Abstract
Boolean Petri nets equipped with \(\textsf {nop}\) allow places and transitions to be independent by being related by \(\textsf {nop}\). We characterize for any fixed \(g\in \mathbb {N}\) the computational complexity of synthesizing \(\textsf {nop}\)-equipped Boolean Petri nets from labeled directed graphs whose states have at most g incoming and at most g outgoing arcs.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Boolean Petri nets are a basic model for the description of distributed and concurrent systems. These nets allow at most one token on each place p in every reachable marking. Therefore, p is considered a Boolean condition that is true if p is marked and false otherwise. A place p and a transition t of a Boolean Petri net N are related by one of the following Boolean interactions: no operation (\(\textsf {nop}\)), input (\(\textsf {inp}\)), output (\(\textsf {out}\)), unconditionally set to true (\(\textsf {set}\)), unconditionally reset to false (\(\textsf {res}\)), inverting (\(\textsf {swap}\)), test if true (\(\textsf {used}\)), and test if false (\(\textsf {free}\)). The relation between p and t determines which conditions p must satisfy to allow t’s firing and which impact has the firing of t on p: The interaction \(\textsf {inp}\) (\(\textsf {out}\)) defines that p must be true (false) first and false (true) after t has fired. If p and t are related by \(\textsf {free}\) (\(\textsf {used}\)) then t’s firing proves that p is false (true). The interaction \(\textsf {nop}\) says that p and t are independent, that is, neither need p to fulfill any condition nor has the firing of t any impact on p. If p and t are related by \(\textsf {res}\) (\(\textsf {set}\)) then p can be both false or true but after t’s firing it is false (true). Also, the interaction \(\textsf {swap}\) does not require that p satisfies any particular condition to enable t. Here, the firing of t inverts p’s Boolean value.
Boolean Petri nets are classified by the interactions of I that they use to relate places and transitions. More exactly, a subset \(\tau \subseteq I\) is called a type of net and a net N is of type \(\tau \) (a \(\tau \)-net) if it applies at most the interactions of \(\tau \). So far, research has explicitly discussed seven Boolean Petri net types: Elementary net systems \(\{\textsf {nop}, \textsf {inp}, \textsf {out}\}\) [9], Contextual nets \(\{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {used}, \textsf {free}\}\) [6], event/condition nets \(\{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {used}\}\) [2], inhibitor nets \(\{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {free}\}\) [8], set nets \(\{\textsf {nop}, \textsf {inp}, \textsf {set}, \textsf {used}\}\) [5], trace nets \(\{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {set}, \textsf {res}, \textsf {used}, \textsf {free}\}\) [3], and flip flop nets \(\{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {swap}\}\) [10]. However, since we have eight interactions to choose from, there are actually a total of 256 different types.
This paper addresses the computational complexity of the \(\tau \)-synthesis problem. It consists in deciding whether a given directed labeled graph A, also called transition system, is isomorphic to the reachability graph of a \(\tau \)-net N and in constructing N if it exists. It has been shown that \(\tau \)-synthesis is NP-complete if \(\tau =\{\textsf {nop},\textsf {inp},\textsf {out}\}\) [1], even if the inputs are strongly restricted [14, 17]. On the contrary, in [10], it has been shown that it becomes polynomial if \(\tau =\{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {swap}\}\). These opposing results motivate the question which interactions of I make the synthesis problem hard and which make it tractable. In our previous work of [13, 15, 16], we answer this question partly and reveal the computational complexity of 120 of the 128 types that allow \(\textsf {nop}\).
In this paper, we investigate for fixed \(g\in \mathbb {N}\) the computational complexity of \(\tau \)-synthesis restricted to g-bounded inputs, that is, every state of A has at most g incoming and at most g outgoing arcs. On the one hand, inputs of practical applications tend to have a low bound g such as benchmarks of digital hardware design [4]. On the other hand, considering restricted inputs hopefully gives us a better understanding of the problem’s hardness. Thus, g-bounded inputs are interesting from both the practical and the theoretical point of view. In this paper, we completely characterize the complexity of \(\tau \)-synthesis restricted to g-bounded inputs for all types that allow places and transitions to be independent, that is, which contain \(\textsf {nop}\). Figure 1 summarizes our findings: For the types of §1 and §2, we showed hardness of synthesis without restriction in [15]. In this paper, we strengthen these results to 2- and 3-bounded inputs, respectively, and show that these bounds are tight. The hardness result of the types of §3 originates from [16]. This paper shows that a bound less than 2 makes synthesis tractable. Hardness for the types of §4 to §8 has been shown for 2-bounded inputs in [16]. In this paper, we strengthen this results to 1-bounded inputs. The hardness part for the types of §9 origin from [13]. In this paper, we argue that the bound 2 is tight. Finally, while the results of §10 are new, the ones of §11 have been found in [15].
For all considered types \(\tau \), the corresponding hardness results are based on a reduction of the so-called cubic monotone one-in-three 3SAT problem [7]. All reductions follow a common approach that represents clauses by directed labeled paths. Thus, this paper also contributes a very general way to prove NP-completeness of synthesis of Boolean types of nets.
2 Preliminaries
Transition Systems. A transition system (TS) \(A=(S,E, \delta )\) is a directed labeled graph with states S, events E and partial transition function \(\delta : S\times E \longrightarrow S\), where \(\delta (s,e)=s'\) is interpreted as  . For
. For  we say s is a source and \(s'\) is a sink of e, respectively. An event e occurs at a state s, denoted by
we say s is a source and \(s'\) is a sink of e, respectively. An event e occurs at a state s, denoted by  , if \(\delta (s,e)\) is defined. An initialized TS \(A=(S,E,\delta , s_0)\) is a TS with a distinct state \(s_0\in S\) where every state \(s\in S\) is reachable from \(s_0\) by a directed labeled path. TSs in this paper are deterministic by design as their state transition behavior is given by a (partial) function. Let \(g\in \mathbb {N}\). An initialized TS A is called g-bounded if for all \(s\in S(A)\) the number of incoming and outgoing arcs at s is restricted by g:
, if \(\delta (s,e)\) is defined. An initialized TS \(A=(S,E,\delta , s_0)\) is a TS with a distinct state \(s_0\in S\) where every state \(s\in S\) is reachable from \(s_0\) by a directed labeled path. TSs in this paper are deterministic by design as their state transition behavior is given by a (partial) function. Let \(g\in \mathbb {N}\). An initialized TS A is called g-bounded if for all \(s\in S(A)\) the number of incoming and outgoing arcs at s is restricted by g:  and
and  .
.
Boolean Types of Nets [2]. The following notion of Boolean types of nets serves as vehicle to capture many Boolean Petri nets in a uniform way. A Boolean type of net \(\tau =(\{0,1\},E_\tau ,\delta _\tau )\) is a TS such that \(E_\tau \) is a subset of the Boolean interactions: \(E_\tau \subseteq I = \{\textsf {nop}, \textsf {inp}, \textsf {out}, \textsf {set}, \textsf {res}, \textsf {swap}, \textsf {used}, \textsf {free}\}\). The interactions \(i \in I\) are binary partial functions \(i: \{0,1\} \rightarrow \{0,1\}\) as defined in Fig. 2. For all \(x\in \{0,1\}\) and all \(i\in E_\tau \) the transition function of \(\tau \) is defined by \(\delta _\tau (x,i)=i(x)\). Notice that I contains all binary partial functions \(\{0,1\} \rightarrow \{0,1\}\) except for the entirely undefined function \(\bot \). Even if a type \(\tau \) includes \(\bot \), this event can never occur, so it would be useless. Thus, I is complete for deterministic Boolean types of nets, and that means there are a total of 256 of them. By definition, a Boolean type \(\tau \) is completely determined by its event set \(E_\tau \). Hence, in the following we identify \(\tau \) with \(E_\tau \), cf. Fig. 3. Moreover, for readability, we group interactions by \(\textsf {enter}= \{\textsf {out},\textsf {set},\textsf {swap}\}\), \(\textsf {exit}= \{\textsf {inp},\textsf {res},\textsf {swap}\}\), \(\textsf {keep}^+= \{\textsf {nop},\textsf {set},\textsf {used}\}\), and \(\textsf {keep}^-= \{\textsf {nop},\textsf {res},\textsf {free}\}\).
Left: \(\tau =\{\textsf {nop}, \textsf {out}, \textsf {res}, \textsf {swap}, \textsf {free}\}\). Right: \(\tilde{\tau }=\{\textsf {nop}, \textsf {inp}, \textsf {set}, \textsf {swap}, \textsf {used}\}\). \(\tau \) and \(\tilde{\tau }\) are isomorphic. The isomorphism \(\phi : \tau \rightarrow \tilde{\tau }\) is given by \(\phi (s)=1-s\) for \(s\in \{0,1\}\), \(\phi (i)=i\) for \(i\in \{\textsf {nop},\textsf {swap}\}\), \(\phi (\textsf {out})=\textsf {inp}\), \(\phi (\textsf {res})=\textsf {set}\) and \(\phi (\textsf {free})=\textsf {used}\).
\(\tau \)-Nets. Let \(\tau \subseteq I\). A Boolean Petri net \(N = (P, T, H_0, f)\) of type \(\tau \), (\(\tau \)-net) is given by finite and disjoint sets P of places and T of transitions, an initial marking \(H_0: P\longrightarrow \{0,1\}\), and a (total) flow function \(f: P \times T \rightarrow \tau \). A \(\tau \)-net realizes a certain behavior by firing sequences of transitions: A transition \(t \in T\) can fire in a marking \(M: P\longrightarrow \{0,1\}\) if \(\delta _\tau (M(p), f(p,t))\) is defined for all \(p\in P\). By firing, t produces the next marking \(M' : P\longrightarrow \{0,1\}\) where \(M'(p)=\delta _\tau (M(p), f(p,t))\) for all \(p\in P\). This is denoted by  . Given a \(\tau \)-net \(N=(P, T, H_0, f)\), its behavior is captured by a transition system \(A_N\), called the reachability graph of N. The state set of \(A_N\) consists of all markings that, starting from initial state \(H_0\), can be reached by firing a sequence of transitions. For every reachable marking M and transition \(t \in T\) with
. Given a \(\tau \)-net \(N=(P, T, H_0, f)\), its behavior is captured by a transition system \(A_N\), called the reachability graph of N. The state set of \(A_N\) consists of all markings that, starting from initial state \(H_0\), can be reached by firing a sequence of transitions. For every reachable marking M and transition \(t \in T\) with  the state transition function \(\delta \) of A is defined as \(\delta (M,t) = M'\).
the state transition function \(\delta \) of A is defined as \(\delta (M,t) = M'\).
\(\tau \)-Regions. Let \(\tau \subseteq I\). If an input A of \(\tau \)-synthesis allows a positive decision then we want to construct a corresponding \(\tau \)-net N purely from A. Since A and \(A_N\) are isomorphic, N’s transitions correspond to A’s events. However, the notion of a place is unknown for TSs. So-called regions mimic places of nets: A \(\tau \)-region of a given \(A=(S, E, \delta , s_0)\) is a pair (sup, sig) of support \(sup: S \rightarrow S_\tau = \{0,1\}\) and signature \(sig: E\rightarrow E_\tau = \tau \) where every transition  of A leads to a transition
of A leads to a transition  of \(\tau \). While a region divides S into the two sets \(sup^{-1}(b) = \{s \in S \mid sup(s) = b\}\) for \(b \in \{0,1\}\), the events are cumulated by \(sig^{-1}(i) = \{e \in E \mid sig(e) = i\}\) for all available interactions \(i \in \tau \). We also use \(sig^{-1}(\tau ') = \{e \in E \mid sig(e) \in \tau '\}\) for \(\tau ' \subseteq \tau \). A region (sup, sig) models a place p and the corresponding part of the flow function f. In particular, sig(e) models f(p, e) and sup(s) models M(p) in the marking \(M\in RS(N)\) corresponding to \(s\in S(A)\). Every set \(\mathcal {R} \) of \(\tau \)-regions of A defines the synthesized \(\tau \)-net \(N^{\mathcal {R}}_A=(\mathcal {R}, E, f, H_0)\) with flow function \(f((sup, sig),e)=sig(e)\) and initial marking \(H_0((sup, sig))=sup(s_{0})\) for all \((sup, sig)\in \mathcal {R}, e\in E\). It is well known that \(A_{N^{\mathcal {R}}_A }\) and A are isomorphic if and only if \(\mathcal {R}\)’s regions solve certain separation atoms [2], to be introduced next. A pair \((s, s')\) of distinct states of A defines a state separation atom (SSP atom). A \(\tau \)-region \(R=(sup, sig)\) solves \((s,s')\) if \(sup(s)\not =sup(s')\). The meaning of R is to ensure that \(N^{\mathcal {R}}_A\) contains at least one place R such that \(M(R)\not =M'(R)\) for the markings M and \(M'\) corresponding to s and \(s'\), respectively. If there is a \(\tau \)-region that solves \((s,s')\) then s and \(s'\) are called \(\tau \)-solvable. If every SSP atom of A is \(\tau \)-solvable then A has the \(\tau \)-state separation property (\(\tau \)-SSP). A pair (e, s) of event \(e\in E \) and state \(s\in S\) where e does not occur at s, that is
of \(\tau \). While a region divides S into the two sets \(sup^{-1}(b) = \{s \in S \mid sup(s) = b\}\) for \(b \in \{0,1\}\), the events are cumulated by \(sig^{-1}(i) = \{e \in E \mid sig(e) = i\}\) for all available interactions \(i \in \tau \). We also use \(sig^{-1}(\tau ') = \{e \in E \mid sig(e) \in \tau '\}\) for \(\tau ' \subseteq \tau \). A region (sup, sig) models a place p and the corresponding part of the flow function f. In particular, sig(e) models f(p, e) and sup(s) models M(p) in the marking \(M\in RS(N)\) corresponding to \(s\in S(A)\). Every set \(\mathcal {R} \) of \(\tau \)-regions of A defines the synthesized \(\tau \)-net \(N^{\mathcal {R}}_A=(\mathcal {R}, E, f, H_0)\) with flow function \(f((sup, sig),e)=sig(e)\) and initial marking \(H_0((sup, sig))=sup(s_{0})\) for all \((sup, sig)\in \mathcal {R}, e\in E\). It is well known that \(A_{N^{\mathcal {R}}_A }\) and A are isomorphic if and only if \(\mathcal {R}\)’s regions solve certain separation atoms [2], to be introduced next. A pair \((s, s')\) of distinct states of A defines a state separation atom (SSP atom). A \(\tau \)-region \(R=(sup, sig)\) solves \((s,s')\) if \(sup(s)\not =sup(s')\). The meaning of R is to ensure that \(N^{\mathcal {R}}_A\) contains at least one place R such that \(M(R)\not =M'(R)\) for the markings M and \(M'\) corresponding to s and \(s'\), respectively. If there is a \(\tau \)-region that solves \((s,s')\) then s and \(s'\) are called \(\tau \)-solvable. If every SSP atom of A is \(\tau \)-solvable then A has the \(\tau \)-state separation property (\(\tau \)-SSP). A pair (e, s) of event \(e\in E \) and state \(s\in S\) where e does not occur at s, that is  , defines an event state separation atom (ESSP atom). A \(\tau \)-region \(R=(sup, sig)\) solves (e, s) if sig(e) is not defined on sup(s) in \(\tau \), that is, \(\lnot \delta _\tau (sup(s), sig(e))\). The meaning of R is to ensure that there is at least one place R in \(N^{\mathcal {R}}_A\) such that
, defines an event state separation atom (ESSP atom). A \(\tau \)-region \(R=(sup, sig)\) solves (e, s) if sig(e) is not defined on sup(s) in \(\tau \), that is, \(\lnot \delta _\tau (sup(s), sig(e))\). The meaning of R is to ensure that there is at least one place R in \(N^{\mathcal {R}}_A\) such that  for the marking M corresponding to s. If there is a \(\tau \)-region that solves (e, s) then e and s are called \(\tau \)-solvable. If every ESSP atom of A is \(\tau \)-solvable then A has the \(\tau \)-event state separation property (\(\tau \)-ESSP). A set \(\mathcal {R}\) of \(\tau \)-regions of A is called \(\tau \)-admissible if for every of A’s (E)SSP atoms there is a \(\tau \)-region R in \(\mathcal {R}\) that solves it. The following lemma, borrowed from [2, p.163], summarizes the already implied connection between the existence of \(\tau \)-admissible sets of A and (the solvability of) \(\tau \)-synthesis:
for the marking M corresponding to s. If there is a \(\tau \)-region that solves (e, s) then e and s are called \(\tau \)-solvable. If every ESSP atom of A is \(\tau \)-solvable then A has the \(\tau \)-event state separation property (\(\tau \)-ESSP). A set \(\mathcal {R}\) of \(\tau \)-regions of A is called \(\tau \)-admissible if for every of A’s (E)SSP atoms there is a \(\tau \)-region R in \(\mathcal {R}\) that solves it. The following lemma, borrowed from [2, p.163], summarizes the already implied connection between the existence of \(\tau \)-admissible sets of A and (the solvability of) \(\tau \)-synthesis:
Lemma 1
([2]). A TS A is isomorphic to the reachability graph of a \(\tau \)-net N if and only if there is a \(\tau \)-admissible set \(\mathcal {R}\) of A such that \(N=N^{\mathcal {R}}_A\).
We say a \(\tau \)-net N \(\tau \)-solves A if \(A_N\) and A are isomorphic. By Lemma 1, deciding if A is \(\tau \)-solvable reduces to deciding whether it has the \(\tau \)-(E)SSP. Moreover, it is easy to see that if \(\tau \) and \(\tilde{\tau }\) are isomorphic then deciding the \(\tau \)-(E)SSP reduces to deciding the \(\tilde{\tau }\)-(E)SSP:
Lemma 2
(Without proof). If \(\tau \) and \(\tilde{\tau }\) are isomorphic types of nets then a TS A has the \(\tau \)-(E)SSP if and only if A has the \(\tilde{\tau }\)-(E)SSP.
In particular, we benefit from the isomorphisms that map \(\textsf {nop}\) to \(\textsf {nop}\), \(\textsf {swap}\) to \(\textsf {swap}\), \(\textsf {inp}\) to \(\textsf {out}\), \(\textsf {set}\) to \(\textsf {res}\), \(\textsf {used}\) to \(\textsf {free}\), and vice versa.
Let \(\tau =\{\textsf {nop},\textsf {set}, \textsf {swap}, \textsf {free}\}\). The TSs \(A_1,\dots , A_4\) give examples for the presence and absence of the \(\tau \)-(E)SSP: TS \(A_1\) has the \(\tau \)-ESSP as a occurs at every state. It has also the \(\tau \)-SSP: The region \(R=(sup, sig)\) where \(sup(s_0)=sup(s_2)=1\), \(sup(s_1)=0\) and \(sig(a)=\textsf {swap}\) separates the pairs \(s_0,s_1\) and \(s_2, s_1\). Moreover, the region \(R'=(sup', sig')\) where \(sup'(s_0)=0\) and \(sup'(s_1)=sup'(s_2)=1\) and \(sig'(a)=\textsf {set}\) separates \(s_0\) and \(s_1\). Notice that R and \(R'\) can be translated into \(\tilde{\tau }\)-regions, where \(\tilde{\tau }=\{\textsf {nop}, \textsf {res}, \textsf {swap}, \textsf {used}\}\), via the isomorphism of Fig. 3. For example, if \(s\in S(A_1)\) and \(e\in E(A_1)\) and \(sup''(s)=\phi (sup(s))\) and \(sig''(e)=\phi (sig(e))\) then the resulting \(\tilde{\tau }\)-region \(R''=(sup'', sig'')\) separates \(s_0, s_1\) and \(s_2,s_1\). Thus, \(A_1\) has also \(\tilde{\tau }\)-(E)SSP. TS \(A_2\) has the \(\tau \)-SSP but not the \(\tau \)-ESSP as event a is not inhibitable at the state \(s_2\). TS \(A_3\) has the \(\tau \)-ESSP (a occurs at every state) but not the \(\tau \)-SSP as \(s_1\) and \(s_2\) are not separable. TS \(A_4\) has neither the \(\tau \)-ESSP nor the \(\tau \)-SSP.
3 Hardness Results
In this section, for several types of nets \(\tau \subseteq I\) and fixed \(g\in \mathbb {N}\), we show that \(\tau \)-synthesis is NP-complete even if the input TS A is g-bounded, cf. Fig. 1. Since \(\tau \)-synthesis is known to be in NP for all \(\tau \subseteq I\) [16], we restrict ourselves to the hardness part. All proofs are based on a reduction of the problem cubic monotone one-in-three 3-SAT which has been shown to be NP-complete in [7]. The input for this problem is a Boolean expression \(\varphi =\{\zeta _0,\dots , \zeta _{m-1}\}\) of m negation-free three-clauses \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) such that every variable \(X\in V(\varphi )=\bigcup _{i=0}^{m-1}\zeta _i\) occurs in exactly three clauses. Notice that the latter implies \(\vert V(\varphi )\vert =m\). Moreover, we assume without loss of generality that if \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) then \(i_0< i_1 < i_2\). The question to answer is whether there is a subset \(M\subseteq V(\varphi )\) with \(\vert M\cap \zeta _i\vert =1\) for all \(i\in \{0,\dots , m-1\}\). For all considered types of nets \(\tau \) and corresponding bounds g, we reduce a given instance \(\varphi \) to a g-bounded TS \(A^\tau _\varphi \) such that the following two conditions are true: Firstly, the TS \(A^\tau _\varphi \) has an ESSP atom \(\alpha \) which is \(\tau \)-solvable if and only if there is a one-in-three model M of \(\varphi \). Secondly, if the ESSP atom \(\alpha \) is \(\tau \)-solvable then all ESSP and SSP atoms of \(A^\tau _\varphi \) are also \(\tau \)-solvable. A reduction that satisfies these conditions proves the NP-hardness of \(\tau \)-synthesis as follows: If \(\varphi \) has a one-three-model then the conditions ensure that the TS \(A^\tau _\varphi \) has the \(\tau \)-(E)SSP and thus is \(\tau \)-solvable. Conversely, if \(A^\tau _\varphi \) is \(\tau \)-solvable then, by definition, it has the \(\tau \)-ESSP. In particular, there is a \(\tau \)-region that solves \(\alpha \) which, by the first condition, implies that \(\varphi \) has a one-in-three model. Consequently, \(A^\tau _\varphi \) is \(\tau \)-solvable if and only if \(\varphi \) has a one-in-three model. Due to space restrictions, we omit for all considered types the proof that \(A^\tau _\varphi \) satisfies the second condition, that is, that the solvability of \(\alpha \) implies the (E)SSP. However, the corresponding proofs can be found in the technical report [11].
A key idea, applied by all reductions in one way or another, is the representation of every clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\), \(i\in \{0,\dots , m-1\}\), by a directed labeled path of \(A^\tau _\varphi \) on which the variables of \(\zeta _i\) occur as events:

The reductions ensure that if a \(\tau \)-region (sup, sig) solves the atom \(\alpha \) then \(sup(s_{i,0})\not =sup(s_{i,n})\). This makes the image of this path under (sup, sig) a directed path from 0 to 1 or from 1 to 0 in \(\tau \). Thus, there has to be an event e on the path that causes the state change from \(sup(s_{i,0})\) to \(sup(s_{i,n})\) by sig(e). We exploit this property and ensure that this state change is unambiguously done by (the signature of) exactly one variable event per clause. As a result, the corresponding variable events define a searched model of \(\varphi \) via their signature. The proof of the following theorem gives a first example of this approach, and Fig. 5 shows a full example reduction.
Theorem 1
For any fixed \(g\ge 2\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau =\{\textsf {nop},\textsf {inp},\textsf {free}\}\), \(\tau =\{\textsf {nop},\textsf {inp},\textsf {used}, \textsf {free}\}\), \(\tau =\{\textsf {nop},\textsf {out},\textsf {used}\}\) and \(\tau =\{\textsf {nop},\textsf {out},\textsf {used}, \textsf {free}\}\).
The TS \(A^\tau _\varphi \) for \(\varphi =\{\zeta _0,\dots , \zeta _{5}\}\) with clauses \(\zeta _0=\{X_0,X_1,X_2\},\ \zeta _1= \{X_0,X_2,X_3\},\ \zeta _2= \{X_0,X_1,X_3\},\ \zeta _3= \{X_2,X_4,X_5\},\ \zeta _4=\{X_1,X_4,X_5\},\ \zeta _5= \{X_3,X_4,X_5\}\) . The red colored area sketc.hes the \(\tau \)-region (sup, sig) that solves \((k_1,h_0)\) and corresponds to the one-in-three model \(M=\{X_0,X_4\}\). (Color figure online)
Proof
We argue for \(\tau \in \{\{\textsf {nop},\textsf {inp},\textsf {free}\}, \{\textsf {nop},\textsf {inp},\textsf {used}, \textsf {free}\} \}\), which by Lemma 2 proves the claim for the other types, too.
Firstly, the TS \(A^\tau _\varphi \) has the following gadget H (left hand side) that provides the events \(k_0, k_1\) and the atom \(\alpha =(k_1, h_0)\). Secondly, it has for every clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) the following gadget \(T_i\) (right hand side) that applies \(k_0\), \(k_1\) and \(\zeta _i's\) variables as events.

Finally, \(A^\tau _\varphi \) uses the states \(\bot _0,\dots , \bot _m\) and events \(\ominus _1,\dots \ominus _m\) and \(\oplus _0,\dots ,\oplus _m\) to join the gadgets \(T_0,\dots , T_{m-1}\) and H by  and
and  , for all \(i\in \{0,\dots , m-1\}\), and
, for all \(i\in \{0,\dots , m-1\}\), and  , cf. Fig. 5.
, cf. Fig. 5.
The gadget H ensures that if (sup, sig) is a region that solves \(\alpha \) then \(sup(h_0)=1\) and \(sig(k_1)=\textsf {free}\) which implies \(sup(h_1)=0\) and \(sig(k_0)=\textsf {inp}\). This is because \(sig(k_1)\in \{\textsf {inp},\textsf {used}\}\) and \(sup(h_0)=0\) implies \(sig(k_0)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), which is impossible. Consequently,  and
and  imply \(sup(s)=1\) and \(sup(s')=0\), respectively. The TS \(A^\tau _\varphi \) uses these properties to ensure via \(T_0,\dots , T_{m-1}\) that the region (sup, sig) implies a one-in-three model of \(\varphi \).
imply \(sup(s)=1\) and \(sup(s')=0\), respectively. The TS \(A^\tau _\varphi \) uses these properties to ensure via \(T_0,\dots , T_{m-1}\) that the region (sup, sig) implies a one-in-three model of \(\varphi \).
More exactly, if \(i\in \{0,\dots , m-1\}\) then for \(T_i\) we have by  and
and  that \(sup(t_{i,0})=1\) and \(sup(t_{i,3})=0\). Thus, there is an event \(X_{i_j}\), where \(j\in \{0,1,2\}\), such that \(sig(X_{i_j})=\textsf {inp}\). Clearly, if \(sig(X_{i_j})=\textsf {inp}\) then \(sig(X_{i_\ell })\not =\textsf {inp}\) for all \(j < \ell \in \{0,1,2\}\) as \(X_{i_\ell }\)’s sources have a 0-support. Consequently, there is exactly one variable event \(X\in \zeta _i\) such that \(sig(X)=\textsf {inp}\). Since i was arbitrary, this is simultaneously true for all clauses \(\zeta _0,\dots , \zeta _{m-1}\). Thus, the set \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {inp}\}\) is a one-in-three model of \(\varphi \).
that \(sup(t_{i,0})=1\) and \(sup(t_{i,3})=0\). Thus, there is an event \(X_{i_j}\), where \(j\in \{0,1,2\}\), such that \(sig(X_{i_j})=\textsf {inp}\). Clearly, if \(sig(X_{i_j})=\textsf {inp}\) then \(sig(X_{i_\ell })\not =\textsf {inp}\) for all \(j < \ell \in \{0,1,2\}\) as \(X_{i_\ell }\)’s sources have a 0-support. Consequently, there is exactly one variable event \(X\in \zeta _i\) such that \(sig(X)=\textsf {inp}\). Since i was arbitrary, this is simultaneously true for all clauses \(\zeta _0,\dots , \zeta _{m-1}\). Thus, the set \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {inp}\}\) is a one-in-three model of \(\varphi \).
Conversely, if \(\varphi \) is one-in-three satisfiable then there is a \(\tau \)-region (sup, sig) of \(A^\tau _\varphi \) that solves \(\alpha \). In particular, if M is a one-in-three model of \(\varphi \) then we first define \(sup(\bot _0)=1\). Secondly, for all \(e\in E(A^\tau _\varphi )\) we define \(sig(e)=\textsf {free}\) if \(e=k_1\), \(sig(e)=\textsf {inp}\) if \(e\in \{k_0\}\cup M\) and else \(sig(e)=\textsf {nop}\). Since \(A^\tau _\varphi \) is reachable, by inductively defining \(sup(s_{i+1})=\delta _\tau (sup(s_i), sig(e_i))\) for all paths  , this defines a fitting region (sup, sig), cf. Fig. 5.
, this defines a fitting region (sup, sig), cf. Fig. 5.
This proves that \(\alpha \) is \(\tau \)-solvable if and only if \(\varphi \) is one-in-three satisfiable.
In the remainder of this section, we present the remaining hardness results in accordance to Fig. 1 and the corresponding reductions that prove them.
Theorem 2
For any fixed \(g\ge 3\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau =\{\textsf {nop},\textsf {set},\textsf {res}\}\cup \omega \) and \(\emptyset \not =\omega \subseteq \{\textsf {used},\textsf {free}\}\).
Proof
The TS \(A^\tau _\varphi \) has the following gadgets \(H_0, H_1\) and \(H_2\) (in this order):

The gadget \(H_0\) provides \(\alpha =(k_0,h_{0,2})\). By symmetry, \(A^\tau _I\) is \(\{\textsf {nop},\textsf {set},\textsf {res},\textsf {used}\}\)-solvable if and only if it is \(\{\textsf {nop},\textsf {set},\textsf {res},\textsf {free}\}\)- or \(\{\textsf {nop},\textsf {set},\textsf {res},\textsf {free}, \textsf {used}\}\)-solvable. Thus, in the following we assume \(\tau =\{\textsf {nop},\textsf {set},\textsf {res},\textsf {used}\}\), \(sig(k_0)=\textsf {used}\) and \(sup(h_{0,2})=0\) if (sup, sig) \(\tau \)-solves \(\alpha \). As a result, by \(sig(k_0)=\textsf {used}\), implying \(sup(h_{0,1})=1\), and \(sup(h_{0,2})=0\) we have \(sig(k_1)=\textsf {res}\). Especially, if  then \(sup(s)=1\) and if
then \(sup(s)=1\) and if  then \(sup(s)=0\). Thus, \(sup(h_{1,0})=sup(h_{2,1})=1\) and \(sup(h_{1,1})=sup(h_{2,0})=0\) which implies \(sig(k_2)=\textsf {res}\) and \(sig(k_3)=\textsf {set}\).
then \(sup(s)=0\). Thus, \(sup(h_{1,0})=sup(h_{2,1})=1\) and \(sup(h_{1,1})=sup(h_{2,0})=0\) which implies \(sig(k_2)=\textsf {res}\) and \(sig(k_3)=\textsf {set}\).
The construction uses \(k_2\) and \(k_3\) to produce some neutral events. More exactly, the TS \(A^\tau _\varphi \) implements for all \(j\in \{0,\dots , 16m-1\}\) the following gadget \(F_{j}\) that uses \(k_2\) and \(k_3\) to ensure that the events \(z_j\) are neutral:

By \(sig(k_2)=\textsf {res}\) and \(sig(k_3)=\textsf {set}\) we have \(sup(f_{j,1})=0\) and \(sup(f_{j,4})=1\). This implies  and
and  and thus \(sig(z_j)=\textsf {nop}\).
and thus \(sig(z_j)=\textsf {nop}\).
Finally, for every \(i\in \{0, \dots , m-1\}\) and clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\), the TS \(A^\tau _\varphi \) has the following four gadgets \(T_{i,0}, T_{i,1}T_{i,2}\) and \(T_{i,3}\) (in this order):




\(T_{i,0},\dots , T_{i,4}\) ensure that there is exactly one \(X\in \zeta _i\) with \(sig(X)=\textsf {res}\): By \(sig(k_0)=\textsf {used}\) and \(sig(k_1)=\textsf {res}\) we get \(sup(t_{i,0,0})=sup(t_{i,1,0})=sup(t_{i,2,0})=sup(t_{i,3,7})=1\) and \(sup(t_{i,0,7})=sup(t_{i,1,7})=sup(t_{i,2,7})=sup(t_{i,3,0})=0\). Since \(z_{16i}, \dots , z_{16i+11}\) are neutral, this implies \(sup(t_{i,0,6})=sup(t_{i,1,6})=sup(t_{i,2,6})=0\) and that there is a variable event with a \(\textsf {res}\)-signature. Moreover, by \(sup(t_{i,3,0})=0\) and \(sup(t_{i,3,7})=1\) and the neutrality of \(z_{16i+12}, \dots , z_{16i+15}\) there is an event of \(y_{3i}, y_{3i+1}, y_{3i+2}\) with a \(\textsf {set}\)-signature. We argue that there is exactly one variable event with a \(\textsf {res}\)-signature: By \(sup(t_{i,0,6})=sup(t_{i,1,6})=sup(t_{i,2,6})=0\), we have \(sig(X)\not \in \{\textsf {set},\textsf {used}\}\) for all \(X\in \{X_{i_0}, X_{i_1}, X_{i_2}\}\). Hence, if \(sig(X_{i_0})=\textsf {res}\) then \(sup(t_{i,0,2})=\dots =sup(t_{i,0,6})=0\) which implies \(sig(y_{3i+1})\not =\textsf {set}\) and \(sig(y_{3i+2})\not =\textsf {set}\) and thus \(sig(y_{3i})=\textsf {set}\). By \(sig(y_{3i})=\textsf {set}\) we have \(sup(t_{i,1,2})=sup(t_{i,1,4})=1\) which implies \(sig(X_{i_1})\not =\textsf {res}\) and \(sig(X_{i_2})\not =\textsf {res}\).
If \(sig(X_{i_1})=\textsf {res}\), then \(sup(t_{i,0,4})=sup(t_{i,1,2})=0\) which implies \(sig(y_{3i})\not =\textsf {set}\) and \(sig(y_{3i+2})\not =\textsf {set}\) and thus \(sig(y_{3i+1})=\textsf {set}\). By \(sig(y_{3i+1})=\textsf {set}\) we have \(sup(t_{i,0,2})=sup(t_{i,2,2})=1\) which implies \(sig(X_{i_0})\not =\textsf {res}\) and \(sig(X_{i_2})\not =\textsf {res}\).
Since \(sig(X_{i_0})=\textsf {res}\) or \(sig(X_{i_1})=\textsf {res}\) implies \(sig(X_{i_2})\not =\textsf {res}\), we conclude that \(sig(X_{i_2})=\textsf {res}\) implies \(sig(X_{i_0})\not =\textsf {res}\) and \(sig(X_{i_1})\not =\textsf {res}\). Thus, there is exactly one variable of the i-th clause with a signature \(\textsf {res}\). Hence, the set \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {res}\}\) is a one-in-three model of \(\varphi \).
To finally build \(A^\tau _\varphi \), we use the states \(\bot =\{\bot _0,\dots , \bot _{20m+2}\}\) and the events \(\oplus =\{\oplus _{0},\dots , \oplus _{20m+2}\}\) and \(\ominus =\{\ominus _{1},\dots , \ominus _{20m+2}\}\). The states of \(\bot \) are connected by  and
and  for \(j\in \{0,\dots , 20m+1\}\). Let \(x=16m+3\) and \(y=19m+3\). For all \(i\in \{0,1,2\}\), for all \(\ell \in \{0,\dots , 16m-1\}\) and for all \(j\in \{0,\dots , m\}\) we add the following edges that connect the gadgets \(H_0,H_1,H_2\) and \(F_0,\dots , F_{16m-1}\) and \(T_{0,0},T_{0,1},T_{0,2},\dots , T_{m-1,0},T_{m-1,1}T_{m-1,2}\) and
for \(j\in \{0,\dots , 20m+1\}\). Let \(x=16m+3\) and \(y=19m+3\). For all \(i\in \{0,1,2\}\), for all \(\ell \in \{0,\dots , 16m-1\}\) and for all \(j\in \{0,\dots , m\}\) we add the following edges that connect the gadgets \(H_0,H_1,H_2\) and \(F_0,\dots , F_{16m-1}\) and \(T_{0,0},T_{0,1},T_{0,2},\dots , T_{m-1,0},T_{m-1,1}T_{m-1,2}\) and

If M is a one-in-three model of \(\varphi \) then \(\alpha \) is \(\tau \)-solvable by a \(\tau \)-region (sup, sig): If \(s\in \{h_{0,0}, h_{1,0}, h_{2,1}\}\) or \(\{f_{j,0} \mid j\in \{0,\dots , 16m-1\}\}\) then \(sup(s)=1\). The support values of the states of \(T_{i,0},\dots , T_{i,3}\), where \(i\in \{0,\dots , m-1\}\), are defined in accordance to which event of \(X_{i_0}, X_{i_1}, X_{i_2}\) belongs to M. The red colored area above sketches \(X_{i_0}\in M\). Moreover, we define \(sup(s)=0\) for all \(s\in \bot \). Let \(e\in E(A^\tau _\varphi )\setminus \oplus \). We define \(sig(e)=\textsf {used}\) if \(e=k_0\) and \(sig(e)=\textsf {res}\) if \(e\in \{k_1\}\cup M\). For all \(i\in \{0,\dots , m-1\}\) and clauses \(\{X_{i_0}, X_{i_1}, X_{i_2}\}\) and all \(j\in \{0,1,2\}\) we set \(sig(e)=\textsf {set}\) if \(e=y_{3i+j}\) and \(X_{i_j}\in M\). Otherwise, we define \(sig(e)=\textsf {nop}\). For all events \(e\in \oplus \) and edges  of A we define \(sig(e)=\textsf {set}\) if \(sup(s')=1\) and, otherwise, \(sig(e)=\textsf {nop}\). The resulting \(\tau \)-region (sup, sig) of \(A^\tau _\varphi \) solves \(\alpha \). \(\square \)
of A we define \(sig(e)=\textsf {set}\) if \(sup(s')=1\) and, otherwise, \(sig(e)=\textsf {nop}\). The resulting \(\tau \)-region (sup, sig) of \(A^\tau _\varphi \) solves \(\alpha \). \(\square \)
Theorem 3
For any fixed \(g\ge 2\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if (1) \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set}\}\) or \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {used}\}\) or \(\tau =\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\cup \omega \) and \(\omega \subseteq \{\textsf {out},\textsf {used},\textsf {free}\}\) or if (2) \(\tau =\{\textsf {nop},\textsf {out},\textsf {res}\}\) or \(\tau =\{\textsf {nop},\textsf {out},\textsf {res},\textsf {free}\}\) or \(\tau =\{\textsf {nop},\textsf {out},\textsf {res},\textsf {set}\}\cup \omega \) and \(\omega \subseteq \{\textsf {inp},\textsf {used},\textsf {free}\}\).
Proof
We present a reduction for the types of (1). By Lemma 2, this proves the claim also for the types of (2). The TS \(A^\tau _\varphi \) has the following gadget H:

The intention of the gadget H is to provide the atom \(\alpha =(k, h_{0,6})\) and the events of \(Z=\{z_0,\dots , z_{3m-1}\}\), \(V=\{v_0,\dots , v_{3m-1}\}\) and \(W=\{w_0,\dots , w_{3m-1}\}\).
Moreover, the TS \(A^\tau _\varphi \) has the following two gadgets \(F_0\) and \(F_1\) and for all \(i\in \{0,\dots , 6m-2\}\) the following gadget \(G_i\) (in this order):

Finally, the TS \(A^\tau _\varphi \) has for every clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\), \(i\in \{0,\dots , m-1\}\), the following gadgets \(T_{i,0}, T_{i,1}\) and \(T_{i,2}\) (in this order):


In the following, we argue that \(H,F_0,F_1\) and \(G_0,\dots , G_{m-2}\) collaborate like this: If (sup, sig) is a \(\tau \)-region solving \(\alpha \) then either \(sig(k)=\textsf {inp}\), \(V\subseteq sig^{-1}(\textsf {enter})\) and \(W\subseteq sig^{-1}(\textsf {keep}^-)\) or \(sig(k)=\textsf {out}\) and \(V\subseteq sig^{-1}(\textsf {exit})\) and \(W\subseteq sig^{-1}(\textsf {keep}^+)\). Moreover, we prove that this implies by the functionality of \(T_{0,0},\dots , T_{m-1,2}\) that \(M=\{X\in V(\varphi ) \mid sig(X)\not =\textsf {nop}\}\) is a one-in-three model of \(\varphi \).
Let (sup, sig) be a \(\tau \)-region that solves \(\alpha \). Since the interactions \(\textsf {res},\textsf {set}\) and \(\textsf {nop}\) are defined on both 0 and 1, this implies \(sig(k)\in \{\textsf {inp},\textsf {out},\textsf {used},\textsf {free}\}\). If \(sig(k)=\textsf {used}\) then \(sup(s)=sup(s')=1\) for every transition  . Hence, we have \(sup(f_{0,3})=sup(f_{1,1})=sup(h_{0,4})=1\). By definition of \(\textsf {inp}, \textsf {res}\) we have that
. Hence, we have \(sup(f_{0,3})=sup(f_{1,1})=sup(h_{0,4})=1\). By definition of \(\textsf {inp}, \textsf {res}\) we have that  and \(sig(e)\in \{\textsf {inp},\textsf {res}\}\) implies \(sup(s)=0\). Consequently, by
and \(sig(e)\in \{\textsf {inp},\textsf {res}\}\) implies \(sup(s)=0\). Consequently, by  and
and  we get \(sig(z_0), sig(q_0)\in \textsf {keep}^+\) and thus \(sup(h_{0,4})=sup(h_{0,5})=sup(h_{0,6})=1\) which contradicts
we get \(sig(z_0), sig(q_0)\in \textsf {keep}^+\) and thus \(sup(h_{0,4})=sup(h_{0,5})=sup(h_{0,6})=1\) which contradicts  . Hence, \(sig(k)\not =\textsf {used}\). Similarly, \(sig(k) =\textsf {free}\) implies \(sup(h_{0,6})=0\), which is a contradiction. Thus, we have that \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\) or \(sig(k)=\textsf {out}\) and \(sup(h_{0,6})=1\).
. Hence, \(sig(k)\not =\textsf {used}\). Similarly, \(sig(k) =\textsf {free}\) implies \(sup(h_{0,6})=0\), which is a contradiction. Thus, we have that \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\) or \(sig(k)=\textsf {out}\) and \(sup(h_{0,6})=1\).
As a next step, we show that \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\) together imply \(sig(v_0)\in \textsf {enter}\) and \(sig(z_0)\in \textsf {keep}^-\). By \(sig(k)=\textsf {inp}\) and  and
and  we get \(sup(h_{0,1})=0\) and \(sup(h_{0,3})=1\). Moreover, by
we get \(sup(h_{0,1})=0\) and \(sup(h_{0,3})=1\). Moreover, by  and \(sup(h_{0,6})=0\) we obtain \(sig(z_0)\in \textsf {keep}^-\), which by \(sup(h_{0,1})=0\) implies \(sup(h_{0,2})=0\). Finally, \(sup(h_{0,2})=0\) and \(sup(h_{0,3})=1\) imply \(sig(v_0)\in \textsf {enter}\). Notice that this reasoning purely bases on \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\). Moreover, \(A^\tau _\varphi \) uses for every \(j\in \{0,\dots , 6m-2\}\) the TS \(G_j\) to ensure \(sup(h_{0,6})=sup(h_{1,6})=\dots =sup(h_{6m-1,6})\). This transfers \(z_0\in \textsf {keep}^-\) and \(v_0\in \textsf {enter}\) to \(V\subseteq \textsf {enter}\) and \(W\subseteq \textsf {keep}^-\). In particular, by \(sig(k)=\textsf {inp}\) we have \(sup(g_{i,0})=sup(g_{i,1})=1\) and \(sup(g_{i,2})=sup(g_{i,3})=0\), that is, \(sig(c_i)=\textsf {nop}\). Hence, if \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\) then \(sup(h_{i,6})=0\) for all \(i\in \{0,\dots , 6m-1\}\). Perfectly similar to the discussion for \(z_0\) and \(v_0\) we obtain that \(V\subseteq sig^{-1}(\textsf {enter})\) and \(W\subseteq sig^{-1}(\textsf {keep}^-)\), respectively. Similarly, \(sig(k)=\textsf {out}\) and \(sup(h_{0,6})=1\) imply \(V\subseteq sig^{-1}(\textsf {exit})\) and \(W\subseteq sig^{-1}(\textsf {keep}^+)\).
and \(sup(h_{0,6})=0\) we obtain \(sig(z_0)\in \textsf {keep}^-\), which by \(sup(h_{0,1})=0\) implies \(sup(h_{0,2})=0\). Finally, \(sup(h_{0,2})=0\) and \(sup(h_{0,3})=1\) imply \(sig(v_0)\in \textsf {enter}\). Notice that this reasoning purely bases on \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\). Moreover, \(A^\tau _\varphi \) uses for every \(j\in \{0,\dots , 6m-2\}\) the TS \(G_j\) to ensure \(sup(h_{0,6})=sup(h_{1,6})=\dots =sup(h_{6m-1,6})\). This transfers \(z_0\in \textsf {keep}^-\) and \(v_0\in \textsf {enter}\) to \(V\subseteq \textsf {enter}\) and \(W\subseteq \textsf {keep}^-\). In particular, by \(sig(k)=\textsf {inp}\) we have \(sup(g_{i,0})=sup(g_{i,1})=1\) and \(sup(g_{i,2})=sup(g_{i,3})=0\), that is, \(sig(c_i)=\textsf {nop}\). Hence, if \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\) then \(sup(h_{i,6})=0\) for all \(i\in \{0,\dots , 6m-1\}\). Perfectly similar to the discussion for \(z_0\) and \(v_0\) we obtain that \(V\subseteq sig^{-1}(\textsf {enter})\) and \(W\subseteq sig^{-1}(\textsf {keep}^-)\), respectively. Similarly, \(sig(k)=\textsf {out}\) and \(sup(h_{0,6})=1\) imply \(V\subseteq sig^{-1}(\textsf {exit})\) and \(W\subseteq sig^{-1}(\textsf {keep}^+)\).
We now argue that \(T_{i,0},\dots , T_{m-1,2}\) ensure that \(M=\{X\in V(\varphi )\mid sig(X)\not =\textsf {nop}\}\) is a one-in-three model of \(\varphi \). Let \(i\in \{0,\dots , m-1\}\) and \(sig(k)=\textsf {inp}\) and \(sup(h_{0,6})=0\) implying \(V\subseteq sig^{-1}(\textsf {enter})\) and \(W\subseteq sig^{-1}(\textsf {keep}^-)\). By \(sig(k)=\textsf {inp}\) and \(V\subseteq sig^{-1}(\textsf {enter})\) and \(W\subseteq sig^{-1}(\textsf {keep}^-)\) we have that \(sup(t_{i,0,2})=sup(t_{i,1,2})=sup(t_{i,2,2})=1\) and \(sup(t_{i,0,5})=sup(t_{i,1,5})=sup(t_{i,2,5})=0\). As a result, every event \(e\in \{X_{i_0}, X_{i_1}, X_{i_2}\}\) has a 0-sink, which implies \(sig(e)\in \{\textsf {nop},\textsf {inp},\textsf {res}\}\), and every event \(e\in \{x_{i_0}, x_{i_1}, x_{i_2}\}\) has a 1-sink, which implies \(sig(e)\in \{\textsf {nop},\textsf {out},\textsf {set}\}\). By \(sup(t_{i,0,2})=1\) and \(sup(t_{i,0,5})=0\) there is a \(X\in \{X_{i_0}, X_{i_1}, X_{i_2}\}\) such that \(sig(X)\in \{\textsf {inp},\textsf {res}\}\). We argue that \(sig(Y)=\textsf {nop}\) for \(Y\in \{X_{i_0}, X_{i_1}, X_{i_2}\}\setminus \{X\}\). If \(sig(X_{i_0})\in \{\textsf {inp},\textsf {res}\}\) then \(sup(t_{i,0,3})=0\) which implies \(sig(x_{i_0})\in \{\textsf {out},\textsf {set}\}\) and, therefore, \(sup(t_{i,1,4})=1\). Since \(sig(X_{i_1}), sig(X_{i_2})\not \in \{\textsf {out}, \textsf {set}\}\) and \(sig(x_{i_1}), sig(x_{i_2})\not \in \{\textsf {inp}, \textsf {res}\}\), it holds \(sup(t_{i,0,3})=sup(t_{i,0,4})=0\) and \(sup(t_{i,1,3})=sup(t_{i,1,4})=1\), respectively. Thus, for all \(e\in \{X_{i_1}, X_{i_2}\}\), there are edges  and
and  such that \(sup(s)=0\) and \(sup(s')=1\). This implies \(sig(e)=\textsf {nop}\). Similarly, if \(sig(X_{i_1})\in \{\textsf {inp},\textsf {res}\}\), then \(sig(X_{i_0})=sig(X_{i_2})=\textsf {nop}\), and if \(sig(X_{i_2})\in \{\textsf {inp},\textsf {res}\}\), then \(sig(X_{i_0})=sig(X_{i_1})=\textsf {nop}\). Hence, every clause \(\zeta _i\) has exactly one variable event with a signature different from \(\textsf {nop}\). This makes \(M=\{X\in V(\varphi )\mid sig(X)\not =\textsf {nop}\}\) a one-in-three model of \(\varphi \). Similarly, if \(sig(k)=\textsf {out}\) and \(sup(h_{0,6})=1\), then M is also a one-in-three model of \(\varphi \).
such that \(sup(s)=0\) and \(sup(s')=1\). This implies \(sig(e)=\textsf {nop}\). Similarly, if \(sig(X_{i_1})\in \{\textsf {inp},\textsf {res}\}\), then \(sig(X_{i_0})=sig(X_{i_2})=\textsf {nop}\), and if \(sig(X_{i_2})\in \{\textsf {inp},\textsf {res}\}\), then \(sig(X_{i_0})=sig(X_{i_1})=\textsf {nop}\). Hence, every clause \(\zeta _i\) has exactly one variable event with a signature different from \(\textsf {nop}\). This makes \(M=\{X\in V(\varphi )\mid sig(X)\not =\textsf {nop}\}\) a one-in-three model of \(\varphi \). Similarly, if \(sig(k)=\textsf {out}\) and \(sup(h_{0,6})=1\), then M is also a one-in-three model of \(\varphi \).
To join the gadgets and finally build \(A^\tau _\varphi \), we use the states \(\bot =\{\bot _0,\dots , \bot _{9m+1}\}\) and the events \(\oplus =\{\oplus _{0},\dots , \oplus _{9m+1}\}\) and \(\ominus =\{\ominus _{1},\dots , \ominus _{9m+1}\}\). The states of \(\bot \) are connected by  for \(j\in \{0,\dots , 9m+1\}\). Let \(x=6m+2\). For all \(i\in \{0,\dots , 6m-2\}\), for all \(j\in \{0,\dots , m-1\}\) and for all \(\ell \in \{0,1,2\}\) we add the following edges that connect the gadgets \(H_0, F_0,F_1, G_0,\dots , G_{6m-2}\) and \(T_{0,0},T_{0,1},T_{0,2}\) up to \(T_{m-1,0},T_{m-1,1},T_{m-1,2}\) to \(A^\tau _\varphi \):
for \(j\in \{0,\dots , 9m+1\}\). Let \(x=6m+2\). For all \(i\in \{0,\dots , 6m-2\}\), for all \(j\in \{0,\dots , m-1\}\) and for all \(\ell \in \{0,1,2\}\) we add the following edges that connect the gadgets \(H_0, F_0,F_1, G_0,\dots , G_{6m-2}\) and \(T_{0,0},T_{0,1},T_{0,2}\) up to \(T_{m-1,0},T_{m-1,1},T_{m-1,2}\) to \(A^\tau _\varphi \):

If M is a one-in-three model of \(\varphi \) then there is a \(\tau \)-region (sup, sig) of \(A^\tau _\varphi \) that solves \(\alpha \). The red colored area of the figures introducing the gadgets indicates already a positive support of some states. In particular, if \(s\in \{h_{j,0}, h_{j,3} \mid j\in \{0,\dots , 6m-1\}\}\) or \(s\in \{f_{0,0}, f_{0,2}, f_{0,3}, f_{1,0},f_{1,1} \}\) \(s\in \{g_{j,0}, g_{j,1} \mid j\in \{0,\dots , 6m-2\}\}\) then \(sup(s)=1\). The support values of the states of \(T_{i,0},\dots , T_{i,2}\), where \(i\in \{0,\dots , m-1\}\), are defined in accordance to which of the events \(X_{i_0}, X_{i_1}, X_{i_2}\) belongs to M. The red colored area above sketches the situation where \(X_{i_0}\in M\). Moreover, for all \(s\in \bot \), we define \(sup(s)=0\). Let \(e\in E(A^\tau _\varphi )\setminus \oplus \). We define \(sig(e)=\textsf {inp}\) if \(e\in \{k\}\cup M\). For all \(i\in \{0,\dots , m-1\}\) and clauses \(\{X_{i_0}, X_{i_1}, X_{i_2}\}\) and all \(j\in \{0,1,2\}\) we set \(sig(e)=\textsf {set}\) if \(e=n\) or \(e\in \{v_j,p_j\mid j\in \{0,\dots , 3m-1\}\}\) or \(e=x_{i_j}\) and \(X_{i_j}\in M\). Otherwise, we define \(sig(e)=\textsf {nop}\). Finally, for all events \(e\in \oplus \) and edges  of A we define \(sig(e)=\textsf {set}\) if \(sup(s')=1\) and, otherwise, \(sig(e)=\textsf {nop}\).
of A we define \(sig(e)=\textsf {set}\) if \(sup(s')=1\) and, otherwise, \(sig(e)=\textsf {nop}\).
Joining of 1-Bounded Gadgets. In the following, we consider types \(\tau \) where \(\tau \)-synthesis from 1-bounded inputs is NP-complete. All gadgets \(A_0,\dots , A_n\) of the reductions are directed paths  on pairwise distinct states \(s^i_0,\dots , s^i_n\). For all types, the joining is the concatenation
on pairwise distinct states \(s^i_0,\dots , s^i_n\). For all types, the joining is the concatenation

with fresh states \(\bot _1,\dots ,\bot _n\) and events \(\ominus _1,\dots \ominus _n,\oplus _1,\dots \oplus _n\).
Theorem 4
For any fixed \(g\ge 1\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau =\{\textsf {nop}, \textsf {inp},\textsf {out},\textsf {set}\}\cup \omega \) or \(\tau =\{\textsf {nop}, \textsf {inp},\textsf {out},\textsf {res}\} \cup \omega \) and \(\omega \subseteq \{\textsf {used}, \textsf {free}\}\).
Proof
Our construction proves the claim for \(\tau =\{\textsf {nop}, \textsf {inp},\textsf {set},\textsf {out}\}\cup \omega \) with \(\omega \subseteq \{\textsf {used}, \textsf {free}\}\). By Lemma 2, this proves the claim also for the other types.
The TS \(A^\tau _\varphi \) has the following gadgets \(H_0, H_1,H_2\) and \(H_3\) (in this order):

If \(\textsf {used}\in \tau \) then \(A^\tau _\varphi \) has the following gadget \(H_4\):

For all \(i\in \{0,\dots , m-1\}\), the TS \(A^\tau _\varphi \) has for the clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) and the variable \(X_i\in V(\varphi )\) the following gadgets \(T_i\) and \(B_i\), respectively:

The gadget \(H_0\) provides the atom \(\alpha =(k_0,h_{0,6})\). Moreover, the gadgets \(H_0,\dots , H_4\) ensure that if (sup, sig) is a \(\tau \)-region solving \(\alpha \) then \(sig(k_0)=\textsf {out}\) and \(sig(k_1)\in \{\textsf {out}, \textsf {set}\}\). In particular, \(H_4\) prevents the solvability of \(\alpha \) by \(\textsf {used}\). As a result, such a region implies \(sup(t_{i,1})=1\), \(sup(t_{i,4})=0\) and \(sup(b_{i,1})=0\) for all \(i\in \{0,\dots , m-1\}\). On the one hand, by \(sup(b_{i,1})=0\) for all \(i\in \{0,\dots , m-1\}\) we have \(sig(X)\not \in \{\textsf {out}, \textsf {set}\}\) for all \(X\in V(\varphi )\). On the other hand, by \(sup(t_{i,1})=1\) and \(sup(t_{i,4})=0\) there is an event \(X\in \{X_{i_0}, X_{i_1},X_{i_2}\}\) such that \(sig(X)=\textsf {inp}\). Since no variable event has an incoming signature we obtain immediately \(sig(Y)\not =\textsf {inp}\) for \(Y\in \{X_{i_0}, X_{i_1},X_{i_2}\}\setminus \{X\}\). Thus, \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {inp}\}\) is a one-in-three model of \(\varphi \).
We argue that \(H_0,\dots , H_4\) behave as announced. Let (sup, sig) be a region that solves \((k_0,h_{0,6})\). If \(sig(k_0)=\textsf {inp}\) then \(sup(h_{0,6})=0\) and \(sig(h_{0,7})=1\), implying \(sig(o)\in \{\textsf {out},\textsf {set}\}\) and \(sup(h_{0,3})=1\). Thus, there is an event \(e\in \{k_1, z_0,z_1\}\) with \(sig(e)=\textsf {inp}\). By \(sig(k_0)=\textsf {inp}\) we have \(sup(h_{1,1})=sup(h_{2,1})=1\) and \(sup(h_{3,1})=0\) implying \(sig(e)\not =\textsf {inp}\) for all \(e\in \{k_1, z_0,z_1\}\), a contradiction.
If \(sig(k_0)=\textsf {free}\) then \(sup(h_{0,6})=1\) and \(sup(h_{0,1})=sup(h_{0,7})=sup(h_{1,1})=0\) which implies \(sig(o)=\textsf {inp}\) and \(sup(h_{0,2})=1\). By \(sup(h_{0,1})=0\) and \(sup(h_{0,2})=1\) we have \(sig(z_0)\in \{\textsf {out}, \textsf {set}\}\) which by \(sup(h_{1,1})=0\) is a contradiction.
If \(sig(k_0)=\textsf {used}\) then \(sup(h_{0,6})=0\) and \(sup(h_{0,1})=sup(h_{0,7})=sup(h_{1,1})=sup(h_{2,1})=1\). This implies \(sig(o)\in \{\textsf {out},\textsf {set}\}\) and \(sup(h_{0,3})=1\). Thus, by \(sup(h_{0,6})=0\) there is an event \(e\in \{k_1,z_0,z_1\}\) with \(sig(e)=\textsf {inp}\). By \(sup(h_{1,1})=sup(h_{2,1})=1\), we have \(e\not \in \{z_0,z_1\}\). If \(sig(k_1)=\textsf {inp}\) then \(sup(h_{4,1})=0\) and \(sup(h_{4,2})=1\), implying \(sig(z_0)\in \{\textsf {out},\textsf {set}\}\) and \(sup(h_{0,6})=1\). This is a contradiction. Altogether, this proves \(sig(k_0)\not \in \{\textsf {inp},\textsf {used},\textsf {free}\}\).
Consequently, we obtain \(sig(k_0)=\textsf {out}\) and \(sup(h_{0,6})=1\) which implies \(sig(o)=\textsf {inp}\) and \(sup(h_{0,3})=0\). By \(sup(h_{0,6})=1\), this implies that there is an event \(e\in \{k_1,z_0,z_1\}\) with \(sig(e)\in \{\textsf {out}, \textsf {set}\}\). Again by \(sig(k_0)=\textsf {out}\), we have \(sup(h_{1,1})=sup(h_{2,1})=0\), which implies \(e=k_1\). The signatures \(sig(k_0)=\textsf {out}\) and \(sig(k_1)\in \{\textsf {out},\textsf {set}\}\) and the construction of \(T_0,\dots , T_{m-1}\) and \(B_0,\dots , B_{m-1}\) ensure that \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {inp}\}\) is a one-in-three model of \(\varphi \): By \(sig(k_0)=\textsf {out}\) and \(sig(k_1)\in \{\textsf {out},\textsf {set}\}\) we have \(sup(t_{i,1})=1\) and \(sup(t_{i,4})=sup(b_{i,1})=0\) for all \(i\in \{0,\dots , m-1\}\). By \(sup(t_{i,1})=1\) and \(sup(t_{i,4})=0\), there is an event \(X\in \zeta _i\) such that \(sig(X)=\textsf {inp}\). Moreover, by \(sup(b_{i,1})=0\), we get \(sig(X_i)\not \in \textsf {enter}\) for all \(i\in \{0,\dots , m-1\}\). Thus, X is unambiguous and thus M is a searched model.
Conversely, if M is a one-in-three model of \(\varphi \) then there is a \(\tau \)-region (sup, sig) that solves \(\alpha \). The red colored area above sketches states with a positive support. Which states of \(T_{i}\), besides of \(t_{i,0}, t_{i,1}\) and \(t_{i,5}\), get a positive support depends for all \(i\in \{0,\dots , m-1\}\) on which of \(X_{i_0}, X_{i_1},X_{i_2}\) belongs to M. The red colored area above sketches the case \(X_{i_0}\in M\). Moreover, we define \(sup(s)=1\) if \(s=b_{i,0}\) and \(X_i\in M\) or if \(s\in \bot \). The signature is defined as follows: \(sig(k_1)=\textsf {set}\); for all \(e\in E(A^\tau _\varphi )\setminus \{k_1\}\) and all  , if \(sup(s')>sup(s)\), then \(sig(e)=\textsf {out}\); if \(sup(s)>sup(s')\), then \(sig(e)=\textsf {inp}\); else \(sig(e)=\textsf {nop}\). \(\square \)
, if \(sup(s')>sup(s)\), then \(sig(e)=\textsf {out}\); if \(sup(s)>sup(s')\), then \(sig(e)=\textsf {inp}\); else \(sig(e)=\textsf {nop}\). \(\square \)
Theorem 5
For any \(g\ge 1\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau =\{\textsf {nop}, \textsf {inp}, \textsf {set}, \textsf {free}\}\) or \(\tau =\{\textsf {nop}, \textsf {inp}, \textsf {set}, \textsf {used}, \textsf {free}\}\) or \(\tau =\{\textsf {nop}, \textsf {out}, \textsf {res}, \textsf {used}\}\) or \(\tau =\{\textsf {nop}, \textsf {out}, \textsf {res}, \textsf {used}, \textsf {free}\}\).
Proof
Our reduction proves the claim for \(\tau =\{\textsf {nop}, \textsf {inp}, \textsf {set}, \textsf {free}\}\) and \(\tau =\{\textsf {nop}, \textsf {inp}, \textsf {set}, \textsf {used}, \textsf {free}\}\) and thus by Lemma 2, for the other types, too.
The TS \(A^\tau _\varphi \) has the following gadgets \(H_0\) and \(H_1\) providing the atom \((k_0,h_{0,3})\):

For all \(i\in \{0,\dots , m-1\}\), the \(A^\tau _\varphi \) for the clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) and the variable \(X_i\in V(\varphi )\) the gadgets \(T_i\) and \(B_i\) as previously defined for Theorem 4. The gadgets \(H_0\) and \(H_1\) ensure that a \(\tau \)-region (sup, sig) solving \((k_0,h_{0,3})\) satisfies \(sig(k_0)=\textsf {free}\) and \(sig(k_1)=\textsf {set}\). This implies \(sup(t_{i,1})=1\) and \(sup(t_{i,4})=sup(b_{i,2})=0\) for all \(i\in \{0,\dots , m-1\}\). By \(sup(t_{i,1})=1\) and \(sup(t_{i,4})=0\), there is an event \(X\in \zeta _i\) such that \(sig(X)=\textsf {inp}\) and, by \(sup(b_{i,2})=0\) for all \(i\in \{0,\dots , m-1\}\), we have \(sig(X)\not =\textsf {set}\) for all \(X\in V(\varphi )\). Thus, the event \(X\in \zeta _i\) is unique and \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {inp}\}\) is a one-in-three model.
We briefly argue that \(H_0\) and \(H_1\) perform as announced: Let (sup, sig) be a \(\tau \)-region that solves \(\alpha \). If \(sig(k_0)=\textsf {inp}\) then \(sup(h_{1,1})=0\) and \(sup(h_{1,2})=1\) which implies \(sig(z_0)=\textsf {set}\) and thus \(sup(h_{0,3})=1\), a contradiction. Hence, \(sig(k_{0})\not =\textsf {inp}\). If \(sig(k_0)=\textsf {used}\) then \(sup(h_{0,1})=sup(h_{1,2})=1\) and \(sup(h_{0,3})=0\). Consequently, \(sig(z_0)=\textsf {inp}\) or \(sig(k_1)=\textsf {inp}\) but this contradicts \(sup(h_{1,2})=1\) and \(sup(h_{0,3})=0\). Thus, \(sig(k_0)\not =\textsf {used}\). Thus, we have \(sig(k_0)=\textsf {free}\) and \(sup(h_{0,3})=1\), which implies that one of \(k_1,z_0\) has a \(\textsf {set}\)-signature. By \(sig(k_0)=\textsf {free}\), we get \(sup(h_{1,3})=0\) and thus \(sig(k_1)=\textsf {set}\).
If M is a one-in-three model of \(\varphi \) then we can define an \(\alpha \) solving region similar to the one of Theorem 4, where we replace \(sig(k_0)=\textsf {inp}\) by \(sig(k_0)=\textsf {free}\).
Theorem 6
For any fixed \(g\ge 1\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau =\{\textsf {nop}, \textsf {inp},\textsf {res},\textsf {swap}\}\cup \omega \) or \(\tau =\{\textsf {nop}, \textsf {out},\textsf {set},\textsf {swap}\}\cup \omega \) and \(\omega \subseteq \{\textsf {used},\textsf {free}\}\).
Proof
The TS \(A^\tau _\varphi \) has the following gadgets \(H_0, H_1, H_2\) and \(H_3\):

The gadgets \(H_0,\dots , H_3\) provide the atom \(\alpha =(k,h_{0,2})\) and ensure that a \(\tau \)-region (sup, sig) solving \(\alpha \) satisfies \(sig(k)=\textsf {inp}\) and \(sup(h_{0,2})=0\). The TS \(A^\tau _\varphi \) has the following gadgets \(F_0, F_1\) and for all \(j\in \{0,\dots , 10\}\) the gadget \(G_j\):

For all \(j\in \{0,\dots , 10\}\), the gadgets \(F_0,F_1, G_j\) ensure \(sig(u_j)=\textsf {swap}\) for any \(\tau \)-region (sup, sig) solving \(\alpha \).
For all \(i\in \{0,\dots , m-1\}\), the TS \(A^\tau _\varphi \) has for the clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) some gadgets \(T_{i,0},\dots , T_{i,6}\) and \(B_i\). The purpose of these gadgets is to make the one-and-three satisfiability of \(\varphi \) and the solvability of \(\alpha \) the same. In particular, the TS \(T_{i,0}\) is defined by:

The gadgets \(T_{i,1}, T_{i,2}\) and \(T_{i,3}\) are defined (in this order) as follows:

Moreover, the gadgets \(T_{i,4}, T_{i,5}\) and \(T_{i,6}\) are defined like this:

Finally, the gadget \(B_i\) is defined as follows:

Let (sup, sig) be a \(\tau \)-region solving \(\alpha \). We first argue that the gadgets \(H_0,\dots ,H_3\) and \(F_0,F_1\) and \(G_0,\dots , G_{10}\) ensure that a \(\tau \)-region (sup, sig) solving \(\alpha \) satisfies \(sig(k)=\textsf {inp}\), \(sup(h_{0,2})=0\) and \(sig(u_0)=\dots =sig(u_{10})=\textsf {swap}\).
If \(sig(k)=\textsf {free}\) and \(sup(h_{0,2})=1\) then  implies \(sup(s)=sup(s')=0\). Especially, by \(sup(h_{0,1})=0\) and \(sup(h_{0,2})=1\) we have \(sig(y_0)=\textsf {swap}\). Moreover, by \(sup(h_{2,1})=sup(h_{2,4})=0\) and \(sig(y_0)=\textsf {swap}\) we have that \(sup(h_{2,2})=sup(h_{2,3})=1\). This implies \(sig(y_1)\in \{\textsf {nop},\textsf {used}\}\). By \(sup(h_{1,1})=0\) and
implies \(sup(s)=sup(s')=0\). Especially, by \(sup(h_{0,1})=0\) and \(sup(h_{0,2})=1\) we have \(sig(y_0)=\textsf {swap}\). Moreover, by \(sup(h_{2,1})=sup(h_{2,4})=0\) and \(sig(y_0)=\textsf {swap}\) we have that \(sup(h_{2,2})=sup(h_{2,3})=1\). This implies \(sig(y_1)\in \{\textsf {nop},\textsf {used}\}\). By \(sup(h_{1,1})=0\) and  this implies \(sig(y_1)=\textsf {nop}\) and thus \(sup(h_{1,2})=0\). Furthermore, by \(sup(h_{1,2})=sup(h_{1,3})=0\) and
this implies \(sig(y_1)=\textsf {nop}\) and thus \(sup(h_{1,2})=0\). Furthermore, by \(sup(h_{1,2})=sup(h_{1,3})=0\) and  this implies \(sig(y_0)\not =\textsf {swap}\), a contradiction. Thus, we have \(sig(k)\not =\textsf {free}\).
this implies \(sig(y_0)\not =\textsf {swap}\), a contradiction. Thus, we have \(sig(k)\not =\textsf {free}\).
If \(sig(k)=\textsf {used}\) and \(sup(h_{0,2})=0\) then  implies \(sup(s)=sup(s')=1\). Thus, we get \(sup(h_{0,1})=sup(h_{0,3})=sup(h_{1,3})=1\) which with \(sup(h_{0,2})=0\) implies \(sig(y_0)=sig(v)=\textsf {swap}\). Moreover, \(sup(h_{1,3})=1\) and \(sig(y_0)=\textsf {swap}\) imply \(sup(h_{1,2})=0\). By \(sup(h_{1,1})=1\), this implies \(sig(y_1)\in \{\textsf {inp},\textsf {res}\}\). Finally, \(sup(h_{3,3})=1\) and \(sig(v)=sig(y_0)=\textsf {swap}\) imply \(sup(h_{3,1})=1\). This contradicts \(sig(y_1)\in \{\textsf {inp},\textsf {res}\}\). Thus, \(sig(k)\not =\textsf {used}\). Altogether, this shows that \(sig(k)=\textsf {inp}\) and \(sup(h_{0,2})=0\), which implies \(sig(v)=\textsf {swap}\).
implies \(sup(s)=sup(s')=1\). Thus, we get \(sup(h_{0,1})=sup(h_{0,3})=sup(h_{1,3})=1\) which with \(sup(h_{0,2})=0\) implies \(sig(y_0)=sig(v)=\textsf {swap}\). Moreover, \(sup(h_{1,3})=1\) and \(sig(y_0)=\textsf {swap}\) imply \(sup(h_{1,2})=0\). By \(sup(h_{1,1})=1\), this implies \(sig(y_1)\in \{\textsf {inp},\textsf {res}\}\). Finally, \(sup(h_{3,3})=1\) and \(sig(v)=sig(y_0)=\textsf {swap}\) imply \(sup(h_{3,1})=1\). This contradicts \(sig(y_1)\in \{\textsf {inp},\textsf {res}\}\). Thus, \(sig(k)\not =\textsf {used}\). Altogether, this shows that \(sig(k)=\textsf {inp}\) and \(sup(h_{0,2})=0\), which implies \(sig(v)=\textsf {swap}\).
By \(sig(k)=\textsf {inp}\) we have \(sup(f_{0,1})=sup(f_{1,1})=sup(g_{j,1})=0\) and \(sup(f_{0,3})=sup(f_{1,3})=sup(g_{j,4})=1\). By \(sig(v)=\textsf {swap}\), this implies \(sup(f_{0,2})=sup(f_{1,2})=0\) and thus \(sig(z_0), sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\). Moreover, \(sup(g_{j,1})=0\), \(sup(g_{j,4})=1\) and \(sig(z_0), sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) imply \(sup(g_{j,2})=0\) and \(sup(g_{j,3})=1\) and thus \(sig(u_j)=\textsf {swap}\).
Let \(i\in \{0,\dots ,m-1\}\). We now show that \(T_{i,0},\dots , T_{i,6}\) and \(B_i\) collaborate as announced. By \(sig(k)=\textsf {inp}\) and \(sig(u_{9})=sig(u_{10})=\textsf {swap}\), we have \(sup(b_{i,1})=1\) for all \(i\in \{0,\dots , m-1\}\). Since  for all \(i\in \{0,\dots , m-1\}\), the gadget \(B_i\) ensures for all \(X\in V(\varphi )\) that
for all \(i\in \{0,\dots , m-1\}\), the gadget \(B_i\) ensures for all \(X\in V(\varphi )\) that  and \(sup(s)\not =sup(s')\) imply \(sig(X)=\textsf {swap}\).
and \(sup(s)\not =sup(s')\) imply \(sig(X)=\textsf {swap}\).
The gadget \(T_{i,0}\) works like this: By \(sig(k)=\textsf {inp}\) we get that \(sup(t_{i,0,1})=0\) and \(sup(t_{i,0,8})=1\). Consequently, the image  of the path
of the path  performs an odd number of state changes between 0 to 1 in \(\tau \). Since \(sig(u_0)=\dots =sig(u_3)=\textsf {swap}\), the events \(u_0,\dots , u_3\) perform an even number of state changes. Thus, either all of \(X_{i_0}, X_{i_1}, X_{i_2}\) are mapped to \(\textsf {swap}\) or exactly one of them. The construction of \(T_{i,1},\dots , T_{i,6}\) guarantees that there is exactly one variable event mapped to \(\textsf {swap}\).
performs an odd number of state changes between 0 to 1 in \(\tau \). Since \(sig(u_0)=\dots =sig(u_3)=\textsf {swap}\), the events \(u_0,\dots , u_3\) perform an even number of state changes. Thus, either all of \(X_{i_0}, X_{i_1}, X_{i_2}\) are mapped to \(\textsf {swap}\) or exactly one of them. The construction of \(T_{i,1},\dots , T_{i,6}\) guarantees that there is exactly one variable event mapped to \(\textsf {swap}\).
In particular, the gadgets \(T_{i,4}, T_{i,5}\) and \(T_{i,6}\) ensure that if \(e\in \{w_{3i}, w_{3i+1} ,w_{3i+2}\}\) then \(sig(e)\not \in \{\textsf {nop},\textsf {used}\}\). We argue for \(w_{3i}\): By \(sig(k)=\textsf {inp}\) we get \(sup(t_{i,4,1})=0\) and \(sup(t_{i,4,4})=1\) which, by \(sig(u_7)=sig(u_8)=\textsf {swap}\), implies \(sup(t_{i,4,2})=1\) and \(sup(t_{i,4,3})=0\). Clearly, this implies \(sig(w_{3i})\not \in \{\textsf {nop},\textsf {used}\}\). Similarly, we obtain that \(sig(w_{3i+1})\not \in \{\textsf {nop},\textsf {used}\}\) and \(sig(w_{3i+2})\not \in \{\textsf {nop},\textsf {used}\}\).
Finally, the gadgets \(T_{i,1}, T_{i,2}\) and \(T_{i,3}\) ensure that no two variable events of the same clause can have a swap signature: By \(sig(k)=\textsf {inp}\) we get that \(sup(t_{i,1,1})=0\) and \(sup(t_{i,1,7})=1\) which with \(sig(u_4)=sig(u_5)=sig(u_6)=\textsf {swap}\) implies \(sup(t_{i,1,3})=0\) and \(sup(t_{i,1,6})=0\). Thus, if \(sig(X_{i_0})=sig(X_{i_1})=\textsf {swap}\) then \(sup(t_{i,1,4})=sup(t_{i,1,5})=1\) which implies \(sig(w_{3i})\in \{\textsf {nop}, \textsf {used}\}\), a contradiction. Similarly, one uses \(T_{i,2}\) and \(T_{i,3}\) to show that neither \(X_{i_0}\) and \(X_{i_2}\) nor \(X_{i_1}\) and \(X_{i_2}\) can simultaneously be mapped to \(\textsf {swap}\). As i was arbitrary, there is exactly one variable per clause that is mapped to \(\textsf {swap}\). Thus, \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {swap}\}\) is a one-in-three model of \(\varphi \).
Conversely, a one-in-three model M of \(\varphi \) allows a \(\tau \)-region (sup, sig) that solves \(\alpha \): The red colored area above indicates which states of \(H_0,\dots , H_3\), \(F_0,F_1\), \(G_0,\dots , G_{10}\) and \(T_{0,4},T_{0,5},T_{0,6},\dots , T_{m-1,4},T_{m-1,5},T_{m-1,6}\) have positive support. Moreover, we define \(sup(s)=1\) for all \(s\in \bot \). Which states of \(T_{i,0}, \dots , T_{i,3}\), where \(i\in \{0,\dots , m-1\}\), besides of k’s sources get a positive support depends on which of \(X_{i_0}, X_{i_1}, X_{i_2}\) belongs to M. The red colored area sketches the situation for \(X_{i_0}\in M\). It is easy to see that there is for all \(e\in E(A^\tau _\varphi )\) a fitting sig-value making (sup, sig) a (solving) \(\tau \)-region where \(sig(k)=\textsf {inp}\) and \(sup(h_{0,2})=0\). \(\square \)
Theorem 7
For any fixed \(g\ge 1\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {swap}\}\cup \omega \) and \(\omega \subseteq \{\textsf {out},\textsf {res},\textsf {used},\textsf {free}\}\) or if \(\tau =\{\textsf {nop},\textsf {out},\textsf {res},\textsf {swap}\}\cup \omega \) and \(\omega \subseteq \{\textsf {inp},\textsf {set},\textsf {used},\textsf {free}\}\).
Proof
We present the reduction for the types built by \(\tau =\{\textsf {nop}, \textsf {inp},\textsf {set},\textsf {swap}\}\cup \omega \) where \(\omega \subseteq \{\textsf {out}, \textsf {res}, \textsf {used}, \textsf {free}\}\). Again, the other types are covered by Lemma 2.
The TS \(A^\tau _\varphi \) has the following gadgets \(H_0,H_1,H_2\) and \(H_3\):

If \(\tau \cap \{\textsf {used},\textsf {free}\}\not =\emptyset \) then \(A^\tau _\varphi \) has also the following gadgets \(H_4,\dots , H_{12} \):

The gadgets \(H_0,\dots , H_3\) (\(H_4,\dots , H_{12}\), if added) provide \(\alpha =(k,h_{3,3})\). They ensure that if (sup, sig) \(\tau \)-solves \(\alpha \), then \(sig(k)\in \{\textsf {inp},\textsf {out}\}\). The TS \(A^\tau _\varphi \) adds the following gadgets \(F_0,F_1,F_2\) and, for all \(i\in \{0,\dots , 13\}\), the gadgets \(G_i, N_i\):

The gadgets \(F_0,F_1,F_2\) and \(G_0,N_0,\dots , G_{13}, N_{13}\) guarantee that if (sup, sig) solves \(\alpha \) then \(sig(u_i)=\textsf {swap}\). Similarly to the reduction of Theorem 6, the TS \(A^\tau _\varphi \) has for every \(i\in \{0,\dots , m-1\}\) gadgets \(T_{i,0},\dots , T_{i,6}\) and \(B_i\) to make the one-in-three satisfiability of \(\varphi \) and the \(\tau \)-solvability of \(\alpha \) the same. These gadgets and the ones for Theorem 6 have basically the same intention. However, since the current types have different interactions, the peculiarity of these gadgets is slightly different. In particular, \(A^\tau _\varphi \) has for each clause \(\zeta _i=\{X_{i_0}, X_{i_1}, X_{i_2}\}\) the following gadget \(T_{i,0}\):

Moreover, the gadgets \(T_{i,1}, T_{i,2}\) and \(T_{i,3}\) are defined as follows:

Furthermore, the gadgets \(T_{i,4}, T_{i,5}\) and \(T_{i,6}\) are defined by

Finally, the TS \(A^\tau _\varphi \) has for all \(i\in \{0,\dots , m-1\}\) the following gadget \(B_i\):

We briefly argue for the announced functionality of the gadgets. Let (sup, sig) be a \(\tau \)-region solving \(\alpha \). If \(sig(k)=\textsf {free}\) then \(sup(h_{3,3})=1\) and  implies \(sup(s)=sup(s')=0\). Since \(sup(h_{3,1})=0\) and \(sup(h_{3,3})=1\), there is an event \(e\in \{v_0,v_1\}\) such that \(sig(e)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). If \(sig(v_0)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), then, by \(sup(h_{1,1})=0\), we get \(sig(v_{0})=\textsf {swap}\). Moreover, if \(sig(v_1)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), which implies \(sig(h_{3,2})=1\), then, by \(sup(h_{2,3})=0\), we get \(sig(v_1)=\textsf {swap}\). By \(sig(v_1)=\textsf {swap}\) and \(sup(h_{2,3})=0\), we get \(sup(h_{2,2})=1\). By \(sup(h_{1,1})\), this implies \(sig(v_0)=\textsf {swap}\). Thus, in any case we get \(sig(v_0)=\textsf {swap}\). By \(sig(v_0)=\textsf {swap}\) and \(sup(h_{4,3})=sup(h_{5,1})=0\) we obtain \(sup(h_{4,2})=sup(h_{5,2})=1\) which implies \(sig(x)=\textsf {swap}\). Using this and \(sup(s)=sup(s')=0\) if
implies \(sup(s)=sup(s')=0\). Since \(sup(h_{3,1})=0\) and \(sup(h_{3,3})=1\), there is an event \(e\in \{v_0,v_1\}\) such that \(sig(e)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). If \(sig(v_0)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), then, by \(sup(h_{1,1})=0\), we get \(sig(v_{0})=\textsf {swap}\). Moreover, if \(sig(v_1)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), which implies \(sig(h_{3,2})=1\), then, by \(sup(h_{2,3})=0\), we get \(sig(v_1)=\textsf {swap}\). By \(sig(v_1)=\textsf {swap}\) and \(sup(h_{2,3})=0\), we get \(sup(h_{2,2})=1\). By \(sup(h_{1,1})\), this implies \(sig(v_0)=\textsf {swap}\). Thus, in any case we get \(sig(v_0)=\textsf {swap}\). By \(sig(v_0)=\textsf {swap}\) and \(sup(h_{4,3})=sup(h_{5,1})=0\) we obtain \(sup(h_{4,2})=sup(h_{5,2})=1\) which implies \(sig(x)=\textsf {swap}\). Using this and \(sup(s)=sup(s')=0\) if  , we have that \(sup(h_{j,2})=1\) for all \(j\in \{6,\dots , 11\}\). This implies \(sig(y_0)=sig(y_1)=sig(y_2)=\textsf {swap}\). By \(sup(h_{12,1})=sup(h_{12,4})=0\), the image of
, we have that \(sup(h_{j,2})=1\) for all \(j\in \{6,\dots , 11\}\). This implies \(sig(y_0)=sig(y_1)=sig(y_2)=\textsf {swap}\). By \(sup(h_{12,1})=sup(h_{12,4})=0\), the image of  is a path from 0 to 0 in \(\tau \). The number of state changes between 0 and 1 on such a path is even. This contradicts \(sig(y_0)=sig(y_1)=sig(y_2)=\textsf {swap}\). Thus, \(sig(k)\not =\textsf {free}\). The assumption that \(sig(k)=\textsf {used}\) and \(sup(h_{3,3})=0\) yields a contradiction, too.
is a path from 0 to 0 in \(\tau \). The number of state changes between 0 and 1 on such a path is even. This contradicts \(sig(y_0)=sig(y_1)=sig(y_2)=\textsf {swap}\). Thus, \(sig(k)\not =\textsf {free}\). The assumption that \(sig(k)=\textsf {used}\) and \(sup(h_{3,3})=0\) yields a contradiction, too.
We conclude that \(sig(k)=\textsf {inp}\) and \(sup(h_{3,3})=0\). This implies \(sig(v_0)\not \in \{\textsf {out},\textsf {set}\}\) and if  , then \(sup(s)=1\) and \(sup(s')=0\). Thus, by \(sup(h_{2,1})=0\) and \(sup(h_{2,3})=1\) there is an event \(e\in \{v_0,v_1\}\) such that \(sig(e)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). If \(e=v_0\) then \(sig(v_0)=\textsf {swap}\). Moreover, if \(e=v_1\) then \(sup(h_{3,2})=1\) which with \(sup(h_{3,3})=0\) and \(sup(h_{1,1})=1\) implies \(sig(v_0)=\textsf {swap}\). Consequently, any case implies \(sig(v_0)=\textsf {swap}\). This results in \(sig(u_j)=\textsf {swap}\) for all \(j\in \{0,\dots , 13\}\) as follows. By \(sup(f_{0,3})=sup(f_{1,3})=1\) and \(sig(v)=\textsf {swap}\) we obtain \(sup(f_{0,2})=sup(f_{1,2})=0\) which with \(sup(f_{0,1})=sup(f_{1,1})=0\) implies \(sig(z_0), sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\). Moreover, by \(sig(z_0), sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) and \(sup(f_{2,1})=0\) we get \(sup(f_{2,3})=0\) which with \(sup(f_{2,4})=1\) implies \(sig(z_2)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). By \(sig(z_0)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) and \(sup(g_{i,1})=0\), we get \(sup(g_{i,2})=0\). Furthermore, \(sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) and \(sup(g_{i,4})=1\) yields \(sig(z_1)=\textsf {nop}\) and \(sup(g_{i,3})=1\). This implies \(sig(u_i)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). Finally, by \(sup(n_{i,1})=0\) and \(sig(z_2)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), we get \(sup(n_{i,1})=1\) and, by \(sup(n_{i,4})=1\) and \(sig(v_0)=\textsf {swap}\), we have \(sup(n_{i,3})=0\). Since \(sig(u_i)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), this yields \(sig(u_i)=\textsf {swap}\) for all \(i\in \{0,\dots , 13\}\).
, then \(sup(s)=1\) and \(sup(s')=0\). Thus, by \(sup(h_{2,1})=0\) and \(sup(h_{2,3})=1\) there is an event \(e\in \{v_0,v_1\}\) such that \(sig(e)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). If \(e=v_0\) then \(sig(v_0)=\textsf {swap}\). Moreover, if \(e=v_1\) then \(sup(h_{3,2})=1\) which with \(sup(h_{3,3})=0\) and \(sup(h_{1,1})=1\) implies \(sig(v_0)=\textsf {swap}\). Consequently, any case implies \(sig(v_0)=\textsf {swap}\). This results in \(sig(u_j)=\textsf {swap}\) for all \(j\in \{0,\dots , 13\}\) as follows. By \(sup(f_{0,3})=sup(f_{1,3})=1\) and \(sig(v)=\textsf {swap}\) we obtain \(sup(f_{0,2})=sup(f_{1,2})=0\) which with \(sup(f_{0,1})=sup(f_{1,1})=0\) implies \(sig(z_0), sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\). Moreover, by \(sig(z_0), sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) and \(sup(f_{2,1})=0\) we get \(sup(f_{2,3})=0\) which with \(sup(f_{2,4})=1\) implies \(sig(z_2)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). By \(sig(z_0)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) and \(sup(g_{i,1})=0\), we get \(sup(g_{i,2})=0\). Furthermore, \(sig(z_1)\in \{\textsf {nop},\textsf {res},\textsf {free}\}\) and \(sup(g_{i,4})=1\) yields \(sig(z_1)=\textsf {nop}\) and \(sup(g_{i,3})=1\). This implies \(sig(u_i)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\). Finally, by \(sup(n_{i,1})=0\) and \(sig(z_2)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), we get \(sup(n_{i,1})=1\) and, by \(sup(n_{i,4})=1\) and \(sig(v_0)=\textsf {swap}\), we have \(sup(n_{i,3})=0\). Since \(sig(u_i)\in \{\textsf {out},\textsf {set},\textsf {swap}\}\), this yields \(sig(u_i)=\textsf {swap}\) for all \(i\in \{0,\dots , 13\}\).
The gadgets \(T_{i,0},\dots , T_{i,6}\), where \(i\in \{0,\dots , m-1\}\), use \(sig(k)=\textsf {inp}\) and \(sig(u_i)=\textsf {swap}\) for all \(i\in \{0,\dots , 13\}\) similarly to the ones of Theorem 6 to ensure that \(M=\{X\in V(\varphi ) \mid sig(X)=\textsf {swap}\}\) is a one-in-three model of \(\varphi \): By \(sup(t_{i,4,6})=sup(t_{i,5,6})=sup(t_{i,6,6})=1\) and \(sig(u_{5})=sig(u_{6})=\textsf {swap}\) we have \(sup(t_{i,4,4})=sup(t_{i,5,4})=sup(t_{i,6,4})=1\) for all \(i\in \{0,\dots , m-1\}\). Thus, if \(X\in V(\varphi )\),  and \(sup(s)\not =sup(s')\) then \(sig(X)=\textsf {swap}\). Using this, one argues in a manner quite similar to that of the proof of Theorem 6 that \(T_{i,0},\dots , T_{i,6}\) collaborate in such a way that there is exactly one variable event \(X\in \{X_{i_0}, X_{i_1}, X_{i_2}\}\) such that \(sig(X)=\textsf {swap}\). Thus, M is a corresponding model. Moreover, if \(sig(k)=\textsf {out}\) and \(sup(h_{3,3})=1\) then we obtain again that \(sig(u_i)=\textsf {swap}\) for all \(i\in \{0,\dots , 13\}\) which also guarantees that M is a searched model.
and \(sup(s)\not =sup(s')\) then \(sig(X)=\textsf {swap}\). Using this, one argues in a manner quite similar to that of the proof of Theorem 6 that \(T_{i,0},\dots , T_{i,6}\) collaborate in such a way that there is exactly one variable event \(X\in \{X_{i_0}, X_{i_1}, X_{i_2}\}\) such that \(sig(X)=\textsf {swap}\). Thus, M is a corresponding model. Moreover, if \(sig(k)=\textsf {out}\) and \(sup(h_{3,3})=1\) then we obtain again that \(sig(u_i)=\textsf {swap}\) for all \(i\in \{0,\dots , 13\}\) which also guarantees that M is a searched model.
Conversely, if M is a one-in-three model of \(\varphi \) then we can define analogously to Theorem 6 a \(\tau \)-region solving \(\alpha \). \(\square \)
Theorem 8
([12]). For any fixed \(g\ge 1\), deciding if a g-bounded TS A is \(\tau \)-solvable is NP-complete if \(\tau \in \{\textsf {nop},\textsf {inp},\textsf {out}\}\cup \{\textsf {used},\textsf {free}\}\).
Proof
The claim follows directly from our result of [12]. There we use 1-bounded cycle free gadgets to prove that synthesis of (pure) b-bounded Petri nets is NP-complete. The joining of [12] yields a 2-bounded TS. However, it is easy to see that the 1-bounded joining of this paper fits, too. The (pure) 1-bounded Petri net type is isomorphic to \(\{\textsf {nop},\textsf {inp},\textsf {out},\textsf {used}\}\) (\(\{\textsf {nop},\textsf {inp},\textsf {out}\}\)). By symmetry, \(\tau \)-solving ESSP atoms by \(\textsf {used}\) is equivalent to solving them by \(\textsf {free}\). \(\square \)
4 Polynomial Time Results
Theorem 9
For any fixed \(g < 2\), one can decide in polynomial time if a g-bounded TS A is \(\tau \)-solvable if \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set}\}\) or \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {used}\}\) or \(\tau =\{\textsf {nop},\textsf {out},\textsf {res}\}\) or \(\tau =\{\textsf {nop},\textsf {out},\textsf {res},\textsf {free}\}\) or \(\tau =\{\textsf {nop},\textsf {set},\textsf {res}\}\cup \omega \) with non-empty \(\omega \subseteq \{\textsf {inp},\textsf {out},\textsf {used},\textsf {free}\}\).
Proof
If A is \(\tau \)-solvable then no event e of A occurs twice in a row. Otherwise, the SSP atom \((s',s'')\) of a sequence  is not \(\tau \)-solvable. Thus, in what follows, we assume that A has no event occurring twice in a row. Moreover, it is easy to see that a 1-bounded TS
is not \(\tau \)-solvable. Thus, in what follows, we assume that A has no event occurring twice in a row. Moreover, it is easy to see that a 1-bounded TS  is a simple directed path on pairwise distinct states \(s_0,\dots , s_m\) or a directed cycle, that is, all states \(s_0,\dots , s_m\) except \(s_0\) and \(s_m\) are pairwise distinct. This proof proceeds as follows. First, we assume that \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set}\}\) and that A is a directed cycle and argue that the \(\tau \)-solvability of a given ESSP atom (k, s) or a SSP atom \((s,s')\) of A is decidable in polynomial time. Secondly, we argue that the presented algorithmic approach is applicable to directed paths, too. Thirdly, we show that the procedure introduced for \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\) can be extended to \(\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {used}\}\). By Lemma 2, this proves the claim for \(\{\textsf {nop},\textsf {out},\textsf {res}\}\) and \(\{\textsf {nop},\textsf {out},\textsf {res},\textsf {free}\}\), too. After that we investigate the case where \(\tau =\{\textsf {nop},\textsf {set},\textsf {res}\}\cup \omega \) with non-empty \(\omega \subseteq \{\textsf {inp},\textsf {out},\textsf {used},\textsf {free}\}\). We argue that it is sufficient to decide the \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\)- and \(\{\textsf {nop},\textsf {res},\textsf {set},\textsf {used}\}\)-solvability of A and that this is doable in polynomial time. The corresponding procedures again modify those introduced for \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\).
is a simple directed path on pairwise distinct states \(s_0,\dots , s_m\) or a directed cycle, that is, all states \(s_0,\dots , s_m\) except \(s_0\) and \(s_m\) are pairwise distinct. This proof proceeds as follows. First, we assume that \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set}\}\) and that A is a directed cycle and argue that the \(\tau \)-solvability of a given ESSP atom (k, s) or a SSP atom \((s,s')\) of A is decidable in polynomial time. Secondly, we argue that the presented algorithmic approach is applicable to directed paths, too. Thirdly, we show that the procedure introduced for \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\) can be extended to \(\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {used}\}\). By Lemma 2, this proves the claim for \(\{\textsf {nop},\textsf {out},\textsf {res}\}\) and \(\{\textsf {nop},\textsf {out},\textsf {res},\textsf {free}\}\), too. After that we investigate the case where \(\tau =\{\textsf {nop},\textsf {set},\textsf {res}\}\cup \omega \) with non-empty \(\omega \subseteq \{\textsf {inp},\textsf {out},\textsf {used},\textsf {free}\}\). We argue that it is sufficient to decide the \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\)- and \(\{\textsf {nop},\textsf {res},\textsf {set},\textsf {used}\}\)-solvability of A and that this is doable in polynomial time. The corresponding procedures again modify those introduced for \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\).
Let \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set}\}\) and A be 1-bounded (cycle) TS with event \(k\in E(A)\) that occurs m times. Since A is a cycle, we can assume that k occurs at A’s initial state:  . Moreover, since k does not occur twice in a row, its occurrences partition A into m k-free subsequences \(I_0,\dots , I_{m-1}\) such that
. Moreover, since k does not occur twice in a row, its occurrences partition A into m k-free subsequences \(I_0,\dots , I_{m-1}\) such that  , \(i\in \{0,\dots , m-1\}\), and \(s^{m-1}_{n_{m-1}}=\iota \), cf. Fig. 6.
, \(i\in \{0,\dots , m-1\}\), and \(s^{m-1}_{n_{m-1}}=\iota \), cf. Fig. 6.
Obviously, defining \(sup(\iota )=1\), \(sig(k)=\textsf {inp}\) and \(sig(e)=\textsf {set}\) for all \(e\in E(A)\setminus \{k\}\) inductively yields a region (sup, sig) solving the ESSP atoms (k, s) where  . Thus, it remains to consider the case
. Thus, it remains to consider the case  . Since
. Since  , there is an \(i\in \{0,\dots , m-1\}\) such that s is a state of the i-th subsequence \(I_i\). In particular, there is a \(j\in \{1,\dots ,n_i-1 \}\) such that \(s=s^i_j\). The state \(s^i_j\) divides \(I_i\) into the sequences
, there is an \(i\in \{0,\dots , m-1\}\) such that s is a state of the i-th subsequence \(I_i\). In particular, there is a \(j\in \{1,\dots ,n_i-1 \}\) such that \(s=s^i_j\). The state \(s^i_j\) divides \(I_i\) into the sequences  and
and  , cf. Fig. 6.
, cf. Fig. 6.
If (sup, sig) is a region that solves \(\alpha \) then \(sig(k)=\textsf {inp}\) and \(sup(s^i_j)=0\) is true. This implies for all \(\ell \in \{0,\dots , m-1\}\) that \(sup(s^\ell _0)=0\) and \(sup(s^\ell _{n_\ell })=1\). Thus, it remains to define the signature of the events of \(\bigcup _{\ell =0}^{m-1}E(I_\ell )\) such that  , for all \(\ell \in \{0,\dots , m-1\}\setminus \{i\}\), and
, for all \(\ell \in \{0,\dots , m-1\}\setminus \{i\}\), and  and
and  .
.
If there is for all \(\ell \in \{0,\dots ,m-1\}\setminus \{i\}\) an event \(e_\ell \in E(I_\ell )\) such that \(e_\ell \not \in E(I^0_i)\) and if there is an event \(e_i\in E(I^1_i)\) so that \(e_i\not \in E(I^0_i)\) then \(sup(\iota )=1\), \(sig(k)=\textsf {inp}\), \(sig(e_\ell )=\textsf {set}\) for all \(\ell \in \{0,\dots , m-1\}\), and \(sig(e)=\textsf {nop}\) for all \(e\in E(A)\setminus \{k,e_0,\dots ,e_\ell \}\) yields a \(\tau \)-region (sup, sig) of A that solves \(\alpha \). Clearly, whether A satisfies this property is decidable in polynomial time.
Otherwise, there is a sequence \(I\in \{I_0,\dots , I_{i-1}, I^1_i,I_{i+1},\dots , I_{m-1}\}\) so that \(E(I)\subseteq E(I^0_i)\). Thus, if (sup, sig) is a \(\tau \)-region that solves \(\alpha \) then there is a \(\ell \in \{1,\dots , j-1\}\) such that \(sig(y^i_{\ell })=\textsf {set}\). Consequently, there has to be a \(\ell ' \in \{\ell +1,\dots , j\}\) such that \(sig(y^i_{\ell '})=\textsf {inp}\) and, in particular, \(sig(y^i_{\ell ''})=\textsf {nop}\) for all \(\ell ''\in \{\ell '+1,\dots ,j\}\). Using this, one finds that (sup, sig) implies a region \((sup',sig')\) that solves \(\alpha \) and gets along with at most two \(\textsf {inp}\)-events. More exactly, defining \(sup'(\iota )=1\), \(sig'(k)=sig'(y^i_{\ell '})=\textsf {inp}\), \(sig'(e)=\textsf {nop}\) for all \(e\in \{y^i_{\ell '+1}, \dots , y^i_{j}\}\) and \(sig'(e)=\textsf {set}\) for all \(e\in E(A)\setminus (\{k,y^i_{\ell '},\dots , y^i_j\})\) yields a valid \(\tau \)-region \((sup', sig')\) that solves \(\alpha \). Since (sup, sig) was arbitrary, these deliberations show that in the second case the atom \(\alpha \) is \(\tau \)-solvable if and only if there is a corresponding region \((sup',sig')\). This yields the following polynomial procedure that decides whether \(\alpha \) is \(\tau \)-solvable: For \(\ell \) from j to 2 test if \((sup_\ell , sig_\ell )\) (inductively) defined by \(sup_\ell (\iota )=1\), \(sig_\ell (y^i_\ell )=\textsf {inp}\), \(sig_\ell (y^i_{\ell '})=\textsf {nop}\) for all \(\ell '\in \{\ell +1,\dots , j\}\) and \(sig_\ell (e)=\textsf {set}\) for all \(e\in E(A)\setminus (\{k,y^i_{\ell },\dots , y^i_j\})\) yields a \(\tau \)-region of A. If the test succeeds for any iteration then return yes, otherwise return no.
We can modify this approach to test the \(\tau \)-solvability of an SSP atom \(\beta =(s,s')\) as follows. Since  is a cycle we can assume without loss of generality that \(s=\iota \) and \(s'=s_i\) for some \(i\in \{1,\dots , m-1\}\). The states \(\iota \) and \(s_i\) partition A into two subsequences
is a cycle we can assume without loss of generality that \(s=\iota \) and \(s'=s_i\) for some \(i\in \{1,\dots , m-1\}\). The states \(\iota \) and \(s_i\) partition A into two subsequences  and
and  . If \(\beta \) is solvable by a region \((sup', sig')\) such that \(sup'(\iota )=1\) and \(sup'(s_i)=0\) then there is an event \(e\in I_0\) such that \(sig(e)=\textsf {inp}\). In particular, there is a region (sup, sig) as follows: \(sup(\iota )=1\), \(sig(e_j)=\textsf {inp}\) and \(j\in \{1,\dots , i\}\), \(sig(e_{\ell })=\textsf {nop}\) for all \(\ell \in \{j+1,\dots , i\}\) and \(sig(e)=\textsf {set}\) for all \(e\in E(A)\setminus \{e_j,\dots , e_i\}\). Similar to the approach for \(\alpha \), we can check if such a region exists in polynomial time. Moreover, the case where \(sup(\iota )=0\) and \(sup(s_i)=1\) works symmetrically.
. If \(\beta \) is solvable by a region \((sup', sig')\) such that \(sup'(\iota )=1\) and \(sup'(s_i)=0\) then there is an event \(e\in I_0\) such that \(sig(e)=\textsf {inp}\). In particular, there is a region (sup, sig) as follows: \(sup(\iota )=1\), \(sig(e_j)=\textsf {inp}\) and \(j\in \{1,\dots , i\}\), \(sig(e_{\ell })=\textsf {nop}\) for all \(\ell \in \{j+1,\dots , i\}\) and \(sig(e)=\textsf {set}\) for all \(e\in E(A)\setminus \{e_j,\dots , e_i\}\). Similar to the approach for \(\alpha \), we can check if such a region exists in polynomial time. Moreover, the case where \(sup(\iota )=0\) and \(sup(s_i)=1\) works symmetrically.
So far we have shown that the \(\tau \)-solvability of (E)SSP atoms of A are decidable in polynomial time if A is a cycle. If  is a directed path then its cycle extension \(A_c\) has a fresh event \(\oplus \not \in E(A)\) and is defined by
is a directed path then its cycle extension \(A_c\) has a fresh event \(\oplus \not \in E(A)\) and is defined by  . The event \(\oplus \) is unique thus an (E)SSP atom of A is solvable by a \(\tau \)-region of A if and only if it is solvable by a \(\tau \)-region of \(A_c\). Thus, we can decide the solvability of atoms of A via \(A_c\). Altogether, this proves that the \(\tau \)-solvability of (E)SSP atoms of 1-bounded inputs is decidable in polynomial time. Since we have at most \(\vert S\vert ^2+\vert E\vert \cdot \vert S\vert \) atoms to solve, the decidability of the \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\)-solvability for 1-bounded TS is polynomial.
. The event \(\oplus \) is unique thus an (E)SSP atom of A is solvable by a \(\tau \)-region of A if and only if it is solvable by a \(\tau \)-region of \(A_c\). Thus, we can decide the solvability of atoms of A via \(A_c\). Altogether, this proves that the \(\tau \)-solvability of (E)SSP atoms of 1-bounded inputs is decidable in polynomial time. Since we have at most \(\vert S\vert ^2+\vert E\vert \cdot \vert S\vert \) atoms to solve, the decidability of the \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\)-solvability for 1-bounded TS is polynomial.
Similar to the discussion for \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set}\}\), one argues that the following assertion is true: If \(\tau =\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {used}\}\) then there is a \(\tau \)-region \((sup', sig')\) with \(sig'(k)=\textsf {used}\) and \(sup(s^i_j)=0\) if and only if there is a \(\tau \)-region (sup, sig) and an number \(\ell \in \{1,\dots , j\}\) such that \(sup(\iota )=1\), \(sig(k)=\textsf {used}\), \(sig(y^i_\ell )=\textsf {inp}\), \(sig(y^i_{\ell '})=\textsf {nop}\) for all \(\ell '\in \{\ell +1,\dots ,j\}\) and \(sig(e)=\textsf {set}\) for all \(e\in E(A)\setminus \{k,y^i_\ell ,\dots , y^i_j\}\). Clearly, the procedure introduced for \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\) can be extended appropriately to a procedure that works for \(\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {used}\}\).
It remains to investigate the case where \(\tau =\{\textsf {nop},\textsf {res},\textsf {set}\}\cup \omega \) with non-empty \(\omega \subseteq \{\textsf {inp},\textsf {out},\textsf {used},\textsf {free}\}\). For a start, let’s argue that deciding the \(\tau \)-solvability is equivalent to deciding the \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\)-solvability or the \(\{\textsf {nop},\textsf {res},\textsf {set},\textsf {used}\}\)-solvability of A. This can be seen as follows: If (sup, sig) is a region that solves an ESSP atom \(\alpha =(k,s)\) such that \(sig(k)=\textsf {inp}\) then there is a \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\)-region \((sup', sig')\) that solves (k, s), too. The region \((sup',sig')\) originates from (sup, sig) by \(sup'=sup\), \(sig'(k)=\textsf {inp}\) and for all \(e\in E(A)\setminus \{k\}\) by \(sig'(e)=\textsf {nop}\) if \(sig(e)\in \{\textsf {nop},\textsf {used},\textsf {free}\}\), \(sig'(e)=\textsf {res}\) if \(sig(e)\in \{\textsf {inp},\textsf {res}\}\) and, finally, \(sig'(e)=\textsf {set}\) if \(sig(e)\in \{\textsf {out},\textsf {set}\}\). Similarly, one argues that \(\alpha \) is \(\tau \)-solvable such that \(sig(k)=\textsf {out}\) if and only if it is \(\{\textsf {nop},\textsf {out},\textsf {res},\textsf {set}\}\)-solvable. Moreover, \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\) and \(\{\textsf {nop},\textsf {out},\textsf {res},\textsf {set}\}\) are isomorphic thus \(\tau \)-solvability with \(\textsf {inp}\) or \(\textsf {out}\) reduces to \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\)-solvability. Similarly, the \(\tau \)-solvability with \(\textsf {used}\) or \(\textsf {free}\) reduces to \(\{\textsf {nop},\textsf {res},\textsf {set}, \textsf {used}\}\)-solvability. It is easy to see that the procedure introduced for \(\{\textsf {nop},\textsf {inp},\textsf {set}\}\) can be extended to the types \(\{\textsf {nop},\textsf {inp},\textsf {res},\textsf {set}\}\) and \(\{\textsf {nop},\textsf {res},\textsf {set}, \textsf {used}\}\). The only difference is that we now search for an event \(y^i_\ell \) such that \(sig(y^i_\ell )=\textsf {res}\) instead of \(sig(y^i_\ell )=\textsf {inp}\).
Finally, we observe that a SSP atom \(\beta =(s,s')\) is \(\tau \)-solvable if and only if it is \(\{\textsf {nop},\textsf {res},\textsf {set}\}\)-solvable. The states s and \(s'\) induce again a partition \(I_0\) and \(I_1\) of A and we can adapt the approach above to \(\{\textsf {nop},\textsf {res},\textsf {set}\}\). \(\square \)
Theorem 10
For any fixed \(g\in \mathbb {N}\), deciding whether a g-bounded TS A is \(\tau \)-solvable is polynomial if one of the following conditions is true:
-
1.
\(\tau =\{\textsf {nop},\textsf {inp},\textsf {free}\}\) or \(\tau =\{\textsf {nop},\textsf {inp},\textsf {used}, \textsf {free}\}\) or \(\tau =\{\textsf {nop},\textsf {out},\textsf {used}\}\) or \(\tau =\{\textsf {nop},\textsf {out},\textsf {used}, \textsf {free}\}\) and \(g < 2\).
-
2.
\(\tau =\{\textsf {nop}, \textsf {set}, \textsf {res}\} \cup \omega \) and \(\emptyset \not =\omega \subseteq \{\textsf {used}, \textsf {free}\}\) and \(g < 3\).
-
3.
\(\tau =\tau '\cup \omega \) and \(\tau '\in \{\{\textsf {nop},\textsf {set},\textsf {swap}\}, \{\textsf {nop},\textsf {res},\textsf {swap}\}, \{\textsf {nop},\textsf {res},\textsf {set}, \textsf {swap}\} \}\) and \(\emptyset \not =\omega \subseteq \{\textsf {used},\textsf {free}\}\) and \(g < 2\).
-
4.
\(\tau \in \{ \{\textsf {nop}, \textsf {inp}\}, \{\textsf {nop},\textsf {inp},\textsf {used}\}, \{\textsf {nop},\textsf {out}\}, \{\textsf {nop},\textsf {out},\textsf {free}\} \}\) or \(\tau \in \mathcal {T}=\{\{\textsf {nop},\textsf {set},\textsf {swap}\}, \{\textsf {nop},\textsf {res},\textsf {swap}\}, \{\textsf {nop},\textsf {set},\textsf {res}\}, \{\textsf {nop},\textsf {set},\textsf {res},\textsf {swap}\}\}\),
Proof
-
(1):
It is easy to see that A is a loop,
 or that A is cycle free, since there is an unsolvable SSP atom otherwise. Moreover, if an event e occurs twice consecutively,
or that A is cycle free, since there is an unsolvable SSP atom otherwise. Moreover, if an event e occurs twice consecutively,  , then \((s,s')\) is not \(\tau \)-solvable. Thus, for every \(e\in E(A)\) there is a \(s\in S(A)\) such that (e, s) has to be solved by \(sig(e)=\textsf {inp}\) (\(sig(e)=\textsf {out}\)) and \(sup(s)=0\) (\(sup(s)=1\)). If e occurs twice on the directed path A then such a region does not exist. On the other hand, A is \(\tau \)-solvable if every event occurs exactly once. Consequently, A is \(\tau \)-solvable if and only if it is 1-bounded and every event occurs exactly once.
, then \((s,s')\) is not \(\tau \)-solvable. Thus, for every \(e\in E(A)\) there is a \(s\in S(A)\) such that (e, s) has to be solved by \(sig(e)=\textsf {inp}\) (\(sig(e)=\textsf {out}\)) and \(sup(s)=0\) (\(sup(s)=1\)). If e occurs twice on the directed path A then such a region does not exist. On the other hand, A is \(\tau \)-solvable if every event occurs exactly once. Consequently, A is \(\tau \)-solvable if and only if it is 1-bounded and every event occurs exactly once. -
(2):
Since ESSP atoms of a \(\tau \)-solvable input A are only solvable by \(\textsf {used}\) and \(\textsf {free}\), we have that if
 then
then  . If \(s=s''\not =s'\) or if \(s,s',s''\) are pairwise distinct then \((s,s')\) is not \(\tau \)-solvable. This implies
. If \(s=s''\not =s'\) or if \(s,s',s''\) are pairwise distinct then \((s,s')\) is not \(\tau \)-solvable. This implies  . As a result, \(\tau \)-solvable inputs have the shape
. As a result, \(\tau \)-solvable inputs have the shape 
Thus, if the loop erasement \(A'\) of A originates from A by erasing all loops
 , that is,
, that is, 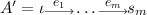 , then deciding the \(\tau \)-solvability of A reduces to deciding if \(A'\) has the \(\tau \)-SSP and if all ESSP atoms (e, s) with
, then deciding the \(\tau \)-solvability of A reduces to deciding if \(A'\) has the \(\tau \)-SSP and if all ESSP atoms (e, s) with  of \(A'\) are \(\tau \)-solvable. This is doable in polynomial time by the approach of Theorem 9.
of \(A'\) are \(\tau \)-solvable. This is doable in polynomial time by the approach of Theorem 9. -
(3):
Since ESSP atoms of an input A are only solvable by \(\textsf {used}\) and \(\textsf {free}\), if
 and \(s\not =s'\) then
and \(s\not =s'\) then  . If
. If  and \(s,s',s'', s'''\) are pairwise different, then the SSP atom \((s',s''')\) is not \(\tau \)-solvable. As a consequence, \(\tau \)-solvable inputs can have at most 3 different states.
and \(s,s',s'', s'''\) are pairwise different, then the SSP atom \((s',s''')\) is not \(\tau \)-solvable. As a consequence, \(\tau \)-solvable inputs can have at most 3 different states. -
(4):
Let \(\tau \in \{\{\textsf {nop}, \textsf {inp}\}, \{\textsf {nop},\textsf {inp},\textsf {used}\}\}\). If A is \(\tau \)-solvable, then for all \(e\in E(A)\) holds
 . Otherwise, \((e,\iota )\) is not \(\tau \)-solvable. Similarly, if \(\tau \in \mathcal {T}\), then ESSP atoms are not \(\tau \)-solvable thus, every event occurs at \(\iota \). A is g-bounded. This implies \(\vert E(A)\vert \le g\). Thus, A has at most \(2\cdot \vert \tau \vert ^g\) \(\tau \)-regions. Since g is fixed, \(\tau \)-synthesis is polynomial by brut-force. By Lemma 2, the claim follows.
. Otherwise, \((e,\iota )\) is not \(\tau \)-solvable. Similarly, if \(\tau \in \mathcal {T}\), then ESSP atoms are not \(\tau \)-solvable thus, every event occurs at \(\iota \). A is g-bounded. This implies \(\vert E(A)\vert \le g\). Thus, A has at most \(2\cdot \vert \tau \vert ^g\) \(\tau \)-regions. Since g is fixed, \(\tau \)-synthesis is polynomial by brut-force. By Lemma 2, the claim follows.
\(\square \)
5 Conclusion
In this paper, we fully characterize the computational complexity of \(\textsf {nop}\)-equipped Boolean Petri nets from g-bounded TS for any fixed \(g\in \mathbb {N}\). Our results show that if \(\tau \)-synthesis is hard then it remains hard even for low bounds g. Moreover, they also show that when g becomes very small, sometimes it makes the difference between hardness and tractability, cf. Fig. 1 §1–§3 and §9, but sometimes it does not, cf. Fig. 1 §4–§7. In this sense, the parameter g helps to recognize interactions that contribute to the power of a type. By Theorem 3 and Theorem 9, \(\{\textsf {nop}, \textsf {inp},\textsf {set}\}\)-synthesis is hard if \(g\ge 2\) and tractable if \(g < 2\), respectively. By Theorem 5, \(\{\textsf {nop},\textsf {inp},\textsf {set},\textsf {free}\}\)-synthesis remains hard for all \(g \ge 1\). Thus, if restricted to 1-bounded inputs then the test interaction \(\textsf {free}\) makes the difference between hardness and tractability of synthesis. Surprisingly enough, by Theorem 9, replacing \(\textsf {free}\) by \(\textsf {used}\) makes synthesis from 1-bounded TS tractable again. It remains future work, to characterize the computational complexity of synthesis for the remaining 128 types which do not contain \(\textsf {nop}\). Moreover, since \(\tau \)-synthesis generally remains hard even for (small) fixed g, the bound of a TS is ruled out for FPT-algorithms. Future work might be concerned with parameterizing \(\tau \)-synthesis by the dependence number of the searched \(\tau \)-net: If \(N=(P, T, f, M_0)\) is a Boolean net, \(p\in P\) and if the dependence number \(d_p\) of p is defined by \(d_p=\vert \{ t\in T\mid f(p,t)\not =\textsf {nop}\} \vert \) then the dependence number d of N is defined by \(d=\text {max}\{ d_p \mid p\in P\}\). At first glance, d appears to be a promising parameter for FPT-approaches because this parameterization puts the problem into the complexity class XP: Since a \(\tau \)-region of \(A=(S,E,\delta , \iota )\) is determined by \(sup(\iota )\) and sig, for each (E)SSP atom \(\alpha \) there are at most \(2\cdot \vert \tau \vert ^d\cdot \sum _{i=0}^d \left( {\begin{array}{c}\vert E\vert \\ i\end{array}}\right) \) fitting \(\tau \)-regions solving \(\alpha \). Thus, by \(\vert \tau \vert \le 8\), \(\tau \)-synthesis parameterized by d is decidable in \(\mathcal {O}(\vert E\vert ^d \cdot \vert S\vert \cdot \text {max}\{\vert S\vert ,\vert E\vert \} )\).
References
Badouel, E., Bernardinello, L., Darondeau, P.: The synthesis problem for elementary net systems is NP-complete. Theor. Comput. Sci. 186(1–2), 107–134 (1997)
Badouel, E., Bernardinello, L., Darondeau, P.: Petri Net Synthesis. Texts in Theoretical Computer Science. An EATCS Series, Springer (2015)
Badouel, E., Darondeau, P.: Trace nets and process automata. Acta Inf. 32(7), 647–679 (1995)
Cortadella, J.: Private correspondance (2017)
Kleijn, J., Koutny, M., Pietkiewicz-Koutny, M., Rozenberg, G.: Step semantics of Boolean nets. Acta Inf. 50(1), 15–39 (2013)
Montanari, U., Rossi, F.: Contextual nets. Acta Inf. 32(6), 545–596 (1995)
Moore, C., Robson, J.M.: Hard tiling problems with simple tiles. Discrete Comput. Geom. 26(4), 573–590 (2001)
Pietkiewicz-Koutny, M.: Transition systems of elementary net systems with inhibitor arcs. In: Azéma, P., Balbo, G. (eds.) ICATPN 1997. LNCS, vol. 1248, pp. 310–327. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63139-9_43
Rozenberg, G., Engelfriet, J.: Elementary net systems. In: Petri Nets. Lecture Notes in Computer Science, vol. 1491, pp. 12–121. Springer (1996)
Schmitt, V.: Flip-flop nets. In: Puech, C., Reischuk, R. (eds.) STACS 1996. LNCS, vol. 1046, pp. 515–528. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-60922-9_42
Tredup, R.: The complexity of synthesizing \({\sf nop}\)equipped boolean nets from \(g\)-bounded inputs (technical report), to appear in CoRR (2019)
Tredup, R.: Hardness results for the synthesis of b-bounded Petri Nets. In: Donatelli, S., Haar, S. (eds.) PETRI NETS 2019. LNCS, vol. 11522, pp. 127–147. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21571-2_9
Tredup, R.: Tracking down the bad guys: reset and set make feasibility for flip-flop net derivatives NP-complete. ICE. EPTCS 304, 20–37 (2019)
Tredup, R., Rosenke, C.: Narrowing down the hardness barrier of synthesizing elementary net systems. In: CONCUR. LIPIcs, vol. 118, pp. 16:1–16:15. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2018)
Tredup, R., Rosenke, C.: The complexity of synthesis for 43 Boolean Petri Net types. In: Gopal, T.V., Watada, J. (eds.) TAMC 2019. LNCS, vol. 11436, pp. 615–634. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-14812-6_38
Tredup, R., Rosenke, C.: On the hardness of synthesizing Boolean nets. In: ATAED@Petri Nets/ACSD. CEUR Workshop Proceedings, vol. 2371, pp. 71–86. CEUR-WS.org (2019)
Tredup, R., Rosenke, C., Wolf, K.: Elementary net synthesis remains NP-complete even for extremely simple inputs. In: Khomenko, V., Roux, O.H. (eds.) PETRI NETS 2018. LNCS, vol. 10877, pp. 40–59. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-91268-4_3
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer-Verlag GmbH Germany, part of Springer Nature
About this chapter
Cite this chapter
Tredup, R. (2021). The Complexity of Synthesizing \(\textsf {nop}\)-Equipped Boolean Petri Nets from g-Bounded Inputs. In: Koutny, M., Kordon, F., Pomello, L. (eds) Transactions on Petri Nets and Other Models of Concurrency XV. Lecture Notes in Computer Science(), vol 12530. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-63079-2_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-63079-2_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-63078-5
Online ISBN: 978-3-662-63079-2
eBook Packages: Computer ScienceComputer Science (R0)











 or that A is cycle free, since there is an unsolvable SSP atom otherwise. Moreover, if an event e occurs twice consecutively,
or that A is cycle free, since there is an unsolvable SSP atom otherwise. Moreover, if an event e occurs twice consecutively,  , then
, then  then
then  . If
. If  . As a result,
. As a result, 
 , that is,
, that is, 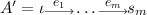 , then deciding the
, then deciding the  of
of  and
and  . If
. If  and
and  . Otherwise,
. Otherwise,