Abstract
We consider multi-agent systems where agents actions and beliefs are determined aleatorically, or “by the throw of dice”. This system consists of possible worlds that assign distributions to independent random variables, and agents who assign probabilities to these possible worlds. We present a novel syntax and semantics for such system, and show that they generalise Modal Logic. We also give a sound and complete calculus for reasoning in the base semantics, and a sound calculus for the full modal semantics, that we conjecture to be complete. Finally we discuss some application to reasoning about game playing agents.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
This paper proposes a probabilistic generalisation of modal logic for reasoning about probabilistic multi-agent systems. There has been substantial work in this direction before [1, 6, 13]. However, here, rather than extending a propositional modal logic with the capability to represent and reason about probabilities, we revise all logical operators so that they are interpreted probabilistically. Thus we differentiate between reasoning about probabilities and reasoning probabilistically. Interpreting probabilities as epistemic entities suggests a Bayesian approach [2], where agents assess the likelihood of propositions based on a combination of prior assumptions and observations.
We provide a lightweight logic, the aleatoric calculus, for reasoning about systems of independent random variables, and give an extension, the modal aleatoric calculus for reasoning about multi-agent systems of random variables. We show that this is a true generalisation of modal logic and provide some initial proof theoretic results. The modal aleatoric calculus allows agents to express strategies in games or theories of how other agents will act, and we present a basic demonstration of this.
2 Related Work
There has been significant and long-standing interest in reasoning about probability and uncertainty, to apply the precision of logical deduction in uncertain and random environments. Hailperin’s probability logic [9] and Nilsson’s probabilistic logic [16] seek to generalise propositional, so the semantics of true and false are replaced by probability measures. These approaches in turn are generalised in fuzzy logics [19] where real numbers are used to model degrees of truth via T-norms. In [18] Williamson provide an inference system based on Bayesian epistemology.
These approaches lose the simplicity of Boolean logics, as deductive systems must deal with propositions that are not independent. This limits their practicality as well defined semantics require the conditional probabilities of all atoms to be known. However, these approaches have been successfully combined with logic programming [12] and machine learning [3]. Feldman and Harel [7] and Kozen [14] gave a probabilistic variation of propositional dynamic logic for reasoning about the correctness of programs with random variables. Importantly, this work generalises a modal logic (PDL) as a many valued logic.
More general foundational work on reasoning probabilistically was done by de Finetti [4] who established an epistemic notion of probability based on what an agent would consider to be a rational wager (the Dutch book argument). In [15], Milne incorporates these ideas into the logic of conditional events. Stalnaker has also considered conditional events and has presented conditional logic [17]. Here, conditional refers to the interpretation of one proposition being contingent on another, although this is not quantified nor assigned a probability.
The other approach to reasoning about uncertainty is to extend traditional Boolean and modal logics with operators for reasoning about probabilities. Modal and epistemic logics have a long history for reasoning about uncertainty, going back to Hintikka’s work on possible worlds [11]. More recent work on dynamic epistemic logic [5] has looked at how agents incorporate new information into their belief structures. There are explicit probabilistic extensions of these logics, that maintain the Boolean interpretation of formulae, but include probabilistic terms [6, 10]. Probabilistic terms are converted into Boolean terms through arithmetic comparisons. For example, “It is more likely to snow than it is to rain” is a Boolean statement, whereas the likelihood of snow is a probabilistic statement.
3 Syntax and Semantics
We take a many-valued approach here. Rather than presenting a logic that describes what is true about a probabilistic scenario, we present the Modal Aleatoric Calculus (\(\mathbf {MAC}\)) for determining what is likely. The different is subtle: In probabilistic dynamic epistemic logic [13] it is possible to express that the statement “Alice thinks X has probability 0.5” is true; whereas the calculus here simply has a term “Alice’s expectation of X” which may have a value that is greater than 0.5. We present a syntax for constructing complex terms in this calculus, and a semantics for assignment values to terms, given a particular interpretation or model.
3.1 Syntax
The syntax is given for a set of random variables X, and a set of agents N. We also include constants \(\top \) and \(\bot \). The syntax of the dynamic aleatoric calculus, \(\mathbf {MAC}\), is as follows:
where \(x\in X\) is a variable and \(i\in N\) is a modality. We typically take an epistemic perspective, so the modality corresponds to an agent’s beliefs. As usual, we let \(v(\alpha )\) refer to the set of variables that appear in \(\alpha \). We refer to \(\top \) as always and \(\bot \) as never. The if-then-else operator \((\alpha ? \beta \!:\!\gamma )\) is read if \(\alpha \) then \(\beta \) else \(\gamma \) and uses the ternary conditional syntax of programming languages such as C. The conditional expectation operator \((\alpha \! \mid \! \beta )_i\) is modality i’s expectation of \(\alpha \) given \(\beta \) (the conditional probability i assigns to \(\alpha \) given \(\beta \)).
3.2 Semantics
The modal aleatoric calculus is interpreted over probability models similar to the probability structures defined in [10], although they have random variables in place of propositional assignments.
Definition 1
Given a set S, we use the notation PD(S) to notate the set of probability distributions over S, where \(\mu \in PD(S)\) implies: \(\mu :S\longrightarrow [0,1]\); and either \(\varSigma _{s\in S} \mu (s) = 1\), or \(\varSigma _{s\in S}\mu (s) = 0\). In the latter case, we say \(\mu \) is the empty distribution.
Definition 2
Given a set of variables X and a set of modalities N, a probability model is specified by the tuple \(P =(W, \pi , f)\), where:
-
W is a set of possible worlds.
-
\(\pi :N\longrightarrow W\longrightarrow PD(W)\) assigns for each world \(w\in W\) and each modality \(i\in N\), a probability distribution \(\pi _i(w)\) over W. We will write \(\pi _i(w,v)\) in place of \(\pi (i)(w)(v)\).
-
\(f:W\longrightarrow X\longrightarrow [0,1]\) is a probability assignment so for each world w, for each variable x, \(f_w(x)\) is the probability of x being true.
Given a model P we identify the corresponding tuple as \((W^P, \pi ^P, f^P)\). A pointed probability model, \(P_w = (W, \pi ,f,w)\), specifies a world in the model as the point of evaluation.
We note that we have not placed any restraints on the function \(\pi \). If \(\pi \) were to model agent belief we might expect all worlds in the probability distribution \(\pi _i(w)\) to share the same probability distribution of worlds. However, at this stage we have chosen to focus on the unconstrained case.
Given a pointed model \(P_w\), the semantic interpretation of a \(\mathbf {MAC}\) formula \(\alpha \) is \(P_w(\alpha )\in [0,1]\) which is the expectation of the formula being supported by a sampling of the model, where the sampling is done with respect to the distributions specified by \(\pi \) and f.
Definition 3
The semantics of the modal aleatoric calculus take a pointed probability model, \(f_w\), and a proposition defined in \(\mathbf {MAC}\), \(\alpha \), and calculate the expectation of \(\alpha \) holding at \(P_w\). Given an agent i, a world w and a \(\mathcal {MAC}\) formula \(\alpha \), we define i’s expectation of \(\alpha \) at w as
Then the semantics of \(\mathbf {MAC}\) are as follows:
We say two formulae, \(\alpha \) and \(\beta \), a semantically equivalent (written \(\alpha \cong \beta \)) if for all pointed probability models \(P_w\) we have \(P_w(\alpha ) = P_w(\beta )\).
The concept of sampling is intrinsic in the rational of these semantics. The word aleatoric has its origins in the Latin for dice-player (aleator), and the semantics are essentially aleatoric, in that they use dice (or sample probability distributions) for everything. If we ask whether a variable is true at a world, the variable is sampled according to the probability distribution at that world. Likewise, to interpret a modality the corresponding distribution of worlds is sampled, and the formula is evaluated at the selected world. However, we are not interested in the result of any one single sampling activity, but in the expectation derived from the sampling activity.
This gives us an interesting combination approaches for understanding probability. Aleatoric approaches appeal to frequentist interpretations of probability, where likelihoods are fixed and assume arbitrarily large sample sizes. This contrasts the Bayesian approach where probability is intrinsically epistemic, where we consider what likelihood an agent would assign to an event, given the evidence they have observed. Our approach can be seen as an aleatoric implementation of a Bayesian system. By this we mean that: random variables are aleatoric, always sampled from a fixed distribution, and modalities are Bayesian, always conditioned on a set of possible worlds.
The if-then-else operator, \((\alpha ? \beta \!:\!\gamma )\), can be imagined as a sampling protocol. We first sample \(\alpha \), and if \(\alpha \) is true, we proceed to sample \(\beta \) and otherwise we sample \(\gamma \). We imagine an evaluator interpreting the formula by flipping a coin: if it lands heads, we evaluate \(\beta \); if it lands tails, we evaluate \(\gamma \). This corresponds to the additive property of Bayesian epistemology: if A and B are disjoint events, then \(P(A\ {or}\ B) = P(A)+P(B)\) [2]. Here the two disjoint events are \(\alpha \) and \(\beta \) and \(\lnot \alpha \) and \(\gamma \), but disjointedness is only guaranteed if \(\alpha \) and \(\lnot \alpha \) are evaluated from the same sampling.
The conditional expectation operator \((\alpha \! \mid \! \beta )_i\) expresses modality i’s expectation of \(\alpha \) marginalised by the expectation of \(\beta \). This is, as in the Kolmogorov definition of conditional probability, i’s expectation of \(\alpha \wedge \beta \) divided by i’s expectation of \(\beta \). The intuition for these semantics corresponds to a sampling protocol. The modality i samples a world from the probability distribution and samples \(\beta \) at that world. If \(\beta \) is true, then i samples \(\alpha \) at that world and returns the result. Otherwise agent i resamples a world from their probability distribution, and repeats the process. In the case that \(\beta \) is never true, we assign \((\alpha \! \mid \! \beta )_i\) probability 1, as being vacuously true.
Abbreviations: Some abbreviations we can define in \(\mathcal {MAC}\) are as follows:
where a and b are natural numbers. We will show later that under certain circumstances these operators do correspond with their Boolean counterparts. However, this is not true in the general case. The formula \(\alpha \wedge \beta \) does not interpret directly as \(\alpha \) is true and \(\beta \) is true. Rather it is the likelihood of \(\alpha \) being sampled as true, followed by \(\beta \) being sampled as true. For this reason \(\alpha \wedge \alpha \) is not the same as \(\alpha \). Similarly \(\alpha \vee \beta \) is the likelihood of \(\alpha \) being sampled as true, or in the instance that it was not true, that \(\beta \) was sampled as true.
The modality \(E_i \alpha \) is agent i’s expectation of \(\alpha \) being true, which is just \(\alpha \) conditioned on the uniformly true \(\top \). The operator \(\Box _i\alpha \) corresponds to the necessity operator of standard modal logic, and uses a property of the conditional operator: it evaluates \((\alpha \! \mid \! \beta )_i\) as vacuously true if and only if there is no expectation that \(\beta \) can ever be true. Therefore, \((\bot \! \mid \! \lnot \alpha )_i\) can only be true if modality i always expects \(\lnot \alpha \) to be false, and thus for the modality i, \(\alpha \) is necessarily true. The formula \(\alpha ^{\frac{a}{b}}\) allows us to explicitly represent degrees of belief in the language. It is interpreted as \(\alpha \) is true at least a times out of b. Note that this is not a statement saying what the frequency of \(\alpha \) is. Rather it describes the event of \(\alpha \) being true a times out of b. Therefore, if \(\alpha \) was unlikely (say true 5% of the time) then \(\alpha ^{\frac{9}{9}}\) describes an incredibly unlikely event.
3.3 Example
We will give simple example of reasoning in \(\mathbf {MAC}\). Suppose we have an aleator (dice player), considering the outcome of a role of a die. While the dice is fair, our aleator does not know whether it is a four sided die or a six sided die. We consider a single proposition: \(p_1\) if the result of throw of the die is 1. The aleator considers two worlds equally possible: \(w_4\) where the die has four sides, and \(w_6\) where the die has 6 sides. The probability model \(P = (W, \pi , f)\) is depicted in Fig. 1: We can formulate properties such as “at least one of the next two throws will be a 1”: \(p_1^{\frac{1}{2}} = (p_1 ? \top \!:\!p_1)\). We can calculate \(P_{w_4}(p_1^{\frac{1}{2}}) = \frac{7}{16}\), while \(P_{w_6}(p_1^{\frac{1}{2}}) = \frac{11}{36}\). Now if we asked our aleator what are the odds of rolling a second 1, given the first roll was 1, we would evaluate the formula \((p_1\! \mid \! p_1)_a\) (where a is our aleator), and in either world this evaluates to \(\frac{5}{24}\). Note that this involves some speculation from the aleator.
4 Axioms for the Modal Aleatoric Calculus
Having seen the potential for representing stochastic games, we will now look at some reasoning techniques. First we will consider some axioms to derive constraints on the expectations of propositions, as an analogue of a Hilbert-style proof system for modal logic. In the following section we will briefly analyse the model checking problem, as a direct application of the semantic definitions.
Our approach here is to seek a derivation system that can generate equalities that are always valid in \(\mathbf {MAC}\). For example, \(\alpha \wedge \beta \simeq \beta \wedge \alpha \) will be satisfied by every world of every model. We use the relation \(\simeq \) to indicate that two formulae are equivalent in the calculus, and the operator \(\cong \) to indicate the expectation assigned to each formula will be equal in all probability models. We show that the calculus is sound, and sketch a proof of completeness in the most basic case.
4.1 The Aleatoric Calculus
The aleatoric calculus, AC, is the language of \(\top ,\ \bot ,\ x\) and \((\alpha ? \beta \!:\!\gamma )\), where \(x\in X\). The interpretation of this fragment only depends on a single world and it is the analogue of propositional logic in the non-probabilistic setting. The axioms of the calculus are:
We also have the rules of transitivity, symmetry and substitution for \(\simeq \):
where \(\alpha [x\backslash \gamma ]\) is \(\alpha \) with every occurrence of the variable x replaced by \(\gamma \). We let this system of axioms and rules be referred to as \(\mathfrak {AC}\).
As an example of reasoning in this system, we will show that the commutativity of \(\wedge \) holds:
The axiom system \(\mathfrak {AC}\) is sound. The majority of these axioms are simple to derive from Definition 3, and all proofs essentially show that the semantic interpretation of the left and right side of the equation are equal. The rules Trans and Sym come naturally with equality, and the rule Subs follows because at any world, all formulae are probabilistically independent.
We present arguments for the soundness of the less obvious tree and swap in the long version of the paper [8].
Lemma 1
The axiom system \(\mathfrak {AC}\) is sound for AC.
Proof
This follows from Lemmas 2 and 3 presented in [8], and Definition 3.2. Also, from the semantics we can see that the interpretation of subformulae are independent of one another, so the substitution rule holds, and the remaining rules follow directly from the definition of \(\simeq \).
To show that \(\mathfrak {AC}\) complete for the aleatoric calculus, we aim to show that any aleatoric calculus formula that are semantically equivalent can be transformed into a common form. As the axioms of \(\mathfrak {AC}\) are equivalences this is sufficient to show that the formulae are provably equivalent. The proofs are presented in the long version of the paper.
A tree form Aleatoric Calculus formula is either atomic, or it has an atomic random variable condition and both its left and right subformulae are in tree form.
Definition 4
The set of all tree form Aleatoric Calculus formulae \(T \subset \varPhi \) is generated by the following grammar:
Lemma 2
For any Aleatoric Calculus formula there exists an equivalent (by \(\simeq \)) tree form formula.
Definition 5
A path in a tree form aleatoric calculus formula is a sequence of tokens from the set \({\{}x, \overline{x} \mid x \in X{\}}\) corresponding to the outcomes of random trials involved in reaching a terminal node in the tree. We define the functions  and
and  to be the set of paths that terminate in a \(\top \) or a \(\bot \) respectively:
to be the set of paths that terminate in a \(\top \) or a \(\bot \) respectively:



where \(^\frown \) is the sequence concatenation operator:
We say two paths are multi-set equivalent if the multiset of tokens that appear in each path are equivalent, and define  to be the set of all paths through a formula.
to be the set of all paths through a formula.
Lemma 3
For any tree form aleatoric calculus formula \(\alpha \):

where \(P(\overline{x}) = (1 - P(x))\).
Proof
This follows immediately from the Definition 3.
Lemma 4
Suppose that \(\phi \) is a formula in tree form such that  (resp.
(resp.  ). Then, for any \(i<n\) there is some formula \(\phi _a^i\) such that:
). Then, for any \(i<n\) there is some formula \(\phi _a^i\) such that:
-
1.
\(\phi \simeq \phi _a^i\)
-
2.
 (resp.
(resp.  )
) -
3.
\(\phi \) and \(\phi _a^i\) agree on all paths that do not have the prefix \((a_0,\ldots , a_{i-1}\). That is, for all
 , where for some \(j<i\), \(b_j \ne a_j\), we have
, where for some \(j<i\), \(b_j \ne a_j\), we have  if and only if
if and only if 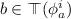 and
and  if and only if
if and only if  .
.
Lemma 5
Given a pair of multi-set equivalent paths a and b in a tree form aleatoric calculus formula, \(\phi \), such that  and
and  , we can find a formula \(\phi _a^b\simeq \phi \) where
, we can find a formula \(\phi _a^b\simeq \phi \) where
-
1.
 and
and 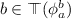
-
2.
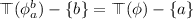 ,
, -
3.
 .
.
Lemma 6
For any pair of tree form aleatoric calculus formulae, \(\phi \) and \(\psi \), there exists a pair of tree forms \(\phi '\simeq \phi \) and \(\psi '\simeq \psi \), such that  .
.
Theorem 1
For any pair of semantically equivalent aleatoric calculus formulae \(\phi \) and \(\psi \), we can show \(\phi \simeq \psi \).
Proof
By Lemma 2 it is possible to convert both formulae in question, \(\phi \) and \(\psi \), into tree form, respectively \(\phi ^\tau \) and \(\psi ^\tau \). By Lemma 6 it is then possible to convert \(\phi ^\tau \) and \(\psi ^\tau \) to a pair of equivalent formulae, respectively \(\varPhi \) and \(\varPsi \), with the same structure (so  ), but possibly different leaves (so
), but possibly different leaves (so  is possibly not the same as
is possibly not the same as  . By Lemma 5 it is possible to swap any multiset-equivalent paths between
. By Lemma 5 it is possible to swap any multiset-equivalent paths between  and
and  . By Lemma 3 two formula, \(\varPhi \) and \(\varPsi \), with the same structure are semantically equivalent if and only if there is a one-to-one correspondence between paths of \(\varPhi \) and \(\varPsi \) such that corresponding paths a and b are multi-set equivalent, and
. By Lemma 3 two formula, \(\varPhi \) and \(\varPsi \), with the same structure are semantically equivalent if and only if there is a one-to-one correspondence between paths of \(\varPhi \) and \(\varPsi \) such that corresponding paths a and b are multi-set equivalent, and  if and only if
if and only if  . Therefore, if and only if the two formulae are equivalent we are able to define \(\varPhi '\) by swapping paths between
. Therefore, if and only if the two formulae are equivalent we are able to define \(\varPhi '\) by swapping paths between  and
and  such that \(\varPhi ' = \varPsi \). As all steps are performed using the axioms and are reversible, this is sufficient to show \(\phi \simeq \psi \).
such that \(\varPhi ' = \varPsi \). As all steps are performed using the axioms and are reversible, this is sufficient to show \(\phi \simeq \psi \).
4.2 The Modal Aleatoric Calculus
The modal aleatoric calculus includes the propositional fragment, as well as the conditional expectation operator \((\alpha \! \mid \! \beta )_i\) that depends on the modality i’s probability distribution over the set of worlds.
The axioms we have for the conditional expectation operator are as follows:
We let the axiom system \(\mathfrak {MAC}\) be the axiom system \(\mathfrak {AC}\) along with the axioms A0-A5.
We note that the conditional expectation operator \((x\! \mid \! y)_i\) is its own dual, but only in the case that agent i does not consider x and y to be mutually exclusive: \((\lnot x\! \mid \! y)_i\simeq (x\! \mid \! y)_i\rightarrow \Box _i(\lnot (x\wedge y)).\) We can see this in the following derivation:
The main axiom in \(\mathfrak {MAC}\) is the axiom A0 which is a rough analogue of the K axiom in modal logic. We note that in this axiom:
if we substitute \(\top \) for y and \(\bot \) for w, we have: \(E_i x\wedge (y\! \mid \! x)_i\simeq E_i(x\wedge y)\) whenever agent i considers x possible (so that \((\bot \! \mid \! \lnot x)_i\simeq \bot \)). In that case we can “divide” both sides of the semantic equality by \(P_w(E_i x)\) which gives the Kolmogorov definition of conditional probability:
Axioms A1 and A2 deal with formulas of the type \((\bot \! \mid \! \alpha )_i\). The probability associated with such formulas is non-zero if and only if \(\alpha \) is impossible in all the successor states, so in these states, we are able to substitute \(\alpha \) with \(\bot \).
Finally axioms A3 and A4 allow us to eliminate conditional expectation operators.
As with the aleatoric calculus, soundness can be shown by deriving equivalence of the semantic evaluation equations, although the proofs are more complex.
Lemma 7
The system \(\mathfrak {MAC}\) is sound for \(\mathbf {MAC}\).
Proof
The nontrivial cases of A0 and A1 are presented in the long version of the paper [8]. and the axioms A2, A3 and A4 follow immediately from the semantics.
Given its correspondence to axiomatizations of modal logic and adequacy for proving small equivalences, we conjecture that \(\mathfrak {MAC}\) is complete for the given semantics.
5 Expressivity
In this section we show that the modal aleatoric calculus generalises the modal logic K. The syntax and semantics of modal logic are given over a set of atomic propositions Q. The syntax of \(\mathrm {K}_n\) is given by:
where \(q\in Q\), and the operators are respectively and, not, necessary. The semantics of \(\mathrm {K}_n\) are given with respect to an epistemic model \(M = (W,R,V)\) where W is the nonempty, countable set of possible worlds, \(R\subseteq W\times W\) is the accessibility relation, and \(V:Q\longrightarrow 2^W\) is an assignment of propositions to states. We require that:
We describe the set of worlds \(\Vert \alpha \Vert ^M\) in the model \(M = (W,R,V)\) that satisfy the formula \(\alpha \) by induction as follows:
where \(\forall u\in W\), \(uR^\alpha = u^R\cap \Vert \alpha \Vert ^M\), if \(uR^\alpha \cap \Vert \alpha \Vert ^M\ne \emptyset \) and \(uR^\alpha = uR\), otherwise.
We say \(\mathbf {MAC}\) generalises K if there is some map \(\varLambda \) from pointed epistemic models to pointed probability models, and some map \(\lambda \) from K formulae to \(\mathbf {MAC}\) formulae such that for all pointed epistemic models \(M_w\), for all K formulae \(\phi \), \(w\in \Vert \phi \Vert ^M\) if and only if \(\varLambda (M_w)(\lambda (\phi )) = 1\).
We suppose that for every atomic proposition \(q\in Q\), there is a unique atomic variable \(x_q\in X\). Then the map \(\varLambda \) is defined as follows: Given \(M = (W,R,V)\) and \(w\in W\), \(\varLambda (M_w) = P_w\) where \(P = (W,\pi ,f)\) and
-
\(\forall u,v\in W\), \(\pi _i(u,v)>0\) if and only if \(v\in uR\)Footnote 1.
-
\(\forall w\in W\), \(\forall q\in Q\), \(f_w(x_q)=1\) if \(w\in V(q)\) and \(f_w(x_q) = 0\) otherwise.
This transformation replaces the atomic propositions with variables that, at each world, are either always true or always false, and replaces the accessibility relation at a world w with a probability distribution that is non-zero for precisely the worlds accessible from w. It is clear that there is a valid probability model that satisfies these properties.
We also define the map \(\lambda \) from K to \(\mathbf {MAC}\) with the following induction:
Lemma 8
For all epistemic models \(M = (W,R,V)\), for all \(w\in W\), for all K formula \(\phi \), we have \(w\in \Vert \phi \Vert ^M\) if and only if \(\varLambda (M_w)(\lambda (\phi )) = 1\).
The proof may be found in the long version of this paper [8].
6 Case Study
We present a case study using some simple actions in a dice game illustrating the potential for reasoning in AI applications. A simple version of the game pigFootnote 2 uses a four sided dice, and players take turns. Each turn, the player rolls the dice as many times as they like, adding the numbers the roll to their turn total. However, if they roll a 1, their turn total is set to 0, and their turn ends. They can elect to stop at any time, in which case their turn total is added to their score.
To illustrate the aleatoric calculus we suppose that for our dice we have two random variables, odd and gt2 (greater than 2). Every roll of the dice can be seen as a sampling of these two variables: 1 is an odd number not greater than 2, and so on. Now we suppose that there is some uncertainty to the fairness of the dice, so it is possible that there is a 70% chance of the dice rolling a number greater than 2. However, we consider this unlikely and only attach a 10% likelihood to this scenario. Finally, we suppose there is an additional random variable called risk which can be used to define a policy. For example, we might roll again if the risk variable is sampled as true. This scenario if visualised in Fig. 2, and the formalization of relevant properties is given in Fig. 3.
These formulas show the different types of information that can be represented: bust and four are true random variables (aleatoric information), whereas ifBust and if-4-1 are based on an agent’s mental model (Bayesian information). Finally roll describes the condition for a policy to roll again. In a dynamic extension of this calculus, given prior assumptions about policies, agents may apply Bayesian conditioning to learn probability distributions from observations.
7 Conclusion
The modal aleatoric calculus is shown to be a true generalisation of modal logic, but gives a much richer language that encapsulates probabilistic reasoning and degrees of belief. We have shown that the modal aleatoric calculus is able to describe probabilistic strategies for agents. We have provided a sound axiomatization for the calculus, shown it is complete for the aleatoric calculus and we are working to show that the axiomatization is complete for the modal aleatoric calculus. Future work will consider dynamic variations of the logic, where agents apply Bayesian conditioning based on their observations to learn the probability distribution of worlds.
Notes
- 1.
We note this function is not deterministic, but this does not impact the final result.
- 2.
https://en.wikipedia.org/wiki/Pig_(dice_game).
References
Baltag, A., Smets, S.: Group belief dynamics under iterated revision: fixed points and cycles of joint upgrades. In: Proceedings of 12th TARK, pp. 41–50 (2009)
Bovens, L., Hartmann, S.: Bayesian Epistemology. Oxford University Press, Oxford (2003)
Cohen, W.W., Yang, F., Mazaitis, K.R.: TensorLog: deep learning meets probabilistic DBs. arXiv preprint arXiv:1707.05390 (2017)
De Finetti, B.: Theory of Probability: A Critical Introductory Treatment. Wiley, Chichester (1970)
van Ditmarsch, H., van der Hoek, W., Kooi, B.: Dynamic Epistemic Logic. Synthese Library, vol. 337. Springer, Dordrecht (2007)
Fagin, R., Halpern, J.Y., Megiddo, N.: A logic for reasoning about probabilities. Inf. Comput. 87(1–2), 78–128 (1990)
Feldman, Y.A., Harel, D.: A probabilistic dynamic logic. In: Proceedings of the Fourteenth Annual ACM Symposium on Theory of Computing, pp. 181–195 (1982)
French, T., Gozzard, A., Reynolds, M.: A modal aleatoric calculus for probabalistic reasoning: extended version (2019). http://arxiv.org/abs/1812.11741
Hailperin, T.: Boole’s Logic and Probability: A Critical Exposition from the Standpoint of Contemporary Algebra, Logic and Probability Theory. North-Holland Pub. Co., Amsterdam (1976)
Halpern, J.Y.: Reasoning About Uncertainty. MIT Press, Cambridge (2017)
Hintikka, J.: Knowledge and Belief. Cornell University Press, Ithaca (1962)
Hommersom, A., Lucas, P.J.: Generalising the interaction rules in probabilistic logic. In: 22nd International Joint Conference on Artificial Intelligence (2011)
Kooi, B.P.: Probabilistic dynamic epistemic logic. J. Log. Lang. Inf. 12(4), 381–408 (2003)
Kozen, D.: A probabilistic PDL. J. Comput. Syst. Sci. 30(2), 162–178 (1985)
Milne, P.: Bruno de Finetti and the logic of conditional events. Br. J. Philos. Sci. 48(2), 195–232 (1997)
Nilsson, N.J.: Probabilistic logic. Artif. Intell. 28(1), 71–87 (1986)
Stalnaker, R.C., Thomason, R.H.: A semantic analysis of conditional logic 1. Theoria 36(1), 23–42 (1970)
Williamson, J.: From Bayesian epistemology to inductive logic. J. Appl. Log. 11(4), 468–486 (2013)
Zadeh, L.A.: Fuzzy sets. In: Fuzzy Sets, Fuzzy Logic, And Fuzzy Systems: Selected Papers by Lotfi A Zadeh, pp. 394–432. World Scientific (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
French, T., Gozzard, A., Reynolds, M. (2019). A Modal Aleatoric Calculus for Probabilistic Reasoning. In: Khan, M., Manuel, A. (eds) Logic and Its Applications. ICLA 2019. Lecture Notes in Computer Science(), vol 11600. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-58771-3_6
Download citation
DOI: https://doi.org/10.1007/978-3-662-58771-3_6
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-58770-6
Online ISBN: 978-3-662-58771-3
eBook Packages: Computer ScienceComputer Science (R0)






 (resp.
(resp.  )
) , where for some
, where for some  if and only if
if and only if 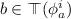 and
and  if and only if
if and only if  .
. and
and 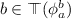
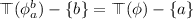 ,
, .
.
