Simulation of Piezoelectric Sensor and Actuator Devices

Abstract

In this chapter, we will study the fundamentals of the FE method, which are important for simulating the behavior of piezoelectric sensors and actuators. The focus lies on linear FE simulations. Section 4.1 deals with the basic steps of the FE method, e.g., Galerkin?s method. Subsequently, the FE method will be applied to electrostatics (see Sect. 4.2), the mechanical field (see Sect. 4.3), and the acoustic field (see Sect. 4.4). At the end, we will discuss the coupling of different physical fields because this represents a decisive step for reliable FE simulations of piezoelectric sensors and actuators. For a better understanding, the chapter also contains several simulation examples.

Nowadays, computer simulations play a key role in the design, optimization, and characterization of piezoelectric sensor and actuator devices. The primary reason for this lies in the fact that simulations as an important step in computer-aided engineering (CAE) allow to predict the device behavior without fabricating expensive prototypes. Consequently, we can accelerate the device design, which goes hand in hand with reduced development costs and a reduced time to market. Simulations allow, furthermore, to determine quantities (e.g., inside a material), which cannot be measured at reasonable expense.

There exist various approaches for simulations of technical devices. The most important are finite difference methods [17], finite element methods [27], boundary element methods [4] as well as approaches that are based on lumped circuit elements (see Sect. 7.5) [15]. Hereafter, we will exclusively concentrate on the finite element (FE) method because this method is very well suited for numerical simulation of piezoelectric sensor and actuator devices. The main advantages of the FE method are listed below [14].

• Numerical efficiency: The FE method yields sparsely populated and symmetric matrices for the resulting algebraic system of equations. Hence, the storage and solution of the algebraic system of equations can be conducted in an efficient way.

• Complex geometry: We are able to discretize complex two-dimensional and three-dimensional computational domains with the aid of appropriate finite elements, e.g., triangles and tetrahedron elements.

• Analysis possibilities: The FE method can be used for static, transient, harmonic, and eigenfrequency analysis of the investigated problem.

However, the FE method also exhibits certain disadvantages. For instance, the FE method may lead to a considerable discretization effort, especially for large computational domains. Another inherent disadvantage is that each computational domain has to be spatially bounded. If an open domain is required for the numerical simulation (e.g., free-field radiation of an ultrasonic transducer), we will need special techniques such as absorbing boundary conditions.

One can choose from a large number of FE software packages (FE solvers), which are commercially available. The software packages ANSYS [1], COMSOL Multiphysics [6], NACS [22], and PZFlex [19] are some well-known representatives. They differ in the supported physical fields as well as in the coupling of these fields.

In this chapter, we will study the fundamentals of the FE method, which are important for simulating the behavior of piezoelectric sensors and actuators. The focus lies on linear FE simulations. Section 4.1 deals with the basic steps of the FE method, e.g., Galerkin’s method. Subsequently, the FE method will be applied to electrostatics (see Sect. 4.2), the mechanical field (see Sect. 4.3), and the acoustic field (see Sect. 4.4). At the end, we will discuss the coupling of different physical fields because this represents a decisive step for reliable FE simulations of piezoelectric sensors and actuators. For a better understanding, the chapter also contains several simulation examples. Further literature concerning the FE method can be found in [3, 12, 14, 20, 23, 27].

4.1 Basic Steps of Finite Element Method

Figure 4.1 illustrates the basic steps of the FE method. The starting point are always partial differential equations (PDEs) for the physical fields within the investigated technical problem, e.g., the physical fields that are involved in the piezoelectric sensor and actuator. In a next step, this so-called strong formulation of the PDE gets multiplied by an appropriate test function, which yields a variational form. After partial integration (integration by parts) of the resulting product over the whole computational domain, we obtain the so-called weak formulation of the PDE. In the final step, we apply Galerkin’s method by approximating both the aimed quantity and the test function with finite elements. This leads to an algebraic system of equations.

Fig. 4.1

Basic step of FE method

In the following subsection, we will detail the basic steps of the FE method for a one-dimensional PDE. Section 4.1.2 treats spatial discretization of computational domains and efficient computation. In Sect. 4.1.3, the difference between Lagrange and Legendre ansatz functions will be discussed. Finally, we introduce an appropriate scheme for time discretization, which is important for transient FE simulations.

4.1.1 Finite Element Method for a One-Dimensional Problem

In order to demonstrate the idea of the FE method, let us consider a one-dimensional (1-D) hyperbolic partial differential equation. Such partial different equation commonly occurs for mechanical problems. It comprises derivations with respect to time as well as to space. The starting point of the FE method is the strong formulation of the PDE

$$\begin{aligned} -\frac{\partial ^2 u \!\left( x,t \right) }{\partial x ^2} + c \frac{\partial ^2 u \!\left( x,t \right) }{\partial t ^2}&= f\!\left( x,t \right) \;. \end{aligned}$$

(4.1)

Here, the expression $u\!\left( x,t \right)$ represents the aimed quantity (e.g., mechanical displacement) depending on both space x and time t. The term c stands for a constant, and $f\!\left( x,t \right)$ is a known excitation (source) term that varies with space and time. In addition to (4.1), boundary and initial conditions are required to uniquely solve the hyperbolic PDE. For the spatial computational domain $x\in \!\left[ a,b \right]$ and the investigated time interval $t\in \!\left[ 0,T \right]$, appropriate conditions are

$u_{a}$ and $u_{b}$ refer to constant boundary conditions for the aimed quantity $u\!\left( x,t \right)$, which have to be fulfilled at any time. Oftentimes, these conditions are called Dirichlet boundary conditions. In case of $u_{a}=0$, we have a homogeneous and, otherwise, i.e., $u_{a}\ne 0$, an inhomogeneous Dirichlet boundary conditions. Apart from such boundary conditions, homogeneous or inhomogeneous Neumann boundary conditions can be specified defining the first-order derivative $\partial u / \partial x$ with respect to space at the boundary of the spatial computational domain. The initial conditions $u_0\!\left( x \right)$, $\dot{u}_0\!\left( x \right)$, and $\ddot{u}_0\!\left( x \right)$ indicate $u\!\left( x,t \right)$, its first-order and second-order derivate with respect to time at $t=0$ in the spatial computational domain $x\in \!\left[ a,b \right]$.

To achieve a clearly arranged form of partial differential equations in strong formulation including boundary conditions (BC) as well as initial conditions (IC), we introduce a compact scheme, which is also used later on. For the 1-D hyperbolic PDE, this scheme reads as

Weak Formulation of the PDE

A fundamental step of the FE method is to transform the PDE from its strong formulation into the weak formulation. Thereby, we multiply the original PDE with an arbitrary test function $w\!\left( x \right)$ and integrate the resulting product over the whole spatial computational domain. The test function has to fulfill only two criteria: (i) $w\!\left( x \right)$ vanishes at Dirichlet boundaries and (ii) the first-order derivative of $w\!\left( x \right)$ with respect to space exists in the weak sense. For the hyperbolic PDE in (4.1), the multiplication by the test function $w\!\left( x \right)$ and integration over the spatial computational domain $x\in \!\left[ a,b \right]$ results in

$$\begin{aligned} \int \limits _{a}^{b} w\!\left( x \right) \!\left[ -\frac{\partial ^2 u \!\left( x,t \right) }{\partial x ^2} + c \frac{\partial ^2 u \!\left( x,t \right) }{\partial t ^2} - f\!\left( x,t \right) \right] \mathrm {d}x = 0\;. \end{aligned}$$

(4.2)

The first term can be simplified by means of partial integration, which has to be replaced for higher dimensional PDEs with Green’s first integration theorem

$$\begin{aligned} \int \limits _{a}^{b} w\!\left( x \right) \frac{\partial ^2 u\!\left( x,t \right) }{\partial x ^2} \mathrm {d}x = \left. \!\left[ w\!\left( x \right) \frac{\partial u\!\left( x,t \right) }{\partial x} \right] \right| _{a}^{b} - \int \limits _{a}^{b}\frac{\partial w\!\left( x \right) }{\partial x} \frac{\partial u\!\left( x,t \right) }{\partial x} \mathrm {d}x \;. \end{aligned}$$

(4.3)

Since the test function $w\!\left( x \right)$ vanishes at Dirichlet boundaries (i.e., $w\!\left( a \right) =w\!\left( b \right) =0$), the weak formulation of (4.1) finally becomes

$$\begin{aligned} \int \limits _{a}^{b} \!\left[ \frac{\partial w\!\left( x \right) }{\partial x} \frac{\partial u\!\left( x,t \right) }{\partial x} + c w \!\left( x \right) \frac{\partial ^2 u \!\left( x,t \right) }{\partial t ^2} \right] \mathrm {d}x = \int \limits _{a}^{b} w\!\left( x \right) f\!\left( x \right) \mathrm {d}x \;. \end{aligned}$$

(4.4)

In contrast to the strong formulation, the dimension of the spatial derivative of the aimed quantity $u\!\left( x,t \right)$ has been reduced by one. As the weak formulation incorporates Neumann boundary conditions $\partial u\!\left( x,t \right) / \partial x$, they are called natural conditions. Dirichlet boundary conditions demand additional consideration in further steps of the FE method and are, therefore, frequently referred to as essential conditions.

Galerkin’s Method

Within Galerkin’s Method, the spatial computational domain is subdivided into cells, the so-called finite elements. In case of the studied 1-D hyperbolic PDE, we divide the domain $\left[ a,b \right]$ into M sufficiently small intervals $\left[ x_{i-1},x_i \right] ~\forall ~i=1,\ldots ,M$ where each interval border $x_{i}$ is a node. The chosen intervals have to satisfy the properties:

• Ascending order of node positions, i.e., $x_{i-1}<x_{i}~\forall ~i=1,\ldots , M$.

• Computational domain is completely covered, i.e., $\left[ a,b \right] =\bigcup \limits _{i=1}^{M} \!\left[ x_{i-1},x_{i} \right]$.

• No intersection of intervals, i.e., $\left[ x_{i-1},x_{i} \right] \cap \!\left[ x_{j-1},x_j \right] =0~\forall ~i\ne j$.

Without limiting the generality, the 1-D computational domain can be equidistantly discretized yielding the node positions (interval width h)

$$\begin{aligned} x_{i}=a+ih~\forall ~i=0,\ldots , M \qquad \text {with}~h=\frac{b-a}{M} \;. \end{aligned}$$

(4.5)

Based on the spatial discretization of the computational domain, we subsequently approximate both the aimed quantity $u\!\left( x,t \right)$ and the test function $w\!\left( x \right)$. Since, here, only the spatial properties of $u\!\left( x,t \right)$ are investigated, the dependency on time t is omitted.

Spatial approximation in the FE method is conducted with a linear combination of ansatz functions¹ featuring local support. For the 1-D problem, each of these ansatz functions is just different from zero in the interval $\left[ x_{i-1},x_{i+1} \right]$. Due to the fact that the weak formulation contains solely spatial derivatives up to one, several types of ansatz functions are suitable. For the sake of simplicity, let us choose piecewise linear hat functions $N_i \!\left( x \right)$ defined as (see Fig. 4.2)

$$\begin{aligned} N_{i} \!\left( x \right) = {\left\{ \begin{array}{ll} 0 &{} \quad \mathrm {for} \quad x_{0} \le x \le x_{i-1} \\ \dfrac{x-x_{i-1}}{h} &{} \quad \mathrm {for} \quad x_{i-1}< x \le x_{i} \\ \dfrac{x_{i+1}-x}{h} &{} \quad \mathrm {for} \quad x_{i}< x \le x_{i+1} \\ 0 &{} \quad \mathrm {for} \quad x_{i+1} < x \le x_{M} \end{array}\right. } \end{aligned}$$

(4.6)

for $i=1,\ldots ,M-1$. The functions $N_0 \!\left( x \right)$ and $N_M \!\left( x \right)$ at the boundary of the computational domain are defined in a similar manner.

Fig. 4.2

Piecewise linear hat functions $N_{i} \!\left( x \right)$ utilized to approximate aimed quantity of considered 1-D hyperbolic PDE ($x_0=a$ and $x_M=b$)

The linear hat functions fulfill the required properties $N_{i}\!\left( x_{j} \right) =1~\forall ~i=j$ and $N_{i}\!\left( x_{j} \right) =0~\forall ~i\ne j$. By means of these functions, the approximations $\mathsf {u}\!\left( x \right)$ and $\mathsf {w}\!\left( x \right)$ of $u\!\left( x \right)$ and $w\!\left( x \right)$, respectively, are given by

$$\begin{aligned} u\!\left( x \right) \approx \mathsf {u} \!\left( x \right)&= \sum \limits _{i=1}^{M-1} N_{i} \!\left( x \right) \mathsf {u}_{i} + N_0 \!\left( x \right) u_{a} + N_{M} \!\left( x \right) u_{b} \end{aligned}$$

(4.7)

$$\begin{aligned} w\!\left( x \right) \approx \mathsf {w} \!\left( x \right)&= \sum \limits _{i=1}^{M-1} N_{i}\!\left( x \right) \mathsf {w}_{i} \end{aligned}$$

(4.8)

where $\mathsf {u}_i=\mathsf {u}\!\left( x_i \right)$ and $\mathsf {w}_i=\mathsf {w}\!\left( x_i \right)$ represent approximated values at node $x_i$. Note that between two neighboring nodes, the approximation of $u\!\left( x \right)$ and $w\!\left( x \right)$ depends on the chosen ansatz functions. In the particular case, the interim values are evaluated according to linear equations. However, because we are able to apply ansatz functions of higher order (see Sect. 4.1.3), the approximation can be performed more precisely.

Inserting (4.7) and (4.8) in the weak formulation (4.4) of the PDE leads to the terms (argument x omitted)

$$\begin{aligned} \int \limits _{a}^{b} \frac{\partial w}{\partial x} \frac{\partial u}{\partial x} \mathrm {d}x&= \int \limits _{a}^{b} \frac{\partial }{\partial x} \!\left[ \sum \limits _{i=1}^{M-1} N_i \mathsf {w}_i \right] \frac{\partial }{\partial x} \!\left[ \sum \limits _{j=1}^{M-1} N_j\mathsf {u}_j + N_0 u_a + N_M u_b \right] \mathrm {d}x \nonumber \\&= \sum \limits _{i=1}^{M-1} \mathsf {w}_i \left\{ \sum \limits _{j=1}^{M-1} \mathsf {u}_j \int \limits _{a}^{b} \frac{\partial N_i}{\partial x} \frac{\partial N_j }{\partial x} \mathrm {d}x \right. \nonumber \\&\left. \quad \quad \quad \quad + \int \limits _{a}^{b} \frac{\partial N_i}{\partial x} \!\left[ \frac{\partial N_0}{\partial x} u_a + \frac{\partial N_M}{\partial x} u_b \right] \mathrm {d}x \right\} \end{aligned}$$

(4.9)

$$\begin{aligned} \int \limits _{a}^{b} c w \frac{\partial ^2 u}{\partial t ^2} \mathrm {d}x&=\int \limits _{a}^{b} c \!\left[ \sum \limits _{i=1}^{M-1} N_i \mathsf {w}_i \right] \!\left[ \sum \limits _{j=1}^{M-1} N_j \frac{\partial ^2 \mathsf {u}_j}{\partial t ^2} \right] \mathrm {d}x \nonumber \\&= \sum \limits _{i=1}^{M-1} \mathsf {w}_i \!\left\{ \sum \limits _{j=1}^{M-1} \frac{\partial ^2 \mathsf {u}_j}{\partial t ^2} \int \limits _{a}^{b} c N_i N_j \mathrm {d}x \right\} \end{aligned}$$

(4.10)

$$\begin{aligned} \int \limits _{a}^{b} w f \mathrm {d}x&= \int \limits _{a}^{b} \!\left[ \sum \limits _{i=1}^{M-1} N_i \mathsf {w}_i \right] f \mathrm {d}x = \sum \limits _{i=1}^{M-1} \mathsf {w}_i \!\left\{ \int \limits _{a}^{b} N_i f \mathrm {d}x \right\} \;. \end{aligned}$$

(4.11)

Thereby, integrals and sums were interchanged which is possible since $\mathsf {u}_j$ and $\mathsf {w}_i$ are constants and, therefore, do not depend on space. We may also omit sums over the approximated test function (i.e., $\sum _{i=1}^{M-1}\mathsf {w}_i$) due to the fact that $w\!\left( x \right)$ can be chosen almost arbitrarily and these sums appear identical in all terms. As a result, the expressions in the bracket $\left\{ \bullet \right\}$ exclusively remain from (4.9)–(4.11). By additionally introducing the matrix and vector components

$$\begin{aligned} \mathsf {M}_{ij} =&\int \limits _{a}^{b} c N_i \!\left( x \right) N_j \!\left( x \right) \mathrm {d}x \end{aligned}$$

(4.12)

$$\begin{aligned} \mathsf {K}_{ij} =&\int \limits _{a}^{b} \frac{\partial N_i \!\left( x \right) }{\partial x} \frac{\partial N_j \!\left( x \right) }{\partial x} \mathrm {d}x \end{aligned}$$

(4.13)

$$\begin{aligned} \mathsf {f}_i =&\int \limits _{a}^{b} N_{i} (x) f \mathrm {d}x - \int \limits _{a}^{b} \frac{\partial N_i \!\left( x \right) }{\partial x} \!\left[ \frac{\partial N_0 \!\left( x \right) }{\partial x} u_a + \frac{\partial N_M \!\left( x \right) }{\partial x} u_b \right] \mathrm {d}x\,, \end{aligned}$$

(4.14)

one is able to rewrite the resulting algebraic system of equations in matrix form (second-order time derivative $\ddot{\varvec{\mathsf {u}}}=\partial ^2 \varvec{\mathsf {u}} / \partial t^2$)

$$\begin{aligned} \varvec{\mathsf {M}} \ddot{\varvec{\mathsf {u}}} + \varvec{\mathsf {K}} \varvec{\mathsf {u}} = \varvec{\mathsf {f}} \;, \end{aligned}$$

(4.15)

which is still continuous in time. Herein, $\varvec{\mathsf {M}}$ and $\varvec{\mathsf {K}}$, both of dimension $(M-1)\times (M-1)$, stand for the mass matrix and stiffness matrix, respectively. Since the ansatz functions feature local support, the matrices are sparsely populated. The vector $\varvec{\mathsf {f}}$ with length $M-1$ is the right-hand side of the algebraic system of equations. The solution of (4.15) provides the vector $\varvec{\mathsf {u}}=\!\left[ \mathsf {u}_1,\mathsf {u}_2,\ldots ,\mathsf {u}_{M-1} \right] ^\mathrm {t}$ with length $M-1$ containing approximated results of the aimed quantity $u\!\left( x_{i} \right)$ for every node $x_{i}$.

4.1.2 Spatial Discretization and Efficient Computation

Usually, one has to deal with two-dimensional (2-D) and three-dimensional (3-D) problems in practice, e.g., numerical simulations for sensors and actuators. Thus, the spatial computational domain $\varOmega$ cannot be subdivided into line intervals but demands alternative finite elements in $\mathbb {R}^2$ and $\mathbb {R}^3$. In the same manner as the line intervals for 1-D problems, the finite elements have to satisfy the properties (i) complete covering of the computational domain and (ii) no intersection of elements. Figure 4.3 shows appropriate finite elements for 2-D (triangular and quadrilateral elements) and 3-D (tetrahedron and hexahedron elements) spaces. Due to local support of the ansatz functions on the nodes within the elements, they are frequently referred to as nodal (Lagrangian) finite elements.²

Fig. 4.3

Finite elements to spatially discretize 2-D and 3-D computational domains $\varOmega$: a triangular element for $\mathbb {R}^2$; b quadrilateral element for $\mathbb {R}^2$; c tetrahedron element for $\mathbb {R}^3$; d hexahedron element for $\mathbb {R}^3$; e spatial discretization (also denoted as mesh or computational grid) of a 2-D computational domain by means of triangles

With a view to assembling $\varvec{\mathsf {f}}$, $\varvec{\mathsf {M}}$, and $\varvec{\mathsf {K}}$ of the algebraic system of equations (4.15), we have to calculate spatial derivatives of the ansatz functions and integrals over the subdomain of a finite element (see, e.g., (4.12)). Especially for fine spatial discretizations in 3-D problems, this procedure provokes remarkable computational effort. To optimize the assembly, the so-called parent elements are introduced which exhibit uniform geometric dimensions. The parent elements are defined in a local coordinate system (see Fig. 4.4). For such elements, we are able to efficiently evaluate both, spatial derivatives of ansatz functions and their numerical integrations. By means of a unique transform, the parent element defined in local coordinates gets subsequently transformed into global coordinates of the spatial computational domain $\varOmega$. After assembling the equations for all finite elements to global system matrices, the resulting algebraic system of equations in (4.15) can finally be efficiently solved with problem-specific algebraic methods, e.g., multigrid methods [5, 14].

Fig. 4.4

a Original finite element and parent element for 1-D; global coordinate x; local coordinate $\xi$; b original quadrilateral finite element and parent element for 2-D; global coordinate system $\left( x,y \right)$; local coordinate system $\left( \xi ,\eta \right)$

4.1.3 Ansatz Functions

As a matter of principle, FE simulations require ansatz functions featuring local support. This means that each ansatz function has to be just different from zero in the considered finite element and in the immediately neighboring ones. Lagrange and Legendre ansatz functions provide local support, and therefore, they are applicable for the FE method [2, 11, 14]. In the following, let us take a closer look at these most important categories of ansatz functions.

Lagrange Ansatz Functions

Lagrange ansatz functions are widely utilized for FE simulations in all sectors of engineering. The underlying procedure is commonly referred to as h-version of the FE method or in abbreviated form h-FEM. For the 1-D case (see Sect. 4.1.1), the Lagrange ansatz function $N_i^{p_{\mathrm {d}}} \!\left( \xi \right)$ for node i is defined as

$$\begin{aligned} N_i^{p_{\mathrm {d}}} \!\left( \xi \right) = \prod _{\begin{array}{c} j = 1 \\ j \ne i \end{array}}^{p_{\mathrm {d}}+1} \frac{\xi -\xi _j}{\xi _i - \xi _j} \end{aligned}$$

(4.16)

leading to $N_i^{p_{\mathrm {d}}} \!\left( \xi _i \right) = 1$. Here, $p_{\mathrm {d}}$ stands for the order (i.e., polynomial degree) of the Lagrange polynomial and $\xi _{i}$ is the position of the ith node within the finite element. As (4.16) shows, each node has its own ansatz function. If we assume 1-D parent elements (see Fig. 4.4a) ranging from $-1$ to 1 and nodes that are equally distributed, the node positions will result in

$$\begin{aligned} \xi _i = -1 + \frac{2\!\left( i-1 \right) }{p_{\mathrm {d}}}\qquad i=1,\ldots ,p_{\mathrm {d}}+1 \;. \end{aligned}$$

(4.17)

Thus, the number of nodes $n_{\mathrm {nodes}}=p_{\mathrm {d}}+1$ within a single finite element increases for increasing order of the Lagrange polynomial. Moreover, the relation

$$\begin{aligned} \sum \limits _{i=1}^{p_{\mathrm {d}}+1} N_i^{p_{\mathrm {d}}} \!\left( \xi \right) =1 \quad \forall ~ \xi \in \!\left[ -1,1 \right] \;. \end{aligned}$$

(4.18)

holds which means, in other words, that the complete set of ansatz functions is needed to compute the aimed quantity between the nodes. Table 4.1 contains the resulting Lagrange ansatz functions $N_i^{p_{\mathrm {d}}} \!\left( \xi \right)$ and the node positions $\xi _{i}$ for $p_{\mathrm {d}}=1$ as well as $p_{\mathrm {d}}=2$. Figure 4.5 displays the ansatz function up to $p_{\mathrm {d}}=3$.

Table 4.1 Lagrange ansatz functions $N_i^{p_{\mathrm {d}}} \!\left( \xi \right)$ and node positions $\xi _i$ for polynomial degree 1 and 2 in case of 1-D parents elements, i.e., $\xi \in \!\left[ -1,1 \right]$

Fig. 4.5

Lagrange and Legendre ansatz functions $N_i^{p_{\mathrm {d}}} \!\left( \xi \right)$ for 1-D up to polynomial degree $p_{\mathrm {d}}=3$ and node positions $\xi _i$ within parent element $\xi \in \!\left[ -1,1 \right]$

By means of increasing order $p_{\mathrm {d}}$ in h-FEM, we can choose coarser spatial discretization for the computational domain without losing precision in simulations. In doing so, the total number of finite elements $n_{\mathrm {elem}}$ is reduced and one would expect remarkably reduced computational effort. However, due to additional nodes within the finite elements for $p_{\mathrm {d}}>1$, the number of unknown quantities for each element becomes larger which has to be considered in the view of computation time.

Legendre Ansatz Functions

FE simulations utilizing Legendre ansatz functions are oftentimes called p-version of the FE method (p-FEM). The Legendre ansatz functions $N_i^{p_{\mathrm {d}}}\!\left( \xi \right)$ for a parent element ($\xi \in \!\left[ -1,1 \right]$; see Fig. 4.4) are defined as

$$\begin{aligned} N_1^{p_{\mathrm {d}}}\!\left( \xi \right)&=\frac{1-\xi }{2} \qquad N_2^{p_{\mathrm {d}}} \!\left( \xi \right) = \frac{1+\xi }{2} \end{aligned}$$

(4.19)

$$\begin{aligned} N_i^{p_{\mathrm {d}}}\!\left( \xi \right)&=\phi _{i-1} \!\left( \xi \right) \quad \forall ~ i=3,\ldots ,p_{\mathrm {d}}+1\;. \end{aligned}$$

(4.20)

The expression $\phi _{i}\!\left( \xi \right)$ represents the integrated Legendre polynomial $L_i$ and results from

$$\begin{aligned} \phi _i \!\left( \xi \right)&= \int \limits _{-1}^{\xi } L_{i-1} \!\left( x \right) \mathrm {d}x \end{aligned}$$

(4.21)

$$\begin{aligned} L_i \!\left( x \right)&= \frac{1}{2^i !} \frac{\partial ^i}{\partial x^i} \!\left( x^2-1 \right) ^i \;. \end{aligned}$$

(4.22)

Similar to Lagrange ansatz functions, the amount of Legendre ansatz functions rises for increasing polynomial degree $p_{\mathrm {d}}$. The ansatz functions of lower order remain, however, unchanged which means that the set of ansatz functions for $p_{\mathrm {d}}+1$ includes all ansatz functions of order $p_{\mathrm {d}}$. On account of this fact, they are also named hierarchical ansatz functions.

There are various benefits of p-FEM over h-FEM. For instance, we can use different orders of ansatz functions in p-FEM for neighboring finite elements. Besides, the polynomial degree $p_{\mathrm {d}}$ may be altered in different spatial directions for 2-D and 3-D simulations, which is especially useful to avoid the so-called locking effects in FE simulations for thin mechanical structures (e.g., cantilevers). In case of equal polynomial degrees in different spatial directions, the simulation procedure is referred to as isotropic p-FEM and otherwise anisotropic p-FEM.

The accuracy of numerical simulations in p-FEM is basically achieved by increasing $p_{\mathrm {d}}$ instead of choosing a finer computational grid. As a result, p-FEM requires a less amount of nodes to spatially discretize the computational domain than h-FEM. Nevertheless, we have to handle an increasing number of unknowns for the nodes since each ansatz function is weighted individually. Furthermore, p-FEM will only make sense if the investigated geometry allows a coarse computational grid. Despite these shortcomings, the targeted use of p-FEM leads to strongly reduced calculation times for smooth and high-frequency problems, e.g., numerical simulation of high-frequency fields in simply shaped mechanical structures.

4.1.4 Time Discretization

Up to now, we have treated solely the dependence on space for the FE method. However, one is mainly concerned with physical processes depending also on time. In order to incorporate time in the FE procedure, an appropriate time discretization is required. Let us discuss the fundamentals of time discretization for the 1-D hyperbolic PDE (4.1). Similar to 1-D space discretization, the investigated time interval $\left[ 0,T \right]$ is subdivided into N sufficiently small subintervals (time step $t_{i}$)

$$\begin{aligned} \!\left[ 0,T \right] =\bigcup \limits _{i=1}^{N} \!\left[ t_{i-1},t_{i} \right] ~\qquad \text {with}~0<t_1<t_2<\ldots<t_{N-1}<t_{N}=T \;. \end{aligned}$$

(4.23)

Without limiting the generality, we may assume equidistant time sampling, i.e., a constant time step size $\varDelta t$ given by

$$\begin{aligned} \varDelta t = t_{i} - t_{i-1} = \frac{T}{N} \;. \end{aligned}$$

(4.24)

The evaluation of the time discretization within the FE method is prevalently performed according to the so-called Newmark scheme [12, 14]. For the spatially discretized hyperbolic PDE in matrix form (4.15), the Newmark scheme contains three substeps, which are briefly explained below. To achieve compact expressions, we use the nomenclature

$$\begin{aligned} \varvec{\mathsf {u}}\!\left( t_{i} \right) =\!\left[ \mathsf {u}_1\!\left( t_{i} \right) ,\ldots ,\mathsf {u}_{M-1}\!\left( t_{i} \right) \right] ^\mathrm {t}=\varvec{\mathsf {u}}^{(i)}=\!\left[ \mathsf {u}_{1}^{(i)},\ldots ,\mathsf {u}_{M-1}^{(i)} \right] ^\mathrm {t}\;. \end{aligned}$$

(4.25)

• 1. Compute predictor step: Starting from the known quantities $\varvec{\mathsf {u}}^{(i)}$, $\dot{\varvec{\mathsf {u}}}^{(i)}$, and $\ddot{\varvec{\mathsf {u}}}^{(i)}$ for time step $t_{i}$, the predicted values result from

  

  (4.26)
  

  (4.27)

• 2. Solve algebraic system of equations: The predicted value $\tilde{\varvec{\mathsf {u}}}$ is then utilized to pose an algebraic system of equations

  $$\begin{aligned} \varvec{\mathsf {M}}^{\star } \ddot{\varvec{\mathsf {u}}}^{(i+1)}&= \varvec{\mathsf {f}}^{(i+1)} - \varvec{\mathsf {K}}\tilde{\varvec{\mathsf {u}}} \end{aligned}$$

  (4.28)
  $$\begin{aligned} \varvec{\mathsf {M}}^{\star }&= \varvec{\mathsf {M}} + \beta _{\mathrm {N}} \!\left( \varDelta t \right) ^2 \varvec{\mathsf {K}} \;. \end{aligned}$$

  (4.29)

  Here, $\smash {\varvec{\mathsf {M}}^{\star }}$ represents the effective mass matrix.³ The solution of (4.28) yields $\smash {\ddot{\varvec{\mathsf {u}}}^{(i+1)}}$ for the subsequent time step $t_{i+1}$.

• 3. Perform corrector step: By means of $\ddot{\varvec{\mathsf {u}}}^{(i+1)}$, we are able to correct the predicted values $\tilde{\varvec{\mathsf {u}}}$ and

  

  (4.30)
  

  (4.31)

  As a result, $\smash {\varvec{\mathsf {u}}^{(i+1)}}$, $\smash {\dot{\varvec{\mathsf {u}}}^{(i+1)}}$ as well as $\smash {\ddot{\varvec{\mathsf {u}}}^{(i+1)}}$ are now known and the predicted values can be calculated for time step $t_{i+2}$.

The parameters $\beta _{\mathrm {N}}$ and $\gamma _{\mathrm {N}}$ determine the type of integration with respect to time and, moreover, the stability of the integration procedure. For example, $\beta _{\mathrm {N}}=0$ and $\gamma _{\mathrm {N}}=0.5$ yield an explicit time integration. $\beta _{\mathrm {N}}=0.25$ and $\gamma _{\mathrm {N}}=0.5$ result in an implicit time integration, which is unconditionally stable (A-stable) for all choices of time step sizes $\varDelta t$. Note that stability of the integration procedure is necessary but not sufficient for precise simulation results. In case of a rough time discretization, one is concerned with numerical dispersion yielding, e.g., distorted pulses for transient simulations. To avoid such numerical dispersions, the time step size has to be chosen sufficiently small. In summary, FE simulations incorporating time discretization provide an approximation of the aimed quantity with respect to both space and time.

4.2 Electrostatics

In order to apply the FE method to quasi-static electric or electrostatic fields (see Sect. 2.1.2), an appropriate PDE is required which results from the combination of (2.9, p. 10)–(2.11). The PDE reads as

$$\begin{aligned} -\nabla \cdot \varepsilon \nabla V_{\mathrm {e}} = q_{\mathrm {e}} \end{aligned}$$

(4.32)

where $\varepsilon$ is the electric permittivity, $V_{\mathrm {e}}$ the electric scalar potential, and $q_{\mathrm {e}}$ the volume charge density, respectively. In compact form, the strong formulation of the PDE in 3-D becomes (computational domain $\varOmega$)⁴

The term $\mathbf {n}$ indicates the normal vector with respect to the boundary $\partial \varOmega$ of $\varOmega$. Due to the fact that electrostatic fields do not depend on time, initial conditions are useless here. This also holds for quasi-static electric fields.

According to the first basic step of the FE method, the strong form (4.32) is transformed into weak form with a scalar test function $w\!\left( \mathbf {r} \right)$. After applying Green’s first integration theorem, the weak form results in

$$\begin{aligned} \int \limits _{\varOmega } \varepsilon \nabla w \cdot \nabla V_{\mathrm {e}} \mathrm {d}\varOmega - \int \limits _{\varOmega } w q_{\mathrm {e}} \mathrm {d}\varOmega = 0 \;. \end{aligned}$$

(4.33)

Spatial discretization (Galerkin’s method) of $w\!\left( \mathbf {r} \right)$ and $V_{\mathrm {e}}\!\left( \mathbf {r} \right)$ yields then the algebraic system of equations

$$\begin{aligned} \varvec{\mathsf {K}}_{V_{\mathrm {e}}} \varvec{\mathsf {v}}_{\mathrm {e}} = \varvec{\mathsf {f}}_{V_{\mathrm {e}}} \;. \end{aligned}$$

(4.34)

If we utilize Lagrange ansatz functions, the vector $\varvec{\mathsf {v}}_{\mathrm {e}}$ will contain the approximated values of $V_{\mathrm {e}}$ at the nodes of the spatially discretized computational domain $\varOmega$. The stiffness matrix $\varvec{\mathsf {K}}_{V_{\mathrm {e}}}$ and the right-hand side $\varvec{\mathsf {f}}_{V_{\mathrm {e}}}$ of (4.34) are given by (ansatz functions $N_i$)

$$\begin{aligned} \varvec{\mathsf {K}}_{V_{\mathrm {e}}}&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {K}}^l \; ; \qquad&\varvec{\mathsf {K}}^l&= \!\left[ \mathsf {k}_{ij}^l \right] \; ; \qquad&\mathsf {k}_{ij}^l&=\int \limits _{\varOmega ^l} \varepsilon \!\left( \nabla N_i \right) ^\mathrm {t}\nabla N_j \mathrm {d}\varOmega \end{aligned}$$

(4.35)

$$\begin{aligned} \varvec{\mathsf {f}}_{V_{\mathrm {e}}}&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {f}}^l \; ; \qquad&\varvec{\mathsf {f}}^l&= \!\left[ \mathsf {f}_{i}^l \right] \; ; \qquad&\mathsf {f}_{i}^l&=\int \limits _{\varOmega ^l} \nabla N_i q_{\mathrm {e}} \mathrm {d}\varOmega \;. \end{aligned}$$

(4.36)

$n_{\mathrm {elem}}$ stands for the number of finite elements (e.g., hexahedra in $\mathbb {R}^3$) used to spatially discretize $\varOmega$. For each finite element (index l), the element matrix $\varvec{\mathsf {K}}^l$ is composed of the components $\smash {\mathsf {k}_{ij}^l}$, which result from the integral over the element domain $\smash {\varOmega ^l}$. The same procedure is carried out to calculate the right-hand side $\varvec{\mathsf {f}}^l$. At this point, it should be emphasized that the dependence of $\varepsilon$ as well as of $q_{\mathrm {e}}$ on space has to be considered. Finally, $\varvec{\mathsf {K}}^l$ and $\varvec{\mathsf {f}}^l$ are fully assembled (assembling operator $\bigwedge$) for all elements leading to $\varvec{\mathsf {K}}_{V_{\mathrm {e}}}$ and $\varvec{\mathsf {f}}_{V_{\mathrm {e}}}$, respectively.

Example

Fig. 4.6

Two views showing geometric arrangement of rectangular plate capacitor with dielectric material between electrodes (relative permittivity $\varepsilon _{\mathrm {r}}$); drawings are not in scale

As a practical example for electrostatics, let us study a plate capacitor with two identical electrodes of rectangular shape, which are assumed to be infinitely thin. The dielectric medium between the electrodes exhibits the relative permittivity $\varepsilon _{\mathrm {plate}}=20$. Figure 4.6 displays the geometric arrangement in two views. By means of the plate length $l_{\mathrm {plate}}=10\,\mathrm{mm}$, the plate width $w_{\mathrm {plate}}=5\,\mathrm{mm}$, and the plate distance $d=1\,\mathrm{mm}$, we can analytically approximate the capacity value $C_{\mathrm {plate}}$ with (2.23, p. 13), which leads to

$$\begin{aligned} C_{\mathrm {plate}} = \frac{\varepsilon _{\mathrm {plate}} \, \varepsilon _0 \, l_{\mathrm {plate}} \,w_{\mathrm {plate}}}{d} = 8.854\,\mathrm{pF}\;. \end{aligned}$$

(4.37)

If one applies this simple analytical approximation, stray fields outside the electrodes will be neglected. Consequently, the approximated $C_{\mathrm {plate}}$ is too small. The impact of these stray fields on $C_{\mathrm {plate}}$ can be determined with the aid of the FE method for the 3-D case. In doing so, the computational domain $\varOmega$ has to contain a certain border area surrounding the plate capacitor (see Fig. 4.6) because the boundary condition $\partial V_{\mathrm {e}} / \partial \mathbf {n}$ implies field lines that are in parallel to the boundary $\partial \varOmega$. The border area is assumed to be air. Stray fields will not be formed in the simulation results when we do not use such border area. Without limiting the generality, the computational domain of the plate capacitor is extended by the margin $l_{\mathrm {marg}}$ on each side and in each spatial direction. The overall computational domain comprising plate capacitor as well as border area features, thus, the geometric dimensions $(l_{\mathrm {plate}}+2 l_{\mathrm {marg}}) \times (w_{\mathrm {plate}} + 2 l_{\mathrm {marg}}) \times (d + 2 l_{\mathrm {marg}})$. The following FE simulations were performed with quadratic Lagrange ansatz functions, i.e., h-FEM with $p_{\mathrm {d}}=2$.

Figure 4.7 shows the simulation result for the electric scalar potential $V_{\mathrm {e}}\!\left( x,z \right)$ in the xz-plane. Thereby, the margin was set to $l_{\mathrm {marg}}=5\,\mathrm{mm}$. The bottom electrode was set to ground (i.e., $0\,\mathrm{V}$), whereas the electric potential of the top electrode amounts $+10\,\mathrm{V}$. It can be clearly seen that there arise considerable electric potentials in the border area of the plate capacitor. Owing to this fact, the stray fields in the border area are not negligible.

Fig. 4.7

Simulated electric potential $V_{\mathrm {e}}\!\left( x,z \right)$ in xz-plane (i.e., $y=0\,\mathrm{mm}$) of plate capacitor; margin $l_{\mathrm {marg}}=5\,\mathrm{mm}$; 3-D computational gird comprises 161693 tetrahedron elements

The obtained simulation result also enables the calculation of $C_{\mathrm {plate}}$. The calculation is based on the energy density $w_{\mathrm {elec}}$ of the electric field, which is with the electric field intensity $\mathbf {E}=-\nabla V_{\mathrm {e}}$ and the electric flux density $\mathbf {D}$ given by

$$\begin{aligned} w_{\mathrm {elec}}=\frac{1}{2} \mathbf {E} \cdot \mathbf {D} = \frac{1}{2} \varepsilon _{\mathrm {r}}\varepsilon _0 \mathbf {E} \cdot \mathbf {E} = \frac{1}{2} \varepsilon _{\mathrm {r}}\varepsilon _0 \left\| \mathbf {E} \right\| _2 = \frac{1}{2} \varepsilon _{\mathrm {r}}\varepsilon _0 \left\| \nabla V_{\mathrm {e}} \right\| _2 \;. \end{aligned}$$

(4.38)

Since the total electric energy $W_{\mathrm {elec}}$ depends on $C_{\mathrm {plate}}$ and the potential difference U between top and bottom electrodes, we can exploit $w_{\mathrm {elec}}$ to determine $C_{\mathrm {plate}}$. The underlying relations read as

$$\begin{aligned} W_{\mathrm {elec}} = \frac{1}{2} C_{\mathrm {plate}} U^2 \qquad \longrightarrow \qquad C_{\mathrm {plate}}=\frac{2 W_{\mathrm {elec}}}{U^2}\;. \end{aligned}$$

(4.39)

$W_{\mathrm {elec}}$ results from summing the energy $W_{\mathrm {elec}}^i$ of all finite elements within $\varOmega$, i.e.,

$$\begin{aligned} W_{\mathrm {elec}} = \sum \limits _{i=1}^{n_{\mathrm {elem}}} W_{\mathrm {elec}}^i \qquad \text {with} \qquad W_{\mathrm {elec}}^i = \frac{1}{2}\int \limits _{\varOmega ^i} \varepsilon _{\mathrm {r}}\varepsilon _0 \left\| \nabla V_{\mathrm {e}} \right\| _2 \mathrm {d}\varOmega \;. \end{aligned}$$

(4.40)

Table 4.2 lists calculated capacity values for different margins. If the margin is small (e.g., $l_{\mathrm {marg}}=0.1\,\mathrm{mm}$), $C_{\mathrm {plate}}$ will be close to the approximation in (4.37). This follows from the neglected stray fields. As expected, $C_{\mathrm {plate}}$ increases for increasing $l_{\mathrm {marg}}$. For the considered configuration, margins greater than $10\,\mathrm{mm}$ cause only a slight increase in $C_{\mathrm {plate}}$. In general, the computation time of the FE simulation drastically increases for increasing $l_{\mathrm {marg}}$ because the number of finite elements $n_{\mathrm {elem}}$ grows rapidly.

Table 4.2 Resulting capacity value $C_{\mathrm {plate}}$ from FE simulation with respect to considered margin $l_{\mathrm {marg}}$ of plate capacitor (see Fig. 4.6)

4.3 Mechanical Field

The PDE in linear continuum mechanics describing the mechanical field of a solid deformable body in an infinitely small fraction at position⁵ $\mathbf {r}$ is defined as (see 2.68, p. 23 in Sect. 2.2.3)

$$\begin{aligned} \mathcal {B}^\mathrm {t}\!\left[ {\mathbf {c}} \right] \mathcal {B} \mathbf {u} + \mathbf {f}_{\mathrm {V}} = \varrho _0 \ddot{\mathbf {u}} \end{aligned}$$

(4.41)

with the displacement vector $\mathbf {u}\!\left( \mathbf {r},t \right)$, the differential operator $\mathcal {B}$ (2.40, p. 18), the stiffness tensor $\left[ {\mathbf {c}} \right]$, the prescribed volume force $\mathbf {f}_{\mathrm {V}}$, and the material density $\varrho _0$, respectively. In the 3-D case, the compact form of (4.41) for the computational domain $\varOmega$ reads as (boundary $\partial \varOmega$ of $\varOmega$)

$\overline{\varOmega }$ represents the computational domain without its Dirichlet boundary. The expression $\mathbf {n}$ denotes the normal vector with respect to the boundary $\varGamma _{\mathrm {n}}$ of $\varOmega$ and $\mathbf {T}_{\mathrm {n}}$ the resulting mechanical stress perpendicular to this boundary. Either $\mathbf {T}_{\mathrm {n}}$ or $\mathbf {u}_{\mathrm {e}}$ have to be assigned as boundary condition to obtain a unique solution of the PDE. Without limiting the generality, we set both boundary conditions to zero, i.e., $\mathbf {T}_{\mathrm {n}}=0$ and $\mathbf {u}_{\mathrm {e}}=0$. Hence, the weak form of (4.41) after utilizing Green’s first integration theorem is given by

$$\begin{aligned} \int \limits _{\varOmega } \varrho _0 \mathbf {w} \cdot \ddot{\mathbf {u}} \; \mathrm {d}\varOmega + \int \limits _{\varOmega } \!\left( \mathcal {B} \mathbf {w} \right) ^\mathrm {t}\!\left[ {\mathbf {c}} \right] \mathcal {B} \mathbf {u} \; \mathrm {d}\varOmega = \int \limits _{\varOmega } \mathbf {w} \cdot \mathbf {f}_{\mathrm {V}} \; \mathrm {d}\varOmega \end{aligned}$$

(4.42)

where $\mathbf {w}\!\left( \mathbf {r} \right)$ is an appropriate test function. Since the displacement $\mathbf {u}$ is a vector quantity, $\mathbf {w}$ has also to be a vector quantity. Moreover, in contrast to the electrostatic field, the ansatz functions $N_i$ for spatial discretization of $\varOmega$ need to be applied for each component within Galerkin’s method. For Lagrange ansatz functions, the approximation $\varvec{\mathfrak {u}}$ of the displacement vector in 3-D (space dimensions $n_{\mathrm {d}}=3$; $\{1,2,3\}\,{\widehat{=}}\,\{x,y,z\}$) computes as

$$\begin{aligned} \mathbf {u}\!\left( \mathbf {r} \right) \approx \varvec{\mathfrak {u}} \!\left( \mathbf {r} \right)&=\sum \limits _{j=1}^{n_{\mathrm {d}}} \sum \limits _{i=1}^{n_{\mathrm {nodes}}} N_{i} \!\left( \mathbf {r} \right) \mathfrak {u}_{i,j} \,\mathbf {e}_j \qquad \text {with}~\mathfrak {u}_{i,j} = \varvec{\mathfrak {u}}\!\left( \mathbf {r}_{i} \right) \cdot \mathbf {e}_j \end{aligned}$$

(4.43)

or alternatively by introducing the approximated vector $\varvec{\mathfrak {u}}_{i}=\!\left[ \mathfrak {u}_{i,x},\mathfrak {u}_{i,y},\mathfrak {u}_{i,z} \right] ^\mathrm {t}=\varvec{\mathfrak {u}}\!\left( \mathbf {r}_i \right)$ at node i as

$$\begin{aligned} \varvec{\mathfrak {u}} \!\left( \mathbf {r} \right)&=\sum \limits _{i=1}^{n_{\mathrm {nodes}}} \varvec{\mathsf {N}}_{i} \!\left( \mathbf {r} \right) \varvec{\mathfrak {u}}_{i}\;; \quad \varvec{\mathsf {N}}_i \!\left( \mathbf {r} \right) = \!\left[ \begin{array}{ccc} N_i \!\left( \mathbf {r} \right) &{} 0 &{} 0 \\ 0 &{} N_i \!\left( \mathbf {r} \right) &{} 0 \\ 0 &{} 0 &{} N_i \!\left( \mathbf {r} \right) \end{array} \right] \;. \end{aligned}$$

(4.44)

$\mathbf {e}_j$ stands for the unit vector pointing in direction j and $n_{\mathrm {nodes}}$ is the total amount of all nodes within the $n_{\mathrm {elem}}$ finite elements, which are used to spatially discretize the computational domain $\overline{\varOmega }$. Finally, the algebraic system of equations in matrix form becomes

$$\begin{aligned} \varvec{\mathsf {M}}_{\mathbf {u}} \ddot{\varvec{\mathsf {u}}} + \varvec{\mathsf {K}}_{\mathbf {u}} \varvec{\mathsf {u}} = \varvec{\mathsf {f}}_{\mathbf {u}}\;. \end{aligned}$$

(4.45)

The mass matrix $\varvec{\mathsf {M}}_{\mathbf {u}}$, stiffness matrix $\varvec{\mathsf {K}}_{\mathbf {u}}$ and right-hand side $\varvec{\mathsf {f}}_{\mathbf {u}}$ are assembled according to

$$\begin{aligned} \varvec{\mathsf {M}}_{\mathbf {u}}&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {M}}^l \; ; \qquad&\varvec{\mathsf {M}}^l&= \!\left[ \varvec{\mathsf {m}}_{ij}^l \right] \; ; \qquad&\varvec{\mathsf {m}}_{ij}^l&=\int \limits _{\varOmega ^l} \varrho _0 \varvec{\mathsf {N}}_i ^\mathrm {t}\varvec{\mathsf {N}}_j \mathrm {d}\varOmega \end{aligned}$$

(4.46)

$$\begin{aligned} \varvec{\mathsf {K}}_{\mathbf {u}}&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {K}}^l \; ; \qquad&\varvec{\mathsf {K}}^l&= \!\left[ \varvec{\mathsf {k}}_{ij}^l \right] \; ; \qquad&\varvec{\mathsf {k}}_{ij}^l&=\int \limits _{\varOmega ^l} \mathcal {B}_i ^\mathrm {t}\!\left[ {\mathbf {c}} \right] \mathcal {B}_j \mathrm {d}\varOmega \end{aligned}$$

(4.47)

$$\begin{aligned} \varvec{\mathsf {f}}_{\mathbf {u}}&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {f}}^l \; ; \qquad&\varvec{\mathsf {f}}^l&= \!\left[ \mathsf {f}_{i}^l \right] \; ; \qquad&\mathsf {f}_{i}^l&=\int \limits _{\varOmega ^l} \varvec{\mathsf {N}}_i ^\mathrm {t}\mathbf {f}_{\mathrm {V}} \mathrm {d}\varOmega \end{aligned}$$

(4.48)

with

$$\begin{aligned} \mathcal {B}_i=\!\left[ \begin{array}{cccccc} \frac{\partial N_i}{\partial x} &{} 0 &{} 0 &{} 0 &{} \frac{\partial N_i}{\partial z} &{} \frac{\partial N_i}{\partial y} \\ 0 &{} \frac{\partial N_i}{\partial y} &{} 0 &{} \frac{\partial N_i}{\partial z} &{} 0 &{} \frac{\partial N_i}{\partial x} \\ 0 &{} 0 &{} \frac{\partial N_i}{\partial z} &{} \frac{\partial N_i}{\partial y} &{} \frac{\partial N_i}{\partial x} &{} 0 \end{array} \right] ^\mathrm {t}\; . \end{aligned}$$

(4.49)

The assembling procedure is similar to the previously discussed FE method for electrostatics. Note that here, the vector $\varvec{\mathsf {u}}$ of unknowns takes the form

$$\begin{aligned} \varvec{\mathsf {u}}=\!\left[ \mathfrak {u}_{1,x},\mathfrak {u}_{1,y},\mathfrak {u}_{1,z},\mathfrak {u}_{2,x},\ldots ,\mathfrak {u}_{n_{\mathrm {nodes}},x},\mathfrak {u}_{n_{\mathrm {nodes}},y},\mathfrak {u}_{n_{\mathrm {nodes}},z} \right] ^\mathrm {t}\end{aligned}$$

(4.50)

and, thus, contains three times as much components as in case of scalar quantities.

In many practical situations, the FE method for mechanical problems can be considerably simplified. The (i) plane strain state, the (ii) plane stress state, and the (iii) axisymmetric stress–strain relations are three fundamental simplifications in continuum mechanics.

• Plane strain state: Let us assume an elastic body, which is large in one direction (e.g., z-direction) and features equal cross sections (e.g., in xy-plane) perpendicular to this dimension. If the boundary conditions and forces acting on the body are identical for each cross section, the dependence of the displacements (e.g., $\mathrm {u}_{\mathrm {z}}$) and strains (e.g., $S_{\mathrm {yz}}$) on the dominating body dimension can be neglected.

• Plane stress state: We will be able to utilize this state if, for instance, the considered elastic body represents a thin plate (e.g., in xy-plane) made of homogeneous isotropic material, which is loaded by forces acting within the plate plane. For such configurations, several components of the stress tensor (e.g., $T_{\mathrm {zz}}$) and the strain tensor (e.g., $S_{\mathrm {yz}}$) can be set to zero.

• Axisymmetric stress–strain relation: This simplification can be applied when the investigated geometry and the material arrangement are axisymmetric. In that case, a cylindrical-coordinate system (radius r, height z, angle $\varTheta$) can be introduced, where both, displacements (e.g., $\mathrm {u}_{\varTheta }$) and strains (e.g., $S_{r \varTheta }$), do not depend on $\varTheta$.

As a result of the three fundamental simplifications, the original mechanical problem in 3-D changes to a 2-D problem. The required mesh to spatially discretize the computational domain is substantially reduced yielding a smaller number of nodes $n_{\mathrm {nodes}}$ and, thus, an algebraic system of equations with less unknown quantities.

4.3.1 Types of Analysis

Several different types of analysis are commonly utilized in numerical simulations based on the FE method. To discuss the basic types of analysis, we start with an extended version of (4.45) for the algebraic system of equations in mechanics

$$\begin{aligned} \varvec{\mathsf {M}}_{\mathbf {u}} \ddot{\varvec{\mathsf {u}}} + \varvec{\mathsf {D}}_{\mathbf {u}} \dot{\varvec{\mathsf {u}}} + \varvec{\mathsf {K}}_{\mathbf {u}} \varvec{\mathsf {u}} = \varvec{\mathsf {f}}_{\mathbf {u}} \;. \end{aligned}$$

(4.51)

Here, the (damping) matrix $\varvec{\mathsf {D}}_{\mathbf {u}}$ accounts for attenuation within the investigated elastic body.

Static Analysis

In case of static analysis, we presume that the aimed quantity (i.e., $\varvec{\mathsf {u}}$), the boundary conditions as well as the right-hand side $\varvec{\mathsf {f}}_{\mathbf {u}}$ do not depend on time t. Hence, one can state $\ddot{\varvec{\mathsf {u}}}=\dot{\varvec{\mathsf {u}}}=0$ and, therewith (4.51), takes the form

$$\begin{aligned} \varvec{\mathsf {K}}_{\mathbf {u}} \varvec{\mathsf {u}} = \varvec{\mathsf {f}}_{\mathbf {u}}\;. \end{aligned}$$

(4.52)

So, the mass matrix $\varvec{\mathsf {M}}_{\mathbf {u}}$ and damping matrix $\varvec{\mathsf {D}}_{\mathbf {u}}$ have no influence on the result. As for the electrostatic field in Sect. 4.2, initial conditions are useless for the static analysis.

Transient Analysis

Both the external loads and the aimed quantity $\varvec{\mathsf {u}}$ may vary with respect to time in case of a transient analysis. Therefore, we are not able to simplify (4.51). In addition to the spatial computational domain, the investigated time interval $\left[ 0,T \right]$ is discretized. For each time step $t_{i}$,

$$\begin{aligned} \varvec{\mathsf {M}}_{\mathbf {u}} \ddot{\varvec{\mathsf {u}}}^{(i)} + \varvec{\mathsf {D}}_{\mathbf {u}} \dot{\varvec{\mathsf {u}}}^{(i)} + \varvec{\mathsf {K}}_{\mathbf {u}} \varvec{\mathsf {u}}^{(i)} = \varvec{\mathsf {f}}_{\mathbf {u}}^{(i)} \end{aligned}$$

(4.53)

has to be fulfilled. According to the Newmark scheme (see Sect. 4.1.4), the solution $\varvec{\mathsf {u}}^{(i+1)}$ for the subsequent time step $t_{i+1}$ results from three computation substeps.

• 1. Compute predictor step:

  

  (4.54)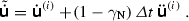
  

  (4.55)

• 2. Solve algebraic system of equations:

  

  (4.56)
  

  (4.57)

• 3. Perform corrector step:

  

  (4.58)
  

  (4.59)

The parameters $\beta _{\mathrm {N}}$ and $\gamma _{\mathrm {N}}$ determine the type of integration, i.e., explicit or implicit integration.

It seems only natural that the transient analysis needs much more computational effort than the static analysis. Especially for large computational grids and long periods of time, this may lead to numerical simulations, which cannot be solved in a reasonable amount of time anymore.

Harmonic Analysis

If the behavior of a system in case of harmonic excitation with frequency f has to be figured out, we can perform a transient analysis with an appropriate excitation signal. However, to achieve the steady state of the system, a sufficiently long period of time $\left[ 0,T \right]$ is required for the simulation, which is usually accompanied by an unacceptable computational effort. On account of this fact, a harmonic analysis should be carried out instead. In doing so, the algebraic system of equations (4.53) in time domain is transformed into the complex frequency domain. The time-dependent expressions $\varvec{\mathsf {f}}_{\mathbf {u}}$ and $\varvec{\mathsf {u}}$ as well as the time derivatives are replaced by (angular frequency $\omega =2\pi f$)

$$\begin{aligned} \varvec{\mathsf {f}}_{\mathbf {u}}&\longrightarrow \hat{\varvec{\mathsf {f}}}_{\mathbf {u}} \cdot \mathrm {e}^{\mathrm {j}\omega t} \;;&\varvec{\mathsf {u}}&\longrightarrow \hat{\varvec{\mathsf {u}}} \cdot \mathrm {e}^{\mathrm {j}\varvec{\varphi }_{\mathbf {u}}} \cdot \mathrm {e}^{\mathrm {j}\omega t} \end{aligned}$$

(4.60)

$$\begin{aligned} \frac{\partial }{\partial t}&\longrightarrow \mathrm {j}\omega \;;&\frac{\partial ^2 }{\partial t ^2}&\longrightarrow -\omega ^2 \end{aligned}$$

(4.61)

$\hat{\varvec{\mathsf {f}}}_{\mathbf {u}}$ and $\hat{\varvec{\mathsf {u}}}$ stand for the amplitudes of both the right-hand side $\varvec{\mathsf {f}}_{\mathbf {u}}$ and the mechanical displacements $\varvec{\mathsf {u}}$ at the nodes of the spatially discretized computational domain, respectively. $\varvec{\varphi }_{\mathbf {u}}$ is a vector containing the phase for the displacement components at each node.⁶ So, the vectors $\hat{\varvec{\mathsf {u}}}$ and $\varvec{\varphi }_{\mathbf {u}}$ feature the same length. The combination of (4.51), (4.60), and (4.61) leads to

$$\begin{aligned} \!\left( - \omega ^2 \varvec{\mathsf {M}}_{\mathbf {u}} + \mathrm {j}\omega \varvec{\mathsf {D}}_{\mathbf {u}} + \varvec{\mathsf {K}}_{\mathbf {u}} \right) \hat{\varvec{\mathsf {u}}} \cdot \mathrm {e}^{\mathrm {j}\varvec{\varphi }_{\mathbf {u}}}= \hat{\varvec{\mathsf {f}}}_{\mathbf {u}}\;, \end{aligned}$$

(4.62)

which is in contrast to (4.51) a complex-valued algebraic system of equations. The solution of this system of equations provides for each node both the amplitude and the phase of the displacement components at frequency f.

Eigenfrequency Analysis

To predict the resonance behavior of a system by means of harmonic analysis, one has to investigate a certain frequency range in which resonance is expected. This procedure may take very long computation time. A time-efficient alternative to the harmonic analysis is the eigenfrequency analysis. Thereby, the system behavior is studied without considering the damping matrix $\varvec{\mathsf {D}}_{\mathbf {u}}$ and the right-hand side $\varvec{\mathsf {f}}_{\mathbf {u}}$ of (4.51). As for the harmonic analysis, we perform a transform into the complex frequency domain yielding the eigenvalue equation

$$\begin{aligned} \!\left[ - \!\left( 2 \pi f \right) ^2 \varvec{\mathsf {M}}_{\mathbf {u}} + \varvec{\mathsf {K}}_{\mathbf {u}} \right] \hat{\varvec{\mathsf {u}}} \cdot \mathrm {e}^{\mathrm {j}\varvec{\varphi }_{\mathbf {u}}} = 0 \;. \end{aligned}$$

(4.63)

The solution of this equation is a pairwise combination of the so-called eigenfrequencies $f_{\!\left( i \right) }$ representing the eigenvalues and eigenvectors $\hat{\varvec{\mathsf {u}}}_{\;\!\left( i \right) } \mathrm {e}^{\mathrm {j}\varvec{\varphi }_{\mathbf {u},\!\left( i \right) }}$. In other words, for each eigenfrequency, one obtains amplitude and phase for the aimed quantity at the nodes of the computational domain. Each eigenvector indicates an eigenmode of the mechanical system.

From the physical point of view, excitations at the eigenfrequency result in a system behavior according to the eigenvectors. In case of an undamped mechanical systems (i.e., $\varvec{\mathsf {D}}_{\mathbf {u}}=0$), the displacements and, consequently, vibrations at this frequency might be rather high. Note that for such a system, the eigenfrequencies coincide with the resonance frequencies of the system.

4.3.2 Attenuation within Mechanical Systems

Each mechanical system is subject to a certain attenuation, which arises due to inner friction. For example, when a one-sided clamped beam is excited by a pulse, the resulting mechanical vibrations will decay. To incorporate attenuation within the FE method, we often add an expression that is proportional to the mechanical velocity $\dot{\varvec{\mathsf {u}}}$ of the mechanical system. The so-called damping matrix $\varvec{\mathsf {D}}_{\mathbf {u}}$ represents the proportionality factor. The resulting algebraic system of equation was already shown in (4.51).

It seems only natural that attenuation can only be considered in a realistic manner if an appropriate damping matrix $\varvec{\mathsf {D}}_{\mathbf {u}}$ is used. Many FE formulations exploit the Rayleigh damping model to determine $\varvec{\mathsf {D}}_{\mathbf {u}}$. The idea of this damping model lies in linearly combining mass matrix $\varvec{\mathsf {M}}_{\mathbf {u}}$ and stiffness matrix $\varvec{\mathsf {K}}_{\mathbf {u}}$ of the system. Therefore, $\varvec{\mathsf {D}}_{\mathbf {u}}$ is given by

$$\begin{aligned} \varvec{\mathsf {D}}_{\mathbf {u}} = \alpha _{\mathrm {M}} \varvec{\mathsf {M}}_{\mathbf {u}} + \alpha _{\mathrm {K}} \varvec{\mathsf {K}}_{\mathbf {u}} \end{aligned}$$

(4.64)

with the mass proportional damping coefficient $\alpha _{\mathrm {M}}$ and the stiffness proportional damping coefficient $\alpha _{\mathrm {K}}$. According to [3], a mode superposition analysis including attenuation yields (ith eigenfrequency $\smash {f_{\!\left( i \right) }}$)

$$\begin{aligned} \alpha _{\mathrm {M}} + \alpha _{\mathrm {K}} \!\left[ 2 \pi f_{\!\left( i \right) } \right] ^2 = 4 \pi f_{\!\left( i \right) } \xi _{\text {d},i}\;. \end{aligned}$$

(4.65)

The expression $\xi _{\text {d},i}$ denotes the modal damping ratio for the ith eigenmode (i.e., at the ith eigenfrequency) and computes as

$$\begin{aligned} \xi _{\text {d},i} = \frac{\alpha _{\mathrm {M}} + \alpha _{\mathrm {K}} \!\left[ 2 \pi f_{\!\left( i \right) } \right] ^2}{ 4 \pi f_{\!\left( i \right) }}\;. \end{aligned}$$

(4.66)

The frequency-dependent damping ratio $\xi _{\mathrm {d}}\!\left( f \right)$ results from the same formula by replacing $f_{\!\left( i \right) }$ with f. $\xi _{\mathrm {d}}\!\left( f \right)$ takes a minimum at $f_{\!\left( i \right) }$ and increases exponentially for $f<f_{\!\left( i \right) }$ and linearly for $f>f_{\!\left( i \right) }$.

The Rayleigh damping model is applicable for transient as well as harmonic analysis based on FE method. However, strictly speaking, the frequency-dependent damping ratio $\xi _{\mathrm {d}}\!\left( f \right)$ will only lead to a good approximation of attenuation if the considered frequency is close to a eigenfrequency. That is the reason why other damping models are applied instead. A common damping model assumes constant attenuation; i.e., $\xi _{\mathrm {d}}$ does not depend on frequency. We can achieve a constant value of $\xi _{\mathrm {d}}$ by means of $\alpha _{\mathrm {M}}=0$ and $\alpha _{\mathrm {K}}=\alpha _{\mathrm {d}}/(2\pi f)$ (see (4.65)) with the damping coefficient $\alpha _{\mathrm {d}}$. By inserting this in (4.64), the damping matrix results in $\varvec{\mathsf {D}}_{\mathbf {u}}=\alpha _{\mathrm {d}} \varvec{\mathsf {K}}_{\mathbf {u}} / (2 \pi f)$. For harmonic FE simulations (4.62), the influence of attenuation remains, thus, constant because the frequency f cancels out in the expression $\mathrm {j}\omega \varvec{\mathsf {D}}_{\mathbf {u}}$. Therefore, attenuation exclusively depends on the product $\alpha _{\mathrm {d}} \varvec{\mathsf {K}}_{\mathbf {u}}$.

Instead of directly introducing a damping matrix $\varvec{\mathsf {D}}_{\mathbf {u}}$ in the FE method, it is possible to consider attenuation for harmonic simulations by using complex-valued material parameters. In case of a mechanical system, this means that the stiffness tensor changes to the complex-valued version

$$\begin{aligned} \!\left[ {\underline{\mathbf {c}}^E} \right] = \!\left[ {\mathbf {c}^E} \right] _{\mathfrak {R}} + \mathrm {j}\!\left[ {\mathbf {c}^E} \right] _{\mathfrak {I}} = \!\left[ {\mathbf {c}^E} \right] _{\mathfrak {R}} \!\left[ 1 + \mathrm {j}\alpha _{\mathrm {d}} \right] \;. \end{aligned}$$

(4.67)

While the real part $\smash {\!\left[ {\mathbf {c}^E} \right] _{\mathfrak {R}}}$ coincides with the original material parameters, the imaginary part $\smash {\!\left[ {\mathbf {c}^E} \right] _{\mathfrak {I}}}$ rates attenuation. The damping coefficient $\alpha _{\mathrm {d}}$ in (4.67) corresponds to the previous definition with $\varvec{\mathsf {D}}_{\mathbf {u}}$ since the imaginary part yields again the expression $\alpha _{\mathrm {d}} \varvec{\mathsf {K}}_{\mathbf {u}}$ in the algebraic system of equations.

4.3.3 Example

Let us study the mechanical behavior of a one-sided clamped copper beam by means of the FE method. The decisive material parameters density, Young’s modulus, and Poisson’s ratio were set to $\varrho _0=8930\,\mathrm{kg\,m}^{-3}$, $E_{M}=126.2\,\mathrm {GPa}$, and $\nu _{P}=0.37$, respectively (see Table 2.5 on p. 26). Figure 4.8a shows the geometric setup for this cantilever beam (length $l_{\mathrm {beam}}=10\,\mathrm{mm}$; height $h_{\mathrm {beam}}=0.5\,\mathrm{mm}$) in the xy-plane. For the sake of simplicity, we assume that the geometric dimension in z-direction is very large compared to $h_{\mathrm {beam}}$ as well as $l_{\mathrm {beam}}$. Moreover, the boundary conditions and external forces acting on the structure are supposed to be equal for each cross section in parallel to the xy-plane. The mechanical problem can, therefore, be treated as plane strain state; i.e., it is sufficient to apply the FE method for the 2-D case (see Fig. 4.8b). The clamping on the left hand side implies that there both the displacements $\mathrm {u}_{\mathrm {x}}$ in x-direction and the displacements $\mathrm {u}_{\mathrm {y}}$ in y-direction equal zero. At the right upper end, the beam is loaded with an external static force of $F=10\,\mathrm{N}$ in negative y-direction. The following FE simulations were performed with quadratic Lagrange ansatz functions, i.e., h-FEM with $p_{\mathrm {d}}=2$.

Fig. 4.8

a Geometric setup of cantilever beam with length $l_{\mathrm {beam}}=10\,\mathrm{mm}$ and height $h_{\mathrm {beam}}=0.5\,\mathrm{mm}$ in xy-plane; b 2-D computational grid comprising 1208 triangles

Since the quantities do not depend on time, we can conduct a static analysis according to (4.52). Figure 4.9 displays the computed bending line $\mathrm {u}_{\mathrm {y}}\!\left( x \right)$, which refers to the centerline of the cantilever beam, i.e., at $y=0$. As expected, the beam deflects in negative y-direction. The deflection at the right beam end amounts $2.18\,\upmu \mathrm{m}$.

Fig. 4.9

Simulation result for bending line $\mathrm {u}_{\mathrm {y}}\!\left( x \right)$ of beam’s centerline

For such a simple arrangement, the beam deflection can also be approximated in an analytical manner. The simplest approximation for the bending line results from the Euler–Bernoulli beam theory, which supposes small mechanical deformations, negligible shear deformations as well as plane cross sections of the beam that are always perpendicular to the beam’s centerline during deformation [24, 26]. According to the Euler–Bernoulli beam theory, the deflection $\mathrm {u}_{\mathrm {y}}\!\left( x=l_{\mathrm {beam}} \right)$ of the right beam end computes as

$$\begin{aligned} \mathrm {u}_{\mathrm {y}}\!\left( x=l_{\mathrm {beam}} \right) =\frac{4 F l_{\mathrm {beam}}^3}{E_{\mathrm {M}} h_{\mathrm {beam}}^3} \end{aligned}$$

(4.68)

for the plane strain state. This leads to the approximated deflection of $2.54\,\upmu \mathrm{m}$. The deviation from the FE simulation stems from the simplifications in the course of the Euler–Bernoulli beam theory.

In Fig. 4.10a and b, one can see the simulated displacement $\mathrm {u}_{\mathrm {x}}\!\left( x,y \right)$ in x-direction and the simulated displacement $\mathrm {u}_{\mathrm {y}}\!\left( x,y \right)$ in y-direction along the cantilever beam for $F=10\,\mathrm{N}$. Not surprisingly, the maximum of $\left| \mathrm {u}_{\mathrm {x}}\!\left( x,y \right) \right|$ is much smaller than of $\left| \mathrm {u}_{\mathrm {y}}\!\left( x,y \right) \right|$. Figure 4.10c depicts the simulated von Mises stress $T_{\mathrm {mis}}\!\left( x,y \right)$, which is here defined as (arguments x and y omitted)

$$\begin{aligned} T_{\mathrm {mis}}=\sqrt{\!\left( T_{\mathrm {xx}} + T_{\mathrm {yy}} \right) ^2 \!\left( \nu _{\mathrm {P}}^2 - \nu _{\mathrm {P}} + 1 \right) + T_{\mathrm {xx}} T_{\mathrm {yy}} \!\left( 2\nu _{\mathrm {P}}^2 - 2 \nu _{\mathrm {P}} -1 \right) + 3 T_{\mathrm {xy}}^2} \end{aligned}$$

(4.69)

with the normal stresses $T_{\mathrm {xx}}$ and $T_{\mathrm {yy}}$ and the shear stress $T_{\mathrm {xy}}$. Especially close to the clamping (i.e., the left beam end), $T_{\mathrm {mis}}\!\left( x,y \right)$ takes high values at the top and bottom sides of the beam.

Fig. 4.10

Simulation result for a displacement $\mathrm {u}_{\mathrm {x}}\!\left( x,y \right)$ in x-direction, b displacement $\mathrm {u}_{\mathrm {y}}\!\left( x,y \right)$ in y-direction, and c von Mises stress $T_{\mathrm {mis}}\!\left( x,y \right)$ along cantilever beam; color bars relate directly to figure above

Fig. 4.11

Simulated normalized eigenmodes $\mathrm {u}_{\mathrm {y}}\!\left( x \right)$ along cantilever beam and eigenfrequencies $f_{\!\left( i \right) }$ for first five eigenmodes

Finally, we regard an eigenfrequency analysis (see (4.63)). Figure 4.11 shows the simulated first five eigenmodes and eigenfrequencies $f_{\!\left( i \right) }$ for transverse vibrations of the cantilever beam. As expected, higher eigenfrequencies are accompanied by an increasing amount of local minima and maxima along the beam. The eigenfrequencies for transverse vibrations can also be analytically approximated by [24]

$$\begin{aligned} f_{\!\left( i \right) } = \frac{\lambda _{(i)}^2}{2 \pi l_{\mathrm {beam}}^2} \sqrt{\frac{E_{\mathrm {M}} h_{\mathrm {beam}}^2}{12 \varrho _0}}\;. \end{aligned}$$

(4.70)

For the first five eigenmodes, the expression $\lambda _{(i)}$ equals

$$\begin{aligned} \lambda _{(i)} = \{1.875;4.694;7.855;10.996;14.137\}\;, \end{aligned}$$

(4.71)

which yields the eigenfrequencies

$$\begin{aligned} f_{\!\left( i \right) } = \{3036;19028;53284;104417;172591\}\,\mathrm{Hz}\;. \end{aligned}$$

(4.72)

Again, the deviations between the simulation results and the analytical approximations stem from simplifications that are performed for the approximation. If the Poisson’s ratio $\nu _{\mathrm {P}}$ is set to zero for the FE simulations, the obtained eigenfrequencies will coincide much better with the approximations in (4.72).

4.4 Acoustic Field

In Sect. 2.3.3, we derived the linear acoustic wave equation for the sound pressure $p_{\sim }$ and the acoustic velocity potential $\varPsi$. For the sound pressure, the wave equation at position $\mathbf {r}$ reads as

$$\begin{aligned} \frac{1}{c_0^2} \ddot{p}_{\sim } - \varDelta p_{\sim } = f_p \end{aligned}$$

(4.73)

with the sound velocity $c_0$ and the excitation function $f_p$ generating acoustic waves in the medium. The compact form of (4.73) for the 3-D computational domain $\varOmega$ including boundary as well as initial conditions becomes

Similar to the FE method for the mechanical field (see Sect. 4.3), either $p_{\mathrm {e}}$ or $p_{\mathrm {n}}$ have to be prescribed as boundary condition of the PDE. To simplify the following expressions, we set these boundary conditions to zero. Therewith, the weak form after applying Green’s first integration theorem results in (scalar test function $w\!\left( \mathbf {r} \right)$)

$$\begin{aligned} \int \limits _{\varOmega } \frac{1}{c_0^2} w \ddot{p}_{\sim } \mathrm {d}\varOmega + \int \limits _{\varOmega } \nabla w \cdot \nabla p_{\sim } \mathrm {d}\varOmega - \int \limits _{\varOmega } w f \mathrm {d}\varOmega =0\;. \end{aligned}$$

(4.74)

The subsequent spatial discretization of $w\!\left( \mathbf {r} \right)$ and $p_{\sim }\!\left( \mathbf {r} \right)$ according to Galerkin’s method leads to the algebraic system of equations in matrix form

$$\begin{aligned} \varvec{\mathsf {M}}_p \ddot{\varvec{\mathsf {p}}} + \varvec{\mathsf {K}}_p \varvec{\mathsf {p}} = \varvec{\mathsf {f}}_p\;. \end{aligned}$$

(4.75)

For Lagrange ansatz functions, the vector $\varvec{\mathsf {p}}$ contains approximated values of the sound pressure $p_{\sim }$ at the nodes of the spatially discretized computational domain $\varOmega$. The mass matrix $\varvec{\mathsf {M}}_p$, stiffness matrix $\varvec{\mathsf {K}}_p$, and right-hand side $\varvec{\mathsf {f}}_p$ are given by (number $n_{\mathrm {elem}}$ of finite elements; ansatz function $N_i$)

$$\begin{aligned} \varvec{\mathsf {M}}_p&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {M}}^l \; ; \qquad&\varvec{\mathsf {M}}^l&= \!\left[ \mathsf {m}_{ij}^l \right] \; ; \qquad&\mathsf {m}_{ij}^l&=\int \limits _{\varOmega ^l} \frac{1}{c_{0}^2} N_i N_j \mathrm {d}\varOmega \end{aligned}$$

(4.76)

$$\begin{aligned} \varvec{\mathsf {K}}_p&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {K}}^l \; ; \qquad&\varvec{\mathsf {K}}^l&= \!\left[ \mathsf {k}_{ij}^l \right] \; ; \qquad&\mathsf {k}_{ij}^l&=\int \limits _{\varOmega ^l} \!\left( \nabla N_i \right) ^\mathrm {t}\nabla N_j \mathrm {d}\varOmega \end{aligned}$$

(4.77)

$$\begin{aligned} \varvec{\mathsf {f}}_p&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {f}}^l \; ; \qquad&\varvec{\mathsf {f}}^l&= \!\left[ \mathsf {f}_{i}^l \right] \; ; \qquad&\mathsf {f}_{i}^l&=\int \limits _{\varOmega ^l} N_i f_p \mathrm {d}\varOmega \;. \end{aligned}$$

(4.78)

To account for attenuation during the wave propagation, an appropriate damping matrix $\varvec{\mathsf {D}}_p$ has to be introduced in addition.

Again, different types of analysis can be performed. In contrast to the mechanical field, the static analysis makes no sense because sound pressure is an alternating quantity. For the transient analysis, we subdivide the investigated time interval [0, T] into sufficiently small subintervals and apply the Newmark scheme according to Sect. 4.1.4. In case of harmonic and eigenfrequency analysis, the algebraic system of equations (4.75) in matrix form has to be transformed into the complex frequency domain.

Alternatively to the sound pressure $p_{\sim }$, one is able to conduct the FE method for the acoustic field by means of the acoustic velocity potential $\varPsi$. The decision if $p_{\sim }$ or $\varPsi$ is utilized primarily depends on the prescribed boundary conditions of the investigated acoustic problem. Principally, we distinguish between three different cases.

• Pressure as boundary condition, i.e., $p_{\sim }=p_{\mathrm {e}}~\text {on}~\partial \varOmega$: The acoustic problem should be studied with the PDE for $p_{\sim }$.

• Normal component of the particle velocity as boundary condition, i.e., $\mathbf {n} \cdot \mathbf {v}_{\sim }=v_{\mathrm {n}}~\text {on}~\partial \varOmega$: Since there is a unique and simple relation between particle velocity and acoustic velocity potential (2.122, p. 34), the acoustic field should be calculated with the PDE for $\varPsi$. The sound pressure results from (2.123).

• Mixed boundary conditions, i.e., $p_{\sim }=p_{\mathrm {e}}~\text {on}~\varGamma _{\mathrm {e}}$ and $\mathbf {n} \cdot \mathbf {v}_{\sim }=v_{\mathrm {n}}~\text {on}~\varGamma _{\mathrm {n}}$: Both quantities are appropriate to solve the acoustic problem. However, we have to convert the boundary conditions into the used quantity.

4.4.1 Open Domain Problems

When the acoustic field of a sound source is studied, we will be mostly interested in the free-field radiation. Actually, the computational domain for numerical simulations based on FE is always limited. On account of this fact, boundary conditions or methods mimicking the so-called open domain are indispensable. The previously discussed boundary conditions cause, however, reflections of the impinging acoustic waves. Consequently, they are not appropriate for free-field simulations. To obtain an open computational domain, several techniques have been developed. In the following, we briefly discuss two famous approaches, namely (i) the absorbing boundary condition (ABC) and (ii) the perfectly matched layer (PML).

Absorbing Boundary Conditions

Let us consider a sinusoidal 1-D pressure wave propagating in x-direction with the sound velocity $c_0$. The acoustic wave may travel in both positive x-direction and negative x-direction. In the complex domain, the solution of the linear wave equation for these waves is given by

$$\begin{aligned} \underline{p}_{\sim }^+ \!\left( x,t \right)&= \hat{p}_{\sim } \mathrm {e}^{\mathrm {j}\!\left( \omega t - kx \right) } \end{aligned}$$

(4.79)

$$\begin{aligned} \underline{p}_{\sim }^- \!\left( x,t \right)&= \hat{p}_{\sim } \mathrm {e}^{\mathrm {j}\!\left( \omega t + kx \right) } \end{aligned}$$

(4.80)

with the sound pressure amplitude $\hat{p}_{\sim }$, the angular frequency $\omega$, and the wave number $k=\omega /c_0$, respectively. Furthermore, we assume at $x_{\mathrm {bound}}$ a virtual boundary $\varGamma _{\mathrm {bound}}$ where the relation

$$\begin{aligned} \!\left( \frac{\partial }{\partial t} + c_0 \frac{\partial }{\partial x} \right) = 0 \end{aligned}$$

(4.81)

has to be fulfilled. Inserting (4.79) and (4.80) in (4.81) reveals that the relation is only satisfied for waves traveling in positive x-direction, i.e., $\underline{p}_{\sim }^+$. Hence, these waves can pass the boundary (see Fig. 4.12). In contrast, waves traveling in negative x-direction are totally reflected at the boundary.

Fig. 4.12

According to ABC, acoustic waves $p_{\sim }^+$ traveling in positive x-direction will pass virtual boundary $\varGamma _{\mathrm {bound}}$ at $x_{\mathrm {bound}}$ and waves $p_{\sim }^-$ traveling in negative x-direction will be totally reflected there

If (4.81) is applied to the FE method at the boundary $\partial \varOmega$ of the computational domain $\varOmega$, one will achieve an open computational domain. We are, thus, able to simulate free-field radiation of an acoustic source. Since this procedure solely affects entries in the damping matrix $\varvec{\mathsf {D}}_p$, which refer to $\partial \varOmega$, the relation (4.81) is usually named absorbing boundary condition.

It is important to mention that an ABC will only work perfectly when the pressure waves impinge perpendicularly onto the boundary. However, in many practical situations, it is impossible to choose a boundary geometry ensuring perpendicular sound incidence for each excitation signal. That is why alternative methods are oftentimes demanded to mimic an open computational domain, e.g., the perfectly matched layer technique.

Perfectly Matched Layer

With a view to explaining the basic idea of the PML technique, we assume a plane acoustic wave propagating in positive x-direction. The wave impinges perpendicularly onto an interface at $x=0$ of two media (medium 1 and medium 2; see Fig. 4.13a), which feature different acoustic properties. For this configuration, the reflection coefficient $r_{\mathrm {pres}}$ for the incident pressure wave becomes (see (2.139, p. 38))

$$\begin{aligned} r_{\mathrm {pres}} = \frac{Z_{\mathrm {aco2}} - Z_{\mathrm {aco1}}}{Z_{\mathrm {aco1}} + Z_{\mathrm {aco2}}} \end{aligned}$$

(4.82)

with the acoustic impedances $Z_{\mathrm {aco1}}$ and $Z_{\mathrm {aco2}}$ of medium 1 and medium 2, respectively. The acoustic impedances for plane waves are defined as

$$\begin{aligned} Z_{\mathrm {aco1}} = \varrho _1 c_1 \qquad \text {and} \qquad Z_{\mathrm {aco2}}=\varrho _2 c_2 \;. \end{aligned}$$

(4.83)

From (4.82), it can be easily deduced that there will not occur any reflection at the interface if $Z_{\mathrm {aco1}}=Z_{\mathrm {aco2}}$ holds. We can fulfill this condition by choosing appropriate combinations of sound velocities and densities for the two media. Without limiting the generality, let us consider the following combination

$$\begin{aligned} \varrho _2&= \varrho _1 \!\left( 1-\mathrm {j}\alpha _{\xi x} \right) \end{aligned}$$

(4.84)

$$\begin{aligned} c_2&= \frac{c_1}{1 - \mathrm {j}\alpha _{\xi x}} \end{aligned}$$

(4.85)

where $\alpha _{\xi x}$ is an arbitrary positive number. Therewith, the (complex-valued) wave number $\underline{k}_2$ in medium 2 results in ($k_1=\omega / c_1$)

$$\begin{aligned} \underline{k}_2 = \frac{\omega }{c_2} = k_1 \!\left( 1 - \mathrm {j}\alpha _{\xi x} \right) \;. \end{aligned}$$

(4.86)

Replacing $k_2$ in the solution of the linear wave equation for sound pressure waves in medium 2, which travel in positive x-direction (cf. (4.79)), with (4.86) yields

$$\begin{aligned} \underline{p}_{\sim }^+ \!\left( x,t \right) = \hat{p}_{\sim } \mathrm {e}^{\mathrm {j}\!\left( \omega t - \underline{k}_2 x \right) } = \hat{p}_{\sim } \mathrm {e}^{\mathrm {j}\!\left( \omega t - k_1 x \right) } \underbrace{\mathrm {e}^{-\alpha _{\xi x} x}}_{\text {damping}} \;. \end{aligned}$$

(4.87)

The expression $\mathrm {e}^{-\alpha _{\xi x} x}$ causes attenuation due to the fact that $\alpha _{\xi x}$ (attenuation coefficient) was assumed to be a positive number. As a result, the amplitude of the propagating pressure wave gets exponentially reduced in medium 2 (see Fig. 4.13a).

Fig. 4.13

a Sound pressure wave $p_{\sim } \!\left( x,t \right)$ propagating in x-direction and impinging perpendicularly onto interface of medium 1 and medium 2; b refraction at interface of $\varOmega _{\mathrm {orig}}$ and $\varOmega _{\mathrm {PML}}$; particle velocity $\mathbf {v}_{\sim }$; c setting of attenuation coefficients $\alpha _{\xi x}$ and $\alpha _{\xi y}$ in 2-D within PML layer that surrounds $\varOmega _{\mathrm {orig}}$

To utilize this principle in the FE method for 2-D as well as 3-D acoustic problems, the original computational domain $\varOmega _{\mathrm {orig}}$ has to be surrounded by an additional computational region $\varOmega _{\mathrm {PML}}$, the so-called perfectly matched layer (see Fig. 4.13c). In this layer, propagating acoustic waves are attenuated until they are reflected at the outer boundary $\partial \varOmega _{\mathrm {PML}}$ of $\varOmega _{\mathrm {PML}}$. During the propagation of the reflected waves back to the interface $\partial \varOmega _{\mathrm {orig}}$ of $\varOmega _{\mathrm {PML}}$ and $\varOmega _{\mathrm {orig}}$, further attenuation is present. The intensity of the reflected acoustic wave will, therefore, be negligible if a sufficient thickness of the PML as well as a proper attenuation coefficient is chosen.

Note that the PML technique does not only require acoustic impedances matching of $\varOmega _{\mathrm {orig}}$ and $\varOmega _{\mathrm {PML}}$ for sound pressure waves impinging perpendicular onto their interface $\partial \varOmega _{\mathrm {orig}}$ but also for oblique incident sound. In order to arrange impedance matching, we locally split the incident wave $p_{\sim }$ into plane waves $p_{\sim x}$, $p_{\sim y}$ and $p_{\sim z}$ propagating in x-, y-, and z-direction, respectively, i.e.,

$$\begin{aligned} p_{\sim }= p_{\sim x} + p_{\sim y} + p_{\sim z}\;. \end{aligned}$$

(4.88)

The splitting is conducted according to the components of the particle velocity $\mathbf {v}_{\sim }=\!\left[ v_{\sim x}, v_{\sim y},v_{\sim z} \right] ^\mathrm {t}$ at the interface in the PML layer (see Fig. 4.13b). Moreover, individual attenuation coefficients $\alpha _{\xi x}$, $\alpha _{\xi y}$, and $\alpha _{\xi z}$ are applied in the different spatial directions (see Fig. 4.13c). By means of this technique, reflections of oblique incident pressure waves are avoided at the interface $\partial \varOmega _{\mathrm {orig}}$, which leads to an open computational domain. It is possible to incorporate the PML technique in the FE method for analysis in the complex frequency domain (i.e., harmonic and eigenfrequency) and in modified form also for transient analysis [13]. However, the additional region $\varOmega _{\mathrm {PML}}$ implies increasing computational effort.

Fig. 4.14

Rotationally symmetric configuration of computational domain $\varOmega$ with radius $R_{\varOmega }=100\,\mathrm{mm}$ for piston-type ultrasonic transducer; circular active surface with radius $R_{\mathrm {T}}=10\,\mathrm{mm}$; amplitude $\hat{v}_{\mathrm {n}}=1\,\mathrm{mm\,s}^{-1}$ of surface normal velocity; absorbing boundary conditions at $\varGamma _{\mathrm {ABC}}$

4.4.2 Example

As a practical example for acoustics, let us study the sound field, which is generated by a piston-type ultrasonic transducer featuring a circular active surface (radius $R_{\mathrm {T}}=10\,\mathrm {mm}$) and a uniform surface normal velocity. The ultrasonic transducer operates in water with a sound velocity of $c_0=1500\,\mathrm{ms}^{-1}$. Owing to the symmetry of the transducer, we can restrict the computational domain $\varOmega$ to a rotationally symmetric configuration. Figure 4.14 illustrates the considered 2-D geometric arrangement, whereby the rotation axis coincides with the z-axis. $\varOmega$ is a quarter circle with radius $R_{\varOmega }=100\,\mathrm{mm}$.

The active surface of the piston-type transducer gets emulated by a line of radial dimension $R_{\mathrm {T}}$ that oscillates sinusoidally with the velocity amplitude $\hat{v}_{\mathrm {n}}=1\,\mathrm{mm\,s}^{-1}$ at the frequency $f_{\mathrm {ex}}$. Therefore, we have to prescribe $\hat{v}_{\mathrm {n}}$ along $R_{\mathrm {T}}$. The remaining part $\varGamma _{\mathrm {n}}$ of the lower limit of $\varOmega$ was assumed to be acoustically hard, i.e., $\hat{v}_{\mathrm {n}}=0$. Due to the rotationally symmetric configuration, this also refers to the z-axis. With a view to simulating free-field radiation, absorbing boundary conditions were used at the boundary $\varGamma _{\mathrm {ABC}}$. The following FE simulations were performed with quadratic Lagrange ansatz functions, i.e., h-FEM with $p_{\mathrm {d}}=2$.

Figure 4.15 contains simulation results for the normalized sound pressure distribution⁷ $\hat{p}_{\sim }\!\left( \rho ,z \right)$, which were obtained by a harmonic FE analysis. The excitation frequency $f_{\mathrm {ex}}$ was varied from $50\,\mathrm{kHz}$ up to $1\,\mathrm{MHz}$. Not surprisingly, $\hat{p}_{\sim }\!\left( \rho ,z \right)$ strongly depends on $f_{\mathrm {ex}}$. The underlying causes will be thoroughly investigated in Sect. 7.2.

Fig. 4.15

Simulated normalized sound pressure distribution $\hat{p}_{\sim }\!\left( \rho ,z \right)$ for excitation frequency $f_{\mathrm {ex}}$ a $50\,\mathrm{kHz}$, b $100\,\mathrm{kHz}$, c $500\,\mathrm{kHz}$, and d $1\,\mathrm{MHz}$; normalization with respect to maximum amplitude $\hat{p}_{\sim \text {max}}$

Note that the required computation time of the harmonic FE simulation varies widely for the considered values of $f_{\mathrm {ex}}$. This originates from the size of the used computational grid because reliable FE simulations call for a sufficiently fine grid. In the present case, one wavelength $\lambda _{\mathrm {aco}}=c_0/f_{\mathrm {ex}}$ of the sound wave was discretized by triangular elements with side lengths smaller than $\lambda _{\mathrm {aco}}/10$. As a result, $\varOmega$ comprises 2469 triangles for $f_{\mathrm {ex}}=50\,\mathrm{kHz}$ and 977043 triangles for $f=1\,\mathrm{MHz}$, respectively. It seems only natural that such an increasing amount of finite elements has a significant impact on the required computation time. Especially when a transient FE analysis is desired, this fact may lead to an unacceptable computational effort.

4.5 Coupled Fields

If numerical simulations are carried out for piezoelectric sensors and actuators, one will always be concerned with the coupling of different physical fields. The (quasi-static) electric field is coupled to the mechanical field inside the piezoelectric material. For ultrasonic transducers, we have to additionally regard the coupling of mechanical and acoustic fields. In the following, the relevant coupling conditions as well as their incorporation into the FE method will be discussed.

4.5.1 Piezoelectricity

As for single physical fields (e.g., mechanical field), the numerical simulation of piezoelectricity demands appropriate PDEs. These equations are obtained by combining the material law of piezoelectricity with fundamental relations of mechanical and (quasi-static) electric fields. To account for the coupling of electric and mechanical quantities inside the piezoelectric material, let us utilize the material law for linear piezoelectricity in e-form and Voigt notation (see Sect. 3.3)

$$\begin{aligned} \mathbf {T}&= \!\left[ {\mathbf {c}^E} \right] \mathbf {S} - \!\left[ {\mathbf {e}} \right] ^\mathrm {t}\mathbf {E} \end{aligned}$$

(4.89)

$$\begin{aligned} \mathbf {D}&= \!\left[ {\mathbf {e}} \right] \mathbf {S} + \!\left[ {\varvec{\varepsilon }^S} \right] \mathbf {E} \end{aligned}$$

(4.90)

with the mechanical stress $\mathbf {T}$, the mechanical strain $\mathbf {S}$, the electric flux density $\mathbf {D}$, and the electric field intensity $\mathbf {E}$. The tensors $\left[ {\mathbf {c}^E} \right]$, $\left[ {\mathbf {e}} \right]$, and $\left[ {\varvec{\varepsilon }^S} \right]$ contain the elastic stiffness constants for constant electric field intensity, the piezoelectric stress constants and the electric permittivities for constant mechanical strain, respectively. In the next step, we insert this material law into Navier’s equation (see (2.42, p. 18))

$$\begin{aligned} \varrho _0 \ddot{\mathbf {u}} - \mathcal {B}^\mathrm {t}\mathbf {T}&= \mathbf {f}_{\mathrm {V}} \end{aligned}$$

(4.91)

as well as into the Law of Gauss (see (2.9, p. 10))

$$\begin{aligned} \nabla \cdot \mathbf {D} = q_{\mathrm {e}}\;. \end{aligned}$$

(4.92)

Here, $\mathbf {u}$, $\varrho _0$, $\mathbf {f}_{\mathrm {V}}$, and $q_{\mathrm {e}}$ stand for the mechanical displacement, the material density, the volume force, and the volume charge density, respectively. Since piezoelectric materials are electrically insulating, they do not contain any free volume charges, i.e., $q_{\mathrm {e}}=0$. Under consideration of this fact and by applying the relations

$$\begin{aligned} \mathbf {S}=\mathcal {B} \mathbf {u} \qquad \text {and} \qquad \mathbf {E}=-\nabla V_{\mathrm {e}}\;, \end{aligned}$$

(4.93)

we arrive at coupled partial differential equations for $\mathbf {u}$ and the electric potential $V_{\mathrm {e}}$

$$\begin{aligned} \varrho _0 \ddot{\mathbf {u}} - \mathcal {B}^\mathrm {t}\!\left( \, \!\left[ {\mathbf {c}^E} \right] \mathcal {B} \mathbf {u} + \!\left[ {\mathbf {e}} \right] ^\mathrm {t}\nabla V_{\mathrm {e}} \right)&= \mathbf {f}_{\mathrm {V}} \end{aligned}$$

(4.94)

$$\begin{aligned} \nabla \cdot \!\left( \, \!\left[ {\mathbf {e}} \right] \mathcal {B} \mathbf {u} - \!\left[ {\varvec{\varepsilon }^S} \right] \nabla V_{\mathrm {e}} \right)&= 0 \;, \end{aligned}$$

(4.95)

which are applicable for FE simulations of piezoelectric materials. The consideration of distinct boundary conditions for the mechanical field as well as for the electric field requires the fundamental equations (4.91) and (4.92) in addition.

FE Method for Piezoelectric Coupling

Each PDE in (4.94) and (4.95) contains both aimed quantities, i.e., $\mathbf {u}$ and $V_{\mathrm {e}}$. Therefore, one has to handle a coupled problem within the FE method for piezoelectricity. Let us show the basic steps by means of a plate-shaped piezoelectric material, which is shown in Fig. 4.16. The top area (loaded electrode; $\varGamma _{\mathrm {L}}$) and the bottom area (grounded electrode; $\varGamma _{\mathrm {G}}$) of the plate are completely covered with electrodes that are assumed to be infinitely thin. Due to the electrodes, the electric potential $V_{\mathrm {e}}$ is equal on $\varGamma _{\mathrm {L}}$ as well as on $\varGamma _{\mathrm {G}}$, respectively. With a view to simplifying the FE procedure, we set the boundary conditions for the electric and the mechanical fields to (boundary $\partial \varOmega$ of $\varOmega$)

Fig. 4.16

Plate-shaped piezoelectric material covered with infinitely thin electrodes on bottom area $\varGamma _{\mathrm {G}}$ and top area $\varGamma _{\mathrm {L}}$

Thus, the electrodes feature prescribed electric potentials, the mechanical displacements at $\varGamma _{\mathrm {G}}$ are fixed, and the piezoelectric material is not mechanically clamped. Moreover, gravity forces within the body are neglected, i.e., $\mathbf {f}_{\mathrm {V}}=0$. By applying $\mathbf {w}\!\left( \mathbf {r} \right)$ (vector quantity) as test function for the displacement $\mathbf {u}$ and $w\!\left( \mathbf {r} \right)$ (scalar quantity) for the electric potential $V_{\mathrm {e}}$, the weak form of (4.94) results in

$$\begin{aligned} \int \limits _{\varOmega } \varrho _0 \mathbf {w} \cdot \ddot{\mathbf {u}} \;\mathrm {d}\varOmega + \int \limits _{\varOmega } \!\left( \mathcal {B} \mathbf {w} \right) ^\mathrm {t}\!\left[ {\mathbf {c}^E} \right] \mathcal {B} \mathbf {u} \; \mathrm {d}\varOmega + \int \limits _{\varOmega } \!\left( \mathcal {B} \mathbf {w} \right) ^\mathrm {t}\!\left[ {\mathbf {e}} \right] ^\mathrm {t}\nabla V_{\mathrm {e}} \; \mathrm {d}\varOmega&= 0 \end{aligned}$$

(4.96)

$$\begin{aligned} \int \limits _{\varOmega } \!\left( \nabla w \right) ^\mathrm {t}\!\left[ {\mathbf {e}} \right] \mathcal {B} \mathbf {u} \; \mathrm {d}\varOmega - \int \limits _{\varOmega } \!\left( \nabla w \right) ^\mathrm {t}\!\left[ {\varvec{\varepsilon }^S} \right] \nabla V_{\mathrm {e}} \; \mathrm {d}\varOmega&=0 \;. \end{aligned}$$

(4.97)

In the next step, we introduce Lagrange ansatz functions for $\mathbf {u}$, $\mathbf {w}$, $V_{\mathrm {e}}$, and w (see Sects. 4.2 and 4.3). Finally, this procedure leads to the algebraic system of equations in matrix form

$$\begin{aligned} \!\left[ \begin{array}{cc} \varvec{\mathsf {M}}_{\mathbf {u}} &{} 0 \\ 0 &{} 0 \end{array} \right] \!\left[ \begin{array}{c} \ddot{\varvec{\mathsf {u}}} \\ \ddot{\varvec{\mathsf {v}}}_{\mathrm {e}} \end{array} \right] + \!\left[ \begin{array}{cc} \varvec{\mathsf {K}}_{\mathbf {u}} &{} \varvec{\mathsf {K}}_{\mathbf {u} V_{\mathrm {e}}} \\ \varvec{\mathsf {K}}_{\mathbf {u} V_{\mathrm {e}}}^\mathrm {t}&{} - \varvec{\mathsf {K}}_{V_{\mathrm {e}}} \end{array} \right] \!\left[ \begin{array}{c} \varvec{\mathsf {u}} \\ \varvec{\mathsf {v}}_{\mathrm {e}} \end{array} \right] = \!\left[ \begin{array}{c} 0 \\ 0 \end{array} \right] \end{aligned}$$

(4.98)

with the vectors $\varvec{\mathsf {u}}$ and $\varvec{\mathsf {v}}_{\mathrm {e}}$ representing approximated values for $\mathbf {u}$ and $V_{\mathrm {e}}$ at the nodes of the computational domain $\varOmega$, respectively. The matrices $\varvec{\mathsf {M}}_{\mathbf {u}}$, $\varvec{\mathsf {K}}_{\mathbf {u}}$ and $\varvec{\mathsf {K}}_{V_{\mathrm {e}}}$ as well as the right-hand side $\varvec{\mathsf {f}}_{V_{\mathrm {e}}}$ are assembled according to Sects. 4.2 and 4.3. The additional matrix $\varvec{\mathsf {K}}_{\mathbf {u} V_{\mathrm {e}}}$ is a consequence of piezoelectric coupling and computes as (number $n_{\mathrm {elem}}$ of elements within $\varOmega$)

$$\begin{aligned} \varvec{\mathsf {K}}_{\mathbf {u} V_{\mathrm {e}}}&= \bigwedge \limits _{l=1}^{n_{\mathrm {elem}}} \varvec{\mathsf {K}}^l \; ; \qquad&\varvec{\mathsf {K}}^l = \!\left[ \varvec{\mathsf {k}}_{ij}^l \right] \; ; \qquad&\varvec{\mathsf {k}}_{ij}^l=\int \limits _{\varOmega ^l} \mathcal {B}_i ^\mathrm {t}\!\left[ {\mathbf {e}} \right] ^\mathrm {t}\tilde{\mathcal {B}}_j \mathrm {d}\varOmega \end{aligned}$$

(4.99)

with

$$\begin{aligned} \tilde{\mathcal {B}}_j = \!\left[ \frac{\partial N_j}{\partial x} , \frac{\partial N_j}{\partial y} , \frac{\partial N_j}{\partial z} \right] ^\mathrm {t}\;. \end{aligned}$$

(4.100)

The FE method also enables for piezoelectric coupling different types of analysis, i.e., static, transient, harmonic as well as eigenfrequency analysis. For the static analysis, derivatives with respect to time are omitted in the algebraic system of equations. In the same manner as for mechanical and acoustic fields, (4.98) has to be transformed into the complex frequency domain in case of harmonic and eigenfrequency analysis. To conduct a transient analysis, one can apply the Newmark scheme (see Sect. 4.1.4).

At this point, it should be mentioned that the coupled algebraic system of equations in (4.98) does not contain any attenuation. In fact, attenuation occurs in every real system and, thus, has also to be regarded here. We can easily incorporate attenuation in the FE method for piezoelectricity if complex-valued material parameters are used (see Sect. 4.3.2).

There exist extended versions of the conventional FE method for piezoelectricity since piezoelectric devices demand external electronic components for electrical excitation or readout. This does not only refer to piezoelectric sensors and actuators but also to vibration-based energy harvesting devices that exploit piezoelectric materials. For such energy harvesting devices, we mostly need a special electric matching network, which converts AC voltage to DC voltage [7, 9]. Due to piezoelectric coupling, the electric matching network has a certain retroactive effect on the harvesting devices, which changes the output of the entire system. One can realistically analyze the behavior of the entire system if the mutual coupling between energy harvesting device and electric matching network is considered in the FE method. Possible work-arounds and solutions for this task can be found in [8, 10, 25].

Example

Various piezoelectric sensors and actuators are based on piezoceramic disks. On this account, let us study the behavior of such a piezoceramic disk by means of the FE method. The considered disk (diameter $d_{\mathrm {S}}=30\,\mathrm{mm}$; thickness $t_{\mathrm {S}}=2\,\mathrm{mm}$) is made of the piezoceramic material PZT-5A and polarized in thickness direction. The decisive material parameters can be found in Table 3.5 on p. 67. Both the top and bottom surfaces of the disk are completely covered by infinitely thin electrodes. Furthermore, we assume free mechanical vibrations, which means that the disk is not clamped and there do not act external forces.

Due to the symmetry of the disk, it makes sense to restrict the computational domain $\varOmega$ to a rotationally symmetric configuration. Figure 4.17a shows the 2-D geometric arrangement of the utilized FE model. Along the rotation axis (z-axis), the mechanical displacements $\mathrm {u}_{\rho }$ in radial direction have to be zero. At the remaining boundaries of $\varOmega$ (i.e., $\varGamma _{\mathrm {G}}$, $\varGamma _{\mathrm {S}}$, and $\varGamma _{\mathrm {L}}$), the normal component of the mechanical stresses was set to zero because of free mechanical vibrations. Figure 4.17b displays the used structured computational grid, which consists of 480 square elements with an edge length of $0.25\,\mathrm{mm}$. Again, the FE simulations were performed with quadratic Lagrange functions, i.e., h-FEM with $p_{\mathrm {d}}=2$.

Fig. 4.17

a Rotationally symmetric configuration of computational domain $\varOmega$ for piezoceramic disk with diameter $d_{\mathrm {S}}=30\,\mathrm{mm}$ and thickness $t_{\mathrm {S}}=2\,\mathrm{mm}$; bottom electrode $\varGamma _{\mathrm {G}}$; top electrode $\varGamma _{\mathrm {L}}$; b 2-D computational grid comprising 480 squares

At the beginning, we will take a look at the complex-valued electrical impedance $\underline{Z}_{\mathrm {T}}\!\left( f \right)$ of the piezoceramic disk since this frequency-resolved quantity is often essential for practical applications. In the complex domain, $\underline{Z}_{\mathrm {T}}\!\left( f \right)$ reads as (frequency f)

$$\begin{aligned} \underline{Z}_{\mathrm {T}}\!\left( f \right) = \frac{\underline{u}_{\mathrm {T}}\!\left( f \right) }{\underline{i}_{\mathrm {T}}\!\left( f \right) } = \frac{\hat{u}_{\mathrm {T}} \cdot \mathrm {e}^{\mathrm {j}(2 \pi f t + \varphi _u)}}{\hat{i}_{\mathrm {T}} \cdot \mathrm {e}^{\mathrm {j}(2 \pi f t + \varphi _i)}} = \frac{\hat{u}_{\mathrm {T}}}{\hat{i}_{\mathrm {T}}} \mathrm {e}^{\mathrm {j}(\varphi _u - \varphi _i)} \end{aligned}$$

(4.101)

with the complex representations of the electric potential $\underline{u}_{\mathrm {T}}$ between top and bottom electrodes and the electric current $\underline{i}_{\mathrm {T}}$. The expressions $\hat{u}_{\mathrm {T}}$ and $\smash {\hat{i}_{\mathrm {T}}}$ stand for the amplitudes of both quantities, whereas $\varphi _u$ and $\varphi _i$ indicate the phase angles. One way to calculate $\underline{Z}_{\mathrm {T}}\!\left( f \right)$ is based on prescribing $\underline{u}_{\mathrm {T}}\!\left( f \right) =\underline{V}_{\mathrm {e}}\!\left( f \right)$ at the top electrode $\varGamma _{\mathrm {L}}$, while the bottom electrode $\varGamma _{\mathrm {G}}$ is set to ground. In doing so, we require the electric current $\underline{i}_{\mathrm {T}}\!\left( f \right)$, which results from the electric charge $\underline{Q}_{\mathrm {T}}\!\left( f \right)$ on $\varGamma _{\mathrm {L}}$ through

$$\begin{aligned} \underline{i}_{\mathrm {T}}\!\left( f \right)&= \mathrm {j}2 \pi f \underline{Q}_{\mathrm {T}}\!\left( f \right) = \mathrm {j}2 \pi f \int \limits _{\varGamma _{\mathrm {L}}} \underline{\mathbf {D}}\!\left( f \right) \cdot \mathbf {n} \,\mathrm {d}\varGamma \nonumber \\&= \mathrm {j}2 \pi f \int \limits _{\varGamma _{\mathrm {L}}} \!\left\{ \,\!\left[ {\mathbf {e}} \right] \mathcal {B} \underline{\mathbf {u}}\!\left( f \right) - \!\left[ {\varvec{\varepsilon }^S} \right] \nabla \underline{V}_{\mathrm {e}} \!\left( f \right) \right\} \, \mathrm {d}\varGamma \;. \end{aligned}$$

(4.102)

Here, the electric flux density $\mathbf {D}$ has been replaced by the term in the brackets of (4.95). $\underline{\mathbf {u}}\!\left( f \right)$ and $\underline{V}_{\mathrm {e}} \!\left( f \right)$ denote complex representations of the mechanical displacement $\mathbf {u}$ and electric potential $V_{\mathrm {e}}$, respectively. By evaluating (4.101), we are, thus, able to compute $\underline{Z}_{\mathrm {T}}\!\left( f \right)$. For FE simulations, this means that one has to sum the resulting electric charges along $\varGamma _{\mathrm {L}}$. It is recommended to perform a harmonic FE analysis for reasons of efficiency. Alternatively to prescribing the electric potential, one can prescribe the charge on the top electrode. The electric impedance results then from determining the electric potential on $\varGamma _{\mathrm {L}}$.

Figure 4.18 depicts the calculated magnitude $\left| \underline{Z}_{\mathrm {T}}\!\left( f \right) \right|$ of the frequency-resolved electrical impedance for the considered piezoceramic disk. It can be clearly seen that the impedance curve contains pronounced local extrema. While local minima in $\left| \underline{Z}_{\mathrm {T}}\!\left( f \right) \right|$ indicate resonances of mechanical vibrations, local maxima are related to antiresonances. The reason that resonances as well as antiresonances of mechanical vibrations become visible in the impedance curve lies in piezoelectric coupling. The combination of local minimum and maximum in the frequency range 60–$90\,\mathrm{kHz}$ refers to mechanical vibrations in radial direction of the disk. At higher frequencies, there exist further combinations, which arise due to the overtones of these vibrations. However, the pronounced combination in the frequency range $800\,\mathrm{kHz}$–$1.3\,\mathrm{MHz}$ refers to mechanical vibrations in thickness direction. In Chap. 5, we will address the significance of impedance curves for material characterization.

Fig. 4.18

Frequency-resolved electrical impedance $\left| \underline{Z}_{\mathrm {T}}\!\left( f \right) \right|$ (magnitude) of considered piezoceramic disk with diameter $d_{\mathrm {S}}=30\,\mathrm{mm}$ and thickness $t_{\mathrm {S}}=2\,\mathrm{mm}$; piezoceramic material PZT-5A

Now, let us discuss the mechanical displacement $\mathrm {u}$ of the piezoceramic disk as a further simulation result. As a matter of principle, the FE method provides this quantity in each point of the computational domain. Figure 4.19 shows the normalized displacement amplitudes $\hat{\mathrm {u}}_{\rho }\!\left( \rho ,z \right)$ and $\hat{\mathrm {u}}_{\mathrm {z}}\!\left( \rho ,z \right)$ in radial and thickness direction, respectively. Thereby, three different excitation frequencies f were selected, namely $10\,\mathrm{kHz}$, $70\,\mathrm{kHz}$, and $1\,\mathrm{MHz}$. The frequency $70\,\mathrm{kHz}$ lies in the range of the vibration resonance in radial direction, whereas $1\,\mathrm{MHz}$ is close to the vibration resonance in thickness direction. For low excitation frequencies, the disk seems to vibrate uniformly in both directions. In contrast, high excitation frequencies cause a superposition of different vibration modes, which becomes apparent in strong local variations of $\hat{\mathrm {u}}_{\rho }\!\left( \rho ,z \right)$ and $\hat{\mathrm {u}}_{\mathrm {z}}\!\left( \rho ,z \right)$.

Fig. 4.19

Normalized displacement amplitudes of piezoceramic disk for different excitation frequencies f; (left) displacement amplitudes $\hat{\mathrm {u}}_{\rho }\!\left( \rho ,z \right)$ in radial direction; (right) displacement amplitudes $\hat{\mathrm {u}}_{\mathrm {z}}\!\left( \rho ,z \right)$ in thickness direction; bright and dark colors indicate large and small amplitude values, respectively

Figure 4.20 depicts $\hat{\mathrm {u}}_{\mathrm {z}}\!\left( \rho \right)$ at the top surface $\varGamma _{\mathrm {L}}$ of the piezoceramic disk for different excitation frequencies. The displacement amplitude values were normalized to the amplitude $\hat{V}_{\mathrm {e}}$ of the applied excitation voltage. In accordance with Fig. 4.19, $\hat{\mathrm {u}}_{\mathrm {z}}\!\left( \rho \right)$ remains almost constant at low frequencies and varies strongly at high frequencies. Besides, Fig. 4.20 reveals that electric excitations close to the vibration resonance in thickness direction generate extremely high values of $\hat{\mathrm {u}}_{\mathrm {z}}\!\left( \rho \right)$. The maximum value for $1\,\mathrm{MHz}$ is more than ten times greater than that for $10\,\mathrm{kHz}$. Because large displacements at high frequencies imply high surface velocities, ultrasonic transducers, which are based on thickness vibrations of piezoceramic disks, should be operated close to resonance.

Fig. 4.20

Displacement amplitudes $\hat{u}_z \!\left( \rho \right)$ at top surface $\varGamma _{\mathrm {L}}$ of piezoceramic disk for different excitation frequencies; normalization with respect to amplitude $\hat{V}_{\mathrm {e}}$ of excitation voltage

4.5.2 Mechanical–Acoustic Coupling

The coupling of mechanical and acoustic fields in the FE method is decisive to study sound radiation of sources and sound reception of receivers, e.g., ultrasonic transducers. In general, we can distinguish between weak coupling and strong coupling.

• Weak coupling: In this situation, the mechanical field serves as source for the acoustic field. Thereby, the acoustic field is assumed to have no influence on the mechanical field. Weak coupling is convenient to calculate the sound radiation pattern of an ultrasonic transducer in air.

• Strong coupling: The mechanical field couples to the acoustic field and vice versa, i.e., coupling in both directions. As a result, the acoustic field alters the mechanical field. Strong coupling has to be considered for ultrasonic transducers operating in water.

Solid–Fluid Interface

To study mechanical–acoustic coupling, let us take a look at an interface $\varGamma _{\mathrm {int}}$ of a solid (elastic body) and a fluid (nonviscous liquid or gas), which is shown in Fig. 4.21. At each point of this interface, the normal components of both the mechanical velocity $\mathbf {v}_{\mathrm {mech}}$ in the solid and the acoustic particle velocity $\mathbf {v}_{\sim }$ in the fluid have to coincide. With the normal vector $\mathbf {n}$, this continuity relation is given by

$$\begin{aligned} \text {condition I:} \quad \mathbf {n} \cdot \!\left( \mathbf {v}_{\mathrm {mech}} - \mathbf {v}_{\sim } \right) = 0\;. \end{aligned}$$

(4.103)

Fig. 4.21

Interface $\varGamma _{\mathrm {int}}$ between solid and fluid; normal components of mechanical velocity $\mathbf {v}_{\mathrm {mech}}$ and acoustic particle velocity $\mathbf {v}_{\sim }$ coincide at $\varGamma _{\mathrm {int}}$

Moreover, the fluid causes a certain pressure load on the solid at the interface $\varGamma _{\mathrm {int}}$. This pressure load $\mathbf {f}_{\varGamma }$ corresponds to the mechanical stress $\mathbf {T}_{\mathrm {\mathbf {n}}}$ acting perpendicular to the surface of the solid and, consequently, computes as

$$\begin{aligned} \text {condition II:} \quad \mathbf {f}_{\varGamma } = \mathbf {T}_{\mathbf {n}} = -\mathbf {n} p_{\sim } \;. \end{aligned}$$

(4.104)

Note that both conditions have to be applied for strong coupling. In contrast, weak coupling is solely based on condition I.

By using the basic relations for linear continuum mechanics and acoustics

$$\begin{aligned} \mathbf {v}_{\mathrm {mech}}=\frac{\partial \mathbf {u}}{\partial t}\;, \quad \mathbf {v}_{\sim } = -\nabla \varPsi \quad \text {and} \quad p_{\sim }=\varrho _{\mathrm {0f}} \frac{\partial \varPsi }{\partial t}\;, \end{aligned}$$

(4.105)

we can derive the two coupling conditions (condition I and II) at the solid–fluid interface for the acoustic pressure $p_{\sim }$ and the acoustic velocity potential $\varPsi$, respectively. Table 4.3 contains the resulting equations for the different formulations.

Table 4.3 Coupling conditions (condition I and II) at the solid–fluid interface $\varGamma _{\mathrm {int}}$ for pressure and potential formulation; fluid density $\varrho _{\mathrm {0f}}$ in the equilibrium state

FE Method for Mechanical–Acoustic Coupling

The numerical simulation of coupled mechanical–acoustic problems demands consideration of the coupling conditions at the interface $\varGamma _{\mathrm {int}}$. In doing so, these conditions are incorporated as appropriate boundary conditions in the PDEs. Without limiting the generality, let us assume that deformations of the mechanical system are the only source for the acoustic field and the boundary conditions at the outer boundary of $\varOmega _{\mathrm {fluid}}$ are zero. Then, the weak forms for the mechanical domain $\varOmega _{\mathrm {solid}}$ and acoustic domain $\varOmega _{\mathrm {fluid}}$ in potential formulation become (density $\varrho _{\mathrm {0s}}$ of the solid)

$$\begin{aligned} \int \limits _{\varOmega _{\mathrm {solid}}} \varrho _{\mathrm {0s}} \mathbf {w} \cdot \ddot{\mathbf {u}} \; \mathrm {d}\varOmega + \int \limits _{\varOmega _{\mathrm {solid}}} \!\left( \mathcal {B} \mathbf {w} \right) ^\mathrm {t}\!\left[ {\mathbf {c}} \right] \mathcal {B} \mathbf {u} \; \mathrm {d}\varOmega - \int \limits _{\varGamma _{\mathrm {int}}} \mathbf {w} \cdot \mathbf {T}_{\mathbf {n}} \; \mathrm {d}\varGamma&= \int \limits _{\varOmega _{\mathrm {solid}}} \mathbf {w} \cdot \mathbf {f}_{\mathrm {V}} \; \mathrm {d}\varOmega \end{aligned}$$

(4.106)

$$\begin{aligned} \int \limits _{\varOmega _{\mathrm {fluid}}} \frac{1}{c_0^2} w \; \ddot{\varPsi } \; \mathrm {d}\varOmega + \int \limits _{\varOmega _{\mathrm {fluid}}} \nabla w \cdot \nabla \varPsi \; \mathrm {d}\varOmega + \int \limits _{\varGamma _{\mathrm {int}}} w \; \mathbf {n} \cdot \nabla \varPsi \; \mathrm {d}\varGamma&= 0 \end{aligned}$$

(4.107)

with the test function $\mathbf {w}\!\left( \mathbf {r} \right)$ (vector quantity) for the mechanical field and $w\!\left( \mathbf {r} \right)$ (scalar quantity) for the acoustic field. While for strong coupling, the interface integrals $\smash {\int _{\varGamma _{\mathrm {int}}}}$ are required for both fields, weak coupling is solely based on the interface integral in (4.107).

Now, we can insert in (4.106) and (4.107) the coupling conditions from Table 4.3, which yields

$$\begin{aligned} \int \limits _{\varOmega _{\mathrm {solid}}} \varrho _{\mathrm {0s}} \mathbf {w} \cdot \ddot{\mathbf {u}} \; \mathrm {d}\varOmega + \int \limits _{\,\,\,\varOmega _{\mathrm {solid}}} \!\left( \mathcal {B} \mathbf {w} \right) ^\mathrm {t}\!\left[ {\mathbf {c}} \right] \mathcal {B} \mathbf {u} \; \mathrm {d}\varOmega + \int \limits _{\varGamma _{\mathrm {int}}} \varrho _{\mathrm {0f}} \mathbf {w} \cdot \mathbf {n} \frac{\partial \varPsi }{\partial t} \; \mathrm {d}\varGamma&= \int \limits _{\varOmega _{\mathrm {solid}}} \mathbf {w} \cdot \mathbf {f}_{\mathrm {V}} \; \mathrm {d}\varOmega \end{aligned}$$

(4.108)

$$\begin{aligned} \int \limits _{\varOmega _{\mathrm {fluid}}} \frac{1}{c_0^2} w \; \ddot{\varPsi } \; \mathrm {d}\varOmega + \int \limits _{\varOmega _{\mathrm {fluid}}} \nabla w \cdot \nabla \varPsi \; \mathrm {d}\varOmega - \int \limits _{\varGamma _{\mathrm {int}}} w \; \mathbf {n} \cdot \frac{\partial \mathbf {u}}{\partial t} \; \mathrm {d}\varGamma&= 0 \;. \end{aligned}$$

(4.109)

Subsequently to introducing Lagrange ansatz functions for $\mathbf {u}$, $\mathbf {w}$, $\varPsi$, and w (see Sects. 4.3 and 4.4), we end up with a symmetric algebraic system of equations in matrix form

$$\begin{aligned} \!\left[ \begin{array}{cc} \varvec{\mathsf {M}}_{\mathbf {u}} &{} 0 \\ 0 &{} - \varrho _{\mathrm {0f}} \varvec{\mathsf {M}}_{\varPsi } \end{array} \right] \!\left[ \begin{array}{c} \ddot{\varvec{\mathsf {u}}} \\ \ddot{\varvec{\varPsi }} \end{array} \right] + \underbrace{\!\left[ \begin{array}{cc} 0 &{} \varvec{\mathsf {C}}_{\mathbf {u}\varPsi } \\ \varvec{\mathsf {C}}_{\mathbf {u}\varPsi }^\mathrm {t}&{} 0 \end{array} \right] }_{\text {coupling}} \!\left[ \begin{array}{c} \dot{\varvec{\mathsf {u}}} \\ \dot{\varvec{\varPsi }} \end{array} \right] + \!\left[ \begin{array}{cc} \varvec{\mathsf {K}}_{\mathbf {u}} &{} 0 \\ 0 &{} - \varrho _{\mathrm {0f}} \varvec{\mathsf {K}}_{\varPsi } \end{array} \right] \!\left[ \begin{array}{c} \varvec{\mathsf {u}} \\ \varvec{\varPsi } \end{array} \right] = \!\left[ \begin{array}{c} \varvec{\mathsf {f}}_{\mathbf {u}} \\ 0 \end{array} \right] \;. \end{aligned}$$

(4.110)

The vector $\varvec{\mathsf {u}}$ contains approximated values of the mechanical displacement at the nodes of $\varOmega _{\mathrm {solid}}$ and $\varvec{\varPsi }$ those of the acoustic velocity potential in $\varOmega _{\mathrm {fluid}}$. The matrices $\varvec{\mathsf {M}}_{\mathbf {u}}$, $\varvec{\mathsf {M}}_{\varPsi }$, $\varvec{\mathsf {K}}_{\mathbf {u}}$, $\varvec{\mathsf {K}}_{\varPsi }$, and the right-hand side $\varvec{\mathsf {f}}_{\mathbf {u}}$ are assembled as discussed in Sects. 4.3 and 4.4. By means of the matrix $\varvec{\mathsf {C}}_{\mathbf {u} \varPsi }$, we perform the coupling of the mechanical and acoustic fields. $\varvec{\mathsf {C}}_{\mathbf {u} \varPsi }$ is composed as

$$\begin{aligned} \varvec{\mathsf {C}}_{\mathbf {u} \varPsi } = \sum \limits _{l=1}^{n_{\mathrm {int}}} \varvec{\mathsf {C}}_{\mathbf {u} \varPsi }^l \; ; \qquad \varvec{\mathsf {C}}_{\mathbf {u} \varPsi }^l = \!\left[ \varvec{\mathsf {c}}_{ij}^l \right] \; ; \qquad \varvec{\mathsf {c}}_{ij}^l=\int \limits _{\varGamma _{\mathrm {e}}} \varrho _{\mathrm {0f}} \!\left( \varvec{\mathsf {N}}_i N_j \right) \cdot \mathbf {n} \;\mathrm {d}\varGamma \end{aligned}$$

(4.111)

with the part $\varGamma _{\mathrm {e}}$ of $\varGamma _{\mathrm {int}}$ and the number $n_{\mathrm {int}}$ of finite elements along the interface. Note that in case of weak coupling, $\varvec{\mathsf {C}}_{\mathbf {u} \varPsi }$ is omitted in the first line of (4.110). Therefore, the mechanical system can be computed directly without considering the acoustic field. The calculation of the acoustic field demands mechanical quantities at the interface $\varGamma _{\mathrm {int}}$ of $\varOmega _{\mathrm {solid}}$ and $\varOmega _{\mathrm {fluid}}$.

Alternatively to the potential formulation, one is able to investigate mechanical–acoustic coupling with the pressure formulation. However, the resulting algebraic system of equations in matrix form is not symmetric anymore, which involves increasing computational effort.

As for the mechanical and acoustic fields, different types of analysis are possible here. A static analysis makes no sense because the acoustic field is based on alternating quantities. For the harmonic and eigenfrequency analysis, we transform (4.110) into the complex frequency domain. The transient analysis can be carried out again according to the Newmark scheme (see Sect. 4.1.4).

Although $\varvec{\mathsf {C}}_{\mathbf {u} \varPsi }$ refers to the first derivative with respect to time, it should not be confused with attenuation. In order to take attenuation into account within the coupled mechanical–acoustic system, we can use appropriate complex-valued material parameters.

The conventional mechanical–acoustic coupling demands computational grids that coincide at the interface $\varGamma _{\mathrm {int}}$ of mechanical domain $\varOmega _{\mathrm {solid}}$ and acoustic domain $\varOmega _{\mathrm {fluid}}$. However, in many practical situations, we want to conduct independent spatial discretizations in both domains. This is especially important because the mechanical domain often calls for a finer computational grid (e.g., due to complicated structures) than the acoustic domain. An approach to get rid of the limitation at $\varGamma _{\mathrm {int}}$ is called nonconforming grids [14]. The idea of this approach lies in appropriately modifying the coupling matrix $\varvec{\mathsf {C}}_{\mathbf {u} \varPsi }$ in (4.111). Note that similar approaches also exist for other fields, e.g., electromagnetics.

In many cases, the acoustic domain $\varOmega _{\mathrm {fluid}}$ in mechanical–acoustic coupling is rather large. Owing to the comparatively low sound velocities of fluids (e.g., air), the acoustic wavelength takes small values, which implies a fine computational grid. Even though $\varOmega _{\mathrm {fluid}}$ is homogeneous, the required computational grid causes an excessive computational effort, especially for transient FE analysis. A potential remedy for the calculation of the pulse-echo behavior of ultrasonic transducers was suggested by Lerch et al. [16]. They model the piezoelectric ultrasonic transducer as well as a thin fluid layer with the FE method. The wave propagation inside the remaining fluid is described by the Helmholtz integral. Close to the transducer, the FE method gets coupled to the Helmholtz integral. A similar approach was recently presented in [18, 21]. Instead of the Helmholtz integral, the wave propagation in the fluid is described by the so-called spatial impulse response (SIR; see Sect. 7.1.2) of the ultrasonic transducer. Since there exist piecewise continuous solutions of the SIR for some shapes of the active transducer surface (e.g., piston-type transducer), this approach enables a highly efficient calculation of the sound field in the fluid. The method was successfully exploited to determine transient output signals of an acoustic microscope, which is based on a high-frequency ultrasonic transducer.