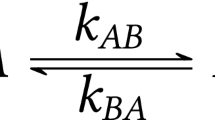In this chapter we consider the decay of an optically excited state of a donor molecule in a fluctuating medium. The fluctuations are modelled by time-dependent decay rates k (electron transfer), \(k_{-1}\) (backreaction), \(k_{da}\) (deactivation by fluorescence or radiationless transitions) and \(k_{cr}\) (charge recombination to the groundstate) (Fig. 9.1).

The time evolution is described by the system of rate equations

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}W(D^{*})= & {} -k(t)W(D^{*})+k_{-1}(t)W(D^{+}A^{-})-k_{da}W(D^{*})\nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}W(D^{+}A^{-})= & {} k(t)W(D^{*})-k_{-1}(t)W(D^{+}A^{-})-k_{cr}W(D^{+}A^{-}) \end{aligned}$$
(9.1)

which has to be combined with suitable equations describing the dynamics of the environment. First we discuss a simple dichotomous model [32] where the fluctuations of the rates are modeled by a random process switching between two values representing two different configurations of the environment. We solve the master equation and discuss the limits of fast and slow solvent fluctuations. In the second part, we apply continuous time random walk processes to model the diffusive motion. For an uncorrelated Markovian process, the coupled equations are solved with the help of the Laplace transformation. The results are generalized to describe the powertime law as observed for CO rebinding in myoglobin at low temperatures.

1 Dichotomous Model

The fluctuations of the rates are modeled by random jumps between two different configurations (±) of the environment which modulates the values of the rates. The probabilities of the two states are determined by the master equation

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( \begin{array}{c} W(+)\\ W(-) \end{array}\right) =\left( \begin{array}{cc} -\alpha &{} \beta \\ \alpha &{} -\beta \end{array}\right) \left( \begin{array}{c} W(+)\\ W(-) \end{array}\right) \end{aligned}$$
(9.2)
Fig. 9.1
figure 1

Electron transfer in a fluctuating medium. The rates are time dependent

Full size image

which has the general solution

$$\begin{aligned} W(+)= & {} C_{1}+C_{2}\mathrm{e}^{-(\alpha +\beta )t}\nonumber \\ W(-)= & {} C_{1}\frac{\alpha }{\beta }-C_{2}\mathrm{e}^{-(\alpha +\beta )t}. \end{aligned}$$
(9.3)

Obviously the equilibrium values are

$$\begin{aligned} W_{eq}(+)=\frac{\beta }{\alpha +\beta }\quad W_{eq}(-)=\frac{\alpha }{\alpha +\beta } \end{aligned}$$
(9.4)

and the correlation function is (with \(Q_{\pm }=\pm 1\))

$$\begin{aligned}<Q(t)Q(0)>= & {} W_{eq}(+)(P(+,t|+, 0)-P(-,t|+, 0))\nonumber \\+ & {} W_{eq}(-)(P(-,t|-, 0)-P(+,t|-, 0))\nonumber \\= & {} (W_{eq}(+)-W_{eq}(-))^{2}+4W_{eq}(+)W_{eq}(-)\mathrm{e}^{-(\alpha +\beta )t}\nonumber \\= & {} <Q>^{2}+\,(<Q^{2}>-<Q>^{2})\mathrm{e}^{-(\alpha +\beta )t}. \end{aligned}$$
(9.5)

Combination of the two systems of equations (9.1, 9.2) gives the equation of motion

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\mathbf {W}=A\mathbf {W} \end{aligned}$$
(9.6)

for the four-component state vector

$$\begin{aligned} \mathbf {W}=\left( \begin{array}{c} W(D^{*},+)\\ W(D^{*},-)\\ W(D^{+}A^{-},+)\\ W(D^{+}A^{-},-) \end{array}\right) \end{aligned}$$
(9.7)

with the rate matrix

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\alpha -k^{+}-k_{da} &{} \beta &{} k_{-1}^{+} &{} 0\\ \alpha &{} -\beta -k^{-}-k_{da} &{} 0 &{} k_{-1}^{-}\\ k^{+} &{} 0 &{} -\alpha -k_{-1}^{+}-k_{cr} &{} \beta \\ 0 &{} k^{-} &{} \alpha &{} -\beta -k_{-1}^{-}-k_{cr} \end{array}\right) . \end{aligned}$$
(9.8)

Generally, the solution of this equation can be expressed by using the left- and right eigenvectors and the eigenvalues \(\lambda \) of the rate matrix which obey

$$\begin{aligned} A\mathbf {R}_{\nu }=\lambda _{\nu }\mathbf {R}_{\nu } \end{aligned}$$
(9.9)
$$\begin{aligned} \mathbf {L}_{\nu }A=\lambda _{\nu }\mathbf {L}_{\nu }. \end{aligned}$$
(9.10)

For the initial values \(\mathbf {W}(0)\) the solution is given byFootnote 1

$$\begin{aligned} \mathbf {W}(t)=\sum _{\nu =1}^{4}\frac{(\mathbf {L}_{\nu }\bullet \mathbf {W}(0))}{(\mathbf {L}_{\nu }\bullet \mathbf {R}_{\nu })}\mathbf {R}_{\nu }\mathrm{e}^{\lambda _{\nu }t}. \end{aligned}$$
(9.11)

In the following we consider a simplified case of gated transfer with \(k_{da}=k_{cr}=k_{-1}^{\pm }=k^{-}=0\) (Fig. 9.2). Then the rate matrix becomes

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\alpha -k^{+} &{} \beta &{} 0 &{} 0\\ \alpha &{} -\beta &{} 0 &{} 0\\ k^{+} &{} 0 &{} -\alpha &{} \beta \\ 0 &{} 0 &{} \alpha &{} -\beta \end{array}\right) . \end{aligned}$$
(9.12)

As initial values we chose

$$\begin{aligned} W_{0}=\left( \begin{array}{c} W_{eq}(+)\\ W_{eq}(-)\\ 0\\ 0 \end{array}\right) =\left( \begin{array}{c} \frac{\beta }{\alpha +\beta }\\ \frac{\alpha }{\alpha +\beta }\\ 0\\ 0 \end{array}\right) . \end{aligned}$$
(9.13)
Fig. 9.2
figure 2

Gated electron transfer

Full size image

There is one eigenvalue \(\lambda _{1}=0\) corresponding to the eigenvectors

$$\begin{aligned} R_{1}=\left( \begin{array}{c} 0\\ 0\\ \beta \\ \alpha \end{array}\right) \quad L_{1}=\left( \begin{array}{cccc} 1&1&1&1\end{array}\right) . \end{aligned}$$
(9.14)

This reflects simply conservation of \(\sum _{\nu =1}^{4}W_{\nu }\) in this special case. The contribution of the zero eigenvector is

$$\begin{aligned} \frac{\mathbf {L}_{1}\bullet \mathbf {W}(0)}{\mathbf {L}_{1}\bullet \mathbf {R}_{1}}\mathbf {R}_{1}=\frac{1}{\alpha +\beta }\left( \begin{array}{c} 0\\ 0\\ \beta \\ \alpha \end{array}\right) =\left( \begin{array}{c} 0\\ 0\\ W_{eq}(+)\\ W_{eq}(-) \end{array}\right) . \end{aligned}$$
(9.15)

A second eigenvalue \(\lambda _{2}=-(\alpha +\beta )\) corresponds to the equilibrium in the final state \(D^{+}A^{-}\) where no further reactions take place

$$\begin{aligned} \mathbf {R}_{2}=\left( \begin{array}{c} 0\\ 0\\ 1\\ -1 \end{array}\right) \quad \mathbf {L}_{2}=\left( \begin{array}{cccc} \alpha&-\beta&\alpha&-\beta \end{array}\right) . \end{aligned}$$
(9.16)

The contribution of this eigenvalue is

$$\begin{aligned} \frac{L_{2}\bullet P_{0}}{L_{2}\bullet R_{2}}R_{2}=0 \end{aligned}$$
(9.17)

since we assumed equilibrium in the initial state. The remaining two eigenvalues are

$$\begin{aligned} \lambda _{3,4}=-\frac{\alpha +\beta +k}{2}\pm \frac{1}{2}\sqrt{(\alpha +\beta +k)^{2}-4\beta k} \end{aligned}$$
(9.18)

and the resulting decay will be in general biexponential. We consider two limits:

1.1 Fast Solvent Fluctuations

In the limit of small k we expand the square root to find

$$\begin{aligned} \lambda _{3,4}=-\frac{\alpha +\beta }{2}\pm \frac{\alpha +\beta }{2}-\frac{k}{2}\pm \frac{\alpha -\beta }{\alpha +\beta }\frac{k}{2}+\cdots \end{aligned}$$
(9.19)

One of the eigenvalues is

$$\begin{aligned} \lambda _{3}=-(\alpha +\beta )-\frac{\alpha }{\alpha +\beta }k+\cdots \end{aligned}$$
(9.20)

In the limit of \(k\rightarrow 0\) the corresponding eigenvectors are

$$\begin{aligned} \mathbf {R}_{3}=\left( \begin{array}{c} 1\\ -1\\ -1\\ 1 \end{array}\right) \quad \mathbf {L}_{3}=\left( \begin{array}{cccc} \alpha&-\beta&0&0\end{array}\right) \end{aligned}$$
(9.21)

and will not contribute significantly. The second eigenvalue

$$\begin{aligned} \lambda _{4}=-\frac{\beta }{\alpha +\beta }k+\cdots =-W_{eq}(+)k \end{aligned}$$
(9.22)

is given by the average rate. The eigenvectors are

$$\begin{aligned} \mathbf {R}_{4}=\left( \begin{array}{c} \beta \\ \alpha \\ -\beta \\ -\alpha \end{array}\right) \quad \mathbf {L}_{4}=\left( \begin{array}{cccc} 1&1&0&0\end{array}\right) \end{aligned}$$
(9.23)

and the contribution to the dynamics is

$$\begin{aligned} \frac{\left( \mathbf {L}_{4}{\cdot }\mathbf {W}_{0}\right) }{\left( \mathbf {L}_{4}\cdot \mathbf {R}_{4}\right) }\mathbf {R}_{4}\mathrm{e}^{\lambda _{4}t}=\frac{1}{\alpha +\beta }\left( \begin{array}{c} \beta \\ \alpha \\ -\beta \\ -\alpha \end{array}\right) \mathrm{e}^{\lambda _{4}t}. \end{aligned}$$
(9.24)

The total time dependence is approximately given by

$$\begin{aligned} W=\left( \begin{array}{c} W_{eq}(+)\mathrm{e}^{\lambda _{4}t}\\ W_{eq}(-)\mathrm{e}^{\lambda _{4}t}\\ W_{eq}(+)(1-\mathrm{e}^{\lambda _{4}t})\\ W_{eq}(-)(1-\mathrm{e}^{\lambda _{4}t}) \end{array}\right) . \end{aligned}$$
(9.25)

1.2 Slow Solvent Fluctuations

In the opposite limit we expand the square root for small \(k^{-1}\) to find

$$\begin{aligned} \lambda _{3,4}=-\frac{\alpha +\beta }{2}-\frac{k}{2}\pm \frac{1}{2}\left( k+(\alpha -\beta )+2\alpha \beta k^{-1}+\cdots \right) \end{aligned}$$
(9.26)
$$\begin{aligned} \lambda _{3}=-\beta +\frac{\alpha \beta }{k}+\cdots \end{aligned}$$
(9.27)
$$\begin{aligned} \mathbf {R}_{3}=\left( \begin{array}{c} 0\\ 1\\ 0\\ -1 \end{array}\right) \quad \mathbf {L}_{3}=\left( \begin{array}{cccc} \alpha&k&0&0\end{array}\right) \end{aligned}$$
(9.28)
$$\begin{aligned} \lambda _{4}=-k-\alpha +\cdots \end{aligned}$$
(9.29)
$$\begin{aligned} \mathbf {R}_{4}=\left( \begin{array}{c} k\\ -\alpha \\ -k\\ \alpha \end{array}\right) \quad \mathbf {L}_{4}=\left( \begin{array}{cccc} 1&0&0&0\end{array}\right) \end{aligned}$$
(9.30)

and the time evolution is approximately

$$\begin{aligned} W(t)=\left( \begin{array}{c} \dfrac{\beta }{\alpha +\beta }\mathrm{e}^{-kt}\\ \dfrac{\alpha }{\alpha +\beta }(\mathrm{e}^{-\beta t}-\frac{\beta }{k}\mathrm{e}^{-kt})\\ \dfrac{\beta }{\alpha +\beta }(1-\mathrm{e}^{-kt})\\ \dfrac{\alpha }{\alpha +\beta }(1-\mathrm{e}^{-\beta t}+\frac{\beta }{k}\mathrm{e}^{-kt}) \end{array}\right) . \end{aligned}$$
(9.31)

This corresponds to an inhomogeneous situation. One part of the ensemble is in a favorable environment and decays with the fast rate k. The rest has to wait for a suitable fluctuation which appears with a rate of \(\beta \).

1.3 Numerical Example

Figure 9.3 shows the transition from fast to slow solvent fluctuations.

Fig. 9.3
figure 3

Nonexponential decay. Numerical solutions of (9.12) are shown for \(\alpha =0.1, \beta =0.9\), (a) \(k=0.2\), (b) \(k=2\), (c) \(k=5\), (d) \(k=10\). Dotted curves show the two components of the initial state, solid curves show the total occupation of the initial state

Full size image

2 Continuous Time Random Walk Processes

Diffusive motion can be modeled by random walk processes along a one dimensional coordinate.

2.1 Formulation of the Model

The fluctuations of the coordinate X(t) are described as random jumps [33, 34]. The time intervals between the jumps (waiting time ) and the coordinate changes are random variables with independent distribution functions

$$\begin{aligned} \psi (t_{n+1}-t_{n})\quad \text {and}\quad f(X_{n+1}, X_{n}). \end{aligned}$$
(9.32)
Fig. 9.4
figure 4

Continuous time random walk

Full size image

The probability that no jump happened in the interval \(0\cdots t\) is given by the survival function

$$\begin{aligned} \varPsi _{0}(t)=1-\int _{0}^{t}\psi (t')\mathrm{d}t'=\int _{t}^{\infty }\psi (t')\mathrm{d}t' \end{aligned}$$
(9.33)

and the probability of finding the walker at position X at time t is given by (Fig. 9.4)

$$\begin{aligned} P(X,t)=P(X, 0)\int _{t}^{\infty }\psi (t')dt'+\int _{0}^{t}dt'\int _{-\infty }^{\infty }dX'\psi (t-t')f(X,X')P(X', t'). \end{aligned}$$
(9.34)

Two limiting cases are well known from the theory of collisions. The correlated process with

$$\begin{aligned} f(X, X')=f(X-X') \end{aligned}$$
(9.35)

corresponds to weak collisions. It includes normal diffusion processes as a special case. For instance if we chose

$$\begin{aligned} \psi (t_{n+1}-t_{n})=\delta (t_{n+1}-t_{n}-\varDelta t) \end{aligned}$$
(9.36)

and

$$\begin{aligned} f(X-X')=p\delta (X-X'-\varDelta X)+(1-p)\delta (X-X'+\varDelta X) \end{aligned}$$
(9.37)

we have

$$\begin{aligned} P(X,t+\varDelta t)=pP(X-\varDelta X,t)+qP(X+\varDelta X, t),\quad p+q=1 \end{aligned}$$
(9.38)

and in the limit \(\varDelta t\rightarrow 0\), \(\varDelta X\rightarrow 0\) Taylor expansion gives

$$\begin{aligned} P(X,t)+\frac{\partial P}{\partial t}\varDelta t+\cdots =P(X, t)+\frac{\partial P}{\partial X}(q-p)\varDelta X+\frac{\partial ^{2}P}{\partial X^{2}}\varDelta X^{2}+\cdots \quad \end{aligned}$$
(9.39)

The leading terms constitute a diffusion equation

$$\begin{aligned} \frac{\partial P}{\partial t}P=(q-p)\frac{\varDelta X}{\varDelta t}\frac{\partial P}{\partial X}+\frac{\varDelta X^{2}}{\varDelta t}\frac{\partial ^{2}P}{\partial X^{2}} \end{aligned}$$
(9.40)

with drift velocity \((q-p)\frac{\varDelta X}{\varDelta t}\) and diffusion constant \(\frac{\varDelta X^{2}}{\varDelta t}\).

The uncorrelated process, on the other hand with

$$\begin{aligned} f(X, X')=f(X) \end{aligned}$$
(9.41)

corresponds to strong collisions. This kind of process can be analyzed analytically and will be applied in the following.

The (normalized) stationary distribution \(\varPhi _{eq}\) of the uncorrelated process obeys

$$\begin{aligned} \varPhi _{eq}(X)= & {} \varPhi _{eq}(X)\int _{t}^{\infty }\psi (t')dt'+f(X)\int _{0}^{t}dt'\psi (t-t')\int _{-\infty }^{\infty }dX'\phi _{eq}(X')\nonumber \\= & {} \varPhi _{eq}(X)\int _{t}^{\infty }\psi (t')dt'+f(X)\int _{0}^{t}dt'\psi (t') \end{aligned}$$
(9.42)

which shows that

$$\begin{aligned} f(X)=\varPhi _{eq}(X). \end{aligned}$$
(9.43)

2.2 Exponential Waiting Time Distribution

Consider an exponential distribution of waiting times

$$\begin{aligned} \psi (t)=\tau ^{-1}\mathrm{e}^{-t/\tau }\quad \varPsi _{0}(t)=\int _{t}^{\infty }\tau ^{-1}\mathrm{e}^{-t'/\tau }dt'=\mathrm{e}^{-t/\tau }. \end{aligned}$$
(9.44)

It can be obtained from a Poisson process which corresponds to the master equation

$$\begin{aligned} \frac{\mathrm{d}P_{n}}{\mathrm{d}t}=-\tau ^{-1}P_{n}+\tau ^{-1}P_{n-1}\quad n=0,1,2\ldots \end{aligned}$$
(9.45)

with the solution

$$\begin{aligned} P_{n}(0)=\delta _{n, 0},\quad P_{n}(t)=\frac{(t/\tau )^{n}}{n!}\mathrm{e}^{-t/\tau } \end{aligned}$$
(9.46)

if we identify the survival function with the probability to be in the initial state \(P_{0}\)

$$\begin{aligned} \varPsi (t)=P_{0}(t)=\mathrm{e}^{-t/\tau }. \end{aligned}$$
(9.47)

The general uncorrelated process (9.34) becomes for an exponential distribution

$$\begin{aligned} P(X,t)=P(X, 0)\mathrm{e}^{-t/\tau }+\int _{0}^{t}dt'\tau ^{-1}\mathrm{e}^{-(t-t')/\tau }\int dX'f(X,X')P(X', t'). \end{aligned}$$
(9.48)

Laplace transformation gives

$$\begin{aligned} \tilde{P}(X,s)=P(X, 0)\frac{1}{s+\tau ^{-1}}+\frac{\tau ^{-1}}{s+\tau ^{-1}}\int dX'f(X,X')\tilde{P}(X', s) \end{aligned}$$
(9.49)

which can be simplified

$$\begin{aligned} \left( s+\tau ^{-1}\right) \tilde{P}(X,s)=P(X, 0)+\tau ^{-1}\int dX'f(X,X')\tilde{P}(X', s). \end{aligned}$$
(9.50)

Back transformation gives

$$\begin{aligned} \left( \frac{\mathrm{d}}{\mathrm{d}t}+\tau ^{-1}\right) P(X, t)=\tau ^{-1}\int dX'f(X,X')P(X', t) \end{aligned}$$
(9.51)

and finally

$$\begin{aligned} \frac{\partial }{\partial t}P(X, t)=-\frac{1}{\tau }P(X, t)+\frac{1}{\tau }\int dX'f(X,X')P(X', t) \end{aligned}$$
(9.52)

which is obviously a Markovian process, since it involves only the time t. For the special case of an uncorrelated process with exponential waiting time distribution, the motion can be described by

$$\begin{aligned} \frac{\partial }{\partial t}P(X,t)=\mathcal {L}P(X, t) \end{aligned}$$
(9.53)
$$\begin{aligned} \mathcal {L}P(X, t)=-\frac{1}{\tau }\left( P(X, t)-\phi _{eq}(X)<P(t)>\right) . \end{aligned}$$
(9.54)

2.3 Coupled Equations

Coupling of motion along the coordinate X with the reactions gives the following system of equations [35, 36]

$$\begin{aligned} \frac{\partial }{\partial t}P(X, t)= & {} \left( -k(X)+\mathcal {L}_{1}-\tau _{1}^{-1}\right) P(X, t)+k_{-1}(X)C(X,t)\nonumber \\ \frac{\partial }{\partial t}C(X, t)= & {} \left( -k_{-1}(X)+\mathcal {L}_{2}-\tau _{2}^{-1}\right) C(X,t)+k(X)P(X, t) \end{aligned}$$
(9.55)

where \(P(X, t)\varDelta X\) and \(C(X, t)\varDelta X\) are the probabilities of finding the system in the electronic state \(D^{*}\) or \(D^{+}A^{-}\), respectively, \(\mathcal {L}_{1,2}\) are operators describing the motion in the two states and the rates \(\tau _{1,2}^{-1}\) account for depopulation via additional channels. For the uncorrelated Markovian process (9.54) the rate equations take the form

$$ \frac{\partial }{\partial t}\left( \begin{array}{c} P(X,t)\\ C(X, t) \end{array}\right) =-\left( \begin{array}{cc} k(X)+\tau _{1}^{-1}+\tau ^{-1} &{} -k_{-1}(X)\\ -k(X) &{} k_{-1}(X)+\tau _{2}^{-1}+\tau ^{-1} \end{array}\right) \left( \begin{array}{c} P(X,t)\\ C(X, t) \end{array}\right) $$
$$\begin{aligned} +\tau ^{-1}\left( \begin{array}{cc} \phi _{1}(X)\\ &{} \phi _{2}(X) \end{array}\right) \left( \begin{array}{c}<P(t)>\\ <C(t)> \end{array}\right) \end{aligned}$$
(9.56)

which can be written in matrix notation as

$$\begin{aligned} \frac{\partial }{\partial t}\mathbf {R}(X,t)=-A(X)\mathbf {R}(X, t)+\tau ^{-1}B(X)<\mathbf {R}(t)>. \end{aligned}$$
(9.57)

Substitution

$$\begin{aligned} \mathbf {R}(X,t)=\exp \left\{ -A(X)\mathbf {U}(X, t)\right\} \end{aligned}$$
(9.58)

gives

$$ -A(X)\mathbf {R}(X,t)+\exp \left\{ -A(X)\frac{\partial }{\partial t}\mathbf {U}(X, t)\right\} $$
$$\begin{aligned} =-A(X)\mathbf {R}(X, t)+\tau ^{-1}B(X)<\mathbf {R}(t)> \end{aligned}$$
(9.59)
$$\begin{aligned} \frac{\partial }{\partial t}\mathbf {U}(X, t)=\tau ^{-1}\exp \left\{ A(X)t\right\} B(X)<\mathbf {R}(t)>. \end{aligned}$$
(9.60)

Integration gives

$$\begin{aligned} \mathbf {U}(X,t)=\mathbf {U}(X, 0)+\tau ^{-1}\int _{0}^{t}\exp \left\{ A(X)t'\right\} B(X)<\mathbf {R}(t')>dt' \end{aligned}$$
(9.61)
$$\begin{aligned} \mathbf {R}(X,t)\,{=}\,\exp (-A(X)t)\mathbf {R}(X, 0)+\tau ^{-1}\int _{0}^{t}\exp (A(X)(t'-t))B(X)<\mathbf {R}(t')>dt' \end{aligned}$$
(9.62)

and the total populations obey the integral equation

$$\begin{aligned}<\mathbf {R}(t)>=<\exp (-At)\mathbf {R}(0)>+\tau ^{-1}\int _{0}^{t}<\exp (A(t'-t))B> <\mathbf {R}(t')>dt' \end{aligned}$$
(9.63)

which can be solved with the help of a Laplace transformation

$$\begin{aligned} \tilde{\mathbf {R}}(s)=\int _{0}^{\infty }\mathrm{e}^{-st}<\mathbf {R}(t)>dt \end{aligned}$$
(9.64)
$$\begin{aligned} \int _{0}^{\infty }\mathrm{e}^{-st}\exp (-At)dt=(s+A)^{-1} \end{aligned}$$
(9.65)
$$\begin{aligned} \int _{0}^{\infty }\mathrm{e}^{-st}\mathrm{d}t\int _{0}^{t}<\exp (A(t'-t))B> <\mathbf {R}(t')>dt'=<(s+A)^{-1}B>\tilde{\mathbf {R}}(s). \end{aligned}$$
(9.66)

The Laplace transformed integral equation

$$\begin{aligned} \tilde{\mathbf {R}}(s)=<(s+A)^{-1}\mathbf {R}(0)>+\tau ^{-1}<(s+A)^{-1}B>\tilde{\mathbf {R}}(s) \end{aligned}$$
(9.67)

is solved by

$$\begin{aligned} \tilde{\mathbf {R}}(s)=\left[ 1-\tau ^{-1}<(s+A)^{-1}B>\right] ^{-1}<(s+A)^{-1}\mathbf {R}(0)>. \end{aligned}$$
(9.68)

We assume that initially the system is in the initial state D* and the motion is equilibrated

$$\begin{aligned} \mathbf {R}(X, 0)=\left( \begin{array}{c} \phi _{1}(X)\\ 0 \end{array}\right) . \end{aligned}$$
(9.69)

For simplicity, we treat here only the case of \(\tau _{12}\rightarrow \infty \). Then we have

$$\begin{aligned} A=\left( \begin{array}{cc} k+\tau ^{-1} &{} -k_{-1}\\ -k &{} k_{-1}+\tau ^{-1} \end{array}\right) \end{aligned}$$
(9.70)
$$\begin{aligned} (s+A)^{-1}= & {} \frac{1}{(s+\tau ^{-1})(s+\tau ^{-1}+k+k_{-1})}\left( \begin{array}{cc} s+\tau ^{-1}+k_{-1} &{} k_{-1}\\ k &{} s+\tau ^{-1}+k \end{array}\right) \nonumber \\ \end{aligned}$$
(9.71)

and with the abbreviations

$$\begin{aligned} \alpha =\left( 1+\frac{1}{s+\tau ^{-1}}(k+k_{-1})\right) ^{-1} \end{aligned}$$
(9.72)

and

$$\begin{aligned} <f(X)>_{1,2}\,=\int \phi _{1,2}(X)f(X)dX \end{aligned}$$
(9.73)

we find

$$\begin{aligned}&<(s+A)^{-1}\mathbf {R}(0)>\nonumber \\= & {} \left\langle \frac{\phi _{1}\alpha }{(s+\tau ^{-1})^{2}}\left( \begin{array}{c} \alpha ^{-1}(s+\tau ^{-1})-k\\ k \end{array}\right) \right\rangle =\left( \begin{array}{c} \dfrac{1}{s+\tau ^{-1}}-\dfrac{1}{(s+\tau ^{-1})^{2}}<\alpha k>_{1}\\ \dfrac{1}{(s+\tau ^{-1})^{2}}<\alpha k>_{1} \end{array}\right) \nonumber \\ \end{aligned}$$
(9.74)

as well as

$$\begin{aligned}&<(s+A)^{-1}B>\nonumber \\= & {} \left( \begin{array}{cc} \dfrac{1}{s+\tau ^{-1}}-\dfrac{1}{(s+\tau ^{-1})^{2}}<\alpha k>_{1} &{} \dfrac{1}{(s+\tau ^{-1})^{2}}<\alpha k_{-1}>_{2}\\ \dfrac{1}{(s+\tau ^{-1})^{2}}<\alpha k>_{1} &{} \dfrac{1}{s+\tau ^{-1}}-\dfrac{1}{(s+\tau ^{-1})^{2}}<\alpha k_{-1}>_{2} \end{array}\right) \nonumber \\ \end{aligned}$$
(9.75)

and the final result becomes

$$\begin{aligned} \tilde{\mathbf {R}}(s)= & {} \frac{1}{s(s^{2}+\tau ^{-1}(s+<\alpha k>_{1}+<\alpha k_{-1}>_{2}))}\nonumber \\\times & {} \left( \begin{array}{c} s(s+\tau ^{-1})-s<\alpha k>_{1}+\tau ^{-1}<\alpha k_{-1}>_{2}\\ (s+\tau ^{-1})<\alpha k>_{1} \end{array}\right) . \end{aligned}$$
(9.76)

Let us discuss the special case of thermally activated electron transfer. Here

$$\begin{aligned}<\alpha k>_{1},<\alpha k_{-1}>_{2}\ll 1 \end{aligned}$$
(9.77)

and the decay of the initial state is approximately given by

$$\begin{aligned} P(s)=\frac{(s+\tau ^{-1})+\tau ^{-1}s^{-1}<\alpha k_{-1}>_{2}}{(s^{2}+\tau ^{-1}s^{-1}(1+<\alpha k>_{1}+<\alpha k_{-1}>_{2})}=\frac{s+K_{2}}{s^{2}+s(K_{1}+K_{2})} \end{aligned}$$
(9.78)

with

$$\begin{aligned} K_{2}= & {} \tau ^{-1}\left( 1+s^{-1}\int dX\phi _{2}(X)\frac{k_{-1}(X)}{1+\dfrac{1}{s+\tau ^{-1}}(k(X)+k_{-1}(X))}\right) \end{aligned}$$
(9.79)
$$\begin{aligned}\approx & {} \int dX\phi _{2}(X)\frac{k_{-1}(X)}{1+\tau (k(X)+k_{-1}(X)}\end{aligned}$$
(9.80)
$$\begin{aligned} K_{1}= & {} \int dX\phi _{1}(X)\frac{k(X)}{1+\tau (k(X)+k_{-1}(X))}. \end{aligned}$$
(9.81)

This can be visualized as the result of a simplified kinetic scheme

$$\begin{aligned} \frac{d}{dt}<P>= & {} -K_{1}<P>+K_{2}<C>\end{aligned}$$
(9.82)
$$\begin{aligned} \frac{d}{dt}<C>= & {} K_{1}<P>-K_{2}<C> \end{aligned}$$
(9.83)

with the Laplace transform

$$\begin{aligned} s\tilde{P}-P(0)= & {} -K_{1}\tilde{P}+K_{2}\tilde{C}\end{aligned}$$
(9.84)
$$\begin{aligned} s\tilde{C}-C(0)= & {} K_{1}\tilde{P}+K_{2}\tilde{C} \end{aligned}$$
(9.85)

which has the solution

$$\begin{aligned} P=\frac{sP_{0}+K_{2}(P_{0}+C_{0})}{s(s+K_{1}+K_{2})}\quad C=\frac{sC_{0}+K_{1}(C_{0}+P_{0})}{s(s+K_{1}+K_{2})}. \end{aligned}$$
(9.86)

In the time domain we find

$$\begin{aligned} P(t)=\frac{K_{2}+K_{1}\mathrm{e}^{-(K_{1}+K_{2})t}}{K_{1}+K_{2}}\quad C(t)=\frac{K_{1}}{K_{1}+K_{2}}\left( 1-\mathrm{e}^{-(K_{1}+K_{2})t}\right) . \end{aligned}$$
(9.87)

Let us now consider the special case that the back reaction is negligible and \(k(X)=k\Theta (X)\) (Fig. 9.5). Here, we have

$$\begin{aligned} \tilde{P}(s)=\frac{s(s+\tau ^{-1})-s<\alpha k>_{1}}{s(s^{2}+\tau ^{-1}(s+<\alpha k>_{1}))} \end{aligned}$$
(9.88)
$$ <\alpha k>_{1}=\int dX\phi _{1}(X)\frac{k(X)}{1+\frac{k(X)}{s+\tau ^{-1}}}=\int _{0}^{\infty }\phi _{1}(X)\frac{k}{1+\frac{k}{s+\tau ^{-1}}}dX $$
$$\begin{aligned} =bk\dfrac{s+\tau ^{-1}}{k+s+\tau ^{-1}}\quad b=\int _{0}^{\infty }\phi _{1}(X)dX\quad a=1-b=\int _{-\infty }^{0}\phi _{1}(X)dX \end{aligned}$$
(9.89)
$$\begin{aligned} \tilde{P}(s)=\frac{\left( s+\tau ^{-1}-bk\dfrac{s+\tau ^{-1}}{k+s+\tau ^{-1}}\right) }{\left( s^{2}+\tau ^{-1}(s+bk\dfrac{s+\tau ^{-1}}{k+s+\tau ^{-1}})\right) }=\frac{s+\tau ^{-1}+k(1-b)}{s^{2}+s(\tau ^{-1}+k)+bk\tau ^{-1}}. \end{aligned}$$
(9.90)

Inverse Laplace transformation gives a biexponential behaviour

$$\begin{aligned} P(t)=\frac{(\mu _{+}+k(1-2b))\mathrm{e}^{-t(k+\mu _{-})/2}-(\mu _{-}+k(1-2b))\mathrm{e}^{-t(k+\mu _{+})/2}}{\mu _{+}-\mu _{-}} \end{aligned}$$
(9.91)

with

$$\begin{aligned} \mu _{\pm }=\tau ^{-1}\pm \sqrt{k^{2}+\tau ^{-2}+2k\tau ^{-1}(1-2b)}. \end{aligned}$$
(9.92)
Fig. 9.5
figure 5

Slow solvent limit

Full size image

If the fluctuations are slow \(\tau ^{-1}\ll k\) then

$$\begin{aligned} \sqrt{k^{2}+\tau ^{-2}+2k\tau ^{-1}(1-2b)}=k+(1-2b)\tau ^{-1}+\cdots \end{aligned}$$
(9.93)
$$\begin{aligned} \mu _{+}=k+2(1-b)\tau ^{-1}+\cdots \quad \mu _{-}=-k+2b\tau ^{-1}+\cdots \end{aligned}$$
(9.94)

and the two time constants are approximately

$$\begin{aligned} \frac{k+\mu _{+}}{2}=k+\cdots \quad \frac{k+\mu _{-}}{2}=b\tau ^{-1}+\cdots \end{aligned}$$
(9.95)

3 Powertime Law Kinetics

The last example can be generalized to describe the powertime law as observed for CO rebinding in myoglobin at low temperatures. The protein motion is now modeled by a more general uncorrelated process.Footnote 2

We assume that the rate k is negligible for \(X<0\) and very large for \(X>0\). Consequently only jumps \(X<0\rightarrow X>0\) are considered. Then the probability obeys the equation

$$\begin{aligned} P(X, t)_{|X<0}= & {} P(X, 0)\int _{t}^{\infty }\psi (t')dt'+\int _{-\infty }^{0}dX'\int _{0}^{t}dt'\psi (t-t')f(X)P(X', t')\nonumber \\= & {} \phi _{eq}(X)\varPsi _{0}(t)+\phi _{eq}(X)\int _{0}^{t}dt'\psi (t-t')\int _{-\infty }^{0}dX'P(X', t')\nonumber \\ \end{aligned}$$
(9.96)
$$\begin{aligned} \varPsi _{0}(t)=\int _{t}^{\infty }\psi (t')dt'\quad \tilde{\varPsi _{0}}(s)=\frac{1-\tilde{\psi }(s)}{s} \end{aligned}$$
(9.97)

and the total occupation of inactive configurations is

$$\begin{aligned} P_{<}(t)= & {} \int _{-\infty }^{0}dX\phi _{eq}(X)\left( \varPsi _{0}(t)+\int _{0}^{t}dt'\psi (t-t')P_{<}(t')\right) \nonumber \\= & {} a\left( \varPsi _{0}(t)+\int _{0}^{t}dt'\psi (t-t')P_{<}(t')\right) . \end{aligned}$$
(9.98)

Laplace transformation gives

$$\begin{aligned} \tilde{P}_{<}(s)=a\left( \tilde{\varPsi }_{0}(s)+\tilde{\psi }(s)\tilde{P}_{<}(s)\right) \end{aligned}$$
(9.99)

with

$$\begin{aligned} a=\int _{-\infty 0}^{0}dX\phi _{eq}(X) \end{aligned}$$
(9.100)

and the decay of the initial state is given by

$$\begin{aligned} \tilde{P}_{<}(s)=\frac{a\tilde{\varPsi }_{0}(s)}{1-a\tilde{\psi }(s)}=\frac{1}{s+\frac{1-a}{a\tilde{\varPsi _{0}(s)}}}. \end{aligned}$$
(9.101)

For a simple Poisson process (9.44) with

$$\begin{aligned} \tilde{\varPsi }_{0}=\frac{1}{s+\tau ^{-1}} \end{aligned}$$
(9.102)

this gives

$$\begin{aligned} \tilde{P}_{<}(s)=\frac{a}{s+(1-a)\tau ^{-1}} \end{aligned}$$
(9.103)

which reproduces the exponential decay found earlier in the slow solvent limit (9.95)

$$\begin{aligned} P_{<}(t)=a\mathrm{e}^{-t\,(1-a)/\tau }. \end{aligned}$$
(9.104)

The long time behaviour is given by the asymptotic behavior for \(s\rightarrow 0\). As \(P_{<}(t)\rightarrow 0\) for \(t\rightarrow \infty \) this is also the case for \(\tilde{P}_{<}(s)\) in the limit \(s\rightarrow 0\). Hence the asymptotic behaviour must be

$$\begin{aligned} \tilde{P}_{<}(s)\approx \frac{a\tilde{\varPsi _{0}(s)}}{1-a}\rightarrow 0\quad s\rightarrow 0 \end{aligned}$$
(9.105)
$$\begin{aligned} P_{<}(t)\rightarrow \frac{a}{1-a}\varPsi _{0}(t)\quad t\rightarrow \infty . \end{aligned}$$
(9.106)

In order to describe a powertime law at long times

$$\begin{aligned} P_{<}(t)\rightarrow t^{-\beta }\quad t\rightarrow \infty \end{aligned}$$
(9.107)
$$\begin{aligned} \tilde{P}_{<}(s)\rightarrow s^{\beta -1}\quad s\rightarrow 0 \end{aligned}$$
(9.108)

the waiting time distribution has to be chosen as

$$\begin{aligned} \varPsi _{0}(t)\sim \frac{1}{(zt)^{\beta }}\quad t\rightarrow \infty . \end{aligned}$$
(9.109)

which implies

$$\begin{aligned} \tilde{\varPsi }_{0}(s)\sim z^{-\beta }s^{\beta -1} \end{aligned}$$
(9.110)

where \(z^{-1}\) is the characteristic time for reaching the asymptotics. Finally, we find

$$\begin{aligned} \tilde{P}_{<}(s)\sim \frac{1}{s+\frac{1-a}{a}z^{\beta }s^{1-\beta }}=\frac{1}{s(1+(\tilde{z}/s)^{\beta })}. \end{aligned}$$
(9.111)

In the time domain this corresponds to the Mittag–Leffler functionFootnote 3

$$\begin{aligned} P_{<}(t)=\sum _{l=0}^{\infty }\frac{(-1)^{l}(\tilde{z}t)^{\beta l}}{\varGamma (\beta l+1)}=E_{\beta }(-(\tilde{z}t)^{\beta }) \end{aligned}$$
(9.112)

which can be approximated by the simpler function

$$\begin{aligned} \frac{1}{1+(t/\tau )^{\beta }}. \end{aligned}$$
(9.113)