In this chapter we study chemical equilibrium reactions. In thermal equilibrium of forward and backward reactions, the overall reaction rate vanishes and the ratio of the rate constants gives the equilibrium constant which usually shows an exponential dependence on the inverse temperature.Footnote 1 We derive the van’t Hoff relation for the equilibrium constant and discuss its statistical interpretation.

1 Arrhenius Law

Reaction rate theory goes back to Arrhenius who in 1889 investigated the temperature-dependent rates of inversion of sugar in the presence of acids. Empirically, a temperature dependence is often observed of the form

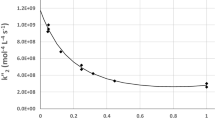
$$\begin{aligned} k(T)=A\mathrm{e}^{-E_{a}/k_{B}T} \end{aligned}$$
(14.1)

with the activation energy \(E_{a}\). Considering a chemical equilibrium (Fig. 14.1)

$$\begin{aligned} \text{ A }\begin{array}{c} k\\ \rightleftharpoons \\ k' \end{array}\text{ B }. \end{aligned}$$
(14.2)

This gives for the equilibrium constant

$$\begin{aligned} K=\frac{k}{k'} \end{aligned}$$
(14.3)

and

$$\begin{aligned} \ln K=\ln k-\ln k'=\ln A-\ln A'-\frac{E_{a}-E_{a}'}{k_{B}T}. \end{aligned}$$
(14.4)
Fig. 14.1
figure 1

Arrhenius law

Full size image

In equilibrium the thermodynamic forces vanish

$$\begin{aligned}&T=const\end{aligned}$$
(14.5)
$$\begin{aligned}&A=\sum _{k}\mu _{k}\nu _{k}=0. \end{aligned}$$
(14.6)

For dilute solutions with

$$\begin{aligned} \mu _{k}=\mu _{k}^{0}+k_{B}T\ln c_{k} \end{aligned}$$
(14.7)

we have

$$\begin{aligned} \sum _{k}\mu _{k}^{0}\nu _{k}+k_{B}T\sum _{k}\nu _{k}\ln c_{k}=0 \end{aligned}$$
(14.8)

which gives the van’t Hoff relation for the equilibrium constant

$$\begin{aligned} \ln (K_{c})=\sum _{k}\nu _{k}\ln c_{k}=-\frac{\sum _{k}\mu _{k}^{0}\nu _{k}}{k_{B}T}-\frac{\varDelta G^{0}}{k_{B}T}. \end{aligned}$$
(14.9)

The standard reaction free energy can be divided into an entropic and an energetic part

$$\begin{aligned} -\frac{\varDelta G^{0}}{k_{B}T}=\frac{-\varDelta H^{0}}{k_{B}T}+\frac{\varDelta S^{0}}{k}. \end{aligned}$$
(14.10)

Since volume changes are not important at atmospheric pressure, the free reaction enthalpy gives the activation energy difference

$$\begin{aligned} E_{a}-E_{a}'=\varDelta H^{0}. \end{aligned}$$
(14.11)

A catalyst can only change the activation energies but never the difference \(\varDelta H^{0}\).

2 Statistical Interpretation of the Equilibrium Constant

The chemical potential can be obtained as

$$\begin{aligned} \mu _{k}=\left( \frac{\partial F}{\partial N_{k}}\right) _{T,V,N_{k}'}=-k_{B}T\left( \frac{\partial \ln Z}{\partial N_{k}}\right) _{T,V, N_{k}'}. \end{aligned}$$
(14.12)

Using the approximation of the ideal gas we have

$$\begin{aligned} Z=\prod \frac{z_{k}^{N_{k}}}{N_{k}!} \end{aligned}$$
(14.13)

and

$$\begin{aligned} \ln Z\approx \sum _{k}N_{k}\ln z_{k}-N_{k}\ln N_{k}+N_{k} \end{aligned}$$
(14.14)

which gives the chemical potential

$$\begin{aligned} \mu _{k}=-k_{B}T\ln \frac{z_{k}}{N_{k}}. \end{aligned}$$
(14.15)

Let us consider a simple isomerization reaction

$$ \text{ A }\rightleftharpoons \text{ B }. $$

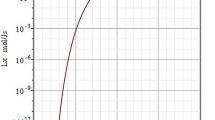
The partition functions for the two species are (Fig. 14.2)

$$\begin{aligned} z_{A}=\sum _{n=0,1\ldots }\mathrm{e}^{-\epsilon _{n}(A)/k_{B}T}\quad \quad z_{B}=\sum _{n=0,1,\ldots }\mathrm{e}^{-\epsilon _{n}(B)/k_{B}T}. \end{aligned}$$
(14.16)

In equilibrium

$$\begin{aligned}&\mu _{B}-\mu _{A}=0\end{aligned}$$
(14.17)
$$\begin{aligned}&-k_{B}T\ln \frac{z_{B}}{N_{B}}=-k_{B}T\ln \frac{z_{A}}{N_{A}}\end{aligned}$$
(14.18)
$$\begin{aligned}&\frac{z_{B}}{z_{A}}=\frac{N_{B}}{N_{A}}=(N_{B}/V)(N_{A}/V)^{-1}=K_{c}\end{aligned}$$
(14.19)
$$\begin{aligned}&K_{c}=\frac{\sum _{n=0,1,\ldots }\mathrm{e}^{-\epsilon _{n}(B)/k_{B}T}}{\sum _{n=0,1\ldots }\mathrm{e}^{-\epsilon _{n}(A)/k_{B}T}}=\frac{\sum _{n=0,1,\ldots }\mathrm{e}^{-(\epsilon _{n}(B)-\epsilon _{0}(B))/k_{B}T}}{\sum _{n=0,1\ldots }\mathrm{e}^{-(\epsilon _{n}(A)-\epsilon _{0}(A))/k_{B}T}}\mathrm{e}^{-\varDelta \epsilon /k_{B}T}. \end{aligned}$$
(14.20)

This is the thermal distribution over all energy states of the system.

Fig. 14.2
figure 2

Statistical interpretation of the equilibrium constant

Full size image