Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Let \(\mathcal C\) be a family of sets in \(\mathbb R^d\), and let \(P\subseteq \mathbb {R}^d\). We say that \({\mathcal C}\) is an m-fold covering of P if every point of P belongs to at least m members of \(\mathcal C\). A 1-fold covering is called a covering. Clearly, the union of m coverings is an m-fold covering. We will be mostly interested in the case when P is a large region or the whole space \(\mathbb {R}^d\).

Sphere packings and coverings have been studied for centuries, partially because of their applications in crystallography, Diophantine approximation, number theory, and elsewhere. The research in this field has been dominated by density questions of the following type: What is the most “economical” (i.e., least dense) m-fold covering of space by unit balls or by translates of a fixed convex body? It is suggested by many classical results and physical observations that, at least in low-dimensional spaces, the optimal arrangements are typically periodic, and they can be split into several lattice-like coverings [14, 15]. Does a similar phenomenon hold for all sufficiently “thick” multiple coverings, without any assumption on their densities?

About 15 years ago, a similar problem was raised for large scale ad hoc sensor networks; see Feige et al. [13], Buchsbaum et al. [6]. In the – by now rather extensive – literature, it is usually referred to as the sensor cover problem. In its simplest version it can be phrased as follows. Suppose that a large region P is monitored by a set of sensors, each having a circular range of unit radius and each powered by a battery of unit lifetime. Suppose that every point of P is within the range of at least m sensors, that is, the family of ranges of the sensors, \(\mathcal C\), forms an m-fold covering of P. If \(\mathcal C\) can be split into k coverings \(\mathcal C_1,\ldots ,\mathcal C_k\), then the region can be monitored by the sensors for at least k units of time (Fig. 1). Indeed, at time i, we can switch on all sensors whose ranges belong to \(\mathcal C_i\; (1 \le i \le k)\). We want to maximize k, in order to guarantee the longest possible service. Of course, the first question is the following.

Problem 1

(Pach, 1980 [31]). Is it true that every m-fold covering of the plane with unit disks splits into two coverings, provided that m is sufficiently large?

Fig. 1.
figure 1

Two simple examples.

Full size image

In a long unpublished manuscript, Mani and Pach [27] claimed that the answer to this question was in the affirmative with \(m\le 33\). Pach [35] warned that this “has never been independently verified.” Winkler [42] even conjectured that the statement is true with \(m=4\). For more than 30 years, the prevailing conjecture has been that for any open plane convex body (i.e., bounded convex set) C, there exists a positive integer \(m=m(C)\) such that every m-fold covering of the plane with translates of C splits into two coverings. This conjecture was proved in [32] for centrally symmetric convex polygons C. It took almost 25 years to generalize this statement to all convex polygons [38, 40]. Moreover, it was proved by Aloupis et al. [3] and Gibson and Varadarajan [19] that in these cases, for every integer k, every at least bk-fold covering splits into k coverings, where \(b=b(C)\) is a suitable positive constant. See [33, 34, 36], for surveys.

Here we disprove the above conjecture by giving a negative answer to Problem 1.

Theorem 1

For every positive integer m, there exists an m-fold covering of the plane with open unit disks that cannot be split into 2 coverings.

Our construction can be generalized as follows.

Theorem 2

Let C be any open plane convex set, which has two parallel supporting lines with positive curvature at their points of tangencies. Then, for every positive integer m, there exists an m-fold covering of the plane with translates of C that cannot be split into 2 coverings.

As was mentioned above, for every open convex polygon Q, there exists a smallest positive integer m(Q) such that every m(Q)-fold covering of the plane with translates of Q splits into 2 coverings. We have that \(\sup m(Q)=\infty \), where the sup is taken over all convex polygons Q. Otherwise, we could approximate the unit disk with convex n-gons with n tending to infinity. By compactness, we would conclude that the unit disk C satisfies \(m(C)<+\infty \), which contradicts Theorem 1.

Problem 2

Does there exist, for any \(n>3\), an integer m(n) such that every convex n-gon Q satisfies \(m(Q)\le m(n)\)?

For any triangle T, there is an affine transformation of the plane that takes it into an equilateral triangle \(T_0\). Therefore, we have \(m(T)=m(T_0)\) and m(3) is finite. For \(n=4\), Problem 2 is open.

In spite of our sobering negative answer to Problem 1 and its analogues in higher dimensions (cp. [27]), there are important classes of multiple coverings such that all of their members are splittable. According to our next, somewhat counter-intuitive result, for example, any m-fold covering of \(\mathbb {R}^d\) with unit balls can be split into 2 coverings, provided that no point of the space is covered by too many balls. (We could innocently believe that heavily covered points make it only easier to split an arrangement.)

Theorem 3

For every \(d\ge 2\), there exists a positive constant \(c_d\) with the following property. For every positive integer m, any m-fold covering of \(\mathbb {R}^d\) with unit balls can be split into two coverings, provided that no point of the space belongs to more than \(c_d2^{m/d}\) balls.

Theorem 3 was one of the first geometric applications of the Lovász local lemma [10], and it was included in [2]. Here, we establish a more general statement (see Theorem 5.2).

One may also believe that unbounded convex sets behave even worse than the bounded ones. It turns out, however, that this is not the case.

Theorem 4

Let C be an unbounded open convex set and let P be a finite set of points in the plane. Then every 3-fold covering of \(P\subset \mathbb {R}^2\) with translates of C can be split into two coverings of P.

In fact, using a standard compactness argument, Theorem 4 also holds if P is any compact set in the plane. However, Theorem 4 does not generalize to higher dimensions. Indeed, it follows from the proof of Theorem 1 that, for every positive integer m, there exists a finite family \(\mathcal C\) of open unit disks in the plane and a finite set \(P\subset \mathbb {R}^2\) such that \(\mathcal C\) is an m-fold covering of P that cannot be split into two coverings. Consider now an unbounded convex cone \(C'\) in \(\mathbb {R}^3\), whose intersection with the plane \(\mathbb {R}^2\) is an open disk. Take a system of translates of \(C'\) such that their intersections with the plane coincide with the members of \(\mathcal C\). These cones form an m-fold covering of P that cannot be split into two coverings.

For interesting technical reasons, the proof of Theorem 4 becomes much easier if we restrict our attention to multiple coverings of the whole plane. In fact, in this case, we do not even have to consider multiple coverings! Moreover, the statement remains true in higher dimensions.

Proposition 5

Let C be an unbounded line-free open convex set in \(\mathbb {R}^d\). Then every covering of \(\mathbb {R}^d\) with translates of C can be split into two, and hence into infinitely many, coverings.

The reason why we assume here that C is line-free (i.e., does not contain a full line) is the following. If C contains a straight line, then it can be obtained as the direct product of a line l and a \((d-1)\)-dimensional open convex set \(C'\). Any arrangement \(\mathcal C\) of translates of C in \(\mathbb {R}^d\) is combinatorially equivalent to the \((d-1)\)-dimensional arrangement of translates of \(C'\), obtained by cutting \(\mathcal C\) with a hyperplane orthogonal to l. In particular, the problem whether an m-fold covering of \(\mathbb {R}^d\) with translates of C can be split into two coverings reduces to the respective question about m-fold coverings of \(\mathbb {R}^{d-1}\) with translates of \(C'\).

Proposition 5 is false already in the plane without the assumption that C is open. However, every 2-fold covering of the plane with translates of an unbounded C can be split into two coverings. We omit the proof as it reduces to a simple claim about intervals.

However, in higher dimensions, the similar claim is false.

Theorem 6

There is a bounded convex set \(C'\subset \mathbb {R}^3\) with the following property. One can construct a family of translates of \(C=C'\times [0,\infty )\subset \mathbb {R}^4\) which covers every point of \(\mathbb {R}^4\) infinitely many times, but which cannot be split into two coverings.

Our construction is based on an example of Naszódi and Taschuk [30], and explores the fact that the boundary of \(C'\) can be rather “erratic.” We do not know whether sufficiently thick coverings of \(\mathbb {R}^3\) by translates of an unbounded line-free convex set can be split into two coverings or not.

In the sequel, we will study the equivalent “dual” form of the above questions. Consider a family \(\mathcal C=\{C_i : i\in I\}\) of translates of a set \(C\subset \mathbb {R}^d\) that form an m-fold covering of \(P\subseteq \mathbb {R}^d\). Suppose without loss of generality that C contains the origin 0. For every \(i\in I\), let \(c_i\) denote the point of \(C_i\) that corresponds to \(0\in C\). In other words, we have \(\mathcal C=\{ C+c_i : i\in I\}\). Assign to each \(p\in P\) a translate of \(-C\), the reflection of C about the origin, by setting \(C^*_p=-C+p\). Observe that

$$p\in C_i \;\; \Longleftrightarrow \;\; c_i\in C^*_p.$$

In particular, the fact that \(\mathcal C\) forms an m-fold covering of P is equivalent to the following property: Every member of the family \(\mathcal C^*=\{C^*_p : p\in P\}\) contains at least m elements of \(\{c_i : i\in I\}\). Thus, Theorem 1 can be rephrased in the following dual form.

Theorem 1’. For every \(m\ge 2\), there is a set of points \(P^*=P^*(m)\) in the plane with the property that every open unit disk contains at least m elements of \(P^*\), and no matter how we color the elements of \(P^*\) with two colors, there exists a unit disk such that all points in it are of the same color.

A set system not satisfying this condition is said to have property B (in honor of Bernstein) or is 2-colorable (see [9, 29, 39]). Generalizations of this notion are related to conflict-free colorings [12] and have strong connections, e.g., to the theory of \(\varepsilon \)-nets, geometric set covers and to combinatorial game theory [1, 18, 21, 34, 41].

The rest of this paper is organized as follows. In the next three sections, we prove Theorem 1’ in 3 steps. In Sect. 2, we exhibit a family of non-2-colorable m-uniform hypergraphs \(\mathcal {H}(k,l)\). In Sect. 3, we construct planar “realizations” of these hypergraphs, where the vertices correspond to points and the (hyper)edges to unit disks, preserving the incidence relations. In Sect. 4, we extend this construction, without violating the colorability condition, so that every disk contains at least m points. The proof of a more general version of Theorem 3, using the Lovász local lemma, can be found in Sect. 5. Finally, in Sect. 6 we make some concluding remarks and mention a couple of open problems.

The proof of Theorem 2, a generalization of Theorem 1 to bounded plane convex bodies with a smooth boundary, and the proofs of our results related to multiple coverings with unbounded convex sets, Theorem 4, Proposition 5, and Theorem 6, can be found in the full version of the paper available online.

2 A Family of Non-2-colorable Hypergraphs \(\mathcal {H}(k,l)\)

In this section we define, for any positive integers k and l, an abstract hypergraph \(\mathcal {H}(k,l)\) with vertex set V(k, l) and edge set E(k, l). The hypergraphs \(\mathcal {H}(k,l)\) are defined recursively. The edge set E(k, l) will be the disjoint union of two sets, , where the subscripts R and B stand for red and blue. All edges belonging to \(E_R(k,l)\) will be of size k, all edges belonging to \(E_B(k,l)\) will be of size l. In other words, \(\mathcal {H}(k,l)\) is the union of a k-uniform and an l-uniform hypergraph. If \(k=l=m\), we get an m-uniform hypergraph (Fig. 2).

Definition 2.1

Let k and l be positive integers.

  1. 1.

    For \(k=1\), let V(1, l) be an l-element set. Set \(E_R(1,l):=V(1,l)\) and \(E_B(1,l):=\{V(1,l)\}\).

  2. 2.

    For \(l=1\), let V(k, 1) be a k-element set. Set \(E_R(k,1):=\{V(k,1)\}\) and \(E_B(k,1):=V(k,1)\).

  3. 3.

    For any \(k,l>1\), we pick a new vertex p, called the root, and let

    $$\begin{aligned} E_R(k,l):=\{e\cup \{p\} \,:\, e\in E_R(k-1,l)\} \cup E_R(k,l-1), \end{aligned}$$
Fig. 2.
figure 2

The hypergraph \(\mathcal {H}(3,3)\) with (arbitrarily) 2-colored vertices. There is a blue (dashed) set with 3 blue vertices or a red (solid) set with 3 red vertices. (Color figure online)

Full size image

By recursion, we obtain that

$$|V(k,l)|={k+l\atopwithdelims ()k}-1,$$
$$|E_R(k,l)|={k+l-1\atopwithdelims ()k},\,\, |E_B(k,l)|={k+l-1\atopwithdelims ()l},$$
$$|E(k,l)|=|E_R(k,l)|+|E_B(k,l)|= {k+l\atopwithdelims ()k}.$$

Lemma 2.2

([37]). For any positive integers k, l, the hypergraph \(\mathcal {H}(k,l)\) is not 2-colorable. Moreover, for every coloring of V(k, l) with red and blue, there is an edge in \(E_R(k,l)\) such that all of its k vertices are red or an edge in \(E_B(k,l)\) such that all of its l vertices are blue.

For completeness, here we include the proof of Lemma 2.2 from [37]. The induction on two parameters, k and l, is similar to the proof of Ramsey’s theorem by Erdős and Szekeres [11].

Proof

We will prove that for every coloring of V(k, l) with red and blue, there is an edge in \(E_R(k,l)\) such that all of its k vertices are red or an edge in \(E_B(k,l)\) such that all of its l vertices are blue.

Suppose first that \(k=1\). If any vertex in V(1, l) is red, then it is a red singleton edge in \(\mathcal {H}(1,l)\). If all vertices in V(1, l) are blue, then the (only) edge \(V(1,l)\in E_B(1,l)\) contains only blue points. Analogously, the assertion is true if \(l=1\).

Suppose next that \(k, l >1\). Assume without loss of generality that the root p is red. Consider the subhypergraph \(\mathcal {H}(k-1,l)\subset \mathcal {H}(k,l)\) induced by the vertices in \(V(k-1,l)\). If it has a monochromatic red edge \(e\in E_R(k-1,l)\), then \(e\cup \{p\}\in E_R(k,l)\) is red. If there is a monochromatic blue edge in \(E_B(k-1,l)\), then we are again done, because it is also an edge in \(E_B(k,l)\).

For other interesting properties of the hypergraphs \(\mathcal {H}(k,l)\) related to hereditary discrepancy, see Matoušek [28].

3 Geometric Realization of the Hypergraphs \(\mathcal {H}(k,l)\)

The aim of this section is to establish the following weaker version of Theorem 1’.

Theorem 1”. For every \(m\ge 2\), there exists a finite point set \(P=P(m)\subset \mathbb {R}^2\) and a finite family of unit disks \(\mathcal C=\mathcal C(m)\) with the property that every member of \(\mathcal C\) contains at least m elements of P, and no matter how we color the elements of P with two colors, there exists a disk in \(\mathcal C\) such that all points in it are of the same color.

We realize the hypergraph \(\mathcal {H}(k,l)\) defined in Sect. 2 with points and disks. The vertex set V(k, l) is mapped to a point set \(P(k,l)\subset \mathbb {R}^2\), and the edge sets, \(E_R(k,l)\) and \(E_B(k,l)\), to families of open unit disks, \(\mathcal C_R(k,l)\) and \(\mathcal C_B(k,l)\), so that a vertex belongs to an edge if and only if the corresponding point is contained in the corresponding disk. The geometric properties of this realization are summarized in the following lemma.

Given two unit disks \(C,C'\), let \(d(C,C')\) denote the distance between their centers. We fix an orthogonal coordinate system in the plane so that we can talk about the topmost and the bottommost points of a disk.

Lemma 3.1

For any positive integers k, l and for any \(\varepsilon >0\), there is a finite point set \(P=P(k,l)\) and a finite family of open unit disks with the following properties.

  1. 1.

    Any disk \(C\in \mathcal C_R(k,l)\) (resp. \(\mathcal C_B(k,l)\)) contains precisely k (resp. l) points of P.

  2. 2.

    For any coloring of P with red and blue, there is a disk in \(\mathcal C_R(k,l)\) such that all of its points are red or a disk in \(\mathcal C_B(k,l)\) such that all of its point are blue. In fact, P and \(\mathcal C(k,l)\) realize the abstract hypergraph \(\mathcal {H}(k,l)\) in the above sense.

  3. 3.

    For the coordinates (x, y) of any point from P, we have \(-\varepsilon<x<\varepsilon \) and \(-\varepsilon ^2<y<\varepsilon ^2\).

  4. 4.

    For the coordinates (x, y) of the center of any disk from \(\mathcal C_R(k,l)\), we have \(-\varepsilon<x<\varepsilon \) and \(-\varepsilon ^2<y-1<\varepsilon ^2\).

  5. 5.

    For the coordinates (x, y) of the center of any disk from \(\mathcal C_B(k,l)\), we have \(-\varepsilon<x<\varepsilon \) and \(-\varepsilon ^2<y+1<\varepsilon ^2\).

  6. 6.

    The topmost and the bottommost points of a disk \(C\in \mathcal C(k,l)\) are not covered by the closure of any other member of \(\mathcal C(k,l)\).

Looking at our construction from “far away” the two families \(\mathcal C_R\) and \(\mathcal C_B\) look like two touching disks, with all points of P very close to the touching point. The segments connecting the centers of disks from different families are almost vertical with all members of \(\mathcal C_R\) lying “above” all members of \(\mathcal C_B\). We prove the lemma by induction. Most conditions are needed for the induction to go through. Condition 6 is an exception: it will be used in Sect. 4.

Fig. 3.
figure 3

The construction.

Full size image

Proof

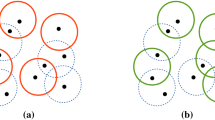
We give a recursive construction. We can assume that \(\varepsilon <1/10\). It is easy to see that, for \(k=1\) or \(l=1\), there exists such a family of unit disks for any \(\varepsilon >0\), see Fig. 3(a). The family \(\mathcal C(2,2)\) is depicted in Fig. 3(b), where the main idea of the induction may already be visible.

Suppose that \(k,l\ge 2\) and we have already constructed \(P(k-1,l)\) and \(\mathcal C(k-1,l)\), and \(P(k,l-1)\) and \(\mathcal C(k,l-1)\), for some \(\varepsilon (k-1,l)<\varepsilon /100\) and \(\varepsilon (k,l-1)<\varepsilon /100\), respectively. To obtain P(k, l), we place the root p of \(\mathcal {H}(k,l)\) into the origin (0, 0), and we shift (translate) \(P(k-1,l)\) and \(P(k,l-1)\) into new positions such that their roots are at \((-\varepsilon /3, -\varepsilon ^2/10)\) and \((\varepsilon /3, \varepsilon ^2/10)\), respectively. With a slight abuse of notation, the shifted copies will also be denoted \(P(k-1,l)\) and \(P(k,l-1)\). See Fig. 3. In this way, it is guaranteed that for the coordinates (x, y) of any point of P, we have

$$-\varepsilon<-(\varepsilon /3+\varepsilon (k-1,l)+\varepsilon (k,l-1))<x<\varepsilon /3+\varepsilon (k-1,l)+\varepsilon (k,l-1)<\varepsilon $$

and

$$-\varepsilon ^2<-(\varepsilon ^2/10+\varepsilon ^2(k-1,l)+\varepsilon ^2(k,l-1))<y<\varepsilon ^2/3+\varepsilon ^2(k-1,l)+\varepsilon ^2(k,l-1)<\varepsilon ^2.$$

Thus, property 3 of the lemma holds.

The family \(\mathcal C(k,l)\) is defined as the union of two previously defined families, \(\mathcal C(k-1,l)\) and \(\mathcal C(k,l-1)\), translated by the same vectors as \(P(k-1,l)\) and, resp. \(P(k,l-1)\) were. Again, we use the same symbols to denote the translated copies. To verify properties 4 and 5, we only have to repeat the above calculations, with the y-coordinates being shifted 1 higher (resp. 1 lower).

Now we show that our set of points P(k, l) and set of disks \(\mathcal C(k,l)\) realize the hypergraph \(\mathcal {H}(k,l)\) (properties 1 and 2). It is easy to see that if \(C\in \mathcal C_R(k-1,l)\) and \(s\in P(k,l-1)\), then \(s\notin C\) but \(p=(0,0)\in C\). The coordinates of the center of C are \(\big (-\varepsilon /3\pm \varepsilon (k-1,l), 1-\varepsilon ^2/10\pm \varepsilon ^2(k-1,l)\big )\) (where here and in the following, \(\pm z\) denotes a number that is between \(-z\) and z), so the distance of p from C is at most \((\varepsilon /3+\varepsilon (k-1,l))^2+(1-\varepsilon ^2/10+\varepsilon ^2(k-1,l))^2<1\). On the other hand, the coordinates of s are \(\big (\varepsilon /3\pm \varepsilon (k,l-1), \varepsilon ^2/10\pm \varepsilon ^2(k,l-1)\big )\), thus the square of its distance from the center of C is at least

$$\big (2\varepsilon /3-\varepsilon (k-1,l)-\varepsilon (k,l-1)\big )^2+\big (1-2\varepsilon ^2/10-\varepsilon ^2(k-1,l)-\varepsilon ^2(k,l-1)\big )^2>1.$$

Analogously, if \(C\in \mathcal C_B(k,l-1)\) and \(s\in P(k-1,l)\), then \(s\notin C\) but \(p=(0,0)\in C\).

Let \(C\in \mathcal C_R(k,l-1)\) and \(s\in P(k-1,l)\). We prove that \(p, s\notin C\). The coordinates of the center of C are \(\big (\varepsilon /3\pm \varepsilon (k,l-1), 1+\varepsilon ^2/10\pm \varepsilon (k,l-1)\big )\). Therefore, the distance of p from the center of C is at least \((\varepsilon /3-\varepsilon (k,l-1))^2+(1+\varepsilon ^2/10-\varepsilon (k,l-1))^2>1\). The calculation for s is similar in the case \(C\in \mathcal C_R(k-1,l)\). Analogously, we have that if \(C\in \mathcal C_B(k-1,l)\) and \(s\in P(k,l-1)\), then \(p, s\notin C\). As the disks in \(\mathcal C(k,l-1)\) (resp. \(\mathcal C(k-1,l)\)) contain precisely the same points of \(P(k,l-1)\) (resp. \(P(k-1,l)\), as before the shift, we have obtained a geometric realization of \(\mathcal {H}(k,l)\), and properties 1 and 2 hold.

It remains to prove that the topmost and the bottommost points of a disk \(C\in \mathcal C(k,l)\) are not covered by any other member of \(\mathcal C(k,l)\) (property 6). Using that our construction and disks are centrally symmetric, it is enough to prove the statement for the topmost points. If \(C\in \mathcal C_R(k,l-1)\), the coordinates of its topmost point are \(\big (\varepsilon /3\pm \varepsilon (k,l-1), 2+\varepsilon ^2/10\pm \varepsilon ^2(k,l-1)\big )\). If \(C\in \mathcal C_R(k-1,l)\), the coordinates of its topmost point are \(\big (-\varepsilon /3\pm \varepsilon (k-1,l), 2-\varepsilon ^2/10\pm \varepsilon ^2(k-1,l)\big )\). If \(C\in \mathcal C_B(k,l-1)\), the coordinates of its topmost point are \(\big (\varepsilon /3\pm \varepsilon (k,l-1), -2+\varepsilon ^2/10\pm \varepsilon ^2(k,l-1)\big )\). If \(C\in \mathcal C_B(k-1,l)\), the coordinates of its topmost point are \(\big (-\varepsilon /3\pm \varepsilon (k-1,l), -2-\varepsilon ^2/10\pm \varepsilon ^2(k-1,l)\big )\).

If \(C\in \mathcal C_R(k,l-1)\), by the induction hypothesis, its topmost point cannot be covered by any other disk from \(\mathcal C(k,l-1)\). Nor can it be covered by any other disk, as the topmost points of all other disks are below it (i.e., have smaller y-coordinates). If \(C\in \mathcal C_R(k-1,l)\), then the square of the distance of its topmost point from the center of some \(C'\in \mathcal C_R(k,l-1)\) is at least

$$\big (2\varepsilon /3 -\varepsilon (k,l-1)-\varepsilon (k-1,l)\big )^2 + \big (1-2\varepsilon ^2/10 -\varepsilon ^2(k,l-1)-\varepsilon ^2(k-1,l)\big )^2>1.$$

If \(C\in \mathcal C_B(k,l-1)\), then the distance of its topmost point from the center of some \(C'\in \mathcal C_R(k-1,l)\) is also at least

$$\big (2\varepsilon /3 -\varepsilon (k,l-1)-\varepsilon (k-1,l)\big )^2 + \big (1-2\varepsilon ^2/10 -\varepsilon ^2(k,l-1)-\varepsilon ^2(k-1,l)\big )^2>1.$$

In all other cases, trivially, the corresponding distances are also larger than 1. This completes the proof of property 6 and hence the lemma.

4 Adding points to P – Proof of Theorem 1’

In this section, we extend the proof of Theorem 1” to establish Theorem 1’ (which is equivalent to Theorem 1). Note that the only difference between Theorems 1” and 1’ is that in the latter it is also required that every unit disk of the plane contains at least m elements of the point set \(P^*=P^*(m)\). The set \(P=P(m,m)\) constructed in Lemma 3.1, does not satisfy this condition. In order to fix this, we will add all points not in \(\cup \mathcal C(m,m)\) to the set P (or rather a sufficiently dense discrete subset of \(\mathbb {R}^2\setminus \cup \mathcal C(m,m)\)). In order to show that the resulting set \(P^*\) meets the requirements of Theorem 1’, all we have to show is the following.

Lemma 4.1

No (open) unit disk \(C\notin \mathcal C(k,l)\) is entirely contained in \(\cup \mathcal C(k,l)\).

For future purposes, we prove this statement in a slightly more general form. In what follows, we only assume that C is an open convex body with a unique topmost point t and a unique bottommost point b, which divide the boundary of C into two closed arcs. They will be referred to as the left boundary arc and a right boundary arc.

Definition 4.2

A collection \(\mathcal C\) of translates of C is said to be exposed if the topmost and bottommost points of its members do not belong to the closure of any other member of \(\mathcal C\).

By the last condition in Lemma 3.1, the collections of disks \(\mathcal C(k,l)\) constructed in the previous section are exposed. We prove the following generalization of Lemma 4.1.

Lemma 4.3

Let \(\mathcal C\) be a finite exposed collection of translates of an open convex body C with unique topmost and bottommost points. If \(C\notin \mathcal C\), then \(C\not \subseteq \cup \mathcal C\).

For the proof, we need a simple observation.

Proposition 4.4

If the right boundary arcs of two translates of C intersect, then the closure of one of the translates must contain the topmost or bottommost point of the other.

Proof

Let \(C_1\) and \(C_2\) be the two translates, and let \(\gamma _i\) denote the closed convex curve formed by the right boundary arc of \(C_i\) and the straight-line segment connecting its two endpoints (the topmost and the bottommost points of \(C_i\)). The curves \(\gamma _1\) and \(\gamma _2\) are translates of each other, and since they intersect, they must cross twice. (At a crossing, one curve comes from the exterior of the other, then it shares an arc with it, which may be a single point, and enters the interior.) It cannot happen that both crossings occur between the right boundary arcs, because they are convex and translates of each other. Therefore, one of the two crossings involves the straight-line segment of one the curves, say, \(\gamma _1\). But since the condition is that the right boundary arcs intersect, one of the two endpoints of this straight-line segment, either the topmost or the bottommost point of \(C_1\), lies in the closure of \(C_2\).

Proof

(of Lemma 4.3 ). Suppose, for contradiction, that \(C\subseteq \cup \mathcal C\). By removing some members of \(\mathcal C\) if necessary, we can assume that \(\mathcal C\) is a minimal collection of translates that covers C. Then C must have a point which belongs to (at least) three translates, \(C_1, C_2, C_3\in \mathcal C\). None of the topmost and bottommost points of these translates can be covered by C, otherwise, it would also be covered by another member of \(\mathcal C\), contradicting the assumption that \(\mathcal C\) is exposed.

Thus, C intersects either the left or the right boundary arc of every \(C_i\). Without loss of generality, suppose that C intersects the right boundary arcs of \(C_1\) and \(C_2\). These right boundary arcs must intersect inside C, otherwise \(C_1\cap C\subseteq C_2\cap C\) or \(C_2\cap C\subseteq C_1\cap C\), and \(\mathcal C\) would not be minimal. Therefore, we can apply Proposition 4.4 to conclude that one of them must contain the topmost or bottommost point of the other.

Remark 1

In the construction described in Lemma 3.1, every disk in \(\mathcal C(m,m)\) contains at most \(|P(m,m)|<2^{2m}\) points. At the last stage, we added many new points to P. We can keep the maximum number of points of P lying in a unit disk bounded from above by a function f(m). What is the best upper bound? The bound given by our construction depends on \(\varepsilon (m,m)\le 100^{-2m}\varepsilon (1,1)\).

5 Bounded Coverings

We prove Theorem 3 in a somewhat more general form. For the proof we need the following consequence of the Lovász local lemma.

Lemma 5.1

(Erdős-Lovász [10]). Let \(k,m\ge 2\) be integers. If every edge of a hypergraph has at least m vertices and every edge intersects at most \({k^{m-1}/4(k-1)^m}\) other edges, then its vertices can be colored with k colors so that every edge contains at least one vertex of each color.

Let \(\mathcal C\) be a class of subsets of \(\mathbb R^d\). Given n members \(C_1,\ldots ,C_n\) of \(\mathcal C\), assign to each point \(x\in \mathbb R^d\) a characteristic vector \(c(x)=(c_1(x),\ldots ,c_n(x))\), where \(c_i(x)=1\) if \(x\in C_i\) and \(c_i(x)=0\) otherwise. The number of distinct characteristic vectors shows how many “pieces” \(C_1,\ldots , C_n\) cut the space into. The dual shatter function of \(\mathcal C\), denoted by \(\pi ^*_{\mathcal C}(n)\), is the maximum of this quantity over all n-tuples \(C_1,\ldots ,C_n\in \mathcal C\). For example, when \(\mathcal C\) is the family of open balls in \(\mathbb R^d\), it is well known that

$$\begin{aligned} \pi ^*_{\mathcal C}(n)\le {n-1\atopwithdelims ()d}+\sum _{i=0}^d {n\atopwithdelims ()i}\le n^d, \end{aligned}$$
(1)

provided that \(2\le d\le n\).

Theorem 5.2

Let \(\mathcal C\) be a class of open sets in \(\mathbb R^d\) with diameter at most D and volume at least v. Let \(\pi (n)=\pi ^*_{\mathcal C}(n)\) denote the dual shatter function of \(\mathcal C\), and let \(B^d\) denote the unit ball in \(\mathbb R^d\). Then, for every positive integer m, any m-fold covering of \(\mathbb R^d\) with members of \(\mathcal C\) splits into two coverings, provided that no point of the space is covered more than \(\frac{v}{(2D)^d Vol B^d}\pi ^{-1}(2^{m-3})\) times, where \(Vol B^d\) is the volume of \(B^d\).

Proof

Given an m-fold covering of \(\mathbb R^d\) in which no point is covered more than M times, define a hypergraph \(\mathcal {H}=(V,E)\), as follows. Let V consist of all members of \(\mathcal C\) that participate in the covering. To each point \(x\in \mathbb R^d\), assign a (hyper)edge e(x): the set of all members of the covering that contain x. (Every edge is counted only once.) Since every point x is covered by at least m members of \(\mathcal C\), every edge \(e(x)\in E\) consists of at least m points.

Consider two edges \(e(x),e(y)\in E\) with \(e(x)\cap e(y)\ne \emptyset \). Then there is a member of \(\mathcal C\) that contains both x and y, so that y must lie in the ball B(x, D) of radius D around x. Hence, all members of the covering that contain y lie in the ball B(x, 2D) of radius 2D around x. Since the volume of each of these members is at least v, and no point of B(x, 2D) is covered more than M times, we obtain that B(x, D) can be intersected by at most \(M Vol B(x,2D)/v=M(2D)^d Vol B^d/v\) members of the covering. By the definition of the dual shatter functions, those members of the covering that intersect B(x, D) cut B(x, D) into at most \(\pi (M(2D)^d Vol B^d/v)\) pieces, each of which corresponds to an edge of \(\mathcal {H}\). Therefore, for the maximum number N of edges of \(\mathcal {H}\) that can intersect the same edge \(e(x)\in E\), we have

$$N\le \pi (M(2D)^d Vol B^d/v).$$

According to Lemma 5.1 (for \(k=2\)), in order to show that the covering can be split into two, i.e., the hypergraph \(\mathcal {H}\) is 2-colorable, it is sufficient to assume that \(N\le 2^{m-3}\). Comparing this with the previous inequality, the result follows.

In the special case where \(\mathcal C\) is the class of unit balls in \(\mathbb R^d\), we have \(v=Vol B^d\), \(D=2\), and, in view of (1), \(\pi ^{-1}(z)\ge z^{1/d}\). Thus, we obtain Theorem 3 with \(c_d=2^{-2d-3/d}\).

If we want to decompose an m-fold covering into \(k>2\) coverings, then the above argument shows that it is sufficient to assume that

$$\pi (M(2D)^d Vol B^d/v)\le k^{m-1}/4(k-1)^m.$$

In case of unit balls, this holds for \(M\le c_{k,d}(1+\frac{1}{k-1})^{m/d}\) with \(c_{k,d}=k^{-1/d}4^{-d-1/d}\).

Two sets are homothets of each other if one can be obtained from the other by a dilation with positive coefficient followed by a translation. It is easy to see [20] that for \(d=2\), the dual shatter function of the class \(\mathcal C\) consisting of all homothets of a fixed convex set C is at most \(n^2-n+2\le n^2\), for every \(n\ge 2\). In this case, Theorem 5.2 immediately implies

Corollary 5.3

Every m-fold covering \(\mathcal C\) of the plane with homothets of a fixed convex set can be decomposed into two coverings, provided that no point of the plane belongs to more than \(2^{(m-11)/2}\) members of \(\mathcal C\).

Naszódi and Taschuk [30] constructed a convex set C in \(\mathbb R^3\) such that the dual shatter function of the class of all translates of C cannot be bounded from above by any polynomial of n. Therefore, for translates of C, the above approach breaks down. We do not know how to generalize Theorem 3 from balls to arbitrary convex bodies in \(\mathbb R^d\), for \(d\ge 3\).

For some related combinatorial results, see Bollobás et al. [5].

6 Open Problems and Concluding Remarks

Theorem 2 states that, if C is a plane convex body with two antipodal points at which the curvature is positive, then for every m, there exists an m-fold covering of \(\mathbb {R}^2\) with translates of C that does not split into two coverings. We also know that this statement is false for any convex polygon. But what happens if C “almost satisfies” the condition concerning the antipodal point pair?

Problem 3

Does there exist an integer m such that every m-fold covering of \(\mathbb {R}^2\) with translates of an open semidisk splits into two coverings?

Another question, which surprisingly is widely open even in a completely abstract setting, is the following.

Problem 4

Suppose that for a body C, there is an integer m such that every m-fold covering of \(\mathbb {R}^d\) with translates of C splits into two coverings. Does it follow that for every \(k>2\), there is an integer \(m_k\) such that every \(m_k\)-fold covering of \(\mathbb {R}^d\) with translates of C splits into k coverings? Is it true that (for the smallest such \(m_k\)) even \(m_k=O_C(k)\)?

According to Theorem 4, every 3-fold cover of a finite point set by the translates of an unbounded open convex set splits into two coverings. Keszegh and Pálvölgyi [25] recently extended this theorem to splitting any \((3k-2)\)-fold so-called pseudohalfplane arrangement into k coverings. The \(3k-2\) can probably be always improved to \(2k-1\), which was done in special cases, e.g., for translates of an unbounded open convex set.

As was stated in the introduction, for every triangle (in fact, for every convex polygon) C, there is an integer m(C) such that every m-fold covering of the plane with translates of C splits into two coverings. Keszegh and the Pálvölgyi [22] extended this theorem to m-fold coverings with homothets of a triangle. (Two sets are homothets of each other if one can be obtained from the other by a dilation with positive coefficient followed by a translation.) Using the idea of the proof of our Theorem 1, Kovács [26] has recently showed that the analogous statement is false for homothets of any convex polygon with more than 3 sides. For further results about decomposition of multiple coverings, see [4, 5, 7, 8, 19, 23, 24].