Keywords

1 Introduction

The information contained in the infrared image and the visible image is quite different and forms a complementary relationship, since the infrared image sensor’s approach of acquiring the target information’s band range and imaging mode is different from the visual one [1]. Through the fusion of the infrared image and the visible image, combing the complementary information and the redundant information of the two kinds of images, the fused image of the target has clear outline, rich information and the perception ability of the image sensor can be largely extended.

Wavelet has become an important means in image fusion for its well-known time frequency localization analysis properties. However, the advantages of the wavelet transform primarily are embodied in the analysis and process towards the one-dimensional segmentation smooth and function of bounded variation. When it has been applied in two-dimensional or higher dimensional case, the separable wavelet formed by one-dimensional wavelet has limited direction, and then cannot optimally represent line singularity or face singularity high-dimensional function [2]. Therefore, the wavelet transform can only reflect the point singularity of the signal, and can not reflect the two-dimensional image’s marginal, linear, characteristics.

Tetrolet transform is a geometric adaptive transform having tetromino support and the potential to adapt to the directional features of an image, it can be better applied in the image fusion [3].

2 Tetrolet Transform

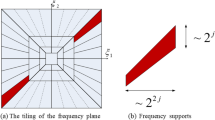
A new adaptive Haar wavelet transform, called tetrolet transform provides efficient image representation. Tetrolet is wavelet based efficient and effective transform, whose supports tetrominoes which are shapes are made by connecting four equal-sized squares. The corresponding filter bank algorithm is simple but enormously effective. In every level of the filter bank algorithm the low-pass image is divided into 4 × 4 blocks. Then in each block a local tetrolet basis is determined, which is adapted to the image geometry in this block. In discrete wavelet transformation (DWT), horizontal and vertical directions only preferred, which fails to achieve optimal results with images that contain geometric structures in other directions. To improve the treatment of orientated geometric image structures, tetrolet transform is introduced [4–9].

In the Haar filter bank, the low-pass filter and the high-pass filters are just given by the averaging sum and the averaging differences of each four pixel values which are arranged in a 2 × 2 square. Then we can determine the low-pass part \( a^{l} = \left( {a^{l} [i,j]} \right)_{i,j = 0}^{{\frac{N}{2} - 1}} \) with

$$ a^{l} [i,j] = \sum\limits_{{\left( {i^{{\prime }} ,j^{{\prime }} } \right) \in I_{i,j} }} { \in \left[ {0,L\left( {i^{{\prime }} ,j^{{\prime }} } \right)} \right]} a\left[ {i^{{\prime }} ,j^{{\prime }} } \right] $$
(1)

as well as the three high-pass parts for l = 1, 2, 3, \( w_{l}^{1} = \left( {w_{l}^{1} \left[ {i,j} \right]} \right)_{i,j = 0}^{{\frac{N}{2} - 1}} \) with

$$ w_{l}^{1} [i,j] = \sum\limits_{{\left( {i^{{\prime }} ,j^{{\prime }} } \right) \in I_{i,j} }} { \in \left[ {l,L(i^{{\prime }} ,j^{{\prime }} )} \right]} a\left[ {i^{{\prime }} ,j^{{\prime }} } \right] $$
(2)

where the coefficients ∈[l, m], l, m = 0, …, 3 are entries from the Haar wavelet transform matrix

$$ W = (a[l,m])_{l,m = 0}^{3} = \frac{1}{2}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 1 \\ 1 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 1 \\ { - 1} & { - 1} \\ \end{array} } \\ {\begin{array}{*{20}c} 1 & { - 1} \\ 1 & { - 1} \\ \end{array} } & {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \\ \end{array} } \right) $$
(3)

The decomposition algorithm of tetrolet transform is processed by four ways, which are as follows:

  1. (1)

    Divide the image into 4 × 4 blocks.

  2. (2)

    Find the sparsest tetrolet representation in each block.

  3. (3)

    Rearrange the low- and high-pass coefficients of each block into a 2 × 2 block.

  4. (4)

    Store the tetrolet coefficients (high-pass part).

  5. (5)

    Apply Steps 1 to 4 to the low-pass image.

Input image is considered as \( a^{0} = \left( {a\left| {i,j} \right|} \right)_{i,j = 0}^{N - 1} \)

with \( N = 2^{J} ,J \in N \) then J − 1 levels can be applied. In the \( rth \) level, r1, …, J − 1, the following computations are performed.

  1. Step 1:

    Divide the low-pass image \( a^{r - 1} \) into blocks \( Q_{i,j} \) of size 4 × 4, \( i,j = 0, \ldots ,\frac{N}{{4^{r} }} - 1 \).

  2. Step 2:

    In each block of \( Q_{i,j} \) there are 117 admissible tetromino coverings are considered, i.e., \( c = 1, \ldots ,117 \). For each tiling c Haar wavelet transform is applied to the four tetromino subsets \( I_{s}^{(c)} ,s = 0,1,2,3 \) In this way, four low-pass coefficients and 12 Tetrolet coefficients are obtained for each tiling of c. More precisely, in \( Q_{i,j} \) we compute analogously to (1) and (2) the pixel averages for every admissible tetromino configuration \( c = 1, \ldots ,117 \) by \( a^{r,(c)} = (a^{r,(c)} [s])_{s = 0}^{3} \) with

    $$ a^{r,(c)} [s] = \sum\limits_{{(m,n) \in I_{g}^{(c)} }} { \in [0,L(m,n)]a^{r - 1} } [m,n] $$
    (4)

    as well as the three high-pass parts l = 1, 2, 3, \( w_{l}^{r,(c)} = (w_{l}^{r,(c)} [s])_{s = 0}^{3} \) with

    $$ w_{l}^{r,(c)} [s] = \sum\limits_{{(m,n) \in I_{g}^{(c)} }} { \in [l,L(m,n)]a^{r - 1} } [m,n] $$
    (5)

    where the coefficients \( \in [l,L(m,n)] \) are given in (3) and where L is the bijective mapping, which relating the four index pairs (m, n) of \( I_{g}^{(c)} \) with the values 0, 1, 2, and 3 in descending order. That means, by the one-dimensional indexing J (m, n) the smallest index is identified with the value 0, while the largest with 3.

    Then the covering \( c^{*} \) is chose such that the l−1-norm of the 12 Tetrolet coefficients becomes minimal

    $$ c^{*} = \mathop {\arg \hbox{min} }\limits_{c} \sum\limits_{i = 1}^{3} {\left\| {w_{l}^{r,(c)} } \right\|}_{1} = \mathop {\arg \hbox{min} }\limits_{c} \sum\limits_{l = 1}^{3} {\sum\limits_{g = 0}^{3} {\left| {w_{l}^{r,(c)} [s]} \right|} } $$
    (6)

    Hence, for every block \( Q_{i,j} \) we get an optimal Tetrolet decomposition [\( a^{r,(c*)} ,W_{1}^{r,(c*)} ,W_{2}^{r,(c*)} ,W_{3}^{r,(c*)} \)]. By doing this, the local structure of the image block is adapted.

    The best covering c* is a covering whose tetrominoes do not intersect an important structure like an edge in the image a r−1. Because the tetrolet coefficients become as minimal as possible a sparse image representation will be obtained. For each block Qi,j the covering c* is stored such that has been chosen, since this information is necessary for reconstruction. If the optimal covering is not unique, then the tiling c* has taken that already chosen most frequently in the previous blocks. Thus, the coding of the used coverings becomes cheaper.

  1. Step 3:

    In order to be able to apply further levels of the tetrolet decomposition algorithm, the entries of the vectors \( a^{r,(c*)} \) are arranged and \( W_{l}^{r,(c*)} \) into 2 × 2 matrices using a reshape function R,

    $$ a_{{|Q_{i,j} }}^{r} = R(a^{r,(c*)} ) = \left( {\begin{array}{*{20}c} {a^{r,(c*)} [0]} & {a^{r,(c*)} [2]} \\ {a^{r,(c*)} [1]} & {a^{r,(c*)} [3]} \\ \end{array} } \right) $$
    (7)

    and in the same way \( w_{{l|Q_{i,j} }}^{r} = R(w_{l}^{r,(c*)} ) \) for l = 1, 2, 3. For an efficient representation in the next level, a suitable arrangement of the low-pass values is essential. That means, the order of labeling the tetrominoes of c* in each block Qi, j by s = 1, 2 and 3 is very important. The labeling should be done in a way, such that the geometry of the tiling is suitably mapped to \( \left( {\begin{array}{*{20}c} 0 & 2 \\ 1 & 3 \\ \end{array} } \right) \). Therefore the four shapes of the chosen partition c* are labeled by comparing with the square case.

  2. Step 4:

    After finding a sparse representation in every block Qi, j for \( i,j = 0, \ldots ,\frac{N}{{4^{r} }} - 1 \), the low-pass matrix is stored.

    $$ a^{r} = (a_{{|Q_{i,j} }}^{r} )_{i,j = 0}^{{\frac{N}{{4^{r} }} - 1}} $$
    (8)

    and the high-pass matrices

    $$ w_{l}^{r} = (w_{{l|Q_{i,j} }}^{r} )_{i,j = 0}^{{\frac{N}{{4^{r} }} - 1}} $$
    (9)

    L = 1, 2, 3, replacing the low-pass image a r−1 by the matrix

    $$ \left( {\begin{array}{*{20}c} {a^{r} } & {w_{2}^{r} } \\ {w_{1}^{r} } & {w_{3}^{r} } \\ \end{array} } \right) $$
    (10)

    After a suitable number of decomposition steps, a shrinkage procedure to the Tetrolet coefficients in order to get a sparse image representation is applied.

    $$ S_{\lambda } (x) = \left\{ {\begin{array}{*{20}l} {x,} \hfill & {\left| x \right| \ge \lambda } \hfill \\ {0,} \hfill & {\left| x \right| \ge \lambda } \hfill \\ \end{array} } \right. $$
    (11)

For the reconstruction of the image, low-pass coefficients are needed from the coarsest level and the Tetrolet coefficients as usual. Additionally, the information about the respective covering in each level and block is necessary.

3 The Infrared and Visible Image Fusion Algorithm Based on Tetrolet

The paper introduced the tetrolet into fusion of the infrared and visible image. The characters of the tetrolet can be better used in extracting the geometric features of the source image and provide more information for the fused image. When the fusion is processing, the different scales and different directional subbands can adopt different fusion rules. The better fused effect can be achieved through sufficiently digging original multi-source image’s visual information.

The high frequency subband after the tetrolet decomposition contains a lot of high frequency information of the image. The bigger coefficient’s absolute value corresponds to the certain directional interval’s significant characteristic, for example: marginal, linear, regional boundary, etc. The coefficients can better depict the image’s structure’s information, and have great influence upon human’s vision. The low frequency subband contains most of low frequency information of the image, and is the primary perception part of the human’s eyes to the image content. The paper judges and processes the fusion according to the characteristics of the low frequency subband and the high frequency subband with corresponding fusion rules, and the subband coefficient would thereby acquired.

According to the human visual system’s characteristics, we can know that the human’s eyes are not sensitive to the individual pixel’s gray value. The distinctness of the image is decided by the all pixels in certain region. To improve the fused image’s clearness, the pixel’s regional feature should be considered in the design of fusion algorithm. Therefore, the coefficient with the bigger regional variance value should be adopted as the fused image’s high frequency subband coefficient in tetrolet transform.

The specific fusion rules are show in the following:

  1. (1)

    Tetrolet decomposition is applied in the visible image V and the infrared image I in the level L. the high frequency subband \( V_{l}^{k} \) and \( I_{l}^{k} \left( {k = 1,2 \ldots ,2^{nl} ,l = 1,2, \ldots ,L} \right) \) and the low frequency subband \( V_{L}^{0} \) and \( I_{L}^{0} \). L is the value of the largest possible decomposition level. \( 2^{nl} \) is the directional value of each level’s decomposition.

  2. (2)

    The coefficient of the low frequency subband remains constant. The paper chooses two images’ average value of the coefficient of the low frequency subband as the fused image’s low frequency subband coefficient.

  3. (3)

    As for the high frequency subband’s coefficient, in the largest decomposition level L, the largest value of the two images which corresponds to decomposition scale values has been adopted as the fused image’s coefficient.

  4. (4)

    As for other \( L - 1 \) level high frequency coefficient, the maximum principle of the local variance has been adopted, that is to say, in the transform domain, calculating the corresponding point \( N \times N \) neighborhood’s local variance \( C_{X}^{k} \)(X as V or I), and choosing the highest coefficient of the variance as the fused image’s corresponding point’s coefficient.

At last, tetrolet inverse transformation has been applied to the fused image’s coefficient, and we get the fused image F.

4 Experiments

The paper has adopted several different approaches to fuse the two registrated infrared and visible images. The Fig. 1 presents a group of image fusion experimental results which is based on multi-image fusion approach. The Fig. 1a, b are infrared and visible image respectively. The Fig. 1c is the fused image based on the contrast pyramid decomposition. Figure 1d is the fused image based on the Laplacian pyramid decomposition. Figure 1f is the fused image based on the paper’s approach (Tetrolet). Among these, the approaches CP, DWT and LP have adopted the same fusion rule as this paper. In calculating the local variance, the \( N \times N \) = 3 × 3; LP, CT, DWT and tetrolet decomposition are all 3 levels.

Fig. 1
figure 1

Comparison of image fusion based on different rules. a Infrared image. b Visible image. c Fusion image using CP. d Fusion image using LP. e Fusion image using DWT. f Fusion image using Tetrolet

Full size image

From Fig. 1a–f are all much clearer than the infrared image (a), and contains the information of the visible image. But the Fig. 1c is a little obscure. There are some noisy spots in Fig. 1d. Compared with the figure (f), the figure (e) is much more obscure in the marginal part of the letter. Therefore, the fused figure (f) which is based on tetrolet transform has better visual effect.

To quantitatively evaluate the performances of the fusion approaches applied in the infrared and invisible image, we adopted many evaluation parameters to evaluate the approach mention in this paper and other approaches quantitatively. As the Table 1 shows, if the entropy and standard deviation acquired by a certain fusion approach is relatively larger, but the cross entropy is relatively smaller, and then we can say that the fusion approach is better. From the Table 1, as far as the infrared and the visible image are concerned, the tetrolet fusion approach which is put forward by the paper is better than LP, DWT and CP fusion approaches.

Table 1 Comparison of statistical parameters about fusion results according to different fusion rules
Full size table

5 Conclusions

The paper put forward an infrared and visible fusion algorithm which is based on the tetrolet transform. Compared with the traditional wavelet transform, tetrolet has anisotropy and translation invariance. The tetrolet transform can preserve the infrared and visible image’s feature information, enhance the fused image’s space detail representation ability, and improve the fused image’s information.