Finite Reasoning Procedures for Dynamic Games

Abstract

In this chapter we focus on the epistemic concept of common belief in future rationality (Perea [37]), which describes a backward induction type of reasoning for general dynamic games. It states that a player always believes that his opponents will choose rationally now and in the future, always believes that his opponents always believe that their opponents choose rationally now and in the future, and so on, ad infinitum. It thus involves infinitely many conditions, which might suggest that this concept is too demanding for real players in a game. In this chapter we show, however, that this is not true. For finite dynamic games we present a finite reasoning procedure that a player can use to reason his way towards common belief in future rationality.

1 Introduction

If you make a choice in a game, then you must realize that the final outcome does not only depend on your own choice, but also on the choices of your opponents. It is therefore natural that you first reason about your opponents in order to form a plausible belief about their choices, before you make your own choice. Now, how can we formally model such reasoning procedures about your opponents? And how do these reasoning procedures affect the choice you will eventually make in the game? These questions naturally lead to epistemic game theory– a modern approach to game theory which takes seriously the fact that the players in a game are human beings who reason before they reach their final decision.

In our view, the most important idea in epistemic game theory is common belief in rationality ([43], see also [12]). It states that a player, when making his choice, chooses optimally given the belief he holds about the opponents’ choices. Moreover, the player also believes that his opponents will choose optimally as well, and that their opponents believe that the other players will also choose optimally, and so on, ad infinitum. This idea really constitutes the basis for epistemic game theory, as most – if not all – concepts within epistemic game theory can be viewed as some variant of common belief in rationality. See [36] for a textbook that gives a detailed overview of most of these concepts in epistemic game theory.

For dynamic games there is a backward induction analogue to common belief in rationality, namely common belief in future rationality [37]. This concept states that a player, at each of his information sets, believes that his opponents will choose rationally now and in the future. Here, by an information set we mean a stage in the game where this player has to make a choice. However, common belief in future rationality does not require a player to believe that his opponents have chosen rationally in the past! On top of this, the concept states that a player also always believes that his opponents, at each of their information sets, believe that their opponents will choose rationally now and in the future, and so on, ad infinitum.

For dynamic games with perfect information, various authors have used some variant of the idea of common belief in future rationality as a possible foundation for backward induction. See [2, 5, 19, 40]. Among these contributions, the concept of stable belief in dynamic rationality in [5] matches completely the idea of common belief in future rationality, although they restrict attention to non-probabilistic beliefs. Perea [32] provides an overview of the various epistemic foundations for backward induction that have been offered in the literature.

Some people have criticized common belief in rationality because it involves infinitely many conditions, and hence – they argue – it will be very difficult for a player to meet each of these infinitely many conditions. The same could be said about common belief in future rationality. The main purpose of this chapter will be to show that this critique is actually not justified, provided we stick to finite games. We will show, namely, that in dynamic games with finitely many information sets, and finitely many choices at every information set, common belief in future rationality can be achieved by reasoning procedures that use finitely many steps only!

Let us be more precise about this statement. Suppose a player in a dynamic game holds not only conditional beliefs about his opponents’ strategies, but also conditional beliefs about his opponents’ conditional beliefs about the other players’ strategies, and so on, ad infinitum. That is, this player holds a full belief hierarchy about his opponents – an object that is needed in order to formally define common belief in future rationality. Such belief hierarchies can be efficiently encoded within an epistemic model with types. This is a model in which for every player there is a set of so-called “types”, and where there is a function that assigns to every type of player i a string of conditional beliefs about the opponents’ strategies and types – one conditional belief for every information set. Within such an epistemic model, we can then derive for every type a full hierarchy of conditional beliefs about the opponents’ strategies and beliefs. So, the “types” in this epistemic model, together with the functions that map types to conditional beliefs on the opponents’ strategies and types, can be viewed as encodings of the conditional belief hierarchies that we are eventually interested in. This construction is based on Harsanyi’s [21] seminal way of encoding belief hierarchies for games with incomplete information. If a belief hierarchy can be derived from an epistemic model with finitely many types only, we say that this belief hierarchy is finitely generated. Such finitely generated belief hierarchies will play a central role in this chapter, as we will show that they are “sufficient” when studying common belief in future rationality in finite dynamic games.

Let us now come back to the question whether common belief in future rationality can be achieved by finite reasoning procedures. As a first step, we show in Sect. 3 that for a finitely generated belief hierarchy, it only takes finitely many steps to verify whether this given belief hierarchy expresses common belief in future rationality or not. So, although common belief in future rationality involves infinitely many conditions, checking these conditions can be reduced to a finite procedure whenever we consider belief hierarchies that are finitely generated. This procedure can thus be viewed as an ex-post procedure which can be used to evaluate a given belief hierarchy, but it does not explain how a player arrives at such a belief hierarchy.

In Sect. 4 we go one step further by asking how a player can reason his way towards common belief in future rationality. To that purpose, we present a finite reasoning procedure such that (a) this procedure will always lead the player, within finitely many steps, to belief hierarchies that express common belief in future rationality, and (b) for every strategy that is possible under common belief in future rationality the procedure generates a belief hierarchy supporting this strategy. So, in a sense, the reasoning procedure yields an exhaustive set of belief hierarchies for common belief in future rationality. This reasoning procedure can be viewed as an ex-ante procedure, as it describes how a player may reason before forming his eventual belief hierarchy, and before making his eventual choice. The reasoning procedure we present in Sect. 4 is based on the backward dominance procedure  [37], which is a recursive elimination procedure that delivers all strategies that can rationally be made under common belief in future rationality.

So far, the epistemic game theory literature has largely focused on ex-post procedures, but not so much on ex-ante procedures. Indeed, most concepts within epistemic game theory can be viewed as ex-post procedures that can be used to judge a given belief hierarchy on its reasonability, but do not explain how a player could reason his way towards such a belief hierarchy. A notable exception is Pacuit [28] – another chapter within this volume that also explicitly investigates how people may reason before arriving at a given belief hierarchy. A lot of work remains to be done in this area, and in my view this may constitute one of the major challenges for epistemic game theory in the future: to explore how people may reason their way towards a plausible belief hierarchy. I hope that this volume will make a valuable contribution to this line of research.

Overall, our main contribution in this chapter is thus to (a) describe a reasoning process that a player can use to reason his way towards (an exhaustive set of) belief hierarchies expressing common belief in future rationality and (b) to show that this reasoning process only involves finitely many steps. Hence, we see that in finite dynamic games the concept of common belief in future rationality can be characterized by finite reasoning procedures. Static games are just a special case of dynamic games, where every player only makes a choice once, and where all players choose simultaneously. It is clear that in static games, the concept of common belief in future rationality reduces to the basic concept of common belief in rationality. As such, the results in this chapter immediately carry over to common belief in rationality as well. Hence, also the concept of common belief in rationality in finite static games can be characterized by finite reasoning procedures, just by applying the reasoning procedures in this chapter to the special case of static games.

This chapter can therefore be seen as an answer to the critique that epistemic concepts like common belief in rationality and common belief in future rationality would be too demanding because of the infinitely many conditions. We believe this critique is not justified.

Similar conclusions can be drawn for various other epistemic concepts in the literature, like permissibility [10, 11], proper rationalizability [2, 41] and common assumption of rationality  [14] for static games with lexicographic beliefs, and common strong belief in rationality  [8] for dynamic games. For each of these epistemic concepts there exists a finite recursive procedure that yields all choices (or strategies, if we have a dynamic game) that can rationally be chosen under the concept. We list these procedures, with their references, in Table 1. An overview of these epistemic concepts and their associated recursive procedures can be found in my textbook [36].

Table 1. Overview of epistemic concepts and their recursive procedures

Among these procedures, iterated elimination of weakly dominated choices is an old algorithm with a long tradition in game theory, and it is not clear where this procedure has been described for the first time in the literature. The procedure already appears in early books by Luce and Raiffa [23] and Farquharson [18].

The concept of common strong belief in rationality by Battigalli and Siniscalchi [8] can be seen as a counterpart to common belief in future rationality, as it establishes a forward induction type of reasoning, whereas common belief in future rationality constitutes a backward induction type of reasoning. More precisely, common strong belief in rationality requires a player to believe that his opponent has chosen rationally in the past whenever this is possible, whereas common belief in future rationality does not require this. On the other hand, common belief in future rationality requires a player to always believe that his opponent will choose rationally in the future, whereas common strong belief in rationality does not require this if the player concludes that his opponent has made mistakes in the past. A more detailed comparison between the two concepts can be found in [34].

The outline of the chapter is as follows. In Sect. 2 we formally define the idea of common belief in future rationality within an epistemic model. Section 3 presents a finite reasoning procedure to verify whether a finitely generated belief hierarchy expresses common belief in future rationality or not. In Sect. 4 we present a finite reasoning procedure which yields, for every strategy that can rationally be chosen under common belief in future rationality, some belief hierarchy expressing common belief in future rationality which supports that strategy. We conclude the chapter with a discussion in Sect. 5. For simplicity, we stick to two-player games throughout this chapter. However, all ideas and results can easily be extended to games with more than two players.

2 Common Belief in Future Rationality

In this section we present the idea of common belief in future rationality [37] and show how it can be formalized within an epistemic model with types.

2.1 Main Idea

Common belief in future rationality [37] reflects the idea that you believe, at each of your information sets, that your opponent will choose rationally now and in the future, but not necessarily that he chose rationally in the past. Here, by an information set for player i we mean an instance in the game where player i must make a choice. In fact, in some dynamic games it is simply impossible to believe, at certain information sets, that your opponent has chosen rationally in the past, as this information set can only be reached through a suboptimal choice by the opponent. But it is always possible to believe that your opponent will choose rationally now and in the future. On top of this, common belief in future rationality also states that you always believe that your opponent reasons in precisely this way as well. That is, you always believe that your opponent, at each of his information sets, believes that you will choose rationally now and in the future. By iterating this thought process ad infinitum we eventually arrive at common belief in future rationality.

2.2 Dynamic Games

We now wish to formalize the idea of common belief in future rationality. As a first step, we formally introduce dynamic games. As already announced in the introduction, we will restrict attention to two-player games for simplicity, although everything in this chapter can easily be generalized to games with more than two players. At the same time, the model of a dynamic game presented here is a bit more general than usual, as we explicitly allow for simultaneous choices by players at certain stages of the game.

Definition 1

(Dynamic Game). A dynamic game is a tuple $\varGamma =(I,X,Z,(X_{i},C_{i},H_{i},u_{i})_{i\in I})$ where

• (a) $I=\{1,2\}$ is the set of players;

• (b) X is the set of non-terminal histories. Every non-terminal history $x\in X$ represents a situation where one or more players must make a choice;

• (c) Z is the set of terminal histories. Every terminal history $z\in Z$ represents a situation where the game ends;

• (d) $X_{i}\subseteq X$ is the set of histories at which player i must make a choice. At every history $x\in X$ at least one player must make a choice, that is, for every $x\in X$ there is at least some i with $x\in X_{i}.$ However, for a given history x there may be various players i with $x\in X_{i}.$ This models a situation where various players simultaneously choose at x. For a given history $x\in X,$ we denote by $I(x):=\{i\in I:x\in X_{i}\}$ the set of active players at x; 

• (e) $C_{i}$ assigns to every history $x\in X_{i}$ the set of choice s $C_{i}(x)$ from which player i can choose at x; 

• (f) $H_{i}$ is the collection of information sets for player i. Formally, $H_{i}=\{h_{i}^{1},...,h_{i}^{K}\}$ where $h_{i}^{k}\subseteq X_{i}$ for every k,  the sets $h_{i}^{k}$ are mutually disjoint, and $X_{i}=\cup _{k}h_{i}^{k}.$ The interpretation of an information set $h\in H_{i}$ is that at h player i knows that some history in h has been realized, without knowing precisely which one;

• (g) $u_{i}$ is player i’s utility function, assigning to every terminal history $z\in Z$ some utility $u_{i}(z)$ in $\mathbb {R}$.

Throughout this chapter we assume that all sets above are finite. The histories in X and Z consist of finite sequences of choice-combinations

$$\begin{aligned} ((c_{i}^{1})_{i\in I^{1}},(c_{i}^{2})_{i\in I^{2}},...,(c_{i}^{K})_{i\in I^{K}}), \end{aligned}$$

where $I^{1},...,I^{K}$ are nonempty subsets of players, such that

• (a) $\emptyset$ (the empty sequence) is in X, 

• (b) if $x\in X$ and $(c_{i})_{i\in I(x)}\in \prod \nolimits _{i\in I(x)}C_{i}(x),$ then $(x,(c_{i})_{i\in I(x)})\in X\cup Z,$

• (c) if $z\in Z,$ then there is no choice combination $(c_{i})_{i\in \hat{I}}$ such that $(z,(c_{i})_{i\in \hat{I}})\in X\cup Z,$

• (d) for every $x\in X\cup Z,$ $x\ne \emptyset ,$ there is a unique $y\in X$ and $(c_{i})_{i\in I(y)}\in \prod \nolimits _{i\in I(y)}C_{i}(y)$ such that $x=(y,(c_{i})_{i\in I(y)}).$

Hence, a history $x\in X\cup Z$ represents the sequence of choice-combinations that have been made by the players until this moment.

Moreover, we assume that the collections $H_{i}$ of information sets are such that

• (a) two histories in the same information set for player i have the same set of available choices for player i. That is, for every $h\in H_{i},$ and every $x,y\in h,$ it holds that $C_{i}(x)=C_{i}(y).$ This condition must hold since player i is assumed to know his set of available choices at h. We can thus speak of $C_{i}(h)$ for a given information set $h\in H_{i};$

• (b) two histories in the same information set for player i must pass through exactly the same collection of information sets for player i,  and must hold exactly the same past choices for player i. This condition guarantees that player i has perfect recall, that is, at every information set $h\in H_{i}$ player i remembers the information he possessed before, and the choices he made before.

Say that an information set h follows some other information set $h^{\prime }$ if there are histories $x\in h$ and $y\in h^{\prime }$ such that $x=(y,(c_{i}^{1})_{i\in I^{1}},(c_{i}^{2})_{i\in I^{2}},...,(c_{i}^{K})_{i\in I^{K}})$ for some choice-combinations $(c_{i}^{1})_{i\in I^{1}},(c_{i}^{2})_{i\in I^{2}},...,(c_{i}^{K})_{i\in I^{K}}.$ The information sets h and $h^{\prime }$ are called simultaneous if there is some history x with $x\in h$ and $x\in h^{\prime }.$ Finally, we say that information set h weakly follows $h^{\prime }$ if either h follows $h^{\prime },$ or h and $h^{\prime }$ are simultaneous.

Note that the game model is quite similar to coalition logic in  [29], and the Alternating-Time Temporal Logic in [1]. See also the chapter by Bulling, Goranko and Jamroga [24] in this volume, which uses the Alternating-Time Temporal Logic.

Fig. 1.

Example of a dynamic game Here, $\emptyset$ and $h_{1}$ are information sets for player 1, and $\emptyset ,h_{2.1}$ and $h_{2.2}$ are information sets for player 2

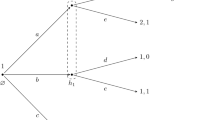
To illustrate the concepts defined above, let us have a look at the example in Fig. 1. At the beginning of the game, $\emptyset ,$ player 1 chooses between a and b,  and player 2 simultaneously chooses between c and d. So, $\emptyset$ is an information set that belongs to both players 1 and 2. If player 1 chooses b,  the game ends, and the utilities are as depicted. If he chooses a,  then the game moves to information set $h_{2.1}$ or information set $h_{2.2},$ depending on whether player 2 has chosen c or d. Player 1, however, does not know whether player 2 has chosen c or d,  so player 1 faces information set $h_{1}$ after choosing a. Hence, $h_{2.1}$ and $h_{2.2}$ are information sets that belong only to player 2, whereas $h_{1}$ is an information set that belongs only to player 1. Note that information sets $h_{1},h_{2.1}$ and $h_{2.2}$ follow $\emptyset ,$ and that player 2’s information sets $h_{2.1}$ and $h_{2.2}$ are simultaneous with player 1’s information set $h_{1}.$ At $h_{1},h_{2.1}$ and $h_{2.2},$ players 1 and 2 simultaneously make a choice, after which the game ends.

2.3 Strategies

In the literature, a strategy for player i in a dynamic game is usually defined as a complete choice plan that specifies a choice for player i at each of his information sets – also at those information sets that cannot be reached if player i implements this strategy. Indeed, this is the original definition introduced by Von Neumann [27] which has later become the standard definition of a strategy in game theory. There is however a conceptual problem with this classical definition of a strategy, namely how to interpret the specification of choices at information sets that cannot be reached under this same strategy. Rubinstein [39] interprets these latter choices not as planned choices by player i, but rather as the beliefs that i’s opponents have about i’s choices at these information sets. Rubinstein thus proposes to separate a strategy for player i into a choice part and a belief part: the choices for player i at information sets that can be reached under the strategy are viewed as planned choices by player i, and constitute what Rubinstein calls player i’s plan of action, whereas the choices at the remaining information sets are viewed as the opponents’ beliefs about these choices. A nice discussion of this interpretation of a strategy can be found in [9] – another chapter in this volume. In fact, a substantial part of Bonanno’s chapter concentrates on the concept of a strategy in dynamic games, and explores the subtleties that arise if one wishes to incorporate this definition of a strategy into a formal epistemic model. For more details on this issue we refer to Bonanno’s chapter [9].

In this chapter, however, we wish to clearly distinguish between choices and beliefs, as we think these are two fundamentally distinct objects. More precisely, our definition of a strategy concentrates only on choices for player i at information sets that can actually be reached if player i sticks to his plan. That is, our definition of a strategy corresponds to what Rubinstein [39] calls a plan of action.

Formally, for every $h,h^{\prime }\in H_{i}$ such that h precedes $h^{\prime },$ let $c_{i}(h,h^{\prime })$ be the choice at h for player i that leads to $h^{\prime }.$ Note that $c_{i}(h,h^{\prime })$ is unique by perfect recall. Consider a subset $\hat{H}_{i}\subseteq H_{i},$ not necessarily containing all information sets for player i, and a function $s_{i}$ that assigns to every $h\in \hat{H}_{i}$ some choice $s_{i}(h)\in C_{i}(h).$ We say that $s_{i}$ possibly reaches an information set h if at every $h^{\prime }\in \hat{H}_{i}$ preceding h we have that $s_{i}(h^{\prime })=c_{i}(h^{\prime },h).$ By $H_{i}(s_{i})$ we denote the collection of player i information sets that $s_{i}$ possibly reaches. A strategy for player i is a function $s_{i},$ assigning to every $h\in \hat{H}_{i}\subseteq H_{i}$ some choice $s_{i}(h)\in C_{i}(h),$ such that $\hat{H}_{i}=H_{i}(s_{i}).$

For a given information set h,  denote by $S_{i}(h)$ the set of strategies for player i that possibly reach h. By S(h) we denote the set of strategy profiles $(s_{i})_{i\in I}$ that reach some history in h.

In the game of Fig. 1, the strategies for player 1 are (a, e), (a, f) and b,  whereas the strategies for player 2 are (c, g), (c, h), (d, i) and (d, j). Note that within our terminology, b is a complete strategy for player 1 as player 1, by choosing b,  will make sure that his subsequent information set $h_{1}$ cannot be reached, and hence we do not have to specify what player 1 would do if $h_{1}$ would be reached. Note also that player 1 cannot make his choice dependent on whether $h_{2.1}$ or $h_{2.2}$ is reached, since these are information sets for player 2 only, and player 1 does not know which of these information sets is reached. As such, (a, e) is a complete strategy for player 1. For player 2, (c, g) is a complete strategy as by choosing c player 2 will make sure that $h_{2.2}$ cannot be reached, and hence we do not have to specify what player 2 would do if $h_{2.2}$ would be reached. Similarly for his other three strategies.

In this example, the sets of strategies that possibly reach the various information sets are as follows:

$$\begin{aligned} S_{1}(\emptyset )= & {} S_{1},\qquad S_{2}(\emptyset )=S_{2}, \\ S_{1}(h_{1})= & {} S_{1}(h_{2.1})=S_{1}(h_{2.2})=\{(a,e),(a,f)\}, \\ S_{2}(h_{1})= & {} S_{2},\qquad S_{2}(h_{2.1})=\{(c,g),(c,h)\},\qquad S_{2}(h_{2.2})=\{(d,i),(d,j)\}. \end{aligned}$$

2.4 Epistemic Model

We say that a strategy is rational for you at a certain information set if it is optimal at that information set, given your conditional belief there about the opponent’s strategy choice. In order to believe that your opponent chooses rationally at a certain information set, you must therefore not only hold conditional beliefs about the opponent’s strategy choice, but also conditional beliefs about the opponent’s conditional beliefs about your strategy choice. This is what we call a second-order belief. Moreover, if we go one step further and want to model the event that you believe that your opponent believes that you choose rationally, we need not only your belief about the opponent’s beliefs about your strategy choice, but also your belief about the opponent’s beliefs about your beliefs about the opponent’s strategy choice – that is, your third-order belief. Consequently, formally defining the idea of common belief in future rationality requires us to consider infinite belief hierarchies, specifying your conditional beliefs about the opponent’s strategy choice, your conditional beliefs about the opponent’s conditional beliefs about your strategy choice, and so on ad infinitum.

A problem with infinite belief hierarchies is that writing them down explicitly is an impossible task, since we would need to write down infinitely many beliefs. So is there a way to efficiently encode such infinite belief hierarchies without writing too much? The answer is “yes”, as we will see right now. Note that your belief hierarchy specifies first-order beliefs about the opponent’s strategy choice, second-order beliefs about the opponent’s first-order beliefs about your strategy choice, third-order beliefs about the opponent’s second-order beliefs, and so on. Hence we conclude that your belief hierarchy specifies conditional beliefs about the opponent’s strategy choice and the opponent’s belief hierarchy. Now let us call every belief hierarchy a type. Then, every type can be identified with its conditional beliefs about the opponent’s strategy choice and the opponent’s type. This elegant and powerful idea goes back to Harsanyi (1967–1968), who used it to model infinite belief hierarchies in games with incomplete information.

Let us now implement this idea of encoding infinite belief hierarchies formally. Fix some finite dynamic game $\varGamma$ with two players.

Definition 2

(Finite Epistemic Model). A finite epistemic model for the game $\varGamma$ is a tuple $M=(T_{1},T_{2},b_{1},b_{2})$ where

• (a) $T_{i}$ is the finite set of types for player i,  and

• (b) $b_{i}$ assigns to every type $t_{i}\in T_{i}$ and every information set $h\in H_{i}$ some probabilistic belief $b_{i}(t_{i},h)\in \varDelta (S_{j}(h)\times T_{j})$ about opponent j’s strategy-type pairs.

Remember that $S_{j}(h)$ denotes the set of strategies for opponent j that possibly reach h. By $\varDelta (S_{j}(h)\times T_{j})$ we denote the set of probability distributions on $S_{j}(h)\times T_{j}.$ So, within an epistemic model every type holds at each of his information sets a conditional belief about the opponent’s strategy choice and the opponent’s type, as we discussed above. For every type $t_{i}\in T_{i}$ we can now derive its complete belief hierarchy from the belief functions $b_{i}$ and $b_{j}.$ Namely, type $t_{i}$ holds at information set $h\in H_{i}$ a conditional belief $b_{i}(t_{i},h)$ on $S_{j}(h)\times T_{j}.$ By taking the marginal of $b_{i}(t_{i},h)$ on $S_{j}(h)$ we obtain $t_{i}$’s first-order belief at h on j’s strategy choice. Moreover, $t_{i}$ holds at information set $h\in H_{i}$ a conditional belief about j’s possible types. As each of j’s types $t_{j}$ holds first-order conditional beliefs on i’s strategy choices, we can thus derive from $b_{i}$ and $b_{j}$ the second-order conditional belief that $t_{i}$ holds at $h\in H_{i}$ about j’s first-order beliefs about i’s strategy choice. By continuing this procedure we can thus deduce, for every type $t_{i}$ in the model, each of its belief levels by making use of the belief functions $b_{i}$ and $b_{j}.$ In this way, the epistemic model above can be viewed as a short and convenient way to encode the infinite belief hierarchy of a player.

By means of this epistemic model we can in particular model the belief revision of players during the game. Consider two different information sets h and $h^{\prime }$ for player i,  where $h^{\prime }$ comes after h. Note that type $t_{i}$’s conditional belief at $h^{\prime }$ about j’s strategy choice may be different from his conditional belief at h,  and hence a type $t_{i}$ may revise his belief about j’s strategy choice as the game moves from h to $h^{\prime }.$ Moreover, $t_{i}$’s conditional belief at $h^{\prime }$ about j’s type may be different from his conditional belief at h,  and hence a type $t_{i}$ may revise his belief about j’s type – and hence about j’s conditional beliefs – as the game moves from h to $h^{\prime }.$ So, all different kinds of belief revisions – about the opponent’s strategy, but also about the opponent’s beliefs – can be captured within this epistemic model.

Table 2. An epistemic model for the game in Fig. 1

As an illustration, consider the epistemic model in Table 2, which is an epistemic model for the game in Fig. 1. So, we consider two possible types for player 1, $t_{1}$ and $t_{1}^{\prime },$ and one possible type for player 2, $t_{2}.$ Player 2’s type $t_{2}$ believes at the beginning of the game that player 1 chooses b and is of type $t_{1},$ whereas at $h_{2.1}$ and $h_{2.2}$ this type believes that player 1 chooses strategy (a, f) and is of type $t_{1}^{\prime }.$ In particular, type $t_{2}$ revises his belief about player 1’s strategy choice if the game moves from $\emptyset$ to $h_{2.1}$ or $h_{2.2}.$ Note that player 1’s type $t_{1}$ believes that player 2 chooses strategy (c, h),  whereas his other type $t_{1}^{\prime }$ believes that player 2 chooses strategy (d, i). So, type $t_{2}$ believes at $\emptyset$ that player 1 believes that player 2 chooses (c, h),  whereas $t_{2}$ believes at $h_{2.1}$ and $h_{2.2}$ that player 1 believes that player 2 chooses (d, i). Hence, player 2’s type $t_{2}$ also revises his belief about player 1’s belief if the game moves from $\emptyset$ to $h_{2.1}$ or $h_{2.2}.$ By continuing in this fashion, we can derive the full belief hierarchy for type $t_{2}.$ Similarly for the other types in this model.

Note that in our definition of an epistemic model we require the sets of types to be finite. This imposes a restriction on the possible belief hierarchies we can encode, since not every belief hierarchy can be derived from a type within an epistemic model with finite sets of types. For some belief hierarchies we would need infinitely many types to encode them. Belief hierarchies that can be derived from a finite epistemic model will be called finitely generated.

Definition 3

(Finitely Generated Belief Hierarchy). A belief hierarchy $\beta _{i}$ for player i is finitely generated if there is some finite epistemic model $M=(T_{1},T_{2},b_{1},b_{2}),$ and some type $t_{i}\in T_{i}$ in that model, such that $\beta _{i}$ is the belief hierarchy induced by $t_{i}$ within M.

Throughout this chapter we will restrict attention to finite epistemic models, and hence to finitely generated belief hierarchies. We will see in Sect. 4 that this is not a serious restriction within the context of common belief in future rationality, as every strategy that is optimal for some belief hierarchy – not necessarily finitely generated – that expresses common belief in future rationality, is also optimal for some finitely generated belief hierarchy that expresses common belief in future rationality. Moreover, finitely generated belief hierarchies are much easier to work with than those that are not finitely generated.

2.5 Common Belief in Future Rationality: Formal Definition

Remember that common belief in future rationality states that you always believe that the opponent chooses rationally now and in the future, you always believe that the opponent always believes that you choose rationally now and in the future, and so on, ad infinitum. Within an epistemic model we can state these conditions formally.

We first define what it means for a strategy $s_{i}$ to be optimal for a type $t_{i}$ at a given information set h. Consider a type $t_{i},$ a strategy $s_{i}$ and an information set $h\in H_{i}(s_{i})$ that is possibly reached by $s_{i}.$ By $u_{i}(s_{i},t_{i}$ | h) we denote the expected utility from choosing $s_{i}$ under the conditional belief that $t_{i}$ holds at h about the opponent’s strategy choice.

Definition 4

(Optimality at a Given Information Set). Consider a type $t_{i},$ a strategy $s_{i}$ and a history $h\in H_{i}(s_{i}).$ Strategy $s_{i}$ is optimal for type $t_{i}$ at h,  if $u_{i}(s_{i},t_{i}$ | $h)\ge u_{i}(s_{i}^{\prime },t_{i}$ | h) for all $s_{i}^{\prime }\in S_{i}(h).$

Remember that $S_{i}(h)$ is the set of player i strategies that possibly reach h. So, not only do we require that player i’s single choice at h is optimal at this information set, but we require that player i’s complete future choice plan from h on is optimal, given his belief at h about the opponent’s strategies. That is, optimality refers both to player i ’s choice at h and all of his future choices following h.

Bonanno [9] uses a different definition of optimality in his chapter, as he only requires the choice at h to be optimal at h, without requiring optimality for the future choices following h. Hence, Bonanno’s definition can be seen as a local optimality condition, whereas we use a global optimality condition here.

Note that, in order to verify whether strategy $s_i$ is optimal for the type $t_i$ at h, we only need to look at $t_i$’s first-order conditional belief at h about j’s strategy choice, not at $t_i$’s higher-order beliefs about j’s beliefs. In particular, it follows that every strategy $s_i$ that is optimal at h for some type $t_i$ – possibly not finitely generated – is also optimal for a finitely generated type $t^{\prime }_i$. Take, namely, any finitely generated type $t^{\prime }_i$ that has the same first-order beliefs about j’s strategy choices as $t_i$. We can now define belief in the opponent’s future rationality.

Definition 5

(Belief in the Opponent’s Future Rationality). Consider a type $t_{i}$ and an information set $h\in H_{i}.$ Type $t_{i}$ believes at h in j’s future rationality if $b_{i}(t_{i},h)$ only assigns positive probability to j’s strategy-type pairs $(s_{j},t_{j})$ where $s_{j}$ is optimal for $t_{j}$ at every $h^{\prime }\in H_{j}(s_{j})$ that weakly follows h. Type $t_{i}$ believes in the opponent’s future rationality if he does so at every information set $h\in H_{i}$.

So, to be precise, a type that believes in the opponent’s future rationality believes that the opponent chooses rationally now (if the opponent makes a choice at a simultaneous information set), and at every information set that follows. As such, the correct terminology would be “belief in the opponent’s present and future rationality”, but we stick to “belief in the opponent’s future rationality” so as to keep the name short.

Note also that belief in the opponent’s future rationality means that a player always believes – at each of his information sets – that his opponent will choose rationally in the future. This corresponds exactly to what Baltag, Smets and Zvesper [5] call stable belief in dynamic rationality, although they restrict to non-probabilistic beliefs in games with perfect information. In their terminology, stable belief means that a player believes so at every information set in the game, whereas dynamic rationality means that at a given information set, a player chooses rationally from that moment on – hence mimicking our condition of optimality at an information set. So, when we say belief in belief in the opponent’s future rationality we actually mean stable belief in the sense of [5].

We can now formally define the other conditions in common belief in future rationality in an inductive manner.

Definition 6

(Common Belief in Future Rationality). Consider a finite epistemic model $M=(T_{1},T_{2},b_{1},b_{2}).$

• (Induction start) A type $t_{i}\in T_{i}$ is said to express 1-fold belief in future rationality if $t_{i}$ believes in j’s future rationality.

• (Induction step) For every $k\ge 2,$ a type $t_{i}\in T_{i}$ is said to express k-fold belief in future rationality if at every information set $h\in H_{i},$ the belief $b_{i}(t_{i},h)$ only assigns positive probability to j’s types $t_{j}$ that express $(k-1)$-fold belief in future rationality.

Type $t_{i}\in T_{i}$ is said to express common belief in future rationality if it expresses k-fold belief in future rationality for all k.

Finally, we define those strategies that can rationally be chosen under common belief in future rationality. We say that a strategy $s_{i}$ is rational for a type $t_{i}$ if $s_{i}$ is optimal for $t_{i}$ at every $h\in H_{i}(s_{i}).$ In the literature, this is often called sequential rationality. We say that strategy $s_{i}$ can rationally be chosen under common belief in future rationality if there is some epistemic model $M=(T_{1},T_{2},b_{1},b_{2}),$ and some type $t_{i}\in T_{i},$ such that $t_{i}$ expresses common belief in future rationality, and $s_{i}$ is rational for $t_{i}.$

3 Checking Common Belief in Future Rationality

Some people have criticized the concept of common belief in rationality, because one has to verify infinitely many conditions in order to conclude that a given belief hierarchy expresses common belief in rationality. The same could be said about common belief in future rationality. We will show in this section that this is not true for finitely generated belief hierarchies. Namely, verifying whether a finitely generated belief hierarchy expresses common belief in future rationality or not only requires checking finitely many conditions, and can usually be done very quickly. To that purpose we present a reasoning procedure with finitely many steps which, for a given finitely generated belief hierarchy, tells us whether that belief hierarchy expresses common belief in future rationality or not.

Consider an epistemic model $M=(T_{1},T_{2},b_{1},b_{2})$ with finitely many types for both players. For every type $t_{i}\in T_{i},$ let $T_{j}(t_{i})$ be the set of types for player j that type $t_{i}$ deems possible at some of his information sets. That is, $T_{j}(t_{i})$ contains all types $t_{j}\in T_{j}$ such that $b_{i}(t_{i},h)(c_{j},t_{j})>0$ for some $h\in H_{i}$ and some $c_{j}\in C_{j}.$ We recursively define the sets of types $T_{j}^{k}(t_{i})$ and $T_{i}^{k}(t_{i})$ as follows.

Algorithm 1

(Relevant Types for $t_{i}$ ) Consider a finite dynamic game $\varGamma$ with two players, and a finite epistemic model $M=(T_{1},T_{2},b_{1},b_{2})$ for $\varGamma .$ Fix a type $t_{i}\in T_{i}.$

• (Induction start) Let $T_{i}^{1}(t_{i}):=\{t_{i}\}$.

• (Induction step) For every even round $k\ge 2,$ let $T_{j}^{k}(t_{i}):=\cup _{t_{i}\in T_{i}^{k-1}(t_{i})}T_{j}(t_{i}).$ For every odd round $k\ge 3,$ let $T_{i}^{k}(t_{i}):=\cup _{t_{j}\in T_{j}^{k-1}(t_{i})}T_{i}(t_{j}).$

So, $T_{j}^{2}(t_{i})$ contains all the opponent’s types that $t_{i}$ deems possible, $T_{i}^{3}(t_{i})$ contains all types for player i which are deemed possible by some type $t_{j}$ that $t_{i}$ deems possible, and so on. This procedure eventually yields the sets of types $T_{i}^{*}(t_{i})=\cup _{k}T_{i}^{k}(t_{i})$ and $T_{j}^{*}(t_{i})=\cup _{k}T_{j}^{k}(t_{i})$. These sets $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ contain precisely those types that enter $t_{i}$’s belief hierarchy in some of its levels, and we will call these the relevant types for $t_{i}.$ Since there are only finitely many types in M,  there must be some round K such that $T_{j}^{*}(t_{i})=T_{j}^{K}(t_{i}),$ and $T_{i}^{*}(t_{i})=T_{i}^{K+1}(t_{i}).$ That is, this procedure must stop after finitely many rounds.

If we would allow for infinite epistemic models, then the algorithm above could be extended accordingly through the use of higher ordinals and transfinite induction. But since we restrict our attention to finite epistemic models here, usual induction will suffice for our purposes.

Now, suppose that type $t_{i}$ expresses common belief in future rationality. Then, in particular, $t_{i}$ must believe in j’s future rationality. Moreover, $t_{i}$ must only consider possible opponent’s types $t_{j}$ that believe in i’s future rationality, that is, every type in $T_{j}^{2}(t_{i})$ must believe in the opponent’s future rationality. Also, $t_{i}$ must only consider possible types for j that only consider possible types for i that believe in j’s future rationality. In other words, all types in $T_{i}^{3}(t_{i})$ must believe in the opponent’s future rationality. By continuing in this fashion, we conclude that all types in $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ believe in the opponent’s future rationality. So, we see that every type $t_{i}$ that expresses common belief in future rationality, must have the property that all types in $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ believe in the opponent’s future rationality.

However, we can show that the opposite is also true! Consider, namely, a type $t_{i}$ within a finite epistemic model $M=(T_{1},T_{2},b_{1},b_{2})$ for which all types in $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ believe in the opponent’s future rationality. Then, in particular, every type in $T_{i}^{1}(t_{i})$ believes in j’s future rationality. As $T_{i}^{1}(t_{i})=\{t_{i}\},$ it follows that $t_{i}$ believes in j’s future rationality. Also, every type in $T_{j}^{2}(t_{i})$ believes in the opponent’s future rationality. As $T_{j}^{2}(t_{i})$ contains exactly those types for j that $t_{i}$ deems possible, it follows that $t_{i}$ only deems possible types for j that believe in i’s future rationality. By continuing in this way, we conclude that $t_{i}$ expresses common belief in future rationality. The two insights above lead to the following theorem.

Theorem 1

(Checking Common Belief in Future Rationality). Consider a finite dynamic game $\varGamma$ with two players, and a finite epistemic model $M=(T_{1},T_{2},b_{1},b_{2})$ for $\varGamma .$ Then, a type $t_{i}$ expresses common belief in future rationality, if and only if, all types in $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ believe in the opponent’s future rationality.

Note that checking whether all types in $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ believe in the opponent’s future rationality can be done within finitely many steps. We have seen above, namely, that the sets of relevant types for $t_{i}$ – that is, the sets $T_{i}^{*}(t_{i})$ and $T_{j}^{*}(t_{i})$ – can be derived within finitely many steps, and only contain finitely many types. So, within a finite epistemic model, checking for common belief in future rationality only requires finitely many reasoning steps. Consequently, if we take a finitely generated belief hierarchy, then it only takes finitely many steps to verify whether it expresses common belief in future rationality or not.

4 Reasoning Towards Common Belief in Future Rationality

In this section our goal is more ambitious, in that we wish to explore how a player can reason his way towards a belief hierarchy that expresses common belief in future rationality. More precisely, we offer a reasoning procedure that generates a finite set of belief hierarchies such that, for every strategy that can rationally be chosen under common belief in future rationality, there will be a belief hierarchy in this set which supports that strategy. In that sense, the reasoning procedure yields an exhaustive set of belief hierarchies.

The reasoning procedure will be illustrated in the second part of this section by means of an example. The reader should feel free to jump back and forth between the description of the procedure and the example while reading the various steps of the reasoning procedure. This could certainly help to clarify the different steps of the procedure. On purpose, we have separated the example from the description of the procedure, so as to enhance readability.

4.1 Procedure

To see how this reasoning procedure works, let us start with exploring the consequences of “believing in the opponent’s future rationality”. For that purpose, we will heavily make use of the following lemma, which appears in [30].

Lemma 1

(Pearce’s Lemma (1984)). Consider a static two-person game $\varGamma = (S_1, S_2, u_1, u_2)$, where $S_i$ is player i’s finite set of strategies, and $u_i$ is player i’s utility function. Then, a strategy $s_i$ is optimal for some probabilistic belief $b_i \in \varDelta (S_j)$, if and only if, $s_i$ is not strictly dominated by a randomized strategy.

Here, a randomized strategy $r_{i}$ for player i is a probability distribution on i’s strategies, that is, i selects each of his strategies $s_{i}^{\prime }$ with probability $r_{i}(s_{i}^{\prime }).$ And we say that the strategy $s_{i}$ is strictly dominated by the randomized strategy $r_{i}$ if $r_{i}$ always yields a higher expected utility than $s_{i}$ against any strategy $s_{j}$ of player j.

One way to prove Pearce’s lemma is by using linear programming techniques. More precisely, one can formulate the question whether $s_{i}$ is optimal for some probabilistic belief as a linear program. Subsequently, one can write down the dual program, and show that this dual program corresponds to the question whether $s_{i}$ is strictly dominated by a randomized strategy. By the duality theorem of linear programming, which states that the original linear program and the dual program have the same optimal value (see, for instance [16]), it follows that $s_{i}$ is optimal for some probabilistic belief, if and only if, it is not strictly dominated by a randomized strategy.

Now, suppose that within a dynamic game, player i believes at some information set $h\in H_{i}$ that opponent j chooses rationally now and in the future. Then, player i will at h only assign positive probability to strategies $s_{j}$ for player j that are optimal, at every $h^{\prime }\in H_{j}$ weakly following h,  for some belief that j can hold at $h^{\prime }$ about i’s strategy choice.

Consider such a future information set $h^{\prime }\in H_{j}$; let $\varGamma ^{0}(h^{\prime })=(S_{j}(h^{\prime }),S_{i}(h^{\prime }))$ be the full decision problem for player j at $h^{\prime },$ at which he can only choose strategies in $S_{j}(h^{\prime })$ that possibly reach $h^{\prime },$ and believes that player i can only choose strategies in $S_{i}(h^{\prime })$ that possibly reach $h^{\prime }.$ From Lemma we know that a strategy $s_{j}$ is optimal for player j at $h^{\prime }$ for some belief about i’s strategy choice, if and only if, $s_{j}$ is not strictly dominated within the full decision problem $\varGamma ^{0}(h^{\prime })=(S_{j}(h^{\prime }),S_{i}(h^{\prime }))$ by a randomized strategy $r_{j}.$

Putting these things together, we see that if i believes at h in j’s future rationality, then i assigns at h only positive probability to j ’s strategies $s_{j}$ that are not strictly dominated within any full decision problem $\varGamma ^{0}(h^{\prime })$ for player j that weakly follows h. Or, put differently, player i assigns at h probability zero to any opponent’s strategy $s_{j}$ that is strictly dominated at some full decision problem $\varGamma ^{0}(h^{\prime })$ for player j that weakly follows h. That is, we eliminate any such opponent’s strategy $s_{j}$ from player i’s full decision problem $\varGamma ^{0}(h)=(S_{i}(h),S_{j}(h))$ at h.

We thus see that, if player i believes in j’s future rationality, then player i eliminates, at each of his full decision problems $\varGamma ^{0}(h),$ those opponent’s strategies $s_{j}$ that are strictly dominated within some full decision problem $\varGamma ^{0}(h^{\prime })$ for player j that weakly follows h. Let us denote by $\varGamma ^{1}(h)$ the reduced decision problem for player i at h that remains after eliminating such opponent’s strategies $s_{j}$ from $\varGamma ^{0}(h).$

Next, suppose that player i does not only believe in j’s future rationality, but also believes that j believes in i’s future rationality. Take an information set h for player i,  and an arbitrary information set $h^{\prime }$ for player j that weakly follows h. As i believes that j believes in i’s future rationality, player i believes that player j,  at information set $h^{\prime },$ believes that player i will only choose strategies from $\varGamma ^{1}(h^{\prime }).$ Moreover, as i believes in j’s future rationality, player i believes that j will choose rationally at $h^{\prime }.$ Together, these two insights imply that player i believes at h that j will only choose strategies $s_{j}$ that are not strictly dominated within $\varGamma ^{1}(h^{\prime }).$ Or, equivalently, player i eliminates from his decision problem $\varGamma ^{1}(h)$ all strategies $s_{j}$ for player j that are strictly dominated within $\varGamma ^{1}(h^{\prime }).$ As this holds for every player j information set $h^{\prime }$ that weakly follows h,  we see that player i will eliminate, from each of his decision problems $\varGamma ^{1}(h),$ all opponent’s strategies $s_{j}$ that are strictly dominated within some decision problem $\varGamma ^{1}(h^{\prime })$ for player j that weakly follows h.

Hence, if player i expresses up to 2-fold belief in future rationality, then he will eliminate, from each of his decision problems $\varGamma ^{1}(h),$ all opponent’s strategies $s_{j}$ that are strictly dominated within some decision problem $\varGamma ^{1}(h^{\prime })$ for player j that weakly follows h. Let us denote by $\varGamma ^{2}(h)$ the reduced decision problem for player i that remains after eliminating such opponent’s strategies $s_{j}$ from $\varGamma ^{1}(h).$

By continuing in this fashion, we conclude that if player i expresses up to k-fold belief in future rationality – that is, expresses 1-fold, 2-fold, ... until k-fold belief in future rationality – then he believes at every information set $h\in H_{i}$ that opponent j will only choose strategies from the reduced decision problem $\varGamma ^{k}(h).$ This leads to the following reasoning procedure, known as the backward dominance procedure [37]. The procedure is closely related to Penta’s [31] backwards rationalizability procedure, and is equivalent to Chen and Micali’s [15] backward robust solution.

Algorithm 2

(Backward Dominance Procedure). Consider a finite dynamic game $\varGamma$ with two players.

• (Induction start) For every information set h,  let $\varGamma ^{0}(h)=(S_{1}(h),S_{2}(h))$ be the full decision problem at h.

• (Induction step) For every $k\ge 1,$ and every information set h,  let $\varGamma ^{k}(h)=(S_{1}^{k}(h),S_{2}^{k}(h))\,$ be the reduced decision problem which is obtained from $\varGamma ^{k-1}(h)$ by eliminating, for both players i,  those strategies $s_{i}$ that are strictly dominated at some decision problem $\varGamma ^{k-1}(h^{\prime })$ weakly following h at which i is active.

Suppose that h is an information set at which player i is active. Then, the interpretation of the reduced decision problem $\varGamma ^{k}(h)=(S_{1}^{k}(h),S_{2}^{k}(h))$ is that at round k of the procedure, player i believes at h that opponent j chooses some strategy in $S_{j}^{k}(h).$ As the sets $S_{j}^{k}(h)$ become smaller as k becomes bigger, the procedure thus puts more and more restrictions on player i’s conditional beliefs about j’s strategy choice. However, since in a finite dynamic game there are only finitely many information sets and strategies, this procedure must stop after finitely many rounds! Namely, there must be some round K such that $S_{1}^{K+1}(h)=S_{1}^{K}(h)$ and $S_{2}^{K+1}(h)=S_{2}^{K}(h)$ for all information sets h. But then, $S_{j}^{k}(h)=S_{j}^{K}(h)$ for all information sets h and every $k\ge K+1,$ and hence the procedure will not put more restrictions on i’s conditional beliefs about j’s strategy choice after round K. This reasoning procedure is therefore a finite procedure, guaranteed to end within finitely many steps.

Above we have argued that if player i reasons in accordance with common belief in future rationality, then his belief at information set h about j’s strategy choice will only assign positive probability to strategies in $S_{j}^{K}(h).$ As a consequence, he can only rationally choose a strategy $s_{i}$ that is optimal, at every information set $h\in H_{i},$ for such a conditional belief that only considers j’s strategy choices in $S_{j}^{K}(h).$ But then, by Lemma 1, strategy $s_{i}$ must not be strictly dominated at any information set $h\in H_{i}$ if we restrict to j’s strategy choices in $S_{j}^{K}(h).$ That is, $s_{i}$ must be in $S_{i}^{K}(\emptyset ),$ where $\emptyset$ denotes the beginning of the game. We can thus conclude that every strategy $s_{i}$ that can rationally be chosen under common belief in future rationality must be in $S_{i}^{K}(\emptyset )$ – that is, must survive the backward dominance procedure at the beginning of the game.

We can show, however, that the converse is also true! That is, every strategy in $S_{i}^{K}(\emptyset )$ can be supported by a belief hierarchy that expresses common belief in future rationality. Suppose, namely, that player i has performed the backward dominance procedure in his mind, which has left him with the strategies $S_{i}^{K}(h)$ and $S_{j}^{K}(h)$ at every information set h of the game. Then, by construction, every strategy $s_{i}\in S_{i}^{K}(h)$ is not strictly dominated on $S_{j}^{K}(h^{\prime })$, for every information set $h^{\prime }$ weakly following h at which i is active. Thus, by Lemma 1, every strategy $s_{i}\in S_{i}^{K}(h)$ is optimal, at every $h^{\prime }\in H_{i}$ weakly following h, for some probabilistic belief $b_{i}^{s_{i},h}(h^{\prime })\in \varDelta (S_{j}^{K}(h^{\prime })).$ Similarly, every strategy $s_{j}\in S_{j}^{K}(h)$ will be optimal, at every $h^{\prime }\in H_{j}$ weakly following h, for some probabilistic belief $b_{j}^{s_{j},h}(h^{\prime })\in \varDelta (S_{i}^{K}(h^{\prime })).$

First, we define the sets of types

$$\begin{aligned} T_{i}= & {} \{t_{i}^{s_{i},h}:h\in H\text { and }s_{i}\in S_{i}^{K}(h)\} \text{ and } \\ T_{j}= & {} \{t_{j}^{s_{j},h}:h\in H \text{ and } s_{j}\in S_{j}^{K}(h)\}, \end{aligned}$$

where H denotes the collection of all information sets in the game. The superscript $s_{i},h$ in $t_{i}^{s_{i},h}$ indicates that, by our construction of the beliefs that we will give in the next paragraph, the strategy $s_{i}$ will be optimal for the type $t_{i}^{s_{i},h}$ at all player i information sets weakly following h.

Subsequently, we define the conditional beliefs of the types about the opponent’s strategy-type pairs to be

$$\begin{aligned} b_{i}(t_{i}^{s_{i},h},h^{\prime })(s_{j},t_{j})=\left\{ \begin{array}{rl} b_{i}^{s_{i},h}(h^{\prime })(s_{j}), &{} \text{ if } t_{j}=t_{j}^{s_{j},h^{ \prime }} \\ 0, &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

for every $h^{\prime }\in H_{i},$ and

$$\begin{aligned} b_{j}(t_{j}^{s_{j},h},h^{\prime })(s_{i},t_{i})=\left\{ \begin{array}{rl} b_{j}^{s_{j},h}(h^{\prime })(s_{i}), &{} \text{ if } t_{i}=t_{i}^{s_{i},h^{ \prime }} \\ 0, &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

for all $h^{\prime }\in H_{j}.$

This yields an epistemic model M. Hence, every type $t_{i}^{s_{i},h}$ for player i,  at every information set $h^{\prime }\in H_{i},$ only considers possible strategy-type pairs $(s_{j},t_{j}^{s_{j},h^{\prime }})$ where $s_{j}\in S_{j}^{K}(h^{\prime }),$ and his conditional belief at $h^{\prime }$ about j’s strategy choice is given by $b_{i}^{s_{i},h}(h^{\prime }).$ By construction, strategy $s_{i}\in S_{i}^{K}(h)$ is optimal for $b_{i}^{s_{i},h}(h^{\prime })$ at every $h^{\prime }\in H_{i}$ weakly following h. As a consequence, strategy $s_{i}\in S_{i}^{K}(h)$ is optimal for type $t_{i}^{s_{i},h}$ at every $h^{\prime }\in H_{i}$ weakly following h. The same holds for player j. Since type $t_{i}^{s_{i},h},$ at every information set $h^{\prime }\in H_{i},$ only considers possible strategy-type pairs $(s_{j},t_{j}^{s_{j},h^{\prime }})$ where $s_{j}\in S_{j}^{K}(h^{\prime }),$ it follows that type $t_{i}^{s_{i},h},$ at every information set $h^{\prime }\in H_{i},$ only considers possible strategy-type pairs $(s_{j},t_{j}^{s_{j},h^{\prime }})$ where strategy $s_{j}$ is optimal for $t_{j}^{s_{j},h^{\prime }}$ at every $h^{\prime \prime }\in H_{j}$ weakly following $h^{\prime }.$ That is, type $t_{i}^{s_{i},h}$ believes in the opponent’s future rationality.

Since this holds for every type $t_{i}^{s_{i},h}$ in this epistemic model M,  it follows directly from Theorem 1 that every type in the epistemic model M above expresses common belief in future rationality.

Now, take some strategy $s_{i}\in S_{i}^{K}(\emptyset ),$ which survives the backward dominance procedure at the beginning of the game. Then, we know from our insights above that $s_{i}$ is optimal for the type $t_{i}^{s_{i},\emptyset }$ at every $h\in H_{i}$ weakly following $\emptyset$ – that is, at every $h\in H_{i}$ in the game. As the type $t_{i}^{s_{i},\emptyset }$ expresses common belief in future rationality, we thus see that every strategy $s_{i}\in S_{i}^{K}(\emptyset )$ can rationally be chosen by some type $t_{i}^{s_{i},\emptyset }$ that expresses common belief in future rationality. In other words, for every strategy $s_{i}\in S_{i}^{K}(\emptyset )$ that survives the backward dominance procedure at $\emptyset$, there is a belief hierarchy expressing common belief in future rationality – namely the belief hierarchy induced by $t_{i}^{s_{i},\emptyset }$ in the epistemic model M – for which $s_{i}$ is optimal. This insight thus leads to the following theorem.

Theorem 2

(Reasoning Towards Common Belief in Future Rationality). Consider a finite dynamic game $\varGamma$ with two players. Suppose we apply the backward dominance procedure until it terminates at round K. That is, $S_{1}^{K+1}(h)=S_{1}^{K}(h)$ and $S_{2}^{K+1}(h)=S_{2}^{K}(h)$ for all information sets h.

For every information set h,  both players i,  every strategy $s_{i}\in S_{i}^{K}(h)\,,$ and every information set $h^{\prime }\in H_{i}$ weakly following h,  let $b_{i}^{s_{i},h}(h^{\prime })\in \varDelta (S_{j}^{K}(h^{\prime }))$ be a probabilistic belief on $S_{j}^{K}(h^{\prime })$ for which $s_{i}$ is optimal.

For both players i, define the set of types

$$\begin{aligned} T_{i}=\{t_{i}^{s_{i},h}:h\in H \,{ and }\, s_{i}\in S_{i}^{K}(h)\}, \end{aligned}$$

and for every type $t_{i}^{s_{i},h}$ and every $h^{\prime }\in H_{i}$ define the conditional belief

$$\begin{aligned} b_{i}(t_{i}^{s_{i},h},h^{\prime })(s_{j},t_{j})=\left\{ \begin{array}{rl} b_{i}^{s_{i},h}(h^{\prime })(s_{j}), &{} \,{ if }\, t_{j}=t_{j}^{s_{j},h^{ \prime }} \\ 0, &{} { otherwise} \end{array} \right. \end{aligned}$$

about j’s strategy-type pairs. Then, all types in this epistemic model M express common belief in future rationality. Moreover,

• (1) for every strategy $s_{i}\in S_{i}^{K}(\emptyset )$ that survives the backward dominance procedure at $\emptyset$ there is a belief hierarchy in M expressing common belief in future rationality for which $s_{i}$ is optimal at all $h\in H_{i}$ possibly reached by $s_{i}$ – namely the belief hierarchy induced by $t_{i}^{s_{i},\emptyset };$

• (2) for every strategy $s_{i}\notin S_{i}^{K}(\emptyset )$ that does not survive the backward dominance procedure at $\emptyset$, there is no belief hierarchy whatsoever expressing common belief in future rationality for which $s_{i}$ is optimal at all $h\in H_{i}$ possibly reached by $s_{i}$.

So, whenever a strategy $s_{i}$ is optimal for some belief hierarchy that expresses common belief in future rationality, this reasoning procedure generates one. In that sense, we can say that this reasoning procedure yields an “exhaustive” set of belief hierarchies. Note also that this is a reasoning procedure with finitely many steps, as the backward dominance procedure terminates after finitely many rounds, after which we only have to construct finitely many types – one for each information set h and each surviving strategy $s_{i}\in S_{i}^{K}(h)$ at h.

The theorem above also shows that finitely generated belief hierarchies are sufficient when it comes to exploring common belief in future rationality within a finite dynamic game. Suppose, namely, that some strategy $s_{i}$ is optimal, at all $h\in H_{i}$ possibly reached by $s_{i},$ for some belief hierarchy – not necessarily finitely generated – that expresses common belief in future rationality. Then, according to part (2) in the theorem, strategy $s_{i}$ must be in $S_{i}^{K}(\emptyset )$. But in that case, the procedure above generates a finitely generated belief hierarchy for which the strategy $s_{i}$ is optimal – namely the belief hierarchy induced by the type $t_{i}^{s_{i},\emptyset }$ within the finite epistemic model M. So we see that, whenever a strategy $s_{i}$ is optimal for some belief hierarchy – not necessarily finitely generated – that expresses common belief in future rationality, then it is also optimal for a finitely generated belief hierarchy that expresses common belief in future rationality.

Corollary 1

(Finitely Generated Belief Hierarchies are Sufficient). Consider a finite dynamic game $\varGamma$ with two players. If a strategy $s_{i}$ is optimal for some belief hierarchy – not necessarily finitely generated – that expresses common belief in future rationality, then it is also optimal for a finitely generated belief hierarchy that expresses common belief in future rationality.

Here, whenever we say that $s_{i}$ is optimal for some belief hierarchy, we mean that it is optimal for this belief hierarchy at every information set $h\in H_{i}$ possibly reached by $s_{i}.$ This corollary thus states that, if we wish to verify which strategies can rationally be chosen under common belief in future rationality, then it is sufficient to stick to finite epistemic models. In that sense, the corollary bears a close resemblance to the finite model property in modal logic (see, for instance, [20]).

Fig. 2.

Example of a dynamic game $\emptyset$ denotes the beginning of the game, and $h_1$ denotes the information set that follows the choice a

4.2 Example

We shall now illustrate the reasoning procedure above by means of an example. Consider the dynamic game in Fig. 2. At the beginning, player 1 can choose between a and b. If he chooses b,  the game ends, and the utilities for players 1 and 2 will be (4, 4). If he chooses a, the game continues, and players 1 and 2 must simultaneously choose from $\{c,d,e,f\}$ and $\{g,h,i,j\},$ respectively. The utilities for both players in that case can be found in the table following choice a. Let us denote the beginning of the game by $\emptyset ,$ and the information set following choice a by $h_{1}.$ Hence, $\emptyset$ and $h_{1}$ are the two information sets in the game. At $\emptyset$ only player 1 makes a choice, whereas both players 1 and 2 are active at $h_{1}.$

We will first run the backward dominance procedure for this example, and then build an epistemic model on the basis of that procedure, following the construction in Theorem 2.

There are two information sets in this game, namely $\emptyset$ and $h_{1}$. The full decision problems at both information sets are given in Table 3.

Table 3. Full decision problems in the game of Fig. 2

We will now start the backward dominance procedure. In round 1, we see that within the full decision problem $\varGamma ^{0}(\emptyset )$ at the beginning of the game, the strategies (a, d), (a, e) and (a, f) are strictly dominated for player 1 by b. So, we eliminate (a, d), (a, e) and (a, f) from $\varGamma ^{0}(\emptyset ),$ but not – yet – from $\varGamma ^{0}(h_{1}),$ as $h_{1}$ follows $\emptyset .$ Moreover, within the full decision problem $\varGamma ^{0}(h_{1})$ at $h_{1},$ player 1’s strategy (a, f) is strictly dominated by (a, d) and (a, e),  and hence we eliminate (a, f) from $\varGamma ^{0}(h_{1})$ and $\varGamma ^{0}(\emptyset ).$ Note, however, that we already eliminated (a, f) at $\varGamma ^{0}(\emptyset ),$ so we only need to eliminate (a, f) from $\varGamma ^{0}(h_{1})$ at that step. For player 2, no strategy is strictly dominated within $\varGamma ^{0}(\emptyset )$ or $\varGamma ^{0}(h_{1}),$ so we cannot yet eliminate any strategy for player 2. This leads to the reduced decision problems $\varGamma ^{1}(\emptyset )$ and $\varGamma ^{1}(h_{1})$ in Table 4.

Table 4. Reduced decision problems after round 1 of backward dominance procedure

We now turn to round 2. Within $\varGamma ^{1}(h_{1}),$ player 2’s strategy j is strictly dominated by i. Hence, we can eliminate strategy j from $\varGamma ^{1}(h_{1}),$ but also from $\varGamma ^{1}(\emptyset ),$ as $h_{1}$ follows $\emptyset .$ No other strategies can be eliminated at this round. This leads to the reduced decision problems $\varGamma ^{2}(\emptyset )$ and $\varGamma ^{2}(h_{1})$ in Table 5.

Table 5. Reduced decision problems after round 2 of backward dominance procedure

In round 3, player 1’s strategy (a, e) is strictly dominated by (a, d) within $\varGamma ^{2}(h_{1}),$ and hence we can eliminate (a, e) from $\varGamma ^{2}(h_{1}).$ This leads to the final decision problems in Table 6, from which no further strategies can be eliminated.

Table 6. Final decision problems in the backward dominance procedure

Note, for instance, that strategy i is not strictly dominated for player 2 within $\varGamma ^{3}(h_{1}),$ as it is optimal for the belief that assigns probability 0.5 to (a, c) and (a, d).

We will now build an epistemic model on the basis of the final decision problems $\varGamma ^{3}(\emptyset )$ and $\varGamma ^{3}(h_{1}),$ using the construction in Theorem 2. At $\emptyset ,$ the surviving strategies are (a, c) and b for player 1, and g, h and i for player 2. That is, $S_{1}^{3}(\emptyset )=\{(a,c),b\}$ and $S_{2}^{3}(\emptyset )=\{g,h,i\}.$ Moreover, at $h_{1}$ the surviving strategies are given by $S_{1}^{3}(h_{1})=\{(a,c),(a,d)\}$ and $S_{2}^{3}(h_{1})=\{g,h,i\}.$ These strategies are optimal, at $\emptyset$ and/or $h_{1},$ for the following beliefs:

• strategy $(a,c)\in S_{1}^{3}(\emptyset )$ is optimal, at $\emptyset ,$ for the belief $b_{1}^{(a,c),\emptyset }(\emptyset )\in \varDelta (S_{1}^{3}(\emptyset ))$ that assigns probability 1 to h;

• strategy $(a,c)\in S_{1}^{3}(\emptyset )$ is optimal, at $h_{1}$ following $\emptyset ,$ for the belief $b_{1}^{(a,c),\emptyset }(h_{1})\in \varDelta (S_{1}^{3}(h_{1}))$ that assigns probability 1 to h;

• strategy $b\in S_{1}^{3}(\emptyset )$ is optimal, at $\emptyset ,$ for the belief $b_{1}^{b,\emptyset }(\emptyset )\in \varDelta (S_{1}^{3}(\emptyset ))$ that assigns probability 1 to g;

• strategy $(a,d)\in S_{1}^{3}(h_{1})$ is optimal, at $h_{1},$ for the belief $b_{1}^{(a,d),h_{1}}(h_{1})\in \varDelta (S_{1}^{3}(h_{1}))$ that assigns probability 1 to g;

• strategy $g\in S_{2}^{3}(\emptyset )$ is optimal, at $h_{1}$ following $\emptyset ,$ for the belief $b_{2}^{g,\emptyset }(h_{1})\in \varDelta (S_{1}^{3}(h_{1}))$ that assigns probability 1 to (a, c);

• strategy $h\in S_{2}^{3}(\emptyset )$ is optimal, at $h_{1}$ following $\emptyset ,$ for the belief $b_{2}^{h,\emptyset }(h_{1})\in \varDelta (S_{1}^{3}(h_{1}))$ that assigns probability 1 to (a, d);

• strategy $i\in S_{2}^{3}(\emptyset )$ is optimal, at $h_{1}$ following $\emptyset ,$ for the belief $b_{2}^{i,\emptyset }(h_{1})\in \varDelta (S_{1}^{3}(h_{1}))$ that assigns probability 0.5 to (a, c) and probability 0.5 to (a, d).

On the basis of these beliefs we can now construct an epistemic model as in Theorem 2. So, for both players i, both information sets h,  and every strategy $s_{i}\in S_{i}^{3}(h),$ we construct a type $t_{i}^{s_{i},h},$ resulting in the type sets

$$\begin{aligned} T_{1}=\{t_{1}^{(a,c),\emptyset },t_{1}^{b,\emptyset },t_{1}^{(a,c),h_{1}},t_{1}^{(a,d),h_{1}}\}\text { and }T_{2}=\{t_{2}^{g, \emptyset },t_{2}^{h,\emptyset },t_{2}^{i,\emptyset },t_{2}^{g,h_{1}},t_{2}^{h,h_{1}},t_{2}^{i,h_{1}}\}. \end{aligned}$$

The conditional beliefs for the types about the opponent’s strategy-type pairs can then be based on the beliefs above. By using the construction in Theorem 2, this yields the following beliefs for the types:

$$\begin{aligned} b_{1}(t_{1}^{(a,c),\emptyset },\emptyset )= & {} (h,t_{2}^{h,\emptyset }),{ \qquad }b_{1}(t_{1}^{(a,c),\emptyset },h_{1})=(h,t_{2}^{h,h_{1}}), \\ b_{1}(t_{1}^{b,\emptyset },\emptyset )= & {} (g,t_{2}^{g,\emptyset }),{ \qquad }b_{1}(t_{1}^{b,\emptyset },h_{1})=(g,t_{2}^{g,h_{1}}), \\ b_{1}(t_{1}^{(a,c),h_{1}},\emptyset )= & {} (h,t_{2}^{h,\emptyset }),{ \qquad }b_{1}(t_{1}^{(a,c),h_{1}},h_{1})=(h,t_{2}^{h,h_{1}}), \\ b_{1}(t_{1}^{(a,d),h_{1}},\emptyset )= & {} (g,t_{2}^{g,\emptyset }),{ \qquad }b_{1}(t_{1}^{(a,d),h_{1}},h_{1})=(g,t_{2}^{g,h_{1}}), \\&\\ b_{2}(t_{2}^{g,\emptyset },h_{1})= & {} ((a,c),t_{1}^{(a,c),h_{1}}), \\ b_{2}(t_{2}^{g,h_{1}},h_{1})= & {} ((a,c),t_{1}^{(a,c),h_{1}}), \\ b_{2}(t_{2}^{h,\emptyset },h_{1})= & {} ((a,d),t_{1}^{(a,d),h_{1}}), \\ b_{2}(t_{2}^{h,h_{1}},h_{1})= & {} ((a,d),t_{1}^{(a,d),h_{1}}), \\ b_{2}(t_{2}^{i,\emptyset },h_{1})= & {} (0.5)\cdot ((a,c),t_{1}^{(a,c),h_{1}})+(0.5)\cdot ((a,d),t_{1}^{(a,d),h_{1}}), \\ b_{2}(t_{2}^{i,h_{1}},h_{1})= & {} (0.5)\cdot ((a,c),t_{1}^{(a,c),h_{1}})+(0.5)\cdot ((a,d),t_{1}^{(a,d),h_{1}}). \end{aligned}$$

Here, $b_{2}(t_{2}^{i,\emptyset },h_{1})=(0.5)\cdot ((a,c),t_{1}^{(a,c),h_{1}})+(0.5)\cdot ((a,d),t_{1}^{(a,d),h_{1}})$ means that type $t_{2}^{i,\emptyset }$ assigns at $h_{1}$ probability 0.5 to the event that player 1 chooses (a, c) while being of type $t_{1}^{(a,c),h_{1}},$ and assigns probability 0.5 to the event that player 1 chooses (a, d) while being of type $t_{1}^{(a,d),h_{1}}.$

By Theorem 2 we know that all types so constructed express common belief in future rationality, and that for every strategy that can rationally be chosen under common belief in future rationality there is a type in this model for which that strategy is optimal. Indeed, the backward dominance procedure delivers the strategies (a, c), b, g, h and i at $\emptyset ,$ and hence we know from  [37] that these are exactly the strategies that can rationally be chosen under common belief in future rationality. Note that

• strategy (a, c) is optimal, at $\emptyset$ and $h_{1},$ for the type $t_{1}^{(a,c),\emptyset }$;

• strategy b is optimal, at $\emptyset ,$ for the type $t_{1}^{b,\emptyset }$;

• strategy g is optimal, at $h_{1},$ for the type $t_{2}^{g,\emptyset }$;

• strategy h is optimal, at $h_{1},$ for the type $t_{2}^{h,\emptyset }$; and

• strategy i is optimal, at $h_{1},$ for the type $t_{2}^{i,\emptyset }.$

So, for every strategy that can rationally be chosen under common belief in future rationality, we have constructed – by means of the epistemic model above – a finitely generated belief hierarchy that expresses common belief in future rationality, and that supports this strategy.

Note, however, that there is some redundancy in the epistemic model above. Namely, it is easily seen that the types $t_{1}^{(a,c),\emptyset }$ and $t_{1}^{(a,c),h_{1}}$ have identical belief hierarchies, and so do $t_{1}^{b,\emptyset }$ and $t_{1}^{(a,d),h_{1}}$. The same holds for $t_{2}^{g,\emptyset }$ and $t_{2}^{g,h_{1}},$ for $t_{2}^{h,\emptyset }$ and $t_{2}^{h,h_{1}},$ and also for $t_{2}^{i,\emptyset }$ and $t_{2}^{i,h_{1}}.$ Hence, we can substitute $t_{1}^{(a,c),\emptyset }$ and $t_{1}^{(a,c),h_{1}}$ by a single type $t_{1}^{(a,c)},$ and we can substitute $t_{1}^{b,\emptyset }$ and $t_{1}^{(a,d),h_{1}}$ by a single type $t_{1}^{b}.$ Similarly, we can substitute $t_{2}^{g,\emptyset }$ and $t_{2}^{g,h_{1}}$ by a single type $t_{2}^{g},$ we can substitute $t_{2}^{h,\emptyset }$ and $t_{2}^{h,h_{1}}$ by a single type $t_{2}^{h},$ and $t_{2}^{i,\emptyset }$ and $t_{2}^{i,h_{1}}$ by $t_{2}^{i}.$ This eventually leads to the smaller – yet equivalent – epistemic model with type sets

$$\begin{aligned} T_{1}=\{t_{1}^{(a,c)},t_{1}^{b}\} \text{ and } T_{2}= \{t_{2}^{g},t_{2}^{h},t_{2}^{i}\} \end{aligned}$$

and beliefs

$$\begin{aligned} b_{1}(t_{1}^{(a,c)},\emptyset )= & {} b_{1}(t_{1}^{(a,c)},h_{1})=(h,t_{2}^{h}) \\ b_{1}(t_{1}^{b},\emptyset )= & {} b_{1}(t_{1}^{b},h_{1})=(g,t_{2}^{h}) \\&\\ b_{2}(t_{2}^{g},h_{1})= & {} ((a,c),t_{1}^{(a,c)}), \\ b_{2}(t_{2}^{h},h_{1})= & {} ((a,d),t_{1}^{b}), \\ b_{2}(t_{2}^{i},h_{1})= & {} (0.5)\cdot ((a,c),t_{1}^{(a,c)})+(0.5)\cdot ((a,d),t_{1}^{b}). \end{aligned}$$

This redundancy is typical for the construction of the epistemic model in Theorem 2. In most games, the epistemic model constructed in this way will contain types that are “duplicates” of each other, as they generate the same belief hierarchy.

5 Discussion

5.1 Algorithms as Reasoning Procedures

In this chapter we have presented an algorithm that leads to belief hierarchies expressing common belief in future rationality, and it is based on the backward dominance procedure proposed in [37]. The difference is that in this chapter we interpret this algorithm not as a computational tool for the analyst, but rather as a finite reasoning procedure that some player inside the game can use (a) to verify which strategies he can rationally choose under common belief in future rationality, and (b) to support each of these strategies by a belief hierarchy expressing common belief in future rationality.

Hence, one of the main messages in this chapter is that the algorithm above for common belief in future rationality does not only serve as a computational tool for the analyst, but can also be used by a player inside the game as an intuitive reasoning procedure. Compare this to the concepts of Nash equilibrium [25, 26] for static games, and sequential equilibrium [22] for dynamic games. There is no easy, finite iterative procedure to find one Nash equilibrium – let alone all Nash equilibria – in a game. In particular, there is no clear reasoning procedure that a player inside the game can use to reason his way towards a Nash equilibrium. Besides, we believe that Nash equilibrium imposes some implausible conditions on a player’s belief hierarchy, as it requires a player to believe that his opponent is correct about the actual beliefs he holds (see [4, 13, 33, 38] and [3, p.5]). In view of all this, we think that Nash equilibrium is not a very appealing concept if we wish to describe the reasoning of players about their opponents. The same actually holds for the concept of sequential equilibrium.

5.2 Finitely Generated Belief Hierarchies

In this chapter we have restricted our attention to finitely generated belief hierarchies – that is, belief hierarchies that can be derived from an epistemic model with finitely many types. By doing so we actually exclude some belief hierarchies, as not every belief hierarchy can be generated within a finite epistemic model. If we wish to include all possible belief hierarchies in our model, then we must necessarily look at complete type spaces for dynamic games as constructed in [7].

But for our purposes here it is actually sufficient to concentrate on finitely generated belief hierarchies. Theorem 2 implies, namely, that whenever a strategy $s_{i}$ is optimal for some belief hierarchy – not necessarily finitely generated – that expresses common belief in future rationality, then $s_{i}$ is also optimal for some finitely generated belief hierarchy that expresses common belief in future rationality. Moreover, finitely generated belief hierarchies have the advantage that they are particularly easy to work with, and that checking for common belief in future rationality can be done within finitely many steps, as is shown in Theorem 1.