Maximal Material Yield in Gemstone Cutting

Abstract

The fabrication of faceted gems from rough gems, when viewed mathematically, is a problem of maximal material yield. Here, one or more jewels must be embedded within an irregularly shaped rough stone such that the total value of the jewels is maximal. Both the position and the shape of the embedded stones can vary, which distinguishes this problem from the cutting and packing problems known in the literature. On the modeling side, there are three extremely interesting challenges: separating the continuous parameters, significant for yield maximization, from the discrete parameters, describing the facets, finding a mathematically tractable description of the esthetic requirements of the faceted stones, and reformulating the containment and/or non-overlapping conditions into tractable constraints. The methods of general semi-infinite optimization lend themselves to this last-named challenge. The numerical solution of such optimization problems having a practical nature is difficult and, in the mathematical literature, one frequently finds only conceptual solution approaches. Among other things, this chapter describes a novel approach and shows how it can be successfully applied to the problem.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Optimum Material Usage—A Must with Expensive Resources

The quest for optimum material cutting is one of the basic principles of industrial production, since the sales price of a manufactured good is not only a function of the production costs, but often depends predominantly on the necessary raw material usage. Hence, the range of problems involving maximizing material usage is large.

A tradesman papering walls, for example, will seek to minimize the number of rolls of wallpaper he uses. In so doing, he will try to manage his use of remnants so that the final waste pieces are as small as possible. A carpenter cutting molding to size deals with the same challenge, as does a metalworker using ready-made metal profiles. This one-dimensional problem—only the length of the pieces matters here—is known in the mathematical literature as the Cutting Stock Problem (see [18, 38], for example). Even in its simple form, it proves to be NP-hard, which is the same as saying that there can be no efficient algorithm for minimizing waste.

Cutting shapes from standard wooden panels, pieces of clothing from fabric rolls, or shoe elements from leather hides represents an even more difficult material usage optimization problem; here, in addition to the geometry of the cut-outs, one must also consider their orientation—as with a fiber’s running direction in a fabric—or cut around flaws in the material—as with knots in a wooden board or injuries to the animal supplying the hide.

Analogous problems also exist in three dimensions: a dispatcher, for example, when picking and packing goods will search for the smallest package that will hold all the pieces, in order to minimize shipping costs. A diamond or colored-gemstone producer will also strive to cut the largest and thus most valuable jewels possible from the raw material he receives from the mine, taking into consideration the preferred orientation and such flaws as cracks and inclusions (see Fig. 1). In the literature, the optimization task in the 2D or 3D situation is often referred to as a Nesting Problem (see [19], for example).

Fig. 1

Exploiting gemstones: raw stones and a selection of cut jewels from Paul Wild oHG

1.1 Gemstone Production—An Ancient Craft Using Scarce Raw Materials

This chapter deals with the optimal cutting of gemstones, although most of the methods developed here can be applied in an analogous manner to the other examples mentioned earlier. To promote a better understanding of the practical questions, we have compiled some background information about gemstone cutting.

For more than 500 years, the most common form of jewel has been the faceted stone. This is a cut and polished gemstone whose surface consists of small, planar areas known as facets. The gemstone is divided into three elements: the crown, the girdle, and the pavilion (see Fig. 2).

Fig. 2

The elements of a faceted stone

The crown and pavilion are polyhedral. The girdle is bordered by planar or curved surfaces and determines the base form of the faceted stone. There are many faceted stone shapes, the best-known of which are shown in Fig. 3.

Fig. 3

The best-known faceted stone shapes, from left to right: baguette, emerald, antique, oval, round, and pear

Along with the base form, there are various basic types of crown and pavilion cuts, which we will subsequently refer to as facetings (see Fig. 4, [25]). Some are possible for every base form; others are not. Moreover, with some cuts, the number of facets is pre-defined, whereas for others, the number of facets depends on the size of the finished stone.

Fig. 4

The round shape in a brilliant cut and a step cut; Fig. 2 depicts the Portuguese cut.

Besides its base form and cut, a faceted stone is also characterized by a variety of size parameters, such as the height, length, and width of the crown, girdle, and pavilion. For optical and esthetic reasons, there are upper and lower limits on certain ratios between these parameters, which we will refer to subsequently as proportions. With diamonds, for example, the transparency of the material and the laws of optics dictate that faceting patterns and proportions be held within very narrow limits, in order to promote the most favorable light transmission paths. Here, it is typical that standard faceted stone shapes are merely scaled to fit the raw material and rotated in order to maximize yield. With colored gemstones, the rules for proportions and faceting are significantly less stringent. This has a favorable impact on the optimization tolerances, but it also makes the resulting mathematical problem considerably harder to solve. For this reason, we consider the more general problem of colored gemstone cutting in the following discussion.

In the past, size-dependent cuts and weak constraints on proportions led to the facets not being cut directly into the raw material. The process chain for producing a faceted stone contains four steps:

• (1) Sectioning: First, the raw material is sectioned into “clean” pieces containing no flaws or cracks, which we will refer to as rough stones. In the end, each rough stone delivers one faceted stone.

• (2) Pre-forming: Here, the rough stones are coarsely pre-cut, or ebauched. This defines the base form and the approximate proportions of the subsequent faceted stone.

• (3) Grinding: Next, the facets of the preferred cut are applied to these pre-cut forms.

• (4) Polishing: Finally, the facets are polished to a high gloss finish.

A faceted stone is appraised according to four criteria, the so-called Four C’s: Carat, Clarity, Color, and Cut. The carat is a measure of weight equaling 0.2 grams. The value of a faceted stone is directly proportional to its weight. The clarity indicates the absence of inclusions, cracks, and surface flaws. The greater the clarity, the more valuable the faceted stone. The natural color of a gemstone and/or the enhanced effect created during its processing also have a substantial impact on the value of a faceted stone. Because this factor can hardly by influenced, however, it will not be discussed further. The cut of a faceted stone has a decisive influence on its ability to reflect and refract light. An increase in a faceted stone’s reflective and refractive characteristics increases its value. Moreover, the faceting contributes significantly to a stone’s overall esthetic qualities.

The value of a faceted stone is thus appraised according to its weight and its esthetic qualities.

Today, gemstones and diamonds are still manufactured largely by hand. Although industrial saws and modern grinding machines are used here, all geometric determinations rely solely on the practiced eye and skilled craftsmanship of the jewel makers. Because the processes involved are complex and expensive, and because there are not enough apprentices learning the trade in the old industrialized nations, most production has long since shifted to the countries of South Asia.

In the first processing step, the sectioning of larger stones into rough stones so as to avoid flaws in the material, about half of the raw material is lost. In converting the rough stones from step (1) into faceted stones in steps (2)–(4), approximately two-thirds more of the precious material is lost. Thus, the loss of weight from the original raw material to the finished product is about five-sixths of the total.

1.2 Automation as a Chance for Better Material Utilization

Given the losses described above, it is natural to ask if mathematical modeling and algorithmic concepts that optimize the sectioning of raw material and the embedding of a faceted stone in a rough stone might not be able to significantly increase the yield above that achieved by the skill of the craftsman. In order to answer this question, however, a number of challenges must be met, the most important of which are mentioned here:

• Data acquisition: The first step toward using mathematical models is collecting input data. Here, the geometry of the rough stones must be depicted for the entire process (steps 1–4) by means of 3D imaging. This can be accomplished using CT technology, for example. However, due to the limited resolution of the available technology, it is very difficult to represent hairline cracks and very small air inclusions in the material. If one assumes only clean individual stones (steps 2–4), then the digitalization can be limited to depicting the stones’ surfaces, which can be accomplished with stripe projection or laser scanning technology.

  How does one prepare the large data sets so that they are suited for the subsequent optimization problems?

• Mathematical model: Two questions must be answered when dealing with optimization problems: What is feasible? and What is good? Neither of these questions can be easily answered for colored gemstone production. Weak constraints on the proportion rules and the large variety of base forms and faceting patterns make it hard to completely describe the alternative sets mathematically. Even harder is bringing the wish for maximum weight—which is directly proportional to volume—into harmony with minimum esthetic demands, which depend on individual taste and cultural background.

  How does one mathematically formulate esthetic requirements?

• Exploitation algorithms: From a mathematical perspective, the resulting optimization problems are extremely complex. This is due less to the above-mentioned large data sets arising from the digitalization of rough stones than to the geometric principles, which, although actually quite simple, are laborious to mathematize. These principles demand that the resulting faceted stones must be completely contained within the rough stone and may not overlap each other. A second issue is the simultaneous existence of continuous variables, such as size and proportion, and discrete variables, such as the number of facets.

  How does one mathematically model the containment and non-overlapping conditions? Is it conceivable to de-couple the combinatorics of the faceting from the optimal sizing of the proportions?

• Fully-automated production process: If one wants to use mathematical models and algorithmic concepts to optimize the cutting of rough gemstones, it becomes necessary to automate production; one cannot simply present a craftsman with a good plan and then wish him luck with it. Simple studies show that even the smallest deviations from the optimal positioning of the faceted stones in the rough stone can lead to marked deteriorations in yield. Thus, there is no way around the implementation of an industrial production process involving the use of CNC technology.

  How can one clamp the individual work pieces during processing? How can the geometry be transferred from one process step to the next with the required precision? Which handling technology should be used? Which saws, grinders, and polishers are appropriate? Can one continue to use the techniques of manual production, or will it be necessary to develop new ways and means?

2 Optimum Volume Yield—Is This a Mathematically Challenging Problem?

A person less trained in mathematics might think: a problem that is so easy to put into words and so easy to understand cannot be so difficult to solve. After all, it’s just a matter of packing a few faceted stones into a rough stone in an economically favorable manner; what’s so hard about that? Unfortunately, this first impression is deceptive, and a look in the mathematical literature or a search of the Internet under the keywords Cutting Stock or Nesting Problem brings a rude awakening. Only the simplest variants, such as rectangular or ball packaging, are well understood mathematically—and even these have only been partially solved. More generalized problem statements and solution approaches are extremely rare. Thus, in 2003, as the ITWM began work on this problem, the first task was to find a model that suited the problem.

2.1 Mathematically Modeling the Optimization Problem—Or, what Is an Acceptable Design for a Jewel?

The central question for modeling the problem is how to mathematically describe a faceted stone. The initial idea of describing the most common convex base forms as polyhedrons failed, since the girdle that separates the crown from the pavilion is, in many cases, a smooth, curved surface, whereas the crown and pavilion have a polyhedral structure. Another question is even more complicated: what is the class of acceptable facet patterns belonging to a given base form? The craftsmen have rules-of-thumb for the number of facets on the girdle, and these depend on the size of the stone; they know the approximate number of facet rows or steps on the crown and pavilion; they know the size of the limiting angles between the facets and the girdle. Facets should decrease in height as one moves away from the girdle; they should be kite-shaped on Portuguese cut stones and the half-axes should divide the kites approximately into golden cuts; and much more. Regarding the proportions, the following guidelines apply: the crown contributes about one-third of the total height, the pavilion, about 50–55 %, and the girdle makes up the rest. The pavilion should not be too “bellied,” but not too slender either—otherwise, too much volume is lost, etc. And the most important point of all is this: at the end of the day, the stone must be beautiful; rules and guidelines alone are not enough.

The above discussion indicates the all too typical dilemma of putting mathematical optimizations into practice: the mathematician needs clear-cut rules to do his work. The alternative set—in this case, the feasible faceted stones—from which favorable solutions should ultimately be selected, must be described exactly, according to fixed rules. There is no room for vagueness. Moreover, to optimize, one also needs a target quantity to help in comparing the quality of two possible solutions. At first glance, this would seem to be simple for gemstone cutting: the stones should be as large as possible. This increases the number of carats, i.e., the weight, thus raising their value. At second glance, however, there is a problem here as well.

If the stone is merely large, but not beautiful, no one will buy it. Therefore, we need a definition of “beautiful” that can be incorporated into the description of the alternative set. Or, at a minimum, we need measurement quantities that correlate well with “beautiful,” so that we can then optimize them as objectives in balance with solutions that are “large” or “heavy.”

The geometric problem that seems at first so easy to formulate now proves to be mathematically challenging indeed. Gemstone cutting seems somehow to be an art or perhaps a craft—in any event, not a science. Peering over the shoulder of the practitioner might provide us with some clues. How does a cutter answer the above questions? Does he simply start cutting away, or does he use rules-of-thumb containing mathematical principles that we can imitate with our models?

Observations of the craftsman at work are quite revealing: after sectioning the raw material, he then closely inspects the shape of a resulting rough stone to see which base form the final faceted stone might have and how this base form is oriented inside the rough stone. Then he starts by cutting the base form’s girdle. The crown and pavilion are coarsely pre-formed; as of this point, there are no facets. This pre-forming process determines the proportions of the stone, the height ratio and degree of belliedness as well as the base angles to the girdle. After pre-forming, the facet rows and counts are assigned and the crown and pavilion are faceted. Figure 5 shows the pre-cut form and intended proportions for the faceted stone depicted in Fig. 2.

Fig. 5

Pre-cut form and proportions for a round-cut stone: table diameter and total height in relation to girdle diameter

The manual production process is thus divided into two parts: pre-forming and faceting. This inspired us, in our mathematical modeling, to de-couple the continuous variables, such as the height and proportions of the faceted stone, from the discrete variables, such as the number of rows and facets in a given facet pattern.

The approach of de-coupling continuous and discrete variables simplifies the structure of the optimization problem significantly and allows the esthetic boundary conditions to be more easily described in the reduced variable sets. But what is the best way to implement this approach?

The implementation involves introducing a parameterized equivalent to the smooth pre-cut form, which we refer to as the calibration body. This is then optimized toward the end of maximizing material yield. Considerations regarding the appearance of a suitable faceting are relegated to a second step, which is discussed in detail in Sect. 5.1

Let us now turn to the optimization problem of the parameterized calibration body. For a single stone, this is closely related to the design-centering problem known in the literature (see [30]), when one describes the quantities relevant for the proportions, such as height, width, and degree of belliedness, as calibration body parameters (i.e., design parameters) and takes position and scaling as further degrees of freedom for the optimization. If one now places limits on the proportion parameters so as to ensure a more-or-less satisfactory esthetic result, then one is left with the question of how to achieve the largest possible volume of a parameterized gem design.

In the following discussion, the requirement that the faceted stone be completely contained within the rough stone is called the containment condition. This is simple and easy to understand, but how can it be mathematically implemented?

Putting it another way, the containment condition requires that each point of the design, that is, the calibration body, must also be a point of the container, that is, the rough stone. We have here, then, an infinite number of constraints for a finite number of parameters, which must be fulfilled for a feasible calibration body. Problems of this sort are referred to as semi-infinite optimization problems. Further challenges revolve around the questions of whether one can mathematically describe in a similar manner the localization of flaws in the resulting jewel or the non-overlapping of two faceted stones in cases where more than one jewel is embedded in a single rough stone. This non-overlapping condition is closely allied to the containment condition. The approach to dealing with both of these questions is discussed in Sect. 4.

A generalization results when one also requires minimum separation distances. Thus, when sectioning raw material into blanks or embedding multiple stones in one rough stone, it is important to arrange the blanks or stones so as to maintain the minimum separation distances required for the production process. Moreover, the production process may also demand adherence to other arrangement principles. For example, if circular saw technology is being used, one must ensure that the arrangement allows for consecutively executed through-cuts, also known as guillotine cuts (for more, see Sect. 6.2).

2.2 The Algorithms—How to Find Optimal Solutions

If one keeps to the above modeling approach, the algorithmic challenge in gaining an optimal calibration body then becomes developing numerical solution concepts for semi-infinite optimization problems that robustly solve high-dimensional, non-convex problems in an acceptable computation time.

To do so, one must first work on reducing the problem size. Here, the goal is to depict the rough stone—discretized via volume or surface data—using the most economical representation possible. Ideally, this is accomplished in a model-friendly form that allows for reduction to a finite problem (see Sect. 5.1.3). To depict the rough stone, one enlists the smallest possible number of simple, smooth parametrical functions that permits numerically non-problematical evaluation.

What remains is a global optimization problem, which commonly has numerous local extreme solutions. If one can characterize the local extremes in the general case using a first-degree optimality condition—such as the Karush–Kuhn–Tucker condition (KKT condition)—then the challenge is to select a suitable strategy for finding an approximately globally optimal solution. Here, there is no generic approach. A hybrid strategy must be found for enumerating favorable local extremes and/or excluding unfavorable ones.

When one has found good calibration bodies for approximating feasible faceted stones, then one can turn to the second optimization task: finding a favorable faceting; that is, one that both follows the standard rules of the gemstone cutter’s art and minimizes volume reduction of the calculated calibration body. At first, it seems obvious that using enough small facets should guarantee such an approximation. However, upon closer inspection, it becomes clear that the standard facet patterns used in the gemstone industry do not allow every calibration body to be approximated adequately. Thus, a certain coupling of faceting and base form once again sneaks in through the back door, so to speak. For fixed facet patterns, the problem of faceting can also be modeled as a non-linear global optimization problem. Here, the question arises as to how one can suitably integrate into the optimization problem the number of facets and facet rows as free optimization variables.

3 ITWM Projects Dealing with This Topic

3.1 Projects with the Gemstone Industry

The idea of increasing material yield during gemstone production by using mathematical optimization methods and automation was prompted by Paul Wild oHG (oHG = general partnership). This family-managed, mid-sized firm located in Kirschweiler, Rheinland-Pfalz, near Idar-Oberstein, is one of Europe’s leading producers of precious colored gemstones. The Company has its own mines in Africa, South America, and Asia, which ensure its supply of raw materials. Production of jewelry stones takes place predominantly in Asia, whereas administration and sales are headquartered in Kirschweiler.

As is typical for the industry, Wild’s jewelry stone production was carried out exclusively by hand until 2003. Up to that point, there had been no significant attempts to industrialize or automate production processes. Some experiments in improving yields in the 1990’s using a semi-automatic installation from Israel gave managing director Markus P. Wild the idea that it ought to indeed be possible to produce colored gemstones in a fully-automated industrial process, one optimized for each individual rough stone. Since 2003, Markus P. Wild has been pursuing this vision, in collaboration with the Fraunhofer-Gesellschaft and other partners from the machine engineering sector.

3.1.1 First Steps—Preliminary Feasibility and Profitability Studies

The Spring of 2003 marked the first contact between Markus P. Wild and the Fraunhofer-Gesellschaft. As a result, the Fraunhofer Institute for Industrial Mathematics ITWM, in Kaiserslautern, the Fraunhofer Institute for Applied Optics and Precision Engineering IOF, in Jena, and the Fraunhofer Institute for Manufacturing Technology and Advanced Materials IFAM, in Bremen, were commissioned in the Fall of 2003 and 2004 to conduct a series of preliminary studies toward the end of preparing a concept for the automatic production of colored jewelry stones:

• A study into 3D measurement of raw gemstones by means of the stripe projection method (Fraunhofer IOF, Jena)

• A study into calculating optimal cutting volumes of colored raw gemstones (Fraunhofer ITWM, Kaiserslautern)

• A study into bonding colored gemstones to metallic processing pins by means of UV-hardened or hot-melt adhesives (Fraunhofer IFAM, Bremen)

In the course of these preliminary studies, the basic feasibility of colored gemstone production with regard to pre-forming, grinding, and polishing in an industrial process was adequately verified. Thus, the development of an automatic cutting process in the context of an industrial research project could be started with acceptable prospects for success. This project was funded from 2005 to 2007 by the mid-sized company promotion foundation of Rheinland-Pfalz via the Investitions- und Strukturbank (ISB). An experimental setup was developed that was able to demonstrate, with scientific rigor, the feasibility of fully-automated colored gemstone processing.

3.1.2 Pioneer Work—The First Industrial Automation of Pre-forming, Grinding, and Polishing

The preliminary results were promising, and considerably higher volume yields could be achieved while still retaining excellent quality for the automatically processed jewelry stones. Thus, as a follow-up to the ISB-sponsored R&D endeavor, Wild oHG commissioned the construction of a fully-automated CNC-controlled production line. Although the most significant technological risks had been dealt with in the context of the ISB project, there were still some hurdles to overcome before a practicable industrial process could be implemented on the new production equipment. These were indeed overcome and, since 2008, the world’s first fully automated production line for colored gemstones has been in operation at Wild oHG.

The operation of the production line quickly showed that, for efficient utilization, an integrated, multi-criteria decision-making process would be needed that considers all of the four C’s–carat, color, clarity, and cut. In cooperation with the Fraunhofer ITWM in Kaiserslautern, in the course of a project sponsored by the German Economics Ministry from 2009 to 2011, a novel decision-support system was developed that facilitates the different types of production decisions: Proposals resulting from the cutting optimization are visualized within the rough stones before production starts; interactive 3D representation permits comparisons of the variants of proportion and faceting; production supervisors can check the quality of the variants before cutting begins; and the marketing department can integrate customers into the decision-making process via the Internet.

The research work in the Fraunhofer ITWM-Wild consortium was praised in the press and described as trailblazing. More than 70 articles appeared in such newspapers and journals as Die Zeit, FAZ (Frankfurter Allgemeine Zeitung), Handelsblatt, and Bild der Wissenschaft. Moreover, the accomplishments of the research consortium were honored in 2009 with the Joseph-von-Fraunhofer prize in a ceremony attended by the German Chancellor Angela Merkel.

The decision was finally made at the end of 2009 to guide the gemstone production machine to series maturity and bring it to market. In 2010, a modular pilot machine was built at the Fraunhofer Center in Kaiserslautern and, starting in the same year, control software was developed (see Fig. 6). The machine has been ready for marketing since the autumn of 2013, and is now being shown to potential buyers. The statements of interest that have already been received from more than 70 companies and technology brokers around the world are indeed very promising. Property rights that protect the machine concept have been granted. To this point, demonstrations at trade fairs have been avoided, so as not to aid potential product counterfeiters located in areas outside the patent protection zone.

Fig. 6

Pilot-production prototype developed at the Fraunhofer ITWM (Photo: G. Ermel, Fraunhofer ITWM)

3.1.3 The New Horizon—Automating the Sectioning Process

The earlier projects, dating from the years up to 2008, revolved primarily around the question of how to garner a single faceted stone from a rough stone. Beginning in 2009, however, the question of how to automate the sectioning process moved into the sights of the project group gathered around Wild oHG. Although one can produce individual stones from clean raw material by merely collecting data about the stone surface, one must collect volume data for the sectioning process, in order to distinguish between exploitable material and impurities, inclusions, and cracks. The method of choice for gaining such 3D data is high-resolution computer tomography (CT). Thus, Wild oHG commissioned testing of CT devices for their suitability for collecting volume data about colored raw gemstones. In 2010, a suitable system based on a two-frequency measurement process was located in the industry. The system was not yet being produced serially, however.

In addition to collecting volumetric data, automating the sectioning process also required a comprehensive study into which cutting technology would be appropriate for such automation. As with the cutting of individual stones, imitation of the manual production process seemed to be the safest path. To this point in time, raw material had always been sectioned by the most experienced craftsmen with the aid of diamond-studded circular saws. In 2009, Wild oHG and the Fraunhofer ITWM initiated the project “Development of a fully-automated sectioning process for colored gemstones,” which was sponsored by the ISB Rheinland-Pfalz and concluded in late June, 2011. The results confirmed that one can indeed use a circular saw to section a colored gemstone in a fully automated process. A prototype of a sectioning machine was then built in the manufacturing center in Kirschweiler. During the actual operation of this machine, however, several obstacles became apparent that made its practical use uneconomical. Thus, some other technologies were also taken into consideration. In 2013, Wild oHG eventually bought a high-pressure waterjet cutting machine. An extension of the ISB-sponsored sectioning project, conducted in cooperation with the Fraunhofer ITWM, is now aiming for a fully-automated sectioning process based on the use of CT and waterjet cutting technologies. A detailed discussion of the sectioning process can be found in Sect. 6.

3.2 Relevant Competences of the ITWM Optimization Department and Related Projects

Since the beginning of its cooperation with Wild oHG, the Fraunhofer ITWM’s Optimization Department has been systematically expanding its competences in modeling and solving industrial problems with semi-infinite optimization. Alongside the main project of gemstone cutting, questions stemming from other domains having comparable structures are also being treated with the help of these techniques.

In the area of nonlinear optimization, the Department has been utilizing its own algorithms from its inception. But it has also drawn upon commercial methods stemming mainly from the academic world, which are each adapted individually to the problem being treated. Here, a broad field of work is the hierarchic decomposition of problems into simpler sub-problems, or complexity reduction by means of adaptive discretization, or model reduction in optimization problems through the use of simplified/surrogate models.

In addition to those of the gemstone project, the following problems have been modeled and solved with the aid of semi-infinite optimization methods:

• Optimizing cooling systems of injection molds and pressure casting dies

• Optimizing the applicator position for radio frequency ablation

Both of these optimization problems deal with how to optimally distribute heat in a geometrically complex environment. With injection and pressure casting, a cavity must be cooled as homogeneously as possible; with radio frequency ablation, tumor tissue must be heated as homogeneously as possible. In each case, a suitable, enveloping isotherm must be established around the cooling or heating zone. If one models the heat distribution at equilibrium, then the requirement that the cooling or heating zone lie within the suitable isotherm is analogous to the containment condition of a faceted stone within a rough stone. Moreover, as with the gemstone problem, one can describe the non-overlapping of cooling channels and mold cavities or the non-puncturing of blood vessels by the applicator using semi-infinite constraints, which permits usage of the algorithm from the gemstone application.

Along with the above-mentioned semi-infinite modeling examples, the Fraunhofer ITWM’s Optimization Department also considers numerous other decomposition problems from various industrial branches. Due to their character, however, these are solved using discrete enumeration techniques:

• Optimal arrangement of electronic components and switches for system-in-package applications

• Optimal cross-sections for cutting conifer woods in large sawmills

• Optimal cutting patterns for pants in the textile industry

• Optimal layouts for photovoltaic installations

3.3 Scientific Studies and Collaborations Involving Optimal Volume Yield

A whole series of scientific inquiries from the aforementioned domains led to graduate theses and publications. In a seminal degree thesis, semi-infinite optimization methods were applied for the first time to the problem of optimizing the material yield of gemstones. More specifically, [11] deals with the approximation of the rough stone using planes and quadrics and the volume optimization of a faceted stone using generalized semi-infinite optimization on the basis of a simple calibration-body model. The ideas originating here were then further developed and supplemented in a dissertation [16]. The topics of this work are volume optimization using realistic calibration-body models, as well as modeling multi-body embedding problems as a generalized semi-infinite optimization problem and developing a feasible method for generalized semi-infinite optimization problems. The most significant results were published in [2, 10, 12].

Other sub-problems were treated in three degree theses. In [6], the authors calculated the faceting for a given calibration body using methods of 3D-body reconstruction from two-dimensional drawings. The goal in [3] was to improve the rough stone approximation using splines. The topic in [7] was generating better starting points by comparing the rough stone geometries.

An alternative to the semi-infinite modeling approach for volume optimization of a faceted stone is described in [4]. Here, the idea was to apply methods of collision detection from algorithmic geometry to triangulations of the rough and faceted stones.

The more complex problems of sectioning and embedding multiple designs in one container are probed in the dissertation [14]. This study involved volume optimizing multiple calibration bodies using generalized semi-infinite optimization; extending the modeling of multi-body embedding problems as a generalized semi-infinite optimization problem; and developing two methods for generalized semi-infinite optimization problems.

One method used in this context to solve the semi-infinite optimization problems is to reformulate them as usual nonlinear problems (see Sect. 4.5.1). These are ill-posed, however, in the sense that the usual regularity requirements are not all fulfilled. As a consequence, the customary solution methods don’t work directly; first, a regularization is required, that is, a softening of the original problem to a similar one having better characteristics. In [5], this idea of softening was transferred to the surface-minimized packing of rectangles, formulated as a nonlinear optimization problem to prevent the optimization from getting stuck in local optima.

The related thematic areas of cooling systems and radio frequency ablation mentioned in the previous section each yielded a dissertation [13, 15], and the latter also resulted in a publication [1].

Our studies into gemstone cutting also resonated strongly in the mathematical community. Along with a cover story in the SIAM news on gemstone cutting, the work was reported on in the American Mathematical Society’s Mathematical Moments and a podcast was created.

In addition to the already mentioned Joseph von Fraunhofer Prize, awarded for the gemstone project, the two first-mentioned dissertations were also honored with a prize by the Kreissparkassen Foundation of the University City of Kaiserslautern for the best dissertations of the year in the field of mathematics.

4 Modeling and Solving Maximum Material Yield Problems

From a mathematical perspective, volume optimization in gemstone cutting represents a cutting and packing problem, more precisely, a maximum material yield problem $( \mathsf{MaxMY} )$.

In maximum material yield problems, the goal is to work out from a large body—the so-called container—a set of smaller bodies—the so-called designs–so that as little of the container material as possible is left over as scrap. If the container has flaws in it, the designs must also avoid these.

When modeling such problems, two different types must be distinguished:

• (1) If the designs are fixed in size, then one searches within the set of all designs that can be generated from the container for the subset that best exploits it.

• (2) If the designs are variable in size and possibly also in shape, then one searches for the variant of the designs that fits in the container and possesses the largest total volume.

Notation Conventions

Let ℕ be the set of natural numbers $\{ 1,2,\ldots\}$, $\mathbb{N}_{0} := \mathbb{N}\cup\{ 0 \}$, $\mathbb{R}_{+}$, the set of non-negative real numbers, and $\mathbb{R}_{++}$, the set of positive real numbers.

We denote the set of real $m$-dimensional vectors as $\mathbb{R}^{m}$. The denotations $\mathbb{R}^{m}_{+}$ and $\mathbb{R}^{m}_{++}$ transfer accordingly. Vectors are essentially column vectors and printed in lower-case, bold type: $\mathbf{a}$. We denote the null vector with $\mathbf{0}$.

We denote the set of real $m \times n$ matrices with $\mathbb{R}^{m \times n}$. Matrices are printed in upper-case, bold type: $\mathbf {A}$. The matrix $\mathrm{diag} ( \mathbf{a} )$ is the diagonal matrix, which possesses the components of the vector $\mathbf {a}$ as diagonal elements.

Sets (of scalars, vectors, etc.) are printed in upper-case, normal type: $A$. We denote the cardinality with $|A|$, the interior with $\mathrm{int} ( A )$, and the power set of a set $A$ with $2^{A}$.

We denote the gradients of a differentiable function $f : \mathbb {R}^{m} \rightarrow\mathbb{R}$ at the point $\bar{\mathbf{x}}$ with $\nabla f(\bar{\mathbf{x}})$. If the function depends on two (or more) vectors, that is, $f : \mathbb{R}^{m} \times\mathbb{R}^{n} \rightarrow\mathbb{R}$, then $\nabla_{\mathbf{x}} f(\bar {\mathbf{x}}, \bar{\mathbf{y}})$ is the vector of the first-order derivatives of $f$ in $(\bar{\mathbf{x}}, \bar{\mathbf{y}})$ with regard to the $\mathbf{x}$ variables. Optimization problems are printed in upper-case, sans serif type: $\mathsf{P}$.

4.1 Set-Theoretical Models

In the following section, we formalize the verbal description and derive a set-theoretical model for both types of maximum material yield problems.

4.1.1 Problems with Fixed Designs

We first turn to type (1) problems, which we call maximum material yield problems with fixed designs $( \mathsf{MaxMY}\mbox{-}\mathsf{FD} )$. With $C$, we denote the container, with $F_{k}$, $k \in K := \{ 1,\ldots,r \}$, the flaws, and with $D_{l}$, $l \in L := \{ 1,\ldots,s \}$, the designs. Each of these objects is represented by a non-empty, compact subset of $\mathbb{R}^{n}$, $n \in\mathbb{N}$ (in general $n \in\{ 2,3 \}$).

While the container can be given with its flaws in an arbitrary position, we assume that the designs are located in a defined position. In order to be able to verify whether a design can be arranged in the container without overlapping the other designs and the flaws, the designs must be transformed into the container. For a maximum material yield problem with fixed designs, for which design rotations are not allowed, we search for a subset $L^{*} \subseteq L$ of designs and translation vectors $\boldsymbol{\sigma}_{l} \in\varSigma_{l} \subseteq\mathbb{R}^{n}$, $l \in L^{*}$, such that the design $D_{l}$ translated by $\boldsymbol{\sigma}_{l}$ (see Fig. 7, left) fulfills for $l \in L^{*}$ all arrangement conditions (containment in the container, non-overlapping with flaws, and non-overlapping with other designs).

Fig. 7

Left, translation, right, rotation and translation of a triangular design $D$

If design rotation is allowed, one also searches for parameters $\boldsymbol{\theta}_{l} \in\varTheta_{l}$, $l \in L^{*}$, of a rotation matrix $\mathbf{R} = \mathbf{R}(\boldsymbol{\theta}_{l}) \in\mathbb{R}^{n \times n}$, so that the design $D_{l}$, which is rotated by means of $\mathbf{R}(\boldsymbol {\theta}_{l})$ and translated by $\boldsymbol{\sigma}_{l}$ (see Fig. 7, right), fulfills the arrangement conditions for $l \in L^{*}$. In many practical applications, the ranges $\varTheta_{l}$, $l \in L$, of the rotation parameters are severely restricted or even finite sets.

This therefore yields the following set-theoretical model for maximum material yield problems with fixed designs:

$$\begin{aligned} \mathsf{MaxMY}\mbox{-}\mathsf{FD} {:} \quad \max\limits _{{\scriptstyle {\scriptstyle L^{*} \subseteq L\atop\scriptstyle \boldsymbol {\sigma}_{l} \in\varSigma_{l}}\atop\scriptstyle \boldsymbol{\theta}_{l} \in \varTheta_{l}}} & \sum _{l \in L^{*}} \mathrm{Vol}(D_{l}) \\ \mbox{s.t. } & \mathbf{R}(\boldsymbol{\theta}_{l}) D_{l} + \boldsymbol{\sigma}_{l} \subseteq C, \\ & \quad l \in L^{*}, \end{aligned}$$

(1)

$$\begin{aligned} & \mathbf{R}(\boldsymbol{\theta}_{l}) D_{l} + \boldsymbol{\sigma}_{l} \cap\mathrm{int} ( F_{k} ) = \emptyset, \\ & \quad l \in L^{*}, \ k \in K, \end{aligned}$$

(2)

$$\begin{aligned} & \mathbf{R}(\boldsymbol{\theta}_{l_{1}}) D_{l_{1}} + \boldsymbol{\sigma}_{l_{1}} \cap\mathrm{int} \bigl( \mathbf{R}( \boldsymbol{\theta}_{l_{2}}) D_{l_{2}} + \boldsymbol{ \sigma}_{l_{2}} \bigr) = \emptyset, \\ & \quad l_{1},l_{2} \in L^{*}, \ l_{1} < l_{2}, \end{aligned}$$

(3)

where $\mathrm{int} ( A )$ refers to the interior of the set $A$, thus allowing the designs to contact one another as well as the flaws.

4.1.2 Problems with Variable Designs

We now consider type (2) problems, which we call maximum material yield problems with variable designs $( \mathsf{MaxMY}\mbox{-}\mathsf{VD} )$. In addition to the previously introduced notation, we use $\mathbf{p}_{l} \in\mathbb{R}^{d_{l}}$ to denote the size and form parameters of the $l$-th design and $P_{l}$ to denote the associated set of the feasible parameter values. The simplest example of a purely size-variable design is a circle with variable radius. An example of a design that is both size and form variable is a so-called superellipse:

$$ D^{\mathrm{SE}}(\mathbf{p}) := \biggl\{ \mathbf{y} \in \mathbb{R}^{2} \biggm| \biggl( \frac{y_{1}^{2}}{p_{1}^{2}} \biggr)^{p_{3}} + \biggl( \frac{y_{2}^{2}}{p_{2}^{2}} \biggr)^{p_{3}} \leq1 \biggr\} ,\quad \mathbf{p} \in P = \mathbb{R}^{3}_{++}. $$

(4)

Variations in $p_{1}$ or $p_{2}$ yield changes in size; variations in $p_{3}$ yield changes in form. For $p_{3} = 1/3$, $D^{\mathrm{SE}}(\mathbf{p})$ is a generalized astroid; for $p_{3} = 1/2$, a rhombus; for $p_{3} = 1$, a usual ellipse; and for $p_{3} \rightarrow \infty$, $D^{\mathrm{SE}}(\mathbf{p})$ approaches a rectangle (see Fig. 8).

Fig. 8

Superellipse for $p_{1} = 2$ and $p_{2} = 1$ and various values of $p_{3}$, from left to right: $p_{3} = 1/3$, $p_{3} = 1/2$, $p_{3} = 1$, and $p_{3} = 50$

Because the designs are now at least size-variable, the search for an optimal subset of the set of all designs no longer makes sense, since, in principle, the designs of each subset can be arranged in the container if they are only made small enough.

Therefore, for maximum material yield problems with variable designs, we have the following set-theoretical model:

$$\begin{aligned} \mathsf{MaxMY}\mbox{-}\mathsf{VD} {:} \quad \max\limits _{{\scriptstyle {\scriptstyle \boldsymbol{\sigma }_{l} \in\varSigma _{l} \atop\scriptstyle \boldsymbol{\theta}_{l} \in\varTheta_{l} }\atop\scriptstyle \mathbf{p}_{l} \in P_{l}}} & \sum _{l \in L} \mathrm{Vol} \bigl(D_{l}( \mathbf{p}_{l}) \bigr) \\ \mbox{s.t. }& \mathbf{R}(\boldsymbol{\theta}_{l}) D_{l}( \mathbf{p}_{l}) + \boldsymbol{\sigma}_{l} \subseteq C, \\ & \quad l \in L, \end{aligned}$$

(5)

$$\begin{aligned} & \mathbf{R}(\boldsymbol{\theta}_{l}) D_{l}( \mathbf{p}_{l}) + \boldsymbol{\sigma}_{l} \cap \mathrm{int} ( F_{k} ) = \emptyset, \\ & \quad l \in L, \ k \in K, \end{aligned}$$

(6)

$$\begin{aligned} & \mathbf{R}(\boldsymbol{\theta}_{l_{1}}) D_{l_{1}}( \mathbf{p}_{l_{1}}) + \boldsymbol{\sigma}_{l_{1}} \cap \mathrm{int} \bigl( \mathbf{R}(\boldsymbol{\theta}_{l_{2}}) D_{l_{2}}( \mathbf{p}_{l_{2}}) + \boldsymbol{\sigma}_{l_{2}} \bigr) = \emptyset, \\ & \quad l_{1},l_{2} \in L, \ l_{1} < l_{2}. \end{aligned}$$

(7)

Whereas the model MaxMY-FD possesses a combinatorical component, the model MaxMY-VD does not. Nonetheless, it is also conceivable here that one might vary over subsets of the set of considered designs or various design numbers. What the two models have in common is the structure of the constraints, which we now turn to in the following discussion.

4.2 Handling Containment and Non-overlapping Conditions

The set-theoretical constraints (1) to (3) or (5) to (7) are of two different types. Whereas constraints (1) and (5) represent containment conditions, the other equations represent non-overlapping conditions. However, each type can be transformed into the other: A set $A~\subseteq~\mathbb{R}^{n}$ is contained in a set $B\subseteq\mathbb{R}^{n}$ if and only if it does not overlap with the complement $\mathbb{R}^{n}\setminus B$ of set $B$:

$$A\subseteq B\quad\iff\quad A\cap\mathrm{int} \bigl( \mathbb{R}^{n} \setminus B \bigr)=\emptyset. $$

Therefore, in the following discussion, we will also use the expression “non-overlapping” as a substitute for “containment.”

However, the abstract formulation of the constraints (1) to (3) or (5) to (7) isn’t numerically tractable.

In order to obtain computable problems, the set-theoretical constraints must be transformed into usual constraints of mathematical optimization.

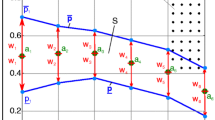
In some cases, this is possible on the basis of geometrical considerations. For example, a circle is contained within a second circle if and only if the distance between their centers is less than or equal to the difference between the radii of the second and first circles (see Fig. 9, left). Moreover, two circles do not overlap if and only if the distance between their centers is greater than or equal to the sum of their radii (see Fig. 9, right).

Fig. 9

Positional relationship of two circles: left, containment; right, non-overlapping

In cases involving complicated objects, this kind of approach is usually fruitless. In the following discussion, we describe two generally valid solution approaches. The first approach uses the methods of computational geometry, more precisely, collision detection. The second approach presupposes a functional description of the objects and transforms the set-theoretical constraints into semi-infinite ones.

4.3 Treating the Non-overlapping Constraints Using Collision Detection Methods

In the present context, we understand the term “collision detection” (see [24], for example) to refer to methods used primarily in the fields of computer games and physical simulations to quickly establish whether two objects are overlapping or not. The methods were developed for three-dimensional space and presuppose that the objects are given explicitly as either triangulations—where an object’s surface is approximated by means of triangles—or as polyhedrons. The critical feature of these methods is the efficiency with which non-overlapping can be tested. One way to make the test as efficient as possible is to pre-process the triangulations by placing a box around each triangle. The boxes are then, in turn, repeatedly pooled together in an appropriate fashion. The result is a tree of boxes, a so-called bounding box tree (BBT), in which each box covers one part of the object, and the box at the root of the tree covers it entirely (see Fig. 10). If a triangulation is now given, one can use the tree to quickly determine which of its triangles might possibly be intersected by the surface of a second object. In this way, one must usually only test a relatively small number of triangles, even when the triangulation contains many of them, as is typically the case for the triangulation of rough stone, for example. For problems with fixed designs, one can directly verify non-overlapping in this fashion, since translation and rotation can be applied directly to the triangulation and the BBT. For problems with variable designs, the triangulation and associated BBT must be newly generated each time. Often, this can prove too costly. In our case, however, the complex triangulation of the rough stone remains unchanged, and the triangulation of a faceted stone and its corresponding BBT can be generated quickly. The application of this idea to gemstone cutting is described in detail in [4].

Fig. 10

Design of a BBT in 2D: each line of the starting object is covered by a box. These are then iteratively pooled together—pair-wise, for example—and covered by another box, until only one remains. To check whether the point at the upper right is contained within the object, one need only test the shaded boxes.

4.4 Transforming the Non-overlapping Conditions into Semi-Infinite Constraints

Let us turn now to the re-formulation of non-overlapping conditions as semi-infinite constraints. First, we introduce our understanding of the latter. Let $2^{A}$ denote the power set, i.e., the set of all subsets, of a set $A$ and let $|A|$ denote its cardinality.

Definition 1

(Semi-infinite constraint, infinite index set)

Let $m,n \in\mathbb{N}$, $g : \mathbb{R}^{m} \times\mathbb{R}^{n} \rightarrow\mathbb{R}$ be a scalar-valued function, and let $Y : \mathbb{R}^{m} \rightarrow2^{\mathbb{R}^{n}}$ be a set-valued mapping with $|Y(\mathbf{x})| = \infty$ for all $\mathbf{x} \in \mathbb{R}^{m}$. Then, the condition

$$ g(\mathbf{x}, \mathbf{y}) \leq0\quad\text{for all } \mathbf{y} \in Y(\mathbf{x}) $$

(8)

is called a general semi-infinite constraint. If $Y(\mathbf {x}) \equiv\bar{Y} \subset\mathbb{R}^{n}$ for all $\mathbf{x} \in \mathbb{R}^{m}$, then the condition (8) is called a standard semi-infinite constraint. In both cases, the set $Y(\mathbf{x})$ is referred to as the infinite index set.

If the function $g$ does not depend on $\mathbf{x}$, this does not affect the terminology.

For our subsequent analysis, we summarize the translation, rotation, and size/shape parameters for each design $D_{l}$, $l \in L$ in a vector $\tilde{\mathbf{p}}_{l}$; introduce the set of feasible parameter values $\tilde{P}_{l} := \varSigma_{l} \times\varTheta_{l} \times P_{l}$; and write $D_{l}(\tilde{\mathbf{p}}_{l})$ instead of $\mathbf {R}(\boldsymbol{\theta}_{l})D_{l}(\mathbf{p}_{l}) + \boldsymbol{\sigma}_{l}$.

If the container can be represented as the solution set of a system of inequalities, that is, if

$$ C = \bigl\{ \mathbf{y} \in\mathbb{R}^{n} \bigm| c_{i}( \mathbf{y}) \leq0, \ i \in I_{0} \bigr\} , $$

where $I_{0}$ is a finite index set and $c_{i}$, $i \in I_{0}$, are real-valued functions, then the transformation of the containment conditions (1) or (5) into semi-infinite constraints is straightforward (see Fig. 11 for a graphical illustration):

$$ D_{l}(\tilde{\mathbf{p}}_{l}) \subseteq C \quad \Leftrightarrow\quad c_{i}(\mathbf{y}) \leq0\quad \text{for all } \mathbf{y} \in D_{l}(\tilde{\mathbf{p}}_{l}), \ i \in I_{0}. $$

Fig. 11

Transformation of a containment condition into a semi-infinite constraint

For the semi-infinite reformulation of the non-overlapping conditions, two approaches were introduced and investigated in [16] and [14]: mutual separation and separation by hyperplane. Because only the second approach can be applied in cases where there are additional, relevant requirements stemming from the production technology (see Sect. 6.2) we will restrict our discussion to this approach. The foundation for this discussion consists of a so-called separation theorem:

Theorem 1

(Separation theorem, see [20], for example)

Let $A,B \subset\mathbb{R}^{n}$ be two non-empty, convex sets, of which at least one is open. Then $A$ and $B$ are non-overlapping if and only if a vector $\boldsymbol{\eta} \in\mathbb{R}^{n} \setminus\{ \mathbf{0} \}$ and a number $\beta\in\mathbb{R}$ exist, such that the following holds:

$$ \boldsymbol{\eta}^{T} \mathbf{y} \leq\beta\quad\textit{for all } \mathbf{y} \in A $$

and

$$ \boldsymbol{\eta}^{T} \mathbf{z} \geq\beta\quad\textit{for all } \mathbf{z} \in B. $$

The hyperplane $H(\boldsymbol{\eta},\beta) := \{ \mathbf{y} \in \mathbb{R}^{n} \mid\boldsymbol{\eta}^{T} \mathbf{y} = \beta\}$, which separates the sets $A$ and $B$, is called a separating hyperplane.

If the flaws and designs are convex, the above theorem delivers a semi-infinite formulation of the non-overlapping conditions (2) and (3) or (6) and (7) (for a graphical illustration, see Fig. 25, right, with $\delta= 0$):

• (1) $D_{l}(\tilde{\mathbf{p}}_{l}) \cap\mathrm{int} ( F_{k} ) = \emptyset$ if and only if a vector $\boldsymbol{\eta }_{l,k}^{\mathrm{DF}} \in\mathbb{R}^{n} \setminus\{ \mathbf{0} \}$ and a number $\beta_{l,k}^{\mathrm{DF}}$ exist, such that

  $$ \bigl(\boldsymbol{\eta}_{l,k}^{\mathrm{DF}}\bigr)^{T} \mathbf{y} \leq\beta _{l,k}^{\mathrm{DF}}\quad\text{for all } \mathbf{y} \in D_{l}(\tilde {\mathbf{p}}_{l}) $$

  (9)

  and

  $$ \bigl(\boldsymbol{\eta}_{l,k}^{\mathrm{DF}}\bigr)^{T} \mathbf{z} \geq\beta _{l,k}^{\mathrm{DF}}\quad\text{for all } \mathbf{z} \in F_{k}. $$

  (10)

• (2) $D_{l_{1}}(\tilde{\mathbf{p}}_{l_{1}}) \cap\mathrm{int} ( D_{l_{2}}(\tilde{\mathbf{p}}_{l_{2}}) ) = \emptyset$ if and only if a vector $\boldsymbol{\eta}_{l_{1},l_{2}}^{\mathrm{DD}} \in \mathbb{R}^{n} \setminus\{ \mathbf{0} \}$ and a number $\beta _{l_{1},l_{2}}^{\mathrm{DD}}$ exist, such that

  $$ \bigl(\boldsymbol{\eta}_{l_{1},l_{2}}^{\mathrm{DD}}\bigr)^{T} \mathbf{y} \leq\beta _{l_{1},l_{2}}^{\mathrm{DD}}\quad\text{for all } \mathbf{y} \in D_{l_{1}}(\tilde{\mathbf{p}}_{l_{1}}) $$

  (11)

  and

  $$ \bigl(\boldsymbol{\eta}_{l_{1},l_{2}}^{\mathrm{DD}}\bigr)^{T} \mathbf{z} \geq\beta _{l_{1},l_{2}}^{\mathrm{DD}}\quad\text{for all } \mathbf{z} \in D_{l_{2}}(\tilde{\mathbf{p}}_{l_{2}}). $$

  (12)

Whereas the conditions (9), (11), and (12) represent general semi-infinite constraints, condition (10) is a standard semi-infinite one. The condition $\boldsymbol{\eta} \neq \mathbf{0}$ is problematic from an optimization perspective, but can be suitably reformulated by means of normalization, for example, $\| \boldsymbol{\eta} \|_{2}^{2} = 1$, where $\| \cdot\|_{2}$ is the Euclidean norm.

Let

$$ \mathbf{x} := \bigl(\tilde{\mathbf{p}}_{1}, \ldots, \tilde{\mathbf {p}}_{s}, \boldsymbol{\eta}_{1,1}^{\mathrm{DF}}, \beta_{1,1}^{\mathrm{DF}},\ldots, \boldsymbol{\eta}_{s,r}^{\mathrm{DF}}, \beta_{s,r}^{\mathrm{DF}}, \boldsymbol {\eta}_{1,2}^{\mathrm{DD}}, \beta_{1,2}^{\mathrm{DD}},\ldots, \boldsymbol {\eta}_{s-1,s}^{\mathrm{DD}}, \beta_{s-1,s}^{\mathrm{DD}}\bigr) $$

be the vector of all parameters (design and hyperplane parameters) and let

$$ X := \left \{ \mathbf{x} \left\vert \textstyle\begin{array}{rcl} \tilde{\mathbf{p}}_{l} & \in& \tilde{P}_{l},\ l \in L, \\ \bigl\| \boldsymbol{\eta}_{l,k}^{\mathrm{DF}} \bigr\| _{2}^{2} & = & 1,\ l \in L,\ k \in K, \\ \bigl\| \boldsymbol{\eta}_{l_{1},l_{2}}^{\mathrm{DD}} \bigr\| _{2}^{2} & = & 1,\ l_{1},l_{2} \in L,\ l_{1} < l_{2} \end{array}\displaystyle \right. \right \} $$

be the set of feasible parameter values. Then, the reformulation of a maximum material yield problem with variable designs as a so-called general semi-infinite optimization problem using the separation by hyperplanes approach becomes:

$$\begin{aligned} \mathsf{GSIP}_{\mathsf{MaxMY}\mbox{\scriptsize{-}}\mathsf{VD}}{:} \quad \max\limits _{\mathbf{x} \in X} & \sum _{l \in L} \mathrm{Vol} \bigl(D_{l}( \mathbf{p}_{l}) \bigr) \\ \mbox{s.t. }& c_{i}(\mathbf{y}) \leq0\quad \mbox{for all } \mathbf{y} \in D_{l}(\tilde{\mathbf{p}}_{l}), \\ & \quad i \in I_{0}, \ l \in L, \end{aligned}$$

(13)

$$\begin{aligned} & \left . \textstyle\begin{array}{@{}l@{\quad}l} \bigl(\boldsymbol{\eta}_{l,k}^{\mathrm{DF}} \bigr)^{T} \mathbf{y} - \beta _{l,k}^{\mathrm{DF}} \leq0 & \mbox{for all } \mathbf{y} \in D_{l}(\tilde{\mathbf{p}}_{l}), \\ \bigl(\boldsymbol{\eta}_{l,k}^{\mathrm{DF}} \bigr)^{T} \mathbf{z} - \beta _{l,k}^{\mathrm{DF}} \geq0 & \mbox{for all } \mathbf{z} \in F_{k}, \end{array}\displaystyle \right \} \\ & \quad l \in L, \ k \in K, \end{aligned}$$

(14)

$$\begin{aligned} & \left . \textstyle\begin{array}{@{}l@{\quad}l} \bigl(\boldsymbol{\eta}_{l_{1},l_{2}}^{\mathrm{DD}} \bigr)^{T} \mathbf {y} - \beta _{l_{1},l_{2}}^{\mathrm{DD}} \leq0 & \mbox{for all } \mathbf{y} \in D_{l_{1}}(\tilde{\mathbf{p}}_{l_{1}}), \\ \bigl(\boldsymbol{\eta}_{l_{1},l_{2}}^{\mathrm{DD}} \bigr)^{T} \mathbf {z} - \beta _{l_{1},l_{2}}^{\mathrm{DD}} \geq0 & \mbox{for all } \mathbf{z} \in D_{l_{2}}(\tilde{\mathbf {p}}_{l_{2}}), \end{array}\displaystyle \right \} \\ & \quad l_{1},l_{2} \in L,\ l_{1} < l_{2}. \end{aligned}$$

(15)

4.5 Solution Methods for General Semi-Infinite Optimization Problems

Now that we know how a maximum material yield problem can be transformed into a general semi-infinite optimization problem, the question arises as to how such problems can be solved numerically. We now want to answer this question.

Let us consider optimization problems of the following form:

$$\begin{aligned} \textstyle\begin{array}[b]{l@{\quad}cl} \mathsf{GSIP}{:} & \displaystyle\min\limits_{\mathbf{x} \in X \subseteq\mathbb {R}^{m}} & f(\mathbf{x}) \\ & \mbox{s.t. } & g_{i}(\mathbf{x}, \mathbf{y}) \leq0 \quad \mbox{ for all } \mathbf{y} \in Y(\mathbf{x}), \ i \in I, \end{array}\displaystyle \end{aligned}$$

(16)

with

$$ Y(\mathbf{x}) := \bigl\{ \mathbf{y} \in\mathbb{R}^{n} \bigm| v_{j}(\mathbf {x}, \mathbf{y}) \leq0, \ j \in J \bigr\} \quad \text{and} \quad \bigl|Y(\mathbf{x})\bigr| = \infty\quad\text{for all } \mathbf{x} \in X, $$

(17)

$I := \{ 1,\ldots, p \}$ and $J := \{ 1,\ldots, q \}$, as well as real-valued, sufficiently smooth functions $f$, $g_{i}$, $i \in I$, and $v_{j}$, $j \in J$. According to Definition 1, we identify such an optimization problem either as:

• a g eneral(ized) s emi- i nfinite p rogram, if the set-valued mapping $Y$ depends on $\mathbf{x}$, or as

• a (standard) s emi- i nfinite p rogram, if the set-valued mapping $Y$ is constant.

The latter is then referred to as an SIP, rather than a GSIP.

The consideration of multiple infinite index sets, a situation that arises for maximum material yield problems, can proceeded directly. For clarity’s sake, we will restrict ourselves in the following discussion to one infinite index set.

For a comprehensive introduction to semi-infinite optimization, we refer the reader to the review article [29] and the book [36] for the SIP problem class and to the review articles [28, 40] and the monographs [39, 50] for the more general GSIP problem class.

Even if the difference between general and standard semi-infinite problems initially appears to be minimal, the former are substantially more complicated structurally and much more difficult to solve numerically.

For the remainder of this section, we make the following assumptions, which we need for our further considerations and which can be fulfilled very easily for maximum material yield problems by means of a suitable modeling approach.

Assumption 1

For all $\mathbf{x} \in X$, the set $Y(\mathbf{x})$ is non-empty and compact.

Assumption 2

For all $\mathbf{x} \in X$, the functions $g_{i}(\mathbf{x}, \cdot)$, $i \in I$, are concave and the set $Y(\mathbf{x})$ is convex.

Assumption 3

For all $\mathbf{x} \in X$, the set $Y(\mathbf{x})$ possesses a Slater point, that is, a point $\hat{\mathbf{y}}(\mathbf{x})$, such that $v_{j}(\mathbf{x}, \hat{\mathbf{y}}(\mathbf{x})) < 0$, $j \in J$, holds.

The key to both the theoretical and the numerical treatment of semi-infinite optimization problems lies in their two-level structure. The parametric lower-level problems from GSIP are given by

$$\begin{aligned} \textstyle\begin{array}[b]{l@{\quad}cl} \mathsf{Q}_{i}(\mathbf{x}){:} & \displaystyle\max\limits_{\mathbf {y} \in\mathbb {R}^{n}} & g_{i}(\mathbf{x}, \mathbf{y}) \\ & \mbox{s.t. }& v_{j}(\mathbf{x}, \mathbf{y}) \leq0, \quad j \in J. \end{array}\displaystyle \end{aligned}$$

(18)

The term $\varphi_{i}(\mathbf{x})$ denotes the optimal value of $\mathsf{Q}_{i}(\mathbf{x})$. Accordingly, the function $\varphi_{i}$ is called the optimal value function. Obviously, a point $\mathbf {x} \in X$ is feasible for GSIP if and only if $\varphi _{i}(\mathbf{x}) \leq0$ for all $i \in I$. The main challenge for the numerical solution of semi-infinite optimization problems is that evaluating $\varphi_{i}(\mathbf{x}) \leq0$ requires computing a global solution of the problem $\mathsf{Q}_{i}(\mathbf{x})$. This is a very difficult task in general. Under Assumptions 2 and 3, however, the lower-level problems are convex, regular optimization problems. This makes a global solution computable. Moreover, under Assumptions 1 to 3, the optimal value functions $\varphi_{i}$, $i \in I$, are well defined and continuous. Thus, the feasible set of GSIP

$$\begin{aligned} M :=& \bigl\{ \mathbf{x} \in X \bigm| g_{i}(\mathbf{x}, \mathbf{y}) \leq0 \text{ for all } \mathbf{y} \in Y(\mathbf{x}), \ i \in I \bigr\} \\ =& \bigl\{ \mathbf{x} \in X \bigm| \varphi_{i}(\mathbf{x}) \leq0, \ i \in I \bigr\} \end{aligned}$$

is closed, and a minimum value exists.

To date, solution methods for general semi-infinite optimization problems have been developed primarily from a conceptual perspective. To the best of our knowledge, comprehensive numerical evaluations exist only for the explicit smoothing approach from [39, 42]. These evaluations can be found in [39], [16], and [12]. All in all, the methods developed so far are based on two concepts:

• (1) the generalization of methods for standard semi-infinite optimization problems and

• (2) the transformation of a general semi-infinite optimization problem into a standard semi-infinite optimization problem.

The methods stemming from concept (1) can be further subdivided:

• (A) discretization and exchange methods (see [46, 47]),

• (B) methods based on local reduction of the general semi-infinite problem (see [43–45, 48]), and

• (C) methods based on the reformulation of GSIP into a related problem, so-called lift-&-project approaches (see [23, 42] and [10]).

We now introduce two methods that were developed at the ITWM in connection with two dissertations [14, 16] and tested by means of gemstone cutting problems.

4.5.1 A Feasible, Explicit Smoothing Method

The first method (see [16] and [10]) consists of a modification of the explicit smoothing approach from [39, 42]. With this modification, the solutions generated in the method for the surrogate problem are feasible for the original problem. We first introduce briefly the explicit smoothing approach and then take a closer look at the aforementioned modification.

Explicit Smoothing Approach

Under Assumption 1, the semi-infinite constraints (16) are equivalent to the conditions

$$ \max_{\mathbf{y} \in Y(\mathbf{x})} g_{i}(\mathbf{x},\mathbf{y}) \leq0,\quad i \in I $$

(see [41]). Thus, GSIP can be written as a b i- l evel p rogram:

$$\begin{aligned} \mathsf{BLP}_{\mathsf{GSIP}}{:} \quad \min\limits _{{\scriptstyle \mathbf {x}, \atop\scriptstyle \mathbf{y}_{1},\ldots,\mathbf{y}_{p}}}& f(\mathbf{x}) \\ \mbox{s.t. } & g_{i}(\mathbf{x}, \mathbf{y}_{i}) \leq0, \end{aligned}$$

(19)

$$\begin{aligned} & \mathbf{y}_{i} \mbox{ solves } \mathsf{Q}_{i}( \mathbf{x}), \quad i \in I. \end{aligned}$$

(20)

Under Assumptions 2 and 3, each global solution $\mathbf{y}_{i}$ of the lower-level problem $\mathsf{Q}_{i}(\mathbf{x})$, $i \in I$, can be characterized by the first-order optimality conditions:

$$\begin{aligned} \nabla_{\mathbf{y}} \mathscr{L}_{i}(\mathbf{x},\mathbf {y}_{i},\boldsymbol{\mu}_{i}) = & \boldsymbol{0}, \\ \mathrm{diag}(\boldsymbol{\mu}_{i}) \mathbf{v}(\mathbf{x},\mathbf {y}_{i}) = & \boldsymbol{0}, \\ \boldsymbol{\mu}_{i} \geq& \boldsymbol{0}, \\ \mathbf{v}(\mathbf{x},\mathbf{y}_{i}) \leq& \boldsymbol{0}, \end{aligned}$$

where

$$ \mathscr{L}_{i}(\mathbf{x},\mathbf{y},\boldsymbol{\mu}) := g_{i}(\mathbf{x},\mathbf{y}) - \boldsymbol{\mu}^{T} \mathbf{v}(\mathbf {x},\mathbf{y}) $$

is the Lagrangian function of problem $\mathsf{Q}_{i}(\mathbf{x})$, $\boldsymbol{\mu}_{i}$ is the $\mathbf{y}_{i}$-associated vector of Lagrange multipliers, $\mathrm{diag} ( \boldsymbol{\mu}_{i} )$ is the diagonal matrix with diagonal elements $\mu_{j}^{i}$, $j \in J$, and

$$ \mathbf{v}(\mathbf{x}, \mathbf{y}) := \bigl(v_{1}(\mathbf{x}, \mathbf {y}),\ldots, v_{q}(\mathbf{x}, \mathbf{y})\bigr)^{T}. $$

Therefore, $\mathsf{BLP}_{\mathsf{GSIP}}$ can be written as a m athematical p rogram with c omplementarity c onstraints:

$$\begin{aligned} \mathsf{MPCC}_{\mathsf{GSIP}}{:} \quad \min\limits _{{\scriptstyle {\scriptstyle \mathbf {x}, \atop\scriptstyle \mathbf{y}_{1},\ldots,\mathbf{y}_{p},}\atop\scriptstyle \boldsymbol{\mu }_{1},\ldots,\boldsymbol{\mu}_{p}}} & f(\mathbf{x}) \\ \mbox{s.t. }& g_{i}(\mathbf{x}, \mathbf{y}_{i}) \leq0, \end{aligned}$$

(21)

$$\begin{aligned} & \nabla_{\mathbf{y}} \mathscr{L}_{i}(\mathbf{x}, \mathbf{y}_{i}, \boldsymbol{\mu}_{i}) = \mathbf{0}, \end{aligned}$$

(22)

$$\begin{aligned} & -\mathrm{diag} ( \boldsymbol{\mu}_{i} ) \mathbf{v}( \mathbf{x}, \mathbf{y}_{i}) = \mathbf{0}, \end{aligned}$$

(23)

$$\begin{aligned} & \boldsymbol{\mu}_{i} \geq\mathbf{0}, \end{aligned}$$

(24)

$$\begin{aligned} & -\mathbf{v}(\mathbf{x}, \mathbf{y}_{i}) \geq\mathbf{0}, \quad i\in I. \end{aligned}$$

(25)

At this point, we do indeed have a reformulation of GSIP as a finite, one-level optimization problem. However, for optimization problems with complementarity constraints, classical regularity conditions such as MFCQ—which are of tremendous significance for numerical methods—are generally not fulfilled at any feasible point (see [37]). (Explicit) smoothing represents one possibility of regularization. The idea here is to replace the “malignant” conditions (23) with the conditions

$$ -\mathrm{diag}(\boldsymbol{\mu}_{i}) \mathbf{v}(\mathbf{x},\mathbf {y}_{i}) = \tau^{2} \mathbf{1}, \quad i \in I, $$

(26)

where $\tau> 0$ is a perturbation parameter and $\mathbf{1} = (1,\ldots,1)^{T} \in\mathbb{R}^{q}$. In this way, $\mathsf {MPCC}_{\mathsf{GSIP}}$ is embedded into a parametric family of optimization problems

$$\begin{aligned} \mathsf{P}_{\tau}{:} \quad \min\limits _{{\scriptstyle {\scriptstyle \mathbf{x},\atop\scriptstyle \mathbf{y}_{1},\ldots,\mathbf{y}_{p},}\atop\scriptstyle \boldsymbol{\mu }_{1},\ldots,\boldsymbol{\mu}_{p}}} & f( \mathbf{x}) \\ \mbox{s.t. } & g_{i}(\mathbf{x}, \mathbf{y}_{i}) \leq0, \\ & \nabla_{\mathbf{y}} \mathscr{L}_{i}(\mathbf{x}, \mathbf{y}_{i}, \boldsymbol{\mu}_{i}) = \mathbf{0}, \\ & -\mathrm{diag} ( \boldsymbol{\mu}_{i} ) \mathbf{v}( \mathbf{x}, \mathbf{y}_{i}) = \tau^{2} \mathbf{1}, \\ & \boldsymbol{\mu}_{i} \geq\mathbf{0}, \\ & -\mathbf{v}(\mathbf{x}, \mathbf{y}_{i}) \geq\mathbf{0}, \quad i \in I. \end{aligned}$$

In [42], the authors show that the degenerateness of the complementarity constraints (23) is eliminated via the regularization described above, and that $P_{\tau}$ can be solved using standard software for nonlinear optimization problems. A solution of $\mathsf{P}_{0} = \mathsf{MPCC}_{\mathsf{GSIP}}$ can now be found by solving a sequence of problems $\mathsf{P}_{\tau_{k}}$, where $\{ \tau_{k} \}_{k \in\mathbb{N}_{0}} \subset\mathbb{R}_{++}$ is a monotonically decreasing null sequence:

Whereas problem $\mathsf{MPCC}_{\mathsf{GSIP}}$ is an equivalent formulation for GSIP, the parametric problem $\mathsf{P}_{\tau}$ represents for $\tau> 0$ merely an approximation.

In [39], the author shows that the explicit smoothing approach possesses an external approximation property (see Fig. 12 also):

Theorem 2

([39])

Let $M_{\tau}$ be the projection of the feasible set of $\mathsf {P}_{\tau}$ in the $\mathbf{x}$-space. Then:

• (i) For all $0 < \tau_{1} < \tau_{2}$, $M_{\tau_{1}} \subset M_{\tau_{2}}$.

• (ii) For all $\tau> 0$, $M \subset M_{\tau}$.

A negative effect of this external approximation property is that the $\mathbf{x}$-components of the solutions of $\mathsf{P}_{\tau}$ can be infeasible for GSIP for all $\tau> 0$, although the infeasibility vanishs in the limiting case. This is a serious problem when the feasibility of the iterates plays a role.

Feasibility in the Explicit Smoothing Approach

The dissertation [16] (and the article [10]) show how the drawback of the iterates’ infeasibility can be redressed by a simple modification of the conditions (21). We will now outline how this works.

Whereas the conditions (23) to (25) characterize the global solutions of the lower-level problems, the conditions (24) to (26) describe for $\tau> 0$ the global solutions of the so-called log-barrier problems (see [39, 42]):

$$ \mathsf{Q}_{i}^{\tau}(\mathbf{x}): \quad\max _{\mathbf{y} \in \mathbb{R}^{n}} \ b_{i}^{\tau}(\mathbf{x}, \mathbf{y}) := g_{i}(\mathbf {x}, \mathbf{y}) + \tau^{2} \sum _{j=1}^{q} \ln\bigl(-v_{j}(\mathbf{x}, \mathbf{y})\bigr), \quad i \in I. $$

(27)

Using the duality theory of convex optimization, the optimal value functions $\varphi_{i}$, $i\in I$, can be estimated from above and thus the feasible set of GSIP can be approximated from the interior (see Fig. 12).

Lemma 1

([16])

For $\tau> 0$ and $i \in I$, let $\mathbf{y}_{i}^{\tau}(\mathbf{x})$ be a global solution of $\mathsf{Q}_{i}^{\tau}(\mathbf{x})$. Then,

$$ \varphi_{i}(\mathbf{x}) = \max_{\mathbf{y} \in Y(\mathbf{x})} \ g_{i}(\mathbf{x}, \mathbf{y}) \leq g_{i}\bigl(\mathbf{x}, \mathbf{y}_{i}^{\tau }(\mathbf{x})\bigr) + q \tau^{2}, $$

where $q$ is the number of functions  $v_{j}$, $j \in J$, describing the index set $Y(\mathbf{x})$.

Thus, the original constraints of the upper level (21) can be replaced by the conditions

$$ g_{i}(\mathbf{x}, \mathbf{y}_{i}) + q \tau^{2} \leq0,\quad i \in I, $$

(28)

which yields the parametric optimization problem

$$\begin{aligned} \hat{\mathsf{P}}_{\tau}{:} \quad \min\limits _{{\scriptstyle {\scriptstyle \mathbf{x},\atop\scriptstyle \mathbf{y}_{1},\ldots,\mathbf{y}_{p},}\atop\scriptstyle \boldsymbol{\mu }_{1},\ldots,\boldsymbol{\mu}_{p}}} & f(\mathbf{x}) \\ \mbox{s.t. } & g_{i}(\mathbf{x}, \mathbf{y}_{i}) + q \tau^{2} \leq0, \\ & \nabla_{\mathbf{y}} \mathscr{L}_{i}(\mathbf{x}, \mathbf{y}_{i}, \boldsymbol{\mu}_{i}) = \mathbf{0}, \\ & -\mathrm{diag} ( \boldsymbol{\mu}_{i} ) \mathbf{v}(\mathbf{x}, \mathbf{y}_{i}) = \tau^{2} \mathbf{1}, \\ & \boldsymbol{\mu}_{i} \geq\mathbf{0}, \\ & -\mathbf{v}(\mathbf{x}, \mathbf{y}_{i}) \geq\mathbf{0}, \quad i \in I. \end{aligned}$$

This modification leads to an internal approximation of the feasible set of GSIP (see Fig. 12 also):

Theorem 3

([16])

Let $\hat{M}_{\tau}$ be the projection of the feasible set of $\hat {\mathsf{P}}_{\tau}$ in the $\mathbf{x}$-space. Then, for all $\tau > 0$, $\hat{M}_{\tau} \subset M$.

A combination of the internal approximation property of $\hat{M}_{\tau}$ with the external one of $M_{\tau}$ leads to a “sandwiching result:”

Corollary 1

([16])

Let $\{ \tau_{k} \}_{k \in\mathbb{N}_{0}} \subset\mathbb{R}$ be a monotonically decreasing null sequence. Then,

$$ \bigcup_{k \in\mathbb{N}_{0}} \hat{M}_{\tau_{k}} \subseteq M \subseteq \bigcap_{k \in\mathbb{N}_{0}} M_{\tau_{k}}. $$

This result significantly improves the termination criteria, which depend on the problem structure: For a given $\tau> 0$, the objective function value for each point in $\hat{M}_{\tau}$ is an upper bound on the optimum value of GSIP, while the global minimum value of $f$ delivers a lower bound over $M_{\tau}$. Thus, in cases where the latter minimum value is numerically available, the difference between the upper and lower bounds can be used as a termination criterion.

Analogously to Algorithm 1, an optimal solution of GSIP is to be found by solving the problems $\hat{\mathsf{P}}_{\tau_{k}}$ for a monotonically decreasing null sequence $\{ \tau_{k} \}_{k \in\mathbb{N}_{0}} \subset\mathbb {R}_{+}$. What is problematical here, however, is the fact that the set $\hat{M}_{\tau}$ can be empty for large values of $\tau$, due to the modification employed. For example, this occurs when the set defined by the tightened constraints (28)

$$ G_{\tau}(\mathbf{x}) := \bigl\{ \mathbf{y} \in\mathbb{R}^{n} \bigm| g_{i}(\mathbf{x}, \mathbf{y}) \leq-q \tau^{2}, \ i \in I \bigr\} , $$

which, in the context of maximum material yield problems with only one design and no flaws, corresponds to a “shrunken” container,

$$ C_{\tau} := \bigl\{ \mathbf{y} \in\mathbb{R}^{n} \bigm| c_{i}(\mathbf{y}) \leq-q \tau^{2}, \ i \in I_{0} \bigr\} , $$

(29)

is empty. Therefore, in a first phase, one must find a threshold value $\bar{\tau}$ with $\hat{M}_{\tau} \neq\emptyset$ for all $\tau \leq \bar{\tau}$ and a $\mathbf{x} \in\hat{M}_{\bar{\tau}}$, before one then, in the second phase, proceeds as in Algorithm 1. For details, please refer to [16] and [10].

Algorithm 1

Explicit smoothing method, [39, 42]

Fig. 12

Under- and over-estimation of the optimal value function $\varphi$ by $\varphi_{\tau}$ and $\varphi_{\tau} + q \tau^{2}$

Finally, we want to graphically illustrate how the explicit smoothing method (Algorithm 1) and its feasible variant work, by means of a d esign c entering problem:

$$ \mathsf{DC}: \quad\max_{\mathbf{x} \in X \subseteq\mathbb{R}^{m}} \ \mathrm{Vol}\bigl(D(\mathbf{x}) \bigr)\quad \mbox{s.t. } D(\mathbf{x}) \subseteq C, $$

that is, by means of a maximum material yield problem with one variable design and no flaws. Here, an ellipse is to be embedded with maximal area in the following container (see Fig. 13):

$$ C^{\mathrm{CT}} := \left \{ \mathbf{y} \in \mathbb{R}^{2} \left\vert \textstyle\begin{array}{rcl} -y_{1} - y_{2}^{2} & \leq& 0, \\ 1/4 y_{1} + y_{2} - 3/4 & \leq& 0, \\ -y_{2} - 1 & \leq& 0. \end{array}\displaystyle \right. \right \} $$

(30)

Fig. 13

The container $C^{\mathrm{CT}}$

One possible description of an ellipse is as the affine image of the unit circle:

$$\begin{aligned} D^{\mathrm{E}}(\mathbf{x}) :=& \bigl\{ \mathbf{A}(\mathbf{x}) \mathbf {y} + \mathbf{c}(\mathbf{x}) \in\mathbb{R}^{2} \big\vert \|\mathbf {y} \|_{2}^{2} \leq1 \bigr\} \\ =& \bigl\{ \mathbf{y} \in\mathbb{R}^{2} \big\vert \bigl[ \mathbf {y}- \mathbf{c}(\mathbf{x}) \bigr]^{T} \bigl[ \mathbf{A(\mathbf{x})} \mathbf{A(\mathbf{x})}^{T} \bigr]^{-1} \bigl[ \mathbf{y}- \mathbf {c}(\mathbf{x}) \bigr] - 1 \leq0 \bigr\} \end{aligned}$$

(31)

with

$$ \mathbf{c}(\mathbf{x}) := \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} , \qquad\mathbf{A}( \mathbf{x}) := \begin{pmatrix} x_{3} & x_{5} \\ 0 & x_{4} \end{pmatrix} , \quad\text{and} \quad\mathbf{x} \in X := \mathbb{R}^{2} \times \mathbb{R}^{2}_{++} \times\mathbb{R}_{+}. $$

The area of an ellipse with this parameterization is:

$$ \mathrm{Vol}_{2}(\mathbf{x}) = \pi x_{3} x_{4}. $$

The formulation of the design-centering problem $\mathsf{DC}^{\mathrm{E}\mbox{\scriptsize{-}}\mathrm{CT}}$ as a general semi-infinite optimization problem becomes:

$$\begin{aligned} \mathsf{GSIP}_{\mathsf{DC}^{\mathrm{E}\mbox{\scriptsize{-}}\mathrm{CT}}}{:} \quad -\min\limits _{\mathbf {x} \in X} & -\pi x_{3} x_{5} \\ \mbox{s.t. } & -y_{1} - y_{2}^{2} \leq0 \quad \mbox{for all } \mathbf{y} \in D^{\mathrm{E}}(\mathbf{x}), \\ & 1/4 y_{1} + y_{2} - 3/4 \leq 0\quad\mbox{for all } \mathbf{y} \in D^{\mathrm{E}}(\mathbf{x}), \\ & -y_{2} - 1 \leq0\quad\mbox{for all } \mathbf{y} \in D^{\mathrm{E}}(\mathbf{x}). \end{aligned}$$

We turn first to the explicit smoothing method (Algorithm 1). We have chosen as null sequence the geometrical sequence $\{ 1/2^{k} \}_{k \in \mathbb{N}_{0}}$ and as starting point $\mathbf{x}^{0}$ the (infeasible) point $(0,0,1,1,0)$; that is, the unit circle (see Fig. 14(a) also). We have obtained an initial configuration for the solutions of the lower-level problems and the associated Lagrange multipliers by solving the log barrier problems (27). Algorithm 1 terminates when the relative error in either the solutions or the associated function values is less than or equal to $10^{-6}$ and the violation of the feasibility of the solution with regard to the underlying general semi-infinite problem is less than or equal to $10^{-6}$. Figure 14 graphically illustrates the iterative solution of the problems $\mathsf{P}_{\tau_{k}}$, $k \in\mathbb{N}_{0}$.

Fig. 14

Area-maximal design-centering of an ellipse into the container $C^{\mathrm{CT}}$ using the explicit smoothing method (Algorithm 1) [light blue-container, green-design, red-solutions of the log barrier problems (27)]: (a) initial situation ($\tau= 0.5$), (b) after solution of problem $\mathsf{P}_{0.5}$, (c) after solution of problem $\mathsf{P}_{0.25}$, and (d) final situation (after a total of 12 iterations, that is, for $\tau= 0.000244140625$).

Using the same example, we want to now look at the feasible variant of the explicit smoothing method. To do so, we use the same null sequence and starting point. The initialization of the solutions of the lower-level problems, as well as of the associated Lagrange multipliers, takes place as above. For termination, we now only have to consider the relative error in the solutions and in the “optimum values,” since a feasible solution of a problem $\hat{\mathsf{P}}_{\tau_{k}}$ is, per construction, also feasible for the next problem $\hat{\mathsf{P}}_{\tau_{k+1}}$. Figure 15 graphically illustrates the algorithmic procedure. Both the actual container (in light blue) and the “shrunken” container $C_{\tau}$ (in dark blue; see (29)) are depicted. With this example, it is not necessary to execute a first phase for finding a suitable threshold value $\bar{\tau}$ and feasible solution for $\mathsf{GSIP}_{\mathsf{DC}^{\mathrm{E}\mbox{\scriptsize{-}}\mathrm{CT}}}$, since the “shrunken” container is not empty.

Fig. 15

Area-maximal design-centering of an ellipse into the container $C^{\mathrm{CT}}$ using the feasible explicit smoothing method [light blue-container, dark blue-“shrunken” container, green-design, red-solutions of the log barrier problems (27)]: (a) initial situation ($\tau= 0.5$), (b) after solution of problem $\hat{\mathsf{P}}_{0.5}$, (c) after solution of problem $\hat{\mathsf{P}}_{0.25}$, and (d) final situation (after a total of 7 iterations, that is, for $\tau= 0.0078125$)

4.5.2 A Transformation-Based Discretization Method

We now introduce a second method developed at the ITWM for solving general semi-infinite optimization problems with convex lower-level problems. This method cleverly combines the solution approaches “discretization of infinite index sets” and “transformation into a standard semi-infinite problem,” thereby circumventing the weak points of each approach. We will first discuss the two solution approaches separately.

Discretization Methods for Standard Semi-Infinite Optimization Problems

In this section, we consider standard semi-infinite optimization problems, that is, optimization problems of the form

$$\begin{aligned} \mathsf{SIP} {:} \quad \min\limits _{\mathbf{x} \in X \subseteq\mathbb {R}^{m}} & f(\mathbf{x}) \\ \mbox{s.t. }& g_{i}(\mathbf{x}, \mathbf{y}) \leq0 \quad \mbox{for all } \mathbf{y} \in Y, \ i \in I, \end{aligned}$$

where $I := \{ 1,\ldots,p \}$, $Y$ is a non-empty, compact, infinite (index) set, and $f$, $g_{i}$, $i \in I$, are real-valued, sufficiently smooth functions. For $\hat{Y} \subset Y$, we introduce the optimization problem

$$\begin{aligned} \mathsf{SIP}(\hat{Y}){:} \quad \min\limits _{\mathbf{x} \in X \subseteq \mathbb{R}^{m}} & f(\mathbf{x}) \\ \mbox{s.t. }& g_{i}(\mathbf{x}, \mathbf{y}) \leq0 \quad \mbox{for all } \mathbf{y} \in\hat{Y}, \ i \in I, \end{aligned}$$

If the set $\hat{Y}$ is finite, $\mathsf{SIP}(\hat{Y})$ is referred to as a discretized SIP problem.

The basic idea of discretization methods is to successively calculate solutions of discretized SIP problems $\mathsf{SIP}(\dot {Y}^{k})$, $k \in\mathbb{N}_{0}$, using a solution method for finite optimization problems, where $\{ \dot{Y}^{k} \}_{k \in\mathbb{N}_{0}}$ is a sequence of finite subsets of $Y$ that converges to the set $Y$ in the Hausdorff distance. The sequence $\{ \dot{Y}^{k} \}_{k \in\mathbb {N}_{0}}$ is either established a priori or defined adaptively. In the latter case, information from the $k$-th discretization step is enlisted for defining $\dot{Y}^{k+1}$. These considerations can be algorithmically applied as follows:

It is not necessary that the starting point $\mathbf{x}^{0}$ in step 1 is feasible for SIP. In the simplest case, $Y^{k+1} := Y$ can be chosen in steps 1 and 5. In step 4, essentially any method for solving finite optimization problems can be used. The only two requirements here are that it can handle infeasible starting points and high-dimensional problems. Except for small $m$ and $| \dot{Y}^{k} |$, however, it is not appropriate to use a generic solution method, since such methods often solve sub-problems having the same number of constraints as the problem itself. Thus, they do not take advantage of the fact that the constraints of a discretized SIP problem stem from only a few functions. For this reason, proprietary methods have been developed to solve these special finite optimization problems (see, for example, [27, 31, 32]).

In order for the method to converge, it is crucial in step 7 to compute a global solution, or at least a good approximation.

Transformation of a General into a Standard Semi-Infinite Problem

In order to be able to use discretization techniques for solving general semi-infinite optimization problems, the methods must either be generalized for the case of variable index sets or the general semi-infinite optimization problem must be transformed into an equivalent standard problem.

In principle, it is possible to generalize discretization and exchange methods for standard semi-infinite optimization problems to the general semi-infinite case. An additional challenge here, however, along with the rapidly growing size of the induced finite problems, is the $\mathbf{x}$-dependency of the index set $Y(\mathbf{x})$, and, thus, of its discretization. In order to guarantee that the feasible sets of the optimization problems induced by the discretizations are closed, the discretization points must be so designed that they depend at least continuously on $\mathbf{x}$, which is non-trivial (see [47]).

Using suitable assumptions, the transformation of a general into a standard semi-infinite optimization problem is, in principle, at least locally possible (see [45, 49]). However, such a transformation is only of practical use when it is globally defined. The ideal situation is as follows:

Assumption 4

Let there be a non-empty, compact set $Z \subset\mathbb{R}^{\tilde {n}}$ and a mapping $\mathbf{t} : \mathbb{R}^{m} \times Z \rightarrow \mathbb{R}^{n}$ that is at least continuous, such that $\mathbf {t}(\mathbf{x},Z) = Y(\mathbf{x})$ for all $\mathbf{x} \in X \subseteq\mathbb{R}^{m}$.

Under this assumption, the general semi-infinite constraints

$$ g_{i}(\mathbf{x}, \mathbf{y}) \leq0\quad \text{for all } \mathbf{y} \in Y(\mathbf{x}), \ i \in I, $$

are clearly equivalent to the standard semi-infinite constraints

$$ \tilde{g}_{i}(\mathbf{x}, \mathbf{z}) := g_{i}\bigl( \mathbf{x}, \mathbf {t}(\mathbf{x}, \mathbf{z})\bigr) \leq0\quad \text{for all } \mathbf{z} \in Z, \ i \in I. $$

For one-dimensional index sets $Y(\mathbf{x}) = [a(\mathbf{x}), b(\mathbf{x})]$, with $a(\cdot) \leq b(\cdot)$, such a transformation can be designed simply by means of a convex combination of the interval limits; for higher dimensional index sets, there exists such a transformation when it is star-shaped (see [45]), which is the case under Assumptions 1 to 3.

However, the transformation entails a serious disadvantage: it can destroy the convexity in the lower-level that is so important for the convergence of the discretization method (see [14], for example).

Combination of Both Techniques

We now outline how the above-mentioned disadvantage can be circumvented, thus allowing the solution of transformable general semi-infinite optimization problems using discretization methods. For details, the reader is referred to [14] (along with [8] and [9]).

We begin by introducing the standard semi-infinite optimization problem induced by the transformation:

$$\begin{aligned} \widetilde{\mathsf{SIP}}: \quad \min\limits _{\mathbf{x} \in X \subseteq\mathbb{R}^{m}} & f( \mathbf{x}) \\ \mbox{s.t. }& \tilde{g}_{i}(\mathbf{x}, \mathbf{z}) \leq0 \quad \mbox{for all } \mathbf{z} \in Z, \ i \in I, \end{aligned}$$

with $\tilde{g}_{i}(\mathbf{x}, \mathbf{z}) := g_{i}(\mathbf{x}, \mathbf{t}(\mathbf{x}, \mathbf{z}))$, $i \in I$. We denote its lower-level problems by

$$ \tilde{\mathsf{Q}}_{i}(\mathbf{x}): \quad\max_{\mathbf{z} \in Z} \ \tilde{g}_{i}(\mathbf{x}, \mathbf{z}), \quad i \in I. $$

As already seen, the feasible sets, and thus the local and global solutions of GSIP and $\widetilde{\mathsf{SIP}}$, coincide. Consequently, a solution for the underlying general semi-infinite problem can be obtained by solving the induced standard problem. A similar result is also obtained with the global solutions of the corresponding lower-level problems.

Theorem 4

([14])

Let $\mathbf{x} \in X$ and $i \in I$. Then, the point $\mathbf{z}^{*}$ is a global solution of $\tilde{\mathsf{Q}}_{i}(\mathbf{x})$ if and only if $\mathbf{y}^{*} = \mathbf{t}(\mathbf{x},\mathbf{z}^{*})$ is a global solution of $\mathsf{Q}_{i}(\mathbf{x})$.

One can thus calculate a global solution for the non-convex problem $\tilde{\mathsf{Q}}_{i}(\mathbf{x})$ by finding a global solution of the convex problem $\mathsf{Q}_{i}(\mathbf{x})$ and transforming it via $\mathbf{t}(\mathbf{x}, \cdot)$ in $Z$. This makes it unnecessary to solve the non-convex problems $\tilde{\mathsf{Q}}_{i}(\mathbf{x})$, $i \in I$, using time-consuming methods of global optimization.

Using the insights from Theorem 4, we can now adapt the relevant steps in Algorithm 2 and obtain a discretization method for transformable general semi-infinite optimization problems:

Algorithm 2

General discretization method for $\mathsf{SIP}$ problems, [34, 35]

The requirements for the transformation-based discretization method are the same as those for Algorithm 2. If no starting discretization $\dot{Y}^{0}(\mathbf{x}^{0})$ from $Y(\mathbf {x}^{0})$ is available for step 2, one can be obtained by solving the lower-level problems and transforming the solutions. A feasible starting point for step 7 can be calculated from a feasible point from $Z$ via the transformation $\mathbf{t}(\mathbf{x}, \cdot )$. With regard to the curvature behavior of the involved functions, only the convexity of the lower-level problems is presupposed in the above method, and not the convexity of the objective function $f$ and the functions $g_{i}(\cdot,\mathbf{y})$, $i \in I$, for all $\mathbf {y}$. Therefore, the result $\mathbf{x}^{*}$ of Algorithm 3 is only as “optimal” as the results of the method used to solve the discretized SIP problems in step 5. Incidentally, this is also the case for the explicit smoothing method (Algorithm 1) and its feasible variant.

Algorithm 3

Transformation-based discretization method for $\mathsf{GSIP}$ problems, [14] and [8]

Finally, we want to illustrate how the transformation-based discretization method works, by means of an example. And here, we’ll employ the same example used for the explicit smoothing method. Our goal, therefore, is once again the area-maximal embedding of an ellipse in the container $C^{\mathrm{CT}}$. For the transformation-based discretization method, we not only need a function to describe the ellipse and an area computation formula, we also need a description of the ellipse as an image of a compact set under a continuously differentiable mapping. As mentioned previously, we model the ellipse as a translated and distorted unit circle. Accordingly, one possible transformation is

$$ \mathbf{t} : \mathbb{R}^{5} \times[0,1]^{2} \rightarrow \mathbb {R}^{2} \quad\text{with} \quad\mathbf{t}(\mathbf{x},\mathbf{z}) := \mathbf{A}(\mathbf{x}) \begin{pmatrix} z_{1} \cos(2 \pi z_{2}) \\ z_{1} \sin(2 \pi z_{2}) \end{pmatrix} + \mathbf{c}(\mathbf{x}), $$

where $\mathbf{A}(\mathbf{x})$ and $\mathbf{c}(\mathbf{x})$ are chosen as above.

As starting point $\mathbf{x}^{0}$, we have again selected the (infeasible) point $(0,0,1,1,0)$ (see Fig. 16(a), also), and as feasibility tolerance, $\varepsilon= 10^{-6}$. The initial discretization $\dot{Y}^{0}(\mathbf{x}^{0})$ consists of the solutions of the lower-level problems. Figure 16 illustrates graphically the successively refined discretization and the solution of the discretized SIP problems $\widetilde{\mathsf{SIP}}(\dot{Z}^{k})$, $k \in\mathbb{N}_{0}$.

Fig. 16

Area-maximal design-centering of an ellipse into the container $C^{\mathrm{CT}}$ using the transformation-based discretization method (Algorithm 3) [light blue-container, green-design, red-points of the current discretization, dark blue-points of the greatest violation of the container constraints, which are added to the current discretization for the next calculation]: (a) initial situation with calculated starting discretization, (b) after solving problem $\widetilde{\mathsf{SIP}}(\dot{Z}^{0})$, (c) after solving $\widetilde{\mathsf{SIP}}(\dot{Z}^{1})$, and (d) final situation (after a total of 30 refinements)

5 Industrial Project I—Automation of Pre-forming, Grinding, and Polishing

In Sect. 1.1, we described how gemstones are processed by hand in the traditional manufacturing setting and outlined the new automated approach developed for producing colored gemstones over the past decade—an approach derived from the traditional jewel-maker’s craft. In this section, we elaborate on the resulting modeling questions and algorithmic solution approaches and discuss the implementation of the automating equipment and software.

5.1 Questions for Modeling an Optimization Problem—Describing Alternative Sets and Quality Measures

In order to make mathematical optimization methods of practical use, one needs an available feasibility or alternative set and well-defined target quantities, which should be characterized as favorably as possible. An easily formulated optimization goal is to maximize the material yield, that is, the sellable volume fraction of a rough stone. A simple feasibility requirement is the containment condition, that is, the requirement that the desired faceted stone is completely contained within the rough stone and that there exists, where necessary for processing reasons, an additional safety buffer between the faceted stone and the edge of the rough stone.

The esthetic requirements are markedly more difficult. For example, the cut pattern of a stone has a significant impact on the final appearance of the faceted stone. Here, a constellation of problems becomes apparent: First, beauty, as the saying goes, is in the eye of the beholder; that is, it is subjective. Second, the subjective appraisal of a person, a jeweler for example, is elusive and difficult to fix precisely. Thus, the esthetic aspect represents one of the greatest modeling challenges.

Basic Approach

For a given rough stone, esthetically motivated conditions are placed on the proportions, and volume optimal solutions are then defined for each faceted stone base form being considered (round, oval, octagonal, etc.). The variously shaped and proportioned faceted stones thus calculated are then presented to a decision-maker via a graphic user interface. On the basis of what he considers to be the most favorable combination of material yield and esthetic considerations, the decision-maker then selects a faceted stone shape for production.

As described in Sect. 2.1, the division of the manual production process into two parts, pre-forming and faceting, motivated us to divide the modeling into two parts as well, by decoupling the continuous and discrete variables. We accomplish this by introducing the calibration body as a parameterized equivalent to the smooth pre-grinding form. We can optimize the calibration body, with an eye on the material yield and proportions, without first having to commit to a particular faceting pattern. In the following subsections, we discuss in greater detail the description of the calibration body, the faceting, and the rough stone modeling.

5.1.1 Faceted Stone Shapes and Calibration Body

A calibration body is characterized in part by its parameterization; parameters include, for example, position in rough stone, height, length, width, and degree of belliedness. Some are generic parameters that are independent of the faceted stone shape and others are shape specific. The parameters’ feasibility domains ensure that the proportions remain within zones that result in esthetically appealing jewels. After one has defined specific values for the parameters, then the most appropriate faceting pattern can be chosen.

The calibration body is also characterized by smooth functions $\mathbf {v} : \mathbb{R}^{m} \times\mathbb{R}^{3} \rightarrow\mathbb{R}^{q}$, which establish, in dependency on the parameters $\mathbf{x} \in\mathbb{R}^{m}$, whether a point $\mathbf{y} \in\mathbb{R}^{3}$ is indeed located within the calibration body ($v_{j}(\mathbf{x}, \mathbf{y}) \leq0$ for all $j=1,\ldots,q$), or whether it is not ($v_{j}(\mathbf{x}, \mathbf {y}) > 0$ for at least one $j \in\{1,\ldots,q\}$). The choice of functions depends of course on the shape of the faceted stone.

On the basis of a simple faceted stone shape with a circular girdle base form, we will now explain how a calibration body can be described and parameterized and how the esthetic requirements fit into the analysis.

Parameterizing a Calibration Body

With the help of six real-valued parameters and a suitable coordinate system, one can represent the absolute position and rotation of a calibration body within the rough stone. The description of the actual extent of the faceted stone shape depends on the base form. For a round stone it can be described using seven more parameters, as depicted in Fig. 17. For the three faceted stone elements—crown, girdle, and pavilion—the three heights $h_{C}$, $h_{G}$, and $h_{P}$ are further parameters; for the crown and girdle, there is a radius $r_{T}$ and a radius $r_{G}$ for the table and the girdle; and for the crown and pavilion, there is one more parameter each, $\tau_{C}$ and $\tau_{P}$, which describe the degree of belliedness or curvature. For other, more complicated faceted stone shapes, there are additional parameters, such as the ratio of the length to the height of the girdle base form.

Fig. 17

Parameterization of the round faceted stone shape using heights and radii and degree of belliedness for pavilion and crown

Alternatively, one can also choose a scaling-invariant parameterization. Here, the radius of the girdle is set to 1, and all other parameters that specify a length are replaced by the ratio of that length to the girdle radius. Thus, we obtain the new parameters $\tilde{h}_{C}:=\frac{h_{C}}{r_{G}}$, $\tilde{h}_{G}:=\frac{h_{G}}{r_{G}}$, $\tilde{h}_{P}:=\frac{h_{P}}{r_{G}}$, and $\tilde{r}_{T}:=\frac{h_{C}}{r_{G}}$. The parameters $\tau_{C}$ and $\tau_{P}$ remain unchanged. Later, in the algorithmic section, we will make use of the advantages of this scaling-invariant parameterization.

Calibration Body Proportions

The feasible value domain of the parameters is very important for the esthetic appearance of the final faceted stone. For example, parameters that specify lengths must fulfill certain proportion requirements. The ratio of the girdle radius to the crown radius, for example, is restricted by both an upper and a lower bound. The same holds true for the ratio of the total calibration body height to the girdle radius or to the individual heights of the pavilion, girdle, and crown. Likewise, there are upper and lower bounds for the belliedness parameters $\tau _{P}$ and $\tau_{C}$. It is not easy to make a good choice for the combination of these bounds, since this choice depends very strongly on the esthetic sensibilities of the decision-maker. A guideline for the mathematical model should be to not make the feasibility intervals too small, otherwise the latitude for volume optimization and the incorporation of esthetic considerations becomes too limited.

Functions for Describing a Calibration Body

In order to be able to use the methods from Sect. 4.5, the calibration body must be described by convex, differentiable functions. Using the parameters described above, we specify for our example of the round faceted stone a corresponding description. Here, the calibration body is given as $D^{\text{Round}}(\mathbf{x}) := \{ \mathbf{y} \in\mathbb{R}^{3} \mid\mathbf{v}(\mathbf{x}, \mathbf{y}) \leq0\}$ and we define $\mathbf{v}$ as follows:

$$ \mathbf{v} : \mathbb{R}^{7} \times\mathbb{R}^{3} \rightarrow \mathbb{R}^{5} : y \mapsto \textstyle\begin{cases} y_{1}^{2}+y_{2}^{2}-r_{P}(y_{3}) & \text{lateral boundary of the pavilion}\\ y_{1}^{2}+y_{2}^{2}-r_{C}(y_{3}) & \text{lateral boundary of the crown}\\ y_{1}^{2}+y_{2}^{2}-r^{2}_{G} & \text{lateral boundary of the girdle}\\ y_{3}-h_{C}-h_{G}& \text{boundary of the table}\\ -y_{3}-h_{P} & \text{boundary at the pavilion apex} \end{cases} $$

(32)

The functions $r_{P}$ and $r_{C}$ specify the radius for a given height $y_{3}$ and are dependent upon $\tau_{P}$, $\tau_{C}$, $r_{C}$, and $r_{G}$. The curvatures of pavilion and crown depend upon $\tau_{P}$ and $\tau_{C}$, respectively. We refer the reader to [16] for a more detailed description of $r_{P}$ and $r_{C}$. There, and in [14] as well, one can find formulas for calculating calibration body volumes via the appropriate integrations. Figure 18 shows an approximation of the set $D^{\text{Round}}$.

Fig. 18

Calibration body of the round faceted stone

5.1.2 Calculating the Facetings

The step from a calibration body to a beautiful faceting is more complex than one might imagine. The obvious idea of simply laying the corners of the facets on the margin of the calibration body won’t work, since the resulting system of equations is over-defined, at least for the Portuguese cut.

As already hinted in Sect. 2.1, the challenges of defining suitable facetings result from numerous aspects that must be considered: The faceting determines the reflection of light and thus the stone’s sparkle and inner flame. Here, the setting angles are crucial. These angles must be neither too sharp nor too shallow, in order to ensure optimal reflection. The number of rows and the number of facets per row are also important criteria and depend on the size and material characteristics of the stone. In general, the larger the stone, the more facets it should have. The faceting must have the same axes of symmetry as the corresponding faceted stone shape. Moreover, an attractive cut pattern is one in which all the facets in a given row have approximately the same setting angle and are about the same height and width. The facets should also decrease in size as one moves away from the girdle.

Two approaches have proven successful for calculating the faceting. The first consists of iteratively adding rows of facets, starting at the girdle and working outwards towards the pavilion’s apex and the crown’s table. Here, a shallower setting angle is specified for each succeeding row. With this approach, however, the possibilities for influencing the faceting pattern are limited. In the second approach, the desired final facets are given at the start and parameterized via their corner points and the normals of the associated levels. If one now formulates as equations the fact that two neighboring facets share two corners or that all the facets in a given row are to have the same setting angle, then one obtains a system of equations that, although over-defined, can nevertheless be solved approximately after appropriate relaxation. This approach is explicit and allows one to exactly control the resulting faceting pattern. It also requires substantially more effort, since a different type of equation system must be set up for each faceted stone shape. Under some circumstances, however, as depicted in Fig. 19, it delivers clearly more attractive faceting than the first approach, which cannot always guarantee good results.

Fig. 19

2D projection of a pavilion faceting pattern for the antique stone shape: left, using the iterative approach, which delivers an unsatisfactory result; right, using the explicit approach

5.1.3 Describing the Rough Stone

The geometric shape of the rough stone must be captured in a suitable manner in order to make it accessible to the optimization algorithms. One possibility for digitalizing the rough stone utilizes data about its surface. Using a 3D scanner with either the stripe projection or laser scanning procedure, surface point clouds are recorded for the rough stone, which one can then convert to a surface model by means of triangulation.

In the terminology of the material cutting field, the rough stone forms the container. If we want to use the solution method from Sect. 4.5, however, then triangulation as a description of the container is hardly suited, since tremendous point clouds arise on the surface for exactness requirements of about 5–10 micrometers. Instead, the convex hull of the net is used, and larger indentations, that is, differences between the rough stone net and the convex hulls, are additionally described by means of quadrics. Because one can represent the inside of the convex hulls by a potentially large number of linear inequalities, this method yields a description of the container consisting of linear and convex quadratic functions.

5.2 Algorithmic Implementation

In the following, we introduce two alternative methods for achieving a maximum material yield.

The first method is based on Algorithm 1 from Sect. 4.5.1. We consider a hierarchic formulation of the problem: First, optimize the volume of the calibration body; then, approximate this calibration body using a suitable faceting pattern with as little volume loss as possible. In a post-optimization step, we can scale and/or rotate the resulting faceted stone into the rough stone in a volume-optimized manner.

The calibration body modeling described in Sect. 5.1.1 conforms to the formal design description requirements needed for the algorithm. The container is likewise described functionally, as discussed in the previous section. In principle, then, Algorithm 1 can be applied. In practice, however, the problem arises that, due to the many functions describing the container—hereafter referred to as container functions—the algorithm becomes very slow. This problem is dealt with by initially considering only a very small portion of the container functions. One iteratively applies the algorithm to the selected subset of container functions, calculates a solution for this relaxed problem, and checks to see whether the resulting faceted stone is feasible with regard to all container functions. If not, one expands the selected subset by including the violated container functions. Using this new, expanded selection, one then re-calculates and begins the next iteration. In practice, this procedure leads to a solution after a few iterations. This solution is feasible for the starting problem, but nonetheless, even in the final iteration, only a small number of container functions must be taken into consideration. Using the calibration body parameters found in this way, one now calculates the faceting. Because the container functions do not map the rough stone exactly and only the calibration body is considered in the optimization, the faceted stone must be adjusted by slight translation, rotation, and scaling operations in a final step, in order to ensure that it lies completely within the rough stone surface described by the triangulation.

The second approach is based on the treatment of the non-overlapping condition described in Sect. 4.3 and works directly with the triangulation of the rough stone. This allows the original surface description to be used directly. The faceting can also be understood as a triangulation if the girdle is suitably discretized. The main challenge inherent in this second approach is to quickly develop a faceting when the calibration body parameters change. Here, one advantage is that the triangulation resulting from a faceting is very small relative to the triangulation of the rough stone. A second advantage is that a change affecting the position of the faceted stone does not lead to a re-calculation of the faceting. For the algorithmic implementation of this approach, one now uses the scaling-invariant parameterization described above with scaling parameter $s$. The problem of maximum material yield can now be described as the search for a maximum scaling parameter $s^{*}$. Because the containment of the design within the container for a given $s$ can be quickly verified, the optimal value $s^{*}$ can also be quickly determined—for example using a bisection approach. In general, as shown in [4], $s^{*}$ depends continuously on the scaling-invariant parameters, so that common optimization methods can be used for the resulting optimization problem.

5.3 Automating the Grinding and Polishing Process—The Technical Challenges

In addition to the virtualization of design and container required to make the maximum material yield problem mathematically and informationally accessible, there are also technical challenges to be mastered, such as holding and guiding the stone during the work steps and automating the grinding and polishing processes.

The starting point for successfully industrializing gemstone production is the approach used in the hand manufacturing process, which is to be suitably refined and automated. The entire process consists of the following steps:

• 1. The rough stone is manually glued to a measurement pin.

• 2. It is then measured and digitalized using a 3D scanner (see Fig. 21).

• 3. An optimal faceted stone is virtually embedded in the measured rough stone via mathematical optimization, as described in Sect. 5.2.

• 4. The corresponding difference images are converted into re-gluing, grinding, and polishing plans and transferred to the machines.

• 5. The rough stone is transferred from the measurement pin to a processing pin, while preserving the coordinate system (see Fig. 20).

  Fig. 20

  

  A rough stone glued to a measurement pin and the re-gluing procedure

  Fig. 21

  

  A configuration for generating a three-dimensional representation of the rough stone via the stripe projection method (Photo: G. Ermel, Fraunhofer ITWM)

• 6. Transfer to the processing station; grinding and polishing of the girdle and the front side (see Fig. 22).

  Fig. 22

  

  Grinding a stone’s first processing side

• 7. Transfer to the pin re-positioning station; axial re-positioning on a second processing pin.

• 8. Transfer to the processing station; grinding and polishing of the back side.

• 9. The processing pin is removed by hand; the faceted stone is now finished.

The goal in designing the process was a level of accuracy in all steps such that an absolute accuracy of 5–10 micrometers could be achieved for the overall production. To describe here in detail all of the technical requirements and their mechanical engineering solutions would exceed the scope of our discussion. The pictures, however, do offer some impressions of the pre-series prototype at the Fraunhofer ITWM, which fulfilled the targeted requirements.

5.4 Automating the Grinding and Polishing Processes—The Software Challenges

Along with the technical challenges, there were also five software development problems to be solved:

• 1. Implementing the optimization algorithm: Here, the primary challenge is to efficiently implement the above-described approaches and to ensure that they are also robust in the face of very rare, pathological, numerical cases that might not arise until the process has been in operation for a length of time.

• 2. Scalable parallelization: Due to the high computing time requirements—about ten faceted stone shapes must be calculated for each stone—parallel execution of the optimization is necessary. Here, the calculations are distributed on multiple CPUs.

• 3. Centralized data-keeping is a critical element: It not only has to support the parallelization of the calculations, it must also maintain in readiness a consistent view of the data for machine controlling and the user interface. Here, the extensive functionality of modern databases is very helpful.

• 4. The machine control system must manage the various stations of the machines for grinding, polishing, pin re-positioning, scanning, and transporting the stone and must pick up error functions and breakdowns.

• 5. As the interface between operator and machine, the user display must include components for controlling and configuring the machines, for showing the virtual rough stones and calculated faceted stones with hardware-optimized 3D depictions, and for starting and configuring the optimization calculations. Here, the ease-of-use of the software and the resulting user experience—hopefully, a positive one—play an important role.

Because of the variety of functions, a professional software design is indispensable. Although the code was created originally in a dissertation according to purely scientific considerations, the current process software now has a modular, maintainable, and extendable structure, in which the individual components can be added or removed, as needed.

6 Industrial Project II—Gemstone Sectioning

After looking at the optimal conversion (with respect to cut and volume) of a rough stone to a faceted one in Industrial Project I, we now turn to the “gemstone sectioning” project. Here, several faceted stones are to be produced from a single rough stone, while maximizing the total volume of the final jewels and avoiding flaws. With this endeavor, we move one step closer to the goal of solving the complete gemstone cutting problem.

6.1 Description of the Problem

We recall that the (main) task of gemstone cutting consists of transforming a rough stone marred with surface flaws, inclusions, and cracks into faceted stones in such a way that their total value is as high as possible. Here, we consider only the volume as value-determining criterion and require that the finished faceted stones be free of flaws. The implementation of the esthetic requirements can be accomplished analogously to Sect. 5.

In order to produce several faceted stones from a single rough stone, the latter must first be sectioned into blanks, each of which yields one faceted stone. This raises the following two questions:

How many faceted stones should be produced from the rough stone, that is, into how many blanks should the rough stone be sectioned? What does such a sectioning look like?

Although, in the manual production process, “sectioning” and “grinding” are separate work steps, generally performed by different persons, the sawyer is already giving some thought to how the blanks should look in order to yield large-volume and esthetically pleasing faceted stones.

The standard tool for sectioning rough stones is the circular saw, with which only straight cuts are possible. While it is indeed possible to cut out a wedge-shaped blank using a circular saw, we want to assume that each cut is a through-cut, which is referred to in the trade as a guillotine cut. Moreover, since each cut consumes valuable material, one uses narrow-kerf blades and tries to keep the cuts short and few in number when sectioning the rough stone.

6.2 Modeling

From a mathematical perspective, the above problem is once again of the maximum material yield type. Here, however, we need to generalize the non-overlapping condition, since the faceted stones must have a specified minimum distance from one another to allow for the kerf width. As an additional requirement, they must also be present in a guillotine arrangement in order to be amenable to circular saw technology (see Fig. 23). In the following discussion, we illustrate how both requirements can be mathematically modeled in the context of Sects. 4.1 and 4.4, that is, for arbitrarily shaped containers and designs.

Fig. 23

Guillotine arrangement of five elliptical designs with minimum distances in a container described by lines and quadrics

6.2.1 Minimum Distance Between the Designs

We first look at the requirement that the designs must have a specified minimum distance $\delta> 0$ from each other.

In some cases, geometrical considerations allow one to deduce practicable conditions. For example, two circles have at least the distance $\delta$ between them if and only if the distance between their centers is greater than or equal to the sum of their radii plus $\delta$ (see Fig. 24).

Fig. 24

Two circles with distance $\delta$

For more complicated designs, this approach is not usually expedient. However, as with the non-overlapping condition, describing the designs by means of functions also allows one here to implement this requirement using semi-infinite constraints. In [14], two modeling approaches were proposed for accomplishing this aim: via Euclidean (norm) distance and via separating hyperplane.

The first approach is intuitive. Two designs have a minimum distance $\delta$ between them if and only if each point of one design has at least a distance $\delta$ from each point of the other design (see Fig. 25, left). The mathematical formulation for this is

$$ \| \mathbf{y} - \mathbf{z} \|_{2} \geq\delta\quad\text{for all } ( \mathbf{y}, \mathbf{z}) \in D_{1}(\tilde{\mathbf{p}}_{1}) \times D_{2}(\tilde{\mathbf{p}}_{2}), $$

which is clearly of semi-infinite nature.

Fig. 25

Ensuring a minimum distance between two elliptical designs: left, using the Euclidean (norm) distance; right, using a separating hyperplane

The second approach, as the name implies, is based on the separation of the designs by means of hyperplanes. On the one hand, we know that the non-overlapping of two convex designs can be guaranteed by means of a separating hyperplane (see Sect. 4.4). On the other hand, the distance of a point from a hyperplane can be directly calculated by inserting the point into the hyperplane equation $\boldsymbol{\eta}^{T} \mathbf{y} = \beta$, if the normal vector $\boldsymbol{\eta}$ of the hyperplane is normalized to 1, that is, if $\| \boldsymbol{\eta} \|_{2} = 1$. If we now require that all points of one design lie on one side of the hyperplane and are at least a distance ${\delta}/{2}$ away from it, and that all points of the other design lie on the other side of the hyperplane and are at least the same distance away from it, then the designs have a minimum distance $\delta$ between them (see Fig. 25, right). These requirements can be formulated mathematically as the inequalities

$$ \boldsymbol{\eta}_{0}^{T} \mathbf{y} - \beta\leq- \frac{\delta}{2} \quad\text{for all } \mathbf{y} \in D_{1}(\tilde{ \mathbf{p}}_{1}) $$

and

$$ \boldsymbol{\eta}_{0}^{T} \mathbf{z} - \beta\geq \frac{\delta}{2} \quad\text{for all } \mathbf{z} \in D_{2}(\tilde{ \mathbf{p}}_{2}), $$

which are both semi-infinite in nature. Here, $\boldsymbol{\eta}_{0}$ denotes the normalized unit vector.

6.2.2 Guillotine Arrangements of Designs

We now show how the requirement of a guillotine arrangement can be implemented for maximum material yield problems.

In order to take advantage of such an arrangement using a saw, it is necessary, of course, to leave space for the saw kerf between the planned designs. However, in the following considerations, for clarity’s sake, we require no minimum distance between the designs. As shown in the previous section, this requirement can be easily integrated into the model at a later stage.

Guillotine cutting problems have been investigated mathematically since the mid-1960s ([26]). The most frequently considered problem is the so-called two-dimensional orthogonal guillotine cutting problem (see Fig. 26):

Fig. 26

Arrangement of smaller rectangles in a larger rectangle: guillotine arrangement, left; non-guillotine arrangement, right

2DOGCP: Can a given set of orthogonally rotatable rectangles be cut out of a large rectangle by a series of linear cuts that run either parallel or orthogonal to the sides of the large rectangle, i.e., by a series of guillotine cuts?

To date, only minor modifications of this standard problem have been investigated: guillotine arrangement of equally sized circles in a rectangle (see [21, 22]) and guillotine cuts of cuboids (see [33]), as well as hyper-cuboids (see [17]).

All familiar models and solution methods take advantage of the simple and fixed geometry of the designs and the container. The designs are translatable; rotation, in contrast, when allowed at all, is only permitted in $90^{\circ}$ steps. The guillotine cuts run orthogonal or parallel to each other.

For the gemstone cutting problem, however, these kinds of guillotine arrangements are not suitable, due to the irregularity of the rough stone and the shape and parametrization of the faceted stones; they would lead to smaller jewels and, thus, lower yields. Instead, we want here to allow the guillotine cuts to be made in an arbitrary position, both absolutely and relative to one another, so that we can “generate” more jewel volume.

In keeping with 2DOGCP, we can, however, introduce our understanding of a guillotine arrangement of arbitrary convex designs (general guillotine cutting problem; see Fig. 23, also) and how one achieves it:

GGCP: Let there be an arrangement of a set of convex designs in a container. The arrangement is call a general guillotine arrangement when the container can be sectioned into pieces by a series of straight, through-cuts, i.e., guillotine cuts, such that each piece contains exactly one design and no design is cut into during the sectioning of the container.

A guillotine cut is therefore a hyperplane, which not only separates two designs from each other, but also one set of designs from another set of designs. In other words, in guillotine arrangements, the non-overlapping of the designs (and maintenance of a minimum distance) is always guaranteed by separating hyperplanes. Here, however, fewer hyperplanes are required than for an arbitrary arrangement. Thus, the number of optimization parameters is smaller. The number and structure of the semi-infinite constraints, however, is the same for guillotine arrangements as for arbitrary arrangements.

The procedure in GGCP generates a fully binary tree, whose nodes correspond to the container portions resulting from the successive sectioning process. Here, the inner nodes represent the guillotine cuts and the leaves represent the designs (see Fig. 27).

Fig. 27

Representation of the guillotine arrangement from Fig. 23 using a fully binary tree

When the number of designs reaches four or more, then there will be at least two possible guillotine arrangements. Here, to find the best one, all the structurally different arrangements must be calculated. The number of possible guillotine arrangements increases exponentially with the number of designs.

6.3 Algorithmic Implementation

To numerically solve this problem, we have chosen to use the transformation-based discretization method introduced in Sect. 4.5.2, since this works very nicely when most of the constraint functions are affine linear and the infinite index sets are very close to polyhedral. For gemstone cutting problems involving a guillotine arrangement of the faceted stones, these prerequisites are either met outright, or can be contrived (see [14]).

6.3.1 Modeling the Faceted Stones

For the transformation-based discretization method, one needs a functional description of the faceted stone shape and a representation of this description as the image of a compact set under a continuously differentiable mapping. Due to the complexity of the faceted stone shapes, it is impossible to represent any shape as the image of a single set. However, if one considers the crown, girdle, and pavilion separately, then this can indeed be done. If the shapes are very complex, further subdivisions may even be necessary.

For illustration purposes, we want to consider the girdle of a round shaped stone. For representations of the crown and pavilion—along with other shapes—as the image of one or more compact sets under continuously differentiable mapping, we refer the reader to [14]. As we know from Eq. (32), the girdle of the round shape

$$ \left \{ \mathbf{y} \in\mathbb{R}^{3} \left\vert \textstyle\begin{array}{rcl} y_{1}^{2} + y_{2}^{2} - r_{G}^{2} & \leq& 0 \\ 0 \leq y_{3} & \leq& h_{G} \end{array}\displaystyle \right. \right \} $$

is a cylinder with radius $r_{G}$ and height $h_{G}$. Using the polar coordinate representation of a cylinder, this is, accordingly, the image of the set $[0,1]^{3}$ under the mapping $\mathbf {t}((h_{G},r_{G}),\cdot) : \mathbb{R}^{3} \rightarrow\mathbb{R}^{3}$, with

$$ \mathbf{t}(\mathbf{x}, \mathbf{z}) := \begin{pmatrix} z_{2} r_{G} \cos(2 \pi z_{1}) \\ z_{2} r_{G} \sin(2 \pi z_{1}) \\ z_{3} h_{G} \end{pmatrix} . $$

6.3.2 Modeling the Rough Stone and Its Flaws

From Sect. 5.1.3, we already know how to model the rough stone surface so that the above problem can be (re-)formulated and solved as a general semi-infinite optimization problem. Therefore, in this section, we will only describe how to model the flaws. We recall that for the convexity of the lower-level problems, which result from reformulating the non-overlapping conditions between the designs and the flaws, both the designs and the flaws must be convex (see Sect. 4.4). While the former always are, the latter may not be. Thus, they must be approximated by convex sets. The simplest such approximation consists of enclosing a flaw, or enclosing the triangulation of its surface, by means of a sphere with minimal radius. A better external approximation is delivered by a so-called Löwner–John ellipsoid. This is an ellipsoid that encloses a set of points and has minimal volume. Finally, the convex hull of each flaw triangulation is calculated. Due to the multi-step nature of the problem solution (see Sect. 6.3.3), one approximates the flaws with various bodies, as illustrated in Fig. 28.

Fig. 28

Enclosing a flaw: from left to right, triangulation of its surface, smallest enclosing sphere, Löwner–John ellipsoid, convex hull of the triangulation

6.3.3 Determining the Starting Point

We now describe how to initialize the transformation-based discretization method (Algorithm 3, Sect. 4.5.2) for gemstone cutting problems. In this context, the starting point in step 1 of the method corresponds to assigning the initial translation, rotation, and size/shape parameters of all faceted stone designs, along with the parameters of all separating planes. The starting discretizations in step 2 correspond to an initial discretization of the faceted stone designs and flaws.

When calculating the initial faceted stone designs and separating plane parameters, we are motivated by the fact that this is a maximum material yield problem. For this reason, we proceed as follows: The problem of volume-maximal embedding of a given number of spheres in a polyhedral container with spherical surfaces and internal cavities (flaws) represents the simplest maximum material yield problem in $\mathbb{R}^{3}$ and can be reduced directly to a finite optimization problem, that is, a problem with a finite number of constraints. Therefore, in the first step, we solve such a problem. Except when centering a single sphere, we are dealing here with a non-convex optimization problem. Therefore, in general, a standard solution method for nonlinear problems will find no global solution. Hence, a calculated solution is repeatedly disturbed and re-optimized (a technique of global optimization known as Monotonic Basin Hopping (MBH)), so as to find a best possible local, perhaps even global, solution.

Unlike spheres, faceted stones have different extensions in the directions of the three main axes. For this reason, spheres are not very well suited for use as surrogate models. Therefore, in the second step, we shift to an elliptical representation of the various objects and solve the corresponding multi-body design centering problem. This, too, can still be formulated as a finite optimization problem. Due to its non-convexity, we use MBH here as well, so as to find the best possible local solution.

We ultimately obtain an initial assignment of the faceted stone design parameters by embedding their discretization in the arranged design ellipsoid while maximizing the volume of the faceted stone design. To solve the semi-infinite reformulation of the gemstone cutting problem, we shift to a polyhedral representation of the surfaces and inner cavities. We refer the reader to [14] for details regarding the entire starting point calculation (see Fig. 31, also, for a graphical illustration).

6.3.4 A Numerical Example

In conclusion, we want to use a numerical example to illustrate the problem dimensions of the resulting optimization problems, as well as the run-times and iteration counts of the transformation-based discretization method.

We implemented both the multi-body design centering problems and the transformation-based discretization method in Matlab (R2012a). To solve the finite reformulations of the multi-body design centering problems and the discretized SIP problems in the context of the transformation-based discretization method, we used the SQP method of the fmincon routine of the Optimization Toolbox V6.1, with standard settings and first-order derivatives. The calculations were performed on a 32 bit Windows laptop PC with Intel Core Duo T2500 2.0 GHz processor and 2.0 GB RAM.

In this example, we do not consider the requirement of maintaining a minimum distance, since it is difficult for the observer to verify this in the two-dimensional representation of the three-dimensional situation. For the same reason, we have dispensed with the requirement that only a guillotine arrangement is allowed.

The rough stone we have selected contains three inclusions. We consider a triangulation of the rough stone surface with 576 triangles (see Fig. 29, left). We approximate these with 9 planes and one quadric (see Fig. 29, right). The convex hull of the approximated surface cavity has 24 corner points. We have enclosed the surface triangulations of each of the three inclusions in one sphere and one ellipsoid (see Fig. 29, right). Their convex hulls have 25, 38, and 50 corner points, respectively.

Fig. 29

Rough stone with three inclusions: left, surface triangulation; right, approximating the rough stone surface with planes and a sphere, and enclosing the inclusions using spheres

Within this rough stone, we want to embed one to five faceted stone designs of the baguette shape (see Fig. 3) with maximum total volume. We let 3 be the maximum number of non-improvements in the MBH for the design centering of both spheres and ellipsoids. The transformation-based discretization method terminates when the maximum violation of the solution feasibility with regard to the underlying general semi-infinite problem is less than or equal to $10^{-3}$. The initial discretization of a baguette-shaped faceted stone design consists of 10 points and is shown in Fig. 30.

Fig. 30

The initial discretization of a baguette-shaped faceted stone design: left, top view; right, side view

Table 1 shows the problem dimensions of the general semi-infinite optimization problems resulting from the maximal material yield problems. Table 2 shows the results of the calculations for the embedding of one to five baguette-shaped faceted stone designs in the rough stone approximation under consideration. The abbreviations in the tables can be deciphered as follows:

# D:

: Number of designs

D:

: Designs: S = Sphere(s), E = Ellipsoid(s), FD = Faceted Stone Designs

# V:

: Number of problem variables

# FC:

: Number of finite constraints

# g’s:

: Number of constraint functions of the semi-finite constraints

# IIS:

: Number of infinite index sets

# SIC:

: Number of semi-infinite constraints

# I:

: Number of loop executions for monotonic basin hopping or transformation-based discretization method for refining the discretization

$t$ :

: CPU-time in seconds

MBH-V:

: Absolute improvement of objective function value in percent as a result of MBH

Vol:

: Volume yield in percent

Table 1 Problem dimensions of the resulting general semi-infinite optimization problems for the embedding of one to five faceted stone designs in the rough stone approximation

Table 2 Embedding of one to five spheres, ellipsoids, and baguette-shaped faceted stone designs in the rough stone approximation: problem dimensions of the finite problems, CPU-times, and volume yields

Figures 31, 32, and 33 illustrate the calculated solutions.

Fig. 31

Multi-step procedure for solving gemstone cutting problems: from spherical to elliptical to polyhedral shaped objects

Fig. 32

Calculated solution for three baguette-shaped faceted stone designs, as viewed from two perspectives

Fig. 33

Calculated solutions for two, four, and five baguette-shaped faceted stone designs

6.4 Automating the Sectioning Process

The technical goal of this project was to automate the sectioning of raw material into blanks that can be further processed. Here, we wanted to carry over as many of the manual processing steps as possible into the automated process.

The sawing technology used in the manual process is the circular saw. Here, wooden clamps are used to hold the rough stones in place for sawing. This holding technology is not suited for automation, however, since it is impossible to predict how deeply the rough stone will sink into the wooden clamps. For an automated process, the stone must adhere precisely to the coordinate system, a problem that was ultimately solved in the following manner: The rough stone is cast in synthetic resin and the resulting block then milled down to a cuboid (see Fig. 34). The resin cuboid is glued to a cutting underlay into which the cutting disc is free to penetrate. The cutting underlay is clamped to a T-grooved plate, which is then fixed in a vice.

Fig. 34

Milled-to-size resin cuboid with enclosed rough stone

The circular saw is designed so that the cutting disc remains stationary, and the resin cuboid is aligned according to the cut to be executed. To allow this alignment, the vice is mounted on a rotary-swivel table that can be shifted orthogonally and parallel to the cutting disc. The cut is then made by guiding the clamping system against the cutting disc (see Fig. 35).

Fig. 35

Sawing by guiding the properly aligned resin cuboid into the cutting disc

For this project, we needed to be able to detect flaws in the interior of the rough stone, which ruled out stripe projection as a means of data collection. Instead, we decided upon computer tomography. The rough stones, including resin cuboids, were digitalized using the ITWM’s own computer tomography equipment.

Along with the optimization algorithms, we implemented two other modules that deal with the execution of the guillotine cuts: The first is a program for virtually executing the guillotine cuts and then visualizing the resulting blanks. The second is a program for calculating the machine data (angle settings of the rotation axes and position of the linear axes) for the saw prototypes in preparation for performing the actual cutting sequence.

The original plan was to have the cuts automatically executed once the resin cuboid was aligned properly. This proved to be impracticable, however, due to two problems that arose with the very first cutting trials: When initiating the cut, if the cutting disc penetrates too quickly into the resin surface or at too obtuse an angle, it can slide off and tilt. The same thing can happen when the resin work piece is withdrawn from the cutting disc. Therefore, cut initiation and work piece withdrawal must both be performed manually under the guidance of an experienced cutter.

Ultimately, the sectioning process was carried out as follows:

• 1. Preparation: encasing the rough stone in synthetic resin and milling the resulting resin cast into cuboid form

• 2. Computer tomography and preparation of volume data: photographing the resin cuboid, segmenting the resin cuboid and rough stone, and analyzing flaws

• 3. Intermediate check 1: re-adjusting the flaw classification

• 4. Preparation of volume data for optimization: generating surface data and approximating the resin cuboid, the rough stone surface, and the flaws

• 5. Optimization: calculating the optimum sectioning plan with respect to volume

• 6. Intermediate check 2: selecting a sectioning plan

• 7. Generation of machine data

• 8. Preparation of the cut: Gluing resin cuboid to an acrylic glass plate, fastening the acrylic glass plate to a aluminum T-groove plate with clamping jaws, clamping the aluminum T-groove plate in the vice of the retaining jig, aligning the retaining jig according to the calculated angles and translations

• 9. Sawing the resin cuboid: manual cut initiation, further cutting with automatic feed-in, manual withdrawal of work piece

• 10. Detaching resin cuboid

• 11. Repetition of steps 7/8 to 10 until all calculated cuts have been performed

• 12. Final check

One problem with this process is the difficulty of guaranteeing sufficient workplace safety. Given the large forces generated by the cutting disc, manual guidance of the resin cuboid is simply too dangerous. Therefore, alternative approaches must be considered. One such alternative that appears promising is the use of high-pressure waterjet cutting for the sectioning process. This approach is discussed below.

6.5 Sectioning by Waterjet Cutting

In our deliberations over the best way to section the raw material, we initially rejected waterjet cutting technology, since the cutting kerfs generated by the waterjet were too wide. In 2011, however, innovations in this technology rendered its use in the gemstone industry feasible. A series of test runs commissioned by Wild oHG in Sweden and Switzerland demonstrated that a high-pressure waterjet, when combined with the correct abrasive, could indeed be used to cut gemstones without transferring significant forces into the stones, and at the same time keeping the kerf width and the depth-of-cut within acceptable bounds. Therefore, high-pressure waterjet cutting technology continues to be investigated within the framework of a current research project.

The powerful waterjet used to section the material has considerably more degrees of freedom than the guillotine cuts. As a consequence, the cut surfaces resulting from waterjet cutting are not necessarily planar, but are, in general, so-called developable surfaces, as depicted in Fig. 36. To model this approach for sectioning and solving the associated maximum material yield problem, the approaches used so far will have to be generalized in future research projects.

Fig. 36

Two polyhedral designs separated by a developable surface

7 Outlook

The problem of optimum material yield in gemstone cutting is an outstanding example of using mathematical methods in the age of computer-supported, customized production. Here, one must not only master the challenges of the machine and software technology, but also the challenges presented by the mathematics involved. When Paul Wild oHG commissioned the Fraunhofer ITWM to initiate this work, there was no practicable mathematical method for calculating optimum faceted stone designs that could simply be taken off the shelf and applied to solving the problems posed in this project. It was necessary to take available algorithmic concepts for problems having containment and non-overlapping conditions and develop or alter them, so as to produce numerically robust methods that could produce results for the complex problems existing here in a reasonable amount of time.

New mathematics resulted from the ITWM projects through the development of a method of feasible solutions for general semi-infinite problems (GSIP), and a new class of methods for solving GSIPs was developed, to wit, the transformation-based discretization method. Moreover, it was demonstrated that sectioning problems and the treatment of inclusions can also be handled using the GSIP model class.

Despite these visible successes, there are still many fascinating questions waiting to be answered and problems that have not been adequately solved.

One exciting example is the sectioning of stones using waterjet technology. To date, we have only investigated guillotine cuts, as executed with circular saw technology. The new technology offers more freedom to design the cuts, which leads to the question of how this more generalized sectioning technology can be described mathematically. How can one calculate optimal sectioning processes? Which is better suited, the semi-infinite formulation or the method based on collision detection? In a new project, planned together with Wild oHG, there are exactly these questions that we will be tackling in our continuing effort to use the tools of mathematics to optimize the cutting of precious stones.