Mapping Kernels Between Rooted Labeled Trees Beyond Ordered Trees

Abstract

In this paper, we investigate several mapping kernels to count all of the mappings between two rooted labeled trees beyond ordered trees, that is, cyclically ordered trees such as biordered trees, cyclic-ordered trees and cyclic-biordered trees, and degree-bounded unordered trees. Then, we design the algorithms to compute a top-down mapping kernel, an LCA-preserving segmental mapping kernel, an LCA-preserving mapping kernel, an accordant mapping kernel and an isolated-subtree mapping kernel for biordered trees in O(nm) time and ones for cyclic-ordered and cyclic-biordered trees in O(nmdD) time, where n is the number of nodes in a tree, m is the number of nodes in another tree, D is the maximum value of the degrees in two trees and d is the minimum value of the degrees in two trees. Also we design the algorithms to compute the above kernels for degree-bounded unordered trees in O(nm) time. On the other hand, we show that the problem of computing label-preserving leaf-extended top-down mapping kernel and label-preserving bottom-up mapping kernel is #P-complete.

This work is partially supported by Grant-in-Aid for Scientific Research 24240021, 24300060, 25540137, 26280085 and 26370281 from the Ministry of Education, Culture, Sports, Science and Technology, Japan.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A tree kernel is one of the fundamental method to classify rooted labeled trees (trees, for short) through support vector machines (SVMs). Many researches to design tree kernels for ordered trees, in which an order among siblings is fixed, have been developed (cf., [2, 6, 14–17]). We call them ordered tree kernels.

A mapping kernel [15–17] is a powerful and general framework for tree kernels based on counting all of the mappings (and their variations) as the set of one-to-one node correspondences [18]. It is known that the minimum cost of (Tai) mappings coincides with an edit distance between trees. Also, as the properties of mapping kernels, almost ordered tree kernels are classified into the framework of mapping kernels [15], and a mapping kernel is positive definite if and only if the mapping is transitive, that is, closed under the composition [16, 17].

On the other hand, few researches to design tree kernels for unordered trees, in which an order among siblings is arbitrary, have been developed. We call them unordered tree kernels. One of the reasons is that the problem of counting all of the subtrees for unordered trees is #P-complete [6].

In order to avoid such difficulty, the unordered tree kernel have been developed as counting all of the specific substructures. For example, Kuboyama et al. [9] and Kimura et al. [7] have designed the unordered tree kernel counting all of the bifoliate q-grams and all of the subpaths, respectively.

As a tractable mapping kernel for unordered trees, Hamada et al. [3] have introduced an agreement-subtree mapping kernel for phylogenetic trees (leaf-labeled binary unordered trees). Also they have given a new proof of intractability of computing a mapping kernel for unordered trees, simpler than Kashima et al. [6], such that the problem of counting the number of leaves with the same labels in leaf-labeled tree is #P-complete, which is based on the problem of counting all of the matchings in a bipartite graph.

It is known that, by introducing several conditions to mappings, we deal with several variations of mappings and they form the hierarchy of mappings [5, 8, 21, 23]. Every variation of mappings provides not only a variation of the edit distance as the minimum cost of all the mappings [5, 8, 22, 23] but also a tree kernel as the number of all the mappings [8, 10, 15].

Note that the problem of computing the tractable variations of the edit distance between unordered trees such as a top-down distance [1, 13], an LCA-preserving segmental distance [23], an LCA-preserving distance [27], an accordant distance [8, 10, 22] and an isolated-subtree distance [25, 26] is essential to solve the minimum weighted maximum matching in a bipartite graph [22, 26, 27]. On the other hand, it is essential for the above #P-completeness [3, 6] to reduce from the problem of counting all of the matchings in a bipartite graph.

Recently, as trees extended from ordered trees and restricted to unordered trees, Yoshino and Hirata [24] have introduced the following three kinds of a cyclically ordered tree that is an unordered tree preserving the adjacency among siblings in a tree as possible. Let $v_1,\ldots ,v_n$ be siblings from left to right. We say that a tree is biordered if it allows two orders $v_1,\ldots ,v_n$ and $v_n,\ldots ,v_1$. Also we say that a tree is cyclic-ordered if it allows a cyclic order $v_i,\ldots ,v_n,v_1,\ldots ,v_{i-1}$ for every i ($1\le i\le n$). Furthermore, we say that a tree is cyclic-biordered if it allows cyclic orders $v_i,\ldots ,v_n,v_1,\ldots ,v_{i-1}$ and $v_{i-1},\ldots ,v_1,v_n,\ldots ,v_i$ for every i ($1\le i\le n$). Then, they have designed the algorithm to compute an alignment distance [4] between cyclically ordered trees in polynomial time. Note that the algorithm does not use the maximum matching for a bipartite graph. It is a simple extension of the algorithm (or recurrences) of computing the alignment distance between ordered trees [4].

Hence, in this paper, we first investigate several mapping kernels such as a top-down mapping kernel, an LCA-preserving segmental mapping kernel, an LCA-preserving mapping kernel, an accordant mapping kernel and an isolated-subtree mapping kernel for cyclically ordered trees. Then, we design the algorithms to compute all of the above mapping kernels for biordered trees in O(nm) time and ones for cyclic-ordered and cyclic-biordered trees in O(nmdD) time, where n is the number of nodes in a tree, m is the number of nodes in another tree, D is the maximum value of the degrees in two trees and d is the minimum value of the degrees in two trees.

Next, by focusing that the agreement subtree mapping kernel is applied to full binary trees, we investigate the above kernels for bounded-degree unordered trees. Then, we design the algorithms to compute all of the above mapping kernels in O(nm) time, which follows from the algorithms to compute ones for unordered trees in $O(nmD^D)$ time, which is exponential to D.

On the other hand, for unordered trees, we show that the problem of computing the label-preserving leaf-extended top-down mapping kernel and the label-preserving bottom-up mapping kernel is #P-complete. Note here that the proof of the above #P-completeness [3, 6] cannot apply to top-down and bottom-up mapping kernels for unordered tree directly. Also, the degrees of unordered trees in this proof are not bounded.

2 Preliminaries

A tree is a connected graph without cycles. For a tree $T=(V,E)$, we denote V and E by V(T) and E(T), respectively. Also the size of T is |V| and denoted by |T|. We sometime denote $v\in V(T)$ by $v\in T$. We denote an empty tree by $\emptyset$.

A rooted tree is a tree with one node r chosen as its root. We denote the root of a rooted tree T by r(T). A(n ordered) forest is a sequence $[T_1,\ldots ,T_n]$ of trees which we denote by $T_1\bullet \cdots \bullet T_n$ or $\bullet _{i=1}^n T_i$. In particular, for two forests $F_1=T_1\bullet \cdots \bullet T_n$ and $F_2=S_1\bullet \cdots \bullet S_m$, we denote the forest $T_1\bullet \cdots \bullet T_n\bullet S_1\bullet \cdots \bullet S_m$ by $F_1\bullet F_2$. For a forest F, we denote the tree rooted by v whose children are trees in F by v(F).

For each node v in a rooted tree with the root r, let ${ UP}_r(v)$ be the unique path (as trees) from v to r. The parent of $v (\ne r)$, which we denote by ${ par}(v)$, is its adjacent node on ${ UP}_r(v)$ and the ancestors of $v (\ne r)$ are the nodes on ${ UP}_r(v)-\{v\}$. We denote the set of all ancestors of v by ${ anc}(v)$. We say that u is a child of v if v is the parent of u. The set of children of v is denoted by ${ ch}(v)$. A leaf is a node having no children. We denote the set of all leaves in T by ${ lv}(T)$. A node that is neither a leaf nor a root is called an internal node. We call the number of children of v the degree of v and denote it by d(v), that is, $d(v)=|{ ch}(v)|$. Also we define $d(T)=\max \{d(v)\mid v\in T\}$ and call it the degree of T.

In this paper, we use the ancestor orders $<$ and $\le$, that is, $u< v$ if v is an ancestor of u and $u\le v$ if $u<v$ or $u=v$. We say that w is the least common ancestor (LCA for short) of u and v, denoted by $u\sqcup v$, if $u\le w$, $v\le w$ and there exists no $w'$ such that A (complete) $w'< w$, $u\le w'$ and $v\le w'$. A (complete) subtree of $T=(V,E)$ rooted by v, denoted by T[v], is a tree $T'=(V',E')$ such that $r(T')=v$, $V'=\{u\in V\mid u\le v\}$ and $E'=\{(u,w)\in E\mid u,w\in V'\}$.

We say that a rooted tree is labeled if each node is assigned a symbol from a fixed finite alphabet $\varSigma$. For a node v, we denote the label of v by l(v), and sometimes identify v with l(v). Also let $\varepsilon \not \in \varSigma$ denote a special blank symbol and define $\varSigma _\varepsilon =\varSigma \cup \{\varepsilon \}$.

Let $v\in T$ and $v_i,v_j\in { ch}(v)$ such that $v_i$ the i-th child of v and $v_j$ the j-th child of v. Then, we say that $v_i$ is to the left of $v_j$ if $i\le j$. Then, for every $u,v\in T$, $u\preceq v$ if either u is to the left of v (when both u and v are the children of the same node in T) or there exist $u',v'\in { ch}(u\sqcup v)$ such that $u\le u'$, $v\le v'$ and $u'$ is to the left of $v'$. Hence, we say that a rooted tree is ordered if a left-to-right order among siblings is fixed; unordered otherwise. Furthermore, in this paper, we introduce cyclically ordered trees by using the following functions $\sigma _{p,n}^+(i)$ and $\sigma _{p,n}^{-}(i)$ for $1\le i,p\le n$.

$$\begin{aligned} \sigma _{p,n}^+(i) = ((i+p-1)~\text{ mod }~n)+1, \,\,\, \sigma _{p,n}^{-}(i) = ((n-i-p+1)~\text{ mod }~n)+1. \end{aligned}$$

Definition 1

(Cyclically Ordered Trees). Let T be a tree and suppose that $v_1,\ldots ,v_n$ are the children of $v\in T$ from left to right.

• 1. We say that T is biordered if T allows the orders of both $v_1,\ldots ,v_n$ and $v_n,\ldots ,v_1$.

• 2. We say that T is cyclic-ordered if T allows the orders $v_{\sigma _{p,n}^+(1)},\ldots ,v_{\sigma _{p,n}^+(n)}$ for every $1\le p\le n$.

• 3. We say that T is cyclic-biordered if T allows the orders $v_{\sigma _{p,n}^+(1)},\ldots ,v_{\sigma _{p,n}^+(n)}$ and $v_{\sigma _{p,n}^{-}(1)},\ldots ,v_{\sigma _{p,n}^{-}(n)}$ for every $1\le p\le n$.

Sometimes we use the scripts $o,b,c,{ cb}$, u, and the notation of $\pi \in \{o,b,c,{ cb},u\}$.

It is obvious that the cyclically ordered trees are an extension of ordered trees and a restriction of unordered trees. The number of orders among siblings of a node v in ordered trees, biordered trees, cyclic-ordered trees, cyclic-biordered trees and unordered trees is 1, 2, d(v), 2d(v) and d(v)!, respectively. Also it holds that, when $d(T)=2$, T is unordered iff it is biordered, cyclic-ordered or cyclic-biordered, and when $d(T)=3$, T is unordered iff it is cyclic-biordered.

3 Mapping

In this section, we introduce a Tai mapping and its variations, and then the distance as the minimum cost of all the mappings.

Definition 2

(Tai Mapping [18]). Let $T_1$ and $T_2$ be trees and $M\subseteq V(T_1)\times V(T_2)$.

• 1. We say that a triple $(M,T_1,T_2)$ is an ordered Tai mapping from $T_1$ to $T_2$, denoted by $M\in \mathcal{M}_{{\textsc {Tai}}}^o(T_1,T_2)$, if every pair $(u_1,v_1)$ and $(u_2,v_2)$ in M satisfies the following conditions.

  • (i) $u_1=u_2$ iff $v_1=v_2$ (one-to-one condition).

  • (ii) $u_1\le u_2$ iff $v_1\le v_2$ (ancestor condition).

  • (iii) $u_1\preceq u_2$ iff $v_1\preceq v_2$ (sibling condition).

• 2. We say that a triple $(M,T_1,T_2)$ is an unordered Tai mapping from $T_1$ to $T_2$, denoted by $M\in \mathcal{M}_{{\textsc {Tai}}}^u(T_1,T_2)$, if M satisfies the conditions (i) and (ii).

In the following, let $u_1,u_2,u_3,u_4\in { ch}(u)$ and $v_1,v_2,v_3,v_4\in { ch}(v)$.

• 3. We say that a triple $(M,T_1,T_2)$ is a biordered Tai mapping from $T_1$ to $T_2$, denoted by $M\in \mathcal{M}_{{\textsc {Tai}}}^b(T_1,T_2)$, if M satisfies the above conditions (i) and (ii) and the following condition (iv).

  • (iv) For every $u\in T_1$ and $v\in T_2$ such that $(u_1,v_1),(u_2,v_2),(u_3,v_3)\in M$, one of the following statements holds.

    • 1. $u_1\preceq u_2\preceq u_3$ iff $v_1\preceq v_2\preceq v_3$.

    • 2. $u_1\preceq u_2\preceq u_3$ iff $v_3\preceq v_2\preceq v_1$.

• 4. We say that a triple $(M,T_1,T_2)$ is a cyclic-ordered Tai mapping from $T_1$ to $T_2$, denoted by $M\in \mathcal{M}_{{\textsc {Tai}}}^c(T_1,T_2)$, if M satisfies the above conditions (i) and (ii) and the following condition (v).

  • (v) For every $u\in T_1$ and $v\in T_2$ such that $(u_1,v_1),(u_2,v_2),(u_3,v_3)\in M$, one of the following statements holds.

    • 1. $u_1\preceq u_2\preceq u_3$ iff $v_1\preceq v_2\preceq v_3$.

    • 2. $u_1\preceq u_2\preceq u_3$ iff $v_2\preceq v_3\preceq v_1$.

    • 3. $u_1\preceq u_2\preceq u_3$ iff $v_3\preceq v_1\preceq v_2$.

• 5. We say that a triple $(M,T_1,T_2)$ is a cyclic-biordered Tai mapping from $T_1$ to $T_2$, denoted by $M\in \mathcal{M}_{{\textsc {Tai}}}^{ cb}(T_1,T_2)$, if M satisfies the above conditions (i) and (ii) and the following condition (vi).

  • (vi) For every $u\in T_1$ and $v\in T_2$ such that $(u_1,v_1),(u_2,v_2),(u_3,v_3),(u_4,v_4)\in M$, one of the following statements holds.

    • 1. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_1\preceq v_2\preceq v_3\preceq v_4$.

    • 2. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_2\preceq v_3\preceq v_4\preceq v_1$.

    • 3. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_3\preceq v_4\preceq v_1\preceq v_2$.

    • 4. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_4\preceq v_1\preceq v_2\preceq v_3$.

    • 5. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_4\preceq v_3\preceq v_2\preceq v_1$.

    • 6. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_3\preceq v_2\preceq v_1\preceq v_4$.

    • 7. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_2\preceq v_1\preceq v_4\preceq v_3$.

    • 8. $u_1\preceq u_2\preceq u_3\preceq u_4$ iff $v_1\preceq v_4\preceq v_3\preceq v_2$.

We will use M instead of $(M,T_1,T_2)$ simply and call a Tai mapping a mapping simply.

Definition 3

(Variations of Tai Mapping). Let $T_1$ and $T_2$ be trees, $\pi \in \{o,b,c,{ cb},u\}$ and $M\in \mathcal{M}_{{\textsc {Tai}}}^\pi (T_1,T_2)$. Here, we denote $M-\{({ r}(T_1),{ r}(T_2))\}$ by $M^-$.

• 1. We say that M is a top-down mapping [1, 13] (or a degree-1 mapping), denoted by $M\in \mathcal{M}_{{\textsc {Top}}}^\pi (T_1,T_2)$, if M satisfies the following condition.

  $$\begin{aligned} \forall (u,v)\in M^- \Bigl (({ par}(u),{ par}(v))\in M\Bigr ). \end{aligned}$$

• 2. We say that M is an LCA-preserving segmental mapping [23], denoted by $M\in \mathcal{M}_{{\textsc {LcaSg}}}^\pi (T_1,T_2)$, if there exists a pair $(u,v)\in T_1\times T_2$ such that $M\in \mathcal{M}_{{\textsc {Top}}}^\pi (T_1[u],T_2[v])$.

• 3. We say that M is an LCA-preserving mapping (or a degree-2 mapping [27]), denoted by $M\in \mathcal{M}_{{\textsc {Lca}}}^\pi (T_1,T_2)$, if M satisfies the following condition.

  $$\begin{aligned} \forall (u_1,v_1),(u_2,v_2)\in M \Bigl ((u_1\sqcup u_2,v_1\sqcup v_2)\in M\Bigr ). \end{aligned}$$

• 4. We say that M is an accordant mapping [8] (or a Lu’s mapping [12]), denoted by $M\in \mathcal{M}_{{\textsc {Acc}}}^\pi (T_1,T_2)$, if M satisfies the following condition.

  $$\begin{aligned} \forall (u_1,v_1),(u_2,v_2),(u_3,v_3)\in M \Bigl ( u_1\sqcup u_2=u_1\sqcup u_3 \iff v_1\sqcup v_2=v_1\sqcup v_3 \Bigr ). \end{aligned}$$

• 5. We say that M is an isolated-subtree mapping [21] (or a constrained mapping [25, 26]), denoted by $M\in \mathcal{M}_{{\textsc {Ilst}}}^\pi (T_1,T_2)$, if M satisfies the following condition.

  $$\begin{aligned} \forall (u_1,v_1),(u_2,v_2),(u_3,v_3)\in M \Bigl (u_3<u_1\sqcup u_2\iff v_3<v_1\sqcup v_2\Bigr ). \end{aligned}$$

• 6. We say that M is a bottom-up mapping [8, 20, 22], denoted by $M\in \mathcal{M}_{{\textsc {Bot}}}^\pi (T_1,T_2)$, if M satisfies the following condition.

  $$\begin{aligned} \forall (u,v)\in M \,\,\left( \begin{array}{l} \forall u'\in T_1[u] \exists v'\in T_2[v]\Bigl ((u',v')\in M\Bigr )\\ \wedge \forall v'\in T_2[v] \exists u'\in T_1[u]\Bigl ((u',v')\in M\Bigr ) \end{array}\right) \!. \end{aligned}$$

Proposition 1

( cf. [8, 23]). For $\pi \in \{o,b,c,{ cb},u\}$ and trees $T_1$ and $T_2$, the following statement holds:

$$\begin{aligned} \begin{array}{c} \mathcal{M}_{{\textsc {Top}}}^\pi (T_1,T_2)\subset \mathcal{M}_{{\textsc {LcaSg}}}^\pi (T_1,T_2)\subset \mathcal{M}_{{\textsc {Lca}}}^\pi (T_1,T_2)\\ \subset \mathcal{M}_{{\textsc {Acc}}}^\pi (T_1,T_2)\subset \mathcal{M}_{{\textsc {Ilst}}}^\pi (T_1,T_2). \end{array} \end{aligned}$$

Furthermore, for $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$, $\mathcal{M}_{{\textsc {Bot}}}^\pi (T_1,T_2)$ is incomparable with $\mathcal{M}_{\text{ A }}^\pi (T_1,T_2)$

4 Mapping Kernels

Let $\pi \in \{o,b,c,{ cb},u\}$ and $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$ unless otherwise noted. A mapping between forests $F_1$ and $F_2$ is defined as a mapping M between trees $v(F_1)$ and $v(F_2)$ such that $(v,v)\not \in M$. We define $\mathcal{M}_{\text{ A }}^\pi (F_1,F_2)$ as similar as $\mathcal{M}_{\text{ A }}^\pi (T_1,T_2)$. Let $\sigma :\varSigma \times \varSigma \rightarrow \mathbf{R}^+$ be a similarity function. The similarity $\sigma (M)$ of a mapping $M\in \mathcal{M}_{\text{ A }}^\pi (T_1,T_2)$ between two trees $T_1$ and $T_2$ is defined as $\displaystyle { \sigma (M)=\prod _{(u,v)\in M}\sigma (l(u),l(v)) }$. The similarity between two forests $F_1$ and $F_2$ is defined as follows:

$$\begin{aligned} \displaystyle { \mathcal{K}_{\text{ A }}^\pi (F_1,F_2)=\sum _{M\in \mathcal{M}_{\text{ A }}^\pi (F_1,F_2)}\sigma (M) }. \end{aligned}$$

Corollary 1

For $\pi \in \{o,b,c,{ cb},u\}$ and $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$, $\mathcal{K}_{\text{ A }}^\pi$ is positive definite.

Proof

Since $\mathcal{M}_{\text{ A }}^\pi$ is closed under the composition [8, 23, 27] and by [16], the statement holds. $\square$

Kuboyama [8] has introduced the recurrences to compute $\mathcal{K}_{\text{ A }}^o(T_1,T_2)$ for $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca }\}$ implicitly and $\mathtt{A}\in \{\text{ Acc },\text{ Ilst }\}$ explicitly illustrated in Fig. 1. Note the underlined formulas that denote the difference between similar formulas.

Fig. 1.

The recurrences of computing $\mathcal{K}_{\text{ A }}^o(T_1,T_2)$ for $\mathtt{A}\in \{\text{ Top },\text{ LcaSg }, \text{ Lca }, \text{ Acc }$, $\text{ Ilst }\}$ [8].

Theorem 1

( cf. , Kuboyama [8]). For $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$, the recurrences in Fig. 1 correctly compute $\mathcal{K}_{\text{ A }}^o(T_1,T_2)$ in O(nm) time, where $n=|T_1|$ and $m=|T_2|$.

4.1 Mapping Kernels for Cyclically Ordered Trees

In this section, we extend the recurrences in Fig. 1 to the recurrences to compute $\mathcal{K}_{\text{ A }}^\pi (T_1,T_2)$ for $\pi \in \{o,b,c,{ cb}\}$ and $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$.

For $u(F_1)$ and $v(F_2)$, let $F_1{=}[T_1[u_1],\ldots ,T_1[u_s]]$ and $F_2{=}[T_2[v_1],\ldots ,T_2[v_t]]$, that is, ${ ch}(u)=\{u_1,\ldots ,u_s\}$, ${ ch}(v)=\{v_1,\ldots ,v_t\}$, $d(u)=s$ and $d(v)=t$. Also let $1\le p\le s$ and $1\le q\le t$. We denote the forests $[T_1[u_{\sigma _{p,s}^+(1)}],\ldots ,T_1[u_{\sigma _{p,s}^+(s)}]]$ and $[T_2[v_{\sigma _{q,t}^+(1)}],\ldots ,T_2[v_{\sigma _{q,t}^+(t)}]]$ by $F_1^p$ and $F_2^q$. Furthermore, we denote the forests $[T_1[u_{\sigma _{p,s}^{-}(1)}],\ldots ,T_1[u_{\sigma _{p,s}^{-}(s)}]]$ and $[T_2[v_{\sigma _{q,t}^{-}(1)}],\ldots ,T_2[v_{\sigma _{q,t}^{-}(t)}]]$ by $F_1^{-p}$ and $F_2^{-q}$. It is obvious that $F_1=F_1^1$ and $F_2=F_2^1$.

Furthermore, the values of p and q in $F_1^p$, and $F_2^q$ are (1) $p=q=1$ if $\pi =o$, (2) $p=\pm 1$ and $q=\pm 1$ if $\pi =b$, (3) $1\le p\le s$ and $1\le q\le t$ if $\pi =c$ and (4) $1\le p\le s$, $-s\le p\le -1$, $1\le q\le t$ and $-t\le q\le -1$ if $\pi ={ cb}$. Hence, we prepare the following sets: (1) $o(s)=o(t)=\{1\}$, (2) $b(s)=b(t)=\{-1,1\}$, (3) $c(s)=\{1,\ldots ,s\}$, $c(t)=\{1,\ldots ,t\}$, and (4) ${ cb}(s)=\{-s,\ldots ,-1,1,\ldots ,s\}$, ${ cb}(t)=\{-t,\ldots ,-1,1,\ldots ,t\}$. We refer these sets to $\pi (s)$ and $\pi (t)$ for $\pi \in \{o,b,c,{ cb}\}$.

Then, we design the recurrences to compute $\mathcal{K}_{\text{ A }}^\pi (T_1,T_2)$ illustrated in Fig. 2.

Fig. 2.

The recurrences of computing $\mathcal{K}_{\text{ A }}^\pi (T_1,T_2)$ for $\pi \in \{o,b,c,{ cb}\}$ and $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$.

Theorem 2

For $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$, the recurrences in Fig. 2 correctly compute $\mathcal{K}_{\text{ A }}^b(T_1,T_2)$ in O(nm) time and $\mathcal{K}_{\text{ A }}^c(T_1,T_2)$ and $\mathcal{K}_{\text{ A }}^{ cb}(T_1,T_2)$ in O(nmdD) time, where $n=|T_1|$, $m=|T_2|$, $d=\min \{d(T_1),d(T_2)\}$ and $D=\max \{d(T_1),d(T_2)\}$.

Proof

In the formulas of $\mathcal{K}_{\text{ Top }}^\pi$ and $\mathcal{T}_{\text{ Lca }}^\pi$, the number of $\mathcal{F}_{\text{ Top }}^\pi (F_1^p,F_2^q)$ and $\mathcal{F}_{\text{ Lca }}^\pi (F_1^p,F_2^q)$ is 1 if $\pi =o$, 4 if $\pi =b$, $d(u)\cdot d(v)$ if $\pi =c$ and $2d(u)\cdot 2d(v)$ if $\pi ={ bc}$. Also in the formulas of $\mathcal{T}_{\text{ Acc }}^\pi$ and $\mathcal{T}_{\text{ Ilst }}^\pi$, the number of $\mathcal{F}_{\text{ Acc }}^\pi (F_1^p,F_2^q)$ and $\mathcal{F}_{\text{ Ilst }}^\pi (F_1^p,F_2^q)$ is 1 if $\pi =o$, $4+2+2+4=12$ if $\pi =b$, $d(u)\cdot d(v)+d(u)+d(v)+d(u)\cdot d(v)=2d(u)\cdot d(v)+d(u)+d(v)$ if $\pi =c$ and $2d(u)\cdot 2d(v)+2d(u)+2d(v)+2d(u)\cdot 2d(v)=8d(u)\cdot d(v)+2d(u)+2d(v)$ if $\pi ={ bc}$. Then, we can compute these recurrences in O(1) time if $\pi \in \{o,b\}$, whereas in $O(d(u)\cdot d(v))=O(dD)$ time if $\pi \in \{c,{ cb}\}$. Hence, the time complexity in the statement holds. Also we can show the correctness by extending Theorem 1. $\square$

4.2 Mapping Kernels for Bounded-Degree Unordered Trees

In this section, we extend the recurrences in Fig. 1 to the recurrences to compute $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ for $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$.

For nonnegative integers s and t, let $B_{s,t}$ be a complete bipartite graph $(X\cup Y,E)$ such that $X=\{1,\ldots ,s\}$ and $Y=\{1,\ldots ,t\}$, and ${ BM}(s,t)$ the set of all maximum matchings in $B_{s,t}$. For every $M\in { BM}(s,t)$, it holds that $M\subset E$ and $|M|=\min \{s,t\}$.

For $u(F_1)$ and $v(F_2)$, let $F_1=[T_1[u_1],\ldots ,T_1[u_s]]$ and $F_2=[T_2[v_1],\ldots$, $T_2[v_t]]$, that is, ${ ch}(u)=\{u_1,\ldots ,u_s\}$, ${ ch}(v)=\{v_1,\ldots ,v_t\}$, $d(u)=s$ and $d(v)=t$. Then, for $M\in { BM}(s,t)$, we denote the ordered forests $\bullet _{(i,j)\in M}T_1[u_i]$ and $\bullet _{(i,j)\in M}T_2[v_j]$ by $F_1^M$ and $F_2^M$, where we assume that trees in a forest are ordered along the order of M. Furthermore, for an ordered forest F, let ${ pm}(F)$ be the set of all permuted forests of F. Then, Fig. 3 illustrates the recurrences of computing $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$.

Fig. 3.

The recurrences of computing $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ for $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc }, \text{ Ilst }\}$.

Theorem 3

For $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst }\}$, the recurrences in Fig. 3 correctly compute $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ in $O(nmD^D)$ time, where $n=|T_1|$, $m=|T_2|$ and $D=\max \{d(T_1),d(T_2)\}$. Hence, if the degrees of unordered trees are bounded by some constant, then we can compute $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ in O(nm) time.

Proof

Since $|{ BM}(s,t)|={}_sP_t$ and the number of all permuted forests of $F_1$ (resp., $F_2$) is ${}_sP_1$ (resp., ${}_tP_1$), the number of occurrences of the formula $\mathcal{F}_{\text{ A }}^u(F_1^M,F_2^M)$ is bounded by $D^D$ and the number of occurrences of the formulas $\mathcal{F}_{\text{ A }}^u(u(F_1),F_2')$ and $\mathcal{F}_{\text{ A }}^u(F_1',v(F_2))$ for $\mathtt{A}\in \{\text{ Acc },\text{ Ilst }\}$ is bounded by $D^D$. In both cases, the number of occurrences of the formulas is $O(D^D)$. Since every pair $(u,v)\in T_1\times T_2$ is called just once, we can compute $K_\mathtt{A}^u(T_1,T_2)$ in $O(nmD^D)$ time by using dynamic programming. Hence, the time complexity in the statement holds. Also we can show the correctness by extending Theorem 1. $\square$

5 #P-Completeness for Unordered Trees

Since we cannot apply the #P-completeness of [3, 6] to the top-down mapping kernel for unordered trees directly, in this section, we show that the problem of counting all the specific top-down mappings (or bottom-up mappings) is #P-complete.

Let M be a mapping between $T_1$ and $T_2$. We say that M is label-preserving (or an indel mapping) if it always holds that $l(u)=l(v)$ for every $(u,v)\in M$. Also we say that M is leaf-extended if, for every $(u,v)\in M$, there exists $(u',v')\in M$ such that $u\in { anc}(u')$, $v\in { anc}(v')$, $u'\in { lv}(T_1)$ and $v'\in { lv}(T_2)$. Then, we deal with a label-preserving leaf-extended top-down mapping M between unordered trees $T_1$ and $T_2$, which we denote $M\in \mathcal{M}_{{\textsc {llTop}}}^u(T_1,T_2)$.

Theorem 4

( cf. , [3]). The problem of counting all the mappings in $\mathcal{M}_{{\textsc {llTop}}}^u(T_1,T_2)$ is #P-complete.

Proof

Valiant [19] has shown that the problem of counting all the matchings in a bipartite graph, which we denote #BipartiteMatching, is #P-complete. Then, we give two trees such that the number of all the label-preserving leaf-extended top-down mapping between them is equal to the output of #Bipartite Matching. Here, for a forest F and a node v such that $l(v)=a$, we denote v(F) by a(F).

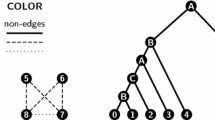
Let $G=(X\cup Y,E)$ be a bipartite graph. For $v\in X\cup Y$, we denote a neighbor of v by N(v). It is obvious that $N(v)\subseteq Y$ if $v\in X$ and $N(v)\subseteq X$ if $v\in Y$. Then, we construct $T_x=a(\{xy\mid y\in N(x)\})$ for every $x\in X$ and $T_1=a(\{T_x\mid x\in X\})$. Similarly, we construct $T_y=a(\{xy\mid x\in N(y)\})$ for every $y\in Y$ and $T_2=a(\{T_y\mid y\in Y\})$. Here, we regard an edge xy in G as the label of a leaf in $T_x$ and $T_y$. Figure 4 illustrates an example of the above construction of $T_1$ and $T_2$ from a bipartite graph G.

Fig. 4.

A bipartite graph G and the trees $T_1$ and $T_2$.

For a matching $B\subseteq E$ in G we construct the label-preserving leaf-extended top-down mapping M between $T_1$ and $T_2$ such that:

$$\begin{aligned} \begin{array}{rcl} M&{}=&{}\left\{ \begin{array}{l@{~~~}l} \emptyset &{} \text{ if } B=\emptyset ,\\ \displaystyle {\{(r(T_1),r(T_2))\}\cup \bigcup _{xy\in B}M_{xy}} &{} \text{ if } B\ne \emptyset , \end{array} \right. \\ M_{xy}&{}=&{}\left\{ \begin{array}{l} (u_1,v_1), (u_2,v_2)\\ \quad \in V(T_x)\times V(T_y) \end{array} \left| \begin{array}{@{~~}l} u_1={ par}(u_2), v_1={ par}(v_2),\\ u_2\in { lv}(T_x), v_2\in { lv}(T_y) \\ l(u_1)=l(v_1)=a, l(u_2)=l(v_2)=xy \end{array} \right. \right\} \!. \end{array} \end{aligned}$$

For example, let B be a matching $\{12,21,33\}$ in G illustrated in Fig. 4 as think lines. Then, the label-preserving leaf-extended top-down mapping M between $T_1$ and $T_2$ is illustrated by dashed lines.

Note that, by the definition of $T_x$ and $T_y$, $M_{xy}$ is a label-preserving leaf-extended top-down mapping between $T_x$ and $T_y$. Also $M_{xy}$ is corresponding to an element xy in a matching of G. Furthermore, no label-preserving leaf-extended top-down mapping $M_{xy}$ between $T_1$ and $T_2$ contains more than one path from the root to leaves in $T_x$ or $T_y$, that is, $M_{xy}$ contains zero or one path in $T_x$ and $T_y$.

Hence, a matching B in G determines the label-preserving leaf-extended top-down mapping M between $T_1$ and $T_2$ uniquely and vice versa. Then, the number of all the matchings in G which is the output of #BipartiteMatching is equal to the number of all the label-preserving leaf-extended top-down mappings between $T_1$ and $T_2$. Hence, the statement holds. $\square$

Fig. 5.

Trees $T_1$ and $T_2$ in Corollary 2.

Finally, we denote all the label-preserving bottom-up mappings between unordered trees $T_1$ and $T_2$ by $\mathcal{M}_{{\textsc {lBot}}}^u(T_1,T_2)$. Then, the proofs of [3, 6] or the above proof imply the following corollary. Here, it is sufficient to construct a matching B in Fig. 4 to a mapping $\displaystyle { \bigcup _{xy\in B}\{(u,v)\in { lv}(T_x)\times { lv}(T_y)\mid l(u)=l(v)=xy\}}$ as Fig. 5, for example.

Corollary 2

( cf. , [3, 6]). The problem of counting all the mappings in $\mathcal{M}_{{\textsc {lBot}}}^u(T_1,T_2)$ is #P-complete.

6 Conclusion

In this paper, for mapping $\mathtt{A}\in \{\text{ Top },\text{ LcaSg },\text{ Lca }\}$, we have designed the recurrences to compute $\mathcal{K}_{\text{ A }}^o(T_1,T_2)$ and $\mathcal{K}_{\text{ A }}^b(T_1,T_2)$ in O(nm) time and to compute $\mathcal{K}_{\text{ A }}^c(T_1,T_2)$ and $\mathcal{K}_{\text{ A }}^{ cb}(T_1,T_2)$ in O(nmdD) time. Also, we have designed the recurrences to compute $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ in $O(nmD^D)$ time, which implies that we can compute $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ in O(nm) time if the degrees of $T_1$ and $T_2$ are bounded by some constant. On the other hand, we show that the problem of computing $\mathcal{K}_{\text{ llTop }}^u(T_1,T_2)$ and $\mathcal{K}_{\text{ lBot }}^u(T_1,T_2)$ are #P-complete.

For $\mathcal{M}_{{\textsc {Aln}}}$ (alignable mapping [8], less-constrained mapping [11]), from [4, 24], we conjecture that we can compute $\mathcal{K}_{\text{ Aln }}^b(T_1,T_2)$ in $O(nmD^2)$ time, $\mathcal{K}_{\text{ Aln }}^\pi (T_1,T_2)$ in $O(nmdD^3)$ time ($\pi \in \{c,{ cb}\}$) and $\mathcal{K}_{\text{ Aln }}^u(T_1,T_2)$ in polynomial time if the degrees of $T_1$ and $T_2$ are bounded by some constant. Hence, it is a future work to investigate whether or not the above conjecture is correct.

In the proof of Theorem 4 and Corollary 2, the condition of label-preserving and leaf-extended are essential. If these condisions are not met, we must count all the other (standard) top-down or bottom-up mappings that are not label-preserving or leaf-extended. In order to show that the problem of counting all the mappings in $\mathcal{M}_{{\textsc {Top}}}^u(T_1,T_2)$, $\mathcal{M}_{{\textsc {Bot}}}^u(T_1,T_2)$ and then $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ for $\mathtt{A}\in \{\text{ LcaSg },\text{ Lca },\text{ Acc },\text{ Ilst },\text{ Aln }\}$ are all #P-complete, we must use the Cook-reduction [6, 19] from #BipartiteMatching, which is more complex than the proof of Theorem 4. On the other hand, this paper has shown that we can compute $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ for bounded-degree unordered trees. Hence, it is an important future work to investigate whether or not the problem of computing $\mathcal{K}_{\text{ A }}^u(T_1,T_2)$ is #P-complete when degrees are unbounded.