Concurrent Secure Computation via Non-Black Box Simulation

Abstract

Recently, Goyal (STOC’13) proposed a new non-black box simulation techniques for fully concurrent zero knowledge with straight-line simulation. Unfortunately, so far this technique is limited to the setting of concurrent zero knowledge. The goal of this paper is to study what can be achieved in the setting of concurrent secure computation using non-black box simulation techniques, building upon the work of Goyal. The main contribution of our work is a secure computation protocol in the fully concurrent setting with a straight-line simulator, that allows us to achieve several new results:

• We give first positive results for concurrent blind signatures and verifiable random functions in the plain model as per the ideal/real world security definition. Our positive result is somewhat surprising in light of the impossibility result of Lindell (STOC’03) for black-box simulation. We circumvent this impossibility using non-black box simulation. This gives us a quite natural example of a functionality in concurrent setting which is impossible to realize using black-box simulation but can be securely realized using non-black box simulation.

• Moreover, we expand the class of realizable functionalities in the concurrent setting. Our main theorem is a positive result for concurrent secure computation as long as the ideal world satisfies the bounded pseudo-entropy condition (BPC) of Goyal (FOCS’12). The BPC requires that in the ideal world experiment, the total amount of information learnt by the adversary (via calls to the ideal functionality) should have “bounded pseudoentropy”.

• We also improve the round complexity of protocols in the single-input setting of Goyal (FOCS’12) both qualitatively and quantitatively. In Goyal’s work, the number of rounds depended on the length of honest party inputs. In our protocol, the round complexity depends only on the security parameter, and is completely independent of the length of the honest party inputs.

Our results are based on a non-black box simulation technique using a new language (which allows the simulator to commit to an Oracle program that can access information with bounded pseudoentropy), and a simulation-sound version of the concurrent zero-knowledge protocol of Goyal (STOC’13). We assume the existence of collision resistant hash functions and constant round semi-honest oblivious transfer.

D. Gupta, A. Sahai—Research supported in part from a DARPA/ONR PROCEED award, a DARPA/ARL SAFEWARE award, NSF Frontier Award 1413955, NSF grants 1228984, 1136174, 1118096, and 1065276, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through the U.S. Office of Naval Research under Contract N00014-11-1-0389. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.

D. Gupta—Work done in part while interning at Microsoft Research India.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Secure computation protocols enable a set of mutually distrustful parties to securely perform a task by interacting with each other. Traditional security notions for secure computation [21, 49] were defined for the stand-alone setting where security holds only if a single protocol session is executed in isolation. In today’s connected world (and especially over internet), many instances of these protocols may be executing concurrently. In such a scenario, a protocol that is secure in the classical stand-alone setting may become completely insecure [5, 37]. Ambitious efforts have been made to generalize the results for the stand-alone setting, starting with concurrently-secure zero-knowledge protocols [7, 14, 34, 45, 47].

However, in the plain model, the effort to go beyond the zero-knowledge functionality were, unfortunately, less than fully satisfactory. In fact, for the plain model far reaching unconditional impossibility results were shown in a series of works [1, 5, 8, 19, 24, 37, 38]. Two notable exceptions giving positive results in the plain model are the works on bounded concurrency [36, 43, 44] (where there is an a-priori fixed bound on the total number of concurrent sessions in the system and the protocol in turn can depend on this bound), and, the positive results for a large class of functionalities in the so called “single input” setting [24]. In this setting, there is a server interacting with multiple clients concurrently with the restriction that the server (if honest) is required to use the same input in all sessions. There is a large body of literature on getting concurrently secure computation in weaker models such as using a super-polynomial time simulator, or a trusted setup. A short survey of these works is given later in this section. We emphasize that in this work, we are interested in concurrently secure computation protocols with no trusted set up assumptions where the security holds according to standard ideal/real paradigm.

An intriguing functionality that cannot be realized in the fully concurrent setting by these results is blind signatures in the plain model. The blind signature functionality, introduced by [11], allows users to obtain unforgeable signatures on messages of their choice without revealing the message being signed to the signer (blindness property). The question of whether a concurrently-secure protocol for this functionality can be constructed as per the ideal/real model simulation paradigm has been open so far. Moreover, given the impossibility result for concurrent blind signatures for black box simulation by Lindell [37], it is clear that we need to use non-black box techniques. Until recently, no non-black box technique was known which applies to full concurrency with polynomial time simulation. However, Goyal [25] recently proposed new non-black box simulation techniques for (fully) concurrent zero-knowledge with straight line simulation. Unfortunately, the result of Goyal is limited to the setting of concurrent zero-knowledge. We ask the question: Can we construct non-box black techniques for (fully) concurrent secure computation, building upon the work of Goyal [25]?

Our Contributions. The main contribution of our work is a secure computation protocol in the fully concurrent setting with a straight-line simulator, that allows us to achieve several new results. In short, we expand the class of realizable functionalities in the concurrent setting and give the first positive results for concurrent blind signatures and verifiable random functions in the plain model as per the ideal/real world security definition. Moreover, the round complexity of our protocol depends only on the security parameter and hence, improves the round complexity of [24] both qualitatively and quantitatively. Finally, our work can be seen as a unifying framework, which essentially subsumes all the previous work on positive results for concurrent secure computation achieving polynomial time simulation based security in the plain model. For detailed description of our results, see Sect. 1.1.

Other Models. In order to circumvent the above mentioned impossibility results in the plain model, there has been quite some work studying various trust assumptions such as common reference string (CRS) model and tamper proof hardware tokens [3, 10, 32]. Another interesting line of work has studied weaker security definitions [16, 39, 42, 46] while still remaining in the plain model, and most notably obtains positive results in models like super polynomial time simulation [6, 9, 17, 46] and input indistinguishable security [17, 39].

Note that these trust assumptions and these relaxed notions of security are sometimes restrictive and are not applicable to many situations. We again emphasize that the focus of this work is concurrent secure computation in the plain model achieving polynomial time simulation. In the plain model, there are point to point authenticated channels between the parties, but there is no global trusted third party.

What Goes Wrong in Concurrent Setting in Plain Model? A well established approach to constructing secure computation protocols is to use the GMW compiler: take a semi-honest secure computation protocol and “compile” it with zero-knowledge arguments. The natural starting point in the concurrent setting is to follow the same principles: somehow compile a semi-honest secure computation protocol with a concurrent zero-knowledge protocol (actually compile with concurrent non-malleable zero-knowledge [5]). Does such an approach (or minor variants) already give us protocols secure according to the standard ideal/real world definition in the plain model?

There is a fundamental problem with this approach which poses a key bottleneck in a number of previous works (see [17, 24, 26, 28–30]). All known concurrent zero-knowledge simulators in the fully concurrent setting work by rewinding the adversarial parties. Such an approach is highly problematic for secure computation in the concurrent setting, where the adversary controls the scheduling of the messages of different sessions. For instance, consider the following scenario: Due to nesting of sessions by the adversary, a rewinding based simulator may need to execute some sessions more than once. Since the adversary can choose a different input in each execution (e.g. based on transcript so far), the simulator would have to query the ideal functionality for than once. However, for any session, the simulator is allowed at most one query! Indeed, such problems are rather inherent as indicated by various impossibility results [5, 38].

Trying to solve this bottleneck of “handling extra queries” in various ways has inspired a number of different works which revolve around a unified theme: first construct a protocol where the simulator requires multiple queries per session in the ideal world, and then, somehow manage to either eliminate or answer these extra queries by exploiting some property of the specific setting in question. Examples of these include Resettable and Stateless computation [29, 30], Multiple Ideal Query model [26–28], Single-Input setting [24], Leaky Ideal Query model [26], etc¹.

Indeed, as is natural to expect, there are limitations on how much one can achieve using the above paradigm of constructing protocols. A very natural question that arises is whether there exists a different approach which allows us to construct concurrent secure computation protocols in the plain model without the need of additional output queries? Moreover, if such a different approach does exist, we know that due to impossibility results [1, 5, 8, 19, 24, 37, 38], there will be some limitations on the scope of its applicability. This leads to some more natural questions. What all can we achieve using this approach? In particular, can we expand the class of realizable functionalities in the concurrent setting? Can we improve the parameters (e.g. round complexity) of the protocols which exist in the plain model?

1.1 Our Results

The key contribution of this work is a new way of approaching the problem of concurrent secure computation in the plain model facilitated by recent advances in concurrent non-black box simulation [25]. We give a protocol with non-black box and straightline simulator. Since, very informally, our simulator does not rely on rewinding at all, we are able to avoid the key bottleneck of additional output queries to the ideal functionality during the rewinds.

However, our simulator has to overcome a number of additional obstacles not present in [25]. Note that unlike secure computation, an adversary in concurrent zero-knowledge does not receive any outputs. Dealing with the outputs given to the adversary in each session is a key difficulty we have to overcome. In particular, one might think that a straightline simulator for concurrent zero-knowledge should give a concurrently secure computation protocol trivially for all functionalities and in particular for concurrently secure oblivious transfer. Note that this cannot be true given unconditional impossibility results for oblivious transfer. For more on such technical hurdles, please refer to the technical overview (Sect. 1.2).

Informally stated, our main theorem is a general positive result for concurrent secure computation as long as the ideal world satisfies our so called bounded pseudo-entropy condition (BPC). Very informally, the bounded pseudoentropy condition requires that in the ideal world experiment, the total amount of information learnt by the adversary (via calls to the trusted party) should have “bounded pseudoentropy”. The origin of the bounded pseudoentropy condition comes from a conjecture of Goyal [24]. More precisely, the bounded pseudoentropy condition says the following:

Definition 1

(Bounded Pseudoentropy Condition (BPC)). An ideal world experiment satisfies bounded pseudoentropy condition if there exists $B\in \mathbb {N}$ and a PPT algorithm $\mathcal {T}$ such that for all $m = m(n)$ concurrent sessions, for all adversarial input vectors $\mathbf {I}$ (where an element of the vector represents the input of the adversary in that session), there exists a set S of possible output vectors such that the following conditions are satisfied

• All valid output vectors corresponding to the input vector $\mathbf {I}$ of the adversary are contained in S. Observe that for a given $\mathbf {I}$, for different honest party input vectors, the output vectors may be different. We require that any such output vector be contained in S. Furthermore, $|S| \le 2^B$.

• For every $\mathbf {O} \in S$, $\mathcal {T}(\mathbf {I}, \mathbf {O}) = 1$, and for every $\mathbf {O} \notin S$, $\mathcal {T}(\mathbf {I}, \mathbf {O}) = 0$. That is, the set S is efficiently recognizable.

Intuitively, this condition says the following: The adversary might be scheduling an unbounded polynomial number of sessions and gaining information from each of the outputs obtained. However for any vector of adversarial inputs, the number of possible output vectors is bounded (and hence so is the information that adversary learns). Further note that this condition places a restriction only on the ideal world experiment, which consists of the functionality being computed and the honest party inputs. There is no restriction on the ideal world adversary, which may follow any (possibly unbounded state) polynomial time strategy.

It can be seen that in concurrent zero-knowledge, as well as, in the bounded concurrency setting, the BPC is satisfied. Also note that the class of ideal worlds which satisfy BPC is significantly more general compared to the single input setting of [24]. For a formal proof of this claim, refer to Sect. 2. In our work, we prove the following main theorem.

Theorem 1

Assume the existence of collision resistant hash functions and constant-round semi-honest oblivious transfer. If the ideal world for the functionality $\mathcal {F}$ satisfies the bounded pseudoentropy condition in Definition 1, then for any constant $\epsilon$, there exists a $O(n^\epsilon )$ round real world protocol $\varPi$ which securely realizes the ideal world for functionality $\mathcal {F}$.

To understand the power of our result, a positive result for all ideal worlds satisfying BPC allows us to get the following “concrete” results:

• Resolving the Bounded Pseudoentropy Conjecture. Goyal [24] considered the so called “single input setting” and obtained a positive result for many functionalities in the plain model. Goyal further left open the so called bounded pseudoentropy conjecture which if resolved would give a more general and cleaner result (see [24] for the exact statement).

  Our BPC is inspired from this conjecture (and can be seen as one way of formalizing it). Thus, Theorem 1 allows us to resolve the bounded pseudoentropy conjecture in the positive. Our positive result for the BPC subsumes most known positive results for concurrent secure computation in the plain model such as for zero-knowledge [34, 45, 47], bounded concurrent computation [36, 43, 44], and the positive results in the single input setting [24].

• Improving the Round Complexity of Protocols in the Single Input Setting. The round complexity of the construction of Goyal [24] in the single input setting was a large polynomial depending not only upon the security parameter but also on the length of the input and the nature of the functionality. For example, for concurrent private information retrieval, the round complexity would depend multiplicatively of the number of bits in the database and the security parameter. Our construction only has $n^\epsilon$ rounds, where n is the security parameter. Therefore, we obtain a significant qualitative improvement in the round complexity for protocols in the single input setting.

• Expanding the Class of Realizable Functionalities, and, Getting Blind Signatures. The blind signature functionality is an interesting case in the paradigm of secure computation both from theoretical as well as practical standpoints. The question of whether concurrent blind signatures (secure as per the ideal/real model simulation paradigm) exist is currently unresolved. Lindell [36, 38] showed an impossibility result for concurrent blind signature based on black-box simulation. This result has also been used as a motivation to resort to weaker security notions (such as game based security) or setup assumptions in various subsequent works (see e.g., [15, 18, 20, 31, 33, 41]). We show that a positive result for BPC directly implies a construction of concurrent blind signatures secure in the plain model as per the standard ideal/real world security notion. Prior to our work, the only known construction of concurrently secure blind signatures was according to the weaker game based security notion due to Hazay et al. [31].

  This implies that concurrent blind signatures is a “natural” example of a functionality which is impossible to realize using black-box simulation but can be securely realized using non-black box simulation in the concurrent setting.² The only previous such example known [29] was for a reactive (and arguably rather contrived) functionality. Another concrete (and related) example of a new functionality that can be directly realized using our techniques is that of a secure verifiable random function.

It would also be interesting to see what our approach yields in the plain model for different settings and security notions where the previous rewinding based approach has been useful (such as resettable computation, super-polynomial simulation, etc.). We leave that as future work.

1.2 Our Techniques

Our protocol and analysis for the concurrent secure computation is admittedly quite complex and we face a number of hurdles on the way. Below, we try to sketch the main difficulties and our ideas to circumvent them at a high level.

To construct concurrent secure computation, we roughly follow the  [21] strategy of first constructing an appropriate zero-knowledge protocol, and then “somehow compiling” a semi honest secure computation protocol using that. In our concurrent setting, in order to avoid the multiple output queries per session, we need a concurrently secure protocol for zero-knowledge with a straightline simulator. Recently, the first such protocol was given by Goyal [25] based on non-black box techniques³.

Another property of the zero-knowledge protocol which is crucial for compilation is simulation-soundness. Our first (and arguably smaller) technical hurdle is to construct a simulation-sound version of Goyal’s protocol. This is necessary because the simulator would rely on the soundness of the proofs given by the adversary while simulating the proofs where it is acting as the prover. Another issue is that in our protocol for concurrent secure computation, the adversary is allowed to choose the statement proved till a very late stage in the protocol. Hence, we need simulation-soundness to hold even when the statements to prove are being chosen adaptively by the adversary. We note that this issue is somewhat subtle to deal with. Our construction of simulation-sound concurrent zero-knowledge relies on the following ingredients: Goyal’s concurrent simulation strategy, a robust non-malleable commitment scheme [35], and a special language to be used in the universal arguments. The final construction along with a description of the main ideas is given in Sect. 3.

The next (and arguably bigger) difficulty is the following. In secure computation, the adversary receives an output in each session (this is unlike the case of zero-knowledge). It turns that it is not clear how to handle these outputs while performing non-black box simulation. Note that some such challenge is inherent in the light of the long list of general impossibility results known [5, 38]. Before we describe the challenge faced in detail, it would be helpful to recall how the non-black box techniques based on [2] work at a high level.

• Non-black Box Technique. In each session, the simulator has to commit to a program $\varPi$, which has to generate the adversary’s random string r in that session. In the transcript between the commitment to $\varPi$ and r, there may be messages of other sessions, which $\varPi$ has to regenerate. Even if the program $\varPi$ consists of the entire state of the simulator and the adversary at the point of the commitment, it runs into a problem in the case of secure computation (where the adversary is getting non-trivial output in each session).

• Key Challenge. Note that to reach from the commitment of $\varPi$ to the message r, the simulator makes use of some external information: namely the outputs it learns by querying the ideal functionality as it proceeds in the simulation. This information, however, is not available with the program $\varPi$ (since the simulator may query the ideal functionality after the program $\varPi$ was committed to). Also, note that the number of outputs learnt could be any unbounded polynomial. Hence, it is not clear how to regenerate the transcript.

The first obvious solution, which does not work, is to allow the program $\varPi$ to take inputs of unbounded length. This would allow the simulator to pass all the outputs obtained to the program $\varPi$. But now the soundness of the protocol seems to be completely compromised. On the other hand, if $\varPi$ does not receive all the outputs, it cannot regenerate the transcript!

To resolve this issue, we use the idea of “Oracle programs” due to Deng, Goyal, and Sahai [13]. The program $\varPi$, while running, is allowed to make any (polynomially unbounded) number of queries (to be answered by the simulator) as long as the response to each query is information theoretically fixed by the query. The soundness is still preserved: an adversarial prover still cannot communicate any information about the verifier’s random string r to $\varPi$. However, the program $\varPi$ can still access a potentially unbounded length string using such an “Oracle interface”.

Unfortunately, the above idea is still not sufficient for our purpose: the outputs given by the ideal functionality are not fixed given the adversary’s input in the session. Here we rely on the fact that we are only considering the ideal worlds which satisfy the bounded pseudoentropy condition. Very roughly, it is guaranteed that the entire output vector has only bounded pseudoentropy (B), given the input of the adversary. Moreover, given the adversary’s input vector, all possible output vectors are efficiently testable by the PPT algorithm $\mathcal {T}$. In other words, for every vector of queries, there is only a bounded (although potentially exponential) number of response vectors accepted by $\mathcal {T}$. We allow the program $\varPi$ to make any number of queries such that the response vector is accepted by $\mathcal {T}$. More details regarding our precise language for non-black box simulation may be found in Fig. 1. This idea allows the simulator to supply the entire output vector (learnt from the ideal functionality) to $\varPi$ while still preserving soundness. The soundness proof relies on the fact that the queries only allow for communication of up to B-bit string to $\varPi$, which is still not sufficient for communicating the string r.

Finally, there are additional challenges due to the requirement of straightline extraction. Towards that end, we rely on input indistinguishable computation introduced by Micali, Pass, and Rosen [39]. Challenges also arise with performing hybrid arguments in the setting where the code of the simulator itself is committed (because of non-black box simulation). The full construction along with the main ideas is given in Sect. 4.

Other Related Work: Though Goyal et al. [25] gave the first protocol for concurrent zero-knowledge with a straightline simulator, recently, Chung et al. [12] gave a constant round concurrent zero-knowledge protocol for uniform adversaries based on a new assumption of P-certificates, which is also straightline simulatable. Their protocol represents an exciting idea which opens an avenue for getting constant round concurrently secure computation protocols (albeit for uniform adversaries only, and, based on a new assumption). We believe that our techniques could also be applicable in constructing concurrent secure computation protocols using the protocol of [12].

2 Concurrently Secure Computation: Our Model

In this section, we begin by giving a brief sketch of our model. For formal description (building upon the model of [38]) of our model, see full version. In this work, we consider a malicious, static and probabilistic polynomial time adversary that chooses whom to corrupt before the execution of the protocol and controls the scheduling of the concurrent executions. Additionally, the adversary can choose the inputs of different sessions adaptively. We denote the security parameter by n. We give a real world/ideal world based security definition. There are k parties $Q_1, Q_2, \ldots , Q_k$, where each party may be involved in multiple sessions with possibly interchangeable roles. In the ideal world, there is a trusted party for computing the desired two-party functionality $\mathcal {F}: \{0,1\}^{r_1} \times \{0,1\}^{r_2} \rightarrow \{0,1\}^{s_1} \times \{0,1\}^{s_2}$. Let the total number of executions be $m = m(n)$. Note that there is no a-priori bound on the number of sessions m and the adversary can start any (possibly unbounded) polynomial number of sessions. On the other hand, in the real world there is no trusted party and the two parties involved in a session, say $P_1$ and $P_2$, execute a two party protocol $\varPi$ for computing $\mathcal {F}$. Our security definition requires that any adversary in the real model can be emulated by an adversary in the ideal model.

2.1 Our Result and Its Applications

As mentioned in the introduction, our main result (see Theorem 1, Sect. 1.1) is a general positive result for concurrent secure computation as long as the ideal world satisfies the bounded pseudo-entropy condition (Definition 1, Sect. 1.1).

Next, we show that our theorem not only subsumes the positive results of [24] in the single input setting but also improves the round complexity.

Comparing Our Results with [24]. In [24], Goyal showed that if the ideal world satisfies the “key technical property” (KTP), then there exists a real world protocol which securely realizes this ideal world. The key technical property, taken verbatim from [24], is as follows:

Definition 2

(Key Technical Property (Definition 3, [24])). The key technical property (KTP) of an ideal world experiment requires the existence of a PPT predictor $\mathcal {P}$ satisfying the following conditions. For all sufficiently large n, there exists a bound D such that for all adversaries and honest party inputs,

For the ideal worlds which satisfy KTP, [24] gave a $O(n^3 D^2)$ round secure protocol which realizes the functionality, where D is the parameter in Definition 2.

In our full version, we prove the following lemma:

Lemma 1

If an ideal world experiment satisfies the key technical property (Definition 2), then it also satisfies the bounded pseudoentropy condition (Definition 1).

As mentioned before, the round complexity of Goyal [24] is $O(n^3 D^2)$ which is a polynomial in security parameter n as well as D (which depends upon length of single input as well as nature of functionality). Our Theorem 1 and Lemma 1 imply a quantitative and qualitative improvement in round complexity. This leads to lower round protocols for applications like private database search, secure set intersection, computing $k^{th}$ ranked element etc. For details see the full version.

Moreover, [24] only gave a positive result for functionalities with hardness free ideal world, i.e. in the ideal world the trusted party is not required to perform any cryptographic operations. There is no such restriction in our setting. In fact, we show that blind signatures and verifiable random functions satisfy the bounded pseudoentropy condition. More interestingly, they do not satisfy the key technical property. We next describe our results for these functionalities.

Blind Signatures. Blind signatures, introduced by [11], allow users to obtain signatures on messages of their choice without revealing the message being signed to the signer (blindness property). In addition, they also need to satisfy the unforgeability property of the digital signature schemes. In this work, we give the following positive result for concurrent blind signatures.

Theorem 2

Assume the existence of collision resistant hash functions and constant-round semi-honest oblivious transfer. Then for any constant $\epsilon$, there exists a $O(n^\epsilon )$ round secure protocol which realizes the ideal world for concurrent blind signature functionality.

We prove this theorem by using unique signatures [22] as the underlying signature scheme and showing that blind signatures satisfy the bounded pseudoentropy condition when the underlying signature scheme is unique. (Note that Lindell’s black box impossibility result also holds in this setting.) A signature scheme is said to be unique if for each public key and each message, there exists at most one valid signature which verifies.

We can model blind signature as a two party computation between the signer and the user for the circuit for generating signatures. Note that the circuit will have the verification key $\mathsf {vk}$ hardcoded. At the end of the protocol, the user outputs a valid signature $\sigma$ if obtained, and signer always outputs $\bot$. Now we show that this functionality satisfies BPC for $B= 0$ and $\mathcal {T}$ algorithm which is same as the signature verification algorithm. Note that if the adversary is playing the role of the user, its output is unique and is completely determined by its input message since $\mathsf {vk}$ is fixed by the function being computed. If the adversary is playing the role of the signer, its output is always $\bot$. Hence, set S will contain only one output vector, which is information theoretically fixed by the adversary inputs and the ideal world experiment (which fixes the verification keys for all the sessions). The algorithm $\mathcal {T}$ simply verifies the user’s signatures w.r.t. corresponding $\mathsf {vk}$ and ensures that signer’s outputs are $\bot$.

Finally note that blind signatures will not satisfy the key technical property. Consider the case when the adversary is acting as the user in all the sessions. By the unforgeability property of the scheme, any PPT predictor which receives k valid input/output (message/signature) pairs cannot predict the signature on the next message with non-negligible probability. Also, note that blind signatures will not satisfy the generalized key technical property discussed in the full version [23] for the same reason.

Verifiable Random Functions. Verifiable random functions (VRFs) were introduced by Micali, Rabin, and Vadhan [40]. They combine the properties of pseudo-random functions with the verifiability property. Intuitively, they are pseudo-random functions with a public key and proofs for verification. Along with pseudo-randomness, they are required to satisfy uniqueness, i.e., given the public key, for any input x, there is a unique y which can verify. In this work, we show the following:

Theorem 3

Assume the existence of collision resistant hash functions and constant-round semi-honest oblivious transfer. Then for any constant $\epsilon$, there exists a $O(n^\epsilon )$ round concurrent real world protocol which realizes the ideal world experiment for verifiable random functions.

We again prove this theorem by showing that VRFs satisfy BPC for $B= 0$ and $\mathcal {T}$ algorithm which is same as verification algorithm. Here, we again rely on the uniqueness property. Finally, note that VRFs too will not satisfy the key technical property due to pseudo-randomness guarantee. For details see the full version.

3 Our Simulation-Sound Non-Black Box Zero-Knowledge Protocol

Constructing a family of polynomially many zero-knowledge protocols which are simulation-sound with respect to each other under (unbounded polynomially many) concurrent executions is one of the difficulties in constructing protocols for fully concurrent multi-party computation (MPC). Simulation-soundness, introduced by Sahai [48], means that the soundness of each of the proofs given by the adversary should hold even when the adversary is getting unbounded polynomial number of simulated proofs. To avoid the problem of providing multiple outputs due to a rewinding based simulator for concurrent MPC, we need to construct simulation-sound zero-knowledge protocols which are straight-line simulatable. Note that Pass [43] also gave a construction of polynomially many protocols which are concurrent zero-knowledge and simulation-sound w.r.t. each other in the restricted setting of bounded concurrency. In this work, we construct such simulation-sound zero-knowledge protocols building upon the non-black box public coin concurrent zero-knowledge protocol of Goyal [25].

First, we give a brief overview of [25]. Some of the text has been taken verbatim from [25]. One of the main technical ideas in  [25] is to have $N= n^\epsilon$ non-black box slots, for any constant $\epsilon$ (each consisting of a commitment to a machine and a verifier challenge string). Each slot is followed by a universal argument (UA) execution. Any of the UA’s in a session may be picked for simulation. If a UA is picked for simulation, to make the analysis go through, the simulator could choose of any of the previously completed slots and prefer the slots which are computationally lighter. In a UA execution, the prover proves that in one of the completed slots, the machine committed successfully outputs the verifier challenge string. Other main idea was to have encrypted executions of the UAs (using its public coin property) to hide the location of the convincing UA executions in the transcript. Finally there is an execution of a witness-indistinguishable argument of knowledge (WIAOK), where the prover proves that either the statement $x \in L$ or there exists a decryption of one of the UAs which is accepting. In the subsequent discussion, we will refer to the part of the protocol with non black box slots and encrypted UAs as the preamble phase and last phase as the wiaok phase.

Two main ideas are required to transform the above described protocol into simulation-sound zero-knowledge protocols, which can then be used to construct protocols for concurrent MPC. Firstly, observe that unless the parties have identities it is impossible to construct a simulation-sound protocol because a man-in-the-middle attack cannot be prevented. Hence, we focus on a setting where each party has a unique identity of $n$ bits. Let $\mathsf {NMCom}$ be a k-robust identity-based non-malleable commitment scheme. Now, after the preamble phase of the protocol, the prover with identity $\mathsf {id}$ gives a non-malleable commitment to the witness under its identity $\mathsf {id}$. More precisely, the prover, having witness w to $x \in L$, gives a commitment $c = \mathsf {NMCom}(w)$ under his identity $\mathsf {id}$. In the final wiaok phase, the prover proves that either there exists a w such that $c = \mathsf {NMCom}(w)$ and $w \in R_L(x)$ or one of the UA executions was convincing. We will be able to prove the simulation-soundness of our protocol using the non-malleability and k-robustness of $\mathsf {NMCom}$. Note that (as described later) our protocol will be simulation-sound even when the adversary is allowed to choose the statements to be proven adaptively till the point when he gives this non-malleable commitment.

Secondly, in our UA executions we will use a special generalized language $\varLambda$ (see Fig. 1) for the UA executions. Here, along with [13] kind of queries $\mathsf {decommit}(\cdot )$ whose response is information theoretically fixed given the query itself, we will also have a second kind of queries, which we will denote by $\mathsf {output}(\cdot )$. Note that though the responses of these queries is not information theoretically fixed, they have a bounded pseudoentropy. Next, we give some intuition about the use of these oracle queries.

Fig. 1.

Our language for zero-knowledge with non-black-box simulation

Intuition Behind the Oracle Queries $\mathsf {output}(\cdot )$ in Language $\varLambda$ . The algorithm $\mathcal {T}$ and the bound $B$ are introduced to capture the information learnt by the adversary. When only concurrent sessions of zero-knowledge are running, there is no information passed to the adversary, hence we can have $\mathcal {T}$ to reject all outputs and still be able to simulate the view of the adversary. This notion will be important for the concurrent executions of multiparty computation because the adversary learns non-trivial information from calls to the trusted party. In particular, it learns the output of the function in each session. We will use the oracle queries $\mathsf {output}(\cdot )$ to communicate the information learnt from the trusted party to the adversary in the ideal world. But still to get our positive result, we will need to bound the amount of information learnt by the adversary. The bound $B$ will be the number of bits of information passed on to the adversary. This is intuitively captured by the condition that there are only $2^B$ vectors of oracle responses which might be accepted by $\mathcal {T}$. Looking ahead, the description of $\mathcal {T}$ will depend on the functionality being computed.

Formal Protocol Description. Let $\textsc {com}(\cdot )$ denote a non-interactive perfectly binding commitment scheme. Whenever we need to be explicit about the randomness, we denote by $\textsc {com}(s;r)$ a commitment to a string s computed with randomness r. Unless stated otherwise, all commitments in the protocol are executed using this commitment scheme. Let $\mathsf {NMCom}$ be the k-robust non-malleable commitment scheme, where k is a parameter computed later. Let $\mathsf {len}= n^2 + B+ \eta$, where $B$ and $\eta$ are parameters computed later.

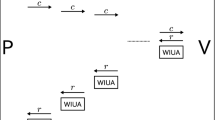
The common input to P and V is the security parameter $n$. The input to P is x in the language $L \in NP$, and a witness w to $x \in L$. Let $\mathsf {id}$ be the $n$ bit identity of the prover. Our protocol $\langle P,V\rangle$ or $c\mathcal {ZK}_\mathsf {id}$, where $\mathsf {id}$ is the identity of the prover, proceeds as follows: Parts of the protocol have been taken verbatim from [25].

• 1. The verifier V chooses a random collision resistant hash function h from a function family $\mathcal {H}$ and sends it to P.

• 2. For $i \in [n^6]$, the protocol proceeds as follows:⁴

  • The prover P computes $z_i = \textsc {com}(h(0))$ and sends it to V.

  • The verifier V selects a challenge string $r_i \mathop {\leftarrow }\limits ^{\$} \{0,1\}^{\mathsf {len}}$ and sends it to the prover P. The above two messages (consisting of the prover commitment and the verifier challenge) are referred to as a “slot”.

  • The prover P and the verifier V will now start a three-round public coin universal argument (of knowledge) [4] where P proves to V that there exists $j \le i$ , s.t., $\tau _j (= (h, z_j, r_j))$ is in the language $\varLambda$ (see Fig. 1).

    The three messages of this UA protocol are called as the first UA message, verifier UA challenge, and, the last UA message. Observe that the UA does not just refer to the slot immediately preceding it but rather has a choice of using any of the slots that have completed in the protocol so far.

  • The prover computes the first UA message and sends a commitment to this message to the verifier. The honest prover will simply commit to a random string of appropriate size.

  • The verifier now sends the UA challenge message.

  • The prover computes the last UA message and again sends only a commitment to this message to the verifier. The honest prover will simply commit to a random string of appropriate size.

• 3. The prover declares the statement $x \in L$ and commits to the witness w using the non-malleable commitment scheme $\mathsf {NMCom}$ under prover’s identity $\mathsf {id}$. Note that a cheating prover can adaptively choose the statement x here.

• 4. Finally, the prover proves the following statement to V using WIAOK

  • 1. The value committed to in Step 3 is a value w such that it is a valid witness to $x \in L$, (i.e. $w \in R_L(x)$), or

  • 2. There exists i such that the i-th UA execution was “convincing”. That is, there exists an $i \in [n^6]$ such that there exists an opening to the prover first and last UA messages such that an honest verifier would have accepted the transcript of the UA execution.

  An honest prover simply commits to the witness for $x \in L$ in Step 3 and uses the first part of the statement to complete the witness-indistinguishable argument of knowledge protocol.

  Observe that a witness to the second part of the above statement would be the opening of the commitments to the UA first and last messages. Hence, the size of the witness is fixed and depends only upon the communication complexity of the 3-round UA system being used.

Remark 1

We call the Steps 1 and 2 of the protocol as non-black box preamble, step 3 as the nmcom phase and step 4 as the wiaok phase.

Parameter k . We set k to be the round complexity of WIAOK. Hence, we set $k = 3$.

Parameter $B$ . Note that the parameter $B$ in $\mathsf {len}$ is same as the one in Fig. 1, i.e. the parameter specified for algorithm $\mathcal {T}$ in the description of language $\varLambda$.

Setting the Parameter $\eta$ . Let $\eta$ be the sum of the following: prover’s maximum communication complexity in different primitives used in the protocol described above, and communication complexity of $\mathsf {NMCom}$. More precisely, we set

$$ \eta = \mathsf {max}( c_{z}, c_{\textsc {ua}1}, c_{\textsc {ua}2}, c_{\textsc {wiaok}}, c_{\mathsf {NMCom},S}) + c_{\mathsf {NMCom},R}, $$

where $c_{z}$ is the length of the slot begin message z, $c_{\textsc {ua}1}$ is the length of the UA first message, $c_{\textsc {ua}2}$ is the length of the UA last message, $c_{\textsc {wiaok}}$ is the prover’s communication complexity in the final WIAOK execution, $c_{\mathsf {NMCom},S}$ is the sender’s communication complexity in $\mathsf {NMCom}$ and $c_{\mathsf {NMCom},R}$ is the receiver’s communication complexity in $\mathsf {NMCom}$.

Looking ahead, (very informally) while proving the simulation-soundness of the above protocol, different parts of the protocol will be taken externally and $\mathsf {NMCom}$ given by the adversary will be exposed to an external receiver, etc. Hence, different parts of the protocol will be given externally to the machine committed by the simulator as part of the string $y_1$ in $\varLambda$.

Note that the entire $\langle P, V\rangle _{}$ protocol is run w.r.t. to language $\varLambda$ having a specific algorithm $\mathcal {T}$ and bound $B$. We will prove that the security properties hold for any such $\mathcal {T}$ and bound $B$ when $\eta$ is chosen as above. Next, we prove the soundness of the protocol for any fixed value of $B$. Then we will prove the simulation-soundness of the protocol. Our ZK simulator will not use the oracle queries of the type $\mathsf {output}(\cdot )$. Later on our MPC simulator will make a non-trivial use of these oracle queries.

The proof of security of simulation-sound non-black box zero-knowledge protocol proceeds along the lines discussed in the introduction (see Sect. 1.2). We give a detailed formal proof of security in the full version.

4 Concurrently Secure Computation: Our Protocol

In this section, we will describe our protocol $\varSigma$ for concurrently secure computation for ideal world experiments which satisfy the bounded pseudoentropy condition (Definition 1) for some parameter $B\in \mathbb {N}$ and algorithm $\mathcal {T}$.

Our Construction. In order to describe our construction, we first recall the notation associated with the primitives that we use in our protocol. Let $\textsc {com}(\cdot )$ denote the commitment function of a non-interactive perfectly binding commitment scheme. Let $\langle P, V\rangle _{}$ denote the simulation-sound non-black box concurrent zero-knowledge protocol as described in Sect. 3 with length of challenge strings modified to be $\mathsf {len}= n^2 + B+ \theta$, where $\theta$ is a parameter computed later. Let $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$ be the constant round protocol for input indistinguishable computation [17, 39]. Let $\mathsf {NMCom}$ be the k-robust non-malleable commitment scheme, where k is a parameter computed later. Further, let $\langle P_\mathsf{wi },V_\mathsf{wi } \rangle$ denote a witness indistinguishable argument and let $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ denote a constant round semi-honest two party computation protocol $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ that securely computes $\mathcal {F}$ in the stand-alone setting as per the standard definition of secure computation.

Let $P_{1}$ and $P_{2}$ be two parties with inputs $x_{1}$ and $x_{2}$. Let $n$ be the security parameter. Protocol $\varSigma =\langle P_{1}, P_{2}\rangle$ proceeds as follows:

I. Non-Black Box Simulation Phase

• 1. $P_{1}\Rightarrow P_{2}:$ $P_{1}$ and $P_{2}$ engage in the preamble phase of $\langle P, V\rangle _{}$ where $P_{1}$ is the prover. Next, in the nmcom phase, $P_{1}$ creates a non-malleable commitment $\mathsf {com}_{1}$ to bit 0, i.e. $\mathsf {com}_{1}=\mathsf {NMCom}(0)$ and sends $\mathsf {com}_{1}$ to $P_{2}$. $P_{1}$ and $P_{2}$ now engage in the wiaok phase where $P_{1}$ proves that either (1) $\mathsf {com}_{1}$ is a commitment to 0 , or (2) there exists i such that the i-th UA execution in the preamble phase was “convincing".

• 2. $P_{2}\Rightarrow P_{1}:$ $P_{2}$ now acts symmetrically. $P_{1}$ and $P_{2}$ engage in the preamble phase of $\langle P, V\rangle _{}$ where $P_{2}$ is the prover. Next, $P_{2}$ creates a non-malleable commitment $\mathsf {com}_{2}$ to bit 0, i.e. $\mathsf {com}_{2}=\mathsf {NMCom}(0)$ to bit 0 and sends $\mathsf {com}_{2}$ to $P_{1}$. $P_{1}$ and $P_{2}$ now engage in the wiaok phase where $P_{2}$ proves that either (1) $\mathsf {com}_{2}$ is a commitment to 0 , or (2) there exists i such that the i-th UA execution in the preamble phase was “convincing”.

Informally speaking, the purpose of this phase is to aid the simulator in obtaining a “trapdoor” to be used during the simulation of the other two phases of the protocol.

Fig. 2.

The functionality $f_{\mathsf {com}_{1},\mathsf {com}_{2}}$

II. Input Indistinguishable Computation Phase. Intuitively speaking, in this phase, the parties “commit” to their inputs and random coins (to be used in the final secure computation phase) by engaging in a execution of $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$ for the functionality $f_{\mathsf {com}_{1},\mathsf {com}_{2}}$ described in Fig. 2. More precisely, $P_{1}$ and $P_{2}$ engage in an execution of $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$ for the functionality $f_{\mathsf {com}_{1},\mathsf {com}_{2}}$ where $P_{1}$ plays the role of $P_{1}^\mathsf{iic }$, while $P_{2}$ plays the role of $P_{2}^\mathsf{iic }$ as follows:

• 1. $P_{1}$ first samples a random string $r_{1}$ (of appropriate length, to be used as $P_{1}$’s randomness in the execution of $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ in Phase III) and uses input $z_1 = x_{1}\Vert r_{1}$ and ${\mathsf {td}}_1 = \bot$ in execution of $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$ for $f_{\mathsf {com}_{1},\mathsf {com}_{2}}$.

• 2. $P_{2}\Rightarrow P_{1}:$ $P_{2}$ now acts symmetrically. $P_{2}$ first samples a random string $r_{2}$ (of appropriate length, to be used as $P_{2}$’s randomness in the execution of $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ in Phase III) and uses input $z_2 = x_{2}\Vert r_{2}$ and ${\mathsf {td}}_2 = \bot$ in execution of $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$ for $f_{\mathsf {com}_{1},\mathsf {com}_{2}}$.

Informally speaking, the purpose of this phase is to aid the simulator in extracting the adversary’s input and randomness with the help of the trapdoor obtained in the previous phase. As we will show later, an adversary will never be able to input a valid trapdoor.

III. Final Secure Computation Phase. ⁵ In this phase, $P_{1}$ and $P_{2}$ engage in an execution of $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ where $P_{1}$ plays the role of $P_{1}^\mathsf{sh }$, while $P_{2}$ plays the role of $P_{2}^\mathsf{sh }$. Since $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ is secure only against semi-honest adversaries, parties first run a coin-flipping protocol to enforce that the coins of each party are truly random. We then compile the semi-honest $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ with $\langle P_\mathsf{wi },V_\mathsf{wi } \rangle$ to ensure correct behavior on part of each party. More precisely, after sending each protocol message, a party also gives a proof using $\langle P_\mathsf{wi },V_\mathsf{wi } \rangle$ that the message generated is consistent with the transcript so far and the input used in the previous phase. More precisely, this phase proceeds as follows:

• 1. $P_{1}\leftrightarrow P_{2}:$ $P_{1}$ samples a random string $r'_{2}$ (of same length as $r_2$) and sends it to $P_{2}$. Similarly, $P_{2}$ samples a random string $r'_{1}$ (of same length as $r_1$) and sends it to $P_{1}$. Let $r''_{1}=r_{1}\oplus r'_{1}$ and $r''_{2}=r_{2}\oplus r'_{2}$. Now, $r''_{1}$ and $r''_{2}$ are the random coins that $P_{1}$ and $P_{2}$ will use during the execution of $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$.

• 2. Let q be the number of rounds in $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$, where one round consists of a message from $P_{1}^\mathsf{sh }$ followed by a reply from $P_{2}^\mathsf{sh }$. Let transcript $T_{1,j}$ (resp., $T_{2,j}$) be defined to contain all the messages exchanged between $P_{1}^\mathsf{sh }$ and $P_{2}^\mathsf{sh }$ before the point $P_{1}^\mathsf{sh }$ (resp., $P_{2}^\mathsf{sh }$) is supposed to send a message in round j. For $j=1,\ldots ,q$:

  • (a) $P_{1}\Rightarrow P_{2}:$ Compute $\beta _{1,j} =P_{1}^\mathsf{sh }(T_{1,j},x_{1},r''_{1})$ and send it to $P_{2}$. $P_{1}$ and $P_{2}$ now engage in an execution of $\langle P_\mathsf{wi },V_\mathsf{wi } \rangle$, where $P_{1}$ proves the following statement:

    • i. either there exist values $\hat{x}_{1}$, $\hat{r}_{1}$ and $\hat{{\mathsf {td}}}_1$ such that (a) the $f_{\mathsf {com}_{1},\mathsf {com}_{2}}$ is valid with respect to the value $\hat{z}_1 = \hat{x}_{1}\Vert \hat{r}_{1}$ and $\hat{{\mathsf {td}}}_1$ and (b) $\beta _{1,j}=P_{1}^\mathsf{sh }(T_{1,j},\hat{x}_{1},\hat{r}_{1}\oplus r'_{1})$

    • ii. or, the non-malleable commitment $\mathsf {com}_{1}$ is a commitment to bit 1.

  • (b) $P_{2}\Rightarrow P_{1}:$ $P_{2}$ now acts symmetrically.

This completes the description of the protocol $\varSigma =\langle P_{1}, P_{2}\rangle$. Note that $\varPi$ consists of several instances of WI, such that the proof statement for each WI instance consists of two parts. Specifically, the second part of the statement states that prover committed to bit 1 in the non-black box simulation phase. In the sequel, we will refer to the second part of the proof statement as the trapdoor condition. Further, we will call the witness corresponding to the first part of the statement as real witness and that corresponding to the second part of the statement as the trapdoor witness.

Setting the Parameters k and $\theta$. We will set k to be the maximum round complexity among UA, WIAOK, $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$ and $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$. We will set $\theta$ to be the sum of the following: a party’s maximum communication complexity in different primitives used in the protocol described above (excluding when it acts as a verifier in $\langle P, V\rangle _{}$), and communication complexity of $\mathsf {NMCom}$. More precisely,

$$ \theta = \mathsf {max}(c_{z}, c_{\textsc {ua}1}, c_{\textsc {ua}2}, c_{\textsc {wiaok}}, c_{\textsc {wi}}, c_{\textsc {iic}}, c_{\textsc {tpc}}, c_{\mathsf {NMCom},S}) + c_{\mathsf {NMCom},R}, $$

where $c_{z}$ is the length of the message z (the slot begin message), $c_{\textsc {ua}1}$ is the length of the UA first message, $c_{\textsc {ua}2}$ is the length of the UA last message, $c_{\textsc {wiaok}}$ is the prover’s communication complexity in the final WIAOK execution, $c_{\textsc {wi}}$ is the prover’s communication complexity in WI, $c_{\textsc {iic}}$ is the communication complexity of any party in $\langle P_{1}^\mathsf{iic }, P_{2}^\mathsf{iic } \rangle$, $c_{\textsc {tpc}}$ is the total communication complexity of the semi-honest two party computation $\langle P_{1}^\mathsf{sh }, P_{2}^\mathsf{sh } \rangle$ for the functionality $\mathcal {F}$, $c_{\mathsf {NMCom},S}$ is the sender’s communication complexity in $\mathsf {NMCom}$ and $c_{\mathsf {NMCom},R}$ is the receiver’s communication complexity in $\mathsf {NMCom}$. Looking ahead, while proving the security of the above protocol, different parts of the protocol will be taken externally and $\mathsf {NMCom}$ given by the adversary will be exposed to external receiver, etc. Hence, all of these will be given externally to the machine committed by the simulator as part of the string $y_1$ in $\varLambda$.

The proof of Theorem 1 proceeds along the lines discussed in the introduction (see Sect. 1.2). For a complete proof refer to the full version of the paper.