Abstract
This chapter uses the structure graph to describe the direct interactions among the signals within a dynamical system. This graph allows to analyse the redundancies within a system, which can be exploited for fault diagnosis and control reconfiguration. A dynamical model is interpreted as a set of constraints, which leads to a bipartite graph representing the system structure. Faults indicate violations of the constraints. The analysis shows how component faults can be found by defining and utilising analytic redundancy relations.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This chapter investigates the structural properties of dynamical systems by analysing their structural model. The structural model of a system is an abstraction of the behavioural model in the sense that instead of the constraints themselves only the structure of the constraints is considered. The structure graph is a representation of the links between constraints and the variables and parameters occurring in each constraint. The structure is represented by a bipartite graph , which is independent of the nature of the constraints, and of the variables and parameter values. Structural analysis can hence describe systems described by quantitative or qualitative relations, by equations, by rules or by tabular relations. The structure graph will be shown to represent a qualitative and easy-to-obtain model of the system.
Structural analysis is based on a description of the normal behaviour of a system, through describing the normal behaviour of each component and the relation (connection) the components have to variables we wish to consider in the system. Using this approach, we will be able to diagnose whether a violation of a normal behaviour has happened. This means we are no longer bound to describe all possible faults that could happen in components of a system, as was the case with FMEA and Fault Propagation Analysis methods presented in Chap. 4. Instead, the starting point of analysis is a set of constraints, a set of nominal input–output relations, which describe the system as a set of components, the normal behaviour of each component and the topology of the components that constitute the system. Any violation of a constraint is considered to be a fault, without specifying the physical reason behind each possible fault.
The structural model will be shown to be represented by a structure graph, composed of constraints and variables. This graph is independent of the value of the system parameters, and structural properties are deducted using graph theory for graphs that are partitioned into two sets: constraints and variables. The properties of this bipartitioned graph are explored in great detail in this chapter.
In spite of their apparent simplicity, structural models provide significant information for use in fault diagnosis and fault-tolerant control. This approach is able to identify those constraints, and related components of the system, which are—or are not—monitorable, to provide calculation of residuals from the analytic redundancy relations (ARR) that exist in a system, and to find those components whose failure can be tolerated through reconfiguration.
In this chapter, structural investigations concern
-
identification of the monitorable part of the system, i.e. the subset of the system components whose faults can be detected and possibly isolated,
-
direct generation of residuals for a system that is specified by its structure graph: the behaviour described through constraints, the known and the unknown variables.
-
how analytical redundancy relations (ARRs) are calculated with ease for linear or nonlinear systems,
-
how analytical redundancy relations in structural representation are transformed to residuals in analytical form for use in fault diagnosis by algorithmic manipulations on the structure graph (matching and backtracking),
-
how to design residuals that meet specific fault diagnosis requirements, namely being insensitive to disturbances and can be structured (i.e. sensitive to certain faults and insensitive to others),
-
demonstrate structural results for active isolation of possible faults in the structure (violation of constraints) through imposing test signals on inputs to isolate an otherwise non-isolable structural defect,
-
discuss possibilities for reconfiguration to estimate and to control some variables of interest in case of sensor, actuator or system component failures.
These important properties are found by the analysis of the structure graph and its canonical decomposition. In order to introduce the canonical decomposition, matchings on a bipartite graph are first presented and their interpretation is given. Causality is introduced and adds orientation to the bipartite structure graph. Matching of unknown variables in the structure graph is then investigated and it is shown how ARRs are found among the constraints that are not needed for a particular matching. It is shown how a set of ARRs and the set of constraints through which they are calculated, lead to the important notions of structural detectability and isolability. It is also shown how ARRs generated by structural analysis by design become insensitive to unknown disturbances or to unknown parameters. Further, structural controllability is discussed and fault tolerance is investigated through analysis of the structural properties that exist for reconfiguration of a system in case of component failures. The chapter finally summarises essential design procedures based on the structural analysis methods.
2 Structural Model
2.1 Structure as a Bipartite Graph
This section introduces the structural model of a system as a bipartite graph which represents the links between a set of variables and a set of constraints . It is an abstraction of the behavioural model, because it merely describes which variables are connected by which constraints, but it does not say how these constraints look like. Hence, the structural model shows the basic features and properties of a system, which are independent of the system parameters.
Behaviour model. The behavioural model of a system is defined by a pair
where
-
\(\mathcal{Z}=\left\{ z_{1},\,z_{2},\ldots ,z_N\right\} \) is a set of variables and parameters and
-
\(\mathcal{C}=\left\{ c_{1},\,c_{2},\ldots ,c_\mathrm{M}\right\} \) is a set of constraints.
According to the granularity of the variables (quantitative, qualitative, fuzzy) and of the time (continuous, discrete), the constraints may be expressed in several different forms like algebraic and differential equations, difference equations, rules, etc.
Example 5.1
A differential-algebraic model Consider the sets
where \(\mathcal{X}_\mathrm{a}\) is the set of variables \({{\varvec{x}}}_\mathrm{a}\) that appear only in algebraic constraints, and \(\mathcal{X}_\mathrm{d}\) the set of variables \({{\varvec{x}}}_\mathrm{d}\) whose derivative obeys some differential constraints \({\varvec{g}}\). A differential-algebraic model is given by
Note that it is possible to define a separate set of variables \(\dot{{{\varvec{x}}}}_\mathrm{d}\) for the derivatives and a separate set of constraints
so that the sets of variables and constraints have to be extended:
where \(\frac{\mathrm {d}}{\mathrm {d}t}\) stands for the differential constraints (5.4) and all the constraints (5.1)–(5.3) are algebraic.
The behaviour model of a dynamical system links present and past values of its variables (for discrete time systems) or variables and their time derivatives up to a certain order (for continuous-time systems). Giving two variables the names \({{\varvec{x}}}(t)\) and \(\dot{{{\varvec{x}}}}(t)\) does not guarantee that the second one is the time derivative of the first one. This is only true thanks to the analyst’s interpretation, and this fact has to be represented, for automatic treatment, by separate constraints like (5.4). \(\square \)
Two basic assumptions express the fact that a model defined by some set of constraints is well formed. These assumptions are used in the sequel.
Assumption 5.1
-
(a)
All the constraints in \(\mathcal{C}\) are compatible.
-
(b)
All the constraints in \(\mathcal{C}\) are independent.
Assumption 5.1(a) means that the set of the constraints is associated with a sound model, namely a model whose set of solutions is not empty. In other words, the constraints do not carry any contradiction.
Assumption 5.1(b) means that the model is minimal in the sense that no constraint defines (at least locally) the same set of solutions as another one, or more generally that in \(\mathcal{C}\) there do not exist two different subsets \(\mathcal{C}'\) and \(\mathcal{C}^\mathcal{00}\) such that
holds, where \(V(\mathcal{C})\) is the set of solutions associated with the constraint set \(\mathcal{C}\). It will be seen that this assumption may or may not hold, depending on the redundancy which is present in the system.
Example 5.2
Dependent constraints Consider the two constraints
They are obviously not independent, since one has \(V(c_{1})\cap V(c_{2})=V(c_{1})\). In fact, constraint \(c_{1}\) is sufficient to describe the set of the system solutions, and one has the implication
Structure graph. The structure of a system is represented by a bipartite graph. A graph is bipartite if its set of vertices can be separated into two disjoint sets \(\mathcal{C}\) and \(\mathcal{Z}\) in such a way that every edge has one endpoint in \(\mathcal{C}\) and the other one in \(\mathcal{Z}\).
Definition 5.1
(Structural model, structure graph) The structural model of the system \(\mathcal{S}=(\mathcal{C},\,\mathcal{Z})\) is a bipartite graph
where \(\mathcal{E}\subset \mathcal{C}\times \mathcal{Z}\) is the set of edges defined as follows:
\(\mathcal{G}\) is also called the structure graph or the structure .
In the representation of a system as a pair \(\mathcal{S}=(\mathcal{C}, \mathcal{Z})\), the set \(\mathcal{C}\) includes the constraints describing the relations among the variables, whereas the vertex set \(\mathcal{C}\) of the graph \(\mathcal{G}\) includes only the names of these constraints, which are used as the names of vertices. Nevertheless, the same symbol \(\mathcal{C}\) is used in \(\mathcal{S}\) and \(\mathcal{G}\).
The bipartite graph is an undirected graph, which can be interpreted as follows: All the variables and parameters \(z_j \in \mathcal{Z}\) that are connected with a given constraint-vertex \(c_i\in \mathcal{C}\) have to satisfy the equation or rule that this constraint-vertex represents. The structure graph can be built for rather general models including models of the form of differential and algebraic equations.
In the following figures, the variable-vertices \(z_j \in \mathcal{Z}\) will be represented by circles while the constraint-vertices \(c_i \in \mathcal{C}\) will be represented by bars. Note that the edges are not oriented. The incidence matrix of the bipartite graph is used to represent the graph as a set \(\mathcal{E}\) of edges in an algebraic manner. The rows of this matrix are associated with the constraints and the columns with the variables. A “1” in the intersection of row \(c_{i}\) and column \(z_{j}\) indicates the existence of the edge \(\left( c_{i},\,z_{j}\right) \in \mathcal{E}\). For an example, cf. (5.5).
Example 5.3
Structure graph of a linear system Consider a linear system described by four constraints \(\{c_{1},\,c_{2},\,c_{3},\,c_{4}\}\) with five variables \(\left\{ x_{1},\,x_{2},\,\dot{x}_{1},\,\dot{x}_{2},\,u\right\} \) as follows:
Its structure graph has the incidence matrix

leading to the bipartite graph depicted in Fig. 5.1. \(\square \)
Example 5.4
Tank system Consider a tank system where the inflow \(q_i(t)\) is controlled via a level sensor and an electric pump and the outflow \(q_o(t)\) is realised through an output pipe (Fig. 5.2).
The system consists of the components {tank, input valve, output pipe, level sensor, level control algorithm}. A continuous-variable continuous-time model is given by the following constraints:
u is the control variable, y the sensor output, \(h_{0}\) the given set point, and r and k are given parameters. h denotes the liquid level, \(q_{i}\) and \(q_{o}\) the flow into or out of the tank. \(\alpha \) is a valve constant. Each component introduces one constraint. The separate constraint
expresses the fact that \(\dot{h}(t)\) is the derivative of the level h(t).
This behavioural model of the tank system without controller leads to the structure graph with the following incidence matrix:

Every column of the matrix corresponds to a circle-vertex and every row to a bar-vertex. The structure graph is shown in Fig. 5.3.
If the controller is introduced, the graph is extended by a new bar-vertex for \(c_{5}\) and two new circle-vertices for \(h_{0}\) and r. Furthermore, if the parameter k appearing in constraint \(c_{3}\) is considered now as an important variable (rather than a fixed given parameter like the valve constant \(\alpha \)), a circle-vertex is introduced for k and linked with \(c_{3}\). These steps lead to the following extended incidence matrix:

For simplicity, only the ones appear in this matrix and empty boxes are zero. Figure 5.4 shows the extended graph. \(\square \)
Remark 5.1
(Structural representation by digraphs) For nonlinear systems
a popular structural representation uses the directed graph (digraph), whose set of vertices is the set of the input, output and state variables and whose edges are defined by the following rules:
-
An edge exists from vertex \(x_{k}\) (resp. from vertex \(u_\mathrm{l}\)) to vertex \(x_{i}\) if and only if the state variable \(x_{k}\) (resp. the input variable \(u_\mathrm{l}\)) really occurs in function \(f_{i}\) (i.e. \(\frac{\partial f_{i}}{\partial x_{k}}\)—resp. \(\frac{\partial f_{i}}{\partial u_\mathrm{l}}\)—is not identically zero).
-
An edge exists from vertex \(x_{k}\) to vertex \(y_{j}\) if and only if the state variable \(x_{k}\) really occurs in the function \(g_{j}\).
In the digraph representation edges are interpreted as “mutual influences” between variables: an edge from \(x_{k}\) to \(x_{i}\) means that the time evolution of the derivative \(\dot{x}_{i}(t)\) depends on the time evolution of \(x_{k}(t)\). Similarly, an edge from \(x_{k}\) to \(y_{j}\) means that the time evolution of the output \(y_{j}(t)\) depends on the time evolution of the state variable \(x_{k}(t)\). In contrast to the bipartite graph, the signals \(x_i\) and \(\dot{x}_i\) are not distinguished but represented by the same vertex \(x_i\). \(\square \)
Example 5.5
Digraph of a linear system The digraph which describes the structure of the system
is shown in Fig. 5.5. Obviously, the constraints given in the behavioural model are not explicitly represented. \(\square \)
2.2 Subsystems
Instead of considering the whole set of constraints which describe the behavioural model of a system, it is sometimes convenient to consider only subsets of constraints. A subsystem is defined by the set of constraints together with the set of variables that occur in these constraints. This subsection introduces the vocabulary connected with subsets of the constraints.
The symbol 2\(^{\mathcal{C}}\) denotes the set of all the subsets of \(\mathcal{C}\) (also denoted as the power set of \(\mathcal{C}\)). Let \(\mathcal{G} = (\mathcal{C},\,\mathcal{Z},\,\mathcal{E})\) be the structure graph of the system \(\mathcal{S}=(\mathcal{C},\,\mathcal{Z})\) and Q be a mapping between a set of constraints and the set of variables used in these constraints:
Q associates with any subset \(\phi \) of constraints, the subset \(Q(\phi )\) of those variables which intervene in at least one of them. Correspondingly, the mapping R associates a set of variables with a set of constraints where these variables appear:
Definition 5.2
(Subsystem) For a system \(\mathcal{S}=(\mathcal{C}, \mathcal{Z})\), a subsystem is a pair \((\phi ,\,Q(\phi ))\) with \(\phi \in \) \(2^{\mathcal{C}}.\) The subgraph that is related with subsystem \((\phi ,\,Q(\phi ))\) represents the subsystem structure.
According to this definition, a subsystem is any subset \(\phi \) of the system constraints together with the set \(Q(\phi ) \subset \mathcal{Z}\) of related variables. There are no specific requirements on the choice of the elements in \(\phi \subseteq 2^\mathcal{C}\). Of course, only some of them are of interest in applications:
-
First, subsystems can be associated with some physical interpretation. Complex systems are often decomposed into subsystems which have a physical or a functional meaning. For example, a boiler can be decomposed into a steam generator, the instrumentation scheme and a control system. These subsystems are associated with subsets of constraints, so that the fault of one or several subsystems results in some of these constraints being changed.
-
Second, subsystems can be associated with special properties. For example, fault diagnosis is possible only for subsystems which exhibit redundancy properties as shown later.
Example 5.6
Q and R mappings for the tank example Consider the following incidence matrix for the single-tank system.

Examples for the mappings Q and R are:
Hence, the pair
is a subsystem and its structure is described by the subgraph with the incidence matrix

2.3 Structural Properties
Two systems which have the same structure are said to be structurally equivalent. Consequently, the structure graph \(\mathcal{G}\) defines a class \(\mathcal{S}(\mathcal{G})\) of structurally equivalent systems. In particular, systems which only differ by the value of their parameters belong to the same class.
The class of systems defined by the structure graph is large, because the structure is independent of the form in which the constraints are expressed. For example, suppose that the level sensor in the single-tank system does not provide an analog output but a quantised one. Then its operation is described by the following table, where \(\alpha ,\,\beta ,\,\gamma \) are given constants:

For structural considerations the important information included in this table is the fact that the sensor reading y and the tank level h are connected and, hence, in the structure graph there exist edges between the variable-vertices for y and h towards the constraint-vertex for the sensor. This fact is obviously independent of the quantisation. Hence, the structure of the sensor is exactly the same for analog and for symbolic sensor readings.
Structural properties are properties of the system class \(\mathcal{S}(\mathcal{G})\) rather than of a single system \(\varSigma \in \mathcal{S}(\mathcal{G})\), because they are properties of the graph \(\mathcal{G}\). The relation between the results of the structural analysis and the results of a numerical analysis of a single system is depicted in Fig. 5.6. The arrows from the left to the right part of the figure show the abstraction process, which leads from the numerical values of the system parameters to the links among the variables represented by the structure of the constraints. Accordingly, the properties of the system class are abstractions of properties of the (numerical) systems that are structurally equivalent.
As the aim of structural analysis is to elaborate properties that belong to the graph \(\mathcal{G}\), but are relevant for all or at least for most of the systems \(\varSigma \in \mathcal{S}(\mathcal{G})\), the analysis usually concerns two similar properties P and \(P'\), where P is a property defined for a single system \(\varSigma \) and \(P'\) is a property of the graph \(\mathcal{G}\). With respect to the figure, one has to ensure that the “inverse abstraction” process from the properties of the class \(\mathcal{S}(\mathcal{G})\) towards the single system \(\varSigma \) is known. For most of the structural properties \(P'\) that are investigated in structural analysis there exists a property P such that the following relation holds:
If the system \(\varSigma \in \mathcal{S}(\mathcal{G})\) has the property P, then the system class \(\mathcal{S}(\mathcal{G})\) has the property \(P'\).
Hence, the requirement that the graph \(\mathcal{G}\) possesses the property \(P'\) is a necessary condition for the system \(\varSigma \in \mathcal{S}(\mathcal{G})\) to have the property P.
Example 5.7
Observability and structural observability Consider the static system
for which the internal variables \(x_1\) and \(x_2\) should be determined for measured outputs \(y_1\) and \(y_2\). Every single system \(\varSigma \) is characterised by Eq. (5.10) together with a parameter vector  . The system \(\varSigma \) is said to be observable if the model (5.10) can be used to determine \(x_1\) and \(x_2\) in terms of \(y_1\) and \(y_2\), which is obviously the case if and only if the matrix \({{\varvec{A}}}({{\varvec{\theta }}})\) is invertible. Hence,
. The system \(\varSigma \) is said to be observable if the model (5.10) can be used to determine \(x_1\) and \(x_2\) in terms of \(y_1\) and \(y_2\), which is obviously the case if and only if the matrix \({{\varvec{A}}}({{\varvec{\theta }}})\) is invertible. Hence,
is a necessary and sufficient condition for the observability of the system \(\varSigma \), where n is the number of unknown variables to be observed. For observability analysis, which concerns the left arrow “Numerical analysis” in Fig. 5.6, Eq. (5.11) has to be checked.
On the other hand, a structural analysis abstracts from the parameter values and uses a graph with the incidence matrix

where \(c_1\) and \(c_2\) denote the first and the second equation in (5.10) and the symbol \([\;\cdot \;]\) denotes the qualitative value of the matrix element considered. The qualitative value \([a({{\varvec{\theta }}})]\) is equal to 1 if the argument \(a({{\varvec{\theta }}})\) does not vanish for all parameter vectors  ; otherwise it is zero.
; otherwise it is zero.
The system class \(\mathcal{S}(\mathcal{G})\) includes all systems \(\varSigma \) described by Eq. (5.10) for arbitrary parameter vectors that are consistent with the entries of the matrix \({{\varvec{E}}}\). Hence, if \({{\varvec{E}}}\) has a vanishing element, the corresponding element of the matrix \({{\varvec{A}}}\) vanishes for all \(\varSigma \in \mathcal{S}(\mathcal{G})\). This system class is said to be structurally observable if at least one system \(\varSigma \in \mathcal{S}(\mathcal{G})\) exists that is observable (according to the definition given above). That is, there has to exist at least one parameter vector \({{\varvec{\theta }}}\) for which the relation \(\det {{\varvec{A}}}\not =0\) holds. This is obviously the case if and only if the structural rank of the matrix \({{\varvec{E}}}\) is two or, more generally,
The structural rank of a matrix \({{\varvec{E}}}\) is the maximum number of non-zero elements in different rows and columns of \({{\varvec{E}}}\). The arrow “structural analysis” in Fig. 5.6 means to test Eq. (5.12).
The important aspect of this example is the fact that for the single system the notion of observability and for a class of systems the notion of structural observability has been defined in such a way that a system has to belong to a structurally observable system class if the system should be observable. Both definitions are closely related to one another, but these properties are not the same! The structural observability of the system class, which can be tested by the graph, is a necessary condition for the observability of the system.
However, to belong to a structurally observable system class is not sufficient for a system to be observable. Think of the system \(\varSigma \) with \(a=b=c=d=1\). This system violates the condition for observability (as \(\det {{\varvec{A}}}= 0\)) although it belongs to a structurally observable system class. An important aspect of the structural investigations in the next sections concerns the relations among these properties, in particular, the elaboration of conditions under which the structural properties of a system class do not transfer to the (numerical) properties of every single system of this class. For the observability properties considered in this example, this condition is given by
which means that the rank of a matrix cannot exceed the structural rank of the graph that represents the structure of this matrix. \(\square \)
An important question asks under what conditions the structural property \(P'\) of \(\mathcal{S}(\mathcal{G})\) does not transfer to the numerical property P of \(\varSigma \in \mathcal{S}(\mathcal{G})\). Two cases can be distinguished with respect to the example above:
-
1.
In the first case, parameters \({{\varvec{\theta }}}\) always satisfy the relation \(\det {{\varvec{A}}}= 0\) and thus the structural property is never translated into an actual property. This situation is excluded in structural analysis, because the parameters are always supposed to be independent, which means that they span the whole space
 . As an algebraic relation like \(\det {{\varvec{A}}}= 0\) defines a manifold in the parameter space
. As an algebraic relation like \(\det {{\varvec{A}}}= 0\) defines a manifold in the parameter space  , it cannot be satisfied by all
, it cannot be satisfied by all  . Otherwise, the equation \(\det {{\varvec{A}}}= 0\) should have been included in the system model.
. Otherwise, the equation \(\det {{\varvec{A}}}= 0\) should have been included in the system model. -
2.
In the second case, the parameters \({{\varvec{\theta }}}\) of the system under investigation satisfy the relation \(\det {{\varvec{A}}}= 0\), and thus the structural property is not translated into an actual property for that particular system. Structural analysis, however, implies the interesting conclusion that under mild assumptions on the functions \(a,\,b,\,c,\,d\) there always exists a parameter vector \(\tilde{{{\varvec{\theta }}}}\) in the neighbourhood of \({{\varvec{\theta }}}\) for which the actual property coincides with the structural one.
In conclusion, (numerical) properties P can only occur if the corresponding structural properties \(P'\) are satisfied. They can certainly not be true if the structural properties are not satisfied. Furthermore:
Structural properties are properties which hold for actual systems almost everywhere in the space of their independent parameters.
Hence, it is extremely unlikely that the system under consideration has a parameter vector for which a structural property does not imply the corresponding numerical property.
2.4 Known and Unknown Variables
The system variables and parameters can be classified as known and unknown ones. The system inputs and outputs are examples of variables that are usually known. Similarly, model parameters which have been previously identified are known. Unknown variables are not directly measured, though there might exist some way to compute their value from the values of known ones. In the tank example, the last four columns of the incidence matrix \(\left\{ h,\,\dot{h},\,q_{i},\,q_{o}\right\} \) correspond to unknown variables, while the first five ones correspond to known variables and parameters \(\left\{ u,\,y,\,h_{0},\,r,\,k\right\} \).
Following that decomposition, the set of the variables is partitioned into
where \(\mathcal{K}\) is the subset of the known variables and parameters and \(\mathcal{X}\) is the subset of the unknown ones. Similarly, the set of constraints is partitioned into
where \(\mathcal{C}_{\mathcal{K}}\) is the subset of those constraints which link only known variables and \(\mathcal{C}_{\mathcal{X}}\) includes those constraints in which at least one unknown variable appears. \(\mathcal{C}_{\mathcal{K}}\) is the largest subset of constraints such that \( Q(\mathcal{C}_{\mathcal{K}})\,\subseteq \, \mathcal{K}\). Obviously, the relations defining control algorithms belong to \(\mathcal{C}_{\mathcal{K}}\) because they introduce constraints among the sensor output, the control objectives (set points, tracking references, final states) and the control input, which are all known variables.
According to the partition of \(\mathcal{Z}\) and \(\mathcal{C}\), the graph \(\mathcal{G}=(\mathcal{C},\,\mathcal{Z},\,\mathcal{E})\) can be decomposed into two subgraphs which correspond to the two subsystems \((\mathcal{C}_{\mathcal{K}},\,Q(\mathcal{C}_{\mathcal{K}}))\) and \((\mathcal{C}_{\mathcal{X}},\,\mathcal{Z})\). The behavioural model of the subsystem \((\mathcal{C}_{\mathcal{K}},\,Q(\mathcal{C}_{\mathcal{K}}))\) involves only known variables. In some further developments, it will be of interest to focus on the subsystem \((\mathcal{C}_{\mathcal{X}},\,\mathcal{Z})\) which leads to the reduced structure graph . This graph includes only those constraints that refer to at least one unknown variable \(z_{i}\in \mathcal{X}\).
A fundamental question of fault diagnosis concerns the determination of unknown variables from known variables by means of constraints. The question whether this is possible or not depends only upon the structure of the subgraph \((\mathcal{C}_{\mathcal{X}},\,\mathcal{X},\,\mathcal{E}_{\mathcal{X}})\) that results from the complete structure graph \(\mathcal{G}\) by deleting all known variables \(z_{i}\in \mathcal{K}\) together with the corresponding edges. Therefore, in all further examples of structure graphs the known variables are marked grey.
Example 5.8
Analysis of the structure graph of the tank system Consider the tank, whose structure graph is given in Fig. 5.4. Assume that the input u and the output y are known signals and, furthermore, \(h_0\), r and k are known parameters. Then the decomposition of the variable set
into set of known and unknown variables yields the sets
By selecting all constraints whose variables are all in the set \(\mathcal{K}\), the set \(\mathcal{C}_{\mathcal{K}}=\{c_{5}\}\) is obtained. All other constraints are comprised in the set
Obviously, \(Q(\mathcal{C}_\mathcal{K}) \subseteq \mathcal{K}\) and
hold. The incidence matrix of the structure graph can be reorganised as follows:

The known variables are in the left columns and the constraint that refers merely to known variables in the first row. The reduced structure graph which corresponds to the subsystem \((\mathcal{C}_\mathcal{X},\, \mathcal{Z})\) is given by the lower part of the incidence matrix. As the variables \(h_0\) and r do not appear in this part of the matrix, their columns are deleted. Hence, the reduced structure graph has the incidence matrix:

The reduced graph is shown in Fig. 5.7a.
For diagnosis, another decomposition of the variables into known and unknown ones is used. The parameters like k, \(h_0\) and r are assumed to be fixed and, hence, ignored in the structure graph. The remaining variables represent signals, some of which are measured and the others are unknown. Hence, for the tank system the fixed parameter k is deleted from the structure graph, which results in the following incidence matrix and in the graph depicted in Fig. 5.7b:

The diagnosis problem for the tank system can be posed as the problem to decide whether the “grey signals” u and y are consistent with the model whose structure is shown in Fig. 5.7b. \(\square \)
3 Matching in Bipartite Graphs
The basic tool for the structural analysis is the concept of matching in bipartite graphs, which is introduced in this section. In loose terms, a matching is a causal assignment which associates with every unknown system variable a constraint that can be used to determine the variable. Unknown variables which do not appear in a matching cannot be calculated. Variables which can be matched in several ways can be determined in different (redundant) ways. The last situation provides a means for fault detection and for reconfiguration.
3.1 Definitions
Matching is a general notion that has been introduced for bipartite graphs. It is introduced here in general terms for bipartite graphs \(\mathcal{G} = (\mathcal{C},\,\mathcal{Z},\,\mathcal{E})\), but illustrated for structure graphs of dynamical systems.
Edges of the graph \(\mathcal{G}\) are said to be disjoint if they have no vertex in common (neither in \(\mathcal{C}\) nor in \(\mathcal{Z}\)).
Definition 5.3
(Matching) A matching \(\mathcal{M} \subseteq \mathcal{E}\) is a set of disjoint edges of a bipartite graph \(\mathcal{G}\).
In general, different matchings can be defined on a given bipartite graph as illustrated in Fig. 5.8 by the bold edges. These matchings are given by the following set of disjoint edges:
The examples show that a set \(\mathcal{M}\) of edges is called matching even if it does not include a maximum number of disjoint edges. If it does, it is said to be a maximum matching.
A maximum matching is hence a matching such that no edge of the graph \(\mathcal{G}\) can be added without violating the requirement that the edges have to be disjoint. Since the set of matchings \({{\varvec{M}}}\) is only partially ordered, it follows that there is in general more than one maximum matching. The “size” of a matching \(\mathcal{M}\) is its cardinality \(|\mathcal{M}|\). In general, the relation
holds. The maximum cardinality over the set of matchings is called the matching number and is denoted by
In the incidence matrix, a matching is represented by selecting at most one “1” in each row and in each column and marking it by “①”. Each ① represents an edge of the matching. No other edge should contain the same variable (thus it is the only one in the row) or the same constraint (it is the only one in the column). The set \({{\varvec{M}}}\) of all matchings of a graph is a subset of 2\(^\mathcal{E}\).
Structural analysis deals with matchings that include all vertices \(c \in \mathcal{C}\) or all vertices \(z \in \mathcal{Z}\).
Definition 5.4
(Complete matching) A matching is called complete with respect to \(\mathcal{C}\) if \(\left| \mathcal{M} \right| =\left| \mathcal{C}\right| \) holds. A matching is called complete with respect to \(\mathcal{Z}\) if \(\left| \mathcal{M}\right| =\left| \mathcal{Z}\right| \) holds.
For a matching \(\mathcal{M}\) that is complete with respect to \(\mathcal{C}\), each constraint belongs to exactly one edge of the matching:
Similarly, for a matching that is complete with respect to \(\mathcal{Z}\), every variable belongs to an edge:
Structural analysis is mainly concerned with \(\mathcal{Z}\)-complete matchings, because such matchings show a way how to determine all unknown variables of the system.
It is useful to define matchings, maximum matchings and complete matchings by considering either the whole structure of the system or only subgraphs which refer to subsets of the constraint set and the variable set. Since only unknown variables in \(\mathcal X\) need be determined by a constraint, variables in \(\mathcal K\) like control input and measurements are already known, the matching can be accomplished for the reduced structure graph containing all unknown variables rather than for the whole structure graph. As the incidence matrices and the graphical representations are given for the complete graph, and since backtracking to known variables is needed at a later stage in order to obtain residuals, matchings are preferably done using the complete structure graph, but we can illustrate some properties of matching by considering the reduced structure graph.
Example 5.9
Matchings on the reduced structure graph of the tank system To illustrate the notion of maximum and complete matchings, consider the reduced structure graph of the single-tank system. Only the unknown signals and the constraints among them are concerned with. The edges of a matching are identified by a thick line in the drawings and by “①” in the incidence matrices.

As in the matchings unknown variables are associated with a constraint by means of which they can be determined, an intuitive graphical representation of the matchings is given in Fig. 5.9 where the constraints are drawn on the left-hand side and the variables on the right-hand side. The thick edges indicate the matching. The graphs are the same as in Fig. 5.7b.
Figure 5.9a shows an incomplete matching. It is not complete with respect to the constraints because constraints \(c_{2} \) and \(c_{4}\) are not matched, nor is it complete with respect to the variables because \(q_\mathrm{o}\) is not matched. However, no edge can be added to the matching without violating Definition 5.3.
Two complete matchings with respect to the set of unknown variables are shown in Fig. 5.9b, c. There is no matching that is complete with respect to \(\mathcal{C}_\mathcal{X}\), because the number of constraints is larger than the number of variables. Note that it is not guaranteed for the structure graphs that a complete matching exists, neither with respect to \(\mathcal{C}_\mathcal{X}\) nor with respect to \(\mathcal{X}\). \(\square \)
3.2 Oriented Graph Associated with a Matching
Defining a matching on a structure graph introduces some orientations of the edges which, until now, were undirected. Constraints which appear in the system description have no direction, because all variables have the same status. For example, the tank constraint
can be used to compute any of the three variables whenever the two other variables are known. It is written in the non-oriented form to stress that the constraint itself has no preference for any of the three variables. Once a matching is chosen, this symmetry is broken, because each matched constraint is now associated with one matched variable and some non-matched ones.
For a given constraint, matched and non-matched variables are identified in the graph incidence matrix by ① or 1, respectively. For example, according to the matching in Fig. 5.9a, the constraint \(c_1\) described by Eq. (5.13) is used to compute \(q_{i}(t)\). This interpretation of a matching as a set of constraints that can be used to determine the value of unknown variables is valid if there exists an order, in which the constraints can be used for such a calculation. However, a matching may result in an “algebraic loop” (Fig. 5.15), which will be discussed in more detail later, where several constraints together define the value of a set of variables. Then the interpretation of a matching as a correspondence between unknown variables and constraints that can be used to determine the variables is valid only for the set of variables and the set of constraints rather than for single variables and single constraints.
In the graphical representation, the unsymmetries associated with a matching are represented by transforming the originally non-oriented edges into oriented ones. Since some constraints might not be matched, the following rules are applied:
-
Matched constraints: The edges adjacent to a matched constraint are provided with an orientation
-
from the non-matched (input) variables towards the constraint,
-
from the constraint towards the matched (output) variable (Fig. 5.10a).
-
-
Non-matched constraints: All the variables are considered as inputs and, hence, all edges are oriented from the variables to the constraint (Fig. 5.10b).
Matched (a) and a non-matched constraint (5.13) (b)
To understand the reason for these rules, consider a matching \(\mathcal{M}\) and choose an edge \((c,\,x)\in \mathcal{M}\). Then the variable x can be considered as the output of the constraint c while the other variables appearing in the set \(Q(c)\backslash \{x\}\) are the inputs.Footnote 1 The interpretation is that the matching represents some causality assignment by which the constraint c is used to compute the variable x assuming the other variables to be known. An explicit representation of the constraint c that can be used to determine x is denoted by
For non-matched constraints, all variables are considered as inputs and no variable of Q(c) can be considered as an output. Hence, the constraint can be written in the form
like Eq. (5.13). If the zero on the right-hand side is considered as output, the constraint can be associated with a ZERO vertex like in Fig. 5.10b. Using no label at all is considered as an implicit ZERO label.
Example 5.10
Determination of unknown variables of the tank system For the single-tank system, the reduced graph shown in Fig. 5.7b and the three matchings shown in Fig. 5.9 yield the oriented graphs depicted in Fig. 5.11. The directed edges show how the internal variables \(q_i, q_o, h\) and \(\dot{h}\) can be determined for known values of u and y.
As Matching 1 is incomplete, the unknown variable \(q_{o}\) cannot be computed as shown in the graph. Matchings 2 and 3 are complete with respect to \(\mathcal{X}\) but incomplete with respect to \(\mathcal{C}_\mathcal{X}\). The non-matched constraint \(c_{1}\) or \(c_{4}\), respectively, leads to a ZERO output, that is, they have to hold for the variables \(q_i\) and \(\dot{h}\) or h and y that have been determined by other constraints or have been measured, respectively. \(\square \)
Note that subgraphs whose input and output nodes are all known provide the system input–output relations. By using Matching 2 in Fig. 5.11 the two following input–output relations are found. The first one is provided by the constraint \(c_{5}\), which links only known variables and is, therefore, deleted when drawing the reduced graph. The second one results from the non-matched constraint \(c_{1}\)
where \(\gamma _{i}(z)\) denotes the output of constraint \(c_{i}\) for the input z.
Alternated chains and reachability. The oriented graph that is obtained from the causal interpretation of the structure graph with a matching has the following property: Any existing path between two nodes (variables or constraints) alternates successively variables and constraints nodes. Such a path is called an alternated chain . Its length is the number of constraints that are crossed along the path. Note that if a non-matched constraint belongs to an alternated chain, the chain ends with the ZERO variable that is associated with the non-matched constraint.
Alternated chains can be used to define the notion of reachability.
Definition 5.5
(Reachability) A variable \(z_{2}\) is reachable from a variable \(z_{1}\) if there exists an alternated chain from \(z_{1}\) to \(z_{2}\). A variable \(z_{2}\) is reachable from a subset \(\chi \subseteq \mathcal{Z}\backslash \left\{ z_{2}\right\} \) of variables if there exists some variable \(z_{1}\in \chi \) such that \(z_{2}\) is reachable from \(z_{1}\). A subset \(\mathcal{Z}_{2}\) of variables is reachable from a subset \(\mathcal{Z}_{1}\) of variables if any variable of \(\mathcal{Z}_{2}\) is reachable from some variable of \(\mathcal{Z}_{1}.\)
Example 5.11
Alternated chains in the tank system Alternated chains associated with the oriented graph of the tank system are the following:
It can be seen that any variable of the set \(\left\{ q_{i},\,q_{o},\,h,\,\dot{h}\right\} \) is reachable from y. \(\square \)
3.3 Causal Interpretation of Oriented Structure Graphs
The aim of this subsection is to discuss the causal interpretation of the oriented bipartite graph associated with a matching.
As stated above, selecting a pair \((c,\,z)\) to belong to a matching implies a causality assignment, by which the constraint c is used to compute the variable z, assuming the other variables to be known. The oriented bipartite graph which results from a causality assignment is named a causal graph . Causal graphs are used in qualitative reasoning, alarm filtering or in providing the computation chain needed for the numerical or formal determination of some variables of interest, as shown by the above interpretation. Although this interpretation is straightforward for simple algebraic constraints, it has to be considered more carefully when strongly coupled subgraphs or differential constraints are present. The following paragraphs deal with these situations.
Algebraic constraints. Let \(c\in \mathcal{C}\) be an algebraic constraint, Q(c) the set of the variables occurring in c and \(n_{c}=\) \(\left| Q(c)\right| \). In the structural analysis, the following assumption is made:
Assumption 5.2
Any algebraic constraint \(c\in \mathcal{C}\) defines a manifold of dimension \(n_{c}-1\) in the space of the variables Q(c).
Since the constraint has to be satisfied at any time t, the variables of the set Q(c) are not independent of each other. Assumption 5.2 means that only \(n_{c}-1\) variables can be chosen arbitrarily while the remaining variable is given by the constraint c. Hence, there is at least one variable \(z\in Q(c)\) such that \(\frac{\partial c}{\partial z}\ne 0\) holds almost everywhere in the space of the variables Q(c).Footnote 2 Therefore, from the implicit function theorem , its value can be deduced (at least locally) from the constraint c and the values of the \(n_{c}-1\) other variables. This is exactly the causal interpretation of matching the variable z with constraint c. Stated differently, the constraint c decreases by one the degrees of freedom associated with the variables Q(c).
Example 5.12
Algebraic constraints Consider the constraint
where \(x_{1}\) and \(x_{2}\) are two unknowns, \(a_{1}\) and \(b_{1}\) are parameters, and \(y_{1}\) is known. This constraint obviously defines a one-dimensional surface in the space of all vectors \((x_{1},x_{2})^\mathrm{T}\). Thus only one degree of freedom is left because only one of the unknowns can be chosen arbitrarily, the possible value(s) of the other one being deduced from (5.14).
The set \(Q(c_1)\) of variables is given by
because, for example,
holds, which illustrates the use of the derivative \(\frac{\partial c}{\partial z}\) used above.
Note that the structural point of view considers the most general case of any pair of parameters \(a_{1}\) and \(b_{1}.\) Particular cases result if \(a_{1}\) or \(b_{1}\) equals to zero, where Eq. (5.14) would still define a one-dimensional manifold, or if \(a_{1}\) and \(b_{1}\) both equal to zero. In the latter case \(c_{1}\) would not define a one-dimensional manifold when \(y_{1}=0\), because any point \((x_{1},\,x_{2})^\mathrm{T}\) in the two-dimensional space would satisfy the constraint, and there would be no solution when \(y_{1}\ne 0\). \(\square \)
The fact that at least one variable can be matched in a given constraint under the causal interpretation does not mean that any variable has this property. An obvious situation in which \((c,\,x)\) cannot be matched is when c is not invertible with respect to x. The constraint shown in Fig. 5.12 defines a manifold of dimension 1 in  , and it is always possible to compute \(x_{2}\) once \(x_{1}\) is given. Matching \(x_{2}\) with this constraint can obviously be interpreted as explained above. However, the interpretation does not apply to the matching of \(x_{1}\), because \(\frac{\partial c}{\partial x_{1}}\) is not different from zero almost everywhere, thus, the constraint c cannot be used to compute \(x_{1}\) whatever be the value of \(x_{2}\).
, and it is always possible to compute \(x_{2}\) once \(x_{1}\) is given. Matching \(x_{2}\) with this constraint can obviously be interpreted as explained above. However, the interpretation does not apply to the matching of \(x_{1}\), because \(\frac{\partial c}{\partial x_{1}}\) is not different from zero almost everywhere, thus, the constraint c cannot be used to compute \(x_{1}\) whatever be the value of \(x_{2}\).
Differential constraints. The case of differential constraints has to be considered carefully. Differential constraints can always be represented as
which means that the functions \(x_{1}(t)\) and \(x_{2}(t)\) cannot be chosen independently of one other. This differential constraint has two possible matchings:
-
If the trajectory \(x_{1}(t)\) is known, its derivative can always be computed (from an analytical point of view, derivatives are here supposed to exist, and from a numerical point of view, there might be problems rised by the presence of noise, which are not considered here). It follows that the constraint can always be matched for \(x_{2}\) which is then uniquely defined. This is called derivative causality.
-
If, on the other hand, \(x_{2}(t)\) is known, matching this constraint for \(x_{1}\) (which is called integral causality ) leads to the computation
$$\begin{aligned} x_{1}(t)=x_{1}(0)+\int _{0}^t x_{2}(\sigma )\, \mathrm {d}\sigma , \end{aligned}$$(5.16)which does not determine \(x_{1}(t)\) uniquely, unless the initial condition \(x_{1}(0)\) is known.
Let \((x_{1}(t),\,x_{2}(t))^\mathrm{T}\) be two functions which satisfy the constraint d. Then, any linear combination \((x_{1}(t)+\alpha ,\,x_{2}(t))^\mathrm{T},\) where \(\alpha \) is any constant function, also satisfies the constraint d. Thus, computing \(x_{1}\) from constraint d may be possible or impossible, depending on the context. Initial values are known in a simulation context, since they are under the control of the user, but this is generally not true in a fault diagnosis context. Hence, the use of integral causality needs to be carefully considered or just avoided.
Remark 5.2
(Consequences for residual generation) Parity space or identification-based residual generation approaches aim at eliminating the unknown initial values by using the system input–output relations which are obtained through derivative causality. The observer-based approaches use integral causality by implementing an auxiliary system—the observer—which provides results that are (asymptotically) independent of the estimate of the initial state. \(\square \)
In summary, different cases have to be considered as far as the counterpart of Assumption 5.2 is concerned stating that a differential constraint (5.15) defines a manifold of dimension \(n_c-1\) in the space of the variables Q(c):
-
If \(x_{1}(t)\) is known, \(x_{2}(t)\) can be matched with constraint d which leads to differential causality. This provides a unique result for \(x_2(t)\). Assumption 5.2 is satisfied since constraint d leaves only one degree of freedom in the determination of \((x_{1}(t),\,x_{2}(t))\).
-
If \(x_{2}(t)\) and the initial value \(x_{1}(0)\) are known, \(x_{1}(t) \) can be matched with constraint d using integral causality. This situation leads to a unique result obtained from Eq. (5.16). Assumption 5.2 is satisfied since constraint d leaves only one degree of freedom in the determination of \((x_{1}(t),\,x_{2}(t))\).
-
If only \(x_{2}(t)\) is known, Assumption 5.2 is not satisfied, because whatever matching is used, two degrees of freedom (the constant function \(\alpha \), and the input function \(x_{2}(t)\)) remain for the determination of \((x_{1}(t),\,x_{2}(t))\).
Direction of calculability in the structure graph. To show direction of calculability (causality) in a structure graph, the symbol \(\mathbf{x}\) is used in position (i, j) indicates that the variable in column j cannot be calculated from the constraint in row i. This is illustrated in Example 5.14 where h cannot be calculated from \(c_6\).
Example 5.13
First-order system A model whose solution exists but is not unique, as the result of Assumption 5.2 being not satisfied, is given by the following single-input first-order system:
Constraint \(c_{1}\) is algebraic and expresses the fact that the vector \((x_{1},\,x_{2})^\mathrm{T}\) lives in a linear manifold of dimension one for every known input u. Constraint \(c_{2}\) does not allow to decrease the dimension of the unknown vector. If \(x_{1}\) were known (which is not the case), one could compute its derivative \(x_{2}\), but the knowledge of \(x_{2}\) (which could be obtained as a function of \(x_{1}\) and u in constraint \(c_{1}\)) is of no help to compute \(x_{1}\) because one should proceed by integration and the initial value \(x_{1}(0)\) is unknown. \(\square \)
Example 5.14
Derivative causality in the tank system Consider the following matching in the tank structural model.

Although it is complete with respect to the variables \(\left\{ h,\,\dot{h},\,q_{i},\,q_{o}\right\} \), it cannot be used for the computation of these variables because it introduces an integral causality, where h should be computed from \(\dot{h}\) by constraint \(c_{6}\), while its initial value is not known because constraint \(c_{4}\) is not matched.
Derivative causality can be forced, if necessary. To represent this situation, the symbol \(\mathbf{x}\) is used, which forbids integral matchings. The previous matching will not be obtained if the tank structural model is written as

where \(\mathbf{x}\) means that although there is an edge between \(c_{6}\) and h, h cannot be matched with \(c_{6}\). Instead, \(c_{6}\) is used to match \(\dot{h}\). \(\square \)
Strongly connected subgraphs. In the oriented graph associated with a matching, strongly connected parts may occur for which the stepwise causal interpretation does not lead to a sequence of calculations of the unknown variables, but another approach is needed to obtain a matching. A subset of vertices is said to be strongly connected if there exists a path between any pair of vertices belonging to this subset.
Strongly connected subgraphs are structures within the graph, which consist of constraints and unknown variables that need be solved simultaneously.
The causal interpretation of a strongly connected subgraph is that the constraints and variables belonging to the subgraph can be matched when all the other variables (not matched in the strongly connected subgraphs) are known. Suppose that \(n_\mathrm{v}\) variables are constrained by a subsystem of \(n_\mathrm{l}\) constraints, and there is a matching such that they form a cyclic structure (loop). Then, \(n_\mathrm{l}\) variables are internal (matched within the loop), and \(n_\mathrm{v}-n_\mathrm{l}\) variables are external (not matched within the strongly connected subgraph).
An example of strongly connected constraints are three linear equations with two variables and both variables enter into each of the equations. Since there is no equation (constraint) with only one unknown variable, two of the equations need be solved simultaneously to determine the two unknowns. Alternatively, one constraint is chosen to express one of the variables by the other, and this result is inserted in one of the other constraints to solve for the second variable.
In more general terms, in structural analysis, an algebraic loop is always supposed to have a unique solution (more precisely: a finite number of solutions), which in the space of unknown variables corresponds to the intersection of \(n_\mathrm{l}\) manifolds of dimension \(n_\mathrm{l}-1\), if the external variables are known (by Assumption 5.2). The loop is associated with a subset of \(n_\mathrm{l}\) constraints that is written here as vector equation
where \({{\varvec{x}}}_\mathrm{l}\) and \({{\varvec{x}}}_\mathrm{e}\) are the vectors of the internal and the known external variables, and each component of \({{\varvec{x}}}_\mathrm{l}\) is matched with one constraint in \({\varvec{h}}_\mathrm{l}\).
It is worth noticing that the interpretation associated with causality in single constraints is not directly extendable to strongly connected subgraphs, as shown by the following example:
Example 5.15
Non-invertible constraints Consider the non-invertible constraint from Example 5.12 and suppose now that there are two constraints \(\left\{ c_{1},\,c_{2}\right\} \) of the same form, but with different parameters. The incidence matrix of the structure graph of this system is

A complete matching is given by

The matching illustrated in Fig. 5.13 of \(x_{1}\) with \(c_{1}\) is obtained by choosing the variable that should be computed from one specific constraint.
The correct interpretation comes from the fact that each constraint defines a (different) manifold dimension one in  , and that, in general, such two manifolds intersect in a finite number of points. To get no solution at all would be a particular case (which would not satisfy Assumption 5.1), and an infinite number of solutions would be the result of the two manifolds were the same one (at least locally). \(\square \)
, and that, in general, such two manifolds intersect in a finite number of points. To get no solution at all would be a particular case (which would not satisfy Assumption 5.1), and an infinite number of solutions would be the result of the two manifolds were the same one (at least locally). \(\square \)
The uniqueness of the solution associated with a cyclic structure that contains differential constraints depends upon the context of the problem. Consider a set of \(n_\mathrm{l}+n_{e}\) variables which is constrained by \(n_\mathrm{l}\) differential equations
where \({{\varvec{x}}}_\mathrm{l}\) is the vector of the variables in the loop, \({\varvec{g}}_\mathrm{l}\) are the constraints in the loop, and \({{\varvec{x}}}_{e}\) are the external variables, which are supposed to be known. The system (5.17) has a unique solution only if the initial value \({{\varvec{x}}}_\mathrm{l}(0)\) is known. If this is not the case, the solution will depend on the \(n_\mathrm{l}\) unknowns \({{\varvec{x}}}_\mathrm{l}(0)\) and thus it will belong to a manifold of dimension \(n_\mathrm{l}\). Such a differential loop is called non-causal .
Example 5.16
Differential loop in the tank example Consider the following matching

which is complete with respect to the variable set \(\left\{ h,\,\dot{h},\,q_{i},\,q_{o}\right\} \), and in which differential causality is now used for constraint \(c_{6}\). The matching results in the differential loop \(h-c_{6}-\dot{h}-c_{1}-q_{0}-c_{3}-h\), which is shown in Fig. 5.14. Although the matching is complete with respect to the set of unknown variables, it is impossible to determine h(t), because the initial value h(0) is unknown. \(\square \)
Following a classical graph-theoretic approach, a loop can be condensed into one single node, which represents a subsystem of constraints to be solved simultaneously. Another approach is to avoid loops (whenever possible) by some transformation of the constraints, leading to diagonal or triangular system structures.
Example 5.17
Treatment of loops Consider a subsystem with \(\mathcal{Z}=\{x_{1},\,x_{2},y_{1},\,y_{2}\}\), \(\mathcal{C}=\left\{ c_{1},\,c_{2}\right\} \). The variables are real numbers, the constraints are linear, \(y_{1},\,y_{2}\) are supposed to be known, and the problem to be solved concerns the computation of \(x_{1},\,x_{2}\) by using the constraints
The incidence matrix of the structure graph and a complete matching w.r.t. \(\left\{ x_{1},\,x_{2}\right\} \) is given as follows:

Figure 5.15a shows the resulting loop in the associated oriented graph. In the structure graph it is supposed that b and \(\gamma \) are non-zero. The linear equations \(c_1\) and \(c_2\) are solvable under the condition \(b\,\gamma -c\,\beta \ne 0\), which cannot be seen from structural considerations.
Figure 5.15b illustrates the condensation in which the loop is “condensed” into one single node, which means that the two equations with two unknowns are solved simultaneously, but no detail is given by the condensed structure graph about how this is done.
Transforming the constraints may also lead to a loop-free oriented graph, because it may give the system a diagonal or a triangular structure. For example, the two following systems are equivalent to (5.18):
and
Figure 5.16 illustrates the loop-free graphs associated with the transformed systems (5.19) and (5.20). Note that the new systems result from manipulations which are not purely structural, but which are done on the behaviour model. \(\square \)
4 Structural Decomposition of Systems
4.1 Canonical Subsystems
This section recalls a classical result from bipartite graph theory, which states that any finite-dimensional graph can be decomposed into three subgraphs with specific properties: an over-constrained, a just-constrained and an under-constrained subgraph. This decomposition is canonical, i.e. for a given system, it is unique. The three subgraphs and the associated subsystems play a major role in the structural analysis and lead to the important structural properties of observability, controllability, monitorability and reconfigurability.
The following definition shows the consequences of the existence of complete matchings for the solution of constraint sets that are structurally described by a bipartite graph \(\mathcal{G}\).
Definition 5.6
( Over-constrained, just-constrained, under-constrained graph) A graph \(\mathcal{G} = (\mathcal{C},\,\mathcal{Z},\,\mathcal{E})\) is called
-
over-constrained if there is a complete matching on the variables \(\mathcal{Z}\) but not on the constraints \(\mathcal{C}\),
-
just-constrained if there is a complete matching on the variables \(\mathcal{Z}\) and on the constraints \(\mathcal{C}\),
-
under-constrained if there is a complete matching on the constraints \(\mathcal{C}\) but not on the variables \(\mathcal{Z}\).
In an over-constrained graph, there remains a complete matching on \(\mathcal{Z}\) after any single constraint has been removed from the set \(\mathcal{C}\).
Example 5.18
Property of the reduced graph of the tank system. Matching 2 of the structure graph of the tank system shown in Example 5.9 is complete with respect to the variables, but there is still one non-matched constraint. Hence, the reduced graph of the tank system is over-constrained.

It can be furthermore noticed that any of the five constraints can be removed, and there still is a complete matching on the resulting graph. \(\square \)
A graph \(\mathcal{G}\) may fail to conform to any of the three properties defined above. In this case, it can be proved that there exists a unique decomposition of \(\mathcal{G}\) into three subgraphs, which are defined by the partitions
of the sets \(\mathcal{Z}\) and \(\mathcal{C}\). The subgraphs are denoted by
where \(\mathcal{E}^-\), \(\mathcal{E}^0\) and \(\mathcal{E}^+\) are the subsets of \(\mathcal{E}\) with the edges that connect vertices of \(\mathcal{C}^-\) with \(\mathcal{Z}^-\), \(\mathcal{C}^0\) with \(\mathcal{Z}^0\) or \(\mathcal{C}^+\) with \(\mathcal{Z}^+\), respectively. Note that the sets \(\mathcal{E}^-\), \(\mathcal{E}^0\) and \(\mathcal{E}^+\) do not represent a partition of the edge set \(\mathcal{E}\) of the overall graph, but a subset of it. As the important fact of this decomposition, the graphs \(\mathcal{G}^-\), \(\mathcal{G}^0\) and \(\mathcal{G}^+\) are under-constrained, just-constrained or over-constrained, respectively. This decomposition has been introduced by Dulmage and Mendelsohn in 1958 and is, therefore, also called the DM decomposition .
Theorem 5.1
(DM decomposition of bipartite graphs) Each bipartite graph \(\mathcal{G} = (\mathcal{C}, \mathcal{Z}, \mathcal{E})\) can be decomposed into three subgraphs, which have the following properties:
-
Over-constrained subgraph \(\mathcal{G}^+\), which possesses a \(\mathcal{Z}\)-complete matching that is not \(\mathcal{C}\)-complete,
-
Just-constrained subgraph \(\mathcal{G}^0\), which possesses a complete matching,
-
Under-constrained subgraph \(\mathcal{G}^-\), which possesses a \(\mathcal{C}\)-complete matching that is not \(\mathcal{Z}\)-complete.
As the choice of matchings for a graph is not unique it is important to state that the DM decomposition is unique. That is, the freedom in choosing matchings with the completeness properties mentioned in the theorem is restricted to the subsets of the vertices, which result from the decomposition (5.21).
As a consequence of the graph decomposition, the corresponding system \(\mathcal{S}=(\mathcal{C}, \mathcal{Z})\) can be decomposed into three subsystems:
In analogy with the corresponding subgraphs, these subsystems are classified as follows:
-
\(\mathcal{S}^{+}\) is called the over-constrained subsystem (also called the over-determined subsystem) and abbreviated as SO. It has more constraints than variables.
-
A structurally over-constrained system \(\mathcal{S}\) is said to be proper structurally over-constrained (PSO) if \(\mathcal{S} = \mathcal{S}^+\).
-
\(\mathcal{S}^{0}\) is called the just-constrained subsystem. It has the same number of unknown variables and constraints if the variables of the set \(\mathcal{Z}^0\) are interpreted as known variables (\(|\mathcal{Z}^0| = |\mathcal{C}^0|\)).
-
\(\mathcal{S}^{-}\) is called the under-constrained subsystem (under-determined subsystem). It has less constraints than variables (\(|\mathcal{Z}^-| < |\mathcal{C}^-|\)).
Subsystems which cannot be decomposed into smaller ones are said to be minimal subsystems.
Example 5.19
DM decomposition of a bipartite graph The example graph in Fig. 5.17 illustrates the situation that a system \(\mathcal{S}\) simultaneously can comprise the three subgraphs mentioned above:
with the associated incidence matrices

The subgraph \(\mathcal{G}^+\) drawn on the left part has a \(\mathcal{Z}\)-complete matching marked by the thick edges. Hence, this graph is over-constrained. The middle subgraph \(\mathcal{G}^0\) possesses a complete matching and is just-constrained, whereas the right subgraph \(\mathcal{G}^-\) has a \(\mathcal{C}\)-complete matching and is under-constrained. Note that the vertices are ordered such that the edges belonging to the matchings form a kind of “main diagonal” of the matrices. The edges that connect two subgraphs do not contribute to these matchings.
The incidence matrix of the overall graph \(\mathcal{G}\) can be ordered in such a way that it contains the sub-matrices \({{\varvec{E}}}^+\), \({{\varvec{E}}}^0\) and \({{\varvec{E}}}^-\) together with further entries, which represent the edges connecting the subgraphs,

Due to the ordering of the vertices in both sets, the matchings in all the three subgraphs build a diagonal line, in which the more abstract representation of Fig. 5.18 is drawn as the diagonal black line. The figure shows in an intuitive way those regions of the incidence matrix where the non-zero elements appear (grey) and those which include only zero entries (white). It further shows that the subgraph \(\mathcal{G}^+\) has more vertices from the set \(\mathcal{C}\) than from the set \(\mathcal{Z}\), because the relation
holds. Hence, the corresponding subsystem has more constraints than variables and is, hence, over-determined. For the other two subgraphs the relations
hold.
Whether or not all the three subgraphs appear in an overall graph \(\mathcal{G}\) is not directly related to the cardinalities of \(\mathcal{C}\) and \(\mathcal{Z}\). That is, even if the graph has more \(\mathcal{Z}\)-vertices than \(\mathcal{C}\)-vertices, it may still comprise a part that is over-constrained.
The DM decomposition includes more information about the graph, namely the connection among the variables and the constraints. The DM decomposition is unique, which means that the partition (5.21) of the sets \(\mathcal{C}\) and \(\mathcal{Z}\) is unique. Whatever complete matchings are used, the same vertices appear in the three subgraphs in all resulting decompositions. What depends upon the matchings used is the order of the vertices in the incidence matrix after the ① entries have been brought into the main diagonal. For example, if in the subgraph \(\mathcal{G}^+\) the matching
is used, which is \(\mathcal{Z}\)-complete as well, the order of the rows for \(c_1\) and \(c_3\) in the matrix \({{\varvec{E}}}\) has to be exchanged, but the DM decomposition remains the same. \(\square \)
For later use, it is convenient to define a measure of structural redundancy, which is associated with the over-constrained part of a system, \(\mathcal{S}^{+}\).
Definition 5.7
(Structural redundancy measure) Given a set of constraints \(\mathcal C\), and let \(Q(\mathcal{C}) \subseteq \mathcal{Z}\) be the subset of variables in \(\mathcal Z\) connected to at least one constraint in \(\mathcal{C}\). The structural redundancy measure is
Example 5.20
DM decomposition of the single-tank system Rearranging the rows and columns related to unknown variables of the structure graph for the single-tank system introduced in Example 5.4 on p. 124, the incidence matrix becomes:

As the ①-elements of a maximum matching show, the single-tank system is over-constrained:
The decomposition is independent of the known variables, which are added to the right of the table for completeness. The structural redundancy measure is
If \(c_2\) was removed from the system, the modified system would be just-constrained with
and \(\varrho (\mathcal{C}) = 0\). \(\square \)
Further decomposition of the just-constrained subgraph. The graph \(\mathcal{G}^0 = (\mathcal{C}^0, \mathcal{Z}^0, \mathcal{E}^0)\) can be further decomposed as it will be explained in this paragraph. As stated above, this graph includes a set of \(n^0\) constraints that can be used to determine the same number of variables. The decomposition introduced now splits these sets of constraints and variables in such a way that the smaller constraint sets can be used consecutively to determine the associated unknown variables. What happens in this decomposition can be seen in Fig. 5.19, where the incidence matrix of the just-constrained subgraph is a lower block triangular matrix.
The decomposition starts after the edges of the just-constrained subgraph have been given the directions described in Sect. 5.3.2, namely the orientation from the \(\mathcal{C}\)-vertex towards the \(\mathcal{Z}\)-vertex for all edges belonging to the complete matching and the opposite direction for all remaining edges. Then the resulting oriented graph is decomposed into strongly connected components. The paths have to be built in accordance with the directions of the edges. As the structure graph is bipartite, the sets of strongly connected vertices include vertices of both kinds. If the corresponding subsets of \(\mathcal{C}^0\) and \(\mathcal{Z}^0\) are enumerated in the same way, the decomposition of the just-constrained subgraph \(\mathcal{G}^0\) results in partitions of these sets:
where q is the number of strongly connected components obtained. If the rows and columns of the incidence matrix belonging to the just-constrained subgraph are ordered accordingly, the lower block-diagonal matrix shown in the middle of Fig. 5.19 results.
Example 5.21
Decomposition of the just-constrained subgraph Figure 5.20 shows the subgraph \(\mathcal{G}^0\) of the bipartite graph introduced in Example 5.19. The edges have the prescribed orientation from the \(\mathcal{C}\)-vertex towards the \(\mathcal{Z}\)-vertex for all edges belonging to the complete matching and the opposite direction for the other edges. The grey fields mark the three different strongly connected components. The constraint \(c_6\) and the variable-vertex \(z_7\) belong together, because the edge \(c_6 \rightarrow z_7\) belongs to the matching used in the DM decomposition. For the same reason, \(c_7\) and \(z_6\) represent a strongly connected component.
After ordering the vertices according to this decomposition, the following incidence matrix \({{\varvec{E}}}^0\) is obtained:

Hence, the just-constrained subgraph of this example can be further decomposed into three subgraphs that can be used consecutively for determining the unknown variables. Note that the variables \(z_5\) and \(z_7\) will be determined by the constraint \(c_5\) or \(z_7\), respectively, and these results will influence the determination of the variable \(z_6\) by using the constraint \(c_6\). This fact illustrates that the order of the subsets is important to retain the causality of the graph and, hence, the order of the computation of the unknown variables. \(\square \)
4.2 Interpretation of the Canonical Decomposition
This subsection addresses the canonical subsystems with respect to existence of solutions, thus providing a key for later analysis of structural observability and controllability.
First, it is clear that Assumption 5.1 (a) on p. 122 must be satisfied by each of the subsets of constraints \(\mathcal{C}^{+},\,\mathcal{C}^{0}\) and \(\mathcal{C}^{-}\). If this was not true, the system model would have no solution, which contradicts with the fact that it describes the behaviour of a physical system (which indeed has a solution).
Second, from the structural point of view, any algebraic constraint is assumed to satisfy Assumption 5.2 on p. 141, thus, a subset of n variables completely matched within a subset of n constraints is uniquely defined, while the result depends on the causality and on the existence of differential loops when constraints of the form
are considered. Finally, it will be seen that there are cases in which Assumption 5.1 (b) cannot hold true.
Static systems. The behavioural model of static systems contains only algebraic constraints. In the over-constrained subsystem \((\mathcal{C}^{+},\,Q(\mathcal{C}^{+}))\) the variables in the set \(\mathcal{Z}^{+}=Q(\mathcal{C}^{+})\) have to satisfy more than \(n^{+}=|\mathcal{Z}^{+}|\) constraints. Since there are more manifolds than variables, no solution can exist if they also satisfy Assumption 5.1 (b). As the model should have at least one solution for a given physical system, one concludes that the constraints in \(\mathcal{C}^{+}\) are not independent, i.e. the system description is redundant . In other words, for the system to have a solution, some compatibility conditions must hold. Structural analysis always assumes the most general case, i.e. the minimum number of relations between the system parameters. This means that the number of independent constraints is maximal, thus leading to the following equivalent conclusions:
-
The over-constrained subsystem has a unique solution (more generally, it has a finite number of solutions).
-
The number of independent constraints in \(\mathcal{C}^{+}\) is \(n^{+}\).
-
The number of compatibility conditions is \(\left| \mathcal{C}^{+}\right| -n^{+}.\)
In the just-constrained subsystem , \((\mathcal{C}^{0},\,Q(\mathcal{C}^{0}))\) , the \(n^{0}\) variables in the set \(\mathcal{Z}^{0}\) have to satisfy exactly \(n^{0}\) constraints, which satisfy Assumptions 5.2 and 5.1(a). A unique solution exists, which is the intersection of the manifolds associated with the constraints \(\mathcal{C}^{0}\), which are assumed to satisfy Assumption 5.1(b). This being the most general case, structural analysis proposes the following conclusions:
-
The just-constrained subsystem has a unique solution.
-
The number of independent constraints in \(\mathcal{C}^{0}\) is \(n^{0}\).
-
There is no compatibility condition.
In the under-constrained subsystem , \((\mathcal{C}^{-},\,Q(\mathcal{C}^{-}))\) , the \(n^{-}\) variables in the set \(\mathcal{Z}^{-}\) have to satisfy less than \( n^{-}\) constraints, which satisfy Assumptions 5.2 and 5.1(a). All what the model can tell is that the unique solution of the physical system belongs to the intersection of less than \(n^{-}\) manifolds, and thus the solution is not uniquely defined by the model. It belongs to a manifold of dimension \(n^{-}-\) \(\left| \mathcal{C}^{-}\right| \) if the constraints also satisfy Assumption 5.1(b). This being the most general case, structural analysis proposes the following conclusions:
-
The under-constrained subsystem has no unique solution.
-
The constraints in \(\mathcal{C}^{-}\) are independent.
-
There is no compatibility condition.
Example 5.22
Compatibility conditions in an over-constrained subsystem Consider the set of linear constraints
where \({\varvec{a}}=(a_{1},\,a_{2},\,a_{3})^\mathrm{T}\) and \({{\varvec{b}}}=(b_{1},\,b_{2},\,b_{3})^\mathrm{T}\) are known parameter vectors and \({{\varvec{y}}}=(y_{1},\,y_{2},\,y_{3})^\mathrm{T}\) is a known signal vector. This system is clearly over-constrained with respect to the unknown variables \(( x_{1},\,x_{2})\). However, whether or not this system of linear equations has a solution depends upon the following cases:
-
1.
\(\mathrm{rank}\,({\varvec{a}},\,{{\varvec{b}}},\,{{\varvec{y}}})=3\), i.e. \({\varvec{a}}\), \({{\varvec{b}}}\) and \({{\varvec{y}}}\) are linearly independent vectors. The system (5.25) has no solution, because the three constraints are incompatible. Assumptions 5.1 and 5.2 cannot hold simultaneously.
-
2.
If \(\mathrm{rank}\,({\varvec{a}},\,{{\varvec{b}}},\,{{\varvec{y}}}) =2\), one solution exists. Note that the parameters and the known variables are no longer independent but the matrix \(({\varvec{a}}, \; {{\varvec{b}}}, \; {{\varvec{y}}})\) has a vanishing eigenvalue and
$$ {{\varvec{y}}}= \lambda {\varvec{a}}+ \mu {{\varvec{b}}}$$leads to the unique solution \(x_{1}=\lambda \) and \(x_{2}=\mu \).
-
3.
If \(\mathrm{rank}\,({\varvec{a}},\,{{\varvec{b}}},\,{{\varvec{y}}})=1\), the matrix \(({\varvec{a}}\; {{\varvec{b}}}\; {{\varvec{y}}})\) has two null eigenvalues. Any pair \((x_{1},x_{2})\) such that \(x_{1}+x_{2}-\lambda \mu =0\) satisfies Eq. (5.25). Note that in that case, two compatibility conditions exist, and Assumption 5.1 does not hold.
-
4.
The last case is \(\mathrm{rank}\,({\varvec{a}},\,{{\varvec{b}}},\,{{\varvec{y}}})=0\), i.e. \({\varvec{a}}={{\varvec{b}}}={{\varvec{y}}}={{\varvec{0}}}\). In this case, all parameters are specified and any pair
 satisfies the system of equations. Assumption 5.2 does not hold.
satisfies the system of equations. Assumption 5.2 does not hold.
Since Eq. (5.25) is the behavioural model of a physical system, it should exhibit at least one solution. Then obviously the most general situation is Case 2 in which only one relation holds between the parameters. This is what assumed in any structural analysis. \(\square \)
Example 5.23
Structural analysis of a tail lamp Figure 5.21 shows the simplified circuit of a tail lamp of a car, which is represented by the following constraints:
with the set of variables
The structure graph is shown in Fig. 5.22a. In the analysis the circuit is considered for closed switches, where the model can be reformulated as a set of linear equations, which is given by
where the variable v is the known input voltage.
For given v, the reduced graph has the canonical decomposition shown by the arrows in Fig. 5.22b. It is interesting to see that for linear static systems this decomposition determines the structural rank of the matrix \({{\varvec{A}}}\), which is given by the maximum number of entries that can be chosen in different rows and different columns as indicated by the ① in the following scheme:

The structural rank is determined for the structure matrix \([{{\varvec{A}}}]\) rather than the matrix \({{\varvec{A}}}\) itself. Therefore, all non-vanishing elements have been replaced by “1” in the structural rank condition. The ① correspond to the oriented edges in the graph and, hence, make a complete matching. The system is just-constrained.
The DM decomposition also shows how to determine the unknown variables \(i_1\), \(i_2\), \(v_2\) and \(v_1\). The more detailed decomposition leads to the subsystems
Accordingly, in the first step, the constraint \(c_1\) is used to determine \(v_1\) in terms of the known variable v
Then the constraint set \(\{c_2, c_3, c_4\}\) has to be used to determine the further three variables by solving the linear equation
for given \(v_1\). The complete matching of this subsystem leads to an algebraic loop. Hence, the constraints \(c_2\), \(c_3\) and \(c_4\) have to be used simultaneously to determine the three unknown variables (Fig. 5.23).
In this example, again, the difference between structural and numerical properties can be seen. As the structural rank of the matrix \({{\varvec{A}}}\) is four, for almost all parameters occurring in the matrix the inverse \({{\varvec{A}}}^{-1}\) exists and the linear equations have a unique solution. For exceptional cases, for which the determinant of \({{\varvec{A}}}\) vanishes, the constraint set has no solution. For the tail lamp, this exceptional case is given by the equality
Hence, for all parameter values that do not satisfy this equality, that is, for all parameters with
the structural rank transfers to the numerical rank of \({{\varvec{A}}}\) and the model of the circuit has a unique solution for any given input voltage v. \(\square \)
Dynamical systems. Remember that, when differential constraints are considered, matching all the variables in a subsystem guarantees that there is a unique solution under integral causality, i.e. if the initial conditions are known. Under derivative causality, the solution is unique if and only if there is a matching which avoids differential loops.
Let \(n_{1}^{+}\) (respectively, \(n_{1}^{0},\,n_{1}^{-}\)) be the maximum number of variables which can be matched in the over-constrained subsystem (respectively, in the just-constrained or the under-constrained subsystems) without introducing any differential loop. One obviously has \(n_{1}^{+}\le n^{+},\;n_{1}^{0}\le n^{0},\;n_{1}^{-}\le n^{-}\).
An over-constrained or a just-constrained subsystem is called causal if there exists a complete matching with respect to the variables \(\mathcal{Z}^{+}\) and \(\mathcal{Z}^{0}\) which do not contain any differential loop, i.e. if \(n_{1}^{+}=n^{+}\) or \(n_{1}^{0}=n^{0}\) holds. The under-constrained subsystem cannot be causal, because there does not exist any complete matching with respect to \(\mathcal{Z}^{-}\).
Example 5.24
Causal over-constrained system The following system
is over-constrained with respect to the variables \((x_{1},\,x_{2})\), where u is supposed to be known. The system is causal because \((x_{1},\,x_{2})\) can be matched with \((c_{1},\,c_{2})\) without introducing a differential loop. Thus, there is a unique solution, which is obtained from the intersection of the two manifolds associated with \((c_{1},\,c_{2})\):
\(a-\alpha \) is assumed not to be zero. Moreover, the constraint \(c_{3}\) is redundant, and acts as a compatibility condition which has to be satisfied for the system solution to exist, namely
If the constraint \(c_{2}\) does not exist, then the system is just-constrained but not causal. Its solution is defined up to the constant \(x_{1}(0)\), which is unknown under differential causality. \(\square \)
5 Matching Algorithms
From the definition, a matching can be represented in the incidence matrix of the bipartite graph by selecting at most one “1” in each row and in each column. This subsection shows how the selection should be done in order to find maximum matchings. An intuitive simple algorithm, referred to as ranking, is first introduced. This algorithm uses the causal interpretation of matchings and is well suited to understand the matching process but it cannot handle cases with strongly coupled subgraphs. As a general approach, the classical maximum matching algorithm is introduced and is followed by a maximum flow algorithm that can find all matchings in an elegant way that, however, is computationally heavy. A very efficient algorithm is then reviewed, which is based on directly finding all minimal structurally over-determined sets (MSO sets) in a structure graph. Examples are provided to show the use of the different algorithms.
5.1 Ranking Algorithm
According to the causal interpretation described above, a complete causal matching over the unknown variables identifies the computations to be done in order to express the unknown variables as a function of the variables that are known or have already been determined. If the matching is not complete with respect to the constraints, non-matched constraints exist that must be satisfied by the variables obtained. These facts are the basis of the following constraint propagation (or ranking) algorithm, which can be used to find a matching. The idea of this intuitive algorithm is to start with a known variable and to “propagate” the knowledge, step by step, by matching the variables which are present in constraints where all other involved variables are matched or known. The algorithm is not able to provide a matching in cases where subsystems are so closely coupled that a set of constraints and variables need be solved simultaneously. Such problems require more elaborate algorithms that are introduced later in this section.

In the first step, all known variables in the set \(\mathcal{K}\) are marked and all unknown variables remain unmarked. In the second step, every constraint that contains at most one unmarked variable is assigned rank 1. It is matched for the unmarked variables (or for ZERO, if there is none), and the variable is marked. This step is repeated with an increasing rank number, until no new variables can be matched.
If every matched variable is also given a number, the rank can be interpreted as the number of steps needed to calculate the corresponding variable from the known ones.
The ranking algorithm stops before a complete matching is obtained if there exist unmarked variables still to be determined, but if all constraints include more than one unmarked variable. This situation occurs, for example, if two constraints have to be used simultaneously to determine two variables (e. g. the constraints \(c_1\) and \(c_2\) for the variables \(x_1\) and \(x_2\) in Example 5.17).
Example 5.25
Ranking of constraints for the single-tank system The ranking algorithm is applied to the tank example as follows. As \(u,\,y\) are known, only the variable set \(\{q_{i},\,q_{o},\,h,\,\dot{h}\}\) has to be matched.
-
Starting set (rank 0): \(\{u,\,y\}\)
-
First step (rank 1): match \(q_{i}\) with \(c_{2}\), match h with \(c_{4}\)
-
Second step (rank 2): match \(q_{0}\) with \(c_{3}\), match \(\dot{h}\) with \(c_{6}\)
-
End (every variable is matched)
The obtained matching is the following one:

Hence, the ranking algorithm can be used to get a complete matching for the tank system. \(\square \)
Example 5.26
Two-tank system The two-tank system introduced in Sect. 2.1 will be considered with u as the known control input and \(q_\mathrm{m}\) as the measured outflow. The following equations lead to the structure graph in Fig. 5.24:
\(A,\,k_1,\,k_2\) and \(k_\mathrm{m}\) are known parameters. \(c_\mathrm{L}\) is the unknown parameter describing the size of the fault. It can be assumed to be zero for the faultless case. In the structure graph the constraints \(c_1,\,c_2,\,c_3\) and \(d_4\) representing the Tank 1 are separated from constraints \(c_6,\,d_7,\,c_8\) and \(c_\mathrm{m}\) describing the Tank 2.
The following matching is found using the ranking algorithm, where the last column shows the rank of the constraints obtained.

The matching obtained can alternatively be represented as follows:

As the ranking algorithm may stop when encountering strongly connected subgraphs, more generic approaches to matching are introduced below.
5.2 General Matching Algorithm
Let \(\mathcal{M}\) be a matching on a graph \(\mathcal{G}\). An edge is said to be weak with respect to \(\mathcal{M}\) if it does not belong to \(\mathcal{M}\). A vertex is weak with respect to \(\mathcal{M}\) if it is only incident to weak edges. An \(\mathcal{M}\)-alternating path is a path whose edges are alternating in \(\mathcal{M}\) and not in \(\mathcal{M}\) (or conversely). An \(\mathcal{M}\)-augmenting path is an alternating path whose end vertices are both weak with respect to \(\mathcal{M}\) . An \(\mathcal{M}\)-alternating tree with root v is a collection of disjoint \(\mathcal{M}\)-alternating paths with the common root v.
The basic matching algorithm is built on the following theorem:
Theorem 5.2
(Berge 1957) A matching \(\mathcal{M}\) in a graph \(\mathcal{G}\) is maximum if and only if there exists no \(\mathcal{M}\) -augmenting path in \(\mathcal{G}\) .
The idea of the proof of the theorem is that if an augmenting path would exist, a new matching of size \(|\mathcal{M}|+1\) would be obtained by exchanging the roles of the matched and non-matched edges in the path, as illustrated by the following example. This step is called the transfer from the old to the new matching along the \(\mathcal{M}\)-augmenting path.
Example 5.27
An \(\mathcal{M}\) -augmenting path A matching \(\mathcal{M}\) of size 3 is given by the bold edges in the bipartite graph of Fig. 5.25 (left).
It can be checked that there exists an \(\mathcal{M}\)-augmenting path, namely
and, therefore, this matching is not maximum. By exchanging weak (dashed lines) and matched (solid line) edges, the following matching of size 4 is found:
Based on the theorem above, the following algorithm extends an initially given matching step-by-step by finding an augmenting path and augmenting the size of the current matching by transferring it, until no further augmenting path can be found and, therefore, the latest determined matching is maximum.

The initial matching can be the empty matching \(\mathcal{M}_{0}=\left\{ \right\} \). In Step 2, the cardinality of the matching is increased by one.
Example 5.28
Maximum matching algorithm Let \(\mathcal{M}_{0}=\left\{ \left( x_{1},c_{2}\right) \!,\left( x_{3},c_{3}\right) \!,\right. \left. \left( x_{4},c_{6}\right) \right\} \) be the initial matching shown on Fig. 5.25. The weak edges are
There are four weak vertices, namely \(\left\{ c_{1},x_{2},c_{4},c_{5}\right\} \). For the first iteration, choosing \( c_{1}\) as the root gives the alternating tree shown on Fig. 5.26a where the current matching is shown in dashed lines. It is easily seen that there are two \(\mathcal{M}_{0}\)-augmenting paths, namely \(c_{1}-x_{1}-c_{2}-x_{2}\) and \(c_{4}-x_{4}-c_{6}-x_{5}\). Since these paths are disjoint, the two transfers can be done simultaneously, resulting in the matching
The weak edges are now
and the weak vertices are \(\left\{ x_{3},c_{3},c_{5}\right\} \). Choosing \(c_{3}\) as the root results in the alternated tree of Fig. 5.26b, which exhibits the \(\mathcal{M}_{1}\)-augmenting path \(x_{3}-c_{2}-x_{2}-c_{5}\). Performing the transfer gives the new matching
which is maximum, because the set of weak edges is now
and there remains only one single weak vertex \(c_{3}\). \(\square \)
Example 5.29
Application to the single-tank system The aim is to search for a maximum matching with respect to the reduced structure graph of the single-tank system.

Let \(\mathcal{M}_{0}=\left\{ {}\right\} .\) Then all vertices are weak. Selecting, e.g. h as the root gives the alternated tree
\(\nearrow \) | \(c_{6}\) | \(\rightarrow \) | \(\dot{h}\) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
h | \(\longrightarrow \) | \(c_{4}\) | ||||||||
\(\searrow \) | \(c_{3}\) | \(\rightarrow \) | \(q_{o}\) | \(\rightarrow \) | \(c_{1}\) | \(\rightarrow \) | \(q_{i}\) | \(\rightarrow \) | \(c_{2}\), |
where two disjoint \(\mathcal{M}_{0}\)-augmenting paths are given by \(c_{6}-\dot{h}\) and \(h-c_{3}-q_{o}-c_{1}-q_{i}-c_{2}\) providing the new matching \( \mathcal{M}_{1}=\left\{ \left( \dot{h},c_{6}\right) ,\left( h,c_{3}\right) \! ,\left( q_{o},c_{1}\right) \!,\left( q_{i},c_{2}\right) \right\} \) which is complete with respect to the unknown variables and, hence, the algorithm ends. \(\square \)
5.3 Maximum Flow Algorithm
Finding a maximum matching in a bipartite graph can be transformed into a maximum flow problem. The procedure is as follows: Construct a network \(\mathcal{N}\) associated with the graph \(\mathcal{G} = \left( \mathcal{C},\mathcal{Z}, \mathcal{E}\right) \) by orienting all edges from \(\mathcal{Z}\) to \(\mathcal{C}\), by inserting a source vertex S with arcs to all vertices of \(\mathcal{Z}\) and a sink vertex T with arcs from all vertices of \(\mathcal{C}\), and by connecting T to S as shown on Fig. 5.27. Furthermore, assign the capacity of all arcs from S to \(\mathcal{Z}\) and from \(\mathcal{C}\) to T as 1. The capacities of all other arcs are set to \(\infty \). Then, the maximum flow on \(\mathcal{N}\) is associated with a maximum matching as stated in the following theorem.
Theorem 5.3
In a bipartite graph \(\mathcal{G}\), the matching number \(\nu (\mathcal{G})\) equals the maximum flow through the network \(\mathcal{N}\) that is associated to the graph \(\mathcal{G}\).
Therefore, a maximum matching can be found by applying the classical maximum flow algorithm of Ford and Fulkerson, which in the case of bipartite graphs is called “the Hungarian method” . Like the preceding algorithm, this algorithm assumes a given matching \(\mathcal{M}\) is known and attempts to extend \(\mathcal{M}\) by finding an augmenting path. This is done by marking vertices on weak edges so as to follow possible augmenting paths.

Example 5.30
Determination of a maximum matching by the Hungarian method Let \(\mathcal{M}_{0}=\left\{ \left( x_{1},c_{2}\right) \!,\left( x_{3},c_{3}\right) \! ,\left( x_{4},c_{6}\right) \right\} \) be the initial matching shown on Fig. 5.25. The table below shows the initial labelling and the sequence of labels obtained as Steps 2 and 3 alternate. The bar over vertices \(c_{1},c_{4}\) and \(c_{5}\) indicate that these vertices are weak with respect to the current matching.

The table demonstrates the Steps 2 and 3 of the algorithm. However, in this example, the first iteration would stop as early as after Step 2-1 because the weak vertex \(c_{5}\) has been labelled (END 1). Tracking the labels backwards until a *-vertex is found gives the \(\mathcal{M}_0\)-augmenting path \(c_{5}-x_{2},\) which results in the augmented matching
from which the next iteration starts. \(\square \)
Example 5.31
Hungarian method applied to the single-tank system With \(\mathcal{M}_{0}=\left\{ \left( \dot{h},c_{6}\right) \right\} \) being the initial matching, the first iteration gives the labels

before END 1 occurs and the matching can be updated as
The second iteration gives

before END 1 occurs. The \(\mathcal{M}_{1}\)-augmenting path is given by \( c_{4}-h-c_{3}-q_{0}\) and leads to the new matching
This matching is complete with respect to the unknown variables and stops the algorithm. Note that the solution is different from the one previously found, which illustrates the fact that maximum matchings are not unique. \(\square \)
The above algorithm is computationally very heavy and experience showed that alternative algorithms were needed to cope with industrial scale systems.
5.4 Minimal Over-Determined Subsystems Approach
The Minimal Structurally Over-determined (MSO) set approach offers another way to find all analytical redundancy relations. The idea in the method is to calculate all subsets \(\mathcal{M}_\mathrm{MSO} \subseteq \mathcal{S}^+\) of an over-constrained structure graph, which have exactly one constraint more than the just-constrained subsystem. The structural redundancy measure for such subset is \(\varrho (\mathcal{M}_\mathrm{MSO}) = 1\) according to Eq. (5.22). Therefore, each MSO set will comprise at least one constraint that can be used as an ARR. The number of ARRs generated in this way will be larger than the set of ARRs found from a single complete matching, but less or equal to the number of ARRs generated by the brute-force approach of generating all possible complete matchings and get a set of ARRs for each of these matchings.
The reason to generate more than the minimal set of ARRs available from a single complete matching is that structural isolability can be enhanced by considering more than the minimal number of ARRs.
Definition 5.8
(Minimal structurally over-constrained subsystem) A minimal structurally over-determined subsystem (MSO subsystem) is a part of the over-constrained part of a system graph from which removal of one constraint will make the subsystem to become just-constrained.
The procedure to find MSO sets is based on examining the set \(\mathcal M\) of constraints of a proper structurally over-constrained structure graph. The PSO property means \(\mathcal{M} = \mathcal{C}^+\). Denoting the set of unknown variables in \(\mathcal{X}\) that are connected to at least one constraint in \(\mathcal{M}\) by \(Q(\mathcal{M})\), then
(cf. Eq. (5.22)). Removing one constraint \(c_i\) from the set \(\mathcal{M}\) reduces the structural redundancy by one,
The set of constraints \(\mathcal{M}\) is an MSO set if \(\mathcal{M}\) is PSO and \(\varrho (\mathcal{M}) = 1\).
These observations led to a computationally very efficient way to determine the set of all possible ARRs for a system. The following computational procedure is used recursively [187]:

This procedure is used in the following algorithm to determine all MSO sets in a structure graph.

The above algorithm finds MSO sets more than once. This can be avoided by finding equivalence classes of constraints and make an extension of the basic algorithm that is described in [187].
Example 5.32
Determination of MSO sets This example shows how MSO sets and thereby ARRs are generated for the single-tank example with extended measurements. Assume that the flow \(q_{o}\) is measured in addition to the input u and the inflow \(q_i\), which leads to an additional measurement constraint

This structure graph is over-constrained with \(\varrho (\mathcal{M}) = 2\).
Algorithm 5.5 determines the four MSO sets listed below.

The table has to be interpreted as follows: The MSO set \(\mathcal{M}_1\) includes the constraint \(c_3(h,q_o) = 0\) as an ARR and uses \(c_4\) to calculate h and \(c_7\) to calculate \(q_o\). Each of the MSO sets is, by the definition of the MSO subsystem, also an ARR.
Algorithm 5.5 finds four MSO sets for this example. By comparison, the Ranking Algorithm 5.1 finds one complete matching of the unknown variables and two ARRs, \(c_1\) and \(c_3\), according to the following matching table:

\(\square \)
6 Structural Diagnosability and Isolability
A system is said to be structurally diagnosable or monitorable if it is possible to test whether the system constraints are satisfied or not. This section is concerned with the analysis of system monitorability and with fault detection and isolation algorithms based on Analytical Redundancy Relations (ARRs) .
Analytical redundancy occurs and analytical redundancy relations become available when there are constraints that are not needed to match the unknown variables in a system. These additional constraints, as well as all others, need be satisfied when the system obeys normal behaviour, so the additional, or redundant, constraints can test whether the system behaviour is normal. Violation of a constraint that is used to calculate an ARR would leave the ARR as not satisfied.
Residuals are derived from ARRs. A residual will only depend on known variables but the ARR might not represent causal computations. The analytical form of a residual is a signal r(t) that can be calculated by causal operations in real time by inserting the instantaneous values of known variables: the input u(t) and measurements y(t). A residual signal r(t) is therefore obtained from the corresponding arr(t) through filtering of the entire arr(t).
The terms analytical redundancy relation and residual generator are often used as synonyms in the literature, although strictly speaking, the ARRs are found without any consideration to stability and causality while a residual generator needs to be both stable and causal to generate a signal r(t) that has the properties needed for fault diagnosis. This is further elaborated in Chap. 6.
Analytical redundancy-based fault diagnosis tries to identify faults by comparing the actual behaviour of the system, which is observed through the time evolution of the known variables, with the behaviour described by the system constraints. This comparison can be performed only if some redundant information exists. For diagnosis it is not sufficient that the known variables and the set of constraints allow to determine all unknown variables. There must be available at least one constraint more with which one can test whether the obtained variables are consistent with the model representing the faultless behaviour of the system. ARRs are the constraints that express this redundancy.
In this section, the analytical redundancy relation-based approach to fault diagnosis is first briefly recalled and stated in the frame of structural analysis, leading to characterise the structurally monitorable part of the system. Finding residuals that are robust, meaning they are insensitive to disturbances or to unknown parameters, are then discussed and residuals that are sensitive to certain structural faults, but not to others (structured residuals) are then addressed.
6.1 Analytical Redundancy-Based Fault Detection and Isolation
Analytical redundancy relations are static or dynamical constraints that will be satisfied (equal to zero) when the system operates according to its normal operation model. Once ARRs are found, the fault detection procedure checks whether they are satisfied or not, and if not, the fault isolation procedure identifies the system components which are to be suspected. The existence of ARR is thus a prerequisite to the elaboration of fault diagnosis procedures. Moreover, in order for the fault diagnosis procedure to work properly, ARR should have the following properties:
-
Robust, i.e. insensitive to unknown input and unknown parameters. This insures that they are satisfied when no fault is present, so that false alarms are not issued.
-
Sensitive to faults: This insures that they are not satisfied when a constraint is violated, i.e. a fault is present, so that faults are detected.
-
Structured: This insures that in the presence of a given fault, only a subset of the ARRs is not satisfied, thus allowing to recognise the fault that occurred from the subset of ARRs that are satisfied and the subset that is not satisfied.
Faults. In structural analysis, a fault is defined as a violation in a constraint. A system is the interconnection of a number of components, each of which is described by its behavioural model in normal operation. Let \(\left\{ C_{i},i=1, 2,\ldots , N\right\} \) be the set of the system components. Each of them is a subsystem \((\phi _{i},\,Q(\phi _{i}))\) which imposes the set of constraints \(\phi _{i}\) to the system variables \(Q(\phi _{i})\), where \(Q(\phi _{i})\cap \mathcal{X}\) are unknown (unmeasured state variables, unknown input, unknown parameters) while \(Q(\phi _{i})\cap \mathcal{K}\) are known (input, output, known parameters). A fault in component \(C_{i} \) is defined as a change in at least one of the constraints \(\varphi \in \phi _{i}\).Footnote 3 Note that this general definition of faults allows to consider different fault modes associated with the same component. Each subset of \(\phi _{i}\) can in fact be considered as a fault mode of \(C_{i}\). Note also that since only the structure is of interest, there is no need to define, nor to model the nature of the change (e.g. using additive or multiplicative fault models).
Example 5.33
Representation of faults in an insulated pipe Consider an insulated pipe and suppose that one is interested in modelling the mass and the heat transfers. A simple model is given by the two constraints
where \(q_{i}\) and \(q_{o}\) are the input and the output flow of the (incompressible) fluid, and \(\theta _{i}\) (respectively, \(\theta _{o}\)) is the input (respectively, the output) fluid temperature. A defect in the insulation would obviously result in \(\varphi _{2}\) being violated, while a leak in the pipe would be modelled by \(\varphi _{1}\) and \(\varphi _{2}\) being violated. \(\square \)
Direct redundancy. Consider a constraint \(\varphi \in \mathcal{C}_{\mathcal{K}}\), where \(\mathcal{C}_{\mathcal{K}}\) is the subset of constraints such that \(Q(\mathcal{C}_{\mathcal{K}})\subseteq \mathcal{K}\) and let C be the component to which \(\varphi \) belongs. This constraint is an ARR because it links only known variables, and it can be checked in real time if it is satisfied or not, by taking the numerical values of the known variables, putting them into constraint \(\varphi \), and testing whether the result is ZERO or not. If the constraint is not satisfied, it can be concluded that the system is not in normal operation, while if the constraint is satisfied it can only be said that the normal operation hypothesis is not falsified by the values of the observations.
In practical situations, variables are not very precisely known, measurements are corrupted by noise, and models only approximate the system behaviour. Thus, the obtained value for the constraint will never be exactly zero, even in normal operation. Let \(r_{\varphi }(\mathcal{K})\) be the obtained value. \(r_{\varphi }(\mathcal{K})\) is called the residual associated with ARR \(\varphi \), and fault detection boils down to decide whether the residual is small enough so that the ZERO hypothesis can be accepted. Fault isolation obviously follows fault detection because only a fault in component C could cause constraint \(\varphi \) not to be satisfied.
In all systems, the control algorithms are direct ARRs, because the subset \(\mathcal{C}_{\mathcal{K}}\) includes the constraints which describe them. Hence, they can be used to check whether the controller is working properly. Although this might be of practical interest, such direct redundancy relations are of little interest as far as structural analysis is concerned, because the result is obvious. Therefore, the aim of the following part of this chapter is to find ARRs in the subsystem \(\left( \mathcal{C}_{\mathcal{X}},\mathcal{Z}\right) \) which includes unknown variables.
Deduced redundancy. Consider some constraint \(\varphi \in \mathcal{C}_{\mathcal{X}}\) and again let C be the component to which \(\varphi \) belongs. Let \(\mathcal{X}_{\varphi }=Q(\varphi )\cap \mathcal{X}\) be the subset of unknowns which appear in constraint \(\varphi \), and suppose that
holds, where \(\mathcal{X}_\mathrm{obs}\) is the subset of the observable variables. Then, any variable \(x\in \mathcal{X}_{\varphi }\) can be expressed as a function of the known ones (possibly including their derivatives) using the model. Suppose that there exists at least one alternated chain with target x which does not include constraint \(\varphi \). This means that even if constraint \(\varphi \) is removed, x can still be matched and computed as a function of the known variables, which indicates that constraint \(\varphi \) belongs to an over-constrained subsystem, as it will be seen later. Then, this alternated chain can be used to compute x as a function of the known variables, and one can put the obtained expression into \(\varphi \), which produces an ARR. The associated residual \(r_{\varphi }(\mathcal{K}) \) should be ZERO when the system operates properly.
However, fault isolation will be slightly different because the residual associated with \(\varphi \) will be non-zero not only if C is not performing well, but also if the actual values of the \(\mathcal{\mathcal{X}}_{\varphi }\) variables are different from those computed from the observations via the normal operation model. This may happen when the fault changes some constraint which belongs to an alternated chain whose target is in \(\mathcal{X}_{\varphi }\). The conclusion is that when \(r_{\varphi }(\mathcal{K}) \) is non-zero, there is an associated set of components to be suspected instead of a single one.Footnote 4 It can be easily determined from the graph-based interpretation.
Example 5.34
Single-tank system Consider the tank whose structure graph is shown in Fig. 5.3. There are two redundancy relations for this system. The first one is given by constraint \(c_{5}\) and is of no interest because it is a direct redundancy relation which only duplicates the control algorithm. The second one is given by \(c_{2}\) which should be satisfied when the system operates normally and which will be false if one of the constraints \(\{c_{1},\,c_{2},\,c_{3},\,c_{4}\}\) is not satisfied (\(c_{6}\) is a mathematical constraint which is not linked with any hardware or software component and thus it cannot be faulty). \(\square \)
6.2 Structurally Monitorable Subsystems
Unfortunately, not every fault can be detected. Therfore, it is important to find ways for distinguishing diagnosable faults or diagnosable subsystems from undiagnosable ones. Such ways will be described in this subsection.
Definition 5.9
(Structurally monitorable subsystem) The structurally diagnosable (monitorable) part of the system is the subset of the constraints for which there exists ARRs that are structurally sensitive to their change.
Such subsystems can be characterised by the following theorem:
Theorem 5.4
(Structural monitorability) The following two necessary conditions for a fault \(\varphi \) to be structurally diagnosable (monitorable) are equivalent:
-
(i)
\(\mathcal{X}_{\varphi }\) is structurally observable—according to (5.27)—in the system \((\mathcal{C}\backslash \{\varphi \},\,\mathcal{Z})\).
-
(ii)
\(\varphi \) belongs to the structurally observable over-constrained part of the system \((\mathcal{C},\,\mathcal{Z})\).
Let \(\left( \mathcal{C}_{\mathcal{X}},\,\mathcal{X}\right) \) be a structurally observable over-constrained subsystem. Then there exists a subset \(\mathcal{S}_{\mathcal{X}} \subset \mathcal{C}_{\mathcal{X}}\) of \(n=\left| \mathcal{X}\right| \) constraints which (from a structural point of view) can be solved uniquely for the variables \(\mathcal{X}\).Footnote 5 These variables can thus be computed as functions of the known variables \(\mathcal{K}\). Putting the obtained values into the remaining constraint set \(\mathcal{R}_{\mathcal{X}}=\mathcal{C}_{\mathcal{X}}\backslash \mathcal{S}_{\mathcal{X}}\) (the symbol \(\mathcal{R}\) is used as a mnemonic for Remaining, or Redundant), one obtains \(\left| \mathcal{C}_{\mathcal{X}}\right| -\left| \mathcal{X}\right| \) relations which link only known variables and which are, therefore, redundancy relations. For a more convenient notation the function
is introduced for the computation of the unknown variables, leading to expressions for the set of constraints \(\mathcal{C}_{\mathcal{X}}\) in the equivalent form
where \(\circ \) means the substitution of \(\mathcal{X}\) by \(\varGamma _{\mathcal{X}}(\mathcal{K})\).
In general, several different complete matchings can be found in a given causal over-constrained subsystem, which lead to different means of computing the unknown variables \(\mathcal{X}\) from the known ones. This fact will be used for the elaboration of fault-tolerant observation schemes but it can also provide another interpretation of redundancy, since obviously the unknown variables \(\mathcal{X}\) have to be the same for all matchings. For example, suppose that two matchings exist such that \(\mathcal{X}\) is associated with \(\mathcal{S}_{\mathcal{X}}\subset \mathcal{C}_{\mathcal{X}}\) in the first one, leading to the relation \(\mathcal{X}=\varGamma _{\mathcal{X}}(\mathcal{K})\), and with \(\mathcal{P}_{\mathcal{X}}\subset \mathcal{C}_{\mathcal{X}}\) in the second one, leading to \(\mathcal{X}=\varLambda _{\mathcal{X}}(\mathcal{K})\). The redundancy relations
directly follow from the fact that the two results should be the same.
Example 5.35
Sensor redundancy A good illustration of this idea is provided by sensor hardware redundancy. Suppose that two sensors measure the same unknown variable x. The measurement equations are given by
where \(\varepsilon _{1}\) and \(\varepsilon _{2}\) denote measurement noise with known distribution. The structure graph has the following incidence matrix.

Here, \(\varepsilon _{1}\) and \(\varepsilon _{2}\) are considered as known variables because their probability distribution is known. This system is over-constrained with \(\mathcal{C}_\mathcal{X}=\{c_{1},\,c_{2}\}\) and \(\mathcal{X}=\{x\}\). The unknown x can be matched with each of the two constraints and, hence, be calculated by each of the sensor equations. This is not only true from the structural point of view but x can be determined numerically if \(\frac{\mathrm {d}c_{1}}{\mathrm {d}x}\) and \(\frac{\mathrm {d}c_{2}}{\mathrm {d}x}\) are both non-zero. Otherwise at least one of the sensors would be completely useless.
For the matching

the oriented graph is given by Fig. 5.28, in which the unknown x is computed by
and \(c_{2}\) is used as a redundancy relation which can be written as
Choosing the second possible matching

provides
and the redundancy relation
Since two matchings exist, the value of x can be computed either from the first or from the second one and leads to the redundancy relation
6.3 Finding Analytic Redundancy Relations
As explained in the preceding sections, redundancy relations are obtained from over-constrained subgraphs of the reduced structure graph. They are composed of alternated chains, which start with known variables and end with non-matched constraints whose output is labelled ZERO. Designing a set of residuals calls for building maximum matchings on the given structure graph, and identifying the redundancy relations as the non-matched constraints in which all the unknowns have been matched, and subsequently expressing the non-matched constraints by known variables through backtracking to known variables, according to the matching. This section gives a complete illustration of this procedure.
Example 5.36
Finding an analytic redundancy relation for the single-tank system For the single-tank example, the incidence matrix of its reduced structure graph was given in Example 5.9:

The result of the ranking algorithm is shown in the following table and in Fig. 5.29. The matching is identical with the second matching in Example 5.9. Note that a new column has been introduced to mark constraints which have the output ZERO. Since ZERO is not a variable, it may be matched several times.

Sorted according to the rank, the following constraint set is obtained:

If the reduced structure graph is redrawn according to the ranking of the constraints, Fig. 5.29 is obtained. The figure shows how the internal variables \(q_i, h, q_o\) and \(\dot{h}\) can be successively determined. The constraints are ordered according to their associated rank. Finally, the constraint \(c_1\) is used to test whether the variables obtained are consistent with the model.
As all constraints are ranked, the system is fully observable and monitorable. By solving the constraints for the matched variables, the following equations are obtained. The right-hand column shows the path of the matching.
These equations can be simplified to obtain the redundancy relations in one analytic expression:
The order of operations on constraints was
As all variables on the right-hand side of the two equations are known, these equations can be applied to the known variables u and y, which are marked by grey circles in Fig. 5.29, to illustrate this fact. \(\square \)
6.4 Structural Detectability and Isolability
Assume that the over-constrained subsystem has been determined by finding a complete matching on the unknown variables. Then, the main results of structural analysis are obtained from the following steps:
-
1.
List all analytic redundancy relations that exist for the system.
-
2.
For all these relations, determine an explicit form if the constraints are explicitly known.
-
3.
List which violations of constraints are detectable.
-
4.
List which violations of constraints are isolable.
Calculate residuals from structural analysis. After a matching has been found, the set \(\mathcal{C}^{(u)}\subset \mathcal{C}\) of unmatched constraints
is determined. To obtain analytical redundancy relations for diagnosis, also referred to as parity relations, the unknown variables in each \(c \in \mathcal{C}^{(u)}\) must be substituted by known ones entering through matched constraints. Backtracking along alternated chains in the matching will facilitate such an elimination of the unknown variables. Finally, each unmatched constraint c will give one parity relation r to be used for diagnosis, and a violation of any constraint that was used in constructing the parity relation will give a non-zero residual when all known variables enter by their real-time values.
Furthermore, analytical redundancy relations show which residuals depend on which constraints. One view on these relations is the Boolean mapping, the dependability matrix or signature matrix,
from which structural detectability can be analysed. It can be checked that the following definition is the practical translation of the monitorability condition in Theorem 5.6.
Lemma 5.1
(Structural detectability) A violation of a constraint c is structurally detectable if and only if it has a non-zero Boolean signature in some residual r
Moreover, since for a given constraint c the set of all parity relations can be partitioned into those in which its Boolean signature is zero and those in which its Boolean signature is non-zero, the following result is straightforward.
Lemma 5.2
(Structural isolability) A violation of a constraint \(c_i\) is structurally isolable if and only if it has a unique signature in the residual vector, i.e. column \(m_i\) of M is independent of all other columns in M
Example 5.37
Nonlinear parity relations for ship Consider the nonlinear model of a ship with dual measurements of heading angle \(\psi \) and with no disturbance from waves:
The set of unknown variables is \(\mathcal{X}=\{ \delta , \omega _{3}, \dot{\omega }_{3},\psi , \dot{\psi } \}\), the set of known variables is \(\mathcal{K} = \{y_{1}, y_{2}, y_{3}, y_4\}\). A complete matching on the unknown variables is traced in the left column below, the right column shows the backtracking to known variables.
The way constraints are used in the three parity relations as follows,
As a violation of any constraint is mapped onto the residuals, all faults are detectable. Considering isolability, five columns are independent: \(m_1, m_2, m_3, d_2\). Hence it is only violations in these constraints that are structurally isolable.
The matching obtained is summarised in condensed form in the following table:

The detectability and isolability properties are conveniently summarised in tabular form as follows, where d and i denote structural detectability and isolability, n that a constraint cannot fail.

The analytical form of the parity relations is obtained from the symbolic expressions from the backtracking. This gives the expected result,
6.5 Design of Robust and Structured Residuals
Robust residuals. The set of constraints that describe the nominal operation of a system might fail to represent all aspects of its actual behaviour. Discrepancies follow from the existence of unknown inputs (disturbances) and from the fact that system parameter values are never exactly known (uncertain parameters). Such discrepancies might result in residuals firing false alarms.
Example 5.38
Residual discrepancies caused by unknown inputs The unknown variables of the single-tank system were computed from the following constraints:
Component | Constraint | Constraint expression |
|---|---|---|
Pump | \(c_{2}:\) | \(q_{i}(t)=\alpha \cdot u(t)\) |
Level sensor | \(c_{4}:\) | \(h(t)=y(t)\) |
Output pipe | \(c_{3}:\) | \(q_{0}(t)=k\sqrt{h(t)}\) |
Derivative constraint | \(c_{6}:\) | \(\dot{h}(t)=\frac{\mathrm {d}}{\mathrm {d}t}h(t)\) |
Putting these expressions into the constraint
the residual
is obtained. Assume that the level sensor output is affected by a constant bias \(\delta \) (unknown input):
Component | Nominal constraint | Actual constraint |
|---|---|---|
Level sensor | \(h(t)=y(t)\) | \(h(t)=y(t)-\delta \). |
Simple calculations show that the residual computed using the nominal model constraints would have a non-zero value:
Case | Residual value |
|---|---|
Nominal | \(\dot{y}(t)+k\sqrt{y(t)}-\alpha u(t)=0\) |
Sensor bias | \(\dot{y}\left( t\right) -\alpha \cdot u(t)+k\sqrt{ y(t)-\delta }=k\left( \sqrt{y(t)-\delta }-\sqrt{y(t)}\right) \ne 0\). |
Hence, although the system is faultless, the residual is non-zero due to the measurement bias \(\delta \). \(\square \)
Example 5.39
Residual discrepancies caused by uncertain parameters Consider now the two following cases for the single-tank system
Component | Nominal constraint | Actual constraint |
|---|---|---|
Pump | \(q_{i}(t)=\alpha \cdot u(t)\) | \(q_{i}(t)=\bar{\alpha } \cdot u(t)\) |
Output pipe | \(q_{0}(t)=k\sqrt{y(t)}\) | \(q_{0}(t)=\bar{k}\sqrt{y(t)}\). |
which refer to uncertainties in the pump and output pipe parameters. Then, the residual computed using the nominal model constraints would have the following values:
Case | Residual value |
|---|---|
Behaviour without uncertainty | \(\dot{y}(t)+k\sqrt{y(t)}-\alpha u(t)=0\) |
Uncertainty of the pump model | \(\dot{y}\left( t\right) +k\sqrt{y(t)}-\bar{\alpha } u(t)=\left( \alpha -\bar{\alpha }\right) u(t)\ne 0\) |
Uncertainty of the output pipe model | \(\dot{y}(t) -\alpha u(t)+\bar{k}\sqrt{y(t)}=(\bar{k}-k) \sqrt{y(t)}\ne 0\). |
Again, a non-zero residual results not from a fault, but from uncertainties of a parameter. \(\square \)
Robustness refers to the property that residuals would not fire any false alarm as the result of unknown inputs acting on the system or as the result of uncertainties in the values of the system parameters. One means of designing robust residuals is the exact decoupling approach, in which the designed residuals are insensitive to unknown input and unknown or uncertain parameters. Therefore, they are satisfied when no fault is present for any value of the unknown input or uncertain parameters. Note that the robustness problem is automatically solved in structural analysis, using the exact decoupling approach presented in Chap. 6, because it exhibits ARRs which are, by definition, only dependent on known variables. Unknown variables which affect the structurally monitorable subsystem are eliminated so that no residual can depend on them. When unknown variables cannot be eliminated, the part of the system they affect is not monitorable. When uncertain parameters are present, the solution to the exact decoupling problem is simply to design the fault diagnosis system considering them as unknown variables (this boils down to use the subset of residuals in which no uncertain parameter intervenes). The consequence is that the number of ARRs will in that case be smaller.
Structured residuals. As defined above, the structure of a residual is the set of the constraints which can be suspected when this residual is not ZERO. Let \(\mathcal{R}\) be a set of residuals, and let \(\varPhi (r)\in 2^{\mathcal{C}} \) be the structure of residual \(r\in \mathcal{R}\). This means that r is expected to be non-zero when at least one of the constraints in \(\varPhi (r)\) is faulty. Similarly, when some constraint \(\varphi \in \mathcal{C}\) is faulty, then all the residuals whose structure contains \(\varphi \) are expected to be non-zero. The pattern of ZERO and non-zero residuals associated with a given fault is called its signature.
Faults which have different signatures are isolable from each other, while faults which share the same signature are non-isolable. Let \(\mathcal{R}=\mathcal{R}_{0}(t)\mathcal \;{\cup }\; \mathcal{R}_{1}(t)\) be the decomposition of the set of residuals provided at some given time t by the decision procedure, where \(\mathcal{R}_{0}(t)\) is the subset of the ZERO residuals and \(\mathcal{R}_{1}(t)\) is the subset of non-zero ones. The subset of suspected constraints (the constraints which might be unsatisfied) at time t is given by
Note that it is possible to define the subset of exonerated constraints (the constraints which are certainly satisfied) at time t by
but one must be aware that this supposes all faults to be detectable. Exoneration is based on the assumption that if a constraint is not satisfied then it will necessarily show through the residuals whose structure it belongs to. The diagnosis at time t is
In order to obtain good isolability properties, it may be of interest to find residuals with given structure. Suppose that one wishes to have residuals which are insensitive to the structural faults of a subset of constraints \(\mathcal{C}^{\prime }\) and are sensitive to the structural faults of the subset of constraints \(\mathcal{C}\,\backslash \mathcal{C}^{\prime }\). A direct approach towards such residuals is to consider only the system \((\mathcal{C}\,\backslash \mathcal{C}^{\prime },\,\mathcal{Z})\) in the design process. However, from the structural monitorability condition, it is seen that the residuals can be made sensitive only to the faults in the monitorable subsystem of \((\mathcal{C}\,\backslash \mathcal{C}^{\prime },\,\mathcal{Z})\), which may be smaller than that of \((\mathcal{C},\,\mathcal{Z}),\) because the former contains less constraints.
Example 5.40
Two-tank system The two-tank system introduced in Sect. 2.1 will first be considered with u as the known control input and \(q_\mathrm{m}\) as the measured outflow. The following equations lead to the structure graph in Fig. 5.24.
\(A,\,k_1, \, k_2\) are known parameters. \(c_\mathrm{L}\) is the unknown parameter describing the size of the fault. It can be assumed to be zero for the faultless case. In the structure graph the constraints \(c_1,\,c_2,\,c_3\) and \(d_4\) representing the Tank 1 are separated from constraints \(c_6,\,d_7,\,c_8\) and \(m_1\) describing the Tank 2.
The following matching is found using the ranking algorithm, where the last column shows the rank of the constraints obtained.

The equations shown on the left are already solved for the matched variable. The corresponding oriented graph is shown in Fig. 5.30. Simplifying these equations results in the following redundancy relation,
with
Equations (5.33)–(5.35) can be used to monitor the two-tank system. By using Eq. (5.35), \(h_2(t)\) and, hence, \(\dot{h}_2\)(t) can be determined for given measurement \(q_\mathrm{m}(t)\). Then Eq. (5.34) yields \(h_1(t)\) and \(\dot{h}_1(t)\). Finally, Eq. (5.33) is checked for known u(t), \(q_\mathrm{m}(t)\) and for \(h_1(t)\), \(\dot{h}_1(t)\) and \(\dot{h}_2(t)\) just obtained.
After redrawing the structure graph, Fig. 5.31 is obtained. This graph shows in which order the constraints can be used to determine all internal variables for given measurement \(q_\mathrm{m}\). Finally, constraint \(c_3\) is used to test the consistency of the variables with the model. The resulting value is denoted by r(t). This residual should vanish to indicate that the measured values \(q_\mathrm{m}(t)\) and u(t) at time t are consistent with the set of constraints and, hence, we must assume that no fault is present. For this example, the residual has the physical meaning of the loss of liquid through a leakage.
A simulation result is depicted in Fig. 5.32 which shows from top to bottom the signals \(u(t),\,x_1(t)\) and \(x_2(t)\), the measurement \(q_\mathrm{m}(t)\) and the right-hand side of Eq. (5.33). Note that the states are reconstructed very nicely. The residual shows the occurrence of the fault very precisely and without any delay. The little spike at time 155 s is due to the reversal of the flow direction in the connection pipe, which represents a singular point in the linearised system.
The signal arr(t) is non-causal due to the two differentiations. To construct a residual, low-pass filtering need be applied to get a causal residual generator. In Laplace transform notation,
here illustrated by a second-order low-pass filter with two real eigenvalues. It is essential that it is never the signals \(\dot{h}_1\) and \(\dot{h}_2\) from \(h_1\) or \(h_2\), respectively, which are low-pass filtered, but the entire ARR expression. Otherwise, due to the phase lag introduced by filtering, the residual given by Eq. (5.33) might no longer be zero for the faultless case.
Simulation results of the two-tank system. From top to bottom input u; tank levels \(h_1,\,h_2\); measured \(q_\mathrm{m}\); reconstructed levels \(h_1,\,h_2\); right-hand side of Eq. (5.33)
Structured residuals. Assume now that the flow \(q_{12}\) between the two tanks can be measured in addition to the input u and the outflow \(q_\mathrm{m}\), which leads to the additional measurement constraint
The system is over-constrained with two remaining constraints that lead to two residuals:

This matching results in the oriented graph shown in Fig. 5.33. Following the orientation of the edges, it is easy to see that the first parity relation depends only on the variables
while the second depends on
These two conditions can be used to selectively monitor Tank 1 and Tank 2. Only a fault in the connection flow \(q_{12}\) or its measurement would affect both constraints.
From the graph two ARRs \(arr_1(t)\) and \(arr_2(t)\) are obtained:
with
These residuals are structured in the sense that they become non-zero if Tank 1 or Tank 2 is affected by some fault. Hence, the additional measurement makes it possible not only to detect a fault in the overall system but to identify the affected component.
Structural isolability using the MSO approach. The ranking algorithm obtained one complete matching of the unknown variables. The matching can be represented in condensed form as follows, where 0 in a column denotes that the constraint is unmatched and used as an ARR.

Giving rise to the two ARRs listed above, structural detectability and isolability is shown in

where d denotes structurally detectable, i structurally isolable and n that the particular constraint cannot fail. Differential constraints cannot fail as these are just definitions that relate a variable \(\dot{h}\) with h through a differential operator. The result is that only one constraint is structurally isolable. Using the MSO set approach, the following MSO sets are received:

The fields either contain the matched unknown variables, zeros to indicate an unmatched constraints or nothing if constraints are not used in the MSO set. Four MSO sets are determined.
Using all four MSO sets and ARRs, the resulting detectability and isolability properties are shown in the following table:

Using all four ARR’s from MSO sets 1–4 results in enhanced isolability, now including both measurements. \(\square \)
It is a general finding that use of several ARR’s in parallel can enhance isolability. Violation of some constraints remain only detectable, and isolating these as possible sources of a fault requires another approach, referred to as active fault isolation.
6.6 Active Fault Isolation
Active structural isolation is an extension of the passive technique considered so far, where residuals were formed from ARRs by backtracking to known variables, input u(t) and measurements y(t), and evaluating the residual r(t) in real time. This approach was seen to lead to cases where some violations of constraints could only be detected but not isolated. We also encountered cases where violation of one of the constraints within a group could be pinpointed as the possible source of violation but isolation could not be achieved, i.e. we could not distinguish which of the constraints within the group had been violated (groupwise isolability).
Active fault isolation employs a perturbation in one or more of the input signals, once it has been detected that some fault is present, to attempt to determine which individual constraints have been violated.
Active isolation is needed if faults are groupwise isolable, i.e. within the group individual faults are detectable but not structurally isolable to an individual constraint. This does not necessarily imply that isolation cannot be achieved in other ways. Exciting the system with an input signal perturbation may make it possible to discriminate different responses of the same residual set, or from input to output in the system, when different constraints within the group are faulty. The following observation is obvious:
Lemma 5.3
Active structural isolation is possible if and only if both a structural condition and a quantitative condition are true.
-
Structural condition: The known variables in the set of residuals associated with a group of non-structurally isolable constraints include at least one control input.
-
Quantitative condition 1: The transfer from control inputs to residuals is affected differently by faults on different constraints.
-
Quantitative condition 2: The transfer from control inputs to outputs is affected differently by faults on different constraints.
Active structural isolation is possible if the structural condition and one or both of the quantitative conditions are met. In order to express the quantitative condition in rigorous terms, we need the following definitions, which are based on reachability and monitorability.
Definition 5.10
(Presence in path from input to residual or to output) Let \(z_j\) denote residual \(r_j\) or output \(y_j\). Let \(p^{(i,j)}\) \(=\{c_{f},c_{g},\ldots ,c_{h}\}\) be a path through the structure graph from input \(u_{i}\) to \(z_{j}\) and \(\prod ^{(i,j)}\) the union of valid paths from \(u_{i}\) to \(z_{j}\). Let
A constraint \(c_{h}\) is present in a path from \(u_{i}\) to \(z_{j}\), and the path includes the constraint \(c_{h}\in C_\mathrm{reach}^{(i,j)}\) if \(c_{h}\) is reachable from \(u_{i}\) and is monitorable from \(z_j\).
Lemma 5.4
Active structural isolability is from input to residual or to output. Two constraints \(c_{g}\) and \(c_{h}\) are actively isolable from residual, respectively, output signatures if
This Lemma advises an easily verifiable way to determine whether one or more constraints, which are only groupwise isolable with the passive approach outlined earlier, could be subjected to active isolation.
Active isolation is employed once a fault has been detected but the exact location could not be determined because the event only possess groupwise structural isolability with the set of residuals used.
Algorithmic aspects. A path through a graph can be determined from the adjacency matrix (cf. Chap. 4)
to show which nodes in a graph are connected. As the graph is bipartite, the adjacency matrix is easily obtained from the incidence matrix \({{\varvec{S}}}\) as
The adjacency matrix shows the result of a walk of length 1. A walk of length n will be described by \({{\varvec{A}}}^{n}.\) Reachability of element i from element j in the graph is determined by investigating the element (i, j) in the sequence of matrices
where cn is the number of elements in \(\{C,K_{i},K_{m}\}\). With the ith column of \({{\varvec{A}}}\) being an input, and the jth row an output, or the residual associated with the zero variable belonging to an unmatched constraint, a path of length m exists from i to j if and only if \({{\varvec{A}}}_{ij}^{m}\ne 0.\) The nodes passed on the walk are determined by tracing the non-zero elements of \({{\varvec{A}}}^{m}, {{\varvec{A}}}^{m-1},\ldots , {{\varvec{A}}}^{1}.\) While this algebraic method is intuitive and is related to the structure graph \({{\varvec{S}}}\), it is computationally inefficient for large systems and algorithmic methods exist that can find all paths from a given input to any variable in a graph.
Example 5.41
Active diagnosis Let a system be given by the structure graph shown in Fig. 5.34. The set of inputs is \(\mathcal{K}_{i}=\left\{ u_{1}, u_{2}\right\} \), the set of outputs \(\mathcal{K}_{m}=\left\{ y_{1}, y_{2}, y_{3}\right\} \), unknown variables are \(\mathcal{X}=\{x_{1}, x_{2}, x_{3}, x_{4}\}.\) The associated incidence matrix is shown in the following table:

A complete matching on the unknown variables can be achieved using the ranking algorithm, leaving \(c_{6}\) and \(c_{3}\) as unmatched constraints. The path found by the matching is the following:
and
The analytical redundancy relations associated with \(c_{3}\) and \(c_{6}\) constitute two parity relations for the system considered in the example and two residual generators are
The dependency matrix between residuals and constraints shown in

imply the detectability and the isolability as achievable from the two residuals. Linearly independent columns show that violation of constraint \(c_{6}\) can be isolated. The sets
are blockwise isolable but violation of any of the individual constraints will only be detectable.
In a fault-tolerant control setting, inputs \(u_{1}\) and \(u_{2}\) can be individually perturbed by the control system. The set of paths through constraints from \(u_{1}\) to the outputs are represented in the reachability table

The reachability from \(u_{2}\) is shown in

Following Lemma 5.4, it is easily seen that \(\{c_{1},c_{2},c_{3}\}\) are structurally isolable when active isolation is employed, while \(c_{4}\) remains detectable. \(\square \)
7 Structural Controllability and Structural Observability
Structural controllability and structural observability are two notions that have been introduced long ago with the aim to show that dynamical systems have the properties of controllability and of observability mainly for structural reasons. The well-known rank conditions on the controllability matrix or the observability matrix can only be satisfied if the non-zero entries of these matrices satisfy structural conditions.
This short section should show that as far as controllability and observability are concerned, structural results obtained by the analysis methods explained in this chapter by means of a bipartite graph are rather similar to those results that have been derived in control theory by a structural representation of linear dynamical systems by directed graphs.
7.1 Observability and Computability
Known and unknown variables. As before, the set of system variables \(\mathcal{Z}\) is decomposed into the sets \(\mathcal{K}\) of known variables and the set \(\mathcal X\) of unknown variables. Known variables are available in real time, while unknown variables are not directly measured. Observability is the system property that allows to determine all unknown variables from all known variables. Analysing the system observability coincides with identifying ways in which those unknown variables can be calculated.
Consider the general system described by the Eqs. (5.1)–(5.4)
with the set of known variables \(\mathcal{\mathcal{K}}=\{{{\varvec{u}}}, \,{{\varvec{y}}}\}\), the set of unknown variables \(\mathcal{X}=\{{{\varvec{x}}}_\mathrm{a}, \, {{\varvec{x}}}_\mathrm{d}, \,\dot{{{\varvec{x}}}}_\mathrm{d}\}\) and the set of constraints \(\mathcal{C}=\{{\varvec{g}}, {{\varvec{m}}}, {\varvec{h}}, \frac{\mathrm {d}}{\mathrm {d}t}\}\). According to the decomposition of \(\mathcal{Z}\) into \(\mathcal{K}\cup \mathcal{X},\, \mathcal{C}\) is decomposed into \(\mathcal{C}_{\mathcal{K}}\cup \mathcal{C}_{\mathcal{X}}\):
\(\mathcal{C}_{\mathcal{K}}\) is the largest subset of constraints such that \(Q(\mathcal{C}_{\mathcal{K}})\subseteq \mathcal{K}\). For the aim to analyse the possibility of computing the unknowns in \(\mathcal{X}\), only the subgraph \((\mathcal{C}_{\mathcal{X}},\,\mathcal{X},\,\mathcal{E}_{\mathcal{X}})\) needs to be decomposed.
7.2 Structural Observability Conditions
For the canonical decomposition
of the subgraph \((\mathcal{C}_{\mathcal{X}},\,\mathcal{X},\,\mathcal{E}_{\mathcal{X}})\) associated with the system (5.37)–(5.40), structural observability can be characterised as follows:
Theorem 5.5
(Structural observability) A necessary and sufficient condition for system (5.37)–(5.40) to be structurally observable is that, under derivative causality,
-
1.
all the unknown variables are reachable from the known ones,
-
2.
the over-constrained and the just-constrained subsystems are causal,
-
3.
no under-constrained subsystem exists.
Condition 1 says that there does not exist any subsystem whose behaviour is not reflected in the behaviour of the known variables, while Conditions 2 and 3 impul that all the variables can be matched using causal matchings and thus are uniquely defined once the known variables are given.
Example 5.42
Non-reachability Consider the following incidence matrix, in which the variable \(x_{3}\) is not reachable from the output.

The constraint set associated with such a structure graph has the form
It is seen that Subsystem 2 can by no means be observable. \(\square \)
Example 5.43
Observability of a nonlinear system Consider the following nonlinear dynamical system with two state variables, two input signals, one parameter \(\theta \) and one sensor:
This system is over-constrained and satisfies the three conditions of the above theorem. The following matching allows to compute the state.

The variable \(x_{2}\) can be reached from the known variables if and only if the matching \((c_{1},\,x_{2})\) can be used, which means that the two conditions
simultaneously have to hold. If not, the system is not observable, because there is no matching by means of which \(x_{2}\) could be computed under derivative causality.
This example illustrates the fact that structural properties provide results which are valid for almost every value of the system parameters and variables. \(\square \)
7.3 Observability and Structural Observability of Linear Systems
Let us consider the linear time-invariant system
where \({{\varvec{x}}}\) and \({{\varvec{y}}}\) are of dimensions n and p. In linear system theory it has been proved that the state is observable if and only if the following condition holds
for which a necessary condition is
Equation (5.45) means, in structural terms, that the unknown variable \({{\varvec{x}}}\) belongs to a causal just-constrained or over-constrained subsystem, when derivative causality is imposed. The structure graph is

where \({{\varvec{d}}}\) are the derivative constraints, which express that dots mean derivatives, \({{\varvec{m}}}\) are the constraints (5.43) from the measurement, and \({{\varvec{c}}}\) are the system constraints (5.42). \({{\varvec{S}}}_{C}\) and \({{\varvec{S}}}_{A}\) are the structures associated with matrices \({{\varvec{C}}}\) and \({{\varvec{A}}}\). Since no variable in \({{\varvec{x}}}\) can be matched from any constraint in \({{\varvec{d}}}\), the system \((\{{{\varvec{c}}}, {{\varvec{m}}}\},\;\{\dot{{{\varvec{x}}}}, {{\varvec{x}}}, {{\varvec{y}}}\})\) must be over-constrained with respect to \({{\varvec{x}}}\). It can be noted that this requirement does not constitute a sufficient condition, because the system parameters might have values such that (5.44)—or (5.45)—is not satisfied.
Example 5.44
Observability of linear systems Consider the unobservable linear time-invariant system
where the parameters \(a,\,b,\,c,\,d,\,e,\,f\) can take any real value. Its structure graph has the incidence matrix

where the constraints \(c_1,\,c_2,\,c_3\) represent the system (5.46), the constraints \(d_1,\,d_2,\,d_3\) express the derivative link between the \(x_1,\,x_2,\,x_3\) and the \(\dot{x}_1,\,\dot{x}_2,\dot{x}_3\) and m is the measurement Eq. (5.47). This system can be decomposed into a just-constrained part \(\mathcal{C}_{\mathcal{X}}^{0}=\{c_{1},\,c_{2},\,d_{3},m\}\), \(\mathcal{X}^{0}=\{\dot{x}_{1},\,\dot{x}_{2},\,\dot{x}_{3},\,x_{3}\}\) from which \(\dot{x}_{1},\,\dot{x}_{2},\,\dot{x}_{3}\) and \(x_{3}\) can be computed as functions of y for almost all values of the parameters, and an under-constrained part \(\mathcal{C}_{\mathcal{X}}^{-}=\{ c_{3},\,d_{1},\,d_{2}\}\), \(\mathcal{X}^{-}=\{x_{1},\,x_{2}\} \) in which \( x_{1}\) and \(x_{2}\) should both be computed from the single constraint \(c_{3}\). It can be checked that adding \(\dot{y}\) and the associated constraints, the subsystem \( \left( \{ c_{3},\,d_{1},\,d_{2}\}, \{x_{1},\,x_{2}\} \right) \) remains under-constrained and that this will always be the case when higher derivatives \(y^{(i)}\) will be considered. Consequently, the information available from the sensor is enough to place the vector \((x_{1},\,x_{2})^\mathrm{T}\) in a subspace of dimension one (since they are linked by one constraint which is known to be linear), but is not enough to compute this vector completely. The observability matrix
is not full rank, whatever the coefficients \(a,\,b,\,c,\,d,\,e,\,f\) are, and it can be checked that no more than the linear form \(ax_{1}+bx_{2}\) can be determined from the observation \((y,\dot{y},\ldots , y^{(s)})\) for any \(s\ge 1\).
Consider now the case that the second state variable is measured:
Then the system is observable. The structure graph has the incidence matrix

and the following causal matching shows that all the components of the state can be computed from y and its derivatives.

7.4 Graph-Based Interpretation and Formal Computation
Since an oriented graph can be associated with each matching, the observability property can be analysed from a graph-theoretical point of view. Let x be an observable variable. Then x can be matched with a constraint the input of which is either known or a set of observable variables. By repeating this argument, it follows that for x to be observable, it is necessary that there exists at least one subgraph (a set of alternated chains) which links this variable with the known variables \({{\varvec{u}}}\) and \({{\varvec{y}}}\) and where no unobservable variable acts as an input in any constraint of this subgraph. This subgraph with the observable target variable x may contain algebraic loops, but it does not contain any differential loop.
The constraints along the alternated chains show the computations which are to be performed in order to compute x. If these constraints are combined, a formal expression of x in terms of known variables can be obtained. A simple algebraic constraint in the chain means that the matched variable is computed as a function of the non-matched ones. An algebraic loop shows that a set of constraints has to be solved simultaneously. A derivative constraint means that the non-matched variable has to be derivated in order to obtain the matched variable (remember that only derivative causality is allowed). The number of derivative constraints which are included between a given input and the target variable shows the maximum order of derivations needed on this input for computing this target.
Note that this interpretation expresses that x belongs to a just- or an over-constrained causal subsystem. If x were to belong to an under-constrained subsystem, the corresponding subgraph would have less constraints than variables, i.e. some unknown variables would be input signals to constraints while being output of no other constraint.
For example, Fig. 5.35 shows the two graphs associated with the linear systems (5.46), (5.47) and (5.48), (5.49) which are non-observable or observable, respectively. It can be seen that in the first case, either \(x_{2}\) or \(x_{1}\) stands as an unknown input of constraint \(c_{3}\) while in the second case, both can be matched thus providing all the states with known predecessors at some level.
When different estimation subgraphs with the same target variable exist, they provide different computation schemes for the same variable. This feature is of interest when monitorability and reconfigurability are considered as discussed in the next section.
7.5 Structural Controllability
Controllability is a property which describes the links between the unknown variables and the input variables, independently of the fact that some unknown variables might be measured or not. Thus, it can be analysed from the structure graph in which the measurement constraints have been removed. Roughly speaking, controllability is concerned with the possibility of finding controls so as to achieve objectives, which are defined in terms of the values one wishes the system variables to be given.
The reachable set of a system is the set of states in which the system can be brought by an appropriate control input. Global controllability is a strong property, which states that the reachable set is the whole state space. Local controllability is a weaker property, which requires that any point in the open ball around a reachable point is also reachable. For linear systems, local and global properties coincide.
Let us first consider static systems \(\left( \mathcal{C},\,\mathcal{Z}\right) \) like
where \(\mathcal{C}=\{{\varvec{h}}\}\), \(\mathcal{Z}=\{{{\varvec{x}}}_\mathrm{a}, {{\varvec{u}}}\}\). For such systems, global controllability means that Eq. (5.50) can be solved for the unknown variables \({{\varvec{u}}}\) for any value of the known (wished) variables \({{\varvec{x}}}_\mathrm{a}\), thus justifying the decomposition of \(\mathcal{Z}\) into \(\mathcal{Z}=\mathcal{K}\cup \mathcal{X},\) with \(\mathcal{K}=\{{{\varvec{x}}}_\mathrm{a}\}\), \(\mathcal{X}=\{{{\varvec{u}}}\}\).
Theorem 5.6
(Controllability of static systems) Necessary and sufficient conditions for system (5.50) to be structurally controllable are the following:
-
(i)
The vertices of \(\mathcal{K}\) are reachable in the structure graph from the input,
-
(ii)
The canonical decomposition of \((\mathcal{C}_{\mathcal{X}},\,\mathcal{X},\,\mathcal{E}_{\mathcal{X}})\) contains no over-constrained subsystem.
If \(\mathcal{K}\) were not reachable from the input, there would be a decomposition of \({{\varvec{x}}}_\mathrm{a}\) into \({{\varvec{x}}}_\mathrm{a}^{\prime }\) (the reachable part), and \({{\varvec{x}}}_\mathrm{a}^{\prime \prime }\) (the unreachable part), such that the model can be written as
There is no solution to this model for any \({{\varvec{x}}}_\mathrm{a}\), namely when \({{\varvec{x}}}_\mathrm{a}\) is such that the part \({{\varvec{x}}}_\mathrm{a}^{\prime \prime }\) does not satisfy the second equation. On the other hand, if the canonical decomposition contains an over-constrained subsystem, the known variables satisfy some compatibility condition, which results in the existence of some manifold
and in the impossibility to find any control \({{\varvec{u}}}\) when the wished system states lie out of this manifold.
The case of dynamical systems is more complex, and except for linear systems, only the reachability condition of the above result can be extended. Consider the general system
where the known variables are \(\mathcal{K}=\{{{\varvec{x}}}_\mathrm{a}, \dot{{{\varvec{x}}}}_\mathrm{d}\}\), the unknown variables are \(\mathcal{X}=\{{{\varvec{x}}}_\mathrm{d}, {{\varvec{u}}}\}\) and the constraints are \(\mathcal{C}=\{{\varvec{g}}, {{\varvec{m}}}, \frac{\mathrm {d}}{\mathrm {d}t}\}\). As the initial conditions \({{\varvec{x}}}_\mathrm{d}(0)\) are known, derivative as well as integral causality can be used.
Theorem 5.7
(Reachability condition) A necessary condition for system (5.51)–(5.53) to be structurally controllable is that the vertices of \(\mathcal{K}\) can be reached in the structure graph from the input \({{\varvec{u}}}\).
This condition says that there does not exist any subsystem whose dynamical behaviour is independent of the input. The “no over-constrained subsystem” condition cannot be extended to the general case, but it holds for linear systems. For simplicity, let us drop algebraic equations, and consider the system (5.54), (5.55) with the known variables \(\mathcal{K}=\{\dot{{{\varvec{x}}}}_\mathrm{d}\}\), the unknown variables \(\mathcal{X}=\{{{\varvec{x}}}_\mathrm{d}, {{\varvec{u}}}\}\), and the constraints \(\mathcal{C}=\{{\varvec{g}}, \frac{\mathrm {d}}{\mathrm {d}t}\}\).
Theorem 5.8
(Linear continuous systems) If the constraints \({\varvec{g}}\) are linear, necessary and sufficient conditions for system (5.54), (5.55) to be structurally controllable are the following:
-
(i)
The vertices of \(\mathcal{K}\) are reachable in the structure graph from the input,
-
(ii)
the canonical decomposition of \((\mathcal{C}_{\mathcal{X}},\,\mathcal{X},\,\mathcal{E}_{\mathcal{X}})\) contains no over-constrained subsystem.
The existence of an over-constrained subsystem would imply that the known variables (here \(\dot{{{\varvec{x}}}}_\mathrm{d}\)) satisfy some compatibility conditions. For linear systems, these would be expressed as
where \({{\varvec{\alpha }}}\) is some constant vector, from which it follows that any system trajectory would belong to the manifold
Consequently, it is not possible to drive the system state to any point in the state space.
Condition (ii) does not extend to nonlinear systems, because in order to define a manifold the compatibility constraints (5.56) which would now be nonlinear should also be integrable. This property does not follow from structural considerations.
8 Structural Analysis in Summary
Structural analysis is an important tool, which is of interest in the early stage of the control and supervision system design. It can be employed even before detailed models are available, the structural analysis only needs that the principal behaviours of a system are specified in order to perform a useful and quite comprehensive analysis. Diagnosability and isolability of a behavioural fault (violation of a constraint) in a system can be made based on such sparse information. Analytical redundancy relations for use in diagnosis can be generated either from a complete matching and subsequent backtracking through the matching to known variables, or by using the minimal structurally over-determined (MSO) sets approach followed by a similar backtracking.
Disturbances or unknown parameters are handled in a structural analysis by defining such unknown quantities as additional unknown variables. When performing a matching, one additional constraint will be needed in the just-determined subsystem to calculate each additional unknown input. This means the available ARRs will reduced in number but will be insensitive to these unknown quantities. It is a salient feature of structural analysis that it generates ARRs equally well for linear and nonlinear systems.
The fault diagnosis and fault-tolerant control results it provides are the identification of the diagnosable part of the system, and the identification of the reconfiguration possibilities of the estimation the control scheme. Since detailed behaviour models need only to be developed for those parts of the system, structural analysis is also a tool for deciding which modelling investments must be done for the design of the control and supervision system.
The structural properties hold for the class \(\mathcal{S}(\mathcal{G})\) defined by the structure graph \(\mathcal{G}\) and, hence, for “almost all” single systems included in this class. Only in exceptional cases, the system under consideration does not have a property that the structural analysis has found for the corresponding class. This relation has been demonstrated in this chapter by several examples.
Observability analysis is the main step to identify the diagnosable part, which is the over-constrained subsystem within the observable one. Furthermore, structural analysis not only provides the computation mechanisms for the estimation algorithms and their reconfiguration, but it can also suggest which sensors should be implemented so as to change the status of system components from undiagnosable to diagnosable.
Structural analysis cannot help in defining fault accommodation strategies, because these strategies are aimed at investigating the means of achieving the system objectives, in spite of faults, without changing its structure. On the contrary, structural analysis is of prime importance as far as reconfiguration is concerned, because the results are expressed with reference to graph properties, whose changes can be analysed when vertices and edges disappear, as the consequence of switching off some system components, after a fault has occurred.
In summary, the following algorithm describes the design procedure for diagnosis based on structural analysis.

9 Exercises
Exercise 5.1
Structural analysis for industrial actuator Make a structural model of the actuator shown in Fig. 5.36.
-
1.
Determine the sets \(\mathcal{K}\) (known variables), \(\mathcal{X}\) (unknown variables) and \(\mathcal{Z}\) (all variables).
-
2.
List the set of constraints that describe the system shown in Fig. 5.36.
-
3.
Derive the incidence matrix and draw the structure graph.
-
4.
Ignore causality and determine a complete matching on \(\mathcal{X}\) that is non-causal.
-
5.
Use the ranking algorithm to determine a complete causal matching on \(\mathcal{X}\). List the unmatched constraints.
-
6.
Determine the parity relations found from the unmatched constraints by backtracking the structure graph to known variables along the paths of the matching,
$$ c_{i}(\mathcal{K}_i)=0 \wedge \; \mathcal{K}_i \subseteq \mathcal{K}. $$ -
7.
Express the parity relations in analytical form using the constraints from question 2. \(\square \)
Exercise 5.2
Structural analysis with unknown input Consider the speed control loop of Fig. 5.37, where \(n_\mathrm{ref}\) is the reference speed.
-
1.
Using the known variables
$$ \mathcal{K}=\left\{ i_{m},n_{m},\theta _{m}, n_\mathrm{ref}\right\} $$and the unknown variables
$$ \mathcal{X}=\left\{ i, Q_l, n, \dot{n}, \theta , \dot{\theta } \right\} , $$determine the set of constraints that describe the system.
-
2.
Build the structure graph for the system. Describe the graph as an incidence matrix and draw the graph.
-
3.
Apply the ranking algorithm on the graph to determine at least one causal matching. List which constraints remain unmatched.
-
4.
For each unmatched constraint, determine a parity relation \( c_{i}(\mathcal{K}_i)=0, \; \mathcal{K}_i \subseteq \mathcal{K}\). \(\square \)
Exercise 5.3
Parity relations for single-axis satellite This exercise considers structural analysis for a single-axis satellite described by the block diagram in Fig. 5.38. The figure illustrates a single axis of a satellite.
There are two input signals \(u_{1}\) and \(u_{2}\) to actuators 1 and 2, respectively, one unknown input d, and five measurements: \(y_{1}\) measures the state \(x_{1}\), \(y_{2}\) and \(y_{3}\) measure \(x_{2}\); \(y_{4}\) and \(y_{5}\) measure torque from actuators 1 and 2, respectively.
-
1.
Determine the sets of known variables, \(\mathcal{K}\), and unknown variables \(\mathcal{X}\). Verify that the intersection \(\mathcal{Z}=\mathcal{K} \cup \mathcal{X}\) gives the total set of variables.
-
2.
Determine the set of constraints that describe the system.
-
3.
Determine the causal structure graph for the system. Represent the graph as an incidence matrix and as a drawing.
-
4.
Use the ranking algorithm on the graph to find one or more complete matchings. List which constraints remain unmatched.
-
5.
From the unmatched constraints, determine the parity relations in analytic form:
$$ c_{i}(\mathcal{K}_i)=0, \; \mathcal{K}_i\subseteq \mathcal{K}. $$
You may wish to use the MATLAB programme SaTool to cope with the complexity of matching or for checking your results. A GNU open source license of SaTool is available from the book homepage. \(\square \)
Exercise 5.4
Parity relations and addition of a sensor Let a system be composed of 3 interconnected components, \(c_{1},c_{2},c_{3}\). Each component is described by one constraint according to the system
The variables \(x_{1},x_{2}\) which characterise the operation of components \(c_{1},c_{2}\) are not measured, only the output y of component \(c_{3}\) is known.
-
1.
Draw the structure graph of the system.
-
2.
Find a redundancy relation which allows to detect a fault in one of the components.
-
3.
Would it be worth to add a fourth component, that would measure \(x_{1}\) according to
$$ c_{4}:z(t)=x_{1}(t) $$z is now an extra known variable, but of course component n\({{}^\circ }4\) may also be faulty. \(\square \)
Exercise 5.5
A specialised arithmetic circuit The following specialised computation circuit is composed of 3 multipliers \(M_{1}\), \(M_{2}\) and \(M_{3}\) and two adders \(A_{1}\) and \(A_{2}\) (Fig. 5.39).
-
1.
Write the model of each system component.
-
2.
Give the incidence matrix of the structure graph (distinguish the known and the unknown variables).
-
3.
Find the analytical redundancy relations by eliminating the unknown variables.
-
4.
For each ARR, give the list of the components the faults of which it is sensitive to.
-
5.
Is there any non-detectable or non-isolable fault?
-
6.
What are the possible diagnostics associated with the following measurements?.

Exercise 5.6
Diagnosability analysis of an ABS test bed An ABS (anti-lock braking system) test bed is schematically drawn in Fig. 5.40. In a simplified version, the test bed has two wheels, where the lower wheel is powered by a motor, whereas the upper wheel has a brake with the braking torque \(M_\mathrm{B}\). The wheel angular velocities are denoted by \(\omega _1\) and \(\omega _2\), the forces between the wheels by \(F_\mathrm{z}\), the lateral force by \(F_\mathrm{x}\) and the masses and inertias by \(m_1\), \(m_2\), \(J_1\) and \(J_2\). The wheel vertical force \(F_\mathrm{z}\) is determined by the geometry of the test bed including the air pressure in the tyres (which may be too low by fault).
The model of the test bed is given below:
Measurable signals are \(M_\mathrm{B}(t)\), \(\omega _1(t)\), \(\omega _2(t)\) whereas the signals \(\dot{\omega }_1(t)\), \(\dot{\omega }_2(t)\) may be measured if this is necessary for fault diagnosis.
-
1.
Draw the structure graph.
-
2.
Analyse the test bed and determine analytical redundancy relations for fault diagnosis.
-
3.
Which signals have to be measured to make the test bed detectable or isolable? \(\square \)
10 Bibliographical Notes
Offering a way to advise how to solve large sets of equations, structural concepts and bipartite graphs were introduced and seminal theoretical results for bipartite graphs were obtained in [17, 86, 87]. The structural approach was first brought into the field of fault in [76].
Decomposition of large systems. Structural concepts have been used since the 1960 and 1970s for the decomposition of large systems of equations in view of their hierarchical resolution [142, 341]. An important issue in that field is also the solvability of large scale differential and algebraic equation systems, for which [193, 371] addressed and employed structural analysis.
Algorithms. Algorithms to compute maximum matchings were studied along with the penetration of electronic computers into engineering research motivated by important applications in operational analysis and in chemical engineering. An algorithm of complexity \(O(\mathcal{N}^{3})\) to find maximum matchings was proposed in [89], while [150] found an algorithm of complexity \(O(\mathcal{N}^{2.5})\) for bipartite graphs. Maximum matchings can also be found from the solutions to the assignment problem [189], or from the maximum flow problem [110, 111]. For details on the algorithms and more bibliographical notes, refer to [17, 62, 131, 206]. Theorem 5.2 was proved in [17].
Looking into maximal isolability and minimum computational complexity, it turned out that finding all possible analytical redundancy relations through finding all possible complete matchings was impractical if not impossible for industrial size systems. Inspired by experience from automotive diagnosis, references [184, 187] proposed to find MSO sets as a more direct way to determined all possible ARRs for a given system and an alternative decomposition of the structure graph and an extremely efficient algorithm (cf. Algorithm 5.4).
Observability, controlability. The technique has also been used for analysis of system structural properties like observability and controllability, where most works use a digraph representation and address linear systems [130, 195, 196, 232]. They have also been extended to the design of multivariable control systems, including considerations like disturbance rejection [286, 301].
Fault diagnosis. In the field of fault diagnosis, structural concepts have been used since the beginning of the 1990s, for the analysis of system monitorability [76] and for the design of structured residuals [126], which provide straightforward decision procedures for fault isolation [69]. An overview can be found in [325].
Realisability and optimization. Issues with realisation of residual generators in large systems caused the development of selection procedures [19], continued by implementations with mixed causality in [337, 352] considered further into issues of causal computations. Furthermore, [354] suggested algorithms for realizability constrained selection of residual generators.
Applications. Significant applications in marine systems were described in [23, 28, 159]. A significant effort related to diagnosis in car engines and for other automotive applications were reported in [350, 352]. Application to large 3-phase systems was discussed in [180]. Diagnosis to determine downhole drilling incidents in [387] and combined diagnosis, active fault isolation and fault-tolerant control was demonstrated for thruster assisted position mooring for offshore production vessels in [238].
Finally, structural concepts have been applied to the problem of sensor selection [57, 230], for component-oriented analysis [370] and for service diagnosis [372, 373].
Relations to AI. The Artificial Intelligence approach to causality in device behaviour [158], which is used in the theory of model-based diagnosis, is also very close to the concept of matching in bipartite graphs. Since the obtained models are mainly under a graphic form, the theory of bond graphs has brought about many specific tools for structural analysis.
Multiple faults and active isolation. Structural analysis was also found useful to cope with the complexity of analysis in cases of multiple faults [23]. An extension of the structural analysis to advise on possibilities of active isolation was suggested in [33] with an application reported in [238].
Algorithms and software tools. The SaTool software environment (GNU public license) that has been used for several examples in this book was introduced in [31]. A large framework for diagnosis design in the automotive industry was presented in [107]. Efficient algorithms for finding structurally minimal over-determined sets were suggested in [187], and [6] compared different algorithms.
Notes
- 1.
In Eq. (5.8), Q has been defined as a mapping from the power set of the set of constraints towards the power set of the set of variables. It is used here also for a single constraint c where for notational convenience \(Q(\{c\})\) is written as Q(c).
- 2.
The term \(\frac{\partial c}{\partial z}\) denotes the derivative of the left-hand side of the constraint \(c(z_1, z_2\ldots )=0\).
- 3.
The notation \(\varphi \) is used—as a mnemonic for “fault”—instead of c which was a mnemonic for “constraint”.
- 4.
This set is called the structure of the residual in the control community and it is called a conflict in the Artificial Intelligence community.
- 5.
The symbol \(\mathcal{S}\) is used as a mnemonic for “solve”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Blanke, M., Kinnaert, M., Lunze, J., Staroswiecki, M. (2016). Structural Analysis. In: Diagnosis and Fault-Tolerant Control. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-47943-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-47943-8_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-47942-1
Online ISBN: 978-3-662-47943-8
eBook Packages: EngineeringEngineering (R0)








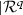 . As an algebraic relation like
. As an algebraic relation like  , it cannot be satisfied by all
, it cannot be satisfied by all  . Otherwise, the equation
. Otherwise, the equation 













 satisfies the system of equations. Assumption
satisfies the system of equations. Assumption 



















