Comparing Semantics Under Strong Timing of Petri Nets

Abstract

The intention of the note is towards a framework for developing, studying and comparing observational semantics in the setting of a real-time true concurrent model. In particular, we introduce trace and bisimulation equivalences based on interleaving, step and causal net semantics in the setting of Petri nets with strong timing, i.e. Petri nets whose transitions are labeled with time firing intervals, can fire only if their lower time bounds are attained, and are forced to fire when their upper time bounds are reached. We deal with the relationships between the equivalences showing the discriminating power of the approaches of the linear-time – branching-time and interleaving – partial order spectra. This allows studying in complete detail the timing behaviour in addition to the degrees of relative concurrency and nondeterminism of processes.

This work is supported in part by DFG-RFBR (project CAVER, grants BE 1267/14-1 and 14-01-91334).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the core of every theory of systems lies a notion of equivalence between systems: it indicates which particular aspects of systems behaviors are considered to be observable. In concurrency theory, a variety of observational equivalences have been promoted, and the relationships between them have been quite well-understood.

In order to investigate the performance of systems (e.g. the maximal time used for the execution of certain activities and average waiting time for certain requests), many time extensions have been defined for a non-interleaving model of Petri nets. On the other hand, there are few mentions of a fusion of timing and partial order semantics, in the Petri net literature. In [6], processes of timed Petri nets (under the asap hypothesis) have been defined by an algebra of the so-called weighted pomsets. The paper [5] has provided and compared timed step sequence and timed process semantics for timed Petri nets. A method to compute all valid timings for a causal net process of a time Petri net has been put forward in [1]. Branching processes (unfoldings) of time Petri nets have been constructed in [4].

To the best of our knowledge, the incorporation of timing into equivalence notions on Petri nets is even less advanced. In this regard, the paper [2] is a welcome exception, where the testing approach has been extended to Petri nets with associating clocks to tokens and time intervals to arcs from places to transitions. Also, it is worth mentioning the paper [3] that compares different subclasses of timed Petri nets with strong timing semantics on the base of timed interleaving language and bisimulation equivalences.

The intention of the note is towards developing, studying and comparing trace and bisimulation equivalences based on interleaving, step, and partial order (causal net) semantics in the setting of Petri nets with strong timing (elementary net systems whose transitions are labeled with time firing intervals, can fire only if their lower time bounds are attained, and are forced to fire when their upper time bounds are reached).

2 Time Petri Nets

In this section, we define some terminology concerning time Petri nets which were introduced in [1] and extend elementary net systems with timing constraints (time intervals) on the firings of transitions.

The domain $\mathbb {T}$ of time values is the set of natural numbers. We denote by $[\tau _1,\tau _2]$ the closed interval between two time values $\tau _1,\tau _2\in \mathbb {T}$. Infinity is allowed at the upper bounds of invervals. Let $Interv$ be the set of all such intervals. We use $Act$ to denote an alphabet of actions.

Definition 1

A (labeled over $Act$) time Petri net is a tuple $\mathcal{TN} = ((P$, $T$, $F$, $M_0$, $L)$, $D)$, where $(P,T,F,M_0,L)$ is a Petri net with a set $P$ of places, a set $T$ of transitions $(P\cap T = \emptyset )$, a flow relation $F\subseteq (P\,\times \,T)\cup (T\,\times \,P)$, an initial marking $\emptyset \ne M_0 \subseteq P$, a labeling function $L:T\rightarrow Act$, and $D : T \rightarrow Interv$ is a static timing function associating with each transition a time interval.

For $x \in P\cup T$, let $^{\bullet } x =\{y\mid (y,x)\in F\}$ and $x^{\bullet } =\{y\mid (x,y)\in F\}$ be the preset and postset of $x$, respectively. For $X\subseteq P\cup T$, define $^{\bullet }X=\bigcup _{x\in X}^{\bullet }x$ and $X^{\bullet }=\bigcup _{x\in X}x^{\bullet }$. For a transition $t\in T$, the boundaries of the interval $D(t)\in Interv$ are called the earliest firing time $Eft$ and latest firing time $Lft$ of $t$.

A marking $M$ of $\mathcal{TN}$ is any subset of $P$. A transition $t$ is enabled at a marking $M$ if $^{\bullet }t \subseteq M$ (all its input places have tokens in $M$), otherwise the transition is disabled. Let $En(M)$ be the set of transitions enabled at $M$. We call a non-empty subset $U\subseteq T$ a step enabled at a marking $M$, if ($\forall t\in U\mathrel {\scriptscriptstyle \diamond }t\in En(M)$) and ($\forall t\ne t'\in U\mathrel {\scriptscriptstyle \diamond }^{\bullet }t\cap ^{\bullet }t' = \emptyset$).

Consider the behavior of the time Petri net $\mathcal{TN}$. A state of $\mathcal{TN}$ is a triple $(M,I,GT)$, where $M$ is a marking, $I: En(M)\longrightarrow \mathbb {T}$ is a dynamic timing function, and $GT\in \mathbb {T}$ is a global time moment. The initial state of $\mathcal{TN}$ is a triple $S_0=(M_0,I_0,GT_0)$, where $M_0$ is an initial marking, $I_{0}(t)=0$, for all $t\in En(M_{0})$, and $GT_0=0$.

A step $U \subseteq T$ enabled at a marking $M$ is fireable from a state $S=(M,I,GT)$ after a delay time $\theta \in \mathbb {T}$ if ($\forall t\in U\mathrel {\scriptscriptstyle \diamond }Eft(t)\le I(t)+\theta$) and ($\forall t'\in En(M) \mathrel {\scriptscriptstyle \diamond }I(t')+\theta \le Lft(t')$). Let $Contact(S)=\{t\in U\mid$ $U$ is a step fireable from a state $S=(M,I,GT)$ after some delay time $\theta \in \mathbb {T}$ and $(M \setminus ^{\bullet }t)\cap t^{\bullet }\ne \emptyset )\}$.

The firing of a step $U$ fireable from a state $S =(M,I,GT)$ after a delay time $\theta$ leads to the new state $S'=(M',I',GT')$ given as follows:

• (i) $M'=(M\setminus ^{\bullet }U)\cup U^{\bullet }$,

• (ii) $\forall t' \in T\mathrel {\scriptscriptstyle \diamond }I'(t') = \left\{ \begin{array}{ll} I(t')+ \theta , &{} \text{ if } t' \in En(M\setminus ^{\bullet }U),\\ 0, &{} \text{ if } t' \in En(M')\setminus En(M\setminus ^{\bullet }U),\\ \text{ undefined }, &{} \text{ otherwise, } \end{array} \right.$

• (iii) $GT'=GT+\theta$.

In this case, we write $S\mathop {\longrightarrow }\limits ^{(U,\theta )}S'$, and, moreover, $S\mathop {\longrightarrow }\limits ^{(A,\theta )}S'$, if $A=L(U)=\sum _{t\in U}L(t)$. A finite or infinite sequence of the form: $S=S^0$ $\mathop {\longrightarrow }\limits ^{(U_1,\theta _1)}$ $S^1$ $\mathop {\longrightarrow }\limits ^{(U_2,\theta _2)}S^2$ $\ldots$, is a step firing sequence of $\mathcal{TN}$ from the state $S$. Then, $(U_1,\theta _1)$ $(U_2,\theta _2)$ $\ldots$ is called a step firing schedule of $\mathcal{TN}$ from $S$. The sequence is an interleaving firing schedule of $\mathcal{TN}$ from $S$, if $|U_i|=1$, for all $i\ge 1$. Define the step (interleaving) language of $\mathcal{TN}$ as follows: $\mathcal{L}_{s(i)}(\mathcal{TN})=\{(A_1,\theta _1)\ldots (A_k,\theta _k) \mid$ $(U_1,\theta _1)$ $\ldots$ $(U_k,\theta _k)$ is a step (interleaving) firing schedule of $\mathcal{TN}$ from the initial state $S_0$, and $A_k=L(U_k)$ ($k\ge 0$)}.

A state $S$ of $\mathcal{TN}$ is reachable if it appears in some step firing sequence of $\mathcal{TN}$ from the initial state $S_0$. Let $RS(\mathcal{TN})$ denote the set of all reachable states of $\mathcal{TN}$. We call $\mathcal{TN}$ $T$ -restricted if $^{\bullet } t\ne \emptyset \ne t^{\bullet }$ for all transitions $t\in T$; contact-free if $Contact(S)=\emptyset$ for all $S\in RS(\mathcal{TN})$; time-progressive if for every infinite step firing schedule $(U_1,\theta _1)$ $(U_2,\theta _2)$ $(U_3,\theta _3)$ $\ldots$ of $\mathcal{TN}$ from some $S\in RS(\mathcal{TN})$, the series $\theta _1 + \theta _2 + \theta _3+\ldots$ diverges. In what follows, we will consider only $T$-restricted, contact-free and time-progressive time Petri nets.

Fig. 1.

An example of a time Petri net

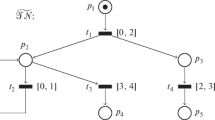
Example 1

Figure 1 shows a time Petri net $\mathcal{TN}$. Both $\sigma = (\{t_1, t_3\}, 3)$ and $\sigma ' = (\{t_1, t_3\}, 3) (\{t_2\}, 2) (\{t_1, t_3\}, 2) (\{t_4,t_5\}, 2)$ are step firing schedules of $\mathcal{TN}$ from $S_0= (M_0, I_0, GT_0)$, where $M_0 = \{p_1, p_2\}$, $I_0(t) = \left\{ \begin{array}{ll} 0, &{} \text{ if } t\in \{t_1, t_3\},\\ {undefined}, &{} \text{ otherwise, } \end{array} \right.$ and $GT_0=0$. Furthermore, $\widehat{\sigma } = (\{t_2\}, 2) (\{t_1, t_3\}, 2) (\{t_4,t_5\}, 2)$ is a step firing schedule of $\mathcal{TN}$ from $S = (M, I, GT)$, where $M = \{p_3, p_4\}$, $GT = 3$, and $I(t) = \left\{ \begin{array}{ll} 0, &{} \text{ if } t \in \{t_2, t_4, t_5\}\\ {undefined}, &{} \text{ otherwise. } \end{array} \right.$ It is easy to see that $\mathcal{TN}$ is really $T$-restricted, contact-free and time-progressive.

3 Time Process Semantics

First, consider definitions related to time partial orders.

Definition 2

A (labeled over $Act$) time partial order is a tuple $\eta =(X,\prec ,\lambda ,\tau )$ consisting of a set $X$; a transitive, irreflexive relation $\prec$; a labeling function $\lambda :X\rightarrow Act$; and a timing function $\tau : X \rightarrow \mathbb {T}$ such that $e\prec e'\Rightarrow \tau (e)\le \tau (e')$. As usual, we write $x\preceq y$ for $x \prec y$ or $x = y$. Often $\prec$ is called a strict partial order, while $\preceq$ is a partial order, i.e. a reflexive, antisymmetric and transitive relation.

Time partial order sets over $Act$, $\eta =(X,\prec ,\lambda ,\tau )$ and $\eta '=(X',\prec ',\lambda ',\tau ')$, are isomorphic (denoted $\eta \sim \eta '$) iff there is a bijective mapping $\beta :X \rightarrow X'$ such that (i) $x \prec y\ \iff \ \beta (x) \prec ' \beta (y)$, for all $x,y\in X$; (ii) $\lambda (x)=\lambda '(\beta (x))$ and $\tau (x)=\tau '(\beta (x))$, for all $x \in X$. The isomorphic class of a time partial order over $Act$, $\eta$, is called a time pomset over $Act$ and denoted as $pom(\eta )$.

Next, define the concept of a time causal net.

Definition 3

A (labeled over $Act$) time causal net is a finitary, acyclic net $TN=(B, E, G,l,\tau )$ with a set $B$ of conditions, a set $E$ of events, a flow relation $G \subseteq (B\,\times \,E)\cup (E\,\times \,B)$ such that $\{e\mid (e,b)\in G\}=\{e\mid (b,e)\in G\}=E$, and, for any $b \in B$, $|\{e\mid (e,b)\in G\}|=|\{e\mid (b,e)\in G\}|\le 1$, a labeling function $l:E\rightarrow Act$, and a time function $\tau : E \rightarrow \mathbb {T}$ such that $e\ G^+\ e' \Rightarrow \tau (e)\le \tau (e')$. Let $\tau (TN)=\sup \{\tau (e)\mid e\in E\}$.

Time causal nets over $Act$, $TN=(B$, $E$, $G$, $l$, $\tau )$ and $TN'=(B'$, $E'$, $G'$, $l'$, $\tau ')$, are isomorphic (denoted $TN \simeq TN'$) iff there exists a bijective mapping $\beta : B \cup E \rightarrow B' \cup E'$ such that (i) $\beta (B)=B'$ and $\beta (E)=E'$; (ii) $x\ G\ y\iff \beta (x)\ G'\ \beta (y)$, for all $x, y \in B \cup E$; (iii) $l(e)=l'(\beta (e))$ and $\tau (e)=\tau '(\beta (e))$, for all $e \in E$.

Specify additional notions and notations for a time causal net $TN$. Let $^{\bullet } x =\{y\mid (y,x)\in G\}$ and $x^{\bullet } =\{y\mid (x,y)\in G\}$, for $x \in B\cup E$; $^{\bullet }X=\bigcup _{x\in X}^{\bullet }x$ and $X^{\bullet }=\bigcup _{x\in X}x^{\bullet }$, for $X\subseteq B\cup E$; and $^{\bullet }TN=\{b \in B \mid ^{\bullet }b=\emptyset \}$, $TN^{\bullet }=\{b \in B \mid b^{\bullet }=\emptyset \}$. Also, $\prec =G^+$ and $\preceq =G^*$. For a downward-closed (w.r.t. $\preceq$) subset $E'\subseteq E$, define the set $Cut(E')=(E'^{\bullet } \ \cup \ ^{\bullet }TN)\setminus ^{\bullet }E'$. A downward-closed subset $E'\subseteq E$ is called timely sound if $\tau (e')\le \tau (e)$, for all $e'\in E'$ and $e\in E\setminus E'$. Clearly, $\eta (TN)=(E,\prec \cap (E\,\times \,E),l,\tau )$ is a time partial order. For $x,x'\in B\cup E$, $x \ \smile \ x'\iff \lnot ((x\prec x')\ \vee \ (x'\prec x)\ \vee \ (x=x'))$ (concurrency). A subset $\emptyset \ne E'\subseteq E$ is a step of TN iff $e \ \smile \ e'$ and $\tau (e)=\tau (e')$, for all $e, e'\in E'$. In this case, let $\tau (E')=\tau (e)$ for some $e\in E'$. An s-linearization of a time causal net $TN$ is a finite or infinite sequence $\rho =V_1 V_2\ldots$ of steps of $TN$, such that every event of $TN$ is included in the sequence exactly once, and both causal and time orders are preserved: $(e_i\prec e_j\vee \tau (e_i) < \tau (e_j)) \Rightarrow i < j$, for all $e_i\in V_i$ and $e_j\in V_j$ ($i,j\ge 1$). An $s$-linearization $\rho$ of $TN$ is called an i-linearization of $TN$, if $|V_i|=1$, for all $i\ge 1$. For an $s$-linearization $\rho =V_1 V_2\ldots$ of $TN$, define $E^k_{\rho } = \bigcup _{1\le i\le k} V_i$ ($k\ge 0$). Clearly, $E^k_{\rho }$ is a downward-closed subset of $E$.

Given time causal nets $TN=(B, E, G,l,\tau )$, $\widehat{TN}=(\widehat{B},\widehat{E},\widehat{G},\widehat{l},\widehat{\tau })$ and $TN'=(B',E',G',l',\tau ')$, $TN$ is a prefix of $TN'$ (denoted ${TN}\mathop {\longrightarrow }\limits ^{{}}{TN'}$) if $B \subseteq B'$, $E$ is a finite, downward-closed and timely sound subset of $E'$, $G=G'\cap (\,\times \,E\cup E\,\times \,B)$, $l=l'\mid _{E}$, and $\tau =\tau '\mid _{E}$; $\widehat{TN}$ is a suffix of $TN'$ w.r.t. TN if $\widehat{E}=E'\setminus E$, $\widehat{B}=B'\setminus B\cup TN^{\bullet }$, $\widehat{G}=G'\cap (\widehat{B}\,\times \,\widehat{E}\cup \widehat{E}\,\times \,\widehat{B})$, $\widehat{l}=l'\mid _{\widehat{E}}$, and $\widehat{\tau }=\tau '\mid _{\widehat{E}}$. We write ${TN}\mathop {\longrightarrow }\limits ^{{\widehat{TN}}}{TN'}$ iff ${TN}\mathop {\longrightarrow }\limits ^{{}}{TN'}$ and $\widehat{TN}$ is a suffix of $TN'$ w.r.t. $TN$.

We are now ready to define the notion of a time process of $\mathcal{TN}$ enabled at some marking.

Definition 4

Given a time Petri net $\mathcal{TN}=(P,\ T,\ F,\ M_0,\ L,\ D)$ with its marking $M$, a pair $\pi =(TN, \varphi )$ with a time causal net $TN=(B$, $E$, $G$, $l$, $\tau )$ and a mapping $\varphi : B \cup E \rightarrow P \cup T$ is a time process of $\mathcal{TN}$ enabled at $M$ iff the following conditions hold:

• $\varphi (B)\subseteq P$, $\varphi (E)\subseteq T$,

• the restriction of $\varphi$ to $^{\bullet }e$ is a bijection between $^{\bullet }e$ and $^{\bullet }\varphi (e)$ and the restriction of $\varphi$ to $e^{\bullet }$ is a bijection between $e^{\bullet }$ and $\varphi (e)^{\bullet }$, for all $e\in E$,

• the restriction of $\varphi$ to $^{\bullet }TN$ is a bijection between $^{\bullet }TN$ and $M$,

• $l(e)=L(\varphi (e))$, for all $e \in E$.

We use $\mathcal{EN}(\mathcal{TN})$ ($\mathcal{EN}(\mathcal{TN},M)$) to denote the set of time processes of $\mathcal{TN}$ enabled at the initial marking $M_0$ (a marking $M$).

Given a time process $\pi =(TN, \varphi )\in \mathcal{EN}(\mathcal{TN},M)$, a state $S=(M,I,GT)$ of $\mathcal{TN}$, and a subset $B'\subseteq B_{TN}$, the latest global time moment when tokens appear in all input places of the transition $t\in En(\varphi (B'))$ is defined as follows:

$$\mathbf{TOE}_{\pi ,S}(B',t) = \max \Big (\{\tau _{TN}(^{\bullet }b) \mid b \in B'_{[t]} \setminus ^{\bullet }TN \} \cup \{\overline{GT}\}\Big ),$$

where $B'_{[t]} = \{b \in B' \mid \varphi _{TN}(b) \in ^{\bullet }t \}$, $\overline{GT}=GT-I(t)$, if $B'_{[t]}\subseteq ^{\bullet }TN$, and $\overline{GT}=GT$, otherwise. Notice that the above is an extension of the definition of $\mathbf{TOE}(\cdot ,\cdot )$ from [1] to the case of time processes of $\mathcal{TN}$ enabled at an arbitrary marking and not only at the initial one.

Definition 5

A time process $\pi =(TN, \varphi )\in \mathcal{EN}(\mathcal{TN},M)$ is fireable from a state S iff for all $e \in E$ it holds:

• (i) $\tau (e) \ge GT$,

• (ii) $\tau (e) \ge {\varvec{TOE}}_{\pi ,S}(^{\bullet }e, \varphi (e)) + Eft(\varphi (e))$,

• (iii) $\forall t \in En(\varphi (C_e))\mathrel {\scriptscriptstyle \diamond }\tau (e) \le {\varvec{TOE}}_{\pi ,S}(C_e, t) + Lft(t)$, where $C_e=Cut(Earlier(e)=\{e'\in E\mid \tau (e')<\tau (e)\})$.

The time process $\pi _0=(TN_0=(B_0,\emptyset ,\emptyset ,\emptyset ,\emptyset )$, $\varphi _0)$ of $\mathcal{TN}$ fireable from the initial state is called the initial time process of $\mathcal{TN}$. We use $\mathcal {FI}(\mathcal{TN})$ ($\mathcal {FI}(\mathcal{TN},S)$) to denote the set of time processes of $\mathcal{TN}$ fireable from the initial state (a state $S\in RS(\mathcal{TN})$). The pomset language of $\mathcal{TN}$ is given by $\mathcal{L}_{pom}(\mathcal{TN})=\{pom(\eta (TN))\mid$ $\pi =(TN,\varphi )\in \mathcal {FI}(\mathcal{TN})\}$.

We now intend to realize for a time Petri net the relationships between its firing schedules from reachable states and its time processes fireable from the states. For $\pi =(TN,\varphi )\in \mathcal {FI}(\mathcal{TN},S)$, define the function $FS_{\pi ,S}$ which maps any $s$-linearization $\rho =V_1 V_2\ldots$ of $TN$ to the sequence of the form: $FS_{\pi ,S}(\rho )=(\varphi (V_1),\tau (V_1)-GT)$ $(\varphi (V_2),\tau (V_2)-\tau (V_1))$ $\ldots$.

Lemma 1

• Given $\pi =(TN,\varphi )\in \mathcal {FI}(\mathcal{TN},S=(M,I,GT))$ and an $s(i)$-linearization $\rho = V_1V_2 \ldots$ of $TN$, $FS_{\pi ,S}(\rho )$ is a step (interleaving) firing schedule of $\mathcal{TN}$ from the state $S$.

• For any step (interleaving) firing schedule $\sigma$ of $\mathcal{TN}$ from a state $S\in RS(\mathcal{TN})$, there is a unique (up to an isomorphism) time process $\pi =(TN,\varphi )\in \mathcal {FI}(\mathcal{TN}, S)$ such that $FS_{\pi ,S}(\rho ) = \sigma$, where $\rho$ is an $s(i)$-linearization of $TN$.

Notice that the items of the Lemma are extensions of Theorems 19 and 21 from [1] to the cases of $s$-linearizations on time processes of $\mathcal{TN}$ fireable from arbitrary reachable states and step firing schedules of $\mathcal{TN}$ from the states.

For $\pi =(TN, \varphi ),\pi '=(TN',\varphi ')\in \mathcal{FI}(\mathcal{TN})$, we write ${\pi }\mathop {\longrightarrow }\limits ^{{\widehat{\pi }=(\widehat{TN},\widehat{\varphi })}}{\pi '}$ iff ${TN}\mathop {\longrightarrow }\limits ^{{\widehat{TN}}}{TN'}$, $\varphi =\varphi '|_{B\cup E}$, and $\widehat{\varphi }=\varphi '|_{\widehat{B}\cup \widehat{E}}$.

Theorem 1

If $\pi =(TN, \varphi )$, $\pi ' =(TN', \varphi ')\in \mathcal {FI}(\mathcal{TN})$ such that ${\pi }\mathop {\longrightarrow }\limits ^{{\widehat{\pi }}}{\pi '}$, then $\widehat{\pi }=(\widehat{TN},\widehat{\varphi })\in \mathcal {FI}(\mathcal{TN},S=(M,I,GT))$, where $M=\varphi (TN^{\bullet })$, $I(t) = \left\{ \begin{array}{ll} \tau (TN)-\mathbf{TOE}_{\pi ,S_0}(TN^{\bullet },t), &{} \text{ if } t \in En(M)\\ \text{ undefined }, &{} \text{ otherwise, } \end{array} \right.$ and $GT=\tau (TN)$.

From now on, we write ${\pi }\mathop {\longrightarrow }\limits ^{{u}}{\pi '}$ iff ${\pi }\mathop {\longrightarrow }\limits ^{{\widehat{\pi }}}{\pi '}$ and $u=pom(\eta ({\widehat{TN}}))$.

Fig. 2.

An example of a time causal net

Example 2

The time causal net $TN' = (B',\ E',\ G',\ l',\ \tau ')$ is depicted in Fig. 2, where the net elements are accompanied by their names, and the values of the functions $l'$ and $\tau '$ are indicated nearby the events. Define the time causal nets $TN = (B,\ E,\ G,\ l,\ \tau )$, with $B = \{b_1, \ldots , b_4 \}$, $E = \{e_1, e_3\}$, $G = G' \cap (B\,\times \,E\cup E\,\times \,B)\}$, $l = l'\mid _{E}$, $\tau = \tau ' \mid _{E}$, and $\widehat{TN} = (\widehat{B},\ \widehat{E},\ \widehat{G},\ \widehat{l},\ \widehat{\tau })$, with $\widehat{B} = B' \setminus B \cup \{b_3, b_4\}$, $\widehat{E} = E' \setminus E$, $\widehat{G} = G' \cap (\widehat{B}\,\times \,\widehat{E} \cup \widehat{E}\,\times \,\widehat{B})$, $\widehat{l} = l'\mid _{\widehat{E}},\ \widehat{\tau } = \tau ' \mid _{\widehat{E}}$. It is easy to see that $TN$ is a prefix of $TN'$, $\widehat{TN}$ is a suffix of $TN'$ w.r.t. $TN$, and, moreover, ${TN}\mathop {\longrightarrow }\limits ^{{\widehat{TN}}}{TN'}$.

Define a mapping $\varphi '$ from the time causal net $TN'$ to the time Petri net $\mathcal{TN}$ (see Fig. 1) as follows: $\varphi '(b_{i}) = p _i$ ($1 \le i \le 6$), $\varphi '(b_{i}) = p _{i-6}$ ($7 \le i \le 10$), and $\varphi '(e_{i}) = t _i$ ($1 \le i \le 5$), $\varphi '(e_6) = t_1$, $\varphi '(e_7) = t_3$. Next, for the time causal nets $TN$ and $\widehat{TN}$, set $\varphi = \varphi ' \mid _{E \cup B}$ and $\widehat{\varphi } = \varphi ' \mid _{\widehat{E} \cup \widehat{B}}$, respectively. Obviously, $\pi ' = (TN', \varphi ')$ and $\pi = (TN, \varphi )$ are time processes of $\mathcal{TN}$ enabled at $M_0$.

Take $S = (M,I,GT)$ as specified in Example 1, $\widetilde{B} = \{b_3, b_4\}$, and $t_2 \in En(\varphi '(\widetilde{B}))$. Calculate $\mathbf{TOE}_{\pi ',S}(\widetilde{B},t_2) = \max \Big (\{\tau _{TN'}(^{\bullet }b)\mid b\in \widetilde{B}_{[t_2]}\setminus ^{\bullet }TN' \} \cup \{\overline{GT}\}\Big ) = \max \Big (\{\tau '(e_1)=3, \tau '(e_3)=3\} \cup \{3\}\Big ) = 3$.

It is not difficult to check that $\pi ' = (TN', \varphi ')$, $\pi = (TN, \varphi )\in \mathcal {FI}(\mathcal{TN})$. For the $s$-linearization $\rho = \{e_1, e_3\}$ $\{e_2\}$ $\{e_6, e_7\}$ $\{e_4,e_5\}$ of $TN'$, we get $FS_{\pi ',S_0}(\rho ) = \sigma ' = (\{t_1, t_3\}, 3)$ $(\{t_2\}, 2)$ $(\{t_1, t_3\}, 2)$ $(\{t_4,t_5\}, 2)$ (see Example 1), in support of Lemma 1. Furthermore, we can write ${\pi }\mathop {\longrightarrow }\limits ^{{\widehat{\pi }=(\widehat{TN},\widehat{\varphi })}}{\pi '}$ because ${TN}\mathop {\longrightarrow }\limits ^{{\widehat{TN}}}{TN'}$, $\varphi = \varphi ' \mid _{E \cup B}$ and $\widehat{\varphi } = \varphi ' \mid _{\widehat{E} \cup \widehat{B}}$. Then, $\widehat{\pi } \in \mathcal {FI}(\mathcal{TN}, S)$, due to Theorem 1.

4 Hierarchy of Equivalences

We start with defining interleaving, step and partial order equivalences for time Petri nets.

Definition 6

Time Petri nets $\mathcal{TN}$ and $\mathcal{TN}'$ labeled over $Act$ are:

• interleaving (step) trace equivalent (denoted $\mathcal{TN}\equiv _{i(s)}\mathcal{TN}'$) iff $\mathcal{L}_{i(s)}(\mathcal{TN})=\mathcal{L}_{i(s)}(\mathcal{TN}')$,

• interleaving (step) bisimilar (denoted ) iff there is a relation $R\subseteq RS(\mathcal{TN})\,\times \,RS(\mathcal{TN}')$ such that $(S_{0}, S' _{0}) \in R$ ($S_{0}$ and $S'_{0}$ are the initial states of $\mathcal{TN}$ and $\mathcal{TN}'$, respectively) and for all $(S,S')\in R$ it holds:

  • if $S \mathop {\longrightarrow }\limits ^{\omega }S_1$ with $\omega \in (Act\,\times \,\mathbb {T})^*$ (with $\omega \in (\mathbb {N}^{Act}\,\times \,\mathbb {T})^*$) in $\mathcal{TN}$, then $S'\mathop {\longrightarrow }\limits ^{\omega }S'_1$ in $\mathcal{TN}'$ and $(S_1,S'_1)\in R$,

  • and vice versa,

• pom-trace equivalent (denoted $\mathcal{TN}\equiv _{pom}\mathcal{TN}'$) iff $\mathcal{L}_{pom}(\mathcal{TN})=\mathcal{L}_{pom}(\mathcal{TN}')$,

• pom-bisimulation equivalent (denoted $\mathcal{TN}{\leftrightarrow _{\!\!\!\!\!\!-}}_{pom}\mathcal{TN}'$) if there is a relation $R\subseteq \mathcal {FI}(\mathcal{TN})\,\times \,\mathcal {FI}(\mathcal{TN}')$ such that $(\pi _{0}, \pi ' _{0}) \in R$ ($\pi _{0}$ and $\pi '_{0}$ are the initial time processes of $\mathcal{TN}$ and $\mathcal{TN}'$, respectively) and for all $(\pi , \pi ')\in R$ it holds:

  • if ${\pi }\mathop {\longrightarrow }\limits ^{{u}}{\pi _1}$ ($u$ is a time pomset over $Act$) in $\mathcal{TN}$, then ${\pi '}\mathop {\longrightarrow }\limits ^{{u}}{\pi _1'}$ in $\mathcal{TN}'$ and $(\pi _1,\pi _1')\in R$,

  • and vice versa.

Finally, we state the relationships between the equivalences.

Theorem 2

Let . Then,

$$\mathcal{TN}\leftrightarrow _{\star } \mathcal{TN}' \ \Rightarrow \ \mathcal{TN}\rightleftharpoons _{*} \mathcal{TN}'$$

iff there is a directed path from $\leftrightarrow _{\star }$ to $\rightleftharpoons _{*}$ in Fig. 1.

Fig. 3.

A hierarchy of equivalences

Fig. 4.

Examples of equivalent and non-equivalent time Petri nets

Proof

‘$\Leftarrow$’ All the implications in Fig. 1 follow from the Definitions, Lemma and Theorems given above.

‘$\Rightarrow$’ We now demonstrate that it is impossible to draw any arrow from one equivalence to the other such that there is no directed path from the first equivalence to the second one in the graph in Fig. 3. For this purpose, we contemplate the time Petri nets depicted in Fig. 4. It is easy to see that $\mathcal{TN}_1$ and $\mathcal{TN}_2$ are $\equiv _{pom}$–equivalent but not ${\leftrightarrow _{\!\!\!\!\!\!-}}_{i}$–equivalent because in $\mathcal{TN}_2$, for example, the execution of an action $a$ after time moment 5 is always possible from the state reachable by the execution of an action $b$ after time moment 0 but it is not the case in $\mathcal{TN}_1$. Next, $\mathcal{TN}_2$ and $\mathcal{TN}_3$ are ${\leftrightarrow _{\!\!\!\!\!\!-}}_{i}$–equivalent but not $\equiv _{s}$–equivalent because, for example, in $\mathcal{TN}_3$ the execution of the step consisting of an action $a$ and $b$ from the initial state after time moment 0 is possible but it is not the case in $\mathcal{TN}_2$. Finally, $\mathcal{TN}_3$ and $\mathcal{TN}_4$ are ${\leftrightarrow _{\!\!\!\!\!\!-}}_{s}$–equivalent but not $\equiv _{pom}$–equivalent because, for example, there is a time process of $\mathcal{TN}_4$ fireable from the initial state where the execution of an action $b$ at time moment 0 causally precedes the execution of an action $a$ at time moment 5 but it is not the case in $\mathcal{TN}_3$.