Abstract
This Chapter introduces parameterized, or parametric, Model Order Reduction (pMOR). The Sections are offered in a prefered order for reading, but can be read independently. Section 5.1, written by Jorge Fernández Villena, L. Miguel Silveira, Wil H.A. Schilders, Gabriela Ciuprina, Daniel Ioan and Sebastian Kula, overviews the basic principles for pMOR. Due to higher integration and increasing frequency-based effects, large, full Electromagnetic Models (EM) are needed for accurate prediction of the real behavior of integrated passives and interconnects. Furthermore, these structures are subject to parametric effects due to small variations of the geometric and physical properties of the inherent materials and manufacturing process. Accuracy requirements lead to huge models, which are expensive to simulate and this cost is increased when parameters and their effects are taken into account. This Section introduces the framework of pMOR, which aims at generating reduced models for systems depending on a set of parameters.
Section 5.2, written by Gabriela Ciuprina, Alexandra Ştefănescu, Sebastian Kula and Daniel Ioan, provides robust procedures for pMOR. This Section proposes a robust specialized technique to extract reduced parametric compact models, described as parametric SPICE-like netlists, for long interconnects modeled as transmission lines with several field effects such as skin effect and substrate losses. The technique uses an EM formulation based on partial differential equations (PDE), which is discretized to obtain a finite state space model. Next, a variability analysis of the geometrical data is carried out. Finally, a method to extract an equivalent parametric circuit is proposed.
Section 5.3, written by Michael Striebel, Roland Pulch, E. Jan W. ter Maten, Zoran Ilievski, and Wil H.A. Schilders, covers ways to efficiently determine sensitivity of output with respect to parameters. First direct and adjoint techniques are considered with forward and backward time integration, respectively. Here also the use of MOR via POD (Proper Orthogonal Decomposition) is discussed. Next, techniques in Uncertainty Quantification are described. Here pMOR techniques can be used efficiently.
Section 5.4, written by Kasra Mohaghegh, Roland Pulch and E. Jan W. ter Maten, provides a novel way in extending MOR to Differential-Algebraic Systems. Here new MOR techniques for reducing semi-explicit system of DAEs are introduced. These techniques are extendable to all linear DAEs. Especially pMOR techniques are exploited for singularly perturbed systems.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Singular Value Decomposition
- Proper Orthogonal Decomposition
- Multiple Input Multiple Output
- Model Order Reduction
- Uncertainty Quantification
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Parametric Model Order Reduction
Model Order Reduction (MOR) techniques are a set of procedures which aim at replacing a large-scale model of a physical system by a lower dimensional model which exhibits similar behavior, typically measured in terms of its input-output response.Footnote 1 Reducing the order or dimension of these models, while guaranteeing that the input-output response is accurately captured, is crucial to enable the simulation and verification of large systems [1–3, 33]. Since the first attempts in this area [31], the methods for linear model reduction have greatly evolved and can be broadly characterized into two types: those that are based on subspace generation and projection methods [13, 27], and those based on balancing techniques [26, 30] (sometimes also referred to as Singular Value Decomposition (SVD)-based [2]). Hybrid techniques that try to combine some of the features of each family have also been presented [18, 19, 21, 29].
Although previously ignored when analyzing or simulating systems, parameter variability can no longer be disregarded as it directly impacts system behavior and performance. Accounting for the effects of manufacturing or operating variability, such as geometric parameters, temperature, etc., leads to parametric models whose complexity must be tackled both during the design and verification phases. For this purpose, Parametric MOR (pMOR, also known as Parameterized MOR) techniques that can handle parameterized descriptions are being considered as essential in the determination of correct system behavior. The systems generated by pMOR procedures must retain the ability to model the effects of both geometric and operating variability, in order to accurately predict behavior and optimize designs.
Several pMOR techniques have been developed for modeling large-scale parameterized systems. Although the first approaches were based on perturbation based techniques, such as [17, 25], the most common and effective ones appear to be extensions of the basic projection-based MOR algorithms [27, 29] to handle parameterized descriptions. An example of these are multiparameter moment-matching pMOR methods [8] which can generate accurate reduced models that capture both frequency and parameter dependence. The idea is to match, via different approaches, generalized moments of the parametric transfer function, and build an overall projector. Sample-based techniques have been proposed in order to contain the large growth in model order for multiparameter, high accuracy systems [28, 37]. They rely on sampling the joint multi-dimensional frequency and parameters space. This approach allows the inclusion of a priori knowledge of the parameter variation, and provides some error estimation. However, the issue of sample selection becomes particularly relevant when done in a potentially high-dimensional space.
1.1 Representation of Parametric Systems
In order to include parametric systems inside an efficient simulation flow, the parametric dependence should be explicit. This means that it must be possible to access the parameter values and modify them inside the same representation, while avoiding, if possible, re-computing the parametric systems, i.e. to perform another extraction.
Parameters usually affect the geometrical or electrical properties of the layout, and thus, most of these variations can be represented as modifications of the values of the system matrices inside a state-space descriptor. For this reason, in most cases, the input and output ports are not affected by these variations (this of course depends on how the system is built), and in the case when they are in fact affected, these variations can be shifted to the inner states. The variability leads to a dependence of the extracted circuit elements on several parameters, of electrical or geometrical origin. This dependence results in a parametric state-space system representation, which in descriptor form can be written as
where \(C,G \in \mathbb{R}^{n\times n}\) are again, respectively, the dynamic and static matrices, \(B \in \mathbb{R}^{n\times p}\) is the matrix that relates the input vector \(u \in \mathbb{R}^{p}\) to the inner states \(x \in \mathbb{R}^{n}\) and \(L \in \mathbb{R}^{q\times n}\) is the matrix that links those inner states to the outputs \(y \in \mathbb{R}^{q}\). The elements of the matrices C and G, as well as the states of the system x, depend on a set of P parameters λ = [λ 1, λ 2, …, λ P ] which model the effects of the mentioned uncertainty. This time-domain descriptor yields a parametric dependent frequency response modeled via the transfer function
for which we seek to generate a reduced order approximation, able to accurately capture the input-output behavior of the system for any point in the parameter space
In general, one attempts to generate a reduced order model whose structure is, as much as possible, similar to the original, i.e. exhibiting a similar parametric dependence. The “de facto” standard used in most of the literature for representing a parametric system is based on a Taylor series expansion with respect to the parameters (shown here for first order in the frequency domain):
where G 0 and C 0 are the nominal values of the matrices, whereas G i and C i are the sensitivities with respect to the parameters. Novel extraction methodologies can efficiently generate such sensitivity information [5, 12].
A nice feature of this representation is that this explicit parameter dependence allows to obtain a reduced, yet similar representation when a projection scheme is applied
where \(\hat{C}_{i} = V ^{T}C_{i}V\), \(\hat{G}_{i} = V ^{T}G_{i}V\), \(\hat{B} = V ^{T}B\) and \(\hat{L} = \mathit{LV }\).
Some questions may be raised about the order neccessary for an accurate representation of the parametric model. This depends on the range of variation and the effect of each parameter, and therefore is not trivial to ascertain.
However, some literature presents interesting results in this area [4, 6], with the conclusion that low order (first order in most cases) Taylor series are a good and useful approximation to the real parametric system. As it will be shown later, this statement has important consequences from the point of view of some parametric algorithms, especially those which rely on moment matching techniques.
1.2 Reduction of Parametric Systems
The most straight-forward approach for the reduction of such a parametric system is to apply nominal techniques. A first possibility is to apply nominal reduction methodologies on the perturbed system. This means that the model in (5.4) is evaluated for a set of parameter values. This model is no longer parametric, and thus standard reduction methodologies can be applied on it. However, once a “perturbed” system is evaluated and reduced, the parameter dependence is lost, and thus the result is a system which is no longer parametric, and therefore only accurate for a set of parameters.
A slightly different approach that overcomes this issue is to apply the projection on the Taylor series approximation. In this case, depending on the framework applied, we can distinguish two cases:
-
First, in a projection methodology, the projector is computed from the nominal system, and later applied on the nominal and on the sensitivity matrices, obtaining a model as in (5.5).
-
Second, in the case of Balanced Truncation realizations, the computation of the Gramians is done via the nominal system, but the balancing and the truncation is done both on the nominal matrices and on the sensitivities.
These methods, although not oriented to accurately capture the behavior of the system under variation of the parameters, can yield good approximations in cases of small variations or mild effect of the parameters. However, they are not reliable, and their performance heavily depends on the system.
1.2.1 Pertubation Based Parametric Reduction
The first attemps to handle and reduce systems under variations were focused on perturbation techniques.
One of the earliest attempts to address this variational issue was to combine perturbation theory with moment matching MOR algorithms [25] into a Perturbation-based Projector Fitting scheme. To model the variational effects of the interconnects, an affine model was built for the capacitance and conductance matrices,
where now C 0 and G 0 are the nominal matrix values, i.e., the value of the matrices under no parameter variation, and C i and G i , i = 1, …, P, are their sensitivities with respect to those parameters. For small parameter variations, the projection matrix obtained via a moment-matching type algorithm such as PRIMA also may show small perturbations. To capture such effect, several samples in the parameter space were drawn G(λ 1, …, λ P ) and C(λ 1, …, λ P ), and for each sample PRIMA was applied resulting a projector. A fitting methodology was later applied in order to determine the coefficients of a parameter dependent projection matrix
To obtain a reduced model, both the parametric system and the projector are evaluated with the parameter set. Projection is applied and the reduced model obtained. However, this reduced model is only valid for the used parameter set. If a reduced model for a different parameter set is needed, the evaluation and projection must be applied again, what makes hard to include this method in a simulation environment.
Another method combined perturbation theory with the Truncated Balanced Realization (TBR) [26, 30] framework. A perturbation matrix was theoretically obtained starting from the affine models shown in (5.6) [17]. This matrix was applied via a congruence transformation over the Gramians to address the variability, obtaining a set of perturbed Gramians. These in turn were used inside a Balancing Truncation procedure. As with most TBR-inspired methods, this one is also expensive to compute and hard to implement. The above methods have obvious drawbacks, perhaps the most glaring of which is the heavy computation cost required for obtaining the reduced models and the limitation that comes from perturbation based approximations, possibly leading to inaccuracy in certain cases.
1.2.2 Multi-dimensional Moment Matching
Most of the techniques in the literature extend the moment matching paradigm [13, 27, 34] to the multi-dimensional case. They usually rely on the implicit or explicit matching of the moments of the parametric transfer function (5.2). These moments depend not only on the frequency, but on the set of parameters affecting the system, and thus are denoted as multi-dimensional or multi-parameter moments.
This family of algorithms assumes that a model based on the Taylor Series expansion can be used for approximating the behavior of the conductance and capacitance, G(λ) and C(λ), expressed as a function of the parameters
where \(G_{i_{1},\ldots,i_{P}}\) and \(C_{i_{1},\ldots,i_{P}}\) are the multidimensional Taylor series coefficients. This Taylor series can be extended up to the desired (or required) order, including cross derivatives, for the sake of accuracy. If this formulation is used, the structure for parameter dependence may be maintained if the projection is not only applied to the nominal matrices, but to the sensitivities as well.
Multiple methodologies follow these basic premises, but they differ in how and which such moments are generated and used in the projection stage.
The Multi-Parameter Moment Matching method [8] relies on a single-point expansion of the transfer function (5.2) in the joint space of the frequency s and the parameters λ 1, …, λ P , in order to obtain a power series in several variables,
where \(M_{k,k_{s},k_{1},\ldots,k_{P}}\) is a k-th (k = k s + k 1 + … + k P ) order multi-parameter moment corresponding to the coefficient term \(s^{k_{s}}\,\lambda _{1}^{k_{1}}\ldots \lambda _{P}^{k_{P}}\).
A basis for the subspace spanned from these moments can be built and the resulting orthonormal basis V can be used as a projection matrix for reducing the original system
This parametrized reduced model matches up to the k-th order multi-parameter moment of the original system.
However, the main inefficiencies of this method are twofold:
-
On the one hand, this method generates pure multi-dimensional moments (see Eq. (5.9)), which means that the number of moments grows dramatically (all the possible combinations for a given order must be done) when the number of parameters is increased, even for a modest number of moments for each parameter. For this reason, the reduced model size grows exponentially with the number of parameters and the moments to match.
-
On the other hand, the process parameters fluctuate in a small range around their nominal value, whereas the frequency range is much larger, and a higher number of moments are necessary in order to capture the global response for the whole frequency range. This algorithm treates the frequency as one parameter more, which turns to be highly innefficient.
An improvement of the previous approach is to perform a Low-Rank Approximation of the multi-dimensional moments [22]. An SVD-based low-rank approximation of the generalized moments, G −1 G i and G −1 C i (which are related to the multidimensional moments), is applied. Then, separate subspaces are built from these low-rank approximations for every parameter. The global projector is obtained from the orthonormalization of the nominal moments (computed via Arnoldi for example), and the moments of the subspaces related to the parameters. The projector is applied on the Taylor Series approximation to obtain a reduced parametric model. This approach, although providing more flexibility and improving the matching, requires the low-rank SVD of the generalized moments, which comes at a cost of O(n 3), i.e., limiting its applicability to small-medium size problems.
A different multi-dimensional moment matching approach was also presented in [16], called Passive Parameterized Time-Domain Macro Models. It relies on the computation of several subspaces, built separately for each dimension, i.e. the frequency s (to which respect k s block moments are obtained in a basis denoted as Q s ) and the parameter set λ (generating the basis Q i which match \(k_{\lambda _{i}}\) block moments with respect to parameter λ i ). These independent subspaces can be efficiently computed using standard nominal approaches, e.g. PRIMA. Once all the subspaces have been computed, an orthonormal basis can be obtained so that its columns span the joint of all subspaces. For example, in the affine Taylor Series representation, using Krylov spaces Kr(A, B, k) (matrix A, multi-columns vector B, moments k):
where subscript i refers to the i-th parameter λ i , and the parameter related moments have been generalized to any shifted frequency s. QR stands for the QR-factorization based orthonormalization. Applying the resulting matrix V in a projection scheme ensures that the parametric Reduced Order Model matches k s moments of the original system with respect to the frequency, and k i moments with respect to the parameter λ i . If the cross-term moments are needed for accuracy reasons, the subspace that spans these moments can also be included by following the same scheme.
A different approach is explored in CORE [23]. Here an explicit moment matching with respect to the parameters is first done, via Taylor-series expansion, followed by an implicit moment matching in frequency (via projection). The first step in done by expanding the state space vector x and the matrices G and C in its Taylor Series only with respect to the parameters,
where G 0, …, 0, C 0, …, 0 and x 0, …, 0(s) are the nominal values for the matrices and the states vector, respectively. The remaining \(G_{i_{1},\ldots,i_{P}}\), \(C_{i_{1},\ldots,i_{P}}\) and \(x_{i_{1},\ldots,i_{P}}\) are the sensitivities with respect to the parameters. Explicitly matching the coefficients of the same powers leads to an augmented system, in which the parametric dependence is shifted to the output related matrix L A :
The second step applies a typical nominal moment matching procedure (e.g. PRIMA [27]) to reduce this augmented system. This is possible because the matrices G A , C A and B A used to build the projector do not depend on the parameters. The projector is latter applied on all the matrices of the augmented system in (5.14). Furthermore, the Block Lower Triangular structure of the system matrices G A and C A can be exploited in recursive algorithms to speed-up the reduction stage. This two-step approach allows to increase the number of the matched multi-parameter moments with respect to other techniques, for a similar reduced order. In principle, in spite of the larger size of the augmented model, the order of the reduced system can be much smaller than in the previous cases. On the other hand, the structure of the dependence with respect to the parameters is lost, since the parametric dependence is shifted to the later projected output related L matrix. The projection mixes all the parameters, losing the possibility of modifying them without need of recomputation. This method also has the disadvantage that the explicit computation of the moments with respect to the parameters can lead to numerical instabilities. The method, although stability-preserving, is unable to guarantee passivity preservation.
Some algorithms [24, 37] try to match the same moments as CORE, but in a more numerical stable and efficient fashion, using Recursive and Stochastic Approaches. They generalize the CORE paradigm up to an arbitrary expansion order with respect to the parameters, and apply an iterative procedure in order to compute the frequency moments related to the nominal matrices, and the ones obtained from the parametric part (this means, to obtain a basis for each block of states x i in (5.14), but without building such system).
where s k is the expansion point for the Krylov subspace generation, and V i j is the j-th moment with respect to the frequency for the i-th parameter. This general recursive scheme, here presented for first order with respect to the parameters, can be extended to any (independent) order with respect to each parameter.
The technique in [37] uses a tree graph scheme, in which each node is associated to a moment, and the branches represent recursive dependences among moments. Each tree level contains all the moments of the same multi-parameter order. On this tree, a random sampling approach is used to select and generate some representative moments, preventing the exponential growth.
On the other hand, the technique in [24] advocates for an exhaustive computation at each parameter order. This means that all the moments for zero-parameter order (i.e. nominal), are computed until no rank is added. The same procedure is repeated for first order with respect to all parameters. If the model is not accurate, more order with respect to the parameters can be added.
Notice that both schemes provide a large degree of flexibility, as different orders with respect to each parameter and with respect to the frequency can be applied. In both approaches, the set of all the moments generated is orthonormalized, so an overall projector is obtained. This is used inside a congruence transformation on the Taylor Series approximation (5.4), to generate a reduced model in the same representation. Another advantage of these methodologies is that the passivity is PRIMA-like preserved, and the basis is built in a numerical stable fashion.
1.2.3 Multi-dimensional Sampling
Another option present in the literature relies on sampling schemes for capturing the variational nature of the parametric model. They are applied for the building of a projector to later apply congruence tranformation on the original model.
A simple generalization of the multi-point moment matching framework [11] to a multi-dimensional space can be done via Variational Multi-Point Moment Matching. Small research has been devoted to this family of approaches, but one algorithm can be found in [22]. The flexibility it provides is also one of its main drawbacks, as the methodology can be applied in a variety of schemes, from a single-frequency multi-parameter sampling to a pure multi-dimensional sampling. From these expansion points, several moments are computed following a typical moment matching scheme. The orthonormalization of the set of moments provides the overall projector which is applied in a congruence reduction scheme. However, it is hard to determine the number and placement of samples, and the number of moments to match with respect to the frequency and to the parameters.
Another scheme, which overcomes some of the issues of the previous approach is the Variational Poor Man’s TBR [28]. This approach is based on the statistical interpretation of the algorithm (see [29] for details) and enhances its applicability to multiple dimensions. In this interpretation, the Gramian X λ is seen as a covariance matrix for a Gaussian variable x λ , obtained by exciting the (presumed stable) system with u involving white noise. Rewriting the Gramian as
where p(λ) is the probability density of λ in the parameter space, S λ . Just as in PMTBR, a quadrature rule can be applied in the overall parameter plus frequency space to approximate the Gramian via numerical computation. But in this case the weights are chosen taking into account the Probability Density Function (PDF) of λ i and the frequency constraints. This can be generalized to a set of parameters, where a joint PDF of all the parameters can be applied on the overall parameter space, or the individual PDF of each parameter can be used. This possibility represents an interesting advantage, since a-priori knowledge of the parameters and the frequency can be included in order to constrain the sampling and yield a more accurate reduced model. The result of this approach is an algorithm which generates Reduced Order Models whose size is less dependent on the number of parameters. In the deterministic case, an error analysis and control can be included, via the eigenvalues of the SVD. However, in the variational case only an expected error bound can be given:
where r is the reduced order and n the original number of states. On the other hand, in this method the issue of sample selection, already an important one in the deterministic version, becomes even more relevant, since the sampling must now be done in a potentially much higher-dimensional space.
1.3 Practical Consideration and Structure Preservation
Inside the pMOR realm, the moment matching algorithms based on single point expansion may not be able to capture the complete behavior along the large frequency range required for common RF systems, and may lead to excessively large models if many parameters are taken into account. Therefore the most suitable techniques for the reduction seem to be the multipoint ones. Among those techniques, Variational PMTBR [28] offers a reliable framework with some interesting features that can be exploited, such as the inclusion of probabilistic information and the trade off between size and error, which allows for some control of the error via analysis of the singular values related to the dropped vectors. On the other hand, it requires a higher computational effort than the multi-dimensional moment matching approaches, as it is based on multidimensional sampling schemes and Singular Value Decomposition (SVD), but the compression ratio and reliability that it offers compensates this drawback. The effort spent in the generation of such models can be amortized when the reduced order model generated is going to be used multiple times. This is usually the case for parametric models, as the designer may require several evaluations for different parameter sets (e.g. in the case of Monte Carlo simulations, or optimization steps). Furthermore, this technique offers some extra advantages when combined with block structured systems [14], such as the block-wise error control with respect to the global input-output behaviour, which can be applied to improve the efficiency of the reduction. This means that each block can be reduced to a different order depending on its relevance in the global response.
An important point to recall here is that the block division may not reflect different sub-domains. Different sub-divisions can be done to address different hierarchical levels. For instance, it may be interesting to divide the complete set in sub-domains connected by hooks, which generates a block structured matricial representation. But inside each block corresponding to a sub-domain, another block division may be done, corresponding either to smaller sub-domains or to a division related to the different kind of variables used to model each domain (for example, in a simple case, currents and voltages). This variable related block structure preservation has already been advocated in the literature [15] and may help the synthesis of and equivalent SPICE-like circuit [35] in the case that is required. Figure 5.1 presents a more intuitive depiction of the previous statements, in which a two domain example is shown with its hierarchy, and each domain has also some inner hierarchy related to the different kind of variables (in this case, voltages and currents, but it can also be related to the electric and magnetic variables, depending on the formulation and method used for the generation of the system matrices).
Two-level hierarchy: domain level (given by the numbers, 1 and 2) and variable level (voltages v k and currents i k )
The proposed flow starts from a parametric state-space descriptor, such as (5.1), which exhibits a multi-level hierarchy, and a block parametric dependence (as different parameters may affect different sub-domains). The matrices of size n have K domains, each with size n i , n = ∑ i n i . For instance, for the static part,
where λ {ij} is the set of parameters affecting \(G_{\mathit{ij}} \in \mathbb{R}^{n_{i}\times n_{j}}\). Then we perform the multi-dimensional sampling, both in the frequency and the parameter space. For each point we generate a matrix or vector z j (a matrix in case B includes multiple inputs)
where C(λ) and G(λ) are the global matrices of the complete domain, with n degrees of freedom (dofs). To generate the matrix \(z_{j} \in \mathbb{R}^{n\times m}\), with m the number of global ports, we can apply a direct procedure, meaning a factorization (at cost O(n β), with 1. 1 ≤ β ≤ 1. 5 for sparse matrices) and a solve (at cost O(n α), with 1 ≤ α ≤ 1. 2 for sparse matrices). Novel sparse factorization schemes can be applied to improve the efficiency [9, 10]. In cases when a direct method may be too expensive iterative procedures may be used [32].
The choice of the sampling points may be an issue, as there is no clear scheme or procedure that is known to provide an optimal solution. However, as stated in [28], the accuracy of the method does not depend on the accuracy of the quadrature (and thus in the sampling scheme), but on the subspace generated. For this reason, a good sampling scheme is to perform samples in the frequency for the nominal system, and around these nominal samples, perform some parametric random sampling in order to capture the vectors that the perturbed system generates. The reasoning behind this scheme is that for small variations, such as the ones resulting from process parameters, the subspace generated along the frequency is generally more dominant than the one generated by the parameters. In addition, under small variations, the nominal sampling can be used as a good initial guess for an iterative solver to generate the parametric samples. For the direct solution scheme, to generate P samples (and thus Pm vectors) for the global system has a cost of O(Pn α +Pn β). Note that since m is the number of global (or external) ports, the number of vectors is smaller than if we take all the hooks into account.
The next step is the orthonormalization, via SVD, of the Pm vectors for generating a basis of the subspace in which to project the matrices. Here an independent basis V i , \(i \in \left \{1,\ldots,K\right \}\), can be generated for each i-th sub-domain. To this end the columns in z j are split according to the block structure present in the system matrices (i.e., the n i rows for each block), and an SVD is performed on each of these set of vectors, at a cost of O(n i (Pm)2), where n i is the size of the corresponding block, and n = ∑ i n i . For each block, the independent SVD allows to drop the vectors less relevant for the global response (estimated by the dropped singular value ratio, as presented in [28]). This step generates a set of projectors, \(V _{i} \in \mathbb{R}^{n_{i}\times q_{i}}\), with q i ≪ n i the reduced size for the i-th block of the global system matrix. These projectors can be placed in the diagonal blocks of an overall projector, that can be used for reducing the initial global matrices to an order q = ∑ i q i . This block diagonal projector allows a block structure (and thus sub-domain) preservation, increasing the sparsity of the ROM with respect to that of the standard projection. This sparsity increase is particularly noticeable in the case of the sensitivities (if a Taylor series is used as base representation), as the block parameter dependence is maintained (e.g. in the static matrix)
The total cost for the procedure can be approximated by
1.4 Examples
1.4.1 L-Shape
As a first example we present a simple L-shape interconnect structure depending on the width of the metal layer. Figure 5.2 shows the frequency response for a fixed parameter value, of the nominal system, the Taylor series approximation (both of order 313), and the reduction models obtained with several parametric approaches:
-
Nominal reduction of the Taylor Series, via PRIMA, of order 25,
-
Multi-dimensional moment matching, via CORE, of order 25,
-
Multi-dimensional moment matching, via Passive Parameterized Time-Domain Macro Models technique, of order 20,
-
And Multi-dimensional sampling, via Variational PMTBR, of order 16.
Figure 5.3 shows the same example, but in this case the response of the systems with respect of the parameter variation, for a given frequency point. It is clear that the parametric Model Order Reduction techniques are able to capture the parametric behavior, whereas the nominal approach (PRIMA) fails to do so, even for high order.
(Top): Frequency response of the L-shape example. The original, both the nominal and the Taylor series for a fixed parameter value, of order 313, and the reductions via PRIMA, CORE, Passive Parameterized Time-Domain Macro Models (PP TDM), and variational PMTBR (VPMTBR), of different orders. (Bottom): Relative error of the reduction models with respect to the original Taylor series approximation
Parameter impact on the response of the L-shape example. The EM model for several parameter values (of order 313), the Taylor series approximation (of order 313 as well), and the reductions via PRIMA, CORE, PP TDM, and VPMTBR, of different orders
Topology of the U-shape: (Up) cross view, (Down) top view. Parameters: distance between conductors, d, and thickness of the metal, h
1.4.2 U-Coupled
This is a simple test case, which has two U-shape conductors; each of the conductors ends represent one port, having one terminal voltage excited (intentional terminal, IT) and one terminal connected to ground. A clear illustration of the setting is given by Fig. 5.4. The distance (d) separating the conductors and the thickness (h) of the corresponding metal layer are parameterized. The complete domain is partitioned into three sub-domains, each of them connected to the others via a set of hooks (both electric, EH, and magnetic, MH). The domain hierarchy and parameter dependence are kept after the reduction, via Block Structure Preserving approaches. The Full Wave EM model was obtained via Finite Integration Technique (FIT) [7], and its matrices present a Block Structure that follows the domain partitioning. Table 5.1 shows the characteristics of the original system. Each sub-domain is affected by a parameter. The left and right sub-domains contain the conductors, and thus are affected by the metal thickness h. The middle domain width varies with the distance between the two conductors, and thus is affected by parameter d. For each parameter the first order sensitivity is taken into account, and a first order Taylor Series (TS) formulation is taken as the original system.
For the reduction we apply three techniques. First, a Nominal Block Structure Preserving (BSP) PRIMA [36], with a single expansion point and matching 50 moments, is applied. This leads to a 100-vector generated basis, that after BSP expansion produces a 300-dofs Reduced Order Model (ROM). Second, a BSP procedure coupled with a Multi-Dimensional Moment Matching (MDMM) approach [16], is tried. The basis will match 40 moments with respect to the frequency, and 30 moments with respect to each parameter. The orthonormalized basis has 196 vectors, that span a BSP ROM of size 588. Third, the proposed BSP VPMTBR, with 60 multidimensional samples, and a relative tolerance of 0. 001 for each block, is studied. This process generates different reduced sizes for each block: 85, 90 and 85, with a global size of 260.
U-coupled: Relative error (dB) in | H 12(s) | for (Up) the nominal response, and (Down) the perturbed response at a single parameter set. The curves represent: BSP PRIMA, BSP VPMTBR, and BSP MDMM
U-coupled: Variation of | H 12 | vs. the variation of the parameter d at 59. 6 GHz for the original TS and the three BSP ROMs
Figure 5.5 shows the relative error in the frequency transfer function at a parameter set point for the three ROMs w.r.t. the Taylor series. PRIMA and MDMM approaches fail to capture the behavior with the order set, but the proposed approach performs much better even for a lower order. Figure 5.6 shows the response change with the variation of parameter d at a single frequency point (Parameter Impact). PRIMA and MDMM only present accuracy for the nominal point, whereas the proposed method maintains the accuracy for the parameter range.
1.4.3 Double Spiral
Layout configuration of the Double Spiral example (view from the top)
This is an industrial example, composed by two square integrated spiral inductors in the same configuration as the previous example (See Fig. 5.7). The complete domain has two ports, and 104, 102 Dofs. The example also depends on the same two parameters, the distance d between spirals, and the thickness h of the corresponding metal layer. In this case a single domain is used, but the BSP approach is applied on the inner structure provided by the different variables in the FIT method (electric and magnetic grid). For the reduction, the proposed BSP VPMTBR methodology is benchmarked against a nominal BSP PRIMA (400 dofs) methodology, and compared with the original Taylor Series formulation. The ROM size in this case is 142 and 165 respectively for the blocks. The results are presented in the Figs. 5.8 and 5.9. Figure 5.8 shows the frequency relative error of the ROMs with respect to the original Taylor Series. PRIMA, although accurate for the nominal response, fails to capture the parametric behavior, whereas the proposed method succeeds in modeling such behavior. This is also the conclusion that can be drawn from the parameter impact in Fig. 5.9.
Double Spiral: Relative error (dB) in | H 12(s) | for (Up) the nominal response, and (Down) the perturbed response at a single parameter set
Double Spiral: | H 12 | vs. the variation of the parameter d at a frequency point for the original TS and the ROMs: PRIMA, and VPMTBR
1.5 Conclusions
We conclude that Parametric Model Order Reduction techniques are essential for addressing parameter variability in the simulation of large dynamical systems.
Representation of the state space based on Taylor series expansion with respect to the parameters provide the flexibility and accuracy required by efficient simulation. This reresentation approach can be combined with projection-based methods to generate structural equivalent reduced models.
Single-point based moment-matching approaches are suitable for small variations and local approximations, but usually suffer from several drawbacks when applied to EM based models operating in a wide frequency range. Multi-point based approaches, although computationally more expensive, are more reliable and generate more compressed models. Thus, the generation cost can be amortized in the simulation stages.
Combination of the projection methodologies with Block Structure Preserving approaches can be done efficiently in parametric environments. Further advantages can be obtained in this case, such as different compression order for each block based on its relevance in the global behavior, higher degree of sparsification of the nominal matrices, and in particular, of the sensitivities, and the maintenance of the block domain hierarchy and block parameter dependence after reduction.
Decomposition of the interconnect net in 2D TLs and 3D junctions
2 Robust Procedures for Parametric Model Order Reduction of High Speed Interconnects
Due to higher integration and increasing of running frequency, full Electromagnetic Models (EM) are needed for an accurate prediction of the real behavior of integrated passives and interconnects in currently designed chips [45].Footnote 2 In general, if on-chip interconnects are sorted with respect to their electric length, they may be categorized in three classes: short, medium and long. While the short interconnects have simple circuit models with lumped parameters, the extracted model of the interconnects longer than the wave length has to consider the effect of the distributed parameters, as well. Fortunately, the long interconnects have usually the same cross-sectional geometry along their extension. If not, they may be decomposed in straight parts connected by junction components (Fig. 5.10). The former are represented as transmission lines (TLs) whereas the latter are modeled as common passive 3D components.
Due to the fact that the lithographic technology is pushed today to work at its limit, the variability of geometrical and physical properties cannot be neglected. That is why, to obtain robust devices, the variability analysis is necessary even during the design stage [44, 55].
This Section proposes a robust specialized technique to extract reduced parametric compact models, described as parametric SPICE like netlists, for long interconnects modeled as transmission lines with several field effects such as skin effect and substrate losses. The technique uses an EM formulation based on partial differential equations (PDE), which is discretized to obtain a finite state space model. Next, a variability analysis of the geometrical data is carried out. Finally, a method to extract an equivalent parametric circuit is proposed. The procedure is validated by applying it on a study case for which experimental data is available.
2.1 Field Problem Formulation: 3D – PDE Models
Long interconnects and passive components with significant high frequency field effects, have to be modeled by taken into consideration Full Wave (FW) electromagnetic field equations. Typical examples of such parasitic effects are: skin effect and proximity, substrate losses, propagation retardation and crosstalk. Only Maxwell equations in FW regime
complemented with the constitutive equations which describe the material behavior:
can model these effects. While material constants are known for each subdomain (Si, Al, SiO2), vectorial fields \(\boldsymbol{B},\boldsymbol{H},\boldsymbol{E},\boldsymbol{D}:\varOmega \times [0,T) \rightarrow \mathbb{R}^{3}\) and the scalar field \(\rho:\varOmega \times [0,T) \rightarrow \mathbb{R}\) are the unknowns of the problem. They can be univocal determined in the simple connected set Ω, which is the computational domain, for zero initial conditions (\(\boldsymbol{B} =\boldsymbol{ 0},\boldsymbol{D} =\boldsymbol{ 0}\) for t = 0), if appropriate boundary conditions are imposed.
According to authors’ knowledge, the best boundary conditions which allow the field-circuit coupling are those given by the electric circuit element (ECE) formulation [54]. Considering \(S_{1}^{{\prime}},S_{2}^{{\prime}},\ldots,S_{n}^{{\prime}}\subset \partial \varOmega\) a disjoint set of surfaces, called terminals (Fig. 5.11), the following boundary conditions are assumed:
ECE – electric circuit element with multiple terminals
Condition (5.24) interdicts the magnetic coupling between the domain and its environment, (5.25) interdicts the galvanic coupling and the capacitive coupling through the boundary excepting for the terminals and (5.26) interdicts the variation of the electric potential over the terminal, thus allowing the connection of the device to exterior electric circuit nodes. For each terminal, k = 1, …, n the voltage and the current can be univocal defined:
where C k ′ is an arbitrary path on the device boundary ∂ Ω, that starts on S k ′ and ends on S n ′, where, by convention, the n-th terminal is considered as reference, i.e. u n = 0. If we assume that the terminals are excited in voltage, then u k , k = 1, 2, …, n − 1 are input signals and i k , k = 1, 2, …, n − 1 are output signals. Equations (5.24) ÷ (5.26) define a multiple input multiple output (MIMO) linear system with n − 1 inputs and n − 1 outputs, but with a state space of infinite dimension. In the weak form of Maxwell’s equations, state variables, \(\boldsymbol{H},\boldsymbol{E}\) belong to the Sobolev space H(curl, Ω) [39]. Uniqueness theorem of the ECE field problem [54] generates the correct formulation of the transfer function \(\mathbf{Y}(s): \mathbb{C} \rightarrow \mathbb{C}^{(n-1)\times (n-1)}\), which represents the matrix of the terminals admittance for a complex frequency s. The relation
defines a linear transformation in the frequency domain of the terminal voltages vector \(\mathbf{u} \in \mathbb{C}^{n-1}\) to the currents vector \(\mathbf{i} \in \mathbb{C}^{n-1}\).
2.2 Numeric Discretization and State Space Models
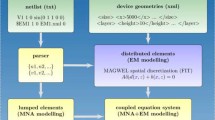
PDE models are too complex for designers needs. The approach we propose for the extraction of the electric models is schematically represented in Fig. 5.12. The left block corresponds to the formulation described in the previous section.
Three levels of abstraction for a component model and its corresponding equations
The next important step in the EM modeling is the discretization of the PDEs. One of the simplest methods to carry out this, is based on the Finite Integration Technique (FIT), a numerical method able to solve field problems based on spatial discretization “without shape functions”. Two staggered orthogonal (Yee type) grids are used as discretization mesh [42]. The centers of the primary cells are the nodes of the secondary cells. The degrees of freedom (dofs) used by FIT are not local field components as in FEM or in FDTD, but global variables, i.e., electric and magnetic voltages u e , u m , electric currents i, and magnetic and electric fluxes ϕ, ψ assigned to the grid elements: edges and faces, respectively. They are associated to these grids elements in a coherent manner (Fig. 5.13).
Dofs for FIT numerical method in the two dual grids cells
By applying the global form of electromagnetic field equations on the mesh elements (elementary faces and their borders), a system of differential algebraic equations (DAE), called Maxwell Grid Equations (MGE) is obtained:
Electric (left) and magnetic (right) equivalent FIT circuits
FIT combines MGE with Hodge’s linear transform operators, which approximate the material behavior (5.23):
The main characteristics of the FIT method are:
-
There is no discretization error in the MGE fundamental Eqs. (5.29) ÷ (5.33). All numerical errors are hold by the discrete Hodge operators (5.34).
-
An equivalent FIT circuit (Fig. 5.14), having MGE + Hodge as equations may be easily build. The graphs of the two constituent mutually coupled sub-circuits are exactly the two dual discretization grids; therefore the complexity of the equivalent circuit has a linear order with respect to the number of grid-cells [49].
-
MGE are:
-
Sparse: matrices \(\boldsymbol{G}_{m},\boldsymbol{C}_{e}\) and \(\boldsymbol{G}_{e}\) are diagonal and matrices \(\boldsymbol{C},\boldsymbol{D}\) have maximum six non-zero entries per row,
-
Metric-free: matrices C – the discrete-curl and D – the discrete-div operators have only 0, +1 and −1 as entries,
-
Mimetic: in Maxwell equations curl and div operators are replaced by their discrete counterparts C and D, and
-
Conservative: the discrete form of the discrete charge conservation equation is a direct consequence of both Maxwell and as well as of the MGE equations.
-
Due to these properties the numerical solutions have no spurious modes.
Considering FIT Eqs. (5.29), (5.31), and (5.34) with the discrete forms of boundary conditions (5.24) ÷ (5.27) a linear time-invariant system is defined having the same input-output quantities as (5.28), but the state equations:
where \(\boldsymbol{x} = [\boldsymbol{u}_{m}^{T},\boldsymbol{u}_{e}^{T},\boldsymbol{i}^{T}]^{T}\) is the state space vector, consisting of electric voltages \(\boldsymbol{u}_{e}\) defined on the electric grid used by FIT, magnetic voltages \(\boldsymbol{u}_{m}\) defined on the magnetic grid and output quantities \(\boldsymbol{i}\). Equations can be written such that only two semi-state space matrices (\(\boldsymbol{C}\) and \(\boldsymbol{G}\)) are affected by geometric parameters (denoted by α in what follows). Considering all terminals voltage-excited, the number of inputs is always equal to the number of outputs. Since output currents are components of the state vector, the matrix \(\boldsymbol{L} =\boldsymbol{ B^{T}}\) is merely a selection matrix.
For instance, the structure of the matrices in the case of voltage excitation is the following:
There are six sets of rows, corresponding to the six sets of equations. The first group of equations is obtained by writing Faraday’s law for inner elementary electric loops. \(\boldsymbol{G}_{m}\) is a diagonal matrix holding the magnetic conductances that pass through the electric loops. The block \(\left [\begin{array}{cc} \boldsymbol{B}_{1} & \boldsymbol{B}_{2} \end{array} \right ]\) has only 0, 1, − 1 entries, describing the incidence of inner branches and branches on the boundary to electric faces. The second group corresponds to Ampere’s law for elementary magnetic loops. \(\boldsymbol{C}_{i}\) and \(\boldsymbol{G}_{i}\) are diagonal matrices, holding the capacitances and electric conductances of the inner branches. The third group represents Faraday’s law for electric loops on the boundary. \(\boldsymbol{B}_{\mathit{Sl}}\) has only 0, 1, − 1 entries, describing the incidence of electric branches included in the boundary to the electric boundary faces. The forth row is obtained from the current conservation law for all nodes on the boundary excepting for the nodes on the electric terminals. \(\boldsymbol{G}_{\mathit{Sl}}\) and \(\boldsymbol{C}_{\mathit{Sl}}\) hold electric conductances and capacitances directly connected to boundary. The fifth set of equations represents current conservation for electric terminals. \(\boldsymbol{G}_{\mathit{TE}}\) and \(\boldsymbol{C}_{\mathit{TE}}\) hold electric conductances and capacitances that are directly connected to electric terminals. \(\boldsymbol{S}_{E}\) is the connexion matrix between electric branches and terminals path. The last row is the discrete form of (5.27), obtained by expressing the voltages of electric terminals as sums of voltages along open paths from terminals to ground, \(\boldsymbol{P}_{E}\) being a topological matrix that holds the paths that connect electric terminals to ground.
Thus, the top left square block of \(\boldsymbol{C}\) is diagonal and the top left square bloc of \(\boldsymbol{G}\) is symmetric. The size of this symmetric bloc corresponds to the useful magnetic branches and to the useful inner electric branches. Its size is dominant over the size of the matrix, therefore, solving or reduction strategies that take into consideration this particular structure are useful.
The discretized state-space system given by (5.35) describes the input output relationship in the frequency domain
similar to (5.28), but having as transfer (circuit) function:
which is a rational function with a finite number of poles.
In conclusion, the discretization of the continuous model leads to a model represented by a MIMO linear time invariant system described by the state equations of finite size. Even if this is an important step ahead in the extraction procedure, the state space dimension is still too large for designer’s needs, therefore a further modeling step aiming an order reduction is required.
2.3 Transmission Lines: 2D + 1D Models
In this section, aiming to reduce the model extraction effort, we will exploit the particular property of interconnects of having invariant transversal section along their extent. We assume that the field has a similar structure as a transversal electromagnetic wave that propagates along the line. The typical interconnect configuration (Fig. 5.15) considered consists of n parallel conductors having rectangular cross section, permeability μ = μ 0, permittivity ɛ = ɛ 0 and conductivity σ k , k = 1, 2, ⋯ , n, placed in a SiO2 layer (σ d , ɛ d , possibly dependent on y) placed above a silicon substrate (σ s , ɛ s ).
Typical interconnect configuration
If the field is decomposed in its longitudinal (oriented along the line, which is assumed to lie along the Oz axis) and the transversal components (oriented in the xOy plane)
then Maxwell’s Equations can be separated into two groups:
called transversal equations and
called propagation equations.
The following hypotheses are adopted:
-
The volume charge density ρ and the displacement current density \(\frac{\partial \mathbf{E}} {\partial t}\) are neglected both in conductors and in the substrate.
-
The following “longitudinal” terms E z = 0, H z = 0 are canceled in the transversal equations, neglecting the field generated by eddy currents.
-
The longitudinal conduction current is neglected in dielectric J z = 0, but not in the conductors.
-
Since the conductances σ k of the conductors are much bigger than the dielectric conductance σ d , the transversal component of the electric field is neglected in the line conductors and in the substrate:
$$\displaystyle{ \mathbf{E}_{t} = \frac{1} {\sigma _{k}}\mathbf{J}_{t} =\boldsymbol{ 0}. }$$(5.42)
Under these hypotheses the transversal equations have the following form (where (k) = conductor, (s) = substrate, (d) = dielectric):
identical with the steady state electromagnetic field equations. For this reason, the electric field admits a scalar electric potential V (x, y, z, t), whereas the magnetic field admits a vector magnetic potential A(x, y, z, t) = k A(x, y, z, t) with longitudinal orientation, so that:
Thus, the propagation equations become:
By assuming an asymptotic behavior of potentials, the integration of the propagation equations yields to:
where C is a curve in the plane z = constant, which starts from the infinity and stops in the computation point of the field H z , n is the normal to the curve, oriented so that the line element is
From (5.42) it follows that the potential V is constant on every transversal cross-section of the conductors and zero in the substrate:
From relations (5.43) and (5.44) it follows that, in the transversal plane, the electric field has the same distribution as an electrostatic field. By using the uniqueness theorem of the electrostatic field it results that the function V (x, y, z, t) is uniquely determined by the potentials of the conductors V k . Consequently, due to the linearity, the per unit length (p.u.l.) charge of conductors and the current loss through the dielectric are:
where c km is the p.u.l. capacitance, and g km is the p.u.l. conductance between the conductor k and the conductor m.
By integrating E z equation from (5.47) over the surface S k and H z equation from (5.47) along the path ∂ S k which bounds this surface, the following propagation equations for potentials are obtained:
where \(r_{k}^{0} = 1/(\sigma _{k}A_{S_{k}})\) is the p.u.l. d.c. resistance of the conductor k, and
are the average values of the two potentials on the cross-section of the conductor k.
By computing the average values of the magnetic potential as in [58] and by substituting (5.50), (5.51) in (5.52) the following expressions are obtained in zero initial conditions:
where l km 0 are the p.u.l. external inductances (self inductances for k = m and mutual inductances for k ≠ m) of the conductors (k) and (m) where the return current is distributed on the surface of the substrate, and l km (t) are “transient p.u.l. inductances”, defined as the average values on S k of the vector potential A obtained in zero initial conditions by a unity step current injected in conductor (m).
For zero initial conditions for the currents i m (z, 0) = 0, for the potential v m (z, 0) = 0 and for the field \(\boldsymbol{B}_{k}^{0}(s) =\boldsymbol{ 0}\), the Laplace transform of (5.54) and (5.55) can be written as:
which is identical to the operational form of the classical Transmission Lines (TLs) Telegrapher’s equations, but where the p.u.l. inductances depend on s (implicitly on the frequency in a time-harmonic regime). In order to extract these dependencies, a magneto-quasi-static (MQS) field problem has to be solved.
2.4 Numeric Extraction of Line Parameters
Models with various degrees of fineness can be established for TLs. The coarsest ones are circuit models with lumped parameters, such as the pi equivalent circuit for a single TL shown in Fig. 5.16. As expected, the characteristic of such a circuit is appropriate only at low frequencies, over a limited range, and for short lines. Even chaining similar cells, the result is not appropriate.
The coarsest model for a single transmission line: a pi equivalent circuit
At high frequencies, the distributed effects have to be considered as an important component of the model. Proper values for the line parameters can be obtained only by simulating the electromagnetic field. The extraction of line parameters is the main step in TLs modeling since the behavior of a line with a given length can be computed from them. For instance, for a multiconductor transmission line, from the per unit length parameters matrices R, L, C and G the transfer matrix for a line of length l can be computed as
From them, other parameters (impedance, admittance or scattering) can be computed. The simplest method to extract constant matrices of the line resistance R, capacitance C and inductance L, respectively, is to solve the field equations numerically in steady-state electric conduction (EC), electrostatics (ES) and magnetostatics (MS) regimes. Empirical formulas may also be found in the literature, such as the ones given in [62] for the line capacitance. None of them take the frequency dependence of p.u.l. parameters into account.
A first attempt to take into consideration the frequency effect, which becomes important at high frequencies, is to compute the skin depth in the conductor and to use a better approximation for the resistance. In [52] we proposed a much more accurate estimation of frequency dependent line parameters based on the numerical modeling of the EM field including the semiconductor substrate. The previous section is the theoretical argument of this approach in which two complementary problems are solved, the first one describing the transversal behavior of the line from which Y l (ω) = G(ω) + jω C(ω) is consequently extracted, and the second one describing the longitudinal behavior of the line from which Z l (ω) = R(ω) + jω L(ω) is extracted.
Since the first field problem is dedicated to the computation of the transversal capacitances between wires and their loss conductances, according to the previous section, the natural choice is to solve a 2D problem of the transversal electro-quasi-static (EQS) field in dielectrics, considering the line wires as perfect conductors with given voltage. The boundary conditions are of Dirichlet type V = 0 on the lower electrode, and open boundary conditions (e.g. Robin, SDI or appropriate ELOB [50]) on the other three sides. A dual approach, such as dFIT [51] allows a robust and accurate parameter extraction.
The second field problem focuses on the longitudinal electric and the generated transversal magnetic field. Consequently, a short line-segment (with only one cell layer) is considered. The magneto-quasi-static (MQS) regime of the EM field is appropriate for the extraction of Z l (ω). However, for our simulations we used a our FIT solver for Full Wave (FW) ECE problems. The magnetic grid is 2D, thus ensuring the TM mode of propagation.
In order to eliminate the transversal distribution of the electric field, the lower electrode is prolongated over the entire far-end cross-section of the rectangular computational domain, which thus has perfect electric conductor (PEC) boundary conditions E t = 0 on two of their faces. On the three lateral faces, open-absorbing boundary conditions are the natural choice, whereas on the near-end cross-section the natural boundary conditions are those of the Electric Circuit Element (ECE): B n = 0, n × curlH = 0 excepting for the wire traces, where E t = 0. These conditions ensure the correct definition of the terminals voltages, and consequently of the impedance/admittance matrix (Fig. 5.17).
Boundary conditions for the full wave – transversal magnetic problem
The pi equivalent circuit for a simulated short line segment. Parameters are evaluated from field simulations
These boundary conditions are the field representation of the line segment with short-circuit at the far-end, whereas the 2D EQS problem is the field representation of the segment-line with open far-end.
The transversal component is finally subtracted from the FW-TM simulation to obtain an accurate approximation of the line impedance, as given by
This subtraction is carried out according to a pi-like equivalent net for the simulated short segment (Fig. 5.18). Finally, the line parameters are:
where
where Δ l is the length of the considered line-segment and Z TM is the impedance matrix extracted from the TM field solution.
This numerical approach to extract the line parameters, named the two fields method, is more robust and may be applied without difficulties to multi-wire lines. The obtained values of the line parameters are frequency dependent, taking into consideration proximity and skin effects as well as losses induced in the conducting substrate.
2.5 Variability Analysis of Line Parameters
The simplest way to analyze the parameter variability is to compute first order sensitivities. These are derivatives of the device characteristics with respect to the design parameters. The sensitivities of the line parameters are essential to estimate the impact of small variations on the device behavior. Moreover, the sensitivity of the terminal behavior of interconnects can also be estimated.
For instance, in the case of a single TL, having the global admittance given by
the sensitivities of the terminal admittance with respect to a parameter can be computed as:
where the sensitivities of
can be computed if the sensitivities of the p.u.l. parameters ∂ R∕∂ α, etc. are known.
In the case of a multiconductor TL with n conductors the sensitivity of the admittance matrix Y of dimension (2n × 2n) is computed by means of the sensitivity of the transfer matrix
also of dimension (2n × 2n), knowing that
In the formulas above, all the sub-blocks are of dimensions (n × n). For instance
The transfer matrix T is computed with (5.57) and its sensitivity is
where
Thus, the basic quantities needed to estimate the sensitivity of the admittance are the sensitivities of the p.u.l. parameters. By using a direct differentiation technique, as explained in [41] the sensitivities of the EQS and TM problems with respect to the parameters that vary, i.e. \(\partial \mathbf{Y}_{\mathit{EQS}}/\partial \alpha \quad \mbox{ and}\quad \partial \mathbf{Z}_{\mathit{TM}}/\partial \alpha\) are computed. Then, the sensitivity of the MQS mode is computed by taking the derivative of (5.58):
Finally, the sensitivities of the p.u.l. parameters are:
The values of the sensitivities thus obtained depend on the frequency as well.
2.6 Parametric Models Based on Taylor Series
Continuous improvements in today’s fabrication processes determine smaller chip sizes and smaller device geometries. Process variations induce changes in the properties of metallic interconnect between devices.
Simple parametric models are often obtained by truncating the Taylor series expansion for the quantity of interest. This requires the computation of the derivatives of the device characteristics with respect to the design parameters [55]. Let us assume that \(y(\alpha _{1},\alpha _{2},\cdots \,,\alpha _{n}) = y(\boldsymbol{\alpha })\) is the device characteristic which depends on the design parameters \(\boldsymbol{\alpha }= [\alpha _{1},\alpha _{2},\cdots \,,\alpha _{n}]\). The quantity y may be, for instance, the real or the imaginary part of the device admittance at a given frequency or any of the p.u.l. parameters. The parameter variability is thus completely described by the real function, y, defined over the design space S, a subset of \(\mathbb{R}^{n}\). The nominal design parameters correspond to the particular choice \(\boldsymbol{\alpha }_{0} = [\alpha _{01}\alpha _{02}\cdots \alpha _{0n}]\).
2.6.1 Additive Model (A)
If y is smooth enough then its truncated Taylor Series expansion is the best polynomial approximation in the vicinity of the expansion point \(\boldsymbol{\alpha }_{0}\). For one parameter (n = 1), the additive model is the first order truncation of the Taylor series:
If we denote by y(α 0) = y 0 the nominal value of the output function, by \(\frac{\partial y} {\partial \alpha } (y_{0}) \frac{\alpha _{0}} {y_{0}} = S_{\alpha }^{y}\) the relative first order sensitivity and by (α −α 0)∕α 0 = δ α the relative variation of the parameter α, then the variability model based on (5.73) defines an affine [60] or additive model (A):
To ensure a relative validity range of the first order approximation of the output quantity less a given threshold t 1, the absolute variation of the parameter must be less than
where D 2 is an upper limit of the second order derivative of the output quantity y with respect to parameter α [41].
For the multiparametric case, one gets:
Similar with one parameter case, the relative sensitivities w.r.t. each parameter are denoted by \(\frac{\partial y} {\partial \alpha _{k}}(\boldsymbol{\alpha }_{0})\frac{\alpha _{0k}} {y_{0}} = S_{\alpha _{k}}^{y}\) and the relative variations of the parameters by δ α k = (α k −α 0k )∕α 0k , the additive model (A) for n parameters being given by:
Thus, each new independent parameter taken into account adds a new term to the sum [52]. The additive model is simply a normalized standard version of a linearly truncated Taylor expansion.
Instead of using this truncated expansion may be numerically favorable to expand some transformation F(y) of y instead. Two particular choices for F have practical importance: identity and inversion as it will be indicated below.
2.6.2 Rational Model (R)
The rational model is the additive model for the reverse quantity 1∕y. It is obtained from the first order truncation of the Taylor Series expansion for the function 1∕y. For n = 1, if we denote by \(r(\alpha ) = \frac{1} {y(\alpha )}\), it follows that:
We define the relative first order sensitivity of the reverse circuit function:
Consequently, we obtain the rational model for n = 1:
It can be easily shown that the reverse relative sensitivity is \(S_{\alpha }^{\frac{1} {y} } = -S_{\alpha }^{y}\). For the multiple parameter case, the rational model is:
If the circuit function y is for instance the admittance, its inverse 1∕y is the impedance. In the time domain, these two transfer functions correspond to a device excited in voltage or in current, respectively. Consequently, the choice between additive and rational models for the variability analysis of the circuit functions in frequency domain can be interpreted as a change in the terminal excitation mode in the time domain state representation. Choosing the appropriate terminal excitation, the validity range of the parametric model based on first order Taylor series approximation can be dramatically extended.
2.7 Parametric Circuit Synthesis
We have shown in [48] that one of the most efficient order reduction method for the class of problems we address is the Vector Fitting (VFIT) method proposed in [47], improved in [43, 46] and available at [61]. It finds the transfer function matching a given frequency characteristic. Thus, in the frequency domain, for the output quantity \(\boldsymbol{y}(s)\), this procedure finds the poles p m (real or complex conjugate pairs), the residuals \(\boldsymbol{k}_{m}\) and the constant terms \(\boldsymbol{k}_{0}\) and \(\boldsymbol{k}_{\infty }\) of a rational approximation of the output quantity (e.g an admittance):
The resulting approximation has guaranteed stable poles and the passivity can be enforced in a post-processing step [43]. The transfer function (5.82) can be synthesized by using the Differential Equation Macromodel (DEM) [57]. Our aim is to extend DEM to take into consideration the parameterization.
To simplify the explanations, we assume a single input single output system, excited in voltage. It follows that the output current is given by (5.83), where x m (s) is a new variable defined by (5.84).
By applying the inverse Laplace transformation to (5.83) and (5.84), relationships (5.85) and (5.86) are obtained:
If we use the following matrix notations
then equations of the system (5.85), (5.86) can be written in a compact form as
2.7.1 Case of Real Poles
In the case in which all poles (and consequently, all the residuals) are real, Eq. (5.85) can be synthesized by the circuit shown in Fig. 5.19 which consists of a capacitor having the capacitance k 0, in parallel with a resistor having the conductance k ∞ , in parallel with q voltage controlled current sources, their parameters being the residuals k m .
Equivalent circuit for the output equation if all poles are real
Sub-circuit corresponding to a real pole
Equation (5.86) can be synthesized by the circuit in Fig. 5.20, where x m is the voltage across a unity capacitor, connected in parallel with a resistor having the conductance − p m and a voltage controlled current source, controlled by the input voltage u.
We would like to include the parametric dependence into the VFIT model and in the synthesized circuit. To keep the explanations simple, we assume that there is only one parameter that varies, i.e. the quantity α is a scalar. Assuming that keeping the order q is satisfactory for the whole range of the variation of this parameter, this means that (5.82) can be parameterized as:
Without loss of generality, we can assume that the additive model is more accurate than the rational one. If not, the reverse quantity is used, which is equivalent, for our class of problems, to change the excitation of terminals from voltage excited to current excited, and use an additive model for the impedance \(\boldsymbol{z} =\boldsymbol{ y}^{-1}\). The additive model (5.74) can be written as
where here \(\boldsymbol{y}\) is a matrix function. By combining (5.91) and (5.92) we obtain an approximate additive model based on VFIT:
From (5.91) it follows that the sensitivity of the VFIT approximation needed in (5.93) is
The sensitivity \(\partial \boldsymbol{y}/\partial \alpha\) can be evaluated with (5.62) for as many frequencies as required and thus the sensitivities of poles and residues in (5.94) can be computed by solving the linear system (5.94) by least square approximation. Finally, by substituting (5.94) and (5.91) in (5.93), the final parameterized and frequency dependent model is obtained:
Expression (5.95) has the advantage that it has an explicit dependence with respect both to the frequency s = j ω and parameter α, is easy to implement and feasible to be synthesized as a net-list having components with dependent parameters, as explained below.
If we denote by
where k ∗ = k ∗(α 0) then Eq. (5.95) can be written as
where
The output current is thus
where the first term can be synthesized with a circuit similar to the one in Fig. 5.19 but where the k ∗ parameters depend on α, and the second term
adds q new parallel branches to the circuit (Fig. 5.21). It is useful to write (5.101) as
The part that depends on s in (5.102) can be synthesized by a second order circuit, such as the one in Fig. 5.22.
Parameterized circuit corresponding to the output equation
Second order subcircuit, with a voltage controlled current source
Second order subcircuit corresponding to a real pole
The current through the coil is
To obtain the expression in (5.102) it is necessary that LC = 1∕p m 2, LG = −2∕p m , for instance, we can chose G = −p m , L = 2∕p m 2, C = 1∕2. Thus, the parameterized circuit is given by the sub-circuits in Figs. 5.21, 5.20 and 5.23. The circuit that corresponds to the output equations has new branches with current controlled current sources. Only this sub-circuit contained parameterized components.
Another possibility to derive a parameterized circuit is to do as follows. In (5.101) we denote by
and by
Relationships (5.104) and (5.105) are equivalent to
which correspond in the time domain to
Equations (5.108) and (5.109) can be synthesized with the subcircuit shown in Fig. 5.24. In this case the circuit that corresponds to the output equation is the one in Fig. 5.25. In brief, the parameterized reduced order circuit can be either the one in Figs. 5.21, 5.20 and 5.23 or in Figs. 5.25, 5.20 and 5.24. In both approaches only the circuit that corresponds to the output equation is parameterized. The second approach has the advantage that can be generalized for a transfer function having complex poles as well.
Subcircuit corresponding to the second order term (second approach)
Parameterized circuit corresponding to the output equation (second approach)
2.7.2 Case of Complex Poles
2.7.2.1 Nominal Differential Equation Macromodel
If some of the q poles are complex, then they appear in conjugated pairs since they are the roots of the characteristic equation corresponding to a real matrix. We assume for the beginning that the transfer function has only one pair of complex conjugate poles: p = a +jb and p ∗ = a −jb. In this case the transfer function is
The numerator can be a real polynomial in s only if k 1 and k 2 are complex conjugated residues: k 1 = c +jd, k 2 = c −jd. In this case, the matrices in (5.87) are
In order to obtain a real coefficient equation, a matrix transformation is introduced. The system (5.89) becomes
where
Let
The transformation \(\boldsymbol{\hat{A}} =\boldsymbol{ V }\boldsymbol{A}\boldsymbol{V }^{-1}\) is a similarity transformation, preserving the eigenvalues of the matrix and thus the characteristic polynomial of the system.
The two equations corresponding to the complex conjugated pair of poles
become after applying the similarity transformation
If there are several pairs of complex conjugated poles, Eq. (5.118) will be true for any of these pairs and, by renaming p → p m , \(\hat{x}_{1} \rightarrow \hat{ x}_{m}^{{\prime}}\), \(\hat{x}_{2} \rightarrow \hat{ x}_{m}^{{\prime\prime}}\), a → a m , b → b m , the synthesized circuit is shown in Fig. 5.26.
Sub-circuit corresponding to a pair of complex conjugate poles
In general, if the system has q poles out of which q r are real and q c = (q − q r )∕2 are pairs of complex conjugate poles, then the synthesis will be done as follows: for each real pole m = 1, …, q r , let k m be the residue corresponding to the pole; for each pair of complex conjugate poles m = 1, …, q c let the pole be p m ′ = a m + jb m , with the corresponding residue k m ′ = c m + jd m . An equivalent circuit for the output equation is shown in Fig. 5.27. It consists of the following elements connected in parallel:
-
A capacitance k 0;
-
A conductance k ∞ ,
-
q r voltage controlled current sources (having the parameter k m , controlled by the voltages x m ),
-
q c voltage controlled current sources (having the parameter \(-\sqrt{2}c_{m}\), controlled by the voltages \(\hat{x}_{m}^{{\prime}}\))
-
q c voltage controlled current sources (having the parameter \(\sqrt{2}d_{m}\), controlled by the voltages \(\hat{x}_{m}^{{\prime\prime}}\)).
The voltages x m are defined on the q r subcircuits that correspond to real poles (Fig. 5.20) and the voltages \(\hat{x}_{m}^{{\prime}}\), \(\hat{x}_{m}^{{\prime\prime}}\) are defined on the q c subcircuits that correspond to the pair of complex conjugate poles (Fig. 5.26).
Sub-circuit corresponding to a pair of complex conjugate poles
2.7.2.2 Parametric DEM
To derive the parametric circuit in the case of complex poles, we could proceed as we did in the first approach for real poles. This would conduce to a transfer function of order 4, which is not obvious how it can be synthesized. The second approach can be extended to the case of complex poles, as follows.
Let’s consider Eqs. (5.108) and (5.109) written for a pair of complex conjugate poles p 1 = a +jb, p 2 = a −jb:
By using the matrix notations
it follows that (5.119) ÷ (5.122) can be written in a compact form as
and by applying the similarity transformation described in the previous section it follows that
where \(\boldsymbol{V }\boldsymbol{A}\boldsymbol{V }^{-1}\) is given by (5.115). It is straightforward to derive that
Thus, the Eqs. (5.124) and (5.125) corresponding to the two complex-conjugated poles become after applying the similarity transformation
Sub-circuit corresponding to a pair of complex conjugate poles
If there are several pairs of complex conjugated poles, equations above will be true for any of these pairs and, by renaming p → p m , \(\hat{g}_{1} \rightarrow \hat{ g}_{m}^{{\prime}}\), \(\hat{g}_{2} \rightarrow \hat{ g}_{m}^{{\prime\prime}}\), \(\hat{f}_{1} \rightarrow \hat{ f}_{m}^{{\prime}}\), \(\hat{f}_{2} \rightarrow \hat{ f}_{m}^{{\prime\prime}}\), \(a \rightarrow a_{m}\), b → b m , the synthesized circuit is shown in Fig. 5.28.
The new terms added in the output equations are
Parametric sub-circuit corresponding to the output equation
In general, if the system has q poles out of which q r are real and q c = (q − q r )∕2 are pairs of complex conjugate poles, then the parametric synthesis will be done as follows: for each real pole m = 1, …, q r , let k m be the residue corresponding to the pole; for each pair of complex conjugate poles m = 1, …, q c let the pole be p m ′ = a m + jb m , with the corresponding residue k m ′ = c m + jd m . The equivalent circuit for the parametric output equation is shown in Fig. 5.29. It consists of the following elements connected in parallel:
-
A parameterized capacitance k 0(α) = k 0 + (α −α 0)∂ k 0∕∂ α,
-
A parameterized conductance k ∞ (α) = k ∞ + (α −α 0)∂ k ∞ ∕∂ α,
-
q r voltage controlled current sources (having as parameter the parameterized value k m (α) = k m + (α −α 0)∂ k m ∕∂ α, controlled by the voltages x m ),
-
q c voltage controlled current sources (having as parameter the parameterized value \(-\sqrt{2}c_{m}(\alpha )\), controlled by the voltages \(\hat{x}_{m}^{{\prime}}\)),
-
q c voltage controlled current sources (having the parameter \(\sqrt{2}d_{m}(\alpha )\), controlled by the voltages \(\hat{x}_{m}^{{\prime\prime}}\)),
-
q r voltage controlled voltage sources (having the parameter (α −α 0)k m , controlled by the voltages f m ,
-
q c voltage controlled current sources (having the parameter \(-\sqrt{2}c_{m}(\alpha -\alpha _{0})\), controlled by the voltages \(\hat{f}_{m}^{{\prime}}\)),
-
q c voltage controlled current sources (having the parameter \(\sqrt{2}d_{m}(\alpha -\alpha _{0})\), controlled by the voltages \(\hat{f}_{m}^{{\prime\prime}}\)).
The voltages x m are defined on the q r subcircuits that correspond to real poles (Fig. 5.20), the voltages \(\hat{x}_{m}^{{\prime}}\), \(\hat{x}_{m}^{{\prime\prime}}\) are defined on the q c subcircuits that correspond to the pair of complex conjugate poles (Fig. 5.26), the voltages f m are defined on the q r subcircuits that correspond to real poles (Fig. 5.24), the voltages \(\hat{f}_{m}^{{\prime}}\) and \(\hat{f}_{m}^{{\prime\prime}}\) are defined on the q c subcircuits that correspond to the complex poles (Fig. 5.28).
2.8 Case Study
In order to validate our approach and to evaluate different parametric models which can be extracted by the proposed procedure, several experiments have been performed on a test structure that consists of a microstrip (MS) transmission line having one Aluminum conductor embedded in a SIO2 layer. The line has a rectangular cross-section, parameterized by several parameters (Fig. 5.30). The return path is the grounded surface placed at y = 0. The nominal values used are: h 1 = 1 μm, h 2 = 0. 69 μm, h 3 = 10 μm, a = 130. 5 μm, p 1 = h 1, p 2 = h 2, p 3 = 3 μm, x max = 264 μm. In order to comply with designer’s requirements, the model should include the field propagation along the line, taking into consideration the distributed parameters and the high frequency effects.
Stripline parameterized structure
Frequency characteristic Re(S11): numerical model vs. measurements
2.8.1 Validation of the Nominal Model
The first step of the validation refers to the simulation of the nominal case for which measurements (S parameters) are available from the European project FP5/ Codestar (http://www.magwel.com/codestar/). By using dFIT + dELOB [52], at low frequencies, the following values are obtained:
which are coherent with the values obtained from the measurements at low frequencies, and validates the grid used and the extension of the boundary used in the numerical model. Then, by using the method described in Sect. 5.2.4 the dependence of p.u.l. parameters with respect to the frequency was computed. The comparison between the resulting S parameters and the measurements is shown in Fig. 5.31 and it validates the nominal model. The sensitivities of the p.u.l. parameters are computed using the CHAMY software [40], by direct differentiation method applied to the state space equations [41]. They could also be computed by Adjoint Field Technique (AFT) [38, 53].
2.8.2 Parametric Models
In this section, the accuracy of several parametric models for the line capacitance is investigated.
The first sets of tests considered only one parameter that varies, namely the width of the line, p 3. The nominal value chosen was p 3 = 3 μm and samples in the interval [1, 5] μm were considered. The reference result was obtained by simulated the samples separately (each sample was discretized and solved). These were compared with the approximate values obtained from models A and R (Fig. 5.32). As expected intuitively, the dependence w.r.t. p 3 is almost linear and the A model is better than the R model. Considering the relative variation of the parameters less than 15 % (which is the typical limit for the technological variations nowadays) the relative variation of the output parameter is obtained (Fig. 5.32, right). The errors of both affine and rational first order models for p.u.l. parameters are given in Table 5.2. Model A based on the first order Taylor series approximation has a maximal error for technologic variations 1.78 % for p.u.l. resistance when p 3 is variable, whereas model R has an approximation error of only 0.6 % for the same range of the technological variations for p.u.l. capacitance when p 3 is variable. Using (5.75) one can be easily identify which is the best model for any case.
Left: Reconstruction of the p.u.l. C from Taylor Series first order expansion; Right: Relative error w.r.t. the relative variation of parameter p 3
The second set of tests considered two parameters that vary simultaneously: p 1 and p 3. For reference, a set of samples in [0. 8, 1. 2] × [2, 4] μm were considered. The p.u.l. capacitance was approximated using the additive, rational and multiplicative models described above. In this case, a new model M is computed using an additive model for p 3 and a rational one for p 1, which is the best choice. Fig. 5.33, left compares the relative variation of the errors w.r.t. a relative variation of parameter p 1 for a variation of p 3 of 5 %. Model M provides lower errors (maximum error is 2 %) than models A (3.7 %) and R (2.2 %). Figure 5.33, right illustrates that in the range from 20 to 40 % model M is the best one if we look at the variation w.r.t. p 3 for a variation of p 1 of 10 %.
Left: Relative error w.r.t. the relative variation of parameter p 1, for a variation of p 3 of 5 %; Right: Relative error w.r.t. the relative variation of parameter p 3, for a variation of p 1 of 10 %
Thus, by using the appropriate multiplicative models in the modeling of the technological variability, the necessity of higher order approximations can be eliminated.
2.8.3 Frequency Dependent Parametric Models
In this case, the parameter considered variable is h 2. The sensitivity of the admittance with respect to this parameter has been calculated according to (5.62), using EM field solution. By applying Vector Fitting, a transfer function with 8 poles has been obtained. This conduced to an overdetermined system of size (236, 26) which has been solved with an accuracy (relative residual) of 3.7 % (Fig. 5.34-left). Finally, the relative error of the A-VFIT model is 1.09 % compared to the relative error of the A model which is 0.95 % for a relative variation of the parameter of 10 % (in Fig. 5.34-right the three curves are on top of each other).
Left: variation of the admittance sensitivity with respect to the frequency; right: reference simulation vs. answer obtained from the frequency dependent parametric model (5.95)
2.9 Conclusions
The paper describes an effective procedure to extract reduced order parametric models of on-chip interconnects allowing model order reduction in coupled field (PDE) – circuit (DAE) problems. These models consider all EM field effects at high frequency, described by 3D-FW Maxwell equations. The proposed procedure is summarized by the following steps:
-
Step 1 – Solve two field problems (2D EQS and FW-TM) and compute frequency dependent p.u.l. parameters and their sensitivities with respect to the geometric parameters that vary;
-
Step 2 – Compute admittance for the real length of the line and its sensitivities with respect to the variable parameters;
-
Step 3 – Choose the A/R variation model, i.e. the appropriate terminal excitation (admittance or impedance);
-
Step 4 – Apply Vector Fitting for the nominal case in order to extract a rational model for the circuit function with respect to the frequency;
-
Step 5 – Compute sensitivities of poles and residues of the circuit function by solving a least square problem;
-
Step 6 – Assemble the frequency dependent parametric model by using the compact expression (5.95) or by synthesis of a SPICE like parametric netlist having frequency constant parameters.
Step 1 is dedicated to the extraction of the frequency dependent p.u.l. line parameters in a more robust and flexible way than the inversion of the equation of the short line segment. It is based on the solving of two field problems: 2D-EQS field which describes the transversal effects such as capacitive coupling whereas EMQS-TM field describes the longitudinal effects such as inductive, skin effect and eddy currents. The longitudinal propagation is described by the classic TL equations, but with frequency dependent p.u.l. line parameters.
Then (step 2), variability models for TL structures considering the dependency of p.u.l. parameters w.r.t. geometric parameters, at a given frequency were analyzed. A detailed study of the line sensitivity was made by using numeric techniques. For one parameter case, the proposed methods avoid the evaluation of higher order sensitivities, but keeping a high level of accuracy by introducing models based on a rational approximation in the frequency domain. The multi-parametric case has been analyzed, in addition, a multiplicative parametric model (M) has been proposed. This is based on the assumption that the quantity of interest can be expressed with separated variables, for which A and/or R models are used. Model M is sometimes better than A and R models obtained from Taylor Series expansion. Its specific terms (products of first order sensitivities) can thus approximate higher order, cross-terms of Taylor Series. In order to automatically select the best first order model for a multiparametric problem, the validity ranges of direct and reversed quantities have to be evaluated (step 3). Once we establish the best model (A or R) for each parameter, the M model will be easily computed by multiplication of individual submodels. Our numerical experiments with the proposed algorithm in all particular structures we investigated prove that the technological variability (e.g. ± 20 % variation of geometric parameters, which is typical for the technology node of 65 nm) can be modeled with acceptable accuracy (relative errors under 5 %) using only first order parametric models for line parameters. This is one of the most important results of our research.
Next, a rational approximation in the frequency domain, obtained with Vector Fitting (step 4) is combined with a first order Taylor Series approximation. The sensitivities of poles, residues and constant terms are computed by solving an over-determined system of linear equations (step 5). The main advantage of this approach is that the final result is amenable to be synthesized with a small parameterized circuit (step 6). This method relies on the differential equation macromodel which is extended in order to take into account the variability. It also assumes that a first order Taylor Series expansion for the parameter that varies is accurate enough for the frequency range of interest. As shown in our previous work, there is a specific excitation type of terminals for which this assumption is acceptable for a certain frequency range. The passivity of the obtained circuit is guaranteed by the fact that the transfer function used as input for the synthesis procedure is passive as it is obtained by a fitting procedure with passivity enforcement.
Thus, the proposed method allows one to obtain parameterized reduced order circuits, having equivalent behavior as on-chip interconnects. These equivalent circuits described in SPICE language are extracted by considering all electromagnetic field effects in interconnects at very high frequency. This method applied to extract the reduced order model of the system described by PDE is a robust and efficient one, being experimentally validated.
The advantages of the proposed approach are:
-
Its high accuracy, due to the consideration of all field effects at high frequency;
-
Fast model extraction due to the reduced order of degrees of freedom in the numerical approach;
-
High efficiency of the model order reduction step due to the use of Vector Fitting; in all interconnect studied cases, extracted models with an order less than 10 had an acceptable accuracy for designers.
-
Simple geometric variability models based only on first order sensitivities, with extended valability domain due to the appropriate excitation;
-
Appropriate variation model for frequency and length of interconnects, due to the transmission lines approach;
-
The reduced SPICE models are simple and compact, containing ideal linear elements with lumped frequency independent constant parameters: capacitances, resistances and voltage controlled current sources; these element parameters have very simple affine variation in the case of the geometric variability.
The proposed method was successfully applied to model technological variability, without being necessary the use of higher order sensitivities.
3 Model Order Reduction and Sensitivity Analysis
Several types of parameters p = (d, s, θ) influence the behaviour of electronic circuits and have to be taken into account when optimizing appropriate performance functions f(p): design parameters d, manufacturing process parameters s, and operating parameters θ.Footnote 3 The impact of changes of design parameters, e.g., the width and length of transistors or the values of resistors, plays a key role in the design of integrated circuits. Deviations from the nominal values defined in the design phase arise in the manufacturing process. Hence, to guarantee that the physical circuit shows the performances that were specified, the design has to be robust with respect to variations in the manufacturing phase. It has to be analysed how sensitive to parameter changes an integrated circuit and its performance is.
The manufacturing process parameters have a statistical impact, f.i., for the oxide thickness threshold. Examples of operating parameters are temperature and supply voltage.
Sensitivity can ease calculations on statistics (for instance by including the sensitivity in calculating the standard deviation of quantities that nearly linearly depend on independent normal distributed parameters [91]: if \(\boldsymbol{F}(\boldsymbol{p}) \approx \boldsymbol{ F}_{0} +\boldsymbol{ A}\boldsymbol{p}\) with p i ∼ N(0, σ i ) then \(\sigma ^{2}(\boldsymbol{F}_{i}) \approx \sum _{j}a_{\mathit{ij}}^{2}\sigma _{j}^{2}\) (σ(F i ), and σ j being the standard deviation of F i and p j , resp.).
For optimizing one wants to minimize a performance function f(p) while also several constraints have to be satisfied. The performance function f(p) and the constraint functions c(p) can be costly to evaluate and are subject to noise (for instance due to numerical integration effects). For both, the dependency on p can be highly nonlinear. Here there is interest in derivative free optimization [118], or to response surface model techniques [79, 80, 92, 117]. Partly these approaches started because in circuit simulation, sensitivities of f(p) and c(p) with respect to p are not always provided (several model libraries do not yet support the calculation of sensitivities). However, when the number of parameters increases adjoint sensitivity methods become of interest [74, 75]. For transient integration of linear circuits this is described in [76, 77]. In [96] a more general procedure is described that also applies to nonlinear circuits and retains efficiency by exploiting (nonlinear) techniques from Model Order Reduction.
A special sensitivity problem arises in verification of a design after layouting. During the verification the original circuit is extended by a huge number of ‘parasitics’, linear elements that generate additional couplings to the system. To reduce their effect the dominant parasitics should be detected in order to modify the layout.
Adjoint equations are also used for goal achievement. One example is in global error estimation in numerical integration [73, 99].
In this Section we describe adjoint techniques for sensitivity analysis in the time domain and indicate how MOR techniques like POD (Proper Orthogonal Decomposition) may fit here. Next we give a short introduction into Uncertainity Quantification which techniques provide an alternative way to perform sensitivity analysis. Here pMOR (parameterized MOR) techniques can be exploited.
3.1 Recap MNA and Time Integration of Circuit Equations
Modified Nodal Analysis (MNA) is commonly applied to model electrical circuits [86, 90]. Including the parameterization the dynamical behaviour of a circuit is then described by network equations of the general form
The state variables \(\mathbf{x}(t,\mathbf{p}) \in \mathbb{R}^{n}\), i.e., the potentials at the network’s nodes and the currents through inductors and current sources, are the unknowns in this system. They depend implicitly on the parameters gathered in the vector \(\mathbf{p} \in \mathbb{R}^{n_{p}}\), because the voltage-charge and current-flux relations of capacitors and inductors, subsumed in \(\mathbf{q}(\cdot,\cdot ) \in \mathbb{R}^{n}\), the voltage-current relations of resistive elements, appearing in \(\mathbf{j}(\cdot,\cdot ) \in \mathbb{R}^{n}\) and the source terms \(\mathbf{s}(\cdot,\cdot ) \in \mathbb{R}^{n}\), i.e., the excitation of the circuit, may depend on the parameterization. The elements’ characteristics q, j are usually nonlinear in the state variables x, e.g., when transistors or diodes are present in the design at hand.
If, however, all elements behave linear with respect to x, the MNA equations are of the form
where \(\dot{\mathbf{x}}\) denotes total differentiation, (d∕dt) x(t, p) with respect to time. C(p) and G(p) are real n × n-matrices that might depend nonlinearly on the parameters p.
Usually the network equations (5.133) state a system of Differential-Algebraic Equations (DAEs), i.e., (∂∕∂ x) q(x, p) (or C(p)) does not have full rank along the solution trajectory x(t, p).
In transient analysis the network equations (5.133) are solved on a time-interval \([t_{0},t_{\text{end}}] \subset \mathbb{R}\), where the parameter vector p is fixed and a (consistent) initial value \(\mathbf{x}_{0,\mathbf{p}}:= \mathbf{x}(t_{0},\mathbf{p}) \in \mathbb{R}^{n}\) is chosen. As the system can usually not be solved exactly, numerical integration, e.g., BDF (backward differentiation formulas) or RK (Runge-Kutta) methods are used to compute approximations \(\mathbf{x}_{i,\mathbf{p}} \approx \mathbf{x}(t_{i},\mathbf{p})\) to the state variables on a discrete timegrid \(\{t_{0},\mathop{\ldots },t_{l},\mathop{\ldots },t_{K} = t_{\text{end}}\}\). For a timestep h form t l−1 to t l = t l−1 + h, multistep methods, like the BDF schemes, approximate the time derivative \(\frac{\text{d}} {\text{d}t}\mathbf{q}(\mathbf{x}(t_{l},\mathbf{p}),\mathbf{p})\) by some k-stage operator \(\rho \mathbf{q}(\mathbf{x}_{l,\mathbf{p}},\mathbf{p}):=\alpha \mathbf{q}(\mathbf{x}_{l,\mathbf{p}},\mathbf{p})+\boldsymbol{\beta }\), where \(\alpha =\alpha (h) \in \mathbb{R}\) is the integration coefficient and \(\boldsymbol{\beta }\in \mathbb{R}^{n}\) is made up of history terms q(x μ, p , p) at the timepoints t μ for \(\mu = l - k,\mathop{\ldots },l - 1\). For the backward Euler method, e.g., we have
This results at each discretisation point \(t_{l} \in \{ t_{0},t_{1},\mathop{\ldots },t_{K}\}\) in a nonlinear equation for the state variable x l, p of the form
This nonlinear problem is usually solved with some Newton-Raphson technique, where in each underlying iteration \(\nu = 1,\,2,\mathop{\ldots }\) a linear system with a system matrix of the form
appears. Typically, simplified Newton-Raphson iterqations may be applied. That is, only the evaluation at x l, p (1) is involved. Note, also when applying a onestep method, like an RK-scheme, linear systems, made up of the Jacobian (5.135) arise.
3.2 Sensitivity Analysis
We encounter that the state variables x(t, p) implicitly depend on the the parameters \(\mathbf{p} \in \mathbb{R}^{n_{p}}\). Hence, one is interested in how sensitive the behavior of the circuit with respect to variations in the parameters is. Thinking about “behavior of the system” we can basically have in mind
-
(i)
How do the state variables vary with varying parameters?
-
(ii)
How do measures derived from the state variables, e.g., the power consumption change with varying parameter?
Furthermore, due to usually nonlinear dependence of the element characteristics q and j or C and G, respectively, on the parameters, we are interested in variations around a nominal value \(\mathbf{p}_{0} \in \mathbb{R}^{n_{p}}\).
In the following we will give a brief overview on the different kinds of sensitivities and how they can be treated numerically. For further reading we refer to the PhD thesis by Ilievski [95] and the papers by Daldoss et al. [78], Hovecar et al. [93], Cao et al. [74, 75] and Ilievski et al. [96].
3.2.1 State Sensitivity
In (transient) state sensitivity one is interested, how the trajectories of the state variables x vary with respect to the parameters p around the nominal setting p 0. Hence, the goal is to compute
As described by Daldoss et al. [78] we linearize the nonlinear network equations (5.133b) around the nominal parameter set p 0, i.e., we differentiate with respect to p. We assume that the element functions q, j are sufficiently smooth such that we can exchange the order of differentiation (Schwarz’s theorem) and get:
where \(\mathbf{C}_{x}(t),\mathbf{G}_{x}(t) \in \mathbb{R}^{n\times n}\) and \(\mathbf{C}_{p}(t),\mathbf{G}_{p}(t),\mathbf{S}_{p}(t) \in \mathbb{R}^{n\times n_{p}}\) and x(t, p 0) solves the network problem (5.133a).
The initial sensitivity value \(\boldsymbol{\chi }_{\mathbf{p}_{0}}(t_{0}) =:\boldsymbol{\chi } _{p_{0},0} =:\boldsymbol{\chi }_{ p_{0}}^{\text{DC}}\) can easily be calculated as the sensitivity of the DC-solution \(\mathbf{x}(0,\mathbf{p}_{0}):= \mathbf{x}_{\mathbf{p}_{0}}^{\text{DC}}\) of the network equation (5.133a), satisfying
Obviously, the DAE (5.137) states a linear time varying dynamical system for the state sensitivity \(\boldsymbol{\chi }_{\mathbf{p}_{0}}\), even when (5.133a) was nonlinear. We assume that we have used the backward Euler method to solve the network problem (5.133). Using the same time grid for solving the state sensitivity problem (5.137), we advance from time point t l−1 to t l = t l−1 + h, i.e., we compute \(\boldsymbol{\chi }_{\mathbf{p}_{0},l} \approx \boldsymbol{\chi }_{\mathbf{p}_{0}}(t_{l})\) again with the backward Euler by solving
with
We note, that the partial derivatives with respect to x have already been computed in the transient analysis and are available, if they have been stored. Especially, the system matrix M l is the same as we have used in applying the backward Euler method in the underlying simulation: within the Newton iterations these where the system matrices in the steps where convergence was recorded. Hence, also the decomposition of this matrix is available, such that the system could be solved efficiently. For schemes other than the backward Euler, we can also state, that the solution of the transient sensitivity problem (5.137) needs ingredients that are available (if they have been stored) from the solution of the network problem with the same method and the same step size. A reasoning for this and details on step size control and error estimation can be found in the paper by Daldoss et al. [78].
However, the sensitivities of the element functions q, j and s have to be calculated. In total, the evaluation of the right-hand side rhs l requires \(\mathcal{O}(n_{p} \cdot n^{2}) + \mathcal{O}(n_{p} \cdot n)\) operations [96]. As in addition a lot of data has to be stored, computing the state sensitivities for circuits containing a large number of parameters is not tractable.
3.2.2 Observation Function Sensitivity
Often one is not interested in the sensitivity \(\boldsymbol{\chi }_{\mathbf{p}_{ 0}}(t)\) of the states of the parameter dependent network problem (5.133) but rather in the sensitivity of some performance figures of the system, like e.g., power consumption. These measures can usually be described by some observation function \(\boldsymbol{\varGamma }(\mathbf{x},\mathbf{p}) \in \mathbb{R}^{n_{o}}\) of the form
where the function \(\mathbf{g}: \mathbb{R}^{n} \times \mathbb{R} \times \mathbb{R}^{n_{p}} \rightarrow \mathbb{R}^{n_{o}}\) is such that the partial derivatives ∂ g ∕ ∂ x and ∂ g ∕ ∂ p exist and are bounded. Note that at the left-hand side of (5.141) x = x(. , p), which is a whole waveform in time.
The sensitivity of the observation function \(\boldsymbol{\varGamma }: \mathbb{R}^{n} \times \mathbb{R}^{n_{p}} \rightarrow \mathbb{R}^{n_{o}}\) around some nominal parameter set \(\mathbf{p}_{0} \in \mathbb{R}^{n_{p}}\), clearly is
For problems where the sensitivity of a few observables, i.e., where n o is small but the system depends on a large number n p of parameters, the adjoint method, introduced by Cao et al. in [74, 75] is an attractive approach. In the mentioned papers, the observation sensitivity problem is derived for implicit differential equations of the form
Here we derive the observation sensitivity problem for problem (5.133a) as we usually encounter in circuit simulation. The idea however, follows the idea presented by Cao et al. in the papers mentioned.
The observation function’s sensitivity is not calculated directly. Instead, an intermediate quantity \(\boldsymbol{\lambda }\), defined by a dynamical system, the adjoint model [82] of the parent problem, is calculated.
3.2.3 Adjoint System for Sensitivity Analysis
Instead of considering the definition (5.141) of the observation function \(\boldsymbol{\varGamma }\) directly, we define an augmented observation function
which arises from coupling the dynamics and the observation function \(\boldsymbol{\varGamma }\) by a Lagrangian multiplier \(\boldsymbol{\lambda }(t) \in \mathbb{R}^{n\times n_{o}}\) that we will define more precisely further on.
If \(\mathbf{x}(t,\mathbf{p})\) solves the network equations (5.133a) for p = p 0 it holds \(\boldsymbol{\varUpsilon }(\mathbf{x},\mathbf{p}_{0}) =\boldsymbol{\varGamma } (\mathbf{x},\mathbf{p}_{0})\) and also the sensitivities coincide:
Note, that where it is clear from the context we omit in the following the specifications of the evaluation points, e.g., (x, p 0).
By the definitions (5.141) and (5.144) of the observation function and the augmented observation function, respectively, we get
We have a closer look at the second integral and apply integration by parts:
Recombining this with the observation sensitivity (5.145) and expanding the total derivatives with respect to p we see
where C x , G x , C p , G p and S p are the quantities defined in Eq. (5.137) and
are the partial derivatives of the kernel of the observable and can thus be computed, if the solution trajectory x(t, p 0) is known.
In the present form (5.146) the calculation of the observation function’s sensitivity still demands to know the development of the state sensitivities \(\boldsymbol{\chi }_{\mathbf{p}_{ 0}}(t)\). As the above considerations are valid for any smooth \(\boldsymbol{\lambda }(t) \in \mathbb{R}^{n\times n_{o}}\) we may choose this parameter such that the state sensitivity disappears in the equation. We have already seen that the sensitivity \(\boldsymbol{\chi }_{\mathbf{p}_{ 0}}^{\text{DC}}\) of the circuit’s operating point \(\mathbf{x}_{\mathbf{p}_{0}}^{\text{DC}}\) can easily be calculated. Hence, choosing \(\boldsymbol{\lambda }\) such that
the calculation of the observable function’s sensitivity reduces to evaluating
Equation (5.147a) inherits the basic structure of the underlying network problem (5.133a). Therefore, this equation defining the Lagrangian \(\boldsymbol{\lambda }(t)\), is usually a DAE system. This linear system is called the adjoint system to the underlying network equation. For DAEs of index up to 1, the choice (5.147b) defines a consistent initial value [75]. For systems of index larger and equal to 2, the consistent initialisation is more difficult. As an initial value for \(\boldsymbol{\lambda }\) is specified for the end of the interval [t 0, t end] of interest, the adjoint equation (5.147a) is solved backwards in time.
Several kind of observation functions also need \(\dot{\mathbf{x}} = \frac{\mathrm{d}} {\mathrm{d}t}\mathbf{x}\) in addition to x. For instance when considering jitter one is interesting in the time difference between two subsequent times τ 1 and τ 2 when a specific unknown reaches or crosses a given value c (with equal signs of the time derivative). For the frequency of the jitter we have f = 1∕T = 1∕(τ 2 −τ 1). Let the specific unknown be \(\boldsymbol{x}_{i}(t,\boldsymbol{p})\). The time moment τ for which \(\boldsymbol{x}_{i}(\tau,\boldsymbol{p}) = c\) may be determined by inverse interpolation between two time points t 1 and t 2 and known values \(\boldsymbol{x}_{i}\) obtained by time integration such that \(\boldsymbol{x}_{i}(t_{1},\boldsymbol{p}) < c <\boldsymbol{ x}_{i}(t_{2},\boldsymbol{p})\). Of course τ depends on \(\boldsymbol{p}\), so more precisely we have \(\boldsymbol{x}_{i}(\tau (\boldsymbol{p}),\boldsymbol{p}) = c\). By differentiation we obtain: \(\mathrm{d}(\tau )/\mathrm{d}\boldsymbol{p} = -[\mathrm{d}(\boldsymbol{x}_{i})/\mathrm{d}t]^{-1}\mathrm{d}(\boldsymbol{x}_{i})/\mathrm{d}\boldsymbol{p}\).
Hence we are also interested in a more general case than (5.141)
By a similar analysis as presented in [96] for (5.145)–(5.146) we derive (\(\hat{\dot{\mathbf{x}}} = \partial \dot{\mathbf{x}}/\partial \mathbf{p}\))
which holds for any \(\zeta (t) \in \mathbb{R}^{n\times n_{o}}\). If ζ is chosen such that
a significant reduction occurs in (5.150) and \(\hat{\boldsymbol{x}}(t)\) is not explicitly needed. This generalizes the result in [96] (see also [64]). Note that \(\boldsymbol{\chi }_{\mathbf{p}_{ 0}}(0) =\hat{ \mathbf{x}}(0,\mathbf{p}_{0}) =\hat{ \mathbf{x}}_{\mathrm{DC}}(\mathbf{p}_{0})\), which is the sensitivity of the DC-solution, which one needs to determine explicitly. Some efficiency is gained by calculating \(\zeta ^{T}(0)\mathbf{C}_{x}(0)\hat{\mathbf{x}}_{\mathrm{DC}} = [\mathbf{C}_{x}^{T}(0)\zeta (0)]^{T}\hat{\mathbf{x}}_{\mathrm{DC}}\) (when n p ≫ 1). Note however that (5.152) can be satisfied only when the right-hand side is in the range of C x T. Because in (5.151)–(5.152) the right-hand sides are evaluated at x(t, p), in general, the solution ζ will depend on p, even in the case of constant matrices C x and G x . This is in contrast to [64].
Summing up, the backward adjoint method for computing the sensitivity of the observable \(\boldsymbol{\varGamma }\) with respect to parameter variations around a nominal parameter setting p 0 is carried out by the following steps
-
1.
Solve the network DAE (5.133a) for x = x(t, p 0), on the interval [t 0, t end];
-
2.
Solve the backward adjoint problem (5.147a), subject to the initial condition (5.147b) for \(\boldsymbol{\lambda }\) on the interval [t end, t 0], i.e., backward in time;
-
3.
Compute the observable sensitivity \(d\boldsymbol{\varGamma }\,/\,d\mathbf{p}\) using the expression (5.148).
Carrying out the backward adjoint method, one has to consider several aspects we do not address here. Amongst these are the evaluations of the partial derivatives like C x along the solution trajectory. On the one hand, these derivatives are usually not available as a closed function but are approximated by finite differences. On the other hand, the evaluation points, i.e., points on the trajectory x(t, p 0) are also available as approximations only. Furthermore, the integral in the formula (5.148) has to be approximated by a numerical quadrature. The nodes needed in the according scheme may not be met exactly during transient simulation and/or during the backward integration of the adjoint problem. For further reading on these problems we refer to [95, 96].
However, leaving all these aspects aside, one has to integrate two dynamical systems numerically. First the (nonlinear) forward problem (5.133a) for the states and then the linear backward problem (5.147a). The contribution of the COMSON project for transient sensitivity analysis was to add model order reduction (MOR) to the process. More precisely, the idea elaborated during the project was to solve an order reduced variant of the backward problem where the data needed to apply the reduction is calculated from the forward solving phase. In the next section we will describe the very basic idea of MOR and give a brief introduction to the specific technique that was used in this project.
3.3 Model Order Reduction (with POD)
Solving a dynamical system with any numerical scheme implies to set up and solve a series of linear equations. In circuit simulation typically the dimension of these systems are in a range of 105–109. Both the evaluation of the system matrices and right-hand sides, e.g., M l and rhs l in (5.139)–(5.140), as well as solving the system, i.e., decomposing the system matrices, is computationally costly.
However, in circuit design often the main interest is the analysis of how a circuit block processes an input signal, e.g., if some input signal is amplified or damped by the circuit. That means, one may not be interested in all n internal state variables but only in a limited selection. This concern is described by an input-output variant of the network model. For a linear network problem (5.133b), omitting the parameters for ease of notation, e.g., the corresponding input-output system reads
where \(\mathbf{u}(t) \in \mathbb{R}^{m}\) and \(\mathbf{y}(t) \in \mathbb{R}^{q}\) are the input and the output of the system, injected to and extracted from the system by the matrices \(\mathbf{B} \in \mathbb{R}^{n\times m}\) and \(\mathbf{L} \in \mathbb{R}^{q\times n}\).
As in an input-output setting, the states x represent an auxiliary variable only. The idea of MOR is to replace the high-dimensional dynamical system (5.153) by
where \(\mathbf{z}(t) \in \mathbb{R}^{r}\) and the system matrices \(\hat{\mathbf{C}},\hat{\mathbf{G}} \in \mathbb{R}^{r\times r}\), \(\hat{\mathbf{B}} \in \mathbb{R}^{r\times m}\) and \(\hat{\mathbf{L}} \in \mathbb{R}^{q\times r}\) are chosen such that r ≪ n and \(\tilde{\mathbf{y}}(t) \approx \mathbf{y}(t)\).
There are various methods to construct the reduced variant (5.154) from the full problem (5.153). We refer to Chapter 4 for an overview, as well as to [63, 67, 69, 70, 103, 108–110, 121] for further studies.
A large class of MOR methods are based on projection. These methods determine a subspace of dimension r, spanned by a basis of vectors \(\mathbf{v}_{i} \in \mathbb{R}^{n}\) \((i = 1,\mathop{\ldots },r)\). The original state vector x(t) is approximated by an element of this subspace that can be written in the form Vz(t), where \(\mathbf{V} = \left (\mathbf{v}_{1},\mathop{\ldots },\mathbf{v}_{r}\right ) \in \mathbb{R}^{n\times r}\). Hence, one replaces x(t) by Vz(t) in (5.153) and projects the equation onto the space subspaces spanned by the columns of V by a Galerkin approach. In this way, a dynamical system (5.154) emerges where the system matrices are given by
3.3.1 Proper Orthogonal Decomposition
While other MOR methods start operating from the matrices C, G, B and L, the method of Proper Orthogonal Decomposition (POD) constructs the matrix V, whose columns span the reduced space the system (5.153) is projected on, from the space that is spanned by the trajectory x(t), i.e., the solution of the dynamical system. The method applies to nonlinear systems as well.
Recall, that our aim is to construct a reduced model for the backward adjoint problem (5.147). As this is a linear system from which we know the system matrices only after a solution of the underlying forward network problem (5.133a), POD seems to be the best choice for this task.
The mission POD fulfills is to find a subspace approximating a given set of data in an optimal least-squares sense. The basis of this approach is known also as Principal Component Analysis and Karhunen-Loève theorem from picture and data analysis.
The mathematical formulation of POD [103, 107, 121] is as follows: Given a set of K datapoints \(\mathbf{X}:= \left \{\mathbf{x}_{1},\mathop{\ldots },\mathbf{x}_{K}\right \}\), a subspace \(S \subset \mathbb{R}^{n}\) is searched for that minimizes
where \(\varrho: \mathbb{R}^{n} \rightarrow S\) is the orthogonal projection onto S, which has \(\{\boldsymbol{\varphi }_{1},\mathop{\ldots },\boldsymbol{\varphi }_{r}\}\) as an orthonormal basis of S.
This problem is solved, applying the Singular Value Decomposition (SVD) to the matrix \(\mathbf{X}:= \left (\mathbf{x}_{1},\mathop{\ldots },\mathbf{x}_{K}\right ) \in \mathbb{R}^{n\times K}\), which is called snapshot matrix, as its columns are (approximations to) the solution of the dynamical system (5.153) at timepoints \(t_{1},\mathop{\ldots },t_{K} \in [t_{0},t_{\text{end}}]\). The SVD applied to the matrix X, provides three matrices:
such that
where the columns of \(\boldsymbol{\varPhi }\) and \(\boldsymbol{\varPsi }\) are left and right eigenvectors, respectively, and \(\sigma _{1},\mathop{\ldots },\sigma _{\nu }\) are the singular values of X.
Then, for any r ≤ ν, taking \(\boldsymbol{\varphi }_{1},\mathop{\ldots },\boldsymbol{\varphi }_{r}\) as the first r columns of the matrix \(\boldsymbol{\varPhi }\) is optimal in the sense that it minimizes the projection mismatch (5.156).
Both cases, n ≥ K and n ≤ K, are allowed; in practice one often has n ≫ K.
Finally, the MOR projection matrix V in (5.155) is chosen made up of these basis vectors:
To understand why the first r columns of \(\boldsymbol{\varPhi }\) solve the minimization problem (5.156) one can recall that for \(i = 1,\mathop{\ldots },n\) the ith column \(\boldsymbol{\varphi }_{i}\) of \(\boldsymbol{\varPhi }\) is actually an eigenvector of the correlation (or covariance) matrix of the snapshots with σ i 2 as eigenvalue:
Intuitively the correlation matrix XX T detects the principal directions in the data cloud that is made up of the snapshots \(\mathbf{x}_{1},\mathop{\ldots },\mathbf{x}_{K}\). The eigenvectors and eigenvalues can be thought of as directions and radii of axes of an ellipsoid that incloses the cloud of data. Then, the smaller the radii of one axis is, the less information is lost if that direction is neglected.
We abandon to explain the derivation of POD in detail here as in literature e.g., [63, 103, 121] this is well explained. For details on the accuracy of MOR with POD we refer to papers by Petzold et al. [94, 107].
3.4 The BRAM Algorithm
In [96] it was observed that a forward analysis in time of (5.133a) automatically provides provides snapshots x(t i , p) at time points t i . This can lead to a reduced system of equations for \(\zeta (t) = \mathbf{V}\tilde{\zeta }\) in (5.151)–(5.152)
Then the overall algorithm is described in Algorithm 5.1, without the lines 5–7.
Algorithm 5.1 BRAM: Backward Reduced Adjoint Method
Here it is assumed that the matrices are saved after the forward simulation. It is also assumed that for the adjoint system the same step sizes are used as in the forward run. If not, additional interpolation has to be taken into account to determine the reduced matrices at intermediate solutions and also effort has to be spent in LU-decomposition.
Apart from this discussion, the question is why this should work in general (apart from special cases in [96]). The solution \(\mathbf{x} \approx \mathbf{V}\tilde{\mathbf{x}}\) depends on the right-hand side s of (5.133a). Clearly V T s should contain the dominant behaviour of s. If \(\mathbf{V}^{T}[ \frac{d} {\mathit{dt}}(\frac{\partial \mathbf{F}} {\partial \dot{\mathbf{x}}} )^{T} -\Big (\frac{\partial \mathbf{F}} {\partial \mathbf{x}} \Big)^{T}]\) behaves similarly when compared to the right-hand side of (5.151) we may expect a similar good approximation for the solution \(\zeta \approx \mathbf{V}\tilde{\zeta }\). Because the right-hand side of (5.158) does not depend on ζ this can be checked in advance, before solving (5.158). In the case of power loss through a resistor we have \(\Big(\frac{\partial \mathbf{F}} {\partial \mathbf{x}} \Big)^{T} = (\mathbf{A}\mathbf{x})^{T}\) (for some matrix A) and we have to check if \((\mathbf{A}\mathbf{x})^{T} \approx \mathbf{V}^{T}\tilde{\mathbf{x}}^{T}\mathbf{V}^{T}\mathbf{A}^{T}\).
Another point of attention is that the projection matrix V found implies that we more or less are looking to the sensitivity of the solution \(\tilde{\mathbf{x}}\) of
rather than for the solution \(\boldsymbol{x}\) of (5.133a). By this it is clear that V depends on p and thus
The question is: can we ignore the first term at the right-hand side of (5.161). Here the last term represents the change inside the space defined by the span of the columns of V. The first term represents the effect by the change of this space itself. One may expect that this term is smaller than the last term (‘the first term will in general require more energy’), especially when the reduction is more or less determined by topology. In several tests we made, this first term indeed was much smaller than the other term.
Note that we not intend to solve (5.160) by using a fixed projection matrix V, valid for p = p 0, for several different values of p. The danger of obtaining improper results when doing this was pointed out by [83]. Contrarily, we always apply an up-to-date matrix V(p). However, this example shows that \(\frac{\partial \mathbf{V}} {\partial \mathbf{p}}\) is not always negligible.
One can collect \(\tilde{\mathbf{V}} = [\mathbf{V}(\mathbf{p}_{1}),\ldots,\mathbf{V}(\mathbf{p}_{k})]\) and apply an additional SVD to \(\tilde{\mathbf{V}}\). This procedure provides a larger, uniform, projection matrix V.
In [95] the parameter dependency of the singular values for POD was analysed for a battery charger, for a ring oscillator, and for a car transceiver example. Also the nr of dominant singular values as function of p was studied. Finally the angle between the subspaces for different p was studied. Note that one can use a matlab function for this based on the algorithm by Knyazev-Argentati [98].
Singular values of POD after 3,500 snapshots for a Li-ion charger for different values of the area of a capacitor
Principle vector rotation as a function of the capacitor area for the problem in Fig. 5.35
Finally, in [95] a modification was introduced in Algorithm 5.1 by introducing the lines 5–7. Note that the additional step 6 is cheap. We obtain the solution of the POD-reduced system. In [94, 103, 107, 121] error estimates are determined for the approximation error of the POD approximation. Actually, in step 8, BRAM II determines the sensitivity of the POD solution. In Fig. 5.35 [95] the singular values of POD after 3,500 snapshots within a simulation from t 0 = 0 ms and t end = 200 ms for a Li-ion charger for different values of the area of a capacitor. The parameter p took values p = 30, 32, 34, 36, 38, 40. Clearly the first 100 singular values are enough for a good reconstruction, which as a by-product als shows a high potential for the application of the BRAM methods as the dimension of the problem can be reduced by roughly a factor 35. In Fig. 5.36 [95] the angle in the rotation of the principle vector is studied, the nominal being for p = 30. The apparent jump to 90∘ rotation near the cut off point is due to matrix diagonal zero padding introduced in the general case for principle vector analysis. These large 90∘ rotations are not due to principle vectors influenced by parameter changes and should not be taken into account.
3.5 Sensitivity by Uncertainty Quantification
A modern approach to Uncertainty Quantification is to expand a solution x(t, p) in a series of orthogonal polynomials in which the \(\boldsymbol{p}\) is argument of the (multidimensional) polynomials and the t appears in the coefficients. If the p are subject to variations such a representation is called a generalized Polynomial Chaos (gPC) expansion. Having established the expansion, this provides facilities similar like a response surface model: fast and accurate statistics and sensitivity.
In this section we shortly summarize some basic items. We also point out how a strategy for parameterized Model Order Reduction (pMOR) fits here. This strategy contains a generalization of one of the pMOR algorithms described in Sect. 5.1 of this Chapter.
We will denote parameters by p = (p 1, …, p q )T and assume a probability space given \((\varOmega,\mathcal{A},\mathcal{P})\) with \(\mathcal{P}:\, \mathcal{A}\,\rightarrow \, \mathbb{R}\) (measure; in our case the range will be [0, 1]) and \(\mathbf{p}:\varOmega \;\rightarrow \; Q \subseteq \mathbb{R}^{q}\), \(\omega \mapsto \mathbf{p}(\omega )\). Here we will assume that the p i are independent random variables, with factorizable joint probability density ρ(p).
For a function \(f: Q\; \rightarrow \; \mathbb{R}\), the mean or expected value is defined by
A bilinear form < f, g > is defined by
The last form is convenient when products of more functions are involved. Similar definitions hold for vector- or matrix-valued functions \(\mathbf{f}: Q\; \rightarrow \; \mathbb{R}^{m\times n}\).
We assume a complete orthonormal basis of polynomials \((\phi _{i})_{i\in \mathbb{N}}\), \(\phi _{i}: \mathbb{R}^{q}\; \rightarrow \; \mathbb{R}\), given with < ϕ i , ϕ j > = δ ij (i, j, ≥ 0). When q = 1, ϕ i has degree i. To treat a uniform distribution (i.e., for studying effects caused by robust variations) one can use Legendre polynomials; for a Gaussian distribution one can use Hermite polynomials [100, 123, 124]. Some one-dimensional polynomials are mentioned in Table 5.3. A polynomial ϕ i on \(\mathbb{R}^{q}\) can be defined from one-dimensional polynomials: \(\phi _{\mathbf{i}}(\mathbf{p}) =\prod _{ d=1}^{q}\phi _{i_{d}}(p_{d})\). Actually i orders a vector i = (i 1, …, i q )T; however we will simply write ϕ i , rather then ϕ i . An example is given in (5.164), using Legendre polynomials. Note that, due to normalization, \(L_{0}(p) = 1/\sqrt{2}\), \(L_{1}(p) = \sqrt{3/2}\,p\), \(L_{2}(p) = \frac{1} {2}\sqrt{\frac{5} {3}}\,(3p^{2} - 1)\) – see also [87]. In [88] one finds algorithms how to efficiently generate orthogonal polynomials from a given weight function.
We will denote a dynamical system by
Here F may contain differential operators. The solution \(\mathbf{x} \in \mathbb{R}^{n}\) depends on t and on p. In addition initial and boundary values are assumed. In general these may depend on p as well.
A solution x(t, p) = (x 1(t, p), …, x n (t, p))T of the dynamical system becomes a random process. We assume that second moments < x j 2(t, p) > are finite, for all t ∈ [t 0, t 1] and j = 1, …, n. We express x(t, p) in a Polynomial Chaos expansion
where the coefficient functions v i (t) are defined by
Continuity/smoothness follow from the solution x(t, p) and similarly the construction of expected values and variances.
A finite approximation x m(t, p) to x(t, p) is defined by
For long time range integration m may have to be chosen larger than for short time ranges. Further below we will describe how the coefficient functions v i (t) can be efficiently approximated.
For functions x(t, p) that depend smoothly on p convergence rates for | | x(t, . ) −x m(t, . ) | | , in the norm associated with (5.163), are known. For instance, for one-dimensional functions x(p) that depend on a scalar parameter p such that x (1), …, x (k) are continuous (i.e., derivatives w.r.t. p), one has
Here the L ρ 2-norms include the weighting/density function ρ(. ). Note that the upperbound in (5.170) actually involves a Sobolev-norm. In [72] one also finds upperbounds using seminorms (that involve less derivatives).
For more general distributions ρ(. ) convergence may not be true. For instance, polynomials in a lognormal variable are not dense in L ρ 2. For convergence one needs to require that the probability measure is uniquely determined by its moments [81]. One at least needs that the expected value of each polynomial has to exist. This has a practical impact. The imperfections in a manufacturing process cause some variability in the components of an electronic circuit. To address the variability, corresponding parameters or functions are replaced by random variables or random fields for uncertainty quantification. However, the statistics of the parameters often do not obey traditional probability distributions like Gaussian, uniform, beta or others. In such a case one may have to construct probability distributions or probability density functions, respectively, which approximate the true statistics at a sufficient accuracy. Thereby, one has to match corresponding data obtained from measurements and observations of electronic devices. The resulting probability distribution functions should be continuous and all moments of the random variables should be finite such that a broad class of methods like, e.g., Polynomial Chaos, is applicable.
The integrals (5.167) can be computed by (quasi) Monte Carlo, or by multi-dimensional quadrature. We assume quadrature grid points \(\mathbf{p}^{1},\,\mathbf{p}^{2},\ldots,\mathbf{p}^{K}\) and quadrature weights w k , 1 ≤ k ≤ K, such that
We solve (5.165) for x(t, p k), k = 1, …, K (K deterministic simulations). Here any suitable numerical solver for (5.165) can be used. In fact (5.171) is a (discrete) inner-product with weighting function \(w_{K}(\mathbf{p}) =\sum _{ k=1}^{K}w_{k}\,\delta (\mathbf{p} -\mathbf{p}^{k})\). This approach is called Stochastic Collocation [100, 123, 124]. Afterwards we determine
Here the Polynomial Chaos expansion is just a post-processing step.
Only for low dimensions q, tensor-product grids of Gaussian quadrature are used. Gaussian quadrature points are optimal for accuracy. In higher-dimensional cases (q > 1) one prefers sparse grids [123, 124], like the Smolyak algorithm. Sparse grids may have options for refinement. Note that Gaussian points do not offer this refinement. Stroud-3 and Stroud-5 formulas [116] have become popular [122].
An alternative approach to Stochastic Collocation is provided by Stochastic Galerkin. After, inserting an expansion of the solution, in polynomials in p, into the equations one orthogonally projects the residue of the equations to the subspace spanned by these polynomials. By this, one gets one big system of differential equations in which the v i are the unknowns [100, 123, 124]. In practice, Stochastic Collocation is much more easily combined with dedicated software for the simulation problem at hand than is the case with Stochastic Galerkin. Theoretically the last approach is more accurate. However, statistics obtained with Stochastic Collocation is very satisfactory.
We note that the expansion x(t, p), see (5.166), gives full detailed information when varying p. From this the actual (and probably biased) range of solutions can be determined. These can be different from envelope approximations based on mean and variances.
Because of the orthogonality, the mean of x(t, p) and of x m(t, p) are equal and are given by
Using (5.172), we get an approximative value. The integrals in (5.173) involve all p k together. One may want to consider effects of p i and p j separately. This restricts the parameter space \(\mathbb{R}^{q}\) to a one-dimensional subset with individual distribution densities ρ i (p) and ρ j (p).
A covariance function of x(t, p) can also be easily expressed
This outcome clearly depends on m. A (scalar) variance is given by
where V 0 T(t) = (0 T, v 1 T(t), …, v m T(t))T. Note that this equals
Having a gPC expansion the sensitivity (matrix) w.r.t. p is easily obtained
One may restrict this to S p (t, μ p ), where μ p = E[p] and \(\frac{\partial \mathbf{x}(t,\mathbf{p})} {\partial \mathbf{p}}\) is the solution of the system that is differentiated w.r.t. p at p = μ p . For a scalar quantity x one can order according to a ‘stochastic influence’ based on
Here \(\sigma _{p_{i}}^{2} =\mathrm{ Var}[p_{i}]\). The sensitivity matrix also is subject to stochastic variations. With a gPC expansion one can determine a mean global sensitivity matrix by
Note that the integrals at the right-hand side can be determined in advance and stored in tables.
In [85] (see also [84]) a parameterized system in the frequency domain
is considered. Here s is the (angular) frequency. For this system a parameterized MOR approach is proposed, which exploits an expansion of C(p) and G(p)
In [71] the parameter variation in C and G did come from parameterized layout extraction of RC circuits.
In Algorithm 5.2 it is assumed that a set \(\mathbf{p}^{1},\mathbf{p}^{2},\ldots,\mathbf{p}^{K}\) is given in advance, together with frequencies s 1, s 2, …, s K . Let Ψ k = (s k , p k). Furthermore, let A = s C(p) +G(p) and AX = B, and, similarly, A k = A(Ψ k) = s k C(p k) +G(p k) and A k X k = B.
A projection matrix V (with orthonormal columns v i ) is determined such that \(\mathbf{X}(s,\mathbf{p}) \approx \bar{\mathbf{X}}(s,\mathbf{p}) \equiv \mathbf{V}\hat{\mathbf{X}}(s,\mathbf{p}) \equiv \sum _{i=1}^{K'}\alpha _{i}(s,\mathbf{p})\mathbf{v}_{i}\). Algorithm 5.2 applies a strategy of which a key step is found in [85]. The extension of V is similar to the recycling of Krylov subspaces [102] and used in MOR by [84]. The refinement introduced in [85] is in the selection from the remaining set (steps 5–6). Note that the residues deal with B and with x and not with the effect in y. Hence, one may consider a two-sided projection here. The method of [85] was used in [71] (using expansions of the matrices in moments of p; note that used expressions from layout extraction were linear in p).
Algorithm 5.2 pMOR Strategy in Uncertainty Quantification
This procedure assumes that the evaluation of a matrix A k (and subsequent matrix vector multiplications) is much cheaper than determining a solution X(Ψ k ). Note also that after extending the basis V in the next step the norms of the residues should reduce. This allows for some further efficiency in the algorithm [85]. Finally, we remark that the X k are zero order (block) moments at Ψ k. After determining the LU-decomposition of A k one easily includes higher moments as well when extending the basis.
A main conclusion of this section is that for the Stochastic Collocation the expansions (5.182)–(5.184) are not explicitly needed by the algorithm. This facilitates dealing with parameters that come from geometry, like scaling [111–115]. The evaluation can completely be done within the CAD environment of the simulation tool – in which case the expressions remain hidden.
The selection of the next parameter introduces a notion of “dominancy” from an algorithmic point of view: this parameter most significantly needs extension of the Krylov subspace. To invest for this parameter will automatically reduce work for other parameters (several may even drop out of the list because of small residues).
If first order sensitivity matrices are available, like in C(p) = C 0(p 0) +C ′(p 0)p and in G(p) = G 0(p 0) +G ′(p 0)p one can apply a Generalized Singular Value Decomposition [89] to both pairs (C 0 T(p 0), [C ′]T(p 0)) and (G 0 T(p 0), [G ′]T(p 0)). In [101] this was applied in MOR for linear coupled systems. The low-rank approximations for C ′(p 0) and G ′(p 0) (obtained by a Generalized SVD [89]) give way to increase the basis for the columns of B of the source function. Note that by this one automatically will need MOR methods that can deal with many terminals [68, 97, 120].
In Algorithm 5.2 and in [85] the subspace generated by the basis V is slightly increasing with each new p k . A different approach is to apply normal MOR for each p k , giving bases V k , and next determine V by an SVD or rank-revealing QR-factorization of \([\mathbf{V}_{k},\ldots,\mathbf{V}_{K}]\). In [66] this approach is used to obtain a Piecewise \(\mathcal{H}_{2}\)-Optimal Interpolation pMOR Algorithm.
To efficiently apply parameterized MOR in Uncertainty Quantification is described in [104, 119]. In [105, 106] sensitivity analysis of the variance did provide ways to identify dominant parameters that contribute most to the variance of a quantity of interest. This approach is different from the low-rank approximations (using the Generalized SVD), mentioned above.
4 MOR for Singularly Perturbed Systems
For large systems of ordinary differential equations (ODEs), efficient MOR methods already exist in the linear case, see [125].Footnote 4 We want to generalize according techniques to the case of differential-algebraic equations (DAEs). On the one hand, a high-index DAE problem can be converted into a lower-index system by analytic differentiations, see [127]. A transformation to index zero yields an equivalent system of ODEs. On the other hand, a regularization is directly feasible in case of semi-explicit systems of DAEs. Thereby, we obtain a singularly perturbed problem of ODEs with an artificial parameter. Thus according MOR techniques can be applied to the ODE system. An MOR approach for DAEs is achieved by considering the limit to zero of the artificial parameter.
We consider a simplified, semi-explicit DAE system to illustrate some concepts only
with differential and perturbation index 1 or 2. For the construction of numerical methods to solve initial value problems of (5.185), a direct as well as an indirect approach can be used. The direct approach applies an ɛ-embedding of the DAEs (5.185), i.e., the system changes into
with a real parameter ɛ ≠ 0. Techniques for ODEs can be employed for the singularly perturbed system (5.186). The limit ɛ → 0 yields an approach for solving the DAEs (5.185). The applicability and quality of the resulting method still has to be investigated.
Alternatively, the indirect approach is based on the state space form of the DAEs (5.185) with differential and perturbation index 1 or 2, for nonlinear cases see [139], i.e.,
with z(t) = Φ(y(t)). To evaluate the function Φ, the nonlinear system
is solved for given value y(t). Consequently, the system (5.187) represents ODEs for the differential variables y and ODE methods can be applied. In each evaluation of the right-hand side in (5.187), a nonlinear system (5.188) has to be solved. More details on techniques based on the ɛ-embedding and the state space form can be found in [132].
Although some MOR methods for DAEs already exist, several techniques are restricted to ODEs or exhibit better properties in the ODE case in comparison to the DAE case. The direct or the indirect approach enables the usage of MOR schemes for ODEs (5.186) or (5.187), where an approximation with respect to the original DAEs (5.185) follows. The aim is to obtain suggestions for MOR schemes via these strategies, where the quality of the resulting approximations still has to be analyzed in each method.
In this section, we focus on the direct approach for semi-explicit system of DAEs, i.e., the ɛ-embedding (5.186) is considered. MOR methods are applied to the singularly perturbed system (5.186). Two scenarios exist to achieve an approximation of the behavior of the original DAEs (5.185) by MOR. Firstly, an MOR scheme can be applied to the system (5.186) using a constant ɛ ≠ 0, which is chosen sufficiently small (on a case by case basis) such that a good approximation is obtained. Secondly, a parametric or parameterized Model Order Reduction (pMOR) method yields a reduced description of the system of ODEs, where the parameter ɛ still represents an independent variable. Hence the limit ɛ → 0 causes an approach for an approximation of the original DAEs.
We investigate the two approaches with respect to MOR methods based on an approximation of the transfer function, which describes the input-output behavior of the system in frequency domain.
4.1 Model Order Reduction and ɛ-Embedding
We restrict ourselves to semi-explicit DAE systems of the type (5.189)–(5.190) and introduce w(t) as an output instead of y(t) with exact the same condition. According to (5.185), after linearizing, we can write the system as
The solution x and the matrix C exhibit the partitioning:
w(t) is the output of the system. The order of the system is n = k + l, where k and l are the dimensions of the differential part and the algebraic part (constraints), respectively, defined in the semi-explicit system (5.185). \(\mathbf{B} \in \mathbb{R}^{n\times m}\); \(\mathbf{L} \in \mathbb{R}^{p\times n}\). After taking the Laplace transform, the corresponding p × m matrix-valued rational transfer function is
provided that \(\det (\mathbf{G} + s\mathbf{C})\neq 0\) and x(0) = 0 and u(0) = 0. Following the direct approach [135], the ɛ-embedding changes the system (5.189)–(5.190) into:
where
with the same inner state and input/output as before. For ɛ ≠ 0, the matrix C(ɛ) is regular in (5.191) and the transfer function reads:
provided that det(G + s C(ɛ)) ≠ 0. For convenience, we introduce the notation
It holds M(s, 0) = s C with C from (5.189).
Concerning the relation between the original system (5.189)–(5.190) and the regularized system (5.191) with respect to the transfer function, we achieve the following statement. Without loss of generality, the induced matrix norm of the Euclidean vector norm is applied.
Lemma 5.1
Let \(\mathbf{A},\ \tilde{\mathbf{A}} \in \mathbb{R}^{n\times n}\) , det ( A ) ≠ 0 and \(\|\mathbf{A} -\tilde{\mathbf{A}}\|_{2} =\|\varDelta \mathbf{A}\|_{2}\) where Δ A is small enough. Then it holds:
Proof
It holds
Suppose \(\mathbf{y}:= \mathbf{A}^{-1}\mathbf{x},\ \tilde{\mathbf{y}}:=\tilde{ \mathbf{A}}^{-1}\mathbf{x}\), then the sensitivity analysis of linear systems yields
where the quantity
is the relative condition number. So by substituting the value of κ(A) we have:
then
□
We conclude from Lemma 5.1 that
for example.
Theorem 5.1
For fixed \(s \in \mathbb{C}\) with \(\det (\mathbf{G} + \mathbf{M}(s,0))\neq 0\) and \(\varepsilon \in \mathbb{R}\) satisfying
for some c ∈ (0,1), the transfer functions H (s) and H ɛ (s) of the systems (5.189)–(5.190) and (5.191) exist and it holds
with
Proof
Let A = G +M(s, 0) and \(\tilde{\mathbf{A}} = \mathbf{G} + \mathbf{M}(s,\varepsilon )\). The condition (5.192) guarantees that the matrices \(\tilde{\mathbf{A}}\) are regular. The definition of the transfer functions implies:
We obtain:
Applying the Lemma 5.1, the term at the right-hand side of the expression above becomes:
Thus the proof is completed. □
It is clear that for inequality (5.192) we have:
We conclude from Theorem 5.1 that
for each \(s \in \mathbb{C}\) with G + s C regular. The relation (5.192) gives feasible domains of ɛ
We also obtain the uniform convergence
in a compact domain \(S \subset \mathbb{C}\) and ɛ ≤ δ with:
with \(\tilde{S}:=\{ z \in S: \left \vert z\right \vert \geq 1\}\). Furthermore, Theorem 5.1 implies the property
for fixed ɛ assuming \(\det \mathbf{G}\neq 0\). However, we are not interested in the limit case of small variables s.
For reducing the DAE system (5.189)–(5.190), we have two ways to handle the artificial parameter ɛ, which results in two different scenarios. In the first scenario, we fix a small value of the parameter ɛ. Thus we use one of the standard techniques for the reduction of the corresponding ODE system. Finally, we achieve a reduced ODE (with small ɛ inside). The ODE system with small ɛ represents a regularized DAE. Any reduction scheme for ODEs is feasible. Recent research shows that the Poor Man’s TBR (PMTBR), see [138], can be applied efficiently to the ODE case. Figure 5.37 indicates the steps for the first scenario.
The approach of the ɛ-embedding for MOR in the first scenario
In the second scenario, the parameter ɛ is considered as an independent variable (value not predetermined). We can use the parametric MOR for reducing the corresponding ODE system. The applied parametric MOR is based on [128, 129] in this case. The limit ɛ → 0 yields the results in an approximation of original DAEs (5.189)–(5.190). The existence of the approximation in this limit still has to be analyzed. Figure 5.38 illustrates the strategy for the second scenario.
The approach of the ɛ-embedding for MOR in the second scenario
Theorem 5.1 provides the theoretical background for the both scenarios. We apply an MOR scheme based on an approximation of the transfer function to the system of ODEs (5.191). Let \(\tilde{\mathbf{H}}_{\varepsilon }(s)\) be a corresponding approximation of H ɛ (s).
It follows
for each \(s \in \mathbb{C}\) with \(\det (\mathbf{G} + s\mathbf{C})\neq 0\). Due to Theorem 5.1, the first term becomes small for sufficiently small parameter ɛ. However, ɛ should not be chosen smaller than the machine precision on a computer. The second term depends on the applicability of an efficient MOR method to the ODEs (5.191). Thus \(\tilde{\mathbf{H}}_{\varepsilon }(s)\) can be seen as an approximation of the transfer function H(s) belonging to the system of DAEs (5.189)–(5.190).
4.2 Test Example and Numerical Results
One cell of the RLC transmission line
We consider a substitute model of a transmission line (TL), see [130], which consists of N cells. Each cell includes a capacitor, an inductor and two resistors, see Fig. 5.39. This TL model represents a scalable benchmark problem (both in differential part and algebraic part but not separately), because we can select the number N of cells. The used physical parameters are
We apply modified nodal analysis, see [131], to the RLC circuit and then the state variables \(\mathbf{x} \in \mathbb{R}^{3N+3}\) consist of the voltages at the nodes, the currents traversing the inductances \(L\) and the currents at the boundaries of the circuit:
So far we have 3N + 3 unknowns and only 3N + 1 equations. Thus two boundary conditions are necessary. Equations for the main nodes and the intermediate nodes in each cell are
where the variable h > 0 represents a discretization step size in space. We apply the boundary conditions
with L 1 > 0 and an independent current source u. Now a direct approach (ɛ-embedding) is used. For the first simulation the variable ɛ is fixed to 10−14 and 10−7, respectively, and the PMTBR method [138] is used as a reduction scheme for the ODE system. For all runs we selected the number of cells to N = 300, which results in the order n = 903 of the original system of DAEs (5.189)–(5.190). Figure 5.40 shows the transfer function both for the DAE and the ODE (including ɛ) and the reduced ODE with fixed ɛ for frequencies s = i ω with \(\omega \in \mathbb{R}\). The number in parentheses shows the order of the systems.
Original transfer function for DAE and ODE and reduced transfer function of PMTBR in case of three different parameters ɛ. The frequency ω ranges from 10−8 to 108
Absolute error plot for the transfer function in the ɛ-embedding, reduction carried out by parametric MOR with PIMTAB, ɛ = 0, 10−10, 10−7
Finally the second scenario with parametric MOR is studied. We apply the PIMTAB parametric MOR following [133, 134]. The limit ɛ → 0 gives the result for the reduced DAE.The error plot for the parametric reduction scheme is shown in Fig. 5.41. The error plot shows an overall nice match for the case of ɛ = 0, 10−10 and as the value for the parameter ɛ increases, the accuracy of the method and of the reduction algorithm decreases. It is also important to mention that the order of the reduced system in the second scenario is nearly half of the one in the first scenario.
Table 5.4 shows which value for the parameter ɛ is acceptable for the both scenarios.
4.3 Conclusions
In this section we applied the ɛ-embedding to approximate a linear system of DAEs by a system of ODEs. We did consider the transfer function in the frequency domain as a function of ɛ and proved uniform convergence for frequencies s in a compact region S where the matrix G + s C is regular (and thus its inverse uniformly bounded). This motivated the usage of MOR methods for ODEs. Most of the reduction schemes are designed and adopted for linear ODEs. Well-known methods are PMTBR (Poor Man’s Truncated Balanced Realization [138]) and the spectral zeros preservation MOR of Antoulas [126].
In the first scenario we applied a fixed ɛ and studied for a transmission line model the behavior of the transfer functions of the DAE, of the ODE and of the reduced model obtained with PMTBR for ɛ = 10−14, 10−10, 10−7. Already for the last value the transfer functions between DAE and ODE differ significantly. If we choose bigger values for ɛ, the system is more friendly but the error is larger and the solution will be changed. On the other hand the transfer function obtained by PMTBR is able to approximate quite well the transfer function of the ODE.
In the second approach we applied the parametric MOR technique PIMTAB [133, 134] to the parameterized ODE. Here we do not need to predefine the value of the ɛ. We obtain a parameterized MOR that gives a reduced model for ɛ = 0 for which the transfer function approximates well the one for the DAE [135, 137].
Notes
- 1.
- 2.
- 3.
- 4.
References
References for Section 5.1
Achar, R., Nakhla, M.S.: Simulation of high-speed interconnects. Proc. IEEE 89(5), 693–728 (2001)
Antoulas, A.C.: Approximation of Large-Scale Dynamical Systems. SIAM, Philadelphia (2005)
Benner, P., Mehrmann, V., Sorensen, D.C. (eds.): Dimension Reduction of Large-Scale Systems. Lecture Notes in Computational Science and Engineering, vol. 45. Springer, Berlin/Heidelberg (2005)
Bi, Y.: Effects of paramater variations on integrated circuits. MSc.-Thesis, Delft University of Technology/Technical University Eindhoven, The Netherlands (2007)
Bi, Y., van der Kolk, K.-J., Ioan, D., van der Meijs, N.P.: Sensitivity computation of interconnect capacitances with respect to geometric parameters. In: Proceedings of the IEEE International Conference on Electrical Performance of Electronic Packaging (EPEP), San Jose, CA, USA, pp. 209–212 (2008)
Ciuprina, G., Ioan, D., Niculae, D., Fernández Villena, J., Silveira, L.M.: Parametric models based on sensitivity analysis for passive components. In: Intelligent Computer Techniques in Applied Electromagnetics. Studies in Computational Intelligence Series, vol. 119, pp. 231–239. Springer, Berlin/Heidelberg (2008)
Ciuprina, G., Loan, D., Mihalache, D., Seebacher, E.: Domain partitioning based parametric models for passive on-chip components. In: Roos, J., Costa, L. (eds.) Scientific Computing in Electrical Engineering 2008. Mathematics in Industry, vol. 14, pp. 37–44. Springer, Berlin/Heidelberg (2010)
Daniel, L., Siong, O.C., Low, S.C., Lee, K.H., White, J.K.: A multiparameter moment-matching model-reduction approach for generating geometrically parametrized interconnect performance models. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 23, 678–693 (2004)
Davis, T.A.: Direct Methods for Sparse Linear Systems. The Fundamentals of Algorithms. SIAM, Philadelphia (2006)
Davis, T.A., Palamadai Natarajan, E.: Algorithm 907: KLU, a direct sparse solver for circuit simulation problems. ACM Trans. Math. Softw. 37(3), Article 36 (2010)
Elfadel, I.M., Ling, D.L.: A block rational Arnoldi algorithm for multipoint passive model-order reduction of multiport RLC networks. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 66–71 (1997)
El-Moselhy, T.A., Elfadel, I.M., Daniel, L.: A capacitance solver for incremental variation-aware extraction. In: Proceedings of the IEEE/ACM International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 662–669 (2008)
Feldmann, P., Freund, R.W.: Efficient linear circuit analysis by Padé approximation via the Lanczos process. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 14(5), 639–649 (1995)
Fernández Villena, J., Schilders, W.H.A., Silveira, L.M.: Parametric structure-preserving model order reduction. In: IFIP International Conference on Very Large Scale Integration, VLSI – SoC 2007, Atlanta, pp. 31–36 (2007)
Freund, R.W.: Sprim: structure-preserving reduced-order interconnect macro-modeling. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD) 2004, San Jose, pp. 80–87 (2004)
Gunupudi, P.K., Khazaka, R., Nakhla, M.S., Smy, T., Celo, D.: Passive parameterized time-domain macromodels for high-speed transmission-line networks. IEEE Trans. Microw. Theory Tech. 51(12), 2347–2354 (2003)
Heydari, P., Pedram, M.: Model reduction of variable-geometry interconnects using variational spectrally-weighted balanced truncation. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 586–591 (2001)
Jaimoukha, I.M., Kasenally, E.M.: Krylov subspace methods for solving large Lyapunov equations. SIAM J. Numer. Anal. 31, 227–251 (1994)
Kamon, M., Wang, F., White, J.: Generating nearly optimally compact models from Krylov-subspace based reduced-order models. IEEE Trans. Circuits Syst. II: Analog Digit. Signal Process. 47(4), 239–248 (2000)
Kula, S.: Reduced order models of interconnects in high frequency integrated circuits. Ph.D.-Thesis, Politehnica University of Bucharest (2009)
Li, J.-R., Wang, F., White, J.: Efficient model reduction of interconnect via approximate system Grammians. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 380–383 (1999)
Li, P., Liu, F., Li, X., Pileggi, L.T., Nassif, S.R.: Modeling interconnect variability using efficient parametric model order reduction. In: Proceedings of the Design, Automation and Test in Europe Conference and Exhibition (DATE), Munich, pp. 958–963 (2005)
Li, X., Li, P., Pileggi, L.: Parameterized interconnect order reduction with explicit-and-implicit multi-parameter moment matching for inter/intra-die variations. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 806–812 (2005)
Li, Y., Bai, Z., Su, Y., Zeng, X.: Model order reduction of parameterized interconnect networks via a two-directional Arnoldi process. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 27(9), 1571–1582 (2008)
Liu, Y., Pileggi, L.T., Strojwas, A.J.: Model order reduction of RC(L) interconnect including variational analysis. In: Proceedings of the 36th ACM/IEEE Design Automation Conference (DAC), New Orleans, pp. 201–206 (1999)
Moore, B.: Principal component analysis in linear systems: controllability, observability, and model reduction. IEEE Trans. Autom. Control AC-26(1), 17–32 (1981)
Odabasioglu, A., Celik, M., Pileggi, L.T.: PRIMA: passive reduced-order interconnect macromodeling algorithm. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 17(8), 645–654 (1998)
Phillips, J.: Variational interconnect analysis via PMTBR. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 872–879 (2004)
Phillips, J.R., Silveira, L.M.: Poor Man’s TBR: a simple model reduction scheme. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 24(1), 43–55 (2005)
Phillips, J., Daniel, L., Silveira, L.M.: Guaranteed passive balancing transformations for model order reduction. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 22(8), 1027–1041 (2003)
Pillage, L.T., Rohrer, R.A.: Asymptotic waveform evaluation for timing analysis. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 9(4), 352–366 (1990)
Saad, Y.: Iterative Methods for Sparse Linear Systems. Pws Publishing Co., Boston (1996)
Schilders, W.H.A., van der Vorst, H.A., Rommes, J. (eds.): Model Order Reduction: Theory, Research Aspects and Applications. Mathematics in Industry, vol. 13. Springer, Berlin (2008)
Silveira, L.M., Kamon, M., Elfadel, I., White, J.K.: A coordinate-transformed Arnoldi algorithm for generating guaranteed stable reduced-order models of RLC circuits. In: Proceedings of the International Conference on Computer Aided-Design (ICCAD), San Jose, pp. 288–294 (1996)
Yang, F., Zeng, X., Su, Y., Zhou, D.: RLCSYN: RLC equivalent circuit synthesis for structure-preserved reduced-order model of interconnect. In: Proceedings of the International Symposium on Circuits and Systems, New Orleans, pp. 2710–2713 (2007)
Yu, H., He, L., Tan, S.X.D.: Block structure preserving model order reduction. In: BMAS – IEEE Behavioral Modeling and Simulation Workshop, San Jose, pp. 1–6 (2005)
Zhu, Z., Phillips, J.: Random sampling of moment graph: a stochastic Krylov-reduction algorithm. In: Proceedings of the Design, Automation and Test in Europe Conference and Exhibition (DATE), Nice, pp. 1502–1507 (2007)
References for Section 5.2
Bi, Y., van der Meijs, N., Ioan, D.: Capacitance sensitivity calculation for interconnects by adjoint field technique. In: Proceedings of the 12th IEEE Workshop on Signal Propagation on Interconnects (SPI-2008), pp. 1–4 (2008)
Bossavit, A.: Most general non-local boundary conditions for the Maxwell equations in a bounded region. COMPEL: Int. J. Comput. Math. Electr. Electron. Eng. 19(2), pp. 239–245 (2000)
CHAMELEON-RF website. http://www.chameleon-rf.org
Ciuprina, G., Ioan, D., Niculae, D., Fernandez Villena, J., Silveira, L.: Parametric models based on sensitivity analysis for passive components. In: Wiak, S., Krawczyk, A., Dolezel, I. (eds.) Intelligent Computer Techniques in Applied Electromangetics. Studies in Computational Intelligence, vol. 119, pp. 231–239. Springer, Berlin (2008)
Clemens, M., Weiland, T.: Discrete electromagnetism with the finite integration technique. Prog. Electromagn. Res. 32, 65–87 (2001)
Deschrijver, D., Mrozowski, M., Dhaene, T., De Zutter, D.: Macromodeling of multiport systems using a fast implementation of the vector fitting method. IEEE Microw. Wirel. Compon. Lett. 18(6), 383–385 (2008)
Ferranti, F., Antonini, G., Dhaene, T., Knockaert, L.: Passivity-preserving parameterized model order reduction for PEEC based full wave analysis. In: Proceedings of the 14th IEEE Workshop on Signal Propagation on Interconnects, pp. 65–68 (2010)
Goel, A.K.: High Speed VLSI Interconnections. Wiley Series in Microwave and Optical Engineering. Wiley-IEEE Press, John Wiley & Sons, Hoboken, NJ, USA (2007)
Gustavsen, B.: Improving the pole relocating properties of vector fitting. IEEE Trans. Power Deliv. 21(3), 1587–1592 (2006)
Gustavsen, B., Semlyen, A.: Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 14(3), 1052–1061 (1999)
Ioan, D., Ciuprina, G.: Reduced order models of on-chip passive components and interconnects, workbench and test structures. In: Schilders, W.H.A., van der Vorst, H.A., Rommes, J. (eds.) Model Order Reduction: Theory, Research Aspects and Applications. Mathematics in Industry, vol. 13, pp. 447–467. Springer, Berlin (2008)
Ioan, D., Ciuprina, G., Radulescu, M.: Algebraic sparsefied partial equivalent electric circuit – ASPEEC. In: Anile, A.M., Alì, G., Mascali, G. (eds.) Scientific Computing in Electrical Engineering. Series Mathematics in Industry vol. 9, pp. 45–50. Springer, Berlin (2006)
Ioan, D., Ciuprina, G., Radulescu, M.: Absorbing boundary conditions for compact modeling of on-chip passive structures. COMPEL: Int. J. Comput. Math. Electr. Electron. Eng. 25(3), 652–659 (2006)
Ioan, D., Ciuprina, G., Radulescu, M., Seebacher, E.: Compact modeling and fast simulation of on-chip interconnect lines. IEEE Trans. Magn. 42(4), 547–550 (2006)
Ioan, D., Ciuprina, G., Kula, S.: Reduced order models for HF interconnect over lossy semiconductor substrate. In: Proceedings of the 11th IEEE Workshop on SPI, pp. 233–236 (2007)
Ioan, D., Ciuprina, G., Schilders, W.: Parametric models based on the adjoint field technique for RF passive integrated components. IEEE Trans. Magn. 44(6), 1658–1661 (2008)
Ioan, D., Schilders, W., Ciuprina, G., van der Meijs, N., Schoenmaker, W.: Models for integrated components coupled with their environment. COMPEL: Int. J. Comput. Math. Electr. Electron. Eng. 27(4), 820–828 (2008)
Kinzelbach, H.: Statistical variations of interconnect parasitics: extraction and circuit simulation. In: Proceedings of the 10th IEEE Workshop on Signal Propagation on Interconnects (SPI), pp. 33–36 (2006)
Kula, S.: Reduced order models of interconnects in high frequency integrated circuits. Ph.D.-Thesis, Politehnica University of Bucharest (2009)
Palenius, T., Roos, J.: Comparison of reduced-order interconnect macromodels for time-domain simulation. IEEE Trans. Microw. Theory Tech. 52(9), 2240-2250 (2004)
Răduleţ, R., Timotin, A., Ţugulea, A.: The propagation equations with transient parameters for long lines with losses. Rev. Roum. Sci. Tech. 15(4), 585–599 (1979)
Ştefănescu, A.: Parametric models for interconnections from analogue high frequency integrated circuits. Ph.D.-Thesis, Politehnica University of Bucharest (2009)
Stefanescu, A., Ioan, D., Ciuprina, G.: Parametric models of transmission lines based on first order sensitivities. In: Roos, J., Costa, L.R.J. (eds.) Scientific Computing in Electrical Engineering 2008. Mathematics in Industry, vol. 14, pp. 29–36. Springer, Berlin/Heidelberg (2010)
The Vector Fitting Web Site. http://www.energy.sintef.no/produkt/VECTFIT/index.asp
van der Meijs, N., Fokkema, J.: VLSI circuit reconstruction from mask topology. VLSI J. Integr. 2(3), 85–119 (1984)
References for Section 5.3
Antoulas, A.C.: Approximation of Large-Scale Dynamical Systems. SIAM Publications, Philadelphia (2005)
Armbruster, H., Feldmann, U., Frerichs, M.: Analysis based reduction using sensitivity analysis. In: Proceedings of the 10th IEEE Workshop on Signal Propagation on Interconnects (SPI), pp. 29–32 (2006)
Augustin, F., Gilg, A., Paffrath, M., Rentrop, P., Wever, U.: Polynomial chaos for the approximation of uncertainties: chances and limits. Eur. J. Appl. Math. 19, 149–190 (2008)
Baur, U., Beattie, C., Benner, P., Gugercin, S.: Interpolatory projection methods for parameterized model reduction. SIAM J. Comput. 33, 2489–2518 (2011)
Benner, P.: Advances in balancing-related model reduction for circuit simulation. In: Roos, J., Costa, L.R.J. (eds.) Scientific Computing in Electrical Engineering SCEE 2008. Mathematics in Industry, vol. 14, pp. 469–482. Springer, Berlin/Heidelberg (2010)
Benner, P., Schneider, A.: Model reduction for linear descriptor dystems with many ports. In: Günther, M., Bartel, A., Brunk, M., Schöps, S., Striebel, M. (eds.) Progress in Industrial Mathematics at ECMI 2010. Mathematics in Industry, pp. 137–143. Springer, Berlin/New York (2012)
Benner, P., Mehrmann, V., Sorensen, D. (eds.): Dimension Reduction of Large-Scale Systems. Lecture Notes in Computational Science and Engineering, vol. 45. Springer, Berlin (2005)
Benner, P., Hinze, M., ter Maten, E.J.W. (eds.): Model Reduction for Circuit Simulation. Lecture Notes in Electrical Engineering, vol. 74. Springer, Berlin (2011)
Bi, Y., van der Kolk, K.-J., Fernández Villena, J., Silveira, L.M., van der Meijs, N.: Fast statistical analysis of RC nets subject to manufacturing variabilities. In: Proceedings of the DATE 2011, Grenoble, 14–18 Mar 2011
Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods – Fundamentals in Single Domains. Springer, Berlin (2010)
Cao, Y., Petzold, L.R.: A posteriori error estimation and global error control for ordinary differential equations by the adjoint method. SIAM J. Sci. Comput. 26(2), 359–374 (2004)
Cao, Y., Li, S., Petzold, L.: Adjoint sensitivity analysis for differential-algebraic equations: algorithms and software. SIAM J. Sci. Comput. 149, 171–191 (2002)
Cao, Y., Li, S., Petzold, L., Serban, R.: Adjoint sensitivity for differential-algebraic equations: the adjoint DAE system and its numerical solution. SIAM J. Sci. Comput. 24(3), 1076–1089 (2002)
Conn, A.R., Haring, R.A., Visweswariah, C., Wu, C.W.: Circuit optimization via adjoint Lagrangians. In: Proceedings of the ICCAD, San Jose, pp. 281–288 Nov 1997
Conn, A.R., Coulman, P.K., Haring, R.A., Morrill, G.L., Visweswariah, C., Wu, C.W.: JiffyTune: circuit optimization using time-domain sensitivities. IEEE Trans. CAD ICs Syst. 17(12), 1292–1309 (1998)
Daldoss, L., Gubian, P., Quarantelli, M.: Multiparameter time-domain sensitivity computation. IEEE Trans. Circuits Syst. I: Fund. Theory Appl. 48(11), 1296–1307 (2001)
Echeverría Ciaurri, D.: Multi-level optimization: space mapping and manifold mapping. Ph.D.-Thesis, University of Amsterdam (2007). http://dare.uva.nl/document/45897
Echeverría, D., Lahaye, D., Hemker, P.W.: Space mapping and defect correction. In: Schilders, W.H.A., van der Vorst, H.A., Rommes, J. (eds.) Model Order Reduction: Theory, Research Aspects and Applications. Mathematics in Industry, vol. 13, pp. 157–176. Springer, Berlin/Heidelberg (2008)
Ernst, O.G., Mugler, A., Starkloff, H.-J., Ullmann, E.: On the convergence of generalized polynomial chaos expansions. ESAIM: Math. Model. Numer. Anal. 46, 317–339 (2012)
Errico, R.M.: What is an adjoint model?. Bull. Am. Meteorol. Soc. 78, 2577–2591 (1997)
Feng, L.: Parameter independent model order reduction. Math. Comput. Simul. 68(3), 221–234 (2005)
Feng, L., Benner, P.: A robust algorithm for parametric model order reduction. PAMM Proc. Appl. Math. Mech. 7, 1021501–1021502 (2007)
Fernández Villena, J., Silveira, L.M.: Multi-dimensional automatic sampling schemes for multi-point modeling methodologies. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 30(8), 1141–1151 (2011)
Fijnvandraat, J.G., Houben, S.H.M.J., ter Maten, E.J.W., Peters, J.M.F.: Time domain analog circuit simulation. J. Comput. Appl. Math. 185, 441–459 (2006)
Gautschi, W.: OPQ: a Matlab suite of programs for generating orthogonal polynomials and related quadrature rules (2002). http://www.cs.purdue.edu/archives/2002/wxg/codes
Gautschi, W.: Orthogonal polynomials (in Matlab). J. Comput. Appl. Math. 178, 215–234 (2005)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. The Johns Hopkins University Press, Baltimore (1996)
Günther, M., Feldmann, U., ter Maten, J.: Modelling an discretization of circuit problems. In: Schilders, W.H.A., ter Maten, E.J.W. (eds.) Handbook of Numerical Analysis, Volume XIII. Special Volume: Numerical Methods in Electromagnetics, pp. 523–659, Chapter 6. Elsevier Science, Amsterdam/Boston (2005)
Häusler, R., Kinzelbach, H.: Sensitivity-based stochastic analysis method for power variations. In: Proceedings of the Analog ’06. VDE Verlag (2006)
Hemker, P.W., Echeverría, D.: Manifold mapping for multilevel optimization. In: Ciuprina, G., Ioan, D. (eds.) Scientific Computing in Electrical Engineering SCEE 2006. Series Mathematics in Industry, vol. 11, pp. 325–330. Springer, Berlin/New York (2007)
Hocevar, D.E., Yang, P., Trick, T.N., Epler, B.D.: Transient sensitivity computation for MOSFET circuits. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 4(4), 609–620 (1985)
Homescu, C., Petzold, L.R., Serban, R.: Error estimation for reduced-order models of dynamical systems. SIAM Rev. 49(2), 277–299 (2007)
Ilievski, Z.: Model order reduction and sensitivity analysis. Ph.D.-Thesis, TU Eindhoven (2010). http://alexandria.tue.nl/extra2/201010770.pdf
Ilievski, Z., Xu, H., Verhoeven, A., ter Maten, E.J.W., Schilders, W.H.A., Mattheij, R.M.M.: Adjoint transient sensitivity analysis in circuit simulation. In: Ciuprina, G., Ioan, D. (eds.) Scientific Computing in Electrical Engineering SCEE 2006. Series Mathematics in Industry, vol. 11, pp. 183–189. Springer, Berlin/New York (2007)
Ionutiu, R.: Model order reduction for multi-terminal Systems – with applications to circuit simulation. Ph.D.-Thesis, TU Eindhoven (2011). http://alexandria.tue.nl/extra2/716352.pdf
Knyazev, A.V., Argentati, M.E.: Principle angles between subspaces in an A-based scalar product: algorithms and perturbation estimates. SIAM J. Sci. Comput. 23(6), 2009-2041 (2002). [Algorithm available in Matlab, The Mathworks, http://www.mathworks.com/]
Lang, J., Verwer, J.G.: On global error estimation and control for initial value problems. SIAM J. Sci. Comput. 29(4), 1460-1475 (2007)
Le Maître, O.P., Knio, O.M.: Spectral Methods for Uncertainty Quantification, with Applications to Computational Fluid Dynamics. Springer, Dordrecht (2010)
Lutowska, A.: Model order reduction for coupled systems using low-rank approximations. Ph.D.-Thesis, TU Eindhoven (2012). http://alexandria.tue.nl/extra2/729804.pdf
Parks, M.L., de Sturler, E., Mackey, G., Johnson, D.D., Maiti, S.: Recycling Krylov subspaces for sequences of linear systems. SIAM J. Sci. Comput. 28(5), 1651–1674 (2006)
Pinnau, R.: Model reduction via proper orthogonal decomposition. In: Schilders, W.H.A., van der Vorst, H.A., Rommes, J. (eds.) Model Order Reduction: Theory, Research Aspects and Applications. Mathematics in Industry, vol. 13, pp. 95–109. Springer, Berlin/Heidelberg (2008)
Pulch, R., ter Maten, E.J.W.: Stochastic Galerkin methods and model order reduction for linear dynamical systems. Provisionally accepted for International Journal for Uncertainty Quantification (2015)
Pulch, R., ter Maten, E.J.W., Augustin, F.: Sensitivity analysis of linear dynamical systems in uncertainty quantification. PAMM - Proceedings in Applied Mathematics and Mechanics, Vol. 13, Issue 1, pp. 507–508 (2013) DOI:10.1002/pamm.201310246
Pulch, R., ter Maten, E.J.W., Augustin, F.: Sensitivity analysis and model order reduction for random linear dynamical systems. Mathematics and Computers in Simulation 111, pp. 80–95 (2015) DOI: http://dx.doi.org/10.1016/j.matcom.2015.01.003
Rathinam, M., Petzold, L.R.: A new look at proper orthogonal decomposition. SIAM J. Numer. Anal. 41(5), 1893–1925 (2003)
Schilders, W.H.A.: Introduction to model order reduction. In: Schilders, W.H.A., van der Vorst, H.A., Rommes, J. (eds.) Model Order Reduction: Theory, Research Aspects and Applications. Mathematics in Industry, vol. 13, pp. 3–32. Springer, Berlin/Heidelberg (2008)
Schilders, W.H.A.: The need for novel model order reduction techniques in the electronics industry. In: Benner, P., Hinze, M., ter Maten, E.J.W. (eds.): Model Reduction for Circuit Simulation. Lecture Notes in Electrical Engineering, vol. 74, pp. 3–23. Springer, Berlin (2011)
Schilders, W.H.A., van der Vorst, H.A., Rommes, J. (eds.) Model Order Reduction: Theory, Research Aspects and Applications. Mathematics in Industry, vol. 13. Springer, Berlin/Heidelberg (2008)
Stavrakakis, K.K.: Model order reduction methods for parameterized systems in electromagnetic field simulations. Ph.D.-Thesis, TU-Darmstadt (2012)
Stavrakakis, K., Wittig, T., Ackermann, W., Weiland, T.: Linearization of parametric FIT-discretized systems for model order reduction. IEEE Trans. Magn. 45(3), 1380–1383 (2009)
Stavrakakis, K., Wittig, T., Ackermann, W., Weiland, T.: Three dimensional geometry variations of FIT systems for model order reduction. In: 2010 URSI International Symposium on Electromagnetic Theory, pp. 788–791 (2010)
Stavrakakis, K., Wittig, T., Ackermann, W., Weiland, T.: Model order reduction methods for multivariate parameterized dynamical systems obtained by the finite integration theory. In: 2011 URSI General Assembly and Scientifc Symposium, p. 4 (2011)
Stavrakakis, K., Wittig, T., Ackermann, W., Weiland, T.: Parametric model order reduction by neighbouring subspaces. In: Michielsen, B., Poirier, J.-R. (eds.) Scientific Computing in Electrical Engineering SCEE 2010. Series Mathematics in Industry, vol. 16, pp. 443–451. Springer, Berlin/New York (2012)
Stroud, A.: Approximate Calculation of Multiple Integrals. Prentice Hall, Englewood Cliffs (1971)
SUMO (SUrrogate MOdeling) Lab. IBCN research group of the Department of Information Technology (INTEC), Ghent University (2012). http://www.sumo.intec.ugent.be/
ter Maten, E.J.W., Heijmen, T.G.A., Lin, A., El Guennouni, A.: Optimization of electronic circuits. In: Cutello, V., Fotia, G., Puccio, L. (eds.) Applied and Industrial Mathematics in Italy II, Selected Contributions from the 8th SIMAI Conference. Series on Advances in Mathematics for Applied Sciences, vol. 75, pp. 573–584. World Scientific Publishing Co. Pte. Ltd., Singapore (2007)
ter Maten, E.J.W., Pulch, R., Schilders, W.H.A., Janssen, H.H.J.M.: Efficient calculation of Uncertainty Quantification. In: Fontes, M., Günther, M., Marheineke, N. (eds) Progress in Industrial Mathematics at ECMI 2012, Series Mathematics in Industry Vol. 19, Springer, pp. 361–370 (2014)
Ugryumova, M.V.: Applications of model order reduction for IC modeling. Ph.D.-Thesis, TU Eindhoven (2011). http://alexandria.tue.nl/extra2/711015.pdf
Volkwein, S.: Model reduction using proper orthogonal decomposition (2008). http://www.uni-graz.at/imawww/volkwein/POD.pdf
Xiu, D.: Numerical integration formulas of degree two. Appl. Numer. Math. 58, 1515–1520 (2008)
Xiu, D.: Fast numerical methods for stochastic computations: a review. Commun. Comput. Phys. 5(2–4), 242–272 (2009)
Xiu, D.: Numerical Methods for Stochastic Computations – A Spectral Method Approach. Princeton University Press, Princeton (2010)
References for Section 5.4
Antoulas, A.C.: Approximation of Large-Scale Dynamical Systems. Advances in Design and Control. SIAM, Philadelphia (2005)
Antoulas, A.C.: A new result on passivity preserving model reduction. Syst. Control Lett. 54, 361–374 (2005)
Ascher, U.M., Petzold, L.R.: Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. SIAM, Philadelphia (1998)
Daniel, L., Siong, O.C., Chay, L.S., Lee, K.H., White, J.: A multiparameter moment-matching model-reduction approach for generating geometrically parameterized interconnect performance models. IEEE Trans. Comput. Aided Des. 23(5), 678–693 (2004)
Feng, L., Benner, P.: A robust algorithm for parametric model order reduction based on implicit moment matching. PAMM Proc. Appl. Math. Mech. 7, 1021501–1021502 (2007)
Günther, M.: Partielle differential-algebraische Systeme in der numerischen Zeitbereichsanalyse elektrischer Schaltungen. Nr. 343 in Fortschritt-Berichte VDI Serie 20. VDI, Düsseldorf (2001)
Günther, M., Feldmann, U.: CAD based electric circuit modeling in industry I: mathematical structure and index of network equations. Surv. Math. Ind. 8, 97–129 (1999)
Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 2nd edn. Springer, Berlin (1996)
Li, Y., Bai, Z., Su, Y., Zeng, X.: Parameterized model order reduction via a two-directional Arnoldi process. In: Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), pp. 868–873 (2007)
Li, Y.-T., Bai, Z., Su, Y., Zeng, X.: Model order reduction of parameterized interconnect networks via a two-directional Arnoldi process. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 27(9), 1571–1582 (2008)
Mohaghegh, K.: Linear and nonlinear model order reduction for numerical simulation of electric circuits. Ph.D.-Thesis, Bergische Universität Wuppertal, Germany. Available at Logos Verlag, Berlin (2010)
Mohaghegh, K., Pulch, R., Striebel, M., ter Maten, J.: Model order reduction for semi-explicit systems of differential algebraic systems. In: Troch, I., Breitenecker, F. (eds) Proceedings MATHMOD 09 Vienna – Full Papers CD Volume, pp. 1256–1265 (2009)
Mohaghegh, K., Pulch, R., ter Maten, J.: Model order reduction using singularly perturbed systems, provisionally accepted for J. of Applied Numerical Mathematics (APNUM) (2015)
Phillips, J., Silveira, L.M.: Poor’s man TBR: a simple model reduction scheme. In: Proceedings of the Design, Automation and Test in Europe Conference and Exhibition (DATE), vol. 2, pp. 938–943 (2004)
Schwarz, D.E., Tischendorf, C.: Structural analysis of electric circuits and consequences for MNA. Int. J. Circuit Theory Appl. 28, 131–162 (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Ciuprina, G. et al. (2015). Parameterized Model Order Reduction. In: Günther, M. (eds) Coupled Multiscale Simulation and Optimization in Nanoelectronics. Mathematics in Industry(), vol 21. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-46672-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-46672-8_5
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-46671-1
Online ISBN: 978-3-662-46672-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)