Variable Thrust Angle Constant Thrust Collision Avoidance Maneuver

Abstract

In this paper, variable thrust angle (VTA) constant thrust collision avoidance maneuver is studied. For in-plane motion, robust controllers satisfying the requirements can be designed by solving this optimization problem. For out-plane motion, a new algorithm of constant thrust fitting is proposed through impulse compensation and fuel consumption under theoretical continuous thrust and the actual constant thrust is calculated. Finally, illustrative example is provided to show the effectiveness of the proposed control design method.

1.1 Introduction

During the last few decades, the problem of collision avoidance maneuver has been extensively studied and many results have been reported [1–3]. In addition, the variable thrust angle (VTA) constant thrust maneuver, until recent years, has been the least studied [4, 5]. In our previous studies [6], constant thrust control for collision avoidance maneuver was studied based on C-W equations and analytical solutions. However, the traditional open-loop control method used in our previous studies is not applicable although they are often utilized during the long-distance navigation process. To overcome this problem, robust closed-loop variable thrust angle control laws for constant collision avoidance maneuver to enhance orbital control accuracy is proposed in this paper. It is found that the fuel consumption of constant thrust is less than that of the theoretical continuous using the method proposed in this paper.

The purpose of this paper is to study VTA constant thrust collision avoidance maneuver; in other words, to design robust closed-loop variable thrust angle control laws for in-plane motion. For in-plane motion, robust control laws for constant thrust variable thrust angle, which satisfy the requirements can be designed by solving the convex optimization problem. Then, for out-plane motion, a new algorithm of constant thrust fitting is proposed using the impulse compensation method. Finally, optimal fuel consumption can be obtained by comparing the theoretical continuous thrust and the actual constant thrust, and then the actual working times of the thrusters can be computed using time series analysis method. An illustrative example is provided to show the effectiveness of the proposed control design method.

1.2 The Robust Variable Thrust Angle Control Laws for In-Plane Motion

The relative motion coordinate system can be established as follows: first, the target spacecraft is assumed as a rigid body and in a circular orbit, and the relative motion can be described by Clohessy-Wiltshire equations. Then, the centroid of the target spacecraft $O_{T}$ is selected as the origin of coordinate; the x-axis is opposite to the target spacecraft motion, the y-axis is from the center of the earth to the target spacecraft, and the z-axis is determined by the right-handed rule. Then the collision avoidance process can be divided into in-plane motion and out-plane motion based on the relative motion dynamic model as follows, with the relative motion dynamic model of the in-plane motion:

$$ \left\{ \begin{array}{ll} \textit{\"{x}} - 2\omega \dot{y} = \frac{{F_{x}\,+\,\eta_{x} }}{m} \hfill \\ \textit{\"{y}} + 2\omega \dot{x} - 3\omega^{2} y = \frac{{F_{y}\,+\,\eta_{y} }}{m} \hfill \\ \end{array} \right. $$

(1.1)

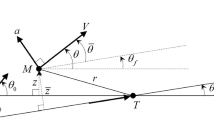
where $\omega$ represents the angular velocity of the target spacecraft. $F_{x} ,F_{y}$ represent the vacuum thrust of the chaser and $\eta_{x} ,\eta_{y}$ represent the sum of the perturbation and nonlinear factors in the x-axis and in the y-axis, respectively. m represents the mass of the chaser at the beginning of the collision avoidance maneuver. Suppose there are six thrusters installed on the chaser as shown in Fig. 1.1.

Fig. 1.1

The thrusters of the chaser

Suppose the actual constant thrusts of the chaser are $F_{x} ,F_{y} ,F_{z}$, the maximum thrusts are $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{x} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{y} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{z}$, and the theoretical continuous thrusts are $F_{x}^{*} ,F_{y}^{*} ,F_{z}^{*}$. The range of the thrust angle in the x-axis $\theta_{x}$ is defined as shown in Fig. 1.2.

Fig. 1.2

Variable thrust angle thrusters

The goal of the collision avoidance maneuver is to design a proper controller for the chaser, such that the chaser can be asymptotically maneuvered to the target position. Define the state error vector $x_{e} (t) = x(t) - x_{t} (t)$, and its state equation can be obtained as

$$ \left\{ \begin{array}{ll} \dot{x}_{e} (t) = (A_{1} + \Delta A)x_{e} (t) + (B_{1} + \Delta B)u(t) \hfill \\ u(t) = Kx_{e} (t) \hfill \\ \end{array} \right. $$

(1.2)

Lyapunov function is defined as follows:

$$ V = x_{e}^{T} (t)Px_{e} (t) $$

(1.3)

where P is a positive definite symmetric matrix. According to the system stability theory, the necessary and sufficient conditions for robust stability of the system are (1.2) as follow:

$$ A^{T} P + PA < 0 $$

(1.4)

Then a multiobjective controller design strategy is proposed by translating a multiobjective controller design problem into a convex optimization problem, and the control input constraints can be met simultaneously. Assuming the initial conditions satisfy the following inequality, where $\rho$ is a given positive constant.

$$ x^{T} (0)Px(0) < \rho $$

(1.5)

Theorem 1.1

If there exist a corresponding dimension of the matrix L, a symmetric positive definite matrix X and two parameters $\varepsilon_{1} > 0,\varepsilon_{2} > 0$ , then the sufficient condition for robust stability exists in a state feedback controller K which can meet the following conditions simultaneously.

$$ \left( {\begin{array}{*{20}c} \Sigma & X & L \\ X & { - \varepsilon_{1} } & 0 \\ {L^{T} } & 0 & { - \varepsilon_{2} } \\ \end{array} } \right) < 0,\;\;\;\;\;\;\;\;\left( {\begin{array}{*{20}c} {\rho I} & {x^{T} (0)} \\ {x(0)} & X \\ \end{array} } \right) < 0, $$

(1.6)

where $\Sigma = XA_{0}^{T} + A_{0} X + L^{T} B_{0} + B_{0} L + \varepsilon_{1} \alpha^{2} I + \varepsilon_{2} \beta^{2} I$ , then the theoretical state feedback controller K can be calculated as follows:

$$ K = LX^{ - 1} = \left( {\begin{array}{*{20}c} {K_{11} } & {K_{12} } & {K_{13} } & {K_{14} } \\ {K_{21} } & {K_{22} } & {K_{23} } & {K_{24} } \\ \end{array} } \right) $$

(1.7)

Then the following results can be obtained.

$$ \left\{ \begin{gathered} \frac{{L_{x} }}{{N_{x} }}\hat{F}_{x} \cos \theta_{x} + \frac{{L_{y} }}{{N_{y} }}\hat{F}_{y} \sin \theta_{y} = k_{11} x_{e} (t) + k_{12} y_{e} (t) + k_{13} \Delta V_{x} + k_{14} \Delta V_{y} \hfill \\ \frac{{L_{x} }}{{N_{x} }}\hat{F}_{x} \sin \theta_{x} + \frac{{L_{y} }}{{N_{y} }}\hat{F}_{y} \cos \theta_{y} = k_{21} x_{e} (t) + k_{22} y_{e} (t) + k_{23} \Delta V_{x} + k_{24} \Delta V_{y} \hfill \\ \end{gathered} \right. $$

(1.8)

Then the thrust angle control laws $\theta_{x} ,\theta_{y}$ which satisfy the robust stability of the in-plane motion can be obtained from Eq. (1.8).

1.3 Constant Thrust Control Laws for the Out-Plane Motion

The relative motion dynamic model of the out-plane motion is

$$ \ddot z + {\omega^2}z = \frac{{{F_z} + {\eta_z}}}{m} $$

(1.9)

For the out-plane motion, a new algorithm of constant thrust fitting is proposed by using the impulse compensation method as follows. Suppose the thrusters in the z-axis can provide different sizes of constant thrust to meet different thrust requirements.

Case I: if the theoretical working time of z-axis thruster in the ith thrust arc $t_{z}^{*} = 0$, then the actual constant thrust of the chaser in the z-axis is $F_{z} = F_{z}^{*} = 0$.

Case II: if the working time of z-axis in the ith thrust arc $\Delta T < t_{z}^{*} < T_{i} = M_{i} \Delta T$, then the constant thrust fitting should be discussed in several subcategories.

Case III: if the theoretical working time of z-axis thruster in the ith thrust arc $t_{z}^{*} = \Delta T < T_{i}$ and $t_{z}^{*}$ can be any one of $M_{i}$ shortest switching time interval in the ith thrust arc. Without loss of generality, suppose that $t_{z}^{*}$ is the first shortest switching time interval and the impulse error in the z-axis in the ith thrust arc $\Delta I_{zi}$ can be calculated as follows:

Step 1: Choose the size of the constant thrust in Case I. There are $N_{z} + 1$ thrust levels can be selected and the level of the constant thrust in Case I can be calculated as follows:

$$ L_{z} = \left[ {\frac{{N_{z} \int\nolimits_{{T_{i} }}^{{T_{i} + \Delta T}} {\left| {F_{z}^{*} (t)} \right|{\text{d}}t} }}{{\hat{F}_{z} \Delta T}}} \right] $$

(1.10)

Step 2: Calculate the impulse error.

$$ \Delta I_{zi} = \text{sgn} (F_{z}^{*} (t))\left| {\int\limits_{{T_{i} }}^{{T_{{i_{i} }} + \Delta T}} {\left| {F_{x}^{*} (t)} \right|\text{d}t - \frac{{L_{z} \hat{F}_{z} \Delta T}}{{N_{z} }}} } \right| $$

(1.11)

Step 3: Determine the value of the impulse compensation threshold. Suppose that the value of the impulse compensation threshold is a positive constant $\gamma > 0$.

• (1) if the impulse error $\Delta I_{zi}$ satisfies the following condition:

  $$ \left| {\int\limits_{{T_{i} }}^{{T_{{i_{i} }} + \Delta T}} {\left| {F_{x}^{*} (t)} \right|} {\text{d}}t - \frac{{\hat{F}_{z} \Delta T}}{{N_{z} }}\left[\frac{{N_{z} \int\nolimits_{{T_{i} }}^{{T_{i} + \Delta T}} {\left| {F_{z}^{*} (t)} \right|} }}{{\hat{F}_{z} \Delta T}}\right]} \right| \le \gamma $$

  (1.12)

  the actual constant thrust of the chaser in the z-axis can be calculated as follows:

  $$ F_{z} = \text{sgn} (F_{z}^{*} (t))\frac{{\hat{F}_{z} \Delta T}}{{N_{z} }}\left[ {\frac{{N_{z} \int\nolimits_{{T_{i} }}^{{T + \Delta T_{i} }} {\left| {\hat{F}_{z}^{*} (t)} \right|{\text{d}}t} }}{{\hat{F}_{z} \Delta T}}} \right] $$

  (1.13)

  then the chaser will not carry out impulse compensation.

• (2) if the impulse error $\Delta I_{zi}$ satisfies the following condition:

  $$ \gamma < \left| {\int\limits_{{T_{i} }}^{{T_{{i_{i} }} + \Delta T}} {\left| {F_{x}^{*} (t)} \right|{\text{d}}t - \frac{{\hat{F}_{z} \Delta T}}{{N_{z} }}\left[\frac{{N_{z} \int\nolimits_{{T_{i} }}^{{T_{i} + \Delta T}} {\left| {F_{z}^{*} (t)} \right|} }}{{\hat{F}_{z} \Delta T}}\right]} } \right| \le \hat{F}_{z} \Delta T $$

  (1.14)

  then the chaser should carry out impulse compensation and the size of the constant thrust impulse compensation of the chaser in the z-axis can be calculated as follows:

  $$ \Delta \tilde{I}_{xi} = F_{5} \Delta T = \frac{{\hat{F}_{z} \Delta T}}{{N_{z} }},(F_{z}^{ * } (t) < 0),\;\;\;\;\;\;\;\Delta \tilde{I}_{xi} = F_{6} \Delta T = - \frac{{\hat{F}_{z} \Delta T}}{{N_{z} }},(F_{z}^{*} (t) > 0) $$

  (1.15)

1.4 Simulation Example

The height of target spacecraft is assumed to be 356 km in a circular orbit, then the mean angular velocity is $\omega = 0.0654 \times 10^{ - 3}\,{\text{rad}}/{\text{s}}$ and the uncertainty parameters is assumed as $\Delta \omega = \pm 1 \times 10^{ - 3}\,{\text{rad}}/{\text{s}}$. The initial mass of the chaser is assumed to be 200 kg at the beginning of collision avoidance maneuver. The size of thrusts is assumed to be ±1,000 N in three axes and the shortest switching time is $\Delta T = 1\;{\text{s}}$. The initial position and velocity of the chaser are assumed to be (1,000, −300, and 200 m) and (−10, 3, and −2 m/s). Suppose the thrusters in three axes can provide 10 different sizes of constant thrust. Suppose the value of the impulse compensation threshold is a positive constant $\gamma = 300\;{\text{Ns}}$.

Figure 1.3 shows the change in x, y, and z and the theoretical thrust $F_{x}, F_{y}, F_{z}$ during collision avoidance maneuver.

Fig. 1.3

The change in position and thrust

The results in Fig. 1.4 show the change of $V_{x}, V_{y} , V_{z}$ and the thrust angles $\theta_{x}, \theta_{y}$ during collision avoidance maneuver.

Fig. 1.4

The change in velocity and the thrust angles

The result in Fig. 1.5 shows the trajectory of chaser during active collision avoidance maneuver. It can be seen that with the switch control, the chaser can get to the 30 target positions smoothly.

Fig. 1.5

The trajectory of the chaser during collision avoidance