Spectroscopic Imaging STM: Atomic-Scale Visualization of Electronic Structure and Symmetry in Underdoped Cuprates

Abstract

Atomically resolved spectroscopic imaging STM (SI-STM) has played a pivotal role in visualization of the electronic structure of cuprate high temperature superconductors. In both the d-wave superconducting (dSC) and the pseudogap (PG) phases of underdoped cuprates, two distinct types of electronic states are observed when using SI-STM. The first consists of the dispersive Bogoliubov quasiparticles of a homogeneous d-wave superconductor existing in an energy range $\vert {}E\vert {} \le {}\varDelta _{0}$ and only upon an arc in momentum space (k-space) that terminates close to the lines connecting k $=$ $\pm {}(\pi {}/a_{0},0)$ to k $=$ $\pm {}(0, \pi {}/a_{0})$. This ‘nodal’ arc shrinks continuously as electron density increases towards half filling. In both phases, the only broken symmetries detected in the $\vert E\vert \le \varDelta _{0}$ states are those of a d-wave superconductor. The second type of electronic state occurs near the pseudogap energy scale $\vert E\vert \sim \varDelta _{1}$ or equivalently near the ‘antinodal’ regions k $=$ $\pm (\pi /a_{0},0)$ and k $=$ $\pm (0, \pi /a_{0})$. These states break the expected 90$^{\circ }$-rotational (C$_{4}$) symmetry of electronic structure within each CuO$_{2}$ unit cell, at least down to 180$^{\circ }$-rotational (C$_{2}$), symmetry. This intra-unit-cell symmetry breaking is interleaved with the incommensurate conductance modulations locally breaking both rotational and translational symmetries. Their wavevector S is always found to be determined by the k-space points where Bogoliubov quasiparticle interference terminates along the line joining $\mathbf k =(0,\pm \pi /a_{0})$ to $\mathbf k =(\pm \pi /a_{0},0)$, and thus diminishes continuously with doping. The symmetry properties of these $\vert E\vert \sim \varDelta _1$ states are indistinguishable in the dSC and PG phases. While the relationship between the $\vert E\vert \sim \varDelta _1$ broken symmetry states and the $\vert E\vert \le \varDelta _{0}$ Bogoliubov quasiparticles of the homogeneous superconductor is not yet fully understood, these two sets of phenomena are linked inextricably because the k-space locations where the latter disappears are always linked by the modulation wavevectors of the former.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Electronic Structure of Hole-doped Cuprates

The CuO$_{2}$ plane electronic structure is dominated by Cu $3d$ and O $2p$ orbitals [1]. Each Cu $d_{x^2-y^2}$ orbital is split energetically into singly and doubly occupied configurations by on-site Coulomb interactions. This results in a ‘charge-transfer’ Mott insulator [1, 2] that is also strongly antiferromagnetic due to inter-copper superexchange [3, 4]. So called ‘hole-doping’, a process distinct from the eponymous one in semiconductors, is achieved by removing electrons from the 2p6 orbitals of the O atoms [5–7].

Fig. 3.1

a Schematic cuprate phase diagram. Here $T_{c}$ is the critical temperature circumscribing a ‘dome’ of superconductivity, $T_\phi$ is schematic of the maximum temperature at which superconducting phase fluctuations are detectable within the pseudogap phase, and $T^{*}$ is the approximate temperature at which the pseudogap phenomenology first appears. b The two classes of electronic excitations in cuprates. The separation between the energy scales associated with excitations of the superconducting state (dSC, denoted by $\varDelta _0$) and those of the pseudogap state (PG, denoted by $\varDelta _1$) increases as $p$ decreases (reproduced from [10]). The different symbols correspond to the use of different experimental techniques. c A schematic diagram of electronic structure within the 1st Brillouin zone of hole-doped CuO$_2$. The dashed lines joining k $=$ $(0,\pm \pi /a_{0})$ to k $=$ $(\pm \pi /a_{0},0)$ are found, empirically, to play a key role in the doping-dependence of electronic structure. The hypothetical Fermi surface (as it would appear if correlations were suppressed) is labeled using two colors, red for the ‘nodal’ regions bounded by the dashed lines and blue for the ‘antinodal’ regions near k $=$ $(0,\pm \pi /a_{0})$ to k $=$ $(\pm \pi /a_{0},0)$

The phase diagram [8] as a function of the number of holes per CuO$_{2}$ measured from half-filling, p, is shown schematically in Fig. 3.1a. Antiferromagnetism exists for p $<$ 2–5 %, superconductivity appears in the range 5–10 % $<$ p $<$ 25–30 %, and a likely Fermi liquid state appears for p $>$ 25–30 %. The highest superconducting critical temperature $T_{c}$ occurs at ‘optimal’ doping $p\sim 16$% and the superconductivity exhibits d-wave symmetry. With reduced p, an unexplained electronic excitation with energy $\vert E\vert \sim \varDelta _{1}$ and that is anisotropic in k-space, [8–13] appears at T* $>$ T $_{c}$. This phase is so called ‘pseudegap’ (PG) because the energy scale $\varDelta _{1}$ could be the energy gap of a distinct electronic phase [9, 10]. Explanations for the PG phase include (i) that it occurs via hole-doping an antiferromagnenic Mott insulator to create a spin-liquid [4, 14–18] or, (ii) that it is a d-wave superconductor but without long range phase coherence [19–24] or, (iii) that it is a distinct electronic ordered phase [25–39].

The energy scales $\varDelta _{1}$ and $\varDelta _{0}$ are associated with two distinct types of electronic excitations [8–11, 40–43] and are observed in underdoped cuprates by many techniques. Further, $\varDelta _{1}$ and $\varDelta _{0}$ deviate continuously from one another with diminishing p (Fig. 3.1b from [10]). Transient grating spectroscopy shows that the $\vert E\vert \sim \varDelta _{1}$ excitations propagate very slowly without recombination into Cooper pairs, while the lower energy ‘nodal’ excitations propagate freely and pair as expected [40]. Andreev tunneling identifies two distinct excitation energy scales which diverge as $\textit{p} \rightarrow {} 0$: the first is identified with the pseudogap energy $\varDelta _{1}$ and the second $\varDelta _{0}$ with the maximum pairing gap energy of Cooper pairs [41]. Raman spectroscopy finds that only the scattering near the d-wave node is consistent with delocalized Cooper pairing [42]. The superfluid density from muon spin rotation evolves with hole-density as if the whole Fermi surface is unavailable for Cooper pairing [43]. Figure 3.1c shows a schematic depiction of the Fermi surface and distinguishes the ‘nodal’ from ‘antinodal’ regions of k-space on red and blue. Momentum-resolved studies of cuprate electronic structure using angle resolved photoemission spectroscopy (ARPES) in the PG phase reveals that excitations with $E\sim -\varDelta _{1}$ occur near the antinodal regions $\mathbf k \cong (\pi /a_{0},0)$; $(0, \pi /a_{0})$, and that $\varDelta _{1}(p)$ increases rapidly as $p\rightarrow 0$ [9–12], while the nodal region of k-space exhibits an ungapped ‘Fermi Arc’ [44] in the PG phase upon which a momentum- and temperature-dependent energy gap opens in the dSC phase [44–50].

Fig. 3.2

a Fourier transform of the conductance ratio map Z(r, E) at a representative energy below $\varDelta _{0}$ for T $_{c}$ $=$ 45K Bi$_{2}$Sr$_{2}$Ca$_{0.8}$Dy$_{0.2}$Cu$_{2}$O$_{8+\delta }$, which only exhibits the patterns characteristic of homogenous d-wave superconducting quasiparticle interference. b Evolution of the spatially averaged tunneling spectra of Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ with diminishing p, here characterized by T $_{c}$(p). The energies $\varDelta _{1}$(p) (blue dashed line) are detected as the pseudogap edge while the energies $\varDelta _{0}(\textit{p})$ (red dashed line) are more subtle but can be identified by the correspondence of the “kink” energy with the extinction energy of Bogoliubov quasiparticles, following the procedures in [57] and [61]. c Laplacian (or equivalent high pass filter) of the conductance ratio map Z(r) at the pseudogap energy $E\,=\,\varDelta _{1}$, emphasizing the local symmetry breaking of these electronic states

Density-of-states measurements report an energetically particle-hole symmetric excitation energy $\vert E\vert =\varDelta _{1}$ that is unchanged in the PG and dSC phases [51, 52]. Figure 3.2b shows the evolution of spatially-averaged differential tunneling conductance ${g}$(E) for Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ [53–55] with the evolution of the pseudogap energy $E\,=\,\pm \varDelta _{1}$ indicated by a blue dashed curve, while that of $\varDelta _{0}$ is shown by red dashed curves (Sect. 3.6). SI-STM uses spatially mapped tunneling spectroscopy to visualize the spatial structure and symmetry of these distinct types of states. For energies $\vert E\vert \le \varDelta _{0}$, the dispersive Bogoliubov quasiparticles of a spatially homogeneous superconductor are always observed [56–62] while the states near $\vert E\vert \sim \varDelta _{1}$ are highly disordered [53–55, 63–70] and exhibit distinct broken symmetries [7, 53, 60–62, 71, 72].

3.2 Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8}$ Crystals

We have studied a sequence of Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ samples with p $\,\cong {}$ 0.19, 0.17, 0.14, 0.10, 0.08, 0.07, 0.06 or with T $_{c}$(K) $=$  86, 88, 74, 64, 45, 37, 20 respectively, and many of these samples were studied in both the dSC and PG phases [53–58, 60–64, 71, 72]. Each sample is inserted into the cryogenic ultra high vacuum of the SI-STM [76] and cleaved to reveal an atomically clean BiO surface. All measurements were made between 1.9 and 65 K using three different cryogenic SI-STMs. These samples were derived from large single crystals with very high quality of Bi$_{2.1}$Sr$_{1.9}$CaCu$_{2}$O$_{8+\delta }$ and Bi$_{2.2}$Sr$_{1.8}$Ca$_{0.8}$Dy$_{0.2}$Cu$_{2}$O$_{8+\delta }$. The crystal growth was carried out in air and at growth speeds of 0.15–0.2 mm/h. Annealing was used to vary the critical temperature of each sample. Oxidation annealing is performed in air or under oxygen gas flow, and deoxidation annealing is done in vacuum or under nitrogen gas flow for the systematic study at different hole-densities [77].

3.3 Spectroscopic Imaging Scanning Tunneling Microscopy

The spectroscopic imaging STM technique consists of making atomically resolved and registered measurements of the STM tip-sample differential tunneling conductance$\mathrm d I/\mathrm d V(\mathbf r , E\,=\,eV)\equiv g(\mathbf r , E\,=\,eV)$ which is a function of both location r and electron energy E. It can simultaneously determine the real space (r-space) and momentum space (k-space) electronic structure both above and below E $_{F}$. Successful implementation of this approach requires quite specialized STM techniques and facilities [76].

SI-STM does suffer from some common systematic errors, the most important and most widely ignored of which emerges from the tunneling current equation itself. The tunneling current is given by

$$\begin{aligned} I\left( \mathbf r ,z,V\right) =C(\mathbf r )e^{-\frac{z(\mathbf {r})}{z_0}}\int \limits _0^{eV}\left[ f(E,T)N(\mathbf {r},E)\right] \left[ 1-f(E,T)\right] N_{\mathrm {Tip}}(E)dE \end{aligned}$$

(3.1)

Here $z$(r) is the tip-surface distance, V the tip-sample bias voltage, N(r, $E$) the sample’s local-density-of-electronic-states, N $_{\mathrm {Tip}}$($E$) the tip density-of-electronic-states, $C(\mathbf r )e^{-\frac{z(\mathbf {r})}{z_0}}$ contains effects of tip elevation, of work function based tunnel-barrier, and of tunneling matrix elements, $f(E,T)$ is the Fermi function. Therefore, as $T\rightarrow 0$ and with $N_\mathrm {Tip}$ and C(r) both equal to constants (3.1) can be simplified as,

$$\begin{aligned} I_s=Ce^{-\frac{z(\mathbf {r})}{z_0}}\int \limits _0^{eV_s}N(\mathbf r ,E)dE\Rightarrow {}Ce^{-\frac{z(\mathbf {r})}{z_0}}=I_s/\int \limits _0^{eV_s}N(\mathbf r ,E)dE \end{aligned}$$

(3.2)

Here V $_{s}$ and I $_{s}$ are the (constant but arbitrary) junction ‘set-up’ bias voltage and current respectively that are used in practice to fix z(r). Taking the energy derivative of (3.1) as T $\rightarrow {}$0 and with N $_\mathrm {Tip}$ and C(r) both equal to constants, and then substituting from (3.2), the measured $g$(r, E) $\equiv {}$dI/dV(r, E $=$ eV) data are then related to N(r, E) by [58, 60–62]

$$\begin{aligned} g(\mathbf r , E=eV)=\frac{eI_s}{\int \limits ^{eV_s}_0{N(\mathbf r ,E')dE'}}N(\mathbf r ,E) \end{aligned}$$

(3.3)

Equation (3.3) shows that when $\int ^{eV_s}_0{N(\mathbf r ,E')dE'}$ is heterogeneous at the atomic scale as it invariably is in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ [53–55, 59–71], the $g$(r, E $=$ eV) data can never be used to measure the spatial arrangements of N(r, E). Mitigation [58, 60–62] of these systematic errors can be achieved by using

$$\begin{aligned} Z(\mathbf r ,E)\equiv \frac{g(\mathbf r , E =+eV)}{g(\mathbf r , E =-eV)}=\frac{N(\mathbf r ,+E)}{N(\mathbf r ,-E)} \end{aligned}$$

(3.4)

which cancels the unknown ‘setup effect’ errors. This approach allows energy magnitudes, distances, wavelengths and spatial symmetries to be measured correctly but at the expense of mixing information derived from states at $\pm {}$ E.

A second very important and frequently overlooked systematic error is the ‘thermal broadening’ which results in an unavoidable energy uncertainty $\delta {E}$ in the energy argument of all types of tunneling spectroscopy. This thermal broadening effect is caused by the convolution of the tip and sample Fermi-Dirac distributions $f\left( E\right) (1-f\left( E\right) )$ in (3.1). As the maximum of this product is $f\left( 0\right) (1-f\left( 0\right) )=\frac{1}{4}$ , the observed FWHM in tunneling conductance due to a delta-function in N(E) at $T=0$ is determined implicitly from

$$\begin{aligned} \left( e^{\frac{E}{k_BT}}+1\right) ^{-1}\left[ 1-\left( e^{\frac{E}{k_BT}}+1\right) ^{-1}\right] =\frac{1}{8} \end{aligned}$$

(3.5)

to be $\delta {E}>3.53k_{B}T$ (or $\delta E>1.28$ meV at $T\,=\,4.2$K). This FWHM is the lower limit of meaningful energy resolution in tunneling spectroscopy, and features in tunnelling spectra whose energy width grows linearly with T with this slope, are due merely to the form of the Fermi function.

A third important systematic error limits k-space resolution when using $\tilde{g}(\mathbf q ,\textit{E})$ and $\tilde{Z}(\mathbf q ,E)$, the power spectral density Fourier transforms of $g$(r, E) and Z(r, E). Because q-space resolution during Fourier analysis is inverse to the r-space field-of-view size, to achieve sufficient precision in $\vert {}$ q(E)$\vert {}$ for discrimination of a non-dispersive ordering wavevector $\mathbf q ^*$ due to an electronic ordered phase from the dispersive wavevectors q(E) due to quantum interference patterns of delocalized states, requires that $g$(r, E) or Z(r, E) be measured in large fields-of-view and with energy resolution at or below $\sim$ $2$ meV for cuprates. Using a smaller FOV or poorer energy resolution in $g$(r, E) studies inexorably generates the erroneous impression of non-dispersive modulations. For example, in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$, no deductions distinguishing between dispersive and non-dispersive excitations can or should be made using Fourier transformed $g$(r,E) data from a FOV smaller than $\sim$ $45$nm-square [57, 62].

A final subtle but important systematic error derives from the slow picometer scale distortions in rectilinearity of the image over the continuous and extended period (of up to a week or more) required for each $g$(r, E) data set to be acquired. This is particularly critical in research requiring a precise knowledge of the spatial phase of the crystal lattice [71, 72]. To address this issue, we recently introduced a post-measurement distortion correction technique that is closely related to an approach we developed earlier to address incommensurate crystal modulation effects [78] in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$. We identify a slowly varying field u(r) [79] that measures the displacement vectoru of each location r in a topographic image of the crystal surface $T(\mathbf r )$, from the location r-u(r) where it should be if $T(\mathbf r )$ were perfectly periodic. Therefore, we consider an atomically resolved topograph $T(\mathbf r )$ with tetragonal symmetry. In SI-STM, the $T(\mathbf r )$ and its simultaneously measured $g(\mathbf r ,E)$ are specified by measurements on a square array of pixels with coordinates labeled as $\mathbf r \,=\,(x,y)$. The power-spectral-density (PSD) Fourier transform of $T(\mathbf r )$, $\vert \tilde{T}(\mathbf q )\vert ^2$— where, $\tilde{T}(\mathbf q )\,$=$\,\mathrm Re \tilde{T}(\mathbf q ) +i\mathrm Im \tilde{T}(\mathbf q )$, then exhibits two distinct peaks representing the atomic corrugations; these are centered at the first reciprocal unit cell Bragg wavevectors $\mathbf Q _a \,$=$\, (Q_{ax},Q_{ay})$ and $\mathbf Q _b \,$=$\, (Q_{bx},Q_{by})$ with $a$ and $b$ labeling the unit cell vectors. Next $T(\mathbf r )$ is multiplied by reference cosine and sine functions with periodicity set by the wavevectors $\mathbf Q _a$ and $\mathbf Q _b$, and whose origin is chosen at an apparent atomic location in $T(\mathbf r )$. The resulting four images are filtered to retain q-regions within a radius $\delta q \,$=$\, \frac{1}{\lambda }$ of the four Bragg peaks; the magnitude of $\lambda$ is chosen to capture only the relevant image distortions. This procedure results in four new images which retain the local phase information $\Theta _a(\mathbf r )$, $\Theta _b(\mathbf r )$ that quantifies the local displacements from perfect periodicity:

$$\begin{aligned} X_a(\mathbf r )=\cos \Theta _a(\mathbf r ),Y_a(\mathbf r )=\sin \Theta _a(\mathbf r ) \end{aligned}$$

(3.6)

$$\begin{aligned} X_b(\mathbf r )=\cos \Theta _b(\mathbf r ),Y_b(\mathbf r )=\sin \Theta _b(\mathbf r ) \end{aligned}$$

(3.7)

Dividing the appropriate pairs of images then allows one to extract

$$\begin{aligned} \Theta _a(\mathbf r )=\tan ^{-1}\frac{Y_a(\mathbf r )}{X_a(\mathbf r )} \end{aligned}$$

(3.8)

$$\begin{aligned} \Theta _b(\mathbf r )=\tan ^{-1}\frac{Y_b(\mathbf r )}{X_b(\mathbf r )} \end{aligned}$$

(3.9)

Of course, in a perfect lattice the $\Theta _a(\mathbf r )$, would be independent of r. However, in the real image T(r), u(r) represents the distortion of the local maxima away from their expected perfectly periodic locations, with the identical distortion occurring in the simultaneous spectroscopic data $g(\mathbf r ,E)$. Considering only the components periodic with the lattice, the measured topograph can therefore be represented by

$$\begin{aligned} T(\mathbf r ) = T_0\left[ \cos \left( \mathbf Q _a\cdot \left( \mathbf r +\mathbf u (\mathbf r )\right) \right) + \cos \left( \mathbf Q _b \cdot \left( \mathbf r +\mathbf u (\mathbf r )\right) \right) \right] \end{aligned}$$

(3.10)

Correcting this for the spatially dependent phases $\Theta _a(\mathbf r )$, $\Theta _b(\mathbf r )$ generated by u(r) requires an affine transformation at each point in (x,y) space. We see that the actual local phase of each of cosine component at a given spatial point r, $\varphi _a(\mathbf r )$, $\varphi _b(\mathbf r )$ can be written as

$$\begin{aligned} \varphi _a(\mathbf r )&= \mathbf Q _a \cdot \mathbf r + \Theta _a(\mathbf r )\end{aligned}$$

(3.11)

$$\begin{aligned} \varphi _b(\mathbf r )&= \mathbf Q _b \cdot \mathbf r + \Theta _b(\mathbf r ) \end{aligned}$$

(3.12)

where $\Theta _i(\mathbf r ) \,$=$\,\mathbf Q _i \cdot \mathbf u (\mathbf r )$; $i \,=\, a,b$ is the additional phase generated by the displacement field $\mathbf u (\mathbf r )$. This simplifies (3.10) to

$$\begin{aligned} T(\mathbf r ) = T_0\left[ \cos \left( \varphi _a(\mathbf r )\right) + \cos \left( \varphi _b(\mathbf r )\right) \right] \end{aligned}$$

(3.13)

which is defined in terms of its local phase fields only, and every peak associated with an atomic local maximum in the topographic image has the same $\varphi _a$ and $\varphi _b$. We then need to find a transformation, using the given phase information $\varphi _{a,b}(\mathbf r )$, to map the distorted lattice onto a perfectly periodic one. This is equivalent to finding a set of local transformations which makes $\Theta _{a,b}$ take on constant values, ${\Theta }_a$ and ${\Theta }_b$, over all space. Thus, let r be a point on the unprocessed (distorted) T(r), and let $\tilde{\mathbf{r }}\,$=$\,\mathbf r -\mathbf u (\mathbf r )$ be the point of equal phase on the ‘perfectly’ lattice-periodic image which needs to be determined. This produces a set of equivalency relations

$$\begin{aligned} \begin{array}{l} \mathbf Q _a \cdot \mathbf r + \Theta _a(\mathbf r ) = \mathbf Q _a \cdot \tilde{\mathbf{r }} +\bar{\Theta }_a \\ \mathbf Q _b \cdot \mathbf r + \Theta _b(\mathbf r ) = \mathbf Q _b \cdot \tilde{\mathbf{r }} +\bar{\Theta }_b \end{array} \end{aligned}$$

(3.14)

Solving for the components of $\tilde{\mathbf{r }}$ and then re-assigning the T(r) values measured at r, to the new location $\tilde{\mathbf{r }}$ in the (x,y) coordinates produces a topograph with virtually perfect lattice periodicity. To solve for $\tilde{\mathbf{r }}$ we rewrite (3.14) in matrix form:

$$\begin{aligned} \mathbf Q \left( \begin{array}{c} \tilde{\mathrm{r }}_1 \\ \tilde{\mathrm{r }}_2 \end{array} \right) = \mathbf Q \left( \begin{array}{c}\mathrm r _1 \\ \mathrm r _2\end{array} \right) - \left( \begin{array}{c} \bar{\theta }_a - \theta _a(\mathbf r ) \\ \bar{\theta }_b - \theta _b(\mathbf r ) \end{array}\right) \end{aligned}$$

(3.15)

where

$$\begin{aligned} \mathbf Q = \left( \begin{array}{cc} Q_{ax} &{} Q_{ay} \\ Q_{bx} &{} Q_{by} \end{array}\right) \end{aligned}$$

(3.16)

Because $\mathbf Q _a$ and $\mathbf Q _b$ are orthogonal, $\mathbf Q$ is invertible allowing one to solve for the displacement field u(r) which maps $\mathbf r$ to $\tilde{\mathbf{r }}$ as

$$\begin{aligned} \mathbf u (\mathbf r ) = \mathbf Q ^{-1} \left( \begin{array}{c} \bar{\theta }_a - \theta _a(\mathbf r ) \\ \bar{\theta }_b - \theta _b(\mathbf r ) \end{array}\right) \end{aligned}$$

(3.17)

with the convention $\bar{\Theta }_i \,$=$\, 0$ that generates a ‘perfect’ lattice with an atomic peak at the origin; this is equivalent to ensuring that there are no imaginary (sine) components to the Bragg peaks in the Fourier transform. Then, by using this technique, one can estimate u(r) and thereby undo distortions in the raw T(r) data with the result that it is transformed into a distortion-corrected topograph $T^{\prime }$(r) exhibiting the known periodicity and symmetry of the termination layer of the crystal. The key step for electronic-structure symmetry determination is then that the identical geometrical transformations to undo u(r) in T(r) yielding $T^{\prime }$(r), are also carried out on every $g$(r, E) acquired simultaneously with the T(r) to yield a distortion corrected $g^{\prime }$(r, E). The $T^{\prime }$(r) and $g^{\prime }$(r, E) are then registered to each other and to the lattice with excellent periodicity. This procedure can be used quite generally with SI-STM data, provided it exhibits appropriately high resolution in both r-space and q-space.

3.4 Effect of Magnetic and Non-magnetic Impurity Atoms

Substitution of magnetic and non-magnetic impurity atoms can probe the microscopic electronic structure of an unconventional superconductor including whether there are sign changes on the order parameter [80–83]. For a BCS superconductor, if the order parameter exhibits s-wave symmetry, then non-magnetic impurity atoms should have little effect because time reversed pairs of states which can undergo Cooper pairing are not disrupted. Magnetic impurity atoms, on the other hand should be quite destructive since they break time reversal symmetry. For unconventional superconductors (non s-wave) this simple situation does not pertain and both magnetic and non-magnetic impurities produce strong pair breaking effects. However, the spatial/energetic structure of the bound and resonant states [80, 84] can be highly revealing of the microscopic order parameter symmetry. These theoretical ideas as summarized in [80] were the basis for SI-STM studies of non-magnetic Zn impurity atoms and magnetic Ni impurity atoms substituted on the Cu sites of Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ [85–87].

Fig. 3.3

a $g$(r, $E\,=\,-1.5$ mV) showing the random dark ‘crosses’ which are the resonant impurity states of a d-wave superconductor, at each Zn impurity atom site. b High resolution $g$(r,$E\,=\,-1.5$ mV). The dark center of scattering resonance in (b) coincides with the position of a Bi atom. The inner dark cross is oriented with the nodes of the d-wave gap. The weak outer features, including the $\sim$ $30$ Å- long “quasiparticle beams” at 45$^{\circ }$ to the inner cross, are oriented with the gap maxima. c The spectrum of a usual superconducting region of the sample, where Zn scatterers are absent (white region in a, b), is shown in blue. The arrows indicate the superconducting coherence peaks that are suppressed near Zn. The data shown in red, with an interpolating fine solid line, are the spectrum taken exactly at the center of a dark Zn scattering site. It shows both the intense scattering resonance peak centered at $\varOmega \,=\,-1.5$ mV, and the very strong suppression of both the superconducting coherence peaks and gap magnitude at the Zn site

For Zn-doped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ near optimal doping, a typical $g$(r, E) of a 50 nm square region at $V\,=\,-1.5$ mV is shown in Fig. 3.3a with the expected overall white background being indicative of a very low $g$(r, E) near the Fermi level. However there are many randomly distributed dark sites corresponding to areas of high $g$(r, E), each with a distinct four-fold symmetric shape and the same relative orientation as clearly seen in Fig. 3.3b. In Fig. 3.3c we show a comparison between spectra taken at their centers and at usual superconducting regions of the sample. The spectrum at the center of a dark site has a very strong intra-gap conductance peak at energy $\varOmega \,=\,-1.5 \pm 0.5$ meV. And, at these sites, the superconducting coherence peaks are strongly diminished, indicating the suppression of superconductivity. All of these phenomena are among the theoretically predicted characteristics of a $\sim$unitary quasiparticle scattering resonance at a single potential-scattering impurity atom in a d-wave superconductor [80].

Fig. 3.4

a, b $g(\mathbf r , E\,=\,\pm 10$ mV) revealing the impurity states at locations of the Ni impurity atoms in this 128 Å $\times$ 128 Å square FOV. At $V_\mathrm{bias }\,=\,+10$ mV, showing the ‘$+$-shaped’ regions of high local density of states associated with the Ni atoms. At $V_\mathrm bias \,=\,-10$ mV, showing the 45$^{\circ }$ spatially rotated ‘X-shaped’ pattern. c $g$(r,E) spectra above a Ni atom (red) and away from the Ni atom (blue).

Studies of Ni-doped samples near optimal doping revealed more intriguing results. Figure 3.4 shows two simultaneously acquired $g$(r, E $=$ eV) maps taken on Ni-doped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ at sample bias V $_\mathrm{bias } \,=\, \pm {}$10mV. At $+10$ mV in Fig. 3.4b ‘$+$-shaped’ regions of higher $g$(r, E) are observed, whereas at $-10$mV in Fig. 3.4a the corresponding higher $g$(r, E) regions are ‘X-shaped’. $g$(r, E) maps at V $_\mathrm{bias } \,=\, \pm {}$19mV show the particle-like and hole-like components of a second impurity state at Ni whose spatial structure is very similar to that at V $_\mathrm{bias } \,=\, \pm {}$10 mV. Figure 3.4c shows the typical spectra taken at the Ni atom site in which there are two clear particle-like $g$(r, E) peaks. The average magnitudes of these on-site impurity-state energies are $\varOmega _{1} \,=\, 9.2\,\pm \,{}$1.1meV and $\varOmega _{2} \,=\, 18.6 \pm {}$0.7 meV. The existence of two states is as expected for a magnetic impurity in a d-wave superconductor [80]. Perhaps most significant, however, is that the magnetic impurity does not appear to suppress the superconductivity (as judged by the coherence peaks) at all, as if magnetism is non destructive to the pairing interaction locally. This is not as expected within BCS-based models of the pairing mechanism.

One of the most interesting observations made during these impurity atom studies, and one which was not appreciated at the time of the original experiments, was that the vivid, clear and theoretically reasonable d-wave impurity states at Zn and Ni disappear as hole density p is reduced below optimal doping in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ [64, 88, 89]. Thus, even though the density of Zn or Ni impurity atoms is the same, the response of the CuO$_{2}$ electronic structure to them is quite different approaching half-filling. In fact, the Zn and Ni impurity states (Figs. 3.3 and 3.4) quickly diminish in intensity and eventually become undetectable at low hole-density [88, 89]. One possible explanation for this strong indication of anomalous electronic structure in underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ could be that the k-space states which contribute to Cooper pairing on the whole Fermi surface at optimal doping, no longer do so at lower p (Sect. 3.6). In this situation, all the Bogoliubov eigenstates necessary for scattering resonances to exist [80, 84] would no longer be available. This hypothesis is quite consistent with the discovery of restricted regions of k-space supporting coherent Bogoliubov quasiparticles that diminish in area with falling hole-density [61] as discussed in Sect. 3.6.

3.5 Nanoscale Electronic Disorder in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$

Nanoscale electronic disorder is pervasive in images of $\varDelta {}_{1}$(r) measured on Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ samples [53–55, 57, 60–71]. The magnitude of $\vert {}\varDelta {}_{1}\vert {}$ ranges from above 130 meV to below 10 meV as p ranges from 0.06 to 0.22. Equivalent nanoscale $\varDelta {}_{1}$(r) disorder is found in Bi$_{2}$Sr$_{2}$CuO$_{6+\delta }$ [59, 68] and in Bi$_{2}$Sr$_{2}$Ca$_{2}$Cu$_{3}$O$_{10+\delta }$ [90].

Fig. 3.5

a Map of the local energy scale $\varDelta _{1}(\mathbf r )$ from a 49 nm field of view (corresponding to $\sim$ $16,000$ CuO$_{2}$ plaquettes) measured on a sample with $T_{c} \,=\, 74$ K. Average gap magnitude $\varDelta _{1}$ is at the top, together with the values of N, the total number of dopant impurity states (shown as white circles) detected in the local spectra. b The average tunneling spectrum, $g(E)$, associated with each gap value in the field of view in a. The arrows locate the “kinks” separating homogeneous form heterogeneous electronic structure and which occur at energy $\sim$ $\varDelta _{0}$. c The doping dependence of the average $\varDelta _{1}$ (blue circles), average $\varDelta _{0}$ (red circles) and average antinodal scattering rate $\Gamma _{2}$* (black squares), each set interconnected by dashed guides to the eye. The higher-scale $\varDelta _{1}$ evolves along the pseudogap line whereas the lower-scale $\varDelta _{0}$ represents segregation in energy between homogeneous and heterogeneous electronic structure

Figure 3.5a shows a typical Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ $\varDelta _{1}$(r) image—upon which the sites of the non-stoichiometric oxygen dopant ions are overlaid as white dots [54]. Figure 3.5b shows the typical $g$(E) spectrum associated with each different value of $\pm \varDelta _{1}$ [53]. It also reveals quite vividly how the electronic structure becomes homogeneous [53–55, 58, 59, 61, 62] for $\vert {}E\vert {}\le {}\varDelta _{0}$ as indicated by the arrows. Samples of Bi$_{2}$Sr$_{2}$CuO$_{6+\delta }$ and Bi$_{2}$Sr$_{2}$Ca$_{2}$Cu$_{3}$O$_{10+\delta }$ show virtually identical effects [59, 68, 90] and imaging $\varDelta _{1}$(r) in the PG phase reveals highly similar [62, 67–69] electronic disorder.

One component of the explanation for these phenomena is that electron-acceptor atoms must be introduced [91] to generate hole doping. This almost always creates random distributions of differently charged dopant ions near the CuO$_{2}$ planes [92]. The dopants in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ are $-$2e oxygen ions charged interstitials and may cause a range of different local effects. For example, electrostatic screening may cause holes to congregate surrounding the dopant locations thereby reducing the energy-gap values nearby [93, 94]. Or the dopant ions could cause nanoscale crystalline stress/strain [95–99] thereby disordering hopping matrix elements and electron-electron interactions within the CuO$_{2}$ unit cell. In Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ the locations of interstitial dopant ions are identifiable because an electronic impurity state occurs at $E\,=\,-0.96$ V nearby each ion [54]. Significant spatial correlations are observed between the distribution of these impurity states and $\varDelta _{1}$(r) maps implying that dopant ion disorder is responsible for much of the $\varDelta _{1}$(r) electronic disorder. The principal effect near each dopant is a shift of spectral weight from low to high energy, with $\varDelta _{1}$ increasing strongly. Simultaneous imaging of the dopant ion locations and $g$(r, E $<$ $\varDelta _{0}$) reveals that the dispersive $g$(r,E) modulations due to scattering of Bogoliubov quasiparticles are well correlated with dopant ion locations meaning that the dopant ions are an important source of such scattering (Sect. 3.6) [53, 54, 56–59, 61, 62].

The microscopic mechanism of the $\varDelta _{1}$-disorder is not yet fully understood. Hole-accumulation surrounding negatively charged oxygen dopant ions does not appear to be the explanation because the modulations in integrated density of filled states are observed to be weak [54]. More significantly, $\varDelta _{1}$ is actually strongly increased nearby the dopant ions [54] that is diametrically opposite to the expected effect from hole-accumulation there. Atomic substitution at random on the Sr site by Bi or by some other trivalent lanthanoid is known to suppress superconductivity strongly [92, 100] possibly due to geometrical distortions of the unit cell and associated changes in the hopping matrix elements. It has therefore been proposed that the interstitial dopant ions might act similarly, perhaps by displacing the Sr or apical oxygen atoms [92, 95, 96, 100] and thereby distorting the unit cell geometry. Direct support for this point of view comes from the observation that quasi-periodic distortions of the crystal unit-cell geometry yield virtually identical perturbations in $g$(E) and $\varDelta _{1}$(r) but now are unrelated to the dopant ions [78]. Thus it seems that the $\varDelta _{1}$-disorder is not caused primarily by carrier density modulations but by geometrical distortions to the unit cell dimensions with resulting strong local changes in the high energy electronic structure. One could also expect the presence of such disorder in Ca$_{2-x}$Na$_{x}$CuO$_{2}$Cl$_{2}$ as Ca is substituted by Na since indeed similar $\varDelta _{1}$ disorder is also observed in this material [60].

Underdoped cuprate $g$(E) spectra always exhibit “kinks” [53–55, 58, 59, 61, 63–66, 68–70] close to the energy scale where electronic homogeneity is lost. They are weak perturbations to N(E) near optimal doping, becoming more clear as p is diminished [53, 55]. Figure 3.5b demonstrates how, in $\varDelta _{1}$-sorted $g$(E) spectra, the kinks are universal but become more obvious for $\varDelta {}$ $_{1}$ $>$50 meV [53, 55]. Each kink can be identified and its energy is labeled by $\varDelta _{0}$(r). By determining $\bar{\varDelta }_0$ as a function of p (Fig. 3.5c), we find that it always divides the electronic structure into two categories [55]. For $\vert E \vert <\bar{\varDelta }_0$ the excitations are spatially coherent in r-space and therefore represent well defined Bogoliubov quasiparticle eigenstates in k-space (Sect. 3.6). By contrast, the pseudogap excitations at $\vert E\vert \sim \varDelta _{1}$ are heterogeneous in r-space and ill defined in k-space (Sect. 3.7).

To summarize: the $\varDelta _{1}$-disorder of Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ is strongly influenced by the random distribution of dopant ions [54] and oxygen vacancies [101]. It occurs through an electronic process in which geometrical distortions of the crystal unit cell appear to play a prominent role [97–102]. While the electronic disorder is most strongly reflected in the states near the pseudogap energy $\vert E\vert \sim \varDelta _{1}$, the states with $\vert E\vert \le \varDelta _{0}$ are homogeneous when studied using direct imaging [53–55, 64] or from quasiparticle interference as described in Sect. 3.6. Therefore this intriguing phenomenon is clearly not heterogeneity of the superconductivity or superconducting energy gap, because in all simultaneously determined images the spatial coherence of Bogoliubov scattering interferences shows the superconducting energy gap to be homogeneous.

3.6 Bogoliubov Quasiparticle Interference Imaging

Bogoliubov quasiparticle interference (QPI) occurs when quasiparticle de Broglie waves are scattered by impurities and the scattered waves undergo quantum interference. In a d-wave superconductor with a single hole-like band of uncorrelated electrons as sometimes used to describe Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$, the Bogoliubov quasiparticle dispersion E(k) would exhibit constant energy contours which are ‘banana-shaped’. The d-symmetry superconducting energy gap would then cause strong maxima to appear for a given E, in the joint-density-of-states at the eight banana-tips k $_{j}$(E); j  $=$  1, 2,..., 8. Elastic scattering between the k $_{j}$(E) should produce r-space interference patterns in N(r,E). The resulting $g$(r,E) modulations should exhibit 16 $\pm {}$ q pairs of dispersive wavevectors in $\tilde{g}(\mathbf q ,\textit{E})$ (Fig. 3.6a).

Fig. 3.6

a The ‘octet’ model of expected wavevectors of quasiparticle interference patterns in a superconductor with electronic band structure like that of Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$. Solid lines indicate the k-space locations of several banana-shaped quasiparticle contours of constant energy as they increase in size with increasing energy. As an example, at a specific energy, the octet of regions of high JDOS are shown as red circles. The seven primary scattering q-vectors interconnecting elements of the octet are shown in blue. b The magnitude of various measured QPI vectors, plotted as a function of energy. Whereas the expected energy dispersion of the octet vectors q $_{i}(E)$ is apparent for $\vert E \vert < 32$mV, the peaks which avoid extinction (q $_{1}^*$ and q $_{5}^*$) shows ultra-slow or zero dispersion above $\varDelta _{0}$ (vertical dashed line). Inset: A plot of the superconducting energy gap $\varDelta (\theta _{k})$ determined from octet model inversion of quasiparticle interference measurements, shown as (open circles) [57]. c Locus of the Bogoliubov band minimum k $_{B}(E)$ found from extracted QPI peak locations q $_{i}(E)$, in five independent Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ samples with increasing hole density. Fits to quarter-circles are shown and, as p decreases, these curves enclose a progressively smaller area. The BQP interference patterns disappear near the perimeter of a k-space region bounded by the lines joining k $=$ $(0,\pm \pi /a_{0})$ and $\mathbf k \,=\,\pm (\pi /a_0,0$). The spectral weights of q $_{2}$, q $_{3}$, q $_{6}$ and q $_{7}$ vanish at the same place (dashed line; see also [61]). Filled symbols in the inset represent the hole count p $=$ 1 $-$ n derived using the simple Luttinger theorem, with the fits to a large, hole-like Fermi surface indicated schematically here in grey. Open symbols in the inset are the hole counts calculated using the area enclosed by the Bogoliubov arc and the lines joining k $=$ $(0, \pm \pi /a_{0})$ and $\mathbf k \,=\, (\pm \pi /\textit{a}_{0}, 0)$, and are indicated schematically here in blue

The set of these wavevectors characteristic of d-wave superconductivity consists of seven: q $_{i}$(E) i $\,=\,$1,...,7 with q $_{i}$($-$ E)  $=$  q $_{i}$($+$ E). By using the point-group symmetry of the first CuO$_{2}$ Brillouin zone and this ‘octet model’, [102–104] the locus of the banana tips k $_{B}$(E)  $=$  (k $_{x}$(E),k $_{y}$(E)) can be determined from:

$$\begin{aligned} \begin{array}{l} 2k_x = q_1,q_{4x}, q_{2x} - q_{2y}, q_{6y}+ q_{6x}, (q_3 + q_7)/\sqrt{2}, q_5 - \sqrt{2}q_7 \\ 2k_y = q_5,q_{4y}, q_{2x} + q_{2y}, q_{6y}- q_{6x}, (q_3 - q_7)/\sqrt{2}, \sqrt{2}q_7 - q_1 \end{array} \end{aligned}$$

(3.18)

The $\varvec{q}_{i}(E)$ are measured from $\vert \tilde{Z} (\varvec{q},E)\vert$, the Fourier transform of spatial modulations seen in $Z(\mathbf r ,E)$ and the k $_{B}(E)$ are then determined by using (3.18) within the requirement that all its independent solutions be consistent at all energies. The superconductor’s Cooper-pairing energy gap $\varDelta$(k) is then determined directly by inverting the empirical data k $_{B}(E\,=\,\varDelta )$.

Near optimal doping in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$, measurements from QPI of k $_{B}(E)$ and $\varDelta (\mathbf k )$ (Fig. 3.6b inset) are consistent with ARPES [57, 105]. And, in Ca$_{2-\textit{x}}$Na$_{x}$CuO$_{2}$Cl$_{2}$ this octet model yields k $_{B}(E)$ and $\varDelta (\mathbf k )$ equally well [58, 59] as indeed the equivalent ‘octet’ approach does in iron-pnictide high temperature superconductors [106]. Therefore, Fourier transformation of Z(r,E) in combination with the octet model of d-wave Bogoliubov QPI yields the two branches of the Bogoliubov excitation spectrum k $_{B}(\pm E)$ plus the superconducting energy gap magnitude $\pm \varDelta (\mathbf k )$ along the specific k-space trajectory k $_{B}$ for both filled and empty states in a single experiment. And, since only the Bogoliubov states of a d-wave superconductor could exhibit such a set of 16 pairs of interference wavevectors with $\mathbf q _{i}(-E)\,=\,\mathbf q _i(+E)$ and all dispersions internally consistent within the octet model, the energy gap $\pm \varDelta$(k) determined by these procedures is definitely that of the delocalized Cooper-pairs.

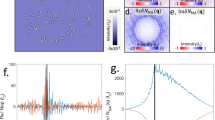
These Bogoliubov QPI imaging techniques are used to study the evolution of k-space electronic structure with diminishing p in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$. In the SC phase, the expected 16 pairs of q-vectors are always observed in $\vert \tilde{Z}(\mathbf q ,E)\vert$ and are found consistent with each other within the octet model (Fig. 3.6a). However, in underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ the dispersion of octet model q-vectors always stops at the same weakly doping-dependent [53, 59, 61] excitation energy $\varDelta _{0}$ and at q-vectors indicating that the relevant k-space states are still far from the boundary of the Brillouin zone (Fig. 3.6c). These observations are quite unexpected in the context of the d-wave BCS octet model. Moreover, for $\vert E \vert >\varDelta _{0}$ the dispersive octet of q-vectors disappears and three ultra-slow dispersion q-vectors become predominant. They are the reciprocal lattice vector Q along with q $_{1}^{*}$ and q $_{5}^{*}$ (see Fig. 3.7a).

Fig. 3.7

a A large FOV $Z(\mathbf r ,E\,=\,48$ mV) image from a strongly underdoped sample showing the full complexity of the electronic structure modulations. Inset: $\vert \tilde{Z}(\mathbf q ,E\,=\,48\,\mathrm mV )\vert$ for underdoped T $_{c}\,=\,50$ K Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$. The (circles) label the location of the wavevectors q $_{1}^*$, q $_{5}^*$ (or S $_{x}$, S $_{y}$ at $E\sim \varDelta _{1}$) and Q $_{x}$, Q $_{y}$ as described in the text. b Doping dependence of line-cuts of $\vert \tilde{Z}(\mathbf q ,E\,=\,48\,\mathrm mV )\vert$ extracted along the Cu-O bond direction Q $_{x}$. Inset: The peak is q $_{5}^*$, and the lines over the data are fits used to extract its location. The short vertical lines indicate the terminating $2k_{y}$ values derived from lower bias data. The vertical dashed lines demonstrate that the q-vectors at energies between $\varDelta _{0}$ and $\varDelta _{1}$ are not commensurate harmonics of a $4a_{0}$ periodic modulation, but instead evolve in a fashion directly related to the extinction point of the Fermi arc. c q $_{1}^*$, q $_{5}^*$, and their sum q $_{1}^*$ + q $_{5}^*$ as a function of p demonstrating that, individually, these modulations evolve with doping while their sum does not change and is equal to the reciprocal lattice vector defining the first Brillouin zone. This indicates strongly that these modulations are primarily a k-space phenomenon

The ultra-slow dispersion incommensurate modulation wavevectors equivalent to q $_{1}^{*}$ and q $_{5}^{*}$ has also been detected by SI-STM in Ca$_{2-\textit{x}}$Na$_{x}$CuO$_{2}$Cl$_{2}$ [58] and Bi$_{2}$Sr$_{2}$CuO$_{6+\delta }$ [59].

We show in Fig. 3.6c the locus of Bogoliubov quasiparticle states k $_{B}$(E) determined as a function of p using QPI. Here we discovered that when the Bogoliubov QPI patterns disappear at $\varDelta _{0}$, the k-states are near the diagonal lines between k $=$ (0, $\pi {}$/a $_{0}$) and k $=$ ($\pi {}$/a $_{0}$, 0) within the CuO$_{2}$ Brillouin zone. These k-space Bogoliubov arc tips are defined by both the change from clearly dispersive states to those whose dispersion is extremely slow or non existent, and by the disappearance of the q $_{2}$, q $_{3}$, q $_{6}$ and q $_{7}$ modulations. Thus, the QPI signature of delocalized Cooper pairing is confined to an arc that shrinks with falling p [61]. This observation has been supported directly by ARPES studies [43, 50] and by QPI studies, [58, 59] and indirectly by analyses of $g$(r, E) by fitting to a multi-parameter model for k-space structure of a dSC energy gap [70].

The minima (maxima) of the Bogoliubov bands k $_{B}(\pm E)$ should occur at the k-space location of the Fermi surface of the non-superconducting state. One can therefore ask if the carrier-density count satisfies Luttinger’s theorem, which states that twice the k-space area enclosed by the Fermi surface, measured in units of the area of the first Brillouin zone, equals the number of electrons per unit cell, $n$. In Fig. 3.7c we show as fine solid lines hole-like Fermi surfaces fitted to our measured k $_{B}$(E). Using Luttinger’s theorem with these k-space contours extended to the zone face would result in a calculated hole-density p for comparison with the estimated p in the samples. These data are shown by filled symbols in the inset showing how the Luttinger theorem is violated at all doping below $p\sim 10\,\%$ if the large hole-like Fermi surface persists in the underdoped region of the phase diagram.

Figure 3.7 provides a doping-dependence analysis of the locations of the ends of the arc-tips at which Bogoliubov QPI signature disappears and where the q $_{1}^*$ and q $_{5}^*$ modulations appear. Figure 3.7a shows a typical Z(r,E $=$ 48mV) where $\varDelta _{0}<E<\varDelta _{1}$ and its $\vert \tilde{Z}(\mathbf q ,E)\vert$ as an inset. Here the vectors q $_{1}^*$ and q $_{5}^*$ are labeled along with the Bragg vectors Q $_{x}$ and Q $_{y}$. Figure 3.7b shows the doping dependence for Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ of the location of both q $_{1}^*$ and q $_{5}^*$ measured from $\vert \tilde{Z} (\mathbf q ,E)\vert$ [61]. The measured magnitude of q $_{1}^*$ and q $_{5}^*$ versus p are then shown in Fig. 3.7c along with the sum q $_{1}^*$ + q $_{5}^*$ which is always equal to 1(2$\pi {}$/a $_{0}$). This demonstrates that, as the Bogoliubov QPI extinction point travels along the line from k $=$ ($0,\,\pi {}$/a $_{0}$) and k $=$ ($\pi {}$/a $_{0}$,0), the wavelengths of incommensurate modulations q $_{1}^*$ and q $_{5}^*$ are controlled by its k-space location [61]. Equivalent phenomena have also been reported for Bi$_{2}$Sr$_{2}$CuO$_{6+\delta }$ [59]. A natural speculation is that “hot spot” scattering related to antiferromagnetic fluctuations is involved in both the disappearance of the Bogoliubov QPI patterns and the appearance of the incommensurate quasi-static modulations at q $_{1}^*$ and q $_{5}^*$ at the diagonal lines between k $=$ (0, $\pi {}$/a $_{0}$) and k $=$ ($\pi {}$/a $_{0}$,0) within the CuO$_{2}$ Brillouin zone [107].

If the PG state of underdoped cuprates is a phase incoherent d-wave superconductor, these Bogoliubov-like QPI octet interference patterns could continue to exist above the transport T $_{c}$. This is because, if the quantum phase $\phi {}$(r, t) is fluctuating while the energy gap magnitude $\varDelta {}$(k) remains largely unchanged, the particle-hole symmetric octet of high joint-density-of-states regions generating the QPI should continue to exist [108–110]. But any gapped k-space regions supporting Bogoliubov-like QPI in the PG phase must then occur beyond the tips of the ungapped Fermi Arc [44]. Evidence for phase fluctuating superconductivity is detectable for cuprates in particular regions of the phase diagram [111–116] as indicated by the region T $_{c}< T < T_{\phi }$ (Fig. 3.1a). The techniques involved include terahertz transport studies, [111] the Nernst effect, [112, 113] torque-magnetometry measurements, [114] field dependence of the diamagnetism, [115] and zero-bias conductance enhancement [116]. Moreover, because cuprate superconductivity is quasi-two-dimensional, the superfluid density increases from zero approximately linearly with p, and the superconducting energy gap $\varDelta$(k) exhibits four k-space nodes, fluctuations of phase $\phi (\mathbf r ,t)$ could strongly impact the superconductivity at low p [19–24].

To explore these issues, the temperature evolution of the Bogoliubov octet in $\vert \tilde{Z}(\mathbf q ,E)\vert$ was studied as a function of increasing temperature from the dSC phase into the PG phase using 48 nm square FOV. Representative $\vert \tilde{Z}(\mathbf q ,E)\vert$ for six temperatures are shown in Fig. 3.8.

Fig. 3.8

(a to x) Differential conductance maps $g(\mathbf r ,E)$ were obtained in an atomically resolved and registered FOV $> 45 \times 45 \,\mathrm nm ^{2}$ at six temperatures. Each panel shown is the $\vert \tilde{Z}(\mathbf q ,E)\vert$ for a given energy and temperature. The QPI signals evolve dispersively with energy along the horizontal energy axis. The temperature dependence of QPI for a given energy evolves along the vertical axis. The octet-model set of QPI wave vectors is observed for every E and T as seen, for example, by comparing (a) and (u), each of which has the labeled octet vectors. Within the basic octet QPI phenomenology, there is no particular indication in these data of where the superconducting transition $T_{c}$, as determined by resistance measurements, occurs

Clearly, the q $_{i}$(E) (i $=$ 1,2,...,7) characteristic of the superconducting octet model are observed to remain unchanged upon passing above T $_{c}$ to at least $T \sim 1.5 T_{c}$. This demonstrates that the Bogoliubov-like QPI octet phenomenology exists in the cuprate PG phase. Thus for the low-energy ($\vert {}$ E $\vert {}$ $<\,$35 mV) excitations in the PG phase, the $\mathbf q _{i}(E)$ ($i\,=\,1,2,\ldots {},7$) characteristic of the octet model are preserved unchanged upon passing above $T_{c}$. All seven q $_{i}(E)$ ($i\,=\,1,2,\ldots {},7$) modulation wavevectors which are dispersive in the dSC phase remain dispersive into the PG phase still consistent with the octet model [62]. The octet wavevectors also retain their particle-hole symmetry $\mathbf q _{i}(+E) \,$=$\, \mathbf q _{i}(-E)$ in the PG phase and the $g$(r, E) modulations occur in the same energy range and emanate from the same contour in k-space as those observed at lowest temperatures [62]. Thus the Bogoliubov QPI signatures detectable in the dSC phase survive virtually unchanged into the underdoped PG phase—up to at least $T \sim 1.5 T_{c}$ for strongly underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ samples. Additionally, for $\vert E \vert \le \varDelta _{0}$ all seven dispersive q $_{i}$(E) modulations characteristic of the octet model in the dSC phase remain dispersive in the PG phase. These observations rule out the existence for all $\vert E\vert \le \varDelta _{0}$ of non-dispersive $g$(E) modulations at finite ordering wavevector Q* which would be indicative of a static electronic order which breaks translational symmetry, a conclusion which is in agreement with the results of ARPES studies. In fact the excitations observable using QPI are indistinguishable from the dispersive k-space eigenstates of a phase incoherent d-wave superconductor [62].

Our overall picture of electronic structure in the strongly underdoped PG phase from SI-STM contains three elements: (i) the ungapped Fermi arc, [44] (ii) the particle-hole symmetric gap $\varDelta {}$(k) of a phase incoherent superconductor, [62] and (iii) the locally symmetry breaking excitations at the $E\sim \varDelta _{1}$ energy scale [53, 60–62, 71, 72] (which remain completely unaltered upon the transition between the dSC and the PG phases [62, 71]). This three-component description of the electronic structure of the cuprate pseudogap phase has recently been confirmed in detail by ARPES studies [49].

3.7 Broken Spatial Symmetries of $E\sim \varDelta _{1}$ Pseudogap States

The electronic excitations in the pseudogap energy range $\vert E\vert \sim \varDelta _{1}$ are associated with a strong antinodal pseudogap in k-space: [11, 12] they exhibit slow dynamics without recombination to form Cooper pairs, [40] their Raman characteristics appear distinct from expectations for a d-wave superconductor, [42] and they appear not to contribute to superfluid density [43]. As described on Sects. 3.4, 3.5 and especially Sect. 3.6, underdoped cuprates exhibit an octet of dispersive Bogoliubov QPI wavevectors q $_{i}$(E), but only upon a limited and doping-dependent arc in k-space. Surrounding the pseudogap energy $E\sim \varDelta _{1}$, these phenomena are replaced by a spectrum of states whose dispersion is extremely slow (Fig. 3.6b) [53, 59–62, 71].

Remarkably, for underdoped cuprates the atomically resolved r-space images of the phenomena in $Z(\mathbf r ,E\sim \varDelta _{1}(\mathbf r ))$ show highly similar spatial patterns. By changing to the reduced energy variables $e(\mathbf r )\,$=$\,E/\varDelta _1(\mathbf r )$ and imaging $Z(\mathbf r ,e)$ it becomes clearer that these modulations exhibit a strong maximum in intensity at $e \,=\, 1$ [61, 62] and that they both break translational symmetry, and reduce the expected C$_{4}$ symmetry of states within the unit cell to at least to C$_{2}$ symmetry [60–62, 71, 72]. Theoretical concerns [117] about a possibly spurious nature to the spatial symmetry breaking in these images were addressed by carrying out a sequence of identical experiments on two very different cuprates: strongly underdoped Ca$_{1.88}$Na$_{0.12}$CuO$_{2}$Cl$_{2}$ ($T_{c}\sim 21K$) and Bi$_{2}$Sr$_{2}$Ca$_{0.8}$Dy$_{0.2}$Cu$_{2}$O$_{8+\delta }$ ($T_{c}\sim 45K$). These materials have completely different crystallographic structures, chemical constituents, dopant-ion species, and inequivalent dopant sites within the crystal-termination layers [60]. Images of the $\vert E\vert \sim \varDelta _{1}$ states for these two systems demonstrate statically indistinguishable electronic structure arrangements [60]. As these virtually identical phenomena at $\vert E\vert \sim \varDelta _{1}$ in these two materials must occur due to the common characteristic of these two quite different materials, the spatial characteristics of $Z(\mathbf r ,e\,=\,1)$ images [60–62, 71] are due to the intrinsic electronic structure of the CuO$_{2}$ plane.

To examine the broken spatial symmetries of the $\vert E\vert \sim \varDelta _{1}$ states within the CuO$_{2}$ unit cell, we use high-resolution $Z(\mathbf r ,e)$ imaging performed in a sequence of underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ samples with $T_{c}$’s between 20 and 55 K. The necessary registry of the Cu sites in each $Z(\mathbf r ,e)$ is achieved by the picometer scale transformation that renders the topographic image T(r) perfectly $a_{0}$-periodic (Sect. 3.3). The same transformation is then applied to the simultaneously acquired $Z(\mathbf r ,e)$ to register all the electronic structure data to this ideal lattice.

Fig. 3.9

a Topographic image $T(\mathbf r )$ of the Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ surface. The inset shows that the real part of its Fourier transform Re $\tilde{T}(\mathbf q )$ does not break C$_{4}$ symmetry at its Bragg points because plots of $\tilde{T}(\mathbf q )$ show its values to be indistinguishable at $\mathbf Q _{x}\,=\,(1,0)2\pi /a_{0}$ and $\mathbf Q _{y}\,=\,(0,1)2\pi /a_{0}$. Thus neither the crystal nor the tip used to image it (and its $Z(\mathbf r ,E)$ simultaneously) exhibits C$_{2}$ symmetry. b The $Z(\mathbf r ,e\,=\,1)$ image measured simultaneously with $T(\mathbf r )$ in (a). The inset shows that the Fourier transform $\vert \tilde{Z}(\mathbf q ,e\,=\,1)\vert$ does break C$_{4}$ symmetry at its Bragg points because Re$\tilde{Z}(\mathbf Q _{x}, e\sim 1)\not \,=\,$ Re$\tilde{Z}(\mathbf Q _{y}, e\sim 1)$. c The value of $O^Q_N(e)$ computed from $Z(\mathbf r ,e)$ data measured in the same FOV as (a) and (b). Its magnitude is low for all $E<\varDelta _{0}$ and then rises rapidly to become well established near $e\sim 1$ or $E\sim \varDelta _{1}$. Thus the pseudogap states in underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ break the expected C$_{4}$ symmetry of CuO$_{2}$ electronic structure. d Topographic image T(r) from the region identified by a small white box) in (a). It is labeled with the locations of the Cu atom plus both the O atoms within each CuO$_{2}$ unit cell (labels shown in the inset). Overlaid is the location and orientation of a Cu and four surrounding O atoms. e The simultaneous $Z(\mathbf r , e\,=\,1)$ image in the same FOV as (d) (the region identified by small white box in (b)) showing the same Cu and O site labels within each unit cell (see inset). Thus the physical locations at which the nematicity measure $O^R_N(e)$ is evaluated are labeled by the dashes. Overlaid is the location and orientation of a Cu atom and four surrounding O atoms. f The value of $O^R_N(e)$ computed from $Z(\mathbf r , e)$ data measured in the same FOV as (a) and (b). As in (c), its magnitude is low for all $E<\varDelta _{0}$ and then rises rapidly to become well established at $e\sim 1$ or $E\sim \varDelta _{1}$

The topograph T(r) is shown in Fig. 3.9a; the inset compares the Bragg peaks of its real (in-phase) Fourier components Re$\tilde{T}(\mathbf Q _{x}$), Re$\tilde{T}(\mathbf Q _{y}$) showing that Re$\tilde{T}(\mathbf Q _{x}$)/Re$\tilde{T}(\mathbf Q _{y}) \,=\, 1$. Therefore T(r) preserves the C$_{4}$ symmetry of the crystal lattice. In contrast, Fig. 3.9b shows that the $Z(\mathbf r ,e\,=\,1)$ determined simultaneously with Fig. 3.9a breaks various crystal symmetries [60–62]. The inset shows that since Re $\tilde{Z}(\mathbf Q _{x}, e\,=\,1$) /Re$\tilde{Z}(\mathbf Q _{y},e\,=\,1) \ne 1$ the pseudogap states break C$_{4}$ symmetry. We therefore defined a normalized measure of intra-unit-cell nematicity as a function of $e$:

$$\begin{aligned} O^Q_N(e)\equiv \frac{{\mathrm{{Re}}}{\tilde{Z}}(\mathbf{Q }_y,{ {e}}) - {\mathrm{{Re}}}{\tilde{Z}}(\mathbf Q _x,{ {e}})}{\bar{Z}(e)} \end{aligned}$$

(3.19)

where $\bar{Z}(e)$ is the spatial average of $Z(\mathbf r ,e)$. The plot of $O^Q_N(e)$ in Fig. 3.9c shows that the magnitude of $O^Q_N(e)$ is low for $e\ll \varDelta _0/\varDelta _1$, begins to grow near $e\sim \varDelta _0/\varDelta _1$, and becomes well defined as $e\sim 1$ or $E\sim \varDelta _1$.

Within the CuO$_{2}$ unit cell itself we directly imaged $Z(\mathbf r ,e)$ [60, 71] to explore where the symmetry breaking stems from. Figure 3.9d shows the topographic image of a representative region from Fig. 3.9a; the locations of each Cu site R and of the two O atoms within its unit cell are indicated. Figure 3.9e shows $Z(\mathbf r ,e)$ measured simultaneously with Fig. 3.9d with same Cu and O site labels. An r-space measure of intra-unit-cell nematicity can also be defined

$$\begin{aligned} O^R_N (e) = \sum _\mathbf R \frac{Z_x(\mathbf R ,e)-Z_y(\mathbf R ,e)}{\bar{Z}(e)N} \end{aligned}$$

(3.20)

where $Z_x(\mathbf R ,e)$ is the magnitude of $Z(\mathbf r ,e)$ at the $O$ site $a_{0}/2$ along the $x$-axis from R while $Z_y(\mathbf R ,e)$ is the equivalent along the y-axis, and N is the number of unit cells. This estimates intra-unit-cell nematicity similarly to $O^Q_N(e)$ but counting only O site contributions. Figure 3.9f contains the calculated value of $O^R_N(e)$ from the same FOV as Fig. 3.9a, b showing good agreement with $O^Q_N(e)$. Thus the intra-unit-cell C$_{4}$ symmetry breaking is specific to the states at $\vert E\vert \sim \varDelta _{1}$, manifestly, because of inequivalence, on the average, of electronic structure at this energy at the two oxygen atom sites within each cell.

Atomic-scale imaging of electronic structure evolution from the insulator through the emergence of the pseudogap to the superconducting state in Ca$_{2-x}$Na$_{x}$CuO$_{2}$Cl$_{2}$ also reveals how the intra-unit-cell C$_{4}$ symmetry breaking emerges from the C$_{4}$ symmetric antiferromagnetic insulator existing at zero hole-doping. Quite remarkably, at lowest finite dopings, nanoscale regions appear exhibiting pseudogap-like spectra and 180$^\circ$-rotational ($C_{2v}$) symmetry, and form unidirectional clusters within a weakly insulating and the $C_{4v}$-symmetric matrix [7]. Therefore ‘hole doping’ in cuprates seems to proceed by the appearance of nanoscale clusters of localized holes within which the intra-unit-cell broken-symmetry pseudogap state is stabilized. A fundamentally two-component electronic structure then exists until these C$_{2v}$-symmetric clusters touch each other at higher doping at which point the long-range high-T $_{c}$ superconductivity emerges in Ca$_{2-x}$Na$_{x}$CuO$_{2}$Cl$_{2}$.

There are also strong incommensurate electronic structure modulations (density waves) in Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$, Ca$_{2-\textit{x}}$Na$_{x}$CuO$_{2}$Cl$_{2}$ and Bi$_{2}$Sr$_{2}$CuO$_{6+\delta }$, for $\varDelta _{0}<\vert {}\textit{E}\vert {}<\varDelta _{1}$ states. They exhibit two ultra-slow dispersion q-vectors, q $_{1}^{*}$ and q $_{5}^{*}$. We find that they evolve with p as shown in Fig. 3.7b, c. The q $_{1}^{*}$ modulations appear as the energy transitions from below to above $\varDelta _{0}$ but disappear quickly leaving only two primary electronic structure elements of the pseudogap-energy electronic structure in $Z(\mathbf q ,E\cong \varDelta _1)$. These occur at the incommensurate wavevector S $_{x}$, S $_{y}$ representing phenomena that locally break translational and rotational symmetry at the nanoscale. The doping evolution of $\vert \mathbf S _{x}\vert \,$=$\,\vert \mathbf S _{y}\vert$ indicates that these modulations are directly and fundamentally linked to the doping-dependence of the extinction point of the arc of Bogoliubov QPI in Sect. 3.6. The rotational symmetry breaking of these incommensurate smectic modulations can be examined by defining a measure analogous to (3.19) of C$_{4}$ symmetry breaking, but now focused only upon the modulations with $\mathbf S _{x}$, $\mathbf S _{y}$:

$$\begin{aligned} O^Q_S(e)\equiv \frac{{\mathrm{Re}}\tilde{ Z}(\mathbf S _\textit{y},\textit{e}) - {\mathrm{Re}}\tilde{ Z}(\mathbf S _\textit{x},\textit{e})}{\bar{Z}(e)} \end{aligned}$$

(3.21)

Low values found for $\vert O^Q_S(e)\vert$ at low $e$ occur because these states are dispersive Bogoliubov quasiparticles [56, 57, 61, 62] and cannot be analyzed in term of any static electronic structure, smectic or otherwise, but $\vert O^Q_S(e)\vert$ shows no tendency to become well established at the pseudogap or any other energy and its correlation lengths are always on the nanometer scale [71].

There is growing interest in possible procedures for measurement of nematic order in STM expeirments as discussed in [74] which identified some challenges inherent in specific approaches. It is important to note that while as they apply to the data presented therein the conclusions of [74] may be true, they are of no relevance for those presented in this section or in [71, 72]. This is because [74] defines “nematicity” by the ratio of the magnitudes measured at the $\mathbf{Q}_x$ $=$ [100] and $\mathbf{Q}_y$ $=$ [010] Bragg peaks of $g(\mathbf{q})$,-the Fourier transform of $g(\mathbf{r})$ in the following fashion

$$\begin{aligned} \frac{|g(\mathbf{Q}_y)|-|g(\mathbf{Q}_x)|}{|g(\mathbf{Q}_y)|+|g(\mathbf{Q}_x)|}, \end{aligned}$$

(3.22)

as is also described in [39]. This is profoundly and essentially different from the definition of nematic order given in (3.19) above; that nematic order parameter $O_N^Q$ is lattice-phase sensitive (and thus atomic site selective) and characterizes the contribution primarily from the oxygen atoms in the CuO$_2$ plane. In contrast, (3.22) as defined in [74] mixes both real and imaginary Fourier Bragg components indiscriminately in a fashion that renders CuO$_2$ intra-unit-cell symmetry breaking extremely difficult, if no impossible, to detect.

At a more practical level, the approaches in [74] and in (3.19) are also highly distinct. In order to obtain $O_N^Q$ given by (3.19), one has first to correct for sub-angstrom scale distorsions in rectilinearity throughout the images of $g(\mathbf r \mathrm , E)$ using the Fujita-Lawler algorithms [71] or similar procedure, and then establish the correct lattice phase with high precision (2$\,\%$ of 2$\pi$), as described in Sect. 3.3. This allows establishment and analysis of the complex elements of the Fourier transform, $\mathrm {Re} T \mathbf{(q)}$ and $\mathrm {Im} T \mathbf{(q)}$, in order to yield a well defined $\mathrm {Re} g \mathbf{(q)}$ and $\mathrm{Im} g \mathbf{(q)}$ only from which $O_N^Q$ can be calculated correctly. We emphasize that this technique not only requires the mathematical steps described in Sect. 3.3, but it also requires spectroscopic measurements using many pixels inside each CuO$_2$ unit-cell. If these measurement specifications, the above lattice-phase definition procedures, and the resulting determination of $\mathrm{Re} g \mathbf{(q)}$ and $\mathrm{Im} g \mathbf{(q)}$ are not all achieved demonstrably, no deductions about the validity of $C_{4v}$ symmetry breaking in the STM data using (3.19) can or should be made. Therefore, whether the (3.22) is valid (or invalid) measure of nematicity as discussed in [74] has no relevance whatsoever for our measurements throughout this section because we use (3.19) along with the procedures described in Sect. 3.3.

In any case, there are simple practical tests for the capability to correctly measure nematicity: observation of adjacent domains with opposite nematic order when using same tip, or the direct detection of the intra-unit-cell symmetry breaking in a characteristic energy associated with the electronic states therein.

In summary: electronic structure imaging in underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ and Ca$_{2-x}$Na$_{x}$CuO$_{2}$Cl$_{2}$ reveal compelling evidence for intra-unit-cell C$_{4}$ sysmetry breaking specific to the states at the $\vert E\vert \sim \varDelta _{1}$ pseudogap energy. These effects exist because of inequivalence, when averaged over all unit cells in the image, of electronic structure at the two oxygen atom sites within each CuO$_{2}$ cell. This intra-unit-cell nematicity coexists with finite q $=$ S $_{x}$, S $_{y}$ smectic electronic modulations, but they can be analyzed separately by using Fourier filtration techniques. The wavevector of smectic electronic modulations is controlled by the point of k-space where the Bogoliubov interference signature disappears when the arc supporting delocalized Cooper pairing approaches the lines between k $=$ $\pm {}$(0,$\pi {}$/a $_{0}$) and k $=$ $\pm {}$($\pi {}$/a $_{0}$,0) (Fig. 3.6b, c). This appears to indicate that the q $=$ S $_{x}$, S $_{y}$ smectic effects are dominated by the same k-space phenomena which restrict the regions of Cooper pairing [61] and are not a characteristic of r-space ordering.

Fig. 3.10

a Smectic modulations along $x$-direction are visualized by Fourier filtering out all the modulations in $Z(\mathbf r , e\,=\,1)$ of the underdoped Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ except those at S $_{x}$. b Smectic modulations along $y$-direction are visualized by Fourier filtering out all the modulations of $Z(\mathbf r , e\,=\,1)$ except those at S $_{y}$. c Smectic modulation around the single topological defect in the same FOV showing that the dislocation core is indeed at the center of the topological defect and that the modulation amplitude tends to zero there. This is true for all the $2\pi$ topological defects identified in (e) and (f). d Phase field around the single topological defect in the FOV in (c). e f Phase field $\phi _{1}(\mathbf r )(\phi _{2}(\mathbf r ))$ for smectic modulations along $x(y)$—direction exhibiting the topological defects at the points around which the phase winds from 0 to 2$\pi {}$. Depending on the sign of phase winding, the topological defects are marked by either white or black dots. The broken red circle is the measure of the spatial resolution determined by the cut-off length (3$\sigma$) in extracting the smectic field from $\tilde{Z}(\mathbf q ,e\,=\,1)$

3.8 Interplay of Intra-unit-cell and Incommensurate Broken Symmetry States

The distinct properties of the $\vert E\vert \sim \varDelta _{1}$ smectic modulations can be examined independently of the $\vert E\vert \sim \varDelta _{1}$ intra-unit-cell C$_{4}$-symmetry breaking, by focusing in q-space only upon the incommensurate modulation peaks S $_{x}$ and S $_{y}$. A coarse grained image of the local smectic symmetry breaking reveals the very short correlation length of the strongly disordered smectic modulations [60, 71, 72]. The amplitude and phase of two unidirectional incommensurate modulation components measured in each $Z(\mathbf r , e\,=\,1)$ image (Fig. 3.10a, b) can be further extracted by denoting the local contribution to the $\mathbf S _{x}$ modulations at position r by a complex field $\Psi _{1}(\mathbf r )$. This contributes to the $Z(\mathbf r ,e\,=\,1)$ data as $\Psi _1(\mathbf r )e^{i\mathbf S _x\cdot \mathbf r }+\Psi _1^*(\mathbf r )e^{-i\mathbf S _x\cdot \mathbf r }\equiv 2\vert \Psi _{1}(\mathbf r )\vert \cos (\mathbf S _{x}\cdot \mathbf r +\phi _{1}(\mathbf r ))$ thus allowing the local phase $\phi _{1}(\mathbf r )$ of $\mathbf S _{x}$ modulations to be mapped; similarly for the local phase $\phi _{2}$(r) of S $_{y}$ modulations.

A typical example of an individual topological defect (within solid white box in Fig. 3.10a) is shown in Fig. 3.10c, d. The dislocation core (Fig. 3.10c) and its associated 2$\pi {}$ phase winding (Fig. 3.10d) are clear. We find that the amplitude of $\Psi _{1}(\mathbf r )$ or $\Psi _{2}(\mathbf r )$ always goes to zero near each topological defect. In Fig. 3.10e, f we show the large FOV images of $\phi _{1}(\mathbf r )$ and $\phi _{2}(\mathbf r )$ derived from $Z(\mathbf r ,e\,=\,1)$ in Fig. 3.10a, b. They show that the smectic phases $\phi _{1}(\mathbf r )$ and $\phi _{2}(\mathbf r )$ take on all values between 0 and $\pm 2\pi$ in a complex spatial pattern. Large numbers of topological defects with 2$\pi$ phase winding are observed; these are indicated by black $(+2\pi )$ and white $(-2\pi )$ circles and occur in approximately equal numbers. These data are all in agreement with the theoretical expectations for quantum smectic dislocations [35].

Fig. 3.11

a Fluctuations of electronic nematicity $\delta O_{n}(\mathbf r ,e\,$=$\,1)$ obtained by subtracting the spatial average $<O_{n}(\mathbf r ,e\,$=$\,1)>$ from $O_{n}(\mathbf r ,e\,=\,1)$. The locations of all 2$\pi$ topological defects measured simultaneously are indicated by black dots. They occur primarily near the lines where $\delta O_{n}(\mathbf r ,e\,=\,1) \,=\,0$. Inset shows the distribution of distances between the nearest $\delta O_{n}(\mathbf r ,e\,=\,1) \,=\,0$ contour and each topological defect; it reveals a strong tendency for that distance to be far smaller than expected at random. b Theoretical $\delta O_{n}(\mathbf r ,e\,=\,1)$ from the Ginzburg Landau functional in the [72] at the site of a single topological defect (bottom). The vector l lies along the zero-fluctuation line of $\delta O_{n}(\mathbf r ,e\,=\,1)$

Simultaneous imaging of two different broken symmetries in the electronic structure provides an unusual opportunity to explore their relationtship empirically, and to develop a Ginzburg-Landau style description of their interactions. The local nematic fluctuation $\delta O_{n}(\mathbf r )\equiv O_{n}(\mathbf r )-<O_{n}>$ (Fig. 3.11a) is the natural small quantity to enter the GL functional. In all cases we then focus upon the phase fluctuations of the smectic modulations (meaning that $\delta O_{n}(\mathbf r )$ couples to local shifts of the incommensurate wavectors) we find that $\delta O_{n}(\mathbf r )\,=\,\mathbf l \cdot \mathbf {\nabla } \phi$ surrounding each topological defect [72] where the vector $\mathbf l \propto (\alpha _{x},\alpha _{y}$) lies along the line where $\delta O_{n}(\mathbf r )\,=\,0$. The resulting prediction is that $\delta O_{n}(\mathbf r )$ will vanish along the line in the direction of l that passes through the core of the topological defect with $\delta O_{n}(\mathbf r )$ becoming greater on one side and less on the other (Fig. 3.11b), and this is what is observed throughout data sets.

Both nematic and smectic broken symmetries have been reported in the electronic/magnetic structure of different cuprate compounds [73, 117–119]. This approach may provide a good starting point to address the interplay between the different broken electronic symmetries and the superconductivity near the cuprate Mott insulator state.

Fig. 3.12

a Image typical of the broken spatial symmetries in electronic structure as measured in the dSC phase at the pseudogap energy $E\sim \varDelta _{1}$ in underdoped cuprates (both Bi$_{2}$Sr$_{2}$CaCu$_{2}$O$_{8+\delta }$ and Ca$_{2-x}$Na$_{x}$CuO$_{2}$Cl$_{2}$). b A schematic representation of the electronic structure in one quarter of the Brillouin zone at lowest temperatures in the dSC phase. The region marked II in front of the line joining $\mathbf k \,=\,(\pi /a_0,0)$ and $\mathbf k \,=\,(0,\pi /a_0)$ is the locus of the Bogoliubov QPI signature of delocalized Cooper pairs. c An example of the characteristic Bogoliubov QPI signature of sixteen pairs of interference wavevectors, all dispersive and internally consistent with the octect model as well as particle-hole symmetric $\mathbf q _i(+E)\,=\,\mathbf q _i(-E)$, here measured at lowest temperatures. d An example of the broken spatial symmetries which are concentrated upon pseudogap energy $E\sim \varDelta _{1}$ as measured in the PG phase; they are indistinguishable from measurements at $T\sim 0$. e A schematic representation of the electronic structure in one quarter of the Brillouin zone at $T\sim 1.5T_c$ in the PG phase. The region marked III is the Fermi arc, which is seen in QPI studies as a set of interference wavevectors $\mathbf q _{i}(E\,=\,0)$ indicating that there is no gap-node at $E\,=\,0$. Region II in front of the line joining $\mathbf k \,=\,(\pi /a_0,0)$ and $\mathbf k \,=\,(0,\pi /a_0)$ is the locus of the phase incoherent Bogoliubov QPI signature. Here all 16 pairs of wavevectors of the octet model are detected and found to be dispersive. Thus although the sample is not a long-range phase coherent superconductor, it does give clear QPI signatures of d-wave Cooper pairs. f An example of the characteristic Bogoliubov QPI signature of sixteen pairs of interference wavevectors, all dispersive and internally consistent with the octet model as well as particle-hole symmetric $\mathbf q _{i}(+E)\,=\,\mathbf q _i(-E)$, but here measured at $T\sim 1.5T_{c}$

3.9 Conclusions

We summarize our empirical understanding of underdoped cuprate electronic structure as derived from SI-STM studies in Fig. 3.12.

In the dSC phase (Fig. 3.12a–c) the Bogoliubov QPI signature of delocalized Cooper pairs exhibiting a spatially homogenous pairing energy gap (Sect. 3.6) exists upon the arc in k-space labeled by region II in Fig. 3.12b. States of this type have energy $\vert E\vert \le \varDelta _{0}$. The Bogoliubov QPI disappears near the lines connecting k $=$ (0, $\pm {}$ $\pi {}$/a $_{0}$) to k $=$ ($\pm {}$ $\pi {}$/a $_{0}$,0)—thus defining a k-space arc which supports the delocalized Cooper pairing. This arc shrinks rapidly towards the k $=$ ($\pm \,\pi /2a_{0},\pm \,\pi /2a_0$) points with falling hole-density in a fashion which could satisfy Luttinger’s theorem if it were actually a hole-pocket bounded from behind by the k $=$ $\pm \,(\pi /a_{0},0)-\mathbf k \pm \,(0,\pi /a_0$) lines. The $\vert E \vert \sim \varDelta _{1}$ pseudogap excitations (Sect. 3.7) are labeled schematically by region I and exhibit a radically different r-space phenomenology locally breaking the expected C$_{4}$ symmetry of electronic structure at least down to C$_2$, by rendering the two oxygen sites electronically inequivalent within each CuO$_{2}$ unit cell (Fig. 3.12a). These intra-unit-cell broken C$_{4}$-symmetry states coexist with incommensurate modulations that break translational and rotational symmetry locally. The wavelengths of these incommensurate modulations q $=$ S $_{x}$, S $_{y}$ are controlled by the k-space locations at which the Bogoliubov QPI signatures disappear; this is the empirical reason why S $_{x}$, S $_{y}$ evolve continuously with doping along the line joining k $=$ $\pm (\pi /a_{0},0)-\mathbf k \pm (0,\pi /a_0$) (Sect. 3.6). In the PG phase (Figs. 3.12d–f), the Bogoliubov QPI signature (Fig. 3.12f) exists upon a smaller part of the same arc in k-space as it did in the dSC phase. This is labeled as region II while the ungapped Fermi-arc (region III) predominates. The $E\sim \varDelta _{1}$ excitations in the PG phase, (Sect. 3.7) are again labeled by region I and exhibit intra-unit-cell C$_{4}$ breaking and q $=$ S $_{x}$, S $_{y}$ incommensurate smectic modulations indistinguishable from those in the dSC phase (Fig. 3.12e). One further point must be reemphasized: the spatially disordered and symmetry breaking states with $E\sim \varDelta _{1}$ are obviously not due to heterogeneity (granularity) of the superconductivity, because the Bogoliubov scattering interference patterns exhibit $\sim$long range spatial coherence, for all dopings and materials studied.

The relationship between the $\vert E\vert \sim \varDelta _{1}$ broken symmetry states (Sects. 3.5, 3.7, 3.8) and the $\vert E\vert \le \varDelta _{0}$ Bogoliubov quasiparticles indicative of Cooper pairing (Sects. 3.4 and 3.6), and thus the relationship between quantum states associated with the heterogeneous pseudogap and those with the homogeneous superconductivity, is not yet understood. However, these two sets of phenomena appear to be linked inextricably. The reason is that the k-space location where the latter disappears always occurs where the Fermi surface touches the lines connecting $(0,\pm \pi /a_{0}$) to $(\pm \pi /a_{0},0)$, while the wavevectors $\mathbf q _{1}^*$ and $\mathbf q _{5}^*$ close to this intersection are those of the incommensurate modulations at $\vert E\vert \sim \varDelta _{1}$.

Finally, site-specific measurements within each $\mathrm {CuO}_{2}$ unit-cell that are segregated into three separate electronic structure images (containing only the Cu sites (Cu(r)) and only the $x/y$-axis O sites ($O_x$(r) and $O_y$(r))) allows sublattice phase resolved Fourier analysis. This has recently revealed directly that the modulations in the $O_x$(r) and $O_y$(r) sublattice electronic structure images consistently exhibit a relative phase of $\pi$. These observations demonstrate by direct sublattice phase-resolved visualization that the cuprate smectic state (density wave) with wavevector S, is in fact a d-form factor density wave [120].