London Theory, Magnetic Penetration Depth, Intermediate State

Abstract

A first phenomenological theory of superconductivity and the Meissner-Ochsenfeld effect was developed by the brothers Fritz and Heinz London in 1935. In particular, their theory provides a value for the so-called magnetic penetration depth, within which the electric shielding currents flow along the surface of the superconductor and the magnetic field still exists in the superconductor. In the following, we refer to the magnetic penetration depth with the symbol $\lambda_{{\text{m}}}$.

A first phenomenological theory of superconductivity and the Meissner-Ochsenfeld effect was developed by the brothers Fritz and Heinz London in 1935. In particular, their theory provides a value for the so-called magnetic penetration depth, within which the electric shielding currents flow along the surface of the superconductor and the magnetic field still exists in the superconductor. In the following, we refer to the magnetic penetration depth with the symbol $\lambda_{{\text{m}}}$.

The brothers Fritz and Heinz London had had to leave Germany as Jews after the National Socialists took over the government and were initially accepted in England. At the Clarendon Laboratory in Oxford, they then contributed (together with other emigrants from Germany) to Oxford’s international leadership in the field of physics at low temperatures.

For a short description of the London theory, we start with the equation of the forces acting on an electron in the electric field E

$$ {\text{m}}\frac{{\partial {\mathbf{v}}_{{\mathbf{s}}} }}{{\partial {\text{t}}}} = \left( { - {\text{e}}} \right)\;{\mathbf{E}} $$

(3.1)

In Eq. (3.1), a dissipative contribution was neglected. The superconducting current density

$$ {\mathbf{j}}_{{\text{s}}} = \left( { - {\text{e}}} \right)\;{\text{n}}_{{\text{s}}} \;{\mathbf{v}}_{{\text{s}}} $$

(3.2)

yields the relationship

$$ {\mathbf{E}} = \left[ {{\text{m}}/\left( {{\text{e}}^{2} \;{\text{n}}_{{\text{s}}} } \right)} \right]\frac{{\partial {\mathbf{j}}_{{\mathbf{s}}} }}{{\partial {\text{t}}}} = {\upmu }_{{\text{o}}} \lambda_{{\text{m}}}^{2} \frac{{\partial {\mathbf{j}}_{{\mathbf{s}}} }}{{\partial {\text{t}}}}. $$

(3.3)

In Eq. (3.3), we introduced the magnetic penetration depth $\lambda_{{\text{m}}}$, which is defined by

$$ \lambda_{{\text{m}}}^{2} = {\text{m}}/\left( {{\upmu }_{{\text{o}}} \;{\text{n}}_{{\text{s}}} \;{\text{e}}^{2} } \right) $$

(3.4)

Here m is the mass, n_s the density and v_s the velocity of the superconducting electrons. µ_o is the vacuum permeability.

Since the superconducting shielding current exactly compensates an external magnetic field, the Maxwell equation

$$ {\text{curl}}\;{\mathbf{H}} = {\mathbf{j}} $$

(3.5)

is a good approximation of the maximum density j_s of the shielding current

$$ {\text{j}}_{{\text{s}}} = {\text{H}}_{{\text{C}}} /{\uplambda }_{{\text{m}}} . $$

(3.6)

On the other hand, the Maxwell equation (B = magnetic flux density) yields

$$ {\text{curl}}\;{\mathbf{E}} = - \frac{{\partial {\mathbf{B}}}}{{\partial {\text{t}}}} $$

(3.7)

together with Eq. (3.3)

$$ {\upmu }_{{\text{o}}} {\mkern 1mu} \lambda_{{\text{m}}}^{2} {\text{curl}}\,\left( {\frac{{\partial {\mathbf{j}}_{{\mathbf{s}}} }}{{\partial {\text{t}}}}} \right) + \frac{{\partial {\mathbf{B}}}}{{\partial {\text{t}}}} = 0. $$

(3.8)

By suppressing the time derivative in Eq. (3.8), Fritz and Heinz London postulated a new equation

$$ {\upmu }_{{\text{o}}} {\mkern 1mu} \lambda_{{\text{m}}}^{2} \,{\text{curl}}\;{\mathbf{j}}_{{\text{s}}} + {\mathbf{B}} = 0. $$

(3.9)

The Maxwell Eq. (3.5) and the relation curl curl x = grad div x − Δ x finally results in

$$ \Delta {\mathbf{H}} = \frac{1}{{{\uplambda }_{{\text{m}}}^{2} }}{\mathbf{H}} $$

(3.10)

with the solution

$$ {\mathbf{H}}\left( {\text{x}} \right) = {\mathbf{H}}\left( 0 \right)\;\exp \;( - {\text{x}}/{\uplambda }_{{\text{m}}} ). $$

(3.11)

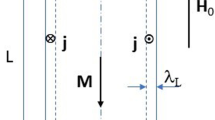
In Fig. 3.1, we show the course of the magnetic field H₀ and the density n_s of the superconducting electrons in the vicinity of the interface between a normal conductor (N) and a superconductor (S). Here we have assumed the geometry of a superconductor whose x-coordinate runs from the surface at ${\text{x}} = 0$ left to the inside of the superconductor and which fills the (left) half space x > 0. The magnetic field H is assumed perpendicular to the x-direction.

Today, Eqs. (3.3) and (3.9) are known as the first and second London equations. They characterize superconductors in contrast to other materials. Physically, Eq. (3.11) means that an external magnetic field inside a superconductor decays exponentially, with the decay occurring within a surface layer of the thickness λ_m. The limiting case T → T_C results in n_s → 0 and therefore λ_m → ∞.

Typical values of the magnetic penetration depth are in the range $\lambda_{{\text{m}}} = 40 - 60{\mkern 1mu} \;{\text{nm}}$. As an important material-specific spatial length, the magnetic penetration depth plays a role in many properties of superconductors.

After the London theory established the fundamental importance of the magnetic penetration depth in superconductors, the Englishman Alfred Brian Pippard pointed out for the first time in 1950 that the superconducting property cannot change abruptly in space and has a certain spatial rigidity. This is expressed by the so-called coherence length $\xi$. Changes in the superconducting properties are only possible at spatial distances greater than the coherence length. This fact is explained by the Ginzburg–Landau theory, which also dates from 1950. The theory is named after the two Russians Vitaly Lazarevich Ginzburg and Lew Dawidowitsch Landau. In Chapter 5, we come back to this.

The two characteristic lengths $\lambda$_m and $\xi$ play a role, for example, at the interfaces between normal and superconducting regions in the same material. Here, the finite value of the coherence length causes a superconducting region to lose its superconducting property and the associated condensation energy density (Eq. (2.4)) already at the distance ξ in front of this interface, thus making a positive contribution $\alpha_{1} = ({\text{H}}_{{\text{C}}}^{2} /8\pi )\xi$ to the interface energy. However, since no gain and therefore no loss of condensation energy occurs within the magnetic penetration depth λ_m, the value $({\text{H}}_{{\text{C}}}^{2} /8\pi )\lambda_{m}$ must still be deducted from this. Finally, for the wall energy of an interface between a normal and a superconducting region, one finds

$$ \alpha = ({\text{H}}_{{\text{C}}}^{2} /8\pi ){\mkern 1mu} (\xi - \lambda_{{\text{m}}} ). $$

(3.12)

In Fig. 3.1, we show the spatial impact of the two lengths ξ and λ_m. In connection with this result Eq. (3.12), it was assumed that the interfacial energy must always be positive and $\xi > \lambda_{{\text{m}}}$ must therefore apply.

Fig. 3.1

Dependence of the density of superconducting electrons, n_s, and the magnetic field H on the distance from the interface between a normal (N) and a superconducting (S) region. The x-coordinate runs in the superconductor from the surface at ${\text{x}} = 0$ left to the interior of the superconductor

When discussing the Meissner-Ochsenfeld effect, we had previously not considered the so-called demagnetization effect. This effect is based on the fact that the magnetic field expulsion increases the magnetic field in the immediate vicinity of the superconductor. This behavior is quantified by the so-called demagnetization coefficient D of the geometry of the superconductor. If we call the magnetic field at the edge of the superconductor H_R, the following applies

$$ {\text{H}}_{{\text{R}}} = {\text{H}}/\left( {1 - {\text{D}}} \right) $$

(3.13)

The coefficient D depends on the geometry and varies in the range 0–1. From Eq. (3.13), we can see that in the range

$$ {\text{H}}_{{\text{C}}} \;\left( {1 - {\text{D}}} \right)\; < \;{\text{H}}\; < \;{\text{H}}_{{\text{C}}} $$

(3.14)

the case H_R > H_C is present and superconductivity must be interrupted. In Table 3.1, we have compiled the demagnetization coefficient D for some geometries.

Table 3.1 Demagnetization coefficient D for different geometries

From Table 3.1, we can see that in the case of a thin plate or cylinder oriented parallel to H, the magnetic field in the outer space is hardly changed by the field expulsion. On the other hand, we expect a large field increase in the case of a plate oriented perpendicular to H, so that the magnetic field at the outer edge quickly becomes larger than the critical magnetic field H_C(T).

In the range marked by Eq. (3.14), superconductivity can no longer be maintained everywhere, and magnetic flux must penetrate the superconductor. In 1937, Landau proposed the existence of a new “intermediate state” for this case, in which normal domains with the local magnetic field H_C and superconducting domains with the local magnetic field zero exist. According to Eq. (3.12), we expect for these domains a wall energy proportional to the length difference $\xi - \lambda_{{\text{m}}}$, where $\xi > \lambda_{{\text{m}}}$.

In Fig. 3.2, we show the intermediate state of a superconducting lead layer of 9.3 µm thickness at 4.2 K for different values of the magnetic field oriented perpendicular to the layer. The images were obtained magneto-optically using a polarization microscope. The normal domains are bright and the superconducting domains are dark. The critical magnetic field of lead at 4.2 K is 550 G (${\text{T}}_{{\text{C}}} = 7.2\;{\text{K}}$).

Fig. 3.2

Intermediate state of a superconducting lead layer of 9.3 µm thickness at 4.2 K in rising (d–f) and falling (j–l) perpendicular magnetic field for the following magnetic field values: d 218 G; e 348 G; f 409 G; j 260 G; k 101 G; l 79 G. Normal domains are bright, superconducting domains are dark