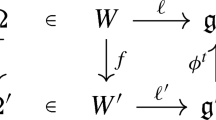Rigid Current Lie Algebras

Abstract

A current Lie algebra is constructed from a tensor product of a Lie algebra and a commutative associative algebra of dimension greater than 2. In this work we are interested in deformations of finite dimensional current Lie algebras and in the problem of rigidity. In particular we prove that a complex finite dimensional current Lie algebra with trivial center is rigid if it is isomorphic to a direct product $\mathfrak {g}\times \mathfrak {g}\times \cdots \times \mathfrak {g}$ where $\mathfrak {g}$ is a rigid Lie algebra.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Current Lie Algebras

If $\mathfrak {g}$ is a Lie algebra over a algebraically closed field $\mathbb {K}$ and $\fancyscript{A}$ a $\mathbb {K}$-associative commutative algebra, then $\mathfrak {g}\otimes \fancyscript{A}$, provided with the bracket

$$ [X\otimes a,Y\otimes b]=[X,Y]\otimes ab $$

for every $X,Y \in \mathfrak {g}$ and $a,b \in \fancyscript{A}$ is a Lie algebra. If $dim (\fancyscript{A})=1$ such an algebra is isomorphic to $\mathfrak {g}$. If $dim (\fancyscript{A})>1$ we will say that $\mathfrak {g}\otimes \fancyscript{A}$ with the previous bracket is a current Lie algebra.

In [16] we have shown that if $\fancyscript{P}$ is a quadratic operad, there is an associated quadratic operad, noted $\tilde{\fancyscript{P}}$ such that the tensor product of a $\fancyscript{P}$-algebra by a $\tilde{\fancyscript{P}}$-algebra is a $\fancyscript{P}$-algebra for the natural product. In particular, if the operad $\fancyscript{P}$ is $\fancyscript{L}ie$, then $\tilde{\fancyscript{L}ie} =\fancyscript{L}ie^!= \fancyscript{C}om$ and a $\fancyscript{C}om$-algebra is a commutative associative algebra. In this context we find again the notion of current Lie algebra.

Remark

In [3], the notion of duplication of algebras constructed by tensor product is presented. If $\mathfrak {g}$ is a Lie algebra, we define on $\mathfrak {g}\otimes \mathfrak {g}$ the product

$$ \mu (X\otimes Y,X'\otimes Y')= [X,Y]\otimes [X',Y']. $$

But, in this case, $\mathfrak {g}\otimes \mathfrak {g}$ is not a Lie algebra, but is related with the notion of $n$-Lie algebras.

In this work we study the deformations of finite dimensional current Lie algebras and we study the rigidity. The notion of rigidity is related to the second group of the Chevalley-Eilenberg cohomology. For the current Lie algebras, this group is not well known. Recently some relations between $H^2(\mathfrak {g}\otimes \fancyscript{A},\mathfrak {g}\otimes \fancyscript{A}),$ $H^2(\mathfrak {g},\mathfrak {g})$ and $H^2_H(\fancyscript{A},\fancyscript{A})$ have been given in [18] but often when $\mathfrak {g}$ is abelian. Let us note also that the scalar cohomology has been studied in [15].

2 Determination of Rigid Current Lie Algebras

In all this work, Lie algebras or associative algebras are of finite dimension over the algebraically closed field $\mathbb {K}$.

2.1 On the Rigidity of Lie Algebras

Let us remind briefly some properties of the variety of Lie algebras (for more details, see [1]). Let $\mathfrak {g}$ be a $n$-dimensional $\mathbb {K}$-Lie algebra. Since the underlying vector space is isomorphic to $\mathbb {K}^n$, there exists a one-to-one correspondance between the set of Lie brackets of $n$-dimensional Lie algebras and the skew-symmetric bilinear maps $\mu : \mathbb {K}^n \times \mathbb {K}^n\rightarrow \mathbb {K}^n$ satisfying the Jacobi identity. We denote by $\mu _{\mathfrak {g}}$ this bilinear map corresponding to $\mathfrak {g}$. In this framework, we can identify $\mathfrak {g}$ with the pair $(\mathbb {K}^n,\mu _{\mathfrak {g}})$. Let us fix definitively a basis $\{X_1,\ldots ,X_n\}$ of $\mathbb {K}^n$. The structure constants $(C_{ij}^k)$ of $\mu _{\mathfrak {g}}$ are given by

$$ \mu _{\mathfrak {g}}(X_i,X_j)=\sum _{k=1}^nC_{ij}^k \ X_k $$

and we can identify $\mu _{\mathfrak {g}}$ with the $N$-tuple $(C_{ij}^k)$ with $N=\frac{n^2(n-1)}{2}$. The Jacobi identity satisfied by $\mu _{\mathfrak {g}}$ is equivalent to the polynomial system :

$$\begin{aligned} \sum _{l=1,\ldots ,n} C_{ij}^lC_{lk}^s+C_{jk}^lC_{li}^s+C_{ki}^lC_{lj}^s=0. \end{aligned}$$

(1)

In this context, a Lie algebra is a point of $\mathbb {K}^N$ whose coordinates $(C_{ij}^k)$ satisfy (1). The set of $n$-dimensional Lie algebras over $\mathbb {K}$ is identified with the algebraic variety $L_n$ embedded into $\mathbb {K}^N$ and defined by the system of polynomial Eq. (1). We will always denote by $\mu$ a point of $L_n$. The algebraic group $GL(n,\mathbb {K})$ acts on $L_n$ by:

$$\begin{aligned} (f,\mu ) \in GL(n,\mathbb {K})\times L_n\longrightarrow \mu _f \ \in L_n \end{aligned}$$

(2)

where $\mu _f$ is given by $\mu _f(X,Y)=f^{-1}(\mu (f(X),f(Y))$ for every $X,Y \in \mathbb {K}^n.$ The orbit $\fancyscript{O}(\mu )$ of $\mu$ related to this action corresponds to the Lie algebras isomorphic to $\mathfrak {g}=(\mathbb {K}^n, \mu ).$ We provide the algebraic variety $L^n$ with the Zariski topology.

Definition 2.1

The Lie algebra $\mathfrak {g}=(\mathbb {K}^n, \mu )$ is rigid if the orbit $\fancyscript{O}(\mu )$ is open in $L_n$.

A way of constructing rigid Lie algebras rests on the Nijenhuis-Richardson Theorem : Let $H^*(\mathfrak {g},\mathfrak {g})$ be the Chevalley-Eilenberg cohomology of $\mathfrak {g}$. If $H^2(\mathfrak {g},\mathfrak {g})=0$ then $\mathfrak {g}$ is rigid. Let us note that the converse is false, numerous examples are described in [1, 9] (in fact, a rigid Lie algebra whose cohomology $H^2(\mathfrak {g},\mathfrak {g})$ is not trivial is such that the affine schema $\fancyscript{L}_n$ given by the Jacobi ideal is not reduced to the point $\mu$ defining $\mathfrak {g}$.)

An intuitive way of defining the notion of rigidity is to consider a rigid algebra as not deformable, that is, any close algebra is isomorphic to it. A general definition of deformations was proposed in [12]. Let $A$ be a commutative $\mathbb {K}$-algebra of valuation such that the residual field $A/\mathfrak {m}$ is isomorphic to $\mathbb {K}$ where $\mathfrak {m}$ is the maximal ideal of $A$. If $\mathfrak {g}$ is a $\mathbb {K}$-Lie algebra then the tensor product $\mathfrak {g}\otimes A$ is an $A$-algebra denoted by $\mathfrak {g}_A$.

Definition 2.2

A deformation of $\mathfrak {g}$ is an $A$-Lie algebra $\mathfrak {g}'_A$ such that the underlying $A$-module is $\mathfrak {g}_A$ and the brackets $[u,v]_{\mathfrak {g}'_A}$ and $[u,v]_{\mathfrak {g}_A}$ of $\mathfrak {g}'_A$ and $\mathfrak {g}_A$ satisfy

$$ [u,v]_{\mathfrak {g}'_A}-[u,v]_{\mathfrak {g}_A} \in \mathfrak {g}\otimes \mathfrak {m}. $$

When $A=\mathbb {C}[[t]]$ we find the classical notion of deformation given by Gerstenhaber. When $A$ is the ring of limited elements in a Robinson non archimedean extension of $\mathbb {C}$, we find the notion of perturbations [8]. If $\mathfrak {g}'_A$ is a deformation of $\mathfrak {g}$ then we have

$$ [u,v]_{\mathfrak {g}'_A}-[u,v]_{\mathfrak {g}_A} =\sum _{i=1}^k \ \varepsilon _1\varepsilon _2 \cdots \varepsilon _i\phi _i $$

where $\varepsilon _i \in \mathfrak {m}$ and $\{\phi _1,\ldots ,\phi _k\}$ a family of independent skew symmetric bilinear maps on $\mathbb {K}^n\times \mathbb {K}^n$ with values in $\mathbb {K}^n$. In particular $\phi _1 \in Z^2(\mathfrak {g},\mathfrak {g})$ and if $\mathfrak {g}'_A$ is isomorphic to $\mathfrak {g}_A$ this map belongs to $B^2(\mathfrak {g},\mathfrak {g})$. We deduce that the deformations of $\mathfrak {g}$ are parameterized by $H^2(\mathfrak {g},\mathfrak {g}).$ In the following, we are going to determine the current Lie algebras which are rigid.

Remark

In [4, 6], we find a similar definition of deformations, but without the hypothesis concerning the valuation. We assume that $A$ is a commutative algebra over the field $\mathbb {K}$ which admits an augmentation $\varepsilon : A \rightarrow \mathbb {K}$. This says that $\varepsilon$ is a $\mathbb {K}$-algebra homomorphism, e.g. $\varepsilon (1_A) = 1$. The ideal $\mathfrak {m}_\varepsilon := Ker (\varepsilon )$ is a maximal ideal of $A$ (Let us note that any maximal ideal of $A$ gives an augmentation). Let us consider a Lie algebra $\mathfrak {g}$ over $\mathbb {K}$, $\varepsilon$ a fixed augmentation of $A$, and $\mathfrak {m}= Ker ( \varepsilon )$ the associated maximal ideal. A global deformation $\lambda$ of $\mathfrak {g}$ with base $(A,\mathfrak {m})$, is a Lie $A$-algebra structure on $\mathfrak {g}\otimes A$ with Lie bracket $[., .]_\lambda$ such that for all $a, b \in A$ and $X, Y \in \mathfrak {g}$,

• 1. $[a \otimes X, b \otimes Y ]_\lambda = (ab \otimes id )[1 \otimes X, 1 \otimes Y ]_\lambda$,

• 2. $\varepsilon \otimes id ([1 \otimes X, 1 \otimes Y ]_\lambda ) = 1\otimes [X, Y ].$

2.2 The Manifold $L_{(p,q)}$

Let $\mathfrak {g}=\mathfrak {g} =\mathfrak {g}_p \otimes \fancyscript{A}_q$ be a $pq$-dimensional current $\mathbb {K}$-Lie algebra where $\mathfrak {g}_p$ is a $p$-dimensional $\mathbb {K}$-Lie algebra and $\fancyscript{A}_q$ a $q$-dimensional associative commutative $\mathbb {K}$-algebra. Let $\{ X_1 ,\ldots , X_p\}$ be a basis of $\mathfrak {g}_p$ and $\{ e_1 ,\ldots , e_q\}$ a basis of $\fancyscript{A}_q$. If we denote by $\{C_{ij}^k \}$ and $\{D_{ab}^c \}$ the structure constants of $\mathfrak {g}_p$ and $\fancyscript{A}_q$ with regards to these basis, then the Lie bracket $\mu _{\mathfrak {g}}=\mu _{\mathfrak {g}_p}\otimes \mu _{\fancyscript{A}_q}$ of $\mathfrak {g}$ where $\mu _{\mathfrak {g}_p}$ is the multiplication of $\mathfrak {g}_p$ and $\mu _{\fancyscript{A}_q}$ the multiplication of $\fancyscript{A}_q$, satisfy:

$$\mu _{\mathfrak {g}}(X_i \otimes e_a, X_j \otimes e_b)=\sum _{k,c} C_{ij}^k D_{ab}^c X_k \otimes e_c,$$

and the structure constants of $\mathfrak {g}$ with respect to the basis $\{ X_i \otimes e_a \}_{i=1,\ldots ,p; \ a=1,\ldots ,q}$ are $\{ C_{ij}^k D_{ab}^c \}.$ Thus, the Jacobi relations are written as

$$ \sum _{l,r} C_{ij}^l C_{lk}^s D_{ab}^r D_{rc}^t +C_{jk}^l C_{li}^s D_{bc}^r D_{ra}^t +C_{ki}^l C_{lj}^s D_{ca}^r D_{rb}^t=0 $$

for any $(s,t)$ in $\left\{ \{1,\ldots ,p \} \times \{1,\ldots ,q \} \right\} .$ These polynomial relations define a structure of algebraic variety denoted by $L_{(p,q)}$ and embedded in the vector space whose coordinates are the structure constants $\{C_{ij}^k D_{ab}^c \}$. It is a closed subvariety of $L_{pq}$. Let $G(p,q)$ be the algebraic group $G(p,q)=GL(p) \times GL(q).$ This group acts naturally on $L_{(p,q)}$ by

$$ (f , \ g).(\mu _{\mathfrak {g}_p}\otimes \mu _{\fancyscript{A}_q})(X\otimes a,Y \otimes b)= f^{-1}(\mu _{\mathfrak {g}_p}(f(X),f(Y)))\otimes g^{-1}(\mu _{\fancyscript{A}_q}(g( a),g( b))). $$

We denote by $\fancyscript{O}_{p,q}(\mathfrak {g}_p \otimes \fancyscript{A}_q )$ the orbit in $L_{(p,q)}$ of $\mu _{\mathfrak {g}}$ corresponding to this action.

Thus, there are two types of deformations:

• The deformations of $\mathfrak {g}$ in the manifold $L_{pq}$. These deformations are parameterized by the second Chevalley-Eilenberg cohomology space $H_C^2(\mathfrak {g},\mathfrak {g})$.

• The deformations of $\mathfrak {g}$ in the manifold $L_{(p,q)}$. They are parameterized by the space $H^2_C(\mathfrak {g}_p,\mathfrak {g}_p) \oplus H^2_H(\fancyscript{A}_q,\fancyscript{A}_q)$ where $H^2_H(\fancyscript{A}_q,\fancyscript{A}_q)$ is the Hochschild cohomology of the associative commutative algebra $\fancyscript{A}_q$ [13, 14, 17].

Definition 2.3

The Lie algebra $\mathfrak {g}_p \otimes \fancyscript{A}_q$ is rigid in $L_{(p,q)}$ if the orbit $\fancyscript{O}_{p,q}(\mu _{\mathfrak {g}})$ is open (in the Zariski sense). It is rigid if the orbit $\fancyscript{O}(\mu _{\mathfrak {g}})$ related to the action of $GL(pq)$ in $L_{pq}$ is open.

It is clear that the rigidity implies the rigidity in $L_{(p,q)}$.

Proposition 2.1

A current Lie algebra $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ is rigid in $L_{(p,q)}$ if and only if $\mathfrak {g}_p$ is rigid in $L_{p}$ and $\fancyscript{A}_q$ is rigid in $\fancyscript{C}om(q)$, the variety of $q$-dimensional associative commutative $\mathbb {K}$-algebras.

In fact, if $\mathfrak {g}_p$ (respectively $\fancyscript{A}_q$) is not rigid in $L_{p}$ (respectively in $\fancyscript{C}om(q)$), then we can find a non isomorphic deformation of $\mathfrak {g}_p$ (respectively $\fancyscript{A}_q$), this gives a non isomorphic deformation of $\mathfrak {g}$. For the general notion of associative rigid algebras see [11].

The main part of this work is to describe rigid current algebras which are rigid (in $L_{pq}$, that is, rigid in the variety of $pq$-dimensional Lie algebras).

Example $p=2, q=2$ $(\mathbb {K}=\mathbb {C}).$ There is, up to isomorphism, only one $2$-dimensional rigid Lie algebra. It is defined by $[X_1,X_2]=X_2$. There is only one $2$-dimensional associative commutative algebra. It is given by $e_1^2=e_1, e_2^2=e_2,e_1e_2=0$ and corresponds to the semi-simple algebra $A_1^2=M_1(\mathbb {K})\times M_1(\mathbb {K})$ where $M_n(\mathbb {K})$ is the algebra of $n$-matrices on $\mathbb {K}.$ The Lie algebra $\mathfrak {g}_2\otimes A_1^2$ is rigid in $L_{(2,2)}$. This algebra is isomorphic to $\mathfrak {g}_2 \times \mathfrak {g}_2.$ It is also rigid in $L_4.$

2.3 Structure of Rigid Current Lie Algebras

Recall that a finite dimensional rigid $\mathbb {K}$-Lie algebra $\mathfrak {g}$ is algebraic (that is, isomorphic to a Lie algebra of an algebraic Lie group) and then admits the decomposition $\mathfrak {g}=\mathfrak {s} \oplus \mathfrak {t} \oplus \mathfrak {n}$ where $\mathfrak {t} \oplus \mathfrak {n}$ is the radical of $\mathfrak {g}$, $\mathfrak {t}$ is a maximal abelian subalgebra whose adjoint operators $ad\, X , X \in \mathfrak {t},$ are semi-simple and $\mathfrak {n}$ is the nilradical [5, 7]. If $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ is rigid, then $\mathfrak {g}_p$ is rigid in $L_p$. If $\mathfrak {g}_p$ is solvable, then so is $\mathfrak {g}$ and we have

$$\mathfrak {g}_p=\mathfrak {t}_p \oplus \mathfrak {n}_p \ \text{ and } \ \ \mathfrak {g}=\mathfrak {t} \oplus \mathfrak {n}.$$

Since $\mathfrak {n}_p \otimes \fancyscript{A}_q$ is a nilpotent ideal of $\mathfrak {g},$ $\mathfrak {n}_p \otimes \fancyscript{A}_p \subset \mathfrak {n}.$

Lemma 2.1

If $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ is rigid, then $\fancyscript{A}_q$ has a non zero idempotent.

Remark

If $\fancyscript{A}_q$ is a nilalgebra, then $\mathfrak {g}$ is nilpotent. In fact if $X \in \mathfrak {g}_p$ and $a \in \fancyscript{A}_q$, we have $[ad(X \otimes a)]^m=(ad\, X)^m \otimes (L_a)^m$ where $L_a:\fancyscript{A}_q \rightarrow \fancyscript{A}_q$ is the left multiplication by $a$. Since $\fancyscript{A}_q$ is a nilalgebra, every element is nilpotent and there exits $m_0$ such that $(L_a)^{m_0}=0.$ Thus $ad ( X\otimes a)$ is a nilpotent operator for any $X$ and $a$. This implies that $\mathfrak {g}$ is nilpotent (this doesn’t imply that $\mathfrak {g}_p$ is nilpotent). Let $f$ be a derivation of $\mathfrak {g}_p.$ Then $f\otimes Id$ is a derivation of $\mathfrak {g}.$ Since $\mathfrak {g}_p$ is rigid, we can find a inner non trivial derivation $ad \, X$ which is diagonal. In this case $ad \, X \otimes Id$ is a non trivial diagonal derivation of $\mathfrak {g}$. By hypothesis $\mathfrak {g}$ is rigid. But any rigid nilpotent Lie algebra is characteristically nilpotent [9], that is, every derivation is nilpotent. We have a contradiction and $\fancyscript{A}_p$ can not be a nilalgebra. Since it is finite dimensional, it admits a non zero idempotent.

Proposition 2.2

If $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ is rigid then $\fancyscript{A}_q$ is an associative commutative rigid unitary algebra in $\fancyscript{C}om(q)$.

Remark

Let $e \ne 0$ be in $\fancyscript{A}_q$ and satisfying $e^2=e.$ The associated Pierce decomposition

$$ \fancyscript{A}_q= \fancyscript{A}^{00}_q \oplus \fancyscript{A}^{10}_q \oplus \fancyscript{A}^{01}_q \oplus \fancyscript{A}^{11}_q $$

where

$$ \fancyscript{A}^{ij}_q=\{ x \in \fancyscript{A}_q \ \text{ such } \text{ that } \ \ e\cdot x=i x,x \cdot e=jx \} $$

reduces to $\fancyscript{A}_q=\fancyscript{A}^{11}_q \oplus \fancyscript{A}^{00}_q$ because $\fancyscript{A}_q$ is commutative and we have $\fancyscript{A}^{11}_q \cdot \fancyscript{A}^{00}_q =\{ 0 \}.$ Thus $\fancyscript{A}_q$ is a direct sum of two commutative algebras. Since $\fancyscript{A}_q$ is rigid, the algebras $\fancyscript{A}^{11}_q$ and $\fancyscript{A}^{00}_q$ are also rigid. The subalgebra $\fancyscript{A}^{11}_q$ is unitary ($e$ is the unit element). From the previous lemma $\fancyscript{A}^{00}_q$ has an idempotent and admits a decomposition

$$ \fancyscript{A}^{00}_q=\fancyscript{A}^{0011}_q \oplus \fancyscript{A}^{0000}_q $$

with $\fancyscript{A}^{0011}_q \ne \{ 0 \}.$ By induction we deduce that

$$ \fancyscript{A}_q =\fancyscript{A}^{1}_q \oplus \ldots \oplus \fancyscript{A}^{p}_q $$

with $\fancyscript{A}^{i}_q$ with unit $e_i$ and $\{ e_1,\ldots ,e_p \}$ is a system of pairwise orthogonal idempotents. Then $e_1 + \cdots +e_p$ is a unit of $\fancyscript{A}_q .$

Theorem 2.1

Let $\mathfrak {g}_p$ be a rigid Lie algebra with solvable non nilpotent radical such that $Z(\mathfrak {g}_p)=\{ 0 \}.$ Then $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ is rigid if and only if $\fancyscript{A}_q=M_1^q(\mathbb {K})$ is given by

$$ e_i^2=e_i \ , i=1,\ldots ,q \ \ \text{ and } \ \ e_i \cdot e_j=0 \ \text{ if } \ i \ne j. $$

Proof Since $\fancyscript{A}_q$ is unitary, the radical of $\mathfrak {g}$ solvable and non nilpotent. Moreover $Z(\mathfrak {g}_p)=\{ 0 \}$ implies that $Z(\mathfrak {g})=\{ 0 \}.$ In fact if $U= \sum _{j,a} \alpha _{ja} X_j \otimes x_a$ is in the center of $\mathfrak {g}$, then $[U,X \otimes 1]=0$ for each $X \in \mathfrak {g}_p.$ Thus

$$ \sum \alpha _{j,a}[X_j ,X] \otimes x_a=0. $$

We have $[\sum _j \alpha _{ja}X_j,X]=0$ for each $a$ and $X.$ So $\sum _j \alpha _{ja}X_j \in Z(\mathfrak {g}_p)$ for any $a.$ Therefore $\alpha _{ja}=0$ for any $a$ and $U=0.$

Consequently, $\mathfrak {g}$ is a rigid Lie algebra with trivial center whose radical is non nilpotent. This implies that all derivations are inner. Let $f$ be a non trivial derivation of $\fancyscript{A}_q$. Since $\fancyscript{A}_q$ is commutative, it is necessarily an outer derivation. Then $Id \otimes f$ is a derivation of $\mathfrak {g}$ and satisfies $(Id \otimes f)(X \otimes 1)=X \otimes f(1)=0$ because $f(1 \cdot 1)=2f(1)=f(1)=0.$ Suppose that $Id \otimes f \in Int(\mathfrak {g})$, that is $Id \otimes f=ad(\sum \alpha _{ij} X_i \otimes x_j).$ Thus $(Id \otimes f)(X \otimes 1)=\sum \alpha _{ij}[X_i,X]\otimes x_j=0$ which implies $\sum \alpha _{ij}[X_i,X]=0$ for any $j$ and $X.$ So $\sum \alpha _{ij}X_i \in Z(\mathfrak {g}_p)$ for any $j.$ Since the center is trivial, then $\sum \alpha _{ij} X_j=0$ for any $j$ and $Id \otimes f \notin Int(\mathfrak {g}).$ There is a contradicion. Therefore $\fancyscript{A}_q$ is such that any external derivation is trivial. We deduce that $\fancyscript{A}_q=M_1^q(\mathbb {K}).$

Remark

• 1. The current Lie algebra $\mathfrak {g}_p \otimes M_1^q(\mathbb {K})$ is isomorphic to $\mathfrak {g}_p \times \cdots \times \mathfrak {g}_p$ with $q$ factors. If $\mathfrak {g}$ is a rigid current algebra with $Z(\mathfrak {g}_p)$ trivial, then it is isomorphic to $\mathfrak {g}_p \times \cdots \times \mathfrak {g}_p$.

• 2. In the theorem, we have a hypothesis concerning the center of $\mathfrak {g}_p$. This hypothesis is probably superfluous. In fact, since the orbit in $L_n$ of a rigid $n$-dimensional Lie algebra is Zariski open, the Zariski closure of this orbit is an algebraic component of $L_n$. This assures that, for a fixed dimension, there exist only a finite number of non isomorphic rigid Lie algebras. But, for all the known examples of rigid Lie algebras, the center is trivial. We can naturally conjecture that any finite dimensional complex rigid Lie algebra has a trivial center.

3 Cohomology and Deformations

The Chevalley-Eilenberg cohomology of current Lie algebras was computed in [18] for the degrees $1$ and $2$. It is shown that the algebra of derivations of $\mathfrak {g}=\mathfrak {g}_p\otimes \fancyscript{A}_q$ is equal to

$$ \begin{array}{ll} \fancyscript{D}er(\mathfrak {g})=&{} \fancyscript{D}er(\mathfrak {g}_p)\otimes \fancyscript{A}_q \oplus Hom_{\mathfrak {g}_p} (\mathfrak {g}_p,\mathfrak {g}_p)\otimes \fancyscript{D}er (\fancyscript{A}_q)\\ &{} \oplus Hom(\mathfrak {g}_p/_{[\mathfrak {g}_p,\mathfrak {g}_p]},Z(\mathfrak {g}_p))]\otimes \frac{End(\fancyscript{A}_q)}{\fancyscript{A}_q+\fancyscript{D}er \fancyscript{A}_q} \end{array} $$

and the first space of cohomology $H^1(\mathfrak {g},\mathfrak {g})$ is

$$ \begin{array}{ll} H^1(\mathfrak {g},\mathfrak {g})=&{} H^1(\mathfrak {g}_p,\mathfrak {g}_p)\otimes \fancyscript{A}_q \oplus Hom_{\mathfrak {g}_p} (\mathfrak {g}_p,\mathfrak {g}_p)\otimes \fancyscript{D}er (\fancyscript{A}_q)\\ &{}\oplus Hom(\mathfrak {g}_p/_{[\mathfrak {g}_p,\mathfrak {g}_p]},Z(\mathfrak {g}_p))]\otimes \frac{Hom(\fancyscript{A}_q,\fancyscript{A}_q)}{\fancyscript{A}_q+\fancyscript{D}er \fancyscript{A}_q}. \end{array} $$

Assume that $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ is a rigid current Lie algebra. Then $\mathfrak {g}_p$ is rigid. Assume also that $Z(\mathfrak {g}_p)=0.$ Then

$$ H^1(\mathfrak {g},\mathfrak {g})=H^1(\mathfrak {g}_p,\mathfrak {g}_p)\otimes \fancyscript{A}_q \oplus Hom_{\mathfrak {g}_p} (\mathfrak {g}_p,\mathfrak {g}_p)\otimes \fancyscript{D}er (\fancyscript{A}_q). $$

If $\mathfrak {g}_p$ is a rigid Lie algebra with non nilpotent radical (we do not know examples of rigid Lie algebras with a nilpotent radical), any derivation of $\mathfrak {g}_p$ is inner. This implies that $H^1(\mathfrak {g}_p,\mathfrak {g}_p)=0$ and $H^1(\mathfrak {g},\mathfrak {g})= Hom_{\mathfrak {g}_p} (\mathfrak {g}_p,\mathfrak {g}_p)\otimes \fancyscript{D}er (\fancyscript{A}_q).$

Proposition 3.1

Let $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ be a current Lie algebra such that $\mathfrak {g}_p$ is rigid with trivial center and a non nilpotent radical. Then $H^1(\mathfrak {g},\mathfrak {g})=0$ if and only if $\fancyscript{D}er(\fancyscript{A}_q)=\{ 0\}.$

Example Consider $\fancyscript{A}_q=M_1^q(\mathbb {K})$. Let $\{ e_i \}$ be a basis of $\fancyscript{A}_q$ satisfying $e_i^2=e_i, e_ie_j=0.$ Let $f$ be in $\fancyscript{D}er(\fancyscript{A}_q).$ We have

$$f(e_i^2)=f(e_i)=2e_if(e_i).$$

This induces $f(e_i)=0$ and finally $f=0.$

A Chevalley-Eilenberg $2$-cochain of $\mathfrak {g}=\mathfrak {g}_p \otimes \fancyscript{A}_q$ decomposes as a finite sum of bilinear forms of type:

$$ \varphi =\psi _1\otimes \varphi _2+\varphi _3\otimes \psi _4 $$

with $\psi _1 \in \fancyscript{C}^2 (\mathfrak {g}_p,\mathfrak {g}_p)$ , $\varphi _2 \in \fancyscript{S}^2(\mathfrak {g}_p,\mathfrak {g}_p)$ and $\varphi _3 \in \fancyscript{S}^2 (\mathfrak {g}_p,\mathfrak {g}_p)$, $\psi _4 \in \fancyscript{C}^2 (\fancyscript{A}_q,\fancyscript{A}_q) ,$ where $\fancyscript{C}^2(\mathfrak {g}_p,\mathfrak {g}_p)$ denotes the space of Chevalley-Eilenberg $2$-cochains of $\mathfrak {g}_p$, $\fancyscript{S}^2(\mathfrak {g}_p,\mathfrak {g}_p)$ the space of symmetric bilinear maps with values in $\mathfrak {g}_p$ and $\fancyscript{C}^2 (\fancyscript{A}_q,\fancyscript{A}_q)$ the space of $2$-cochains of the Harrison cohomology of $\fancyscript{A}_q.$ We deduce using this decomposition that $H^2(\mathfrak {g},\mathfrak {g})=(H^2)' \oplus (H^2)''.$ The first space is computed in ([18], proposition 3.1). We find

$$ (H^2)'= H^2(\mathfrak {g}_p,\mathfrak {g}_p) \otimes \fancyscript{A}_q \oplus \fancyscript{B}(\mathfrak {g}_p,\mathfrak {g}_p) \otimes \frac{H^2_H(\fancyscript{A}_q,\fancyscript{A}_q)}{\fancyscript{P}_+(\fancyscript{A}_q,\fancyscript{A}_q)} \oplus \chi (\mathfrak {g}_p,\mathfrak {g}_p) \otimes \frac{\fancyscript{A}(\fancyscript{A}_q,\fancyscript{A}_q)}{\fancyscript{P}_+(\fancyscript{A}_q,\fancyscript{A}_q)} $$

(see [18] for notations). But the second space was just computed when $\mathfrak {g}_p$ is abelian.

For example assume that we have a primitive infinitesimal deformation of $\mu _1\otimes \mu _2,$ that is, $\mu _1\otimes \mu _2 +\epsilon (\psi _1\otimes \varphi _2+\varphi _3\otimes \psi _4).$ The linear part of the Jacobi identity gives the expression of a $2$-cocycle of Chevalley-Eilenberg cohomology of $\mu _1\otimes \mu _2$. We find:

$$\begin{aligned} \delta _{\mu _1}&{\otimes \mu _2}(\psi _1\otimes \varphi _2+\varphi _3\otimes \psi _4)(X_1,X_2,X_3,a_1,a_2,a_3)\\&=\varSigma \mu _1(\psi _1(X_1,X_2),X_3)\otimes \mu _2(\varphi _2(a_1,a_2),a_3)\\&\quad +\varSigma \mu _1(\varphi _3(X_1,X_2),X_3)\otimes \mu _2(\psi _4(a_1,a_2),a_3)\\&\quad +\varSigma \psi _1(\mu _1(X_1,X_2),X_3)\otimes \varphi _2(\mu _2(a_1,a_2),a_3)\\&\quad +\varSigma \varphi _3(\mu _1(X_1,X_2),X_3)\otimes \psi _4(\mu _2(a_1,a_2),a_3)=0 \end{aligned}$$

for any $X_1,X_2,X_3 \in \mathfrak {g}_p$ and $a_1,a_2,a_3 \in \fancyscript{A}_q,$ and the sum is taken on the cyclic permutations of $(1,2,3)$. We deduce

Proposition 3.2

If $\fancyscript{A}_q$ is unitary then $\psi _1 \in Z^2(\mathfrak {g}_p,\mathfrak {g}_p)$ as soon as $\varphi _2(1,1) \ne 0$.

If $X_1=X_2=X_3$, the above identity reduce to:

$$\mu _1(\varphi _3(X_1,X_1),X_1)\otimes \varSigma \mu _2(\psi _4(a_1,a_2),a_3)=0.$$

Proposition 3.3

If there exits $X \in \mathfrak {g}_p$ such that $\mu _1(\varphi _3(X_1,X_1),X_1) \ne 0$ then

$$\mu _2\bullet \psi _4=0$$

with

$$ \mu _2\bullet \psi _4(a_1,a_2,a_3)=\varSigma \mu _2(\psi _4(a_1,a_2),a_3). $$

Note that $\psi _4$ is a $2$-cocyle for the Harrison cohomology of $\mu _2$ so $\mu _2\bullet \psi _4=\psi _4\bullet \mu _2.$

Suppose that $\mathfrak {g}$ is rigid solvable with trivial center. Then $\fancyscript{A}_q$ is unitary and $\psi _1 \in Z^2(\mathfrak {g}_p,\mathfrak {g}_p)$ as soon as $\varphi _2(1,1) \ne 0.$

4 Application: Associative Commutative Real Rigid Algebras

4.1 Real Rigid Lie Algebras

The study of the rigid real Lie algebras was recently initiated in [2]. Let us point out the principal results. An external torus of derivations of $\mathfrak {n}$ is an abelian subalgebra $\mathfrak {t}$ of $\mathcal{{D}}er(\mathfrak {n})$, the Lie algebra of derivations of $\mathfrak {n}$, such as the elements are semi-simple. This means that complex derivations $f \otimes Id \in \mathfrak {t} \otimes \mathbb {C}$ are simultaneously diagonalizable. If $\mathfrak {t}$ is a maximal (with respect to inclusion) external torus of $\mathfrak {n}$ then $\mathfrak {t} \otimes \mathbb {C}$ is a maximal external torus of $\mathfrak {n} \otimes \mathbb {C}$. From a result of Malcev (see e.g. [10]), all the maximal tori of $\mathfrak {n} \otimes \mathbb {C}$ are conjugated with respect to $\text {Aut}(\mathfrak {n} \otimes \mathbb {C})$ so they have the same dimension (thus a maximal exterior torus is sometimes called a Malcev torus). It is the same for the maximal tori $\mathfrak {t}$ of $\mathfrak {n}$. This dimension is called the rank of $\mathfrak {n}$. But contrary to the complex case, all the tori are not conjugated with respect to the group of automorphisms.

Definition 4.1

Let $\mathfrak {n}$ be a finite dimensional real nilpotent Lie algebra. We call a toroidal index of $\mathfrak {n}$ the number of conjugation classes of a maximal external torus with respect to the group of automorphisms $\text {Aut}_{\mathbb {R}}(\mathfrak {n})$ of $\mathfrak {n}$.

Example The toroidal index of the real abelian Lie algebra $\mathfrak {a}_n$ of dimension $n$ is equal to $[n/2]+1$ where $[p]$ is the integer part of the rational number $p$. In fact, let $\{X_1,\ldots ,X_n\}$ be a basis of $\mathfrak {a}_n$. Let us denote by $f_i$ the derivation defined by $f_i(X_j)=\delta _i ^j X_j$ and by $f_{1,2p}$ the derivation given by

$$ \left\{ \begin{array}{l} f_{1,2p}(X_{2p-1})=X_{2p}, \\ f_{1,2p}(X_{2p})=X_{2p-1}.\\ \end{array} \right. $$

Up to conjugation, the maximal exterior tori are the subalgebras of $gl(n,\mathbb {R})$ generated by

$$ \begin{array}{ll} {\mathfrak {t}}_1=&{}\mathbb {R}\{f_1,\ldots ,f_n\} \\ {\mathfrak {t}}_{2}=&{} \mathbb {R}\{f_{1,2},f_1+f_2,f_3\ldots ,f_n\} \\ {\mathfrak {t}}_{3}=&{} \mathbb {R}\{f_{1,2},f_1+f_2,f_{1,4},f_3+f_4,f_5,\ldots ,f_n\} \\ \ldots \\ {\mathfrak {t}}_{n}=&{} \mathbb {R}\{f_{1,2},f_1+f_2,f_{1,4},f_3+f_4,\ldots ,f_{1,n},f_{n-1}+f_n\} \\ \end{array} $$

if $n$ is even, if not the last relation is replaced by

$$ {\mathfrak {t}}_{n}= \mathbb {R}\{f_{1,2},f_1+f_2,f_{1,4},f_3+f_4,\ldots ,f_{1,n-1},f_{n-2}+f_{n-1},f_n\}. $$

4.2 Real Rigid Associative Commutative Algebras

Let $\mathfrak {r}_2$ be the real nonabelian $2$-dimensional Lie algebra. There exists a basis $\{X_1,X_2\}$ with regard to which the bracket is given by $[X_1,X_2]=X_2.$ Let $\fancyscript{A}_n$ be a $n$-dimensional real rigid commutative associative algebra. Its complexification is isomorphic to $M_1^n(\mathbb {C})$. Thus the real current Lie algebra $\mathfrak {g}=\mathfrak {r}_2 \otimes \fancyscript{A}_n$ is rigid. We deduce that its complexification is rigid and isomorphic to $\mathfrak {r}_2^n$. These remarks allow to write the following decomposition:

$$ \mathfrak {g}=\mathfrak {r}_2 \otimes \fancyscript{A}_n=\mathfrak {t}_n \oplus \mathfrak {a}_n $$

where $\mathfrak {a}_n$ is the $n$-dimensional abelian Lie algebra. We can deduce from this the structure of $\fancyscript{A}_n$. In fact, if $\{Y_1,\ldots ,Y_n\}$ is a basis of $\mathfrak {t}_n$ corresponding to the derivations $f_{1,2},f_1+f_2,\ldots ,f_{1,2s},f_{2s-1}+f_{2s},f_{2s+1},\ldots ,f_n\}$ described in the previous section, the Lie bracket of $\mathfrak {g}$ satisfies

$$ \left\{ \begin{array}{l} \,[Y_1,X_1]=-X_2, \ [Y_1,X_2]=X_1, \\ \,[Y_2,X_1]=X_1, \ [Y_2,X_2]=X_2, \\ \ldots \\ \,[Y_{2s-1},X_{2s-1}]=-X_{2s}, \ [Y_{2s-1},X_{2s}]=X_{2s-1}, \\ \,[Y_{2s},X_{2s-1}]=X_{2s-1}, \ [Y_{2s},X_{2s}]=X_{2s}, \\ \,[Y_i,X_i]=X_i, \ i=2s+1,\ldots ,n. \end{array} \right. $$

Let $\{e_1,\ldots ,e_n\}$ be a basis of $\fancyscript{A}_n$ such that the isomorphism between $\mathfrak {r}_2 \otimes \fancyscript{A}_n$ and $\mathfrak {t}_n \oplus \mathfrak {a}_n$ is given by $U_1 \otimes e_i=Y_i$ and $X_{2i}=U_2 \otimes e_{2i-1}$, $X_{2i-1}=U_2 \otimes e_{2i}$ for $i=1,\ldots ,s$ and $X_j=U_2 \otimes e_j$ for $j=2s+1,..,n.$ The rigid associative algebra $\fancyscript{A}_n$ is thus defined by

$$ \left\{ \begin{array}{l} e_{2i-1}^2=e_{2i-1}, \ \ i=1,\ldots ,s;\\ e_{2i-1}e_{2i}=e_{2i }e_{2i-1}=e_{2i}, \ \ i=1,\ldots ,s;\\ e_{2i}^2=-e_{2i-1}, \ \ i=1,\ldots ,s;\\ e_j^2=e_j, \ \ j=2s+1,\ldots ,n. \end{array} \right. $$

Proposition 4.1

Let $\fancyscript{A}_n$ be a $n$-dimensional real rigid associative algebra. There exists an integer $s$, $1\le s\le n$ and a basis $\{e_1,\ldots ,e_n\}$ of $\fancyscript{A}_n$ such that the multiplication of $\fancyscript{A}_n$ is given by

$$ \left\{ \begin{array}{l} e_{2i-1}^2=e_{2i-1}, \ \ i=1,\ldots ,s;\\ e_{2i-1}e_{2i}=e_{2i }e_{2i-1}=e_{2i}, \ \ i=1,\ldots ,s;\\ e_{2i}^2=-e_{2i-1}, \ \ i=1,\ldots ,s;\\ e_j^2=e_j, \ \ j=2s+1,\ldots ,n. \end{array} \right. $$