Capacity Allocation Model of Air Cargo with the Differences in Transport Time

Abstract

Capacity allocation is the core of air cargo revenue management. Nearly all the existing studies are conducted under the assumption of the equal transport time, overlooking the differences in transport time for the cargo in the actual operating processes. In fact, according to the foregoing differences, air cargo can be divided into urgent and general cargo. Urgent cargo should be transport as soon as possible, while the general one can be delayed within a certain time limit. In the light of the actual cargo loading demand, this paper proposes a dynamic programming model for air cargo capacity allocation so as to get the maximum revenue of a single-leg flight. Then simulation validates the effectiveness of the strategy suggested in this paper.

1 Introduction

In recent years, with the rapid development of international economic and trade, the air cargo industry with its unparalleled advantages maintains a tremendous growth, which has become a new profit growth point for the air transport enterprises. Some well-known airlines such as Lufthansa, KLM Royal Dutch Airlines, have implemented the methods of cargo revenue management by phases and obtained a freight revenue growth of 2–5 %. However, the development of air cargo in China is later than the developed countries, the methods for better management and scientific decision have not been found for the revenue management strategies including capacity optimization, inventory control and pricing. Therefore, some problems have been raised in front of unprecedented development for air cargo. And some of them are determined by the industry particularities. Currently, air cargo is conducted mainly depend on cargo planes and passenger planes, and the transportation by passenger planes has accounted for a great majority of the air cargo business. The retentions of customers’ goods are frequently happened due to the limited capacity of the planes, the obvious uncertainty and variability of the market demands as well as the lack of scientific management methods. This inability of on time transportation not only brings negative influence to the customer relationship but also makes the expensive capacity resources wasted. Owing to the diversity and the different transportation requirements of the goods along with considerable uncertainties in the weight and volume of them, the scientific inventory control for the space has become one of the important issues in the decision-making process for the air cargo industry.

2 Literature Review

The air cargo revenue management can be defined as selling the right cargo products (cargo space and cargo services) to the right customers at the right time for the right price. Due to the perishability of the space in the cargo planes and passenger planes, the strategies of air cargo revenue management can be divided into dynamic pricing, inventory control and overbooking. But the cargo space has multidimensional natures such as weight, volume, shape and size and its capacity is easily affected by the weather, the weight of fuel and passenger baggage, so air cargo revenue management cannot be simply substituted by passenger revenue management.

The research on air cargo revenue management starts from the late 1900s. Kasilingam [5] detailedly analyzes the difference between air cargo revenue management and passenger revenue management for the first time. The author gives the four steps for the analysis of air cargo revenue management, proposes the implementation model, and points out that the strategies for space control is one of the research areas with great potential in the future. The representative research on air cargo revenue management after Kasilingam [5] are as follows: Kasilingam [6] supposes that the capacity, distribution of occurrence rate, overbooking cost and idle cost are given, and develops a simplified one-dimensional model. By minimizing of the sum of the two costs, the author finally obtains the optimal overbooking level. Luo et al. [8] extend the one-dimensional model of Kasilingam to a two-dimensional model for air cargo overbooking. They believe that both the size and weight of the goods can be overbooked. By applying the methods of rectangular approximation and marginal analysis, the authors give out the mathematical model with the objective of minimizing the cost, and obtain the approximate overbooking level. The effectiveness of their model is also verified in practice. On the basis of Luo et al., Moussawi and Cakanyildirim [9] create an overbooking model in order to maximize the revenue, and calculate the approximate optimal level of overbooking. From the viewpoint of the agents, Chew et al. [2] determine the short-term space booking strategies with the lowest transportation costs by establishing of the stochastic dynamic programming model. The model considers the delayed transportation of the goods. But the assumption is only limited to one dimension. And it does not take the revenue of the air cargo companies into account. Rivi Sandhu [11] tries to solve the network transportation problems. The author develops the inventory control model for static planning which considers the revenues both from the passengers and the goods. In this model, the volumes of the goods are simplified to containers with fixed sizes. The author approximately calculates the maximum expected total revenue of the flights across the whole network by the method of Bender dimension reduction. Amaruchkul et al. [1] establish the Markov decision model to discuss the inventory control model for single-leg air cargo revenue management while the volumes of goods are stochastic and multidimensional. When study on the strategies for inventory control in air cargo revenue management, Andreea Popescu et al. [10] divide the goods into small goods (mail, parcels) and bulk goods. They use the linear programming model and dynamic programming model to solve the problem for those two types of goods respectively. The simulation shows that the results of the proposed method are superior to the traditional first-come first transported and static planning methods. Levin and Nediak [7] divide the agents into contract clients and protocol clients. They build a dynamic programming model for inventory and verify the validity of it by a numeral example. Wang and Kao [13] decide the capacity for air cargo overbooking by fuzzy systems with the consideration of the uncertainty environment Huang and Chang [4] consider the randomness of the goods’ volume and weight. They present the algorithm to solve the problems of air cargo revenue management based on the estimates of expected revenue function for the dynamic pricing model. Han et al. [3] think about the capacity allocation problems for the single-leg air cargo revenue management. They assume that the volume, weight and yield of the goods are all stochastic, and the booking process has the Markov property. The decision of whether accept the booking requests or not follows the bid control model. Particularly, as to one piece of goods, it will not be accepted unless its revenue is greater than the opportunity cost. The optimal decision is determined by the maximizing the reward function in the Markov chain.

To sum up, except Chew et al. [2], the current research on air cargo revenue management all under the assumption of first come first transported and the permit of goods delay, overlooking the differences in transport time for the cargo in the actual operating processes. In fact, air cargo can be divided into urgent and general cargo. Urgent cargo should be transport as soon as possible, while the general one can be delayed within a certain time limit. Consequently, associated with the actual operation for the loading of the air cargo, this paper develops a dynamic programming model with the consideration of the differences in transport time for the cargo and the two-dimensional characteristics of the space. The proposed model can provide the inventory control strategies for the single-leg air cargo revenue management. The objective of this paper is to better serve the practice of air cargo revenue management.

3 Modeling

• 1. Problem Statement

Usually the air cargo companies start to receive cargo booking from the day before the scheduled departure time of the flight (that is to say, 48 h in advance). During the peak seasons, the supply of the flight is often unable to meet the demand. Faced with this situation, the traditional practices of the control center is to receive and transport the cargo in accordance with the arrival sequence of it. When the capacity is not enough, the cargo which arrives late will be refused. Throughout the booking process, the arrival of the cargo can be generally divided into two types: urgent cargo and general cargo. The urgent cargo has a higher transportation price and a stricter timeliness requirement for transportation. Delay is usually disallowed for the urgent cargo. On the contrary, general cargo has a lower transportation price and a less strict timeliness requirement for transportation. Usually, an appropriate delay is allowed if the cargo can arrive at the destination within a certain period of time. Although the traditional strategy perfectly ensure that all the received cargo can be transported and the customer satisfaction is maintained at a high level, it ignores the differences in the transportation between the urgent and general cargo: on the one hand, it provides the urgent service to the general cargo with a lower transportation price, which increases an unnecessary cost of service; on the other hand, the later arrived cargo with a higher transportation price will be refused because the received general cargo has occupied the space, which results in the loss of potential benefits. Therefore, in this paper, we mainly focus on minimizing the loss of potential benefits of air cargo, without reducing the quality of service and affecting the perception of customer service. The objective of this study is to maximize the total revenue of a single flight and minimize the punishment cost of delay transportation by reasonable acceptance and transportation of cargo when the loading capacity is constant.

• 2. Modeling

Consider the peak season for transportation (that is to say, the demand is greater than supply), the maximum loading weight and volume of flight $A$ are $k_w$ and $k_v$ respectively. The booking time $t$ is discrete and $0 \le t \le T$. $t=0$ indicates the start of booking. $t = T$ expresses the end of booking which means the plane takes off with full cargo. Describe the problem using dynamic programming: split the intervals into small ones and assume that at each stage $t$, at most one booking requirement will arrive. Suppose there are two types of the booking requirements: $i=1,2,\; i=1$ indicates the urgent cargo and $i=2$ indicates the general cargo. The unit price and penalty cost of requirement $i$ are $h_i$ and $r_i$ respectively. Usually, the urgent cargo cannot be delayed while the appropriate delay for the general cargo is allowed, so $h_1 \rightarrow +\infty ,\; h_2=r_2$. The transportation delay of the received urgent cargo will bring significant loss to the reputation of the air company, so $h_1 \rightarrow +\infty$. The transportation delay of the general cargo is equivalent to the return of the received order. And the order will be received again in the nest flight as compensation. So for the current flight, the revenue of receiving orders turns to be 0, $h_2 = r_2$. In the booking period, the weight $w_i$ and volume $v_i$ of the requirement $i$ are the random variables which respectively follow the distribution of $\phi _i$ and $\psi _i$, and the expected income for requirement $i$ is $r_iw_i$. $p_{it}$ states the arrival probability of requirement $i$ during the time period $t$, and $p_{0t} = 1-\sum _{i=1,2}p_{it}$ expresses the probability of zero booking requirement during the time period $t$.

When $t < T$, the value function $U_t(x_w,x_v)$ represents the maximum expected revenue from time $t$ to the end of booking when the remaining available weight is $x_w$ and the remaining volume is $x_v$. Then the Bellman equation of $U_t(x_w,x_v)$ is:

$$\begin{aligned} U_t(x_w,x_v)=&~\sum \limits _{i=1,2}p_{it}\max \{U_{t+1}(x_w- w_{it},x_v-v_{it}) +r_iw_{it},U_{t+1}(x_w,x_v)\}\nonumber \\&~+p_{0t}U_{t+1}(x_w,x_v). \end{aligned}$$

(54.1)

In this equation, $w_{it}$ and $v_{it}$ indicate the weight and volume of the cargo during arriving period $t$. And they are also the random variables which respectively follow the distribution of $\phi _i$ and $\psi _i$. The economic significance of Eq. (54.1) can be explained as follows: the maximum expected revenue from time $t$ to the end of booking when the remaining available weight is $x_w$ and the remaining volume is $x_v$ should be equal to the sum of the maximum expected revenue when the cargo may arrive at time $t$ and the maximum expected revenue when the cargo may not arrive at time $t$.

When $t = T$ and after the end of the booking, $w_{i{j_i}}$ and $v_{i{j_i}}~(j_i=1,2,\cdots ,J_i)$ indicate weight and size of the $j_i$th cargo of type $i$ which has been accepted. $J_i$ is the total amount of the received cargo of type $i$. $C(J_i)$ is the penalty cost of transportation by plane. Then the optimization problem of cargo loading can be expressed by the following programming model:

$$\begin{aligned}&\min C(J_i)=\sum \limits _{i=1,2}\sum \limits _{j_i=1}^{J_i}h_iw_{i{j_i}}(1-a_{i{j_i}}), \end{aligned}$$

(54.2)

Subject to

$$\begin{aligned}&\sum \limits _{i=1,2}\sum \limits _{j_i=1}^{J_i}w_{i{j_i}}a_{i{j_i}} \le {k_{w}}, \end{aligned}$$

(54.3)

$$\begin{aligned}&\sum \limits _{i=1,2}\sum \limits _{j_i=1}^{J_i}v_{i{j_i}}a_{i{j_i}} \le {k_{v}}, \end{aligned}$$

(54.4)

$$\begin{aligned}&a_{i{j_i}} \in \{ 0,1 \},\quad \forall i=1,2,\;j_i=1,2,\cdots ,J_i. \end{aligned}$$

(54.5)

The objective Eq. (54.2) minimizes the total penalty cost after loading. Equation (54.3) ensure that the total weights of the cargo do not exceed the maximum weight of the plane. Equation (54.4) guarantee that the total volumes of the cargo do not exceed the maximum volume of the plane. In Eq. (54.5), if the decision variable $a_{ij_i}=1$, it means the $j_i$th cargo of type $i$ is loaded on the plane, otherwise $a_{ij_i}=0$. Obviously, Eq. (54.1) satisfies the boundary conditions:

$$\begin{aligned}&{\text {When}}\;x_w = 0\;or\;x_v = 0, U_t(x_w,x_v) = -E[C(J_i)],\end{aligned}$$

(54.6)

$$\begin{aligned}&{\text {When}}\; t=T,U_T(x_w,x_v)=-E[C(J_i)]. \end{aligned}$$

(54.7)

Equation (54.6) means that if the received cargo has reached even exceeded the maximum available weight of the plane, the cargo booking will no longer be accepted in principle. And only the loading problem of the received cargo will be considered. Equation (54.7) represents that when the booking is over and the plane prepares to take off, the cargo booking will no longer be accepted and only the loading problem of the received cargo will be considered.

• 3. Optimal Conditions

$\varDelta {U_{it}}(x_w,x_v) = U_t(x_w,x_v)-U_t(x_w-w_{it},x_v-v_{it})$ represents the opportunity cost of accepting the cargo with type $i$ whose weight and volume are $w_{it}$ and $v_{it}$ when the remaining available weight and volume are $x_w$ and $x_v$ in time $t$. Then Eq. (54.1) can be rewritten as:

$$\begin{aligned} U_t(x_w,x_v)=&\!\sum \limits _{i=1,2}p_{it}\max \{\!U_{t\!+\!1}(x_w\!-\!w_{it}, x_v\!-\!v_{it}) \!+\!r_iw_{it},U_{t\!+\!1}(x_w,x_v)\}\!+\!p_{0t}U_{t+1}(x_w,x_v)\nonumber \\ =&\sum \limits _{i=1,2}p_{it}\max \{r_iw_{it}-\varDelta {U_{i,t+1}}(x_w,x_v),0\}+U_{t+1}(x_w,x_v). \end{aligned}$$

(54.8)

Apparently, the optimal boundary conditions when accepting the cargo of type $i$ are: $r_iw_{it} \ge \varDelta U_{i,t+1}(x_w,x_v)$. That is, when and only when the expected revenue of accepting the cargo with type $i$ is greater than or equal to its opportunity cost, the cargo will be accepted; otherwise, it will not be accepted.

4 Model Solving

We use the idea of dynamic programming dimension reduction (dynamic programming decomposition-Talluri and Van Ryzin [12]) to approximately get the optimal value of the value function $U_t(x_w,x_v), 1\ll t\ll T$. Dynamic programming dimension reduction is the commonly used approximate method for solving the problems of network air transportation. The basic idea of it is to calculate the opportunity cost according to tension of the remaining available resources on each leg of the entire network, allocate the number of tickets with different levels to each leg (fare proration) and finally break down the network problem into $N$ sub-problems in each single leg. In accordance with this idea, this paper first converts the single-leg two-dimension air cargo problem into two-leg one-dimension network problem. Then we approximately calculate the unit opportunity cost of the remaining available weight and volume of the plane in time $t$ by dynamic programming dimension reduction. After that, we will get the expected opportunity cost of the cargo with type $i$ which arrives at time $t$. Finally, we will decide whether to accept the cargo or not. The specific steps are as follows:

Fig. 54.1

Convert the air cargo problem

• 1. Convert the air cargo problem

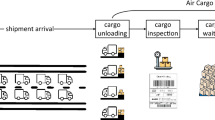
As is shown in Fig. 54.1, the weight and size of the space for cargo planes are defined as leg $(A, B)$ and leg $(B, C)$ which the passenger planes pass through. The maximum available capacity (the maximum weight capacity) of leg $(A, B)$ is $k_w$. And the maximum available capacity (the maximum volume capacity) of leg $(B, C)$ is $k_v$. The unit prices of the urgent and general cargo which have arrived are equivalent to two types of the ticket prices for passengers. The actual volume and weight for a single piece of cargo is equivalent to the quantities of tickets for leg $(A, B)$ and leg $(B, C)$ which are purchased at one time. As a result, the single-leg two-dimension air cargo problem is converted into a two-leg one-dimension network passenger problem. The notations are re-defined as follows:

 

$t$ :

time for booking, $0 \le t \le T. ~ t = 0$ expresses the start of booking. $t = T$ indicates the booking is over and the plane takes off.

$k_w,k_v$ :

maximum available capacity for leg $(A, B)$ and leg $(B, C)$.

$i$ :

$i=1$ indicates the ticket of urgent class, and $i=2$ indicates the ticket of general class.

$p_{it}$ :

states the arrival probability of demand for the $i$th class ticket in time period $t$, and $p_{0t}=1-\sum _{i=1,2}p_{it}$ is the probability of zero booking demand in time period $t$.

$r_i$ :

unit price of the $i$th class ticket.

$h_i$ :

unit penalty cost for the delayed transportation which is paid to the passengers who have bought the $i$th class tickets. $h_1 \gg r_1>h_2=r_2,$ $\text {suppose} ~ h_1=M(M \rightarrow \infty )$.

$w_{it},v_{it}$ :

the booking number of the $i$th class tickets on leg $(A, B)$ and leg $(B, C)$ in time period $t$, and they are also the random variables which respectively follow the distribution of $\phi _i$ and $\psi _i$.

 

• 2. Find the initial approximate solution for the unit opportunity costs of the loading weight and volume on the plane

After the converting step 1, the unit opportunity costs of the loading weight and volume on the plane are equivalent to the unit opportunity costs of resources on leg $(A, B)$ and leg $(B, C)$. In accordance with the assumption, at each stage $t$, at most one booking demand will arrive. Therefore, the number of expected booking for the $i$th class tickets during the whole booking period is: $n_i = \sum _{t=0}^{T_1}p_{it}.$ At the same time, the booking numbers of the $i$th class tickets on leg $(A, B)$ and leg $(B, C)$ in each time period are $w_{it}$ and $v_{it}$. They are the random variables which respectively follow the distribution of $\phi _i$ and $\psi _i$. According to the assumption, the distributions do not change over time, so $E[w_{it}] = E[w_i] = \int _{0}^{+\infty }\phi _i(l)ldl, E[v_{it}] = E[v_i] = \int _{0}^{+\infty }\psi _i(l)ldl.$ Here, $\phi _i$ and $\psi _i$ are the density functions which respectively correspond to the distribution function $\phi _i$ and $\psi _i$: $\phi _i(d) = \int _{-\infty }^{d}\phi _i(l)ldl, \psi _i(d) = \int _{-\infty }^{d}\psi _i(l)ldl$. Apparently, according to the problem, when $l \le 0, \phi _i(l) = \psi _i(l) = 0$.

The multi-objective stochastic programming model with expected value which is used to solve the loading problem above is developed here:

$$\begin{aligned}&\max E\{ \sum \limits _{i=1,2}f_i(x_i)-C(x_i), -C(x_i)\},\nonumber \\&\text {s.t.}\left\{ \begin{array}{l} x_i \ge 0, ~i=1,2,\\ E[f_i(x_i)] = r_i \cdot \min \{x_i,n_i\} \cdot E[x_i].\\ \end{array} \right. \end{aligned}$$

(54.9)

Substituting the above Eqs. (54.2)–(54.5) into Eq. (54.9), it can be converted as:

$$\begin{aligned}&\max d_1^{+}-d_1^{-}-d_2^{+}+d_2^{-}, \end{aligned}$$

(54.10)

Subject to

$$\begin{aligned}&\sum \limits _{i=1,2}\{r_i\cdot \min \{x_i,n_i\}\cdot E[w_i]-\sum \limits _{j_i=1}^{\min \{x_i,n_i\}}h_iE[w_i](1-a_{ij_i})\} -d_1^{+}+d_1^{-} = 0,\end{aligned}$$

(54.11)

$$\begin{aligned}&\sum \limits _{j_i=1}{\min \{x_i,n_i\}}h_iE[w_i](1-a_ij_i)-d_2^{+}+d_2^{-} = 0,\end{aligned}$$

(54.12)

$$\begin{aligned}&\sum \limits _{i=1,2}\sum \limits _{j_i=1}{\min \{x_i,n_i\}}E[w_i]a_ij_i \le k_w,\end{aligned}$$

(54.13)

$$\begin{aligned}&\sum \limits _{i=1,2}\sum \limits _{j_i=1}{\min \{x_i,n_i\}}E[v_i]a_ij_i \le k_v,\end{aligned}$$

(54.14)

$$\begin{aligned}&x_i,d_i^{\pm } \ge 0, a_ij_i \in \{0,1\},\quad \forall i=1,2,\; j_i= 1,2 \cdots ,x_i. \end{aligned}$$

(54.15)

The objective Eq. (54.10) maximizes the total expected net revenue after the acceptance of booking and transportation while minimizing the penalty cost for the delayed transportation. Equation (54.13) indicate that the expected transportation demands on leg $(A, B)$ do not exceed its maximum transportation capacity. Equation (54.14) ensure that the expected transportation demands on leg $(B, C)$ do not exceed its maximum transportation capacity. In Eq. (54.15), the decision variable $x_i$ represents the total number of the accepted bookings for the $i$th class tickets. $a_{ij_i}=1$ means the booking of the $j_i$th tickets with type $i$ is accepted, otherwise $a_{ij_i }=0$.

To make the model easier to solve, set $a_i$ as the total number of orders for the $i$th class tickets which have been transported, then the model above can be simplified to:

$$\begin{aligned}&\max d_1^{+}-d_1^{-}-d_2^{+}+d_2^{-}, \end{aligned}$$

(54.16)

Subject to

$$\begin{aligned}&\sum \limits _{i=1,2}E[w_i]\cdot \{r_ix_i-h_i(x_i-a_i)\}-d_1^{+}+d_1^{-} = 0,\end{aligned}$$

(54.17)

$$\begin{aligned}&\sum \limits _{i=1,2}h_iE[w_i](x_i-a_i)-d_2^{+}+d_2^{-} = 0 ,\end{aligned}$$

(54.18)

$$\begin{aligned}&\sum \limits _{i=1,2}E[w_i]a_i \le k_w,\end{aligned}$$

(54.19)

$$\begin{aligned}&\sum \limits _{i=1,2}E[v_i]a_i \le k_v,\end{aligned}$$

(54.20)

$$\begin{aligned}&a_i-x_i \le 0,\end{aligned}$$

(54.21)

$$\begin{aligned}&x_i-n_i \le 0, \end{aligned}$$

(54.22)

$$\begin{aligned}&a_i,x_i,d_i^{\pm } \ge 0 \quad \forall i=1,2. \end{aligned}$$

(54.23)

Equations (54.16)–(54.20) correspond to Eqs. (54.10)–(54.14) which have not be simplified. The meaning of the decision variable $x_i$ is unchanged. Equation (54.21) ensure that the total number of the transported tickets does not exceed the total number of the received orders. Equation (54.22) states that the expected total number of the accepted orders does not exceed the expected total number of the received orders.

It is very easy to get the optimal solution of the model $\pi _w,\pi _v$ and the optimal solution of the corresponding dual problem $\pi _w,\pi _v$. That is, the initial approximate solution of unit opportunity cost for the resources (the loading weight and volume on the plane) on leg $(A, B)$ and leg $(B, C)$. Particularly, from Eqs. (54.2), (54.12) and (54.18), it is easy to know:

$$\begin{aligned} E[C(J_i)] = E[C(x_i)] = \sum \limits _{i=1,2}h_iE[w_i](x_i-a_i) = d_2^{+}-d_2^{-}. \end{aligned}$$

(54.24)

Therefore, substituting the optimal solution of decision variables $x_i,a_i$ and $x_i,a_i$ in the simplified stochastic programming model into Eq. (54.24), the approximate expected penalty cost for transportation $E[C(J_i)]$ can be obtained.

• 3. Calculate the prorated cargo rate for all types of cargo

The prorated cargo rate for all types of cargo is the prorated resource rate for all types of tickets on the legs. Set $pcr_ij$ as the prorated resource rate for the $i$th class $(i=1,2)$ of tickets on the leg $j~ (j=w,v)$, then: $pcr_{ij} = \max \{0,r_i-\pi _l | _{l \in \{w,v\},l \ne j}\}$. Its economic explanation is: when accepting the $i$th class of cargo and taking out the expected opportunity cost of the occupied weight (volume) of the plane, it is the expected revenue generated by the occupied weight (volume) of the plane. Obviously, when $pcr_{ij}$ is higher, the resources on leg $j$ are more precious as to the $i$th class of cargo.

• 4. Convert Eq. (54.1) into two one-dimension dynamic programming models

The prorated cargo rate for all types of cargo is $pcr_{ij}$. Equation (54.1) can be converted into the following two one-dimension dynamic programming models to solve:

$$\begin{aligned}&U_{wt}\!=\!\sum \limits _{i=1,2}p_{it}\max \{Uw,t\!+\!1(x_w\!-\!1) \!\,+\,\!pcr_{iw},U_{i,t\!+\!1}(x_w)\}\!\,+\,\!p_{0t}U_{w,t\!+\!1}(x_w),\end{aligned}$$

(54.25)

$$\begin{aligned}&U_{vt}=\sum \limits _{i=1,2}p_{it} \max \{Uv,t+1(x_v-1)+pcr_{iv},U_{i,t+1}(x_v)\} +p_{0t}U_{v,t+1}(x_v). \end{aligned}$$

(54.26)

Similarly, Eqs. (54.25) and (54.26) satisfy the boundary conditions: When $x_j = 0, U_{jt}(x_j) = E[C(J_i)], j=w,v,$ When $t=T, U_{jT}(x_j) = E[C(J_i)],\; j=w,v$.

• 5. Calculate the opportunity costs of the loading weight and volume on the plane

Set $\triangle U_{wt}(x_w)$ as the unit opportunity cost of the loading weight on the plane when the remaining weight is $x_w$ at time $t$, then: $\triangle U_{wt}(x_w) = U_{wt}(x_w)-U_{wt}(x_w-1)$. Similarly, set $\triangle U_{vt}(x_v)$ as the unit opportunity cost of the loading volume on the plane when the remaining volume is $x_v$ at time $t$, then: $\triangle U_{vt}(x_v) = U_{vt}(x_v)-U_{vt}(x_v-1).$

• 6. Calculate the expected opportunity costs for all types of cargo

The unit opportunity costs of the loading weight and volume on the plane are $\triangle U_{wt}(x_w)$ and $\triangle U_{vt}(x_v)$ when the remaining weight and volume are $x_w$ and $x_v$ at time $t$. Then the expected opportunity cost of the $i$th class cargo with weight $w_{it}$ and volume $v_{it}$ which arrives at time $t$ is: $EC = \triangle U_{wt} \cdot w_{it}+U_{vt} \cdot v_{it}.$ Therefore, the optimal boundary conditions for accepting the cargo are: $r_iw_{it}-EC \ge 0.$ That is, when and only when the expected revenue of accepting the cargo with type $i$ is greater than or equal to its opportunity cost, the cargo will be accepted; otherwise, it will not be accepted.

5 Simulation Example

We use the simulation example to illustrate the implementation processes of the strategies for the air cargo inventory control when considering the differences in transport time for the cargo. And the following problems are examined:

• 1. Comparing with the traditional first-come-first-transported strategy, is the strategy for the air cargo inventory control when considering the differences in transport time for the cargo better?

• 2. In the implementation process, is there a regular pattern for this inventory control strategy?

5.1 Numerical Example

Flight $A$ starts booking 48 h in advance. The maximum loading weight and volume of it are 15,000 kg and 100 ${\text {m}}^{3}$. The unit transport prices for the urgent cargo and the general cargo are 3.00 and 1.00 Yuan per kg. Usually, the urgent cargo cannot be delayed while the general cargo can be delayed, so the penalty cost of the urgent cargo is 100.00 Yuan per kg while the penalty cost of the general cargo is 1.00 Yuan per kg. In the time interval for booking, the average number of the arrived orders is 245. The urgent cargo accounts for 12 % of the orders which the general cargo accounts for 88 %. The weight and volume of the urgent cargo respectively follow the gamma distribution $\varGamma (3,16)$ and $\varGamma (3,0.0842)$. The weight and volume of the general cargo respectively follow the gamma distribution $\varGamma (4,40)$ and $\varGamma (4,0.2105)$. Suppose that in the whole time interval for booking, the arrivals of both the urgent cargo and general cargo follow Poisson distribution. So the unit opportunity cost of the loading weight and volume on the plane during the peak seasons can be obtained, which is shown in Table 54.1.

Based the data in Table 54.1, the opportunity cost of the arrived cargo can be calculated according to Step 6 in Sect. 54.4. The detailed implementation processes of the strategy for inventory control will be given later (Table 54.2).

5.2 Simulation Strategy

In this section we conduct the simulation for the whole booking processes of Flight $A$ by applying the traditional first-come-first-transported strategy and the proposed strategy (referred to as inventory control strategy) in this paper. Then the differences between the two strategies are compared. By running the simulation program in Matlab for 100 times, the results can be obtained as follows:

The average net revenue of the first-come-first-transported strategy is 16,223.84 Yuan. The average weight rate of this strategy is 99.96 % and the average volume rate is 79.72 %. The average net revenue of the inventory control strategy is 17296.32 Yuan which shows a 6.67 % increase to the first-come-first-transported strategy. The average weight rate of this strategy is 99.79 % and the average volume rate is 78.31 %, which is similar to the former strategy (Table 54.2).

Table 54.1 The numerical value of opportunity cost of weight and volume of air cargo

Table 54.2 The results of simulation

In particular, by applying the first-come-first-transported strategy, the average number of accepted tickets for the general cargo is 90.6 which accounts for 87 % of all the tickets, and the average number of accepted tickets for the urgent cargo is 13.5 which accounts for 13 %. The accepted rate is almost the same as the arrival rate. But by applying the inventory control strategy, the average number of accepted tickets for the general cargo is 90 which accounts for 79 % of all the tickets, and the average number of accepted tickets for the urgent cargo is 24 which accounts for 21 %. The accepted rate of the urgent cargo increases a lot. And 4.7 % of the general cargo is delayed.

6 Conclusion

Air cargo revenue management has gradually become an important method to enhance the competitive advantages of the air companies. This paper develops a dynamic programming model which takes the differences in transport time for the cargo into account and obtains the optimal inventory control strategy for a single leg air cargo revenue management with two types of cargo. Compared with the traditional first-come-first-transported strategy, the proposed inventory control strategy can increase the revenue from two aspects: first, when receiving the orders, the urgent cargo with higher price has a higher priority; second, when transporting the cargo, a small proportion of the general cargo should be delayed in order to ensure all the urgent cargo are transported on time and the perception of the customers are not affected. This paper only focuses on the single leg air cargo revenue management problem with two types of cargo. It is more complicated for the multi-leg problem with multiple types of cargo. In order to better meet the needs of the air cargo companies, further research should be conducted in this field.