Average Run Length Performance Approach to Determine the Best Control Chart When Process Data is Autocorrelated

Abstract

Most conventional Statistical Process Control techniques have been developed under the assumption of the independence of observations. However, due to advances in data sensing and capturing technologies, larger volumes of data are routinely being collected from individual units in manufacturing industries and therefore data autocorrelation phenomena is more likely to occur. Following this changes in manufacturing industries, many researchers have focused on the development of appropriate SPC techniques for autocorrelated data. This paper presents a methodology to be applied when the data exhibit autocorrelation and, in parallel, to evidence the strong capabilities that simulation can provide as a key tool to determine the best control chart to be used, taking into account the process’s dynamic behavior. To illustrate the proposed methodology and the important role of simulation, a numerical example with data collected from a pulp and paper industrial process is provided. A set of control charts based on the exponentially weighted moving average (EWMA) statistic was studied and the in and out-of-control average run length was chosen as performance criteria.The proposed methodology constitutes a useful tool for selecting the best control chart, taking into account the autocorrelated structure of the collected data.

1 Introduction

Traditional statistical process control assumes that consecutive observations from a process are independent. Nowadays, in industrial processes, autocorrelation has been recognized as a natural phenomenon, more likely to be present when:

• Parameters, such as temperature and pressure, are subject to small variations considering the rate at which they are measured;

• The presence of tanks and reactors inducts inertial process elements;

• Data is sequentially sampled in time and with a sampling rate that can be very high, due to high-performance measurement devices.

Chemical and pharmaceutical industries can be pointed as examples of processes where the existence of autocorrelation in data is extremely likely. Only in recent years has autocorrelation become an important issue in statistical process applications, particularly in the industrial field and, due to this fact, a large number of researchers has focused and contributed to this field of knowledge.

Data independency assumption violation is incurred when autocorrelation is present between two consecutive measurements that may cause severe deterioration of standard control chart performance, usually measured in terms of run length (RL), i.e. the number of observations required to obtain an observation outside of the control limits [6, 7].

Several authors have studied and discussed the negative effects of traditional control charts applied to processes with autocorrelated observations [1, 4, 6]. In these cases, there is a significant increase in the number of false alarms, or a considerable loss of control chart sensitivity, caused by incorrect estimation of process parameters. As a consequence, these two situations can produce, respectively: pointless searches for special causes, maybe with costly discontinuity in the production rates; and a loss of sensitivity that may undermine product reputation and discredit this powerful tool.

In order to overcome these limitations, two main approaches have emerged. The first approach uses traditional control charts for independent and identically distributed data (iid) but with suitably modified control limits to take into consideration the autocorrelation structure [4, 9]. The second approach uses time series models to fit to the observations and apply traditional control charts to the residuals from this model [1, 3].

The main goal of this article is to present a methodology that points out the main issues to be considered in both phases of control chart implementation (phase I and II) and to provide a set of guidelines when simulation is used for optimal Control Chart selection with autocorrelated data. A stationary first-order autoregressive AR(1) process was considered in the study with individual observations. As a performance criterion, it was used the average run length (ARL) and their corresponding standard deviation of the run length (SDRL). In this study, a set of widely accepted control charts applicable for monitoring the mean of autocorrelated processes were selected, namely: the residual-based chart or the special control chart (SCC) of Alwan [1] (in both phase I and II), the Exponentially Weighted Moving Average (EWMA) control chart for residuals [3], the EWMAST chart (EWMA for Stationary process) developed by Zang [9] and the MCEWMA chart (Moving-Centerline EWMA), with variable limits proposed by Montgomery and Mastrangelo [5]. Detailed simulation results are provided and suggestions are made.

2 Theoretical Background

1. EWMAST Chart

Zhang [9] proposes the EWMAST chart as being an extension of the traditional EWMA chart designed to monitor a stationary process. This chart uses the autocorrelation function to modify the control limits of the EWMA chart. The EWMA chart is defined by:

$$\begin{aligned} E_t=(1-\lambda )E_{t-1}+\lambda X_t, \end{aligned}$$

(1.1)

where $X_t$ corresponds to data under control at a time $t$, $E_0=\mu$ and the parameter $\lambda (0<\lambda <1)$ is a constant. The approximate variance, according to Zhang [9] is given by:

$$\begin{aligned} \sigma _{\text {EWMAST}}^2\approx \sigma ^2\left( \frac{\lambda }{2-\lambda }\right) \left( 1+ \sum \limits _{k=1}^M\rho _k(1-\lambda )^k(1-(1-\lambda )^{2(M-k)})\right) , \end{aligned}$$

(1.2)

where $\rho _x(k)$ is the process autocorrelation at lag $k$ and $M$ is an integral ${\ge }25$. The control limits of this chart are given by:

$$\begin{aligned} \left\{ \begin{array}{l} LSC_{\text {EWMAST}}=E_0+L^{\text {EWMAST}}\hat{\sigma }_{\text {EWMAST}}\\ \nonumber LC_{\text {EWMAST}}=E_0\\ \nonumber LSC_{\text {EWMAST}}=E_0-L^{\text {EWMAST}}\hat{\sigma }_{\text {EWMAST}},\\ \end{array}\right. \end{aligned}$$

where $L$ is usually equals to 2 or 3.

Note that when the data process are independently and identically distributed, or white noise, $\rho _x(k)=0$ when $k\ne 0$. In this case, the EWMAST chart and the traditional EWMA are de same.

Zhang [9] shows that for stationary AR(1) processes the EWMAST chart performs better than the EWMA residual chart and, that’s an obvious advance for using EWMAST chart is that is no need to build a time series model for stationary process data.

2. MCEWMA Chart

Montgomery and Mastrangelo [5] developed a new chart that brings together all the information on the MM chart, also developed by these authors, in a single one called MCEWMA chart. This chart allows, simultaneously, analyzes the evolution of the process behavior and detect special causes of variation.

Defining the variable $E_t$ by Eq. (1.1) and considering that $\hat{X}_t=E_{t-1}$, the residual $e_t$, at time $t$ is given by: $e_t=X_t-\hat{X}_t=X_t-E_{t-1}$. The control limits and centerline of the MCEWMA chart vary over time and, are defined at time $t$, by:

$$\begin{aligned} \left\{ \begin{array}{l} LSC_t=E_{t-1}+3\sigma _{ep}\\ LC_t=E_{t-1}\\ LSC_t=E_{t-1}-3\sigma _{ep},\\ \end{array}\right. \end{aligned}$$

where the standard deviation of forecast errors, $\sigma _{ep}$, can be estimated by any of the following equations:

$$\begin{aligned} \hat{\sigma }_{ep}=\frac{1}{N}\sum \limits _{t=1}^Ne_t^2,\; (\hat{\sigma }_{ep})_t\cong 1.25\,\text {DAM}_t,\;(\hat{\sigma }_{ep})_t=(1-\alpha )(\hat{\sigma }_{ep})_{t-1}+\alpha |e_t|, \end{aligned}$$

with $\text {DAM}_t$ corresponding to the mean absolute deviation, given by:

$$\begin{aligned} \text {DAM}_t=(1-\alpha )\text {DAM}_{t-1}+\alpha |e_t|, \end{aligned}$$

(1.3)

and $0<\alpha \le 1$.

The MCEWMA chart presents a poor sensitivity in detecting small or moderate changes in the process mean. Taking into account this limitation, Montgomery and Mastrangelo [5] proposed the use of “tracking signal”, which together with the MCEWMA chart help increase its sensitivity in detecting trends. The smoothed-error tracking signal, $Ts(t)$, can be obtained by: $Ts(t)=\left| \frac{Q_t}{\text {DAM}_t}\right|$, where $Q_t=\alpha e_t+(1-\alpha ) Q_{t-1}$ and $\text {DAM}_t$ defined by (1.3), with $0.05 \le \alpha \le 0.15$ as a smoothing constant. When the $Ts(t)$ exceeds a constant $Ks$, typically with values between 0.2 and 0.5, means that the forecast error is biased, indicating a change in the underlying process.

3. EWMA Chart with Residuals

The traditional EWMA chart may also be built using residuals, by using residual values instead of the data collected from the process. The use of these charts significantly increases detection of minor to moderate changes of the expected residual value and its variance $\sigma _e^2$ and, consequently changes in process parameters. The statistic used in the EWMA of residuals chart, to monitor the process mean at time $t$ is given by: $\text {EWMA}_t=(1-\lambda )\text {EWMA}_{t-1}+\lambda e_t$ with $\text {EWMA}_0=0$ and $\theta =1-\lambda$.

The control limits are simply given by: $\pm L^{\text {EWMA}_{res}}\sigma _{\text {EWMA}_{res}}$, where the variance of residual EWMA statistics is:

$$\begin{aligned} \sigma _{\text {EWMA}_{res}}^2\approx \sigma _e^2\left( \frac{\lambda }{2-\lambda }\right) . \end{aligned}$$

(1.4)

3 Methodology

In Fig. 1.1 the proposed methodology is presented, providing a basis for control chart implementation guidance when the assumption of data independence is violated. The methodology, in general, does not differ significantly from the approach that is generally used when the data are independent, but there are important aspects to consider, including the treatment of special variation causes that may arise in Phase I, the correct selection of a set of control charts and the important role that simulation can play in identifying the best control chart to be used in Phase II.

Fig. 1.1

Methodology for phase I and II

1. Phase I:Process Parameter Estimation

The evaluation of process stability and subsequent estimation of its parameters are the main objectives underlying the Phase I. However, it is necessary to verify that the assumptions underlying its implementation are satisfied (independence and normality of data). The verification of the first assumption can be ensured by the interpretation of the sample ACF (autocorrelation function) and the sample PACF (partial autocorrelation function) of the residuals. If there is significant autocorrelation in the data, it is implicit that the second assumption is valid, since the residuals obtained from a well adjusted ARIMA model should be normally distributed with zero mean and constant variance. After fitting an appropriate time series model, a residual-based control chart should be used. The existence of assignable causes indicates the presence of special causes of variation and requires a different treatment that does not pass by mere identification and elimination of those special causes, as if data were uncorrelated. Since autocorrelated data is characterized by having time-oriented observations, when an assignable cause is detected in phase I, the value $y_t$, in that instance, should be replaced by their expected value at time $t$.

The calculation of expected values can be done by applying an outlier’s detection model [2]. After achieving process stability, the final step consists on parameter estimation: residual standard deviation, process mean and process standard deviation.

2. Phase II: Process Monitoring

After evaluating process stability, process monitoring will take place. The first step comprises the identification of a set of candidate control charts. This selection may include control charts with modified control limits (1st approach) and/or control charts with residuals obtained from a time series model (2nd approach). To help with the selection, some guidelines can be found in Montomery [6], Zhang [9], and Sheu and Lu [8]. The choice of a suitable control chart depends, in a large way, on the type of shifts $(\delta )$ in mean and/or standard deviation or changes in ARIMA’s model parameters that are to be detected. The last step to be fulfilled in phase II comprises a comparison of the control chart’s performance through collecting ARL out-of-control $(\text {ARL}_{OC})$ and correspondent SDRL, when the process is subject to shifts/changes in parameters (mean, standard deviation or ARIMA model parameters). Once more, simulation reveals to be a valuable and indispensable tool in achieving this milestone, i.e., defining the optimum control chart to be used in monitoring phase.

4 Case Study

The case study refers to a pulp and paper process, where individual paper pulp viscosity measurements were collected from the bottom of a 100 m high digester. This type of process is characterized as being continuous and highly dynamic. For phase I, a sample of 300 viscosity measurements were obtained, collected every four hours and analyzed in the laboratory. Moreover, this sample represents a period of 50 production days, which is also representative in what respects to process dynamic behavior. For phase II, a sample size of 200 viscosity measurements were collected at the same conditions, corresponding to a period of 33 production days.

1. General

According to phase I showed in Fig. 1.1, underlying control chart assumption verification should be compulsory, especially when data is provided from a continuous and high dynamic process. Nowadays, several commonly available software packages (${\text {Statistica}}^\circledR$, ${\text {Matlab}}^\circledR$, ${\text {Minitab}}^\circledR$) allow a fairly expeditiously assumption check. The present study adopts the use of ${\text {Statistica}}^\circledR$ software package in order to obtain the sample ACF and sample PACF, with the 300 viscosity measurements, both represented in Fig. 1.2.

Fig. 1.2

Sample partial autocorrelation function (PACF) for viscosity

Graphic interpretation clearly shows that data follows an autoregressive first order model, AR(1), evidenced by slow ACF peak decline and existence of only one significant PACF peak.

The time series model that better adjusts to data was obtained with an autoregressive parameter $\phi$ equal to 0.561 (standard error of $\phi$ equal to 0.0528). Process mean obtained from viscosity measurements was $\mu _y=1076.45$, with $\sigma _y=47.923$ (process standard deviation) and $\sigma _s=39.677$ (residual standard deviation).

Since the first-order autor regressive residuals, $\varepsilon _t$, are assumed to be independent and identically distributed (iid) with mean zero and $\sigma _s$ constant, the first residual control chart can be established, considering an ARLIC $= 370$. For this $\text {ARL}_{IC}$ the control limits are given by $\pm 3\times \sigma _s$, taking a numerical value of $\pm 119.0$. For the residual moving range (MR) chart the upper control limit is given by $3\times MR_s/1.128$, with centerline equal to $MR_s$. The numerical values for upper control limit and centerline are 146.2 and 44.7, respectively. The lower control limit is equal to zero.

The residual control charts, $\varepsilon _t-MR_s$, were constructed and the existences of five possible assignable causes were identified (values outside the control limits). According to the methodology in Fig. 1.1, those possible assignable causes cannot simply be eliminated, requiring their replacement with the corresponding expected values. The iterative outlier’s detection model was applied and the corresponding expected value for each outlier was determined and replaced on the original data set. A new data set, ytnew with the same length, is obtained as well as new estimates for process viscosity mean $(\mu _y^{\text {new}}=1{,}074.0)$ and corresponding standard deviation $(\sigma _y^{\text {new}}=44.9)$. The new adjusted time series model is given by:

$$\begin{aligned} y_t^{\text {new}}=0.579y_{t-1}^{\text {new}}+\varepsilon _t, \end{aligned}$$

(1.5)

with standard error of autoregressive parameter, $\sigma _s^{\text {new}}$, equal to 0.0512 and residual standard deviation, $\sigma _y^{\text {new}}$, equal to 36.0. Comparing the new results with the previous ones, there is a slight increase in the autoregressive parameter (with decrease in standard error), followed by an adjustment in the process mean, reducing both the process and residual standard deviations, as expected. Based on the Eq. (1.5) model and in its parameters, new control limits were determined for both control charts: residuals and moving ranges. The numerical values obtained were $\pm 108.0$ for residual control chart, 132.7 and 40.6 for upper and centerline of MR chart, respectively.

2. Phase II

In the present study four control charts were identified as being good candidates, namely MCEWMA with tracking signal, $Ts$, and EWMAST charts, included in the 1st approach; residual control chart (SCC) and residual EWMA chart, considering the 2nd approach.

The methodology and formulas used to construct the first two charts follows the original references, namely Montgomery and Mastrangelo [5] for MCEWMA and Zang [9] for EWMAST. Those three control charts, based on EWMA statistics, were modeled in ${\text {MatLab}}^\circledR$’s software, using Eq. (1.5) to obtain the autoregressive first order model, where errors are independent and identically distributed with mean zero and standard deviation of 36.0. The chart parameters were obtained by simulating data sets of 4,000 values, repeated 10,000 times. For EWMA of residuals and EWMAST, we considered the same smoothing constant $(\theta )$, equal to 0.2. The in-control ARL was fixed on 370, establishing a common performance comparison platform between all candidate control charts. The estimates of control chart parameters are shown in Table 1.1. Mean-square errors are presented in parenthesis in front of each related parameter.

Table 1.1 Estimates of control charts parameters obtained by simulation for the numerical example

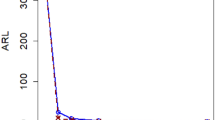
Once control limits for all control charts are established, a competitive analysis was performed by considering the different types of changes that may occur in a process such as mean shifts and disturbances in model parameters. The simulation conditions were the same as in the previous study. The simulation results for the four control charts are presented in Table 1.2 and their corresponding ARL’s and SDRL’s for the mean shifts were determined. The parameter is the size of the mean shift, measured in terms of the standard deviation (new mean = $\mu +\delta \sigma$) and with 0.5 increments.

Table 1.2 ARL’s and SDRL (in parentheses) for SCC, EWMAres, EWMAST and MCEWMA charts

Six changes with 5 % interval in autoregressive parameter $(\phi =0.597)$ were considered in what respects to model parameter disturbances (illustrated in Fig. 1.3).

Fig. 1.3

Sensitive analysis on changes to autoregressive parameter, $\phi$

Both sensitivity analysis methods evidence that EWMAres and EWMAST charts are the best performers in the autoregressive process in the study. Moreover, both present a similar behavior. As expected, SCC and the MCEWMA charts show poor sensitivity when detecting small to moderate shifts in mean, although they exhibit robustness in the presence of model parameter disturbances (Fig. 1.3). In contrast, EWMAres and EWMAST charts decrease their sensitivity whenever the autoregressive parameter decreases and increase their sensitivity whenever the autoregressive parameter increases.

5 Conclusion

Whenever statistical process control monitoring is to be used, great care should be taken to ensure that control chart requirements such as data independence are fulfilled. Ignoring data correlation has direct consequences regarding control chart performance deterioration (increased number of false alarms or decreased sensitivity). Through a case study, the present work evidences the key issues that should be taken into account in the presence of data autocorrelation. The role of simulation is demonstrated to be of great relevance not only to define the control limits that are able to converge on a single ARL value for all charts being used but also to obviate their comparative performance analysis. Considering process dynamic characteristics, AR(1), and taking into account the objective of detecting little to moderate disturbances in the process mean, the best choice dictates the use of EWMAST chart and EWMA residuals.