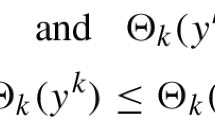A Smoothing Descent Method for Nonconvex TV$^q$-Models

Abstract

A novel class of variational models with nonconvex $\ell _q$-norm-type regularizations ($0<q<1$) is considered, which typically outperforms popular models with convex regularizations in restoring sparse images. Due to the fact that the objective function is nonconvex and non-Lipschitz, such models are very challenging from an analytical as well as numerical point of view. In this work a smoothing descent method with provable convergence properties is proposed for computing stationary points of the underlying variational problem. Numerical experiments are reported to illustrate the effectiveness of the new method.

This research was supported by the Austrian Science Fund (FWF) through START project Y305 “Interfaces and Free Boundaries” and through SFB project F3204 “Mathematical Optimization and Applications in Biomedical Sciences”.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In signal or image recovery from sparse data, it has been observed that models based on nonconvex regularization typically outperform convex ones. In particular, variational models relying on $\ell _q$ -norm-type regularization with $q\in (0,1)$ are of interest [3, 9, 16]. Due to the particular choice of $q$, the associated functional $\Vert v\Vert _q^q:=\sum _i |v_i|^q$ turns out to be nonconvex, nondifferentiable and not even locally Lipschitz continuous, and it is not a norm in the usual sense. These properties imply several challenges from an analytical as well as numerical point of view in the treatment of such problems. In fact, analytically generalized derivative concepts are challenged [7] and, thus, the first-order optimality description becomes an issue. Concerning the numerical solution of general nonsmooth minimization problems, we mention that while convex problems are rather well understood [13, 14, 19] nonconvex ones are still challenging [1, 14]. For nonconvex and non-locally-Lipschitz problems, the literature on methods based on generalized derivatives is rather scarce. However, taking the particular format of the underlying nonsmoothness into account and possibly applying tailored (vanishing) smoothing concepts, in [4, 6, 9, 12, 15, 16] solvers of the associated minimization problems in sparse signal or image recovery were developed recently. In view of these references, we note that [6, 15] requires conditions for the successful analysis which ultimately rule out the $\ell _q$-norm-type regularization, [9] needs a sparsity assumption, and [4] provides a method based on Bergman iterations and specific shrinkage-procedures, but does not include a convergence analysis. In [12] a regularized nonsmooth Newton technique is proposed which relies on some kind of local smoothing.

Motivated by smoothing methods (see for example [6]), in this work, for solving the problem (1) below, we present a descent algorithm combining a Huber-type smoothing (which we call Huberization in the sequel) with elements of the nonsmooth Newton solver from [12]. In fact, the smoothing method provides a mechanism which allows us to drive the Huber-type smoothing of the $\ell _q$-norm to zero, thus, genuinely approaching, along a subsequence, a stationary point of the $\ell _q$-norm-type problem. From the gradient of the Huberized objective, a suitable descent direction for that objective is computed by the so-called $R$-regularized nonsmooth Newton method [12]. By this procedure, a variable-metric-type scaling is applied to the steepest descent direction, thus, improving the convergence behavior of the overall method. Moreover, convergence of the algorithmic scheme towards a stationary point of (1) is established.

The rest of the paper is organized as follows. In Sect. 2, we introduce the nonconvex TV$^q$-model in finite dimension and establish the existence of a solution and the necessary optimality condition. A smoothing descent method and its convergence analysis are presented in Sect. 3. Finally, the proposed method is implemented for various image processing tasks and the results are reported in Sect. 4.

2 Nonconvex TV$^q$-Model

The nonconvex TV$^q$-model considered in this paper is formulated as follows:

$$\begin{aligned} \min _{u\in \mathbb {R}^{|\varOmega |}} f(u):=\sum _{(i,j)\in \varOmega }\left( \frac{\mu }{2}|(\nabla u)_{ij}|^2+\frac{\alpha }{q}|(\nabla u)_{ij}|^q+\frac{1}{2}|(Ku-z)_{ij}|^2\right) . \end{aligned}$$

(1)

Here, $\varOmega$ is a two-dimensional discrete image domain with $|\varOmega |$ being the number of pixels in $\varOmega$, $u\in \mathbb {R}^{|\varOmega |}$ represents the digital image which is to be reconstructed from observed data $z\in \mathbb {R}^{|\varOmega |}$, $\nabla \in \mathbb {R}^{2|\varOmega |\times |\varOmega |}$ is the gradient operator, $|(\nabla u)_{ij}|$ denotes the Euclidean norm of $(\nabla u)_{ij}$ in $\mathbb {R}^2$, $K\in \mathbb {R}^{|\varOmega |\times |\varOmega |}$ is a continuous linear operator (which, for instance, might describe blurring), and $\alpha >0,~0<q<1,~0<\mu \ll \alpha$ are user-chosen regularization parameters. In particular, if $q=1$ and $\mu =0$, then (1) corresponds to the conventional (convex) total variation (TV-) model according to Rudin, Osher and Fatemi [18].

Throughout this paper, we shall assume that

$$\begin{aligned} \mathrm{Ker}\nabla \cap \mathrm{Ker}K=\{0\}. \end{aligned}$$

(2)

Under the condition (2), the existence of a solution of (1) is guaranteed by the following theorem. Its proof can be found in [12].

Theorem 1

(Existence of Solution). There exists a global minimizer for the variational problem (1).

Note that due to the presence of the power-$q$ term the objective $f$ in (1) is not even locally Lipschitz continuous. This causes difficulties when using the Clarke generalized gradient of $f$ [7] for describing stationarity of a point $u$. However, distinguishing smooth and nonsmooth regions of $f$ through the norm of the gradient of $u$, stationary points of (1) can still be characterized by the following Euler-Lagrange-type system:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\mu \varDelta u+K^\top (Ku-z)+\alpha \nabla ^\top (|\nabla u|^{q-2}\nabla u)=0, &{} \mathrm{if~}(\nabla u)_{ij}\ne 0; \\ \nabla u=0, &{} \mathrm{otherwise}. \end{array}\right. } \end{aligned}$$

(3)

The disjunctive nature of the above system, which is due to the nonsmoothness of $f$, causes severe difficulties in the design of solution algorithms. In the following, we propose a smoothing descent method, which generates a sequence that has an accumulation point satisfying (3).

3 Smoothing Descent Method

The smoothing descent method proceeds iteratively as follows. In each iteration, the TV$^q$-objective is smoothed locally around the nondifferentiability by a Huber function which is controlled through the parameter $\gamma >0$. The Huber function reads

$$\begin{aligned} \varphi _{\gamma }(s):= {\left\{ \begin{array}{ll} \frac{1}{q}s^q-(\frac{1}{q}-\frac{1}{2})\gamma ^q, &{} \mathrm{if~} s>\gamma , \\ \frac{1}{2}\gamma ^{q-2}s^2, &{} \mathrm{if~} 0\le s\le \gamma , \end{array}\right. } \end{aligned}$$

and the associated Huberized version of (1) is given by

$$\begin{aligned} \min _{u\in \mathbb {R}^{|\varOmega |}} f_{\gamma }(u):=\sum _{(i,j)\in \varOmega }\left( \frac{\mu }{2}|(\nabla u)_{ij}|^2+\alpha \varphi _{\gamma }(|(\nabla u)_{ij}|)+\frac{1}{2}|(Ku-z)_{ij}|^2\right) . \end{aligned}$$

(4)

The corresponding Huberized Euler-Lagrange equation is

$$\begin{aligned} \nabla f_{\gamma }(u)=-\mu \varDelta u+K^\top (Ku-z)+\alpha \nabla ^\top \left( \max (|\nabla u|,\gamma )^{q-2}\nabla u\right) =0. \end{aligned}$$

(5)

Here the max-operation is understood in a componentwise sense.

Clearly, the Huberized objective $f_\gamma$ is continuously differentiable and bounded from below. Therefore, (4) can be solved by well-known standard solvers for smooth minimization problems; see, e.g., [17]. In this work, however, we utilize a tailored approach by employing the so-called R-regularized Newton scheme which was very recently proposed in [12]. In order to globalize the Newton iteration, a backtracking Armijo line search is used which is particularly tuned to the structure of the problem of interest.

For completeness, we provide a self-contained introduction of the $R$-regularized Newton method in the appendix. Essentially, this method is a generalization of the lagged-diffusivity fixed-point iteration [2, 5, 20], which alleviates diffusion nonlinearity by using information from the previous iterate. Moreover, with the aid of the infeasible Newton technique [11], a sufficient condition can be derived for obtaining a descent direction in each iteration; see Theorem 5 in the appendix. The descent property is important for the Armijo-based line search globalization; see [17] and the references therein for a general account of Armijo’s line search rule.

When (4) is solved with sufficient accuracy, for instance with respect to the residual norm $\Vert f_{\gamma ^k}(u^{k+1})\Vert$, then the Huber parameter is reduced and the current solution serves as the initial guess for solving the next Huberized problem. The resulting overall algorithmic scheme is specified next.

In our experiments, we shall always fix the parameters $\tau =0.1,~\theta =0.8,~\rho =0.1$.

Next we present the convergence analysis for the smoothing descent method. For this purpose, we take $\bar{\gamma }=0$.

Lemma 2

The sequence generated by Algorithm 3 satisfies

$$\begin{aligned} \lim _{k\rightarrow \infty } \gamma ^k=0,\quad \mathrm{and~} \liminf _{k\rightarrow \infty }\Vert \nabla f_{\gamma ^{k}}(u^{k+1})\Vert =0. \end{aligned}$$

Proof

Define the index set

$$\begin{aligned} \mathcal {K}:=\{k:\gamma ^{k+1}=\theta \gamma ^k\}. \end{aligned}$$

(7)

If $\mathcal {K}$ is finite, then there exists some $\bar{k}$ such that for all $k>\bar{k}$ we have $\gamma ^k=\gamma ^{\bar{k}}$ and $\Vert \nabla f_{\gamma ^k}(u^{k+1})\Vert \ge \rho \gamma ^{\bar{k}}$. This contradicts the fact that the first-order method with Armijo line search for solving the smooth problem $\min _u f_{\gamma ^{\bar{k}}}(u)$ generates a sequence $(u^k)$ such that $\liminf _{k\rightarrow \infty }\Vert \nabla f_{\gamma ^{\bar{k}}}(u^k)\Vert =0$, cf. [10]. Thus, $\mathcal {K}$ is infinite and $\lim _{k\rightarrow \infty }\gamma ^k=0$. Moreover, let $\mathcal {K}=(k^l)_{l=1}^\infty$ with $k^1<k^2<...$, then we have $\Vert \nabla f_{\gamma ^{k^l}}(u^{k^l+1})\Vert \le \rho \gamma ^{k^l}\rightarrow 0$ as $l\rightarrow \infty$. Hence, $\liminf _{k\rightarrow \infty }\Vert \nabla f_{\gamma ^{k}}(u^{k+1})\Vert =0$.

Theorem 3

Assume that the sequence $(u^k)$ generated by Algorithm 3 is bounded. Then there exists an accumulation point $u^*$ of $(u^k)$ such that $u^*\in \mathbb {R}^{|\varOmega |}$ satisfies the Euler-Lagrange Eq. (3).

Proof

In view of the result in Lemma 2, there exists a subsequence of $(u^k)$, say $(u^{k'})$, such that $\lim _{k'\rightarrow \infty }\Vert \nabla f_{\gamma ^{k'-1}}(u^{k'})\Vert =0$. Since $(u^{k'})$ is bounded, by compactness there exists a subsequence of $(u^{k'})$, say $(u^{k''})$, such that $(u^{k''})$ converges to some $u^*$ as $k''\rightarrow \infty$. We show that $u^*$ is a solution to (3). On the set $\{(i,j)\in \varOmega :(\nabla u^*)_{ij}=0\}$, the conclusion follows automatically. On the set $\{(i,j)\in \varOmega :(\nabla u^*)_{ij}\ne 0\}$, we have that $\max (|\nabla u^{k''}|,\gamma ^{k''-1})\rightarrow |\nabla u^*|>0$ as $k''\rightarrow \infty$. Therefore, it follows from

$$\begin{aligned} |\nabla f(u^*)|\le |\nabla f_{\gamma ^{k''-1}}(u^{k''})-\nabla f(u^*)|+|\nabla f_{\gamma ^{k''-1}}(u^{k''})|\rightarrow 0, \end{aligned}$$

(8)

that $u^*$ satisfies (3).

4 Numerical Experiments

In this section, we report on numerical results obtained by our algorithm for various tasks in TV$^q$-model based image restoration. The experiments are performed under MATLAB R2009b on a 2.66 GHz Intel Core Laptop with 4 GB RAM.

4.1 Denoising

We first test our algorithm on denoising the “Two Circles” image; see Fig. 1. This image, shown in plot (a), is degraded by zero-mean white Gaussian noise of 7 % and 14 % standard deviation respectively; see plots (b) and (c). The parameters $q=0.75,~\mu =0$ are used in this example. The restored images of two different noisy images are given in plots (d) and (e). In the following, we use the data set in (b) to investigate the numerical behavior of Algorithm 3 in details.

Robustness to Initialization. Note that our algorithm is intended to find a stationary point of the TV$^q$-model (which is often a local minimizer in our numerical experiments). It is worthwhile to check the quality of such local solutions. In Fig. 2, we implement the algorithm starting from three different choices of initializations; see the first row. The corresponding restored images are shown in the second row, which are visually indistinguishable. The energy values of the restorations in (e), (f), (g), (h) are equal to 29.4488, 29.4499, 29.4497, 29.4594, respectively, which also indicates that the restorations have small differences in quality. We remark that choosing a relatively large initial Huber parameter $\gamma ^0$ in general strengthens the robustness of the algorithm against poor initializations.

Choice of Stopping Criteria. As the stopping criteria (step 4) of Algorithm 3 depends on $\bar{\gamma }$, here we suggest an empirical way based on the histogram for choosing a proper $\bar{\gamma }$ in an a posteriori way. As we know, the TV$^q$-model tends to promote a solution with very sparse histogram. This is numerically confirmed by the histogram plots in Fig. 3. Therefore, it is reasonable to terminate the algorithm once there is no longer significant change in the sparsity pattern of the histogram. In our particular example, this suggests that $\bar{\gamma }=10^{-4}$ is a proper choice. The same choice of $\bar{\gamma }$ will be used in all the following experiments.

Miscellaneous Numerical Behavior. We further demonstrate the numerical behavior of the algorithm in Fig. 4. All data points in the plots are taken from those iterations with $k\in \mathcal {K}$; see (7) for the definition of $\mathcal {K}$. As $\gamma ^k$ decreases, our algorithm is well behaved in terms of objective value, PSNR, and residual norm. Qualitatively a similar numerical behavior is observed in the experiments that follow.

Fig. 1.

Denoising: (a) “Two Circles” image. (b) Corrupted with 7 % Gaussian noise. (c) Corrupted with 14 % Gaussian noise. (d) Restoration of (b) with $\alpha =0.05$. (e) Restoration of (c) with $\alpha =0.12$.

Fig. 2.

Initialization test: (a) Observed image as initial guess. (b) Tikhonov regularized image as initial guess. (c) Rotated image as initial guess (d) Random initial guess. (e), (f), (g), and (h) are the restorations from (a), (b), (c), and (d) respectively.

Fig. 3.

Histogram of $u^{k+1}$ ($k\in \mathcal {K}$).

Fig. 4.

Numerical behavior ($k\in \mathcal {K}$): (a) TV$^q$-energy $f(u^{k+1})$. (b) PSNR$(u^{k+1})$. (c) Residual norm $\Vert \nabla f_{\gamma ^k}(u^{k+1})\Vert$.

4.2 Deblurring

In Fig. 5 we test our algorithm in the context of deblurring the 256-by-256 phantom image depicted in plot (a). The original image is blurred by a two-dimensional truncated Gaussian kernel yielding

$$\begin{aligned} (Ku)_{ij}=\sum _{|i'|\le 3,~|j'|\le 3}\exp \left( -\frac{|i'|^2+|j'|^2}{2|\sigma _K|^2}\right) u_{i-i',j-j'}. \end{aligned}$$

Then white Gaussian noise of zero mean and 0.05 standard deviation is added to the blurred image; see (b). We apply our algorithm with $q=0.75,~\alpha =0.01,~\mu =10^{-6}$, and $u^0=z$. In plot (c) the restored image is shown. Its PSNR-value is 27.6672.

Fig. 5.

Deblurring: (a) 256-by-256 Phantom. (b) Noisy blurred image; PSNR=21.7276. (c) Restored image; PSNR=27.6672.

4.3 Compressed Sensing

We also apply our algorithm to a $k$-space compressed sensing problem; see Fig. 6. The observed data $z$ is constructed as follows: $z=SFu_{true},$ where $F$ is the 2D discrete Fourier transform and $S$ is a 20 % k-space random sampling matrix. We reconstruct the image by solving our TV$^q$-model with $q=0.75,~\alpha =0.001,~\mu =10^{-6}$, and $u^0=0$. The corresponding restored image is shown in (e). This result is compared with the reconstruction obtained from the inverse Fourier transform in (c) and the reconstruction obtained from the TV-model in (d) with $q=1,~\alpha =0.02,~\mu =10^{-6}$. In our implementation of the TV-model, $\alpha$ is chosen in order to obtain an image with optimal PSNR. The (convex) TV-model, here as well as in Sect. 4.4, is solved by a primal-dual Newton method [11] with Huber parameter $\bar{\gamma }$. We remark that many other algorithms in the literature may also work efficiently in the same context. In the left part of Table 1, we provide the comparison of the three candidate methods with respect to PSNR and CPU time. It is observed that the inverse Fourier transform is computationally cheap but only yields a poor result. The TV method takes about 6 seconds but still cannot recover the image to fine details. Our TV$^q$ method takes about double the CPU time of TV and provides an almost perfect reconstruction.

Fig. 6.

Compressed sensing: (a) 64-by-64 Phantom. (b) 20 % $k$-space random sampling. (c) Direct reconstruction by FFT. (d) Reconstruction by TV-model. (e) Reconstruction by TV$^q$-model.

4.4 Integral-Geometry Tomography

In Fig. 7, we apply our algorithm to integral-geometry tomography. The given data $z$ in (b), also known as the sinogram, is constructed by taking the 2D Radon transform of the underlying image every 15 degrees (out of 180 degrees). The matrix $K$ in this example is a discrete Radon transform of size 1235-by-4096. We utilize our TV$^q$-model with $q=0.75,~\alpha =0.001,~\mu =10^{-6}$, and $u^0=0$. The restoration is shown in plot (e). This result clearly is superior to the one shown in plot (c), which is obtained by filtered backprojection, and the one shown in plot (d), which is obtained from the TV-model with $q=1,~\alpha =0.02, \mu =10^{-6}$. In our implementation of the TV-model, $\alpha$ is chosen in order to obtain an image with optimal PSNR. In the right part of Table 1, we again compare the three candidate methods with respect to PSNR and CPU time. Similar to the compression sensing example, the TV$^q$ method costs more CPU time than the other two methods (but still less than double the CPU time of the TV method) but yields an almost perfect reconstruction.

Fig. 7.

Integral-geometry tomography: (a) 64-by-64 Phantom. (b) Sinogram. (c) Reconstruction by filtered backprojection. (d) Reconstruction by TV-model. (e) Reconstruction by TV$^q$-model.

4.5 Reconstruction of Multi-coil MRI Raw Data

We now extend the methodology to magnetic resonance imaging (MRI), by considering the following model:

$$\begin{aligned} \min _{u\in \mathbb {R}^{|\varOmega |}} \frac{1}{2}\sum _{l=1}^{L}\Vert K_lu-z_l\Vert ^2+\sum _{(i,j)\in \varOmega }\frac{\alpha _g}{q}|(\nabla u)_{ij}|^{q} +\sum _{(i',j')\in \Xi }\frac{\alpha _w}{q}|(W u)_{i'j'}|^{q}, \end{aligned}$$

(9)

with $K_l:=PF(\sigma _lu)$. Here $\alpha _g$ and $\alpha _w$ are two positive parameters, $L$ is the number of coils of the MRI machine, $(z_l)$ denote the raw data collected by each coil, $(\sigma _l)$ are the given (or precomputed) coil sensitivities, $F$ is the two-dimensional discrete Fourier transform, and $P$ represents some given radial projection operator in the k-space. Moreover, $W:\mathbb {R}^{|\varOmega |}\rightarrow \mathbb {R}^{|\Xi |}$ is a user-chosen transform, typically a 2D discrete wavelet transform, and $\Xi$ denotes the wavelet transformed domain.

Note that in addition to the TV$^q$ regularization, we include the $\ell ^q$-norm of wavelet coefficients in the regularization in order to allow the reconstruction to be richer than patchwise constant images. Nevertheless, our algorithm presented in this paper can be extended without agonizing pain to the problem (9).

Indeed, as a straightforward extension of Theorem 1, the solution of (9) exists provided that $\mathrm{Ker}\nabla \cap \mathrm{Ker}W\cap (\cap _{l=1}^L\mathrm{Ker}K_l)=\{0\}.$ The Euler-Lagrange equation for (9) appears as

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha _g\nabla ^\top p_g+\alpha _wW^\top p_w+\sum \nolimits _{l=1}^LK_l^\top (K_lu-z_l)=0, \\ (p_g)_{ij}=|(\nabla u)_{ij}|^{q-2}(\nabla u)_{ij}, &{}\!\!\!\!\!\!\!\! \mathrm{if~}(i,j)\in \varOmega \wedge (\nabla u)_{ij}\ne 0,\\ (p_w)_{i'j'}=|(Wu)_{(i',j')}|^{q-2}(Wu)_{i'j'}, &{} \!\!\!\!\!\!\!\! \mathrm{if~}(i',j')\in \Xi \wedge (Wu)_{i'j'}\ne 0. \end{array}\right. } \end{aligned}$$

The associated Huberized problem can be analogously formulated as

$$\begin{aligned} \min _{u\in \mathbb {R}^{|\varOmega |}} \frac{1}{2}\sum _{l=1}^{L}\Vert K_lu-z_l\Vert ^2+\alpha _g\sum _{(i,j)\in \varOmega }\varphi _{\gamma }(|(\nabla u)_{ij}|) +\alpha _w\sum _{(i',j')\in \Xi }\varphi _{\gamma }(|(W u)_{i'j'}|), \end{aligned}$$

and the corresponding Huberized Euler-Lagrange equation is given by

$$\begin{aligned} \alpha _g\nabla ^\top \! (\max (|\nabla u|,\gamma )^{q-2}\nabla u)+\alpha _w W^\top \! (\max (|Wu|,\gamma )^{q-2}Wu)+\sum _{l=1}^LK_l^\top \! (K_lu-z_l)=0. \end{aligned}$$

We shall not go into further details but remark that the $R$-regularized method in the appendix can be used to solve the above smooth problem by treating the gradient term and the wavelet term independently. Thus, Algorithm 3 can be implemented.

Table 1. Comparison with respect to PSNR and CPU time (in seconds).

In this experiment, the MRI data are collected from four coils, i.e. $L=4$. We choose $q=0.75,~\alpha _g=10^{-5},~\alpha _w=2\times 10^{-5},$ and $W$ to be the 4th-order Daubechies wavelet transform [8]. The reconstructed images using various numbers of radial projections are shown in Fig. 8. Depending on the resolution (or detail) desired by practitioners, our method helps to reduce the necessary number of k-space samples and therefore to speed up the overall MRI data acquisition.

Fig. 8.

Reconstruction of four-coil MRI raw data.

5 Appendix: $R$-Regularized Newton Method

Here we provide a brief and self-contained description of the $R$-regularized Newton method. The interested readers can find more details in the recent work [12].

A regularized-Newton-type structure generically arises in the classical lagged-diffusivity fixed-point iteration [20]. Let $u^k$ be our current iterate in solving the Huberized problem (4). By introducing a lagged-diffusivity weight

$$\begin{aligned} w^k:=\max (|\nabla u^k|,\gamma )^{q+r-2}, \end{aligned}$$

and a dual variable

$$\begin{aligned} p:=w^k\max (|\nabla u|,\gamma )^{-r}\nabla u, \end{aligned}$$

with $0\le r\le 2-q$, the reweighted Euler-Lagrange Eq. (5) appears as

$$\begin{aligned} \left\{ \begin{array}{l} -\mu \varDelta u+K^\top (Ku-z)+\alpha \nabla ^\top p=0,\\ (w^k)^{-1}\max (|\nabla u|,\gamma )^{r}p=\nabla u. \end{array}\right. \end{aligned}$$

(10)

Given a current approximation $(u^k,p^k)$, we apply a generalized linearization to (10) and obtain the generalized Newton system

$$\begin{aligned} \left[ \begin{array}{cc} -\mu \varDelta +K^\top K &{} \alpha \nabla ^\top ,\\ -\widetilde{C}{}^k(r)\nabla &{} D((m^k)^{2-q}e) \end{array}\right] \left[ \begin{array}{c} \delta u^k \\ \delta p^k \end{array}\right] = \left[ \begin{array}{c} \mu \varDelta u^k-K^\top (Ku^k-z)-\alpha \nabla ^\top p^k \\ \nabla u^k-(m^k)^{2-q}p^k \end{array}\right] , \end{aligned}$$

where

$$\begin{aligned}m^k&:= \max (|\nabla u^k|,\gamma ), \\ (\chi _{\mathcal{A}^k})_{ij}&:=\left\{ \begin{array}{ll} 1, &{} \mathrm{if~}|(\nabla u^k)_{ij}|>\gamma ,\\ 0, &{} \mathrm{otherwise}, \end{array}\right. \\ \widetilde{C}{}^k(r)&:= I-r D(\chi _{\mathcal{A}^{k}}(m^k)^{-q}p^k)\left[ \begin{array}{cc} D(\nabla _xu^k) &{} D(\nabla _yu^k) \\ D(\nabla _xu^k) &{} D(\nabla _yu^k) \end{array}\right] . \end{aligned}$$

Here $D(v)$ denotes a diagonal matrix with the vector $v$ as diagonal entries. For $v\in \mathbb {R}^{|\varOmega |}$ and $p=(p^1,p^2)\in \mathbb {R}^{2|\varOmega |}$, the notation $vp$ is understood as a vector in $\mathbb {R}^{2|\varOmega |}$ such that $(vp)_{ij}=(v_{ij}p^1_{ij},v_{ij}p^2_{ij})$ for all $(i,j)\in \varOmega$.

After eliminating $\delta p^k$, we are left with the linear system

$$\begin{aligned} \widetilde{H}{}^k(r)\delta u^k=-\nabla f_\gamma (u^k), \end{aligned}$$

(11)

where

$$\begin{aligned} \widetilde{H}{}^k(r)&:= -\mu \varDelta +K^\top K+\alpha \nabla ^\top D((m^k)^{q-2}e)\widetilde{C}{}^k(r) \nabla . \end{aligned}$$

The Newton system (11) can be rewritten as

$$\begin{aligned} (H^k+\beta R^k)\delta u^k=-\nabla f_\gamma (u^k), \end{aligned}$$

(12)

with $\beta = 2-q-r$, where $H^k:=\widetilde{H}{}^k(2-q)$ is the Hessian from the non-reweighted primal-dual Newton method [11, 20], and

$$\begin{aligned} R^k:=\alpha \nabla ^\top D(\chi _{\mathcal{A}^{k}}(m^k)^{-2}p^k)\left[ \begin{array}{cc} D(\nabla _xu^k) &{} D(\nabla _yu^k) \\ D(\nabla _xu^k) &{} D(\nabla _yu^k) \end{array}\right] \nabla . \end{aligned}$$

serves as a regularizer on the Hessian $H^k$. This coins the name R-regularization in connection with Newton’s method.

Next we aim to establish a sufficient condition on the $R$-regularization weight $\beta$ in order to guarantee that $\widetilde{H}{}^k(r)$ is positive definite and, therefore, $\delta u^k$ is a descent direction for $f_{\gamma }$ at $u^k$. For this purpose we invoke an infeasible Newton technique [11, 12].

The infeasible Newton technique involves two modifications in constructing the system matrix $\widetilde{H}{}^k(r)$. First, we replace $p^k$ by $p^k_+$, where

$$\begin{aligned} p^k_+:=\frac{\chi _{\mathcal{A}^k}(m^k)^{q-1}p^k}{\max ((m^k)^{q-1},|p^k|)}+(1-\chi _{\mathcal{A}^k})p^k. \end{aligned}$$

Note that the modified $p^k_+$ satisfies its feasibility condition, i.e.

$$\begin{aligned} |(p^k_+)_{ij}|\le |(\nabla u^k)_{ij}|^{q-1}, \quad \mathrm{whenever~}|(\nabla u^k)_{ij}|>\gamma . \end{aligned}$$

(13)

Secondly, we replace $\widetilde{C}{}^k(r)$ by its symmetrization denoted by $\widetilde{C}{}^k_+(r)$, i.e.

$$\begin{aligned} \widetilde{C}{}^k_+(r):=&\frac{\widetilde{C}{}^k(r)+\widetilde{C}{}^k(r)^\top }{2} =I-rD(\chi _{\mathcal{A}^k}(m^k)^{-q})\cdot \nonumber \\&\quad \cdot \left[ \begin{array}{cc} D((p^k_+)_x\nabla _xu^k) &{}\!\! D(\frac{1}{2}((p^k_+)_x\nabla _yu^k+(p^k_+)_y\nabla _xu^k)) \\ D(\frac{1}{2}((p^k_+)_x\nabla _yu^k+(p^k_+)_y\nabla _xu^k)) &{} D((p^k_+)_y\nabla _yu^k) \end{array}\right] . \end{aligned}$$

Accordingly, the system matrix $H^k$ in (12) is replaced by $H^k_+$ with

$$\begin{aligned} H^k_+ := -\mu \varDelta +K^\top K+\alpha \nabla ^\top D((m^k)^{q-2}e)\widetilde{C}{}^k_+(2-q) \nabla , \end{aligned}$$

and the regularizer $R^k$ is replaced by $R^k_+$ with

$$\begin{aligned} R^k_+:=&\alpha \nabla ^\top D(\chi _{\mathcal{A}^{k}}(m^k)^{-2})\cdot \nonumber \\&\cdot \,\left[ \begin{array}{cc} D((p^k_+)_x\nabla _xu^k) &{} D(\frac{1}{2}((p^k_+)_x\nabla _yu^k+(p^k_+)_y\nabla _xu^k)) \\ D(\frac{1}{2}((p^k_+)_x\nabla _yu^k+(p^k_+)_y\nabla _xu^k)) &{} D((p^k_+)_y\nabla _yu^k) \end{array}\right] \nabla . \end{aligned}$$

Lemma 4

Let $0\le r\le 1$ (or equivalently $1-q\le \beta \le 2-q$) and the feasibility condition (13) hold true. Then the matrix $\widetilde{C}{}^k_+(r)$ is positive semidefinite.

The proof of Lemma 4 is given in [12]. Thus, the positive definiteness of the $R$-regularized Hessian $H^k_++\beta R^k_+$ follows immediately from its structure and Lemma 4.

Theorem 5

Suppose the assumptions of Lemma 4 are satisfied. Then the $R$-regularized Hessian $H^k_++\beta R^k_+$ is positive definite.

We remark that our choice of $\mu$ is related to Theorem 6. Under the condition (2), for any positive $\mu$ the matrix $-\mu \varDelta +K^\top K$ is positive definite, and therefore Theorem 6 follows. However, whenever $K$ is injective the same conclusion holds with $\mu =0$. This is why we are allowed to choose $\mu =0$ in the denoising example in Sect. 4.1.

Given the result in Theorem 5, the descent direction $\delta u^k$ in the $R$-regularized Newton method implemented in step 1 of Algorithm 3 can be now obtained by solving the linear system

$$\begin{aligned} (H^k_++\beta R^k_+)\delta u^k=-\nabla f_\gamma (u^k), \end{aligned}$$

with $1-q\le \beta \le 2-q$. Given $\delta u^k$, one can compute $\delta p^k$ as

$$\begin{aligned} \delta p^k=(m^k)^{q-2}(\nabla u^k+\widetilde{C}{}^k(r)\nabla \delta u^k)-p^k, \end{aligned}$$

and then update $u^{k+1}:=u^k+a^k\delta u^k$ and $p^{k+1}:=p^k+a^k\delta p^k$ with some step size $a^k$ determined by the Armijo line search as in step 2 of Algorithm 3.

In all experiments in Sect. 4, we consistently choose $\beta =1-q$. This choice has the interesting interpretation that we actually relax the TV$^q$-model to a weighted TV-model (with weight updating in the outer iterations); see [12].