Keywords

1 Introduction

Earth Rotation Parameters (ERPs) consist of Polar motion and Length of Day as well as Precession and Nutation, which play a key role in the transformation between ICRF and ITRF. Up to now, several Precession and Nutation Model have been built, e.g. IAU1976 precession, IAU 1980 Nutation, IAU 2000, IAU 2000A and IAU 2006. With the accumulation of more geodetic observation data and the improvement of measurement precision, the new precession and nutation model will be constructed with higher precision. The accuracy of the coefficient of IAU 2006 model is achieved with up to 1 µas at J2000.0 [1], which is good enough to realize high precision of coordinate transformation, so ERPs of Polar motion and Length of Day are the most important parameters to limit the current accuracy of conversion between the two coordinate frames.

The first international organization that aimed at determining ERPs is International Latitude Service (ILS), which renamed International Polar Motion Service (IPMS) later. However, due to the limitation of classic optical technologies and instruments, the accuracy of polar motion was about 1 meter. International Time Bureau (BIH) used the Doppler observation data in 1972 and the accuracy was improved to 50 cm [2]. Later the Very Long Baseline Interferometry (VLBI) and Satellite Laser Range (SLR) techniques were used gradually to determined ERP and the relevant precision was improved to 10–20 cm. In 1988, IPMS was replaced by International Earth Rotation Service (IERS) that brought GPS observation to calculate ERP in 1994. Up to now, IERS has used the VLBI, LLR (Lunar Laser Ranging), SLR, GPS and DORIS (Doppler Orbitography by Radiopositioning Integrated on Satellite) observation data to estimate ERPs with a precision of sub-centimeter [3]. A number of estimates and studies on ERP have been conducted from different technologies such as GPS, VLBI, SLR [4–6]. With the development of Global Navigation Satellite Systems (GNSS), the number of International GNSS Service (IGS) tracking stations is increased rapidly. As a result, we have massive GNSS observation data that make possible to calculate ERPs with high precision and high temporal resolution [7]. This paper mainly uses observation data from global uniformly distributed GPS and GLONASS stations to determine ERPs, which are assessed with comparing to the IERS C04 solutions. Furthermore, the impact of ERP errors on aircraft orbit is analyzed and discussed. In addition, ERPs are determined by GNSS data only from regional IGS tracking stations in China and its surrounding areas. Method to improve the precision of ERP calculated by only regional GPS data is also analyzed in order to test ERP estimate with BeiDou regional navigation system with a limited tracking stations at this stage.

2 Principle of ERP Determination and Its Impact on Orbit

2.1 Principle of ERP Determination

As it is well known, the observation equation of GNSS satellites is related to the polar motion and rotation, so the ERPs can be determined using GNSS observation. The vector of observation (\( \vec{\rho } \)) from station to satellite can be expressed by the state vector of satellite (\( \vec{r} \)) and the position vector of station P (\( \vec{r}_{P} \)) in the celestial reference system as follows [8, 9]:

$$ \vec{\rho } = f(\vec{r},\dot{\vec{r}},\vec{r}_{P} ) $$
(11.1)

where \( \dot{\vec{r}} \) is the derivative of \( \vec{r} \). The vector \( \vec{r}_{P} \) in the inertial coordinate system thus can be expressed by the position vector \( \vec{r}_{P0} \) of station in the terrestrial reference system as:

$$ \vec{r}_{P} = PNRW\,\vec{r}_{P0} = P(t)R_{1} ({\Delta} \varepsilon )R_{2} ( - {\Delta} \psi \sin \varepsilon_{0} )R_{3} ( - \theta_{GM} )R_{1} (y_{p} )R_{2} (x_{p} ) $$
(11.2)

where P, N, R and W are the matrix of precession, nutation, earth rotation and polar motion, respectively. The parameters of polar motion (\( x_{p} ,y_{p} \)) and LOD (replaced by Earth rotation angle \( \theta \)) are included in the matrix \( W \) and \( R \), respectively. \( {\Delta} \varepsilon \) and \( {\Delta} \psi \) are precession and nutation. Linearized to one order, Eq. (11.1) can be rewritten as:

$$ \begin{aligned} \vec{\rho } & = f(\vec{r},\dot{\vec{r}},\vec{r}_{P} ) = f_{0} (\vec{r},\dot{\vec{r}},\vec{r}_{p} ) + \frac{\partial f}{{\partial x_{p} }}x_{p} + \frac{\partial f}{{\partial y_{p} }}y_{p} + \frac{\partial f}{\partial \theta }\theta \\ & = f_{0} (\vec{r},\dot{\vec{r}},\vec{r}) + \frac{\partial f}{{\partial \vec{r}_{p} }}\frac{{\partial \vec{r}_{P} }}{{\partial x_{p} }}x_{p} + \frac{\partial f}{{\partial \vec{r}_{p} }}\frac{{\partial \vec{r}_{P} }}{{\partial y_{p} }}y_{p} + \frac{\partial f}{{\partial \vec{r}_{p} }}\frac{{\partial \vec{r}_{P} }}{\partial \theta }\theta \\ \end{aligned} $$
(11.3)

where \( f_{0} (\vec{r},\dot{\vec{r}},\vec{r}) \) is the approximate value calculated by initial ERPs and \( \partial f/\partial \vec{r}_{p} \) is related to the type of observation and expressed by Eq. (11.2). Ignoring the micro items, \( \frac{{\partial \vec{r}_{P} }}{{\partial x_{p} }} \), \( \frac{{\partial \vec{r}_{P} }}{{\partial y_{p} }} \) and \( \frac{{\partial \vec{r}_{P} }}{\partial \theta } \) can be deduced according to Eq. (11.2) as follows:

$$ \frac{\partial f}{{\partial \vec{r}_{p} }} = \frac{{\vec{r} - \vec{r}_{p} }}{{\vec{\rho }}} $$
(11.4)
$$ \frac{{\partial \vec{r}_{P} }}{{\partial x_{p} }} = PNR\frac{\partial W}{{\partial x_{p} }}\vec{r}_{P0} = PNRW\left( {\begin{array}{*{20}c} { - z} \\ 0 \\ x \\ \end{array} } \right) $$
(11.5)
$$ \frac{{\partial \vec{r}_{P} }}{{\partial y_{p} }}{ = }PNR\frac{\partial W}{{\partial y_{p} }}\vec{r}_{P0} = PNRW\left( {\begin{array}{*{20}l} { - x_{p} y} \\ {x_{p} x + z} \\ { - y} \\ \end{array} } \right) $$
(11.6)
$$ \frac{{\partial \vec{r}_{P} }}{\partial \theta }{ = }\frac{{\partial \vec{r}_{P} }}{{\partial \theta_{g} }}\frac{{\partial \theta_{g} }}{\partial \theta } = PN\frac{\partial R}{{\partial \theta_{g} }}W\vec{r}_{P0} \frac{{\partial \theta_{g} }}{\partial \theta } = 2\pi (1 + k)(t - t_{0} )PNRW\left( {\begin{array}{*{20}l} { - y - y_{p} z} \\ {x - x_{p} z} \\ {y_{p} x + x_{p} y} \\ \end{array} } \right) $$
(11.7)

where \( \theta_{g} \) is the Greenwich Apparent Sidereal Time (GAST) and can be expressed as:

$$ \theta_{g} = GAST = 2\pi [GMST(UT0) + (1 + k)UT1] + {\Delta} \psi \cos \xi $$
(11.8)
$$ \begin{aligned} GMST(UT0) = & \,(24110.54841 + 8640184.812866T + 0.093104T^{2} \\ & - 6.2 \times 10^{{ - 6}} T^{3} )/86400 \\ \end{aligned} $$
(11.9)
$$ UT1 = UTC + (UT1 - UTC)_{0} + \theta (t - t_{0} ) $$
(11.10)

The \( T \) is the Julian century of observation epoch. \( (1 + k) \) can be calculated at a given \( T \). \( (UT1 - UTC)_{0} \) is the value of \( (UT1 - UTC) \) at epoch \( t_{o} \). Assuming n satellites with observing by m stations and substituting Eq. (11.4)–(11.7) into Eq. (11.3), we can acquire the error equation set as:

$$ \mathop V\limits_{m \times n,1} = \mathop B\limits_{m \times n,3} \mathop X\limits_{3,1} - \mathop l\limits_{m \times n,1} \quad \mathop P\limits_{m \times n,m \times n} $$
(11.11)

where P is the matrix of weight and other items are expressed as follow:

$$ \mathop B\limits_{m \times n,3} = \left( {\begin{array}{*{20}c} {\frac{{\partial f_{1}^{1} }}{{\partial x_{p} }}} \hfill & {\frac{{\partial f_{1}^{1} }}{{\partial y_{p} }}} \hfill & {\frac{{\partial f_{1}^{1} }}{\partial \theta }} \hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill \\ {\frac{{\partial f_{i}^{j} }}{{\partial x_{p} }}} \hfill & {\frac{{\partial f_{i}^{j} }}{{\partial y_{p} }}} \hfill & {\frac{{\partial f_{i}^{j} }}{\partial \theta }} \hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill \\ {\frac{{\partial f_{m}^{n} }}{{\partial x_{p} }}} \hfill & {\frac{{\partial f_{m}^{n} }}{{\partial y_{p} }}} \hfill & {\frac{{\partial f_{m}^{n} }}{\partial \theta }} \hfill \\ \end{array} } \right),\,\mathop l\limits_{m \times n,1} = \left( {\begin{array}{*{20}c} {\vec{\rho }_{1}^{1} - f_{1}^{1} (\vec{r},\dot{\vec{r}},\vec{r})} \hfill \\ \cdots \hfill \\ {\vec{\rho }_{i}^{j} - f_{i}^{j} (\vec{r},\dot{\vec{r}},\vec{r})} \hfill \\ \cdots \hfill \\ {\vec{\rho }_{m}^{n} - f_{m}^{n} (\vec{r},\dot{\vec{r}},\vec{r})} \hfill \\ \end{array} } \right),\,\mathop v\limits_{m \times n,1} = \left( {\begin{array}{*{20}c} {v_{1}^{1} } \hfill \\ {v_{1}^{2} } \hfill \\ {v_{i}^{j} } \hfill \\ \cdots \hfill \\ {v_{m}^{n} } \hfill \\ \end{array} } \right),\,\mathop X\limits_{3,1} = \left( {\begin{array}{*{20}c} {x_{p} } \\ {y_{p} } \\ \theta \\ \end{array} } \right). $$

Thus according to least-square method, we can determine the value of ERP and assess its precision:

$$ X = \left( {B^{T} PB} \right)^{ - 1} \left( {B^{T} Pl} \right) = \left( {\sum\limits_{i = 1}^{i = k} {B_{i}^{T} P_{i} B_{i} } } \right)^{ - 1} \sum\limits_{i = 1}^{i = k} {B_{i}^{T} P_{i} l_{i} } $$
(11.12)
$$ Q = \sigma_{0}^{2} \left( {\sum\limits_{i = 1}^{i = k} {B_{i}^{T} P_{i} B_{i} } } \right)^{ - 1} $$
(11.13)
$$ \sigma_{0}^{2} = \frac{{V^{T} V}}{n - t} $$
(11.14)

where \( (n - t) \), \( V \), \( \sigma_{0} \) and \( Q \) are the degree of freedom, residual error, unit weighted variance and coefficient matrix, respectively.

2.2 Impact of ERP on Orbit Determination

Geocentric Celestial Reference System (GCRS) is a good quasi-inertial reference frame with its axis fixed, so the orbits of the satellites or spacecraft are estimated in the coordinate system. And then coordinates of satellites are converted to the International Terrestrial Reference System (ITRS) using the Earth Orientation Parameters. The transformation equation can be expressed as Eq. (11.2). Transformation matrix P and N can be calculated according to IAU2000A model with a maximum error less than 0.2 μas [10], which equals to 2.6 cm for navigation satellite orbit. So the orbital errors caused by nutation error and precession error are often ignored. However, the orbital error caused by the changes in polar motion and length of day may reach tens of centimeters or even meters which should be considered in the determination of aircraft orbit or autonomous navigation. Omitting complicated derivation, Eq. (11.15) can represent the orbital error affected by ERP errors. More information can be referred to [11, 12].

$$ \left[ {\begin{array}{*{20}l} {\Delta} X \\ {\Delta} Y \\ {\Delta} Z \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {Y_{S}^{\prime } \cdot {\Delta} \theta + Z_{S}^{\prime } \cdot {\Delta} X_{p} } \\ { - X_{S}^{\prime } \cdot {\Delta} \theta - Z_{S}^{\prime } \cdot {\Delta} Y_{p} } \\ { - X_{p}^{\prime } \cdot Y_{S}^{\prime } \cdot {\Delta} \theta - Y_{p}^{\prime } \cdot X_{S}^{\prime } \cdot {\Delta} \theta - X_{S}^{\prime } \cdot {\Delta} X_{p} + Y_{S}^{\prime } \cdot {\Delta} Y_{p} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Y_{S}^{\prime } \cdot {\Delta} \theta + Z_{S}^{\prime } \cdot {\Delta} X_{p} } \\ { - X_{S}^{\prime } \cdot {\Delta} \theta - Z_{S}^{\prime } \cdot {\Delta} Y_{p} } \\ { - X_{S}^{\prime } \cdot {\Delta} X_{p} + Y_{S}^{\prime } \cdot {\Delta} Y_{p} } \\ \end{array} } \right]$$
(11.15)

where \( {\Delta} X_{p} \), \( {\Delta} Y_{p} \) and \( {\Delta} \theta \) are the error in polar motion and the error in Earth rotation angel calculated by LOD. (\( X_{s}^{\prime } \), \( Y_{s}^{\prime } \), \( Z_{s}^{\prime } \)) represents the coordinate of satellite in inertial system. \( X_{p}^{\prime } \cdot {\Delta} \theta \) and \( Y_{p}^{\prime } \cdot {\Delta} \theta \) are micro items which can be ignored.

3 GNSS Data Processing and Result

3.1 ERP Determination from Global Distribution GNSS Stations

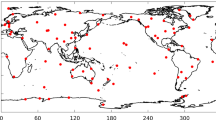
In this paper, 75 IGS tracking stations with global uniform distribution are selected and more than 60 stations can track both GPS and GLONASS. ERPs are determined for 60 days (January 1 to March 1, 2013) using GPS and GLONASS observations. Double-difference mode from Bernese GPS Software is chosen during the data processing with strong constraint of orbit elements and solar pressure. Apart from ERPs, troposphere parameters, stations coordinates and clock error are estimated simultaneously. Other models or strategies are used, including the quasi ionosphere free (QIF), IAU 2000 Precession/Nutation, IERS 2000 sub-daily polar model, OT_CSRC ocean tide file, FES2004 ocean loading correction. Differences of experiment results with respect to IERS C04 solutions at the same time (UTC 12:00:00) are showed in Fig. 11.1. Table 11.1 gives the precision statistic results.

Fig. 11.1
figure 1

Differences of global experiment results w.r.t IERS C04 solutions

Full size image
Table 11.1 Statistics results of global GNSS estimated ERPs w.r.t IERS C04
Full size table

According to the results, it is clear to see that ERPs estimated from GPS observations are much better than those from GLONASS observations in polar motion. The two results are compared with IERS C04. The standard deviations are 0.065 mas and 0.150 mas, respectively. However, the two results present a certain relationship with a similar trend and their precisions are the same in LOD (0.0283 ms and 0.0289 ms). Due to correlations with the orbital elements, LOD is not directly connected to GNSS observations. But it’s possible to estimate the drift in UT1-UTC through adding a constant value to UT1 and adapting the ascending nodes of the satellite orbits by a corresponding value without affecting the ranges between stations and satellites [13]. In addition, satellites orbits are fixed with the precise ephemeris from IGS products and we chose the same baselines during processing the GPS and GLONASS data, which may be responsible for the correlation between the two results in LOD.

3.2 ERPs Estimated from Regional Distribution Stations

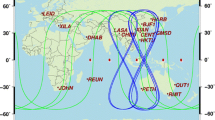
In order to analyze the accuracy of ERP from regional distribution stations, 18 stations in China and its surrounding areas are chosen for testing (from Jan 1 to May 31). These stations are bjfs, bjnm, chan, guao, kunm, lhaz, shao, tnml, twtf, urum, wuhn, alic (Australia), hyde (India), kit3 (Uzbekistan), nuts (Singapore), pert (Australia), pimo (Philippines), ulab (Mongolia). The results from regional GPS observations are compared to IERS C04, and the differences are shown in Fig. 11.2.

Fig. 11.2
figure 2

Differences of regional experiment results w.r.t IERS C04 solutions

Full size image

ERPs are also estimated from regional 11 stations with simultaneously tracking GLONASS (bjfs, bjnm, lhaz, urum, wuhn, alic, hyde, kit3, nuts, pert, ulab). In addition, variance components estimation is used to estimate ERPs from combined GPS+GLONASS observation. Results are compared to the IERS C04 and the differences are shown in Fig. 11.2. Table 11.2 gives the precision statistic of the results from regional observation.

Table 11.2 Statistics result of regional experiment estimate w.r.t IERS C04
Full size table

The results show the precision of ERPs from regional stations is lower than that from global stations, especially in polar motion. It’s not only related to the number of stations, but also the distribution of stations plays a important role. However, the ERP has been improved dramatically by combined GPS and GLONASS. The combined results has been improved by 15.9 % (\( x_{p} \)), 13.6 % (\( y_{p} \)) and 0.0 % (LOD) when compared to the result from only GPS. It’s more significant when compared to the result from GLONASS with 51.5 % (\( x_{p} \)), 58.1 % (\( y_{p} \)) and 19.7 % (LOD). So we can conclude that combined method improves the ERP precision with respect to both GPS and GLONASS alone, which is a good reference when estimating ERPs from regional BDS navigation system observations.

3.3 Impact of ERP Error on Aircraft Orbit Determination

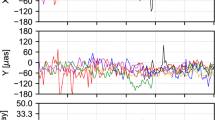
In order to analyze the impact of ERP error on aircraft orbit, ERP values of different precision are used to determinate the orbit of aircraft. Because the impacts from ERP are mainly reflected in the coordinates transformation between ICRF and ITRF, so this paper main focus on this session. Figure 11.3 shows the orbital error of GPS satellites with 0.5 mas error in polar motion and 0.5 ms error in LOD with respect to precise ephemeris from IGS products on September 1, 2013. As shown in Fig. 11.3, ERP has more impact on X and Y direction than Z direction. Although the maximum error is less than 10 cm in Z direction, the error in X and Y direction can reaches to 100 cm. In addition, the orbit is more easily affected by LOD than polar motion which can be interpreted by Eq. (11.15). Because the orbit errors in X and Y direction are caused by LOD and polar motion parameters, however, the orbit error in Z direction is caused only by polar motion parameters. According to the further study, in order to satisfy requirement of centimeter-level accuracy for navigation satellite orbit determination, the error in polar motion should be less than 0.05 mas and error in LOD must be less than 0.01 ms, and the orbit error will be less than 2 cm in every X, Y or Z direction in this case.

Fig. 11.3
figure 3

Errors of orbits due to the effect of ERP error

Full size image

4 Conclusions

Continuous GNSS observations can be used to estimate the ERPs of high precision and high temporal resolution. In this paper, ERP are estimated using GNSS observation in different cases and some conclusions can be drawn.

  1. 1.

    Precision of polar motion can be improved dramatically with more stations and better distribution of stations. However, precision of LOD can’t be improved much only by increasing the number of stations.

  2. 2.

    Due to correlation with the orbital elements, LOD is not directly related to GNSS observations. But UT1-UTC can be acquired by adding a constant to UT1 with a certain correlation.

  3. 3.

    Precision of ERPs estimated from regional GNSS stations is relatively low but can be improved by combined multi-system observations. Combined GPS+GLONASS results in polar motion are improved by 15 % with respect to GPS alone and by 50 % with respect to GLONASS alone.

  4. 4.

    LOD has more effects on satellite orbit than polar motion. In order to satisfy requirement of centimeter-level accuracy for orbit determination of navigation satellite, the error in polar motion should be less than 0.05 mas and the error in LOD must be less than 0.01 ms.