Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Continuum neural field models of the type proposed by Amari [1, 2] (see also Chap. 3) have been used as a model for cortical tissue, describing phenomena such as travelling fronts and pulses of activity [12, 27], stationary and breathing bumps [15, 16, 18, 28], and instabilities leading to pattern formation such as might be responsible for visual hallucinations [6, 22] (see also Chaps. 1, 4, and 7). Much of this work uses the assumption that neural connectivity in the tissue is homogeneous and isotropic. This simplification may give an adequate first order approximation of the behaviour of the tissue in some situations (e.g. fronts of activity in cortical slices [11]), but it is mainly motivated by the fact that it leads to much more tractable equations. There have been several attempts to include more realistic connections in this type of model: for example travelling fronts in a periodically varying connection function have been studied in Refs. [7, 9, 13, 25], whilst Ref. [8] considers a crystal like structure for connectivity such as might be expected in the visual cortex , and long range point connections have been studied in Refs. [5, 24, 26, 29]. Spatial inhomogeneity can also be introduced via external input to the fields [10, 17, 18].

In this chapter we take a different approach, and consider quenched stochastic inhomogeneous connections which are introduced in addition to a homogeneous component. To achieve this we numerically construct spatially continuous, stochastic connection functions. With such a scheme it is not possible to solve the field equations analytically, so instead we use approximation and numerical methods.

We consider a two population continuum model, given in two dimensions by

$$\displaystyle\begin{array}{rcl} \tau _{u}\frac{\partial u} {\partial t} + u(\mathbf{x},t)& =& \int _{\varGamma }w(\mathbf{x},\mathbf{x^{{\prime}}})f\left (u(\mathbf{x^{{\prime}}},t)\right )d\mathbf{x^{{\prime}}}- gv(\mathbf{x},t), \\ \tau _{v}\frac{\partial v} {\partial t} + v(\mathbf{x},t)& =& f\left (u(\mathbf{x},t)\right ), {}\end{array}$$
(8.1)

where Γ denotes the extent of the system. The field u(x, t) describes an excitatory neural population and v(x, t) local inhibition (which can be interpreted either as an inhibitory neural population, or as nonlinear local feedback). We set the time units of the system by choosing τ u  = 1; τ v and g give the relative response time and strength of the inhibition. We employ the usual approximation for the firing rate function , taking it to be a step at threshold θ, i.e. \(f(u) =\varTheta (u-\theta )\) where 0 < θ < 1.

For the inhomogeneous connection function w(x, x ′) we consider two different forms. First in Sect. 8.2 we consider a local inhomogeneity where the connection weight varies with position, but there are no long range connections ; then in Sect. 8.3 we consider a connection function in which long range connections can be introduced by varying a single parameter. In both cases we examine the well known solutions of propagating fronts and pulses of activity in one dimension, before describing a new type of behaviour—namely persistent fluctuations of activity—in both one and two dimensional systems.

We perform numerical simulations of Eq. (8.1) by discretizing space, and then using a 4th order Runge-Kutta algorithm to solve a set of first order ordinary differential equations. If the connection function w(x, x ′) is chosen carefully, the integral on the right hand side of the equation for u(x, t) can be written as a convolution . Although this leads to some loss of generality, the convolution theorem can then be exploited—using a fast Fourier transform algorithm [19] the integral can be very efficiently solved.

2 Local Inhomogeneity in Connection Density

There is some experimental evidence [21] that the number of synapses between two neurons is a Gaussian function of their separation. Thus we adopt a Gaussian connection function, and add to it a small inhomogeneous perturbation. In this section we assume that there are no long distance connections and write our connection function in 1D as

$$\displaystyle{ w(x,x^{{\prime}}) = w_{ H}(x - x^{{\prime}})[1 + A\mathbf{(}w_{ 1}(x) + w_{2}(x^{{\prime}})\mathbf{)}], }$$
(8.2)

where w H is a normalised Gaussian function

$$\displaystyle{ w_{H}(y) = \frac{1} {\sqrt{\pi }}e^{-y^{2} }, }$$
(8.3)

and the constant A gives the magnitude of the inhomogeneous connections. The unit width of the homogeneous function defines the spatial length scale of the connections (and all lengths given in the rest of the chapter are quoted in these units). For w 1 and w 2 we numerically generate functions which vary stochastically (but continuously) in space with Gaussian statistics, zero mean, and unit mean squared, and which are auto-correlated on a length λ (there is no correlation between the functions). We include two different functions (of x and x ′) in order to remove any bi-directionality in the connections; for simplicity each is a different stochastic realisation of the function with the same statistics. This can loosely be thought to represent additional (to the homogeneous) connections into point x and out of point x ′. It is this separability of the connection function which allows the integral to be written as a convolution . Note that although the functions are constructed stochastically, they do not vary with time, so the dynamics of the system are entirely deterministic.

The inhomogeneity is therefore characterised by its magnitude A, and correlation length λ. We identify two different regimes, λ < 1 and λ > 1. The first represents local heterogeneity in the connections, i.e., on length scales less than the width of w H ; the second can be interpreted as variation of connection strength on lengths larger than the width of w H , i.e., locally the connections appear homogeneous, but the overall connection density varies on longer length scales. For the latter case it is important to note that whilst connection density varies on long length scales in this regime, we have not included any long range connections. We also note that since u(x, t) represents a population of excitatory neurons, only a positive connection function makes physical sense. Thus in the present work we only consider values of A that are small enough so that w(x, x ′) remains positive for all x, x ′.

2.1 Travelling Fronts and Pulses

We first examine the effect of local stochastic connectivity on the well known solutions to Eq. (8.1) in 1D, i.e. travelling fronts and pulses [27]. We treat the inhomogeneity as a small perturbation to the system; initially we add a constant additional connection weight γ to a homogeneous function w H (y), later replacing this with the inhomogeneous connections \(\gamma \rightarrow \gamma (x,x^{{\prime}}) = A[w_{1}(x) + w_{2}(x^{{\prime}})]\), and expanding \(\gamma (x,x^{{\prime}}) =\bar{\gamma } +\delta \gamma (x,x^{{\prime}})\) about \(\bar{\gamma }= 0\). We consider the equations

$$\displaystyle\begin{array}{rcl} \tau _{u}\frac{\partial u} {\partial t} + u(x,t)& =& \int _{\varGamma }w_{H}(x - x^{{\prime}})(1+\gamma )f\left (u(x^{{\prime}},t)\right )\mathit{dx}^{{\prime}}- gv(x,t), \\ \tau _{v}\frac{\partial v} {\partial t} + v(x,t)& =& f\left (u(x,t)\right ), {}\end{array}$$
(8.4)

where w H (y) is given in Eq. (8.3). The uniform steady states are found by setting \(\partial _{t}u = \partial _{t}v = 0\) and assuming no x dependence. These are then given by the pairs of values of u and v which simultaneously solve

$$\displaystyle\begin{array}{rcl} u& =& (1+\gamma )f(u) - gv, \\ v& =& f(u). {}\end{array}$$
(8.5)

The stability of the points can be shown in the standard way by expanding \(u(x,t) =\bar{ u} +\delta ue^{\omega t}\) and \(v(x,t) =\bar{ v} +\delta ve^{\omega t}\) in Eq. (8.4), and then finding the eigenvalues ω. There are stable fixed points at \((\bar{u}_{1},\bar{v}_{1}) = (0,0)\) and \((\bar{u}_{3},\bar{v}_{3}) = (1 +\gamma -g,1)\), and an unstable saddle point at \((\bar{u}_{2},\bar{v}_{2}) = (\theta,1)\); note that the fixed point \((\bar{u}_{3},\bar{v}_{3})\) only exists if \(1 +\gamma -g>\theta\). Travelling wave fronts are possible when there are two stable steady states—the front connects a region in the \((\bar{u}_{1},\bar{v}_{1})\) state with a region in the \((\bar{u}_{3},\bar{v}_{3})\) state.

The speed of the front can be found by following Ref. [12]. The equations for u(x, t) and v(x, t) can be solved using the Green’s functions

$$\displaystyle{ \begin{array}{rclcrcl} \eta _{u}(s)& =&\left \{\begin{array}{ll} \frac{1} {\tau _{u}}e^{-s/\tau _{u}}&s \geq 0, \\ 0 &s <0, \end{array} \right.&\ \ \ \mathrm{and}\ \ \ &\eta _{v}(s)& =&\left \{\begin{array}{ll} \frac{1} {\tau _{v}}e^{-s/\tau _{v}}&s> 0, \\ 0 &s \geq 0, \end{array} \right. \end{array} }$$
(8.6)

and a change of variables \(\xi = x - ct\) can be used to transform to a co-moving frame where the front is stationary with shape given by

$$\displaystyle{ q(\xi ) =\int _{ 0}^{\infty }\eta _{ u}(s)\left [\psi _{u}(\xi +\mathit{cs}) - g\psi _{v}(\xi +\mathit{cs})\right ]\mathit{ds}, }$$
(8.7)

where

$$\displaystyle\begin{array}{rcl} \psi _{u}(\xi )& =& \int _{-\infty }^{\infty }(1+\gamma )w_{ H}(y)f\mathbf{(}q(\xi -y)\mathbf{)}dy,{}\end{array}$$
(8.8)
$$\displaystyle\begin{array}{rcl} \psi _{v}(\xi )& =& \int _{0}^{\infty }\eta _{ v}(s)f\mathbf{(}q(\xi +\mathit{cs})\mathbf{)}\mathit{ds}.{}\end{array}$$
(8.9)

The boundary conditions are q(0) = θ, with q(ξ) < θ for ξ > 0, and q(ξ) > θ for ξ < 0. Since the firing rate is taken to be a step function \(f(u) =\varTheta (u-\theta )\), these integrals can be solved, and then the front speed c is given by

$$\displaystyle{ \theta = \left \{\begin{array}{ll} \frac{1+\gamma } {2} \left [1 - e^{ \frac{1} {4c^{2}} }\left (1 -\text{erf}( \frac{1}{2c})\right )\right ]&c> 0, \\ \frac{1+\gamma } {2} \left [1 + e^{ \frac{1} {4c^{2}} }\left (1 + \text{erf}( \frac{1}{2c})\right )\right ]&c <0. \end{array} \right. }$$
(8.10)

which can be solved numerically (a different choice of w H (y) can lead to analytic solutions). Figure 8.1a, b show how c depends on θ and γ; there is a minimum value of γ below which there is no front solution. There is no dependence on τ v or g. It can be shown using the Evans’ function method [14] that when both stable fixed points \((\bar{u}_{1},\bar{v}_{1})\) and \((\bar{u}_{3},\bar{v}_{3})\) exist, the moving front solution is also stable.

Fig. 8.1
figure 1

Plots (a) and (b) show, for the homogeneous system given by Eq. (8.4), how the front propagation speed c varies with θ (at constant γ) and γ (at constant θ) respectively. Note that there is a minimum value of γ below which the front solution does not exist. There is no dependence on τ v or g, and where moving front solutions exist they are stable. Plots (c) and (d) show how the mean and variance of the speed of a front travelling through an inhomogeneous system with two stable steady state solutions depends on the magnitude of the inhomogeneous connections A. Points, diamonds and squares show results for λ = 0. 5, 5 and 10 respectively, averaged over 10 realisations of the stochastic connections. The solid line gives the analytic result for the variance of c derived in the large λ limit (Eq. (8.13)). The other parameters used are θ = 0. 1 and g = 0. 2

Full size image

So far we have proceeded as in Ref. [12], except for the inclusion of the constant γ which represents the additional connections that are added to the system. The extension to spatially varying connections is simply a matter of the replacement \(\gamma \rightarrow \gamma (x,x^{{\prime}}) = A[w_{1}(x) + w_{2}(x^{{\prime}})]\). Equation (8.8) becomes

$$\displaystyle{ \psi _{u}(\xi ) =\int _{ -\infty }^{\infty }\left (1 +\gamma (x,x^{{\prime}})\right )w_{ H}(y)f\mathbf{(}q(\xi -y)\mathbf{)}dy. }$$
(8.11)

We assume for the moment that this replacement does not change the fact that there are two stable steady states; we shall discuss what happens if this is not the case at the end of this section. Considering first the regime where λ is shorter than the unit width of the homogeneous connection function and the length cτ v , we find that the inhomogeneity will be averaged out, and effectively γ(x, x ′) = 0. That is to say, the integral in Eq. (8.11) is effectively an average of γ(x, x ′) over the width of the function w H (y); since in the λ < 1 regime γ(x, x ′) varies on a length scale much shorter than this and has zero mean, we expect behaviour to be the same as the homogeneous case.

In the limit of large λ (which we argued above is biologically relevant), \(w_{2}(x^{{\prime}})\) will vary on length scales much longer than the width of the homogeneous connections w H (y), and so in the integral we can approximate \(w_{2}(x^{{\prime}}) \approx w_{2}(x)\) and then \(\gamma (x,x^{{\prime}}) \approx \gamma (x) = A[w_{1}(x) + w_{2}(x)]\). We then proceed to expand \(\gamma (x) =\bar{\gamma } +\delta \gamma (x)\) about \(\bar{\gamma }= 0\). We argue that the speed c is given by a function c = h(γ) (the solution to Eq. (8.10)), and expand to second order, giving

$$\displaystyle{ c = h(\bar{\gamma }) +\delta \gamma h^{{\prime}}(\bar{\gamma }) + \frac{\delta \gamma ^{2}} {2}h^{{\prime\prime}}(\bar{\gamma }) + \mathcal{O}(\delta \gamma ^{3}). }$$
(8.12)

Since the connection function is composed of Gaussian distributed functions with zero mean, we know that \(\bar{\gamma }= 0\) and \(\langle \delta \gamma ^{2}\rangle = 2A^{2}\), \(\langle \delta \gamma ^{4}\rangle = 6A^{4}\) etc. and the odd moments are zero, with A the amplitude of the inhomogeneity. We can therefore write the mean and variance of the speed

$$\displaystyle\begin{array}{rcl} \langle c\rangle & =& h(0) + A^{2}h^{{\prime\prime}}(0) + \mathcal{O}(\delta \gamma ^{4}), \\ \langle (c -\langle c\rangle )^{2}\rangle & =& 2A^{2}h^{{\prime}}(0)^{2} + \frac{1} {2}A^{4}h^{{\prime\prime}}(0)^{2} + \mathcal{O}(\delta \gamma ^{4}).{}\end{array}$$
(8.13)

From inspection of the plot of c against γ (Fig. 8.1b) there is an approximately linear relationship at γ = 0; thus we approximate the first derivative h ′(0) as a constant (found numerically from Eq. (8.10) to be h ′(0) = 2. 835) and neglect higher derivatives. We therefore expect the mean speed to be independent of A at linear order, and the variance to vary as A 2.

We test these predictions by using numerical simulations of an inhomogeneous system where there are two stable steady states throughout, and where initial conditions have been chosen so as to lead to travelling fronts (for example an initial condition with a discontinuity in the u variable, \(u(x <0,t = 0) = 1,\ u(x> 0,t = 0) = 0,\ v(x,t = 0) = 0\)). Figure 8.1c, d show how the mean and variance of the speed of the front vary with A for several values of λ. The averages are over not only the speed of a single front as it moves through the system, but also over many systems with different realisations of the stochastic connections. We find that for small A the mean speed is approximately constant, but for larger A our approximation fails, as the mean speed starts to decrease. The solid line shows the equation \(2h^{{\prime}}(0)A^{2}\) with h ′(0) = 2. 835, and we find that this becomes a better approximation as λ increases.

As well as travelling front solutions, homogeneous models of this type can also support travelling pulses. Again we investigate the effect of inhomogeneous connections by first considering a homogeneous additional connection weight γ, before expanding about this. As shown in Ref. [12] the derivation of the speed and shape of a travelling pulse follows in a similar manner to that of the front, but with boundary conditions \(q(0) = q(\varDelta ) =\theta\), q(ξ) > θ for 0 ≤ ξ < Δ and q(ξ) < θ otherwise; i.e. the pulse has width Δ. Since this system is isotropic, solutions with c > 0 and c < 0 will be identical under the transformation x → −x, so we only consider c > 0. Analysing Eq. (8.4) with these boundary conditions , we find equations relating c and Δ to g, θ, τ u and γ (similar to Eq. (8.10) for the fronts ). Figure 8.2 shows the dependence of pulse width and speed on γ and g for θ = 0. 1 and τ v  = 1. Note that for some parameters there are two branches of solutions. The stability can again be found by constructing an Evans function , which allows identification of a stable and an unstable branch.

Fig. 8.2
figure 2

Plots showing how the speed and width of a travelling pulse in the homogeneous system given by Eq. (8.4) vary with the constant γ, for different values of the inhibitory population strength g. The upper branches are found to be stable (heavy lines) and the lower branches are unstable (light lines). Other parameters are θ = 0. 1 and τ v  = 1

Full size image

To examine whether the system still supports travelling pulses in the presence of inhomogeneous connections we proceed as before, and replace \(\gamma \rightarrow \gamma (x) =\bar{\gamma } +\delta \gamma (x)\), and consider the λ > 1 case. From Fig. 8.2 we find that stable solutions only exist at γ = 0 for large g, and that they only exist over a narrow range of γ. This means that in a typical system we require large g and small 〈δ γ 2〉 for there to be a significantly large regions where pulses are stable. We observe that in such a system there are regions in which we can initiate a travelling pulse which will move with fluctuating speed and width; the pulse cannot propagate into regions in which locally a stable pulse solution does not exist, i.e. a pulse will die if it encounters such a region.

In summary front solutions exist and are stable in a homogeneous system provided there are two stable steady states and γ is greater than some minimum value which depends on the firing threshold θ (Fig. 8.1b). Pulse solutions are only stable for a small range of γ and g. With inhomogeneous connections fronts can still propagate provided there remains two stable steady states, and pulses can be initiated and propagate only in the regions in which they are locally stable. Fluctuations in the speed of fronts and pulses which arise due to stochasticity in firing, rather than in connectivity are studied in Chap. 9 of this book.

We have so far examined inhomogeneous systems in which there are either one or two stable steady states everywhere in the system; we now turn our attention to what happens if this is not the case.

If we define the function

$$\displaystyle{ W(x) =\int _{ 0}^{L}w_{ H}(x - x^{{\prime}})[1 + A\mathbf{(}w_{ 1}(x) + w_{2}(x^{{\prime}})\mathbf{)}]\mathit{dx}^{{\prime}}- g, }$$
(8.14)

then from Eq. (8.1) one notes that if W(x) > θ for all x, then by setting the derivatives to zero and assuming u(x, t) = u(x) the steady states are given by

$$\displaystyle{ \bar{u}(x) = W(x)f\left (\bar{u}(x)\right ), }$$
(8.15)

i.e. \(\bar{u}_{1}(x) = 0\) and \(\bar{u}_{3}(x) = W(x)\). If the condition W(x) > θ is not true for all x, then in the regions where W(x) < θ there is only one steady state (\(\bar{u}_{1} = 0\) ); for values of x where there are two steady states, the system can exist in the upper state only locally. In such a system a new kind of behaviour can be observed. Broadly speaking, we see patches of high activity, patches of low activity and regions which fluctuate between the two. Such persistent fluctuations have not previously been observed in neural field models without the addition of external input.

2.2 Persistent Fluctuations

In this section we examine in more detail this new type of fluctuating behaviour. In order to qualitatively understand how the fluctuations arise in systems with stochastic inhomogeneous connections we also examine some deterministic inhomogeneous connection functions. We then quantitatively study the patterns of activity in the stochastic system in the fluctuating state, seeking to understand what this behaviour might mean for information transfer across neural tissue. This involves measurements of the mean and mean squared activity, and spatial and temporal correlations in the activity patterns, and consider how these depend on the properties of the underlying connections. The same fluctuating behaviour is seen in both 1D and 2D systems.

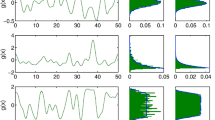
Figure 8.3 shows an example of a 1D system where we observe persistent fluctuations in u(x, t) at some values of x. Also shown is the time evolution of the activity, both at some arbitrarily chosen points in the system, and on average. We find that at some points u appears to oscillate periodically, whilst at others it appears more chaotic. The spatially averaged activityFootnote 1 〈u(x, t)〉 x appears to fluctuate chaotically. (In fact a numerical measurement of the Lyapunov exponents of the discretized approximation of the system shows this to be a limit cycle with an extremely long period.)

Fig. 8.3
figure 3

Top: Plots showing snapshots of the activity u as a function of x at different times t, whilst a 1D system is undergoing persistent fluctuations. Black lines show u(x, t), grey lines show W(x) (Eq. (8.14)), and the dotted line shows θ = 0. 1. Bottom: Plots showing how u varies in time during persistent fluctuations, at different randomly chosen points x i and on average. For all plots the other parameters are g = 0. 8, τ v  = 1, A = 0. 3 and λ = 5

Full size image

So, what parameter values are required in order to see the fluctuating behaviour? Firstly, the inhibition strength g must be large enough in order that there are some regions of the system where there are two stable steady states, and some regions where there is only one. We also find that both the amplitude, A, and and length scale, λ, of the connections must not be too small, otherwise, for some realisations of the connections, the activity drops to the lower steady state across the whole system. To initiate fluctuations there must be some initial excitation in the regions of the system with two stable steady states, either via the initial conditions or a transient external input. The fluctuations are then seen to persist indefinitely once any external input is removed.

The existence of the fluctuating state depends on the particular realisation of the connections, as well as their statistical properties. In order to understand why we do or do not observe persistent fluctuations for a particular realisation of the inhomogeneity, we examine some carefully chosen deterministic inhomogeneous connection functions. Observing the behaviour of this simpler system allows us to more easily understand how the fluctuations arise.

2.2.1 Simple Deterministic Connection Function

In 1D, in the large λ limit the field equations can be written

$$\displaystyle\begin{array}{rcl} \tau _{u}\frac{\partial u} {\partial t} + u(x,t)& =& [1 + A\left (w_{1}(x) + w_{2}(x)\right )]\int _{0}^{L}w_{ H}(x - x^{{\prime}})f\left (u(x^{{\prime}},t)\right )\mathit{dx}^{{\prime}} \\ & &-gv(x,t), \\ \tau _{v}\frac{\partial v} {\partial t} + v(x,t)& =& f\left (u(x,t)\right ), {}\end{array}$$
(8.16)

where we have approximated \(w_{2}(x^{{\prime}}) \approx w_{2}(x)\), since the width of the function w H is much less than λ. If instead of using stochastic functions we choose w 2(x) = 0, and w 1(x) a piecewise linear function, we can construct a system with a region with two stable steady states (\(\bar{u}_{1} = 0\), and \(\bar{u}_{3} = 1\) ), a region with a single steady state (\(\bar{u}_{1} = 0\) ), and a boundary region where w 1(x) has constant gradient. The resulting W(x) as defined by Eq. (8.14) is shown in Fig. 8.4a. If the system is set up with the initial condition u(x, t) ≥ θ for all x, then after a short transient time the result is a region where u(x, t) = 1 for all t, a region where u(x, t) = 0 for all t, and a boundary region where u fluctuates. That is to say, a “bump” in w 1(x) gives rise to a bump of activity with fluctuating boundaries.

In Fig. 8.4b–e we show how periodic fluctuations of the edges of the activity bump occur. A retracting front of activity forms in the “boundary region”; as this front retracts a small growing “side bump” forms. When the peak of this side bump reaches threshold, u grows rapidly and the direction of movement of the front changes. The front moves out into the region which can only support the \(\bar{u}_{1} = 0\) steady state before retracting again, and the process repeats. The fluctuations are therefore a consequence of the non-monotonicity of the front at the edges of the highly connected bump, which originates from the presence of the local inhibitory field. A higher density of connections allows the tissue to reside in an active state and this activity spreads into the region with a lower connection density. In this region there are insufficient excitatory connections to sustain the high activity, and as the inhibitory field v increases the front moves back into the highly connected region. The time scale of the fluctuations is determined by the relaxation time of the inhibition τ v . We also find that the frequency of the fluctuations increases with the gradient of W(x) in the boundary region (as well as depending on θ, τ v , and g). Also the width of the fluctuating region increases as τ v increases.

Fig. 8.4
figure 4

Plot (a) shows an example deterministic W(x) (solid line) with different regions where there are either two or one stable steady states. At the boundary between these regions, W(x) varies continuously and in this example has a constant gradient of 0. 1. The dotted line shows the threshold θ = 0. 1. Plots (b)–(d) show how the activity fluctuates at the edge of the “bump” in W(x), via the generation of a “side bump”. Solid black lines show u(x, t), grey lines show W(x) and dotted lines show the threshold θ. Arrows show the direction of motion of the front. Plot (e) shows how the mean activity varies with time. After an initial transient there is periodic oscillation

Full size image

A slightly different choice of W(x) can produce a bump of activity with fluctuating boundaries which emits travelling pulses. As we saw in the previous section there is a narrow range of values of γ for which stable travelling pulse solutions exist. If the region adjacent to the bump has w 1(x) consistent with this, pulses can propagate into it. The rate at which they are emitted depends on the gradient of the edges of the bump in W(x).

Breathing bumps and pulse emitting bumps have also been observed in homogeneous connection models. In Ref. [10] it was shown that stationary fronts and pulses can be generated in a homogeneous connection model with linear feedback via the introduction of a spatially varying external input; if the magnitude of the input is increased, the system goes through a Hopf bifurcation to an oscillating state. In Ref. [15] spike frequency adaption (where the dynamics of the threshold depend on activity) was introduced, giving rise to stationary bumps which go unstable in favour of breathing solutions. In both of these cases the mechanism for the generation of the oscillations is different to the one described here. Here the oscillations arise as a result of inhomogeneity in the connections.

By examining this simple deterministic inhomogeneity in the connections we obtain a better qualitative understanding of what is taking place in the case of stochastic connection functions. In that case, the observed behaviour is a result of many “breathing bumps” (with characteristic width λ), which fluctuate with a frequency which depends on the local gradient of W(x). These bumps may interact with each other, some emitting pulses. For small A and small λ (i.e. in a regime where regions with W(x) > θ do not have large spatial extent) the retracting fronts of activity may meet before the “side bumps” have grown to reach threshold. The activity collapses into the lower steady state (\(\bar{u}_{1} = 0\) ), and this is typically irreversible. This explains why for some realisations of the stochastic connections (and systems of finite size) we find u(x, t) → 0 for all x after a short transient time. In general, requirements for fluctuations are that W(x) has non-zero gradient (a requirement for the growth of “side bumps”), that θ must be close enough to \(\bar{u}_{1} = 0\), and that the bumps in W(x) are wide enough so that the peaks of the side bumps reach threshold before the retracting fronts meet.

2.3 Activity Patterns and Correlations

We now return to the case of stochastic connections in 1D, and examine how the properties of w 1(x) and w 2(x) effect the fluctuations. The dependence of the magnitude A and length scale λ of the inhomogeneous connections, on the mean and mean squared activity during persistent fluctuations is shown in Fig. 8.5. As one would expect, increasing A leads to an increase in the mean activity 〈u(x, t)〉 x, t . There is also an increase in the amplitude of the fluctuations, i.e. \(\langle u(x,t)^{2}\rangle _{x,t}\) increases. In contrast, variation of λ has little impact on the mean and mean squared activity, except at small λ. In that case, the regions where W(x) > θ are small, and we expect fewer regions where the activity fluctuates; i.e. the majority of the system sits in the lower steady state, leading to a reduced activity on average. We note that for \(A \gtrsim 1/\sqrt{2}\) the connection function becomes unphysical as it is likely that w(x, x ′) will be negative for some x, x ′.

Fig. 8.5
figure 5

Plots showing how the amplitude A and correlation length λ of the connections effect the spatial mean and mean squared of the activity. Top left and right show the effect of varying A at fixed correlation lengths λ = 5 (points) and λ = 0. 5 (diamonds). Bottom left and right show the effect of varying λ at fixed A = 0. 1 (points) and A = 1 (diamonds). All results are averages from 10 realisations of the connections, with errors given by the standard deviation over realisations

Full size image

The length λ can, however, determine the length and time scales of the fluctuations. We define respectively the spatial and temporal correlation functions

$$\displaystyle\begin{array}{rcl} C_{x}(X) = \frac{\langle \delta u_{x}(x,t)\delta u_{x}(x + X,t)\rangle _{x,t}} {\langle \delta u_{x}(x,t)^{2}\rangle _{x,t}},& &{}\end{array}$$
(8.17)
$$\displaystyle\begin{array}{rcl} C_{t}(\tau ) = \frac{\langle \delta u_{t}(x,t)\delta u_{t}(x,t+\tau )\rangle _{x,t}} {\langle \delta u_{t}(x,t)^{2}\rangle _{x,t}},& &{}\end{array}$$
(8.18)

where \(\delta u_{x}(x,t) = u(x,t) -\langle u(x,t)\rangle _{x}\) and \(\delta u_{t}(x,t) = u(x,t) -\langle u(x,t)\rangle _{t}\). As well as averaging over x and t for a single system, we also average over many different simulations with different realisations of the stochastic connections. From the spatial correlation function we can measure a correlation length l, defined to the the length over which C x (X) drops by a factor e −1. As is shown in Fig. 8.6a–c, for large A the correlation length of the fluctuating activity is close to that of the underlying connection functions.Footnote 2 That is to say, as the strength of the inhomogeneity increases, the activity patterns become more entrained to the structure of the connections.

Fig. 8.6
figure 6

Plots (a)–(c) show how the correlation length of the connections effects the correlation length in u(x, t) for different values of A. Results are averages over 10 realisations of the inhomogeneous connections, with error given by the standard deviation. Also shown (grey line) is the average measured correlation length of the functions w 1(x) and w 2(x); the shaded region shows the standard deviation. Plot (d) shows the time correlation function C t (τ) as defined by Eq. (8.18). The grey line is from a system with λ = 0. 4 and the black from λ = 5, both with A = 0. 3. Plot (e) shows the fast Fourier transform of the time correlation functions for the same systems. Finally, (f) shows how the characteristic gradient m rms of the connection function effects the principal frequency of the fluctuating activity (black points). We include results from systems with A = 0. 1, A = 0. 3 and A = 1, with λ varying between 2 and 5 (since our definition of characteristic gradient only makes sense for λ > 1). For comparison (grey points) we also show the frequency of fluctuations from a system with a deterministic connection function containing a single gradient, as shown in Fig. 8.4a

Full size image

We turn now To temporal correlations. In the previous subsection we found that for a single “bump ” in connection density, the frequency of the fluctuations depends on the gradient of the function W(x). To see whether this is also true in the stochastic case we define a “characteristic gradient” of the inhomogeneous component of the connections

$$\displaystyle{ m_{\mathrm{rms}} = A\sqrt{\left <\left (\frac{dw_{1 } } {\mathit{dx}} + \frac{dw_{2}} {\mathit{dx}} \right )^{2}\right>}. }$$
(8.19)

Expanding the square gives

$$\displaystyle{\left <\left (\frac{dw_{1}} {\mathit{dx}} + \frac{dw_{2}} {\mathit{dx}} \right )^{2}\right> = \left <\left (\frac{dw_{1}} {\mathit{dx}} \right )^{2} + \left (\frac{dw_{2}} {\mathit{dx}} \right )^{2} + 2\frac{dw_{1}} {\mathit{dx}} \frac{dw_{2}} {\mathit{dx}} \right> = 2\left <\left (\frac{dw_{1}} {\mathit{dx}} \right )^{2}\right>,}$$

where we have used the fact the \(\langle d_{x}w_{1}\rangle =\langle d_{x}w_{2}\rangle\) and \(\langle d_{x}w_{1}d_{x}w_{2}\rangle = 0\), because there is no correlation between w 1 and w 2 (d x denotes derivative with respect to x). From the construction of the functions w 1 and w 2 we have

$$\displaystyle{ \left <\left (\frac{dw_{1}} {\mathit{dx}} \right )^{2}\right> = \frac{1} {\lambda ^{2}}, }$$
(8.20)

which gives a characteristic gradient of connections in the system of

$$\displaystyle{ m_{\mathrm{rms}} = \frac{A\sqrt{2}} {\lambda }. }$$
(8.21)

We note that this quantity is only relevant in the large λ limit, since we have used the approximation \(w_{2}(x^{{\prime}}) \approx w_{2}(x)\).

To examine how variation of m rms effects the fluctuations, we consider the Fourier transform of the function C t (τ) (Fig. 8.6e), i.e. we look at the frequency of the fluctuations. We take the frequency component with the largest amplitude to be the “principal frequency” of the fluctuations. Figure 8.6f shows how the principal frequency depends on m rms ; also shown is the same measurement for the deterministic inhomogeneity examined in the previous section (Fig. 8.4a). In general as the characteristic gradient of the connections increases, the frequency of the fluctuations increases; for the stochastic connections the frequency reaches a maximum between 0.1 and 0.15 Hz.

2.4 Persistent Fluctuations in 2D

In this section we examine results from 2D simulations. Due to the high computational overhead we consider smaller systems and fewer realisations of the connections than in the 1D case. Although this means that the results for the 2D case may be less reliable, reassuringly we see qualitatively the same behaviour as in 1D.

Fig. 8.7
figure 7

Top: Colour plots of u(x, t) for a 2D system undergoing persistent fluctuations. Parameters are λ = 5, A = 0. 3, g = 0. 8, and θ = 0. 1. The system is a square of side L = 30. Bottom: Plot showing how the input correlation length λ of the underlying 2D connections effects the measured correlation length of the fluctuating activity for various A. The grey lines show the measured correlation length of functions w 1(x) and \(w_{2}(\mathbf{x^{{\prime}}})\) with the shaded region showing the error in this. All results are averaged over five realisations of the stochastic connections

Full size image

We focus on the regime in which we observe persistent fluctuations ; Fig. 8.7 shows snapshots of u(x, t) at different times. We also show the dependence of the correlation length of the stochastic connection functions on the correlations in the activity. The grey solid line shows the measured correlation lengths of the underlying connection functions w 1(x) and \(w_{2}(\mathbf{x^{{\prime}}})\). The points show the measured correlation length of the activity, and we see behaviour the same as in the 1D case; as A increases the patterns in activity become slave to the correlations in the underlying connections.

3 Long Range Connections

In the previous section we described a model of inhomogeneous stochastic connections, however these have all been local in nature. That is to say, there are no connections between distant points, only spatial variation in the local density of connections. As detailed in Ref. [4], stochastic long range connections can be introduced into Eq. (8.1) via the following connection function

$$\displaystyle{ w(\mathbf{x},\mathbf{x^{{\prime}}}) = w_{ H}(\mathbf{x} -\mathbf{x^{{\prime}}}) + Aw_{ I}(\vert \mathbf{x} -\mathbf{x^{{\prime}}}\vert )\left [w_{ 1}(\mathbf{x}) + w_{2}(\mathbf{x^{{\prime}}})\right ]. }$$
(8.22)

As before w H is a homogeneous Gaussian connection function (Eq. (8.3)), and w 1(x) and \(w_{2}(\mathbf{x}^{{\prime}})\) are numerically generated stochastic functions representing additional connections into and out of the tissue at point x and x ′ respectively. This time however we choose these functions such that they are always positive. The function w I can be thought of as an envelope for the inhomogeneous connections; we choose a power law function

$$\displaystyle{ w_{I}(y) = \mathcal{N} \frac{\vert y\vert ^{-\alpha }} {1 + \vert y\vert ^{-\alpha }}, }$$
(8.23)

where the exponent α determines the range of the connections, and \(\mathcal{N}\) is chosen such that \(\int _{\varGamma }w_{I}(y)dy = 1\). If α > 1, w I is a narrow function, and we recover a local connection model; for α < 1, w I is a wide function and can extend throughout the system, i.e. there are a small number of long range connections between distant points. Figure 8.8a–c show typical realisations of w(x, x ′) in 1D for different values of α.

Fig. 8.8
figure 8

Top: Plots showing the connection function in Eq. (8.22) for a 1D system with (a) α = 6, (b) α = 1, and (c) α = 0. 1. Note that the homogeneous peak of w H is present in each case. In (c) the long range “tails” of the inhomogeneous connections have a small amplitude due to the normalisation \(\mathcal{N}\). Bottom: Average coherence (see Eq. (8.26)) of a 1D system with A = 1. 9 and g = 2. 9, averaged over 10 realisations of the connections for α = 6 (solid line) and α = 0. 1 (dotted line). The standard deviation is shown by the shaded regions (Figure adapted from Ref. [4])

Full size image

In the large α (local connections) regime, wave front solutions exist as in Sect. 8.2, provided two stable steady states solutions exist across the whole system. These are given by

$$\displaystyle{ \bar{u}(\mathbf{x}) = W(\mathbf{x})f\left (\bar{u}\right ), }$$
(8.24)

where we now define

$$\displaystyle{ W(\mathbf{x}) = 1 + A\int _{\varGamma }w_{I}(\mathbf{x} -\mathbf{x}^{{\prime}})\left [w_{ 1}(\mathbf{x}) + w_{2}(\mathbf{x}^{{\prime}})\right ]d\mathbf{x}^{{\prime}}- g. }$$
(8.25)

For the small α (long range connections) regime activity no longer propagates throughout the system at a finite speed: due the long range connections a local external stimulus can lead to the system entering the upper steady state at all points in the system.

As with the model described in the previous section, for some choice of parameters A and g, the system can support persistent fluctuations of activity. For the case of local connections (large α) fluctuations arise when there are some regions of the system which have two stable steady states, and other regions in which there is only one. There are regions in which \(u \rightarrow \bar{ u}_{1} = 0\), regions in which \(u \rightarrow \bar{ u}_{3}\), and connecting regions where u fluctuates.

In the regime of long range connections (small α) there is slightly different behaviour. There are fluctuations of activity at every point throughout the system. There are large large regions (where W(x) > θ) in which u fluctuates coherently remaining above θ, and smaller regions where u fluctuates more quickly about θ. As detailed in Ref. [4] the fluctuations originate in regions where W(x) cuts through the threshold θ, much as for the model discussed in the previous section. Here though, due to long range connections spanning the length of the system, this also leads to fluctuations at all other points.

In order to quantify the “coherently” fluctuating regions we use the following quantity to characterize fluctuations at points x and x ′:

$$\displaystyle{ \varGamma (X) = \left <\frac{\langle u(x,t)u(x - X,t)\rangle _{t}^{2}} {\langle u(x,t)^{2}\rangle _{t}\langle u(x - X,t)^{2}\rangle _{t}}\right>_{x}, }$$
(8.26)

where here \(X = x - x^{{\prime}}\), and as before angled brackets with subscripts denote average over space or time. A value of Γ(X) = 1 means that points separated by a distance X have activity which is fluctuating synchronously; a small value of Γ(X) means that fluctuations in these regions are fluctuating interdependently. Figure 8.8 shows that in a system with α < 1 the long range connections give rise to fluctuations which are coherent over large regions of the system. Similar results are obtained for 2D systems.

4 Conclusions

We have demonstrated that travelling front solutions in a continuum neural field model are robust to the addition of small amplitude, inhomogeneous, stochastic (local) connections, provided there is only weak inhibitory feedback. The wavefront connects a region in a quiescent \(\bar{u}_{1} = 0\) steady state with a region in a spatially varying \(\bar{u}_{3} =\bar{ u}_{3}(x)\) steady state, and travels with a time varying velocity. This provides a mechanism for the fluctuation in speed of travelling fronts of activity such as observed in “1D” slices of neural tissue (like those studied in Ref. [11]). Via a simple expansion \(\gamma (x) =\bar{\gamma } +\delta \gamma (x)\) predictions can be made about the dependence of the resulting distribution of front speeds on the magnitude of the inhomogeneity. The mean speed of a front of activity remains largely unaffected by the inhomogeneity. The variance of the speed is independent of A when the inhomogeneity is correlated on lengths shorter than 1, and grows with A 2 if the connections are correlated on lengths longer than 1 (in units of the width of the homogeneous connections). If the magnitude of the inhomogeneity A or the strength of the inhibition g are large enough to destabilise the upper steady state (i.e. W(x) < θ for some x), then there will be regions of the system through which the front cannot propagate.

Persistent fluctuations of activity are a new type of behaviour for continuum neural field models. By studying a simple deterministic connection function we have identified the origin of the fluctuations, and explained why such behaviour is observed for some realisations of the connections, but not others. All of the results presented in this chapter arise from initial conditions where u > θ across the entire system, meaning that the system will show persistent fluctuations if it is able to support them. A more natural scenario would be an initially quiescent system (u = 0), which is then excited by a transient, possibly spatially heterogeneous, external input. This could be likened to an idea initially suggested by Hebb in Ref. [20] known as cortical reverberation; Hebb hypothesised that a particular weak input pattern might elicit a large persistent response from a system, whereas a different, stronger, input pattern may have little effect. In terms of the present model, a short lived spatially varying input pattern may excite some regions of the system into the persistently fluctuating state; a different input (for example to a region where there is no upper steady state) may only excite the system for the duration of the input. This can also be linked to models of working memory [30], where a localised stimulus excites a region into an active state, and this high activity is maintained after the stimulation has ceased.

By examining correlations in the fluctuating activity, we find that, except for very small values of λ and A, the patterns follow the underlying connection functions w 1 and w 2. We expect this in the large λ regime since we can make the approximation that \(w_{2}(x^{{\prime}})\) does not vary within the width of the inhomogeneous connections, and u(x, t) will closely follow W(x). A natural question to ask is “Can we say anything about connectivity from measuring spatial correlations in activity patterns?” This could lead to testable predictions in experimental work, for example using fluorescent dyes [3].

In two dimensional systems with local inhomogeneous connections we find persistent fluctuations which are qualitatively the same as in 1D. Aside from the simple extensions to planar fronts and pulses, one could study, for example, the propagation of high activity from a locally excited region. In a homogeneous system the 2D analogue of planar fronts is an expanding circular region of high activity [23]; in an inhomogeneous model the high activity region would likely be irregularly shaped, and there could be, for example, channels of higher connectivity down which activity could propagate more rapidly, or conversely “barrier” regions with lower connectivity .

Finally we have shown that persistent fluctuations can also be found in systems with long range inhomogeneous connections. By allowing additional connections over long distances, fluctuations can become synchronised in different regions.