Monomial Phase: A Matrix Representation of Local Phase

Abstract

Local phase is a powerful concept which has been successfully used in many image processing applications. For multidimensional signals the concept of phase is complex and there is no consensus on the precise meaning of phase. It is, however, accepted by all that a measure of phase implicitly carries a directional reference. We present a novel matrix representation of multidimensional phase that has a number of advantages. In contrast to previously suggested phase representations it is shown to be globally isometric for the simple signal class. The proposed phase estimation approach uses spherically separable monomial filter of orders 0, 1 and 2 which extends naturally to N dimensions. For 2-dimensional simple signals the representation has the topology of a Klein bottle. For 1-dimensional signals the new phase representation reduces to the original definition of amplitude and phase for analytic signals. Traditional phase estimation using quadrature filter pairs is based on the analytic signal concept and requires a pre-defined filter direction. The new monomial local phase representation removes this requirement by implicitly incorporating local orientation. We continue to define a phase matrix product which retains the structure of the phase matrix representation. The conjugate product gives a phase difference matrix in a manner similar to the complex conjugate product of complex numbers. Two motion estimation examples are given to demonstrate the advantages of this approach.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Background

This chapter presents an overview of traditional phase concepts, and in particular discusses extension of the phase concept to encompass multi-dimensional signals.

Tracing the origin of the word “phase” one finds that it is back-formed as a singular form of modern Latin “phases”, plural of the Greek word “phasis” meaning “appearance”. Latin singular “phasis” was used in English from 1660. Phase is still commonly used to describe the cyclic appearance of the moon (Fig. 1). Non-lunar application is first attested 1841, meaning a difficult period in life is attested from 1913. In general phase refers to a particular or possible way of viewing something, to a stage or period of change or development.

Fig. 1

The word phase is commonly used to describe the cyclic appearance of the moon. In general phase refers to a particular or possible way of viewing something, to a stage or period of change or development. In signal processing phase traditionally refers to a real number in a bounded interval, a phase angle, here denoted θ (Increasing θ show moon phases in the order they appear seen from the southern hemisphere)

The short introduction above is intended to underline the fact that the meaning of a concept is determined by the way it is used and that concepts will naturally evolve to best suit the communication needs of a given group of people. This is no doubt true also in the evolution of science. We will review, investigate, and further develop the concept of phase in the context of signal processing.

In signal processing the precise meaning of a concept is defined by it’s mathematical representation. A meaningful application of most signal processing concepts requires that the data to be processed represent some aspect of the real world in an orderly way. More precisely, it is generally required that an increased difference between real world events results in an increased distance between the data points that represent these events. Working with representations where these requirements are not met would make many signal processing concepts meaningless and would also greatly reduce the possibility of gaining an intuitive understanding of how suitable processing can be carried out. For many real world aspects, however, establishing well-behaved representations is a non-trivial task and in these cases a first and crucial step of any analysis is to find such a representation. In this chapter the required features of a suitable mathematical representation of local phase for N-dimensional signals are discussed and a novel matrix representation is proposed.

1.1 Traditional 1-Dimensional Signal Processing Concepts

Description and estimation of local spatio-temporal structure has a long history and numerous analysis tools have been developed. In addition to local phase, local orientation, frequency, scale, motion, and locality of estimates are prominent examples of features that have been considered central in the analysis. In the field of signal processing phase was originally used as a descriptor for one-dimensional signals. The concept of phase was later broadened to serve as a descriptor of multi-dimensional structure.

Many of the popular image analysis tools related too local phase have roots that can be traced to early work in signal processing and optics, e.g. Riesz transforms [1], Zernike moments [2, 3], and Gabor signals [4]. Regardless of this development the first stages in the analysis remain the same. In most cases the processing starts by performing local linear combinations of image values, e.g. convolution operators.

Important signal descriptors were often first developed for temporal, 1-dimensional signals. Important well-known concepts are the Fourier phase and the shift theorem, describing how the Fourier phase is affected by moving the signal. However, since the sine wave basis functions in the Fourier transform are inherently global, the Fourier phase concept is of limited practical utility. Real world signals are often non-stationary (images, volumes, sequences) and thus local features in time and space are often of more interest. The local phase concept is readily defined via local basis functions and the Hilbert transform [5–7]. The first mention of phase in a 2-dimensional image processing context appears to be found in [8]. Early work on phase in more than one dimension is found in [9–13]. Work on extensions of the Hilbert transform to higher dimensions can be found in [14]. Related work can also be found in references [15–26]. An overview of phase representation in signal processing is given in [27]. More recent relevant work on phase related topics is presented in [28–31]. Specific relations of the cited publications to the present work will be commented on in the proper context below.

1.1.1 The Hilbert Transform

At the heart of the 1-dimensional concepts of local phase, local frequency, and local amplitude lies the Hilbert transform. Denoting the spatial variable by x the Hilbert transform of a signal s(x) is obtained through the following convolution operation. Following the definition and notation of Bracewell [7], we write this as:

$$\displaystyle{ \mathsf{s}_{\!\!_{\mathcal{H}}}(x) = \mathsf{s}(x)\, {\ast}\,\frac{-1} {\pi x} }$$

(1)

where ∗ denotes the convolution operator.¹ Let ω denote the frequency variable and $\mathsf{S}_{\!\!_{\mathcal{H}}}(\omega )$ denote the Fourier transform corresponding to $\mathsf{s}_{\!\!_{ \mathcal{H}}}(x)$. Then, since convolution in the spatial domain corresponds to multiplication in the Fourier domain, the Fourier transform of $\frac{-1} {\pi x}$ is i sign(ω), can be compactly expressed in the Fourier domain:

$$\displaystyle{ \mathsf{S}_{\!\!_{\mathcal{H}}}(\omega ) = i\;\mathsf{S}(\omega )\,\mathrm{sign}(\omega ) }$$

(2)

where sign(ω) equals one for ω > 0, zero for ω = 0 and minus one for ω < 0. Hence, the Fourier transform of $\mathsf{s}_{\!\!_{\mathcal{H}}}$ is obtained by multiplying S by the imaginary unit i and then change sign of the result for negative frequencies. Another way of understanding this transform is that the argument of the frequency components are turned an angle $\frac{\pi }{2}$ in the positive direction for positive frequencies and in the negative direction for negative frequencies.

1.1.2 The Analytic Signal

Having defined the Hilbert transform we can now define the analytic signal, $\mathsf{s}_{_{ A}}$, corresponding to a real signal s. The analytic signal is a complex signal and is uniquely defined as:

$$\displaystyle{ \mathsf{s}_{_{A}}(x) = \mathsf{s}(x) - i\;\mathsf{s}_{\!\!_{\mathcal{H}}}(x) }$$

(3)

As can be seen, the real part of the analytic signal is the original signal itself and the imaginary part is it’s Hilbert transform times − i. This is illustrated in Figs. 2 and 5. To summarize, the relations between a real signal and it’s corresponding analytic signal is, in the spatial and frequency domains given by:

Fig. 2

Figure showing perhaps the simplest possible analytic signal. The real part is a cosine, s(x) = cos(x), and the imaginary part is a sine, $\mathsf{s}\!\!_{_{\mathcal{H}}}(x) = -\sin (x)$. The corresponding analytic signal is a complex exponential, s _A (x) = e ^ix. Color code: white means $\varphi = 0$ (zero phase), dark gray means $\varphi =\pi$, green means $\varphi =\pi /2$ and red means $\varphi = -\pi /2$. The gray ‘glass’ tube represents the signal amplitude. The original signal is shown in black in the center

$$\displaystyle{ \left \{\begin{array}{lll} \mathsf{s}_{A}(x)& = [\,\delta (x)\; +\, \frac{i} {\pi x}\;\,] {\ast}\mathsf{s}(x) & \\ \mathsf{S}_{A}(\omega ) & = [\,1 +\mathrm{ sign}(\omega )\,]\;\,\mathsf{S}(\omega ) = 2\,H(\omega )\,F(\omega )&\ \ \ \ \ \ \ \ \end{array} \right. }$$

(4)

where H(⋅ ) is the Heavyside step function: H(ω) = 1 for u > 0 and H(ω) = 0 for ω < 0. Hence, the analytic signal corresponding to s is obtained by suppressing all it’s negative frequencies and multiplying by two. Two simple examples are:

$$\displaystyle{ \begin{array}{ll} \mathsf{s}(x) =\cos (\omega x)\;\;\;\; \leftrightarrow \;\;\;\;\mathsf{s}_{A}(x) =\;\;\; e^{i\omega x} \\ \mathsf{s}(x) =\sin (\omega x)\;\;\;\; \leftrightarrow \;\;\;\;\;\mathsf{s}_{A}(x) = -\mathit{ie}^{i\omega x} \end{array} }$$

(5)

These two sinusoidal examples have infinite support, the analytic signal has a constant magnitude and the difference can be describes as a shift in phase angle, see Fig. 2.

1.1.3 Analytic Signal Examples

An interesting family of analytic signals, s _A (x), and the corresponding Fourier transforms, S _A (ω), is given by the Poisson distribution related function:

$$\displaystyle{ \left \{\begin{array}{ll} \mathsf{s}_{A}(x) = (1\! + ix)^{-\kappa } \\ \mathsf{S}_{A}(\omega ) = \frac{H(\omega )} {\varGamma (\kappa )} \;\omega ^{\kappa -1}\,e^{-\omega } \end{array} \right. }$$

(6)

where Γ(⋅ ) is the gamma function and κ ( > 0) is a real number determining the shape of the analytic signal. Figure 3 shows four examples from this family of functions in the Fourier domain. Figures 4 and 5 show the corresponding signal in the spatial (or temporal) domain for κ = 4. Figure 4 shows a traditional plot where the ‘wrap around’ discontinuity of the phase angle at ±π can be seen. Figure 4 shows the analytic signal in a three-dimensional space where the phase can be represented as a continuously varying vector in the complex plane, $e^{\varphi (x)}$.

Fig. 3

Fourier domain plots of four different analytic signals (or quadrature filters) from the family of analytic functions given by Eq. (6). Regardless of the value of κ there are no negative frequencies present. From left to right the values of κ are: 2, 4, 8 and 16. The plots have been normalized to have a maximum value of one (Different colors simply indicate different curves)

Fig. 4

Traditional plot of an analytic signal from the family given in Eq. (6) with κ = 4. The figure shows the real part (blue), the imaginary part (red), the amplitude (green) and the phase angle with wrap-around at ±π (black)

Fig. 5

Figure showing a relatively broad-band analytic signal from the family given in Eq. (6). Here κ = 4 implying that the phase angle, $\varphi$, will make two full 2π turns from start to end of the signal. Color code: white means $\varphi = 0$ (zero phase), dark gray means $\varphi =\pi$, green means $\varphi =\pi /2$ and red means $\varphi = -\pi /2$. The gray ‘glass bulb’ represents the signal amplitude. The original signal is shown in black in the center

1.1.4 Local Amplitude, Phase and Frequency

Three traditionally important and fundamental concepts in 1-dimensional signal processing are:

$$\displaystyle{ \begin{array}{ll} \mathrm{The\ local\ amplitude:} &\mathsf{A}(x) \\ \mathrm{The\ local\ phase\ angle:\ \ \ \ }&\varphi (x) \\ \mathrm{The\ local\ frequency:} &\frac{\partial \varphi (x)} {\partial x}\\ \end{array} }$$

(7)

An analytic signal can be directly expressed in terms of amplitude and phase:

$$\displaystyle{ \begin{array}{ll} \mathsf{s}_{A}(x) = \mathsf{A}(x)\;e^{i\,\varphi (x)}\end{array} }$$

(8)

In general, and in particular for analytic signals constructed from a real signal according to Eq. (3), the amplitude varies more slowly than the phase and the two concepts provide a useful complementary local representation of a signal. This way of expressing the analytic signal has found numerous applications in signal processing, [7].

1.1.5 Quadrature Filters

A filter that has the properties of an analytic signal is known as a quadrature filter. The real even part will pick up the even part of the signal and the imaginary odd part will pick up the odd part of the signal. If the desired Fourier response is only known for the even or the odd part the missing part can be generated directly in the Fourier domain by using the sign function.

$$\displaystyle{ \left \{\begin{array}{ll} F_{o}(\omega ) =\mathrm{ sign}(\omega )\,F_{e}(\omega ) \\ F_{e}(\omega ) =\mathrm{ sign}(\omega )\,F_{o}(\omega )\end{array} \right. }$$

(9)

In the spatial domain, the even filter is real and the odd filter is imaginary and it is natural to combine them into a single complex filter, f(x):

$$\displaystyle{ \begin{array}{ll} f(x)& = f_{e}(x) + f_{o}(x) \\ & = m(x)\,e^{i\,\theta (x)}\end{array} }$$

(10)

Equation (10) shows that the filter can be expressed as a product of the filter magnitude, m, and a unitary complex number, e ^{i  θ(x)}. The argument (modulo 2π) of the latter is traditionally referred to as the phase. It is, however, from a representational point of view much preferable to use the unitary complex number, ψ = e ^{i  θ(x)}, as the representation of phase since it is continuous and does not suffer from the wrap-around discontinuity. This will also be consistent with the representation for higher dimensional phase suggested below. When referring to the real argument, θ, we will use the term ‘phase angle’.

Since the Hilbert transform is defined in one dimension the analytic signal is only well-defined for one-dimensional signals as well. The Hilbert transform can, however, be used in higher dimensional spaces if a direction in this space is specified. Local phase estimation based on such directed quadrature filter responses [8, 17] has found extensive use in image processing. The quadrature filter response to a signal, s, can be expressed as a convolution in the spatial domain or as a multiplication in the Fourier domain, i.e.

$$\displaystyle{ \begin{array}{ll} \mathsf{q}(x)& = f(x) {\ast}\mathsf{s}\:\!(x) \\ & = \mathcal{F}^{-1}\!\left [\,F(\omega )\;\mathsf{S}(\omega )\:\right ] \end{array} }$$

(11)

where ∗ denotes the convolution operator, S denotes the Fourier transform of s, $\mathcal{F}^{-1}$ denotes the inverse Fourier transform. The quadrature filter response can also be represented in terms of amplitude, A and phase angle θ or phase ψ:

$$\displaystyle{ \begin{array}{ll} \mathsf{q}(x)& = \mathsf{A}(x)\,e^{i\,\theta (x)} \\ & = \mathsf{A}(x)\psi \:\!(x)\end{array} }$$

(12)

The magnitude of the filter response reflects the signal energy and the argument reflects the relationship between the evenness and oddness of the signal (see Fig. 6).

Fig. 6

Plots of a quadrature filter response to a signal (top) containing four typical events: a positive ‘bump’, a positive gradient edge, a a negative ‘bump’ and a negative gradient edge. The real response is shown in blue, the imaginary in red and the amplitude in gray

1.1.6 Interpretation of Local Phase

The fundamental property of local phase represents the relation between even and odd signal content at specific spatial location. The local phase has a number of interesting invariance and equivariance properties that makes it an important feature in image processing. Local phase estimates are, for example, invariant to signal energy, the phase varies in the same manner regardless if there are small or large signal variations. Further, local phase and spatial position have a tight relationship and local phase generally varies continuously with spatial position thus enabling sub-pixel/voxel resolution. In high frequency areas the phase changes faster than in low frequency areas. The phase angle derivative is called local or instantaneous frequency [7, 16]. Phase also has interesting invariance properties with respect to scaling [9–11]. Figure 7 shows the intensity profile over a number of lines and edges.

Fig. 7

A simple display of the 1-dimensional phase concept. Bottom: an image with varying intensity in the x-direction. Marked with circles are from left to right: a white line, a positive gradient edge, a black line and a negative gradient edge. Middle: the corresponding intensity as a 1-dimensional signal. Top: the local signal shapes placed at the corresponding phase angle positions

In this chapter we will show how the concept of phase can be generalized to higher dimensional signal spaces.

2 Phase Representation for Multi-dimensional Signals

For multidimensional signals the equivalent of the 1-dimensional quadrature filter response amplitude is the structure tensor [15, 29]. Structure tensors are, just as the response amplitude, phase invariant. However, the relationships between the different filters used to produce the structure tensor holds important complementary information about the neighborhood. These relations are the basis for the concept known as local phase. Local phase is a powerful concept in it’s own right and has been successfully used in many applications. As is the case with the structure tensor there is no consensus on the precise meaning of phase. In this chapter we will make an effort to define what the concept of phase should imply.

2.1 General Representational Considerations

At a high level of abstraction a representation of any concept can be viewed in terms of equivariance and invariance. A good representation should vary in a way that precisely reflects changes in the feature that is represented. At the same time the representation should be invariant to changes in features that are considered to leave that which is represented unchanged. The common understanding is that local phase should be equivariant to a relation between oddness and evenness of the signal at a given position. It is also accepted by all that a measure of phase necessarily carries a directional reference, i.e. it should be equivariant with rotation of the signal. That the phase of a signal should be invariant to the signal mean level and the signal amplitude is also not debated. We will, in addition, consider the following properties to apply to a good phase representation for multi-dimensional signals:

• Uniqueness

• Continuity

• A shift invariant manifold metric

The purpose of these requirements is to ensure that common signal processing operations, such as averaging and differentiation, can be meaningfully applied to a spatio-temporal phase field. Precisely what the requirements are taken to imply will be made clear in a proper mathematical setting in Sect. 3.

2.2 Monomial Filters

All local phase estimation approaches are based on the use of a set of filters onto which each local neighborhood is projected. The design of these filters directly determines crucial aspects of the performance of the estimator. The filters should provide an appropriate basis for representing the targeted features of the signal. A natural requirement is that the estimate directly reflects rotations of the neighborhood, i.e. the estimate should be equivariant with rotation, but be invariant to other transformations, e.g. change of scale. Another important aspect, not further discussed here, is the locality of the estimates, see [23].

Here we present a class of filters designed to meet the above requirements, monomial filters. The monomial filters are spherically separable, i.e. defined as a product of one radial and one directional part:

$$\displaystyle{ F(\boldsymbol{\omega }) = R(\rho )\,D(\,\boldsymbol{\hat{\omega }}\,) }$$

(13)

where $\boldsymbol{\omega }$ is the Fourier domain coordinate, $\rho =\| \boldsymbol{\omega }\|$ and $\boldsymbol{\hat{\omega }} = \frac{\boldsymbol{\omega }}{\rho }$.

2.2.1 Radial Part

The radial part is not important for the following discussions on phase and could in principle be set to unity. In practice, however, there will always be a non-constant radial part involved, typically it is a bandpass filter (R(0) = 0), e.g. a lognormal function, [8, 17], a logerf function, [23], or a function given by | S _A (ω) | in Eq. (6).

2.2.2 Directional Matrix

The directional part consists of monomials i.e. products of non-negative integer powers of the components of $\boldsymbol{\hat{\omega }}$. Performing n repeated outer products of $\boldsymbol{\hat{\omega }}$ will contain all order n component products.

$$\displaystyle{ \boldsymbol{D}_{n}(\boldsymbol{\,\boldsymbol{\hat{\omega }}}) = \boldsymbol{\hat{\omega }}^{\otimes n} =\mathop{\underbrace{ \boldsymbol{\hat{\omega }} \otimes \boldsymbol{\hat{\omega }}\,\;\ldots \,\otimes \,\boldsymbol{\hat{\omega }}\,}}\limits _{ n\ \mathrm{entities}} }$$

(14)

For the following investigation of phase only orders 0, 1 and 2 will be needed. In the 2D case, using the notation $\boldsymbol{\hat{\omega }} = (\mu,\,\nu )^{T}$, we have:

$$\displaystyle\begin{array}{rcl} D_{0}(\boldsymbol{\hat{\omega }})& =& 1{}\end{array}$$

(15)

$$\displaystyle\begin{array}{rcl} \boldsymbol{D}_{1}(\boldsymbol{\hat{\omega }})& =& \left (\begin{array}{c} \mu \\ \nu \end{array} \right ){}\end{array}$$

(16)

$$\displaystyle\begin{array}{rcl} \boldsymbol{D}_{2}(\boldsymbol{\hat{\omega }})& =& \left (\begin{array}{cc} \mu ^{2} & \mu \nu \\ \mu \nu & \nu ^{2}\\ \end{array} \right ){}\end{array}$$

(17)

It is worth noting here that $\boldsymbol{D}_{1}(\boldsymbol{\boldsymbol{\hat{\omega }}})$ corresponds to the Riesz transform, [1] in the general case and the Hilbert transform in the one-dimensional case since $\boldsymbol{\hat{\omega }} = \frac{\omega } {\vert \omega \vert } =\mathrm{ sign}(\boldsymbol{\boldsymbol{\omega }})$.

2.2.3 Monomial Filter Matrices

To construct matrices holding proper filters we simply multiply the matrix holding the directional responses, $\boldsymbol{D}_{n}(\boldsymbol{\hat{\omega }})$, with the radial function, R(ρ). For each order n ≥ 0 a monomial filter matrix is defined as:

$$\displaystyle{ \boldsymbol{F}_{n}(\boldsymbol{\omega }) = R(\rho )\,\,\,\boldsymbol{D}_{n}(\boldsymbol{\hat{\omega }}) }$$

(18)

2.3 Monomial Filter Response Matrices

The next step is to apply a monomial filter matrix to a signal, thus obtaining a monomial filter response matrix. This can be done by convolving the signal with each of the filters in the filter matrix and storing the results in the corresponding positions. Using an FFT approach the same result can also be obtained multiplying the Fourier transform of the signal by each filter in the Fourier domain.

Let the spatial domain correspondence of the monomial filter matrix $\boldsymbol{F}_{n}$ be denoted F _n . Each element of F _n contains the convolution kernel of the corresponding FD filter function in $\boldsymbol{F}_{n}$. If the multi-dimensional signal is denoted $\mathsf{s}(\mathbf{x})$, where x denotes the spatial coordinates, the monomial filter response matrix, $\mathsf{\mathbf{Q}}_{n}(\mathbf{x})$, is defined as:

$$\displaystyle{ \mathsf{\mathbf{Q}}_{n}(\mathbf{x}) = \mathbf{F}_{n}(\mathbf{x}) {\ast}\mathsf{s}\:\!(\mathbf{x}) }$$

(19)

where ∗ denotes the convolution operator.

Denoting the Fourier transform of s by S the same relation can be expressed using multiplication in the Fourier domain:

$$\displaystyle{ \mathsf{\mathbf{Q}}_{n}(\mathbf{x}) = \mathcal{F}^{-1}\!\left [\boldsymbol{F}_{ n}(\boldsymbol{\omega })\;\,\mathsf{S}(\boldsymbol{\omega })\:\right ] }$$

(20)

Here $\mathcal{F}^{-1}$ denotes the inverse Fourier transform.

In this general description each element of $\mathsf{\mathbf{Q}}_{n}(\mathbf{x})$ contains the monomial filter responses for the entire signal. Since all filtering operations in this paper are shift invariant we may, in the interest of clarity and without loss of generality, from now on omit to denote the spatial coordinate vector x and only consider the filter matrix response at x = 0.

2.4 Signal Classes

It will be useful for the following discussion to define two different classes of signals. We will here define the sinusoidal and simple signal classes.

2.4.1 Sinusoidal Signals

We first present the simplest possible case, a sinusoidal signal with amplitude A, spatial frequency $\mathsf{\mathbf{u}}$, and zero phase.

$$\displaystyle{ \mathsf{s}(\mathbf{x}) = \mathsf{A}\cos (\mathsf{\mathbf{u}}^{\mathrm{T}}\mathbf{x}) }$$

(21)

For this case the monomial filter response matrix dependence on the signal frequency, $\mathsf{\mathbf{u}}$, is given by:

$$\displaystyle{ \begin{array}{lcl} \mathsf{\mathbf{Q}}_{n}(\mathsf{\mathbf{u}})& =&\:\mathsf{A}\:R(\rho )\;\boldsymbol{D}_{n}(\mathsf{\mathbf{\hat{u}}})\ \ \ \ \ \ \ \mathrm{for\ even\ }n \end{array} }$$

(22)

where $\rho =\| \mathsf{\mathbf{u}}\|$ and $\,\mathsf{\mathbf{\hat{u}}}\, = \frac{\mathsf{\mathbf{u}}} {\rho }$. Note that in this special case of zero phase, i.e. a symmetric signal, the response will be zero for odd n. For odd signals, i.e.

$$\displaystyle{ \mathsf{s}(\mathrm{\mathbf{x}}) = \mathsf{A}\sin (\mathsf{\mathbf{u}}^{\mathrm{T}}\mathbf{x}) }$$

(23)

even orders will be 0 and odd order responses are given by:

$$\displaystyle{ \mathsf{\mathbf{Q}}_{n}(\mathsf{\mathbf{u}}) =\: -i\:\mathsf{A}\:R(\rho )\;\boldsymbol{D}_{n}(\mathsf{\mathbf{\hat{u}}})\ \ \ \ \ \ \ \ \ \mathrm{for\ odd\ \ }n }$$

(24)

For a general sinusoidal with phase θ, i.e.

$$\displaystyle{ \mathsf{s}(\mathbf{x}) = \mathsf{A}\cos (\mathsf{\mathbf{u}}^{\mathrm{T}}\mathbf{x}+\theta ) }$$

(25)

both even and odd order filters will respond and we get:

$$\displaystyle{ \mathsf{\mathbf{Q}}_{n}(\theta,\mathsf{\mathbf{u}}),\:=\: \left \{\begin{array}{rlcl} \mathsf{A}&\!\cos (\theta )\,R(\rho )\,\boldsymbol{D}_{n}(\,\mathsf{\mathbf{\hat{u}}}\,)\ \ \ \ \ &\mathrm{for\ even\ }&n \\ - i\,\mathsf{A}&\!\sin (\theta )\,R(\rho )\,\boldsymbol{D}_{n}(\,\mathsf{\mathbf{\hat{u}}}\,)\ \ \ \ \ \ & \mathrm{for\ odd\ \ } &n \end{array} \right. }$$

(26)

2.4.2 Simple Signals

Following [17] we define simple signals to be signals that can be expressed as:

$$\displaystyle{ \mathsf{s}(\mathbf{x}) = \mathsf{g}(\mathsf{\mathbf{\hat{u}}}^{\mathrm{T}}\mathbf{x}) }$$

(27)

Here g(⋅ ) is any real one variable function and $\mathsf{\mathbf{\hat{u}}}$ is a unit vector giving the orientation of the signal. For this case the monomial filter response matrix dependence on the signal orientation, $\mathsf{\mathbf{\hat{u}}}$, is given by:

$$\displaystyle{ \begin{array}{lcl} \mathsf{\mathbf{Q}}_{n}& =&\:\mathsf{A}_{n}\;\boldsymbol{D}_{n}(\mathsf{\mathbf{\hat{u}}}) \end{array} }$$

(28)

Here A _n is the local amplitude of the filter response. By factoring out the directional dependence, A _n depends only on the radial filter function, R(ρ), and the signal generating function, g(x). By he Fourier slice theorem, [7], we know that the Fourier transform of a simple signal is non-zero only on a line through the origin. This makes for a simple solution. Letting v be a 1-dimensional frequency variable and denoting the Fourier transform of g(x) by G(v) we find the filter response amplitude as:

$$\displaystyle{ \left \{\begin{array}{lll} \mathsf{A}_{n} = \mathsf{A}_{\mathsf{e}} = &\int _{v}R(\vert v\vert )\:\mathsf{G}(v)\:dv\ \ \ \ \ \ \ \ \ &\mathrm{for\ even\ }n \\ \mathsf{A}_{n} = \mathsf{A}_{\mathsf{o}} =&\int _{v}R(\vert v\vert )\:\mathsf{G}(v)\;\mathrm{sign}(v)\,dv\ \ \ \ \ &\mathrm{for\ odd\ }n \end{array} \right. }$$

(29)

Unless explicitly mentioned all signals will in the following be regarded simple.

2.5 Vector Phase Representations

Next we turn to a somewhat more advanced phase representation approach. Monomial quadrature filter sets support a simple yet general definition of phase. We will show how a continuous and consistent N​ +​ 1 dimensional vector phase representation can be constructed.

2.5.1 Monomial Quadrature Filter Matrices

The final step required for attaining filter matrices that can be used for local phase estimation is to concatenate one even and one odd monomial filter matrix to form a monomial quadrature filter matrix, $\boldsymbol{F}_{mn}(\boldsymbol{\omega })$.

$$\displaystyle{ \begin{array}{lcl} \boldsymbol{F}_{mn}(\boldsymbol{\omega })& =&\{\boldsymbol{F}_{m}(\boldsymbol{\omega }),\;\boldsymbol{F}_{\mathsf{n}}(\boldsymbol{\omega })\}\end{array} }$$

(30)

Where the “{}” brackets denotes a simple juxtaposition of the components, i.e. there are no requirements on the types or sizes of the assembled components. The monomial quadrature filter response matrix, $\mathsf{\mathbf{Q}}_{nm}$, is, as before, obtained through convolution in the spatial domain or multiplication in the Fourier domain and we have:

$$\displaystyle{ \mathsf{\mathbf{Q}}_{mn} =\{ \mathsf{\mathbf{Q}}_{m},\;\mathsf{\mathbf{Q}}_{n}\} }$$

(31)

2.5.2 Phase from Orders 0 and 1

The simplest case of phase estimation uses filters of orders 0 and 1, i.e.

$$\displaystyle{ \begin{array}{lcl} \boldsymbol{F}_{\!01}(\mathsf{\mathbf{u}})\:& =&\:\{\boldsymbol{F}_{0}(\mathsf{\mathbf{u}})\:\boldsymbol{,}\:\boldsymbol{F}_{1}(\mathsf{\mathbf{u}})\,\} \\ & =&\:R(\rho )\:\{1\:\boldsymbol{,}\:\,\mathsf{\mathbf{\hat{u}}}\,\}\end{array} }$$

(32)

The filter response using F _​01, the spatial counterpart of $\boldsymbol{F}_{\!01}$, can then be written:

$$\displaystyle{ \begin{array}{ll} \mathsf{\mathbf{Q}}_{01} & = \mathbf{F}_{01} {\ast}\mathsf{s} \\ & =\{\, \mathsf{A}_{e}\;\boldsymbol{,}\;\,\mathsf{A}_{o}\,\,\mathsf{\mathbf{\hat{u}}}\,\,\} \end{array} }$$

(33)

A phase representation, $\boldsymbol{\theta }_{01}$, is then obtained by simply normalizing the filter response matrix, $\mathsf{\mathbf{Q}}_{01}$, using the Frobenius norm.

$$\displaystyle{ \begin{array}{ll} \boldsymbol{\varPsi }_{01} \equiv \,\mathsf{\mathbf{\hat{Q}}}\,_{01} & = \frac{\mathsf{\mathbf{Q}}_{01}} {\|\mathsf{\mathbf{Q}}_{01}\|} \\ & = \frac{\{\,\mathsf{A}_{e}\;\boldsymbol{,}\;\,\mathsf{A}_{o}\,\,\mathsf{\mathbf{\hat{u}}}\,\,\}} {\sqrt{\mathsf{A} _{e }^{2 }+\mathsf{A} _{o }^{2}}} \\ & =\{\cos (\theta )\;\boldsymbol{,}\;\,i\,\sin (\theta )\:\,\mathsf{\mathbf{\hat{u}}}\,\:\} \end{array} }$$

(34)

A color coded representation of the N + 1 dimensional phase for 2-dimensional signals is shown in Fig. 8. The eight plots in Fig. 9 show the local phase when moving in two different directions in a gray scale image using three different types of visualizations.

Fig. 8

Two views (from above and from below) of the color coded 3-dimensional vector phase space for 2-dimensional signals. The color code is as follows: white means θ = 0, increased saturation means higher θ and full saturation means $\theta =\pi /2$. Gray means θ = π. The color indicates the direction, $\varphi$. Green/red indicates x-direction. Blue/yellow indicates y-direction. Black iso-line are drawn for $\theta = \mathit{pi}/4,\pi /2,3\pi /2$ and for $\varphi = 0,\mathit{pi}/2$. Right: the same color coded space seen from below

Fig. 9

Plots of the N + 1 dimensional vector phase space for 2-dimensional signals. Left: 3D coordinate system with direction angle, $\varphi$, and complex phase angle, θ. Middle: the same space color coded seen from above. White means θ = 0, increased saturation means higher θ. Full saturation means $\theta =\pi /2$, the color indicates the direction, $\varphi$. A black iso-line is drawn at $\theta \ =\ \pi /4$. Right: the same color coded space seen from below. Gray means θ = π. A black iso-line is drawn at $\theta = 3\pi /4$

2.6 Relations to Previous Work

Before moving on to discussing higher order phase representations we would like to point out a number of interesting relations to classical concepts and previous work.

2.6.1 One-Dimensional Case

For one-dimensional signals the monomial response matrix, $\mathsf{\mathbf{Q}}_{01}$, reduces to the original definition of amplitude and phase for analytic signals, [7], i.e.

$$\displaystyle{ \mathsf{\mathbf{Q}}_{01} = \vert \mathsf{\mathbf{Q}}_{01}\vert \,\boldsymbol{\varPsi }_{01} = Ae^{i\,\theta } }$$

(35)

2.6.2 Monomial Structure Tensors

Although it is not the focus of the present chapter it seems appropriate to here mention that using the monomial filter response matrix the corresponding local structure tensor is, as outlined in [29], found as:

$$\displaystyle{ \mathsf{\mathbf{T}}_{\mathit{nm}}^{2} = \mathsf{\mathbf{Q}}_{\mathit{ nm}}\,\mathsf{\mathbf{Q}}_{\mathit{nm}}^{T} }$$

(36)

2.6.3 Phase from Directed Quadrature Filters

The construction of classical quadrature filter pairs, [8, 17], is a generalization of the analytic signal concept to higher dimensions but require pre-defined filter directions. A simple approach to local phase analysis of multidimensional signals is to measure a number of 1-dimensional phases from a set of quadrature filters given a number of fixed directions. The complex scalar response of a quadrature filter can, in the traditional manner, be expressed in terms of local amplitude, $\mathsf{A} = \vert \,\mathsf{q}_{\boldsymbol{k}}\vert$, and local phase, $\psi _{\boldsymbol{k}} =\hat{ \mathsf{q}}_{\boldsymbol{k}}$ or phase angle, $\theta _{\boldsymbol{k}} =\mathrm{ arg}(\mathsf{q}_{\boldsymbol{k}})$.

$$\displaystyle{ \begin{array}{lcl} \mathsf{q}_{\boldsymbol{k}}\:& =&\;\mathsf{A}\;\psi _{\boldsymbol{k}}\: =\: \mathsf{A}\;e^{i\theta _{\boldsymbol{k}}} \end{array} }$$

(37)

A problem is that $\psi _{-k} =\psi _{ k}^{{\ast}}$ implying that the same information can end up being represented in two ways, i.e. the representation is not one-to-one. For simple signals the measured phase will be invariant to the filter direction (except for the conjugate problem above) but for non-simple signals the directional dependence of the local phase can be highly complex and difficult to interpret. Although a lot of information about the local phase will be present in the joint outputs of a set of quadrature filters in different directions we do not consider it a preferable starting point for producing a good phase representation.

2.6.4 The N + 1 Dimensional Phase Vector

For 2-dimensional signals the monomial phase, $\boldsymbol{\varPsi }_{01}$, is equivalent to the 3-dimensional vector phase definition for 2-dimensional signals due to Knutsson presented in [10] (1989). For higher dimensional signal spaces it generalizes to the N + 1 dimensional vector phase definition given in [17] (1995), i.e.

$$\displaystyle{ \varPsi _{_{N+1}} = \varPsi _{01} = \frac{\mathsf{\mathbf{Q}}_{01}} {\|\mathsf{\mathbf{Q}}_{01}\|} = \frac{\{\,\mathsf{A}_{0}\;\boldsymbol{,}\;\,\mathsf{A}_{1}\,\,\mathsf{\mathbf{\hat{u}}}\,\,\}} {\sqrt{\mathsf{A} _{0 }^{2 } + \mathsf{A} _{1 }^{2}}} }$$

(38)

2.6.5 Monogenic Signal

The Felsberg monogenic signal, F _M , defined for 2-dimensional signals, [18] (2001), will in our notation be written:

$$\displaystyle{ F_{M} = \mathsf{\mathbf{Q}}_{01} =\{\, \mathsf{A}_{0}\;\boldsymbol{,}\;\,\mathsf{A}_{1}\,\,\mathsf{\mathbf{\hat{u}}}\,\,\} }$$

(39)

In other words it is identical to the monomial filter response matrix using orders 0 and 1. An extension to higher dimensional signals is straight forward and will also be expressed by Eq. (39). This relates directly to the N + 1 dimensional phase vector above and to the conformal monogenic signal, [28, 30].

2.6.6 Monogenic Phase Vector

The monogenic phase, $\varphi _{M}$, defined for 2-dimensional signals, [18] (2001), is found by the following mapping of the monogenic signal:

$$\displaystyle{ \varphi _{M} =\tan ^{-1}\left (\frac{\|\,\mathsf{A}_{1}\,\|} {\mathsf{A}_{0}}\right )\,\mathsf{\mathbf{\hat{u}}}\,_{\perp } }$$

(40)

where tan⁻¹ ∈ [ 0,  π [ and $\,\,\mathsf{\mathbf{\hat{u}}}\,_{\perp } = (-\mathsf{u}_{y},\mathsf{u}_{x})^{T}$ if $\,\mathsf{\mathbf{\hat{u}}}\, = (\mathsf{u}_{x},\mathsf{u}_{y})^{T}$. The definition monogenic phase is formulated in the 3-dimensional monogenic signal space and $\,\mathsf{\mathbf{\hat{u}}}\,_{\perp }$ is obtained via the cross product $(1,0,0)^{T} \times (\mathsf{A}_{0},\,\mathsf{A}_{1}\mathsf{u}_{x},\,\mathsf{A}_{1}\mathsf{u}_{y})^{T}$. Note that, since the definition is based on the cross product, it does not directly generalize to higher dimensions.

2.6.7 Three-Dimensional Case

For three-dimensional signal spaces $\boldsymbol{\varPsi }_{01}$ is equivalent to a unitary quaternion.

3 Higher Order Phase Representations

The N + 1 dimensional phase representation and the monogenic signal definitely have important merits but, as we will show in this section, still leave some things to be desired. The monomial phase approach, however, allows for a higher order phase representation that will meet our requirements.

As a starting point for the discussions regarding higher order phase representations we state that all information except the magnitude should be represented by the phase. For a collection of monomial filter response matrices, $\{\mathsf{\mathbf{Q}}_{n_{i}}\}$, let a generalized phase be defined by:

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}_{\{n_{i}\}}\: =\:\{ \,\mathsf{\mathbf{\hat{Q}}}\,_{n_{i}}\} \equiv \frac{\{\mathsf{\mathbf{Q}}_{n_{i}}\}\ \ \,} {\ \|\{\mathsf{\mathbf{Q}}_{n_{i}}\}\|_{\mathsf{fro}}} }$$

(41)

where ‘fro’ indicates the Frobenius norm (also known as the Hilbert-Schmidt norm) which is simply obtained as the square root of the sum of the absolute squares of all individual scalar elements.

3.1 Local Phase from Orders 0, 1, and 2

We can attain a joint representation of signal orientation and phase using Monomial filters of orders 0, 1 and 2. Consider the following set of filter responses:

$$\displaystyle{ \mathsf{\mathbf{Q}}_{012} = \left \{\alpha \mathsf{Q}_{0},\ \beta \mathsf{\mathbf{Q}}_{1},\ \gamma \,\mathsf{\mathbf{Q}}_{2}\right \} }$$

(42)

Separate amplitude A and phase $\mathsf{\boldsymbol{\varPsi }}$

$$\displaystyle{ \mathsf{A} = \vert \vert \left \{\alpha \mathsf{Q}_{0},\ \beta \mathsf{\mathbf{Q}}_{1},\ \gamma \,\mathsf{\mathbf{Q}}_{2}\right \}\vert \vert _{\mathsf{fro}} }$$

(43)

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }} = \frac{\left \{\alpha \mathsf{Q}_{0},\ \beta \mathsf{\mathbf{Q}}_{1},\ \gamma \,\mathsf{\mathbf{Q}}_{2}\right \}} {\mathsf{A}} }$$

(44)

The filter response set can now be written

$$\displaystyle{ \mathsf{\mathbf{Q}}_{012} = \mathsf{A}\mathsf{\boldsymbol{\varPsi }} }$$

(45)

Note that in practise Q ₀ need not be computed using a separate monomial filter of order 0 since an even/odd monomial filter of order n span all subspaces of lower even/odd order. e.g. for the present case: $\mathsf{Q}_{0} =\mathrm{ trace}(\mathsf{\mathbf{Q}}_{2})$.

3.1.1 Balance Between Order 0, 1 and 2 Components

Equation (44) gives us the general form of a phase representation, however, we have yet to determine the relative weights, α, β and γ, of the individual components To do this it suffices to study the sinusoidal signal case. For a sinusoidal signal with orientation $\,\mathsf{\mathbf{\hat{u}}}\,$ and phase θ we then get the following expression for the phase, $\mathsf{\boldsymbol{\varPsi }}$.

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\,) = \left \{\alpha \cos (\theta ),\ i\,\beta \sin (\theta )\,\mathsf{\mathbf{\hat{u}}}\,^{T},\ \gamma \cos (\theta )\,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\,\right \} }$$

(46)

In order to find appropriate values for α, β and γ we need to add some constraints. We want the behavior of the representation to be as simple as possible and it is natural to require that the sensitivity of the phase representation to a change in local phase angle, as well as a change in local orientation, should be invariant to the local phase. In other words we will, as stated above, require that the metric is shift invariant, i.e. the norm of the partial derivatives with respect to θ and $\mathsf{\mathbf{\hat{u}}}$ should be constants.

$$\displaystyle{ \left \{\begin{array}{lll} \|\frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \theta }\|_{\mathsf{fro}} & =&\mathrm{c}_{1} > 0 \\ \| \frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \,\mathsf{\mathbf{\hat{u}}}\,}\|_{\mathsf{fro}} & =&\mathrm{c}_{2} > 0 \end{array} \right. }$$

(47)

Calculating the squared norm of $\frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \theta }$ gives:

$$\displaystyle{ \begin{array}{ll} \left \|\frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \theta }\right \|_{\mathsf{fro}}^{2} & = \left \|\left \{-\alpha \sin (\theta ),\ i\,\beta \cos (\theta )\,\mathsf{\mathbf{\hat{u}}}\,^{T},\ -\gamma \sin (\theta )\,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\,\right \}\right \|_{ \mathsf{fro}}^{2} \\ & = (\alpha ^{2}\, +\,\gamma ^{2})\sin ^{2}(\theta )\ +\ \beta ^{2}\cos ^{2}(\theta ) \end{array} }$$

(48)

By inspection it is simple to see that if we set

$$\displaystyle{ \beta ^{2} =\alpha ^{2} +\gamma ^{2} }$$

(49)

we get:

$$\displaystyle{ \left \|\frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \theta }\right \|_{\mathsf{fro}}^{2} =\beta ^{2} }$$

(50)

and the first requirement is met.

Finding the solution to the second requirement is slightly more involved. We will revert to the definition of partial derivatives by studying the change when adding an infinitesimal perpendicular vector $\epsilon \,\,\mathsf{\mathbf{\hat{v}}}\,$ to $\,\mathsf{\mathbf{\hat{u}}}\,$ with $\|\,\mathsf{\mathbf{\hat{v}}}\,\| = 1$. Omitting the ε ² terms, we get:

$$\displaystyle{ \begin{array}{ll} &\mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\, +\epsilon \,\mathsf{\mathbf{\hat{v}}}\,) = \\ &\quad = \left \{\alpha \cos (\theta ),\,i\beta \sin (\theta )(\,\mathsf{\mathbf{\hat{u}}}\, +\epsilon \,\mathsf{\mathbf{\hat{v}}}\,)^{T},\,\gamma \cos (\theta )(\,\mathsf{\mathbf{\hat{u}}}\, +\epsilon \,\mathsf{\mathbf{\hat{v}}}\,)(\,\mathsf{\mathbf{\hat{u}}}\, +\epsilon \,\mathsf{\mathbf{\hat{v}}}\,)^{T}\right \} \\ &\quad = \left \{\alpha \cos (\theta ),\,i\beta \sin (\theta )(\,\mathsf{\mathbf{\hat{u}}}\, +\epsilon \,\mathsf{\mathbf{\hat{v}}}\,)^{T},\,\gamma \cos (\theta )[\,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\!\! +\!\epsilon (\,\mathsf{\mathbf{\hat{v}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\!\! +\! \,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{v}}}\,^{T})\,]\right \} \end{array} }$$

(51)

Expressing the difference in $\mathsf{\boldsymbol{\varPsi }}$ yields:

$$\displaystyle\begin{array}{rcl} \!\!\!\!\!\!\!\!\!\!\mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\, +\epsilon \,\mathsf{\mathbf{\hat{v}}}\,) -\mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\,)& =& \left \{0,\ i\beta \sin (\theta )\epsilon \,\mathsf{\mathbf{\hat{v}}}\,^{T},\ \gamma \cos (\theta )\epsilon (\,\mathsf{\mathbf{\hat{v}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\!\! +\! \,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{v}}}\,^{T})\right \}{}\end{array}$$

(52)

Dividing by ε and finding the limit as ε → 0 we arrive at:

$$\displaystyle{ \begin{array}{ll} \frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \,\mathsf{\mathbf{\hat{u}}}\,} & =\lim \nolimits _{\epsilon \rightarrow 0}\frac{\mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\,+\epsilon \,\mathsf{\mathbf{\hat{v}}}\,)-\mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\,)} {\epsilon } \\ & = \left \{0,\ i\beta \sin (\theta )\,\mathsf{\mathbf{\hat{v}}}\,^{T},\ \gamma \cos (\theta )(\,\mathsf{\mathbf{\hat{v}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\!\! +\! \,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{v}}}\,^{T})\right \} \end{array} }$$

(53)

Calculating the squared norm of $\frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \,\mathbf{\hat{u}}}$ gives:

$$\displaystyle{ \left \| \frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \,\mathsf{\mathbf{\hat{u}}}\,}\right \|_{\mathsf{fro}}^{2} =\beta ^{2}\sin ^{2}(\theta ) +\gamma ^{2}\cos ^{2}\|\,\mathsf{\mathbf{\hat{v}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\! + \,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{v}}}\,^{T}\|_{ \mathsf{fro}}^{2} }$$

(54)

and, as we now that $\,\mathsf{\mathbf{\hat{v}}}\,^{T}\,\mathsf{\mathbf{\hat{u}}}\, = 0$

$$\displaystyle{ \left \| \frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \,\mathsf{\mathbf{\hat{u}}}\,}\right \|_{\mathsf{fro}}^{2} =\beta ^{2}\sin ^{2}(\theta ) + 2\,\gamma ^{2}\cos ^{2}(\theta ) }$$

(55)

Setting

$$\displaystyle{ \beta ^{2} = 2\gamma ^{2} }$$

(56)

gives

$$\displaystyle{ \left \| \frac{\partial \mathsf{\boldsymbol{\varPsi }}} {\partial \,\mathsf{\mathbf{\hat{u}}}\,}\right \|_{\mathsf{fro}}^{2} =\beta ^{2} }$$

(57)

and the second requirement is also met showing that this phase representation is shift invariant with respect to $(\,\mathsf{\mathbf{\hat{u}}}\,,\theta )$ for all $(\,\mathsf{\mathbf{\hat{u}}}\,,\theta )$. A shift invariant metric trivially implies that the mapping is continuous. It is also not difficult to see that $\mathsf{\boldsymbol{\varPsi }}$ is unique with respect to $(\,\mathsf{\mathbf{\hat{u}}}\,,\theta )$ and the exercise is left to the devoted reader.

At this stage the only degree of freedom left relates directly to the norm of the representation. The choice will not effect the general behavior of the representation and choosing

$$\displaystyle{ \alpha ^{2} +\beta ^{2} +\gamma ^{2} = 4 }$$

(58)

gives the following particularly simple and unique solution:

$$\displaystyle{ \alpha = 1,\ \ \ \beta = \sqrt{2},\ \ \ \gamma = 1 }$$

(59)

With this choice the phase representation is composed of the following components:

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}(\theta,\,\mathsf{\mathbf{\hat{u}}}\,) = \left \{\cos (\theta ),\ i\,\sqrt{2}\sin (\theta )\,\mathsf{\mathbf{\hat{u}}}\,^{T},\ \cos (\theta )\,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{T}\,\right \} }$$

(60)

3.1.2 A Comment on Some Alternative Phase Representations

The investigation above shows that all three orders are needed to construct a phase representation that meets the shift invariance requirement. This disqualifies, for example, the N + 1 dimensional Haglund-Knutsson-Granlund local phase (1989), [10], and the Felsberg-Sommer monogenic signal (2001), [18], both of which only use orders 0 and 1, and are in fact identical except for an amplitude normalisation. The monogenic phase is a mapping of the monogenic signal and can be viewed as an attempt to construct a concept that is more similar to the traditional phase angle in one-dimensional signal analysis. A consequence of the similarity with the traditional phase angle is that the ‘wrap around’ discontinuity is also inherited. This will not be a problem if the monogenic phase estimate is considered the final result of the analysis, However, if the estimates are used as input to further processing this mapping of the monogenic signal will make it difficult to apply many standard operations, e.g. averaging and differentiation, due to the discontinuous representation.

3.2 A Matrix Representation of Phase

A matrix phase representation that meets all the above requirements is given by:

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,)\ =\ \left (\begin{array}{lll} \ \mathsf{u}\ \ \ \ \ i\,\mathsf{\mathbf{u}}^{_{T}} \\ i\,\mathsf{\mathbf{u}}\ \ \ \ \ \ \mathsf{\mathbf{U}} \end{array} \right )\ =\ \left (\begin{array}{lll} \ \cos (\theta )\ \ \ \ \ \ i\sin (\theta )\,\,\mathsf{\mathbf{\hat{u}}}\,^{^{T} } \\ i\sin (\theta )\,\,\mathsf{\mathbf{\hat{u}}}\,\ \ \ \ \cos (\theta )\,\,\mathsf{\mathbf{\hat{u}}}\,\,\mathsf{\mathbf{\hat{u}}}\,^{^{T} } \end{array} \right ) }$$

(61)

A number of interesting observations regarding this matrix representation can be made. The representation has a Frobenius norm of $\sqrt{ 2}$ and two non-zero eigenvalues with unity norm. The eigenvalues are a complex conjugate pair implying an order 2 sub-determinant of unity. The representation is pseudo-unitary, i.e. unitary in the spanned 2-dimensional subspace, implying:

$$\displaystyle{ \left \{\begin{array}{lll} \boldsymbol{\varPsi }(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,)^{\dag } = \mathsf{\boldsymbol{\varPsi }}(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,)^{+} \\ \mathsf{\boldsymbol{\varPsi }}(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,)^{\dag }\;\mathsf{\boldsymbol{\varPsi }}(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,) = \mathsf{\boldsymbol{\varPsi }}(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,)\;\mathsf{\boldsymbol{\varPsi }}(\,\theta,\,\,\mathsf{\mathbf{\hat{u}}}\,)^{\dag } = \mathsf{\mathbf{P}}_{2}\end{array} \right. }$$

(62)

where ‘^†’ denotes the complex matrix transpose, ‘⁺’ denotes the Moore-Penrose pseudo inverse and $\mathsf{\mathbf{P}}_{2}$ is a projection matrix having two non-zero eigenvalues equal to unity.

3.3 The Phase Space Manifold Is a Klein Bottle

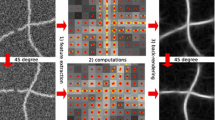
By plotting image patches with different phase and orientation in a regular fashion the intrinsic Klein bottle structure of the phase space manifold is revealed, [32], see Fig. 10 and the caption. A Klein bottle, K, is a non-orientable surface in four dimensions and for 2-dimensional simple signals the phase matrix, Ψ, only needs four degrees of freedom. In general, however, the phase matrix, Ψ, has five degrees of freedom. The fifth dimension is needed to represent the local phase of non-simple signals. That is the general topology of the phase matrix for two-dimensional signals is K × I, where I is an interval of real numbers.

Fig. 10

By plotting image patches with different phase and orientation in a regular fashion the intrinsic Klein bottle structure of the phase space is revealed. Orientation changes from top to bottom and phase changes from left to right. The first and last row and the first and last column represent the same orientation/phase combinations. To match the first and last row one of them has to be taken in reversed order. This shows that, for 2-dimensional signals, the phase manifold is a Klein bottle

3.3.1 Color Code

The five degrees of freedom of the phase matrix, Ψ, are hard to directly visualize in a simple way. To obtain images that holds as much as possible of the phase information we will introduce a color coding scheme. This implies a mapping from five dimensions to the three dimensions of the color space used in Fig. 8. The hue is based on the direction of the imaginary vector part of the phase matrix product, i.e. phase matrix elements Ψ(2, 1) and Ψ(3, 1). Zero-phase (ridge/white line) is coded as white and 180 phase (valley/black line) as gray. See Figs. 11 and 12.

Fig. 11

Plot showing the colors corresponding to the phase at the center of the patches in Fig. 10. The figure provides a link between Figs. 10 and 12. It also shows that the RGB color space is inadequate to represent the Klein bottle topology since all the θ = 0 and all the θ = π patches are white and gray respectively

Fig. 12

Figure showing four views of a three-dimensional sub-space of the phase matrix representation. The Klein bottle structure shows itself like a modified torus (in a way similar to a mobius-band), a tube bent in a circle but before ‘glued’ together inside and outside surfaces trade places. The black lines indicate $\theta = \pm \pi /4$

4 Monomial Phase Products and Phase Angle Differences

An important operation using the complex scalar phase is the complex conjugate product giving a phase angle difference estimate. Let us see if we can use the new high order phase in the same way.

4.1 Direct Products of Phase Matrices

In order to do this we need to decide how an appropriate product of two phase matrices can be defined. Starting with two phase matrices, $\mathsf{\boldsymbol{\varPsi }}_{a}$ and $\mathsf{\boldsymbol{\varPsi }}_{b}$:

$$\displaystyle\begin{array}{rcl} \mathsf{\boldsymbol{\varPsi }}_{a}& =& \left (\begin{array}{c@{\quad }c} \mathsf{a} \quad &i\,\mathsf{\mathbf{a}}^{_{T}} \\ i\,\mathsf{\mathbf{a}}\quad & \mathsf{\mathbf{A}}\\ \quad \end{array} \right ) = \left (\begin{array}{lll} \ \cos (\theta )\ \ \ \ \ \ i\sin (\theta )\,\,\mathsf{\mathbf{\hat{a}}}\,^{^{T} } \\ i\sin (\theta )\,\,\mathsf{\mathbf{\hat{a}}}\,\ \ \ \ \cos (\theta )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{^{T} } \end{array} \right ){}\end{array}$$

(63)

$$\displaystyle\begin{array}{rcl} \mathsf{\boldsymbol{\varPsi }}_{b}& =& \left (\begin{array}{c@{\quad }c} \mathsf{b} \quad &i\,\mathsf{\mathbf{b}}^{_{T}} \\ i\,\mathsf{\mathbf{b}}\quad & \mathsf{\mathbf{B}} \end{array} \right ) = \left (\begin{array}{lll} \ \cos (\phi )\ \ \ \ \ \ i\sin (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,^{^{T} } \\ i\sin (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,\ \ \ \ \cos (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{^{T} } \end{array} \right ){}\end{array}$$

(64)

we will, in analogy with standard matrix multiplication, define the product of two phase matrices to be:

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}_{a}\,\mathsf{\boldsymbol{\varPsi }}_{b} = \left (\begin{array}{c@{\qquad }c} \mathsf{a}\mathsf{b} -\mathsf{\mathbf{a}}^{_{T}}\mathsf{\mathbf{b}} \qquad &i\,(\,\mathsf{a}\mathsf{\mathbf{b}}^{_{T}} + \mathsf{\mathbf{a}}^{_{T}}\mathsf{\mathbf{B}}\,) \\ i\,(\,\mathsf{\mathbf{a}}\mathsf{b} + \mathsf{\mathbf{A}}\mathsf{\mathbf{b}}\,)\qquad & -\mathsf{\mathbf{a}}\mathsf{\mathbf{b}}^{_{T}} + \mathsf{\mathbf{A}}\mathsf{\mathbf{B}} \end{array} \right ) }$$

(65)

Note that the components multiplied here can be scalars, vectors or matrices. All products are, however, standard matrix algebra products.

As mentioned above we wish to investigate the analog of the complex conjugate product for complex numbers. For two phase matrices this translates to the complex transpose product, i.e. terms holding $\mathsf{\mathbf{b}}$ will change sign. Letting ‘ ^† ’ denote the complex conjugate transpose we get:

$$\displaystyle{ \begin{array}{ll} \mathsf{\boldsymbol{\varPsi }}_{a}\,\mathsf{\boldsymbol{\varPsi }}_{b}^{\dag }& = \left (\begin{array}{c@{\qquad }c} \mathsf{a}\mathsf{b} + \mathsf{\mathbf{a}}^{_{T}}\mathsf{\mathbf{b}} \qquad &i\,(\,-\mathsf{a}\mathsf{\mathbf{b}}^{_{T}} + \mathsf{\mathbf{a}}^{_{T}}\mathsf{\mathbf{B}}\,) \\ i\,(\,\mathsf{\mathbf{a}}\mathsf{b} -\mathsf{\mathbf{A}}\mathsf{\mathbf{b}})\qquad & \mathsf{\mathbf{a}}\mathsf{\mathbf{b}}^{_{T}} + \mathsf{\mathbf{A}}\mathsf{\mathbf{B}} \end{array} \right ) \\ & = \left (\begin{array}{c@{\quad }c} \mathsf{c}_{11} \quad &i\,\mathsf{\mathbf{c}}_{12}^{_{T}} \\ i\,\mathsf{\mathbf{c}}_{21}\quad & \mathsf{\mathbf{C}}_{22} \end{array} \right )\end{array} }$$

(66)

The last entry in Eq. (66) simply serves as a way to identify the individual components of $\mathsf{\boldsymbol{\varPsi }}_{a}\,\mathsf{\boldsymbol{\varPsi }}_{b}^{\dag }$. Carrying out the calculations for each component we obtain:

$$\displaystyle{ \begin{array}{lll} \mathsf{c}_{11} & =&\ \ \ \ \cos (\theta )\cos (\phi )\ \ \ \ \ \ \ \ \, +\ \sin (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\, \\ \mathsf{\mathbf{c}}_{12}^{_{T}} & =&\ -\cos (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\ \,\ +\ \sin (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{^{T} } \\ \mathsf{\mathbf{c}}_{21} & =&\ \ \ \ \,\sin (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\ \ \ \ \ \, -\ \cos (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\, \\ \mathsf{\mathbf{C}}_{22} & =&\ \ \ \ \ \sin (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{^{T} } +\ \cos (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{^{T} }\end{array} }$$

(67)

Thus the result in the general case is quite complex, however, setting the orientations of the to phase matrices to be equal will allow us to significantly simplify the expression.

4.1.1 Equal Orientations

For the equal orientation case, i.e. $\mathsf{\mathbf{\hat{b}}} = \mathsf{\mathbf{\hat{a}}}$, we get:

$$\displaystyle{ \begin{array}{lll} \mathsf{c}_{11} & =&\ \ \ \ \ \cos (\theta )\cos (\phi )\ +\ \ \sin (\theta )\sin (\phi ) \\ \mathsf{\mathbf{c}}_{12}^{_{T}} & =&\ [-\cos (\theta )\sin (\phi )\ \, +\ \ \sin (\theta )\cos (\phi )\ ]\ \,\mathsf{\mathbf{\hat{a}}}\,^{T} \\ \mathsf{\mathbf{c}}_{21} & =&\ [\ \ \ \sin (\theta )\cos (\phi )\ \ -\ \ \cos (\theta )\sin (\phi )\ ]\ \,\mathsf{\mathbf{\hat{a}}}\, \\ \mathsf{\mathbf{C}}_{22} & =&\ [\ \ \ \sin (\theta )\sin (\phi )\ \ +\ \ \cos (\theta )\cos (\phi )\ ]\ \,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{^{T} } \end{array} }$$

(68)

Simplifying further and restoring the matrix notation we arrive at the following expression:

$$\displaystyle{ \begin{array}{ll} \mathsf{\boldsymbol{\varPsi }}_{a}\,\mathsf{\boldsymbol{\varPsi }}_{b}^{\dag }& = \left (\begin{array}{c@{\quad }c} \ \cos (\theta -\phi ) \quad &i\,\sin (\theta -\phi )\ \,\mathsf{\mathbf{\hat{a}}}\,^{T} \\ i\,\sin (\theta \!-\!\phi )\ \,\mathsf{\mathbf{\hat{a}}}\,\quad &\cos (\theta -\phi )\ \,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{^{T} } \end{array} \right ) \\ & = \mathsf{\boldsymbol{\varPsi }}(\,\theta -\phi,\,\,\mathsf{\mathbf{\hat{a}}}\,) \\ & = \mathsf{\boldsymbol{\varPsi }}(\,\varDelta \!\theta,\,\,\mathsf{\mathbf{\hat{a}}}\,) \end{array} }$$

(69)

where Δ θ is the difference in phase angle. In other words, it works perfectly for the “same orientation” case. We get a direct analogue to the multiplication of complex numbers.

4.2 A Symmetric Complex Conjugate Phase Product

The simple matrix product analogue defined in Eq. (65) has a significant drawback. The result will not have the same symmetry features as the multiplied phase matrices unless the orientations are identical. For this reason we define a symmetric complex conjugate phase matrix product that will retain the symmetry features also when the orientations differ.

$$\displaystyle{ \begin{array}{ll} \varPsi _{^{\frac{a} {^{b}} }} & \stackrel{\mathrm{def}}{=}\frac{1} {2}(\mathsf{\boldsymbol{\varPsi }}_{a}\,\mathsf{\boldsymbol{\varPsi }}_{b}^{\dag } + \mathsf{\boldsymbol{\varPsi }}_{ b}^{\dag }\,\mathsf{\boldsymbol{\varPsi }}_{ a}) \\ & = \frac{1} {2}\left (\begin{array}{c@{\qquad }c} \mathsf{a}\mathsf{b} + \mathsf{\mathbf{a}}^{_{T}}\mathsf{\mathbf{b}} \qquad &i\,(\,-\mathsf{a}\mathsf{\mathbf{b}}^{_{T}} + \mathsf{\mathbf{a}}^{_{T}}\mathsf{\mathbf{B}}\,) \\ i\,(\,\mathsf{\mathbf{a}}\mathsf{b} -\mathsf{\mathbf{A}}\mathsf{\mathbf{b}}\,)\qquad & \mathsf{\mathbf{a}}\mathsf{\mathbf{b}}^{_{T}} + \mathsf{\mathbf{A}}\mathsf{\mathbf{B}} \end{array} \right ) \\ & + \frac{1} {2}\left (\begin{array}{c@{\qquad }c} \mathsf{b}\mathsf{a} + \mathsf{\mathbf{b}}^{_{T}}\mathsf{\mathbf{a}} \qquad &i\,(\ \ \mathsf{b}\mathsf{\mathbf{a}}^{_{T}} -\mathsf{\mathbf{b}}^{_{T}}\mathsf{\mathbf{A}}\,) \\ i\,(-\mathsf{\mathbf{b}}\mathsf{a} + \mathsf{\mathbf{B}}\mathsf{\mathbf{a}}\,)\qquad & \mathsf{\mathbf{b}}\mathsf{\mathbf{a}}^{_{T}} + \mathsf{\mathbf{B}}\mathsf{\mathbf{A}} \end{array} \right ) \\ & = \left (\begin{array}{cc} \mathsf{c}_{11} &i\,\mathsf{\mathbf{c}}_{12}^{_{T}} \\ i\,\mathsf{\mathbf{c}}_{21}& \mathsf{\mathbf{C}}_{22} \end{array} \right )\end{array} }$$

(70)

Carrying out the calculations for each component we get:

$$\displaystyle{ \begin{array}{lll} \mathsf{c}_{11} & =&\frac{1} {2}\,(\ \ \cos (\theta )\cos (\phi )\ \ \ \ \ \ \ +\ \sin (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\, \\ &\ &\ \ +\,\cos (\theta )\cos (\phi )\ \ \ \ \ \ \ +\ \sin (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\,\mathsf{\mathbf{\hat{a}}}\,\ ) \\ \mathsf{\mathbf{c}}_{12}^{_{T}} & =&\frac{1} {2}\,(-\cos (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\ +\ \sin (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{T} \\ &\ &\ \ \ +\,\cos (\phi )\sin (\theta )\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\ \ -\ \sin (\phi )\cos (\theta )\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,) \\ \mathsf{\mathbf{c}}_{21} & =&\frac{1} {2}\,(\ \ \,\sin (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\ \ \ \ \, -\ \cos (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\, \\ &\ &\ \ \ -\sin (\phi )\cos (\theta )\,\,\mathsf{\mathbf{\hat{b}}}\,\ \ \ \ \, +\ \cos (\phi )\sin (\theta )\,\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\,\mathsf{\mathbf{\hat{a}}}\,\ ) \\ \mathsf{\mathbf{C}}_{22} & =&\frac{1} {2}(\ \ \ \sin (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\ +\ \cos (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{T} \\ &\ &\ \ \ \ +\sin (\theta )\sin (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T}\ +\ \cos (\theta )\cos (\phi )\,\,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{T}\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{T})\end{array} }$$

(71)

Setting $\eta = \,\mathsf{\mathbf{\hat{a}}}\,^{T}\,\mathsf{\mathbf{\hat{b}}}\,$ and simplifying gives:

$$\displaystyle{ \begin{array}{lll} \mathsf{c}_{11} & =&\ \ \ \ \ \ \ \cos (\theta )\cos (\phi )\ +\ \eta \sin (\theta )\sin (\phi ) \\ \mathsf{\mathbf{c}}_{21} & =&\frac{1} {2}\,[\ \ \,(\sin (\theta )\cos (\phi )\ -\ \eta \cos (\theta )\sin (\phi ))\,\,\mathsf{\mathbf{\hat{a}}}\,\\ &\ & + (-\sin (\phi )\cos (\theta )\ +\ \eta \cos (\phi )\sin (\theta )\,)\,\,\mathsf{\mathbf{\hat{b}}}\,\ \ ]\\ \mathsf{\mathbf{c} } _{ 12} & =&\mathsf{\mathbf{c}}_{21} \\ \mathsf{\mathbf{C}}_{22} & =&\frac{1} {2}(\ \ \ \sin (\theta )\sin (\phi )\ +\ \eta \cos (\theta )\cos (\phi )\,)(\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{_{T}}\!\! + \,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{_{T}}) \end{array} }$$

(72)

Expressing using factors 1 ± η we get:

$$\displaystyle{ \begin{array}{lll} \mathsf{c}_{11} & =&\frac{1} {2}[\ \ (1+\eta )(\cos (\theta )\cos (\phi ) +\sin (\theta )\sin (\phi )) \\ &\ &\ \ + (1-\eta )(\cos (\theta )\cos (\phi ) -\sin (\theta )\sin (\phi ))\ ] \\ \mathsf{\mathbf{c}}_{21} & =&\frac{1} {4}[\ [(1+\eta )(\sin (\theta )\cos (\phi ) -\cos (\theta )\sin (\phi )) \\ &\ &\ \ + (1-\eta )(\sin (\theta )\,\cos (\phi ) +\cos (\theta )\sin (\phi ))\,]\,\,\mathsf{\mathbf{\hat{a}}}\, \\ &\ &\ - [(1+\eta )(\sin (\phi )\cos (\theta ) -\cos (\phi )\sin (\theta )) \\ &\ &\ \ \, + (1-\eta )(\sin (\phi )\cos (\theta ) +\cos (\phi )\sin (\theta ))\,]\,\,\mathsf{\mathbf{\hat{b}}}\,\ ]\\ \mathsf{\mathbf{c} } _{ 12} & =&\mathsf{\mathbf{c}}_{21} \\ \mathsf{\mathbf{C}}_{22} & =&\frac{1} {4}[\ [\,(1+\eta )(\sin (\theta )\sin (\phi ) +\cos (\theta )\cos (\phi )) \\ &\ &\ + (1-\eta )(\sin (\theta )\sin (\phi ) -\cos (\theta )\cos (\phi ))\,](\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{_{T}}\!\! + \,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{_{T}})\ ] \end{array} }$$

(73)

Using classical trigonometrics we arrive at:

$$\displaystyle{ \begin{array}{ll} \mathsf{c}_{11} & = \frac{1} {2}[\ \ (1+\eta )\cos (\theta -\phi )\ +\ (1-\eta )\cos (\theta +\phi )\,] \\ \mathsf{\mathbf{c}}_{21} & = \frac{1} {4}[\ (1+\eta )\sin (\theta -\phi )(\,\mathsf{\mathbf{\hat{a}}}\, + \,\mathsf{\mathbf{\hat{b}}}\,)\ + (1-\eta )\sin (\theta +\phi )(\,\mathsf{\mathbf{\hat{a}}}\, -\,\mathsf{\mathbf{\hat{b}}}\,)\,]\\ \mathsf{\mathbf{c}}_{ 12} & = \mathsf{\mathbf{c}}_{21} \\ \mathsf{\mathbf{C}}_{22} & = \frac{1} {4}[\ (1+\eta )\cos (\theta -\phi )\ -\ (1-\eta )\cos (\theta +\phi )\,]\,(\,\,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{b}}}\,^{^{T} }\!\! + \,\mathsf{\mathbf{\hat{b}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{^{T} })\end{array} }$$

(74)

In a final desperate attempt to understand what’s going on we introduce the variables:

• ζ = the angle between the two signal directions $\,\mathsf{\mathbf{\hat{a}}}\,$ and $\,\mathsf{\mathbf{\hat{b}}}\,$

• $\mathbf{s} = \frac{1} {2}(\,\mathsf{\mathbf{\hat{a}}}\, + \,\mathsf{\mathbf{\hat{b}}}\,)$ the mean of the two signal direction vectors

• $\mathbf{d} = \frac{1} {2}(\,\mathsf{\mathbf{\hat{a}}}\, -\,\mathsf{\mathbf{\hat{b}}}\,)$ half of the difference between the two signal direction vectors.

Substituting the new variables and using standard trigonometric identities we find:

$$\displaystyle{ \begin{array}{ll} \mathsf{c}_{11} & =\ \ \cos ^{2}( \frac{\zeta }{2})\,\cos (\theta -\phi )\ \ \ +\ \sin ^{2}( \frac{\zeta }{2})\,\cos (\theta +\phi ) \\ \mathsf{\mathbf{c}}_{21} & =\ [\,\cos ^{2}( \frac{\zeta }{2})\,\sin (\theta -\phi )\,\mathbf{s}\ +\ \sin ^{2}( \frac{\zeta }{2})\,\sin (\theta +\phi )\,\mathbf{d}\,] \\ \mathsf{\mathbf{c}}_{12} & = \mathsf{\mathbf{c}}_{21} \\ \mathsf{\mathbf{C}}_{22} & =\ [\,\cos ^{2}( \frac{\zeta }{2})\,\cos (\theta -\phi )\ \ -\ \sin ^{2}( \frac{\zeta }{2})\,\cos (\theta +\phi )\,]\,(\mathbf{s}\,\mathbf{s}^{^{T} }\! -\,\mathbf{d}\mathbf{d}^{^{T} })\end{array} }$$

(75)

Noting that $\|\mathsf{\mathbf{s}}\| =\cos ( \frac{\zeta }{2})$ and $\|\mathsf{\mathbf{d}}\| =\sin ( \frac{\zeta }{2})$ gives:

$$\displaystyle{ \left \{\begin{array}{lll} \mathsf{\mathbf{s}} =\cos ( \frac{\zeta }{2})\,\mathsf{\mathbf{\hat{s}}}\, \\ \mathsf{\mathbf{d}} =\sin ( \frac{\zeta }{2})\,\mathsf{\mathbf{\hat{d}}}\, \end{array} \right. }$$

(76)

We can now write:

$$\displaystyle{ \begin{array}{lll} \mathsf{c}_{11} & =&\ \ \cos ^{2}( \frac{\zeta }{2})\,\cos (\theta -\phi )\ \ \ \ +\ \sin ^{2}( \frac{\zeta }{2})\,\cos (\theta +\phi ) \\ \mathsf{\mathbf{c}}_{21} & =&\ [\,\cos ^{3}( \frac{\zeta }{2})\,\sin (\theta -\phi )\,\,\mathsf{\mathbf{\hat{s}}}\,\ +\ \sin ^{3}( \frac{\zeta }{2})\,\sin (\theta +\phi )\,\,\mathsf{\mathbf{\hat{d}}}\,\,] \\ \mathsf{\mathbf{c}}_{12} & =&\,\mathsf{\mathbf{c}}_{21} \\ \mathsf{\mathbf{C}}_{22} & =&\ [\,\cos ^{4}( \frac{\zeta }{2})\,\cos (\theta -\phi )\ \ \ -\frac{1} {4}\sin ^{2}(\zeta )\,\cos (\theta +\phi )\,]\:\,\mathsf{\mathbf{\hat{s}}}\,\,\,\mathsf{\mathbf{\hat{s}}}\,^{^{T} } \\ & \ & \!\!\!\! - [\,\frac{1} {4}\sin ^{2}(\zeta )\,\cos (\theta -\phi )\ \ -\ \sin ^{4}( \frac{\zeta }{ 2})\,\cos (\theta +\phi )\,]\:\,\mathsf{\mathbf{\hat{d}}}\,\,\mathsf{\mathbf{\hat{d}}}\,^{^{T} } \end{array} }$$

(77)

Rearranging terms we can finally express $\mathsf{\boldsymbol{\varPsi }}_{ \!\!^{\frac{a} {^{b}} }}$ in a way that will shed some light on what happens when $\,\mathsf{\mathbf{\hat{a}}}\,$ and $\,\mathsf{\mathbf{\hat{b}}}\,$ differs:

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \mathsf{\boldsymbol{\varPsi }}_{\!\!^{\frac{a} {^{b}} }} & =&\cos ^{2}( \frac{\zeta }{2})\ \mathsf{\boldsymbol{\varPsi }}(\,\theta -\phi,\,\,\mathsf{\mathbf{\hat{s}}}\,) \\ &\ & -\cos ^{2}( \frac{\zeta }{2})\left (\begin{array}{lll} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i\,[1 -\cos ( \frac{\zeta }{2})]\:\sin (\theta -\phi )\,\,\mathsf{\mathbf{\hat{s}}}\,^{^{T} } \\ i\,[1 -\cos ( \frac{\zeta }{2})]\:\sin (\theta -\phi )\,\mathsf{\mathbf{\hat{s}}}\,\ \ \ \ \ \ \ \ [1 -\cos ^{2}( \frac{\zeta }{2})]\cos (\theta -\phi )\,\mathsf{\mathbf{\hat{s}}}\,\,\mathsf{\mathbf{\hat{s}}}\,^{^{T} }\!\!\! \end{array} \right ) \\ &\ & +\sin ^{2}( \frac{\zeta }{2})\left (\begin{array}{lll} \!\ \ \ \ \ \ \ \cos (\theta +\phi )\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i\,\sin ( \frac{\zeta }{2})\:\sin (\theta +\phi )\,\,\mathsf{\mathbf{\hat{d}}}\,^{^{T} } \\ i\,\sin ( \frac{\zeta }{2})\:\sin (\theta +\phi )\,\mathsf{\mathbf{\hat{d}}}\,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sin ^{2}( \frac{\zeta }{2})\cos (\theta +\phi )\,\mathsf{\mathbf{\hat{d}}}\,\,\mathsf{\mathbf{\hat{d}}}\,^{^{T} }\!\!\! \end{array} \right ) \\ &\ & -\frac{1} {4}\sin ^{2}(\zeta )\left (\begin{array}{lll} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\mathsf{\mathbf{\hat{0}}}\,^{^{T} } \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\mathsf{\mathbf{\hat{0}}}\,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos (\theta +\phi )\,\mathsf{\mathbf{\hat{s}}}\,\,\mathsf{\mathbf{\hat{s}}}\,^{^{T} } \end{array} \right ) \\ &\ & -\frac{1} {4}\sin ^{2}(\zeta )\left (\begin{array}{lll} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\mathsf{\mathbf{\hat{0}}}\,^{^{T} } \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\mathsf{\mathbf{\hat{0}}}\,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos (\theta -\phi )\,\mathsf{\mathbf{\hat{d}}}\,\,\mathsf{\mathbf{\hat{d}}}\,^{^{T} }\!\!\! \end{array} \right ) \end{array} & &{}\end{array}$$

(78)

We can see that the first term has the same form as the monomial phase matrix representation, except for a scaling with $\cos ^{2}( \frac{\zeta }{2})$, and represents the difference in phase in the mean direction of the two signals. The magnitude of the four additional terms can be roughly described as follows. For the same orientation case, ζ = 0, the additional terms are zero and otherwise no individual additional term has a larger norm than $\sin ^{2}( \frac{\zeta }{2})$ and Eq. (78) can be written:

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}_{\!\!^{\frac{a} {^{b}} }}\ =\ \ \,\cos ^{2}( \frac{\zeta } {2})\ \mathsf{\boldsymbol{\varPsi }}(\,\varDelta \!\theta,\,\,\mathsf{\mathbf{\hat{s}}}\,)\ +\ \sin ^{2}( \frac{\zeta } {2})\mathsf{\boldsymbol{\varPsi }}\!_{\epsilon } }$$

(79)

where Δ​θ is the difference in phase angle, (θ −ϕ), and $\mathsf{\boldsymbol{\varPsi }}\!_{\epsilon }$ is a matrix with terms having a limited magnitude. In other words, as long as the angular difference between the signals is not too large the result is very well-behaved. The experiments in the next section will demonstrate this behavior.

Two comments are appropriate to make here: (1) As is also the case for complex conjugate products of complex numbers, changing the order of the matrices (or complex numbers) will result in a complex transpose of the result, i.e.

$$\displaystyle\begin{array}{rcl} \varPsi _{^{\frac{a} {^{b}} }} = \varPsi _{\!^{ \frac{b} {^{a}} }}^{\dag }& &{}\end{array}$$

(80)

This simply corresponds to the fact that the change of order implies that the reference direction of the motion is reversed. (2) The symmetric complex conjugate phase product is not associative, i.e. if carrying out products of more than two matrices changing the order in which the dyadic products are done may change the result. However, as the estimation always only involves two matrices, this has no consequence in the motion estimation case.

4.3 Monomial Phase and Motion Estimation

Local phase estimation is a key part of many displacement estimation algorithms. In this section we will demonstrate the power of the new phase representation in two different cases. We will refer to the computed phase based measure as the displacement even though the actual displacement in image coordinates is related by a factor dependent on the wavelength of the sine waves used. In all experiments the color coding used for the phase matrix component images on the left hand side is: Green – positive real, Red – negative real, Blue – positive imaginary, Yellow – negative imaginary. The Klein bottle sub-space color coding used for the images on the right hand side is described in Sect. 3.3. The displacement estimate used for the arrows is computed as follows. Expressing the symmetric complex conjugate matrix product, $\mathsf{\boldsymbol{\varPsi }}_{ \!\!^{\frac{a} {^{b}} }}$, as:

$$\displaystyle{ \mathsf{\boldsymbol{\varPsi }}_{\!\!^{\frac{a} {^{b}} }}\ =\ \left (\begin{array}{c@{\qquad }c} \mathsf{c} \qquad &i\,\mathsf{\mathbf{c}}^{_{T}} \\ i\,\mathsf{\mathbf{c}}\qquad & \mathsf{\mathbf{C}} \end{array} \right ) }$$

(81)

the simplest way to compute a displacement vector, $\mathsf{\mathbf{d}}_{\varPsi }$ is:

$$\displaystyle{ \mathsf{\mathbf{d}}_{\varPsi } =\tan ^{-1}\!\left (\frac{\|\,\mathsf{\mathbf{c}}\,\|} {\mathsf{c}}\right )\:\,\mathsf{\mathbf{\hat{c}}}\,\ =\ \varDelta \!\theta \;\,\mathsf{\mathbf{\hat{c}}}\, }$$

(82)

where tan⁻¹ ∈ [ 0,  π [ . This means that the direction of the displacement is given by $\,\mathsf{\mathbf{\hat{c}}}\,$ and the displacement distance is computed as the arc-tangent of the ratio between the magnitude of $\mathsf{\mathbf{c}}$ and the value of c. It is worth noting that the form of Eq. (82) has obvious similarities to the definition of the monogenic phase vector, Eq. (40). However, there are two important differences: Firstly, since the entries here are components of a matrix phase product, the result represents a phase relation rather than a single phase. Secondly, the formulation in Eq. (82) is valid for any signal dimensionality. It is also appropriate to note that in three dimensions Eq. (82) is equivalent to the logarithm of a unitary quaternion, $(\mathsf{q},\,\mathsf{\mathbf{q}})$, i.e. $\tan ^{-1}\left (\frac{\|\ \mathsf{\mathbf{q}}\ \|_{_{\ }}^{^{\ }}\!\!\!} {\mathsf{q}} \right )^{^{\ }}\,\mathsf{\mathbf{\hat{q}}}\,\ =\log (\mathsf{q},\,\mathsf{\mathbf{q}})$.

4.3.1 Two Radial Sine Waves with Different Frequency

The simplest case, shown in Fig. 13 is a pair of radial sine wave patterns with slightly different frequency. The local orientation for this pair is identical and the phase difference grows linearly out from the center. The result in Fig. 13 is as predicted by the theoretical analysis, Eqs. (69), (81) and (82).

Fig. 13

Figure showing a simple scaling example using two radial sine waves with slightly different frequency. The gray scale images show the to different input images. The local orientation is identical in both images but the phase difference grows linearly out from the center. The 3 × 3 groups of color images to the left show the individual components of the phase matrices Ψ _a , Ψ _b (top two) and phase matrix product, $\varPsi _{\!\!^{\frac{a} {^{b}} }}$ (bottom). Here green means positive real, red means negative real, blue means positive imaginary and yellow means negative imaginary. The corresponding color coded phase images are shown to the right. The added arrows indicate the corresponding displacement estimate, $\mathsf{\mathbf{d}}_{\varPsi }$, (bottom right). The arrows correctly show that the phase difference is pointing towards the center with magnitudes increasing linearly from the center. The outer gray circular area is where the difference in phase angle, θ, reaches π and the phase angle difference is interpreted as having the opposite sign

4.3.2 Two Sine Waves with Different Orientations

Figure 14 shows an example with two linear sine wave patterns with 20^∘ difference in orientation. The result is as predicted by the theoretical analysis, Eqs. (79)–(82). This example clearly demonstrates the robustness of the approach.

Fig. 14

Example using two sine waves with the same frequency but with different orientations, the orientation difference here is 20^∘. The layout is the same as in Fig. 13. The result shows that the estimated orientation of the motion corresponds to the average orientation present in the two input images, $\,\mathsf{\mathbf{\hat{s}}}\,$. This is in accordance with Eq. (78) for small differences in orientation. Even though the orientation is relatively large the influence of the additional terms in Eq. (78) is hardly noticeable. The white linear structure going through the center of the result image (bottom right) indicates that the difference in the phase angle, θ is zero. The colors and the arrows correctly show that the phase difference grows linearly perpendicular to the white ‘center-line’. The outer gray linear areas are where the difference in phase angle, θ, reaches π and the phase angle difference is interpreted as having the opposite sign

4.3.3 A Comment on Optical Flow

Motion estimation and phase difference estimation are not identical problems but are related through a distance/phase relation. However, a comparison with the well-known optical flow motion estimation algorithm will highlight some important aspects. Figure 15 shows the result of the classical optical flow algorithm applied to the image pair in Fig. 14. As the gradient in optical flow is taken from a single reference image there are two possible solutions, shown left and right. The two fundamental assumptions made in optical flow are: (1) ‘the image is locally planar’ and (2) ‘the second image is a translated version of the first image’. These to assumptions are in practice rarely a good approximation and are, in fact, severely violated for a simple translated sine wave pattern. As can be expected, using the gray images in Fig. 14 yield optical flow estimates that are quite useless. Although the conjugate phase products results in Fig. 14 are not equivalent to displacement estimates they demonstrate that the monomial phase based model is likely to provide a much more powerful approach in non-trivial cases.

Fig. 15

Figure showing the result when applying the optical flow algorithm to the two gray images in Fig. 14. As the gradient in optical flow is taken from a single reference image there are two possible solutions, shown left and right. Even for these relatively simple cases the fundamental optical flow assumptions are violated and the result is very far from the correct displacement in most locations. The only situation that consistently gives the correct result is when the displacement is zero!

4.4 Averaging of Phase Matrix Products

In many applications the presence of noise can render individual local feature estimates unreliable. A simple, powerful and extensively used method for noise suppression and regularization is low pass filtering of the obtained local estimates. However, and we stress this again, for the averaging operation to be meaningful is required that the feature representation space has the fundamental properties previously discussed in this chapter.

The appropriate spatio-temporal size of the low pass filter is determined by the noise level and how much ‘smoothing’ of the feature field that is acceptable. Here the importance of the symmetric complex conjugate phase product defined in Sect. 4 is highlighted. In motion estimation the motion field will, as a rule, have a much slower spatial variation then the local phase field. This situation is clearly shown in Figs. 13 and 14. Hence, a large low pass filter, that would remove important details of the phase field, can still be used without significant deterioration of the motion field. This will allow robust motion estimates to be attained in difficult and noisy situations.

The averaging operation can be expressed as a weighted summation where the coefficients, w _l sum to unity, i.e. $\sum w_{l} = 1$. Using a bar to denote a weighted average we can express the local average of the phase matrix product as:

$$\displaystyle{ \begin{array}{ll} \overline{\mathsf{\boldsymbol{\varPsi }}}_{\!\!^{\frac{a} {^{b}} }} & =\sum _{l}w_{l}\:\mathsf{\boldsymbol{\varPsi }}_{al}\,\mathsf{\boldsymbol{\varPsi }}_{bl}^{T} \\ & = \left (\begin{array}{lll} \ \ \sum _{l}w_{l}\cos (\varDelta \!\theta _{l})\ \ \ \ \ \ \ \ \ i\,\sum _{l}w_{l}\sin (\varDelta \!\theta _{l})\ \,\mathsf{\mathbf{\hat{a}}}\,_{l}^{T} \\ \,i\,\sum _{l}w_{l}\sin (\varDelta \!\theta _{l})\ \,\mathsf{\mathbf{\hat{a}}}\,_{l}\ \ \ \ \ \ \sum _{l}w_{l}\cos (\varDelta \!\theta _{l})\ \,\mathsf{\mathbf{\hat{a}}}\,_{l}\,\mathsf{\mathbf{\hat{a}}}\,_{l}^{^{T} } \end{array} \right ) \\ & = \left (\begin{array}{c@{\qquad }c} \overline{\mathsf{c}} \qquad &i\;\,\overline{\mathsf{\mathbf{c}}}^{\,T} \\ i\;\,\overline{\mathsf{\mathbf{c}}}\qquad & \overline{\mathsf{\mathbf{C}}} \end{array} \right ) \end{array} }$$

(83)

In the general case the weights, w _l , of the averaging filter can be both spatially variant and signal dependent.

4.4.1 Equal Orientations

Letting all orientations be equal, i.e. $\,\mathsf{\mathbf{\hat{a}}}\,_{l} = \,\mathsf{\mathbf{\hat{a}}}\,;\;\forall l$ and calculating the weighted average, $\overline{z}$, of the complex numbers, z _l , corresponding to the difference phase angles Δ​θ _l in Eq. (83), i.e.

$$\displaystyle\begin{array}{rcl} \overline{z}\: =\:\sum _{l}\:w_{l}\;z_{l}\: =\:\sum _{l}\:w_{l}\;e^{\,i\varDelta \!\theta _{l} }& &{}\end{array}$$

(84)

we find the weighted average phase matrix product as:

$$\displaystyle{ \begin{array}{ll} \overline{\mathsf{\boldsymbol{\varPsi }}}_{\!\!^{\frac{a} {^{b}} }} & = \left (\begin{array}{lll} \ \ \mathrm{Re}(\,\overline{z}\,)\ \ \ \ \ \ \ \ \ i\;\mathrm{Im}(\,\overline{z}\,)\ \,\mathsf{\mathbf{\hat{a}}}\,^{T} \\ \,i\;\mathrm{Im}(\,\overline{z}\,)\ \,\mathsf{\mathbf{\hat{a}}}\,\ \ \ \ \ \ \ \mathrm{Re}(\,\overline{z}\,)\ \,\mathsf{\mathbf{\hat{a}}}\,\,\mathsf{\mathbf{\hat{a}}}\,^{^{T} } \end{array} \right ) \\ & = r\;\mathsf{\boldsymbol{\varPsi }}(\varDelta \!\theta,\,\,\mathsf{\mathbf{\hat{a}}}\,)\end{array} }$$

(85)

where r ≤ 1 is a scalar attaining unity only if all z _l are equal. In fact the value of r will be directly related to the width of the angular distribution of z _l . Again we have a direct analog to complex numbers and it should be noted that, in general, the average phase angle (a bounded real number) will not be the same as the phase angle of the average phase matrix, i.e.

$$\displaystyle{ \varDelta \!\theta \:\neq \;\overline{\varDelta \!\theta _{l}} }$$

(86)

4.4.2 General Averages

Analyzing the behavior of monomial phase matrix averages in the general case is beyond the scope of this chapter. Suffice to say that the averages will, due to the well-behaved representation, be continuous with respect to all entries and that the sub matrix $\overline{\mathsf{\mathbf{C}}}$ will hold information about the directional distribution of $\,\mathsf{\mathbf{\hat{a}}}\,_{l}$. For example, neighborhoods with a high degree of curvature will result in a $\overline{\mathsf{\mathbf{C}}}$ having more than one significantly non zero eigenvalue.

5 Conclusion

We have presented a novel matrix representation of multidimensional phase that has a number of advantages. In contrast to previously suggested phase representations it is shown to be globally isometric, i.e. the metric of the representation is invariant to shifts along the phase matrix manifold. The proposed phase estimation approach uses spherically separable monomial filter of orders 0, 1 and 2 which naturally extends to N dimensions. For 2-dimensional simple signals the representation has the topology of a Klein bottle. Further, we have defined a symmetric conjugate phase matrix product which retains the structure of the phase matrix representation. This product gives a phase difference matrix in a manner similar to the complex conjugate product of complex numbers. We have also shown that the phase matrix representation allows meaningful averages to be calculated as simple weighted summations. Some important advantages of the proposed representation has been demonstrated in two motion estimation examples.

We have to some extent investigated the mathematical properties of our new matrix phase representation. However, as pointed out by one of the reviewers, this matrix representation no doubt merits further investigation in particular regarding geometrical and group theoretical aspects.