A Decentralized Production and Distribution Planning Model in an Uncertain Environment

Abstract

Distributed Decision Making (DDM) is a discipline of decision theory in which decision making power is distributed among several decision making units. Supply Chain planning problems usually involve multiple decision makers, making DDM highly suitable for realistic modelling. Furthermore, due to the complexity and dynamism of supply chain environments, accounting for uncertainty is important when modelling a supply chain planning problem. This chapter contributes to existing knowledge on the one hand with a brief literature review of DDM systems developed in the recent past. On the other hand, it contributes a proposed DDM coordination mechanism for a supply chain planning problem with two distributed decision makers, in a multi-echelon context, with multiple product levels. The DDM system’s performance is evaluated under demand uncertainty by applying a fuzzy approach. Computational results show that the proposed distributed model closely approximated the optimal solutions generated by the centralised model, strengthening the evidence for DDM’s applicability to real problems. Finally, the fuzzy approach is shown to be a useful tool for decision makers in evaluating risk in their supply chain planning decisions.

1 Introduction

A Supply Chain (SC) can be defined as a system of organizations, people, technology, activities, information and resources involved together in the creation of value for an end customer by moving a product or service to that customer. It is imperative that some form of collaboration exists between supply chain members to coordinate their activities and plans for better results. This coordination or alignment as it is also known is referred to as collaborative planning. Formally defined, “collaborative planning is a joint decision making process for aligning plans of individual SC members with the aim of achieving coordination in light of information asymmetry” (Stadtler 2009).

Key elements of this definition are that collaborative planning is a decision making process, and that it is done in light of information asymmetry. The latter simply means that not all SC members have access to the same information. Jung et al. (2008) found that most supply chain planning approaches involve some form of centralized supply chain environment, in which the decision maker has all the required information. However, exactly that is what is lacking in a collaborative planning environment according to Stadtler’s definition.

Distributed Decision Making (DDM) is a discipline of decision theory in which decision making power is distributed among several decision making units. These decisions are interrelated because one decision affects the outcome of another. How to structure these distributed decision problems into a coordinated problem is the central question in Distributed Decision Making. “DDM can therefore be characterized as the design and coordination of connected decisions” (Schneeweiss 2003).

Application of DDM theory to supply chain planning problems started over two decades ago. New approaches however, continue to be developed in the scientific community. As part of the Quantitative Modelling Techniques, DDM will be applied to a centralized supply chain planning model. The centralized model that serves as the basis for this work is the Production and Distribution Planning Model developed by Park (2005). Jung et al.’s (2008) work serves as the basis for creating the distributed model.

The real world complexity and dynamism of Supply Chain environments also imply there is usually a degree of uncertainty regarding SC planning decisions. This uncertainty can greatly influence the effectiveness of decisions taken, meaning it is valuable to consider it in the decision making process. Davis (1993) recognises three main types of uncertainty, supplier uncertainty, process uncertainty and demand uncertainty. Supply uncertainty results from variability in suppliers’ performance. Process uncertainty results from unreliability issues in the production process. The most important type of uncertainty, according to Davis, is demand uncertainty which arises from volatile demand or inaccurate forecasts. Coincidently, demand uncertainty was also required to be included in the Distributed Decision Making model.

The objective of this chapter is therefore twofold:

• 1. To convert a centralized supply chain planning model into a distributed decision making model and compare the performance of both models,

• 2. To apply fuzzy logic theory (possibility theory approach) to the distributed model to incorporate demand uncertainty and comment on its performance and use.

Although the adaptation of Park’s centralised model towards a distributed model is to be done using a similar method to that of Jung et al., many other methods exist in the literature. A review of the literature will be performed to identify existing DDM systems. Especially the coordination mechanisms they employ are interesting since this determines to great extent how the system works. A classification of DDM systems based on characteristics taken from earlier classifications will be attempted to gain a more structured view on the existing body of work. In addition to simply creating this overview, it is hoped that insights will be gained as to how to create a DDM model out of Park’s centralized model.

The following steps are of a more practical nature. The centralized model will have to be decomposed into distributed models after which a coordination mechanism can be designed. Both model’s performance will then be compared with the aid of a commercial modelling program and solver, MLP and CPLEX. The last step to achieve the second objective is model the uncertainty of demand by applying fuzzy possibility theory.

The rest of this section starts with a description of the search methodology and corresponding literature review. The overview of existing DDM systems finishes Sect. 2, and with it the more theoretical half of this report. Section 3 first introduces the generic centralised model before presenting the hands on problem that is to be solved by all the mathematical models. The centralised model is then decomposed into distributed models in Sect. 4, after which the coordination mechanism is also presented. Section 5 has a more elaborate introduction on fuzzy logic theory and presents the distributed model under uncertainty. Section 6 presents the computational results for all three models and contains a discussion of these results, after which Sect. 7 offers some final conclusions and future work.

2 Literature Review

This section contains the theoretical part of this research project. It starts with the search methodology, followed by the discussion of important Distributed Decision Making characteristics and the actual analysis of the existing literature on DDM and mathematical programming.

2.1 Search Methodology

This section outlines the methodology used during the search for relevant scientific literature regarding DDM. First the search terms used are presented, followed by the scientific databases that were consulted. The section is concluded by a representation of the obtained results.

2.1.1 Search Terms

Distinguishing search terms had to be devised to find relevant material. First of all, prior work had to preferably be related to some form of operations, production or supply chain planning. That would fit closer to the problem treated later in the applied part of this research. Second, it was imperative that the mathematical models were distributed or decentralized. Because collaborative planning uses DDM extensively, and coordination mechanisms are essential elements these search terms were also chosen. To increase the possibility of finding mathematical models, abbreviations were added to the former. Finally, reviews, surveys and bodies of knowledge were queried for because they could offer a good starting point for more articles and search terms. The search terms devised before starting the search are presented in Table 1.

Table 1 Search terms devised prior to consulting scientific databases

2.1.2 Scientific Databases and Search Strategy

Four databases of scientific articles were consulted in order to find relevant literature. These were the following: ScienceDirect, Scopus, Emerald Insight and IEEE Explorer. The article titles, abstracts and keywords were queried for matching results. The results for these queries are presented in Sect. 2.1.3. Furthermore, cross checking of oft cited articles was performed to find other relevant material. This was particularly fruitful for the review and survey type results. For the subsequent analysis, priority was generally given to those articles that were most recent and/or cited often.

2.1.3 Obtained Results

Table 2 shows the number of articles found for a particular combination of search terms, for different scientific databases. Differences are accountable to the different search algorithms the databases employ. IEEE explorer e.g., returned many articles when ‘production planning’ was used. Practically no results were left when the term was taken out.

Table 2 Number of articles found with combination of search terms, sorted for scientific database

Table 3 shows the amount of articles that were eventually selected as reference articles, sorted by the journal in which they were published. Only the European Journal of Operational Research provided more than one reference article, with all others providing a single article. The wide range, from chemical engineering to computer engineering shows that distributed decision making is applied in a broad field of disciplines.

Table 3 Reference articles sorted by journal of publication

The final representation of literature search results is given in Table 4. Not many conclusions can be drawn from this table, because not enough articles were analysed to offer a comprehensive picture on the publication dates of articles on DDM in mathematical modelling.

Table 4 Reference articles sorted by year of publication

2.2 Presentation of DDM Characteristics for Analysis of Literature

Due to the sheer variety in mathematic models developed, it should come as no surprise that there exists a similar variety of Distributed Decision Making systems. Various authors have tried to classify those using different distinguishing characteristics. Three of those efforts are discussed here, after which the most relevant characteristics are chosen for the classification in this research.

2.2.1 Review of Earlier Taxonomies and Classification Attempts

Schneeweiss (2003) developed taxonomy to classify and formally describe various hierarchical DDM systems in a unified way. It is important to note first, that Schneeweiss distinguishes between a Top level and a Base level within the hierarchy. The Top level is regarded as the leader in the hierarchy that makes the first decision and the Base level follows the Top level’s instruction. The Base level then engages in its own local decision making. Now, Schneeweiss identified three key characteristics that can be used to characterize DDM systems.

The first characteristic is the state of information. This can be either symmetric, which means that the same information is known to all decision makers in the system, or asymmetric, which means that certain information may be known to one, e.g., Top, but unknown to another, Base e.g.

The second characteristic is the grade of anticipation that decision makers show in their decision making. Two options exist. A reactive anticipation means that the Top level considers a possible reaction of the base-level with respect to a top-level’s possible instructions. For non-reactive anticipation, on the other hand, no specific reaction is taken into account. Reactive anticipation can be perfect, meaning that the Top level has full knowledge of the Base level’s model and thus its reaction. It can also be approximate, when the Base level’s model is approximately known by the Top level. The last possibility is implicit anticipation where only a part of the base level is anticipated. The grade of anticipation employed shows how much ‘bottom-up’ influence in the decision making at Top level there is within the hierarchy.

The final characteristic is defined as the configuration of criteria. Coupling equations of criteria are used to demonstrate the degree of coupling between Top and Base levels. For any form of Top level criterion in which the Base level’s criteria are integrated in-, added to- or even make up entirely the Top level criterion, a DDM is said to be team based. This is because the value of the Top level criterion depends on the Base level through its definition. Of course, the Base level has to comply to the Top level’s instructions so a Base level criterion need not take Top level criteria into account. The three configurations of criteria mentioned are all common in team based DDM systems.

The other possible configuration is non-team. This happens when a Top level’s criterion completely ignores the Base level. In this case, each level is thus completely self-interested and will show what is known as opportunistic behaviour. The goal is always to increase one’s own benefit, even when detrimental to the global solution. Based on these criteria, Schneeweiss classifies DDM systems into three main types. They are shown in Table 5. He notes that many variations to these general types may occur.

Table 5 Three types of DDM systems as identified by Schneeweiss (2003)

Another notable effort is a framework developed by Stadtler (2009), which is meant to classify Collaborative Planning approaches along various characteristics. Three main groups of characteristics are identified, (1) the supply chain structure and the relationships within the supply chain, (2) the decision situation, or which decisions take place, when, with which objectives and with which information, and (3) the characteristics of the collaborative planning schemes. Only the characteristics relevant to DDM models and in particular coordination mechanisms will be discussed here.

Within the relationships between supply chain members involved in CP, their behaviour is important. It can be team, opportunistic (non-team) or somewhere in between, and coincides with one of Schneeweiss’s characteristics. However, Schneeweiss mathematically formalized team and non-team behaviour with the aid of coupling equations and criterions for Top and Base level, whilst Stadtler merely pointing out its importance. Nevertheless, its importance is now clearer than ever and a coordination mechanism must take possible opportunism into account. The required solution is also important for the coordination mechanism. It can be limited to aligning flows of materials, or merely finding a feasible solution. Perhaps an optimal solution for the supply chain as a whole is required, or one step further, a fair solution for all members involved. This was not part of Schneeweiss’s analysis.

Within the decision situation the models that are employed, in which phase there is collaboration and which objectives are employed are all important. However, the most important aspect here is referred to as information status. Which information is shared, how certain can we be of its correctness and is certain information hidden? The latter corresponds to symmetry or asymmetry. Recall that Stadtler by definition regards collaborative planning to involve asymmetric information.

The final group of characteristics is in my opinion the most important with respect to DDM and coordination mechanisms. The presence of a mediator could significantly alter the dynamics of collaboration. How the initial solution is defined is also important. This is mostly done by upstream planning according to Stadtler (2009), but downstream planning or random initial solutions can also be used. The number of plans exchanged between levels, consisting of the number of rounds allowed to reach a solution and the number of offers sent per round can also change how a system works. Finally, with respect to the final results, being able to check optimality or not, and the allowing of side payments could affect a coordination mechanism. The latter could e.g., be used to make a solution fairer to all members.

The final research used for the development of taxonomy is a review on collaborative supply chain planning by Frayret (2009). For collaborative planning, there are three challenges to be dealt with: “the design of a coordination process, …, the design of local decision making processes; and the design and utilization of Advanced Planning and Scheduling systems (APS)” (Frayret 2009). The former is conveniently the main focal point of his classifications. The local decision making processes correspond to what Stadtler referred to as the decision models. APS systems are inherently linked to coordination techniques according to Frayret (2009), but will not be considered further as they are outside the scope of this project.

The coordination processes can once again be divided further, into three groups. The first group is the Coordination Heuristics, which consists of:

• (a) Greedy heuristics and information sharing,

• (b) Distributed local search,

• (c) Distributed search with constraint propagation.

Greedy heuristics and information sharing are the most simple coordination mechanisms. They include upstream planning and variations of it to improve performance. Other examples are when more information is shared, even up to the point where more centralized solving is possible. Distributed local search generally involves an iterative exchange of information between supply chain partners, during which the local levels adjust their own initial plans by searching for local optima. Distributed search occurs when more than one search process is carried out simultaneously. In the distributed local search the members take their local searches in turn. In the distributed search this is not the case, making the search faster.

The second group is Agent Based Coordination, which consists of:

• (a) Knowledge-based coordination,

• (b) Market-based coordination.

Agent Based Coordination is based in agent technology, which uses artificial intelligence (AI) to develop coordination approaches. Agents are pieces of software that represent a certain interest. They can thus be used to represent members of a supply chain. In knowledge-based coordination, a set of agents use protocols that tell them how to interact with other agents. These protocols define all possible actions and model the outcomes of interactions. The protocols thus govern the coordination. In some cases, additional information known as arguments are sent to other agents, with the aim of influencing their actions. The other agent based coordination technique is Market-based coordination. Basically, like in an auction proposals are sent and received by agents. The contents of these proposals are modified to increase or decrease benefits, according to their prior success or failure respectively. Here, the learning or AI aspect of agents becomes clear.

The final coordination technique identified by the author is Mathematical decomposition (6). He claims the main decomposition approach is Lagrangean decomposition. Its general idea is that an originally distributed model is turned into a centralized model, by relaxing the ‘complicating’ constraints where local variables of two or more coupled decision makers appear. A penalty is assigned to violating these relaxed constraints by using Lagrangean multipliers. Then, a distributed and synchronous iterative process is developed to adjust the penalties until the model converges on a feasible solution. One could view it this way. The ‘local’ models (bear in mind that the model is centralized) communicate through these Lagrange multipliers. Values that increase other local decision makers’ penalties are communicated if one’s own non relaxed constraints are violated. The contrary is true when there is slack in those constraints. This is done until all hard constraints are satisfied and penalties are preferably at a minimum. Details on the exact working of mathematical decomposition can be found in works by Nishi et al. (2007), Walther et al. (2008) and Lu et al. (2012).

2.2.2 Selection of Characteristics for Analysis

The state of information is identified by both Schneeweiss and Stadtler, so it seems very important to include that. Stadtler added the degree of uncertainty and the type of information (products, costs, other KPI’s) to the existing characteristic of (a) symmetry of information. Type of information is very specific, so it is ignored. Degree of uncertainty will also be considered next to symmetry, because the end goal of this research is a model that accounts for demand uncertainty.

The grade of anticipation of one level’s criteria by another is also interesting since it greatly influences a Top level’s instruction. The last of Schneeweiss’s characteristics is the configuration of criteria. How a top level decision maker in a hierarchy takes the base criteria into account, is not extremely important. Most important is to know whether it happens or not, because it interests us to know whether decision makers exhibit team- or opportunistic behaviour in a DMM system. This was coincidently Stadtler’s only distinction. The exact configuration is therefore dropped. All three characteristics will be used, but the type identification as performed in (Schneeweiss 2003) will not be employed. The reason is that the characteristics themselves reveal more than a type.

Distinguishing between DDM systems that look for feasible solutions, optimal supply chain solutions or even fair solutions is very interesting. First, optimality is much more difficult to achieve than just a feasible solution. Second, requiring a fair solution has strong implications for the coordination mechanism because the initial mechanism might not produce a fair solution. Also, “computational tests showed that fair solutions sacrifice 37.15 % on average in solution quality” (Stadtler 2009). Related to that is the allowing of side payments at the final solution, as they could diminish that sacrifice. Therefore, these will also be taken into account. Other characteristics identified by Stadtler that will be looked out for is the presence of a mediator, solely because it could completely change how coordination works, how the initial solution is computed, and the number of rounds and offers used in the communication process. Few or many rounds e.g., determine whether or not a system can be operated manually or must be fully automatic.

To conclude, the coordination mechanism distinction from Frayret will also be included in the analysis. Although a certain coordination mechanism may imply one of the earlier characteristics, the actual mechanism will greatly set the studied works apart. It will also be useful for a reader to see which general coordination mechanism is employed to decide whether it interests him/her.

2.3 Analysis of Literature

The articles studied for this project were not all designed for use in supply chain contexts. However, they do all represent some form of distributed decision making system. It proved quite difficult to find distributed decision making systems within the time constraints, so non supply chain systems were also included. Their techniques are what matter most, not only the application area. Each system was analysed for identification of the characteristics chosen in Sect. 2.2. The respective characteristics for each system are summarized in Table 6. The numbers below the characteristics point out their source, and N/A means that information was not provided or not applicable.

Table 6 Classification of studied works

The first DDM system analysed by Cao and Chen (2006) was a decentralized facility location problem. They changed a decentralized two level nonlinear programming model into an equivalent linear single level model. The result was a hierarchical model with a coordination mechanism resembling the upstream planning approach in a supply chain context.

A more advanced system used a distributed local search for local optima. Jung et al. (2008) developed a decentralized supply chain planning framework based on minimal-information sharing between the manufacturer and a third party logistics provider. Each used its own model and kept private information. The coordination mechanism ensured local solutions converged towards a feasible solution, although the levels did not cooperate as a team. Each level strived for local optimisation. However, opportunistic behaviour was not demonstrated as the information they exchanged was truthful.

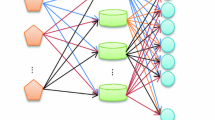
While the different levels in Jung et al.’s model had to wait for input from the other level before proceeding to search for their new local optimum, Gaudreault et al. (2009) developed a system wherein levels concurrently evaluate other level’s earlier decisions instead of one local optimum being processed at any given moment. The authors call this a “distributed discrepancy search procedure” and it is categorized as a distributed search with constrain propagations. The procedure is illustrated in Fig. 1. The top level (agent A, closest to the customer) takes lower levels (tiers further away) into account. This is because the lower levels communicate their locally optimal plans upwards. The optimal solution is thus known to agent A but not to agents B or C. The distributed search for the optimal solution is like a tree. Each agent computes its optimal solution based on the request by the agent directly above him (one tier closer to the customer). It is thus possible that agent C is working on a local solution based on what agent B sent him, whilst at the same time agent A is computing a new solution based on the locally optimal response it got from agent B. More than one solution is thus evaluated at a time.

Fig. 1

Illustration of distributed discrepancy search procedure, Source (Gaudreault et al. 2009)

An example of agent based coordination was found in the work of Wernz and Denshmukh (2010). The specific application was intra-organizational, but the techniques were interesting nonetheless. First of all, the Top level agent and Base level agent are in a hierarchical relationship, but the agents make decisions simultaneously instead of sequentially. There is also two way interaction through reward and influence, which is not seen in any of the other studied works. This anticipation is merely implicit. It would be characterized as a principal agent system according to the definition by Schneeweiss (2003).

The remaining three studied systems employed mathematical decomposition through Lagrangean relaxation of constraints. The first of these by Nishi et al. (2007) was developed to determine the production scheduling and distribution planning for a single stage production system with parallel distributed production units. The novelty is in their use of quadratic penalty terms in the objective function. Walther et al.’s (2008) mathematical decomposition is applied to a supply chain problem, that of a recycling supply chain looking to assign optimal quantities of mass for recycling. The mathematical decomposition of the initial centralized model is performed to create the negotiation mechanism between a head firm and several recycling companies. In these two systems, a master problem serves as a top level coordinator. The sub-problems communicate their local solutions to the master problem to eventually find the optimum. Lu et al.’s (2012) approach also involves Lagrangean relaxation, but they do not introduce a master problem to server as a coordinator of the decomposed original central problem. “Instead, the resulted sub-problems are equally ranked, and a novel self-coordination scheme is developed which enables the solving of sub-problems is coordinated through peer-to-peer communication, rather than communication between each sub-problem and the master problem” Lu et al. (2012).

Interesting similarities between all studied DDM systems is that all deal with asymmetric information, the objective is always to find the SC optimum and never a fair solution, and none of the systems employs a mediator. The biggest differences are found in the team or opportunistic behaviour demonstrated, and of course the coordination mechanisms used. The reader is reminded that the overview of the classification can be found in Table 6.

3 Centralized Deterministic Model

This section presents the centralised deterministic model used as the basis for the applied part of this research project. The model is an adapted form of the production and distribution planning model by Park (2005). First the general model formulation is given, followed by an explanation and the specific configuration of the planning problem. Computational results are given in Sect. 6.

3.1 General Model Formulation

The centralised planning problem considers a supply chain of manufacturing plants and retailers, with a planning horizon of five time periods. The manufacturing plants produce multiple items with a limited production capacity. For every item that is produced in a given time period, a plant dependent fixed set-up cost is incurred that is independent of the lot size. Excess production may be stored at the plant at a holding cost, for which there is no storage capacity limit. The items are structured in a three level bill of materials (BOM). Those items at level two and three of the BOM are consumed for the production of higher level items, according to amounts defined in the BOM. Only the items at level one, which are the final products, are delivered to the retailers.

Plants are capable of producing only a given set of items, with the items distributed over the different plants. Therefore, plants also act as suppliers to each other for the delivery of items used as subcomponents. Only items that are consumed as subcomponents are delivered in between plants. Consequently, the planning problem is a multi-stage problem, with the plants capable of being at various stages, dependent on the items they produce and those items’ positions in the BOM.

Delivery between plants is regarded to be free of charge and free of capacity constraints. Delivery from plants to retailers is performed by means of a fleet of homogeneous vehicles with similar capacities and usage costs. Sending a vehicle from any plant to a retailer incurs a fixed cost (depreciation of vehicle, insurance, driver wages) and a variable cost dependent on the transported item, its quantity and the route (plant—retailer combination). Any one vehicle can only transport one item type and travel one route per time period. The amount of vehicles used can change without incurring costs.

The demand for the final products (level one items) is expressed as a ‘core demand’ and a ‘forecasted demand’. The ‘core demand’ may be considered as the demand by a retailer’s loyal customer base, and must be satisfied. The ‘forecasted demand’ contains the ‘core demand’ and is the total amount of final products that can be sold in a given time period. In the centralised deterministic model, these demands are known with certainty. Any unsatisfied forecasted demand is considered a stock-out, for which a stock-out opportunity cost is incurred. Backordering is not allowed. Every retailer is allowed to keep a finite amount of final products in inventory, for which an inventory cost is incurred.

The objective of the centralised planning problem is to maximise profits over the five time periods. The decision maker has all the data (demand, inventories, production costs etc.) available to him and plans the production and distribution of final product items and subcomponent items. A mixed-integer model is used to solve the centralised production and distribution planning problem. First, the notations used are presented, followed by the model.

Indices

$$ \begin{aligned} i & = plants, i \in \left( {1, \ldots ,I} \right) \\ j & = retailers, j \in (1, \ldots ,J) \\ k & = items, k \in (1, \ldots ,K) \\ t & = time periods, t \in (1, \ldots , T) \\ \end{aligned} $$

Parameters

$$ \begin{aligned} c_{ik} & = {unit\;processing\;cost\;of item\;k\;at\;plant\;i} \\ s_{ik} & = {setup\;cost\;for\; item\;k\;at\;plant\;i} \\ o_{ik} & = {processing\;time\; for\;item\;k\;at\;plant\;i} \\ u_{ik} & = {setup\;time\; for\;item\;k\;at\;plant\;i} \\ h_{ik}^{p} & = {inventory\;holding\;cost\;of\;item\;k\;at\; plant\;i\;per\;period\; t} \\ \lambda_{ik} & = \left\{ {\begin{array}{*{20}c} 1 & {if\;plant\;i\;can\;produce\;item\; k} \\ 0 & {if\;plant\;i\;can\;NOT\;product\;item\;k} \\ \end{array}}\right.\end{aligned} $$

$$ \begin{aligned}\beta_{{ik^{\prime}k}} & = {required\;cuantity\;of\;item\;k\;for\;the\;production\;of\;one\; item} \;k^{\prime} {at\;plant\;i} \\ L_{i} & = {production\;capacity\; of\;plant\;in\;time} \\ d_{ijk} & = {unit\;transportation\;cost\;of\;item\;k\;between\;plant\;i\;and\;retailer\;j} \\ g & = {fixed\;cost\;per\;vehicle} \\ B & = {fixed\;capacity\;per\; vehicle} \end{aligned} $$

$$ \begin{aligned} E_{jkt} & = {demand\;for\;item\;k\;at\;retailer\;j\;in\; period\;t\;that\;must\;be\;filled} \\ F_{jkt} & = {total\;forecast\;demand\;for\;item\;k\;at\;retailer\;j\;in\;period\;t}, E_{jkt} {is\;part\;of\;} F_{jkt} \\ p_{jk} & = {unit\;selling\;price\;of\;item\;k\;at\;retailer\;j} \\ h_{jk}^{r} & = {inventory\;holding\;cost\;of\;item\;k\;at\;retailer\;j\;per\;period\;t} \\ W_{j}^{r} & = {capacity\;for\;units\;of\;inventory\;at\ retailer\;j} \\ v_{jk} & = {stockout\;cost\;per\;unit\;of\;item\; at\;retailer\;j} \\ \end{aligned} $$

$$ \begin{aligned}\beta_{{ik^{\prime}k}} & = {required\;cuantity\;of\;item\;k\;for\;the\;production\;of\;one\; item} \;k^{\prime} {at\;plant\;i} \\ L_{i} & = {production\;capacity\; of\;plant\;in\;time} \\ d_{ijk} & = {unit\; transportation\;cost\;of\;item\;k\;between\;plant\;i\;and\;retailer\;j} \\ g & = {fixed\;cost\;per\;vehicle} \\ B & = {fixed\;capacity\;per\; vehicle} \end{aligned} $$

$$ \begin{aligned}\\ E_{jkt} & = {demand\;for\;item\;k\;at\;retailer\;j\;in\; period\;t\;that\;must\;be\;filled} \\ F_{jkt} & = {total\;forecast\; demand\;for\;item\;k\;at\;retailer\;j\;in\;period\;t}, E_{jkt} {is\;part\;of\;} F_{jkt} \\ p_{jk} & = {unit\;selling\;price\;of\;item\;k\;at\;retailer\;j} \\ h_{jk}^{r} & = {inventory\;holding\;cost\;of\;item\;k\;at\;retailer\;j\;per\;period\;t} \\ \end{aligned} $$

$$ \begin{aligned}W_{j}^{r} & = {capacity\;for\;units\;of\;inventory\;at\ retailer\;j} \\ v_{jk} & = {stockout\;cost\;per\;unit\;of\;item\; at\;retailer\;j} \\ \end{aligned} $$

Decision variables

x _ikt :

= quantity of item k produced in palnt in period t

y_ikt :

$=\left\{ {\begin{array}{*{20}c} 1 & {if\;setup\;must\;be\;performed\;at\;plant\;i\;for\;item\;k\;in\;period t} \\ 0 & {otherwise} \\ \end{array} } \right.$

a ^p _ikt :

= level of inventory of item k at palnt i in period t

C _ikt :

= quantity of item k consumed as subcomponent at palnt in period t

qi _ii′kt :

= quantity of components k shipped form palnt in to plant i′ in period t

qj _ijkt :

= quantity of item k transported form palnt in to retailer j in period t

a ^r _ikt :

= level of inventory of item k at retailer j in period t

z _ijt :

= number of vechile required for distribution form palnt i to retailer j in period t

Z _jkt :

= supply shortage volume of item k for ratailer j in; period t

Si jkt :

= outcome variable with available supply to be sent to Retailers model

Model

Objective function

$$ \begin{aligned} & Max\sum\nolimits_{j} {\sum\nolimits_{k} {p_{jk} } \sum\nolimits_{t} {\left( {a_{jkt - 1}^{r} + \mathop \sum \limits_{i} qj_{ijkt} - a_{jkt}^{r} } \right)} } \\ & - \left( {\sum\nolimits_{i} {\sum\nolimits_{k} {\sum\nolimits_{t} {c_{ik} x_{ikt} } } } + \sum\nolimits_{i} {\sum\nolimits_{k} {\sum\nolimits_{t} {s_{ik} y_{ikt} } } } + \sum\nolimits_{i} {\sum\nolimits_{k} {\sum\nolimits_{t} {h_{ik}^{p} a_{ikt}^{p} } } } } \right) \\ & - \left( {\sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {h_{jk}^{r} a_{jkt}^{r} } } } + \sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {v_{jk} } } } \left( {F_{jkt} - \left( {a_{jkt - 1}^{r} + \sum\nolimits_{i} {qj_{ijkt} - a_{jkt}^{r} } } \right)} \right)} \right) \\ & - \left( {\mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} g*z_{ijt} + \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{k} \mathop \sum \limits_{t} d_{ijk} qj_{ijkt} } \right) \\ \end{aligned} $$

(1)

Subject to

$$ \left( {\sum\nolimits_{k} {x_{ikt} *o_{ik} + y_{ikt} *u_{ik} } } \right) \le L_{i} \quad \forall i\forall t $$

(2)

$$ x_{ikt} \le M*y_{ikt} \quad \forall i\forall k\forall t $$

(3)

$$ x_{ikt} \le M*\lambda_{ik} \quad \forall i\forall k\forall t $$

(4)

$$ C_{ikt} = \sum\nolimits_{{k^{\prime}}} {\beta_{{ik^{\prime}k}} *x_{{ik^{\prime}t}} \quad \forall i\forall k\forall t} $$

(5)

$$ C_{ikt} = \sum\nolimits_{{i^{\prime}}} {qi_{{i^{\prime}ikt}} \quad \forall i\forall k\forall t} $$

(6)

$$ a_{ikt}^{p} = a_{ikt - 1}^{p} + x_{ikt} - \sum\nolimits_{j} {qj_{ijkt} } - \sum\nolimits_{{i^{\prime}}} {qi_{{ii^{\prime}kt}} \quad \forall i\forall k\forall t} $$

(7)

$$ a_{jkt - 1}^{r} + \sum\nolimits_{i} {qj_{ijkt} - a_{jkt}^{r} \ge E_{jkt} \quad \forall j\forall k\forall t} $$

(8)

$$ a_{jkt - 1}^{r} + \sum\nolimits_{i} {qj_{ijkt} - a_{jkt}^{r} \le F_{jkt} \quad \forall j\forall k\forall t} $$

(9)

$$ \sum\nolimits_{k} {a_{jkt}^{r} \le W_{j}^{r} \quad \forall j\forall t} $$

(10)

$$ \sum\nolimits_{k} {qj_{ijkt} \le B*z_{ijt} \quad \forall i\forall j\forall t} $$

(11)

$$ a_{ik0}^{p} = 0, a_{jk0}^{r} = 0,\quad \forall i\forall j\forall k $$

(12)

$$ x_{ikt} \ge 0, a_{ikt}^{p} \ge 0,y_{ikt} \in \left\{ {0,1} \right\},C_{ikt} \ge 0, qi_{{ii^{\prime}kt}} \ge 0, qj_{ijkt} \ge 0, a_{jkt}^{r} \ge 0, z_{ijt} \ge 0, and\; all\; are\; integers\quad \forall i\forall j\forall k\forall t $$

(13)

The objective function (1) expresses the total net profit over the time periods, calculated by subtracting total costs from total revenue. Revenue is the total turnover at all retailers, calculated by multiplying selling price with sales ($a_{jkt - 1}^{r} + \mathop \sum \limits_{i} qj_{ijkt} - a_{jkt}^{r} )$. The costs include production-, inventory holding-, stock-out- and distribution costs. Constraint (2) represents the capacity limit on production at a plant. Constraint (3) forces the incurring of setup costs if items are produced. Constraint (4) makes sure that production of items is only allowed at a plant if that plant is capable of producing that item. For both these constraints, M is a sufficiently large positive number. Constraint (5) determines the amount of an item that is consumed for the production of higher level items, by summing the products of the production quantities of the higher level items with the amount of lower level items consumed for their production. Constraint (7) assures the inventory balance at a plant, with both shipments to retailers and to other plants taken into account. Constraint (8) ensures that the ‘core demand’ is satisfied, whilst constraint (9) ensures that no more is sold (and thus ordered from the plants at some point) than the ‘forecasted demand’. Constraint (10) applies the storage capacity for inventory held by retailers. The amount of vehicles needed for transportation of items to retailers is calculated in constraint (11). Constraint (12) then defines the initial inventory levels at both plants and retailers. Note that these can be changed. The final constraint (13) enforces restrictions of non-negativity, integer and binary nature of decision variables.

The model calculates optimal production quantities $x_{ikt}$ for all items at the different plants for all time periods and optimal amounts $qj_{ijkt}$ to be shipped to the retailers. It will balance setup with inventory holding costs and delivery costs with stock-out costs. It can therefore occur that not all forecasted demand is satisfied, although the inventory storage capacity at retailers exists to minimise the occurrence of demand not being satisfied.

3.2 Specific Configuration of Supply Chain

The supply chain that is used for this research project is represented in Fig. 2. The model’s indices, parameters and decision variables are included to show to which part of the Supply Chain they pertain. The Supply Chain consists of three manufacturing plants and two retailers. There are five time periods and eight items in this problem. Of the items, only items one and two are of level one, and thus sold as end products. Their item number is indicated red for this reason. Furthermore, each item has a specific retailer, with retailer one selling item one and item two being sold by retailer two. The product structure of the final products is also given in the figure, where the required quantities of a subcomponent can be found in the top right corner of each item. Items three and four are the level two items, and items five to eight are at level three.

Fig. 2

Supply chain configuration used for centralised model

The item production capabilities are distributed among the plants in such a manner, that each item is produced at only one plant. Plant one makes items one and three, plant two makes items two and four, and plant three makes items five to eight. As a result, plant three supplies plants one and two with level three subcomponents. Plants one and two make their own level two subcomponents and final products. Because each retailer only sells one product, each plant only delivers to one retailer. The flow of items is represented by the red arrows in Fig. 2.

The configuration presented was determined in the assignment. However, the model has successfully been tested for other configurations. Examples are retailers selling more than one item, plants ‘competing’ by being able to produce the same items and common subcomponents in product structures. The flows could therefore also include the grey dashed arrows. This generality is a useful characteristic, should the model ever need to be applied to a different Supply Chain.

4 Distributed Deterministic Model

Next, the centralised deterministic model is decomposed into two separate models. These separate models each pertain to a different decision maker, one that controls the manufacturing plants and distribution of items, and one that controls the retailers. A coordination mechanism is developed to link the two models and form the distributed deterministic model. The distributed decision making process is also presented to enhance clarity. Computational results are again found in Sect. 6.

4.1 Model Manufacturer

The first decision maker has control over the production of items in the plants, and their distribution to the retailers. It is assumed that distribution of items is part of this decision maker’s model because it is generally the manufacturer’s responsibility to deliver a product to its customer. As done for the centralised model, first the notation is presented, then the model. Additions or changes from the centralised model are highlighted in bold.

Indices

$$ \begin{aligned} i & = plants, i \in \left( {1,2,3} \right) \\ j & = retailers, j \in (1,2) \\ k & = items, k \in (1, \ldots ,8) \\ t & = time periods, t \in (1, \ldots , 5) \\ \end{aligned} $$

Parameters

$$ \begin{aligned} c_{ik} & = {unit\;processing\;cost\;of \;item\;k\;at\;plant\;i} \\ s_{ik} & = {setup\;cost\;for\;item\;k\;at\;plant\;i} \\ o_{ik} & = {processing\;time\;for\;item\;k\;at\;plant\;i} \\ u_{ik} & = {setup\;time\;for\;item\;k\;at\;plant\;i} \\ h_{ik}^{p} & = {inventory\;holding\;cost\;of\;item\;k\;at plant\;i\;per\;period\;t} \\ \lambda_{ik} & = \left\{ {\begin{array}{*{20}c} 1 & {if\;plant\;i\;can\;produce\;item\; k} \\ 0 & {if\;plant\;i\;can\;NOT\;product\;item\;k} \\ \end{array} } \right. \\ \beta_{{ik^{\prime}k}} & = {required\;cuantity\;of\;item\;k\;for\;the\;production\;of\;one\;item}\;k^{\prime}{at plant i} \\ L_{i} & = {production\;capacity\;of\;plant\;i\;in\;time} \\ d_{ijk} & = {unit\;transportation\;cost\;of\;item\;k\;between\;plant\;i\;and\;retailer\;j} \\ g & = {fixed\;cost\;per\;vehicle} \\ B & = {fixed\;capacity\;per\;vehicle} \\ \user2{vi}_{{\user2{jk}}} & = \user2{unit\;supply\;shortage\; penalty\;cost\;of\;retailer\;j\;for\;item\;k} \\ \user2{Sj}_{{\user2{jkt}}} & = \user2{requested\;supply\;quantity\;for\;item\;k\;by\;retailer\;j\;in\;period\;t}\;(\user2{received\;from\;j}) \\ \end{aligned} $$

Decision Variables

$$ \begin{aligned} x_{ikt} & = {quantity\;of\;item\;k\;produced\;in\;plant\;i\;in\;period\;t} \\ y_{ikt} & = \left\{ {\begin{array}{*{20}c} 1 & {if\;setup\;must\;be\;performed\;at\;plant\;i\;for\;item\;k\;in\; period\;t} \\ 0 & {otherwise} \\ \end{array} } \right. \\ a_{ikt}^{p} & = {level\;of\; inventory\;of\;item\;k\;at\;plant\;i\;in\;period\;t} \\ C_{ikt} & = {quantity\; of\;item\;k\;consumed\;as\;subcomponent\;at\;plant\;i\;in\;period\;t} \\ qi_{{ii^{\prime}kt}} & = {quantity\;of\;components\;k\; shipped\;from\;plant\;i\;to\;plant}\; i^{\prime} {in\;period\;t} \\ qj_{ijkt} & = {quantity\;of\;item\;k\;transported\;from\;plant\;i\;to\;retailer\; j\;in\;period\;t} \\ z_{ijt} & = {number\;o\;vehicles\; required\;for\;distribution\;from\;plant\;i\;to\;retailer\;j\;in\;period\;t} \\ \user2{Z}_{{\user2{jkt}}} & = \user2{supply\;shortage\;volume\;of\;item\;k\;for\;retailer\; j\;in ;period\;t} \\ \user2{Si}_{{\user2{jkt}}} & = \user2{outcome\;variable\;with\;available\;supply\;to\;be\; sent\;to\;Retailers\;model} \\ \end{aligned} $$

Model

Objective function

$$ \begin{aligned} & Min \left( {\sum\nolimits_{i} {\sum\nolimits_{k} {\sum\nolimits_{t} {c_{ik} x_{ikt} } } } + \sum\nolimits_{i} {\sum\nolimits_{k} {\sum\nolimits_{t} {s_{ik } y_{ikt} } } } + \sum\nolimits_{i} {\sum\nolimits_{k} {\sum\nolimits_{t} {h_{ik}^{p} a_{ikt}^{p} } } } } \right) \\ & + \left( {\sum\nolimits_{i} {\sum\nolimits_{j} {\sum\nolimits_{t} {g*z_{ijt} } } } + \sum\nolimits_{i} {\sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {d_{ijk} qj_{ijkt} } } } } } \right) \\ & + \sum\nolimits_{\varvec{j}} {\sum\nolimits_{\varvec{k}} {\sum\nolimits_{\varvec{t}} {\varvec{vi}_{{\varvec{jk }}} \varvec{Z}_{{\varvec{jkt}}} \varvec{ }} } } \\ \end{aligned} $$

(14)

Subject to

$$ \left( {\sum\nolimits_{k} {x_{ikt} *o_{ik} + y_{ikt} *u_{ik} } } \right) \le L_{i} \quad \forall i\forall t $$

(15)

$$ x_{ikt} \le M*y_{ikt} \quad \forall i\forall k\forall t $$

(16)

$$ x_{ikt} \le M*\lambda_{ik} \quad \forall i\forall k\forall t $$

(17)

$$ C_{ikt} = \sum\nolimits_{{k^{\prime}}} {\beta_{{ik^{\prime}k}} *x_{{ik^{\prime}t}} \quad \forall i\forall k\forall t} $$

(18)

$$ C_{ikt} = \sum\nolimits_{{i^{\prime}}} {qi_{{i^{\prime}ikt}} \quad \forall i\forall k\forall t} $$

(19)

$$ a_{ikt}^{p} = a_{ikt - 1}^{p} + x_{ikt} - \sum\nolimits_{j} {qj_{ijkt} } - \sum\nolimits_{{i^{\prime}}} {qi_{{ii^{\prime}kt}} \quad \forall i\forall k\forall t} $$

(20)

$$ \sum\nolimits_{\varvec{i}} {\varvec{qj}_{{\varvec{ijkt}}} } + \varvec{Z}_{{\varvec{jkt}}} = \varvec{Sj}_{{\varvec{jkt}}} \quad \forall \varvec{j}\forall \varvec{k}\forall \varvec{t} $$

(21)

$$ \sum\nolimits_{k} {qj_{ijkt} } \le B*z_{ijt} \quad \forall i\forall j\forall t $$

(22)

$$ \sum\nolimits_{\varvec{i}} {\varvec{qj}_{{\varvec{ijkt}}} } = \varvec{Si}_{{\varvec{jkt}}} \quad \forall \varvec{i}\forall \varvec{j}\forall \varvec{k} $$

(23)

$$ a_{ik0}^{p} = 0\quad \forall i\forall k $$

(24)

$$ x_{ikt} \ge 0, a_{ikt}^{p} \ge 0,y_{ikt} \in \left\{ {0,1} \right\},C_{ikt} \ge 0, qi_{{ii^{\prime}kt}} \ge 0, qj_{ijkt} \ge 0, z_{ijt} \ge 0,Z_{jkt} \ge 0,\;and\; all\; are\; integers\quad \forall i\forall j\forall k\forall t $$

(25)

The manufacturer does not know the actual demand for final products. He only knows the requested supply quantities for each item per period as submitted by the retailers. This quantity is represented by a new parameter $Sj_{jkt}$. The manufacturer must endeavour to fill the requested supply quantities to the best of his ability, because it contributes to Supply Chain profitability. To make the model strive for this, a penalty will be incurred for every unit of unfilled requested supply. For this reason, a shortage penalty cost $vi_{jk}$ and a shortage quantity decision variable $Z_{jkt}$ have been defined.

The manufacturer has no knowledge of actual demand or of retail prices. Maximising profit is thus not a valid objective for this model. Instead, the manufacturer will try to minimise its costs while meeting supply, because that should contribute to SC profitability. The objective function (14) now only includes production, setup and inventory holding costs for the plants, distribution costs and supply shortage penalty costs. Because having shortage negatively affects the objective function, the model will try to fill all demand. The penalty cost per unit of shortage must be high enough for the manufacturer to generally prefer production and distributing to incurring the penalty.

Constraints (15–20) are the same as in the centralised model, but constraint (21) replaces the constraints that ensured filling demand. It makes sure that the amount of an item shipped from all the plants to a retailer plus any shortage equal the requested supply quantity by that retailer for that item. If the shipped amounts do not suffice, shortage is positive and the penalty will be incurred. Constraint (22) governs the amount of vehicles needed for transportation of items to retailers, like in the earlier model. Constraint (23) is also new, and calculates the supply of an item k that is available for a retailer in a period t. This decision variable, $Si_{jkt}$, is the connection between the manufacturer’s model and the retailers’ model, because it will be communicated to the retailers after the manufacturer has solved its local problem. The retailers then know the available supply quantities that they can use to satisfy demand with. It will become clear that $Si_{jkt}$ is an input variable for the retailers’ model, just like $Sj_{jkt}$ is for the manufacturer’s model.

4.2 Model Retailers

The second decision maker has control over the retailers. This is a modelling choice, as each retailer could also have its own model, in which case the index j of the retailers would be forsaken. For simplicity, this is not done in this project. The notation and model are first given, with changes or additions highlighted in bold. The explanation of the model follows hereafter.

Indices

$$ \begin{aligned} j & = retailers, j \in (1,2) \\ k & = items,\quad k \in (1,2) \\ t & = time periods, t \in (1, \ldots , 5) \\ \end{aligned} $$

Parameters

$$ \begin{aligned} E_{jkt} & = \textit{demand for item k at retailer j in period t that must be filled} \\ F_{jkt} & = \textit{total forecast demand for item k at retailer j in period t}, E_{jkt} \textit{is part of } F_{jkt} \\ p_{jk} & = \textit{unit selling price of item k at retailer j} \\ h_{jk}^{r} & = \textit{inventory holding cost of item k at retailer j per period t} \\ W_{j}^{r} & = \textit{capacity for units of inventory at retailer j} \\ v_{jk} & = \textit{stockout cost per unit of item k at retailer j} \\ \user2{Si}_{{\user2{jkt }}} & = \user2{offered \;supply\; quantity\; of\; item\; k \;to\; ret}.\user2{ j\; in\; period\; t }\left\{ {\begin{array}{*{20}c} {\user2{first\; iteration\; it \;is\; infinite} } \\ {\user2{then, \;received \;from \;plants}} \\ \end{array} } \right. \\ \end{aligned} $$

Decision Variables

$$ \begin{aligned} \user2{q}_{{\user2{jkt}}} & = \user2{quantity\; of \;item \;k \;requested\; from\; plants\; by\; retailer\; j\; in\; period \;t} \\ a_{jkt}^{r} & = \textit{level of inventory of item k at retailer j in period t} \\ \end{aligned} $$

Model

Objective function

$$ \begin{aligned} & Max \sum\nolimits_{j} {\sum\nolimits_{k} {p_{jk} } } \sum\nolimits_{t} {\left( {a_{jkt - 1}^{r} + \varvec{q}_{{\varvec{jkt}}} - a_{jkt}^{r} } \right)} \\ & - \left( {\sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {h_{jk}^{r} a_{jkt}^{r} } } } + \sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {v_{jk} } } } \left( {F_{jkt} - \left( {a_{jkt - 1}^{r} + \varvec{q}_{{\varvec{jkt}}} - a_{jkt}^{r} } \right)} \right)} \right) \\ \end{aligned} $$

(26)

Subject to

$$ a_{jkt - 1}^{r} + \varvec{q}_{{\varvec{jkt}}} - a_{jkt}^{r} \ge E_{jkt} \quad \forall j\forall k\forall t $$

(27)

$$ a_{jkt - 1}^{r} + \varvec{q}_{{\varvec{jkt}}} - a_{jkt}^{r} \le F_{jkt} \quad \forall j\forall k\forall t $$

(28)

$$ \varvec{q}_{{\varvec{jkt}}} \varvec{ } \le \varvec{Si}_{{\varvec{jkt }}} \quad \forall \varvec{j}\forall \varvec{k}\forall \varvec{t } $$

(29)

$$ \sum\nolimits_{k} {a_{jkt}^{r} } \le W_{j}^{r} \quad \forall j\forall t $$

(30)

$$ \varvec{q}_{{\varvec{jkt}}} = \varvec{Sj}_{{\varvec{jkt }}} \quad \forall \varvec{j}\forall \varvec{k}\forall \varvec{t } $$

(31)

$$ a_{jk0}^{r} = 0,\quad \forall j\forall k $$

(32)

$$ q_{jkt} \ge 0, a_{jkt}^{r} \ge 0, and\; all\; integers\quad \forall j\forall k\forall t $$

(33)

First of all, the index i for the plants is no longer present, because it does not matter for the retailers where their supply comes from, as long as it comes. The parameter $Si_{jkt }$ is the only new parameter, and it is the available supply of an item for a retailer in period t, which is received from the manufacturer’s model. Only for the first iteration of the retailers’ model it is assumed to be infinite. This is because the distributed search for the optimal solution begins at the retailers, as will become apparent in the following sections. Because it does not matter from which plant the supply comes, the decision variable $qj_{ijkt}$ is changed into $q_{jkt}$. The latter now only represents the item quantities requested by a retailer from the manufacturer as a whole.

The objective function (26) is programmed to maximise profits by maximising sales and minimising inventory holding costs and stock-out costs. Constraints (27) and (28) still exist to ensure ‘core demand’ is satisfied and ‘forecasted demand’ not exceeded. The small change in these constraints is that $\sum\nolimits_{i} {qj_{ijkt} }$ is replaced by $q_{jkt}$. Constraint (29) enforces that the requested amounts of items from the manufacturer are at most what the manufacturer has indicated he can provide. Constraint (30) is copied from the centralised model. The sixth constraint is newly added to calculate the input variable for the manufacturer’s model, $Sj_{jkt }$. It is simply equal to $q_{jkt}$, meaning that could also be sent to the manufacturer’s model. However, for uniformity this is changed into $Sj_{jkt }$.

4.3 Coordination Mechanism

The characteristics of the coordination mechanism will now be discussed, drawing from the characteristics identified in Sect. 2. Information sharing in the distributed model is minimal, with only requested quantities and available quantities shared between the two decision makers. The exchange of requested and available supply quantities was inspired by the distributed local search mechanism as developed by Jung et al. (2008) Other information is kept private, accounting for a state of information asymmetry. The information exchanged however, is certain, and truthfully exchanged. The decision makers do not display opportunistic behaviour.

The distributed decision making model can also be characterised as a non-team model. Neither decision maker takes the other’s interest into account, and tries to optimise its own objective function. The other’s response is not anticipated either, making the grade of anticipation non-reactive. Neither decision maker has knowledge of the other’s model implemented in their own model. This makes opportunism a lot more difficult too.

The requested and available quantities are exchanged between the two decision making models directly. No mediator is involved to monitor or perhaps influence the local decisions that are taken. The distributed model starts with the retailer solving his local problem of determining how much to request from the manufacturer based on customer demand. That information is then sent to the manufacturer who returns his response. If the available supply quantity is enough to at least fill ‘core demand’, i.e., the retailers’ model has a feasible solution, the iterative exchange starts. The two models exchange updated solutions back and forth until they reach a feasible solution where all requested items are delivered without shortage. The initial solution used is one that maximises sales, because it is generated by the retailers’ model.

After starting the iterative process, the number of iterations is not fixed in the model. A protocol governing coordination as such has not been programmed. Iterations will be performed manually, continuing until a feasible solution has or has not been reached. A stop criterion is therefore not formally defined. Whether this is a correct choice will become apparent from the computational results, since they will show how many iterations were performed. The expected/desired result is a best solution for the Supply Chain as a whole. Fairness is not considered in the solution, with only the retailers’ model concerned with making money. All the manufacturer’s model does is minimise costs. He obviously does not know how his decisions affect revenue, and will only find out after having the final decision is made.

Side payments are not used to distribute the benefits between the decision makers and thus make it fair. This is also not required because the goal of the DDM model is to find the SC optimum. The other goal of side payments is to ensure each decision maker’s participation. The shortage penalty cost acts as the incentive for the manufacturer to comply with requests from retailers. This could also be modelled alternatively, to let the manufacturer make a profit when he complies with demand, but the penalty method works as well.

4.4 Modifications to Guarantee Feasibility

During initial testing of the distributed models, it was found that unless exorbitant shortage penalty costs $vi_{jk}$ (which were actually higher than the sales price) were applied, the manufacturer’s model would not supply the item with the lowest margin in the first period if capacity was tight. With margin, the difference between the penalty cost and the production-, setup-, inventory holding- and distribution cost is meant. The reason was that the model preferred to produce larger batches of one item in the first period, and then in the next period would start producing the other item. The result was infeasibility in the retailers’ model, because core demand could not be filled.

It is not realistic for a manufacturer to have complete liberty over supply quantities for his customers. A reasonable assumption is that the manufacturer and the retailers have agreed contracts, in which it is agreed that the manufacturer will endeavour to meet at least a percentage of the requested supply. If such a ‘fill rate’ is to be incorporated into the manufacturer’s model, the retailers could theoretically engage in shortage gaming strategies, to ensure they always get enough. This will not happen because of the model formulation, and the corresponding assumption of no opportunism, but in reality this would be very probable. That consideration shows that only in a trusting environment, can DDM really thrive. A fill rate of 67 % of the initially requested supply quantity is reasonable, and also enough to satisfy core demand. The fill rate $FR_{jk}$ will be added as a parameter to the model, so that it can also be changed according to any set of contractual agreements.

The additional constraint for the manufacturer’s model is then:

$$ \sum\nolimits_{i} {qj_{ijkt} } \ge FR_{jk} *Sj_{jkt}^{initial} \quad \forall j\forall k\forall t$$

(34)

The constraint ensures that the delivered quantity of item k is at least the fill rate multiplied by the initially requested supply. $Sj_{jkt}^{initial}$ is entered into the restriction, because the regular $Sj_{jkt}$ is updated after each iteration. However, the minimum amount to be filled is the fraction of the initially requested amount, not of the requested amount in the following iterations.

In reality, this would be easy, because the manufacturer can easily store the initially requested supply and not change it. However, for the model to function, a separate initial retailers’ model must be run to ensure that it stores $Sj_{jkt}^{initial}$ somewhere where it cannot be changed. In ensuing iterations the retailers’ model without the generation of $Sj_{jkt}^{initial}$ is then run.

4.5 The Decision Making Process

The flow of information and the decision making process is represented graphically in Fig. 3. The Distributed Model starts with the generation of the initial sales plan by the retailer, in which he calculates the initially requested supply quantities $Sj_{jkt}^{initial}$. These quantities are sent to the manufacturer who generates a production and distribution plan to best satisfy the requested supply quantities, at minimal cost. If there is no production shortage, then all requested supply can be delivered, which terminates the procedure. If the manufacturer cannot meet all that is requested, the available supply quantity per item, retailer and time period is calculated. This is then sent back to the retailer. He generates a new plan, checking whether he can meet his core customers’ demand. If not, the problem is infeasible. If he can, then he generates a new request quantity and sends it to the manufacturer. The procedure continues until there are no production shortages.

Fig. 3

Decision making process distributed model

5 Distributed Model Under Uncertainty

In this section, the distributed deterministic model is adapted to account for uncertainty in demand. The retailers’ model is the model that takes demand into account. In contrast, the manufacturer has no knowledge of demand. The adaptation to account for uncertainty will therefore be done exclusively on the retailers’ model.

Peidro et al. (2009) found that several approaches exist in scientific literature for developing SC planning models under uncertainty. Most are based on analytical approaches, simulation approaches or hybrids of the former two. The models developed in these approaches generally use probability distributions based on historical data. The fuzzy set theory , pioneered by Zadeh (1965), and possibility theory are the other approaches identified. These are not based on historical data and have been applied with much success to various fields for modelling of uncertainty. Through requirement, possibility theory shall be applied to model demand uncertainty in the DDM model.

Two parameters defined the demand in the retailers’ model; which were ‘core demand’ and ‘forecasted demand’. In possibility theory, these parameters are turned into diffuse coefficients. It is plausible that both parameters can turn out to be somewhat lower, or somewhat higher than initially thought. Consequently, a membership function that expresses that is required. A triangular or ‘Lambda’ membership function is therefore chosen to represent the fuzzy demand parameters. It has a central value with a membership degree of one, and the membership degree decreases the further the parameter moves away from the central value. Outside of two boundary values (one left and one right), the membership degree turns zero, meaning that it is not plausible that demand will take on values outside of a certain interval. Taking ‘core demand’ as an example, the triangular fuzzy coefficient E is defined by three parameters (E1, E2, E3). E1 is the left boundary of the fuzzy set, E2 the central value for which the membership degree equals one, and E3 is the right boundary of the set. The membership functions for ‘core demand’ E and ‘forecasted demand’ F are presented graphically in Fig. 4. One can see that for values in the interval [E1, E3] and [F1, F3], the membership degree $\upmu$ is non-zero.

Fig. 4

Membership functions of fuzzy parameters for ‘core demand’ $\tilde{\varvec{E}}_{{\varvec{jkt}}}$ (left) and ‘forecasted demand’ $\tilde{\varvec{F}}_{{\varvec{jkt}}}$ (right)

Furthermore, it is reasonable to assume that there is less uncertainty for the ‘core demand’, because it comes from a loyal customer base, than there is for the ‘forecasted demand’. A smaller range of values thus belong to the fuzzy set of ‘core demand than of ‘forecasted demand’. This is expressed by a smaller interval (a, b) than (c, d), i.e., the range between the boundary values.

The approach used to change the deterministic model into a fuzzy model is the one used by Jiménez et al. (2007). It was developed to incorporate diffuse coefficients with trapezoidal membership functions into linear programming models. The triangular function is a simplification of the trapezoidal function, for which the two central values of the trapezoid are the same and the function is symmetrical. For the mathematical justification of the method, the reader is referred to the article by Jiménez et al. (2007).

For triangular functions, Jiménez showed that the expected interval of a diffuse coefficient ã = (a₁, a₂, a₃), can be calculated by:

$$ EI\left( {{\tilde{\text{a}}}} \right) = \left[ {E_{1}^{{{\tilde{\text{a}}}}} , E_{2}^{{{\tilde{\text{a}}}}} } \right] = \left[ {\frac{1}{2} *\left( {a_{1} + a_{2} } \right), \frac{1}{2} *\left( {a_{2} + a_{3} } \right)} \right] $$

And the expected value of a diffuse coefficient can then be calculated by:

$$ EV\left( {{\tilde{\text{a}}}} \right) = \left( {\frac{{E_{1}^{{{\tilde{\text{a}}}}} + E_{2}^{{{\tilde{\text{a}}}}} }}{2}} \right) $$

Objective functions and constraints with diffuse coefficients in them subsequently change, although differently. When a diffuse coefficient appears in the objective function, it is replaced by its expected value. In a symmetric triangular membership function this value corresponds with the central value, so no calculations are really required. Constraints change depending on the relationship ($\le , =$ or $\ge$) defined in the constraint. The ‘satisfy core demand’ and ‘not surpass forecasted demand’ constraints affected in the retailers’ model are $\ge$ and $\le$ constraints respectively, which change as follows:

$$ \begin{aligned} ax & \ge b \to \left[ {\left( {1 - \alpha } \right)E_{2}^{a} + \alpha E_{1}^{a} } \right]x \ge \alpha E_{2}^{b} + (1 - \alpha )E_{1}^{b} \\ ax & \le b \to \left[ {\left( {1 - \alpha } \right)E_{1}^{a} + \alpha E_{2}^{a} } \right]x \le \alpha E_{1}^{b} + (1 - \alpha )E_{2}^{b} \\ \end{aligned} $$

Where α is a parameter $\in [0,1]$ set by the decision maker. With α he/she can vary the degree of feasibility of the fuzzy model. A higher value of α makes the fuzzy coefficients assume values that make it harder to find a feasible solution, thus covering for more of the uncertainty.

5.1 Retailers’ Model Formulation Under Uncertainty

The $F_{jkt}$ parameter in the objective function will be replaced with the expected value, so that the model is also generally valid. Because the newly defined fuzzy demand parameters only appear on the right hand sides of the constraints, only the right hand sides of the constraints are affected. The new terms are factored out to preserve linearity. The new fuzzy retailers’ model is thus formulated as following, with bold highlighting the changes:

Indices

$$ \begin{aligned} j & = retailers,\quad j \in (1,2) \\ k & = items,\quad k \in (1,2) \\ t & = time periods,\quad t \in (1, \ldots , 5) \\ \end{aligned} $$

Parameters

$$ \begin{aligned}\vec{\alpha}& = \user2{degree \;of\; feasibility \;parameter \;set\; by\; decision\; maker} \\\vec{\gamma}& = \left( {1 -\vec{\alpha}} \right),\user2{ complement \;of \;degree \;of\; feasibility\; parameter \;set\; by \;decision \;maker} \\ \tilde{\user2{E}}_{{\user2{jkt}}} & = \left( {\user2{E}_{1} ,\user2{ E}_{2} ,\user2{E}_{3} } \right)_{{\user2{jkt}}} , \textit{demand for item k at retailer j in period t that must be filled} \\ \tilde{\user2{F}}_{{\user2{jkt}}} & = \left( {\user2{F}_{1} ,\user2{ F}_{2} ,\user2{F}_{3} } \right)_{{\user2{jkt}}} , \textit{total forecast demand for item k at retailer j in period t} \\ p_{jk} & = \textit{unit selling price of item k at retailer j} \\ h_{jk}^{r} & = \textit{inventory holding cost of item k at retailer j per period t} \\ W_{j}^{r} & = \textit{capacity for units of inventory at retailer j} \\ v_{jk} & = \textit{stockout cost per unit of item k at retailer j} \\ Si_{jkt } & = \textit{offered supply quantity of item k to ret. j in period t} \left\{ {\begin{array}{*{20}c} {\textit{first iteration it is infinite} } \\ {\textit{then, received from plants} } \\ \end{array} } \right. \\ \end{aligned} $$

Decision Variables

$$ \begin{aligned} q_{jkt} & = \textit{quantity of item k requested from plants by retailer j in period t} \\ a_{jkt}^{r} & = \textit{level of inventory of item k at retailer j in period t} \\ \end{aligned} $$

Model

Objective function

$$ \begin{aligned} & Max \sum\nolimits_{j} {\sum\nolimits_{k} {p_{jk} } } \sum\nolimits_{t} {\left( {a_{jkt - 1}^{r} + q_{jkt} - a_{jkt}^{r} } \right)} \\ & - \left( {\sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {h_{jk}^{r} a_{jkt}^{r} } } } + \sum\nolimits_{j} {\sum\nolimits_{k} {\sum\nolimits_{t} {v_{jk} } } } \left( {\left( {\frac{1}{4}\varvec{F}_{1} + \varvec{ }\frac{1}{4}\varvec{F}_{2} + \frac{1}{4}\varvec{F}_{2} + \varvec{ }\frac{1}{4}\varvec{F}_{3} } \right) - \left( {a_{jkt - 1}^{r} + q_{jkt} - a_{jkt}^{r} } \right)} \right)} \right) \\ \end{aligned} $$

(35)

Subject to

$$ a_{jkt - 1}^{r} + q_{jkt} - a_{jkt}^{r} \ge \frac{1}{2}\varvec{\alpha E}_{2} + \frac{1}{2}\varvec{\alpha E}_{3} + \frac{1}{2}\varvec{\gamma E}_{1} + \frac{1}{2}\varvec{\gamma E}_{2} \quad \forall j\forall k\forall t $$

(36)

$$ a_{jkt - 1}^{r} + q_{jkt} - a_{jkt}^{r} \le \frac{1}{2}\varvec{\alpha F}_{1} + \frac{1}{2}\varvec{\alpha F}_{2} + \frac{1}{2}\varvec{\gamma F}_{2} + \frac{1}{2}\varvec{\gamma F}_{3} \quad \forall j\forall k\forall t $$

(37)

$$ q_{jkt} \le Si_{jkt } \quad \forall j\forall k\forall t $$

(38)

$$ \sum\nolimits_{k} {a_{jkt}^{r} } \le W_{j}^{r} \quad \forall j\forall t $$

(39)

$$ q_{jkt} = Sj_{jkt } \quad \forall j\forall k\forall t $$

(40)

$$ a_{jk0}^{r} = 0,\quad \forall j\forall k $$

(41)

$$ q_{jkt} \ge 0, a_{jkt}^{r} \ge 0, and\; all\; are\; integers\quad \forall j\forall k\forall t $$

(42)

6 Computational Results

This section discusses the computational results for the centralised deterministic model, distributed deterministic model and the distributed model under uncertainty. First the experimental design is explained, after which the results are presented. A discussion of the results follows to end the section.

6.1 Experimental Design

Eight different datasets were used to generate solutions with the different models. Three parameters were chosen to be varied to create the different sets. First, demand was given two different behaviours. Both had the same total demand value, but in one instance the demand was stable over the periods, whereas in the other it was very erratic, varying from near nothing to high peaks. Second, production capacity was varied. Low capacity meant that the production capacity constraints were very tight, and that it was never really possible to meet all demand. High capacity was chosen such that there should still be some slackness, meaning cost considerations would govern the decision more than capacity. These same costs were the third parameter to be varied. Combinations of low unit production costs with high setup costs, and high unit production costs with low setup costs were made to change the decisions the manufacturer would make regarding batches. Low setups obviously encouraged smaller batches. The eight combinations created the datasets found in Table 7. Due to space limitations, the details of the created datasets are not presented here, but can be made available upon request.

Table 7 Datasets used in computations

Another very important parameter for the distributed models is the penalty for production shortage applied to the manufacturer. Its value greatly influences the outcome of the manufacturer’s decisions, as was already found by the model choosing not to serve retailers at all if it is chosen too low. Three different values for the production shortage were used; one that is only 60 % of the sales price, one of 90 % and the highest penalty is 120 % of the sales price.

The values for these parameters, and all other parameters were entered into a Microsoft Access database. An Access database was chosen because it can interact with the modelling program employed, MPL. MPL models can extract data from the database and also export their solutions back to the database. This dual interaction was very useful for the exchange of the supply quantity variables $Sj_{jkt}$ and $Si_{jkt}$. The MPL models were solved with the CPLEX solver on a single desktop computer with 4 GB RAM, using an academic license.

6.2 Results Centralised Deterministic Model and Distributed Deterministic Model

The results for the Centralised Deterministic Model (CM) and the Distributed Deterministic Model (DM) are presented in Table 8. Several observations were made whilst studying the data.

Table 8 Computational results for centralised model (CM) and distributed model (DM)

• 1. The biggest percentage gap in the objective value profit between the CM and the DM is 11.2 %. This occurs twice, whilst the second biggest gap is only 4.6 %. In general, the DM looks to be performing reasonably well compared to the CM, with many distributed solutions being close to the optimal solution.

• 2. The biggest percentage gaps occur when setup costs are high in relation to unit production costs. This corresponds to the odd datasets. The explanation is that high setup costs may cause the manufacturer to not want to produce a batch of a certain item, if it has enough in inventory to meet the agreed fill rate. Some of the forecasted demand can then not be met, resulting in lost sales and a suboptimal solution.

• 3. The DM’s performance did not vary much for the production shortage penalties ${\text{vi}}_{\text{jk }}$ of 60 % and 90 % of the sales price. However, for a penalty cost of 120 % of the sales price, DM performance was always equal or better than for the lower penalties, and by quite a margin. For this model therefore, a higher penalty cost seems to lead to better results.

• 4. Computation times were either very short, or extremely long. Two of the 24 runs of the manufacturer’s model took 500 and 600 s respectively. These did not occur for the same dataset either, which seems to suggest that some combinations of data make the problem more difficult to solve optimally, because solutions are closer together.

• 5. One run of the CM also took a very long time, and it was aborted after 10 min (600 s) with a suboptimal solution being accepted. The DM outperformed the CM for all three shortage penalties. Only in this particular case, the DM performed better as the shortage penalty decreased. These two observations imply that for that particular dataset, not serving some of the demand was better. However, I assume that this is due to the dataset configuration and to be considered an anomaly instead of a rule.

• 6. The two most important observations come from the iterations column. In some cases, only one iteration is required because it is optimal for the manufacturer to deliver everything that is requested. This coincides with a stable demand behaviour and high production capacity.

• 7. In all the other runs, only two iterations are sufficient to generate a feasible solution to the problem. The retailers never order less than the available supply quantities. With hindsight, this is due to the decomposition choices made for the centralised model, which requires some further discussion.

Part of the assignment was to apply the same type of coordination mechanism that Jung et al. (2008) developed for their DDM model. The important difference between their model and the adaptation of Park’s (2005) model developed in this chapter, is the model decomposition choices made when decomposing the central model into two distributed models. The decomposition choice to make the manufacturer responsible for delivering the items to the retailers has meant that the only consideration for the retailers is minimising inventory and stock-out costs. This means they will ask for as much as they can possibly sell every period, but no more. Keeping inventory would come into the equation if the distribution costs were also incurred by the retailers. They might then prefer smaller or bigger shipments to avoid nearly empty vehicles, resulting in inventory at the retailers. In that case, the retailers might actually change their requested supply quantities after knowing the available supply quantities, resulting in more iterations. In Jung et al.’s model, the retailer’s place is taken by a third party logistics provider (3PL). He does have to take distribution costs into account, so his optimal local solution may change per received available supply quantity. I want to be clear that the decomposition choice was made on the argumentation given earlier, realism. The increased simplicity of the coordination was not taken into account.

Seeing how the distributed model would behave if the retailers’ model included distribution costs instead of those being part of the manufacturer’s model, would be very interesting. I expect that the amount of iterations would increase, following the above reasoning on managing distribution-, inventory and stock-out costs. The coordination mechanism would also change somewhat, although it would still function in a similar fashion.

Taking all into account, more dynamism in the coordination process would have been revealing regarding the workings of distributed decision making, but the current distributed deterministic model performs well enough to be satisfied with the result.

6.3 Results Distributed Model Under Uncertainty

The optimal solutions for the distributed model under demand uncertainty were generated with a production penalty value $vi_{jk }$ of 120 % of the sales price, because these gave the best results in the earlier computations. Datasets one, four and five were chosen at random for the other parameters.

The parameter α was varied between 0.1 and 1. Recall that a solution for α = 0.1 is very easily found because the uncertain demand parameters take on the most favourable values. That solution is thus the best possible outcome, but it is not very likely, and will probably leave the decision maker with unsold items. One could call it the risky solution. At the other end of the scale, α = 1 gives the worst possible outcome. However, this solution is also certain to be possible, because the demand parameters take on the most unfavourable values that the decision makers believe they can assume. This is thus the risk-averse solution. So, the choice for α depicts the amount of risk the decision maker is willing to accept in his solutions. The computational results for different values of α are given in Table 9.

Table 9 Computational results for distributed fuzzy model with demand uncertainty

The optimal objective values for α = 0.5 correspond with the objective values found by the deterministic DM. This is because of the symmetry in the chosen membership functions. For each dataset, the riskiest solution has the potential to perform 45 % better than the most risk-averse solution. It is therefore for the decision maker to decide how much risk he wants to take with his solutions.

The computation times are mostly quite low, with two notable exceptions. Once, for dataset 1 the entire computation takes 121 s, and for one run with dataset 4 the solver takes a total of 300 s. These are other datasets than took long in the deterministic DM however. Consequently, this enforces the belief that long computation times result from ‘unlucky’ combinations of parameters that give the solver a hard time in finding the optimal solution. This time however, both longer runs did finish inside 10 min and were therefore not aborted prematurely.

7 Conclusions

An analysis of recent Distributed Decision Making related work was given in this chapter. The different works of literature were classified along differing DDM characteristics, with extra attention given to characteristics related to the coordination mechanisms used in DDM systems.

Thereafter, a centralised deterministic mixed-integer model was developed for a Supply Chain planning and distribution problem similar to that of Park (2005), but with the addition of multiple product levels. This model was further developed into a distributed deterministic model and a distributed model which accounted for demand uncertainty by applying possibility theory. The distributed model has demonstrated that it could approximate very closely the centralised model’s performance, in most cases to within a per cent point. With the fuzzy distributed model, it was possible to see what the solutions could deliver in terms of objective value under various risk levels, which showed to be an insightful tool for decision makers dealing with uncertainty.

It should be noted that the objective of this chapter is not to provide a real large scale application for the proposed models. The emphasis in this chapter is on demonstrating how a proposed DDM coordination mechanism for a supply chain planning problem under uncertainty, can obtain solutions very close to those obtained by the centralized model. For this reason and for illustrative purposes, we focus on a small size case study. It is expected that when the size of the problem grows, the computational time will be greater. Further research may investigate the application of metaheuristics approaches and other soft computing techniques in order to handle large scale problems.