Abstract
This chapter develops the adiabatic theory of particle motion from first principles. It is presented as a prime example of “physics as the art of modeling”, in which a complex real system is replaced by a highly simplified virtual, i.e., imagined one. In our case the original system is a charged particle in complex multi-periodic motion in a magnetic field, replaced by a so-called guiding center particle (a model!) of equal mass and charge, moving in a smooth, uncomplicated way (having averaged out the smaller scale turns and loops of the real particle). The instantaneous position of this virtual particle is the guiding center, a point in space whose coordinates depend on the local magnetic field and the properties of the real particle. In addition, we show why the guiding center particle is endowed with a magnetic moment which impersonates average electromagnetic properties of the rapidly cycling motion of the original particle. The notion of drift velocity is introduced, and other fundamental physical magnitudes germane to adiabatic motion are defined; drift velocities are classified into zero order (independent of the particle’s dynamic properties), first order and higher order. The first adiabatic invariant is defined and a simple demonstration of its near-constancy under certain restrictions (the adiabatic conditions) is given. We then discuss in detail what happens to a charged particle in its cyclotron motion when the magnetic field is slowly time-dependent, demonstrating the fundamental role of the often neglected magnetic vector potential. Examples are given for zero and first order drifts in simple field configurations. However simple, these examples (e.g., ion pick-up; adiabatic breakdown; closed vs. open drift orbits and their separatrix; co-rotating vs. convecting regions in an externally imposed electric field) illustrate some important basic properties of particles trapped in the equatorial region of the magnetosphere. In the course of this chapter, we emphasize that magnetic field lines are purely geometric entities, useful for one’s mental representation of magnetic field configurations but, like the notion of a guiding center particle, devoid of any physical reality; nonetheless we give a phenomenological definition of field line velocity again putting to good use the vector potential and its local time variation.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1.1 Introduction: Adiabatic Theory and the Guiding Center Approximation
The equation which describes the motion of a particle of charge q and mass m in a magnetic field \({\boldsymbol B}\), under the action of an electric field \({\boldsymbol E}\) and an external non-electromagnetic force \({\boldsymbol F}\), is given by
Footnote 1The solution \({\boldsymbol r} ={\boldsymbol r}(t,{\boldsymbol r}_{0},{\boldsymbol v}_{0})\) represents the position of the particle as a function of time t, initial position \({\boldsymbol r}_{0}\) and initial velocity \({\boldsymbol v}_{0}\). Equation (1.1) is described from a given inertial frame of reference which we henceforth call the original frame of reference (OFR) (also called the laboratory system).
The solution of (1.1) may represent a very complicated trajectory. For instance, cosmic ray particle orbits in the geomagnetic field usually are of such nature. But under certain conditions of field geometry, external forces and particle energy like those prevalent in the radiation belts during geomagnetically quiet times, standard periodicities appear which then allow a simplified description if one is not interested in the actual instantaneous values of the phases in question, that is, if only average or approximate positions of the particles are wanted. There can be as many as three distinct types of periodicities: (i) the cyclotron motion, a periodicity in the particle’s motion perpendicular to the magnetic field; (ii) the bounce motion, a periodic motion up and down a magnetic field line; and (iii) the drift motion, a periodic motion on a closed surface or drift shell, made up of field lines. Periodicity (i) is always the first to appear and has the highest frequency. It may exist even in absence of (ii) and (iii). For instance, when a not-too-high energy cosmic ray particle approaches the earth in the polar regions, it may have a clear-cut cyclotron motion but no other periodicity. Bounce frequencies are usually orders of magnitude lower than cyclotron frequencies; drift frequencies are orders of magnitude lower than bounce frequencies. Any magnetic field in which particles have the capability of bounce motion (ii) is called a trapping field. If, in addition, periodicity (iii) may occur, we say that it has a configuration of stable trapping.
Cyclotron motion qualitatively represents a helical motion of the particle around a field line (Fig. 1.1). In more precise terms, we say that cyclotron motion exists if at any instant of time we can find a (moving) frame of reference in which an observer sees the particle in a nearly circular periodic orbit, nearly perpendicular to the magnetic field (with single periodicity at least during a few cycles). If such a frame of reference can be found, we say that the guiding center approximation holds, and we call this particular frame of reference the guiding center system (GCS). The geometric center of the orbit is the guiding center; the (average) radius ρ C is called Larmor radius, cyclotron radius or gyroradius. The period associated with the cyclotron motion (time to complete one turn) is called the cyclotron period τ C . If no reference frame can be found in which the orbit is periodic and closed, there is no cyclotron motion. This happens with very high energy cosmic rays in the earth’s field. Note carefully that these are rather qualitative descriptions, and that ρ C and τ C are quantities defined in the yet-to-be-determined GCS.
With the terms “nearly circular”, “nearly periodic”, “nearly perpendicular” we mean that any deviation from “exactly… ” is very small in relation to the order of magnitude of the variable in question. Such approximations are typical for the adiabatic theory of particle motion, about which we may state in “kindergarten terms” that it provides correct answers only as long as “we don’t look too close and are not expecting too detailed information”. A more precise definition and description of the conditions under which adiabatic theory is useful will be given further below.
In the OFR we can picture the motion of a charged particle as the superposition of a displacement of its guiding center with a cyclotron rotation of the particle about the guiding center. By definition, the instantaneous velocity of the guiding center is that of the GCS. The actual position \({\boldsymbol r}\) of the particle can thus be specified by the position \({\boldsymbol r}_{C}\) of the guiding center C, and a cyclotron phase angle \(\varphi\) in the GCS (provided the radius of gyration is known, Fig. 1.2). In many problems dealing with magnetically trapped particles, knowledge of the cyclotron phase is unimportant and the guiding center description is all that one needs. But forgetting \(\varphi\) completely would lead to nasty mistakes!
Cyclotron orbit during one turn τ C . The little orbital displacement vectors \(\delta {\boldsymbol r} ={\boldsymbol v}\delta t\) add up to the vector \(\varDelta {\boldsymbol r}\) in one turn. \(\varDelta {\boldsymbol r}/\tau _{C}\) in the limit \(\delta t \rightarrow 0\) defines the guiding center system velocity \({\boldsymbol V }\). The position \({\boldsymbol r}_{C}\) of the guiding center is defined as the cyclotron-average of the particle position vector \({\boldsymbol r}\) during one turn. In all this it is assumed that adiabatic conditions prevail, i.e., that \(\varDelta {\boldsymbol r} \ll \langle {\boldsymbol r} -{\boldsymbol r}_{C}\rangle\) and τ C ≪ Δ t, a characteristic time interval of “practical interest”
Considering Fig. 1.3, it is reasonable to define the instantaneous guiding center velocity vector \({\boldsymbol V }\) as the average of the particle’s instantaneous velocity vector \({\boldsymbol v}\) in the OFR over a cyclotron period:
In adiabatic theory it is customary to divide the GC velocity into two components with respect to the direction of the local magnetic field (the natural coordinate system, Sect. A.1), each one of which behaves physically in a very distinct manner: \({\boldsymbol V } ={\boldsymbol V }_{\perp } +{\boldsymbol V }_{\parallel }\). The perpendicular velocity \({\boldsymbol V }_{\perp }\) of the GCS is called the particle’s drift velocity \({\boldsymbol V }_{D}\):
because it represents the velocity with which we see the particle “drift away” from the initial field line in the OFR. Likewise, the parallel velocity \({\boldsymbol V }_{\parallel }\) is the average of the particle’s instantaneous parallel velocity \({\boldsymbol v}_{\parallel }\). However, contrary to what happens with vector \({\boldsymbol v}_{\perp }\), whose direction turns a full 2π during one cyclotron period, the parallel velocity vector changes very little, and we can write
Quite generally, the cyclotron-averaging symbol \(\langle \,\ldots \rangle _{\tau }\) represents the integral operator \(1/\tau _{C}\int _{0}^{\tau _{C}}\ldots dt\).Footnote 3
Finally, the position vector of the guiding center is the cyclotron average of the particle’s position vector (Figs. 1.2 and 1.3):
In the GCS (starred quantities), the particle’s instantaneous velocities parallel and transverse to the magnetic field are, respectively,
By definition, for the particle velocity vector in the GCS:
For the moduli:
The latter equation tells us that \(0 \leq \langle {{v}^{{\ast}}_{\perp }}^{2}\rangle _{\tau } \leq \langle {v_{\perp }}^{2}\rangle _{\tau }\). In particular, when the magnitudes \(\langle {v_{\perp }}^{2}\rangle _{\tau }\) and \(\langle {{v}^{{\ast}}_{\perp }}^{2}\rangle _{\tau }\) coincide, V D = 0, i.e., there is no drift. Less trivially, when \(\langle {v_{\perp }}^{2}\rangle _{\tau } ={ V _{D}}^{2}\) we have \({v}^{{\ast}}_{\perp }\equiv 0\) and there is no cyclotron motion: the particle follows, at least locally, an “uncurled” trajectory in the OFR (an example will be discussed in the next section).
For the magnetic and electric fields in a moving GCS the following transformations apply:
Notice that only the transverse part \({\boldsymbol V }_{D}\) of the GCS velocity \({\boldsymbol V }\) contributes to the induced electric field term in (1.9). We have used non-relativistic transformations in anticipation of the fact that, for all practical radiation belt and plasma configurations V D ≪ c (velocity of light)—even if the particles themselves may be relativistic.
Expression (1.9) is particularly important. It indicates that for any given point in a \({\boldsymbol B},{\boldsymbol E}\) field one can always find a moving frame of reference for which the component of \({\boldsymbol E}\) perpendicular to the local \({\boldsymbol B}\) has been “transformed away”, i.e., in which \({\boldsymbol E}_{\perp }^{{\ast}} = 0\) at that point (if both \({\boldsymbol B}\) and \({\boldsymbol E}\) are uniform over a finite domain, one can find one common frame for all points therein). This fact plays a fundamental role both in adiabatic theory and plasma physics.
The velocity \({\boldsymbol U}\) of this special frame at point \({\boldsymbol r}\) (in the OFR) and time t can be obtained by multiplying vectorially the second equation of (1.9) by \({\boldsymbol B}\):
Note that, again, only the perpendicular component \(E_{\perp }\) intervenes in these relations. \(E_{\parallel }\) survives transformation (1.9) intact.Footnote 4
There are different types of drifts (1.3), which appear under different well-defined circumstances. They can be classified into various groups according to whether they depend on the dynamic variables of the particle or according to the restrictive conditions that have to be imposed to guarantee their validity. We shall discuss each group independently on the basis of particular examples.
1.2 Uniform Magnetic Field; Basic Definitions; Magnetic Moment
As the most basic example we consider a charged particle in a uniform, static magnetic field, in absence of any external forces. We rewrite (1.1) in the form:
where \({\boldsymbol p}\) is the particle’s momentum, and \({\boldsymbol v}\) its velocity in the OFR. The right hand side is called the Lorentz force; it is always perpendicular to the particle’s velocity. Therefore, in absence of non-magnetic forces, the speed v and the kinetic energy T remain constant. We can write (1.12) in the form
which also holds relativistically because m = const in this particular case. Also \({\boldsymbol B}\) is constant in space and time. The angle between \({\boldsymbol v}\) and \({\boldsymbol B}\)
is called the particle’s pitch angle. When α > π∕2 it is customary to take the complement to π (angle with the anti-\({\boldsymbol B}\) direction). For the parallel component of (1.13) we have:
This means the motion of the particle projected along a uniform magnetic field is rectilinear uniform. Since \(\vert {\boldsymbol v}\vert = \mathrm{const}\), we also conclude that
For the perpendicular component of (1.12) we can write \(m{\boldsymbol a}_{\perp } = q\vert {\boldsymbol v} \times {\boldsymbol B}\vert _{\perp }\). The acceleration \({\boldsymbol a}_{\perp }\) is therefore always perpendicular to \({\boldsymbol v}_{\perp }\) and its magnitude
in view of (1.15).Footnote 5
This means that the particle’s motion projected on a plane perpendicular to the magnetic field is circular uniform and a ⊥ is the centripetal acceleration.
In the case under discussion, the GCS moves along the magnetic field with velocity
In the GCS, v ⊥ = const and the particle trajectory is a circle with a gyroradius that can be obtained from (1.17):
We have used the starred quantity \(v_{\perp }^{{\ast}}\) to re-emphasize the fact that the gyroradius ρ C is defined in the GCS (in the particular case under discussion, though, v ∗ = v because V D ≡ 0.) Notice that, in view of the factor q in (1.13), positive and negative particles have mutually opposite senses in their cyclotron rotations.
Associated with the particle’s cyclotron motion, we have the cyclotron period (defined in the GCS like ρ C ):
and the cyclotron angular frequency
Expressions (1.19)–(1.21) are valid relativistically, provided one considers m as the relativistic mass m = m 0 γ (m 0 rest mass; \(\gamma = {(1 {-\beta }^{2})}^{-1/2};\beta = {v}^{/}c\)). In the non-relativistic case, ω C and τ C are independent of the particle’s velocity, depending only on the field intensity and the class of particles (q∕m); in other words they are a function of space (a scalar field). This fully justifies the definition of the drift velocity (1.2) as an average over cycle time. Using (1.14), it is useful to express (1.19) and (1.20) in the form:
For electrons and protons, respectively, the constant factors have values:
From now on we shall deal mainly with non-relativistic (γ = 1) cases. It is possible to express the gyroradius in vector form taking into account (1.19) and (1.21):
where \({\boldsymbol e} ={\boldsymbol B}/B\) is a unit vector in the direction of \({\boldsymbol B}\) (see Sect. A.1). The vector \({\boldsymbol \rho }_{C}\) points from the guiding center to the particle. The instantaneous position of the guiding center of a particle of velocity \({\boldsymbol v}\) at point \({\boldsymbol r}\) thus becomes
Since during one cyclotron turn the vector \(\langle {\boldsymbol {v}}^{{\ast}}\rangle _{\tau } = 0\) (1.6), we have \({\boldsymbol r}_{GC} =\langle {\boldsymbol r}\rangle _{\tau }\), as defined earlier.
The motion of a charged particle in a uniform magnetic field is circular helicoidal. Positive particles spiral clockwise around the field lines if we look at them in a direction opposite to \({\boldsymbol B}\); negative particles spiral counter-clockwise (Fig. 1.4). When the pitch angle is \(9{0}^{\circ }\), \({\boldsymbol v}_{\parallel } = 0\) and the motion is perpendicular to \({\boldsymbol B}\); the particle has cyclotron motion only and stays on a circle forever. In that case, the GCS coincides with the OFR. If α = 0, there is no cyclotron motion at all; the particle moves along a straight field line. Notice that in general ρ C is not the radius of curvature of the particle’s trajectory in the OFR (this is true only if \(\alpha = \pi /2\)). For a helicoid, the radius of curvature R C is always greater than the radius of the cylinder around which the helicoid is wound (\(R_{C} = \rho _{C}{/\sin }^{2}\alpha =\rho _{C}{(v/v_{\perp })}^{2}\)).
As viewed from the GCS, the cyclotron motion of a charged particle about the guiding center is equivalent to a circular electric current loop with radius ρ C and intensity \(I = \vert q\vert /\tau _{C} = {q}^{2}B/(2\pi m)\) of the same direction for both positive and negative particles, Fig. 1.5.Footnote 6 The associated magnetic moment \({\boldsymbol M} = I\delta {\boldsymbol S}\) is directed opposite to \({\boldsymbol B}\), of magnitude \(M = I\pi {\rho _{C}}^{2} = m{v_{\perp }^{{\ast}}}^{2}/2B ={ p_{\perp }^{{\ast}}}^{2}/(2mB)\) (1.19). Thus we can write:
The expression of the transverse kinetic energy \({T}^{{\ast}}_{\perp } = 1/2m{v_{\perp }^{{\ast}}}^{2}\) is valid only for the non-relativistic case. It is important to emphasize that \(v_{\perp }^{{\ast}}\) is the modulus of the transverse velocity in the GCS.
In its cyclotron motion, the particle also has an angular momentum or spin about the guiding center \({\boldsymbol l} = m{\boldsymbol \rho }_{C} \times {\boldsymbol {v}}^{{\ast}}\) directed opposite to \({\boldsymbol B}\) for a positive charge and in the same direction for negative particles (Fig. 1.5). Taking into account (1.19) and (1.26) we can write:
Although we have defined (1.26) and (1.27) for the case of a uniform \({\boldsymbol B}\) field in absence of other forces, they are of general validity and, indeed, of crucial importance: M and l are constants of motion within the guiding center approximation, i.e., adiabatic invariants. In other words, the magnetic moment M and the spin l are intrinsic parameters associated with a particle in cyclotron motion. This is the reason why in the Introduction we talked about replacing the original particle with a virtual particle, normally called “guiding center particle” or “magnetized charged particle” of the same mass m and charge q, but in which the “averaged-out” cyclotron motion is represented by just one vector: the magnetic moment \({\boldsymbol M}\) (or the intrinsic angular momentum \({\boldsymbol l}\)) which we mentally picture as being attached to the GC particle. What we lose in this “remodeling” process are the details of the cyclotron motion, specifically, the cyclotron phase of the original particle (angular coordinate of the particle in its cyclotron motion, Fig. 1.2). The full kinetic energy of the particle can be retrieved from the value of M and the local B (1.26), plus the parallel GCS velocity V ∥ . The overall condition for the validity of the guiding center particle model is that the requirements for the GC approximation apply, i.e., that it is possible to identify a frame of reference (the GCS) in which the particle executes a closed-orbit periodic motion (for a more precise definition of the GC approximation, see next section). In the case of Fig. 1.4, a GC particle just moves straight up or down along the magnetic field line with a velocity \({\boldsymbol V }_{\parallel }\) equal to the parallel velocity of the parent particle.
It is important to note that for the external field’s magnetic flux Φ through the cyclotron orbit in the GCS (see (1.26) and (1.27)),
Consequently, Φ is also an adiabatic constant of motion.
The expression (1.28) can be used for a “kindergarten”-level demonstration of the conservation of the magnetic moment M (non-relativistic case). Suppose that in the field configuration under discussion (\(9{0}^{\circ }\) particles in a uniform B-field), the magnetic field intensity changes in time very slowly, so that \(\tau _{C} \ll B/(dB/dt)\). According to Faraday’s law, the induced electric field \({\boldsymbol E}_{I}\) will change the transverse kinetic energy of the particle during one cyclotron turn by \(\delta T_{\perp }^{{\ast}} = q\oint {\boldsymbol E}_{I}{\boldsymbol ds} = q\,d\varPhi /dt\) (absolute values only). To first order (in which we consider ρ C constant), the change per unit time will be (first equality in (1.28)): \(dT_{\perp }/dt \simeq \delta T_{\perp }^{{\ast}}/\tau _{C} = q\,/\tau _{C}\,(d\varPhi /dt) = T_{\perp }^{{\ast}}/B\,(dB/dt)\)—therefore, \(T_{\perp }^{{\ast}}/B = M = \mathrm{const}\). In essence, this means that in the above cyclotron loop model, the current I is a closed current with the well-known property of a superconducting system to react (driven by the induced electric field) to any change of the magnetic field in such a way so as to maintain constant the flux Φ through its own loop. Thus a cycling particle will adjust its cyclotron orbit so as to preserve Φ, hence its magnetic moment M (as long as the variation of the magnetic field satisfies the adiabatic condition). Although we have shown this for the simplest magnetic field configuration possible, it has general validity: the particle doesn’t care why the flux through its cyclotron orbit changes—only that it does!Footnote 7
When the particle velocity is relativistic, it can be demonstrated that the quantity that is conserved is the relativistic magnetic moment
where m 0 is the rest mass and \(T_{r\perp }^{{\ast}}\) the perpendicular relativistic kinetic energy (\(T_{r} = m_{0}{c}^{2}(\gamma -1) = m_{0}{v{}^{2}\gamma }^{2}/(1+\gamma )\)). Since the rest of the book deals mainly with non-relativistic particles, some of the principal equations can be easily converted to relativistic ones by replacing the magnetic moment, wherever it appears, with its relativistic expression (1.29) and the kinetic energy with the relativistic kinetic energy T r (for a full relativistic treatment of adiabatic theory, see [2, 3] also shows the full relativistic expressions of the most important relationships).
Speaking of relativity, it is interesting to briefly examine the cyclotron motion of a charged particle from the quantum physics point of view. The stronger the magnetic field, for a given transverse velocity of the particle the higher will be its cyclotron frequency (1.21) and the smaller its gyroradius (1.19). For ultra-high intensity fields, quantum mechanics must be applied in the description of the cyclotron motion; this situation is of importance in the theoretical study of particles trapped in the magnetic field of a neutron star or black hole. The magnetic field intensities in the environment of such an object may be as high as \(1{0}^{6} - 1{0}^{11}\) Tesla. Consider Heisenberg’s uncertainty relation \(\varDelta x\varDelta p_{x} \geq \hslash /2\) (\(\hslash = \mbox{ Planck}{^\prime}\mbox{s constant}/2\pi = 1.05 \times 1{0}^{-26}\) J). If as a meaningful maximum order of magnitude we insert for Δ x the gyroradius (1.17) and for Δ p x the product mv ⊥ , taking into account (1.27) the uncertainty relation gives a lower limit for the GC particle’s angular momentum: \(l \geq \hslash /2\). In other words, zero is not an option and the intrinsic angular momentum of a GC particle in a magnetic field is quantized. As a matter of fact, the quantum energy levels (called Landau levels, [4]) of an elementary charged particle gyrating in an intense magnetic field B turn out to be
This leads to energy levels of the order of hundreds of keV to thousands of MeV, for electrons trapped in extreme magnetic environments. It also means that the cyclotron frequency is quantized:
Considerations of quantum spin of the original particle and relativistic effects complicate somewhat the picture, but are outside the scope of this book.
1.3 Zero-Order Drifts
We now consider the case of a charged particle in a uniform static magnetic field under the action of an external non-magnetic, non-inertial, interaction force \({\boldsymbol F}\) which is constant in time and space. We divide the force into two components \({\boldsymbol F}_{\parallel }\) and \({\boldsymbol F}_{\perp }\), parallel and perpendicular to \({\boldsymbol B}\), respectively. The equation of motion (1.1) can be split into the following pair:
The first equation tells us that the particle is accelerated along the field line in a “conventional” way by \({\boldsymbol F}_{\parallel }\). Let us assume for the time being that \({\boldsymbol F}_{\parallel } = 0\) (i.e. \({\boldsymbol F} ={\boldsymbol F}_{\perp }\)). This means that the particle will have a constant velocity \(v_{\parallel }\) along the field line and so will the GCS. Thus we only need to determine the GCS’s perpendicular velocity or drift velocity, which we call \({\boldsymbol V }_{F}\). This is the instantaneous velocity of a frame of reference in which the particle executes a circular motion. To find \({\boldsymbol V }_{F}\), we will use the “trick” of creating a motion-induced electric field \({\boldsymbol {E}}^{{\ast}}\) (1.9) in a moving frame of reference such that the external force is balanced out by a force \(q{\boldsymbol {E}}^{{\ast}} = q{\boldsymbol V }_{F} \times {\boldsymbol B}\):
Multiplying vectorially by \({\boldsymbol e}/qB\), where \({\boldsymbol e}\) is again the unit vector in the direction of \({\boldsymbol B}\), we obtain
\({\boldsymbol V }_{F}\) is called the force drift. Since \({\boldsymbol F}_{\parallel }\) does not affect (1.31), this expression is also valid in the more general case when \({\boldsymbol F}_{\parallel }\neq 0\).
As viewed from the OFR, the particle has a cyclotron motion (that in the GCS) plus a translation with constant velocity \({\boldsymbol V }_{F}\) given by (1.31), plus a translation parallel to the field line. If both \({\boldsymbol F}_{\parallel }\) and \({\boldsymbol v}_{\parallel }\) are zero, the resulting motion is a cycloid in a plane perpendicular to B (Fig. 1.6). Notice that \({\boldsymbol V }_{F}\) is always perpendicular to both \({\boldsymbol B}\) and \({\boldsymbol F}\). The particle thus “reacts” perpendicularly to the external force and no average work is done on the particle during its drift motion under the present condition of a uniform field, although in the OFR, the kinetic energy of the particle changes periodically in its cyclotron turns; in the GCS, however, the perpendicular velocity is \(v_{\perp }^{{\ast}} = \mathrm{const}\). Positive and negative particles drift in mutually opposite directions. Most importantly, \({\boldsymbol V }_{F}\) is independent of the particles’ mass and energy. It is called a zero order drift because the only condition for its validity is that the extension of the uniform field domain be large enough to allow the particle to execute its cyclotron or spiral turns undisturbed (domain ≫ ρ C ). Note that for a force field, zero order drifts are a function of position \({\boldsymbol r}\) only—a vector field. We cannot independently impart some arbitrary zero order drift to a particle as an initial condition.
One can easily understand the physical reasons for the drift of a charged particle under the action of a constant external force, perpendicular to \({\boldsymbol B}\). As sketched in Fig. 1.7, the kinetic energy of a particle in the OFR is not constant; during one cycloid turn, the particle is alternatively being accelerated (larger radius of curvature ρ—do not confuse with Larmor radius!) and decelerated by the external force \({\boldsymbol F}\)—v ⊥ is not constant during one turn (see below). It should be clear that in this case the magnetic moment cannot be defined in the OFR.
If the external force is not constant but derives from a general force field \({\boldsymbol F} = -{\boldsymbol \nabla }W\) (W: force field potential), (1.31) still is valid. Let us assume that F ∥ = 0 everywhere, which means that the magnetic field lines lie in electrostatic equipotential surfaces. The force-drift velocity (1.31) is tangent to such an equipotential surface and the guiding center of a \(9{0}^{\circ }\) pitch angle particle will thus follow an equipotential line in a plane perpendicular to the uniform field \({\boldsymbol B}\) (Fig. 1.8). This, however is true only under the assumption that the variation of W over a gyroradius is very small with respect to the particle’s kinetic energy:
This in turn implies that
The particle will execute many overlapping cyclotron turns as it drifts along a W = const curve.
The most important kind of external force is the electric field force \(q{\boldsymbol E}\). The only non-electric external force of interest would be gravitation; it plays a role for plasmas in stellar environments but none in planetary magnetospheres. However, as we shall see later, there are inertial forces of importance (virtual non-interaction-based forces arising in an accelerated frame of reference). With an electric field, the drift velocity (1.31) becomes
This is called the “E-cross-B drift”, for which we shall always use the letter U. Note the crucial fact that the electric charge has canceled out; both positive and negative particles drift in the same direction with the same speed, regardless of their mass and energy (Fig. 1.9). This common electric drift \({\boldsymbol U}\) is identical to the velocity (1.10) of a frame of reference in which the perpendicular component \({\boldsymbol E}_{\perp }\) has been transformed away. It should come as no surprise, for in our case this is, indeed, the frame of reference in which there are no forces other than the Lorentz force acting on the particle—the very definition of the GCS! The fact that \({\boldsymbol U}\) is a drift velocity common to all particles confirms its fundamental role as the bulk velocity of the ensemble of particles that constitute a plasma. In contrast, the charge-dependent force drift (1.31), and other drifts which we shall introduce later, give rise to electric currents in a plasma (Chap. 5).
1.4 Examples of “E Cross B” Drifts; Uniform Magnetic Field of Time-Dependent Intensity
It is instructive to examine the motion of a charged particle in uniform \({\boldsymbol B}\) & \({\boldsymbol E}\) fields as viewed “under a magnifying glass” in the OFR. Consider Fig. 1.10.
The uniform magnetic field is directed out of the paper, and v ∥ = 0. We assume only the direction of \({\boldsymbol U}\) as known, but not its modulus. Call v P and v Q the velocities along the x axis of the particle at points P and Q, respectively (consider one of these velocities as given). We will have, from (1.6) and with \({v}^{{\ast}} = {v}^{{\ast}}_{\perp } = \mathrm{const.}\):
On the other hand, we have the following energy relation:
Therefore, with (1.19)
which is identical to (1.11). But in this case we have not used in any way the transformation (1.9).
The gyroradius ρ C (1.19) can be expressed as a function of v P or v Q :
Note that this is not the radius of curvature of the trajectory in the OFR!
It is interesting to compare the total forces acting in the OFR on the particle at P and Q, respectively:
Both relations represent the constant magnitude of the Lorentz force in the GCS. The different radii of curvature of the orbit at P and Q in the OFR arise from the difference in particle velocities at these points (1.4):
Notice that if \(U = E/B = 1/2\,v_{P}\), we have v ∗ = U and R Q = 0; the trajectory is the limit of an open cycloid (Fig. 1.11).
This shows that a particle can be instantaneously at rest in the OFR and yet possess cyclotron and drift motion!Footnote 8 On the other hand, if \(U = E/B = v_{P}\), we have v ∗ = 0 and R Q = ∞; the trajectory in the OFR is a straight line (in the GCS the particle is at rest!). In this case, in the OFR, the Lorentz force is balanced out by the electric field force at all times (the principle of a velocity spectrometer!).
Returning to the kinetic energy, in the GCS the particle’s T ∗ is constant, as is its speed v ∗. The cyclotron-average kinetic energy transverse to \({\boldsymbol B}\) in the OFR will be \(\langle T_{\perp }\rangle = 1/2m\langle {v}^{2}_{\perp }\rangle\). Taking into account that \({\boldsymbol v}_{\perp } ={\boldsymbol v}_{\perp }^{{\ast}} +{\boldsymbol U}\) (we reintroduce the subindex ⊥ because what follows is valid in general, also for v ∥ ≠ 0), and that by definition (see (1.3) and (1.6)) \(\langle {\boldsymbol v}_{\perp }\rangle ={\boldsymbol U}\) and \(\langle {\boldsymbol v}_{\perp }^{{\ast}}\rangle = 0\), we have
To consolidate the understanding of the electric drift velocity (1.34) (answering for instance the question: When \(B \rightarrow 0\), what does it really mean that the guiding center races away with \(V _{E} \rightarrow \infty \)?) we discuss another simple but illustrative example of possible detailed configurations of charged particle trajectories in a uniform \({\boldsymbol B}\&{\boldsymbol E}\) field. Consider the case of positive particles injected one after another with the same initial velocity \({\boldsymbol v}_{i}\), as shown in Fig. 1.12 (\({\boldsymbol B} \perp {\boldsymbol E} \perp {\boldsymbol v}\)). While each particle is traveling, B (and E) are held constant; initially, the magnetic field is large. Then B is decreased before the next injection. This process is repeated until B reaches zero.
Let us analyze in detail the cyclotron and drift motions of the particles, as they are injected into smaller and smaller magnetic fields. From (1.4) we have
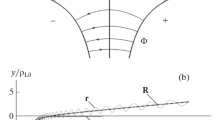
(bars because ρ C > 0 always!). Figure 1.13 (top) shows the graph of the function \(\rho _{C} = \rho _{C}(B)\).
Consider the distinct regions A, B and C, and the “notable points” R and S, where \(B_{R} = 2E/v_{i}\) and \(B_{S} = E/v_{i}\), respectively.
Region A: For large B’s the drift velocity (1.10) and the Larmor radius (1.19) are very small and the particle behaves adiabatically, turning many times before drifting away (see Fig. 1.13, lower graph). As the B decreases, the gyroradius and the drift velocity U increase. In the GCS, the particle velocity v ∗ decreases.
Top: Larmor radius ρ C as a function of | B | for the example of a charged particle of given initial velocity \({\boldsymbol v}_{i}\) injected perpendicularly into uniform \({\boldsymbol B}\) and \({\boldsymbol E}\) fields. Definition of characteristic regions and points discussed in the text. Bottom: Sketch of typical orbits in the OFR for characteristic regions and points. Not in scale!
Point R: The Larmor radius reaches a maximum; in the GCS the velocity v ∗ = U and in the OFR the particle trajectory becomes the limit of an open cycloid, with cuspidal points at which the particle comes momentaneously to rest (see footnote on page 65).
Region B: As the B field decreases further, the gyroradius begins to decrease. The drift velocity continues to increase and the trajectory is an open cycloid with increasing “wavelength” and amplitude—the drift U wins over the velocity v i . In the GCS, the particle velocity v ∗ continues to decrease, and the cyclotron circles become smaller and smaller.
Point S: In the GCS the cyclotron circle has been reduced to a point: the particle is at rest, v ∗ = 0! In the OFR the particle moves in uniform rectilinear motion with speed U (the velocity spectrometer effect mentioned above).
Region C: As the magnetic field intensity continues to decrease, the drift speed increases further, and in the OFR the particle follows an open cycloid with decreasing amplitude and wavelength. However now it is a cycloid turning upwards from the injection point, into the direction of \({\boldsymbol E}\). In this regime the GC velocity is larger than the particle injection velocity; the GCS “races away” from the particle to the right in the figure. An observer in the GCS will in turn see the particle initially moving to the left, being at the lowest point of a circular motion.
The domain \(c \lesssim E/B \lesssim \infty \) deserves special attention. Would this really represent a relativistic or “transrelativistic” situation for the GCS? What is the physical meaning of such apparent nonsense? Obviously we have a breakdown of the very concept of guiding center. Let us not forget that the GC is a purely geometric feature and that the “GC particle” is a virtual artifact, a useful model, product of our imagination—the only physical reality is the original cycling particle! The drift velocity \({\boldsymbol U}\) is also a geometric concept, mathematically tied to the original particle. All this can be summarized by stating that the restriction for the validity of zero-order drifts is that the spatial domain of the \({\boldsymbol B}\) & \({\boldsymbol E}\) field be much larger than the gyroradius ρ C of the particle. More specifically, if L trans and L p are the extensions of the field domain transverse and parallel to the particle drift \({\boldsymbol U}\), respectively, the conditions for adiabatic behavior in a uniform E-cross-B field are
In the second equation N turns is the number of cyclotron turns when the particle drifts the length L p . When according to (1.36) ρ C becomes large enough but the conditions of validity still hold, the particle could, indeed, be accelerated by the E field to relativistic velocities before the Lorentz force wins and the particle turns over and enters a deceleration phase. For a B-value strictly zero, we simply have the case of a particle under the action of just one force (\(q{\boldsymbol E}\)), and the trajectory becomes a parabola in the non-relativistic domain.
The example discussed above shows that what must be used in the expression of M (1.26) and l (1.27) is the perpendicular velocity v ∗ of the particle in the GCS, not in the OFR where the transverse velocity of the particle v ⊥ is variable. For instance, in case S above (\(B = E/v_{i}\)), ρ C = 0, and M and l are both zero! On the other hand, a particle injected into a B& E field with zero initial velocity does have a non-zero magnetic moment \(M = m{E}^{2}/2{B}^{3}\) (the “ion pick-up mechanism” mentioned in the footnote on page 65—best argument yet that the transverse velocity in the definition (1.26) of M is not the velocity in the OFR!). It is important to emphasize again that zero order drifts are independent of the particle’s energy as long as the physical domain of uniform fields is large enough (1.37).
Our next example of \({\boldsymbol E}\) cross \({\boldsymbol B}\) drift, of particular conceptual importance in magnetospheric plasma physics, is that of the drift of a guiding center particle in a purely induced electric field (time-dependent magnetic field, no charges present anywhere)
(see Sect. A.1). The first obvious case should be that of a stationary uniform magnetic field, whose source current system moves rigidly with constant velocity \({\boldsymbol V }_{0}\) with respect to a frame of reference at rest (the OFR). No electric charges are present. A \(9{0}^{\circ }\) pitch angle charged particle would be subjected to an induced electric field drift velocity given by (A.57) of Sect. A.1; in other words, it would drift with the moving frame velocity and thus obviously remain part of the magnetic field system. Notice that this time we have appealed to the vector potential and Maxwell’s equations rather than simply using the postulated rule of field transformation (1.9). Although we only considered a uniform magnetic field in pure translation here, the same procedure applies to rigidly rotating fields like the internal geomagnetic and planetary fields (neglecting external magnetospheric currents): at each point there will be an induced electric field and associated zero-order drift velocity (1.38), which in this case is called corotational drift, causing all trapped particles to corotate with the planet. Of course, additional drifts (see next sections) will complicate the picture. In the case of Earth, the corotational electric field will have a significant effect only on very low energy particles (e.g., the constituents of the plasmasphere), but in the magnetospheres of Giant Planets it plays a very important role even for relativistic electrons of their radiation belts.
As another example of induced electric field drift, we consider a long circular solenoid with a time-dependent current (Fig. 1.14). We again shall assume the scalar potential to be zero (no free electric charges present); the vector potential will be that of relation (A.56) of Sect. A.1, directed as shown in the figure and of magnitude A = B r. We now inject a \(9{0}^{\circ }\) pitch angle particle of energy or magnetic moment such that ρ C ≪ R, radius of the solenoid. If nothing else happens, its guiding center will remain at rest. Now we adiabatically increase the current in the solenoid, such that \(\dot{B} > 0\). An induced electric field will appear as shown in Fig. 1.14, given by (A.58). Independently of its mass, charge and energy, the particle will drift toward the center of the solenoid with an induced drift speed of \(V _{ind} =\dot{ B}\,r\). Due to the conservation of magnetic moment (1.26), its energy will change at a rate \(dT/dt = M\dot{B}\)—i.e., in this example, gradually increase. A whole ensemble of particles trapped in the increasing uniform field would thus be energized and compressed toward the axis.
This example allows us to introduce the concept of field line motion (e.g., [5]) in a phenomenological way. Because the preceding process affects all \(\alpha = 9{0}^{\circ }\) charged particles equally regardless of their nature, if we “paint” a given initial field line by placing such particles all along it, they will all drift together and remain on a common field line (see first corollary at the end of Sect. A.2) in a way governed exclusively by what happens to the magnetic field (its sources) time-wise. It is thus possible to declare the “painted” field line to be the same as the initial one and adopt (1.38) as the ad hoc operational definition of velocity of the point of a field line. Although we only have considered the oversimplified case of a uniform magnetic field, it can be shown that the property of remaining on a common field line applies to any changing magnetic field configuration—as long as there are no potential electric fields (\({\boldsymbol \nabla }\cdot {\boldsymbol E} \equiv 0\) everywhere) and no parallel electric fields are present (\(\partial {\boldsymbol A}/\partial t \cdot {\boldsymbol B} \equiv 0\)).Footnote 9 For the general case, we also must add the condition of near-zero energy (T → 0) for the probe particle, to avoid the action of other drifts (see following sections), which are all energy-dependent. Note that the above ad hoc definition of moving field line is valid even in a vacuum situation; note also that thus defined, it is always perpendicular to the field line in question—a parallel field line velocity cannot be defined in a physically meaningful way (although we may well imagine it, for instance, for the field of a long solenoid being transported parallel to its axis). The reason for using terms like “to declare” and “ad hoc” is related to the fact that, as mentioned in Sect. A.1, a physical distinction between the potential and inductive contributions to an electric field as required prior to use of (1.38) is not possible through a single measurement operation (we would “have to know” the system a priori, or probe it through an experimental protocol by turning off all electrostatic sources).
Finally, we take advantage of the above very simple example to present a better “microscopic” view of the cyclotron acceleration (or deceleration) process ultimately responsible for the conservation of a particle’s magnetic moment under adiabatic conditions. Looking with a magnifying glass at the particle in Fig. 1.14 in the OFR, we see it gyrating in an induced electric field more explicitly shown in Fig. 1.15.
Notice that since the \({\boldsymbol A}\)-vector increases linearly with r, the particle will be alternatively accelerated and decelerated, with the acceleration phase always winning a bit in our example. This causes both the drift toward the axis and the gradual increase in kinetic energy, and is why, in reality, the orbit shown in Fig. 1.15 is not closed in the OFR. Now we can come up with a more convincing analytical, less kindergarten-like, proof of the conservation of magnetic moment—albeit only for a very simple field configuration. In the figure and according to the discussion on page 189 of Sect. A.1, the magnitude of the induced electric field will be \(E_{ind} =\dot{ A} =\dot{ B}(r +\rho _{C}\cos \varphi )\), where \(\varphi\) is the cyclotron phase as measured from the lower point of the orbit. In addition to the near-constant transverse Lorentz force \(q{\boldsymbol v} \times {\boldsymbol B}\), in the case of a varying magnetic field there will be a tangential electric force \(f_{t} = q\,\dot{B}(r +\rho _{C}\cos \varphi )\cos \varphi\), varying from positive to negative during one half-turn. Although under adiabatic condition this tangential force will be much smaller in magnitude than the Lorentz force, the near-circular motion of the gyrating particle is not uniform. The work of this tangential force during a half-turn, i.e., the kinetic energy gain of the particle, turns out \(\varDelta T =\int _{ 0}^{\pi }f_{t}\rho _{C}d\varphi = q\dot{B}{\rho _{C}}^{2}\,\pi /2\). Dividing by τ C ∕2 we obtain the change of kinetic energy per unit time of the gyrating particle in a time dependent (increasing) uniform field: \(\dot{T} = 2\varDelta T/\tau _{C} = 1/2m{v}^{2}\,(\dot{B}/B)\) or \((\dot{T}/T) = (\dot{B}/B)\), which if integrated gives \(T/B = M = \mathrm{const}\). (1.26). In a similar way one can easily figure out the induced drift of the gyrating particle toward the central axis of the solenoid.
As an interesting addendum to this proof we note that if at time t there are several particles of identical velocities on a common cyclotron orbit like the one shown in Fig. 1.15 (i.e., having only different phases), a simple dynamic calculation shows that they would not be on common orbits at later times except at times t n after intervals that are integer multiples of the cyclotron period: \(t_{n} = t + n\,\tau _{C}\). We will find a similar behavior in the case of other periodicities of adiabatic motion (bounce and drift).
1.5 First Order Drifts
We now drop the assumption of a uniform magnetic field. Gradients in the magnetic field (assumed constant in time) cause first order drifts which are energy-dependent. A magnetic field is inhomogeneous when any of the components of the gradient tensor \(\partial B_{i}/\partial x_{k}\) (Sect. A.1) are non-zero in some region of space. There are different kinds of field gradients from the geometrical point of view which play quite distinct roles in adiabatic theory. For the time being, we work only with the vector gradient of the modulus B, which we denote by \({\boldsymbol \nabla }B\). Its components are of course related to those of the tensor gradient (see relation (A.35) of Sect. A.1). We divide this vector into two components, parallel and perpendicular to the magnetic field, respectively (see Sect. A.1, (A.20) and (A.19)):
Each component has a distinct effect on the guiding center motion.
In this section we examine the effect of the perpendicular gradient \({\boldsymbol \nabla }_{\perp }B\). In Sect. A.1 (A.21) and (A.15) it is shown that in a current-free region in which \({\boldsymbol \nabla }_{\perp }B\neq 0\), all field lines are curved; in spite of this, we shall ignore field line curvature for the time being (as we shall see in Sect. 1.6 this is fully justified for \(9{0}^{\circ }\) pitch angle particles in the equatorial (minimum-B) surface of a trapping magnetic field). We shall also assume condition (1.39) to apply: the magnetic field varies very little over the Larmor radius of the particle. If ∇B is the modulus of the gradient of B and B∕∇B is a characteristic length for the change of B, the adiabatic condition can be written in the following equivalent ways:
Let us inject a \(9{0}^{\circ }\) pitch angle particle with velocity \({\boldsymbol v}_{\perp }\) into a field with (almost) straight field lines and a perpendicular gradient (Fig. 1.16). We realize that there must be a drift to the right: for a positive particle the field at points P, R, … is weaker than that at points Q, S, …, causing an alternating change of the radius of curvature of the particle orbit (note carefully that the orbit in the figure is drawn “stretched-out”; because of condition (1.39), the particle really turns many times before appreciably drifting away from the initial position). We now want to find the general expression for the corresponding gradient-B drift velocity \({\boldsymbol V }_{G}\), i.e., the perpendicular velocity of the GCS. First, we note that the particle must move with constant speed v ⊥ in the OFR (rather than in the GCS as happens with force drifts), since there are no external non-magnetic forces acting. As we did in the case of a zero order drift in a uniform B& E field, we shall use the motion-induced electric field trick. Let us assume that the GCS indeed moves to the right with velocity \({\boldsymbol V }_{G}\) as intuitively shown in Fig. 1.16. The particle velocity in the GCS is \({\boldsymbol {v}}^{{\ast}}\) (we drop the obvious subindex ⊥ ); but now the motion-induced electric field \({{\boldsymbol E}}^{{\ast}} = -{\boldsymbol V }_{G} \times {\boldsymbol B}\) (1.9) will alternatively accelerate and decelerate the particle. Therefore, its speed in the GCS will not be constant: the motion in the GCS is circular but non-uniform (reverse situation from the force drift case in the precious section!) In particular, for points P and Q in Fig. 1.17:
B is the magnetic field at the guiding center C.
For a generic cyclotron phase angle \(\varphi\) (Fig. 1.17), and taking into account (1.6) for the speed of the particle in its circular orbit in the GCS,
Therefore, averaging over one cyclotron turn we obtain
Note that in this case of drift in an inhomogeneous magnetic field, the particle velocity in the GCS is not constant (despite the orbit being a closed circle), but its average value is equal to the constant speed in the OFR. In the GCS, conservation of energy leads, for points P and Q in Fig. 1.16, to \(\frac{1} {2}m({v_{P}^{{\ast}}}^{2} -{ v_{ Q}^{{\ast}}}^{2}) = 2\rho _{ C}q{E}^{{\ast}}\). Replacing \(v_{P}^{{\ast}}\), \(v_{Q}^{{\ast}}\) and E ∗ by their expressions in (1.40), we find that V G cancels out, leaving
Notice that in this case, what enters in the expression of the Larmor radius is not the varying velocity in the GCS, but its average value, which in this case happens to be equal to the constant speed in the OFR. The same happens with the magnetic moment. Defined in the GCS, we really must use in its fundamental expression (1.26) the average \(\langle v_{\perp }^{{\ast}}\rangle\). Does this invalidate the derivation of this expression based on a simple circuit model? No, we just have to improve a bit that model: instead of one particle of charge q circling with a velocity \(v_{\perp }^{{\ast}}\) we must “smear” the charge along the circle with a linear charge density \(\lambda = q/(2\pi \rho _{C})\). The current I at any given point will be \(I =\lambda v_{\perp }^{{\ast}}\). If the velocity varies along the circuit, as happens in the case under discussion, conservation of charge requires that \(I =\lambda v_{\perp }^{{\ast}} = \mathrm{const}\). along the circle. Since the resulting magnetic moment only cares about I and not how the latter is made up as a convection current, the model circuit remains intact! Confused? Such nitpicking details do happen in adiabatic theory! It also shows how every model in physics must be constantly and carefully examined in detail regarding its validity and the degree of its approximation to the “reality out there”.
We continue our detailed examination considering Newton’s equation at points P and Q, involving centripetal accelerations:
The last terms are the Lorentz forces in the OFR at points P and Q, respectively. From either of the second equalities we obtain, inserting the above expression for ρ C :
or, finally, for the moduli:
With (1.26) and (1.27), and observing Fig. 1.16, we obtain several versions for the vector expression of the gradient-B drift velocity:
These expressions are non-relativistic; for relativistic particles, we have for the magnitude of V G :
in which
Although the above expression is valid for relativistic particles, the actual values of the drift velocity in typical magnetospheric fields are non-relativistic; as we shall see, this is also the case for other drifts. The first equalities in (1.46) tell us that given a surface perpendicular to the magnetic field, a \(9{0}^{\circ }\) pitch angle particle on it will drift along a B = const. contour. As we shall see in the next section, this is an important result for magnetospheric physics.
Relations (1.46) were proven here for the very restricted case of a \(9{0}^{\circ }\) pitch angle particle in a non-uniform magnetic field with nearly parallel field lines. They have general validity, provided condition (1.39) holds for the magnetic field gradient. Note that in contrast to the zero order drift (1.34), the gradient-B drift velocity depends on the energy, mass and charge of the particle and that, according to (1.45) and (1.43), the adiabatic condition (1.39) leads to
We now complete the “microscopic” examination of this case by returning to the OFR to calculate the different radii of curvature R P and R Q at points P and Q in Fig. 1.16—a difference that is responsible for the shape of the cycloidal orbit in the OFR. Taking the expressions for the Lorentz force at these points (last equalities in (1.44)), and equating them to the centripetal accelerations in the OFR (times mass), we obtain
If condition (1.39) holds, the difference between R P and R Q is, indeed, extremely small, and the cycloid will be tightly closed (Fig. 1.18). As an important remark, we note the following: if we determine the vector expression of the centripetal Lorentz force \({\boldsymbol f}(\varphi )_{L}\) in the GCS as a function of the phase angle (as we did with the velocity \({\boldsymbol {v}}^{{\ast}}\) in (1.41)), we would discover that the gradient-B drift (1.46) is nothing but a force drift caused by the phase-average force \(\langle {\boldsymbol f(\varphi )}_{L}\rangle _{\varphi }\). It does not count as a zero-order drift, however, because the phase-average force is a first-order quantity, it is not energy independent and \(V _{G} \ll v_{\perp }\) always. We will return to this in detail in the next chapter.
Let us summarize some of the principal properties of zero-order and first-order drifts, for non-relativistic, \(9{0}^{\circ }\) pitch angle particles. In the zero-order drift due to the action of an external force, the drift of the particle is independent of its energy; the orbit in the original frame of reference is in general a cycloid and the particle velocity is variable (periodic). In the guiding center frame of reference, the orbit is circular uniform. The constant particle speed in the GCS is equal to the average of the particle speed in the OFR. There are no restrictions on particle energy, as long as there is enough space for the particle to execute its periodic motion. In a first-order drift due to a transverse magnetic field gradient, the drift motion depends on the particle energy; the orbit in the OFR is also a cycloid, but the speed is constant. In the GCS, the orbit is circular, but the speed is variable (periodic). The average speed in the GCS is equal to the constant speed in the OFR. There are restrictions on energy and field gradient.
1.6 Example: Drift of \(9{0}^{\circ }\) Pitch-Angle Particles in the Magnetospheric Equator; Effects of an Electric Field
We shall now analyze the motion of \(9{0}^{\circ }\) pitch angle particles on the equatorial (minimum-B) surface of the earth’s magnetosphere making some simplifying assumptions about magnetic and electrostatic field models. The study of equatorial particles is useful for several reasons: (i) as we shall see later, the equatorial point of a field line represents an equilibrium position for mirroring particles—hence the study of equatorial particles provides “first order” information on the behavior of the off-equatorial population; (ii) the theoretical treatment of equatorial and near-equatorial particles can be done analytically by using simple field models, providing physical insight (though not quantitative accuracy) into fundamental aspects of trapped particle dynamics [7, 8]; (iii) many characteristic effects of spatial field asymmetries are most pronounced for equatorial particles; (iv) more experimental information is available on trapped particles at low geomagnetic latitudes, especially in the outer magnetosphere.
Let us consider the drift motion of charged particles and assume that no external forces are acting (this is nearly the case for radiation belt electrons and protons of energies greater than about 100 keV). The guiding centers of these particles will experience a pure gradient drift (1.46) following constant-B curves; electrons will drift eastwards, protons westwards. Figure 1.19
Experimentally determined average contours of constant magnetic field intensity in the equatorial surface [9]. These contours represent drift paths for energetic, 90\({}^{\circ }\) pitch angle particles. Radial distances are in earth radii (1 R E = 6, 371 km)
sketches the principal features of constant magnetic field intensity contours as observed in systematic measurements [9]. A qualitative examination of the figure leads to the following conclusions:
-
(i)
Within about 7 ∼ 8 earth radii (1 R E = 6, 371 km) all drift paths are closed. In that region an equatorial particle thus remains stably trapped (assuming that there are no external perturbations.)
-
(ii)
The trajectories’ day-night asymmetry increases as one moves away from the earth. Within about 4 R E , they are approximately circles, as prescribed by a dipole-like field. Further out, the asymmetry is such that a given drift path has its closest approach to earth at magnetic midnight.
-
(iii)
Constant-B contours going through the midnight meridian at distances greater than about 7 R E do not close around the earth. Particles drifting along them are trapped in the magnetosphere for only a limited time, running into the boundary at the flanks of the magnetosphere. We call them pseudo-trapped or quasi-trapped particles. The last closed contour represents the “limit of stable trapping” for equatorial particles. (Magnetic field lines through this contour intersect the earth near the equatorward edge of the auroral oval.)
-
(iv)
A satellite in circular orbit (for instance, a geostationary satellite at 6.6 R E from the center of the earth), cuts through different drift paths as the local time or longitude of its position changes. In particular, at midnight it samples the outermost B-ring, at noon the innermost one, of a certain B-range. Assuming that particles are distributed evenly along a drift path, their flux will be only a function of B (see Chap. 4). If this flux decreases outwards (i.e. with decreasing B), a detector on a geostationary satellite measuring equatorial particles will reveal a diurnal variation of its counting rate with maxima occurring at local noon.
-
(v)
Drift paths are closer to each other at midnight. This means that the transverse gradient of the field is larger there. Thus, according to (1.46), a particle’s drift velocity will be larger at night than at noon. As a consequence, stably trapped equatorial particles spend more time on the day side than on the night side during their drift. This difference becomes more pronounced as we approach the limit of stable trapping.
An analytical expression of the equatorial magnetospheric field intensity B 0 at point r 0, ϕ 0 (longitude east of midnight), reasonably good during quiet and moderately disturbed times in the region 1.5–7 R E , is given:
The three terms represent, respectively, (i) the main dipole field (with B E ∼ 30, 438 nT the dipole magnetic field intensity on the Earth surface at r 0 = 1R E ); (ii) the contribution from a uniform field compression by the Chapman-Ferraro boundary currents; and (iii) a day-night asymmetry caused by the cross-tail current. The second and third terms are small compared to the dipole term. To first order, the coefficients b 1 and b 2 depend on the stand-off distance to the subsolar point of the magnetopause; the following relations represent this relationship reasonably well:
Notice the strong dependence with the stand-off distance R s (R s = 10R E corresponds to the normal state of the magnetosphere). The equation of the drift trajectory \(B_{0}(r_{0},\phi _{0}) = \mathrm{const}\). generated by a particle injected at point r 0i , ϕ 0i with a \(9{0}^{\circ }\) pitch angle is, to first order:
Note that only the day-night asymmetry coefficient b 2 appears. This equation represents eccentric circles with closest approach to the earth on the night side (as in Fig. 1.19); their eccentric displacement increases very rapidly with radial distance r 0i . Close to Earth higher order multipoles from the internal geomagnetic field must be taken into account for a more realistic description (Sect. 3.4).
Evaluating the drift velocity (1.46) of a particle along this B 0 = const. contour, we find
This function passes through a maximum at midnight and a minimum at noon. Trapped equatorial particles thus indeed spend more time on the dayside than on the nightside of the magnetosphere, as we have anticipated above.
The drift period τ d is given to first order by
In this case only the compression coefficient b 1 intervenes. For particles of the same energy, τ d increases as B 0 decreases (as the particle’s drift contour radius increases), passes through a maximum for \(B_{0}\mathop{\cong}(20/3)b_{1}\) ( ∼ 160 nT, or a radial distance of approximately 5.8 R E ), and then decreases again. The approximations used to derive these expressions start breaking down at these radial distances (for a more realistic field model the actual position of the contour of maximum drift period is slightly larger than the figure quoted.)
Our next examples involve the drift motion of equatorial particles subject to an electric field \({\boldsymbol E}_{0} = -{\boldsymbol \nabla }V\) parallel to the minimum-B surface (please do not confuse the electric scalar potential V with the drift velocity vector \({\boldsymbol V }_{D}\)!). Each particle will be subjected to a drift that is the vector sum of (1.46) and (1.34):
For equatorial particles, this means that they will drift along curves of constant \(\varPsi = (M/q)B_{0} + V\), which plays the role of an “extended” potential (note that \(q\varPsi = \mathfrak{E}\), total energy of the particle). The functions \(B_{0}(r_{0},\phi _{0})\) and \(V (r_{0},\phi _{0})\) can be determined using analytical or numerical models of the magnetic and electric fields. If the initial position of the particle’s guiding center is \(r_{0i},\phi _{0i}\), the drift trajectory \(r_{0} = r_{0}(\phi _{0})\) is found by solving \(\varPsi = (M/q)B_{0}(r_{0},\phi _{0}) + V (r_{0},\phi _{0}) = (M/q)B_{0i} + V i = \mathrm{const.}\), where the magnetic moment \(M = T_{0}/B_{0} = T_{0i}/B_{0i}\) (non-relativistic case) serves to determine the particle’s kinetic energy along its path. To calculate the time Δ t to reach a given point of its drift path (or to determine the drift period in a closed orbit), it is necessary to integrate the inverse of (1.54): \(\varDelta t =\int (r_{0}/V _{D})d\phi _{0}\) (dl: element of arc of the drift path).
We shall discuss examples using simple analytical approximations for B 0 and W 0. We choose a pure dipole field \(B = B_{E}{(R_{E}/r_{0})}^{3}\), and an electric field consisting of two terms: (i) an ubiquitous corotational field arising from the rotation of the dipole (co-axial rotation in this simplified model), and (ii) a uniform dawn-dusk electric field (assumed to be driven by the solar wind flow). The corotational field is an induced field with the property, mentioned on page 76, that any near-zero energy particle (regardless of its mass and charge) will drift with the local rotational speed (\(v_{corot} =\varOmega _{E}r_{0}\)) in the dipole field: \(E_{corot} = v_{corot}B_{0} =\varOmega _{E}{R_{E}}^{3}B_{E}{r_{0}}^{-2}\) (\(\varOmega _{E} = 7.272\, \times \, 1{0}^{-5}\) rad/s) is the angular rotational speed of the Earth). Despite being an induced field (of the type \(-\partial {\boldsymbol A}/\partial t\); see Sect. A.1), in the domain of interest this expression can be written as the gradient of a potential \(V _{corot} = -\varOmega _{E}{R_{E}}^{3}B_{E}/r_{0}\). Concerning the uniform dawn-dusk electric field \({\boldsymbol E}_{dd}\), its potential is \(V _{dd} = E_{dd}r_{0}\sin \phi _{0}\) (positive, to have \({\boldsymbol E}\) pointing in the − y direction). The final expression of Ψ is then
Taking into account that \({\boldsymbol \nabla }_{\perp } ={\boldsymbol \nabla }_{\perp r} +{\boldsymbol \nabla }_{\perp \phi }\) and that there is a vector product operation in (1.54), the corresponding drift velocity (1.54), in its polar components on the equatorial plane, is given by:
Let us examine some characteristics of the equatorial particle drift paths r 0 = r 0(ϕ), solution of \(\varPsi =\varPsi _{i} = \mathrm{const.}\), where Ψ i is defined by the initial values r 0i , ϕ 0i and \(M = T_{i}/B_{i}\). We begin with analyzing the electric equipotentials, i.e., the drift trajectories of M → 0 equatorial particles. Their equation will be, according to (1.55),
Near the earth, the (negative) corotation potential will prevail (V < 0), and the equipotentials will approximate circles around the Earth; far away, e.g., toward the magnetotail, the equipotentials will approximate straight lines, representing a general sunward drift. The equation for the zero equipotential V 0 = 0 is \({r_{0}}^{2} = (\varOmega _{E}{R_{E}}^{3}B_{E})/(E_{dd}\sin \phi _{0})\). Note that it is valid only for sinϕ 0 > 0, i.e., it lies entirely in the dawn quadrants (see Fig. 1.20).
Its intersection R 0 with the dawn meridian (y-axis) is located at
from the center of the Earth. This value will come handy as a geometric scaling parameter. The larger the electric field, the closer to the Earth the zero potential curve will come (the smaller the corotational region in the figure). The solution of the quadratic equation (1.57) is
The presence of the function sinϕ 0 in the square root indicates that the characteristics of the equipotentials in both dawn quadrants (sinϕ 0 > 0) will in general be different from those in the dusk quadrants. Figure 1.20 sketches the different types of equipotentials for the general case. Since the value of r 0 must come out positive, in the dawn side there can only be one solution (the positive sign of the square root); in the dusk side two different solutions are possible. Note first the existence of two topological regions, a corotation region with closed equipotential lines around the Earth, and the convection region with open equipotentials, where low energy particles flow from the tail toward the front of the magnetosphere. The potential V S of the separatrix (called Alfv\(\mathrm{\acute{e}}\) n layer) limiting both regions will be that for which the two solutions along the dusk meridian (\(\sin \phi _{0} = -1\)) coincide, i.e., for which the square root in (1.59) is zero: \(V _{S} = -2\sqrt{E_{dd } \varOmega _{E }{ R_{E } }^{3 } B_{E}} = -2E_{dd}R_{0}\) (only the negative value of the square root will lead to positive r 0 in (1.59)). The equation of the separatrix will be, taking into account (1.58):
The geometric form is independent of the intensity of the dawn-dusk electric field; the latter only appears in the scaling factor R 0 (1.58). Again, the larger E dd the smaller will be the corotation region. For sinϕ 0 > 0 only the negative sign of the square root is acceptable; for sinϕ 0 < 0 both signs are possible, and two solutions may exist. Observe in the figure the notable points, intersections of the separatrix with the y-axis (sinϕ 0 = ±1) and on the x-axis (for the latter, consider that the limit of the geometric factor in (1.60) for \(\sin \phi _{0} \rightarrow 0\) is 1∕2).
Some words about the concept of field line motion (page 79) in relation to the equipotentials shown in Fig. 1.20. As stated above, these equipotentials are the trajectories of near-zero charged particles, moving with a velocity (1.54) (without the M-term). Would this then also be the velocity of the corresponding field lines? Would the entire magnetic field be convecting and corotating as prescribed by the motion of the field lines’ equatorial points, up to their intersection with the Earth? First of all, we haven’t said anything about the electric field off the minimum-B equator. If all field lines are equipotentials (\({\boldsymbol E}_{\parallel }\equiv 0\)) such a picture might indeed be correct. Yet in the definition of field line velocity, did we not require that the electric field be an induced electric field (1.38)? Well, just as the induced rotational electric field (page 76) can be expressed as the gradient of a scalar in the region of interest, the dawn-dusk electric field \({\boldsymbol E}_{dd}\) was also expressed as a potential field in the region of interest, despite also being an induced field (the moving or changing source currents to be found in the solar wind). So indeed we could visualize the curves of Fig. 1.20 as the trajectories of the equatorial footprints of magnetospheric field lines in our model. Unfortunately, their intersection with the conducting ionosphere substantially complicates the picture. Despite these reservations, the field lines through the closed portion of the separatrix may be viewed as an approximation to the limit of corotating low energy plasma particles that form the plasmasphere. Such limiting surface is called the plasmapause, and Eq. (1.60) may be viewed as “the plasmapause equation”; its form and dependence of a dawn-dusk electric field indeed bear some observed geometric and dynamic characteristics of the plasmapause.
We now turn to particles of arbitrary energy. If, say, \(T_{i} \gtrsim 100\) keV, the electric field drift can be neglected and electrons and protons drift in opposite senses along constant B lines, as discussed in relation to Fig. 1.19. In the intermediate range of energies the drift motion is more complicated. Electrons in general behave rather “normally” because in general the electric drift and the gradient drift point roughly in the same direction. For protons, however, these drifts may point in opposite directions on some parts of the dusk side; depending on which is the greater, the proton drift will be eastward or westward. Figure 1.21a, b
(a) Broken lines: equipotentials for an electric field of potential E dd = 1. 8 kV R E −1. Solid lines: drift paths of electrons injected with 1 keV along the dusk meridian (dots). Notice corotation vs. convection. Equipotentials in the corotation region (not shown) are close, but not equal to the drift paths. (b) Solid lines: drift paths of protons injected with 1 keV along the dusk meridian (dots). Notice three types of paths: corotational, “vortices” not enclosing the earth, and sunward convection
show drift trajectories calculated using (1.54) for 1 keV electrons and protons, respectively, injected on the disk meridian (solid curves), for a dawn-dusk electric field of 1.8 kV/R E . Close to Earth, the electrons are stably trapped; beyond the stagnation point 1 keV electrons are quasi-trapped, being convected into the boundary. There is a reversal of drift sense at the stagnation point. Notice also how corotating electron drift paths approach the earth closer at dawn; their energy there can be up to ten times greater than at dusk. The behavior of protons (Fig. 1.21b), again injected with 1 keV at several positions along the dusk meridian, is more complex. Starting at 3, 4 or 5 R E at dusk, the corotational field takes them eastwards around the earth in orbits similar to those of electrons; the energy-dependent gradient drift, directed opposite to the electric field drift, is negligible. Between 5 and 7 R E on the dusk meridian, we have a zone in which protons get sufficiently accelerated in their eastward drift so that, eventually, the gradient drift takes over and turns them around westwards against the corotation drift, on the same evening side of the earth. After crossing the dusk meridian, these protons are decelerated and the electric field drift takes over again. We thus have closed drift paths which do not encircle the earth. Beyond 7 R E on the dusk meridian, 1 keV protons are quasi-trapped, following a convection pattern toward the Sun.
Thus far we have assumed static conditions. Equation (1.54) can be integrated also for a slowly, adiabatically varying dawn-dusk field (V = V (t)). This can be used to determine the fate of low energy equatorial protons injected from the magnetospheric tail and convecting toward the Earth during conditions of high E dd , and then captured around the Earth in corotating orbits when a decrease in E dd sets in (having the effect of expanding the separatrix). This, in connection with more realistic field models and consideration of local plasma effects, may play a role in substorm ring current injection dynamics.
Notes
- 1.
We shall use rationalized SI (Système International) units throughout this book. q is thus expressed in Coulombs (elementary charge \(= 1.6021 \times 1{0}^{-19}\) Coulombs), B in Tesla ( = 104 Gauss)—see Sect. A.1.
- 2.
For the time being we’ll just consider τ C as a priori known. As we shall see in the next section, in a non-relativistic situation τ C is independent of the particle’s dynamic state, depending only on mass, charge and the local magnetic field.
- 3.
Later we will run into the cyclotron phase average operator, \(\langle \,\,\ldots \rangle _{\varphi } = 1/2\pi \int _{0}^{2\pi }\ldots d\varphi = 1/\tau _{C}\int _{0}^{\tau _{C}}\ldots (d\varphi /dt)dt\). When the cyclotron motion in the GCS is uniform, both operators are identical and will be designated as \(\langle \,\,\rangle _{C} =\langle \,\,\rangle _{\tau } =\langle \,\,\rangle _{\varphi }\). A compilation of all phase averages used in this book is given in a footnote on page 200 of Sect. A.3.
- 4.
In regions where B → 0 (e.g., near a neutral line) the concept of “transforming away E ⊥ ” breaks down. See page 73.
- 5.
Henceforth, whenever the charge q appears in the expression of a scalar quantity as a ⊥ , it will be meant to represent the absolute value of q (unless explicitly stated to the contrary). If on the other hand q appears in the expression of a vector quantity, it is assumed to carry its actual sign; otherwise it will be explicitly written as | q | .
- 6.
Yet another model is to imagine the charge q smeared evenly over the cyclotron circle in the GCS, rotating uniformly with period τ C . See page 92.
- 7.
In Hamiltonian mechanics (e.g., [1]) of point charges in a magnetic field, it is demonstrated that for cyclic variables like the arc \({\boldsymbol l}\) (see Fig. 1.5) the so-called canonical path or action integral \(J =\oint ({\boldsymbol p} + q{\boldsymbol A}) \cdot {\boldsymbol dl}\) is a constant of motion for a single particle (provided that the fields and the forces change very little during one cycle). Taking \({\boldsymbol dl}\) in the direction of a positive particle (Fig. 1.5) and carefully considering that, therefore, the magnetic flux through the cyclotron loop \(\oint {\boldsymbol A} \cdot {\boldsymbol dl}\) is negative, we have \(J_{c} =\oint ({\boldsymbol p} + q{\boldsymbol A}) \cdot {\boldsymbol dl} = 2\pi \rho _{C}mv_{\perp }^{{\ast}}-\pi {\rho _{C}}^{2}B = (2\pi m/q)M\), therefore \(M = \mathrm{const.}\)
- 8.
If we place a charged particle in a B& E field with zero initial velocity (for instance, by ionizing a neutral atom at rest), it will start moving in an open cycloid (Fig. 1.11), with a drift velocity U given by (1.10) and a Larmor radius \(\rho _{C} = mE/q{B}^{2}\). The maximum kinetic energy of the particle (at point P) will be \(T = 2m{(E/B)}^{2} = 2m{U}^{2}\), and the average energy, according to (1.35), will be mU 2. This so-called “ion pick-up” process plays an important role in space physics.
- 9.
Without the first condition we would run into the undesirable situation of having “moving field lines” in a static magnetic field crossed by a static electric field, as for instance in the case of two oppositely charged plates placed parallel to \({\boldsymbol B}\) in the gap of a magnet. It can be shown that the above definition is not only independent of the particular position of the guiding center along the field line but that it is magnetic flux-preserving (i.e., flux tubes preserve their identity). There is nothing artificial with a definition using probe particles placed along a field line: after all, as we know from elementary textbooks, the electric and magnetic field vectors themselves are formally defined by forces on probe particles! Neither is the condition that all ρ be turned off artificial: in elementary electromagnetism books, the self-field of probe charges are also “turned off” (ignored). While it is tempting to exaggerate the physical significance of a purely mathematical-geometric concept such as a field line, we must never lose sight of the fact that the only “physical reality” in electromagnetism is mutually interacting electrically charged matter. Here are some perhaps too strong words from Richard Feynman et al. [6]: “ … not only is it not possible to say whether field lines move or do not move with charges—they may disappear completely in certain coordinate frames …”
References
H. Goldstein, Classical Mechanics (Addison-Wesley, Boston, 1980)
B. Rossi, S. Olbert, Introduction to the Physics of Space (McGraw Hill, New York, 1970)
T.G. Northrop, The Adiabatic Motion of Charged Particles (Interscience, New York, 1963)
S. Eliezer, P. Norreys, J.T. Mendonça, K. Lancaster, Effects of Landau quantization on the equations of state in intense laser plasma interactions with strong magnetic fields. Phys. Plasmas 12(5), 052115 (2005)
J.W. Belcher, S. Olbert, Field line motion in classical electromagnetism. Am. J. Phys. 71, 220–228 (2003)
R.P. Feynman, R.B. Leighton, M. Sands, Feynman Lectures on Physics, vol. II (Addison-Wesley, Boston, 1963)
J.G. Roederer, Geomagnetic field distortions and their effects on radiation belt particles. Rev. Geophys. Space Phys. 10, 599–630 (1972)
M. Schulz, L.J. Lanzerotti, Particle Diffusion in the Radiation Belts (Springer, Berlin, 1974)
D.H. Fairfield, Average magnetic field configuration of the outer magnetosphere. J. Geophys. Res. 73, 7329–7338 (1968)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Roederer, J., Zhang, H. (2014). Particle Drifts and the First Adiabatic Invariant. In: Dynamics of Magnetically Trapped Particles. Astrophysics and Space Science Library, vol 403. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-41530-2_1
Download citation
DOI: https://doi.org/10.1007/978-3-642-41530-2_1
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-41529-6
Online ISBN: 978-3-642-41530-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)