Mechanical Response of Porous Materials: The Gurson Model

Abstract

In this chapter the formulation for damage known as Gurson model is presented. The original formulation, set in a micro-mechanical context, and different adjustments of phenomenological nature are described. The range of the parameters of the model and their influence on the representation are described. The main computational details for the implementation of the model by means of the finite element method are presented and examples of application are given.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fracture Mechanics that uses global fracture parameters, such as $J$ integral or Crack Tip Opening Displacement (CTOD) [34], only in special situations represents the behavior of ductile solids. In polycrystalline metals, ductile fracture is controlled by nucleation, growth and coalescence of microvoids and a local approach provides a clearer picture.

Voids can nucleate from large inclusions and second phase particles, by particle fracture or interfacial decohesion [47]. Once a void has been nucleated, it will grow under plastic deformation and hydrostatic stress. Eventually the voids will connect and ductile fracture by void coalescence will take place.

Thus, four stages, as indicated in Fig. 1 are observed: homogenous deformation with void nucleation and growth, localized deformation and void coalescence.

Fig. 1

Stages in the development of damage: a nucleation, b growth, c coalescence and d fracture

The best known micro-mechanical model for void related damage and fracture is due to Gurson [25, 26] and includes a plastic damage yield condition that depends on a damage parameter (porosity) and a growth law for this damage variable. The original Gurson model has been subjected to many analysis, criticisms and improvements, some of which are reviewed in the present work. The original model assumes a homogenous deformation field and thus is not able to describe interaction effects, void shape changes and the non-homogeneous transformations that lead to coalescence and rupture. Some important modifications are due to Tvergaard [76, 79] who introduced adjustment parameters and to Chu and Needleman [10] who proposed improved nucleation laws for porosity. For this reason the model is sometimes referred to as GTN (for Gurson, Tvergaard, Needleman). Other modifications will be described in Sect. 4. Many of them maintain the same basic variables and general form of the equations and have only a phenomenological (i.e. no micromechanical) base. Application of the Gurson model to practical problems is only possible in a computational context. So, diverse studies have been devoted to the numerical implementation (usually through finite element techniques) of the model. Details of some procedures and application examples are given in Sects. 5 and 6.

2 Gurson Damage Model

2.1 Yield Criterion

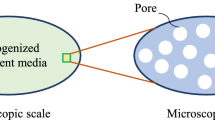
This theory—originally presented by Gurson [25, 26] in a PhD dissertation supervised by J. R. Rice—proposed yield criteria and flow rules for porous materials, focusing the effect of void nucleation and growth, as observed in ductile fracture. Figure 2 (from Gurson [26]), defines macroscopic and microscopic stresses and strains and the spherical model of a unit cell. The isotropic damage variable (in the framework of continuum damage mechanics [32, 33]) is the volumetric void fraction or porosity $f=V_\textit{v}/V$, with $V_\textit{v}$ being the volume of voids in a representative small volume $V$. The volumetric void fraction $f$ is assumed as defined at each point of the continuum.

Fig. 2

Void-matrix aggregate, with random void shapes and orientations, evidencing macroscopic and microscopic tensor quantities, and also the unit cell model studied by Gurson [26]

The macroscopic yield criterion was approximated with an upper bound approach [28]. Aggregates of cells representing voids in a ductile matrix were employed, with the matrix material idealized as rigid-perfectly plastic obeying von Mises yield criterion. Using a distribution of macroscopic flow fields and working with a dissipation integral, upper bounds for the macroscopic stress fields required for yield were determined. Their locus in the stress space determines the yield surface. It was shown that normality of plastic flow holds for this yield surface. The expression proposed by Gurson is

$$\begin{aligned} \varPhi =&\frac{\Sigma _{\mathrm{eq}}^2}{\sigma _0^2} + 2f\cosh \frac{3\Sigma _\mathrm {m}}{2\sigma _0}-1-f^2=0 \nonumber \\ \Sigma _{\mathrm{eq}} =&\sqrt{\frac{3}{2}\Sigma ':\Sigma '}, \quad \Sigma _\mathrm {m} = p = \frac{1}{3}{\mathrm{tr}}\Sigma , \quad \Sigma ' = \Sigma - \Sigma _\mathrm {m}, \end{aligned}$$

(1)

where $\Sigma _{\mathrm{eq}}$ is the macroscopic von Mises equivalent stress, $\Sigma '$ is the deviator of the macroscopic stress, $\Sigma _\mathrm {m}$ is the mean macroscopic stress or pressure, $\Sigma _0$ is the yield stress of the matrix undamaged material and $f$ is the porosity. For $f = 0$ Gurson’s model reduces to the von Mises criterion.

A prior model, the Drucker-Prager theory [18], had already proposed a yield criterion dependent on hydrostatic stress in the general form (the macroscopic stress being now indicated with $\sigma$)

$$\begin{aligned} \varPhi = \sigma _{\mathrm{eq}}-a\sigma _\mathrm {m}-b=0. \end{aligned}$$

(2)

Gurson seminal contribution resides in the establishment of a microstructural relation for the effect of the hydrostatic stress $p$ on the yield function through the consideration of a porosity variable $f$.

In the original Gurson model (Eq. 1), the softening of the material with the increase of void volume fraction is a continuous process, and a complete loss of load carrying capacity would occur only when the void has grown to the ultimate value $f = 1$. Tvergaard [76, 79] compared the bifurcation predictions based on the Gurson model and his own numerical studies for material containing periodic distribution of voids and suggested a modification of the Gurson model. In the most usual notation

$$\begin{aligned} \varPhi = \frac{\sigma _{\mathrm{eq}}}{\sigma _\mathrm {y}} + \sqrt{2\alpha _1f\cosh \alpha _2\frac{3\Sigma _\mathrm {m}}{2\sigma _\mathrm {y}}-1-\alpha _1^2f^2}=0 \end{aligned}$$

(3)

or

$$\begin{aligned} \varPhi = \sigma _{\mathrm{eq}}-\varpi \sigma _\mathrm {y}=0, \end{aligned}$$

(4)

with

$$\begin{aligned} \varpi = \sqrt{1-2\alpha _1f\cosh \left( \alpha _2\frac{3\Sigma _\mathrm {m}}{2\sigma _\mathrm {y}}\right) +\alpha _1^2f^2}. \end{aligned}$$

(5)

The substitution of $\Sigma$ by $\sigma$ is coherent with the fact that the original micromechanical model has been altered to include phenomenological parameters.

Fig. 3

Gurson yield surface for a porous material, showing the influence of pressure and volumetric void fraction

In Fig. 3, yield surfaces for different levels of void content are shown, in a plot of normalized macroscopic deviatory stress versus normalized pressure. It can be seen that the elastic domain depends on the hydrostatic pressure. When the volumetric void fraction $f$ decreases, the influence of pressure also decreases, leading to a larger elastic domain. For $f = 0$, the model reduces to the von Mises criterion, which is independent of the hydrostatic pressure.

The parameter $\alpha _1$ in Eq. (3) is a coefficient multiplying the porosity $f$, to be adjusted by comparing numerical simulations of RVE aggregates and the predictions of the model. Since the element studied by Gurson was a single hollow sphere and thus disregarded interaction among voids, this coefficient introduces somehow the interaction effect. The parameter $\alpha _2$ in Eq. (3) can be understood as a calibrating coefficient acting on the pressure.

The parameter $\alpha _1$ is the inverse of the value $f_\mathrm {U}$, being $f_\mathrm {U}$ the volumetric void fraction that corresponds to rupture in the absence of hydrostatic pressure. From $\varpi (p = 0, \sigma _\mathrm {y}, f) = 0$, results $f_\mathrm {U} = 1/\alpha _1$.

Rupture occurs at a porosity level $f_\mathrm {U}$ in the absence of pressure. If pressure is present, rupture takes place at a porosity value lower than $f_\mathrm {U}$. The combinations of pressure and porosity that lead to rupture are given by

$$\begin{aligned} \varpi = \frac{2}{3\alpha _2}{\mathrm{arccosh}}\frac{1+\alpha _1^2f^2}{2\alpha _1f}-\frac{p}{\sigma _\mathrm {y}}=0. \end{aligned}$$

(6)

Figure 4 shows plots corresponding to Eq. (6) for $\alpha _2 = 1.0$ and $\alpha _2 = 0.7$. Even with this modification, the void volume fraction at which the Gurson model will lose load carrying capacity is still unrealistically large. Both experimental observations [9] and results of cell model analysis by Koplik and Needleman [37] show that the volume fraction of voids at which void coalescence starts is usually less than 15 %.

Fig. 4

Combinations of pressure and porosity values that correspond to loss of strength ($\varpi =0$)

Flow rule: As shown by Gurson [26] the plastic strain rate tensor $D_{ij}^\mathrm {p}$ obeys the normality rule

$$\begin{aligned} D_{ij}^\mathrm {p}=\dot{\lambda }\frac{\partial \varPhi }{\partial \sigma _{ij}}. \end{aligned}$$

(7)

The equivalent plastic strain rate is defined as

$$\begin{aligned} \dot{\varepsilon }^\mathrm {p} = \sqrt{\frac{2}{3}D_{ij}^\mathrm {p}D_{ij}^\mathrm {p}}. \end{aligned}$$

(8)

As in classical plasticity, the relation giving the plastic strain rates as a function of the stress rates is obtained using the consistency condition $\dot{\varPhi }=0$ .

2.2 Evolution Law for the Porosity

In a plastic damage theory it is necessary to have, in addition to the yield criterion and the flow rule, an evolution law for damage (porosity, in this case). The mechanism of damage evolution considered in the original Gurson model was growth. Growth occurs when the voids (pre-existent or nucleated) change their size according to the volume change in the continuum and is controlled by mass conservation through the expression

$$\begin{aligned} \dot{f}_\mathrm {g} = (1-f)D_{ii}^\mathrm {p}, \end{aligned}$$

(9)

which determines that voids increase or decrease their volume according to the volume variation in the continuum.

In the GTN version, two additional mechanisms are included: nucleation and coalescence. Nucleation occurs mainly due to material defects, in the presence of tension. Coalescence is related to the fast rupture process that occurs after the volumetric void fraction reaches a limit, usually indicated by $f_\mathrm {C}$. Coalescence is the union of neighbor voids due to the rupture of a ligament among them (see Fig. 1).

The equations that govern damage evolution are modeled in a simplified form as follows. First, it is assumed that the total void growth rate is given by

$$\begin{aligned} \dot{f} = \left\{ \begin{array}{ll} \dot{f}_\mathrm {n} + \dot{f}_\mathrm {g}&{} \quad f \le f_\mathrm {C}, \\ \dot{f}_\mathrm {c}&{}\;\, f > f_\mathrm {C}, \end{array}\right. \end{aligned}$$

(10)

where $\dot{f}_\mathrm {n}$ is the void nucleation rate, $\dot{f}_\mathrm {g}$ is the void growth rate and $\dot{f}_\mathrm {c}$ is the void coalescence rate. Thus, as long as $f$ is smaller than a characteristic value $f_\mathrm {C}$, only nucleation and growth develop. Above $f_\mathrm {C}$, only coalescence takes place. The nucleation rate is proportional to the rate of the equivalent plastic strain

$$\begin{aligned} \dot{f}_{\mathrm {n}} = A(\varepsilon ^\mathrm {p})\dot{\varepsilon }^\mathrm {p}. \end{aligned}$$

(11)

For $A(\varepsilon ^\mathrm {p})$ Chu and Needleman [10] proposed the statistical distribution

$$\begin{aligned} A(\varepsilon ^\mathrm {p}) = \frac{f_\mathrm {N}}{s_\mathrm {N}\sqrt{2\pi }} \exp \left[ -\frac{1}{2}\left( \frac{\varepsilon ^\mathrm {p}-\varepsilon _\mathrm {N}}{s_\mathrm {N}}\right) ^2\right] , \end{aligned}$$

(12)

where $f_\mathrm {N}$ is the proposed final nucleation void volumetric fraction, $\varepsilon _\mathrm {N}$ is the mean plastic strain value for nucleation and $s_\mathrm {N}$ is the standard deviation for the distribution (see Fig. 5).

Fig. 5

Evolution of porosity in the nucleation stage considering $\varepsilon _\mathrm {N} = 0.2$ and two different $s_\mathrm {N}$ values. As a consequence of the combinations of $\varepsilon _\mathrm {N}$ and $s_\mathrm {N}$ adopted, nucleation is almost complete in both cases

Sometimes it is assumed that nucleation does not take place when the material is in compression. The compression state is indicated by a negative pressure p, and thus $A(\varepsilon ^\mathrm {p}) = 0$ if $p < 0$.

Coalescence is governed [78] by the relation

$$\begin{aligned} \dot{f}_\mathrm {c} = \frac{f_\mathrm {U}-f_\mathrm {C}}{\varDelta \varepsilon }\dot{\varepsilon }^\mathrm {p}, \end{aligned}$$

(13)

where $\varDelta \varepsilon$ is a material parameter that controls how fast the coalescence happens. An alternative way of taking coalescence into account [80] is to replace the volumetric void fraction $f$ in the Gurson yield surface (3) by a corrected volumetric void fraction $f^*$ given by

$$\begin{aligned} f^* = \left\{ \begin{array}{ll} f &{} \quad f < f_\mathrm {C},\\ f_\mathrm {C} + \displaystyle \frac{1.0-f_\mathrm {C}}{f_\mathrm {F}-f_\mathrm {C}}(f-f_\mathrm {C}) &{} \quad f > f_\mathrm {C}, \end{array}\right. \end{aligned}$$

(14)

with $f_F$ being the rupture volumetric void fraction. In this case, only nucleation and growth are considered in Eq. (10). Nucleation and coalescence are irreversible. Thus, it seems natural to model them (Eqs. (11) and (13)) as governed by equivalent plastic strain. The growth mechanism is reversible, so it is modeled (Eq. (9)) as volume change dependent.

Fig. 6

Evolution of porosity for a tensioned material obeying Gurson model. The three mechanisms of voids evolution: nucleation, growth and coalescence can be identified. It is observed that the parameter $\varDelta \varepsilon$ is the equivalent plastic strain increment from the beginning of coalescence until the final rupture of the material

In Fig. 6, the evolution of porosity is shown. The occurrence of the three stages of porosity evolution can be observed: initially, a relative fast nucleation, according to the standard deviation $s_\mathrm {N}$ imposed, placed around equivalent plastic strain 0.1; afterwards, a growth stage until an equivalent plastic strain around 0.5, 0.7 or 0.9 is reached. And finally, the coalescence stage, in which the porosity level changes abruptly, according to the parameter employed. The start of the coalescence stage is defined based on porosity, according to Eq. (13).

2.3 Elastic Constants for the Damaged Material

The presence of embedded voids in a metallic matrix alters also the elastic behavior. Mori and Tanaka [49] relations are usually adopted

$$\begin{aligned} K = \frac{4K_0G_0(1-f)}{4G_0 + 3K_0f},\qquad G = \frac{G_0(1-f)}{\displaystyle 1 + \frac{6K_0 + 12G_0}{9K_0 + 8G_0}f}, \end{aligned}$$

(15)

with $K_0$ and $G_0$ being the undamaged values of compressibility and shear modulus, respectively. There are other proposals to include the effect of porosity on elastic constants [31, 45, 59], leading to similar results for low porosities. Figure 7 shows the dependence of damaged Young’s modulus $E$ on the porosity, evaluated from Eqs. (15) and from [45]. $E_0$ is the undamaged Young’s modulus.

Fig. 7

Dependence of Young’s modulus on the void volumetric fraction as introduced by Mackenzie [45] and Mori and Tanaka [49] equations

2.4 Assessment of Gurson Model

The Gurson model has been assessed using numerical micromechanical techniques. Trillat and Pastor [75] use the static and kinematic methods of limit analysis to check both for the 2D and 3D Gurson expressions. For spherical cavities Gurson criterion seems to be a good analytical expression; in the case of cylindrical cavities Gurson expression seems too restrictive. The 2D formulation is also analyzed in [20], where a modification of the Gurson yield function is proposed.

3 Influence of the Parameter Values on the Behavior of the Damage Model

The material parameters in the Gurson model can be classified as:

• (a) constitutive parameters, related to the Gurson yield surface ($\alpha _1,\alpha _2$);

• (b) initial parameters, associated to the origin of the porosity, whether present in the virgin material ($f_0$) or nucleated by plastic straining ($f_\mathrm {N}$, $s_\mathrm {N}$ and $\varepsilon _\mathrm {N}$);

• (c) critical parameters, related to the interaction between neighbor voids, describing the coalescence stage and the final rupture of the material.

The constitutive parameters $\alpha _1$ and $\alpha _2$ act as multipliers on the volumetric void fraction and on the pressure respectively, introducing the possibility of adjusting the the Gurson yield surface with available experimental or numerical data. To larger values of $\alpha _1$ and $\alpha _2$ correspond a smaller elastic domain. Figure 8 shows the dependence of the Gurson yield surface on the $\alpha _2$ parameter.

Fig. 8

Dependence of Gurson yield surface on $\alpha _2$ parameter presented for $\alpha _2 = 0.7$ and $\alpha _2 = 1.0$

The second group of parameters is related to the origin of the voids. An initial porosity $f_0$ can be employed in two situations: when the material has actually an initial porosity or when voids are developed from inclusions that break or debond from the matrix at a very low strain level. Otherwise, the strain governed nucleation relation proposed by Chu and Needleman [10], described by Eqs. (11) and (12), is used.

The value adopted for $f_\mathrm {N}$ determines the proposed level of nucleated voids. The parameter $\varepsilon _\mathrm {N}$ corresponds to the mean equivalent plastic strain for which nucleation is developed. The nucleation standard deviation $s_\mathrm {N}$ controls the localization of nucleation around $\varepsilon _\mathrm {N}$. Figures 5 and 9 shows two nucleation processes with different $\varepsilon _\mathrm {N}$: to the smaller value (Fig. 9) corresponds an earlier nucleation. In both the figures, plots with different $s_\mathrm {N}$ are presented: to smaller values of $s_\mathrm {N}$ corresponds a faster nucleation, with the nucleation localized around the mean equivalent plastic strain nucleation $\varepsilon _\mathrm {N}$.

Figure 9 shows that the proposed level $f_\mathrm {N}$ is not reached, if $s_\mathrm {N}=0.1$ is employed. This is because the porosity evolution law in the nucleation stage $\dot{f}_n$ is given in a rate form that must be integrated while the material is plastically deformed. If an inadequate relation between $s_\mathrm {N}$ and $\varepsilon _\mathrm {N}$ is employed, a significant part of the porosity evolution rate $\dot{f}_n$ will take place in the “fictitious negative” part of the equivalent plastic strain domain (Fig. 10), and not be integrated, since the equivalent plastic strain is always positive, determining an incomplete nucleation.

Fig. 9

Evolution of porosity in the nucleation stage considering $\varepsilon _\mathrm {N} = 0.1$ and two different $s_\mathrm {N}$ values, showing localized nucleation around $\varepsilon _\mathrm {N}$ if a smaller value of $s_\mathrm {N}$ is employed. Incomplete nucleation can be observed if an inadequate combination of $\varepsilon _\mathrm {N}$ and $s_\mathrm {N}$ is adopted, i.e., a large $s_\mathrm {N}$ value with relation to the $\varepsilon _\mathrm {N}$ value

Fig. 10

Dependence of nucleation evolution rate on equivalent plastic strain. Part of the area under the curve is placed on the “fictitious negative” domain of the equivalent plastic strain

To avoid this problem, a relation between $s_\mathrm {N}$ and $\varepsilon _\mathrm {N}$ in the form $\varepsilon _\mathrm {N} > zs_\mathrm {N}$ must be respected. So, to each value of $z$ corresponds a different level of nucleation. To ensure a nucleation level of at least 95 % of $f_\mathrm {N}$ it is necessary to employ a $z$ value of 1.645. To obtain a nucleation level of 97 % of $f_\mathrm {N}$, $z = 1.882$ must be used and to attain a nucleation level of 99 % of $f_\mathrm {N}$, $z = 2.337$ must be employed.

Another important choice concerns the influence of the pressure sign on the nucleation of voids. One approach is to consider nucleation completely independent of the pressure sign [71, 77]. For a material without initial porosity, this choice leads to a Gurson yield surface which is symmetric with respect to pressure, as indicated in Fig. 11 . On the other hand, if nucleation is associated to debonding between inclusions and metallic matrix, this debonding will decrease whenever the region is submitted to compression. To avoid this contradiction, some proposals consider nucleation only for $p>0$ (tension), imposing $A(\varepsilon ^\mathrm {p})=0$ if $p<0$ [69]. For a material initially free of voids, we will have Gurson behavior for $p>0$ and von Mises behavior for $p<0$ as indicated in Fig. 11. This approach also has drawbacks. Considering a material initially compressed and plastically deformed to an equivalent plastic strain level higher than $\varepsilon _\mathrm {N}$, if the load reversal happens and the hydrostatic stress state on the material changes to tension, nucleation will not take place. In the absence of nucleated voids, there will be no void evolution and the material will continue obeying von Mises yield criterion even for a high level of plastic straining and positive hydrostatic tension [13]. Both nucleation approaches give the same response to monotonic positive hydrostatic pressure.

Fig. 11

Gurson yield surface associated to a material initially voids free, under different nucleation approaches: nucleation only in tension or pressure independent nucleation, symmetric with relation to the pressure sign. If the material is tensioned, both approaches lead to similar results. If the material is compressed, with nucleation only in tension, von Mises behavior is reproduced

The third class of parameters includes those related to the coalescence of voids. Considering the coalescence rate of voids described by the Eq. (13), two material parameters are present: $f_\mathrm {C}$, that indicates the initial level of voids at which coalescence takes place, and $\varDelta \varepsilon$, that indicates how fast coalescence occurs. Considering a material submitted to uniform tension, it can be seen that the coalescence parameters control the final branch of the load-displacement relation presented in Fig. 12: $f_\mathrm {C}$ controls the start of the branch and $\varDelta \varepsilon$ controls its slope. To a small $f_\mathrm {C}$ corresponds a final branch that starts earlier and to a small $\varDelta \varepsilon$ corresponds a steeper one.

Fig. 12

Force versus displacement relations for a tensioned material obeying Gurson behavior. It can be seen that after yielding there is a decay in tension corresponding to nucleation, and that the final branch corresponding to rupture starts earlier or later depending on $f_\mathrm {C}$ and with its slope depending on $\varDelta \varepsilon$

4 Further Developments and New Trends for Gurson Model

The Gurson model has been modified by several authors, particularly in reference to its parameters. There are proposals to make these parameters function of porosity [23, 81], triaxiality [40], shape of voids [36], etc. There are proposals to use kinematical hardening [8, 42]. A thermo mechanical coupling [84] includes the possibility of using parameters dependent on temperature.

Thomason [74] proposes a model that incorporates Rice and Tracey [66] equations, and is able to represent both the growth and the change of void shapes. For this model, the $\alpha _i$ parameters proposed by Tvergaard [76, 79] would be unnecessary. Klöecker and Tvergaard [36] also propose a modification of the Gurson model to take into account changes in void shapes and the coalescence process. Zhang and Niemi [88] present a mechanism of coalescence that avoids the need for determining experimentally the critical value of the coalescence beginning $f_\mathrm {C}$. In this model, the void remains spherical during growth, and the initiation of coalescence is controlled by the triaxiality level.

Voyiadjis and Kattan [81] propose a formulation that introduces damage through a damage tensor. Applying this formulation to simulate Gurson model, they obtain a yield surface with porosity dependent parameters. Wen et al. [82] propose a modification of the Gurson model to take into account void size. They show that the yield surface is larger for materials with very small voids. The effect becomes important for high porosities.

The Gurson model has been used in combination with Fracture Mechanics by Kikuchi et al. [35], Needleman and Tvergaard [52], Koppenhoefer and Dodds Jr. [38] and Skallerud and Zhang [70] employing J integral and by Aravas and McMeeking [3] employing J integral and COD.

Subjects that deserve particular attention are situations with low triaxility and shear stresses, the effect of hardening and the consideration of cyclic loading.

4.1 Non-Spherical Voids

The evolution of the void shape and its effect on the mechanical behavior has been considered by Gologanu et al. [22] and Pardoen and Hutchinson [58].

Gologanu et al. [22] extended the Gurson model to prolate and oblate voids in a plastic material. The stress potential proposed corresponds to an ellipsoidal volume of perfectly plastic material containing a confocal ellipsoidal void,

$$\begin{aligned} \varPhi = C\left( \frac{\Sigma _{\mathrm{eq}}+\eta \Sigma _\mathrm {h}}{\sigma _0}\right) ^2 -2q(g+1)(g+f) \cosh \left( \kappa \frac{\Sigma _\mathrm {h}}{\Sigma _\mathrm {0}}\right) -q^2(g+f)^2 =0, \end{aligned}$$

(16)

with

$$\begin{aligned} \Sigma _\mathrm {h} = 2\alpha _2\left( \frac{\Sigma _{11}+\Sigma _{22}}{2}\right) + (1-2\alpha _2)\Sigma _{33}. \end{aligned}$$

The parameters $C, \eta , q, \alpha _2$ depend on the current void and cell shape. Pardoen and Hutchinson [58] use a potential function similar to Eq. (16) and add a coalescence function that determines the initiation of the coalescence, based on the work of Thomason [74]. Two new variables determine void shape and the relative void spacing. The analysis seems to give satisfactory results for the overall cell behavior (i.e. equivalent stress-strain curves), but a precise prediction of the shape evolution needs the introduction of correction functions.

4.2 Shear Effects

The difficulty of the Gurson formulation to model damage under pure shear has been tackled in a phenomenological form by Nahshon and Hutchinson [50]. An extension of the Gurson model that incorporates damage growth under low triaxial straining in shear-dominated states is proposed. This extension retains the isotropy of the original Gurson model by making use of the third invariant of stress to introduce shear dependence. This extension opens the possibility for computational approaches based on the Gurson model to be extended to shear-dominated failures. This modification assumes that the volume of voids undergoing shear may not increase, but void deformation and reorientation contribute to damage and softening increase. Thus, $f$ is no longer directly tied to the plastic volume change. Instead, it is regarded as an effective damage parameter. The modification, while phenomenological, is nevertheless formulated to be consistent with the mechanism of softening in shear. Specifically, it is proposed that the growth rate expression be written as

$$\begin{aligned} \dot{f} = (1-f)D_{ii}^\mathrm {p} + A \dot{\varepsilon }^\mathrm {p} + k_\omega f\omega _0 \frac{s_{ij}D_{ij}^\mathrm {p}}{\sigma _\mathrm {y}} , \end{aligned}$$

(17)

where $s_{ij}$ is the deviatoric part of the stress tensor and the invariant measure $\omega _0 = \omega (\sigma )$ is defined as

$$\begin{aligned} \omega _0 = \omega (\sigma ) = 1 - \left( \frac{27III_s}{2\sigma _\mathrm {y}^3}\right) ^2 , \end{aligned}$$

(18)

in which $III_s$ is the third invariant of the deviator. In Eq. (17), the first term representing growth of existing voids follows from plastic incompressibility, the second term describes nucleation of new voids, while the last term, introduced by Nahshon and Hutchinson [50], is formulated to be consistent with the mechanism of void softening in shear. Void nucleation is here taken to be plastic strain controlled as suggested by Chu and Needleman [10], so that the coefficient $A$ in Eq. (17) takes the form of Eq. (12).

The model approximates experimental results obtained for various structural alloys that show a marked difference between fracture strains under axisymmetric stress and those under a pure shear stress plus a hydrostatic component or under plane stress states. The shear contribution added to the damage growth rate in Eqs. (17) and (18) does not affect the normality of the plastic flow rule [50].

The proposal above has been critically analyzed by Nielsen and Tvergaard [53], which claims the modification represents damage development in shear, but also gives a contribution to the damage development at plane strain uniaxial tension, even though the stress triaxiality is far from zero.

4.3 Hardening

Gurson [25, 26] had already considered the case of a matrix with isotropic hardening, writing Eq. (1) with $\sigma _0 = \sigma (\bar{E})$, where $\bar{E}$ is given by the evolution law $(1-f)\sigma _0\dot{\bar{E}} = \Sigma _{ij}D_{ij}^\mathrm {p}$. Mear and Hutchinson [48] and Becker and Needleman [6], were the first to introduce linear kinematic hardening into the Gurson yield function. In the case of purely kinematic hardening [48], the proposed criterion is

$$\begin{aligned} \varPhi = \frac{(\Sigma -A)_{\mathrm{eq}}^2}{\sigma _\mathrm {y}^2} + 2f\cosh \left( \frac{3(\Sigma -A)_\mathrm {m}}{2\sigma _\mathrm {y}}\right) -1-f^2=0, \end{aligned}$$

(19)

where $A$ denotes now the back stress (center of the macroscopic elastic domain).

The extensions mentioned above are purely phenomenological. Leblond et al. [39] derived another yield function (the extended Leblond-Perrin-Devaux—LPD model) based on the analysis of a spherical void in a spherical volume element assuming an incompressible isotropic and kinematic hardening matrix material:

$$\begin{aligned} \varPhi = \frac{(\Sigma -A)_{\mathrm{eq}}^2}{\Sigma _1^2} + 2\alpha _1f\cosh \left( \frac{3\alpha _2(\Sigma -A)_\mathrm {m}}{2\Sigma _2}\right) -1-(\alpha _1f)^2=0. \end{aligned}$$

(20)

The two variables $\Sigma _1$ and $\Sigma _2$ replace the isotropic flow stress in the Gurson equation.

Steglich et al. [72] carried out unit cell calculations assuming a non-linear kinematic hardening matrix material surrounding spherical voids. They compared the unit cell results to predictions of the LPD model with non-linear kinematic hardening and found that, in principle, the behavior under constant triaxiality, as observed in the cell calculations, can be described with the model.

5 Computational Details

5.1 Numerical Implementation

The Gurson damage model computational formulation is usually presented in rate form (hypoelasticity). Thus, a numerical scheme must be adopted to integrate the rate equations following the evolution of the internal variables (stresses, damage and plastic strain). A time discretization procedure is adopted, associating to each time $t$ a specific load level. Then, the evolution of internal variables is obtained for subsequent times $t + \varDelta t, t + 2\varDelta t$, etc. The correct integration of rate constitutive equations has a direct implication on the precision of the solution.

Physical and geometrical nonlinearities must be taken into account during the integration process. A convenient way is to consider the physical and geometrical nonlinearities in separate levels. Therefore, the integration of constitutive equations is organized in two stages: first, the evaluation of corotational Cauchy stresses (material nonlinearity); and secondly, the evaluation of stresses, from the previously obtained corotational stresses (geometrical nonlinearity). A good integration scheme must provide incremental stability, precision and incremental objectivity.

Incremental objectivity is assured by the corotational formulation. An integration procedure that has been widely employed is the so called split-operator scheme, with which all strain increase is initially considered as elastic. If the yield surface is exceeded, a plastic corrector is applied.

Ortiz and Popov [57], Runesson et al. [67], Gratacos et al. [24], Lee [41] and Zhang [86] present studies on the stability and precision of different integration schemes. Zhang [85] and Zhang and Niemi [87] present a generalized mid-point algorithm that is an evolution of the algorithm presented by Aravas [2] to integrate constitutive equations with internal variables and isotropic hardening. The algorithm determines the change in corotational stresses and internal variables such as porosity and plastic strain. Beginning at a time $t$ (characterized by a subindex $n$), at which all the stresses and internal variables are known, the algorithm provides the updated values at time $t+\varDelta t$ (subindex $n+1$). It uses a predictor-corrector strategy, partitioning volumetric and deviatory plastic strains. The parameter $\alpha$ controls whether the integration scheme is explicit ($\alpha = 0$) or implicit ($\alpha > 0$). The process is as follows:

• (a) the logarithmic strain $E_{ij}^N$ is decomposed into the sum of an elastic part $E_{ij}^{N,\mathrm {e}}$ and a plastic part $E_{ij}^{N,\mathrm {p}}$; such additive decomposition is adequate when an Updated Lagrangian description (with reference and updated configurations close to updated each other) is employed;

• (b) stresses are determined from the elastic strains;

• (c) the yield surface is determined using the conventional von Mises equivalent stress $q$, the pressure $p$ and the internal variables $H_t$;

• (d) the plastic strain rate is determined using a potential function $g$. In the present case the potential function is the Gurson yield surface, that is associated to Eq. (7);

• (e) the rate $h_t$ of the internal variables $H_t$ is a function of the stress increment and on the value of the internal variables.

Initially, all the strain increment is supposed as being elastic. In this case, plastic strain and porosity remains unchanged in the time step. If the yield surface is violated, a plastic corrector is applied. The integration algorithm can be viewed as a system of non-linear equations to be solved.

$$\begin{aligned} \varDelta E_\mathrm {p}P + \varDelta E_\mathrm {q}Q = 0, \end{aligned}$$

(21)

$$\begin{aligned} \varPhi _{n+1} = \phi \left\{ p_{n+1}, (s_{ij})_{n+1}, (H_t)_{n+1}\right\} = 0, \end{aligned}$$

(22)

$$\begin{aligned} p_{n+1} = p_{n+1}^T + K\{f\}\varDelta E_\mathrm {p} \end{aligned}$$

(23)

$$\begin{aligned} (s_{ij})_{n+1} = (s_{ij})_{n+1}^T -3G\{f\}\varDelta E_\mathrm {q}\frac{(s_{ij})_{n+\alpha }}{q_n}, \end{aligned}$$

(24)

$$\begin{aligned} (\varDelta H_t)_{n+1} = (h_t)_{n+\alpha }\left\{ \varDelta E_\mathrm {p}, \varDelta E_\mathrm {q}, p_{n+\alpha }, (s_{ij})_{n+\alpha }, (H_t)_{n+\alpha }\right\} \end{aligned}$$

(25)

with $K\{f\}$ and $G\{f\}$ being the bulk modulus and shear modulus respectively, both corrected by the porosity. $\varDelta E_\mathrm {p}$ and $\varDelta E_\mathrm {q}$ are related, respectively, to the volumetric and deviatory part of the logarithmic plastic strain increment [87].

The non-linear equations system can be solved by the Newton-Raphson method, taking as variables $\varDelta E_\mathrm {p}$ and $\varDelta E_\mathrm {q}$. Once obtained their values, the next step is to update stresses and internal variables (Eqs. (23), (24) and (25)). The process is repeated until $|(\varPhi )_{n+1}|\le 10{-7}$.

Some additional strategies can be used to enhance the robustness of the integration scheme. Worswick and Pick [83] recommends to employ sub-incrementation, breaking a time step into sub-steps. The number of sub-steps $NSI$ may be chosen as a function of elastic predictor values, determining

$$\begin{aligned} NSI_1 = {\mathrm{INT}}(\varPhi _{n+1}^T/\sigma _\mathrm {y}), \end{aligned}$$

(26)

$$\begin{aligned} NSI_2 = {\mathrm{INT}}({\mathrm{ABS}}(p_{n+1}^T/\sigma _\mathrm {y})), \end{aligned}$$

(27)

and choosing

$$\begin{aligned} NSI = {\mathrm{MAX}}(NSI_1, NSI_2). \end{aligned}$$

(28)

5.2 Mesh-Size Dependence

A subject that deserves particular attention is the influence of mesh size in finite element analysis with the Gurson model as in all situations that involve softening. Then the results become strongly mesh dependent, unless special procedures are employed. Procedures proposed include non-local models, viscoplasticity, gradient plasticity, etc., in order to introduce a characteristic length, related not to the mesh size but to the material structure [1, 5, 15, 16, 46, 51, 60].

Non-local strategies for the Gurson model have been proposed by Leblond et al. [39], Needleman and Tvergaard [52] and Reusch et al. [64, 65].

The use of gradient plasticity formulations considers that the yield surface depends not only on internal variables but also on its gradients. This dependence leads to behavior similar to the nonlocal approach. Gologanu et al. [21] and Ramaswamy and Aravas [62, 63] have studied the application of gradient plasticity together with the Gurson model. A viscoplastic formulation also introduces a characteristic length. In the context of the Gurson damage, viscoplascity is used by Needleman and Tvergaard [52] and Stainier [71].

5.3 Arbitrary Lagrangian-Eulerian Alternative

The Gurson damage model involves two major components: a yield surface that depends on the stress state, virgin yield stress and porosity level, and a law for the evolution of porosity, also dependent on stresses and strains. Thus, the results obtained applying the damage model are only as good as the displacements, stresses and strains used as input data. Modeling the problem with finite elements, the results obtained are in strong dependence on the quality of the mesh employed. In the presence of the finite strains allowed by ductile behavior, errors due to high mesh distortion can be expected. In order to improve the quality of the results some action must be taken. One possibility is to employ remeshing [11, 73]. This is a good option, but usually expensive, because it needs continuous error monitoring to define the exact moment to remesh, a good mesh generator and an experienced user to control the process. Another way of minimizing the mesh distortion is to employ an ALE formulation, in which the mesh is redefined at arbitrary steps, in an automatic way. Both methods may be combined.

Arbitrary Lagrangian-Eulerian formulation (ALE) is a strategy initially developed for hydro-codes [17, 30], and after extended to solid mechanics problems [4, 27, 29, 44, 68], enhancing the quality of the meshes in processes that occur with large deformations. The main characteristic of ALE formulation is the relative movement between finite element mesh and material points. Considering this characteristic, Eulerian and Lagrangian formulations can be understood as particular cases of ALE formulation.

As mesh and material displace independently, a value relating material velocity $v_i$ and mesh velocity $\hat{v}_i$, the convective velocity $c_i$, can be established as $c_i = v_i-\hat{v}_i$. A material rate of a function $g_i$ is defined as $g_i^\bullet = g_i^o + c_jg_{i,j}$, where $g_i^o$ represents the local variation of $f_i$ and $c_jg_{i,j}$ represent the convective effects. Considering the balance of momentum equation in the Lagrangian form and applying equilibrium conditions in the Lagrangian-Eulerian form results

$$\begin{aligned} \sigma _{ij,j} + \rho b_i = \rho \left( v_i^o+c_jv_{i,j}\right) , \end{aligned}$$

(29)

where $\rho$ is the specific mass and $b_i$ is the body force per unit mass. Applying the virtual work principle to Eq. (29) results in

$$\begin{aligned} \int \limits _V\delta u_i\left[ \sigma _{ij,j} + \rho b_i - \rho \left( v_i^o+c_jv_{i,j}\right) \right] \mathrm {d}V = 0. \end{aligned}$$

(30)

A weak form of the equilibrium conditions can be obtained,

$$\begin{aligned} \int \limits _V \rho v_i^o\delta u_i\mathrm {d}V + \int \limits _V \rho c_jv_{i,j}\delta u_i\mathrm {d}V + \int \limits _V\delta u_{i,j}\sigma _{ji}\mathrm {d}V = \int \limits _V \rho b_i \delta u_i\mathrm {d}V + \delta \int \limits _S t_i\delta u_i\mathrm {d}S . \end{aligned}$$

(31)

It is easy to see that in Eq. (31) both the mesh and material velocities are involved. In a finite element implementation, the system of equations resulting of Eq. (31) can be solved by means of two alternative strategies: (a) to define a system considering as the degrees of freedom, those corresponding to the displacements of both the mesh and the material; (b) to solve the problem in a staggered manner [7, 61]. The second alternative considers two stages at each load increment. First, the Updated Lagrange (UL) stage, with the mesh attached to the material, that ends after equilibrium is obtained. Afterwards, in the Eulerian stage, the new mesh position is defined, trying to reduce distortion, and the relevant information is transferred from the old to the new mesh.

6 Numerical Examples

The numerical examples presented in this section were obtained employing two different finite element codes. The first one [69] is a well-known commercial software. The second one, MetaFor, was developed at the University of Liège by Ponthot and Hogge [61], to treat problems of metal forming, and was used under a courtesy license. Both codes have an adequate treatment of geometrical non-linearity and contact. The Gurson model using the ALE formulation and implicit time-integration was implemented on MetaFor [12].

6.1 Indentation of a Block by a Sphere

This example analizes the punching of a block of square section by a sphere [12]. The height of the block is $100$ mm and the transversal section is $140 \times 140$ mm. The sphere has a radius of $50$ mm, and travels $50$ mm in the vertical downward direction. Because of symmetry, a quarter of the problem is modeled. The contact between block and sphere is considered as sliding, with normal penalty factor of $618$ N/m. The material of the block has elastic modulus $E = 206$ GPa, Poisson’s ratio $\nu =0.3$, density $\rho = 7500$ kg/m$^3$. Linear hardening is considered with $\sigma _\mathrm {y} = \sigma _\mathrm {y}^0 + h\varepsilon ^\mathrm {p}$ being $\sigma _\mathrm {y}^0 = 346.4$ MPa, $h = 138$ MPa. For the Gurson model $\alpha _1 = 1.5$, $\alpha _2 = 1.0$, $f_\mathrm {N} = 0.04$, $\varepsilon _\mathrm {N} = 0.5$, $s_\mathrm {N} = 0.1$, $f_\mathrm {C} = 0.15$ and $\varDelta \varepsilon = 0.3$. Results obtained employing MetaFor [61] are presented in Fig. 13, considering both UL and ALE formulations.

Fig. 13

Last configuration achieved: a UL formulation and b ALE formulation

Figure 13a shows that in the case of the UL formulation the elements in the contact zone are highly distorted. The nodes on the contact surface are distant one from another and the contact surface gets far from the spherical surface and closer to a polyhedron. The simulation came to a stop at 82 % of the proposed punch displacement with a message of negative Jacobian. With the ALE formulation, the total proposed punch displacement was attained with a good quality mesh. Figure 14 shows the final porosity distribution obtained with pressure independent void nucleation model [13].

Fig. 14

Final porosity (void volumetric fraction $vvf$) distribution obtained with ALE formulation and pressure independent void nucleation model

6.2 Analysis of Metallic Foams

Analysis of a single sphere: the finite element analysis in this section follows that in [55]. The sphere is modeled as an axisymmetric body with 375 linear quadrilateral elements. Because of symmetry considerations only one half of the sphere is modeled. The platen of the test machine is modeled as a rigid plane with prescribed displacements and the contact procedure is activated.

The sphere analyzed has an external radius of 1.0 mm and wall thickness of 0.1 mm. The material constants used are: elastic modulus $E = 200$ GPa, initial yield stress $200$ MPa and Poisson’s ratio $\nu = 0.3$. In the cases without damage (von Mises yield criterion), kinematic hardening is employed, with a hardened yield stress of $250$ MPa to a unitary plastic strain. When Gurson model is employed, hardening is considered as isotropic with the same magnitude.

Plots of macroscopic stress (defined as the ratio between the sum of the reactions in the compression direction and the surface of the circle corresponding to the projection of the undeformed sphere onto a plane) versus normalized displacement (defined as the relation between the imposed displacement to the top plane and the original radius) are given in Fig. 15.

The plot corresponding to elasto-plastic behavior coincides with Lim et al. [43] results. Two other plots, obtained with the consideration of damage are shown in Fig. 15. One simulation considers 5 % of initial porosity with no void nucleation and the other considers only 5 % void nucleation without initial porosity. In both alternatives damage accumulates in the same region of the sphere.

Fig. 15

Macroscopic stress versus normalized displacement with and without damage

Fig. 16

Final distribution of porosity starting with an initial porosity of 5 %

Figures 16 and 17 show the distribution of porosity at the end of the compression process, corresponding to a normalized displacement of 0.9. The damage parameter reaches 13.4 % when initial porosity is used (Fig. 16) and 9.8 % if only nucleation is considered (Fig. 17). These are fairly high values, but as the damage region is localized, only in small changes in the load-displacement relation (Fig. 15) are observed.

Analysis of a Representative Volume Element (RVE) representing a Metallic Hollow Sphere Structure (MHSS): In this analysis [56] two geometries are studied. The first one, in which the space among the spheres is fully occupied by resin is called syntactic. The second one, in which the space between adjacent spheres is only partially occupied by the resin is called partial. The models used in the analysis are made to fit global densities for the set resin-metal of $1.2$ g/cm$^3$ (syntactic) and $0.6$ g/cm$^3$ (partial). The metal spheres have an external radius of $1.5$ mm and the resin thickness between spheres is $0.36$ mm. The boundary conditions employed in both RVEs are shown in Fig. 18.

Fig. 17

Final distribution of porosity starting with nucleation

Fig. 18

Boundary conditions adopted in partial and syntactic morphologies

Materials constants used are $E = 110$ GPa, $\nu = 0.30$, virgin yield stress $\sigma _\mathrm {y}^0 = 300$  MPa and $\rho = 6.95$ g/cm$^3$ for the metal of the sphere and $E = 24.6$ GPa, $\nu = 0.34$, compression yield stress $\sigma _\mathrm {y}^0 = 113$ MPa, traction yield stress $\sigma _\mathrm {y}^0 = 61.5$ MPa and $\rho = 1.13$ g/cm$^3$ for the resin. Both metal sphere and matrix were modeled as elasto-plastic. Damage is considered only for the metallic spheres. The meshes presented in Fig. 19-left (partial) and in Fig. 19-right (syntactic) are employed.

Fig. 19

Meshes employed to analyze partial and syntactic morphologies

Fig. 20

Load-displacement plots for the case of partial geometry (0.6 g/cm$^3$) considering a RVE confined that keeps on a vertical plane the lateral sides of the cell and a free RVE without restrictions on the lateral sides

Figure 20 shows macroscopic stresses versus normalized displacement obtained simulating the partial geometry behavior. Experimental results [19] are also given. The abrupt changes in stiffness (points 1, 2 and 3 of Fig. 20) observed in the numerical results for a single sphere, free or confined, are due to the new contact zones that appear. This effect is not so apparent in the experimental results which correspond to a conglomerate of spheres with random geometries and properties that smoothed up such details.

Additional results may be found in [14, 54].