Temporal and Spectral Quantification of the ‘Crackle’ Component in Supersonic Jet Noise

Abstract

Measurements of the pressure waveforms along a grid in the far-field of an unheated Mach 3 jet were conducted in order to study crackle. A detection algorithm is introduced which isolates the shock-type structures in the temporal waveform that are responsible for crackle. Ensemble averages of the structures reveal symmetric shocks at shallow angles, while they appear to be asymmetric near the Mach wave angle. Spectral quantification is achieved through time–frequency analyses and shows that crackle causes the expected high-frequency energy gain. The increase in energy due to crackle is proposed as a more reliable metric for the perception of crackle, as opposed to the Skewness of the pressure or pressure derivative.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

There is practical interest in suppressing crackle as it is responsible for the excessive sound power that personnel, working in close proximity to aviation operations, are exposed to. This work aims to quantify crackle in a temporal and spectral sense, which is necessary for a systematic approach in noise reduction. The current experimental campaign, on an unheated shock-free Mach 3 jet, comprises turbulent mixing noise which consists of two components. The first is emitted by large-scale turbulence convection in the jet. These structures radiate Mach waves in a cone with half angle $\phi = { \cos }^{ - 1} (a_{\infty } /U_{c} )$, as measured from the jet axis; $U_{c}$ is the convective speed of the most energetic instability waves. The second component is associated with fine-scale turbulence, which causes an omni-directional sound pattern.

In general, nonlinear acoustic phenomena are a prerequisite to understand the noise that radiates to the far-field from jets with a supersonic convective acoustic Mach number. The topic of nonlinear acoustics governs all forms of acoustic waveform distortion in progressive waves, beyond the change in amplitude from spherical spreading $\left( {p \propto 1/r} \right)$. Two types of nonlinear effects—local and cumulative—can affect the waveform shape and create steep waveform gradients (Hamilton and Blackstock 2008); a review in the context of jet noise can be found in the dissertation by (Baars 2013). The simplest example of cumulative distortion—more pronounced with distance—is a sinusoid that gradually evolves into an N-wave when progressing through a lossless fluid. Conversely, local nonlinear distortions are instantaneous effects, such as a displacement of the source. When observing the pressure waveforms in laboratory-scale jet studies, shock-type structures (Fig. 1) are often ascribed to cumulative steepening. While this might be the case in full-scale jet noise (Gee et al. 2007), it was recently shown that it is nearly impossible to measure these cumulative effects in range-restricted environments using laboratory-scale nozzles (Baars 2013).

Fig. 1

Temporal pressure waveform of far-field jet noise indicating shock-type intermittent events that are responsible for producing crackle

The shock-type waveform structures, which are responsible for crackle, are thus the result of local nonlinear phenomena. When (Ffowcs Williams et al. 1975) investigated crackle, emitted by a static full-scale engine, they formulated it as spasmodic bursts of a rasping fricative sound. They stated that the crackle signatures are formed in the near vicinity of, or within, the turbulent jet. This statement seems to be adapted by most researchers and the current work supports this hypothesis. One of the major challenges in studying crackle are the issues of perception (Gee et al. 2007). Various observers may perceive a waveform as crackle-free, while others do not. Furthermore, there is no unique measure of crackle, i.e. only a few metrics have been applied to jet data in an attempt to assess its presence. The Skewness of the pressure’s PDF was used to establish a criterion (Ffowcs Williams et al. 1975), which has a shortcoming in the sense that the rise times of the compressive waveform parts are omitted. Henceforth, the perception of crackle may be better quantified with statistics of the pressure derivative, as was noticed by (McInerny 1996, Gee et al. 2007). This article presents a new unique measure associated with the crackle structures, based on time-preserving analyses techniques, in particular, wavelet transforms.

2 Experimental Campaign

The experiments were conducted in the fully anechoic jet facility of The University of Texas at Austin, as shown in Fig. 2 (Baars 2013). The jet under investigation comprises a Method of Characteristics contour with an exit gas dynamic Mach number of $M_{e} = 3.00$ and an exit diameter of 1 in (25.4 mm). The nozzle was operated at perfectly expanded conditions with an unheated flow $\left( {T_{0} = 2 8 8. 2\,{\text{K}}} \right)$. The convective Mach number was computed to be $M_{c} = U_{c} /a_{\infty } = 1.43$ and results in a Mach angle of $\phi = 45.6^{^\circ }$ (Baars 2013). Acoustic waveforms were acquired at a rate of 102.4 kS/s using four 1/4 in pressure-field microphones (PCB 377B10) on a translatable beam. The array was used to measure (non-synchronized) pressure waveforms on an (x, r)-grid, spanning from 5 $D_{j}$ to 145 $D_{j}$ in the axial direction and from 25 $D_{j}$ to 95 $D_{j}$ in the radial direction with a uniform spacing of 10 $D_{j}$ (Fig. 2b).

Fig. 2

a The Mach 3 nozzle assembly and translatable microphone array. b Facility plan-view with an indication of the (x,r)-grid measurement positions (○)

3 Quantifying Crackle

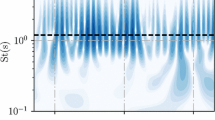
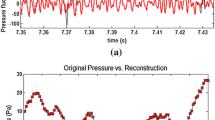
To quantify crackle in a time-preserving fashion, a Shock Detection Algorithm (SDA) is applied to identify temporal instances of sharp pressure rises in the broadband jet noise pressure waveforms. A raw waveform, $p(t)$, is shown in Fig. 3a.

Fig. 3

a Pressure waveform at location B (see Fig. 6a) and the associated PDF. b WPS of the pressure signal and the GWS and shock spectrum

The SDA finds all peaks of the pressure derivative $\dot{p}(t)$ exceeding a threshold of $T = 3 \times 10^{ - 6} \,\sigma /\left( {6{\text{d}}t} \right)$ [kPa/ms]; $\sigma$ is the pressure standard deviation and ${\text{d}}t$ is the discrete time-step of $10^{ - 5} \,{\text{s}}$. Subsequently, shocks in which the pressure jump does not exceed an amplitude of $A = 2.7\sigma$ [Pa] are omitted. The two thresholds are based on an effective acoustic shock thickness of $\Updelta x_{s} = 10^{ - 6} a_{\infty } A/T = 0.0185\;{\text{m}}$. The instances when structures were identified are marked at the top of Fig. 3a. To reveal the temporal waveform structure of crackle, an ensemble-average of all shocks is performed in a local time-frame (shock fronts aligned at $\tau = 0$) at each grid location. Fig. 4 presents the signatures at three locations. In general, shocks are point-symmetric around $\tau = 0$ at shallow angles, while they are less point-symmetric near the Mach wave angle. A contour of the average number of shocks per second is shown in Fig. 6a. The contours follow spherically spreading lines emanating from the end of the potential core (Baars 2013) and shows the absence of shock coalescence.

Fig. 4

Ensemble-averages (black –) of the individual shock structures (grey –) at three locations in the measurement grid (see Fig. 6a for a mapping). Around 6, 28, and 13 k ensemble-averages were taken at locations a θ = 20.2°, loc. A, b θ = 49.1°, loc. B, c θ = 69.8°, loc. C, respectively

The continuous Morlet wavelet transform was applied to extract the energy content as function of time and frequency; the Wavelet Power Spectrum (WPS) is shown in Fig. 3b, for the signal shown in Fig. 3a. With these results, the SDA was verified, since at the instances of shocks (white –), the spectral content is broadband, with an expected high-frequency energy gain associated with the sharp compressive parts in the waveforms. The principle of extracting a measure of the energy increase in the signal due to the presence of these crackle signatures is presented in Fig. 5.

Fig. 5

The laboratory-scale spectrum at grid location B (subscript L) is scaled down to a full-scale scenario (subscript F). Adjacent, the A-weighting is applied to the spectrum, and the shock spectrum is presented (solid black –). The percentage gain (from dashed to solid black) is shown at the bottom

The consequence of the laboratory-scale data is that high-frequency energy appears above the upper bound of the human ear (20 kHz). Therefore, the frequency is scaled down (FfowcsWilliams et al. 1975) by a factor of $\approx 12$ to replicate the perception of a full-scale scenario with the following conditions: $D_{j} = 24$ in, $M_{j} = 1.5$ and $T_{j} = 1,500\;{\text{K}}$ (constant Strouhal # scaling). A-weighting is then applied to account for the relative sound energy perceived by the human ear (Fig. 5).

The spectral content of the crackle structures is obtained by an ensemble-average of the local wavelet spectra at the instances provided by the SDA (white lines in Fig. 3b). The obtained spectrum is denoted as the shock spectrum (see Figs. 5 and 3b). The energy increase due to crackle is measured as the energy gain from the ${\text{GWS}}_{\text{F}} {\text{ - A}}$ spectrum (scaled and A-weighted; computed from the complete signal) to the shock spectrum (143 % for location B). Fig. 6b shows the gain for the entire grid. From the crackle gain contour it is observed that the shock gain is independent of the distance travelled by the sound. More importantly, this measure seems to be an appropriate metric for the perception of crackle, as is concluded from blind jury trials performed at UT Austin. The crackle is perceived dominantly at shallow angles and becomes gradually less pronounced at larger angles.

Fig. 6

a Contours of the average number of shocks/s (normalized by 1,835/s at $\left( {x,r} \right)/D_{j} = \left( {55,45} \right)$, and × 10). b The crackle gain in percentage