Latent Heat of a Traffic Model

Abstract

We have studied the optimal velocity model (Bando et al., Jpn J Indust Appl Math 11:203, 1994; Phys Rev E 51:1035, 1995; J Phys I Fr 5:1389, 1995) for highway traffic. On a microscopic level, traffic flow is described by Bando’s optimal velocity model in terms of accelerating and decelerating forces. We define an intrinsic energy of the model. We find a latent heat when the system undergoes a phase transition from single phase traffic (free flow) to a phase that contains two different, a dense and a dilute phase (congested or stop–and–go flow). Here we report on properties of the latent heat.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We have studied a model for single lane highway traffic, the so called Bando Optimal Velocity Model (OVM) [1, 2]. In the model a vehicle wants always to drive with its optimal velocity with respect to the distance to the vehicle ahead, the so called headway distance. In the model no overtaking is allowed. The model consists of a set of coupled differential equations one for each vehicle. We integrate out the equations of motion of the OVM by a Runge Kutta 4th order numerical method.

The phase diagram of the OVM consists of two phases. One is a high density phase where vehicles have a low velocity (congestion) and the other phase is a low density phase where vehicles run at nearly maximum velocity (free flow). A system can end up in one of these two phases in the entire system or it can end up in a mixed phase state. In the mixed phase state there will be two phase boundaries. The phase boundaries are either at the head of the queue where vehicles leave the congested phase or at the tail where vehicles break and enter the queue (congested phase). If there are too few vehicles in the system a high density phase will not form and all vehicles will be in the low density phase. The OVM undergoes a dynamic phase transition.

Within the framework of the OVM an energy E of the model can be defined [3] and from the energy we can calculate a latent heat E _gap for the system of cars going from a phase of low density to one with a high density.

2 The Bando Optimal Velocity Model

The Bando OVM is a deterministic model for traffic flow. It consists of a one-dimensional circular road (single lane) with periodic boundary conditions, see Fig. 1.

Fig. 1

Vehicles marked by filled circles driving on a closed loop. The arrows indicate the direction and magnitude of the velocity. Δ x is the headway distance

The set of differential equations making up the Bando OVM dynamics are:

$$\displaystyle\begin{array}{rcl} & & \mbox{ dimension}\qquad \qquad \qquad \qquad \quad \mbox{ dimensionless} \\ & & \frac{d} {\mathit{dt}}v_{i} = \frac{1} {\tau } \left (v_{\mathit{opt}}(\varDelta x_{i}) - v_{i}\right )\qquad \frac{d} {\mathit{dt}}u_{i} = \left (u_{\mathit{opt}}(\varDelta y_{i}) - y_{i}\right ){}\end{array}$$

(1a)

$$\displaystyle{ \frac{d} {\mathit{dt}}x_{i} = v_{i}\qquad \frac{d} {\mathit{dt}}y_{i} = \frac{1} {b}u_{i} }$$

(1b)

$$\displaystyle\begin{array}{rcl} & & v_{\mathit{opt}}\left (\varDelta x\right ) = v_{\mathit{max}} \frac{{(\varDelta x)}^{2}} {{D}^{2} + {(\varDelta x)}^{2}}\qquad u_{\mathit{opt}}\left (\varDelta y\right ) = \frac{{(\varDelta y)}^{2}} {1 + {(\varDelta y)}^{2}}{}\end{array}$$

(1c)

$$\displaystyle\begin{array}{rcl} & & \qquad \qquad \qquad \qquad \qquad\qquad b = \frac{D} {v_{\mathit{max}}\tau }{}\end{array}$$

(1d)

The set of three equations to the right are the dimensionless version of the equations to the left. The velocity of the car i is v _i and its position is x _i . The optimal velocity function is v _opt (Δ x). The distance to the vehicle in front, the headway distance, is denoted by $\varDelta x_{i} = x_{i+1} - x_{i}$ (bumper-to-bumper distance) and $c = N/L$ is the homogeneous density, where N is the number vehicles and L is the length of the road. Control parameters are maximal velocity of a vehicle v _max , an interaction distance D and a characteristic time τ. These three control parameters can be combined to a single parameter b in the dimensionless version.

Following [3] the acceleration of a vehicle cars can be split into two contributions

$$\displaystyle{ m \frac{d} {\mathit{dt}}v_{i} = F_{\mathit{acc}}(v_{i}) + F_{\mathit{dec}}(\varDelta x_{i}) }$$

where

$$\displaystyle\begin{array}{rcl} F_{\mathit{acc}}(v_{i})& =& \frac{m} {\tau } \left (v_{\mathit{max}} - v_{i}\right ) \geq 0{}\end{array}$$

(2a)

$$\displaystyle\begin{array}{rcl} F_{\mathit{dec}}(\varDelta x_{i})& =& \frac{m} {\tau } \left (v_{\mathit{opt}}(\varDelta x_{i}) - v_{\mathit{max}}\right )\quad \in [-v_{\mathit{max}}m/\tau,0] \leq 0{}\end{array}$$

(2b)

Adding together Eqs. (2a) and (2b) recovers Eq. (1a) from above

$$\displaystyle{ \frac{d} {\mathit{dt}}v_{i} = \frac{1} {\tau } \left (v_{\mathit{opt}}(\varDelta x_{i}) - v_{i}\right )\;. }$$

The decelerating force Eq. (2b) can be written as (using Eq. (1c))

$$\displaystyle{ F_{\mathit{dec}}(\varDelta x_{i}) = v_{\mathit{max}}\frac{m} {\tau } \left ( \frac{{(\varDelta x)}^{2}} {{D}^{2} + {(\varDelta x)}^{2}} - 1\right )\ <\ 0\;. }$$

(3)

The decelerating force will always be less then zero but approach zero at infinite head away distance Δ x and starting at $-v_{\mathit{max}}m/\tau$ at zero distance.

A potential energy V for the system of N vehicles can be defined as $V =\sum _{ i=1}^{N}\phi (\varDelta x_{i})$ where ϕ(Δ x _i ) is the interaction potential of the i-th car with the car (i + 1) ahead, which is given by (Note $F_{\mathit{dec}}(\varDelta x_{i})\neq - \partial V/\partial x_{i}$ is a violation of Newton’s 3rd law)

$$\displaystyle{ F_{\mathit{dec}}(\varDelta x_{i}) = -\frac{\partial \phi (x_{i+1} - x_{i})} {\partial x_{i}} = \frac{d\phi (\varDelta x_{i})} {d\varDelta x_{i}}. }$$

(4)

Integrating this equation gives

$$\displaystyle{ \phi (\varDelta x) = v_{\mathit{max}}\frac{D\,m} {\tau } \left [ \frac{\pi } {2} -\arctan \left ( \frac{\varDelta x} {D}\right )\right ] }$$

(5)

where the integrating constant is chosen such that ϕ(∞) = 0

The time derivative of the potential V becomes

$$\displaystyle{ \frac{dV } {\mathit{dt}} =\sum \limits _{ i=1}^{N}(v_{ i+1} - v_{i})F_{\mathit{dec}}(\varDelta x_{i})\;. }$$

(6)

The time derivative for the kinetic energy $T =\sum _{ i=1}^{N}\frac{mv_{i}^{2}} {2}$ is

$$\displaystyle{ \frac{d} {\mathit{dt}} \frac{mv_{i}^{2}} {2} = v_{i}m \frac{d} {\mathit{dt}}v_{i} = v_{i}\left (F_{\mathit{acc}}(v_{i}) + F_{\mathit{dec}}(\varDelta x_{i})\right )\;. }$$

(7)

The time derivative of the total energy $E = T + V$ and the energy flux Φ obey the following balance equation

$$\displaystyle{ \frac{\mathit{dE}} {\mathit{dt}} +\varPhi = 0 }$$

(8)

where

$$\displaystyle{ \varPhi = -\sum \limits _{i=1}^{N}\left [v_{ i}F_{\mathit{acc}}(v_{i}) + v_{i+1}F_{\mathit{dec}}(\varDelta x_{i})\right ] }$$

(9)

is the energy flux. It includes both input (from engine) and output (friction) of energy. Energy is not conserved but the driven system will reach a stationary state as time goes on.

3 Bando OVM Numerical Results

The system is started in a configuration close to the homogeneous state and as time goes on in the simulation the system ends up in one of two possible stationary states.

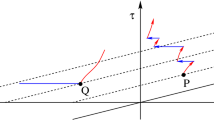
It can end up in a homogeneous flow with all vehicles traveling at the same headway distance. This solution is the fixed point Δ x _i  = Δ x _hom , $v_{i} = v_{\mathit{opt}}\left (\varDelta x_{\mathit{hom}}\right )$ and all vehicles travel with the same velocity. This would give the dashed line in Fig. 2.

The other possibility is that the system reaches a limit cycle. In this solution there is one congested part and one free flow part in the system. Vehicles leave at a steady rate the head of the queue to enter the free flow regime and after a while they will reach the tail of the queue and enter the slowly moving regime. This would give the full line in Fig. 2. Note that there is only one queue in the stationary limit cycle. If there are more queues the system is still evolving and is not stationary. In the leftmost figure in Fig. 3 the reduction of the number of queues can clearly be seen as steps in the energy E as time increases.

Fig. 2

Solution for ρ = 0. 0303 m⁻¹ solid circle. Solution for ρ = 0. 0606 m⁻¹ open circle, but this splits into a limit cycle

Integrating out the equations (Bando OVM equation (1a–1d)) the energy of the system can be calculated. As the system evolves from its initial configuration the number of queues will be reduced till the system reaches the limit solution (t → ∞). After that the energy E of the system will remain constant. In the leftmost Fig. 3 the evolution of the energy to a constant value can be seen clearly.

Fig. 3

In the left figure the solid line (larger density ρ = 0. 0606 m⁻¹) reaches the limit cycle over a series of smaller queues till finally only one queue is present. The dashed line small density ρ = 0. 0303 m⁻¹ reaches the fixed point a homogeneous system. In the right figure the energy as a function of the density of cars. The two joining points of the curves define the latent heat to go from the dense queued state to the free flow

For each particular combination of control parameters N, L and $b = \frac{D} {v_{\mathit{max}}\tau }$ a calculation is made. In the rightmost Fig. 3 one such result is shown combining several runs. In this figure there are two curves shown. Where the curves are on top of each other the system is in a homogeneous limit state. Where the two curves are separated the system is in the limit cycle. The difference in energy between the two joining positions of the curves is the energy as the system evolves from a dense homogeneous system to a dilute homogeneous system via a two phase regime. This energy difference represents a latent heat, here denoted by E _gap .

Fig. 4

In the left figure the latent energy is shown as a function of the control parameter b. In the right figure the same data as in the left figure is analyzed according to the scaling relation

In the leftmost Fig. 4 the latent heat E _gap is presented as a function of the control parameter b in Eq. (1d). The shape of the curve suggests an analysis according to a simple power law:

$$\displaystyle{ E_{\mathit{gap}} = A{(b_{c} - b)}^{\alpha }. }$$

(10)

where A is a constant and b _c is the value for b that gives a zero latent heat. In the rightmost Fig. 4 the result according to Eq. (10) is shown. As is apparent from the figure the power law seems to be fulfilled quit well. The value arrived forα = 0. 4994. The value used for b _c  = 1. 29745. The scaling is rather sensitive to small changes to b _c as the data will not join a straight line for small b _c − b.

4 Conclusions

We have shown how ideas from thermodynamics can be applied to such a many–particle system as traffic flow, based on a microscopic (car–following) description, in analogy to equilibrium physical systems like super saturated vapor forming liquid droplets.

We have calculated the latent heat of the model as the system changes from a low density phase to the a high density phase. We found the there is a scaling behavior in the latent heat for small b _c − b. Results found for the scaling exponent are α = 0. 50 and b _c  = 1. 297.