Speed Transform, a New Time-Varying Frequency Analysis Technique

Abstract

Due to the periodical motions of most machinery in steady state operation, many diagnosis techniques are based on frequency analysis. This is often performed through Fourier transform. Some extensions of these techniques to the more general case of non stationary operation have been proposed. They are based on signal processing advances such as time–frequency representations and adaptive filtering. The technique proposed in this paper is based on the observation that, when under non stationary operation, the vibrations of a machine are still tightly related to the speed variations. It is thus suggested to decompose the vibration signal over a set of time-varying frequency sine waves synchronized with the speed variations, instead of fixed frequency sine waves. This set of time-varying frequency sine waves is shown to be an orthonormal basis of the subspace it spans in the case of linear frequency variations. An insight to the improvement such decomposition can provide for spectral analysis, cyclostationary analysis and time–frequency representation is given. Some application examples are presented over both simulated signals and real-life signals.

1 Introduction

In rotating machinery, under varying rotation speed, the vibration signal is non-stationary and its statistic characteristics vary with time. For such a signal, conventional general harmonic analysis, performed through Fast Fourier Transform (FFT), doesn’t provide accurate information for the spectrum of the signal, due to the non-constant speed. In order to overcome the limitations of this technique, appropriate methods have been dedicated to varying speed cases. The best known methods are Order Tracking analysis by short-time Fourier transform (STFT) [1], windowed Fourier transform (WFT) or angular resampling [2]. These last years, new methods such as Vold Kalman filter [3] or Gabor Order Tracking approach [4] have been introduced. The main characteristic of these methods is that they are based on resampling scheme or sampled STFT. However in many cases, all previous techniques have limited resolution or show a number of gaps [5]. For the STFT, depending on the window used, analysis quality may be affected. Regarding the angular resampling of the vibration signal, its drawback is that the resonance frequencies of the rotating machine are disturbed by the process.

In order to avoid the previous shortcomings, we propose a new technique called Speed Transform (ST) when the speed varies linearly. This new approach consists in expanding the vibration signal into a series of elementary oscillatory functions, whose frequencies depend on the variation of the speed. The main advantage of the new approach is that it adapts to the vibration signal and components so that the resonance frequencies are preserved.

The paper is organized as follows. In Sect. 2, ST is presented in both theoretical and practical implementation aspects. In Sect. 3, ST is applied to simulated data and in Sect. 4 it is applied to real-life data. Our conclusion is presented in Sect. 5.

2 Speed Transform, Theory and Practical Implementation

Applying Fourier analysis to a signal consists in decomposing that signal over a basis of elementary oscillatory functions. The definition of the Fourier transform of a signal $s(t)$ is well known and is given by:

$$ S\left( f \right) = \mathop \smallint \limits_{ - \infty }^{ + \infty } s(t)\;e^{ - 2\pi jft} dt $$

(1)

where the Fourier transform of the signal $s(t)$ is denoted by $S(f)$, $t$ stands for time and $f$ for frequency. When actually applied to vibration signals, it usually comes to a slightly different tool that can be described by:

$$ S\left( f \right) = \frac{1}{2T}\mathop \smallint \limits_{ - T}^{ + T} s(t)\;e^{ - 2\pi jft} dt $$

(2)

It thus consists in evaluating the closeness of the signal $s(t)$ to a set of elementary oscillatory functions $e^{2\pi jft}$ over a finite time interval T, or in other terms, evaluating a mean contribution of each of these $e^{2\pi jft}$ functions to the signal over that interval. In what follows, this practical tool will be considered as Fourier transform.

The tool described by Eq. (2) exhibits a nice asymptotic property. Let us evaluate the closeness of two functions of the basis $e^{{2\pi jf_{1} t}}$ and $e^{{2\pi jf_{2} t}}$ when the time interval tends to infinity, i.e.:

$$ \mathop {\lim }\limits_{T \to + \infty } \frac{1}{2T}\mathop \smallint \limits_{ - T}^{ + T} e^{{ - 2\pi jf_{1} t}} \;e^{{ + 2\pi jf_{2} t}} \;dt = \left[ {\begin{array}{*{20}c} {0\, for\, f_{1} \ne f_{2} } \\ {1\, for\, f_{1} = f_{2} } \\ \end{array} } \right. $$

(3)

This is equal to zero for $f_{1} \ne f_{2}$ (cross terms) and equal to one for $f_{1} \ne f_{2}$ (auto terms). This property allows to evaluate the contribution of any $e^{2\pi jft}$ function to the signal by applying Eq. (2), provided that the time interval is long enough to ensure that the cross-terms vanish.

This tool is thus well fitted to the physical nature of vibration signals under stationary operation. Indeed, the periodical movements of machinery generate periodical components within the temporal moments of the signals. Due to the nice property described by Eq. (3) these periodical components produce spectral lines through Fourier analysis.

Under non stationary operation, Fourier analysis keeps its nice mathematical properties but does not fit any more to the physical model of the data. Indeed, many components of the vibration signal follow the speed variations, so that they are not any more periodic. All the components that are tied to the rotation frequency of the machine spread over a frequency band. Retrieving their amplitude or even detecting them through Fourier analysis thus becomes difficult.

This is why we propose to use a basis of elementary oscillatory functions whose frequencies follow the speed variations. This would allow preserving the main advantage of frequency analysis, which is to fit to the physical model of the data. But what about the mathematical properties of the decomposition over such a time-varying basis? More precisely, do a set of $e^{{2\pi j {\smallint \limits_{0} ^ {t}}\Delta f(u)\,du}}$ functions, whose frequencies $n {{\Updelta}}f(t)$ follow the speed variations, still exhibit the property described by Eq. (3)? We showed (see appendix) that provided the variations of $n{{\Updelta}}f\left( t \right)$ are linear versus time, that mathematical property still holds.

Let us give some specifications for this new analysis tool that will be called speed transform:

• first, the frequencies of the basis functions should all be proportional to the speed variations,

• their frequencies must always be smaller than the Nyquist frequency,

• they should be equi-spaced over the analysis band, in terms of proportion of the rotation speed, rather than in terms of frequency band,

• they should be equi-spaced with such step $\Updelta f\left( t \right)$ that no component tied to the rotation speed could be missed in the analysis interval.

In order to satisfy these specifications, let us first define some expressions: $r\left( t \right)$ will stand for the rotation speed in Hertz and $T = NT_{e}$ for the duration of the vibration signal, with N the total number of samples and $f_{e}$ the sampling period. The different parameters used to generate the basis are shown on Fig. 1. The rotation frequency (in green) and the basis functions frequencies (blue) are represented versus the number of samples in reduced frequency.

Fig. 1

Frequencies of the basis functions

The example is given for a $N\, = \,64$ samples base, with speed variations in reduced frequency given by $r\left( t \right) = 0.1\, + \,0.001*t$. The green plot represents the rotation frequency variation $r\left( t \right)$ and the red one represents the time-varying frequency resolution $\Updelta f\left( t \right)$ of the speed transform. It is proportional to $r\left( t \right)$ and the proportionality coefficient is an integer value k such that $r\left( t \right) = k\Updelta f\left( t \right)$ and $max\left\{ {\Updelta f\left( t \right)} \right\} \le \frac{1}{T}$ in order to have a sufficient resolution not to miss any component. The basis B is composed of $\frac{N}{2} + 1 = 33$ oscillatory functions $b_{n} \left( t \right)$ calculated as follows:

$$ B = \left[ {b_{n} \left( t \right) = e^{2\pi jn \smallint \limits_{0}^{t} \Updelta f\left( u \right)\,du} , 0 \le n \le N/2} \right] $$

(4)

On Fig. 2 is displayed the modulus of the basis correlation matrix. As expected from theory, it is a diagonal matrix with unitary diagonal terms. The non diagonal terms should be zero but some side effects appear due to the fact that the basis functions are finite length. These side effects can be minimized by applying an apodisation window, such as Hamming window, as shown on Fig. 3.

Fig. 2

Modulus of the correlation matrix of the basis

Fig. 3

Modulus of the correlation matrix of the basis computed with apodisation

As usual, the shape of the main lobe and side-lobes depends on the apodisation window. The width of the main lobe and the maximum speed resolution $max\left\{ {\Updelta f\left( t \right)} \right\}$ are both related to the inverse of the length of the signal. This ensures that one of the calculated samples at least will be located on the main lobe. This prevents any component whose variations are not a integer multiples of $\Updelta f\left( t \right)$ from not being detected. In order to improve the amplitude estimation of these components some interpolation can be applied, as in classical spectral analysis.

3 Application to Simulated Data

We first applied this technique to the analysis of simulated toothed gearing vibrations. The features of the simulated experiment are the following ones:

• the two wheels are respectively 20 and 22 toothed ones,

• the rotation frequency of the 20 toothed wheel is variable and given by $f_{20} \left( t \right)\, = \,16\, + \,3 t$, the gearing frequency by $f_{eng} \left( t \right) = 20 f_{20} \left( t \right)$ and the 22 toothed wheel frequency by $f_{22} \left( t \right) = f_{eng} \left( t \right)/22$.

• the vibration signal is given by $s\left( t \right) = s_{eng} \left( t \right) \left( {s_{20} \left( t \right) + s_{22} \left( t \right)} \right)$ with:

• $s_{eng} \left( t \right) = \cos \left( {2\pi \smallint \limits_{0}^{t} f_{eng} (u) du \left( t \right)t + \varphi_{eng} } \right)$ where $\varphi_{eng}$ is a random phase

• $s_{20} \left( t \right) = \mathop \sum \limits_{m = 1}^{8} \cos \left( {2\pi m\smallint \limits_{0}^{t}f_{20} \left( u \right)du + \varphi_{20,m} } \right)$ with $\varphi_{20,m}$ random (resp. $s_{22} \left( t \right)$, $f_{22} \left( t \right)$ and $\varphi_{22,m}$).

• the total number of available samples is $N = 20000$, i. e. a 1s time interval.

The amplitude spectrum of this simulated signal is displayed on Fig. 4. It was calculated by applying a 65,536 sample Fourier transform over the whole signal, with a Hamming apodisation window. Due to the speed variation, the energy of the gearing fundamental and its sidebands spread over several frequency channels. Only the lowest frequencies, corresponding to the inferior sidebands of the 36 toothed wheel modulation, can be separated. This comes from the fact that their frequencies are varying slower than that of the higher frequency components. Nevertheless, though they can be separated, the amplitude displayed on the spectrum is erroneous, since the energy of each sideband is spread over several neighboring frequency channels.

Fig. 4

Amplitude spectrum of the simulated toothed gearing vibration signal

This problem cannot be totally overcome by the use of time–frequency distributions. Two spectrograms were calculated with different frequency resolutions. The spectrogram displayed on Fig. 5 was computed over slices of 1,024 samples, Hamming windowing and a¾ of a slice overlap. The frequency resolution is thus $\Updelta f = 19.53\,Hz$ and the temporal resolution $\Updelta t = 0.05\,s$, which would be enough to follow the temporal variations of the speed but does not allow separating the sidebands. Whereas the second spectrogram (Fig. 6), calculated the same way but over 8,192 sample slices, not only fails to follow the temporal variations ($\Updelta t = 0.4\,s$) but cannot either separate the sidebands, despite a better frequency resolution ($\Updelta f = 2.44\,Hz$), because the sidebands spread over neighboring frequency channels.

Fig. 5

Spectrogram of the vibration signal computed over 1024 sample slices

Fig. 6

Spectrogram of the vibration signal computed over 8192 sample slices

Whereas the speed transform of the signal, displayed on Fig. 7, succeeds in separating all the sidebands and estimating their amplitude. Instead of being represented versus frequency, it is represented versus the proportion of the speed signal that was used to build the speed transform basis. Here the speed signal was that of the 20 toothed wheel, so that all the sidebands corresponding to that wheel appear at harmonic positions of the speed signal. The transform was computed over the whole signal with Hamming windowing and interpolated by 8.

Fig. 7

Speed transform (in black) displayed versus the proportion of the 20 toothed wheel rotation frequency. Green lines are the true 22 toothed sidebands and red ones the true gearing fundamental and true 20 toothed sidebands

4 Application to Real-Life Data

Here the speed transform is applied to the vibration signal of a diesel engine.

In order to build the basis functions $b_{n} \left( t \right) = e^{{2\pi jn\smallint \limits_{0}^{t} \frac {r (u)}{K} du}}$ we first need to estimate from the tachometer signal the function $g\left( t \right) = 2\pi \smallint \limits_{0}^{t}r\left( u \right)\,du$, i.e. the angular position of the shaft, if we suppose that it is zero for $t = 0$. This can be easily done based on the following properties:

• $g\left( t \right)$ must be an order 2 polynomial

• It must be such that $sin\left( {g\left( t \right)} \right) = 0$ at each tick of the tachometer signal

A curve is built by associating an integer multiple of 2π to each tick time and a curve fitting procedure allows finding the order 2 polynomial fitted to that curve. The coefficients of this polynomial are then used to compute the value of $g\left( t \right)$ at any time t.

The speed transform has first been computed on the time interval between 30.6 and 32 s, where the rotation frequency is stationary and equal to 75 Hz (see Fig. 8), in order to compare the result to Fourier transform.

Fig. 8

The rotation speed of the diesel engine estimated from the tachometer signal

The amplitude spectrum and the speed transform calculated on that interval are displayed on Figs. 9 and 10. This confirms that the usual Fourier transform is actually a particular case of the proposed speed transform. Note however a slight improvement of the latter as compared to the former due to the compensation of small speed fluctuations.

Fig. 9

The Amplitude spectrum and speed transform calculated between 30.6 and 32 s

Fig. 10

Zoom on the high frequencies

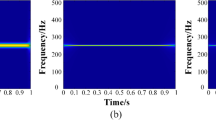
The technique has then been applied between 25 and 30 s, i.e., on a time interval where the speed is linearly increasing. The amplitude spectrum and speed transform are displayed on Figs. 11, 12 and 13. The capability of the speed transform to adjust to linear speed variations is clearly demonstrated, even in the high frequency range. Whereas one can only distinguish the H2 harmonic (firing frequency of the engine) in the Fourier transform, all multiples of the H1 (crankshaft rotation) and H1/2 (thermodynamic cycle) are visible in the speed transform. This opens a valuable perspective for order tracking at virtually no cost as compared to other techniques, such as those based on time-varying filters or angular resampling preconditioning.

Fig. 11

The Amplitude spectrum and speed transform calculated between 25 s and 30 s

Fig. 12

Zoom on the low frequencies

Fig. 13

Zoom on the high frequencies

5 Conclusion

Fourier analysis plays a prominent role in the vibration analysis of rotating machines. Strictly speaking, it applies only to the situation where the machine is rotating at exactly constant speed. The extension of Fourier analysis to non-stationary operation is a current and active field of research. Whereas valuable solutions exist, for instance based on angular resampling, this paper proposed a new speed transform which inherits all the properties of the Fourier transform—in particular the orthonormality of its functional basis—when applied to linear speed variations. This not only has the advantage of simplicity, but it also returns properly scaled results. The speed transform has potential in several applications, and in particular in order tracking. Due to its resemblance to Fourier analysis, it opens a bunch of signal processing possibilities dedicated to non-stationary signals, such as non-stationary demodulation, non-stationary envelope analysis, cyclo-non-stationary analysis, etc. A short-time version of the speed transform is also conceivable to track arbitrary speed variations that can be approximated as piece-wise linear.

Appendix

We are interested in:

$$ \mathop {\lim }\limits_{T \to \infty } I\left( T \right) $$

where:

$$ {\text{I}}\left( {\text{T}} \right) = \frac{1}{2T}\mathop \smallint \limits_{ - T}^{T} e^{{2\pi j\left( {f_{1} \left( t \right) - f_{2} \left( t \right)} \right)t}} dt $$

Let us suppose that the variations of $f_{1} \left( t \right)$ and $f_{2} \left( t \right)$ are linear. In this case, there exist $\alpha \,et\,\beta$ such that:

$$ f_{1} \left( t \right) - f_{2} \left( t \right) = 2\alpha t + \beta $$

Which leads to:

$$ \begin{gathered} I\left( T \right) = \frac{1}{2T}\mathop \smallint \limits_{ - T}^{T} e^{{2\pi j\left( {\alpha t^{2} + \beta t} \right)}} dt \hfill \\ I\left( T \right) = \frac{1}{2T}\mathop \smallint \limits_{ - T}^{T} e^{{2\pi j\left( {\alpha \left( {t + \frac{\beta }{2\alpha }} \right)^{2} - \frac{{\beta^{2} }}{4\alpha }} \right)}} dt = \frac{1}{2T}e^{{ - 2\pi j\frac{{\beta^{2} }}{4\alpha }}} \mathop \smallint \limits_{ - T}^{T} e^{{2\pi j\left( {\alpha \left( {t + \frac{\beta }{2\alpha }} \right)^{2} } \right)}} dt \hfill \\ \end{gathered} $$

The variable is changed from t to x:

$$ \left|{\begin{array}{*{20}{l}} x &= t + \frac{\beta }{2\alpha } \\ dt &= dx \\ - T &+ \frac{\beta }{2\alpha } \le x \le T + \frac{\beta }{2\alpha } \end{array}}\right.$$

Which leads to:

$$ I\left( T \right) = \frac{1}{2T}e^{{ - 2\pi j\frac{{\beta^{2} }}{4\alpha }}} \mathop \smallint \limits_{{ - T + \frac{\beta }{2\alpha }}}^{{T + \frac{\beta }{2\alpha }}} e^{{2\pi j\alpha x^{2} }} dx $$

The integral can be decomposed into three parts:

$$ \mathop \smallint \limits_{{ - T + \frac{\beta }{2\alpha }}}^{{T + \frac{\beta }{2\alpha }}} e^{{2\pi j\alpha x^{2} }} dx = I_{1} + I_{2} + I_{3} $$

with:

$$\left|{\begin{array}{*{20}{l}} {I_{1} = \mathop \smallint \limits_{{ - T + \frac{\beta }{2\alpha }}}^{ - T} e^{{2\pi j\alpha x^{2} }} dx } \\ {I_{2} = \mathop \smallint \limits_{ - T}^{ - T} e^{{2\pi j\alpha x^{2} }} dx } \\{ I_{3} = \mathop \smallint \limits_{T}^{{T + \frac{\beta }{2\alpha }}} e^{{2\pi j\alpha x^{2} }} dx}\end{array}}\right. $$

The integrals $I_{1}$ et $I_{3}$ are finite so that the only problem is to calculate:

$$ \mathop {\lim }\limits_{T \to \infty } \frac{1}{2T}e^{{ - 2\pi j\frac{{\beta^{2} }}{4\alpha }}} I_{2} \left( T \right) $$

Let ${\text{J}}\left( {\text{T}} \right) = \mathop \smallint \limits_{ - T}^{T} e^{{2\pi j\alpha t^{2} }} dt$

$$ \mathop {\lim }\limits_{{{\text{T}} \to + \infty }} {\text{J}}\left( {\text{T}} \right) = J_{\infty } = \mathop \smallint \limits_{ - \infty }^{ + \infty } e^{{2\pi j\alpha t^{2} }} dt $$

Let us change variable t to: $u = \sqrt {2\pi \alpha } \,t$

The expression becomes:

$$ J_{\infty } = \frac{1}{{\sqrt {2\pi \alpha } }}\mathop \smallint \limits_{ - \infty }^{ + \infty } e^{{ju^{2} }} du = \frac{1}{{\sqrt {2\pi \alpha } }}2\mathop \smallint \limits_{0}^{ + \infty } e^{{ju^{2} }} du $$

Which is proportional to the well known Fresnel integral: $\mathop \smallint \limits_{0}^{ + \infty } e^{{ju^{2} }} du = \frac{\sqrt \pi }{2}e^{{j\frac{\pi }{4}}}$

So that $J_{\infty } = \frac{1}{{\sqrt {2\alpha } }}e^{{j\frac{\pi }{4}}}$

This proves that $\mathop {\lim }\limits_{T \to \infty } I\left( T \right) = 0$ whenever $f_{1} \left( t \right) - f_{2} \left( t \right) \ne 0$

If $f_{1} \left( t \right) - f_{2} \left( t \right) = 0$, it is easy to show that $I\left( T \right) = 1$ for any value of T.