Experimental Study on Improved Differential Evolution for System Identification of Hammerstein Model and Wiener Model

Abstract

For nonlinear system of the Hammerstein model and Wiener model, a method for nonlinear system identification is proposed based on differential evolution Algorithm (DE). The based idea of the method is that the problem of nonlinear system identification is changed into optimization problems in parameter space. In order to enhance the performance of the DE identification, put forward a kind of adaptive mutation differential evolution algorithm for scaling factor (MDE), and on this basis, we make an improvement on crossover to make a better performance. To make an analysis for particle swarm optimization (PSO), DE and improved DE, the improvement DE has higher accurate and recognition ability, stronger convergence.

8.1 Introduction

For the linear system identification, theoretical studies have tended to mature, but in real life, actual system is almost nonlinear system, so the research for nonlinear system is necessary [1]. The Wiener model and Hammerstein model [2] which Narendra and Gallman proposed not only simple but also can effectively describe the nonlinear characteristics of dynamic system. Literature [3] based on PSO has a identification for Hammerstein model, although the algorithm has a good robustness, the running speed of the program is relatively slow; Literature [4] based on PSO has a identification for Hammerstein model, QPSO algorithm has more strong nonlinear recognition ability, the program running time is also relatively fast, however, to some extent, identification of the complexity of the operation increased.

Differential evolution (DE) algorithm was first introduced by Storn and Price for global optimization in 1995 [5], as a stochastic global optimizer, DE has appeared as a simple and very efficient optimization technique. The DE’s advantages are easy to implement, require a few control parameters turning and exhibit fast convergence. The DE algorithm is a population-based algorithm using the following operators: crossover, mutation and selection. In recent years, DE is widely applied in neural network [6], parameter identification [7], function optimization [8, 9] and constraint optimization problem [10, 11] and other areas. However, it has been observed that the convergence rate of DE do not meet the expectation in cases of highly multimodal problems. Several variants of DE have been proposed to improve its performance.

8.2 Differential Evolution

In this section we will describe briefly the working of basic DE. Compared with other evolutionary algorithms (EA), DE is a simple yet powerful optimizer with fewer parameters [12]. Scale factor (F) and crossover rate (CR) are two very important control parameters of DE. Setting the parameters to inappropriate values may not only deteriorate the search efficiency, but also lead to solutions with poor quality. Differential evolution’s basic steps can be described as follows [13]:

Mutation operation: The mutation operation of DE applies the vector differentials between the existing population members for determining both the degree and direction of perturbation applied to the individual subject of the mutation operation. The mutation process at each generation begins by randomly selecting three individuals $X_{r1,G} ,$$X_{r2,G}$ and $X_{r3,G} ,$ in the population set of NP elements. The $i{\text{th}}$ perturbed individual, $V_{i,G + 1} ,$ is generated based on the three chosen individuals as follows:

$$ V_{i,G + 1} = X_{r3,G} + F*\left( {X_{r1,G} - X_{r2,G} } \right) $$

(8.1)

where, $i = 1 \cdots NP,$$r{}_{1},r_{2} ,r_{3} \in \left\{ {1 \cdots NP} \right\}$ are randomly selected such that $r_{1} \ne r_{2} \ne r_{3} \ne i,$ F is the control parameter such that $F \in \left[ {0, + 1} \right] .$

Crossover operation: once the mutant vector is generated, the perturbed individual, $V_{i,G + 1} = \left( {V_{1,i,G + 1}, \ldots , V_{n,i,G + 1} } \right) ,$ and the current population member, $X_{i,G} = \left( {X_{1,i,G}, \ldots X_{n,i,G} } \right) ,$ are then subject to the crossover operation, that finally generates the population of candidates, or “trial” vectors, $U_{i,G + 1} = \left( {u_{1,i,G + 1} , \ldots ,u_{n,i,G + 1} } \right) ,$ as follows:

$$ u_{{j,i,G + 1}} = \left\{ {\begin{array}{*{20}c} {v_{{j,i,G + 1}} } & {if\;rand_{j}\, \le\, C_{r} \vee j = k} \\ {x_{{j,i,G}} } & {otherwise} \\ \end{array} } \right. $$

(8.2)

where, $j = 1 \cdots n,\;\;k \in \left\{ {1 \cdots n} \right\}$ is a random parameter’s index, chosen once for each i. The crossover rate, $C_{r} \in \left[ {0,1} \right] ,$ is set by the user.

Selection operation: If the new individual is better than the original one then the new individual is to be an offspring n the next generation $G = t + 1$ else the new individual is discarded and the original one is retained in the next generation.

$$ X_{{i,G + 1}} = \left\{ {\begin{array}{*{20}c} {U_{{i,G + 1}} } & {if\,f\left( {U_{{i,G + 1}} } \right) \le f\left( {X_{{i,G}} } \right)} \\ {X_{{i,G}} } & {otherwise} \\ \end{array} } \right. $$

(8.3)

where, $f\left( {} \right)$ is the fitness function. Each individual of the temporary population is compared with its counterpart in the current population. The one with the lower projective function value will survive generation.

8.2.1 Improvement of DE

To make DE more efficient for different scenarios, efforts are needed to improve its performance and a chaotic algorithm, simulated annealing algorithm or some adaptive methods have been applied in DE.

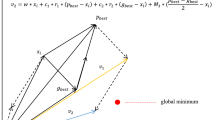
• A. In the differential evolution algorithm, the constant of differentiation $F$ is a scaling factor of the difference vector. It is an important parameter that controls the evolving rate of the population. One of the most useful differential evolution strategies are described in the following.

It is proposed a adaptive scaling factor formula [14]:

$$ M = F_{0} * 2^{\lambda } \quad \lambda = e^{{\left( {1 - \frac{T}{T + 1 - t}} \right)}} $$

(8.4)

where $F_{0}$ is the initial scaling factor, T is the number of iterations and t is the current evolution number. Early in the algorithm, $\lambda = 1,$ make the $M = 2F_{0} ,$ the improvement called MDE.

Early in the algorithm, adaptive mutation operator was $F_{0} - 2F_{0} ,$ it has great value and makes the individuals diversity in the population at the initial generations to overcome the premature. With the algorithm progress, mutation operator gradually reduced, mutation rates is closed to $F_{0}$ later, preserve the excellent individuals, enhance the probability of obtaining the global optimum.

• B. As mentioned in the above subsection, $CR$ is a very important control parameters of DE. At early stage, the diversity of population is large because the population individuals are all different from each other. Small values of $CR$ increase the possibility of stagnation and slow down the search process. On the other hand, if the $CR$ value is relatively high, this will increase the population diversity and improve the convergence. Therefore, the $CR$ must take a suitable value in order to avoid the premature convergence or slow convergence rate. Based on the analysis above, in order to balance between the diversity and the convergence rate, a dynamic nonlinear increased crossover probability method was proposed, which is called KDE, formula is as follows [15]:

$$ CR = CR_{\hbox{max} } + (CR_{\hbox{min} } - CR_{\hbox{max} } ) * (1 - count/gen\_\hbox{max} )^{k} $$

(8.5)

Which $count$ is the current generation number, $gen\_\hbox{max}$ is the maximum number of generations, $CR_{\hbox{min} }$ and $CR_{\hbox{max} }$ denote the maximum and minimum value of the $CR ,$ and $k$ is a positive number. The optimal setting for these parameters are $CR_{\hbox{min} } = 0.5,$$CR_{\hbox{max} } = 0.55$ and $k = 4 .$

In this paper, a new method is put forward. Combining the two kinds of methods include KDE and MDE, which have mentioned above, trying to combine MDE and KDE, make use of MDE can increase the global search of the optimal value of the probability and KDE has a good performance in accuracy.

8.2.2 Hammerstein Model and Wiener Model

• A. Hammerstein model is a special kind of nonlinear system, the structure series composition by a no memory nonlinear gain link and a dynamic linear link, as Fig 8.1 show.

  Fig. 8.1

  

  Hammerstein model

The difference equation of Hammerstein model expressed as:

$$ \left\{ {\begin{array}{*{20}l} {A(q^{{ - 1}} )y(k) = B(q^{{ - 1}} )x(k) + C(q^{{ - 1}} )w(k)} \hfill \\ {x(k) = f(u(k)) = u\left( k \right) + r_{2} u^{2} (k) + \cdots + r_{p} u^{p} (k)} \hfill \\ {A(q^{{ - 1}} ) = 1 + a_{1} q^{{ - 1}} + \cdots + a_{n} q^{{ - n}} } \hfill \\ {B(q^{{ - 1}} ) = b_{0} + b_{1} q^{{ - 1}} + \cdots + b_{t} q^{{ - t}} } \hfill \\ {C(q^{{ - 1}} ) = 1 + c_{1} q^{{ - 1}} + \cdots + c_{m} q^{{ - m}} } \hfill \\ \end{array} } \right. $$

(8.6)

Among them $u(k)$and $y(k)$ are identification system input and output sequence; $w(k)$ is the Gaussian white noise sequence with zero-mean and variance of $\sigma^{2} ,$ $u(k)$and $w(k)$ independent; $x(k)$ is unmeasured intermediate input signal, it is not only linear dynamic input but also the output of the nonlinear part. $q^{ - 1}$ for lag operator, $A(q^{ - 1} )$ $B(q^{ - 1} )$ and $C(q^{ - 1} )$ are lagging operator polynomial; $f( \cdot )$ is no memory for the nonlinear gain. Introducing parameter vector for $\theta_{1} = \left[ {a_{1\;} \;a_{2} \cdots a_{n} \;b_{1} \;b_{2} \cdots b_{t} \;c_{1} \;c_{2} \cdots c_{m} \;r_{1} \;r_{2} \cdots r_{p} } \right]^{T} ,$ identify target is based on a given input $u(k)$ and system output $y(k)$ estimate parameter vector $\theta_{1} ,$ set the estimate of parameter vector $\theta_{1} ,$ $\mathop {\theta_{1} }\limits^{ \wedge } = \left[ {\mathop {a_{1} }\limits^{ \wedge } \;\mathop {a_{2} }\limits^{ \wedge } \cdots \mathop {a_{n} }\limits^{ \wedge } {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {b_{1} \;}\limits^{ \wedge } \mathop {b_{2} }\limits^{ \wedge } \cdots \mathop {b_{t} }\limits^{ \wedge } {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {c_{1} }\limits^{ \wedge } {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {c_{2} }\limits^{ \wedge } \cdots \mathop {c_{m} }\limits^{ \wedge } {\kern 1pt} {\kern 1pt} \mathop {r_{1} \;}\limits^{ \wedge } \mathop {r_{2} }\limits^{ \wedge } \cdots \mathop {r_{p} }\limits^{ \wedge } } \right]^{T}$.

• B. Wiener model is a special kind of nonlinear system, the structure series composition by a no memory nonlinear gain link and a dynamic linear link, as Fig 8.2 shows.

  Fig. 8.2

  

  Wiener model

The difference equation of Wiener model expressed as:

$$ \left\{ \begin{gathered} A(q^{{ - 1}} )z(k) = q^{{ - d}} B(q^{{ - 1}} )u(k) \hfill \\ y(k) = f[z(k)] + e(k) \hfill \\ A(q^{{ - 1}} ) = 1 + a_{1} q^{{ - 1}} + \cdot \cdot \cdot + a_{n} q^{{ - n}} \hfill \\ B(q^{{ - 1}} ) = b_{0} + b_{1} q^{{ - 1}} + \cdot \cdot \cdot + b_{t} q^{{ - t}} \hfill \\ \end{gathered} \right. $$

(8.7)

Among them $u(k)$ and $y(k)$ are identification system input and output sequence, $e(k)$ is white Gaussian noise, $z(k)$ is the linear part of the output. Definition parameter variables $\theta_{2} = [a_{1} \cdot \cdot \cdot a_{n} \mathop {}\limits_{{}}^{{}} b_{0} \cdot \cdot \cdot b_{t} ]^{T} ,$ identify target is based on a given input $u(k)$ and system output $y(k)$ estimate parameter vector $\theta_{2} ,$ set the estimate of parameter vector $\theta_{2} ,$ $\hat{\theta }_{2} = [\hat{a}_{1} \cdot \cdot \cdot \hat{a}_{n} \mathop {}\limits_{{}}^{{}} \hat{b}_{0} \cdot \cdot \cdot \hat{b}_{t} ]^{T} .$

The estimate of the deviation can use the following criterion function to measure.

$$ J(k) =\; \sum\limits_{i = 0}^{L} {\left[ {y(k - i) - \mathop y\limits^{ \wedge } (k - i)} \right]}^{2} $$

(8.8)

The L for identification window length, $y(k - i)$ $\mathop y\limits^{ \wedge } (k - i)$ is $k - i(i = 1, \ldots L)$ moment output measurement signal and estimate.

8.3 Experiment Study

8.3.1 Test Function Used in Simulation Studies

In this paper, aim at the problem of Hammerstein model, using PSO, DE and improved DE do some simulation. For PSO, study gene $c_{1} = 2,c_{2} = 1.6,$ inertia weight $w$ linear decreases along with the iteration times 0.4 from 0.9, maximum speed limit in 1; For DE, the scale factor $F = 0.5$ and the crossover probability $CR = 0.3;$ for MDE, $F_{0} = 0.1 ,$ and $CR = 0.4 ;$ for MKDE, $F_{0} = 0.3,$ $CR_{\hbox{min} } = 0.3,$ $CR_{\hbox{max} } = 0.55.$ population size (NP) between $5 D$ and $10 D,$ D is the number of the goal function decision variables, no less than 4, this lab take $NP = 40,$ the maximum iterations are for 1,200. Each differential evolution algorithm based on each improvement is run 20 times, the results are presented in Tables 8.1, 8.2, where various standard statistical measures including mean, minimum and RMSE. The Hammerstein model select is as follows:

$$ \left\{ {\begin{array}{ll} {A(q^{ - 1} )y(k) = B(q^{ - 1} )x(k) + C(q^{ - 1} )w(k)} \\ {x(k) = f(u(k)) = u(k) + 0.5u^{2} (k) + 0.3u^{3} (k) + 0.1u^{4} (k)} \\ {A(q^{ - 1} ) = 1 - 1.5q^{ - 1} + 0.7q^{ - 2} } \\ {B(q^{ - } ) = q^{ - 1} + 0.5q^{ - 2} } \\ {C(q^{ - 1} ) = 1 + 1.5q^{ - 1} } \\\end{array}} \right. $$

(8.9)

Table 8.1 The numerical comparison of four kinds of algorithm for Hammerstein model

Table 8.2 The numerical comparison of four kinds of algorithm for Wiener model

Wiener model select is as follows:

$$ \left\{ {\begin{array}{*{20}c} {x\left( k \right) = 15x\left( {k - 1} \right) - 07x\left( {k - 2} \right) + u\left( {k - 1} \right) + 0.5u\left( {k - 2} \right)} \hfill \\ {\qquad \qquad \qquad y\left( k \right) = f\left[ {x\left( k \right)} \right] + e\left( k \right),} \hfill \\ {\qquad \qquad f\left[ {x\left( k \right)} \right] = \left\{ \begin{gathered} \sqrt {x\left( k \right)/2,} \:x\left( k \right) \ge 0, \hfill \\ - \sqrt { - x\left( k \right)/2,} \:x\left( k \right) > 0 \hfill \\ \end{gathered} \right.} \hfill \\ \end{array} } \right. $$

(8.10)

The input signal $u(k)$ is zero-mean, variance is 1 of the Gaussian white noise sequence, $w(k)$ is Gaussian white noise which variance is 0.1, identify window width is 500, to identify the parameters of the true value vector is, $\theta_{ 1} = [ { - 1} . 5{\kern 1pt} {\kern 1pt} 0. 7{\kern 1pt} {\kern 1pt} 1. 0{\kern 1pt} {\kern 1pt} 0. 5{\kern 1pt} {\kern 1pt} 1. 5{\kern 1pt} {\kern 1pt} 0. 5{\kern 1pt} {\kern 1pt} 0. 3{\kern 1pt} {\kern 1pt} 0. 1 ]^{\text{T}} ,$ $\theta_{2} = [ { - 1} . 5{\kern 1pt} {\kern 1pt} 0. 7{\kern 1pt} {\kern 1pt} 1. 0{\kern 1pt} {\kern 1pt} 0. 5 ]^{\text{T}} .$ In simulation experiments, define root mean square error (RMSE) to measure precision.

$$ RMSE = \sqrt {\frac{{\sum\limits_{j = 1}^{L} {\left[ {y(j) - \mathop {y(j)}\limits^{ \wedge } } \right]^{2} } }}{L}} $$

(8.11)

8.3.2 Experimental Results

The experiment works on MATLAB7.1 software simulation platform. For Hammerstein model, There are 8 parameters ($a_{1} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} b_{1} {\kern 1pt} {\kern 1pt} b_{2} {\kern 1pt} {\kern 1pt} c_{1} {\kern 1pt} {\kern 1pt} r_{1} {\kern 1pt} {\kern 1pt} r_{2} {\kern 1pt} r_{3}$), this paper drawing results put five linear parameters ($a_{1} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} b_{1} {\kern 1pt} {\kern 1pt} b_{2} {\kern 1pt} {\kern 1pt} c_{1}$) and three nonlinear parameter (${\kern 1pt} r_{1} {\kern 1pt} {\kern 1pt} r_{2} {\kern 1pt} r_{3}$) separate display. Figures 8.3, 8.4, 8.5, 8.6 are respectively the parameter identification results of Hammerstein model system with PSO algorithm DE algorithm and improved DE algorithm, Figs. 8.7, 8.8, 8.9, 8.10 are the results of Wiener model.

Fig. 8.3

Performance curves of PSO algorithm for Hammerstein model

Fig. 8.4

Performance curves of DE algorithm for Hammerstein model

Fig. 8.5

Performance curves of MDE algorithm for Hammerstein model

Fig. 8.6

Performance curves of MKDE algorithm for Hammerstein model

Fig. 8.7

Performance curves of PSO algorithm for Wiener model

Fig. 8.8

Performance curves of DE algorithm for Wiener model

Fig. 8.9

Performance curves of MDE algorithm for Wiener model

Fig. 8.10

Performance curves of MKDE algorithm for Wiener model

Figure 8.3 shows that PSO algorithm identifies Hammerstein model parameters with less iteration, the whole curve relatively smooth, identify the linear parameter within 100 generation, identify the nonlinear parameter in about 300 generation, but its program running time is many times as other algorithm.

Figure 8.4 shows that DE algorithm identify Hammerstein model parameters a little more iteration than PSO algorithm, identify the linear parameter around 200 generation, also identify the nonlinear parameter in about 340 generation, but its running faster and has more accurate identification parameter results.

We can see from Fig. 8.5 that MDE algorithm not only identify Hammerstein model parameters with less iteration, identify the linear parameter around 150 generation, identify the nonlinear parameter around 250 generation, but also its running faster with the most accurate result, and has the maximum probability of getting the global optimal solution.

It is shown in Fig. 8.6 that MKDE algorithm identifies the linear parameters with only about 100 iterations, identify the nonlinear parameters with about 200 iterations. Compare this method with the methods mentioned above, we know that the convergence rate of the MKDE is much fast than the other algorithms.

From Figs. 8.7, 8.8, 8.9, 8.10, we also can see that it is evident that the convergence of DE algorithm is faster than PSO algorithm. Figure 8.7 shows the identification iterations of PSO is about 36 generations and the oscillating amplitude is big before it achieves stability; Fig. 8.8 illustrates that DE algorithm can identify the parameters of Wiener model with 30 iterations, and the oscillating amplitude is smaller than the PSO algorithm; Fig. 8.9 shows that MDE algorithm identify the parameters of Wiener model in about 25 iterations; Fig. 8.10 shows that MKDE algorithm identify the parameters of Wiener model with only about 20 iterations.

In the same parameter setting conditions, we get the data result when the graph output. Take the average of the 30 group data, the results shown in Tables 8.1 and 8.2.

From Tables 8.1 and 8.2, it can be clearly observed that the DE algorithm and the improved DE algorithms perform more or less in a similar result although MKDE outperforms other algorithms. Although MDE can increase global search ability, and MKDE has a better performance both in accuracy and convergence. From Tables 8.1 and 8.2, we can see that the accuracy of PSO algorithm is smaller than the DE and the improved DE. PSO algorithm identifies the parameters is closed to the truth-value, however, the DE algorithm and improved DE can identify the parameters perfectly with little error, especially the MKDE algorithm.

8.4 Conclusions

In this paper we have investigated the performance of DE and the improved DE, the simulation of results showed that relative to the basic DE algorithm, improved DE algorithm some more advanced, the MKDE not only do better than other algorithms in accuracy, but also performs excellent at convergence speed. It turns out that the performance of DE algorithm is very sensitive to the choice of parameters and is related with the feature of problem. The next work we should do is to improve the stability of the DE algorithm.