Abstract
In the previous chapters, the X-ray analysis has been applied to the samples with the electron density distributed uniformly in a macroscopic volume: the constant value for XRR analysis and three-dimensional periodic function in case of HRXRD analysis.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
In the previous chapters, the X-ray analysis has been applied to the samples with the electron density distributed uniformly in a macroscopic volume: the constant value for XRR analysis and three-dimensional periodic function in case of HRXRD analysis. These samples are usually grown with a predicted design to realize certain physical or mechanical properties of a final structure. The natural materials, however, possess in most cases the mixed structure, consisting of a large number of crystallites of various shape and size with random distribution over the sample volume. This kind of physical structure is called a polycrystalline form and it occurs in the majority of existing samples.
The non-destructive X-ray studies explore the properties of polycrystals, which influence the macroscopic characteristics of the products made of polycrystalline materials. There are different methods of X-ray analysis described in numerous monographs: the powder diffractometry performs the chemical and structural analysis of the material [1] and determines the grain size [2] and microstructural imperfections, the texture X-ray analysis studies the preferable orientations of the crystallites [3], X-ray stress analysis evaluates the residual stresses and strains in the samples [4, 5].
The chapter deals with the residual stress analysis, and the theoretical concepts described in previous chapters are used here to interpret the X-ray residual stress measurements. The first section introduces the basic physical definitions used further in X-ray stress analysis. The most difficult part of the theoretical interpretation is a description of the elastic interaction between crystalline grains which influences the microscopic properties of the crystallites. The second section presents the approximations and models used for solution of this problem. The third section considers the powder X-ray diffractometry in a connection with X-ray stress analysis. The forth section deals with the macroscopically isotropic samples, and the expressions for X-ray elastic constants are derived. The covariant methods and vector parametrization of the rotation space group are utilized to simplify the operations with tensors. Finally, the macroscopically anisotropic material are discussed in the fifth section of this chapter.
7.1 X-Ray Stress Measurements
The residual stresses are defined by the distribution of the forces and the moments of forces, which exist in an equilibrium state in the polycrystals. The stresses influence the mechanical properties and the fatigue life of a material under external exposure. The residual stresses are the result of the elastic or plastic deformation of crystallites, and the distribution of the stress in a volume is distinguished by the several scales, \(\sigma = \sigma _I + \sigma _{II} + \sigma _{III}\) [4]: (i) macroscopic, where the stress \(\sigma _I\) is averaged over the large number of grains, (ii) mesoscopic, where \(\sigma _{II}\) is an average stress inside grain, and (iii) microscopic, where \(\sigma _{III}\) describes the fluctuation of local stress inside a crystallite around value \(\sigma _{II}\). The mechanical properties of the sample are defined mostly by macro-residual stress \(\sigma _I\), the evaluation of which by X-ray stress measurements involve the calculation of \(\sigma _{II}\) and \(\sigma _{III}\) as well (Sect. 7.2).
The real microstructure of polycrystals is very complex. For the description of areas with coherent crystallographic structure, there are different spatial scales and naming conventions for micro-objects exist: crystallite, subgrain, dislocation cell, cell-block, grain and others [6]. Depending on the material, these objects have various relationships. In this chapter, we are not focusing on any particular material and therefore use the words crystallite and grain as synonyms.
In according to elastic theory [7], the stress tensor \(\sigma _{ij}(\varvec{r})\) in the position \(\varvec{r}\) is a symmetric tensor of a second rank which defines the force density \(F_i\) acting on the square \(d S_j = n_j dS\) as follows:
where \(n_j\) are the components of a normal vector to the square \(d S\) and the repeating indices are summed up accordingly.
In general case, the components \(\sigma _{ij}(\varvec{r})\) have different values in different crystallites, however, the averaging over all grains results in a macro-residual stress:
which has to be evaluated in the most of the practical applications and is a target of the residual stress analysis.
Thereafter, we consider the basic principles of X-ray diffraction stress analysis for polycrystals with uniform and isotropic distribution of the crystallites [4, 5, 8]. The stresses \(\sigma _{ij}\) in the sample lead to the variation of the interplane distances inside the crystallites, and the value \(d_{hkl}\) for the plane \(\{hkl\}\) depends on the orientation of grain in a polycrystal (Fig. 7.1).
The linear dimension of the grains in polycrystalline materials is essentially less than the extinction length of X-rays, and according to (6.77) the X-ray scattering from a single grain is described by a kinematical diffraction theory. The position of the diffraction peak for the radiation with the wavelength \(\lambda \) is determined by Bragg law:
where angle \(\theta _{hkl}\) is a Bragg angle for reflection \(hkl\). Assuming the value \(d_{hkl}^{(0)}\) and Bragg angle \(\theta _{hkl}^{(0)}\) are known for the investigated crystal under the non-stressed condition, the measurement of the position of the diffraction peak \(\theta _{hkl} \) delivers the elastic deformation of corresponding crystallographic planes:
This value is a component of the strain tensor \(\epsilon _{ij} (\varvec{r})\), which depends on the coordinate and is connected to the stress tensor by Hooke’s law [7]:
where \(s_{ijkl}(\varvec{r})\) is a local compliance tensor, which may vary both inside grain and at the grain boundary (Sect. 7.2). In a primitive model of uniform and isotropic polycrystal consisting of the isotropic grains [5], the averaging over the coordinates in (7.5) establishes the relationship between the measured average strain tensor \(\epsilon _{ij} = \langle \epsilon _{ij} (\varvec{r})\rangle \) in sample, the evaluated macroscopic stress tensor \(\sigma _{ij}\) and the compliance tensor \(S_{ijkl} \), which is referred to the whole polycrystal but for uniform sample contains two parameters \(S_1, 1/2 S_2\) [7] only:
These parameters are expressed through the Young modulus \(E\) and Poisson ratio \(\nu \) as:
Each of three tensors in (7.6) has a simplified form in various coordinate systems used for residual stress analysis (Fig. 7.2).
The coordinate system \(S\) is related to the sample as a whole, and the axis \(z (i = 3)\) coincides with the normal to the sample surface. In the coordinates \(S\), the components of the macroscopic stress tensor \(\sigma _{ij}\) are initially defined. The laboratory coordinate system \(L\) is set to merge the direction of the axis \(z'\) and reciprocal lattice vector \(\varvec{H}\) of crystallites, corresponding to the Bragg angle \(2 \theta _{hkl}\). This direction in a system \(S\) is defined by the unit vector \(\varvec{y}(\psi ,\phi ); \ \varvec{Q} = Q \varvec{y} \approx 2\pi \varvec{y} /d_{hkl}^{(0)} \) with angles \(\psi \) and \(\phi \) (Fig. 7.2). The definition of the vector \(\varvec{y}\) is possible by other parameters, which can be more convenient for interpretation of the measurements from the samples with preferred orientations, see Sect. 7.3. The experimentally measured strain (7.4) defines the component of strain tensor \(\epsilon ^{hkl}_{\psi \phi } = \epsilon _{33}^L\) in a coordinate system \(L\).
Finally, the crystallographic coordinate system \(C\) is defined by the crystallographic axes of crystallites, and the stiffness tensor is set in this coordinate system. Assuming the uniform and isotropic sample model (Sect. 7.2), the parameters \(S_1^C\) and \(S_2^C\) are equal for all grains and calculated from the crystallographic parameters of a crystal composing a crystallite. They also coincide with the macroscopic parameter \(S_1\) and \(S_2\) of polycrystal in Eq. (7.6).
In isotropic polycrystal, the components of the strain tensor (7.6) in system \(S\) are expressed through the value \(\epsilon _{33}^L\) by three components of the rotation operator \(\hat{T} (\varvec{y})\) (Fig. 7.2):
which is the same as vector \((\varvec{y})\) is the system \(S\):
Using the Eqs. (7.6)–(7.9), the relationship between the measured by X-ray diffraction strains and components of the residual stress tensor is:
The Eq. (7.10), named often as fundamental equation of X-ray stress analysis, contains 6 unknown components of the stress tensor. They can be found as a solution of the system of linear equations obtained from the measurement of strain at 6 different angles \(\psi \) and \(\phi \). The values of the diagonal and non-diagonal components of the strain tensor may differ essentially, and thus even small errors in the measured positions of the diffraction peaks make the analysis unstable. Therefore, another analytical methods utilizing the specific features of Eq. (7.10) are used for the treatment of X-ray data. The most commonly used technique is a \(\sin ^2 \psi \) method, introduced for the first time in [9].
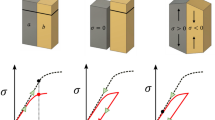
The method is based on the fact, that the boundary conditions of the sample shape are not essential for uniform and isotropic macroscopic polycrystal. Therefore, the coordinate system \(S\) is approaching the system \(P\) of the stress tensor [7], where \(\sigma _{ij} = \sigma _i \delta _{ij}; \ \sigma _i \equiv \sigma _{ii}\) and thus tensor contains the diagonal elements only. In this case, the dependence of the function \(\epsilon ^{hkl}_{\psi \phi }\) on \(\sin ^2 \psi \) at fixed \(\phi \) is defined by a straight line (Fig. 7.3a). Thus, the interpolation of several measurements carried out at different \(\sin ^2 \psi \) and \(\phi = 0\) and \(\phi = \pi /2\) by a straight line makes it possible to calculate values \(\sigma _{11}\) and \(\sigma _{22}\) from the inclination angles of the line. The intersection of the line with the ordinate delivers the value \(\sigma _{33}\).
Typical shapes of the function \(\epsilon ^{hkl}_{\psi \phi }(sin^2 \psi )\) for the measurement of strain by point detector: a linear function in case of diagonal stress tensor, b elliptical function in case of non-zero \(\sigma _{13}\) and \(\sigma _{23}\), c oscillating function in the presence of texture, d parabolic function in case of strong gradient of \(\sigma _{ij} (z)\) toward the normal to the sample surface
As follows from (7.10), the presence of non-diagonal components in \(\sigma _{ij}\), i.e. the deviation in the directions of the axes of \(S\) and \(P\) systems, leads to the dependence of \(\epsilon ^{hkl}_{\psi \phi }\) on the sign of the calculation angle \(\psi \). This fact results in elliptical form of the curves \(\epsilon ^{hkl}_{\psi \phi }(sin^2 \psi )\), which allows to calculate the values \(\sigma _{13}\) and \(\sigma _{23}\), too (Fig. 7.3b).
For anisotropic and non-uniform polycrystals, the method described above does not permit to calculate the components of the stress tensor, however, the curves \(\epsilon ^{hkl}_{\psi \phi }(sin^2 \psi )\) are helpful to investigate qualitatively the distribution of the stresses in the sample, for example, presence of stress gradient or texture (Fig. 7.3c, d).
The quantitative residual stress analysis in case of essential deviations from \(\sin ^2 \psi \) law assumes the averaging of (7.6) by using microscopic models (microstress) for separate grains and their elastic interaction (7.2) as well as the consideration of texture of polycrystalline sample (7.3). In general case, the resulting equations contain a complicated relationship between the microscopic compliance tensor of separate grains and components of macroscopic tensor \(S_{ijkl}\) referred to the whole sample. In the framework of macroscopically isotropic model and in the presence of anisotropy inside grains, the Eq. (7.10) can be used to interpret the experimental data:
Here the coefficients \(S_2^{hkl}\) and \(S_1^{hkl}\) depend on the diffraction vector and can be considered as phenomenological X-ray elastic constants [2] (see Sect. 7.4 for more details).
There are several improved techniques of X-ray measurements, which optimize the study of residual stresses in polycrystals. The grazing-incidence X-ray diffraction (GIXRD) is used for the investigation of stress gradients in surface layers and coatings [8]. At small incidence angles \(\alpha \) near the critical angle of total external reflection \(\alpha _c\), the diffraction peak is formed in the grains located in the depth, which depends on the incidence angle (Fig. 7.4).
The depth, where 63 % of the full intensity of diffraction peak is formed, is called informational depth \(\tau \) and for thick layer it is expressed as [2]:
where \(\beta \) is an imaginary part of the refraction index \(n = 1 - \delta - i \beta \) (see Chap. 1). By varying the incidence angle of X-rays, the stress can be measured from different distances in-depth from the surface. At the angles comparable with \(\alpha _c\), where \(\sin ^2 \alpha _c = 2 \delta \), the refraction of both incident and exit beams becomes essential (Fig. 7.4), which results in the angular shift of the diffraction peak at \(2\theta \) with respect to the Bragg angle \(2 \theta ^{hkl}\) in formula (7.4). The corrections for refraction change also the informational depth and have to be accounted for the reconstruction of stress gradients [10]. The formulas for the corrections are:
The transition layer at the surface sample caused by roughness (Chap. 3) also distorts the informational depth and the corresponding corrections have to be applied for calculation of stress gradients [11].
The Eqs. (7.10) and (7.11) are used above for the experimental geometry, which measures the shift of diffraction peak at fixed indices \((hkl)\), i.e. by varying the direction \(\varvec{y} (\psi )\) of the diffraction vector \(\varvec{Q}\) at fixed length \(Q\). However, these equations are valid for the case of different indices, when the angle \(\psi ^{hkl}\) is connected to the Bragg and the incidence angles as:
and varies from one diffraction peak to another without rotation of sample. This approach is called multiple \(hkl\) stress evaluation and is used in GIXRD geometry to evaluate stress gradients [10, 12]. The Eq. (7.11) is applied in this case in the form [12]:
For determination of the values \(\sigma _{ \phi },\tau _{ \phi }\) and \((\sigma _{11} + \sigma _{22}) \) at fixed \( \phi \), it is enough to measure the strain for 3 reflections. However, the equation system obtained can be badly defined or has no any exact solution due to big difference between \(\sigma _{ \phi }\) and \(\tau _{ \phi }\). Therefore, in practice the multiple measurements are performed and the stress is calculated by fitting the strain for all reflections on the basis of formula (7.15) [10].
The presented above technique of X-ray diffraction stress measurements is commonly used and utilizes a point or linear X-ray detectors, which record the scattered X-ray signal in the diffraction plane corresponding to the angle \(\psi \) (Fig. 7.2). Recently the two-dimensional detectors became popular for residual stress measurements [13]. In that case, the diffraction signal from the uniform polycrystal is exposed as Debye rings with the radius defined by the reflection \((hkl)\) and with variation of the angle along the Debye ring between 0 and \(2 \pi \). The detection of X-ray signal out of the diffraction plane introduces another degree of freedom in the relative arrangement of the coordinate systems and this fact requires the modification of the Eq. (7.11) for residual stress analysis. The derivation of a new equation for two-dimensional data is done in [13]. This technique offers an extended opportunities for stress analysis in the samples with large size of grains and highly textured materials.
Independently on the X-ray measurement technique used for stress analysis, the results are strongly influenced by the selected model of grain interaction and the distribution of grains in a sample, as reflected in the Hooke’s law (7.5). This important issue is discussed in the following sections.
7.2 Grain-Interaction Models
The stress and strain inside the single crystallite (grain) are connected by the Hooke’s law. The Bragg peak, however, is formed by the signals coming from the number of grains with different rotation angle \(\alpha \) (Fig. 7.2). Within this set of grains, there are different magnitudes of microscopic strain and stress observed, which differ from the macroscopic values to be evaluated. Therefore, the relation between the strain \(\epsilon _{ij}(\varvec{g})^{(S)}\) in a single grain (coordinate system \((S)\)) having orientation \(\varvec{g}\) and the macroscopically averaged stress tensor \(\langle \sigma _{ij}\rangle ^{(S)}\) has to be established. This relationship will help to find the dependence between macroscopic stress in a sample and measured experimentally by X-ray diffraction strain. Within the framework of linear elasticity theory, this relationship is expressed as:
The coefficients \(A_{ijkl}(\varvec{g})\) depend non-linearly on the orientation of grain \(\varvec{g}\) and on the stiffness tensor of grain \(c_{ijkl}^{(C)}\).
The problem of calculation of macroscopic parameters of the sample consisting of non-uniform areas has a long history [14]. The determination of averaged elastic, dielectric, electroconductive and thermoconductive properties have a similar mathematical formulations in linear theory. The elastic properties of polycrystal are found from the equations of the elastic equilibrium with the boundary conditions:
where \(c_{ikjl}(\varvec{r})\) is a stiffness tensor, which varies from one crystallite to another when \(\varvec{r}\) varies, \(\Gamma \) is a boundary between regions \((1)\) and \((2)\) with the normal \(\varvec{n}\). The boundary conditions for electrostatics in media have similar form:
where \(\epsilon _{ij}\) is a permittivity, \(\phi \) is a potential and \(D_i\) is an electric displacement field. By substituting \(\epsilon _{ij}\) for the tensor of electroconductivity and \(D_i\) for the current density, we obtain the equations for electroconductive properties of material. By substituting \(\phi \) for the temperature and \(\epsilon _{ij}\) for the tensor of thermal conduction, and \(D_i\) for the heat flux, we obtain the equations for thermoconductive properties, and so on. Thus, the methods developed for one branch of physics can be transformed to another. With regard to the elastic properties, however, the mathematical background is more complex due to the involvement of tensors of higher rank and vectors \(u_i\) instead of the scalar \(\phi \).
There are following approaches to the solution of above-mentioned problem:
-
Exact solutions for certain models, for example, the exact solution of the Eq. (7.17) for adjoined isotropic spheres with similar properties in isotropic surrounding, so called composite sphere assemblage [14, 15]. The number of these models, which allow an exact solution is relatively small.
-
The methods based on the expansion into series over small parameter. The small parameter can be concentration of particles in composite material [14, 16], the anisotropy degree of the crystallites in a sample [17], and so on. In case if the parameter is not small, the series can be used for qualitative analysis [18]. An equivalent formulation of this approach is a chain of the equations Born-Bogolubov-Green-Kirkwood-Ivone [19].
-
The methods for determination of lower and upper boundaries of the macroscopic parameters [14, 18]. These methods are based on the variation principle: the exact solution of the Eqs. (7.17) and (7.18) minimizes the energy.
-
Self-consistent methods, where the ansatz for (7.17) and (7.18) is constructed as follows: the interaction between particles is substituted for the interaction of separate particle with effective media, the properties of which have to be found. The effective permittivity has been found by Bruggeman [20] using this method. For the elastic properties of polycrystalline materials, the self-consistent methods are based on eigenstrain approach [21], where the Eshelby problem is solved for the stress initiated by the inclusions [22]. Based on this approach, Kröner proposed a self-consistent method for calculation of elastic properties of polycrystals known as Eshelby-Kröner model [23].
-
The method based on the simplified models of grain interaction. Instead of solution of (7.17), the ad hoc assumptions are used for distribution of stresses and strains in grains [24]. As a result, the boundary conditions (7.17) are broken, however, the proper selection of model allows to obtain a good fit between experimental data and theory.
-
A numerical solution of (7.17) and (7.18) and further averaging of the prior found fields. This approach is frequently used for optical properties of metamaterials [25]. In opposite to the artificial metamaterials, where the fragments are designed initially, the polycrystalline samples obey many random parameters. For the numerical solution of (7.17), the shape and crystallographic orientation of each crystallite have to be known. The method of finite elements is proved [26, 27] to show a good agreement with analytical methods.
Hereafter, we consider the frequently used models and methods for solution of Eq. (7.16).
7.2.1 Voigt Model
The first grain-interaction model has been proposed by Voigt in 1910 [28]. This model assumes that all crystallites have the same strain \(\epsilon _{ij}\) independently on their orientations. As a result, the microscopic strain equals to the averaged macroscopic one:
Thus, the stress tensor in crystallite with orientation \(\varvec{g}\) is calculated by formula:
where \(c_{ijkl}^{(S)}(\varvec{g})=T^{(SC)}_{ii'jj'kk'll'}(\varvec{g})c_{i'j'k'l'}^{(C)}\) is a stiffness tensor of crystallite with orientation \(\varvec{g}\) in coordinate system \((S)\). To derive the relationship (7.16), the macroscopic stress tensor \(\langle \sigma _{ij}\rangle ^{(S)}\) has to be determined. For determination, the Eq. (7.20) has to be averaged over crystallite orientations \(\varvec{g}\) with respect to the orientation distribution function (ODF) \(f(\varvec{g})\), (see more detailed discussion on ODF and transformation \(T^{(SC)}\) in the Sect. 7.4):
Using (7.19), (7.21) and (7.16), the following statement is obtained for Voigt model:
In this model, the tensor \(A_{ijkl}^{V}\) is independent on the crystallite orientation \(\varvec{g}\), which results in a linear character of \(\sin ^2\psi \) even in the presence of texture.
The Voigt model is a pretty rough approximation for grain interaction, where the boundary conditions of the elasticity theory (7.17) are deliberately not satisfied. The strains are continuous at the boundaries of crystallites, however, the stresses suffer the discontinuity (7.20). The totally opposite situation occurs in a Reuss model.
7.2.2 Reuss Model
The Reuss model [29] assumes all the crystallites have the same stress \(\sigma _{ij}\) independently on the orientation. As a result, the microscopic stress of a single crystallite equals to the macroscopic one averaged over the whole sample:
The strain tensor of a crystallite with the orientation \(\varvec{g}\) is:
where \(s_{ijkl}^{(S)}(\varvec{g})=T^{(SC)}_{ii'jj'kk'll'}(\varvec{g})s_{i'j'k'l'}^{(C)}\) is a compliance tensor of crystallite with orientation \(\varvec{g}\) in a coordinate system \(S\). By comparing (7.24) and (7.16), we conclude:
where tensor \(A_{ijkl}^{R}\) depends on the crystallite orientation \(\varvec{g}\), which leads to the non-linearity of \(\sin ^2\psi \) in the presence of texture.
The Reuss model is similarly rough as the Voigt one: the boundary conditions of the elasticity theory are not fulfilled. In opposite to the Voigt model, the stresses are continuous at the crystallite boundaries and the strains (7.24) are discontinuous.
7.2.3 Hashin-Shtrikman Boundaries for Rigidity Modulus
The models of Voigt and Reuss describe the limiting cases of grain interaction. The microscopic mechanical elastic constants binding \(\langle \sigma _{ij}\rangle \) and \(\langle \epsilon _{ij}\rangle \) are shown in [30] to satisfy the inequality:
Here \(K\) and \(G\) are real values of macroscopic bulk and rigidity moduli, and \(K^{V,R},G^{V,R}\) are the values found by Voigt and Reuss models.
The result (7.26) can be illustrated by analogue with the electrical conductivity [16]. In the Reuss model, all grains have equal stress value, which by analogue with (7.17) and (7.18) corresponds to equal current in all conductors. Thus, the Reuss model is analogous to the sequential connection of the conductors, which results in the highest resistance value. The Voigt model corresponds to the equal voltage on all conductors, and thus is analogous to parallel connection, which gives the minimal resistance. For any other types of connection, the resulting resistance will have an intermediate value between the ones mentioned above.
Despite both Voigt and Reuss models are very approximate, the expressions (7.25) and (7.22) do not depend neither from the grain shape nor from their mutual locations. Is it possible to obtain more accurate limits and to identify which information about the crystallites is required for this purpose, we analyze below the Eq. (7.17) following the work [18].
Let us split stiffness tensor \(c_{ikjl}(\varvec{r})\) into sum of constant tensor \(C_{ikjl}\) which we define later and tensor \(\delta c_{ikjl}(\varvec{r})\) which varies from crystallite to crystallite:
The Eq. (7.17) is then expressed as:
The structure of this equation is similar to one of (6.26): there is a constant differential operator \(C_{ikjl}\frac{\partial ^2}{\partial x_k\partial x_l}\) analogous to \(L_0\) in (6.26) and a fluctuating term. Based on the Eq. (7.28), we have to find the averaged effective parameters of the physical system, and therefore use the methods similar to the ones described in the Sect. 6.2, namely represent (7.28) in an integral form:
where \(G_{ij}(\varvec{r},\varvec{r}')\) is a Green function of the elasticity theory [7, 21]; and the arbitrary solution of the uniform equation \(u_i(\varvec{r})^{(0)}\) is chosen to satisfy the boundary conditions at the border of polycrystal. Then the Green function has to satisfy the condition:
at the boundary of the polycrystal. By integrating and using (7.29) and (7.30), we arrive at:
To calculate the strains, the Eq. (7.31) has to be differentiated:
where due to the symmetry of the stiffness tensor with respect to the transposition of indices Footnote 1 \(\delta c_{jknl}(\varvec{r}')\frac{\partial u_n}{\partial x_l'}=\delta c_{jknl}(\varvec{r}')\epsilon _{nl}\):
The expression (7.32) can be written as:
where symbol : means the convolution over two indices, and \(\varvec{\Gamma }\) is an integral operator [18]:
Using this equation, the expression (7.16) can be re-written in an operator form. By reversing (7.34):
where \(\varvec{1}\) is a unity tensor of 4th rank. We assume that the strain \(\varvec{\epsilon }^{(0)}\) at the boundary of polycrystal is uniform (the general case is discussed in [18]), then the macroscopic strain \(\langle \varvec{\epsilon }\rangle \) is equal to \(\varvec{\epsilon }^{(0)}\):
Applying the Hooke’s law, we obtain for macroscopic values:
and for microscopic values:
After averaging (7.39) and using (7.36), the expression for macroscopic stiffness tensor is:
and the relationship (7.16) is found to be:
Within the accuracy of approximation (7.17), these expressions are exact. However, similarly to the case of (6.33), for the calculation of (7.40) and (7.41) the operators have to be found, which are inverse to the non-local integral operators. This is a challenging problem, and the models of Voigt, Reuss and Eshelby-Kröner are the approximate methods to calculate (7.40) and (7.41).
In the same way as in (6.33), the inverse operators can be represented as an expansion into series, and thus (7.40) is written as:
The first two terms in (7.42) correspond to the Voigt model, whereas the same formula, being constructed not from stiffness tensor \(C\) but from compliance tensor \(S\), will correspond to Reuss model. In both approximations, there is no need to know the shape and mutual arrangement of the crystallites, however, for the calculation of the subsequent term in the series this information is necessary. Indeed, the operator \(\varvec{\Gamma }\) is non-local, and therefore for calculation of the third term in (7.42) the value \(\langle \delta \varvec{c}(\varvec{r}_1) \delta \varvec{c}(\varvec{r}_2) \rangle \) must be known, which is a correlation function of the second order for the elastic properties of polycrystal. To calculate further terms in the series, the correlation functions of higher order must be simulated. In general case, the series (7.42) is divergent, and the special summation techniques have to be applied for the final calculation [18].
Using the derived above equations, the expressions for upper and lower limits of the macroscopic stiffness tensor \(\varvec{C}_{M}\) can be obtained. To isolate the operator \(\varvec{\Gamma }\), the equation (7.34) is re-formulated as [18]:
This equation for fluctuating stress parameter \(\widetilde{\varvec{\sigma }}\) can be considered as a consequence of the minimization of the functional:
Alternatively, using (7.43) the functional \(F[\widetilde{\varvec{\sigma }}]\) is:
where Eq. (7.38) is used and \(V\) is a volume of the polycrystal.
As follows from (7.44), the exact solution of (7.43) delivers the extremum of the functional \(F[\widetilde{\varvec{\sigma }}]\). If the value \(\delta \varvec{c}^{-1}\) is positive definite, Footnote 2 the extremum will be a minimum [18]. For any probe field \(\widetilde{\varvec{\sigma }}_{\text {probe}}\), the following inequality is satisfied:
By reduction of \(F[\widetilde{\varvec{\sigma }}_{\text {probe}}]\) to the form \(V\varvec{\epsilon }^{(0)}:\frac{\varvec{C}_{v}}{2}:\epsilon ^{(0)}\), the Eq. (7.46) delivers the upper limit for \(\varvec{C}_{M}\). Using a similar algorithm for the compliance tensor \(S\), in case of negative definite value \(\delta \varvec{c}^{-1}\), we obtain [18]:
from where the lower limit for \(\varvec{C}_{M}\) is received. To explicitly calculate both limits, the following probe field is used:
where the sum is performed over all grains of polycrystal, and the field inside each grain is assumed to be constant. The function \(\Theta _n(\varvec{r})\) describes the shape of \(n\)-th grain: \(\Theta _n(\varvec{r})\) equals to 1 inside grain and to 0 outside. The coefficients \(\widetilde{\varvec{\sigma }}_{n}\) are determined by the minimization of the functional \(F\), which for the field (7.48) is:
With respect to the coefficients \(\widetilde{\varvec{\sigma }}_{n}\), the expression (7.49) is a quadratic form of type \(\frac{1}{2}\sum \nolimits _{n,m} a_{nm}\widetilde{\sigma _n}\widetilde{\sigma _m}+\sum \nolimits _{n}b_n\widetilde{\sigma _n}\). It can be easily found that the extremum is \(\frac{1}{2}\sum \nolimits _{n}b_n\widetilde{\sigma _n}^*\), where \(\widetilde{\sigma _n}^*\) is a solution of the equation \(\sum \nolimits _{m} a_{nm}\widetilde{\sigma _m}^*+b_n=0\). Applying these expressions to (7.49), the extremum of the functional is found to be:
As follows from (7.50), due to the operator \(\Gamma \) the expression for \(\widetilde{\varvec{\sigma }_n}^*\) is non-local and requires the correlation function for the grain shape. The function \(\Gamma \) is calculated on the basis of Green function with the boundary conditions (7.30). The functions \(\Gamma \) and \(\Gamma ^{\infty }\) calculated for infinite crystal can be connected for fluctuating \(\widetilde{\varvec{\sigma }}\). By neglecting the condition (7.30), the additional term appears in (7.31), which includes the integral over the surface:
In case of uniform boundary conditions, the averaged values \(\langle \varvec{\sigma }\rangle \) and \(\langle \varvec{\epsilon }\rangle \) are also uniform, and we can assume the value \(\langle \widetilde{\varvec{\sigma }}\rangle \) uniform, too. In the integration of (7.51) over the surface, the contribution from \(\langle \widetilde{\varvec{\sigma }}\rangle \) is compensated [18]. By using the Gauss theorem and replacing the displacements by strain, the expression analogous to (7.34) is obtained:
Substituting this expression in (7.50) and applying the translational invariance, we arrive at:
where \(f_{nm}\) is a correlation function of the grain shape.
In the case of spherically symmetric correlation function \(f_{nm}(\varvec{\rho })=f_{nm}(\rho )\), the expression (7.53) can be essentially simplified, and the explicit solution is obtained on the basis of Eshelby tensor. To derive this formula, the Green function of the infinite media is represented as an expansion through the plane waves, and from (7.29) follows:
where \(M_{ij}(\varvec{n})\) is a Chirstoffel tensor (acoustic tensor). Using formula (7.35), the integral in (7.53) is expressed as:
The integral over the directions \(\varvec{n}_{\rho }\) is conveniently calculated in spherical coordinates with the axis \(z\) along \(\varvec{n}\), and further integration over \(k\) by using
and integrating over \(\rho \) by using
modifies (7.55) to the expression:
where
This simple formula is a consequence of the spherical symmetry \(f_{nm}(\varvec{\rho })\) of the grains. The similar results is obtained [18, 31] for the grains of elliptical shape, where the tensor \(\varvec{E}\) is:
where the coordinate system coincides with the ellipse axes, and \(a_1,a_2,a_3\) are the lengths of the semi-axes. The dimensionless tensor \(\varvec{E} : \varvec{C}\) is called an Eshelby tensor [21] which is used for calculation of strain fields for the inclusions inside the sample [22]. Substituting (7.58) into (7.53) and utilizing the equality \(f_{nm}(0) = \delta _{nm}V_n/V\), the following expression is found:
from where the relation between the fluctuating stress \(\widetilde{\varvec{\sigma }}^*_n\) and the average value \(\langle \widetilde{\varvec{\sigma }}^*\rangle \) follows:
By averaging this formula, the connection between \(\langle \widetilde{\varvec{\sigma }}^*\rangle \) and average strain is obtained:
The expressions (7.60) and (7.61) connect the fluctuating stresses \(\widetilde{\varvec{\sigma }}^*_n\) with the average strain \(\epsilon ^{(0)}\). Thus, the functional (7.49) minimized on the class of the functions (7.48) can be expressed through the quadratic form of \(\epsilon ^{(0)}\) according to (7.50). Comparing this result with the equation (7.46), the upper boundary for macroscopic stiffness tensor in case of positively defined \(\delta \varvec{c}_n^{-1}\) (or lower boundary in case of negatively defined \(\delta \varvec{c}_n^{-1}\)) is:
These estimates for the boundaries of the macroscopic rigidity modulus have been proposed by Hashin and Shtrikman [32]. Due to taking into account the correlation properties of the grains by Eshelby tensor, the boundaries are found to be more narrow than the ones provided by Voigt and Reuss.
Using the Eq. (7.48) as a model solution of the Eq. (7.17), the relation (7.16) between the strain in the grain with the orientation \(\varvec{g}\) and the macroscopic stress on the basis of (7.52), (7.62), (7.60), and (7.61), we obtain:
7.2.4 Self-Consistent Model of Eshelby-Kröner
The tensor \(\varvec{C}\) in the expressions (7.27)–(7.52) can be chosen in an arbitrary way, except of the case when using (7.46) and (7.47) the boundaries for macroscopic stiffness tensor \(\varvec{C}_M\) have to be determined. In this case, the positive (negative) definite difference \(\delta \varvec{c}_n\) is required for each grain \(n\). To find the model solution of (7.17) or to minimize the functional (7.44), the tensor \(\varvec{C}\) has to be defined. The easiest way is to set tensor \(\varvec{C}\) equal to the macroscopic stiffness tensor \(\varvec{C}_M\), and then (7.37) and (7.38) are written as:
This assumption sets the value of \(\langle \widetilde{\varvec{\sigma }}^*\rangle \) to zero because of:
As a next step, we minimize the functional (7.44) on the class of probe functions (7.48), and again obtain the formulas (7.59)–(7.61). Using (7.60) and (7.43), the strain of the \(n\)-grain is equal to:
The requirement of the average strain from (7.66) to be equal \(\varvec{\epsilon }^{(0)}\) leads to the equation:
This tensor expression is a system of equations for the determination of the components of the tensor \(\varvec{C}\). Indeed, the tensor \(\varvec{C}\) defines the tensor \(\varvec{E}\) through the Eqs. (7.54) and (7.58), and this relationship is non-linear in general case. The number of independent parameters in averaged tensors (the left part of (7.67) and macroscopic tensors \(\varvec{E}\) and \(\varvec{C}\)) is equal. For example, the tensors are described by two parameters in case of macroscopic isotropy (absence of texture), see details in Sect. 7.4. As a result, the expression (7.67) contains as many independent equations as the number of independent components in tensor \(\varvec{C}\). Due to the procedures of convolution in (7.54) and of integration in (7.58), the relationship between \(\varvec{E}\) and \(\varvec{C}\) is non-linear and cumbersome. As a consequence, the system of equations (7.67) is also non-linear. In a simple case of microscopic isotropy and cubic symmetry of the crystallites, the formula (7.67) leads to the cubic equation (7.147), see [21, 23].
The equations analogous to (7.67) can be obtained in another ways, for example, the macroscopic Hooke’s law (7.65) satisfying to \(\langle \widetilde{\varvec{\sigma }}^*\rangle =0\) results in the following equation, according to (7.61):
For the crystallites of the same shape having equal Eshelby tensors, the equation (7.68) is equivalent to (7.162). However, if the tensor \(\varvec{E}\) varies from one crystallite to another \(\varvec{E}=\varvec{E}_n\), the formulas (7.68) and (7.67) give different results. This situation occurs in case of morphological texture [33, 34] with the grains of anisotropic elliptical shape in different orientations.
The relationship (7.16) for the considered model follows directly from (7.66) and (7.64):
The frequently used method of the derivation of equation (7.67) is based on the model of the inclusions inside the infinite matrix [22, 23]. This approach substitutes the problem of grain interaction by the model of the grain of spherical (elliptical) shape included into infinite effective media, called matrix. The stiffness tensor of matrix is assumed to be equal to the stiffness tensor of polycrystal, which has to be found. To solve this problem, the strain inside \(n\)-th grain has to be determined. The parameter \(\delta \varvec{c}(\varvec{r})\) in the equation (7.28) has the following form:
To determine the strain in \(n\)-th grain, the equation (7.28) has to be solved, which also can be reduced to the formula (7.32). The sample is supposed to be infinite and, therefore, the Green function of infinite media is admitted. By analogue with (7.54) and (7.55), the integral is modified to:
We assume here that the strain inside \(n\)-th grain is uniform and the grain has a spherical shape, and the integral over \(k\) is presented in the form of [31]:
The integral over \(\varvec{r}'\) is easy to calculate in spherical coordinates with the axis \(z\) along the vector \(\varvec{n}\):
here \(R\) is a radius of grain. The expression obtained has a physical meaning of the square of disc formed in the space of \(\varvec{r}'\) by the intersection of the sphere with the radius \(R\) and the plane defined by the equation \(\varvec{n} (\varvec{r}-\varvec{r}')=0\). Finally, for the function (7.71) we obtain:
This formula shows that for the spherical grains the strain inside the grain is uniform. The dependence on the radius \(\varvec{r}\) disappears when the section of the grain by the plane is a curve of the second order, i.e. sphere and ellipse. By substituting (7.74) into (7.32):
The formula (7.66) follows immediately from the expression above, that confirms the equivalence of the approaches based on the variational principle and effective media.
The expressions similar to (7.75) and (7.66) exist also in the electrostatics, for example, the external field causes the uniform field in sphere or ellipsoid [35]. The calculations based on (7.57) result for the sphere with the permittivity \(\epsilon _{0}\) in the tensor \(\varvec{E}\):
The tensor analogous to the tensor Eshelby \(\varvec{E} : \varvec{C}\) in this case is equal to \(\frac{1}{3}\delta _{ij}\) and it is called the tensor of depolarization or demagnitization in electrostatics and magnetostatics, respectively [36]. As follows from (7.66), the electric field \(\varvec{E}_{1}\) inside sphere with permittivity \(\epsilon _1\) and the electric field \(\varvec{E}_0\) in the media with permittivity \(\epsilon _{0}\) are connected as [35]:
The algorithm of the calculation of the properties of composite random media using the method of effective media and the expressions (7.77) and (7.67) has been proposed by Bruggeman [20]. This technique is successfully applied for calculation of optical properties of the composite and nanostructured materials [16].
7.2.5 Grain Interaction in Thin Film. Vook-Witt and Inverse Vook-Witt Models
The considered in the previous sections grain interaction was assumed to take a place in a sample with a large number of grain in all spatial directions. The statistical methods used for calculation of physical parameters are based on this assumption. The important class of the investigated by X-ray stress method samples are thin films and coatings. The number of grains in a lateral direction of film is statistically large enough, however, in the direction of a surface normal it can be small. The entire thickness of the film often contains a single grain [5, 37, 38], and thus the system is rather two-dimensional than three-dimensional. The methods described above are therefore not applicable for coatings in general case.
The averaging over all directions is no longer possible because of the evident anisotropy, which complicates the calculation of the Eq. (7.16). For these samples, the simple phenomenological models of grain interaction are used, which take into account the difference of physical properties in lateral and normal directions.
The frequently used model of such type is a Vook-Witt model [39, 40], which adopts the Voigt model in lateral direction (equal strains), and the Reuss model (equal stresses) in the normal direction. Introducing \(z\) axis along the normal to the film, the strain and stress tensors in \(n\)-th grain are expressed as:
where the symbol \(\cdot \) means the component is being not fixed by the model but found from the elasticity theory.
The strain and stress fields (7.78) can be found from the exact solutions of the elastic equations (7.17) in a certain geometry of the polycrystal. By considering the polycrystalline film as a stack of the parallel infinite plates, the Eq. (7.78) satisfies the boundary conditions (7.17), and the uniform inside the plates strain fields are the solutions of the differential equation (7.17). To find the relation (7.16) based on the assumption (7.78), we formulate the Hooke’s law for \(n\)-th grain:
which expresses the strain \(\varvec{\epsilon }_n\) and the stress \(\varvec{\sigma }_n\) in the grain through the average values \(\langle \varvec{\epsilon }\rangle \) and \(\langle \varvec{\sigma }\rangle \). Keeping in mind the symmetry of the tensors, the formula (7.78) contains six undefined variables:
and the relationship (7.79) gives six equations, accordingly.
To present the following expressions in a simple form, the coordinate free covariant notations [38, 41] are introduced instead of the indices. The assumptions (7.78) can be re-written as [38]:
where the tensor of 4th rank \(\varvec{\varPi }_{||}\) means the projection of the 2nd rank tensor on the plane with the normal \(\varvec{n}\). The projection of the vector onto the plane with the normal \(\varvec{n}\) is performed by the projector \(\varvec{t}\), see (4.20). The projection of the 2nd rank tensor is then written as:
or in the index form [38]:
Here we took into account the fact of the symmetry of the projected tensors over the indices \(k\) and \(l\), which leads to the symmetrization of the projector, see (7.33). To explicitly find the tensor (7.16), the Eq. (7.79) is written in the following form:
Using the model (7.78) and Hooke’s law for the averaged values (7.38), the tensor (7.16) for the \(n\)-th grain is:
To use (7.84), the macroscopic stiffness tensor \(C_M\) has to be determined, which follows from the averaging of (7.84):
In general, there no operator exists, which is inverse to the projectional one, and in (7.85) the operator \(\varvec{1}+\varvec{\beta }:\varvec{\varPi }_{\bot }\) also has no inverse one. Thus, the operator \(C_M\) cannot be determined from (7.85), and we use for this purpose the expression analogous to (7.83) with the compliance tensor \(\varvec{s}_n\). After some transformations, we obtain formula analogous to (7.85) but with \(S_M\), and using \(\varvec{C}_M=\varvec{S}_M^{-1}\) obtain:
This equation does not define \(C_M\) unambiguously similarly to (7.85). However, the operators \(\varvec{1}+\varvec{\beta }:\varvec{\varPi }_{\bot }\) in (7.85) and \(\varvec{\gamma }:\varvec{\varPi }_{\bot }\) in (7.86) are the projectors onto different subspaces, which complement each other. Therefore, the sum of (7.85) and (7.86) with arbitrary coefficient \(k\) defines the function \(C_M\) unambiguously:
The expressions (7.84) and (7.87) comprehensively determine the relationship (7.16). These formulas do not contain the parameters, which describe the correlation properties of the grain locations, as the tensor \(\varvec{E}\) in equations (7.69) and (7.63) does. In this sense, the Vook-Witt model is similar to the models of Voigt and Reuss: the mutual influence of grains is not considered, and the resulting expressions depend only on the fraction of grains with certain orientations and do not depend on the morphology of the polycrystal. The strain inside the grain is uniform.
Both Voigt and Reuss models are the limiting cases of grain interaction. The Vook-Witt model with Voigt approach in a lateral direction and Reuss approach in a normal one, is also a limiting case of the grain interaction. The reversed case of Vook-Witt model with Voigt model in a normal and Reuss model in a lateral directions has been proposed in [37] and is called inverse Vook-Witt model:
By comparing (7.88) and (7.80), the expressions (7.84)–(7.87) in the models of Vook-Witt and inverse Vook-Witt differ by the substitution of \(\varvec{\varPi }_{\bot }\) for \(\varvec{\varPi }_{||}\) and vice versa. In opposite to Vook-Witt model, there is no system exists for which the strain and stress fields found by the inverse Vook-Witt model are the exact solutions [38].
The intermediate cases between Vook-Witt and inverse Vook-Witt models are proposed in [37] to describe the grain interaction by a linear combination of former ones. The alternative approach for the intermediate cases is Eshelby-Kröner model for the elliptical grains [5, 38]. The variable parameter, which makes a balance between both limiting cases is a ratio of semi-axes of the ellipsoid. Generally speaking, the model designed for the bulk polycrystal is not applicable to the thin polycrystalline film. However, in the limiting cases, the Eshelby-Kröner model becomes effectively two-dimensional. For the oblate ellipsoid (\(a_1=a_2>>a_3\), axis \(z\) along normal to the surface), the Eshelby-Kröner model transforms into Vook-Witt model [5] and is an exact solution. The opposite limiting case of the stretched ellipsoid \(a_1=a_2<<a_3\) in the Eshelby-Kröner approach coincides with the infinite cylinder model, which being a two-dimensional model gives different results than the inverse Vook-Witt one [5].
7.3 Residual Stress Analysis as a Particular Case of Powder Diffractometry
The real microstructure of the polycrystals is very complex [42]. X-ray diffraction provides the results of X-ray scattering from a large volume of the sample, and this fact leads to a contribution of numerous factors into the detected X-ray profile. The practical data treatment of the recorded X-ray intensities assumes the use of a simplified sample model parametrized by the effective physical variables [2].
The typical model assumes the polycrystal as consisting of a large number of the crystalline blocks (grains). Each grain has a certain shape, size and orientation of the crystallographic lattice, and may contain the defects of a crystallographic lattice, for instance, dislocations. Due to different reasons (plastic deformation, thermal expansion, etc.), the polycrystal may have the macroscopic residual stresses.
The sketch for calculation of the auto-correlation function of the grain shape (7.92)
Using the results of previous chapter, the intensity of the diffracted X-ray radiation from the polycrystal can be calculated. The dynamical effects are neglected here, because of due to the disorientation of the grains, the typical scale of the correlation function (6.60) given by the correlation length \(l_d\) is less than the size of the grain. This estimate is taken with a certain reserve, because of the presence of the defects diminishes the parameter \(l_d\). The size of the grains is essentially less than the extinction length, and thus the diffraction can be treated as kinematical, according to (6.77). The general expression for the intensity in this case is (6.83):
here \(\varvec{Q}=\varvec{k}_{out}-\varvec{k}_{in}\) is a momentum transfer, \(g(\varvec{r}_1,\varvec{r}_2)\) is a correlation function of polycrystal, \(\varvec{H}\) is a reciprocal lattice vector of the excited reflection. We omitted the constant coefficients in the expression because of in the most of the cases the relative intensities are evaluated within a single diffraction profile. The effects of the instrumental and resolution functions are also neglected, which can be accounted by the special functions [2]. Assuming the disoriented grains, the correlation function of the whole system consists of the sum of the correlation functions of the grains:
Here the sum is taken over all grains of polycrystal, \(\varvec{H}_n\) is a reciprocal lattice vector corresponding to the average lattice of \(n\)-th grain, \(g_n\) is a correlation function inside \(n\)-th grain, \(\Theta _n(\varvec{r})\) is a function describing the shape of \(n\)-th grain, which is equal to unity inside the grain and to zero outside. The defects are supposed to be distributed uniformly inside the grain, and the influence of the grain shape on the strain field is neglected. Under these conditions, the correlation function depends on the relative distance \(\varvec{\rho }=\varvec{r}_1 - \varvec{r}_2\), and using the integration over the variables \(\varvec{r}_1\) and \(\varvec{\rho }\), we obtain:
The integral over \(\varvec{r}_1\) as a function of the distance \(\varvec{\rho }\) is an auto-correlation function of the grain shape: it is a volume of the intersectional area, which is created by the original and the shifted by vector \(\varvec{\rho }\) grains (Fig. 7.3). According to (6.60), the correlation function in the presence of several independent types of defects is a product of correlation functions for each defect type. As follows from (7.91), the influence of the grain shape can also be represented by a correlation function:
where \(V_n\) is a volume of \(n\)-th grain.
The values \(g_n(\varvec{\rho }), g_V(\varvec{\rho })_n\) and \(\varvec{H}_n\) vary from grain to grain. However, the grain shape and volume, the defects inside the grain and the orientation of grain are statistically independent, and these parameters can be averaged separately:
The number of the grains in the sample is usually large and, therefore, the distribution functions can be introduced for the parameters. For the sake of simplicity, the distributions of grain shapes [43] and defects [44] are omitted here. The distribution of the grain orientations (texture) is described by the orientational distribution function [45] \(f(\varvec{g})\):
where \(\varvec{g}\) is a set of three parameters describing the orientation of crystallographic lattice of grain with respect to the sample, \(d V_{\varvec{g}}\) is a total volume of grains, which have an orientation within the interval \(\varvec{g},\varvec{g}+d\varvec{g}\) and \(V\) is a volume of polycrystal. The isotropic distribution of grains corresponds to \(f(\varvec{g})=1\). Taking into account (7.94) the Eq. (7.92) becomes:
where \(g(\varvec{\rho })\) is a product of the averaged correlation functions \(\langle g_n(\varvec{\rho }) \rangle \langle g_V(\varvec{\rho })_n \rangle \), the constant multiplier \(V\) is omitted in further calculations.
For the orientation of the grain \(\varvec{g}\) (parametrization of the rotation group [46]), the Euler angles are frequently chosen. In this parametrization, the law of the parameters composition is quite complex. Therefore we use further the vector parametrization of the rotation group known as Gibbs vector [41, 46]. In this parametrization, the rotation is parametrized by the vector \(\varvec{c}\) with the direction defined by the axis of rotation and with the length equals to \(\tan \phi /2\), where \(\phi \) is a rotation angle. The rotation matrix is expressed through \(\varvec{c}\) as [41, 46]:
where \(\varepsilon _{ikj}\) is the antisymmetric Levi-Cevita pseudo-tensor. The vector parametrization is outstanding among other parameterizations because of its elegant composition law, which enables to express two successive rotations with parameters \({\varvec{c}}^{(1)}\) and \({\varvec{c}}^{(2)}\) as a single rotation with the parameter \({\varvec{c}}^{(12)}\) [41, 46]:
Additionally, the vector parametrization has the following convenient properties:
Using this parametrization, the formula (7.95) is written as:
Here \(1/\pi ^2 (1+\varvec{c}^2)^2\) is a weight function for invariant integration over the rotation group [41], the corresponding weight function for parametrization through the Euler angles is \(\sin \theta /8 \pi ^2\) [47].
The dependence of the reciprocal lattice vector \(\varvec{H}(\varvec{c})\) from the grain orientation \(\varvec{c}\) is conditioned in the following way. The vector \(\varvec{H}\) is defined by Miller indices in the coordinate system \(\varvec{C}\), and due to the stresses of II type it varies both for direction and module from grain to grain. Assuming the small magnitude of strains, the components of vector \(\varvec{H}^{(L)}\) corresponding to the average crystallographic lattice of grain with the orientation \(\varvec{c}\) can be represented as:
here \(\varvec{H}^{(0)}\) corresponds to a non-deformed lattice, and vector \(\delta \varvec{H}_{\bot }(\varvec{c})\) is perpendicular to \(\varvec{H}^{(0)}\).
To calculate (7.99), the vectors \(\varvec{Q}, \varvec{H}\) and \(\varvec{\rho }\) have to be defined in the same coordinate system, say in the system \(L\). The parameter \(\varvec{c}\) in (7.99) then characterizes the transition from the coordinate system \(C\) to the system \(L\), and it is denoted here \(\varvec{c}^{(LC)}\). The grains, which satisfy the Bragg condition \(\varvec{H}^{(C)}(\varvec{c})=\varvec{Q}\), are characterized by the parameter \(\varvec{c}^{(LC)}\) equals to:
where unit vector \(\varvec{n}\) is chosen along \(\varvec{H}^{(C)}\), the vector \(\varvec{y}\) is replaced by the vector \(\varvec{e}_z\) from the coordinate system L (Fig. 7.6). The transformation (7.101) has an evident meaning of the sequences: (i) the rotation around axis \(\varvec{n} \times \varvec{e}_z\) perpendicular to vectors \(\varvec{n}\) and \(\varvec{e}_z\) is applied, which transfers \(\varvec{n}\) into \(\varvec{e}_z\), (ii) the rotation at arbitrary angle \(\alpha \) around \(\varvec{e}_z\) is executed.
The sketch for the coordinate system \(\alpha , c_1^{(||)}, c_2^{(||)}\) defined by (7.102) in the space of the parameters of the rotation group
To integrate over \(d^3 \varvec{c}\) in (7.99), the new coordinate system with the axis \(z\) along \(\varvec{c}(\alpha )\) is introduced in the parameter space \(\varvec{c}\) (Fig. 7.6):
where variation of the parameter \(\alpha \) corresponds to the grains in the Bragg condition, which differ by various \(\alpha \) angles around \(\varvec{H} || \varvec{Q}\); the crystallites with the parameters \(c_1^{(||)}\) and \(c_2^{(||)}\) are deviated from the Bragg condition. Using the Eqs. (7.100) and (7.96) and assuming small strains and deviations from the Bragg angle, the expression (7.99) in the chosen coordinate system is written as:
Here \(J\) is a Jacobian of the transformation, \(K[(x,y),(c_1^{(||)},c_2^{(||)})]\) is a bilinear form on \((x,y)\) and \((c_1^{(||)},c_2^{(||)})\), and its coefficients depend on \(\varvec{n}\) and are of the order of unity.
When integrating (7.103) over \(x\) and \(y\), the fact of a large width of the texture ODF, which is broader than the diffraction peak, results in the estimate:
The largest contribution in (7.103) is made by the values \((c_1^{(||)},c_2^{(||)})\) which are less than \(1/H l_d\) and, therefore, all the terms containing \((c_1^{(||)},c_2^{(||)})\) can be assumed to be constant except of the exponent \(e^{i H_0 K[(x,y),(c_1^{(||)},c_2^{(||)})] }\). This turns the integral over \((c_1^{(||)},c_2^{(||)})\) into delta-function of \(x,y\), and the intensity is proportional to Fourier image \(g(0,0,z)\), that corresponds to (6.134), see Fig. 6.4.3. Alternatively, to integrate over \((c_1^{(||)},c_2^{(||)})\), the integral over \(x,y\) can be replaced by a delta-function, according to criteria (7.104). In other words, the Bragg condition is re-written as \(\delta (\varvec{Q}-\varvec{H}(\varvec{c}))\). The Jacobian, the weight function and other terms cancel each other, and the expression can be obtained:
Thus, the measured X-ray intensity is a sum of intensities from all grains with the orientations different by the angle \(\alpha \) from the vector \(\varvec{H}\).
The residual stress analysis requires the measurement of the intensity maximum in the direction \(\varvec{y}\). The position of the maximum of (7.105) is calculated by using a cumulant expansion:
The correlation function \(g(0,0,z)\) is usually symmetric, and therefore the second term in the cumulative expansion does not influence the diffraction peak position. Provided the third and further odd cumulative terms decrease slower than correlation function, the position of the maximum \(Q_m\) is defined by the first cumulative term:
This equation is equivalent of (7.4).
With the known relationship between the strain and the macroscopic residual stress in the grain, the residual stresses in the sample can be determined on the basis of (7.107). This basic expression for the X-ray stress analysis has been derived using several physical assumptions. For the traditional metallic samples these assumptions are valid in the majority of the cases, however, when analyzing the modern materials possessing the strong texture or intentionally designed nanoscale structure, the above described approximations have to be carefully validated.
7.4 Residual Stress in Macroscopically Isotropic Materials. X-Ray Elastic Constants
The polycrystal is macroscopically isotropic when all crystallite orientations are equiprobable (absence of texture) and all directions inside macroscopical polycrystal are equivalent. The mechanical elastic properties are then defined by two parameters, for example, by bulk and rigidity moduli. The macroscopically isotropic case is realized in the absence of texture in the models of Voigt, Reuss and Eshelby-Kröner for spherical grainsFootnote 3. In the models of Vook-Witt and inverse Vook-Witt, even in the absence of texture there is an anisotropy due to the operators \(\varvec{\varPi }_{\bot }\) and \(\varvec{\varPi }_{||}\), which distinguish the normal direction to the surface.
To determine the stresses by X-ray method, the position of the diffraction peak in the direction \(\varvec{y}\) has to be related to the macroscopic stress \(\langle \sigma _{ij}\rangle ^{(S)}\). As follows from (7.107), the peak shift defines the value:
where the braces mean the averaging over the grains contributing to diffraction. The connection between the stress and the strain in coordinate system \(S\) is given by the Eq. (7.16). To write the expression (7.108) in the coordinate system \(S\), the fact of the coincidence of the direction of vector \(\varvec{H}^{(0)}\) and \(\varvec{y}\) due to the Bragg condition is used (see also the logic of the derivations from (7.105) to (7.107)). Using (7.16), we obtain:
or in indexless form:
To perform the integration over the angle \(\alpha \), the components of the 4-th rank tensor \(\varvec{A}\) have to be transformed from the coordinate system \(C\) into the system \(S\), which is done by four times convolution:
The operation requires the transformation of 81 components resulting in the cumbersome expressions. To make the results compact, the Voigt notations are used [4], which take into account the symmetry property \(c_{ijkl}=c_{(\underline{i}\underline{j})kl}=c_{ij(\underline{k}\underline{l})}=c_{(\underline{ij}\underline{kl})}\). In the result, the 4-th rank tensor is represented as symmetric \(6\times 6\) matrix, which has 21 component. This number is equal to the number of parameters, required to describe the elastic properties of crystal with a lowest monoclinic symmetry. The cubic crystal has 3 independent components, and the transformation (7.111) contains the exceeding number of operations in this case. Below the transformation of (7.111) is described, which takes into account the high symmetry of the tensor [48]. We separate the isotropic part of the tensor, which is not undergoing to the transformations, and the averaging over the orientations is thus reduced to the truncation of the anisotropic components.
From the point of view of the group theory, the 4-th rank tensors form the representation space of the rotation group, and it can be decomposed into irreducible representation (IR) spaces [49]. In the case of a lowest triclinic symmetry, the stiffness (compliance) tensor is decomposed in:
The basis tensors \(\varvec{\sigma }_{s}, \varvec{\delta }_{d,m}, \varvec{\eta }_{m}\) can be calculated with the help of the Clebsch-Gordan coefficients \(C_{j_1,m_1;j_2,m_2}^{j,m}\) starting from the circular vectors:
which are the IR of weight \(l=1\):
The basic tensors (7.112) possess a completeness property (any stiffness or compliance tensor can be expanded using them) and are mutually orthogonal:
where the symbol \({::}\) means the convolution over 4 indices: \(\varvec{a} {::} \varvec{b}^*=a_{ijkl}b^*_{ijkl}\).
The IR decomposition highlights the symmetry properties of the compliance tensor and separates its isotropic and anisotropic parts, e.g. the stiffness tensor for cubic system has the form:
where the Voigt notations are used, \(A=\frac{C_{11}-C_{12}}{2C_{44}}\) is the Zener’s anisotropy factor. In isotropic case \(A=1\), the anisotropic part \(\varvec{\eta }_c\) disappears.
The rotation transformation in the subspace of IR of weight \(l\) is performed by using the angular momentum matrices. For the rotation described by the vector parameter \(\varvec{c}\), the expression is [41]:
where \(\varvec{J}\) is the vector \((J_x,J_y,J_z)\) composed of the matrices of angular momentum.
Besides the transformation of tensors from one coordinate system into another, the multiplication of tensors and the inversion are the important operations for calculation of the tensor \(\varvec{A}\) on the basis of Eqs. (7.22), (7.63) and (7.69). Using the Voigt notations, these operations are reduced to the multiplication and inversion of \(6\times 6\) matrices. This approach, however, does not take into account the symmetry of the tensor. Using the expansion (7.112), the tensors \(\varvec{\sigma }_{1},\varvec{\sigma }_{2},\varvec{\eta }_c\) are shown below to create a closed group with respect to the operation of multiplication (convolution over two indices), which is written as:
Thus, for the macroscopically isotropic media consisting of the grains with a cubic symmetry, the 4-th rank tensor is expanded into tensors \(\varvec{\sigma }_{1},\varvec{\sigma }_{2}\) and \(\varvec{\eta }_c\):
The averaging over the orientations is then reduced to the truncation of anisotropic part:
The necessity to use the special representation of tensors occurs also for the energy functionals (7.44) and (7.45). The inequalities (7.47) and (7.46) make the restrictions to the tensor characteristics determining the system energy and not to the components of the stiffness tensor. The elastic energy of the unity volume of sample \(\varvec{\epsilon }: \varvec{C} : \varvec{\epsilon }/ 2\) is a quadratic form with respect to the strain \(\varvec{\epsilon }\). Because of the elastic energy can not be negative, this quadratic form is always positively defined. To understand which values are restricted by the inequalities for elastic energy, the Voigt notations are used and the \(6\times 6\)stiffness matrix is presented on the basis of eigenvectors:
here \(\lambda _{\nu }\) are the eigenvalues, \(\varvec{e}_{\nu ,i}\) are the eigenvectors, and the summation over \(i\) corresponds to the degenerated eigenvectors. The positive definition means \(\lambda _{\nu }>0\), and the inequality (7.46) is equivalent to the inequalities for eigenvalues \(\lambda _{\nu }^{C}\le \lambda _{\nu }^{C_M}\). Thus, the inequalities (7.47) and (7.46) constrain the eigenvalues of the tensors.
The representation (7.121) is also convenient due to the simplification of the multiplication table (7.118). For example, using the expansion for the crystals with a cubic system [18]:
which coincides with the expression (7.121), the analogue of the above table is written as:
The relation between the expressions (7.122) and (7.119) is simple:
and the product of the tensors and the inverse tensor are:
The inverse relation between representations is found to be:
Thus, the products of the tensors and the inverse tensor are calculated conveniently using the expression (7.122), and the averaging and the transformation between different coordinate systems using the expression (7.119) are simplified. The similar expressions can be constructed for low symmetry tensors, too [50].
As follows from (7.22), (7.25), (7.63) and (7.69), the formula for tensor \(\varvec{A}_n\) for \(n\)-th grain contains the isotropic tensors only (\(\varvec{C}_M\) and \(\varvec{E}\)) and the stiffness tensor of \(n\)-th grain \(\varvec{c}_n\). Applying the tensor operations of summation, multiplication and inversion for isotropic tensors and tensor \(\varvec{c}_n\), the resulting tensor can be presented in the form of (7.119). The tensor \(\varvec{A}_n\) in the coordinate system \(C\) is then written as:
and for the grains composed of the same material, the formula (7.127) does not depend on the orientation of the grain. Because of the isotropic tensors \(\varvec{\sigma }_{1}\) and \(\varvec{\sigma }_{2}\) are not modified with the transformations between the coordinate systems, the integral in (7.110) is calculated as:
where \(\hat{\varvec{T}}^{(SC)}\) is the symbol meaning the transformation of the tensor components either by (7.111) or (7.117).
To calculate the tensor \(\overline{\varvec{\eta }_c}\), we use the basis IR with the weight \(l=4\), where the transformation is performed by the matrices (7.117). For calculation of (7.117), the parametric vector \(\varvec{c}^{(SC)}\) has to be defined as a function of angle \(\alpha \). The expression (7.101) presents the transformation from the coordinate system \(C\) to the system \(L\), and in a way similar to (7.101), the parametric vector \(\varvec{c}^{(SL)}\) can be found, which corresponds to the transition from \(L\) to \(S\):
As a result, the parametric vector \(\varvec{c}^{(SC)}(\alpha )\) is obtained as a combination of the sequential transformations from the system \(C\) to the system \(L\), and then from \(L\) to \(S\):
In this expression, the only transformation depending on the angle \(\alpha \) is the one corresponding to the parametric vector \(\tan \frac{\alpha }{2}\varvec{e}_z\). This fact helps to calculate the integral over \(\alpha \), using the diagonal form of the matrix \(J_z\) and the formula (7.117):
From this equation, for the matrix of transformation in the space IR with the weight \(l=4\), we obtain:
and for \(\varvec{\eta }_c\) the following formula is found:
where the coefficients \({\eta _{c}}_{n'}\), defining the value \(\varvec{\eta }_{c}\) in the expansion over the basis \(\varvec{\eta }_{n'}\) in (7.112) are taken from the equation (7.116). To calculate the function (7.110) with the values (7.128) and (7.133), the direction of vector \(\varvec{y}\) in coordinate system \(S\) and the orientation of the reciprocal lattice vector in the system \(C\) have to be fixed:
The matrices \(\varvec{y}\otimes \varvec{y}:\varvec{\sigma }_{2}\) and \(\varvec{y}\otimes \varvec{y}:\overline{\varvec{\eta }_c}\) are found to be proportional each to other. The Eq. (7.110) can then be presented in a universal form by using X-ray elastic constants (XEC), which leads to the Eq. (7.11) with:
where the dependence on the Miller indices \(hkl\) of the reciprocal lattice vector is given by the invariant \(\Gamma \):
Below we consider XEC for polycrystals of a cubic symmetry for various models of grain interaction.
7.4.1 Voigt Model
According to (7.21) and (7.22), the tensor (7.116) has to be averaged and then inversed. Using formula (7.119), the averaging is carried out by (7.120):
By using the relationship (7.122) and the representation (7.124), the inverse tensor is found with the help of (7.125):
In the formula (7.135) for XEC, using the Eqs. (7.119) and (7.126), we obtain the expression (7.138) in the form of (7.119), and from (7.135):
These expressions are independent on the Bragg reflection \(hkl\).
7.4.2 Reuss Model
The X-ray elastic constants have a simple form if using the components of the compliance tensor \(\varvec{S}\). The tensor \(\varvec{A}\) coincides with the compliance tensor, and in the form of (7.119) is written as:
Substituting this equation into (7.135), we obtain:
7.4.3 Eshelby-Kröner Model
The Voigt and Reuss models are the limiting cases of the grain interaction. The previous section considered the narrower than those two bounds for the bulk elastic modules. The transfer of the results obtained in this section to the XEC bounding has to be done with a caution. The values of XEC are determined by the averaging over the angle \(\alpha \) and not by the averaging over the orientations. As a result, the equation (7.135) contains the dependence on the anisotropic part and on the Miller indices.
Nevertheless, several general conclusions can be made on the basis of the estimates for the boundaries of the macroscopic elastic modules. For simple case of rotationally symmetric biaxial stress state, and from the expression (7.135) for (7.11) we obtain:
As follows from the expressions (7.118) and (7.120), the component \(a_1=3\kappa \) is not mixed with other components in tensor operations, and for all the models the equality \(A_1=\frac{1}{C_{11}+2 C_{12}}\) is satisfied. Thus, according to (7.142), the \(\sin ^2\psi \) plots for all models in case of rotationally symmetric biaxial stress cross the same point at \(\sin ^2\psi =2/3\).
The inclination angle of \(\sin ^2\psi \) plot is defined by the parameters \(A_2\) and \(A_{\eta }\). Using the representation (7.122), the following relationship is received:
The definition (7.136) shows that the inequality is satisfied: \(0\le \Gamma \le 1/3\), which means the values \(1-3\Gamma \) and \(3\Gamma \) are always positive. To determine the limits of the function \(\sin ^2\psi \), the variation limits of \(\mu _A\) and \(\mu _A'\) have to be found. Assuming the strain fields are uniform inside the grain (7.48), the macroscopic compliance tensor depends on the tensor \(\varvec{A}\) as:
The boundaries for macroscopic elastic moduli are defined by the boundaries of parameters \(\kappa _s\) and \(\mu _s\). As follows from (7.144), the limits for \(\mu _s\) determine the limits of the linear combination \(2\mu _A+3\mu '_A\), and thus constrain the limits of the function \(\sin ^2\psi \) only at \(\Gamma =1/5\). However, the models defining the boundaries of the macroscopic moduli are frequently considered to constrain the \(\sin ^2\psi \) plot, too (Fig. 7.7).
a \(\sin ^2\psi \) plot for Cu sample possessing the residual stress of 200 MPa, the Bragg \((200)\) reflection, for the models of Voigt (V) and Reuss (R), and for the boundary models of Hashin-Strickman (HS) and Eshelby-Kröner (E-K). b The dependence \(\mu _A\) at fixed \(C_{11}\) and \(C_{12}\) for the same models. The models determining the boundaries for macroscopic moduli constrain the parameters \(\mu _A\) and \(\mu _A'\); for HS model, the tensor \(\varvec{A}\) from (7.63) has been used
Within the approximation of strain uniformity inside the grain (7.48) and spherical symmetry of the correlation function of grains (7.53), the Eshelby-Kröner model satisfies the equation (7.43), which is due to the self-consistency of the tensor \(\varvec{C}\) in the Eq. (7.67). In the case of macroscopically isotropic media, spherically symmetric correlation function of grain shape and the cubic symmetry of the crystallites, this equation can be essentially simplified [21, 23]. In that case, the tensor \(\varvec{E}\) is found by the analytical integration of (7.57), and for the representation (7.122) we obtain:
To calculate the expression (7.67), the representation (7.122) is used again for multiplication and inversion of tensors and the representation (7.118) for the averaging. As a result, the following equation is derived:
where the parameters \(\kappa _C\) and \(\mu _C\) characterize the macroscopic tensor \(\varvec{C}\), the parameters \(\kappa ,\mu \) and \(\mu '\) describe the stiffness tensor of the crystallite with a cubic symmetry. The system (7.146) contains 2 independent equations, and taking into account the positiveness of values \(\kappa _C,\mu _C,\kappa ,\mu \) and \(\mu '\), we have:
The parameter \(\kappa _C\), which has a physical meaning of a bulk modulus, has the same value for both Voigt and Reuss models, and thus \(\kappa _C=\kappa \) is an exact solution. The cubic equation for \(\mu _C\) has a single positive root, and the expression (7.147) defines comprehensively the tensor \(\varvec{C}\). When tensor \(\varvec{C}\) is known, the XEC are found by substituting (7.69) into (7.135):
7.5 Residual Stress in Macroscopically Anisotropic Materials. X-Ray Stress Factors
In the presence of texture or direction-dependent grain interaction, the relation between strain \(\{\epsilon _H(\varvec{y})\}\) and macroscopic stress in polycrystal can not be presented by Eq. (7.11). To confirm this fact, the changes implemented by a macroscopic anisotropy in the equations (7.108) - (7.136) are considered below. The relationship between the strain \(\{\epsilon _H(\varvec{y})\}\) and the macroscopic stress in polycrystal (7.110) becomes:
The ODF function \(f(\varvec{c})\) is a function of the orientation of the system \(C\) relatively to the system \(S\). The parametric vector (7.130) depending on the vector \(\varvec{y}\) and angles \(\psi ,\phi \) is an argument of ODF, and the right part of (7.149) may have different kinds of dependency from the angles \(\psi \) and \(\phi \). This means the non-linearity of \(\sin ^2\psi \) plot, and the XEC provided by (7.11) and (7.136) are not sufficient for proper data interpretation. In this situation, the expression (7.149) is written in the form:
and the functions \(\varvec{F}(\varvec{y})\) defined in the coordinate system \(S\) are called X-ray stress factors (XSF).
As follows from (7.150), to calculate XSF, the tensor \(\varvec{A}\), which characterizes the grain with the orientation \(\varvec{c}(\alpha )\), has to be found in the coordinate system \(S\). For macroscopically isotropic models, the tensor \(\varvec{A}\) in the coordinate system \(C\) is equal for all crystallites independently on their orientations. Mathematically it is a consequence of the fact that the macroscopic tensors \(\varvec{C}\) and \(\varvec{E}\) are the isotropic tensors, which are independent on the coordinate system. In the case of macroscopically anisotropic polycrystal, the macroscopic tensors are generally anisotropic. As a result, to calculate the tensor \(\varvec{A}\), the operations with the anisotropic tensors have to be carried out in different coordinate systems. The final product of these tensors is not expressed through the tensors themselves, and the analogue of (7.118) can not be constructed using a small number of basic elements. Below we discuss the XSF calculation algorithms for different grain interaction models.
7.5.1 Voigt Model
In accordance with (7.21) and (7.22), the tensor (7.116) has to be averaged and then inverted. The averaging is carried out with an accounting of ODF as described in the Eq. (7.21). After these procedures, the tensor \(\varvec{A}\) being equal for all crystallites is derived in the coordinate system \(S\), and by the reduction of the integral over \(\alpha \) the XSF are:
Here the value \(\langle \varvec{c}\rangle ^{-1}\) is constant and XSF are independent on \(hkl\). The dependence on the angles \(\psi \) and \(\phi \) is contained in the term \(\varvec{y}\otimes \varvec{y}\). As a consequence, the plot of residual stress versus angles \(\psi \) and \(\phi \) depends quadratically on the trigonometric functions, but in general case differs from (7.11).
7.5.2 Reuss Model
In the Reuss model, the tensor \(\varvec{A}\) is equal to the compliance tensor of a crystallite (7.25). Because of the expression for the tensor \(\varvec{A}\) does not contain the operations with macroscopic tensors, the expansion (7.119) can be used, which results similarly to (7.128) in:
This formula can be applied in an analytical form in the important case of the textured materials described by axial or spherical components [51, 52]. The ODF in this case is modeled by simple functions describing the grain groups, which have allocated orientation and the distribution of the directions, for example, ODF in a form of:
here \(\varvec{c}_p\) is a vector-parameter specifying the primary orientation, \(N\) is a normalization constant, \(1/S\) describes the spread of the directions, \(\text {Tr}\) is a trace of the matrix. Using the explicit form of the matrix (7.96), we obtain:
and utilizing the expressions for \(\varvec{c}^{(SC)}(\alpha )\) in (7.130), the ODF dependence on the angle \(\alpha \) is:
where \(\beta _B\) and \(\phi _B\) are the angles defining the unity vector in the coordinate system \(C\) along the reciprocal lattice vector (Fig. 7.2).
The analogous relationships can be found for axial components, with ODF:
where \(\varvec{f}_{p}\) is a vector of primary fiber direction in the coordinate system \(S\), \(\varvec{n}_p\) is a primary fiber vector in the coordinate system \(C\), \(N\) is a normalization coefficient, and \(1/S\) defines the characteristic distribution of the directions. By utilizing the explicit form of the transformation matrix (7.96) and using the expressions for \(\varvec{c}^{(SC)}(\alpha )\) in (7.130), the following formulas are derived:
In both axial and spherical component cases, the dependence of ODF on the angle \(\alpha \) is expressed as \(e^{k_1\cos (\alpha +k_2)}\). Similar to the Eqs. (7.130)–(7.131), the transformation matrix \(\hat{\varvec{T}}^{(SC)}(\alpha )\) in (7.152) has a form \(e^{i n \alpha }\). By using the equation:
with \(I_m\) being a modified Bessel function of \(m\)-th order and applying (7.158), (7.157) and (7.155), we obtain for (7.152):
Here the notations of (7.133) have been used, and the angles \(\omega ,\phi \) for the spherical components are:
and for the case of axial components:
This formula can be generalized for \(\varvec{S}\) tensor of arbitrary symmetry [53].
The expression (7.159) demonstrates the transition from XSF to XEC. From one hand, the relation between the measured strain and the stress (7.11) takes a place in a case of the isotropic material. As follows from (7.159) and (7.152), in isotropic case \(A=1\), the anisotropic part \(S_{\eta }=0\) disappears along with the term of texture. From the other hand, in the limit of the isotropic ODF, the value \(S\) tends to zero, the functions \(I_l(S\omega )\) tend to zero, except of \(I_0(S\omega )\), and we obtain the expression (7.133), which results in (7.11).
7.5.3 Eshelby-Kröner Model
In the presence of texture, the Eq. (7.67) becomes very cumbersome. In opposite to the isotropic case, where the simple analytical expression (7.145) exists, the relation between \(\varvec{E}\) and \(\varvec{C}\) in anisotropic polycrystals is given by cumbersome integrals (7.57) and (7.58). The averaging procedure involves ODF, which again complicates the calculations comparing to the isotropic sample, where the equation (7.120) is valid. As a result, the expressions (7.67) become a system of non-linear equations, where the analytical solution similar to (7.147) is not possible.
\(\sin ^2\psi \) plot for Cu sample with symmetric biaxial stress 200 MPa, for (420) Bragg reflection for Voigt (V), Reuss (R), Eshelby-Kröner (E-K), Vook-Witt (VW), and inverse Vook-Witt (iVW) models. The axial texture with half-width \(1/S=20\) degree is included in the simulations, and \(\varvec{f}_p\) coincides with the normal \(\varvec{n}_p\) in the direction (111). The dashed line shows the value \(\int d \alpha f(\varvec{c}^{(SC)}(\alpha ))\), which is proportional to the intensity of reflection at fixed \(\psi \) and \(\phi \)
The appropriate solution for the textured polycrystals is a construction of the iterative procedure based on (7.67) for calculation of the tensor \(\varvec{C}\) [33, 34]. For example, the Eq. (7.66) is re-written as:
where the second term in the right side equals to zero for the exact solution of (7.67). By expressing the strain \(\epsilon ^{(0)}\) through the stress \(\langle \varvec{\sigma }\rangle \) using the macroscopic compliance tensor \(\varvec{S}=\varvec{C}^{-1}\), the following equation is obtained:
Based on this equation, the iterative scheme can be constructed as follows:
where \(\varvec{E}^{(n)}\) is calculated using \(\varvec{C}^{(n)}={\varvec{S}^{(n)}}^{-1}\). The coefficient \(f\) is determined empirically: the small values of \(f\) provide the convergence, however, require longer iterations, whereas the large values of \(f\) make the iterations unstable. Using (7.69) and (7.150), the expression for XSF is:
with macroscopic tensors \(\varvec{E},\varvec{C},\varvec{S}=\varvec{C}^{-1}\) being defined in the coordinate system \(S\) and stiffness tensor of a separate crystallite \(\varvec{c}\) being defined in the coordinate system \(C\).
7.5.4 Vook-Witt and Inverse Vook-Witt Models
Unlike the above discussed models, the Vook-Witt and inverse Vook-Witt models implement the macroscopic anisotropy in the absence of texture.Footnote 4 The basic expressions (7.84)–(7.87) contain the anisotropic tensors \(\varvec{\varPi }_{\bot }\) and \(\varvec{\varPi }_{||}\), which distinguish the direction of a surface normal among others (Fig. 7.8 and 7.9).
\(\sin ^2\psi \) plot for Cu sample with symmetric biaxial stress 200 MPa and for Bragg reflection (200) in the absence of texture for Voigt (V), Reuss (R), Eshelby-Kröner (E-K), Vook-Witt (VW) and inverse Vook-Witt (iVW) models. The morphologic texture inherent in Vook-Witt and inverse Vook-Witt models leads to the non-linearity even in the absence of the orientational texture
The presence of texture incorporates another source of a macroscopic anisotropy. Basing on the formulas (7.150) and (7.84), the following expression is obtained for XSF:
Here the macroscopic tensors are defined in the coordinate system \(S\), and the stiffness tensor of a separate crystallite \(\varvec{c}\) in a coordinate system \(C\).
Notes
- 1.
The parenthesis near underlined indices mean the symmetrization operation, \(a_{(\underline{i}\underline{j})kl}\equiv \frac{1}{2}(a_{ijkl}+a_{jikl})\). In these notations, the symmetry of stiffness tensor relatively the transposition of indices has a form \(c_{ijkl}=c_{(\underline{i}\underline{j})kl}=c_{ij(\underline{k}\underline{l})}=c_{(\underline{ij}\underline{kl})}\), where the latter equality means the symmetry with respect to the transposition of index pair.
- 2.
To clarify whether the tensor is positive definite, the special representation (7.121) is used (see Sect. 7.4). In this representation, the positive definition corresponds to \(\varvec{C}\,{=}\,(3\kappa _c,2\min (\mu _c,\mu _c'),2\min (\mu _c,\mu _c'))\), and negative definition to \(\varvec{C}\,{=}\,(3\kappa _c,2\max (\mu _c,\mu _c'),2\max (\mu _c,\mu _c'))\), respectively.
- 3.
- 4.
A similar situation occurs in Eshelby-Kröner model with the elliptical grains possessing a certain orientation [5].
References
V.K. Pecharsky, P.Y. Zavalij, Fundamentals of Powder Diffraction and Structural Characterization of Materials (Springer, New York, 2005)
E.J. Mittemeijer, P. Scardi (eds), Diffraction Analysis of the Microstructure of Materials (Springer, Berlin, 2004)
U.F. Kocks, C.N. Tom\(\acute{e}\), H.-R. Wenk, Texture and Anisotropy: Preferred Orientations in Polycrystals and Their Effects on Material Properties (Cambridge University Press, Cambridge, 1998)
I.C. Noyan, J.B. Cohen, Residual Stress: Mesurements by Diffraction and Interpretation (Springer, Berlin, 1987)
U. Welzel, S. Freour, E.J. Mittemeijer, Direction-dependent elastic grain-interaction models a comparative study. Phil. Mag. 85(21), 2391–2414 (2005)
T. Ungár, Dislocation densities, arrangements and character from X-ray diffraction experiments. Mater. Sci. Eng. A 309, 14–22 (2001)
L.D. Landau, E.M. Lifshitz, Theory of Elasticity, vol. 7, 3rd edn (Butterworth-Heinemann, Oxford, 1986)
Mario Birkholz, Thin Film Analysis by X-Ray Scattering (Wiley, Weinheim, 2006)
E. Macherauch, P. Müller, Das \(\sin ^2 \psi \) - Verfahren der röntgenographischen Spannugsmessung. Zeitschrift angewandte Physik 13, 305–312 (1961)
V. Uglov, V. Anischik, S. Zlotski, I. Feranchuk, T. Alexeeva, A. Ulyanenkov, J. Brechbuehl, A. Lazar. Surf. Coat. Technol. 202, 2389 (2009)
A. Benediktovich, H.H. Guerault, I. Feranchuk, V. Uglov, A. Ulyanenkov, Influence of surface roughness on evaluation of stress gradients in coatings. Mater. Sci. Forum 681, 121–126 (2011)
V. Hauk, Structural and Residual Stress Analysis by Nondestructive Methods: Evaluation-Application-Assessment (Elsevier Science, Amsterdam, 1997)
B.B He, Two-dimensional X-ray Diffraction (Wiley, New Jersey, 2009)
Z. Hashin, Analysis of composite materials. J. Appl. Mech. 50(2), 481–505 (1983)
G.W. Milton, The coherent potential approximation is a realizable effective medium scheme. Commun. Math. Phys. 99(4), 463–500 (1985)
R.J. Gehr, R.W. Boyd, Optical properties of nanostructured optical materials. Chem. Mater. 8(8), 1807–1819 (1996)
I.M. Lifshitz, L.N. Rosenzweig, To the theory of elastic properties of the polycrystals. Russ. J. Exp. Theoret. Phys. 16(11), 967–980 (1946)
J.R. Willis, Variational and related methods for the overall properties of composites. Adv. Appl. Mech. 21, 1–78 (1981)
Jr. W.F. Brown, Solid mixture permittivities. J. Chem. Phys. 23(8), 1514–1517 (1955)
D.A.G Bruggeman, The calculation of various physical constants of heterogeneous substances. I. The dielectric constants and conductivities of mixtures composed of isotropic substances. Ann. Phys. 24(132), 636–679 (1935)
T. Mura, Micromechanics of Defects in Solids (Springer, New York, 1987)
J.D. Eshelby, The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A. Math. Phys. Sci. 241(1226), 376–396 (1957)
E. Kröner, Berechnung der elastischen Konstanten des Vielkristallsaus den Konstanten des Einkristalls. Zeitschrift für Physik A Hadrons and Nuclei 151(4), 504–518 (1958)
U. Welzel, J. Ligot, P. Lamparter, A.C. Vermeulen, E.J. Mittemeijer. Stress analysis of polycrystalline thin films and surface regions by x-ray diffraction. J. Appl. Crystallogr. 38(1), 1–29 (2005)
A. Andryieuski, S. Ha, A.A. Sukhorukov, Y.S. Kivshar, A.V. Lavrinenko, Bloch-mode analysis for retrieving effective parameters of metamaterials. Phys. Rev. B 86(3), 035127 (2012)
T. Maas Harald Wern, N. Koch, Self-consistent calculation of the X-ray elastic constants of polycrystalline materials for arbitrary crystal symmetry. Mater. Sci. Forum. 404–407, 127–132 (2002)
R.A. Lebensohn, O. Castelnau, R. Brenner, P. Gilormini, Study of the antiplane deformation of linear 2-d polycrystals with different microstructures. Int. J. Solids Struct. 42(20), 5441–5459 (2005)
W. Voigt, Lehrbuch der Kristallphysik (Leipzig Teubner, 1910)
A. Reuss, Berechnung der Fliessgrenze von Mischkristallen auf Grund der Plastizitatsbedingung fuer Einkristalle. ZAMM J. Appl. Math. Mech. / Zeitschrift fur Angewandte Mathematik und Mechanik 9(1), 49–58 (1929)
R Hill, The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A. 65(5), 349 (1952)
R.J. Asaro, D.M. Barnett, The non-uniform transformation strain problem for an anisotropic ellipsoidal inclusion. J. Mech. Phys. Solids. 23(1), 77–83 (1975)
Z. Hashin, S. Shtrikman, A variational approach to the theory of the elastic behaviour of polycrystals. J. Mech. Phys. Solids. 10(4), 343–352 (1962)
G. Kneer, Uber die Berechnung der Elastitatsmoduln vielkristallner Aggregate mit Textur. physica status solidi (b). 9(3), 825–838 (1965)
N. Koch, U. Welzel, H. Wern, E.J. Mittemeijer, Mechanical elastic constants and diffraction stress factors of macroscopically elastically anisotropic polycrystals: the effect of grain-shape (morphological) texture. Phil. Mag. 84(33), 3547–3570 (2004)
L.D. Landau, E.M. Lifshitz, J.B. Sykes, J.S. Bell, M.J. Kearsley, L.P. Pitaevskii, Electrodynamics of Continuous Media, vol. 364 (Pergamon Press, Oxford, 1960)
J.A. Osborn, Demagnetizing factors of the general ellipsoid. Phys. Rev. 67(11–12), 351–357 (1945)
U. Welzel, M. Leoni, E.J. Mittemeijer, The determination of stresses in thin films; modelling elastic grain interaction. Phil. Mag. 83(5), 603–630 (2003)
D. Faurie, O. Castelnau, R. Brenner, P.O. Renault, E. Le Bourhis, P. Goudeau, In situ diffraction strain analysis of elastically deformed polycrystalline thin films, and micromechanical interpretation. J. Appl. Crystallogr. 42(6), 1073–1084 (2009)
R.W. Vook, F. Witt, Thermally induced strains in evaporated films. J. Appl. Phys. 36(7), 2169–2171 (1965)
M. Leoni, U. Welzel, P. Lamparter, EJ Mittemeijer, J.D. Kamminga, Diffraction analysis of internal strain-stress fields in textured, transversely isotropic thin films: theoretical basis and simulation. Phil. Mag. A. 81(3), 597–623 (2001)
F.I. Fedorov, The Lorentz Group (Nauka, Moscow, 1979)
E.J. Mittemeijer, Fundamentals of Materials Science: The Microstructure-Property Relationship Using Metals as Model Systems (Springer, Heidelberg, 2011)
T. Ungár, J. Gubicza, G. Ribárik, A. Borbély, Crystallite size distribution and dislocation structure determined by diffraction profile analysis: principles and practical application to cubic and hexagonal crystals. J. Appl. Crystallogr. 34(3), 298–310 (2001)
G. Ribarik, T. Ungar, Characterization of the microstructure in random and textured polycrystals and single crystals by diffraction line profile analysis. Special topic section: local and near surface structure from diffraction. Mater. Sci. Eng. A, 528(1), 112–121 (2010)
H.J. Bunge, P.R. Morris, Texture Analysis in Materials Science: Mathematical Methods (Butterworths, London, 1982)
G.A. Korn, T.M. Korn, Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review (Dover Publications, Mineola, 2000)
I.M. Gelfand, R.A. Minlos, Z.Y. Shapiro, H.K. Farahat, Representations of the Rotation and Lorentz Groups and Their Applications, vol. 35 (Pergamon Press, New York, 1963)
A. Benediktovitch, F. Rinaldi, S. Menzel, K. Saito, T. Ulyanenkova, T. Baumbach, I.D. Feranchuk, A. Ulyanenkov, Lattice tilt, concentration, and relaxation degree of partly relaxed InGaAs/GaAs structures. Phys. Status Solidi (a). 208(11), 2539–2543 (2011)
Y.I. Sirotin, M.P. Shaskolskaya, The Basics of Crystallophysics (Nauka, Moscow, 1975)
L.J. Walpole, On the overall elastic moduli of composite materials. J. Mech. Phys. Solids. 17(4), 235–251 (1969)
S. Matthies, K. Helming, T. Steinkopff, K. Kunze, Standard distributions for the case of fibre textures. Phys. Status Solidi (b). 150(1), K1–K5 (1988)
T. Eschner et al., Texture analysis by means of model functions. Textures Microstruct. 21, 139–139 (1993)
A. Benediktovich, I. Feranchuk, A. Ulyanenkov, Calculation of X-ray stress factors using vector parameterization and irreducible representations for SO(3) group. Mater. Sci. Forum. 681, 387–392 (2011)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2014 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Benediktovitch, A., Feranchuk, I., Ulyanenkov, A. (2014). X-Ray Diffraction Residual Stress Analysis in Polycrystals. In: Theoretical Concepts of X-Ray Nanoscale Analysis. Springer Series in Materials Science, vol 183. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-38177-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-642-38177-5_7
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-38176-8
Online ISBN: 978-3-642-38177-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)