Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The design of parallel metaheuristics [1], thanks to the increasing power offered by modern hardware architectures, is a natural research line in order to reduce the execution time of the algorithms, especially when solving problems of a high dimension, highly restricted, and/or time bounded. Parallel metaheuristics are often based on new different search patterns that are later implemented on physically parallel hardware, then improving the quality of results obtained by traditional sequential algorithms and also reducing their execution time. As a consequence, research on parallel metaheuristics has grown substantially in recent years, motivated by the excellent results obtained in their application to the resolution of problems in search, optimization, and machine learning.

Among parallel metaheuristics, Parallel Evolutionary Algorithms (PEAs) have been extensively adopted and are nowadays quite popular, mainly because Evolutionary Algorithms (EAs) are naturally prone to parallelism. For this reason, the study of parallelization strategies for EAs has laid the foundations for working in parallel metaheuristics. The most usual criterion for categorizing PEAs distinguishes three categories [3, 17]: the master–slave model (functional distribution of the algorithm), the distributed or island model (the population is partitioned into a small number of subpopulations that evolve in semi-isolation) [3], and the cellular model (the population is structured in overlapping neighborhoods with limited interactions between individuals) [2]. Although tied to hardware (clusters and multicores, especially), the previous research actually deals a lot with decentralization of search techniques, leaving the running platform sometimes as a background aid just to reduce time.

The use of Graphics Processing Units (GPUs) for general purpose computing (GPGPU) has experienced tremendous growth in recent years. This growth has been based on its wide availability, low economic cost, and inherent parallel architecture and also on the emergence of general purpose programming languages, such as CUDA [11, 20]. This fact has also motivated many scientists from different fields to take advantage of the use of GPUs in order to tackle general problems in various fields like numerical linear algebra [8], databases [21], model order reduction [5], and scientific computing [11].

GPGPU also represents an inspiring domain for research in parallel metaheuristics. Naturally, the first works on GPUs have gone in the direction of implementing the mentioned three categories of PEAs on this new kind of hardware [14]. Thus, many results show the time savings of running master–slave [18], distributed [30], and cellular [28, 29] metaheuristics on GPU, mainly Genetic Algorithms (GAs) [18, 22] and Genetic Programming [9, 14–16, 19] but also other types of techniques like Ant Colony Optimization [6], Differential Evolution [7], and Particle Swarm Optimization [31].

A different approach is not to take a regular existing family of algorithms and port it to a GPU but to propose new techniques based on the architecture of GPUs. Recently, two optimization algorithms have been proposed, Systolic Neighborhood Search (SNS) [4] and Systolic Genetic Search (SGS) [23], based on the idea of systolic computing.

The concept systolic computing was developed at Carnegie-Mellon University by Kung and Leiserson [12, 13]. The basic idea focuses on creating a network of different simple processors or operations that rhythmically compute and pass data through the system. Systolic computation offers several advantages, including simplicity, modularity, and repeatability of operations. This kind of architecture also offers transparent, understandable, and manageable but still quite powerful parallelism. However, this architecture had difficulties in the past, since building systolic computers was not easy and, especially, because programming high-level algorithms on such a low-level hardware was hard, error prone, and too manual. Now with GPUs we can avoid such problems and get only the advantages.

In the leading work on optimization algorithms using systolic computing, the SNS algorithm has been proposed, based on local search [4]. Then, we have explored a new line of research that involved more diverse operations. Therefore, we have proposed a novel parallel optimization algorithm that is based on the synchronous circulation of solutions through a grid of cells and the application of adapted evolutionary operators. We called this algorithm SGS [23]. In SGS [23], solutions flow across processing units according to a synchronous execution plan. When two solutions meet in a cell, adapted evolutionary operators (crossover and mutation) are applied to obtain two new solutions that continue moving through the grid. In this way, solutions are refined again and again by simple low-complexity search operators.

The goal of this work is to evaluate one of the new algorithms that can be proposed based on the premises of SGS. In the first place, we evaluate SGS regarding the quality of solutions obtained. Then, we focus on analyzing the performance of the GPU implementation of the algorithm on four different cards. This evaluation shows how changes produced in GPUs in a period of only 2 years impact on the runtime of the algorithm implemented. Considering the results in a broader perspective, it also shows the impressive progress on the design and computing power of these devices.

This chapter is organized as follows. The next section introduces the SGS algorithm. Section 3 describes the implementation of the SGS on a GPU. Then, Sect. 4 presents the experimental study considering several instances of the Knapsack Problem (KP) evaluated over four different Nvidia’s GPUs. Finally, in Sect. 5, we outline the conclusions of this work and suggest future research directions.

2 Systolic Genetic Search

In a SGS algorithm, the solutions are synchronously pumped through a bidimensional grid of cells. The idea is inspired by the systolic contraction of the heart that makes possible that ventricles eject blood rhythmically according to the metabolic needs of the tissues.

It should be noted that although SGS has points of contact with the behavior of Systolic Arrays (SAs) [10] and both ideas are inspired by the same biological phenomenon, they have an important difference. In SAs, the data is pumped from the memory through the units before returning to the memory, whereas in SGSs the data only circulates through the cells, all time.

At each step of SGS, as it is shown in Fig. 1, two solutions enter each cell, one from the horizontal (\(S_{\mathrm{H}}^{i,j}\)) and one from the vertical (\(S_{\mathrm{V}}^{i,j}\)), where adapted evolutionary/genetic operators are applied to obtain two new solutions that leave the cell, one through the horizontal (\(S_{\mathrm{H}}^{i,j+1}\)) and one through the vertical (\(S_{\mathrm{V}}^{i+1,j}\)).

Fig. 1
figure 1

Systolic cell

Full size image

The pseudocode of the SGS algorithm is presented in Algorithm 1. Each cell applies the basic evolutionary search operators (crossover and mutation) but to different, preprogrammed fixed positions of the tentative solutions that circulate throughout the grid. In this way, the search process is actually structured. The cells use elitism to pass on to the next cells the best solution among the incoming solution and the newly generated one by the genetic operators. The incorporation of elitism is critical, since there is no global selection process as in standard EAs.

Each cell sends the outgoing solutions to the next horizontal and vertical cells that are previously calculated, as shown in the pseudocode. Thus it is possible to define different cell interconnection topologies. In this work, and in order to make the idea of the method more easily understood, we have used a bidimensional toroidal grid of cells, as shown in Fig. 2.

Fig. 2
figure 2

Two-dimensional toroidal grid of cells

Full size image

In order to better illustrate the working principles of SGS, let us consider that the problem addressed can be encoded as binary string, with bit-flip mutation and two-point crossover as evolutionary search operators. We want to remark that the idea of the proposal can be adapted to other representations and operators. In this case (binary representation), the positions in which operators are applied in each cell are computed by considering the coordinates occupied by the cell in the grid, thus avoiding the generation of random numbers. Some key aspects of the algorithm such as the size of the grid and the calculation of the mutation point and the crossover points are discussed next.

2.1 Size of the Grid

The length and width of the grid should allow the algorithm to have a good exploration, but without increasing the population to sizes that compromise performance. In order to generate all possible mutation points at each row, the grid length is l (the length of the tentative solutions), and therefore each cell in a row modifies a different position of the solutions. For the same reason, the natural value for the width of the grid is also l. However, in order to keep the total number of solutions of the population within an affordable value, the width of the grid has been reduced to τ = ⌈lgl⌉. Therefore, the number of solutions of the population is 2 × l ×τ (two solutions for each cell).

2.2 Mutation

The mutation operator always changes one single bit in each solution. Figure 3 shows the general idea followed to distribute the points of mutation over the entire grid.

Fig. 3
figure 3

Distribution of mutation points across the grid

Full size image

Each cell in the same row mutates a different bit in order to generate diversity by encouraging the exploration of new solutions. On the other hand, cells in the same column should not mutate the same bit in order to avoid deteriorating the search capability of the algorithm. For this reason, the mutation points on each row are shifted div(l, τ) places.

Figure 4 shows an example of the mutation points of the cells from column j. The general formula for calculating the mutation point of a cell (i, j) is:

$$\displaystyle{ 1 + \left (\left (i - 1\right )\frac{l} {\tau } + j - 1\right )\mod l, }$$
(1)

where mod is the modulus of the integer division and the division in the formula is an integer division.

Fig. 4
figure 4

Mutation points for column j

Full size image

2.3 Crossover

Figure 5 shows the general idea followed to distribute the crossover points over the entire grid.

Fig. 5
figure 5

Distribution of crossover points across the grid

Full size image

For the first crossover point two different values are used in each row, one for the first l∕2 cells and another one for the last l∕2 cells. These two values differ by div(l, 2τ), while cells of successive rows in the same column differ by div(l, τ). This allows using a large number of different values for the first crossover point following a pattern known a priori. Figure 6 illustrates the first crossover point calculation. The general formula for calculating the first crossover point of a cell (i, j) is:

$$\displaystyle{ 2 + \frac{l} {\tau } (i - 1) + \frac{j - 1} { \frac{l} {2}} \frac{l} {2\tau }, }$$
(2)

where all the divisions in the formula are integer divisions.

Fig. 6
figure 6

First crossover point calculation

Full size image

For the second crossover point, the distance to the first crossover point increases with the column, from a minimum distance of 2 positions to a maximum distance of div(l, 2) + 1 positions. In this way, cells in successive columns exchange a larger portion of the solutions. Figure 7 illustrates the second crossover point calculation, being F 1 the first crossover point for the first l∕2 cells and F 2 the first crossover point for the last l∕2 cells. If the value of second crossover point is smaller than the first one, the values are swapped. The general formula for calculating the second crossover point of a cell (i, j) is:

$$\displaystyle{ 1 + \left (3 + \frac{l} {\tau } \left (i - 1\right ) + \frac{j - 1} { \frac{l} {2}} \frac{l} {2\tau } + \left ((j - 1)\mod \frac{l} {2}\right )\right )\mod l, }$$
(3)

where all the divisions in the formula are integer divisions.

Fig. 7
figure 7

Second crossover point calculation

Full size image

2.4 Exchange of Directions

As the length of the grid is larger than the width of the grid, the solutions moving through the vertical axis would be limited to only τ different mutation and crossover points, while those moving horizontally use a wider set of values. In order to avoid this situation, which can cause the algorithm not to reach its full potential, every τ iterations the two solutions being processed in each cell exchange their directions. That is, the solution moving horizontally leaves the cell through the vertical axis, while the one moving vertically continues through the horizontal.

3 SGS Implementation

This section is devoted to presenting how SGS has been deployed on a GPU. In this work we study the performance of the GPU implementation of SGS in four different Nvidia’s devices, so we provide a general snapshot of GPU devices and briefly comment some important differences between the devices used. Then, all the implementation details are introduced.

3.1 Graphics Processing Units

The architecture of GPUs was designed following the idea of devoting more transistors to computation than traditional CPUs [11]. As a consequence, current GPUs have a large number of small cores and are usually considered many-cores processors.

The CUDA architecture abstracts these computing devices as a set of shared memory multiprocessors (MPs) that are able to run a large number of threads in parallel. Each MP follows the Single Instruction Multiple Threads (SIMT) parallel programming paradigm. SIMT is similar to SIMD but in addition to data-level parallelism (when threads are coherent) allows thread-level parallelism (when threads are divergent) [11, 20].

When a kernel is called in CUDA, a large number of threads are generated on the GPU. The threads are grouped into blocks that are run concurrently on a single MP. The blocks are divided into warps that are the basic scheduling unit in CUDA and consist of 32 consecutive threads. Threads can access data on multiple memory spaces during their lifetime, being the most commonly used: registers, global memory, shared memory, and constant memory. Registers and shared memory are fast memories, but registers are only accessible by each thread, while shared memory can be accessed by any thread of a block. The global memory is the slowest memory on the GPU and can be accessed by any executing thread. Finally, constant memory is fast although is read-only for the device  [27].

The compute capability allows knowing some features of a GPU device. In this work we use a GPU with compute capability 1.1 (a GeForce 9800 GTX+), two with compute capability 1.3 (a Tesla C1060 and a GeForce GTX 285), and one with compute capability 2.0 (a GeForce GTX 480). Table 1 presents some of the most important features for devices with the compute capabilities considered in this work [20].

Table 1 Features according to compute capabilities of the device
Full size table

It should also be noted that the global memory access has improved significantly in devices with newer compute capabilities [20]. In devices with compute capability 1.1, each half-warp must read 16 words in sequence that lie in the same segment to produce a single access to global memory for the half-warp, which is known as coalesced access. Otherwise, when a half-warp reads words from different segments (misaligned reads) or from the same segment but the words are not accessed sequentially, it produces an independent access to global memory for each thread of the half-warp. The access to global memory was improved considerably in devices with compute capabilities 1.2 and 1.3, and threads from the same half-warp can read any words in any order in a segment with a single access (including when several threads read the same word). Finally, the devices with compute capabilities 2.0 include cached access to global memory.

3.2 Implementation Details

Figure 8 shows the structure of the GPU implementation of the SGS algorithm. The execution starts with the initialization of the population that runs in the CPU and solutions are transferred to the global memory of the GPU. Thus, the results obtained working with the same seed are exactly the same for the CPU and GPU implementations. This restriction can increase the runtime of the GPU implementation but simplifies the experimental analysis by focusing in the performance. Then, the constant data required for computing the fitness values is copied to the constant memory of the GPU. At each iteration, the crossover and mutation operators (crossoverAndMutation kernel), the fitness function evaluation (evaluate kernel), and the elitist replacement (elitism kernel) are executed on the GPU. Additionally, the exchange of directions operator (exchange kernel) is applied on the GPU in given iterations (when \(\mathrm{div}(\mathit{generation},\tau ) == 0\)). Finally, when the algorithm reaches the stop condition, the population is transferred back from the GPU to the CPU.

Fig. 8
figure 8

Structure of GPU implementation

Full size image

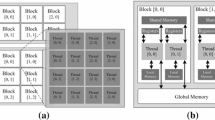
The kernels are implemented following the idea used in [22], in which operations are assigned to a whole block and all the threads of the block cooperate to perform an operation. If the solution length is larger than the number of threads in the block, each thread processes more than one element of the solution but the elements used by a single thread are not contiguous. Thus, each operation is applied to a solution in chunks of the size of the thread block (T in the following figure), as it is shown in Fig. 9.

Fig. 9
figure 9

Threads organization

Full size image

l ×τ Blocks are launched for the execution of crossoverAndMutation kernel (one for each cell). Initially, the global memory location of the solutions of the cell, the global memory location where the resulting solutions should be stored, the crossover points, and the mutation point are calculated from the block identifiers. Then, the crossover is applied to the two solutions, processing the solution components in chunks of size of the thread block. Finally, the thread zero of the block performs the mutation of both solutions.

The elitism, exchange, and evaluate kernels follow the same idea regarding the thread organization and behavior and are also launched for execution organized in l ×τ blocks. The fitness function evaluation (evaluate kernel) uses data from the constant memory of the GPU and an auxiliary structure in shared memory to store the partial fitness values computed by each thread. Finally, it applies a reduction to calculate the full fitness value.

4 Experimental Results

This section describes the problem used for the experimental study, the parameters setting, and the execution platforms. Then, the results obtained are presented and analyzed.

4.1 Test Problem: The Knapsack Problem

The KP is a classical combinatorial optimization problem that belongs to the class of \(\mathcal{N}\mathcal{P}\)-hard problems [25]. It is defined as follows. Given a set of n items, each of them having associated an integer value p i called profit or value and an integer value w i known as weight, the goal is to find the subset of items that maximizes the total profit keeping the total weight below a fixed maximum capacity (W) of the knapsack or bag. It is assumed that all profits and weights are positive, that all the weights are smaller than W (items heavier than W do not belong to the optimal solution), and that the total weight of all the items exceeds W (otherwise, the optimal solution contains all the items of the set).

The most common formulation of the KP is as the integer programming model presented in (4a)–(4c), being x i the binary decision variables of the problem that indicate whether the item i is included or not in the knapsack.

$$\displaystyle\begin{array}{rcl} \mbox{ (KP)}\quad & \mbox{ maximize}\quad & f(\mathbf{x}) =\sum _{ i=1}^{n}p_{ i}x_{i}{}\end{array}$$
(4a)
$$\displaystyle\begin{array}{rcl} & \mbox{ subject to:}\quad & \sum _{i=1}^{n}w_{ i}x_{i} \leq W{}\end{array}$$
(4b)
$$\displaystyle\begin{array}{rcl} & & x_{i} \in \{ 0,1\},\forall i = 1,\ldots,n{}\end{array}$$
(4c)

It should be noted that there are very efficient specific heuristics for solving the KP [26], but we have selected this problem because it is a classical problem that can be used to evaluate the proposed algorithm against similar techniques.

Table 2 presents the instances used in this work. These instances have been generated with no correlation between the weight and the profit of an item (i.e., w i and p i are chosen randomly in [1, R]) using the generator described in [25]. The Minknap algorithm [24], an exact method based on dynamic programming, was used to find the optimal solution of each of the instances.

Table 2 Knapsack instances used in the experimental evaluation and their exact optimal solutions
Full size table

The algorithms studied use a penalty approach to manage infeasibility. In this case, the penalty function subtracts W from the total profit for each unit of the total weight that exceeds the maximum capacity. The formula for calculating the fitness for infeasible solutions is:

$$\displaystyle{ f(\mathbf{x}) =\sum _{ i=1}^{n}p_{ i}x_{i} -\left (\sum _{i=1}^{n}w_{ i}x_{i} - W\right ) \times W. }$$
(5)

4.2 Algorithms

In addition to the algorithm proposed in this chapter, we have included two algorithms, a random search (RS) and a simple GA with and without elitism, in order to compare the quality of the solutions obtained. The former is considered as a sanity check, just to show that our algorithmic proposals are more intelligent than a pure random sampling. On the other hand, the GAs have been chosen because of their popularity in the literature and also they share the same basic search operators (crossover and mutation) so we can properly compare the underlying search engine of the techniques. Briefly, the details of the algorithms used in this work are:

  • RS: The RS algorithm processes the items sequentially. If an item in the knapsack exceeds the maximum capacity, it is discarded. Otherwise, the item is included at random with probability 0.5.

  • Simple Genetic Algorithm (SGA): It is a generational GA with binary tournament, two-point crossover, and bit-flip mutation.

  • Elitist Genetic Algorithm (EGA): It is similar to SGA but with elitist replacement, i.e., each child solution replaces its parent solution only if it has a better (higher) fitness value.

  • SGS: The SGS algorithm presented in Sect. 2.

Each of the algorithms studied has been implemented on CPU. The implementation is straightforward so no further details are provided. Additionally, SGS has been implemented on GPU. Both the CPU and GPU implementations of SGS have exactly the same behavior.

4.3 Parameters Setting and Test Environment

The SGA and EGA parameter values used are 0.9 for the crossover probability and 1∕l for the mutation probability, where l is the length of the tentative solutions. The population size and the number of iterations are defined by considering the features of SGS, using exactly the same values for the two GA versions. In this study, the population size is 2 × l ×τ and the number of iterations is 10 × l (recall that τ = ⌈lgl⌉). Finally, 2 × l ×τ × 10 × l solutions are generated by RS to perform a fair comparison.

The execution platform for the CPU versions of the algorithms is a PC with a Quad Core Xeon E5530 processor at 2.40 GHz with 48 GB RAM using Linux operating system. These CPU versions have been compiled using the -O2 flag and are executed as single-thread applications.

Several GPU cards have been used to evaluate the GPU version of the algorithm. Each Nvidia’s GPU is connected to a PC with different features (see Table 3 for the main characteristics of the entire computing platform). All the PCs use Linux operating system. Table 4 provides the details of each one of the GPUs used in the evaluation (PTMB stands for Peak of Theoretical Memory Bandwidth and MP for Multiprocessors) [20]. The GPU versions were also compiled using the -O2 flag. Considering the features of all the GPU platforms, executions with 32, 64, 128, and 256 threads per block were made.

Table 3 Hardware platforms used for experimental analysis
Full size table
Table 4 GPU cards used for experimental analysis
Full size table

All the results reported in the next subsection are over 50 independent runs and rounded to two significant figures. The CPU and GPU versions of SGS were executed using the same seeds in order that the numerical results of the two versions are exactly the same. The transference times of data between CPU and GPU are always included in the reported total runtime of the GPU version.

4.4 Experimental Analysis

This section describes the experimental analysis conducted to validate SGS. The experiments include a study of the numerical efficiency of the algorithm proposed and a study of the performance of the parallel GPU implementation of SGS.

4.4.1 Numerical Efficiency

Table 5 presents the experimental results regarding the quality of the solutions obtained. The table includes the best and worst solution found, the average solution, the standard deviation, and the number of times the optimal solution is found (#Hits).

Table 5 Experimental results on CPU
Full size table

The results obtained show that SGS is able to find the optimal solution in 7 out of the 8 instances for every run and in the remaining instance (1,000–1,000) in 45 out of 50 trials. EGA also performs well, finding the optimal solution for all the instances, but it is noticeable that SGS is clearly superior to EGA in five instances (200–10,000, 500–1,000, 500–10,000, 1,000–1,000 and 1,000–10,000) concerning the hit rate. Figure 10 graphically displays this fact. It is clear that the structured search of SGS has allowed this algorithm to identify the region where the optimal solution is located for the considered instances. SGS is likely to provide a more robust search under this experimental conditions. On the other hand, SGA only reaches the optimal solution in one of the smallest instance and generally cannot obtain good solutions. Finally, RS presents uncompetitive results with the other algorithms, which means that SGS performs a rather intelligent exploration of the search space. Within the context of this experimental evaluation, the potential of the algorithm proposed in this work regarding the quality of the obtained solutions has been shown.

Fig. 10
figure 10

Hit rate reached by all the algorithms evaluated (no bar means zero hit rate)

Full size image

Table 6 shows the mean runtime in seconds and the standard deviation for SGA, EGA, and SGS executed on CPU. The runtime of RS is not included in the table due to the poor numerical results obtained. The results show that SGS is the best performing algorithm. This is mainly caused because the crossover and mutation points of each cell are calculated from its position on the grid, thus avoiding the generation of random numbers during the execution of the algorithm.

Table 6 Runtime in seconds of CPU versions (mean±std)
Full size table

4.4.2 Parallel Performance

Table 7 shows the mean runtime in seconds and the standard deviation of SGS executed on the GeForce 9800 GTX+, the Tesla C1060, the GeForce GTX 285, and the GeForce GTX 480.

Table 7 Runtime in seconds of SGS on GPU (mean±std), highlighted in bold the shortest runtime for each GPU in each instance
Full size table

Let us start with an analysis of the performance by graphic card. The first results examined are those obtained by the SGS deployment on the oldest of the GPU available in our laboratory, the GeForce 9800 GTX+. The best performance of the algorithm is obtained when using 32 threads per block for all the instances studied. In general, the results reached are poor as the reduction in execution time is less than two when comparing to the runtime of the CPU version. However, these results should be put in perspective. The GPU used is quite old and has very limited capacities, while the CPU used is a powerful server with a large amount of RAM. The main reason of such a poor performance of the algorithm on this GPU is how the access to global memory is handled by devices with compute capability 1.1. Indeed, in the implemented algorithm, the solutions are stored sequentially in global memory and may have an arbitrary length (the length is given by the instance being addressed).

When solutions are read from global memory, the same word should be accessed by different threads of the half-warp (data is stored in 8 bits and the size of the minimum addressable word is 32 bits) and there are misaligned accesses. For these reasons, each thread of the half-warp accesses independently to global memory instead of coalescing the access to global memory for the whole half-warp. This was improved in devices with larger compute capability, as it was commented in Sect. 3.1, and it is verified in the results of the following cards.

The best performance of the algorithm when executed on the Tesla C1060 is obtained when using 32 threads per block for smallest instances and 64 threads per block for the rest of the instances. The results show an impressive reduction of up to 14 times in the runtime with respect to the 9800 GTX+. This reduction is mainly caused by the changes in coalesced access conditions of the devices and the increase in the number of CUDA cores.

The best performance of the algorithm when executed on the GeForce GTX 285 is obtained when using 32 threads per block for smallest instances and 64 threads per block for the rest of the instances. The results show a reduction in the execution time of up to 40 % regarding the Tesla C1060. This result is interesting since both cards have the same compute capability and the same number of cores and multiprocessors. The main difference between both cards is the theoretical peak of memory bandwidth that is 50 % greater in the GTX 285 than in the Tesla C1060 GPU (see Table 4). This fact is the main reason that explains the difference in execution times. It should be noted that the algorithm is divided into three kernels, one for the crossover and mutation, one for the calculation of the fitness values, and one for applying the elitism (in certain iterations there is an additional kernel for the exchange of directions of the solutions). Each of these kernels copy data from global memory to the multiprocessors, apply the operation, and copy the modified data back to the global memory, so the bandwidth of global memory is critical. Another reason that could explain the improvement in the performance is that the processors clock of the GTX 285 is 10 % faster than the processors clock of the Tesla C1060.

Finally, the best performance of the algorithm when executed on the GTX 480 is obtained when using 64 threads per block for smaller instances and 128 threads per block for the bigger instances. The results show an additional reduction in the execution time of up to 73 % regarding the GTX 285. The greatest reductions in runtime are achieved in executions with a large number of threads. This is provoked by the increase in the number of CUDA cores per multiprocessor as well as the inclusion of a double warp scheduler in each multiprocessor in devices with Fermi architecture (like the GeForce GTX 480 card). The results also show that the SGS implementation on a modern GPU can achieve significant performance improvements.

A further analysis on the comparative performance of the CPU and GPU implementations for the same configuration is elaborated next. Figures 11 and 12 show the improvement in performance (in terms of the wall-clock time reduction) of the GPU implementation versus the CPU implementation of SGS on the instances with 100, 200, 500, and 1000 items. The reductions range from 5.09 (100–1,000) to 35.71 (1,000–1,000) for the best setting for the number of threads per block on GTX 480. The tendency for more modern GPU models and for a given GPU card and a given number of threads is clear, the larger the instance, the higher the time reduction. The reason is twofold. On the one hand, larger tentative solutions allow SGS to better profit from the parallel computation of the threads, and on the other hand, the SGS model requires larger populations when the size of the instances increases (the grid has to be enlarged to meet the SGS structured search model), so a higher number of blocks have to be generated and the algorithm takes advantage of the capabilities offered by the GPU architecture. The experimental evaluation also allows to see the impressive evolution of GPUs in a period of only 2 years, since the runtime of SGS in the GeForce 9800 GTX+ is reduced up to 26× when executing in a GeForce GTX 480.

Fig. 11
figure 11

Runtime reduction on GPU versus CPU for the smaller instances

Full size image
Fig. 12
figure 12

Runtime reduction on GPU versus CPU for the larger instances

Full size image

Although the improvements in the performance achieved are satisfactory, there is still room for larger improvements. Indeed, the GPU implementation can be further tuned to the Fermi architecture (GTX 480). If the implementation is tailored to the specific features of this architecture, the runtime of SGS can be reduced even more. In addition to this, most of the kernels used to deploy SGS on GPU have a similar behavior, making it possible to merge all the operations into one, storing intermediate results in shared memory, and thus reducing accesses to global memory.

Finally, to study the performance of the GPU implementation of SGS versus the other algorithms implemented in CPU, we use the number of solutions built and evaluated by the algorithms. Table 8 presents the number of solutions (in millions) built and evaluated for each algorithm per second. The values reported were rounded to have three significant decimals.

Table 8 Solutions (in millions) built and evaluated by the algorithms per second
Full size table

Figure 13 shows the improvement factor when comparing the number of solutions built and evaluated by SGS on GPU against SGA and EGA on CPU. The results obtained show that the GPU implementation of SGS can build and evaluate solutions more than 100 times faster than the CPU implementation of SGA and EGA on CPU for the larger instances considered in this experimental evaluation.

Fig. 13
figure 13

Factor of improvement of SGS on GPU over SGA and EGA on CPU

Full size image

5 Conclusions

In this work we have presented an in-depth study of a relatively new parallel optimization algorithm, the SGS algorithm. SGS is inspired by the systolic contraction of the heart that makes it possible that ventricles eject blood rhythmically according to the metabolic needs of the tissues, and previous ideas of systolic computing. This is just one of the first algorithms that tries to adapt new concepts (not the algorithms themselves) of existing metaheuristics to the very special architecture of a GPU.

The experimental evaluation conducted here showed the potential of the new SGS search model, outperforming three other algorithms for solving the KP in instances with up to 1000 items. The results have also shown that the GPU implementation of SGS speeds up the runtime up to 35 times when executing in a GTX 480 and automatically scales when solving instances of increasing size. The experimental evaluation also showed that the runtime of SGS executed in the oldest GPU available in our laboratory (the 9800 GTX+) can be reduced up to 26× when executed in the newest GPU available in our laboratory (the GTX 480). Finally, the comparative evaluation between the GPU implementation of SGS and the CPU implementation of SGA and EGA showed that SGS can build and evaluate solutions more than 100 times faster for the biggest instances considered in this work.

The lines of work currently explored are the study of the effect of merging the three kernels into one and providing wider impact analysis by solving additional problems to extend the existing evidence of the benefits of this line of research.