Keywords

51.1 Introduction

ReliabilityFootnote 1 is a probability that an item performs its required function under given conditions for a stated time (Birolini 2007). Traditionally, the assessment of system reliability is usually based on failure data. However, when the system is highly reliable, it is very difficult to obtain enough failure data. At this time, degradation data can be an efficient way to estimate the reliability (Meeker et al. 2001). In the last decades, degradation data has played an important role in evaluating system reliability.

As we know that degradation, such as wear, erosion and fatigue, is very common for most mechanical system or components. It can be described by a continuous performance process in terms of time (Zuo et al. 1999; Robinson and Croder 2000; Tseng et al. 2009). In Ref. (Zuo et al. 1999), three kinds of methods for degradation data analysis are presented, including linear regression method, degradation path method, and stochastic process method. The degradation data need to be dealt with so as to fit a known distribution or stochastic process, and the maximum likelihood estimation method, Bayesian method and the least squares method are usually used to estimate the parameters (Robinson and Croder 2000; Tseng et al. 2009). However, in the above researches, the effect of shocking was not considered.

Shock is one of the major reasons that cause failure to mechanical components (Nakagawa 2007). On the one hand, the random shocks will speed up the degradation process. And on the other hand, the degradation process will make the system more vulnerable to the random shocks. Thus, the effect on the degradation due to shocks may not be neglected.

In recent years, the interactions between degradation and random shock process have drawn attentions from academia. Klutke and Yang (2002) derived an availability model for an inspected system subject to continuous degradation and shocks. Li and Pham (2005a, b) considered the reliability and maintenance model for two degradation processes and random shocks. Kharoufeh et al. (2006) derived the system lifetime distribution and the limiting average availability for a failure process involving both degradation and shocks. Deloux et al. (2009) proposed a predictive maintenance policy for a continuously deteriorated system with deterioration and random shocks. Lehman (2009) surveyed two classes of degradation-threshold-shock (DTS) models, including general DTS and DTS with covariates, in which system failure were caused by the competing failure between degradation and trauma. Wang et al. (2011) considered a reliability model by using fuzzy degradation data when degradation and shocks were involved.

Most studies among Ref. (Klutke and Yang 2002; Li and Pham 2005a, b; Kharoufeh et al. 2006; Deloux et al. 2009; Lehmann 2009; Wang et al. 2011) assumed that the degradation process and shock process are independent with each other. However, there exist correlations between the degradation process and the random shocks. Shocks can not only decrease the performance directly, but also speed up the degradation.

Additionally, the above studies used the continuous distribution function or the linear regression method to describe the degradation of the system. In fact, for some system the degradation indices are non-monotonic. In fact, existing methods cannot describe this phenomenon properly.

The Wiener process is a kind of stochastic process with independent increment, and it can be used to describe non-monotonic properties. Due to its good properties of modeling the degradation processes on analysis and computation, the Wiener process has been used in reliability fields by many researchers, e.g. Whitmore (1995), Wang (2011), and Chun Su and Ye Zhang (2010).

In this paper, we consider a combination model for systems subject to random shock and degradation process. The random shock can also cause an abrupt damage to the degradation process. The Wiener process is used to describe the degradation process, and the parameters are estimated by the maximum likelihood estimation method. A case study of fatigue crack growth is provided to illustrate the proposed model and method.

51.2 Reliability Analysis Considering Degradation and Shock

51.2.1 Analysis of Degradation Process

It is assumed that system degradation performance at time t is W (t) and H is the failure threshold. When the degradation performance W (t) exceeds the threshold H for the first time, the component is considered to be failed.

Degradation can be influenced by the random factors from the component itself and the environment. As a consequence, a good statistical model should take into account the sources of variation, and stochastic process is appropriate to describe the degradation of the system.

Suppose that the degradation process, {W(t), t ≥ 0}, obeys a Wiener process:

$$ W(t)=\mu t+\sigma B(t) $$

where μ is the drift parameter; σ is the diffusion parameter; B(t) is the standard Brownian motion.

The Wiener process has the following properties:

  1. 1.

    W(0) = 0;

  2. 2.

    W(t) has continuous sample paths;

  3. 3.

    W(t) has independent increments;

  4. 4.

    W(t) − W(s) ∼ N(μ(t − s), σ2(t − s)) for t > s ≥ 0.

From the properties of the Wiener process, we can obtain that the degradation performance W (t) is normally distributed as

$$ W(t) \sim N(\mu t,{\sigma^2}t) $$

The probability density function can be defined as

$$ f(w)=\frac{1}{{\sqrt{{2\pi t}}\sigma }}\exp \left\{ {-\frac{{{{{(w-\mu t)}}^2}}}{{2{\sigma^2}t}}} \right\} $$

For the Wiener process has many good properties, it has been used by many researchers in reliability field. In this paper, the degradation path is assumed to follow a Wiener process.

51.2.2 Shock Process Analysis

It is known that many factors from the environment can bring shocks to the components. Random shock modeling has been extensively studied for the component under the external shock environments, such as sudden and unexpected usage loads and accidental dropping onto hard surfaces (Nakagawa 2007; Wang et al. 2011). Shocks caused by the random environmental factors usually follow Poison processes. In the literature, four categories of random shock models are considered: cumulative shock model, extreme shock model, run shock model and δ-shock model (Bai et al. 2011). In this paper, the cumulative shock model is considered.

Suppose that random shocks arrive according to a homogeneous Poisson process with rate λ. Let the random variable N(t) denote the number of shocks until time t with the probability

$$ P\{N(t)=n\}=\frac{{{{{(\lambda t)}}^n}}}{n! }{e^{{-\lambda t}}},\begin{array}{*{20}{l}} {} & {n=0,1,2,\cdots } \\ \end{array} $$

In addition, the shock damage sizes are used to measure the instant increase in the degradation and are assumed to be independent identically distributed random variables, denoted as Y j for j = 1, 2, …, ∞. The cumulative damage size of the degradation process due to random shocks until time t is given as

$$ S(t)=\left\{ \begin{aligned} & \sum\limits_{j=1}^{N(t) } {{Y_j}\kern2em \mathrm{if}\ N(t)>0} \\ & 0\kern4em \;\mathrm{if}\ N(t)=0 \\ \end{aligned} \right. $$

where N(t) is the total number of shocks to the system that have arrived by time t.

51.2.3 Reliability Analysis for Combination Model

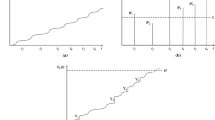
Shown as in Fig. 51.1, the total degradation damage is the cumulative effect of continuous degradation and sudden shocks. Obviously, the degradation is an aging process during field operation, and shock loads can cause additional abrupt damage, which contributes to the degradation process.

Fig. 51.1
figure 00511

The degradation process under random shock

Full size image

Now we establish reliability assessment model by considering a degradation process and the effect that shocks on the degradation process. The failure is defined as that the total degradation amount D(t) drops below certain failure threshold H.

From Fig. 51.1, the total degradation performance including continuous degradation and shock damages can be expressed as

$$ \begin{aligned} D(t)& = W(t)+S(t) \\ & = \mu t+\sigma B(t)+{Y_1}+\cdots +{Y_{N(t) }} \\ \end{aligned} $$

Based on the failure definition, the reliability at time t can be derived as

$$ \begin{aligned} R(t)& = P(D(t)<H) \\ & = P(W(t)+S(t)<H) \\ \end{aligned} $$

If the shocks arrive according to a Poisson process with rate λ, it can be obtained

$$ \begin{aligned} R(t)& = P(W(t)+S(t)<H) \\ & = P\left(W(t)+\sum\limits_{j=1}^{N(t) } {{Y_j}} <H\right) \\ & = \sum\limits_{n=0}^{\infty } {P\left( {W(t)+\sum\limits_{j=1}^{N(t) } {{Y_j}} <H|N(t)=n} \right)} P\left( {N(t)=n} \right) \\ \end{aligned} $$

Furthermore, it is supposed that the damage sizes due to shocks are independent identically distributed normal random variables with the distribution

$$ {Y_j} \sim N({\mu_Y},\sigma_Y^2),\,\,j=1,2,\cdots $$

The corresponding probability density function is

$$ g(y)=\frac{1}{{\sqrt{{2\pi }}{\sigma_Y}}}\exp \left\{ {-\frac{{{{{(y-{\mu_Y})}}^2}}}{{2\sigma_Y^2}}} \right\} $$

Then, we can get

$$ S(t)=\sum\limits_{j=1}^n {{Y_j}} \sim N(n{\mu_Y},n\sigma_Y^2) $$

According to the properties of Wiener process, we can get

$$ W(t) \sim N(\mu t,{\sigma^2}t) $$

Thus,

$$ W(t)+S(t) \sim N(\mu t+n{\mu_Y},{\sigma^2}t+n\sigma_Y^2) $$

And

$$ \begin{aligned} &\,P\left( {W(t)+\sum\limits_{j=1}^{N(t) } {{Y_j}} <H|N(t)=n} \right) \\ &\qquad = P\left( {W(t)+\sum\limits_{j=1}^n {{Y_j}} <H} \right) \\ &\qquad = \Phi (\frac{{H-\mu t-n{\mu_Y}}}{{\sqrt{{{\sigma^2}t+n\sigma_Y^2}}}}) \\ \end{aligned} $$

where \( \Phi (\cdot ) \) is the cumulative distribution function of a standard normally distributed variable.

Then the reliability function R(t) can be derived as

$$ R(t)=\sum\limits_{n=0}^{\infty } {\Phi (\frac{{H-\mu t-n{\mu_Y}}}{{\sqrt{{{\sigma^2}t+n\sigma_Y^2}}}})} \cdot \frac{{\exp (-\lambda t){{{(\lambda t)}}^n}}}{n! } $$

Thus the probability density function of the failure time, \( f(t) \), is derived as

$$ {\fontsize{9.1}{11}\selectfont{\begin{aligned} & f(t)=-\frac{dR(t) }{dt} \\ & = \sum\limits_{n=0}^{\infty } {\left( {\phi (\frac{{H-\mu t-n{\mu_Y}}}{{\sqrt{{{\sigma^2}t+n\sigma_Y^2}}}})} \right.} \cdot \frac{{\exp (-\lambda t){{{(\lambda t)}}^n}}}{n!}\cdot \left. {\frac{{\mu ({\sigma^2}t+n\sigma_Y^2)+\tfrac{1}{2}{\sigma^2}(H-\mu t-n{\mu_Y})}}{{{{{({\sigma^2}t+n\sigma_Y^2)}}^{{{3 \left/ {2} \right.}}}}}}} \right) \\ & \quad - \sum\limits_{n=0}^{\infty } {\Phi (\frac{{H-\mu t-n{\mu_Y}}}{{\sqrt{{{\sigma^2}t+n\sigma_Y^2}}}})} \cdot \frac{{\lambda \exp (-\lambda t){{{(\lambda t)}}^{n-1 }}(n-\lambda t)}}{n! } \\ \end{aligned}}} $$

where \( \phi (\cdot ) \) is the probability density function of a standard normally distributed variable.

51.3 Parameters Estimation of Reliability Model

It is supposed that there are N samples in the test, and each sample has M times of observations. Let W i (t j ) be observation of the ith sample at the corresponding time t j , i =1, 2, …, N; j = 1, 2, …,M. The degradation data for this model can be presented in the form

$$ {W_{{N\times M}}}(t)=\left( {\arraycolsep4pt\begin{array}{*{20}{l}} {{W_1}({t_1})} & \cdots & {{W_1}({t_M})} \\ \vdots & \ddots & \vdots \\ {{W_N}({t_1})} & \cdots & {{W_N}({t_M})} \\ \end{array}} \right) $$

Let

$$ \Delta {W_i}\left( {{t_j}} \right)={W_i}\left( {{t_j}} \right)-{W_i}\left( {{t_j}_{-1 }} \right),\,\,{t_0} = 0 $$

Based on the independent increment property of the Wiener process, the random variable ΔWi(tj) has the following distribution

$$ \Delta {W_i}\left( {{t_j}} \right) \sim N\left( {\mu \Delta {t_j},{\sigma^2}\Delta {t_j}} \right),\ \Delta {t_j}={t_j}-{t_j}_{-1 } $$

So, the probability density function of ΔW i (t j ) is

$$ f(\Delta {W_i}({t_j}))=\frac{1}{{\sqrt{{2\pi \Delta {t_j}}}\sigma }}\exp \left\{ {-\frac{{{{{(\Delta {W_i}({t_j})-\mu \Delta {t_j})}}^2}}}{{2{\sigma^2}\Delta {t_j}}}} \right\} $$

where i = 1, 2, …, N, j = 1, 2, …, M.

Thus the likelihood function of the samples is

$$ \begin{aligned} L(\mu, \sigma )& = \prod\limits_{i=1}^N {\prod\limits_{j=1}^M {f(\Delta {W_i}({t_j}))} } \\ & = \prod\limits_{i=1}^N {\prod\limits_{j=1}^M {\frac{1}{{\sqrt{{2\pi \Delta {t_j}}}\sigma }}\exp \left\{ {-\frac{{{{{(\Delta {W_i}({t_j})-\mu \Delta {t_j})}}^2}}}{{2{\sigma^2}\Delta {t_j}}}} \right\}} } \\ \end{aligned} $$

Taking the logarithm of the likelihood function and the log-likelihood function as

$$ \ln L(\mu, \sigma )=\sum\limits_{i=1}^N {\sum\limits_{j=1}^M {\ln f(\Delta {W_i}({t_j}))} } $$

Differentiating lnL with respect to μ and σ, respectively, we can get

$$ \hat{\mu} = \frac{{\sum\limits_{i=1}^N {\sum\limits_{j=1}^M {\Delta {W_i}({t_j})} } }}{{\sum\limits_{i=1}^N {\sum\limits_{j=1}^M {\Delta {t_j}}}}} $$
$$ {{\hat{\sigma}}^2} =\frac{{\sum\limits_{i=1}^N {\sum\limits_{j=1}^M {{{{(\Delta {W_i}({t_j})-\hat{\mu}\Delta {t_j})}}^2}} } }}{{\sum\limits_{i=1}^N {\sum\limits_{j=1}^M {\Delta {t_j}} } }} $$

51.4 Numerical Examples

Fatigue crack is a common degradation phenomenon for mechanical components. In this section, an example is given to illustrate the proposed models in Sects. 51.2 and 51.3. This example is based on the fatigue crack data of an alloy in (Lu and Meeker 1993). All samples had an initial crack length of 0.90 in.. Figure 51.2 shows the cumulative degradation of the fatigue crack data.

Fig. 51.2
figure 00512

The cumulative degradation of fatigue crack sizes

Full size image

Wang et al. (2011) and some other researchers have used the data to analyze the reliability of the component. Here we will use the same data to illustrate the proposed model, and the results will also be compared with Wang’s results.

Based on the degradation data, we can obtain the degradation increments data. According to the proposed estimated method in Sect. 51.3, the maximum likelihood estimations of μ and σ are obtained as:

$$ \hat{\mu}=4.78\times {10^{-6 }} $$

and

$$ {{\hat{\sigma}}^2}=0.77\times {10^{-7 }} $$

The reliability curves using different estimation methods with the test data as shown in Fig. 51.3, and the details can be seen in Lu and Meeker (1993), Lu et al. (1997). But the effect of shocking is not considered in those paper. From Fig. 51.3, we can find that the reliability curves are nearly the same before12 × 104 -cycle by using different estimation methods, while after 12 × 104 cycle, the estimated reliability curves have a little difference.

Fig. 51.3
figure 00513

Plot of degradation reliability using different methods

Full size image

It is supposed that the random shock process follows a Poisson process, and the shock damage size Y j (j =1, 2,…) is assumed to follow a normal distribution, Y j ∼ N(0.02 in., 0.1 in.); the failure threshold value H = 2.0 in., and the occurrence rate is λ = 1.0.

The probability density function f(t) and the corresponding reliability function R(t) are shown as in Figs. 51.4 and 51.5, respectively.

Fig. 51.4
figure 00514

Plot of failure time distribution

Full size image
Fig. 51.5
figure 00515

Plots of reliability function under different case

Full size image
Fig. 51.6
figure 00516

Plots of reliability function under different methods

Full size image

Additionally, in this paper we will discuss the impacts of shocks to the system reliability. If the damages caused by the random shocks are not considered, it is assumed that Y j  = 0, for j = 1, 2, …. The reliability curve is plotted in Fig. 51.5, and the upper curve is reliability that the random shocks are not considered. Obviously, if we do not account for the effects of shocks, the reliability estimate will be higher. The lower curve is the reliability when the random shocks are accounted for.

As shown in the Fig. 51.5, the effects of shocks are not so significant before t reaches the 5 × 104 cycle, the two reliability curves nearly overlap before that. For the region that t is larger than 5 × 104 -cycle, the two curves begin to separate and the effects of shocks become larger.

Moreover, the degradation path is assumed to follow the normal distribution in (Wang et al. 2011), \( W(t) \sim N(\mu (t),{\sigma^2}(t)) \), where

$$ \mu (t)=0.8767\exp (0.0398t) $$

and

$$ {\sigma^2}(t)=7.7602\times {10^{-5 }}\exp (0.4646t). $$

In order to compare the difference with different methods, the two reliability curves are plot in Fig. 51.6. The upper curve is the reliability under the Wiener process and the lower curve is the reliability under the normal distribution.

From the Fig. 51.6, it can be found that the reliability has a little difference under the Wiener process and normal distribution. Thus, Wiener process is effective for the reliability modeling considering degradation and random shock.

51.5 Conclusion

In this paper, we establish a reliability model for components subject to random shock and degradation process. The random shock can caused an abrupt damage to the degradation process. The Wiener process is used to describe the degradation process, and the maximum likelihood estimation method is used to estimate the parameters of the model.

The case study shows that shocks have obviously impact on the reliability of the component, and the reliability is higher when the impact of shocks is not considered.