Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Once an audio recognition system that functions under idealistic conditions is established, the primary concern shifts towards making it robust in a real-world. The previous chapter touched this issue by illustrating how audio source separation can be exploited to recover a clean speech signal from a mixture. Extraction of the desired signal, however, is not a necessary pre-condition for robust audio recognition. Rather, several options exist for system improvement along the chain of processing, and have proved to be promising especially in the monaural case. Thus, we will next have a look at this issue following the overview given in [1].

First, filtering or spectral subtraction of the signal before can be applied directly after the audio capture. This is realised, for example, in the advanced front-end feature extraction (AFE) or Unsupervised Spectral Subtraction (USS). Then, auditory modelling can be introduced in the feature extraction process. The main influence of noise on audio is irreversible loss of information caused by its random behaviour and a distortion in the feature space that can be compensated by a suited audio representation in the noise condition [2, 3]. Examples of features in this direction include the MFCCs, PLP coefficients [4, 5] or RASTA-PLP features [6, 7] (cf. Sect. 6.2.1). Next along the chain of processing is the option to enhance the extracted features aiming at removal of effects as introduced by noise [8–10]. Exemplary techniques are normalisation methods such as (Cepstral) Mean Subtraction (CMS) [11], MVN [12], or HEQ [9]. Such feature enhancement can also be realised in a model based way, such as by jointly using a Switching Linear Dynamic Model (SLDM) for the dynamic behaviour of audio plus a Linear Dynamic Model (LDM) for additive noise [13]. Later in the chain, one could tailor the learning algorithm to be able to cope with noisy signal input. Alternatives besides HMMs [14], such as Hidden Conditional Random Fields (HCRF) [15], Switching Autoregressive Hidden Markov Models (SAR-HMMs) [16], or other more general DBN structures provide higher flexibility in modelling. For example, the extension of an SAR-HMM to an Autoregressive Switching Linear Dynamical System (AR-SLDS) [17] allows for an explicit noise model leading to higher noise robustness. Another solution is to match the AM (or even LM) or feature space to noisy conditions. This requires a recogniser trained on noisy audio [18]. However, the performance highly dependends on how similar the noise conditions for training and testing are [19]. One can thus distinguish between low to highly matched conditions training. Further, it can be difficult to provide knowledge on the type of noisy condition. This can be eased by so-called multi-condition training, where clean and noisy material with different types of noise is mixed. This is usually not as good as perfectly matched condition between the current test setting and the one learnt previously. However, it provides a good compromise by improving on average over different noise conditions. Besides using noisy material for training, model adaptation can be used to quickly adapt the recogniser to a specific noise condition encountered in the test scenario. This covers widely used techniques such as maximum a posteriori (MAP) estimation [20], maximum likelihood linear regression (MLLR) [21], and minimum classification error linear regression (MCELR) [22].

Given the multiplicity of developed techniques for noise robustness in Intelligent Audio Analysis, a selection of relevant techniques and a good coverage of the different stages along the chain of processing is aimed at in this section. As these techniques are often also tailored to the specific type of noise at hand, relevant special cases such as white noise or babble noise are covered, which are very challenging for speech processing. In the ongoing, let us take a detailed look at the above mentioned options in particular for audio signal preprocessing, feature enhancement, and audio modelling. For the sake of better readability, ‘audio of interest’ such as speech, music, or specific sounds of interest as opposed to noise will partly simply be written as ‘audio’ in this chapter.

1 Audio Signal Preprocessing

The preprocessing of the audio signal for its enhancement shall compensate noise influence prior to the feature extraction [23–25]. Apart from explicit BASS as was shown in the last chapter, one of the frequently used audio and particular speech signal preprocessing [26] standards is the advanced front-end feature extraction introduced in [27] based on two-step Wiener filtering in the time domain. Spectral subtraction such as USS [10] can lead to similar effects at lower computational requirements in comparison to Wiener filtering [28, 29]. These techniques can also be subsumed under broader audio signal preprocessing despite being carried out in the (magnitude) spectogram domain. These two techniques will now be introduced in more detail.

1.1 Advanced Front-End Feature Extraction

The processing in the AFE [27] is shown in Fig. 9.1: Subsequent to noise reduction the denoised waveforms are processed and cepstral features are computed and blindly equalised.

Fig. 9.1
figure 1

Feature extraction in the AFE according to ETSI ES 202 050 V1.1.5

Full size image

Preprocessing in the AFE is based on two-stage Wiener filtering. After denoising in the first stage, a second one carries out additional dynamic noise reduction. In this second stage a gain factorisation unit controls the intensity of filtering dependent on the SNR. Figure 9.2 depicts the components of the two noise reduction cycles: First, a framing takes place. Then, the linear spectrum is estimated per frame, and the power spectral density (PSD) is smoothed along the time axis in the PSD Mean block. An audio activity detection (or VAD in the special case of speech) discriminates between audio and noise, and thus the estimated spectrum of the audio frames and noise are used in the computation of the frequency domain Wiener filter coefficients. To obtain a Mel-warped frequency domain Wiener filter, the linear Wiener filter coefficients are smoothed along the frequency axis using a Mel-filterbank [1]. The Mel-warped Inverse DCT unit (Mel IDCT) determines the impulse response of the Wiener filter prior to the input signal’s filtering. The signal then passes through a second noise reduction cycle using this impulse response. Finally, the DC offset removal block eliminates the constant component of the filtered signal.

Fig. 9.2
figure 2

Two-stage Wiener filtering for noise reduction in the AFE according to ETSI ES 202 050 V1.1.5

Full size image

The Wiener filter approach in the AFE algorithm has the advantage that noise reduction is carried out on the frame-level. Further, the Wiener filter parameters are adapted to the current SNR. This allows to handle non-stationary noise. Important is, however, an exact audio activity detection (or VAD). This can be particularly demanding in the case of negative SNR levels (cf. e.g., Sect. 10.1.2). Overall, the AFE is a rather complex approach sensible to errors and inaccuracies within the individual estimation and transformation steps [1].

1.2 Unsupervised Spectral Subtraction

USS’s [10] spectral subtraction scheme bases on a two-mixture model approach of noisy audio. It aims to distinguish audio and background noise at the magnitude spectogram level. A probability distribution is used to model audio and noise. For the modelling of background noise on silent parts of the time-frequency plane, one usually assumes white Gaussian behaviour for the real and imaginary parts [30, 31]. This corresponds to a Rayleigh probability density function \(f_{N}(m)\) for noise in the magnitude domain:

$$\begin{aligned} f_{N}(m)=\frac{m}{\sigma _{N}^2} e^{-\frac{m^2}{2\sigma _{N}^2}} \end{aligned}$$
(9.1)

For the two-mixture model, only an audio ‘activity’ model modelling large magnitudes is needed besides the Rayleigh silence model. For the audio PDF \(f_{S}(m)\) a threshold \(\delta _{S}\) is defined with respect to the noise distribution \(f_{N}(m)\) such that only magnitudes \(m>\delta _{S}\) are modelled. In [10], a threshold \(\delta _{S}=\sigma _{N}\) is used where \(\sigma _{N}\) is the mode of the Rayleigh PDF. Consequently, magnitudes below \(\sigma _{N}\) are assumed as background noise. Two additional constraints are needed for \(f_{S}(m)\):

  • The derivative \(f_{S}^{\prime }(m)\) of the ‘activity’ PDF may not be zero if \(m\) is just above \(\delta _{S}\); otherwise the threshold \(\delta _{S}\) is meaningless as it could be set to an arbitrarily low value.

  • With \(m\) towards infinity the decay of \(f_{S}(m)\) should be lower than the decay of the Rayleigh PDF to guarantee \(f_{S}(m)\) modelling large amplitudes.

The ‘shifted Erlang’ PDF with \(h=2\) [32] fulfils these two criteria. It can thus be used to model large amplitudes assumed to be audio of interest:

$$\begin{aligned} f_{S}(m)=1_{m>\sigma _{N}} \cdot \lambda _{S}^2 \cdot (m-\sigma _{N}) \cdot e^{-\lambda _{S}(m-\sigma _{N})} \end{aligned}$$
(9.2)

with \(1_{m>\sigma _{N}}=1\) if \(m>\sigma _{N}\) and \(1_{m>\sigma _{N}}=0\) otherwise.

The overall PDF for the spectral magnitudes of the noisy audio signal is

$$\begin{aligned} f(m)=P_{N} \cdot f_{N}(m) + P_{S} \cdot f_{S}(m), \end{aligned}$$
(9.3)

where \(P_{N}\) is the prior for ‘silence’ and background noise, and \(P_{S}\) is the prior for ‘activity’ and audio of interest. The parameters of the derived PDF \(f(m)\) summarised in the set

$$\begin{aligned} \varLambda =\{ P_{N},\sigma _{N},P_{S},\lambda _{S}\} \end{aligned}$$
(9.4)

are independent of time and frequency, and can be trained by the EM algorithm (cf. Sect. 7.3.1) [33]. In the expectation step, posteriors are estimated as

$$\begin{aligned}&p(\mathrm{sil }|m_{f,t},\varLambda )=\frac{P_{N} \cdot f_{N}(m_{f,t})}{P_{N} \cdot f_{N}(m_{f,t}) + P_{S} \cdot f_{S}(m_{f,t})}\end{aligned}$$
(9.5)
$$\begin{aligned}&p(\mathrm{act }|m_{f,t},\varLambda )=1-p(\mathrm{sil }|m_{f,t},\varLambda ). \end{aligned}$$
(9.6)

For the Maximisation step, the moment method is used: An update \(\sigma _{N}\) employing all data takes place before all data with values above the new \(\sigma _{N}\) help to update \(\lambda _{S}\). Two update equations describe the method as follows:

$$\begin{aligned}&\hat{\sigma }_{N}=\frac{\Big [\sum _{f,t}^{ }m_{f,t}^2 \cdot p(\mathrm{sil }|m_{f,t},\varLambda )\Big ]^{\frac{1}{2}}}{\Big [2\sum _{f,t}^{ } p(\mathrm{sil }|m_{f,t},\varLambda )\Big ]^{\frac{1}{2}}}\end{aligned}$$
(9.7)
$$\begin{aligned}&\hat{\lambda }_{S}=\frac{\sum _{m_{f,t}>\hat{\sigma }_{N}} (m_{f,t}-\hat{\sigma }_{N})^{-1} \cdot p(\mathrm{act }|m_{f,t},\varLambda )}{\sum _{m_{f,t}>\hat{\sigma }_{N}} p(\mathrm{act }|m_{f,t},\varLambda )}. \end{aligned}$$
(9.8)

Subsequent to the training of all mixture parameters \(\varLambda =\{ P_{N},\sigma _{N},P_{S},\lambda _{S}\}\) USS with the parameter \(\sigma _{N}\) as floor value is applied:

$$\begin{aligned} m_{f,t}^{ USS}=\max \Big ( 1, \frac{m_{f,t}}{\sigma _{N}} \Big ) \end{aligned}$$
(9.9)

Flooring to a non-zero value is required for MFCC or similar features, as zero magnitude values after spectral subtraction can result in unfavourable dynamics. Overall, USS is a simple and efficient preprocessing method that allows for unsupervised EM fitting on observed data. As a downside, it requires reliable estimation of an audio magnitude PDF which is rather challenging. With the PDFs not depending on frequency and time, USS only handles stationary noises. Further, it only models large magnitudes of the audio of interest. Low audio magnitudes thus cannot be distinguished from background noise.

2 Feature Enhancement

In feature enhancement, enhancement takes place after the extraction of features to reduce a potential mismatch between test and training conditions. Popular methods include CMS [11], MVN [12], HEQ [9], and the Taylor Series approach [34] able to cope with the non-linear effects of noise. There are some further methods tailored to specific types of features, such as in the cepstrum-domain, where a feature compensation algorithm to decompose audio of interest and noise is introduced in [35]. To enhance noisy MFCCs, a SLDM can also be used to model the dynamics of audio of interest and those of additive noise by a LDM [13]. An observation model then describes how audio and noise produce the noisy observations to reconstruct the features of clean audio. An extension [36] includes time-dependencies among the discrete state variables of the SLDM. Further, a state model for the dynamics of noise can help to model non-stationary noise sources [37]. Finally, incremental on-line adaptation of the feature space is possible as by feature space maximum likelihood linear regression (FMLLR) [38]. Again, we will now take a detailed look at selected popular approaches.

2.1 Feature Normalisation

2.1.1 Cepstral Mean Subtraction

To ease the influence of noise and transmission channel transfer functions in cepstral features, CMS [11, 39] provides a simple approach. Its basic principle of mean subtraction can also be applied to practically any other audio LLD. Often, the noise can be considered as comparably stationary when opposed to the rapidly changing characteristics of the audio signal of interest. Thus, a subtraction is carried out of the long-term average cepstral or other feature vector

$$\begin{aligned} {\underline{\mu }}=\frac{1}{T}\sum _{t=1}^{T}{\underline{x}}_{t} \end{aligned}$$
(9.10)

from the observed noise corrupted feature vector sequence of length \(T\):

$$\begin{aligned} {\underline{X}}=\{ {\underline{x}}_{1},{\underline{x}}_{2},\dots ,{\underline{x}}_{t},\dots ,{\underline{x}}_{T}\} \end{aligned}$$
(9.11)

By that, a new estimate \(\tilde{x_{t}}\) of the signal in the feature domain results:

$$\begin{aligned} {\underline{\tilde{x}}}_{t}={\underline{x}}_{t}-{\underline{\mu }}, \; 1\le t \le T \end{aligned}$$
(9.12)

The subtraction of the long-term average is particularly interesting in the cepstral domain. Since the audio spectrum is multiplied by the channel transfer function (cf. Sect. 6.2.1.4), by the logarithm application in the MFCC calculation, this multiplication turns into an addition, and this part can be eliminated by subtraction of the cepstral mean from all input vectors. A disadvantage of CMS, as opposed to HEQ, is the disability to treat non-linear noise effects.

2.1.2 Mean and Variance Normalisation

The subtraction of the mean per feature vector component corresponds to an equalisation of the first moment of the vector sequence probability distribution. If noise has also an influence on the variance of the features, according variance normalisation of the vector sequence can be applied and by that an equalisation of the first two moments. This is known as MVN. The processed feature vector is obtained by

$$\begin{aligned} \tilde{\underline{x}_{t}}=\frac{{\underline{x}}_{t}-{\underline{\mu }}}{{\underline{\sigma }}}. \end{aligned}$$
(9.13)

The division by the vector \({\underline{\sigma }}\) of the standard deviations per feature vector components is computed out element-by-element. The new feature vector’s components have zero mean and unity variance.

2.1.3 Histogram Equalisation

HEQ is a popular technique in digital image processing [40] where it helps raise the contrast of images and alleviates the influence of the lighting conditions. In audio processing, HEQ can improve the temporal dynamics of noise-affected feature vector components. HEQ extends the principle of CMS and MVN to all moments of the probability distribution of the feature vector components [9, 41], and by that compensates non-linear distortions caused by noise.

In HEQ, the histogram of each feature vector component is mapped onto a reference histogram. The underlying assumption is that noise influence can be described as a monotonic partly reversible feature transformation. With success depending on meaningful histograms, HEQ requires several frames for their reliable estimation. A key advantage lending to HEQ’s independence of the noise characteristics is that no assumptions are made on the statistical properties (e.g., normality) of the noise process.

For HEQ, a transformation

$$\begin{aligned} \tilde{x}=F(x) \end{aligned}$$
(9.14)

needs to be found for the conversion of the PDF \(p(x)\) of an audio feature into a reference PDF \(\tilde{p}(\tilde{x})=p_{ ref}(\tilde{x})\). If \(x\) is a unidimensional variable with PDF \(p(x)\), a transformation \(\tilde{x}=F(x)\) modifies the probability distribution, such that the new distribution of the obtained variable \(\tilde{x}\) can be expressed as

$$\begin{aligned} \tilde{p}(\tilde{x})=p(G(\tilde{x}))\frac{\partial G(\tilde{x})}{\partial \tilde{x}} \end{aligned}$$
(9.15)

with \(G(\tilde{x})\) as the inverse transformation corresponding to \(F(x)\). For the cumulative probabilities based on the PDFs, let us consider:

$$\begin{aligned} C(x)&=\int _{-\infty }^{x} p(x^{\prime })dx^{\prime } \nonumber \\&=\int _{-\infty }^{F(x)} p(G(\tilde{x}^{\prime }))\frac{\partial G(\tilde{x})}{\partial \tilde{x}^{\prime }} d\tilde{x}^{\prime } \\&=\int _{-\infty }^{F(x)} \tilde{p}(\tilde{x}^{\prime }) d\tilde{x}^{\prime } \nonumber \\&=\tilde{C}(F(x))\nonumber \end{aligned}$$
(9.16)

By that, the transformation converting the distribution \(p(x)\) into the ‘target’ distribution \(\tilde{p}(\tilde{x})=p_{ ref}(\tilde{x})\) can be expressed as

$$\begin{aligned} \tilde{x}=F(x)=\tilde{C}^{-1}[C(x)]=C_{ ref}^{-1}[C(x)], \end{aligned}$$
(9.17)

where \(C_{ ref}^{-1}(\dots )\) is the inverse cumulative probability function of the reference distribution [1]. Further, \(C(\dots )\) is the feature’s cumulative probability function. To obtain the transformation per feature vector component, a ‘rule of thumb’ is to use 500 uniform intervals between \(\mu _{i}-4\sigma _{i}\) and \(\mu _{i}+4\sigma _{i}\) for the derivation of the histograms. \(\mu _{i}\) and \(\sigma _{i}\) are the mean and standard deviation of the \(i\)th feature vector element. A Gaussian probability distribution with zero mean and unity variance can be used per element as a reference probability distribution, then, however, ignoring higher moments.

From the feature normalisation strategies discussed above, CMS is the simplest. Together with MVN, it is used most frequently. MVN usually leads to better results at slightly increased computational effort. However, these two techniques both provide a linear transformation. This is different for HEQ, which is able to compensate non-linear effects, but requires sufficient audio frames for good results. HEQ further corrects only monotonic transformations. This can cause an information loss, given that random noise behaviour renders the needed transformation non-monotonic.

2.2 Model Based Feature Enhancement

In model based audio enhancement one usually models audio and noise individually plus how these two produce the observation. Then, the features are enhanced to benefit the audio of interest by use of these models. An example is a SLDM to model the dynamics of clean audio of interest [13] that will next be introduced by the mentioned three models for noise, audio, and the combination.

2.2.1 Modelling of Noise

Noise is modelled by a simple LDM with the system equation

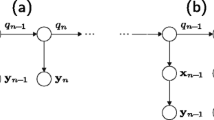
$$\begin{aligned} {\underline{x}}_{t}={\underline{A}}\,{\underline{x}}_{t-1}+{\underline{b}}+{\underline{g}}_{t^{\prime }}, \end{aligned}$$
(9.18)

where the matrix \(\underline{A}\) and the vector \(\underline{b}\) simulate the noise process’s evolution over time. Further, \(\underline{g}_{t}\) is a Gaussian noise source that drives the system. A graphical model representation of this LDM is given in Fig. 9.3. In this and the following visualisations in this section, squares again indicate observations. With LDMs being time-invariant, they can model signals such as coloured stationary Gaussian noises. The LDM is expressed by

$$\begin{aligned} p(\,{\underline{x}}_{t}|{\underline{x}}_{t-1})&=\mathcal{N }(\,{\underline{x}}_{t};{\underline{A}}\,{\underline{x}}_{t-1}+{\underline{b}},{\underline{C}}\,) \end{aligned}$$
(9.19)
$$\begin{aligned} p(\,{\underline{x}}_{1:T})&=p(\,{\underline{x}}_{1})\prod _{t=2}^{T}p(\,{\underline{x}}_{t}|{\underline{x}}_{t-1}), \end{aligned}$$
(9.20)

where \(\mathcal{N }(\,{\underline{x}}_{t};{\underline{A}}{\underline{x}}_{t-1}+\,{\underline{b}},{\underline{C}})\) is a multivariate Gaussian with the mean vector \({\underline{A}}{\underline{x}}_{t-1}+\,{\underline{b}}\) and the covariance matrix \({\underline{C}}\), and \(T\) is the input sequence’s length.

Fig. 9.3
figure 3

LDM for the modelling of noise

Full size image
Fig. 9.4
figure 4

SLDM for the modelling of audio of interest

Full size image

2.2.2 Modelling of Audio of Interest

The SLDM models the audio signal of interest passing through states as in a HMM. It further enforces a continuous state transition in the feature space conditioned on the state sequence. This more complex dynamic model has a hidden state variable \(s_{t}\) at each time \(t\). Like this, \(\underline{A}\) and \(\underline{b}\) depend on the state variable \(s_{t}\):

$$\begin{aligned} \underline{x}_{t}=\underline{A}(s_{t})\underline{x}_{t-1}+\underline{b}(s_{t})+\underline{g}_{t}. \end{aligned}$$
(9.21)

Likewise, the possible state sequences \(s_{1:T}\) describe a non-stationary LDM, as \(\underline{A}\) and \(\underline{b}\) change with time as do the audio features. In Fig. 9.4 the SLDM is shown as graphical model. As one sees, time dependencies are assumed between the continuous variables \(\underline{x}_{t}\), but not between the discrete state variables \(s_{t}\) [13]. An extension in [36] includes time dependencies between the hidden state variables, similar as in enhancing a GMM to a HMM. A SLDM as in Fig. 9.4 is described by

$$\begin{aligned} p(\,\underline{x}_{t},s_{t}|\underline{x}_{t-1})=\mathcal N (\,\underline{x}_{t};\underline{A}(s_{t})\underline{x}_{t-1}+\underline{b}(s_{t}),\underline{C}(s_{t}))\cdot p(s_{t}) \end{aligned}$$
(9.22)
$$\begin{aligned} p(\,\underline{x}_{1:T},s_{1:T})=p(\,\underline{x}_{1},s_{1})\prod _{t=2}^{T}p(\,\underline{x}_{t},s_{t}|\underline{x}_{t-1}). \end{aligned}$$
(9.23)
Fig. 9.5
figure 5

Observation model for noisy audio

Full size image

The EM algorithm can be used for the learning of the parameters of the SLDM, namely \(\underline{A}(s)\), \(\underline{b}(s)\), and \(\underline{C}(s)\). If one sets the number of states to one the SLDM turns into a LDM to compute the parameters \(\underline{A}\), \(\underline{b}\), and \(\underline{C}\) required for the noise modelling LDM.

2.2.3 Observation Model

The observation model describes the relationship of the noisy observation \(\underline{y}_{t}\) and the hidden audio and noise features. In Fig. 9.5, the graphical model representation of such a model is given by the zero variance observation model with SNR inference as in [42]. It is assumed that audio of interest \(\underline{x}_{t}\) and noise \(\underline{n}_{t}\) mix linearly in the time domain. In the cepstral domain, for example, this corresponds to a non-linear mixing.

2.2.4 Posterior Estimation and Enhancement

To reduce the computational complexity of the posterior estimation, an approximation is given by the restriction of the search space size by the generalised pseudo-Bayesian (GPB) algorithm [43]. It neglects distinct state histories with differences more than \(r\) frames in the past. Thus, with \(T\) as the sequence length, the inference complexity reduces from \(S^{T}\) to \(S^{r}\) where \(r\ll T\). In the GPB algorithm, one ‘collapses’, ‘predicts’, and ‘observes’ for each of the audio frames. Estimates of the moments of \(\underline{x}_{t}\) representing the de-noised audio features are computed based on the Gaussian posterior as calculated during the ‘observation’ in the GPB algorithm. In this process, clean features are assumed to be the Minimum Mean Square Error (MMSE) estimate \(E[\underline{x}_{t}|\underline{y}_{1:t}]\). SLDM feature enhancement can lead to outstanding results including the case of coloured Gaussian noise and negative SNR. This comes by the effort of modelling noise. The audio model’s linear dynamics model the the smooth time evolution of typical audio of interest such as speech, music, or certain sound types. The switching states express the piecewise stationarity typical in such audio. However, noise frames are assumed to be independent over time. As a consequence, non-stationary noises are not modelled adequately. Even with the restrictions made in the GPB algorithm, feature enhancement by SLDM is computationally more demanding than the techniques discussed above. Further, as in the AFE (cf. Sect. 9.1), accurate audio activity detection is required to provide correct estimation of the noise LDM.

3 Model Architectures

The most frequently used data-driven model representation of audio are HMMs [14]. Beyond the so far described optimisation options along the chain of Intelligent Audio Analysis, extending HMM topologies to more general DBN layouts can also help to increase noise robustness [15, 17, 44]. Generative models such as HMMs assume conditional independence of the audio feature observations, thus ignoring long-range dependencies as given in most audio of interest [45]. To overcome this, Conditional Random Fields (CRF) [46–48] model a sequence by an exponential distribution given the observation sequence. The HCRF [15, 49] further includes hidden state sequences for the estimation of the conditional probability of a class over an entire sequence. Another interesting option is to model the raw audio signal in the time domain [16]. For example, SAR-HMM [16] provide good results in clean audio conditions. To cope with noise, these can be extended to a Switching Linear Dynamical System (SLDS) [17] to model the dynamics of the raw audio signal and the noise. These alternatives will now be shortly presented.

3.1 Conditional Random Fields

As mentioned above, CRF [46] use an exponential distribution to model a sequence given its observation and by that also non-local dependencies among states and observations. Further, unnormalised transition probabilities are possible. Owing to the ability to enforce a Markov assumption as in HMMs, dynamic programming is applicable for inference. CRFs were also shown beneficial as LM [50].

3.2 Hidden Conditional Random Fields

An extension to HCRF is needed to make the CRF paradigm suited for general audio recognition tasks. This comes, as CRF provide a class prediction per observation and frame of a time sequence rather than for an entire sequence. HCRF overcome this by adding hidden state sequences [49]. Reports of superiority over HMM in the Intelligent Audio Analysis domain include the recognition of phones [15] and non-linguistic vocalisations [51] or the segmentation of meeting speech [52]. A particular strength is the possibility to use arbitrary functions for the observations without complication of the parameter learning.

The HCRF models the conditional probability of a class \(c\), given the sequence of observations \(\underline{X}=\underline{x}_{1},\underline{x}_{2},\dots ,\underline{x}_{T}\):

$$\begin{aligned} p(c|\underline{X},\underline{\lambda })=\frac{1}{z(\,\underline{X},\underline{\lambda })} \sum _{Seq\in c}e^{\underline{\lambda }\,\underline{f}(c,Seq,\underline{X})}, \end{aligned}$$
(9.24)

where \(\underline{\lambda }\) is the parameter vector and \(\underline{f}\) the ‘vector of sufficient statistics’, and \(Seq=s_{1},s_{2},\dots ,s_{T}\) is the hidden state sequence run through during the computation of this conditional probability. The probability is normalised by the ‘partition function’ \(z(\,\underline{X},\underline{\lambda })\) to ensure a properly normalised probability [15]:

$$\begin{aligned} z(\,\underline{X},\underline{\lambda })=\sum _{c} \sum _{Seq\in c} e^{\underline{\lambda }\,\underline{f}(c,Seq,\underline{X})}. \end{aligned}$$
(9.25)

The vector \(\underline{f}\) determines the probability to model. With a suited \(\underline{f}\) a left-right HMM can be imitated [15]. Let us now now restrict the HCRF to a Markov chain, but without the requirements of the transition probabilities to sum to one and real probability densities for the observations. In analogy to a HMM a parametrisation by transition scores \(a_{i,j}\) and observation scores \(b_{j}(\,\underline{x}_{t})\) can then be reached with the parameters \(\underline{\lambda }\), where and \(i\) and \(j\) are states of the model (cf. Sect. 7.3.2). Forward and backward recursions (cf. Sect. 7.3.1) as for a HMM can then further be used.

3.3 Audio Modelling in the Time Domain

Modelling of the raw signal in the time domain is a sparsely pursued option, but can offer easy explicit noise modelling [16]. We will look at SAR-HMMs to this end first, and then at the extension to SLDS.

3.3.1 Switching Autoregressive Hidden Markov Models

The SAR-HMM models the audio signal of interest as an autoregressive (AR) process. The non-stationarity is realised by switching between different AR parameter sets [17] by a discrete switch variable \(s_{t}\) similar to the HMM states. At a time step \(t\)—referring to the sample-level in this case—, exactly one out of \(S\) states is occupied. The state at time step \(t\) depends exclusively on its predecessor with the transition probability \(p(s_{t}|s_{t-1})\). The sample \(v_{t}\) at this time step is assumed as a linear combination of its \(R\) preceding samples superposed by a Gaussian distributed ‘innovation’ \(\eta (s_{t})\). \(\eta (s_{t})\) and the AR weights \(c_{r}(s_{t})\) are the parameter set given by the state \(s_{t}\):

$$\begin{aligned} v_{t}=-\sum _{r=1}^{R}c_{r}(s_{t})v_{t-r}+\eta (s_{t}) \quad \text{ with } \quad \eta \sim \mathcal N (\eta ;0,\sigma ^{2}(s_{t})). \end{aligned}$$
(9.26)

There, \(\eta (s_{t})\) models variations from pure autoregression rather than an independent additive noise process. The joint probability of a sequence of length \(T\) is

$$\begin{aligned} p(s_{1:T},v_{1:T}) = p(v_{1}|s_{1})p(s_{1})\prod _{t=2}^{T}p(v_{t}|v_{t-R:t-1},s_{t})p(s_{t}|s_{t-1}). \end{aligned}$$
(9.27)

Figure 9.6 visualises the SAR-HMM as DBN structure. Switching of the different AR models is forcedly ‘slowed down’ by introducing an constant \(K\). The model then needs to remain in a state for an integer multiple of time steps. This is needed, as considerably more sample values usually exist than features on the frame level.

Fig. 9.6
figure 6

SAR-HMM as DBN structure

Full size image

The EM algorithm can be used for learning of the AR parameters. Based on the forward-backward algorithm (cf. Sect. 7.3.1) the distributions \(p(s_{t}|v_{1:T})\) are learnt. The fact that an observation \(v_{t}\) depends on \(R\) predecessors makes the backward pass more complicated than in the case of an HMM. A ‘correction smoother’ [53] can thus be applied such that the backward pass calculates the posterior \(p(s_{t}|v_{1:T})\) by ‘correcting’ the forward pass’s output.

3.3.2 Autoregressive Switching Linear Dynamical Systems

With the extension of the SAR-HMM to an AR-SLDS, a noise process can explicitly be modelled [17]. The observed audio sample \(v_{t}\) of interest is then modelled as a noisy version of a hidden clean sample that is obtained from the projection of a hidden vector \(\underline{h}_{t}\) with the dynamic properties of a LDS:

$$\begin{aligned} \underline{h}_{t}=\underline{A}(s_{t})\underline{h}_{t-1}+\underline{\eta }_{t}^\mathcal{H }, \quad \text{ with } \quad \underline{\eta }_{t}^\mathcal{H }\sim \mathcal N \big (\,\underline{\eta }_{t}^\mathcal{H };0,\underline{\varSigma }_\mathcal{H }(s_{t})\big ). \end{aligned}$$
(9.28)

The transition matrix \(\underline{A}(s_{t})\) describes the dynamics of the hidden variable that depends on the state \(s_{t}\) at time step \(t\). A Gaussian distributed hidden ‘innovation’ variable \(\underline{\eta }_{t}^\mathcal{H }\) models variations from ‘pure’ linear state dynamics. As for \(\eta _{t}\) in Eq. (9.26) in the case of the SAR-HMM, \(\underline{\eta }_{t}^\mathcal{H }\) is not modelling an independent additive noise source. For the determination of the observed sample at time step \(t\), the vector \(\underline{h}_{t}\) is projected onto a scalar \(v_{t}\):

$$\begin{aligned} v_{t}=\underline{B}\,\underline{h}_{t}+\eta _{t}^\mathcal{V }, \quad \text{ with } \quad \eta _{t}^\mathcal{V }\sim \mathcal N (\eta _{t}^\mathcal{V };0,\sigma _\mathcal{V }^{2}), \end{aligned}$$
(9.29)

where \(\eta _{t}^\mathcal{V }\) models independent additive white Gaussian noise (AWGN) assumed to modify the hidden clean sample \(\underline{B}\underline{h}_{t}\). The DBN structure of the SLDS that models the hidden clean signal and an independent additive noise is found in Fig. 9.7.

Fig. 9.7
figure 7

AR-SLDS as DBN structure

Full size image

The parameters \(\underline{A}(s_{t})\), \(\underline{B}\) and \(\underline{\varSigma }_\mathcal{H }(s_{t})\) of the SLDS can be chosen to mimic the SAR-HMM (cf. Sect. 9.3.3.1) for the case \(\sigma _\mathcal{V }=0\) [17]. Likewise, if \(\sigma _\mathcal{V }\ne 0\) a noise model is included but no training of a new model is needed. With determination of the exact parameters of the AR-SLDS having a complexity of \(\mathcal O (S^T)\), the Expectation Correction (EC) approximation [54] provides an elegant reduction to \(\mathcal O (T)\).

In practice, the AR-SLDS is particularly suited to cope with white noise disturbance, as the variable \(\eta _{t}^\mathcal{V }\) incorporates an AWGN model. It is, however, usually inferior to frame-level feature-based HMM approaches in clean conditions. This may be explained by the difference of the approach to human perception which is not performed in the time-domain. In coloured noise environment the AR-SLDS usually also leads to lower performance than frame-level feature modelling as by SLDMs. A limitation for practical use is the high computational requirement, even with the EC algorithm: As an example, for audio at 16 kHz, \(T\) is 160 times higher than for a feature vector sequence operated on 100 FPS.

Obviously, further model architectures exist that were not shown here, but are well suited to cope with noises, in particular also for non-stationary noise. An example are the LSTM networks as shown in Sect. 7.2.3.4 [55, 56].