Quantitative and Spatial Evaluation of Distance-Based Localization Algorithms

Abstract

Indoor localization, especially in wireless networks (WN) has become an important research focus in computer science during the past ten years. Several approaches exist to estimate a node’s position relative to other devices. Most approaches are based on distance measurements and localization algorithms. In this chapter we provide an overview of common and new localization algorithms. A detailed investigation on the error distribution and the real world behaviour of these algorithms is presented. We also provide a discussion of the evaluation results that leads to open questions and future research approaches.

1 Introduction

With the broad success of location based services the demand for indoor localization functionality has become bigger and bigger. In theory most techniques to satisfy this demand are well known. There are several ways to estimate distances in wireless networks and several algorithms to calculate positions with estimated distances and the position of the corresponding anchor devices in the network. The general usability of a digital positioning system has been proved since 1994 with the general public availability of the Global Positioning System (GPS).

A positioning system for real world indoor use must have several differences to GPS. The main difference is the size of the ranging error that is part of every range estimation. While the GPS satellites use very precise and synchronized clocks, due to cost reasons, only common quartz clocks are used in WNs. Quartz clocks have higher jitter and drift, and consequently are not synchronized. Although there exist several high accuracy time synchronization protocols for use in WN, the achievable accuracy is far too low for precise range estimation. Another big issue for indoor localization is that generally there is no direct line of sight to the node whose distance is to be estimated; thus, multipath effects and signal reflection have a much bigger influence than in the GPS system.

Concerning these issues, several approaches for more error tolerant and more robust algorithms have been published. Because there are no standardized test cases and many researches obviously do not have access to radio ranging hardware, many authors rely on simulation to prove their functionality (see Sect. 2 for examples) and only a small minority uses real world deployments for their evaluation. Moreover, each simulation works with its own settings of the simulation parameters: they all differ in the choice of playing field, placement of anchors, radio range, and ranging error model. With respect to simulation results: we show that the performance of location estimation methods depends on the experimental setting. Thus, choosing a suitable algorithm for a given scenario or deployment is not possible based on these published results. It may even be impossible to conclude whether a method is consistently more precise than another one.

We provide an overview and present a structured analysis of common localization algorithms. The first two steps of our analysis are based on simulations and the third step is based on a real world deployment in an office building. All simulations and all test runs were conducted with the same parameter settings for all algorithms, so the results are comparable and strengths and weaknesses of the discussed algorithms can be seen easily.

In Sect. 2, we review related work and motivate our approach. In Sect. 3, we introduce the algorithms that we consider and explain their basic properties. In Sect. 4, we present our evaluation by simulation. The first part is a quantitative simulation of these algorithms. This simulation is similar to the simulations performed in the publications that introduce each algorithm to show their benefits. Instead of just reproducing the results of those papers, we simulate all algorithms using the same parameter settings to ensure that our comparisons are valid.

In the second part of Sect. 4, we discuss the spatial properties of the selected algorithms. The quantitative evaluation in the first part measures the average performance of each algorithm. Some algorithms show a harmonic performance, i.e., the position estimation error does not correlate well with the position and the placement of anchor nodes. Other algorithms are less harmonic; they perform badly in some areas of the playing field and exceptionally well in other areas. Thus, analyzing the distribution of the position error for each algorithm gives a refined view on the results obtained by our quantitative evaluation. We show that the error distribution doesn’t only depend on the error distribution of the measured distances, but also on the geometrical constellation between node and anchors and the characteristics of the algorithm. We present a new approach that shows that the algorithm itself has a much bigger influence on the resulting error than only viewing the geometrical constellation.

In Sect. 5, we validate the simulation results using a large indoor deployment by executing every algorithm with real world data gathered in our office building. The combined analysis makes the algorithms much more comparable and delivers a much better understanding of the strengths and weaknesses of the algorithms than the original papers where they have been published. In Sect. 6 we present our conclusion.

2 Related Work

Work on evaluating and comparing localization algorithms turns out to be heterogeneous. We are aware of surveys that explain different localization methods, e.g. (Mao et al. 2007), and qualitative surveys, e.g. (Torres-Solis et al. 2010), that review existing algorithms and try to convey the context in which they are best applied. Those surveys are meta-studies and provide little quantitative evaluation.

Surveys that focus on a quantitative comparison are attempted by Biaz and Ji (2005) and by Langendoen and Reijers (2003). Both survey multi-hop methods. Their results are not directly comparable to ours, since we do not limit the radio range. Biaz and Ji are vague on the ranging errors of their simulation, only stating “The actual range error is determined dynamically during the experiment by the production of the maximum variance and a random number between −1 and 1” but they do not state the used probability distribution. Indeed, Biaz and Ji compare algorithms based on their sensitivity to ranging errors using varying settings. We share some experimental setups with Langendoen and Reijers (a centred 3 × 3 grid) but work with different error models.

Comparing published performance evaluations is difficult at best. Table 1 lists the evaluation methods used by the sources to our algorithms. Each publication uses a different setup of the playing field and a different error model. Also the choice of algorithms they compare to varies. Linear Least Squares (LLS) and Bounding Box/Min–Max, (Savvides et al. 2002; Langendoen and Reijers 2003), appear to be the most common choices. Thus, transferring results about, say, Adapted Multi-Lateration (AML) (Kuruoglu et al. 2009) to Least Median of Squares (LMS) (Li et al. 2005) actually requires a new simulation run, as the results were obtained in non-comparable settings.

Table 1 Evaluation settings of common algorithms

Surveys like the ones above usually compare algorithms based on statistical evaluations of simulations. Comparing such results is difficult, because they differ in error model, geometric placement of anchors and density of anchors. These vary, sometimes leading to contradictory conclusions. Thus, we compare all algorithms under the same conditions. We highlight that results can be manipulated by the choices, effectively favouring one algorithm over the other.

Navidi et al. (1998) make a very profound observation about two lateration approaches: trilateration and multilateration. They observe that anchor position influences the position estimation error and call for more research in the domain of anchor placement. This comment also inspired the work on a spatial simulation that we present in part two of Sect. 4.

Yang and Liu (2010) present a slightly similar approach to research the spatial error distribution. Instead of calculating all possible positions on the playing field and visualizing the position error distribution, they calculate one position and visualize the probability for this node to be located on all other positions of the playing field.

Some researchers use the Cramér-Rao Bound (CRB) for estimating the error distribution instead of using simulations. The CRB computes a lower bound on the covariance of the error, usually from the position of the anchors and the statistical error model. For example, an analysis of the CRB has been given by Yang and Scheuing (2005), where they apply it to compute optimal anchor positions. The CRB gives a lower bound on the covariance matrix of an idealised, unbiased position estimator, based on geometric properties of anchor nodes and statistical properties of the range measurement errors. It does not reference the algorithm under consideration. Thus, the CRB only allows to state whether an algorithm is already optimal, provided that the algorithm is analysed analytically or statistically by a simulation similar to ours. This was both observed by Dulman et al. (2008) and Vaghefi and Buehrer (2012), which all observe that the CRB is an inadequate tool for localization. In addition, Yang and Scheuing observe in Proposition 2, that the CRB is a strict lower bound under any Gaussian error model, as no unbiased estimator will attain this bound.

3 Localization Algorithms

For reasons of clarity and comprehensibility we focus our evaluation on six localization algorithms. Three of them are well known algorithms and often used for performance comparison when proposing a new localization algorithm: Multilateration using Nonlinear Least Squares (NLLS) or LLS and Min–Max algorithm. The other three algorithms are more recent and have never been benchmarked under consistent conditions till now: LMS, AML and Iterative Clustering-based Localization Algorithm (ICLA) (Haiyong et al. 2011).

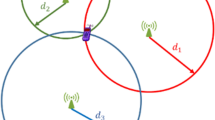
• 1. NLLS: Given $m$ anchor nodes with fixed positions at $b_{i} = \left( {x_{i} ,y_{i} } \right)$ for $i = 1,2, \ldots ,m$ and possibly noisy range measurements $d_{i}$ from these nodes to a non-anchor node located at $u = \left( {x,y} \right)$, multilateration finds the most likely position of the unknown node, denoted by $\hat{u}$. From this information we write a system of equations:

  $$\begin{array}{*{20}c} {\left( {x - x_{1} } \right)^{2} \,+ \,\left( {y - y_{1} } \right)^{2} = d_{1}^{2} } \\ {\left( {x - x_{2} } \right)^{2} \,+\, \left( {y - y_{2} } \right)^{2} = d_{2}^{2} } \\ {\begin{array}{*{20}c} \vdots \\ {\left( {x - x_{m} } \right)^{2} \,+\, \left( {y - y_{m} } \right)^{2} = d_{m}^{2} } \\ \end{array} } \\ \end{array} $$

  (1)

  This problem is usually solved by using a least squares (LS) method, that is, minimizing the sum of the squared residuals between the observed ranges $d_{i}$ and the estimated distances $\left\| {u - b_{i} } \right\|$:

  $$ \mathop u\limits^{} = \arg \mathop {\min }\limits_{u} \mathop \sum \limits_{{i = 1}}^{m} \left( {\left\| {\hat{u} - b_{i} } \right\| - d_{i}^3 } \right) $$

  (2)

  The minimization problem can be solved by using any of the Newton type optimization algorithms (Dennis and Schnabel 1996). These start from an initial guess at the solution and then iterate to gradually improve the estimated position until a local minimum of the objective function in Eq. (2) is found. However, there is a non-negligible probability of falling into a local minimum of the error surface when solving Eq. (2). Therefore, to find an estimate close to the global minimum, LS must run several times with different initial starting points, which is expensive in terms of computing overhead.

• 2. LLS: The nonlinear least squares problem can be linearized by subtracting one of the equations given in Eq. (1) from the remaining $m - 1$ equations. In matrix notation, the linear system can be expressed as $Au = b$ and can be solved by the LS method to provide an estimated location, as given by the closed form solution shown in Eq. (3) (i.e., normal equations).

  $$ \hat{u} = \left( {A^{T} A} \right)^{ - 1} A^{T} b $$

  (3)

  with:

  $$ A = \left( {\begin{array}{*{20}c} {x_{1} - x_{m} } & {y_{1} - y_{m} } \\ {x_{2} - x_{m} } & {y_{2} - y_{m} } \\ {\begin{array}{*{20}c} \vdots \\ {x_{{m - 1}} - x_{m} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {y_{{m - 1}} - y_{m} } \\ \end{array} } \\ \end{array} } \right),b = \frac{1}{2}\left( {\begin{array}{*{20}c} {d_{m}^{2} - d_{1}^{2} + \left\| {b_{1} - u^{3} } \right\|} \\ {d_{m}^{2} - d_{2}^{2} + \left\| {b_{2} - u^{3} } \right\|} \\ {\begin{array}{*{20}c} \vdots \\ {d_{m}^{2} - d_{{m - 1}}^{2} + \left\| {b_{{m - 1}} - u^{3} } \right\|} \\ \end{array} } \\ \end{array} } \right) $$

  (4)

• 3. AML: Similar to multilateration, Adapted Multi-Lateration tries to estimate the position of an unlocalized node using circle intersections. AML consists of three steps: intersection and elimination, first estimation and refinement. At the first step two intersecting circles are arbitrarily chosen. These circles may intersect at one or two points. If there is more than one point, the point with the larger distance to the third anchor is eliminated. At the first estimation step the previously computed intersection point is moved to the middle of the line connecting it with the closest point of the third anchor’s circle. This is done to compensate the errors introduced by range measurements. The calculation is done using the resemblance of triangles. At the last step the position can be further refined. Therefore, the anchors that were not used in the previous steps are added to the position estimation process with the same principle utilized in the second step.

• 4. Min–Max: The Min–Max algorithm, also known as Bounding Box algorithm, is a simple and straightforward method in contrast to the quite expensive number of floating point operations of LLS or NLLS that is required. The main idea is to build a square (bounding box) given by $\left[ {x_{i} - d_{i} ,y_{i} - d_{i} } \right] \times \left[ {x_{i} + d_{i} ,y_{i} + d_{i} } \right]$ around each anchor node $i$ using its location $\left( {x_{i} ,y_{i} } \right)$ and distance estimate $d_{i}$, and then to calculate the intersection of these squares. The final position of the unlocalized node is approximated by the center of the intersection box which is computed by taking the maximum of all coordinate minimums and the minimum of all maximums:

  $$ \left[ {{\text{max}}\left( {x_{i} - d_{i} } \right),{\text{max}}\left( {y_{i} - d_{i} } \right)} \right] \times \left[ {{\text{min}}\left( {x_{i} + d_{i} } \right),{\text{min}}\left( {y_{i} + d_{i} } \right)} \right] $$

  (5)

• 5. ICLA: The ICLA algorithm transforms node localization to an issue of clustering intersection points, which is claimed to be resistant to RSSI errors. The algorithm consists of three main steps. In the first step all intersection points between every two circles centered at the anchors coordinates and with radii equal to the estimated distances are generated. These intersection points cluster around the unlocalized node. In the second step the iterative clustering model (ICM) is applied to get the most representative intersection points for localization. The final step of the algorithm calculates the position of the unlocalized node by taking the centroid of all intersection points of the biggest group that ICM has produced. ICM is the central part of the algorithm. Here, all intersection points are iteratively moved towards their moving direction and merged if a collision occurs. The collision area is a circular area with the radius equal to the size of the moving step. Points with bigger weight exert a larger attracting force to other points and influence their moving direction. Initially, all points have the same weight. At the end of the procedure, all points are classified into several different clusters according to the left points.

• 6. LMS: Multilateration using LLS or NLLS is vulnerable to attacks because of its non-robustness to “outliers”. Due to the summation in the cost function shown in Eq. (2), a single outlier may ruin the estimation. Therefore, Li et al. (2005) propose to minimize the median of residue squares instead, based on the method introduced by (Rousseeuw and Leroy (1987). In this way a single outlier has little influence on the cost function, and won’t bias the estimate considerably. Finding the exact solution of this non-linear optimization problem is computationally expensive. Thus, the authors suggest the following procedure for implementing an approximated solution as the robust LMS algorithm:

• 1. Set $n = 4$ as the appropriate subset size.

• 2. Set $M = \left\{ {\begin{array}{*{20}l} {20,} \hfill & {if N > 6} \hfill \\ {\left( {\begin{array}{*{20}l} N \\ n \\ \end{array} } \right),} \hfill & {otherwise} \hfill \\ \end{array} } \right.$ as the appropriate total number of subsets.

• 3. Randomly draw $M$ subsets of size $n$ from the set of available anchors $\left\{ {\left( {x_{1} ,y_{1} } \right), \ldots ,\left( {x_{N} ,y_{N} } \right)} \right\}$. Estimate a position $\left( {\hat{x}_{ 0} ,\hat{y}_{0} } \right)_{j}$ for each subset $j = 1, 2, \ldots , M$ using LLS and calculate the median of the estimation residuals $r_{ij}^{2}$ to each anchor $i = 1, 2, \ldots , N$.

• 4. Define $m = arg\mathop {\hbox{min} }\limits_{j} med_{i} \left\{ {r_{ij}^{2} } \right\}$, then $\left( {\hat{x}_{ 0} ,\hat{y}_{0} } \right)_{m}$ is the position estimate with the least median of all medians among all subsets.

• 5. Calculate the scale estimate $s_{0} = 1.4826\left( {1 + \frac{5}{N - 2}} \right)\sqrt {med_{i} r_{im}^{2} }$.

• 6. Assign a weight $w_{i}$ to each anchor according to the formula $w_{i} = \left\{ {\begin{array}{*{20}l} {1, \left| {\frac{{r_{i} }}{{s_{0} }}} \right| \le 2.5} \\ {0, otherwise} \\ \end{array} } \right.$, whereas $r_{i} = \sqrt {\left( {x_{i} - \hat{x}_{ 0} } \right)^{2} + \left( {y_{i} - \hat{y}_{0} } \right)^{2} } - d_{i}$ is the residue of the i-th anchor for the location estimate $\left( {\hat{x}_{ 0} ,\hat{y}_{0} } \right)_{m}$.

• 7. Do LLS with weights $\left\{ {w_{i} } \right\}$ and all anchors to compute the final position estimate $\left( {\hat{x}_{ 0} ,\hat{y}_{0} } \right)$. This corresponds to executing LLS with only the anchors with a weight of $w_{i} = 1$.

The main idea of LMS is that at least one subset among all subsets contains only small or no measurement errors. Although smaller subsets increase the probability to have at least one good subset, $n = 4$ is chosen to reduce the chance that the samples are too close to each other to produce a numerically stable position estimate (Li et al. 2005).

4 Simulation

In this section we give a detailed analysis of the six localization algorithms introduced in Sect. 3. First, we give a quantitative analysis of the algorithms using a common error model for the distance measurement procedure. This way, we are able to compare our results with the results of other research papers. Second, we give an insight in the spatial error distribution by analyzing all algorithms with the LS² (Will et al. 2012) simulation engine. This simulator produces images of the error distribution by calculating the position error for every discrete point on the simulated area which easily shows the strengths and weaknesses of a given algorithm. Throughout the simulations we stick mostly to a grid layout of nine anchor nodes to be able to compare the results of the two approaches.

4.1 Quantitative Evaluation

We present simulation results that demonstrate the performance of the selected localization algorithms in different scenarios. We model each measured distance $d_{i}$ between the unlocalized node and the anchor node $i$ as,

$$ d_{i} = \hat{d}_{i} + \epsilon_{LOS} + \epsilon_{NLOS}$$

(6)

where $\hat{d}_{i}$ is the real distance, which is contaminated by measuring errors and non-line of sight (NLOS) errors. The measuring error $\epsilon_{LOS}$ results from the measuring processes in a noisy channel and the NLOS error $\epsilon_{NLOS}$ derives from the blocking of the direct paths. For the sake of comparison, we model $\epsilon_{LOS}$ by a zero mean Gaussian distribution $N(0,\sigma )$ because this is done by the majority of the related research papers. The NLOS error $\epsilon_{NLOS}$ was simulated as an Exponential random variable with the parameter $\lambda$ uniformly distributed, $\lambda \in U(0,b)$ where $b > 0$ is the maximum value of the uniform distribution. For each distance measurement a random value uniformly distributed between 0 (exclusive) and 1 (inclusive) is chosen and if smaller or equal than a predefined probability $p$, $d_{i}$ gets increased by NLOS error. For direct line of sight distance measurements this probability is zero, thus $\epsilon_{NLOS} = 0$. The performance of the localization algorithms is given in terms of mean absolute error (MAE) which is the average of the difference between the real and estimated locations. For all of our simulations we have one unlocalized node which takes 100,000 random positions on a square area and executes each algorithm. The radio range is unlimited in our simulations, so the unlocalized node gets distance measurements to all anchor nodes regardless of its current location.

In our first simulation, we deploy 9 anchor nodes on a square area of increasing size. The side length of the area varies from 10 to 100 m. The anchor nodes are arranged in a grid of 3 × 3 nodes in order that they cover the whole area. The anchor setup can be seen in Fig. 1. There are only line of sight distance measurements with standard deviation $\sigma = 2.3$. Figure 2 shows the results of this simulation, where the vertical axis is the localization error and the horizontal axis is the side length of the square area. The performance of NLLS, LLS, LMS, and ICLA stays pretty much unaffected by an increased area size. The accuracy of ICLA even shows an improvement of 20 % until the side length reaches 60 m. The performance of AML and Min–Max decreases linearly as the side length grows, with Min–Max showing the worst behavior.

Fig. 1

3 × 3 Grid setup

Fig. 2

Localization error to area size

In a second simulation, we deploy the 9 anchor nodes in the same way on a 100 × 100 m² area but continuously decrease the area the anchor nodes span. This can be seen in Fig. 1. At the start, the anchors cover the white square area. When reducing the covered area, the anchors would be deployed on the edges of the grey square area. In each step we reduce the covered area by 10 %. As a result of this, the unlocalized node will more and more take positions outside the grid because the anchors are not any longer the edges of the network. This is a reasonable test because it’s not always possible to have an ideal anchor setup and the movement of mobile nodes is not always predictable in a real world deployment. Again, there are only line of sight distance measurements with $\sigma = 2.3$. Figure 3 shows the results of this simulation where the vertical axis is the localization error and the horizontal axis is the area coverage in percent in relation to the 100 × 100 m² area. In general, AML and especially Min–Max are affected most by the reduction of the covered area. NLLS, LLS, LMS, and ICLA stay relatively unaffected until the coverage ratio drops below a critical margin of 10 %, with NLLS showing the best performance all the time. Area coverage of 1 % also isn’t a reasonable setup because the resulting grid only has a dimension of 10 × 10 m² with a distance of 45 m to the edges of the square area. However, area coverage of 30 % with a grid dimension of 54.8 × 54.8 m² and a distance of 22.6 m to the edges still sounds reasonable. In this scenario localization accuracy drops by 12.3 % (NLLS), 17.4 % (ICLA), 21.8 % (LMS), and 26 % (LLS) compared to the initial situation, whereas the accuracy of AML drops by 44.5 % and that of Min–Max by 206 %.

Fig. 3

Localization error to area coverage

In the next set of simulations, we set the side length of the square area to 50 m and the area coverage to 70 % while sticking to the grid distribution of anchor nodes.

Figure 4 shows the result of a simulation where the line of sight measurement noise is increased constantly. This is done by increasing the standard deviation $\sigma$ of the zero mean Gaussian measurement errors $\epsilon_{LOS}$. All algorithms show a decreased performance in terms of localization accuracy if the measurement noise is increased. The localization error of all algorithms except ICLA rises linearly. ICLA suffers most by an increased measurement noise while NLLS and Min–Max show the best overall performance. Although Min–Max doesn’t start from the same level than the other algorithms it can even outperform AML in the end. When there is no measurement error, only ICLA and Min–Max don’t produce very low estimation error. This is also expected since Min–Max does not produce an ideal solution of the equation system (by using bounding boxes) including anchor coordinates and distances to each of them. ICLA, on the other hand, occasionally clusters more intersection points than needed. This is the case when the unlocalized node is close to anchors and the resulting circles have small radii. As a result, there exist intersection points close to the intersection points of the ideal solution.

Fig. 4

Increasing measurement noise

In our next simulation, we wanted to test the influence of NLOS errors to the chosen localization algorithms. Therefore, we set the line of sight error to $\sigma = 2.3$ and the upper bound of the uniform distribution for parameter $\lambda$ to 3. In each simulation run, we set the probability $p$ for having NLOS errors to a fixed value. Thus, the expected percentage value of non-line of sight distances is close to $p$. The maximum allowed distance estimation error was set to 30 m. In this way all estimation errors larger than 30 m are cut off and reassigned to 30 m. Figure 5 shows that the localization error of ICLA and Min–Max increases gradually with the increase of NLOS distances, which demonstrates good NLOS error tolerance. NLLS, LLS, and AML show large performance degradation in terms of localization accuracy. As expected, LMS can outperform LLS due to its attack resistance in case of large outliers. At 20 % probability of NLOS distances LMS starts to perform better than LLS. This observation even gets more obvious when looking at a simulation run whose results are displayed in Fig. 6. Here, the maximum allowed distance estimation error is increased in steps of 30 m and the probability of NLOS distances is kept fixed at 50 %. LLS and NLLS cannot withstand these large errors due to the summation in the cost function, whereas ICLA and Min–Max stay completely unaffected by larger errors. Even the performance of AML only slightly decreases and is better than LMS in the end.

Fig. 5

Increasing the probability of NLOS distances

Fig. 6

Increasing the maximum allowed distance error

In our last simulation, we reposition the anchors as seen in Fig. 7 and modify the amount of anchors to investigate its influence on the performance of the algorithms. In the first simulation run, we take anchor 1–3, in the second simulation run anchor 1–4 and so on. In this way, there are no collinear anchors and the covered area is always nearly at maximum. All other settings remain the same except that the probability of NLOS distances is set to 30 %. Figure 8 shows the results of this simulation where the vertical axis is the localization error and the horizontal axis is the anchor count. Except for AML whose estimation error increases temporarily when anchor count exceeds 5, the estimation error of the other algorithms decreases. LMS performs better than LLS when the anchor count exceeds 5 because only then can LMS build enough subsets of size 4 to filter out outliers. ICLA doesn’t seem to work well with anchor counts below 5–6 but shows the overall highest performance gain of all algorithms and in the end outperforms even NLLS.

Fig. 7

Grid setup for anchor count simulation

Fig. 8

Increasing the anchor count

Another important aspect when comparing localization algorithms is their computational complexity. Figure 9 shows the average execution times of the six algorithms needed for a single localization with three, six, and nine anchors in our simulation. Min–Max has the smallest execution time since it applies only simple arithmetic operations. The same holds for AML. The execution time of NLLS is much higher than that of LLS because of its iterative approach, whereas LLS uses a closed form solution. The execution time of LMS is around 14 times higher than that of LLS except when the anchor count is lower five because then LMS cannot build subsets of size four. The execution time of ICLA is extremely large compared to all other algorithms.

Fig. 9

Execution times of the six localization algorithms

4.2 Spatial Evaluation

To evaluate the spatial distribution of the position error we executed every algorithm 1,000 times in the LS² simulation engine. LS² calculates the position error for every discrete point on the simulated area using an error model and an algorithm selected by the user. First, we simulated every algorithm with a uniform grid layout for the anchors. We chose nine anchors whose convex hull covers 4 % of the simulation area. The resulting images consist of up to three differently colored areas. The grey area indicates a position error between 100 and 500 % of the expected distance measurement error value; the darker the area, the higher is the error. The green area (if present) indicates a position error lower than the expected distance measurement error; the darker the area, the lower is the error. In the blue area the error is higher than 500 % of the position error and is cropped for better image contrast. The anchors are represented by the small red squares. We chose a uniformly distributed error with an expected value of 5 % of the playing field length for this simulation to minimize the effect of the error model and to maximize the effect of the geometrical constellation of the anchors and the influence of the algorithm. Other error models change the shapes very little but lower the contrast of the resulting images, so they are not as meaningful.

The green area is very important for cooperative localization strategies in WNs, because the position error stays in a reasonable range as long as the node remains in the green area. Otherwise the position error tends to grow much faster than expected.

In Fig. 10 we display the spatial distribution of the six algorithms in descending order of their average position error. As expected, Min–Max has the worst average error. But Min–Max performs much better than all other algorithms if the unlocalized node stays inside the convex hull of the anchors. If the node’s position is more than the inter-anchor distance away from the convex hull, the error grows very fast. NLLS performs completely different. Its overall error distribution is nearly uniform but the weaker regions are inside the convex hull and not outside. This different behavior corroborates that statistical measures like mean error and standard deviation are less precise than analyzing the spatial distribution. LLS and LMS perform nearly similar with LLS having an overall better average result inside the convex hull in this setup. The quality of AML and ICLA is poor in every aspect in this setup. They have no real strengths and get weaker very fast with rising distance to the anchors. It is also remarkable that the spatial error distribution of some algorithms is not symmetric, although the anchors are set up symmetrically. LMS for example performs better in the lower right corner of the convex hull than in the other three corners. Only Min–Max and NLLS are nearly symmetric.

Fig. 10

The average spatial error distribution of the six simulated algorithms (1,000 simulation runs). The algorithms are from left to right: Min–Max (480 % average position error compared to expected distance error), ICLA (408 %), AML (340 %), LMS (202 %), LLS (188 %) and NLLS (138 %)

Especially the comparison between LLS and NLLS shows that LLS has its strengths and is useful in some scenarios even if NLLS performs much better in the average case. Looking only at this setup, the dynamic selection of algorithms (e.g. between Min–Max and NLLS) regarding a roughly estimated position would lead to better results.

The different spatial distributions of the position error of the six algorithms shows that statistical methods like the Cramér-Rao Bound, that do not take the geometrical characteristics of the algorithms into account, are often misleading or not very helpful.

For some applications where you have to guarantee an upper bound of the position error, e.g. in rescue scenarios, the worst case of the spatial distribution is more meaningful than the average case. In Fig. 11 we show the highest position error for every discrete location out of the 1,000 simulation runs. NLLS shows its weaknesses inside the convex hull more clearly, but in contrast to the average results, it looks strictly symmetric. AMLs worst case distribution looks completely different to the average case distribution. The lower right half of the convex hull was one of the weaker regions in Fig. 10 and is the best region in Fig. 11. Again, AMLs performance is very poor in this setup compared to the other algorithms. Min–Max again is the best algorithm if the unlocalized node stays inside the convex hull of the anchor nodes and the worst case distribution is linear weakened compared to the average one.

Fig. 11

Worst case results for NLLS, AML, and Min–Max (1,000 simulation runs)

For the next simulation run, we lowered the number of anchors to four and chose a different layout, where the four anchors are not placed optimal but nearly collinear. The resulting spatial distribution of the position error in Fig. 12 has changed little. NLLS is weaker inside the convex hull and stronger outside, but still remains very homogenous. Min–Max remains very good between the anchors and quickly gets worse with increasing distance to the anchors. Min–Max has still the lowest error for all algorithms inside the convex hull. LMS and LLS perform nearly identically. They remain on a good average level and do not seem to suffer very much from the reduced anchor count. The only outlier is AML, which is the only algorithm of the six that performs better with fewer anchors in a worse layout. We conclude that AML has some design weaknesses and should be optimized to perform better with more anchors, or at least should only use a subset of the given anchors. In its original paper, AML is mainly simulated in a setup with a maximum of four anchors, so their conclusion that AML performs very well seems reasonable only under these limited conditions. ICLA once again is weak under these conditions. This contradicts somewhat to the findings in its original publication where ICLA always showed half the error of Min–Max and also to the previous subsection where ICLA showed better performance. An explanation can be seen in Fig. 4. Because the expected measurement error was much higher in the simulations using LS² than the other ones, the accuracy of ICLA experienced a much larger degradation. This is of particular importance since, as previously mentioned, ICLA suffers the most from an increased measurement noise.

Fig. 12

The average spatial error distribution of the six simulated algorithms (1,000 simulation runs) with 4 anchors. The algorithms are from left to right: ICLA (406 %), Min–Max (382 %), LMS (262 %), LLS (261 %), AML (220 %) and NLLS (138 %)

For the last simulation we placed 9 anchors on a half circle. The results of this simulation can be seen in Fig. 13. The most interesting observation for this constellation is that the size of the green area is significantly bigger for the algorithms with high average errors. This leads to a new perspective in comparing these algorithms, especially for tracking applications where the current position can roughly be estimated. In the case shown in Fig. 13 one could implement a simple algorithm which switches between NLLS and Min–Max depending on the estimated node position.

Fig. 13

The average spatial error distribution of three simulated algorithms (1,000 simulation runs) with 9 anchors. The algorithms are from left to right: NLLS (130 %), LLS (160 %) and Min–Max (360 %)

This observation is also useful for a general comparison and evaluation of localization algorithms. Concentrating only on the average position error as an evaluation metric could lead to wrong conclusions if the spatial distribution is disregarded. The very different spatial distributions of ranging errors for a given scenario also implies that the CRB, which does not consider the algorithm itself, can give only a very vague estimation of the spatial distribution of the position error. For example, Min–Max has a worse average position error, but performs better in real world indoor deployments because the inter-anchor distance is normally low and the node can only move inside the hull of the anchors that are usually mounted to walls. This behaviour can be predicted from the spatial distribution.

5 Experimental Results

In order to measure the effectiveness of the six algorithms with real sensor network data and to be able to compare the results with the executed simulations, we recorded the data of a series of different test runs. The experiments were carried out using a modified version of the Modular Sensor Board (MSB) A2 (Baar et al. 2008) node which is equipped with a Nanotron nanoPAN 5375 (Nanotron Technologies GmbH 2009) transceiver. This hardware enables the sensor nodes to measure inter-node ranges using time of flight (TOF) in the 2.4 GHz frequency band. The experiments took place on the second floor of our Computer Science Department during daytime.

Figure 14 shows one exemplary campaign of measurements following a route among offices, laboratories and with a few people walking around. For the reason of clarity, we plotted only the results of NLLS and Min–Max using a Kalman filter. The starting point is denoted by “S”, the endpoint is denoted by “E” and the total length of the path was about 100 m.

Fig. 14

Position estimates on the second floor of our Computer Science Department

In each run, we used 17 anchors which were deployed throughout the building. Most of the anchors were placed in office rooms with doors closed. Only a small fraction of nodes was placed on the hallway, in case of Fig. 14, there were four nodes. Ground truth was measured with the aid of a robot system developed at our Department using a Microsoft Kinect. This reference system provides about 10 cm positioning accuracy. The robot also carried the unlocalized node and followed a predefined path with a predefined speed. We used the maximum movement speed of the robot, which is 0.5 m/s. In total, we performed over 5,300 localizations when adding up all test runs. The nanoPAN achieves ranging precision of around 2.85 m in average and the RMSE is 4.32 m. However, the ranging error can be as large as 20 m. We even encountered measurement errors up to 75 m in rare cases. Figure 15 shows the distribution of the distance measurement error using all anchor nodes and all runs.

Fig. 15

Histogram of distance measurement error (all runs and anchors)

The quantitative results of the six localization algorithms are shown in Table 2. The average anchor degree throughout all experiments was 7.48. As it can be seen, Min–Max outperforms the other algorithms in terms of localization accuracy with achieving an average error of 2.05 m. This is about twice as good as ICLA, the second best algorithm with an average error of 4.25 m. The good performance of Min–Max is not surprising because the inter-anchor distances were relative short (between 5 and 10 m) and the mobile node took mainly positions within the bounds of the network. As we know from Sect. 4 this is the optimal situation for Min–Max algorithm. This behavior can also be seen in Fig. 16 where the unfiltered estimated locations of Min–Max are displayed. For instance when looking at anchor 11 or 12, one can clearly see that the error is bounded by their coordinates.

Table 2 Quantitative results for the localization task

Fig. 16

Behavior of unfiltered Min–Max algorithm

The fact that the RMSE of NLLS, AML, and ICLA is only slightly larger than the RMSE of the distance measurements tells us that these algorithms performed well relative to the quality of the distance measurements available. The histograms of localization errors of all algorithms can be seen in Fig. 17 where the vertical axis is the absolute frequency and the horizontal axis is the localization error. LLS and therefore also LMS show poor performance compared to the other algorithms. Also the RMSE is much larger than that of the other algorithms. However, LMS can still achieve better localization accuracy than LLS as expected from our simulations.

Fig. 17

Histograms of localization errors in a real environment, the second floor of our Computer Science Department

Obviously, the position accuracy could be improved using some filtering techniques, such as Kalman or particle filters, but the aim of this chapter is to show and compare the performance of the used localization algorithms without using any of those filtering techniques.

Summarizing the results of the simulations and experiments, it can be stated that NLLS shows the overall best performance no matter the area size and coverage ratio. Its spatial error distribution is very uniform which is proved by the simulations done in Sect. 4. It is also among the best algorithms of the real experiment. However, if the measurement noise is not that high, ICLAs performance is very close to that of NLLS. When the average anchor degree is greater than 5 and when operating in indoor environments where the percentage of NLOS distances is certainly higher than 30 % in most of the cases, ICLA outperforms the other localization schemes in terms of accuracy and shows a much better resistance to NLOS errors, even than NLLS. However, this advantage comes at the expense of increased calculation costs compared to all other algorithms.

Min–Max has the advantage of being computationally cheap and insensitive to errors, but it requires a good constellation of anchors; in particular, the desired localization error of Min–Max can be easily adjusted by placing the anchors at the edges of the network and having small inter-anchor distances. This fact is also stated by Savvides et al. (2002) and proved by Langendoen and Reijers (2003). AML works best when the number of used anchors lies between 4 and 5. This corresponds to the findings of Kuruoglu et al. (2009) and is the reason why they limit the number of used anchors to 4 when comparing AML with LLS and Min–Max. They identify the refinement phase of their algorithm as the reason for this behavior. Like Min–Max, AML also profits from a good constellation of anchors, although the impact is not as high as that of Min–Max. We could also prove that LLS performs better than LMS when the attack strength is low (less than 20 % NLOS distances), which is stated by Li et al. (2005). That’s the reason why they implemented an efficient switched LLS-LMS localization scheme to overcome this situation. The desired design goal of being more robust against large distance measurement error due to non-line of sight signal propagation could be validated by our studies. Nevertheless, LMS cannot outperform NLLS unless the distance measurement error is abnormally high which shouldn’t be the case even in indoor deployments.

6 Conclusion

We showed that the error distribution doesn’t only depend on the error distribution of the measured distances, but also on the geometrical constellation between node and anchors and the characteristics of the algorithm. We presented results from both simulations and real experiments that corroborate our theory.

The NLLS algorithm is the best general purpose algorithm of the tested localization algorithms, because its spatial error distribution is very homogenous even if the anchor placement isn’t optimal. ICLA, on the other hand, showed ambiguous behavior. While the algorithm performed weakly in the spatial error distribution analysis, the real experiments and other simulations showed opposite behavior. We discovered that ICLA measurement noise which should be adapted to omission is the reason for the poor performance in Sect. 4.2. If we know the error distribution of the distance measurement device and the operation environment (e.g. indoors), then ICLA provides a good alternative to NLLS. That ICLA should be adapted is also not mentioned in its original publication.

If the errors are large and the unlocalized node is in the convex hull of the anchors, Min–Max also is a good choice for localization. Especially in dense networks with small inter-anchor distances Min–Max outperforms all other algorithms as shown by the experiments in Sect. 5.

The optimal solution for the localization task would be to use a selection algorithm which is capable of analyzing the current situation at each point in time and then applying the ideal method for achieving the lowest positioning error possible.

Future work should address the development of an algorithm that is optimized for geometric constellations typically found in real world deployments. For indoor environments an algorithm should focus on low inter-anchor distances and the performance inside the convex hull of the anchors. For cooperative localization algorithms one should try to achieve a very homogeneous error distribution with position errors lower than the average distance error. To develop such algorithms or an adaptive combination of several algorithms, it would be helpful to get simple estimation for the expected quality of the current anchor setup with the current algorithm.