Keywords

1 Introduction

A crucial part in any source reconstruction procedure is the computation of the bioelectromagnetic field generated by known sources. This computation is known as the forward problem or direct problem and includes the mathematical description of the sources and sensors, as well as the description of the relationship between the source parameters and the simulated data at the sensors. The material (tissue) properties and the distribution of tissues within the volume conductorFootnote 1 are highly complex. This complexity makes the transfer function between sources and measurements non-trivial. Thus, approaches to the forward problem are mainly characterized by the degree of simplification they apply.

First we consider the description of the sources. Microscopically, currents across cell membranes are impressed by chemical processes and concentration gradients. In the pyramidal cells of the cortex, these currents are mainly arranged in a radially symmetric manner around the axes of the dendrites, which causes a cancellation of their far field and therefore invisibility to EEG/MEG. These impressed currents give rise to local ohmic currents inside and outside the cells, governed by a complex interplay of chemical and electrical processes at the microscopic level (involving voltage-gated ion channels, second messenger chains, barriers like cell membranes, etc.). However, these functional and structural details at the cellular level are usually not taken into account when modeling EEG/MEG. Instead, the source area is considered as a black box. All currents within that box, including impressed and passive ohmic currents inside and outside the cells, are represented by a single primary current, usually modeled by means of an equivalent current dipole. The far field of this current is probably dominated by intracellular ohmic currents flowing along the longitudinal axis of the apical dendrites of the pyramidal cells (i.e., perpendicular to the cortical surface). It is assumed that at least a few ten thousands of neurons need to be simultaneously active to produce a measurable effect at the head surface (Murakami and Okada 2006). The extent of the box is implicitly determined by the spatial resolution of the measurement. More specifically, the primary current is normally described as point-like. Under this constraint, the extent of that black box must be small compared to the distance to the sensors. All currents outside the box are defined as volume currents (secondary currents). Thus, the total current density is the sum of primary and secondary current densities: \(\vec{J}\left( {\vec{r}^{'} } \right) = \vec{J}_{p} \left( {\vec{r}^{'} } \right) + \vec{J}_{v} (\vec{r}')\). Since often multiple source componentsFootnote 2 are active at the same time, the measured magnetic fields and electric potentials represent a superposition of all contributions. Each source component can be characterized by a set of parameters (see below) and by the signals it produces at sensor level. These signals are often termed components of the signal (Donchin 1966; Kayser and Tenke 2005). In the literature on source separation the term “source” is often used synonymously for the signal the source component is producing, whereas in the literature on source reconstruction it is used to describe the parameterized source model.

The primary current density \(\vec{J}_{p} (\vec{r}',t)\) is a spatially continuous function. In order to describe it with a finite vector of parameters, two approaches exist. The discretization approach divides the space into sections, within each of which the current density is replaced by the integral over the volume of that section:

$$\vec{d}_{i} (t) = \int\limits_{{V_{i} }} {\vec{J}_{p} (\vec{r}',t)dv}$$
(1)

where \(\vec{d}_{i} (t)\) denotes the dipole moment typically given in nanoamperemeters [nAm]. The discretization approach is based on the topology of the source space. For example, the entire brain volume can be discretized in hexahedral voxels, or the cortical sheet can be discretized into prisms (triangles representing the cortical surface plus a predefined thickness). In each of these elements, the primary current density is modeled by one current dipole.

In many practical applications the primary current density is relatively focal, such that it can be satisfactorily described by a few current dipoles at the centers of activity leading to the multiple dipoles model. The second approach parameterizes the primary current density with the help of a series expansion. The series can also describe extended source configurations centered at the expansion point. Often, the electric potential at the measurement location \(\vec{r}\)expressed by a Taylor series expansion with the origin at position \(\vec{r}'\):

$$\varphi (\vec{r}) = \frac{1}{4\pi \sigma }\left[ {\frac{m}{{\left| {\vec{r} - \vec{r}'} \right|}} + \frac{{\vec{d}(\vec{r} - \vec{r}')}}{{\left| {\vec{r} - \vec{r}'} \right|^{3} }} + \frac{1}{{\left| {\vec{r} - \vec{r}'} \right|^{3} }}\left( {\frac{3}{{\left| {\vec{r} - \vec{r}'} \right|^{2} }}(\vec{r} - \vec{r}')^{T} \bar{q}(\vec{r} - \vec{r}') - tr(\bar{q})} \right) + \cdots } \right]$$
(2)

Here, m is the electric monopole moment, which vanishes due to the charge conservation law:

$$m = - \int\limits_{V} {\nabla \vec{J}_{p} (\vec{r}')dv} ,$$
(3)

\(\vec{d}\) is the dipole moment according to Eq. (1) and \(\bar{q}\) is the quadrupole tensor:

$$\bar{q} = \int\limits_{V} {\vec{J}_{p} (\vec{r}')\vec{r}'^{T} dv}$$
(4)

A truncation of this series, after the dipole term, results in the equivalent current dipole model which represents the entire current density as a point-like current element. Extending this approach to multiple partial volumes yields the same multiple dipoles model, which was derived from the discretization approach above.

The sensor model describes how a sensor transforms a physical quantity into an accessible output. For biomagnetic measurements this typically involves first the transformation of the magnetic flux density into a magnetic flux by integration over the area of a pickup coil. Next this magnetic flux is often combined across several coils in order to suppress far field disturbances. Finally, the magnetic flux is converted into a voltage. Important parameters of this model are the position, orientation, geometrical form, and number of windings of the coils. The exact integration of the flux density over the coil area would be computationally demanding. Thus, often the flux density at the center point of the coil is assumed to represent the constant value over the entire coil area. More accurate approaches involve a weighted average of the flux density at a small number of integration points within the coil area. Magnetic recordings do not require a reference, which is an advantage compared to electric recordings.

Next we consider the description of the relationship between source parameters and the simulated data at the sensors. Maxwell’s equations are the basis for this transfer function. For most non-invasively measured electric and magnetic bio-signals, frequencies are below 1,000 Hz and the spatial dimension is below 1 m. Consequently, the temporal derivatives in the Maxwell equations can be omitted (Plonsey and Heppner 1967), yielding the quasi-static Maxwell equations that disregard capacitive and inductive effects (Table 1). The free volume charge density is not relevant here, since we consider the electric flow field only, which is uncoupled from the electrostatic field due to the vanishing derivative of D in the quasistatic approximation of Ampère’s law (Table 1). The only remaining relevant material parameter is the electrical conductivity.

Table 1 Full and quasi-static Maxwell equations
Full size table

From the definition of the scalar electric potential \(\vec{E} = - \nabla \varphi\) (based on the quasi-static law of Faraday) and Ohm’s law \(\vec{J} = \bar{\sigma } \cdot \vec{E}\), one can derive Poisson’s equation (Eq. 5), while the quasi-static law of Ampère allows (under the assumption of a scalar magnetic permeability \(\bar{\mu } = \mu\)) for computing the magnetic field from the electric potential (Eq. 6).

$$\nabla \bar{\sigma }\nabla \varphi = - \nabla {\vec{\text{J}}}_{\text{p}}$$
(5)
$$\nabla \times \vec{B} = - \mu \left( {\bar{\sigma }\nabla \varphi + \vec{J}_{p} } \right).$$
(6)

This leads to expressions for the electric potential φ and the magnetic induction \(\vec{B}\) at position \(\vec{r}\), arising from N dipoles at positions \(\vec{r}_{i} '\) with moments \(\vec{d}_{i}\), in an infinite volume with homogeneous and isotropic conductivity.

$$\vec{B}_{\infty } (\vec{r}) = \frac{\mu }{4\pi }\sum\limits_{i = 1}^{N} {\vec{d}_{i} \times \frac{{(\vec{r} - \vec{r}_{i} ')}}{{|\vec{r} - \vec{r}_{i} '|^{3} }}} \quad \varphi_{\infty } (\vec{r}) = \frac{1}{4\pi \sigma }\sum\limits_{i = 1}^{N} {\vec{d}_{i} } \frac{{(\vec{r} - \vec{r}_{i} ')}}{{|\vec{r} - \vec{r}_{i} '|^{3} }}$$
(7)

These equations, however, do not provide an acceptable solution for the situation in real biological tissue as they do not take into account the effects of conductivity inhomogeneities. If very simplifying assumptions about the distribution of conductivities are made, analytical or semi-analytical solutions can be used. The human head can be modeled with the help of a series of spherical or ellipsoidal layers (Cuffin and Cohen 1977; Sarvas 1987; de Munck 1988, 1989; Kariotou 2004; Giapalaki and Kariotou 2006). Such models allow for easy computations, but can yield significant errors (Cuffin and Cohen 1977).

More realistic conductivity profiles can be modeled using numerical methods. These methods can be classified into differential and integral methods depending on whether derivatives or integrals are to be approximated. Additionally, methods can be classified according to their basic assumptions and simplifications. A crucial property of the head is the fact that a relatively low-conducting skull encloses the relatively well-conducting brain. In turn, the skull is surrounded by a relatively well-conducting remainder of the head (scalp, muscles, eyes, etc.). This leads to the compartment assumption. Typically, 3 compartments with homogeneous and isotropic conductivity are defined: scalp, skull and brain. The brain compartment subsumes all tissues inside the skull. The skull compartment includes both compact and spongy bone. The scalp compartment summarizes all tissues outside the skull. The compartment approach necessitates the use of an integral-based method.

Alternatively, the compartment assumption can be replaced by a 3D volume discretization. Here, the volume is divided into small elements. The size and number of elements governs the achievable accuracy and is limited by computational resources. Volume discretization approaches are usually treated with differential methods.

The boundary element method (BEM) is an integral method based on the compartment assumption (Barnard et al. 1967a, b; Geselowitz 1967, 1970; Sarvas 1987; Hämäläinen and Sarvas 1989; Stenroos et al. 2007). An alternative approach is the multiple multipole method (MMP) (Haueisen et al. 1996). Here, multipole expansions are used to describe the neuroelectromagnetic field and the expansion coefficients may be computed based on a matching of the boundary conditions at a set of boundary points representing the major conductivity jumps. For modeling the 3D or anisotropic conductivity profile of the head, the finite element method (FEM) (Witwer et al. 1972; Haueisen et al. 1995; Wolters et al. 2004; Hallez et al. 2005) or the finite difference method (FDM) (Witwer et al. 1972; Haueisen et al. 1995; Wolters et al. 2004; Hallez et al. 2005) can be used. Both are differential methods. The entire volume is discretized into small elements and each volume element is assigned a separate conductivity tensor. While FDM is easier to implement, FEM allows for a smoother geometry description of conductivity boundaries. For a review including the FEM and FDM see e.g. (Hallez et al. 2007).

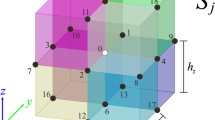
In the following, we will treat analytical methods, BEM, and FEM in more detail, since these methods are most frequently used. Figure 1 shows an example model for BEM and FEM.

Fig. 1
figure 1

Examples for head models. Left boundary element model with the most important conductivity boundaries (inner and outer skull surface, outer surface of the head) described by triangular meshes. Right finite element model built with tetrahedral elements. Colors represent tissue types

Full size image

2 Analytical and Semi-Analytical Methods

In order to obtain analytical or semi-analytical formulations of the forward problem, the geometry of the head and the conductivity distribution have to be described in terms of simple shapes, such as concentric spherical or ellipsoidal shells. In the simplest case, the volume conductor is assumed to be a sphere, which is more or less adapted to the actual head geometry. Under this assumption, for MEG it can be shown that the predicted magnetic field outside the head depends solely on the origin of the sphere as well as the positions and orientations of the sources and the sensors. The conductivity profile including the outer radius, as long as it is spherically symmetric, plays no role. According to Sarvas (1987), the magnetic induction \(\vec{B}\) at sensor position \(\vec{r}\) due to N dipoles at positions \(\vec{r}_{i}^{'}\) with dipole moments \(\vec{q}_{i}\) (i = 1…N) is computed as follows:

$$\vec{a}_{i} = \vec{r} - \vec{r}_{i}^{'}$$
(8)
$$F_{i} = \left| {\vec{a}_{i} } \right|\left( {\left| {\vec{r}} \right|\left| {\vec{a}_{i} } \right| + \left| {\vec{r}} \right|^{2} - \vec{r}_{i}^{'} \vec{r}} \right)$$
(9)
$$\nabla F_{i} = \left( {\left| {\vec{r}} \right|^{ - 1} \left| {\vec{a}_{i} } \right|^{2} + \left| {\vec{a}_{i} } \right|^{ - 1} \vec{a}_{i} \vec{r} + 2\vec{a}_{i} + 2\vec{r}} \right)\vec{r} - \left( {\vec{a}_{i} + 2\vec{r} + \left| {\vec{a}_{i} } \right|^{ - 1} \vec{a}_{i} \vec{r}} \right)\vec{r}_{i}^{'}$$
(10)
$$\vec{B}\left( {\vec{r}} \right) = \frac{\mu }{4\pi }\mathop \sum \limits_{i = 1}^{N} \frac{{F_{i} \vec{q}_{i} \times \vec{r}_{i}^{'} - \vec{q}_{i} \times \vec{r}_{i}^{'} \vec{r}\nabla F_{i} }}{{F_{i}^{2} }}$$
(11)

Another important property of this volume conductor model can be seen from the formula above: a dipole with radial orientation does not contribute to the measured field. Its effect is completely compensated for by the Ohmic return currents.

In contrast, the predicted EEG on the surface of a spherical volume conductor does depend on sources of all orientations, as well as on the conductivities and radii of the different tissue layers. A semi-analytical solution based on Legendre polynomials is given by de Munck (1989). It allows for the inclusion of tissue compartments with different conductivities, bounded by concentric spherical surfaces. It even allows for a simple form of tissue anisotropy, namely the distinction between radial and tangential conductivities.

Although spherical models reflect the basic geometric properties of the head, such as its round shape and the concentric arrangement of the tissue layers, the deviations from the real head shape may lead to substantial errors (Cuffin and Cohen 1977). There are a number of possibilities to improve this situation without giving up the advantages of an analytical solution. One option is the use of ellipsoidal instead of spherical shells, as proposed, for example, by Fieseler (Fieseler 1999) and Kariotou (Kariotou 2004; Giapalaki and Kariotou 2006).

Alternatively, one can use a separate spherical volume conductor model for each sensor. One way to find these local spheres is to fit them locally to a patch of the head (or brain) surface near the respective sensor (Ilmoniemi 1985; Lütkenhöner et al. 1990). This assumes that the description of the tissue boundaries in the immediate vicinity of the respective sensor is most crucial for the accuracy of the forward computation. A more principled, but also computationally more expensive, way to find the best spherical models on a sensor-to-sensor basis was proposed by Huang et al. (1999). They first used a realistic 3-shell boundary element model (see below) to compute solutions in each sensor for a large number of dipoles located in the entire brain (i.e., a leadfield computation, see below). Then, for each sensor, the solutions for the same dipoles were computed using a spherical head model, and the parameters of that spherical model were optimized such that the difference between the boundary element method solution and the spherical solution became minimum. For MEG, a single-compartment boundary element model can be used alternatively. The resulting spheres can then be used to calculate forward solutions for arbitrary dipoles. In principle, this method can be seen as a sophisticated way for interpolating leadfields computed using numerical methods, such as BEM. For a review and evaluation of different methods using multiple spheres, see Lalancette et al. (2011).

Finally, Nolte (2003) proposed an approach, where the solution for a spherical volume conductor is corrected by a superposition of basis functions constructed from spherical harmonics and fitted to the boundary conditions. It can be shown that this approach yields good approximations for non-spherical volume conductors such as the prolate spheroid (Nolte 2003) and even for realistically shaped volume conductors (Stenroos et al. 2012).

3 Numerical Methods

3.1 Boundary Element Method

The BEM is an important and popular field calculation method used in biomagnetism. It can describe the head as an isotropic and piecewise homogeneous volume conductor of realistic shape. In practice, the compartments are designed such that their boundaries represent the most prominent conductivity jumps in the head. These are most often the head surface as well as the outer and inner bounds of the skull. For MEG, the volume currents outside the interior of the skull contribute relatively little to the measurements and therefore the respective compartments (skull, scalp) are often neglected (Hämäläinen and Sarvas 1989). However, it was recently shown that the inclusion of the skull and scalp compartments allows for a relevant improvement in accuracy (Stenroos et al. 2012).

Mathematically, the solution is derived from Poisson’s equation (Eq. 5) and the appropriate Cauchy boundary conditions: (1) the potential has to be continuous across the boundary: \(\varphi^{ + } = \varphi^{ - }\), and (2) the perpendicular component of the current has to be continuous across the boundaryFootnote 3: \(\sigma^{ + } \left( {\nabla_{ \bot } \varphi } \right)^{ + } = \sigma^{ - } \left( {\nabla_{ \bot } \varphi } \right)^{ - }\), where the superscripts ()+ and ()− refer to the values on either side of the boundary and \(\nabla_{ \bot }\) is the derivative with respect to the normal direction of the boundary. There are two different approaches to the solution: direct and indirect BEM. In the direct approach one sets up and solves an equation system for both the potentials and their normal derivatives (Boemmel et al. 1993; Fletcher et al. 1995). A specific variant of direct BEM is the symmetric BEM approach (Kybic et al. 2005). In the indirect approach the potential function is first derived analytically, before applying the BEM (Brebbia et al. 1984; Mosher et al. 1999). This leads to the following expressions for the electric potential and the magnetic induction (Geselowitz 1967, 1970):

$$\frac{{\sigma_{k}^{ + } + \sigma_{k}^{ - } }}{2}\varphi \left( {\vec{r}} \right) = \sigma_{s} \varphi_{\infty } \left( {\vec{r}} \right) - \sum\limits_{j = 1}^{N} {\frac{{\sigma_{j}^{ - } - \sigma_{j}^{ + } }}{4\pi }} \int_{{S_{j} }} {\varphi \left( {\vec{r}^{\prime}} \right)\vec{n}\left( {\vec{r}^{\prime}} \right)\frac{{\vec{r} - \vec{r}^{\prime}}}{{\left| {\vec{r} - \vec{r}^{\prime}} \right|^{3} }}} dS'$$
(12)
$$\vec{B}\left( {\vec{r}} \right) = \vec{B}_{\infty } \left( {\vec{r}} \right) - \frac{\mu }{4\pi }\sum\limits_{j = 1}^{N} {\left( {\sigma_{j}^{ - } - \sigma_{j}^{ + } } \right)} \int_{{S_{j} }} {\varphi \left( {\vec{r}^{\prime}} \right)\vec{n}\left( {\vec{r}^{\prime}} \right) \times \frac{{\vec{r} - \vec{r}^{\prime}}}{{\left| {\vec{r} - \vec{r}^{\prime}} \right|^{3} }}} dS'$$
(13)

Here, σs refers to the conductivity in the source compartment, \(\vec{n}\) is the normal vector of the boundary, \(\vec{r}\) and \(\vec{r}'\) denote the positions where the potential is calculated, S j is the j-th boundary between compartments with different conductivity, N is the number of compartments, and k is the index of the boundary on which the potential is calculated. Both, the magnetic induction and the electric potential are computed as a sum of the respective term for the infinite volume conductor (Eq. 7) and a correction term accounting for the geometry. For the electric potential, Eq. (12) is implicit, since the correction term depends on the potential itself. Equations (12 and 13) can also be interpreted in the following way (Gencer and Acar 2004): in addition to primary sources, causing the infinite volume potential/field, so-called secondary sources are placed on the boundaries, their orientations being perpendicular to the boundaries and their strength being proportional to the electric potential and the size of the conductivity step.

For the numerical implementation of BEM, the potential has to be approximated on the realistically shaped compartment boundaries. This leads to the necessity to discretize these boundaries into small elements and to express the potential on each element. The elements can have different shapes, the most common one being the triangle. The potential can be assumed to be constant on each boundary element or to vary linearly (or, in some cases, quadratically) between the vertices (basis function). The most basic method for the formulation of the resulting problem is the collocation method, where the residual is minimized in all discretization points (i.e., the centroid of elements for constant and the vertices for linear basis functions). Alternatively, one can use the Galerkin method, where the integral of the residual over the surface is approximated by means of the basis functions and then minimized. Numerical simulation with single-shell models have shown that the Galerkin method using linear basis functions usually performs better than the collocation method or the Galerkin method with constant basis functions. However, these differences are generally small (Tissari and Rahola 2003; Stenroos and Haueisen 2008). Although the benefit of the Galerkin is expected to increase with several and closely spaced surfaces, with nowadays frequently used higher mesh densities (>4,000 nodes per surface) the numerical errors due to the use of collocation BEM are smaller than errors due to model simplifications or geometrical errors, assuming that the sources are not too close to the boundary (Mosher et al. 1999; Stenroos and Nenonen 2012).

An important question when practically constructing boundary element models is the discretization of the boundaries, which was shown to critically influence the accuracy of the solution (Haueisen et al. 1997). More precisely, it was shown that when using the collocation method with constant basis functions, the size of triangular elements should not exceed 10 mm or the minimal distance between sources and boundary, whichever is the smaller. When using linear basis functions, the size of the triangles can be up to twice the distance between sources and boundary. These rules also apply to secondary sources, which account for the conductivity discontinuities at the boundaries (see above). Thus, the thickness of tissue layers (e.g., skull compartment) and triangle size is linked in an analogous way. Due to the fact that the distribution of the secondary sources is fairly smooth, the consequences are less severe.

The relatively low conductivity of the skull tends to cause the resulting equation systems to be ill-posed. This is usually ameliorated by the isolated source approach, which first solves the problem assuming a perfectly insulating skull and then applies a correction term (Hämäläinen and Sarvas 1989; Stenroos and Sarvas 2012).

3.2 Finite Element Method

In contrast to the BEM, the FEM principally allows for accounting for the full three-dimensional tensor-valued conductivity function. In practice, of course, this is limited by the chosen discretization. The discretization means the subdivision of the volume into small elements, each endowed with a separate conductivity tensor. Within each element, the electric potential is described by a three-dimensional parameterized function, the so-called Ansatz function. For each element, a Laplace equation is approximated by deriving the Ansatz function twice. For those elements with sources, the Laplace equation turns into a Poisson equation, with an additional term accounting for the source divergence. Since the sources are usually modeled as point-like, a numerical singularity arises, which has to be treated suitably. Finally, the Cauchy boundary conditions between the elements have to be considered. This all leads to a high-dimensional sparse linear system of equations. The sparsity of the system allows, in spite of its large size, for a relatively time and memory efficient solution using dedicated algorithms. Finally, by numerical derivation of the potential, a current is computed, which is then used to compute the magnetic induction at the sensors using the law of Biot-Savart.

The two main types of discretization elements are tetrahedra and hexahedra. While hexahedra perfectly match the shape of medical imaging voxels, which form the main source of information on volume conductor geometry, tetrahedra are especially versatile when it comes to approximating arbitrarily shaped tissue boundaries. However, the node shifting technique largely compensates for this latter disadvantage of the hexahedra approach (Wolters et al. 2007). The representation of the head can be done with uniform elements of the same size (e.g. 1 mm3 voxels) or with elements of varying sizes depending on the segmentation of the tissues and the expected potential gradient. In addition, it is possible to adaptively change the discretization depending on metrics which are derived from intermediate solutions (Schimpf 2007). For example, in hexahedral elements the potential of one element e is given as:

$${\varphi }^{\text{e}} \left( {{\text{x}},{\text{y}},{\text{z}}} \right) = \mathop \sum \limits_{{{\text{j}} = 1}}^{8} {\text{N}}_{\text{j}}^{\text{e}} ({\text{x}},{\text{y}},{\text{z}}){\varphi }_{\text{j}} ,$$
(14)

where \(\varphi_{j}\) are the potentials of the nodes adjacent to the element e, and \(N_{j}^{e}\) are the shape functions describing the parameterized approximation used for each element. Most often, tri-linear shape functions are used (first-order FEM). However, also tri-quadratic functions may be used (second-order FEM). Zhang et al. (2004) suggest that for a relatively low number of elements (~150,000) and high dipole eccentricity second-order FEM provides higher accuracy compared to first order FEM. However, the results of van Uitert et al. (2001) indicate that for small element sizes (less than 2 mm side length) there is no significant advantage of second-order FEM.

Source modeling often assumes a point-like dipole. Although this model is an idealization, it forms the starting point of most source representations in EEG/MEG volume conductor modeling. However, this idealization poses a problem for FEM, as it causes a singularity. Three major approaches were put forward to treat this singularity. First, it is possible to replace the effect of the point-like dipole by making appropriate assumptions on the voltages and/or currents at the surrounding nodes of the dipole. This is equivalent to the introduction of Dirichlet and/or Neumann boundary conditions at nodes in the immediate neighborhood of the dipole. For example, a current dipole can be represented by a number of current monopoles in its surrounding. The entire group of methods can be seen as a variant of Saint-Venant’s principle (blurred dipole representation). In literature, however, the Saint-Venant’s principle only refers to current monopole representations. The second principal approach separates the problem into a source-free numerical problem governed by the Laplace equation and a Poisson problem in the infinite homogeneous space, for which an analytical solution exists. This approach is often called subtraction method (van den Broek et al. 1996; Drechsler et al. 2009). In the third principal approach, the partial integration method, the divergence of the current is projected onto the Ansatz functions and integrated over the volume. By making use of the fact that the current perpendicular to the surface is zero, one can eliminate the derivative of the primary current density and hence the singularity. Comparisons of two or three of the above dipole modeling approaches are given e.g. in (Schimpf et al. 2002; Hallez et al. 2007; Wolters et al. 2007). Although evaluations of all methods in larger studies are still missing, the Saint-Venant’s principle dipole representation seems a suitable choice especially in high resolution FEM models (Haueisen et al. 1995; Schimpf et al. 2002; Wolters et al. 2007). This is supported by the fact that brain activity is characterized by distributed current sources and sinks. Note that for the validity of the approach it is necessary that all sources and sinks are actually located within the tissue of the source areas (e.g. grey matter).

While earlier FEM studies mainly used successive over-relaxation (SOR) and Jacobi preconditioned conjugate gradient methods (Haueisen et al. 2002), multigrid methods nowadays provide a computationally more efficient way of solving the large system of equations. A recent paper showed that high resolution FEM models of the human head can also be computed within reasonable time and memory bounds (Wolters et al. 2007). This makes FEM models suitable for application in clinical studies.

4 Electric Conductivity

4.1 Introduction

A crucial piece of information for all models described above is the distribution of the electric conductivity in the head. Therefore, the determination of conductivity values is of great importance. Electric current flow in the human head is based on the movement of ions. Thus, the electric conductivity is largely determined by the concentration of these ions and the anatomical microstructure representing the restrictions and hindrances to the movement of these ions. Consequently, conductivity is a continuous function of location, i.e. inhomogeneous. Additionally, at each point the conductivity can be different in different directions (e.g. in white matter, the conductivity is higher along the fibers and lower across the fibers). This leads to the concept of anisotropic conductivity, which is mathematically represented by the conductivity tensor \(\bar{\sigma }\). In order to practically handle the tensor-valued continuous function of conductivity, a discretization is required. Naturally, the single elements in full 3D methods like FEM provide a discretization. Here, each element is assigned a value representing the mean conductivity tensor for this element. The conductivity discretization thus depends on the chosen resolution of the model. Often, anisotropic conductivity information is not available. In these cases the tensor is replaced by a scalar conductivity value for each element. Moreover, elements are grouped together and assigned the same scalar conductivity value. This leads, in the simplest case, to a compartment style representation of conductivity in full 3D methods like FEM. Lumped scalar conductivity values are also assigned to entire compartments, such as the skull, the brain, the cerebro-spinal fluid (CSF) or the skin, in analytical sphere and ellipsoid models as well as in BEM models.

4.2 Measurement of Electric Conductivity

Measurements of in vivo electrical conductivity values are difficult to perform for any level of discretization needed in the different types of forward models. The most common direct conductivity measurement approach is the four-electrode method. Here, two electrodes supply a current yielding a current density distribution in the specimen under investigation. The other two electrodes are used to measure a voltage drop within the specimen. From the measured voltage and the given current density, the unknown conductivity can be calculated. Alternatively, a voltage can be impressed and a current can be measured. Assuming a homogeneous specimen, four point-like electrodes can be placed in a row on the specimen, where the outer two supply the current and the inner two measure the voltage. In order to increase the accuracy of the model assumptions and to reduce the sensitivity towards local inhomogeneities of the tissue, the two current supplying electrodes might be extended in two dimensions (e.g. plate electrodes). Sources of error in such measurements are related to the positioning and the polarization of the electrodes as well as the violation of the homogeneity assumption for the specimen. The latter can be partially avoided by using an appropriate model to describe the inhomogeneous structure of the specimen. Moreover, if electrodes are put into tissue, damage is unavoidable. Besides other consequences, this leads to impressed current flow both in the intra- and extracellular space. Thus, the measured conductivity reflects both parts to a varying degree, referred to as apparent conductivity (Ranck 1963; Okada 1994). Another source of error lies in the fact that there is intrinsic electric activity in biological tissue, which interacts with the applied current. The interplay of these sources of error depends on the type of tissue under investigation and on the size and spacing of the electrodes.

For practical and ethical reasons, in vivo conductivity measurements on humans are rarely possible, which leads to the necessity to employ in vitro preparations. However, the conductivity values differ significantly between in vivo and in vitro situations depending on the applied preparation protocol (Galeotti 1902; Crile et al. 1922; Geddes and Baker 1967; Akhtari et al., 2000, 2002). For example, the selection of the tissue samples, the exposure to air and the temperature control during the experiment are critical parameters (Hoekema et al. 2003). Moreover, significant differences in measured conductivity values exist across species (Geddes and Baker 1967; Gabriel et al., 1996). There is inter- and intra-subject variability which can be related to age (Wendel et al. 2010), diseases, environmental factors, and personal constitution (Crile et al. 1922). It was argued that natural heterogeneity and sample–sample variability dominate the measurement uncertainty (Gabriel et al. 2009).

Alternative conductivity measurement methods impress a current and measure the induced magnetic field. For example, in magnetic resonance electric impedance tomography (MREIT) electrodes are used to impress currents into the human body and the induced magnetic flux densities are measured with the help of an MRI scanner (Seo and Woo 2011). The conductivity values are subsequently reconstructed. It is also possible to impress currents with the help of magnetic fields and measure the resulting magnetic field.

Another class of conductivity estimation techniques uses measured electric and/or magnetic data during the source localization procedure. For very simple source configurations, such as the first cortical somatosensory evoked activity, not only the unknown source parameters are estimated in the inverse procedure but also the unknown conductivity values. Naturally, this approach can only be applied for very few unknowns, for example the conductivities of the scalp, skull, and brain compartments. The advantage of this method lies in the direct estimation of the relevant model parameters (Fuchs et al. 1998; Goncalves et al. 2003; Baysal and Haueisen 2004; Gutierrez et al. 2004; Lai et al. 2005). The disadvantage is rooted in the strong model assumptions, also concerning the source configuration.

The direction dependence of the electric conductivity can be estimated based on the measurement of direction dependent water diffusion using diffusion weighted MRI (Basser et al. 1994). With the help of the effective-medium approach, the tensor of the electric conductivity is estimated from the tensor of the measured water diffusion (Tuch et al. 2001), which was successfully validated in (Oh et al. 2006; Bangera et al. 2010) and refined in (Wang et al. 2008). However, this approach is limited due to the complex and unknown relationship between ion mobility and water diffusion.

In spite of all effort so far, getting exact, detailed and reliable conductivity information for head models is still a challenge and will require substantial research effort in the future.

4.3 Conductivity of Single Tissue Types

The following Table 2 gives an account of the conductivity values for single tissues based on existing literature. Tissue conductivity depends, among other factors, on frequency and temperature. Thus, only conductivity values measured at or near body temperature and at low frequencies (d.c. up to 100 kHz) were taken into account. Among the relevant literature, two reviews are most often cited: (Geddes and Baker 1967; Gabriel et al. 1996) (and its more recent extension Gabriel et al. 2009).

Table 2 Isotropic conductivity values of single tissue types used in human head volume conductor modeling
Full size table

4.4 Compartment Conductivities

Since most often three or four compartments are used to describe the volume conductor, these compartment conductivities of the brain, CSF, skull, and scalp are most relevant and considered here. Each compartment-conductivity depends on the complex geometrical arrangement of the tissues determining the compartment. Furthermore, since the compartment conductivity is merely a model for the real conductivity profile, the source configuration also has an influence on the choice of this value. In principle, there are three ways to estimate a compartment conductivity: (i) based on the measurement of single tissues an average for a compartment is computed (either model based or model free); (ii) the conductivity of an entire compartment is directly measured (bulk conductivity); and (iii) the compartment model (conductivity as free parameter) is fitted to purposely performed measurements (e.g. EEG, MEG, DTI), see above.

A number of studies report bulk conductivity measurements. Akhtari et al. (2006) measured freshly excised human neocortex and subcortical white matter in 21 neurosurgical patients and found values of 0.066–0.156 S/m. CSF, as indicated above, has 1.79 S/m. The conductivity values for the skull compartment show large variation. Akhtari et al. (2002) found 0.0085–0.0114 S/m bulk conductivity for live human skull at room temperature, while in an earlier study on a cadaver skull the values ranged from 0.0023 to 0.00584 S/m (Akhtari et al. 2000). Hoekema et al. (2003) found values between 0.032 and 0.08 S/m in a very well controlled study of live human skull in 5 neurosurgical patients. The most comprehensive study on 3 layer live human skull at body temperature was performed by Tang et al. (2008). They demonstrated that the conductivity value largely depends on the local structure of the skull. They distinguished (besides other criteria) between normal and thin spongiform layers and found conductivity values for the 3 layer skull of 0.0126 S/m and 0.00691 S/m, respectively. The standard deviation was about 20 %. Using electric impedance tomography and the model fit approach, Gonçalves et al. (2003) estimated the conductivity of the brain and skull compartment in six subjects to be 0.33 S/m and 0.0082 S/m with a standard deviation of 13 and 18 %, respectively.

For separate EEG or MEG analysis only compartment conductivity ratios are needed. For the often used 3-compartment model this is the ratio of scalp:skull:brain. In the past, the most often used ratio was 1:1/80:1, which was derived from a study by Rush and Driscoll (1968), who measured the impedance of a dry half-skull in fluid and proposed values of 0.33, 0.0042 and 0.33 S/m. Recently, this ratio was questioned by a number of researchers. Oostendorp et al. (2000) performed both measurement on cadaver skull and in vivo on volunteers using electric stimulation and found a ratio of 1:1/15:1. Baysal and Haueisen (2004) used combined MEG/EEG measurements and estimated a ratio of 1:1/22:1. Lai et al. (2005) suggested a ratio of 1:1/25:1. Based on the measurements of Hoekema et al. (2003), a ratio of 1:1/8:1 can be considered. Zhang et al. (2006) estimated 1:1/20:1 based on measurement in two epilepsy patients. The values of Tang et al. (2008) indicate approximate ratios between 1:1/25:1 and 1:1/50:1 and the values of Gonçalves et al. (2003) approximately 1:1/40:1. Dannhauer et al. (2011) report a ratio of 1:1/25:1 to 1:1/47:1 based on the measurements of Akhtari et al. (2002) and a model fit. Although the recent studies show some degree variability, they all agree on the fact that the value of 80 in the long standing ratio of 1:1/80:1 is too high.

5 Leadfield Concept

Results from the forward calculation can be used in inverse procedures directly (e.g., in spatio-temporal dipole fitting) or stored in so-called leadfield matrices. Such matrices represent the forward solutions for sources on a predefined grid. The term leadfield (originally derived from “lead” that stands for a single EEG channel) refers to a function describing the sensitivity of the output of one sensor to the parameters of the source model. For example when using the dipole model, the leadfield is a function of the position and the orientation of a unit strength dipole. Usually, the leadfield is discretized, e.g. the dipoles are positioned on the nodes of a regular grid with canonical orientations (e.g. x, y, z). These leadfield vectors are combined into a leadfield matrix, describing the influence of each unit dipole on each sensor. Accordingly, this matrix is also sometimes called influence matrix or gain matrix. In such a matrix, each row refers to one sensor (one leadfield) and each column describes the influence of one unit dipole (e.g. one unit dipole per canonical direction) on the sensor array. In general, the leadfield matrix is a discretized representation of the forward problem. The discretization has to be such that it adequately approximates the leadfield. When using dipoles in the brain, spatial sampling of 3-10 mm is common. Any dipole orientation can be represented by the superposition of 3 canonical orientations.

6 Conclusion and Outlook

Source localization is increasingly applied in neuroscientific research and clinical studies. The accuracy of source reconstruction depends on the accuracy of the solution of the forward problem. Finite element models are more elaborate compared to boundary element models and can, in principle, account for the anisotropic distribution of connectivity at any level of detail. Until recently, there were three major obstacles for the use of this kind of forward modeling in source reconstruction schemes. (1) The computation was computationally too costly to allow for a repetitive computation of forward solutions as required by inverse algorithms. (2) The possibility to account for the anisotropic conductivity on a voxel basis turns from an advantage to a drawback, if reliable information on these material properties at this level of detail is missing. (3) At the position of the dipoles, singularities occur, which were difficult to treat numerically. While reasons (1) and (3) can be considered to be mostly solved (Wolters et al. 2004; Lew et al. 2009), reason (2) still requires substantial research. Especially diffusion weighted MR imaging promises to offer new ways to estimate material properties at a fine level of detail (Güllmar et al. 2010; Dannhauer et al., 2011; Sengül and Baysal 2012). If there is no reliable information on anisotropic volume conduction BEM can be the method of choice in realistic volume conductor modeling.