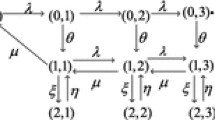Abstract
A single server Markovian queue with repairs and vacations is studied in this paper. Under a linear reward-cost structure, we investigate the behavior of customers with various levels of information regarding the system state. Equilibrium strategies for the customers under different levels of information are derived and the stationary behaviors of the system under these strategies are investigated.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Studies about the economic analysis of queueing systems can go back at least to the pioneering work of Naor [5] who analyzed customers optimal strategies in an observable M/M/1 queue with a simple reward-cost structure. After the work of Naor, Edelson and Hildebrand [3] investigated this model. Then surveys on this subject were showed in [1, 2, 4] respectively. The paper is organized as follows. In Sect. 2, we describe the dynamics of the model and the reward-cost structure. In Sect. 3, we derive the equilibrium strategies for the customers under different levels of information. Finally, in Sect. 4, some conclusions are given.
2 Model Description
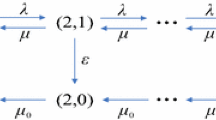
We consider a single-server queue in which customers arrive according to a Poisson process with rate \( \lambda \). We assume that the service times are exponentially distributed with rate \( u \). The server alternates between on and off periods that are also exponentially distributed at rates \( \xi \) and \( \theta \) respectively.
And the server is deactivated and begins a vacation as soon as the queue becomes empty. When a new customer arrives at an empty system, a setup process starts for the server to be activated. The time required to setup is also exponentially distributed with rate \( \beta \). We assume that inter-arrival times, service times and setup times are mutually independent.
We represent the state at time t by the pair (N(t); I(t)), where N(t) denotes the number of customers in the system and I(t) denotes the state of the server. Hereinafter, we define a breakdown period at state 0 and a work period at state1 as well as a vacation period at state 2. We assume that every customer receives reward of R units for completing service. Moreover, there exists a waiting cost of C units per time unit.
In the next sections we obtain customer optimal strategies for joining/balking. We distinguish two cases with respect to the level of information available to customers at their arrival instants:
-
(1)
Fully observable case: Customers are informed about the queue length as well as the sever state (N(t), I(t));
-
(2)
Fully unobservable case: Customers are not informed about the queue length N(t) nor the sever state I(t).
3 Equilibrium Strategies
In this section we show that there exist equilibrium strategies in the two information cases that we defined above.
3.1 Fully Observable Case
We begin with the fully observable case in which there exist equilibrium strategies of threshold type.
Theorem 1
In the fully observable M/M/1 queue with repairs and vacations, there exist a triple of thresholds
Such that the strategy ‘While arriving at time t, observe (N(t), I(t)); enter if \( N(t)\le {n_e}(I(t)) \) and balk otherwise’ is a weakly dominant strategy.
Proof
Consider an arriving customer, his expected net reward if he enter is S(n; i) = \( R-CT(n;i) \), where T(n; i) denotes his expected mean sojourn time given that he finds the system at state (N(t); I(t)) upon his arrival. We have
We denote T 0 by the expected mean service time of a customer, then we get
Then the following equations are obtained easily
By solving \( S(n,i)\ge 0 \) for n, we obtain that customers decide to enter if and only if \( n\le {n_e}\left( {I(t)} \right) \) where n e (0), n e (1) and n e (2) are given by Theorem 1.
3.2 Fully Unobservable Case
In this section we proceed the fully unobservable case. With a mixed strategy, an arriving customer joins with a certain probability q, and the effective arrival rate, or joining rate is \( \lambda q \).
Proposition 1
Consider the fully unobservable model of the M/M/1 queue with repairs and vacations, the expected mean sojourn time of a customer who decides to enter is given by
Proof
Let p(n, i) be the stationary distribution of the corresponding system and the balance equations are presented below.
Define the partial stationary probability generating function of the system as\( {G_i}(z)=\sum\nolimits_{n=0}^{\infty } {p(n,i){z^n},\left( {|z|\le 1,i=0,1,2} \right)} \) and we can get G 0(z), G 1(z) and G 2(z) by solving the above balance equations. Then the mean number of the customers in the system is as follows
Hence, the expected mean sojourn time of a customer who decides to enter upon his arrival can be obtained by using Little’s law \( E\left[ W \right]=E\left[ N \right]/\lambda q \).
Theorem 2
In the fully unobservable model of the M/M/1 queue with repairs and vacations, a unique Nash equilibrium mixed strategy ‘enter with probability q e ’ exists, where q e is given by
Proof
We consider a tagged customer at his arrival instant. If he decide to enter the system, the expected net benefit he gets is
The expected mean sojourn time is strictly increasing for \( q\in (0,1) \), so when \( R\in \left( {C\left( {\frac{1}{\beta }+\frac{{\theta +\xi }}{{\theta \mu }}} \right),C\frac{{\lambda (\xi \beta -\xi \theta -{\theta^2})+\theta (\xi \beta +\theta \beta +\theta \mu )}}{{\theta \beta \left[ {\theta \mu -\lambda (\xi +\theta )} \right]}}} \right) \), (15) has a unique root in (0,1) which gives the first branch of (14). When \( R\in \left[ {\left. {C\frac{{\lambda (\xi \beta -\xi \theta -{\theta^2})+\theta (\xi \beta +\theta \beta +\theta \mu )}}{{\theta \beta \left[ {\theta \mu -\lambda (\xi +\theta )} \right]}},\infty } \right)} \right. \), \( S(q) \) is positive for every q. In other words, the unique equilibrium point is q e = 1 in this case, which gives the second branch of (26).
4 Conclusion
In this paper we studied the equilibrium strategies of the M/M/1 queues with repairs and vacations. The equilibrium balking strategies were investigated for the two kinds of queues. To the author’s knowledge, this is the first time that repairs and vacations are introduced into the queue system at the same time.
References
Burnetas A, Economou A (2007) Equilibrium customer strategies in a single server Markovian queue with setup times. Queueing Syst 56:213–228
Economou A, Kanta S (2008) Equilibrium balking strategies in the observable singleserver queue with breakdowns and repairs. Oper Res Lett 36:696–699
Edelson NM, Hildebrand K (1975) Congestion tolls for Poisson queueing processes. Econometrica 43:81–92
Guo P, Hassin R (2011) Strategic behavior and social optimization in Markovian vacation queues. Oper Res 59:986–997
Naor P (1969) The regulation of queue size by levying tolls. Econometrica 37:15–24
Acknowledgements
This work is supported by National Natural Science Foundation of China (No. 11171019), Program for New Century Excellent Talents in University (NCET-11-0568) and the Fundamental Research Funds for the Central Universities (No. 2011JBZ012).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Li, C., Wang, J., Zhang, F. (2013). Equilibrium Analysis of the Markovian Queues with Repairs and Vacations. In: Zhang, Z., Zhang, R., Zhang, J. (eds) LISS 2012. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-32054-5_89
Download citation
DOI: https://doi.org/10.1007/978-3-642-32054-5_89
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-32053-8
Online ISBN: 978-3-642-32054-5
eBook Packages: Business and EconomicsBusiness and Management (R0)