HiFlow³: A Hardware-Aware Parallel Finite Element Package

Abstract

The goal of this paper is to describe the hardware-aware parallel C++ finite element package HiFlow³. HiFlow³ aims at providing a powerful platform for simulating processes modelled by partial differential equations. Our vision is to solve boundary value problems in an appropriate way by coupling numerical simulations with modern software design and state-of-the-art hardware technologies. The main functionalities for mapping the mathematical model into parallel software are implemented in the three core modules Mesh, DoF/FEM and Linear Algebra (LA). Parallelism is realized on two levels. The modules provide efficient MPI-based distributed data structures to achieve performance on large HPC systems but also on stand-alone workstations. Additionally, the hardware-aware cross-platform approach in the LA module accelerates the solution process by exploiting the computing power from emerging technologies like multi-core CPUs and GPUs. In this context performance evaluation on different hardware-architectures will be demonstrated.

12.1 Introduction

Scientific computing and numerical simulations are very important tasks in research, engineering and development. Mathematics combined with new software design dedicated to state-of-the-art hardware technologies result in high complexity but also break new grounds in the area of scientific computing. HiFlow³ [4] is a parallel hardware-aware finite element software with the goal to provide powerful tools for the solution of complex problems arising in the area of medical engineering, meteorology and energy research. A team at the Engineering Mathematics and Computing Lab (EMCL) at the Karlsruhe Institute of Technology (KIT) is actively developing the software package. The goal of this paper is to present the concept of the software and the three core modules. Benchmark results for an advection-diffusion example comparing different platforms and preconditioners illustrate its usability and flexibility.

The paper is structured as follows. Chapter 2 outlines the design of HiFlow³. The core modules are described in more details in Chaps. 3–5. Finally, benchmarks results for the advection-diffusion example are shown in Chap. 6.

12.2 Motivation, Concepts and Structure of HiFlow³

12.2.1 Fields of Application

A typical application in the research area of medical engineering incorporating the full complexity of physical and mathematical modeling is the United Airways project [2]. Within an interdisciplinary framework its objective is the simulation of the full human respiratory tract including complex and time-dependent geometries with different length scales, turbulences, fluid-structure interaction (e.g. fine hairs and mucus), and effects due to temperature and moisture variations. Due to the complex interaction of the different physical effects it is a great challenge to define robust numerical methods giving accurate simulation results.

12.2.2 Flexibility

The conceptual goal of HiFlow³ is to be a flexible multi-purpose software package. Its modular, transparent and documented structure tries to enable the user to set up a wide range of scenarios with reasonable effort. The core of HiFlow³ is divided into three main modules: Mesh, DoF/FEM and LA; see Fig. 12.1. These three core modules are essential for the solution procedure which is based on the finite element method (FEM) for partial differential equations (PDEs). They are supplemented by other building blocks consisting of e.g. routines for numerical integration, matrix assembly, inclusion of boundary conditions, setting up nonlinear and linear solvers, providing data output for visualization of solutions and error estimators.

Fig. 12.1

Structure of the HiFlow³ core divided into modules and methods

12.2.3 Performance, Parallelism, Emerging Technologies

The huge demand on fast and accurate simulation results for large-scale problems poses considerable challenges on the implementation on modern hardware. Supercomputers and emerging parallel hardware like GPUs offer impressive computing power in the range of Teraflop/s for desktop supercomputing up to Petaflop/s for cutting edge HPC machines. Therefore, an important goal associated with the design of HiFlow³ is the full utilization of the available resources on heterogeneous platforms ranging from large HPC systems to a stand-alone workstation or a coprocessor-accelerated machine. To achieve this goal each core module is in itself parallel. An MPI-layer [12] realizes the communication between different nodes and processors. Furthermore, a hardware-aware computing concept, see Sect. 12.2.4, is implemented on the linear algebra level. This concept and all modules are laid out with respect to scalability in a generic sense. The design of HiFlow³ aims at obtaining high standards with respect to the efficiency without sacrificing the flexibility of the software.

12.2.4 Hardware-Aware Computing

Hardware-aware computing is a multi-disciplinary approach to identify the best combination of applications, physical models, numerical schemes, parallel algorithms, and platform-specific implementations that gives the fastest and most accurate results on a particular platform [3]. Since hardware design and mathematical cognition give rise to different implementation concepts, hardware-aware computing also means to find a balance between the associated opponent guiding lines while keeping the best mathematical quality. All solutions need to be designed in a reliable, robust and future-proof context. The goal is not to design isolated solutions for particular configurations but to develop methodologies and concepts that preferably apply to a wide range of problem classes and architectures or that can be easily extended or adapted. The HiFlow³ project realizes related concepts in the framework of the local multi-platform LAtoolbox [5, 6] within the LA module. Its use of specific implementations of basic routines like local matrix-vector and advanced preconditioning techniques is aimed at exploiting the available computing power of emerging technologies like multi-core CPUs, graphics processing units (GPUs) and multi-GPUs. The structure provided by the LA module allows to build solvers without having detailed information on the underlying platform.

12.3 Mesh Module

The Mesh module provides a set of classes which can be used to represent the computational mesh in a finite element problem. In this section, the main ideas and features of the module are summarized. A more detailed description can be found in [13].

A mesh is a partitioning of a domain into a set of non-overlapping cells. Supported cell types are triangles and quadrilaterals in 2D, and tetrahedra and hexahedra in 3D. The description of the supported shapes are encapsulated in a class hierarchy, whereas the rest of the code is independent of the type and dimension of the cells.

The module can also represent lower-dimensional entities, such as edges and faces. The computation and storage of incidence relations between entities, which together make up the topology of the mesh, is performed in a way that closely follows the approach described in [11].

The geometry of the mesh is defined by assigning coordinates to each vertex, but the extension to more complete representations that could handle cells with curved faces is also possible.

The functionality provided through the Mesh module can be divided into three categories: queries, modifications and communication. The first category includes functions to iterate over the various entities and the topological incidence relations between them; as well as access to the geometrical information and other attributes associated with the entities such as material numbers. The modifying functionality includes creation, refinement and coarsening. A mesh can be created by specifying it entirely in code, or by reading a file. The AVS UCD [1] and VTK [15] formats are supported. For efficient I/O of large meshes, the module supports reading and writing of parallel VTK files. Refinement and coarsening does not have to be uniform, and there is functionality for dealing with the hanging nodes that arise as a result of local refinement.

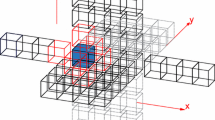
For large-scale computations, the mesh might not fit into the memory of each process. For this reason, the HiFlow³ Mesh module makes it possible to work with meshes that are distributed across a cluster of computers, as shown in Fig. 12.2.

Fig. 12.2

A mesh of a human nose distributed in 16 stripes

Support for distributed meshes is provided by the functions in the communication layer. A distributed mesh is represented by a set of local mesh objects, one on each process. The communication functionality is external to these objects, which themselves are not aware that they are part of a larger, global mesh. This has the advantage that calls to query and modification functions are local to each process, and do not require communication, which facilitates their implementation and use.

The information about how the parts of the global mesh are connected is provided through a data structure that keeps track of which vertices are shared with other processes, and maps vertex identities between processes. With this structure on hand, it is also possible to identify shared entities of higher dimension.

To facilitate the exchange of specific information required for finite element assembly, the Mesh module can also compute and communicate a layer of overlapping “ghost cells”, which can be appended to each local mesh (see Fig. 12.3).

Fig. 12.3

A part of a mesh with the ghost layer

Different strategies can be used when deciding how to divide a mesh between the processes. Currently, the best option is to link via a provided interface to the popular graph partitioning library METIS [10].This enables the computation of a well-balanced partitioning of the mesh over the available processes.

12.4 DoF/FEM Module

In the context of FEM solutions are expressed in terms of linear combinations of some chosen shape functions defined on mesh cells. The degrees of freedom (DoF), which can easily count up to millions of unknowns, represent the number of parameters that define such a discrete function. To this end, local basis functions are defined on reference cells which are mapped into the physical space using transformations, see Fig. 12.4.

Fig. 12.4

Transformations Φ and Ψ map DoF points of biliinear and biquadratic finite element ansatz from reference cells to cells A and B of the mesh, respectively

12.4.1 Submodules

The FEM submodule is dedicated to represent a finite element ansatz in a generic way to ensure extensibility at low memory costs, but still to enable high performance assembly. The basic concept lies in defining three major classes FEType, FEManager and FEInstance, see Fig. 12.5. FEType is an interface class that represents a specific continuous or discontinuous finite element ansatz on a defined reference cell by utilizing the design-pattern singleton stored within FEInstance. For establishing the mapping between a tuple of a mesh cell and a variable to their corresponding singleton, only references are stored. This mapping and all interfaces to out-of-module classes are managed by the FEManager.

Fig. 12.5

Overview of classes for description of finite element functions

Many practical relevant problems require a great number of DoFs (up to millions). These DoFs need to be numbered and interpolated in a unique way depending on arbitrary combinations of finite element ansatz on neighboring cells. One major task of the DoF submodule is to create a mapping between a local DoF Id and a global (mesh wide) DoF Id given by the local numbering strategy in the FEM submodule. The second major task is to interpolate those DoFs, which are restricted due to conditions provided by FEM and cannot be identified. The DoFs in any cell of the considered mesh are determined by a transformation [14] that maps the reference cell to the chosen physical cell and thereby defines the location of the DoF points (see Fig. 12.4).

12.4.2 Partitioning

In a domain decomposition setup, i.e. several processes are used for the solution of one single domain, each part of the domain (subdomain) is dedicated to one process using MPI. Again a unique DoF numeration of all DoFs in the global domain must be determined. For good scaling properties, a parallel and distributed handling of the DoFs is needed, i.e. each process manages the DoFs that are connected to the cells lying in its domain and the class DofPartition is used to create the correspondence with other subdomains from other processors via MPI communication. Each subdomain has information of the neighboring domains by the ghost cells which is a read-only copy of the neighboring cells (one layer neighborship of the processor’s subdomain). To create a DoF numbering with (domain-) global Ids, each process determines in a first step a consecutive numbering of the DoFs within its subdomain, whereas also the ghost layer is treated as if it would belong to the subdomain. The antiquated information stored in this layer must be updated via communication. Hereby, a decision needs to be made, whether a DoF lying on the skeleton of the domain belongs to a subdomain or not, i.e. this DoF is lying on two subdomains, which are sharing it. The implemented procedure states, that the subdomain represented by a unique lower subdomain Id will own the DoF.

12.5 Linear Algebra Module

The LA module handles the basic linear algebra operations and offers linear solvers and preconditioners. It is implemented as a two-level library. The upper (or global) level is an MPI-layer which is responsible for the distribution of data among the nodes and performs cross-node computations, e.g. scalar products and sparse matrix-vector multiplications. The lower (or local) level takes care of the on-node routines offering an interface independent of the given platform.

The MPI-layer of the LA module takes care of communication and computations in the context of FEM. Given a partitioning of the underlying domain (handed over by the mesh module, see Sect. 12.3) the DoF module (see Sect. 12.4) distributes the DoFs according to the chosen finite element approach. This results in a row-wise distribution of the assembled matrices and vectors. Each local sub-matrix is divided into two blocks: a diagonal block representing all couplings and interactions within the subdomain, and an off-diagonal block representing the couplings across subdomain interfaces.

The highly optimized BLAS 1 and 2 routines are implemented in the local multi-platform linear algebra toolbox (lmpLAtoolbox) which is acting on each of the subdomains. By using unified interfaces as an abstraction of the hardware we provide easy-to-use access to the underlying heterogeneous platforms. In this respect the application developer can utilize the LA module without any knowledge of the hardware and the system configuration. The final decision on which specific platform the application will be executed can be taken at run time. Currently, the lmpLAtoolbox support sequential, OpenMP parallel and Intel MKL CPU versions, NVIDIA GPU version and OpenCL back-end which provides access to ATI and NVIDIA GPUs. Due to the flexible design of the library we can add a new back-end and still use the same solvers without modifying them.

The layered structure and organization of both the LA module and the lmpLAtoolbox is depicted in Fig. 12.6. It shows a high-level view of distributed communication and computation across nodes and the node-level computation across several devices in a heterogeneous environment. Details on software description and on the design, as well as performance benchmarks on several platforms can be found in [5, 6, 9].

Fig. 12.6

Structure of the lmpLAtoolbox and LA module for distributed computation and node-level computation across several devices in a homogeneous and heterogeneous environment

Due to the modular setup and the consistent structure, the lmpLAtoolbox can be used as a standalone library independently of HiFlow³. It offers a complete and unified interface for many hardware platforms. Hence, the LA module not only offers fined-grained parallelism but also flexible utilization and cross-platform portability.

12.5.1 Linear Solvers and Preconditioners

The LA module offers a high-level of abstraction by providing unified interfaces for basic matrix and vector routines. Platform-specific implementations are transparent to the user. Thus, linear and non-linear solvers can be implemented easily and generically without any information on the underlying hardware platform while keeping platform-adapted and tuned code. The default solvers in HiFlow³ are preconditioned and non-preconditioned Krylov subspace solvers like – CG and GMRES. For the GPU implementation of the CG solver we offload all of the vector and matrix operations on the device [5, 6], while for the GMRES solver we use hybrid-parallel approach where the basic vector and matrix routine are offloaded but the Krylov subspaces in still build on the CPU [9].

On the node level, we provide very fined-grained parallel preconditioners based on additive, multiplicative (incomplete LU-factorization) and approximate inverse techniques. In order to obtain high degree of parallelism we use multi-coloring decomposition of the matrix for the additive preconditioner and for the ILU(0). For the incomplete factorization with fill-ins we provide new technique for controlling the additional fill-in entries – power(q)-pattern method [8]. By using this algorithm we can execute in parallel the forward and backward sweeps of the LU matrix. An example for a Poisson problem solved with matrix-based multigrid method and with preconditioned CG solver based on HiFlow³ are reported in [7].

12.6 Example: Advection-Diffussion Equation

The goal of this section is to show the simulation workflow in HiFlow³ and benchmark results for different platforms and preconditioning techniques. As an example the well known advection-diffusion equation is chosen. We aim to find $u \in {H}_{0}^{1}(\Omega ) :=\{ v \in {H}^{1}(\Omega ) : v{\vert }_{\partial \Omega } = 0\}$ such that

$$\epsilon (\nabla u,\nabla \phi ) + (\beta \cdot \nabla u,\phi ) = (f,\phi )\quad \forall \phi \in {H}_{0}^{1}(\Omega ),$$

(12.1)

where ( ⋅,  ⋅) denotes the L ²(Ω) scalar product, Ω ∈ ℝ ^d (d = 2, 3) is a Lipschitz domain and f ∈ L ²(Ω) given. ε ∈ ℝ represents the diffusion coefficient and the vector β ∈ ℝ ^d the direction of transport and information flow. Numerical oscillations may occur for small diffusion coefficients, i.e. $\|{\beta \|}_{2} \gg \epsilon$. In order to prevent this, ε and β are chosen depending on the characteristic mesh size h such that for the Peclet number Pe (see [9] and references therein) holds:

$$Pe = \frac{h\|{\beta \|}_{2}} {\epsilon } < 1.$$

For the finite element solution procedure the following steps have to be performed to map the weak formulation of advection diffusion example (12.1) to HiFlow³, see Algorithm 3. In a preprocessing step the domain of interest is discretized by means of a finite element triangulation. The spatial grid is read in, adjusted by global refinement, partitioned using the external library METIS [10] and distributed via MPI. Then, a problem-adapted finite element space with appropriate ansatz functions is chosen. Once these two information are provided a unique global numbering of the DoFs is determined. In the case of distributed memory platforms the DoF-partitioner is used to create the global numbering throughout the whole computational domain by only using its local information and MPI communication across the nodes. In the next step the linear non-symmetric system matrix and the vector for the right hand side can be assembled by local integration over all elements within the triangulation. Data structures for matrices and vectors are provided by the LA module. An adequate linear solver for non-symmetric matrices is combined with different preconditioners to solve the linear system. Finally, output in either sequential or parallel format is provided for the visualization.

12.6.1 Numerical Results and Benchmarks

The numerical experiments on multicore-CPUs and multi-GPU configurations are performed on a dual-socket Intel Xeon (E5450) quad-core platform equipped with an NVIDIA Tesla S1070 system providing two GPUs per socket. The memory capacity of the host CPU system is 16 GB and 4 ×4 GB for the GPUs. We are only using two GPUs associated with a single socket. All simulations are performed in double precision. For the numerical experiments we consider an exact solution given in 2 dimensions by

$$u(x,y) = x\frac{{e}^{{\beta }_{1}x} - {e}^{{\beta }_{1}}} {{e}^{{\beta }_{1}}} \sin (\pi y),\quad (x,y) \in \Omega = (0,1) \times (0,1).$$

The unit square is discretized by quadrilaterals and globally refined such that $h = \frac{1} {{2}^{9}}$. Q ₂ Lagrangian finite elements ansatz function are chosen, which leads to 1, 025² = 1, 050, 625 DoFs. The non-symmetric system matrix has 16 ⋅10⁶ non-zero entries. We use the iterative (preconditioned) GMRES method to solve the problem [10]. The stop criteria for the solver is set to a relative tolerance of 10^− 6, which results for the chosen benchmarks settings in an absolute tolerance about 10^− 9.

The number of iterations and the performance times for the sequential, OpenMP, one and two GPUs are shown of Table 12.1. Clearly, the problem is very ill conditioned and the system is hard to solve without preconditioning. When solving this system on different parallel architectures due to the parallel reduction and the different distribution of the floating-point errors, we obtain different number of iterations. This may be avoided by applying a ‘good’ preconditioner, leading to a well-conditioned system. The corresponding speedup factors for parallel execution and for different preconditioners are presented on Fig. 12.7. The speedup depends on the utilization of the available bandwidth of the platforms – with one core we can utilize one fourth of the bandwidth and therefore the OpenMP implementation is three to four times faster then the sequential version on the CPU. The GPU implementation however is about 9–13 times faster. The speedup profile of the preconditioners is the same for the sequential, OpenMP and GPU version – this is an important characteristic predominant with the high degree of parallelism of our preconditioners.

Fig. 12.7

Speedup comparing different platforms (eight cores CPU, 1 × GPU, 2  × GPU) w.r.t. to single core CPU (left) and speedup of different preconditioners (Multi-colored (symmetric) Gauss-Seidel and ILU(0), and power(q)-pattern ILU(1, 2)) on the four different platforms w.r.t. Jacobi preconditioner (right)

Table 12.1 Number of iterations and solving time of the preconditioned GMRES solver. With (*) we denote when the number of iterations exceeds 100,000 and in this case we stop the solver

For the two GPUs case we apply the preconditioners in the block-Jacobi fashion with two blocks for each GPU. Doing so we decrease the coupling of the precondition matrix, thereby increasing the number of iterations. Even though with two GPUs we may utilize twice the bandwidth, this limits the speedup to less than two.

12.7 Conclusion

The creation of a multi-purpose finite element software package that is portable across a wide variety of platforms including emerging technologies like hybrid CPU and GPU platforms is a challenging and multi-facetted task. The modules Mesh, DoF/FEM and Linear Algebra complemented by auxiliary routines and interfaces provide a broad suite of building blocks for development of modern numerical solvers and application scenarios. The user is freed from a detailed knowledge of the hardware – one only has to familiarize with the provided interfaces and needs to customize the available modules in order to adapt HiFlow³ to his domain-specific problem settings.

With hardware-aware solvers HiFlow³ allows to compute the linear system of differential equations on different back-ends with single source code for all platforms. Besides the solvers, HiFlow³ provides very fined-grain parallel preconditioners for multi- and many-core platforms and to our best knowledge is the first software package providing incomplete LU factorization preconditioners on the GPU devices.