Nonlinear Periodic Phononic Structures and Granular Crystals

Abstract

This chapter describes the dynamic behavior of nonlinear periodic phononic structures, along with how such structures can be utilized to affect the propagation of mechanical waves. Granular crystals are one type of nonlinear periodic phononic structure and are the focus of this chapter. The chapter begins with a brief history of nonlinear lattices and an introduction to granular crystals. This is followed by a summary of past and recent work on one-dimensional (1D) and two-dimensional (2D) granular crystals, which is categorized according to the crystals’ periodicity and dynamical regime. The chapter is concluded with a commentary by the authors, which discusses several possible future directions relating to granular crystals and other nonlinear periodic phononic structures. Throughout this chapter, a richness of nonlinear dynamic effects that occur in granular crystals is revealed, including a plethora of phenomena with no linear analog such as solitary waves, discrete breathers, tunable frequency band gaps, bifurcations, and chaos. Furthermore, in addition to the description of fundamental nonlinear phenomena, the authors describe how such phenomena can enable novel engineering devices and be applied to other nonlinear periodic systems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

7.1.1 Nonlinearity in Periodic Phononic Structures

The effect of structural periodicity on wave propagation has been studied in a wide array of fields. This includes vibrations in spring-mass systems, electrons in crystalline lattices, light waves in photonic periodic structures, cold atoms in optical lattices, and plasmons in networks of Josephson junctions or metal surfaces [1–4]. The preceding chapters of this book have considered, in particular, the effect of structural discreteness and periodicity on the propagation of phonons, sound, and other mechanical waves. Phononic crystals and acoustic metamaterials are examples of materials designed for this purpose. By studying the linear response of these systems, many common properties are revealed, such as the existence of band gaps. However, as the amplitude of the wave excitation is increased, the response of the material can become nonlinear and the wave propagation becomes more complex. As a result, the study of nonlinearity in periodic structures has revealed unique phenomena with no analogs in linear theory. Such phenomena include nonlinear resonances, bifurcations, chaos, self-trapping, and intrinsic localization. Nonlinear devices thus have potential for novel applications such as frequency conversion, energy harvesting, and switching, among others.

Although the role of nonlinearity has been extensively studied in non-phononic periodic structures and metamaterials, such as photonic periodic structures, optical metamaterials, and atomic Bose-Einstein Condensates in optical lattices [5], there are thus-far few examples of nonlinear phononic crystals or nonlinear acoustic metamaterials. Potential sources of nonlinearity in phononic/acoustic materials can be categorized into (1) intrinsic and (2) extrinsic. The former derives from nonlinearities in the material constitutive response (i.e., interatomic forces, nonlinear elasticity, plasticity, or ferroelasticity) [6]. The latter derives from the geometry or topology of the fundamental building blocks (i.e., contact forces between particles [7], deformation of micro-nano mechanical oscillators [8], or the nonlinearity related to geometrical instabilities [9]).

Homogenous materials with nonlinear elastic [6] or nonlinear acoustic responses [10] have long been studied. Nonlinear bulk and surface waves, resulting from the interplay between the intrinsic nonlinearity and geometrical dispersion, have also been studied and observed in solids [11–13]. However, until recently, this research has not been combined with the new capabilities of linear phononic crystals and acoustic metamaterials, as described in the previous chapters of this book. The far most studied nonlinear periodic phononic structures within the sonic regime (0–20 kHz) are granular crystals. Granular crystals are arrays of elastic particles in contact [14] whose nonlinearity results from the geometry of adjacent particles. In addition to granular crystals, some of the few studied examples of nonlinear periodic phononic structures are as follows. In the ultrasonic regime (greater than 1 MHz), nonlinear energy localization has been observed in micromechanical oscillator arrays [15]. Moreover, recent work by Liang B et al. suggested theoretically [16] and later demonstrated experimentally [17] the ability to use nonlinear acoustic materials, e.g., a contrast agent micro-bubble suspension, coupled to a linear superlattice to obtain acoustic rectification. Finally, at much higher frequencies (greater than 1 GHz), several studies have explored mechanical wave propagation in periodic nonlinear structures, focusing on high-amplitude stress wave and thermal phonon propagation. Several studies by Maris and collaborators investigated the propagation of high-amplitude picosecond pulses in crystalline solids, which are a type of naturally occurring nonlinear periodic structure [18, 19]. With respect to the propagation of high-frequency thermal phonons, many studies have focused on the use of nonlinear lattices for thermal rectification. The earliest of these studies were conducted by Terraneo et al. in 2002 [20] and then by Li et al. in 2004 [21]. Later, an experimental study by Chang et al., 2006, also demonstrated thermal rectification using mass-loaded carbon and boron-nitride nanotubes, and attributed the rectification to nonlinear processes [22]. Based on these studies, several following works have extended this concept further to suggest that nonlinear lattices could be used as thermal transistors [23], logic gates [24], and memory [25]. Several computational studies have also investigated and suggested multiple device concepts for thermal rectification building blocks, including carbon nano-cones [26] and graphene ribbons [27].

One of the most common ways to model the behavior of granular crystals, and many other types of nonlinear periodic structures, is to describe them as nonlinear lattices. The study of nonlinear lattices can thus offer many potential lessons and insights into the behavior of nonlinear periodic phononic structures. As such, the section directly following gives a brief history of the major types of nonlinear lattices. The review of nonlinear lattices is then followed by an introduction to granular crystals, which is one of the most widely studied types of nonlinear periodic phononic structures and is the subject matter that comprises the focus of this chapter.

7.1.2 Nonlinear Lattices

Since the first computational experiments in nonlinear mass-spring lattices by Fermi, Pasta, and Ulam in 1955 [28], there has been a wealth of interest in the dynamics of nonlinear lattices. Using one of the first modern computers, Fermi, Pasta, and Ulam (FPU) studied a system where the restoring (spring) force between two adjacent masses was nonlinearly related to the relative displacement between masses, and investigated how long would it take for long-wavelength oscillations to transfer their energy (thermalize) into an equilibrium distribution between all the modes of the system. Instead of the predicted thermalization, they found that over the course of the simulation, most of the energy had returned to the mode with which they had initialized the system in coherent form [29].

This discovery initiated whole fields of research relating to the study of nonlinear waves in discrete lattices [30–32]. This includes many different types of nonlinear lattices inspired by physical systems (in addition to the FPU lattice), and the study of physical phenomena occurring in them. As described in the review by Kevrekidis, P. G. [32], three of the most commonly studied types of nonlinear lattices are the discrete nonlinear Schrödinger (DNLS), the Klein-Gordon (KG), and the FPU lattices. The 1D forms of these lattice equations are as follows:

The DNLS can be written as

$$ j{\dot{u}_i} = - \epsilon ({u_{{i + 1}}} + {u_{{i - 1}}}) - |{u_i}{|^2}{u_i}, $$

the KG as

$$ {\ddot{u}_i} = \epsilon ({u_{{i + 1}}} - 2{u_i} + {u_{{i - 1}}}) - V^\prime ({u_i}), $$

and the FPU as

$$ {\ddot{u}_i} = V^\prime ({u_{{i + 1}}} - {u_i}) - V^\prime ({u_i} - {u_{{i - 1}}}), $$

where ${u_i}$ is the dynamical variable of interest at site $i$, $\epsilon$ is a coupling parameter (constant), $j = \sqrt {{ - 1}}$, and V is a nonlinear potential function [32]. The DNLS equation has been used to describe nonlinear waveguide arrays and Bose-Einstein condensates, among others [32]. Additionally, under small-amplitude assumptions, it is interesting to note that the DNLS can be derived from either the KG or the FPU lattices [33]. The KG system has been used to model systems of coupled pendula, electrical systems, and metamaterials with split ring resonators, among others [32]. In contrast to the KG system, the FPU has no onsite potential term, and instead involves a nonlinear potential based on nearest neighbor interactions (nonlinear springs). The FPU system has been used to describe the behavior of crystalline solids and structures, including granular crystals.

Studies of these lattices have helped to predict and understand the existence of localized nonlinear coherent structures and other nonlinear phenomena in many naturally occurring and artificial nonlinear (not necessarily discrete) systems. Two examples of nonlinear coherent structures, which are particularly applicable to the study of granular crystals are solitary waves and discrete breathers. Solitary waves were first observed by Russel in a shallow water-filled canal in 1844 [34]. Since then they were shown to be a solution of the Korteweg-de Vries (KdV), a nonlinear partial differential equation, and have been discovered in myriad systems and discrete nonlinear lattices of all the above types [35, 36]. Discrete breathers are a type of intrinsic (not tied to any structural disorder) localized mode, and have been the subject of many theoretical and experimental investigations [33, 36, 37]. Discrete breathers have been demonstrated in charge-transfer solids, superconducting Josephson junctions, photonic crystals, biopolymers, micromechanical cantilever arrays, and more [33]. In addition to nonlinear localized structures, the presence of nonlinearity in dynamical lattices makes available an array of useful phenomena including quasiperiodic and chaotic states, sub- and superharmonic generation, bifurcations, the breaking of time-reversal symmetry, and frequency conversion [38–43].

7.1.3 Introduction to Granular Crystals

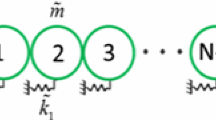
Granular crystals, which can be defined as ordered aggregates of elastic particles in contact with each other, are a type of nonlinear periodic phononic structure (Fig. 7.1). Their nonlinearity emerges from two characteristics: (1) the geometry of the particles is such that the force at the contact between neighboring elements is nonlinearly related to the displacement of the particle centers, as can be described by Hertzian contact [7] and (2) in an uncompressed state, granular crystals cannot support tensile loads, effectively creating an asymmetric potential between neighboring elements. An unusual feature of granular crystals that results from these nonlinearities is the negligible linear range of the interaction forces between neighboring particles in the vicinity of a zero compression force. This results in nonexistent linear sound speed in the uncompressed material. This phenomena has led to the term “sonic vacuum,” which describes a medium where the traditional wave equation does not support a characteristic speed of sound [14].

Fig. 7.1

Granular crystals in one, two, and three dimensions composed by metallic particles confined by supporting walls or confined in a matrix [The three-dimensional image has been adapted from (Daraio, C.; Nesterenko, V.F.; Jin, S.; “Strongly Nonlinear Waves in 3D Phononic Crystals” APS – Shock Compression of Condensed Matter, 197–200, American Institute of Physics, Conference Proceedings, Portland (OR), 2003)]

The study of granular crystals emerged in 1983 with work by Nesterenko that showed analytically, numerically [44], and later experimentally [45], the concept of “sonic vacuum” and the formation and propagation of highly nonlinear solitary waves in one-dimensional granular crystals. Granular crystals have since been shown to support many other unique dynamic phenomena. This wide array of phenomena supported by granular crystals is enabled by a tunable nonlinear response that encompasses linear, weakly nonlinear, and highly nonlinear behaviors, and can be controlled by essentially linearizing the system through the application of a variable static load [14, 46–48].

In their linear and weakly nonlinear dynamic regime, granular crystals have shown the ability to support tunable acoustic band gaps [49, 50] and discrete breathers [51, 52]. In the strongly nonlinear regime, they have been shown to support compact solitary waves [44–46, 48], nonlinear normal modes [53] anomalous reflections [54], and energy-trapping phenomena when interacting with defects and interfaces [55]. Because of this array-rich dynamics, which has been confirmed by theory, numerical simulations, and simple experiments, granular crystals have become one of the most studied examples of nonlinear lattices. Granular crystals have also been proposed and designed for use in numerous engineering applications including tunable vibration filters [50, 56], optimal shock protectors [57], nondestructive evaluation devices [58], acoustic lenses [59], and acoustic rectifiers [60].

As previously described, the nonlinearity of the interaction law results from the Hertzian contact between particles with elliptical contact area [7, 61, 62]. The Hertzian contact relates the contact force F _i,i+1 between two particles (i and i+1) to the relative displacement Δ _i,i+1 of their particle centers, as shown in the following equation:

$$ {F_{{i,i + 1}}} = {A_{{i,i + 1}}}[{\Delta_{{i,i + 1}}}]_{ + }^{{{n_{{i,i + 1}}}}}. $$

Values inside the bracket [s]₊ only take positive values, which denotes the tensionless characteristic of the system (i.e., there is no force between the particles when they are separated). For Δ _i,i+1 = 0 the particles are just touching, Δ _i,i+1 > 0 the particles are in compression, and Δ _i,i+1 < 0 the particles are separated. This tensionless characteristic is one part of the nonlinearity of the Hertzian contact.

For two spheres (or a sphere and a cylinder), the coefficient A _i,i+1 in the Hertz relationship is defined as:

$$ {A_{{i,i + 1}}} = \frac{{4{E_i}{E_{{i + 1}}}\sqrt {\displaystyle{\frac{{{R_i}{R_{{i + 1}}}}}{{{R_i} + {R_{{i + 1}}}}}}} }}{{3{E_{{i + 1}}}(1 - \nu_i^2) + 3{E_i}(1 - \nu_{{i + 1}}^2)}}, \quad {n_{{i,i + 1}}} = \frac{3}{2}, $$

(7.1)

where ${E_i}$, ${\nu_i}$, and ${R_i}$ are the elastic modulus, the Poisson’s ratio, and the radius of the i-th particle, respectively. The ${n_{{i,i + 1}}} = 3/2$ comes from the geometry of the contact between two linearly elastic particles with elliptical contact area, as can be seen in [61]. In addition to assuming that the contact area is elliptical and that both particles remain linearly elastic, the derivation of Hertzian contact assumes that [61]: (1) the contact area is small compared to the dimensions of the particle, (2) the contact surface is frictionless with only normal forces between them, and (3) the motion between the particles is slow enough that the material responds quasi-statically. Variation of the contact geometry will result in a variation of the interaction law stiffness and/or nonlinearity, and ultimately in a variation of the acoustic properties of the crystals. Several recent works have studied this variation theoretically, numerically, and experimentally, by exploring the dynamic response of chains of particles composed of grains with different geometries [63–65] (see Sect. 7.3.5).

The remainder of this chapter describes past and recent work in one-dimensional (1D) and two-dimensional (2D) granular crystals, categorized according to periodicity and dynamical regime.

7.2 One-Dimensional Granular Crystals

The dynamic properties of one-dimensional (1D) granular crystals have been extensively studied, using analytical, numerical, and experimental methods. The following sections describe some of the most interesting physical phenomena supported by these nonlinear systems.

If the stiffness of the contact between two adjacent particles is very low compared to the bulk stiffness of the particles composing the crystal and the contact area small compared to the particle size, 1D granular crystals can be modeled as a system of nonlinear springs and point masses (FPU-like nonlinear lattices). Another perspective from which to approach this same idea is that the characteristic (resonant) frequencies of the particles themselves must be very high compared to the modal frequencies of the granular crystal involving the rigid body-like motion of the particles in the system. Neglecting any dissipation, a statically compressed 1D array of elastic granules can be described by the following system of coupled nonlinear differential equations:

$$ {m_i}{\ddot{u}_i} = {A_{{i - 1,i}}}[{\delta_{{0,i - 1,i}}} + {u_{{i - 1}}} - {u_i}]_{ + }^{{{n_{{i - 1,i}}}}}{ } - {A_{{i,i + 1}}}[{\delta_{{0,i,i + 1}}} + {u_i} - {u_{{i + 1}}}]_{ + }^{{{n_{{i,i + 1}}}}}. $$

(7.2)

For spherical particles we recall that ${n_{{i,i + 1}}} = \frac{3}{2}$ and A _i,i+1 is defined as in (7.1). Here, the static overlap ${\delta_{{0,i,i + 1}}} = {\left( {\frac{{{F_0}}}{{{A_{{i,i + 1}}}}}} \right)^{{2/3}}}$, and ${F_0}$ is the homogeneous static compression force. ${m_i}$is the mass of the ith particle and ${u_i}$ is the dynamic displacement of the $i$th particle from its equilibrium position in the initially statically compressed chain. The bracket ${[s]_{ + }}$ of (7.2) takes the value $s$ if $s > 0$ and the value 0 if $s \le 0,$ which signifies that adjacent beads are not in contact. Within this framework, the dynamic of the system can be tuned to encompass linear, weakly nonlinear, and strongly nonlinear regimes of dynamic behavior, as will be demonstrated for the mono-atomic case in the following section.

7.3 One-Dimensional Monoatomic Granular Crystals

This section focuses on the nonlinear dynamic behavior of a statically compressed 1D monoatomic granular crystal (all particles are the same). A granular crystal composed of identical elastic spherical granules is considered, as shown in Fig. 7.2. For this crystal, ${R_i} = R$, ${m_i} = m = \frac{4}{3}\pi {R^3}{\rho_0}$, and A _i,i+1 of (7.2) is reduced to ${A_{{i,i + 1}}} = A = \frac{{E\sqrt {{2R}} }}{{3\left( {1 - {\nu^2}} \right)}}$, where m is the mass of the sphere, E and ρ ₀ are the Young’s modulus and density of particle material, R is the particle radius, and ν is the Poisson’s ratio. Moreover, it is assumed that the chain is subjected to constant static force ${F_0}$ applied to both ends, resulting in an initial displacement δ ₀ between neighboring particle centers, ${\delta_{{0,i,i + 1}}} = {\left( {\frac{{{F_0}}}{A}} \right)^{{2/3}}} = {\delta_0}$. The particle equations of motion, shown in (7.2) thus reduce to:

Fig. 7.2

One-dimensional monoatomic crystal compressed by a static force ${F_0}$. The crosses represent the initial positions of the particle centers in a statically compressed chain while the black circles denote the current positions [14]

$$ m{\ddot{u}_i} = A[{\delta_0} + {u_{{i - 1}}} - {u_i}]_{ + }^{{3/2}} - A[{\delta_0} + {u_i} - {u_{{i + 1}}}]_{ + }^{{3/2}}, $$

(7.3)

where ${u_i}$ is the displacement of the $i$th bead from its equilibrium position in the initially compressed chain, as shown in Fig. 7.2, and $i \in \{ 2, \cdots, N - 1\}$.

7.3.1 Near-Linear Regime

To approximate the fully nonlinear equations of motion shown in (7.3), a power series expansion of the forces can be taken. For dynamical displacements with amplitude much less than the static overlap, i.e. $\frac{{\left| {{u_{{i - 1}}} - {u_i}} \right|}}{{{\delta_{{0,i}}}}} \ll 1$, one can keep only the harmonic term of the expansion. In this case, the granular crystal can be considered as a linear lattice with spring constant ${K_2} = \frac{3}{2}A\delta_0^{{1/2}}$, where the equations of motion are reduced to:

$$ {m_i}{\ddot{u}_i} = {K_{{2}}}({u_{{i - 1}}} - {u_i}) - {K_{{2}}}({u_i} - {u_{{i + 1}}}). $$

(7.4)

The spectral band of the ensuing linear chain (see Chap. 2 for more details) has an upper cutoff frequency of ${\omega_m} = \sqrt {{4{K_2}/m}}$. As a consequence of the nonlinear relation ${F_0} \propto \delta_0^{{3/2}}$ for the case of the spherical granules, the cutoff frequency (as well as the sound velocity of the 1D monoatomic granular crystal) scales as $F_0^{{1/6}}$. These results have been confirmed experimentally [47, 66].

7.3.2 Weakly Nonlinear Regime

If the dynamic displacements have small amplitudes $\frac{{|{u_{{i - 1}}} - {u_i}|}}{{{\delta_{{0,i}}}}} < 1$ relative to those due to static load, a power series expansion of the forces (up to quartic displacement terms) can be calculated to yield the ${K_2} - {K_3} - {K_4}$ model:

$$ m{\ddot{u}_i} = \sum\limits_{{k = 2}}^4 {{K_k}} [{({u_{{i + 1}}} - {u_i})^{{k - 1}}} - {({u_i} - {u_{{i - 1}}})^{{k - 1}}}], $$

(7.5)

where ${K_2} = \frac{3}{2}A\delta_0^{{1/2}}, \;\;\; {K_3} = - \frac{3}{8}A\delta_0^{{ - 1/2}}, \;\;\; {K_4} = -\frac{3}{{48}}A\delta_0^{{ - 3/2}}$.

This model is an example of the celebrated FPU model. Many theoretical studies have focused on the dynamical properties of this type of nonlinear lattice, revealing the existence of coherent nonlinear structures such as nonlinear periodic waves, solitary waves [67], and discrete breathers [68].

Seeking traveling waves with a characteristic spatial size L that is much larger than the inter-particle distance α = 2R − δ₀, one can apply the so-called long-wavelength or continuum approximation.

Using the replacement:

$$ {u_i} = u(x),{u_{{i\pm 1}}} \approx u\pm a{u_x} + \frac{1}{2}{a^2}{u_{{xx}}}\pm \frac{1}{6}{a^3}{u_{{xxx}}} + \frac{1}{{24}}{a^4}{u_{{4x}}}, $$

(7.6)

equation (7.5) is transformed into the nonlinear Boussinesq equation and into the Korteweg-de Vries equation (see for example [69]). In (7.6), u _x  = ∂u/∂x, and the number of subscripts x denotes the order of the derivative of u. Nesterenko applied this method (taking into account only up to the ${K_3}$ term) to a strongly compressed granular chain, and derived the following KdV equation [14]:

$$ \begin{array}{ccc} { {\xi_{\rm{t}}} + {c_0}{\xi_{{xx}}} + \gamma {\xi_{{xxx}}} + \frac{\sigma }{{2{c_0}}}\xi {\xi_x} = 0,\xi = - {u_x} \hfill} \\\\ \quad c_0^2 = \frac{{A\delta_0^{{1/2}}6{R^2}}}{m},\gamma = \frac{{{c_0}{R^2}}}{6},\sigma = \frac{{c_0^2R}}{{{\delta_0}}}.\end{array}$$

(7.7)

In (7.7), ξ = −u _x , ξ _x = ∂ξ /∂t, and c ₀ is the linear sound speed. The solutions of (7.7) are well known, and include nonlinear periodic waves and solitary waves.

On the other hand, to investigate how quasi-monochromatic plane waves or narrow-band packets evolve by nonlinear effects, one can derive another well-known nonlinear wave equation—the Nonlinear Schrödinger (NLS) equation. This equation predicts many nonlinear phenomena, including second harmonic generation, modulation instability, and the existence of bright and dark solitons [35]. The derivation of the NLS from (7.5) is possible using the method of multiple scales combined with a quasi-discreteness approximation (see [70] for an application of this method to a generic FPU lattice in the form of (7.5) and [71] for a recent application of this method to a monoatomic strongly compressed granular crystal).

Another generic feature of nonlinear lattices is the existence of nonlinear localized modes called discrete breathers (DBs). DBs have been studied extensively in monoatomic FPU chains [68]. One of the mechanisms for the generation of such nonlinear localized modes is the modulational instability (MI) of a plane wave at the band edge. A detailed analysis of this instability (bifurcation) shows that the MI of the upper cutoff mode manifests itself when the coefficients of the FPU lattice are such that $3{K_2}{K_4} - 4K_3^2 > 0$ (see Sect. 4.3 of [33] and references therein). In the monoatomic granular crystal setting, one can show that this inequality does not hold. This is an indication that small-amplitude DBs bifurcating from the upper band mode do not exist in monoatomic granular crystals. However, the existence of dark discrete breathers or large-amplitude DBs remains an interesting open question.

Another interesting weakly nonlinear effect, self-demodulation, was studied by Tournat and collaborators in compressed 1D granular crystals [72]. In this work, they explored how, in a nonlinear medium, two primary frequencies can mix to form a propagating wave with frequency that is the difference of the two primaries.

7.3.3 Highly Nonlinear Regime: Long-Wavelength Approach

A very interesting, non-classical wave behavior appears if the granular material is weakly compressed and the particle displacements are larger than the initial relative displacement δ ₀ resulting from the static compression. This regime is termed the highly nonlinear regime. Most of the studies in 1D monoatomic granular crystals have been devoted to this dynamical regime. This section summarizes the basic steps of the long-wavelength method that Nesterenko applied [14]. A review of alternate analytical approaches and experimental observations will also be presented in the following sections.

Fig. 7.3

Weakly compressed chain of particles. The crosses represent the initial positions of the particles in the statically compressed chain, the black circles correspond to the current positions of spheres, and the open circles the initial positions of the spheres in the uncompressed [14]

Including δ ₀ in displacement ${u_i}$ which is calculated from the particle positions in the uncompressed system (see Fig. 7.3 and [14] for more details), (7.3) becomes:

$$ m{\ddot{u}_i} = A[{u_{{i - 1}}} - {u_i}]_{ + }^{{3/2}} - A[{u_i} - {u_{{i + 1}}}]_{ + }^{{3/2}} $$

(7.8)

In the long-wavelength approximation, the displacements u _i-1 , u _i+1 can be expanded in a power series according to a small parameter ε = a/L up to the fourth order [see (7.6)]. By substituting (7.6) into (7.8), and conducting some additional calculation, a new wave equation is obtained [14]:

$$ \begin{array}{lllll}{u_{{tt}}} = - {c^2}{\left\{ {{{( - {u_x})}^{{3/2}}} + \frac{{{{\text{a}}^2}}}{{12}}\left[ {{{\left( {{{( - {u_x})}^{{3/2}}}} \right)}_{{xx}}} - \frac{3}{8}\left( {{{( - {u_x})}^{{ - 1/2}}}} \right)u_{{xx}}^2} \right]} \right\}_x}, - {u_x} > 0, \hfill \\{c^2} = \frac{{2E}}{{\pi {\rho_0}(1 - {\nu^2})}}. \end{array} $$

(7.9)

Despite the complex nature of the presented strongly nonlinear wave equation, the stationary solutions of (7.9), such as nonlinear periodic and solitary waves, can be found in the form u(x − Vt) [14]. The waveform of a periodic wave with speed V = V _p is given by the following expression:

$$ \xi = {\left( {\frac{{5V_{\rm{p}}^2}}{{4{c^2}}}} \right)^2}{\text{co}}{{\text{s}}^4}\left( {\frac{{\sqrt {{10}} }}{{5a}}x} \right). $$

(7.10)

The dependence of the speed of the periodic wave, V _p, on the minimal and maximum strains is presented in [14].

The solitary shape (for the case when the initial prestrain ξ₀ approaches 0) is one hump of the periodic solution of (7.10), with a finite wave length equal to about five particle diameters. This solitary wave is a supersonic one, similarly to the KdV soliton, but differs from the KdV soliton in other fundamental properties. A unique feature of this solitary wave is the independence of its width on amplitude. Accordingly, this property is quite different from the property of weakly nonlinear KdV solitary wave. Here, the speed of the solitary wave V _s has a nonlinear dependence on maximum strain ξ_m (and particle velocityυ _m):

$$ {V_{\rm{s}}} = \frac{2}{{\sqrt {5} }}c\xi_{\rm{m}}^{{1/4}} = {\left( {\frac{{16}}{{25}}} \right)^{{1/5}}}{c^{{4/5}}}\upsilon_{\rm{m}}^{{1/5}} = {\left( {\frac{{8E}}{{{5}\pi {\rho_0}\left( {1 - {\nu^2}} \right)}}} \right)^{{2/5}}}\upsilon_{\rm{m}}^{{1/5}}. $$

(7.11)

This result shows that the speed of the strongly nonlinear solitary wave V _s does not depend on particle size in the granular material. At the same time it does depend on the elastic properties of the particles (E and v) and their density. The presented theoretical results allow us to design strongly nonlinear granular materials with exceptionally low velocity of signal propagation. Simple estimation based on (7.11) shows that it is possible to create materials with nonlinear impulse speed in the interval 10–100 m/s.

7.3.4 Review of Alternate Strongly Nonlinear Wave Theoretical Approaches

The solitary wave solution (or a soliton with compact support, known also as compacton [73]) presented in the previous section describes well the solitary wave that an impulsive excitation generates in a weakly compressed or uncompressed granular crystal. This was verified in simulations and experiments by different authors (see references below). The rigorous proof of the existence of solitary waves in a monoatomic granular crystal composed of spherical particles was done by MacKay [74], who applied the existence theorem for solitary waves on lattices by Friesecke and Wattis [75]. Ji and Hong extended the proof given by MacKay to the general case of an arbitrary power-law type contact force [76].

An analytical solution of the form tanh(f _n ) for stationary waves in discrete chains, where f _n is represented by a series, was also presented by Sen and Manciu [77]. Their result is very close to a soliton obtained by the long-wavelength approximation. Chatterjee studied the asymptotic description of the tail of the soliton in an uncompressed chain and he revealed that it has a double exponential decay [78]. He also presented a new asymptotic solution for the full solitary wave, which is closer to the results of numerical simulations than the approximate solution given by Nesterenko. A quite different analytic approach for the study of pulse propagation in granular crystals was developed by Lindenberg and collaborators [79, 80]. This method uses the binary collision approximation to reduce the problem of propagation to collisions involving only two granules at a time.

English and Pego [81] studied the shape of the solitary wave that propagates in a 1D granular chain without precompression (δ ₀ = 0). Their method is based on a reformulation of the equations of motion using the difference coordinates ${r_i} = {u_{{i - 1}}} - {u_i}$ such that:

$$ m{\ddot{r}_i} = A\left[ {[{r_{{i + 1}}}]_{ + }^{{3/2}} - 2[{r_i}]_{ + }^{{3/2}} + [{r_{{i - 1}}}]_{ + }^{{3/2}}} \right]. $$

(7.12)

Seeking for traveling wave solutions, ${r_i} = r(x) \equiv r(i - ct)$, one obtains the following advanced delay equation:

$$ r ^{\prime\prime}(x) = \frac{A}{{m{c^2}}}\left[ {{r^{{3/2}}}(x - 1) - 2{r^{{3/2}}}(x) + {r^{{3/2}}}(x + 1)} \right]. $$

(7.13)

By rewriting this equation in an equivalent integral form and studying its asymptotic behavior, they proved that the solitary wave decays super-exponentially. Moreover, they applied an iterative method for the computation of the numerically exact shape of the solitary waves.

Later, Ahnert and Pikovksy [82] applied a different type of quasi-continuum approximation by expanding, up to fourth order, the difference coordinate ${r_i}$ instead of the displacement ${u_i}$. Substituting these expansions in (7.12), they obtained a strongly nonlinear partial differential equation (see (7.6) in [82]) that supports a solitary wave with compact form. The analytic solution has the same form as Nesterenko’s solution, but with slightly different amplitude and width constants. Moreover, they presented an accurate numerical method for the numerical solution of the advanced delay equation (7.13) and they compared the numerically obtained solutions with those of approximated PDEs.

Recently, Starosvetsky and Vakakis [83], working directly on the nonlinear lattice equations with no precompression, developed semi-analytical approaches for computing different families of nonlinear traveling waves. These waves involve both separation and compression between adjacent particles and therefore they cannot be resolved using quasi-continuum approximations. In addition, they showed that these wave families converge to the solitary wave in a certain asymptotic limit. They also solved the reduced advanced delay equation numerically, and applied the method of Pade approximations.

7.3.5 Review of Experiments with Strongly Nonlinear Solitary Waves

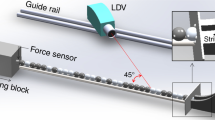
The quantitative agreement of analytical and numerical predictions with experiments, regarding solitary waves in strongly nonlinear granular crystals, was first found by Lazaridi and Nesterenko [45]. They observed for the first time the rapid decomposition of the initial impulse excitation into multiple solitary waves in a distance comparable to the solitary wave width, (Fig. 7.4). Since then there have been several experimental studies and observations of solitary waves and other strongly nonlinear phenomena in multiple settings. Optical observations of strongly nonlinear waves in arrays of photoelastic disks excited by a local explosive loading were reported by Zhu, Shukla, and Sadd [84]. Coste, Falcon, and Fauve [46], and Coste and Gilles [47] conducted a very detailed quantitative study of the speed and shape of solitary waves at different amplitudes. They reported a negligible decay of the solitary wave in chains composed of 50 particles, and they concluded that the solitary waves shape observed in experiments were in very good agreement with the predictions obtained from theoretical solutions such as (7.10).

Fig. 7.4

Evolution of a soliton train excited experimentally by a striker impact (M _s = 10 m, u _s = 0.5 m/s), after a propagation distance of N particles: (a) N = 5, (b) N = 10, (c) N = 20, (d) N = 30, (e) N = 40, (f) N = 60. The vertical scale corresponds to a force of 80 N, the horizontal scale to a total time of 50 μs (a–e) and 100 μs (f) [14]. Figure reproduced from [Nesterenko, V.F., Dynamics of Heterogeneous Materials. 2001, Chapter 1, pp. 70, NY: Springer-Verlag] with permission from the publisher

The relatively low speed of the solitary waves detected by Coste et al. [46] is very unusual for solid materials. In an uncompressed granular system, according to (7.11), the minimum propagation speed of a solitary wave can be close to zero if the amplitude of the disturbance is approaching zero (“sonic vacuum”) [13]. Using polymeric and composite particles [85, 86], for example, one can design granular crystals with a solitary wave speed corresponding to a signal in the interval of 10–100 m/s, an order of magnitude less than that previously observed in experiments by Coste et al. [45]. In addition to the experimental observation of solitary waves, many works relating to highly nonlinear phenomena in granular crystals have followed. Nesterenko et al. showed experimentally the presence of anomalous reflections when highly nonlinear waves interact with interfaces [54], effectively demonstrating for the first time the concept of an acoustic diode. Daraio et al. [48], described in detail the ability to tune the dynamic response of granular crystals by controlling the static precompression and the dynamic excitation applied to the system. Job et al. [87], investigated the behavior of solitary waves interacting with a boundary, showing for the first time the sensitivity of solitary waves to the mechanical properties of an adjacent medium. Thorough experimental, numerical, and theoretical descriptions of the formation, propagation [88], and collision of solitary wave trains were published a few years later [89].

Recently, several experimental works described wave propagation in granular crystals composed of particles with elliptical and cylindrical geometries [63, 64]. Chains composed of ellipsoidal or cylindrical particles were shown to support the formation and propagation of highly nonlinear solitary waves similar to the solitary waves observed in chains of spherical particles. These systems were also found to be highly dependent not only on the particles’ geometry but also on the orientation angles between particles in the chain. This dependence on orientation angle between beads provides an additional free parameter to design acoustic materials with unprecedented transmission properties.

Experimental studies have also described the dynamic response of chains composed of spherical steel particles coated with a soft polymeric material. These studies showed that this type of system also supports the formation and propagation of highly nonlinear solitary waves [85]. However, one interesting property of these systems is that the contact interaction between thin-coated spheres does not follow the classical Hertzian interaction between two solid spheres [90]. The dynamic response of chains composed of coated spheres is governed by a quadratic power law dependence between the contact force, F, and the displacement, δ, instead of the Hertzian, non-integer power of 3/2. This new nonlinear contact interaction dramatically changes the dynamics of solitary wave propagation compared to its counterpart in chains of solid spheres. Here, the spatial width of the wave becomes shorter (3.14 particles size instead of 5), the wave speed (V _s) is relatively slower, and its dependence on force amplitude (F _m) is also different (V _s ~ F ^1/4_m instead of V _s ~ F ^1/6_m ).

Studies of chains of hollow spherical particles also presented interesting nonlinear acoustic phenomena. Highly nonlinear solitary waves were observed to propagate through the system, but the wave properties were different from the highly nonlinear solitary waves in the chains of solid spheres. The spatial width of the solitary wave in chain of hollow spheres was approximately 8 particles (larger than 5 particles, which is the characteristic length of a solitary wave forming in a chain of uniform, solid spheres). The wave speed was found to be proportional to the force amplitude to the power 1/11 [65]. It was shown that such behavior resulted from the unique contact interaction between thin hollow spheres, which for the range of wave amplitude studied, could be approximated by a power-law type relation (F = kδ ⁿ). In this case, the exponent n was found to be smaller than the value 3/2 as in the classical Hertzian interaction between solid spheres. The contact stiffness k and the exponent n were also found to be dependent on the thickness of the hollow sphere’s shell. This dependence of the dynamic behavior of granular crystals on the coating and/or shell thickness of spherical particles provides yet another free parameter to employ in tuning the dynamics of nonlinear acoustic crystals.

7.4 One-Dimensional Diatomic Granular Crystals

By increasing the degree of periodicity, from a homogenous monoatomic granular crystal to a diatomic granular crystal composed of alternating particles, additional interesting phenomena can be accessed. This section describes some of those phenomena characteristic of 1D diatomic granular crystals, including tunable band gaps, discrete breathers (DBs), and highly nonlinear solitary waves with widths up to ten particles.

An example of a 1D diatomic granular crystal is illustrated in the bottom of Fig. 7.1. The equation of motion for the general 1D granular crystal, shown in (7.2), can be reduced to the 1D diatomic crystal model, as follows:

$$ {m_i}{\ddot{u}_i} = A[{\delta_0} + {u_{{i - 1}}} - {u_i}]_{ + }^{{3/2}} - A[{\delta_0} + {u_i} - {u_{{i + 1}}}]_{ + }^{{3/2}}, $$

(7.14)

where the subscript i is the index of the ith particle, the particle masses are ${m_{{2i - 1}}} = m$ and ${m_{{2i}}} = M$. By convention, M is taken to be the larger of the two masses and m to be the smaller of the two masses. Because all contacts (aside from any boundaries) are the same, there is a single Hertzian contact coefficient A and static overlap δ ₀ that are used to represent the system, which have been defined in the previous sections. Within this framework, as before, the dynamic response of the system can be tuned to encompass linear, weakly nonlinear, and strongly nonlinear regimes of dynamic behavior. Also as before, the K ₂ −K ₃ −K ₄ model can be applied in the weakly nonlinear regime, and the K ₂ linearized model in the linear regime.

7.4.1 Near-Linear Regime: Localized Surface Modes

For dynamical displacements with amplitude much less than the static overlap $(\left| {{u_{{i + 1}}} - {u_i}} \right| \ll {\delta_{{0)}}}$, the nonlinear ${K_3}$ and ${K_4}$ terms can be neglected, and the linear dispersion relation of the system can be easily computed. This results in an effectively linear diatomic system of springs and point masses, as was presented in Chap. 2, but with a tunable stiffness K ₂ .

Several previous studies explored the existence of band gaps in highly compressed granular crystals. Initially, studies focused on 1D, two-particle unit cell, arrays of glued [91], welded [92], and elastically compressed spherical particles [49, 51, 56]. These studies demonstrated tunable vibration spectra with two bands of propagation (called the acoustic and optical bands) separated by a band gap in the diatomic case. Boechler et al. [50] later extended this work by investigating the response of one-dimensional diatomic granular crystals with three-particle unit cells, and showing their tunability based on variations of the particles geometry and on the applied static load. In contrast to diatomic granular crystals with two-particle unit cells, the three-particle unit cell granular crystal was shown to contain up to three distinct pass bands and two finite band gaps.

In addition to acoustic and optical band modes, the diatomic semi-infinite harmonic granular crystal also supports a gap mode, provided the crystal has a light particle at the surface and free boundary conditions. This mode is localized at the surface (i.e., at the first particle), and its displacements have the following form [93]:

$$ {u_{{2i + 1}}} = B{( - 1)^i}{\left( {\frac{m}{M}} \right)^i}{{\text{e}}^{{j{\omega_s}t}}} $$

(7.15)

$$ {u_{{2i + 2}}} = B{( - 1)^{{i + 1}}}{\left( {\frac{m}{M}} \right)^{{i + 1}}}{{\text{e}}^{{j{\omega_s}t}}}, $$

with particle number $i \ge 0$, frequency ${\omega_{\rm{s}}} = \sqrt {{{K_2}(1/m + 1/M)}}$ is in the gap of the linear spectrum, and B is an arbitrary constant. This particular mode with frequency in the band gap, that is localized around the surface, proves to have a nonlinear counterpart and to be very closely related to the DB in the strongly discrete regime, as will be described in the following section.

7.4.2 Weakly Nonlinear Regime: Discrete Breathers

By increasing the relative amplitude of the dynamic to static displacements $(|{u_{{i + 1}}} - {u_i}| < {\delta_0})$, and thus entering the weakly nonlinear regime, a type of intrinsic localized mode called a discrete breather (DB) can be supported by the system. DBs have been widely studied in the realm of nonlinear lattices, as previously described [33]. They are nonlinear modes that have frequency within the gap of the linear spectrum and are localized in space. As such, discrete breathers have practical importance as a mechanism to localize vibrational energy in frequency and space without the introduction of any extrinsic disorder.

DBs were rigorously proven to exist in diatomic FPU-type lattices, with alternating heavy and light masses, by Mackay in 1997 [94]. Furthermore, several studies also investigated the specific case of DBs located in the gap between the acoustic and optical bands of anharmonic diatomic lattices [95–97].

A recent study by Theocharis et al. systematically studied the existence and stability of DBs in diatomic granular crystals [52]. Studies in other diatomic anharmonic lattices have shown the existence of up to two types of DBs. The study by Theocharis et al. demonstrated that both types of DBs can arise in granular chains. They examined both of these two families of discrete gap breathers, and studied their existence, stability, and structure throughout the gap of the linear spectrum. The first family was an unstable DB that is centered on a heavy particle and characterized by a symmetric spatial energy profile, and the second family is a potentially stable DB that is centered on a light particle, and is characterized by an asymmetric spatial energy profile.

Although the FPU and granular crystal lattices are analogous in many respects, there exists an important difference because of the additional nonlinearity caused by the tensionless characteristic of the granular crystal lattice. Accordingly, Theocharis et al., contrasted discrete breathers in anharmonic FPU-type diatomic chains with those in diatomic granular crystals, and found that for the case when the DB was very narrow (highly discrete), the asymmetric nature of the latter interaction potential led to a form of hybrid bulk-surface localized solutions (see Fig. 7.5). Figure 7.5 shows the two families of DB solutions at times t = T and t = T/2 (where T is the periodic of the DB), and the profile of a linear surface mode. This similarity between the shapes of the two modes suggests that the temporary creation of a new interior surface, allowed by tensionless characteristic of the system, has contributed to a modified type of intrinsic localized mode.

Fig. 7.5

Top panels: Spatial profile of a DB in the heavy mass-centered symmetric family at times (a) t = 0 and (b) t = T/2. Bottom panels: As with the top panels, but for the light mass centered asymmetric family of DB solutions. The dashed curves correspond to the spatial profile of the surface mode obtained using (7.15). In each panel, a visualization of particle positions is included, along with the corresponding spatial gap openings, for the corresponding time and DB solution. Copyright (2010) by The American Physical Society [52]

The existence of DBs in diatomic granular crystals was experimentally proven in a recent study by Boechler et al. [51]. In this study, the authors utilized the modulational instability (MI) of the lower optical mode to generate DBs in an 80 particle diatomic granular crystal. In the weakly nonlinear regime, granular crystals can be showed to be subject to MI when K ²₃ /K ₂ K ₄ < 3/4. To excite the MI, they drove the granular crystal from one boundary at the lower optical mode frequency, at high amplitude. Upon reaching a critical amplitude for the MI to occur, the anharmonic lattice vibration decayed into a localized DB.

Figure 7.6 shows, as per Boechler et al. [51], an experimental observation of a DB, generated in an 80 particle diatomic granular crystal. This example shows how the interplay of nonlinearity and discreteness/periodicity leads to the localization of vibrational energy within a narrow spatial regime (around the 14th particle from the boundary), at a specific frequency within the gap of the linear spectrum ( f _b  = 8.31 kHz). In panels (a) and (b), far from the center of the DB, a periodic response at the driving frequency ( f _d  = 8.9 kHz) can be seen. Alternatively, in panels (c) and (d), near the center of the DB, a quasiperiodic response appears, which is characterized by the driving frequency and frequency of the generated DB. This spatial localization is further clarified in the spatial profile of the energy distribution shown in panel (e).

Fig. 7.6

Experimental observation of a DB, in an 80 particle granular crystal, at f _b  = 8.31 kHz. (a), (c) Force at particle 2 and 14, respectively. (b), (d) Power spectral density (PSD) for the highlighted time regions in (a), (c) of the same color. Square (circular) markers denote the DB (driving) frequency and PSD amplitude. (e) The ratio of the PSD amplitude at the discrete breather frequency divided by the PSD amplitude of the driving frequency as a function of sensor location. The vertical dashed line in (b) and (d) denotes the lower cutoff frequency of the optical band, and the vertical dashed lines in (a) and (c) denote the time region for the PSD calculation. Image reproduced from [98]

7.4.3 Highly Nonlinear Regime: Strongly Nonlinear Solitary Waves

In this section, the effects of increased periodicity on the propagation of solitary waves in 1D diatomic granular crystals with no static load is described. Solitary waves in such systems were first studied and described by Nesterenko in 2001 [14]. He found that by assuming the mass of one particle type to be much larger than the mass of the other (m ₁ /m ₂ >> 1) and by applying the long wavelength approximation, the resulting wave equation supports a solitary wave solution with a characteristic spatial width of ~10 particles. This demonstrates how an increase in periodicity (or redistribution of the monoatomic particle masses to two neighboring particles) can result in wider solitary wave.

Later, Porter et al. [99] applied the long-wavelength approximation to diatomic granular crystals with arbitrary mass ratios by postulating a “consistency condition” between the displacements of the two particles in the unit cell. They showed that the diatomic chain supports a finite-width soliton-like solution, and they obtained an analytical expression for the width of the solution as a function on the mass ratio. This expression generalizes the previously known limiting cases, namely, m ₁ /m ₂  = 1 (monoatomic) and m ₁ /m ₂ >> 1 (diatomic with ~10 particle length solitary wave width). In the same study, Porter et al. compared these analytical predictions with simulations and experiments and found good agreement.

Recently, Vakakis et al. [100] presented an extensive numerical and theoretical study of solitary waves in diatomic chains. They showed that in a diatomic granular crystal, scattering at the interfaces of the dissimilar light and heavy beads will typically cause a slow disintegration of the traveling wave and the formation of small amplitude oscillating tails. However, they also found that for specific discrete values of the mass ratio between heavy and light particles, the system supports solitary waves which travel without distortion. These discrete values of the mass ratio correspond to the case where the light beads always stay in contact with adjacent heavy beads. For this case, the entire energy of the main pulse is conserved and transferred without loss to the next heavy bead. These solutions can be considered analogous to the propagation of solitary waves in monoatomic granular crystals, in that their velocity profiles decay to zero. Finally, they also observed that the diatomic family of solitary waves propagates faster than the corresponding solitary waves in monoatomic systems.

7.5 One-Dimensional Monoatomic Granular Crystals with Defects

By placing one or more defects into an otherwise perfectly periodic mono-atomic granular crystal, disorder can be introduced into the system. The presence of disorder, and its interplay with the nonlinearity of the system, causes interesting and useful phenomena throughout the granular crystal’s range of dynamic regimes. In contrast to the case of increasing periodicity, introducing disorder adds new ways to break the spatial-symmetry of the granular crystal. In combination with the ability of nonlinear systems to break the time-reversal symmetry of the dynamic response, the introduction of spatially asymmetric disorder can be particularly useful. In the following section several recent studies are described relating to defects in monoatomic granular crystals, including: tunability of defect modes in the linear regime [101], localized nonlinear defect modes and spontaneous symmetry breaking in the weakly nonlinear regime [102], the interplay of solitary waves with defects in the highly nonlinear regime [103], and tunable bifurcation-based acoustic rectification in a driven granular crystal [60].

7.5.1 Near-Linear Regime: Tunable Defect Modes

A strongly compressed (with respect to the dynamic displacements) homogenous granular crystal with light-mass defects will contain exponentially localized modes with frequencies above the acoustic band of the granular crystal, localized around the defect sites. The frequency of these localized defect modes is tunable with changes in static load, similar to the tunability of the linear dispersion relation of a periodic granular crystal.

The existence and tunability of defect modes localized around one and two light-mass defects in a strongly compressed 1D otherwise homogenous granular crystal was investigated first numerically and analytically by Theocharis et al. [101], and then experimentally by Man et al. [101]. In the work by Man et al., they placed one and two light-mass defects near the edge of a 20 stainless-steel particle granular crystal, applied white-noise excitation from the edge of the crystal, and measured the frequency of the defect modes localized in the vicinity of the defects as a function of defect size and relative defect position. The observed defect mode frequencies were compared with eigen-analysis of the linearized 20 particle granular crystal (as described in Theocharis et al. [101]), and analytical expressions based on few-site considerations [100]. They showed that, for a sufficiently small single light mass defect in an otherwise homogenous granular crystal, the frequency of the defect mode can be approximated as [101]:

$$ \begin{array}{lll} {f_{{3{\rm{bead}}}}} \\ \quad= \frac{1}{{2\pi }}\sqrt {{\frac{{2{K_{\rm{Rr}}}M + {K_{\rm{RR}}}m + {K_{\rm{Rr}}}m + \sqrt {{ - 8{K_{\rm{Rr}}}{K_{\rm{RR}}}mM + {{[2{K_{\rm{Rr}}}M + ({K_{\rm{RR}}} + {K_{\rm{Rr}}})m]}^2}}} }}{{2mM}}}}.\end{array} $$

(7.16)

This expression is obtained by solving the eigenvalue problem of the three-particle system in the vicinity of the defect (large particle–defect particle–large particle). Here M is the mass of the homogenous particles, m is the mass of the defect particle, f _3bead is the frequency of the localized defect mode, ${K_{\rm{RR}}} = 3/2{A_{\rm{RR}}}^{{{2}/{3}}}{F_0}^{{{1}/{3}}}$ is the linearized stiffness between two large particles, and ${K_{\rm{Rr}}} = 3/2{A_{\rm{Rr}}}^{{{2}/{3}}}{F_0}^{{{1}/{3}}}$ is the linear stiffness of the contact between a defect-particle and a large particle. A _Rr and A _RR are the Hertz contact coefficients between the respective particles. From this expression, it is clear how the defect modes are tunable with static load, geometry, and material properties.

In both studies [101, 102], it was found that when two defects were placed sufficiently far from each other (outside the localization length of each individual defect mode), the granular crystal presented two isolated linear defect modes with frequencies of a single-defect mode. The further the distance between the defects, the closer the modes are to isolated ones with near-identical frequencies. However, when the defects are brought sufficiently close together (within the localization length of a single-defect mode) each defect was found to affect the other. This caused the formation of a symmetric and anti-symmetric pair of defect modes, with two new separate frequencies, involving both defects.

7.5.2 Weakly Nonlinear Regime: Nonlinear Localized Modes and Symmetry Breaking

If the amplitudes of the dynamic displacements are increased, relative to the static overlap, and thus the nonlinearity of the dynamic response is also increased, the nonlinear localized defect modes depart from their linear counterparts and new phenomena are introduced. In addition to exploring the near-linear behavior of one-dimensional, strongly compressed granular crystals with one or two light-mass defects, Theocharis et al. investigated the behavior of defects in the weakly nonlinear regime [102]. As previously described, by analyzing the problem’s linear limit, they identified the system eigen frequencies and the linear defect modes. Using continuation techniques, they found localized nonlinear defect mode solutions that bifurcate from their linear counterparts and studied their linear stability in detail by computing the Floquet multipliers of the nonlinear periodic solutions.

For the case of a single light-mass defect, it was found that the inherent nonlinearity of the system leads to long-lived localized breathing oscillations, which form robust nonlinear localized modes. Their frequency depends not only on the static load, the geometry, and the material properties of the granular crystal and defect particle, but also on the amplitude of the oscillations. Because of the type of the nonlinearity in the system, the defect mode’s frequency decreases with increasing dynamic amplitude (and nonlinearity). These are examples of two ways where nonlinearity can be used to tune the frequency of a localized mode: by changing the static load, and thus the stiffness of the contacts, or by changing the relative amplitude of the dynamic displacements to the static overlap.

For the case of two defects, nonlinearity can create further interesting phenomenology when the defects are sufficiently close. A particularly intriguing example is the case of next-nearest neighbor defects, where the two defects are separated by one large particle. This resembles the situation of a “double well” potential, which has been studied systematically in various settings, including nonlinear optics [104] and atomic physics [105, 106]. In these settings, it has been predicted analytically (via a two-mode reduction), manifested numerically, and observed experimentally that beyond a certain nonlinearity threshold, a pitchfork bifurcation arises that causes the spontaneous symmetry breaking of the relevant configurations, and results in asymmetric nonlinear modes. The investigations of this phenomena in granular crystals, by Theocharis et al., indicate that this phenomenology is more generic. Figure 7.7 shows the bifurcation of the antisymmetric linear defect mode as a function of the defect mode frequency and relative force between the defect sites, for a next-nearest neighbor configuration. As the antisymmetric defect mode (Fig. 7.7, inset A1) becomes progressively more nonlinear (and decreases in frequency), at a critical point, the mode becomes unstable via a pitchfork-like bifurcation. This bifurcation signals the emergence of two asymmetric modes (Fig. 7.7, insets A2 and A3), which are mirror images of each other and predominantly centered on one of the two defect sites.

Fig. 7.7

Pitchfork bifurcation illustrated by force differential between two next-nearest neighbor defects, as a function of the mode frequency. This shows the transition from a single antisymmetric mode to two (mirror-symmetric between them) asymmetric modes after the onset of the symmetry breaking bifurcation. Insets: spatial profiles and locations of Floquet multipliers $\lambda$ in the complex plane of solutions for different frequencies

The case of the bifurcation of the antisymmetric two-defect mode is a good example of how, through the addition of nonlinearity, sharp transitions can be created between two acutely different states, the spatial symmetry of the dynamic response broken, and new mechanisms accessed to control the distribution and frequency of vibrational energy.

7.5.3 Highly Nonlinear Regime: Transient Localized Modes

By increasing the nonlinearity of the dynamic response further, the interaction of traveling waves with defects in a nonlinear system can be explored. The interaction of highly nonlinear solitary waves with a mass defect placed in a 1D, unloaded granular crystal has been investigated analytically and computationally first by Sen [107–109] and then by Hascoet, in 2000 [110]. This work was later followed by a more in depth numerical and experimental study by Job, in 2009 [103]. Two different physical pictures emerge whether one considers a light or a heavy impurity mass. The scatter of the solitary wave with a light impurity yields transient oscillations of the defect which leads to the emission of lower amplitude solitary waves in both directions [110]. In contrast, a heavy-mass defect is shifted by the solitary wave, a solitary wave is reflected back, and the transmitted wave loses its soliton characteristics and is fragmented into smaller waves of decreasing amplitude [110]. In the work by Job, it was shown that the interaction with a light-mass defect will also lead to the transient excitation of a localized mode [103]. They described how the slow-timescale local compression caused by the solitary wave around the defect site can act analogously to the linearizing static compression described in the previous sections, and create an oscillating localized defect mode [103]. Starosvetsky et al. also analyzed analytically and numerically the interaction of the solitary wave with light mass defects. They used reduced models that take into account only the interaction of the defect mass with its neighboring particles [111].

7.5.4 Driven-Damped Granular Crystals: Quasiperiodicity, Chaos, and Acoustic Rectification

In the previous sections, the existence of linear and nonlinear localized modes surrounding defects in an otherwise homogenous granular crystal was discussed. The transient interaction of traveling solitary waves with defects was also explored. Neither of these cases involved a high-amplitude continuous driving force nor damping. Studying cases with damping and continuous driving is useful for both real-world applications and devices, and involves interesting new phenomena.

In 2011, Boechler et al. [60] studied experimentally and computationally the case of a 1D statically compressed granular crystal that contains a light-mass defect close to one end, and is subject to a harmonic driving force (see left panel of Fig. 7.8). As described in the previous section, a light mass defect will create a localized mode with frequency above the acoustic band of the homogenous part of the granular crystal. Boechler et al. selected the frequency of the driving force to be close to the defect mode frequency. Because the driving force has frequency above the acoustic band of the homogenous granular crystal, the signal cannot propagate through the crystal at that frequency. However, at sufficiently high amplitudes, and only from the boundary that is close to the defect, a jump phenomenon occurs from periodic to quasiperiodic and then chaotic states, where the energy of the driver is redistributed to different frequencies that can transmit through the system. This example illustrates how the combination of nonlinearity, periodicity, driving, and asymmetric disorder can create new material and device capabilities. In this case, this combination allowed energy to propagate predominantly in one direction.

Fig. 7.8

(Left) Schematic diagram of a 1D granular crystal designed for acoustic rectification and switching. (Right) Bifurcation diagram. Right panel reproduced from [60] with permission from the publisher

To understand the nature of the bifurcations, and the jump to the quasiperiodic and chaotic states that allowed the asymmetric acoustic energy transmission, Boechler et al. conducted parametric continuation using the Newton-Raphson (NR) method in phase space [33] and numerical integration of the fully nonlinear equations of motion that describe the granular crystal. Dissipation was taken into account by using linear damping (see more about dissipative effects in the next section). Applying NR, they followed the periodic family of solutions of the driven system as a function of driving amplitude and studied its linear stability. Right panel of Fig. 7.8 shows the maximum dynamic force amplitude (four particles from the actuator) for each solution as a function of the driving amplitude. The stable (unstable) periodic solutions are denoted with solid blue (dashed black) lines. At turning points 1,2, stable and unstable periodic solutions collide and mutually annihilate (saddle-center bifurcation [40]). At points 3,4, the periodic solution changes stability and a new two-frequency stable quasiperiodic state emerges (Naimark-Sacker bifurcation [38]). Following this bifurcation picture, they observed in their experimental setup and numerical simulations that with increasing amplitude, a progression of the system response that followed the low-amplitude stable periodic solution up to point 1, where the system jumps past the unstable periodic solution to the high-amplitude stable quasiperiodic state. Further increase of the driver’s amplitude led to a continued cascade of double period bifurcations and resulted in the merging of distinct frequency peaks, the formation of continuous bands, and chaotic dynamics. As the quasiperiodic and chaotic states redistribute energy from the driver to frequencies within the transmitting band, it is the existence of these states which enables the previously described acoustic rectification.

7.6 Dissipative Granular Crystals

Most of the studies to date involving granular crystals ignore dissipative effects. However, it is clear from the experiments that in many settings dissipation is strong and should be included. The sources of dissipation in granular crystals are many, including friction, plasticity, viscoelasticity, and viscous drag, among others. In the past few years there have been a number of analytical and numerical studies that have introduced dissipative terms into the equations of motion.

In [112], the authors studied the effects of two dissipative mechanisms on pulse propagation in nonlinear chains. The first was an intrinsic mechanism—an incomplete restitution mechanism that resulted in partial trapping of the impulse energy in the internal modes of the grain. The second mechanism was extrinsic—a velocity-dependent friction $f = - \gamma {\dot{u}_i}$. In both cases, they showed that the decay of the energy was well approximated by an exponential function. The attenuation of traveling pulses in 1D unloaded granular crystals due to on-site linear damping $f = - \gamma {\dot{u}_i}$ was also analyzed in [113]. They found an overall exponential decay of the energy, which depends on the exponent of the interaction potential, and causes the pulse to slow down as it propagates. They also showed that the shape and the width of the pulse remained unchanged.

Job and his collaborators studied the interaction of a solitary wave with boundaries in a 1D granular crystal, considering two dissipative mechanisms: internal viscoelasticity and solid friction of the beads due to their weight on the track aligning the granular crystal [114]. Viscoelastic dissipation was taken into account by considering a dissipative force at the contact of the two beads in the form $f = \eta A{\partial_t}([{u_{{i - 1}}} - {u_i}]_{ + }^{{3/2}})$[114], where $\eta$ includes unknown coefficients due to internal friction of the material. Solid friction was included by considering a force $f = \mu mg$. These dissipative terms were also shown to produce broader solitary waves.

In [115] viscous dissipation, depending on the relative velocity between neighboring particles, was included in the model as $f = p(\mathop{{{{\dot{u}}_{{i - 1}}}}}\limits - 2\mathop{{{{\dot{u}}_i}}}\limits + \mathop{{{{\dot{u}}_{{i + 1}}}}}\limits )$, where $p$ is the viscosity coefficient. The authors investigated its influence on the shape of a steady shock wave. Using this type of viscous dissipation, in [116], they solved the following system of nondimensional equations:

$$ {\ddot{u}_i} = [p({\dot{u}_{{i + 1}}} - {\dot{u}_i}) - {({u_i} - {u_{{i + 1}}})^n}]\theta ({u_i} - {u_{{i + 1}}}){ } - [p({\dot{u}_{{i - 1}}} - {\dot{u}_i}) + {({u_{{i - 1}}} - {u_i})^n}]\theta ({u_{{i - 1}}} - {u_i}), $$

where θ is the Heaviside function. They found that the inclusion of this relative velocity-dependent viscous damping may yield interesting effects such as the creation of secondary pulses. A different approach was presented in [117], where the authors provided a quantitative characterization of dissipative effects for solitary wave propagation in 1D granular crystals. They incorporated a phenomenological nonlinear dissipation that depends on the particle’s relative velocities. By using optimization schemes and experiments, they calculated a common dissipation exponent with a material-dependent prefactor.

Most of the above studies concern the attenuation of propagating pulses generated by an impulsive excitation. Recent experiments in 1D compressed granular crystals, subjected to continuous harmonic driving at one end, also revealed a strong attenuation of the signal [60]. To account for the dissipation in these experimental settings, a linear on-site damping term $f = - \gamma {\dot{u}_i}$ with a damping coefficient $\gamma$ was selected to match the experimental results.

7.7 Two-Dimensional Granular Crystals

Given the richness of the nonlinear dynamic phenomena found in one-dimensional systems, higher dimensional nonlinear systems are expected to present a plethora of new dynamic effects. For example, two- and three-dimensional nonlinear systems are expected to present additional families of wave modes not realizable in the 1D case; new types of solitary waves propagating in the axial and lateral directions (particularly interesting for wave energy redirection and wave guiding); complex nonlinear resonance interactions occurring between spatially extended modes and localized waves; and enhanced possibilities for acoustic wave energy localization and trapping across spatial or temporal scales.

The dynamic properties of 2D granular crystals have only been partially characterized. In particular, experimental efforts are few, although such systems are expected to present a variety of novel dynamic phenomena. Several authors have previously proposed models to characterize the dynamic response of two-dimensional, ordered granular media. For example, [118] described a model for a square lattice of elastically interacting particles, which included relative particle rotation. Tournat et al. [119] proposed a theoretical model to describe out-of-plane elastic waves in a monolayer granular membrane consisting of a hexagonal lattice of particles. Their model was the first one to include shear and bending rigidity at the contact between particles, and to calculate dispersion relations that accounted for these effects.

The simplest example of a highly nonlinear 2D granular crystal consists of a uniform, uncompressed square packing of elastic particles in contact with each other. When this system is excited on one side by a uniform, planar waveform, its response is expected to be quasi-one-dimensional [14] and the response of the system can be characterized by a “curtain solution” derived similarly to (7.10). The first experimental characterization of the dynamic behavior of a square packing of particles was provided in [84], using photoelastic elliptical disks, excited by an explosive charge. The same study characterized the stress wave propagation in arrays of elliptical disks of various geometrical packings, and concluded that it is the contact normals and the vector-connecting particles’ centers of mass that primarily influence wave propagation characteristics such as load transfer path and load attenuation. Discrete element numerical models (DEM) were also used to analyze the dynamics of similar systems [120].

The formation and propagation of solitary waves in 2D square granular crystals was reported and studied quantitatively for the first time by Leonard et al. [121] using triaxial accelerometers embedded within selected particles in the crystals. A larger number of studies also explored the dynamic behavior of hexagonal packing under different (near-linear to highly nonlinear) loading conditions [84, 120, 122–128].One of the major difficulties in the experimental realization of acoustic materials based on two-dimensional nonlinear granular lattices is the sensitivity of such systems to the presence of variation in the particles’ geometry. In the ideal configuration, all particles have an equal number of contacts and equal equilibrium forces. The presence of small defects in experiments, however, can lead to the loss of contact between particles or to the local compression in the surrounding particles. Such loss of contacts or local compression ultimately results in a disordered energy transfer between the particles. A few past works studied the effects of imperfections in two-dimensional granular crystals and their role in the stress wave propagation [122–125, 129]. While Hertzian behavior predicts a 1/6 power-law between maximum force and wave speed [47], it was found that the presence of defects tends to increase the wave propagation speed to a 1/4 power law relationship, effectively inducing deviations from the theoretical Hertzian behavior. This deviation from Hertzian behavior was observed only for granular crystals with low precompression. Increasing the precompression applied on hexagonal arrays was seen to cause a transition to a fully Hertzian behavior [122–125]. More recently, Leonard et al. experimentally characterized the dynamic response of regular 2D square granular crystals, and showed that variation in the packing geometry/composition (Fig. 7.9, left) can dramatically vary the directionality of wave propagation [130].

Fig. 7.9

(Left) Dynamic response of two-dimensional granular crystals formed by square-centered packings of different material cylinders and spheres (see inset). Variation of the materials configuration leads to dramatic changes of the wave propagation front, as shown from experiments and numerical simulations [130]. (Right) Design concept of a tunable, nonlinear acoustic lens obtained with a two-dimensional array of particle chains. The formation of the focal spot (i.e., the “sound bullet”) is evident on the host medium on the right [59]. Images reproduced from [130] and [59]

Two-dimensional arrays of particles have also been shown to form tunable acoustic lenses (Fig. 7.9, right) that support the formation of concentrated acoustic pulses at the focal point (“sound bullets”, [59]). The ability to redirect nonlinear acoustic pulses in two-dimensional systems has also been studied by looking at pulse splitting and recombination in y-shaped granular networks [131–133]. These works showed theoretically, numerically, and experimentally the ability to bend and split incident pulses, and redirect mechanical energy as a function of the branch geometry.

Additional work on the dynamic behavior of ordered two-dimensional granular crystals is needed to fully understand the dynamic response of such systems, and to characterize how nonlinear wave formation and propagation depends on the underlying particle arrangement. Variations of the excitation type (impulsive or harmonic forcing) are expected to lead to the discovery of interesting new acoustic/dynamic phenomena including wave guiding, trapping, filtering, and localized breathing modes.

7.8 Future Directions and Conclusions

The preceding chapters of this book have demonstrated how structural periodicity can be utilized to create new materials with unprecedented physical properties. In such materials the individual building blocks are assembled in carefully designed structures, where by working together, they cause the bulk material to present properties greater than those of the individual components. This general concept of obtaining “materials by design” is not new, and has been a long-term quest for chemists and material scientists alike. For instance, chemists have long been trying to engineer crystals and molecules by arranging atoms in specific lattices and geometries, to obtain a specific bulk property. However, by extending this concept past molecules and crystal grains, to specially designed structural building blocks—from the nano to macroscales—a whole new field of possibilities is enabled.

One of the main benefits of such designed materials is that they enable new technological capabilities. New materials with multifunctional properties can be designed, which have both structural and dynamic functionalities. Perhaps more importantly, by creating materials with previously unseen properties, new devices and applications are enabled. Furthermore, as such materials are “designed” by construction, and they can be easily tailored for use in specifically targeted applications.

The range of possible bulk responses from such designed materials depends in part on the complexity of the interaction between the fundamental building blocks. As described in the previous chapters, the design of these periodic structures has historically been based on linear interactions. The presence of nonlinearity in these systems gives added advantages through complexity. This chapter predominately focused on nonlinear dynamic phenomena in granular crystal systems, where the nonlinearity was caused by the geometric inter-particle interactions between elastic particles. As was described, nonlinear dynamics enables the existence of new useful dynamic phenomena and coherent structures. This includes solitary waves, discrete breathers, bifurcations, quasiperiodicity, and chaos, among others. Nonlinearity also enables a dramatic tunability of the material responses, by providing an unprecedented sensitivity to variations of materials and external parameters. However, because of the inherent complexity of nonlinear systems, which enables such useful phenomena, analyzing and predicting the behavior of such systems is also more difficult. In the future, the development of new predictive theoretical and computational tools will be necessary to further guide the development, design, and testing of nonlinear periodic phononic structures.

Some particular future areas of interest, with respect to the study of nonlinear periodic phononic structures, include, but are not limited to the following. As nonlinearity has been applied to spring-mass-like systems, in granular crystals, nonlinearity could also further be applied to the study of nonlinear metamaterials, nonlinear resonant structures, or phononic crystals with nonlinearly elastic components. The study of hybrid linear-nonlinear systems, could lead to the observation of new dynamic phenomena such as the amplitude-dependent filtering of acoustic signals [134].

New material systems where nonlinear material responses interplay with active building blocks or other multi-physical effects is another area that could lead to the discovery of unprecedented material responses. The ability to couple multi-physical effects in periodic structures can also lead to the creation of tunable multifunctional and energy-harvesting devices, such as opto-mechanical sensors [135], or phoXonic systems [136]. For example, the generation of nonlinear modes in nonlinear acoustic crystals could be used as a mechanism for frequency conversion, or the presence of nonlinear localized modes could be exploited for energy localization and harvesting.

Because of the similarity of acoustic and elastic wave propagation to phonon propagation, the effects studied here could also be extended to smaller scales involving heat propagation. For instance, as described in this chapter for acoustics, nonlinear periodic structures have been utilized to create tunable rectifiers based on the onset of bifurcation instabilities. This type of device could provide new ways to control the flow of acoustic energy, enable acoustic logic devices, and be used in novel energy-harvesting systems [60]. However, these same ideas could be scaled down to create new ways to control heat propagation, and enable materials with direction-dependent thermal conductivities or thermal logic devices.

Furthermore, the newly explored phenomena, which occur in granular crystals and other nonlinear periodic phononic structures, should be further explored for their potential in engineering applications. The ability to engineer the dispersion relation through nonlinearities could be implemented in tunable vibration filtering devices and in noise and vibration-insulating systems. Compact solitary waves with robust properties and large amplitudes could find use in biomedical devices with improved resolution and signal-to-noise ratio [59], or in the nondestructive evaluation of materials [58].

The study of nonlinearity in engineered materials like phononic crystals and metamaterials is still at an early stage of development. By understanding the fundamental properties of nonlinear acoustic crystals, nonlinear phononic systems, and nonlinear resonant structures, new physical phenomena can be discovered and lead to a new ability to design and implement materials and devices.