Abstract
A minimal model for the associative algebra A is a quasi-free resolution (T(W),d) such that the differential map d maps W into ⊕
n≥2
W
⊗n. We would like to find a method to construct this minimal model when A is quadratic, that is A=T(V)/(R) where the ideal (R) is generated by R⊂V
⊗2. We will see that the quadratic data (V,R) permits us to construct explicitly a coalgebra  and a twisting morphism
and a twisting morphism  . Then, applying the theory of Koszul morphisms given in the previous chapter, we obtain a simple condition which ensures that the cobar construction on the Koszul dual coalgebra, that is
. Then, applying the theory of Koszul morphisms given in the previous chapter, we obtain a simple condition which ensures that the cobar construction on the Koszul dual coalgebra, that is  , is the minimal model of A.
, is the minimal model of A.
The quadratic hypothesis R⊂V ⊗2 can be weakened by only requiring R⊂V ⊗2⊕V. In this case, we say that the algebra is inhomogeneous quadratic. We show how to modify the preceding method to handle the inhomogeneous quadratic case. Two examples are: the universal enveloping algebra \(U(\mathfrak{g})\) of a Lie algebra \(\mathfrak{g}\) (original example due to J.-L. Koszul) and the Steenrod algebra.
In the process of its internal development and prompted by its inner logic, mathematics, too, creates virtual worlds of great complexity and internal beauty which defy any attempt to describe them in natural language but challenge the imagination of a handful of professionals in many successive generations.
Yuri I. Manin in “Mathematics as metaphor”
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
A minimal model for the associative algebra A is a quasi-free resolution (T(W),d) such that the differential map d maps W into ⊕
n≥2
W
⊗n. We would like to find a method to construct this minimal model when A is quadratic, that is A=T(V)/(R) where the ideal (R) is generated by R⊂V
⊗2 (this is the quadratic hypothesis). We will see that the quadratic data (V,R) permits us to construct explicitly a coalgebra  and a twisting morphism
and a twisting morphism  . Then, applying the theory of Koszul morphisms given in the previous chapter, we obtain a simple condition which ensures that the cobar construction on the Koszul dual coalgebra, that is
. Then, applying the theory of Koszul morphisms given in the previous chapter, we obtain a simple condition which ensures that the cobar construction on the Koszul dual coalgebra, that is  , is the minimal model of A.
, is the minimal model of A.
If one tries to construct by hand the space W, then one is led to take W=V⊕R⊕(R⊗V∩V⊗R)⊕⋯. In fact, \(\mathbb{K}\oplus V\oplus R\oplus (R\otimes V \cap V\otimes R) \) is the beginning of a certain sub-coalgebra of the cofree coalgebra over V, which is uniquely determined by V and R. This is precisely the expected coalgebra  , up to suspension. The twisting morphism κ is simply the composite
, up to suspension. The twisting morphism κ is simply the composite  . The expected condition is the acyclicity of the Koszul complex
. The expected condition is the acyclicity of the Koszul complex  . This is the Koszul duality theory for homogeneous quadratic algebras as introduced by Stewart Priddy in [Pri70]. In practice it is easier to work with algebras instead of coalgebras. When V is finite dimensional we consider the “graded linear dual” of
. This is the Koszul duality theory for homogeneous quadratic algebras as introduced by Stewart Priddy in [Pri70]. In practice it is easier to work with algebras instead of coalgebras. When V is finite dimensional we consider the “graded linear dual” of  which is, up to suspension, a quadratic algebra A
!, usually called the Koszul dual algebra of A.
which is, up to suspension, a quadratic algebra A
!, usually called the Koszul dual algebra of A.
The quadratic hypothesis R⊂V ⊗2 can be weakened by only requiring R⊂V ⊗2⊕V. In this case, we say that the algebra is inhomogeneous quadratic. We show how to modify the preceding method to handle the inhomogeneous quadratic case, also done in [Pri70]. Two examples are: the universal enveloping algebra \(U(\mathfrak{g})\) of a Lie algebra \(\mathfrak{g}\) (original example due to J.-L. Koszul) and the Steenrod algebra. Inhomogeneous Koszul duality theory gives a proof of a general Poincaré–Birkhoff–Witt theorem, which, applied to \(U(\mathfrak{g})\), gives the classical one.
In our treatment of Koszul duality of associative algebras, we keep algebras and coalgebras on the same footing. Working with coalgebras allows us to avoid the finite dimensional hypothesis. Moreover we give conceptual proofs so that they can be generalized to other monoidal categories. Our interest for Koszul duality of associative algebras is to serve as a paradigm for Koszul duality of algebraic operads.
Koszul algebras have applications in many fields of mathematics, which will not be discussed at all here (see the introduction of [PP05]). Classical references on Koszul duality of associative algebras include: S. Priddy [Pri70], Yu.I. Manin [Man87, Man88], R. Fröberg [Frö99], A. Polishchuk and L. Positselski [PP05].
3.1 Quadratic Data, Quadratic Algebra, Quadratic Coalgebra
We start with a quadratic data (V,R) to which we associate an algebra and a coalgebra

In this chapter we suppose that \(\mathbb{K}\) is a field, though most of the definitions and constructions are valid over a commutative ring.
3.1.1 Quadratic Data
By definition a quadratic data (V,R) is a graded vector space V and a graded subspace R⊆V⊗V. A morphism of quadratic data f:(V,R)→(W,S) is a graded linear map f:V→W such that (f⊗f)(R)⊆S.
3.1.2 Quadratic Algebra
The quadratic algebra A(V,R):=T(V)/(R) is, by definition, the quotient of the free associative algebra over V by the two-sided ideal (R) generated by R⊆V ⊗2. In other words, A(V,R) is the quotient of T(V) which is universal among the quotient algebras A of T(V) such that the composite
is 0. It means that, for any such algebra A, there is a unique algebra morphism A(V,R)→A which makes the following diagram commutative:

Since (R) is a homogeneous ideal, it follows that A(V,R) is graded and augmented. This degree is called the weight and denoted as a superscript in parentheses. Explicitly it is given by:
Any basis of V is called a set of generators of A. Any basis {r i } of R determines a set of relations r i =0 in A. By abuse of terminology r i , which should be called a relator, is often called a relation.
A morphism of quadratic data, f:(V,R)→(W,S) induces a natural morphism of weight graded algebras A(V,R)→A(W,S). Any morphism of algebras which respects the weight grading is of this form. But it is not the case for every morphism of algebras.
3.1.3 Quadratic Coalgebra
The quadratic coalgebra C(V,R) is, by definition, the sub-coalgebra of the cofree coassociative coalgebra T c(V) which is universal among the sub-coalgebras C of T c(V) such that the composite
is 0. It means that, for any such coalgebra C, there is a unique coalgebra morphism C→C(V,R) which makes the following diagram commutative:

The coalgebra C(V,R) is weight graded. Explicitly it is given by:
Observe that the restriction of the coproduct of C (that is the deconcatenation) to the weight 2 component C (2)=R is given by
We will say that C(V,R) is cogenerated by V with corelations R in T c(V). Observe that the coalgebra C(V,R) is conilpotent, cf. Sect. 1.2.4.
A morphism of quadratic data, f:(V,R)→(W,S) induces a natural morphism of weight graded coalgebras C(V,R)→C(W,S). Any morphism of coalgebras which respects the weight grading is of this form. But it is not the case for every morphism of coalgebras.
3.1.4 The Graded Framework
Both constructions A(V,R) and C(V,R) can be extended to the category of graded vector spaces. In this framework, V is a graded module and R is a graded sub-module of the graded module V ⊗2. Then the algebra A(V,R), resp. the coalgebra C(V,R), is bigraded by degree and weight (cf. Sect. 1.5.1). Both A(V,R) and C(V,R) are connected weight graded in the sense of Sect. 1.5.10, with trivial differential.
3.2 Koszul Dual of a Quadratic Algebra
We construct the Koszul dual coalgebra and the Koszul dual algebra of a quadratic algebra. We work here in the homogeneous framework. The inhomogeneous framework, where it is only supposed that R⊂V⊕V ⊗2, is treated in Sect. 3.6.
3.2.1 Koszul Dual Coalgebra of a Quadratic Algebra
Let (V,R) be a graded quadratic data. By definition the Koszul dual coalgebra of the quadratic algebra A(V,R) is the coalgebra
where s
2
R is the image of R in (sV)⊗2 under the map V
⊗2→(sV)⊗2, vw↦svsw. The upside down exclamation point  (left exclamation point in the Spanish language) is usually pronounced “anti-shriek”. If V is a graded space concentrated in degree 0, then sV is concentrated in degree 1. Observe that C(sV,s
2
R) is equal to C(V,R) as a coalgebra. The decoration “s” is modifying the degree of the objects. It plays a role when we apply the Koszul sign rule to morphisms. We can omit it in the notation at the expense of changing the signs of the maps accordingly.
(left exclamation point in the Spanish language) is usually pronounced “anti-shriek”. If V is a graded space concentrated in degree 0, then sV is concentrated in degree 1. Observe that C(sV,s
2
R) is equal to C(V,R) as a coalgebra. The decoration “s” is modifying the degree of the objects. It plays a role when we apply the Koszul sign rule to morphisms. We can omit it in the notation at the expense of changing the signs of the maps accordingly.
3.2.2 Koszul Dual Algebra of a Quadratic Algebra
The algebra obtained as the linear dual of the coalgebra  carries a desuspension sign. In the literature, one sometimes finds its unsuspended analog, denoted by A
! and called the Koszul dual algebra of the quadratic algebra
A. Explicitly it is defined by
carries a desuspension sign. In the literature, one sometimes finds its unsuspended analog, denoted by A
! and called the Koszul dual algebra of the quadratic algebra
A. Explicitly it is defined by
and carries the obvious associative algebra structure.
Dualizing linearly the exact sequence
provides the exact sequence
In other words the orthogonal space R ⊥ is defined as the image of (V ⊗2/R)∗ in (V ∗)⊗2 under the isomorphism (V ⊗2)∗≅V ∗⊗V ∗, cf. Sect. 1.2.2.
Proposition 3.2.1.
The Koszul dual algebra A ! admits the following quadratic presentation
Proof.
First notice that the linear dual of the quadratic coalgebra A
¡=C(sV,s
2
R) is the quadratic algebra  . The last step can be proved either directly or by using the notion of Manin products of Sect. 4.5.1: the Koszul dual algebra is equal to
. The last step can be proved either directly or by using the notion of Manin products of Sect. 4.5.1: the Koszul dual algebra is equal to  . □
. □
3.2.3 Koszul Dual Algebra of a Coalgebra
It is also useful to introduce the Koszul dual algebra of a quadratic coalgebra
It follows immediately that
As an immediate consequence we have, under finite dimensionality assumption:
Observe that the coalgebra A ¡ is well-defined even in the graded framework and without any finiteness hypothesis.
3.2.4 Examples
-
1.
Let V be a finite dimensional vector space and let R=0. Then we have A=T(V). Its Koszul dual algebra is the algebra of dual numbers \(A^{!}=D(V^{*}):= \mathbb{K}1\oplus V^{*}\), with trivial multiplication.
-
2.
The symmetric algebra S(V) is the quadratic algebra T(V)/(R), where the space of relations R is the subvector space of V ⊗2 spanned by the elements x⊗y−y⊗x for x,y∈V. The coalgebra Λ c(sV) is the subcoalgebra of T c(sV) satisfying the universal property of Sect. 3.1.3 with the subspace s 2 R=〈sx⊗sy−sy⊗sx|x,y∈V〉. Therefore, its component of weight n is equal to
$$\varLambda^c(sV)^{(n)}= \biggl\langle \sum_{\sigma \in \mathbb{S}_n} \operatorname{sgn}(\sigma) s^n x_{\sigma(1)}\otimes \cdots \otimes x_{\sigma(n)}\Bigm| x_1, \ldots, x_n \in V \biggr\rangle.$$The coalgebra structure is given by the deconcatenation coproduct and is cocommutative. When V is an n-dimensional vector space with basis {x 1,…,x n } in degree 0, one gets the polynomial algebra \(S(V) = \mathbb{K}[x_{1}, \ldots, x_{n}]\). In this case, its Koszul dual algebra is the exterior algebra S(V)!=Λ(V ∗), since R ⊥ is spanned by the elements \(x_{i}^{*}x_{j}^{*}+x_{j}^{*}x_{i}^{*}\), where \(\lbrace x_{1}^{*}, \ldots , x_{n}^{*}\rbrace\) is the dual basis.
-
3.
We refer to [Pri70, Man87, Man88, Frö99, PP05] for many more examples.
3.3 Bar and Cobar Construction on a Quadratic Data
We make explicit the dga coalgebra BA and the dga algebra ΩC in the quadratic case. The Koszul dual objects are shown to be equal to the syzygy degree 0 homology group in both cases.
3.3.1 Bar Construction on a Quadratic Algebra
The bar construction \(\mathrm{B}A:= T^{c}(s\bar{A})\) over the quadratic dga algebra A=A(V,R) (whose differential is trivial) is equipped with a homological degree and a weight grading. We now introduce the syzygy degree.
The weight grading on BA is defined by the sum of the weight of each element: ω(sa 1,…,sa k ):=ω(a 1)+⋯+ω(a k ). Since A is a connected wgda algebra, the augmentation ideal \(\bar{A}\) is concentrated in weight grading ≥1. We define another degree on \(\bar{A}\) by the weight grading of A minus 1. It induces a new nonnegative degree on the bar construction, called the syzygy degree which is equal to ω(a 1)+⋯+ω(a k )−k. The component of syzygy degree d of BA is denoted by Bd A, whereas the homological degree r component is denoted by (BA) r .
Since A has trivial internal differential, the differential on BA reduces to d 2, which raises the syzygy degree by 1 and preserves the weight grading. So it forms a cochain complex with respect to the syzygy degree, which splits with respect to the weight grading. Hence the associated cohomology groups will be bigraded, by the syzygy degree and by the weight grading.
The following diagram depicts this decomposition. The syzygy degree is indicated on the last row, so we delete the notation s for simplicity. We write \(\bar{A}= V \oplus V^{2}/R \oplus V^{3}/(RV+VR)\oplus \cdots \) for more clarity, the tensor product notation being reserved for the one in BA only.

On the weight (3) row the map from V⊗V⊗V is
where [−] denotes the class in the quotient. The other map on this row is
From this description we see immediately that the syzygy degree 0 column forms the cofree coalgebra T c(sV). Hence the Koszul dual coalgebra \(A^{\textrm{!`}}= \mathbb{K}\oplus sV\oplus s^{2}R\oplus \cdots \) is a subspace of this column.
Let  and \(\bar{\Delta }(x)=\sum x_{(1)}\otimes x_{(2)}\). The boundary map of
and \(\bar{\Delta }(x)=\sum x_{(1)}\otimes x_{(2)}\). The boundary map of  is given explicitly by the formula
is given explicitly by the formula
The next proposition shows that  is equal to the kernel of the boundary map.
is equal to the kernel of the boundary map.
Proposition 3.3.1.
Let (V,R) be a quadratic data, A=A(V,R) the quadratic algebra and
 its Koszul dual coalgebra. The natural coalgebra inclusion
its Koszul dual coalgebra. The natural coalgebra inclusion
 induces an isomorphism of graded coalgebras:
induces an isomorphism of graded coalgebras:
Proof.
We claim that, for each n, the inclusion  is exactly the kernel of the horizontal differential, that is H
0(B•
A)(n). It is obvious for n=0 and n=1. For n=2 the boundary map in (BA)(2) is the quotient map V
⊗2→V
⊗2/R, hence its kernel is R. More generally, since the boundary map is a derivation, it is given in degree 0 by the sum of the maps (sV)⊗n→(sV)⊗i⊗sV
⊗2/R⊗(sV)⊗j. So the kernel is
is exactly the kernel of the horizontal differential, that is H
0(B•
A)(n). It is obvious for n=0 and n=1. For n=2 the boundary map in (BA)(2) is the quotient map V
⊗2→V
⊗2/R, hence its kernel is R. More generally, since the boundary map is a derivation, it is given in degree 0 by the sum of the maps (sV)⊗n→(sV)⊗i⊗sV
⊗2/R⊗(sV)⊗j. So the kernel is
□
3.3.2 Cobar Construction on a Quadratic Coalgebra
Like the bar construction, the cobar construction  over the quadratic dga coalgebra C=C(V,R) (whose differential is trivial) has several gradings.
over the quadratic dga coalgebra C=C(V,R) (whose differential is trivial) has several gradings.
We introduce the same definitions as for the bar construction. We consider the weight grading (ΩC)(n), which is the sum of the weights of the elements of  . The syzygy degree of ΩC is induced by the weight of elements of
. The syzygy degree of ΩC is induced by the weight of elements of  minus 1 in the same way. We denote it by Ω
d
C.
minus 1 in the same way. We denote it by Ω
d
C.
Since the internal differential of the coalgebra C is trivial, the differential of the cobar construction ΩC reduces to d 2, which lowers the syzygy degree by 1. Hence, (Ω• C,d 2) becomes a chain complex. Since the differential d 2 preserves the weight of the elements of C, this chain complex splits with respect to the weight: it is isomorphic to the following direct sum of sub-chain complexes ΩC≅⨁ n≥0(ΩC)(n).
The diagram below represents this weight decomposition. The syzygy degree is indicated on the last row, so we delete the notation s −1 for simplicity.

In degrees 0 and 1, the maps R→V ⊗2 and (V⊗R)⊕(R⊗V)→V ⊗3 are simply the inclusions. The map VR∩RV→(V⊗R)⊕(R⊗V) is inc1−inc2 where inc1, resp. inc2 is the inclusion of the first, resp. second, summand. From this description we see immediately that the syzygy degree 0 column forms the free algebra T(s −1 V) and that the algebra
is a quotient of it.
Proposition 3.3.2.
Let
C=C(V,R) be the quadratic coalgebra associated to the quadratic data (V,R), and let
 be its Koszul dual algebra. The natural algebra projection
be its Koszul dual algebra. The natural algebra projection
 induces an isomorphism of graded algebras:
induces an isomorphism of graded algebras:
Proof.
The proof is analogous to the proof of Proposition 3.3.1. □
3.4 Koszul Algebras
For any quadratic data, we define a twisting morphism from the Koszul dual coalgebra to the quadratic algebra. This gives a twisted tensor product, called the Koszul complex, which plays a central role in the Koszul duality theory. We state and prove the main theorem of this chapter which says that the Koszul complex is acyclic if and only if the cobar construction over the Koszul dual coalgebra gives the minimal model of the algebra. The other definitions of a Koszul algebra appearing in the literature are given and we conclude with examples.
3.4.1 The Koszul Complex of a Quadratic Data
Starting with a quadratic data (V,R) we define κ:C(sV,s 2 R)→A(V,R) as the linear map of degree −1 which is 0 everywhere except on V where it identifies sV to V:
Observe that the shift s in the definition of  makes κ a degree −1 map. The following result shows that κ is a twisting morphism.
makes κ a degree −1 map. The following result shows that κ is a twisting morphism.
Lemma 3.4.1.
We have
κ⋆κ=0, and therefore
 .
.
Proof.
Since κ is 0 almost everywhere, the convolution product κ⋆κ is 0 except maybe on V ⊗2. Computing κ⋆κ explicitly on V ⊗2 we find that it is equal to the composite
hence it is 0 as expected.
So the map κ is a twisting morphism by Sect. 2.1.2. □
Proposition 3.4.2.
The twisting morphism κ:C(sV,s 2 R)↠V↣A(V,R) induces a map d κ which makes
(respectively A⊗ κ A ¡) into a weight graded chain complex.
Proof.
The differential d κ was constructed out of κ in Sect. 1.6.1. It is a differential by Lemmas 3.4.1 and 1.6.2. Since κ has degree −1 and weight 0, it is the same for the differential d κ . Hence this chain complex splits with respects to the total weight. □
The chain complex  (resp.
(resp.  ) is called the Koszul complex, or left Koszul complex (resp. right Koszul complex) of the quadratic algebra A(V,R). Its summand
) is called the Koszul complex, or left Koszul complex (resp. right Koszul complex) of the quadratic algebra A(V,R). Its summand  of weight (n) is equal to:
of weight (n) is equal to:
3.4.2 Koszul Criterion
In this section, we derive the main theorem of Koszul duality theory for associative algebras from the preceding chapter.
Proposition 3.4.3.
The maps corresponding to the twisting morphism
 under the isomorphisms of Theorem 2.2.6 are exactly
under the isomorphisms of Theorem 2.2.6 are exactly
 and
and
 .
.
Proof.
By direct inspection. □
Theorem 3.4.4
(Koszul criterion).
Let (V,R) be a quadratic data. Let
A:=A(V,R) be the associated quadratic algebra and let
 be the associated quadratic coalgebra. Then the following assertions are equivalent:
be the associated quadratic coalgebra. Then the following assertions are equivalent:
-
1.
the right Koszul complex
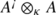 is acyclic,
is acyclic, -
2.
the left Koszul complex
 is acyclic,
is acyclic, -
3.
the inclusion
 is a quasi-isomorphism,
is a quasi-isomorphism, -
4.
the projection
 is a quasi-isomorphism.
is a quasi-isomorphism.
When these assertions hold, the cobar construction on
 gives a minimal resolution of
A.
gives a minimal resolution of
A.
Proof.
Theorem 2.3.1 can be applied to A:=A(V,R),  and to α=κ since by Lemma 3.4.1 κ is a twisting morphism and since the connectivity and weight grading assumptions are satisfied.
and to α=κ since by Lemma 3.4.1 κ is a twisting morphism and since the connectivity and weight grading assumptions are satisfied.
Let us verify that  is the minimal model of A when the Koszul complex is acyclic. First, the dga algebra
is the minimal model of A when the Koszul complex is acyclic. First, the dga algebra  is free as a graded algebra by construction (but not as a dga algebra). Second, its differential
is free as a graded algebra by construction (but not as a dga algebra). Second, its differential  satisfies the minimal hypothesis d(W)⊂⨁
n≥2
W
⊗n also by construction. Third, by Proposition 3.3.2 we have
satisfies the minimal hypothesis d(W)⊂⨁
n≥2
W
⊗n also by construction. Third, by Proposition 3.3.2 we have  and by (4) the resulting map
and by (4) the resulting map  is a quasi-isomorphism. □
is a quasi-isomorphism. □
Observe that starting with C(V,R) instead of A(V,R) with the following twisting morphism

gives the same result up to a shift of grading. So we get Koszul duality theory for coalgebras.
3.4.3 Definition of a Koszul Algebra
A quadratic data (resp. quadratic algebra, resp. quadratic coalgebra) is said to be Koszul if its Koszul complex is acyclic.
By Theorem 3.4.4 we see that A is Koszul if and only if there is an isomorphism  (resp. H
•(ΩA
!)≅A). By Propositions 3.3.1 and 3.3.2, this is equivalent to the vanishing of the (co)homology groups: H
d(B•
A) and
(resp. H
•(ΩA
!)≅A). By Propositions 3.3.1 and 3.3.2, this is equivalent to the vanishing of the (co)homology groups: H
d(B•
A) and  for d>0. More generally, a connected weight graded algebra A is said to be Koszul if the cohomology H
d(B•
A)=0 of its bar construction is concentrated in syzygy degree d=0. In this case, Exercise 3.8.1 shows that A admits a quadratic presentation. Therefore, there is no restriction to treat only the quadratic case.
for d>0. More generally, a connected weight graded algebra A is said to be Koszul if the cohomology H
d(B•
A)=0 of its bar construction is concentrated in syzygy degree d=0. In this case, Exercise 3.8.1 shows that A admits a quadratic presentation. Therefore, there is no restriction to treat only the quadratic case.
The bar–cobar construction ΩBA is always a resolution of A. To simplify it, one idea is to apply the cobar construction to the homology H
•(BA) rather than to BA. When A is Koszul, the homology of BA is exactly  and one gets the resolution
and one gets the resolution  of A. For any quadratic algebra we have the following commutative diagrams:
of A. For any quadratic algebra we have the following commutative diagrams:

The algebra A is Koszul if and only if all these maps are quasi-isomorphisms by Corollary 2.3.2 and Theorem 3.4.4. Both  and ΩBA are models of A and
and ΩBA are models of A and  is the minimal model.
is the minimal model.
With the aforementioned definitions, a quadratic algebra A is Koszul if and only if its Koszul dual coalgebra  is Koszul. The following proposition states the same property with the Koszul dual algebra.
is Koszul. The following proposition states the same property with the Koszul dual algebra.
Proposition 3.4.5.
Let (V,R) be a finite dimensional quadratic data. The quadratic algebra A=A(V,R) is Koszul if and only if its Koszul dual algebra A !=A(V ∗,R ⊥) is Koszul.
Proof.
The left Koszul complex  associated to the twisting morphism
associated to the twisting morphism  is made up of finite dimensional vector spaces in each degree and weight. Its linear dual is equal to the right Koszul complex
is made up of finite dimensional vector spaces in each degree and weight. Its linear dual is equal to the right Koszul complex  , up to suspension. Therefore one is acyclic if and only if the other one is acyclic and we conclude by Theorem 3.4.4. □
, up to suspension. Therefore one is acyclic if and only if the other one is acyclic and we conclude by Theorem 3.4.4. □
3.4.4 Other Equivalent Definitions
In the literature [Löf86, Frö99], one encounters the following equivalent definitions of a Koszul algebra.
Lemma 3.4.6.
Let A=A(V,R) be a quadratic algebra. It is a Koszul algebra if and only if the homology of its bar construction H •(BA) is a sub-coalgebra of T c(sV).
Proof.
It is a direct consequence of Proposition 3.3.1 and Theorem 3.4.4. □
Let A=A(V,R) be a finitely generated quadratic algebra. Recall that the derived Ext-functor \(\mathrm{Ext}^{\bullet}_{A}(\mathbb{K}, \mathbb{K})\) is defined as the homology \(H_{\bullet}(\operatorname{Hom}_{A}(R, \mathbb{K}))\), where \(R\xrightarrow{\sim} \mathbb{K}\) is any projective resolution of \(\mathbb{K}\) in the category of A-modules. It can be endowed with an associative algebra structure called the Yoneda algebra. Considering the quasi-free resolution \(A\otimes_{\iota} \mathrm{B}A \xrightarrow{\sim} \mathbb{K}\), the Ext-functor can be computed by \(\mathrm{Ext}^{\bullet}_{A}(\mathbb{K}, \mathbb{K})=H_{\bullet}((\mathrm{B}A)^{*})\), where (BA)∗ is the degreewise and weightwise dual of BA. Since it is the homology of the linear dual of a dga coalgebra, the Yoneda algebra structure is easily described.
Proposition 3.4.7.
A finitely generated quadratic algebra A(V,R) is Koszul if and only if its Yoneda algebra \(\mathrm{Ext}^{\bullet}_{A}(\mathbb{K}, \mathbb{K})\) is generated by its weight 1 elements.
Proof.
This proposition is linear dual to the previous lemma. □
Another equivalent definition of a Koszul algebra amounts to saying that the ground field \(\mathbb{K}\) has a “linear minimal graded resolution of \(\mathbb{K}\) with free A-modules”. Such a resolution is provided by the Koszul complex  . For the definitions of these terms and a proof of the equivalence, we refer the reader to [Frö99].
. For the definitions of these terms and a proof of the equivalence, we refer the reader to [Frö99].
3.4.5 Examples
The symmetric algebra S(V) and the exterior coalgebra Λ c(sV) are Koszul dual to each other. The tensor algebra and the dual numbers coalgebra are also Koszul dual to each other. Here are the proofs of the acyclicity of the associated Koszul complexes, which proves that they are Koszul.
Proposition 3.4.8.
The Koszul complex (Λ c(sV)⊗S(V),d κ ) is acyclic.
Proof.
Though this statement is true over ℤ, we will prove it only over a characteristic zero field. We represent any element \(\sum_{\sigma \in \mathbb{S}_{p}} \operatorname{sgn}(\sigma) s^{p} x_{\sigma(1)}\otimes \cdots \otimes x_{\sigma(p)}\) of Λ c(sV)(p) simply by x 1∧⋯∧x p , keeping in mind that \(x_{1}\wedge\cdots\wedge x_{p}=\operatorname{sgn}(\sigma) x_{\sigma(1)}\wedge \cdots \wedge x_{\sigma(p)}\) holds for any \(\sigma \in \mathbb{S}_{p}\), like in the Koszul dual algebra Λ(V ∗). (This identification is nothing but the isomorphism between (Λ c(sV))∗ and Λ(V ∗), up to suspension.)
The boundary map
is given by
Define
by the formula
One checks that \(hd+dh=(p+q)\operatorname{id}\). Since we work in characteristic zero it shows that \(\operatorname{id}\) is homotopic to 0 and therefore the complex is acyclic. □
Proposition 3.4.9.
For any graded vector space V, the Koszul complex \(((\mathbb{K}\oplus V)\otimes T(V), d_{\kappa})\) of the quadratic algebra T(V) is acyclic.
Proof.
Since T(V)=A(V,0), we get R=0 and therefore \(C(V,R)\cong \mathbb{K}\oplus V\), where Δ(1)=1⊗1, Δ(v)=v⊗1+1⊗v.
The boundary map d=d κ of the Koszul complex \((\mathbb{K}\oplus V)\otimes T(V)\) is zero on the component \(\mathbb{K}\otimes T(V)\) and is the identification of V⊗T(V) with \(\mathbb{K}\otimes T(V)^{\geq 1}\) on the other component. Indeed, it is a consequence of the formulas for Δ and of κ(1)=0,κ(v)=v.
So, the homology of the Koszul complex is \(\mathop{\mathrm{Ker}}d / \mathop{\mathrm{Im}}d = T(V)/ T(V)^{\geq 1}= \mathbb{K}\) concentrated in bidegree (0,0). Hence the Koszul complex is acyclic. □
3.5 Generating Series
Let (V,R) be a quadratic data such that V is finite dimensional. The weight-graded algebra A(V,R)=⊕ n≥0 A (n) is such that \(A_{0}=\mathbb{K}1\) and A (n) is finite dimensional. By definition the generating series or Hilbert–Poincaré series of A is
Theorem 3.5.1.
If (V,R) is a finite dimensional quadratic data which is Koszul, then the following identity holds between the generating series of A and A !:
Proof.
The Euler–Poincaré characteristic of the sub-chain complex of weight (n) of the Koszul complex of A is equal to  . By definition, it is equal to the coefficient of x
n of \(f^{A^{!}}(x) f^{A}(-x)\). When the quadratic data (V,R) is Koszul, the Koszul complex is acyclic. It implies that the Euler–Poincaré characteristic is equal to 0, for n>0, and it is equal to 1, for n=0, which concludes the proof. □
. By definition, it is equal to the coefficient of x
n of \(f^{A^{!}}(x) f^{A}(-x)\). When the quadratic data (V,R) is Koszul, the Koszul complex is acyclic. It implies that the Euler–Poincaré characteristic is equal to 0, for n>0, and it is equal to 1, for n=0, which concludes the proof. □
Notice that one can also define the generating series of a quadratic coalgebra. In that case, we have  .
.
Let us apply this theorem to the examples of Sect. 3.4.5. When the dimension of V is equal to k, we have
which satisfy \(f^{\mathbb{K}\oplus V}(x)f^{T(V)}(-x)=1\). In the case of the symmetric algebra, we have
which satisfy \(f^{\varLambda(V^{*})}(x)f^{S(V)}(-x)=1\).
Theorem 3.5.1 provides a method to prove that an algebra is not Koszul. One first computes the Hilbert–Poincaré series f A(x) of the quadratic algebra A and then its inverse series f A(−x)−1. If this last one has at least one strictly negative coefficient, then it cannot be the series associated to a quadratic algebra. Therefore, the algebra A is not a Koszul algebra. (See [PP05, Sect. 2.2] for an example.) For a more exhaustive treatment of generating series, we refer the reader to [PP05, Ufn95].
If a chain complex is acyclic, then its Euler–Poincaré characteristic is equal to zero; but the converse is not true. This motivates us to look for quadratic algebras satisfying the functional equation of Theorem 3.5.1 but which fail to be Koszul. Such examples are given in [Pos95, Roo95, Pio01]. In the next section, we give a necessary and sufficient combinatorial condition for an algebra to be Koszul and in Sect. 4.3 we give a sufficient algebraic condition for an algebra to be Koszul.
3.6 Koszul Duality Theory for Inhomogeneous Quadratic Algebras
In the preceding sections, we dealt with Koszul duality of homogeneous quadratic algebras. In [Pri70] Priddy considered more general objects: inhomogeneous quadratic algebras with quadratic and linear relations. They are algebras whose relators contain not only quadratic terms but also possibly linear terms. The main example is the universal enveloping algebra of a Lie algebra: \(U(\mathfrak{g})=T(\mathfrak{g})/(R)\) where the relator is [x,y]−x⊗y+y⊗x. The purpose of this section is to adapt our treatment of Koszul duality theory to this more general framework. The modification consists in adding a suitable internal differential in the construction of the Koszul dual coalgebra.
There exists an even more general case allowing also constant terms in the space of relations, cf. [PP05].
3.6.1 Quadratic-Linear Algebra
A quadratic-linear data (V,R) is a graded vector space V together with a degree homogeneous subspace
So, there may be linear terms in the space of relations. We still denote by A=A(V,R)=T(V)/(R) the associated quotient. We consider q:T(V)↠V ⊗2 the projection onto the quadratic part of the tensor algebra. The image of R under q, denoted qR, is homogeneous quadratic, so (V,qR) is a quadratic data in the sense of Sect. 3.1. We denote by qA its associated algebra: qA:=A(V,qR). We assume that R satisfies the property
If it is not the case, by removing some elements of V one can choose another presentation of A which does satisfy (ql 1). This condition amounts to the minimality of the space of generators of A. Under this assumption, there exists a map φ:qR→V such that R is the graph of φ:
For instance, if \(A=U(\mathfrak{g})\), then φ(x⊗y−y⊗x)=[x,y] and \(qA=S\mathfrak{g}\). The weight grading on T(V) induces a filtration which is compatible with the ideal (R). Hence the quotient algebra A is filtered by F n A:= Im(⨁ k≤n V ⊗k). The assumption R∩V={0} implies \(\mathrm{F}_{1} A=\mathbb{K}\oplus V\). We denote by \(\operatorname{gr}A\) the graded algebra associated to the filtration of A, \(\operatorname{gr}_{n} A:=\mathrm{F}_{n} A/\mathrm{F}_{n-1} A\). We denote by
the resulting epimorphism. It is obviously an isomorphism in weight 0 and 1, but not necessarily in weight 2. A corollary of the present theory shows that p is an isomorphism provided that qA is Koszul, see Theorem 3.6.4. In the example \(A=U(\mathfrak{g})\) the map \(p:S(\mathfrak{g})\to \operatorname{gr}U(\mathfrak{g})\) is the PBW isomorphism.
3.6.2 Koszul Dual Coalgebra
The map φ permits us to construct the composite map
By Proposition 1.2.2 there exists a unique coderivation,  , which extends this composite.
, which extends this composite.
Lemma 3.6.1.
-
(a)
If {R⊗V+V⊗R}∩V ⊗2⊂qR, then the image of the coderivation \(d_{\tilde{\varphi}}\) lives in
 , thereby defining a coderivation
d
φ
of the coalgebra
, thereby defining a coderivation
d
φ
of the coalgebra
 .
. -
(b)
If the condition
$$(ql_2) : \lbrace R\otimes V + V \otimes R \rbrace \cap V^{\otimes 2} \subset R\cap V^{\otimes 2} $$is satisfied, then the coderivation d φ squares to 0.
Proof.
If {R⊗V+V⊗R}∩V
⊗2⊂qR, then we prove that \(d_{\tilde{\varphi}}(C(sV, s^{2}qR)^{(3)}) \subset C(sV, s^{2} qR)^{(2)}=s^{2}qR\). The proof of the general case is done in the same way with the formula  . Since C(sV,s
2
qR)(3) is equal to s
2
qR⊗sV∩sV⊗s
2
qR, any of its elements can be written Y=∑s
2
X⊗sv=∑sv′⊗s
2
X′, with v,v′∈V and X,X′∈qR. The formula for the unique coderivation on the cofree coalgebra T
c(sV) of Proposition 1.2.2 gives
. Since C(sV,s
2
qR)(3) is equal to s
2
qR⊗sV∩sV⊗s
2
qR, any of its elements can be written Y=∑s
2
X⊗sv=∑sv′⊗s
2
X′, with v,v′∈V and X,X′∈qR. The formula for the unique coderivation on the cofree coalgebra T
c(sV) of Proposition 1.2.2 gives

Hence, forgetting the suspension for simplicity, we have

Since \(\operatorname{ker} \varphi=R\cap V^{\otimes 2}\), we get d
φ
2(C(V,qR)(3))={0} if {R⊗V+V⊗R}∩V
⊗2⊂R∩V
⊗2. Once again, the proof of the general case follows from the same pattern using the explicit formula of the coalgebra  . □
. □
Since R∩V ⊗2⊂qR, condition (ql 2) implies {R⊗V+V⊗R}∩V ⊗2⊂qR. Condition (ql 2) amounts to saying that one cannot create new quadratic relations in R by adding an element to the relations of the presentation.
Let (V,R) be a quadratic-linear data satisfying the conditions (ql 1) and (ql 2). By definition the Koszul dual dga coalgebra of A=A(V,R) is the dga coalgebra
3.6.3 Koszulity in the Inhomogeneous Quadratic Framework
A quadratic-linear data (resp. a quadratic-linear algebra) is said to be Koszul if it satisfies conditions (ql 1), (ql 2) and if the quadratic data (V,qR), or equivalently the quadratic algebra qA, is Koszul in the sense of Sect. 3.4.
Notice that for a homogeneous quadratic data, Koszul in the classical sense is Koszul in this sense. In this case, the conditions (ql 1), (ql 2) are trivially satisfied and the inner coderivation d φ vanishes.
3.6.4 Cobar Construction in the Inhomogeneous Quadratic Framework
Under the hypotheses (ql
1) and (ql
2), we have constructed a conilpotent dga coalgebra  . Applying the cobar construction of Sect. 2.2.2, we get a dga algebra
. Applying the cobar construction of Sect. 2.2.2, we get a dga algebra  , whose differential is of the form d
1+d
2. The internal derivation d
1 is the unique derivation which extends d
φ
. The derivation d
2 is induced by the coalgebra structure of
, whose differential is of the form d
1+d
2. The internal derivation d
1 is the unique derivation which extends d
φ
. The derivation d
2 is induced by the coalgebra structure of  .
.
We consider the same map κ in this context

Lemma 3.6.2.
The map
κ
is a twisting morphism in
 , that is
∂(κ)+κ⋆κ=0.
, that is
∂(κ)+κ⋆κ=0.
Proof.
We refine the proof of Lemma 3.4.1, taking care of the internal differential d
φ
of  . The Maurer–Cartan equation becomes −κ∘d
φ
+κ⋆κ=0. The map −κ∘d
φ
+κ⋆κ is equal to 0 everywhere except on
. The Maurer–Cartan equation becomes −κ∘d
φ
+κ⋆κ=0. The map −κ∘d
φ
+κ⋆κ is equal to 0 everywhere except on  where its image is {−φ(X)+X∣X∈qR}=R, which vanishes in A. □
where its image is {−φ(X)+X∣X∈qR}=R, which vanishes in A. □
The twisting morphism κ induces a morphism of dga algebras  by Theorem 2.2.6.
by Theorem 2.2.6.
Theorem 3.6.3.
Let
A
be an inhomogeneous quadratic Koszul algebra satisfying the conditions (ql
1) and (ql
2). Let
 be its Koszul dual dga coalgebra. The morphism of dga coalgebras
be its Koszul dual dga coalgebra. The morphism of dga coalgebras
 is a quasi-isomorphism.
is a quasi-isomorphism.
Proof.
In this proof, we consider the cobar construction as a chain complex graded by the syzygy degree as in Sect. 3.3.2: both the internal differential d
1 of  induced by d
φ
and the differential d
2 induced by the coproduct of the coalgebra
induced by d
φ
and the differential d
2 induced by the coproduct of the coalgebra  lower the syzygy degree by 1. So we have a well-defined nonnegatively graded chain complex.
lower the syzygy degree by 1. So we have a well-defined nonnegatively graded chain complex.
Since  is a weight graded coalgebra, the underlying module
is a weight graded coalgebra, the underlying module  of the bar construction is weight-graded. We consider the filtration F
r
of
of the bar construction is weight-graded. We consider the filtration F
r
of  defined by its weight: the elements of F
r
are the elements of weight less than r. The two components of the differential map d=d
1+d
2 satisfy
defined by its weight: the elements of F
r
are the elements of weight less than r. The two components of the differential map d=d
1+d
2 satisfy
The filtration F
r
is therefore stable under the boundary map d. Since it is bounded below and exhaustive, the associated spectral sequence \(E^{\bullet}_{rs}\) converges to the homology of  by the classical convergence theorem of spectral sequences [ML95, Proposition 3.2, Chap. 11]. Hence, F
r
induces a filtration F
r
on the homology of
by the classical convergence theorem of spectral sequences [ML95, Proposition 3.2, Chap. 11]. Hence, F
r
induces a filtration F
r
on the homology of  such that
such that

The first term of this spectral sequence is equal to  , which is made up of the elements of syzygy degree equal to r+s and grading equal to (r). The differential map d
0 is given by d
2. Since the algebra qA is Koszul, the spectral sequence is equal to \(E^{1}_{rs}=qA^{(r)}\) at rank 1. More precisely \(E^{1}_{rs}\) is concentrated in the line r+s=0: \(E^{1}_{rs}\cong qA^{(r)}\), for r+s=0 and \(E^{1}_{rs}=0\), for r+s≠0. Therefore, the spectral sequence collapses at rank 1.
, which is made up of the elements of syzygy degree equal to r+s and grading equal to (r). The differential map d
0 is given by d
2. Since the algebra qA is Koszul, the spectral sequence is equal to \(E^{1}_{rs}=qA^{(r)}\) at rank 1. More precisely \(E^{1}_{rs}\) is concentrated in the line r+s=0: \(E^{1}_{rs}\cong qA^{(r)}\), for r+s=0 and \(E^{1}_{rs}=0\), for r+s≠0. Therefore, the spectral sequence collapses at rank 1.
In conclusion, the convergence theorem gives

The result of Proposition 3.3.2 still holds in the inhomogeneous case, that is  , with the syzygy degree. Hence the quotient
, with the syzygy degree. Hence the quotient  is equal to gr
r
A and the morphism
is equal to gr
r
A and the morphism  is a quasi-isomorphism. □
is a quasi-isomorphism. □
Notice that, in the inhomogeneous case, this resolution is not minimal because of the internal differential d 1.
3.6.5 Poincaré–Birkhoff–Witt Theorem
Theorem 3.6.4
(Poincaré–Birkhoff–Witt Theorem).
When a quadratic-linear algebra A is Koszul, then the epimorphism \(p : qA \twoheadrightarrow \operatorname{gr} A\) is an isomorphism of graded algebras
Proof.
This theorem was already proved in the proof of the previous theorem, where the convergence of the spectral sequence gave
□
Another proof of this theorem, based on deformation theory, can be found in [BG96]. Even if the Poincaré–Birkhoff–Witt theorem is a direct consequence of the proof of Proposition 3.6.3, it has the following two nontrivial consequences: Corollary 3.6.5 and Proposition 3.6.6.
Corollary 3.6.5.
Let A(V,R) be an algebra with the quadratic-linear presentation (V,R). If the quadratic algebra qA=A(V,qR) is Koszul, then conditions (ql 1) and (ql 2) are equivalent to conditions
Proof.
Condition (ql 1′) is the generalization of condition (ql 1) from R to (R). Condition (ql 2′) is the generalization of condition (ql 2) from R⊗V+V⊗R to (R). In the other way round, if conditions (ql 1) and (ql 2) are satisfied and if the algebra A(V,R) is Koszul, then we get the Poincaré–Birkhoff–Witt isomorphism \(qA\cong \operatorname{gr}A\) of Theorem 3.6.4. In weight 1, it implies condition (ql 1′). In weight 2, it implies qR=q((R)∩{V⊕V ⊗2}), which is equivalent to condition (ql 2′) by condition (ql 1′). □
Conditions (ql 1′) and (ql 2′) amount to say that the ideal generated by R does not create any new quadratic-linear relation. It is equivalent to the maximality of the space of relations in the presentation of the inhomogeneous quadratic algebra. Such conditions can be hard to check in practice because one would have to compute the full ideal generated by R. But this proposition shows that if one finds a quadratic-linear presentation of an algebra satisfying conditions (ql 1), (ql 2) and whose homogeneous quadratic data is Koszul, then the space of relations R is maximal.
Remark.
This result is “Koszul dual” to the Diamond Lemma 4.2.4, since we work with the cobar construction Ω instead of the bar construction B in Sect. 4.2.4. Here it gives, under condition (ql 1),

where condition (ql 2) has to be seen as the particular case of condition (ql 2′) in weight 3. These two conditions refer to the ideal generated by R, whereas the condition of the Diamond Lemma refers to the quotient by some ideal associated to R. Also, in a similar way, we get the following isomorphism between the Koszul dual algebras (of the aforementioned coalgebras): \(qA\cong \operatorname{gr}A \cong A\) as a direct byproduct. This result is better seen as a Diamond Lemma for Gröbner bases, see Sect. 4.3.7.
3.6.6 Acyclicity of the Koszul Complex
As in the quadratic case, the Koszul complex associated to an inhomogeneous Koszul algebra is acyclic.
Proposition 3.6.6.
When
A(V,R) is a quadratic-linear Koszul algebra, its Koszul complexes
 and
and
 are acyclic.
are acyclic.
Proof.
We consider the Koszul complex as a chain complex graded by the weight of the elements of  . The two parts \(d_{\varphi} \otimes \operatorname{id}_{A}\) and \(d^{r}_{\kappa}\) of the differential map lower this degree by −1, so it is a well-defined chain complex.
. The two parts \(d_{\varphi} \otimes \operatorname{id}_{A}\) and \(d^{r}_{\kappa}\) of the differential map lower this degree by −1, so it is a well-defined chain complex.
The natural filtration on A plus the weight grading on  induce an exhaustive and bounded below filtration F
r
on
induce an exhaustive and bounded below filtration F
r
on  . The differential maps satisfy \(d^{r}_{\kappa}: F_{r} \to F_{r}\) and \(d_{\varphi} \otimes \operatorname{id}_{A} : F_{r} \to F_{r-1}\). Therefore, E
0 is equal to
. The differential maps satisfy \(d^{r}_{\kappa}: F_{r} \to F_{r}\) and \(d_{\varphi} \otimes \operatorname{id}_{A} : F_{r} \to F_{r-1}\). Therefore, E
0 is equal to  where
where  is the associated twisting morphism and where \(d^{0}=d^{r}_{\bar{\kappa}}\).
is the associated twisting morphism and where \(d^{0}=d^{r}_{\bar{\kappa}}\).
By the Poincaré–Birkhoff–Witt Theorem, E
0 is equal to the twisted tensor product  of the Koszul quadratic algebra qA, with
of the Koszul quadratic algebra qA, with  being the Koszul twisting morphism. Therefore, it is acyclic and we conclude by the convergence theorem for spectral sequences [ML95, Proposition 3.2, Chap. 11]). □
being the Koszul twisting morphism. Therefore, it is acyclic and we conclude by the convergence theorem for spectral sequences [ML95, Proposition 3.2, Chap. 11]). □
In [Pri70], Priddy called Koszul resolutions, the resolution  (resp.
(resp.  ) of \(\mathbb{K}\) by free A-modules. They provide chain complexes, smaller than the augmented bar construction A⊗
π
BA, which allow one to compute the Tor functors \(\mathrm{Tor}^{A}_{\bullet}(\mathbb{K}, M)\) for any A-module M (see [CE56, ML95] for the definition of Tor functors). In the example of the universal enveloping algebra of a Lie algebra, Priddy recovers the original Koszul resolution [CE56], which computes the Chevalley–Eilenberg homology of Lie algebras, see Sect. 3.6.7. Applied to restricted Lie algebras, this gives May resolutions [May66]. For the Steenrod algebra, it provides resolutions based on the Λ (co)algebra of [BCK+66], see Sect. 3.6.8 for more details.
) of \(\mathbb{K}\) by free A-modules. They provide chain complexes, smaller than the augmented bar construction A⊗
π
BA, which allow one to compute the Tor functors \(\mathrm{Tor}^{A}_{\bullet}(\mathbb{K}, M)\) for any A-module M (see [CE56, ML95] for the definition of Tor functors). In the example of the universal enveloping algebra of a Lie algebra, Priddy recovers the original Koszul resolution [CE56], which computes the Chevalley–Eilenberg homology of Lie algebras, see Sect. 3.6.7. Applied to restricted Lie algebras, this gives May resolutions [May66]. For the Steenrod algebra, it provides resolutions based on the Λ (co)algebra of [BCK+66], see Sect. 3.6.8 for more details.
Dually, the twisted convolution algebra  computes the homology functors \(\mathrm{Ext}^{\bullet}_{A}(\mathbb{K}, A)\) as in [BCK+66] (see Exercise 3.8.11).
computes the homology functors \(\mathrm{Ext}^{\bullet}_{A}(\mathbb{K}, A)\) as in [BCK+66] (see Exercise 3.8.11).
3.6.7 The Example of the Universal Enveloping Algebra
The universal enveloping algebra of a Lie algebra \(\mathfrak{g}\) is \(U(\mathfrak{g}):=T(\mathfrak{g})/(x\otimes y - y \otimes x- [x,y])\). So it is defined as a quadratic-linear algebra with \(V=\mathfrak{g}\). Its associated quadratic algebra is the symmetric algebra on \(\mathfrak{g}\): \(q(U(\mathfrak{g}))\cong S(\mathfrak{g})\).
Proposition 3.6.7.
When the characteristic of the ground field is not 2, the universal enveloping algebra \(U(\mathfrak{g})\) of a Lie algebra \(\mathfrak{g}\) is a Koszul algebra.
Proof.
A direct inspection shows that condition (ql 1) is satisfied. Let us prove that condition (ql 2) is also satisfied. The subspace R∩V ⊗2 of V ⊗2 is equal to {∑x⊗y∣∑[x,y]=0}. Let ξ=∑(x⊗y⊗z−y⊗x⊗z−[x,y]⊗z)+∑(t⊗u⊗v−t⊗v⊗u−t⊗[u,v]) be an element of (R⊗V+V⊗R). It belongs to V ⊗2 if and only if ∑(x⊗y⊗z−y⊗x⊗z)+∑(t⊗u⊗v−t⊗v⊗u)=0. In this case, applying [[−,−],−] to this element, we get 2∑[[x,y],z]+2∑[[t,u],v]=0. This proves that ξ∈R∩V ⊗2 and that (ql 2) holds, when the characteristic of \(\mathbb{K}\) is not 2. Finally, Proposition 3.4.8 shows that \(S(\mathfrak{g})\) is a Koszul algebra, therefore \(U(\mathfrak{g})\) is a Koszul algebra. □
Among other consequences, Theorem 3.6.4 can be applied and gives the “classical” Poincaré–Birkhoff–Witt theorem: there is an isomorphism of graded algebras
which is sometimes stated in terms of the monomial basis of the symmetric algebra.
Proposition 3.6.8.
The Koszul dual dga coalgebra of the universal enveloping algebra \(U(\mathfrak{g})\) is the following dga coalgebra

where d φ is the Chevalley–Eilenberg boundary map defining the homology of the Lie algebra \(\mathfrak{g}\).
Proof.
First, we have  . Recall that \(\varLambda^{c}(s\mathfrak{g})\) is linearly spanned by the elements \(\sum_{\sigma \in \mathbb{S}_{n}} \operatorname{sgn}(\sigma) s^{n} x_{\sigma(1)}\otimes \cdots \otimes x_{\sigma(n)}\), which we denote by x
1∧⋯∧x
n
. The internal differential d
φ
is the unique coderivation which extends φ:x⊗y−y⊗x↦[x,y]. Therefore it is equal to
. Recall that \(\varLambda^{c}(s\mathfrak{g})\) is linearly spanned by the elements \(\sum_{\sigma \in \mathbb{S}_{n}} \operatorname{sgn}(\sigma) s^{n} x_{\sigma(1)}\otimes \cdots \otimes x_{\sigma(n)}\), which we denote by x
1∧⋯∧x
n
. The internal differential d
φ
is the unique coderivation which extends φ:x⊗y−y⊗x↦[x,y]. Therefore it is equal to
which is the Chevalley–Eilenberg differential [CE48, Kos50], see Sect. 13.2.7. □
Corollary 3.6.9.
The twisted tensor product \(U(\mathfrak{g})\otimes_{\kappa}\varLambda^{c}(s\mathfrak{g})\) is a resolution of \(\mathbb{K}\) by free \(U(\mathfrak{g})\)-modules.
Proof.
Direct corollary of Proposition 3.6.6 and Proposition 3.6.7. □
This is the original Koszul resolution which computes Chevalley–Eilenberg homology of Lie algebras [CE56].
3.6.8 The Example of the Steenrod Algebra
The Steenrod algebra
 is the quadratic-linear algebra
is the quadratic-linear algebra

over the characteristic 2 field \(\mathbb{K}=\mathbb{F}_{2}\), where |Sq i|=i and where R Adem stands for the Adem relations

The quadratic analog  is obtained by omitting the linear term \(\binom{j-1}{i} Sq^{i+j}\). The images of the elements \(\lbrace Sq^{i_{1}} \cdots Sq^{i_{k}}; i_{l}\geq 2 i_{l+1} \rbrace\) form a basis of
is obtained by omitting the linear term \(\binom{j-1}{i} Sq^{i+j}\). The images of the elements \(\lbrace Sq^{i_{1}} \cdots Sq^{i_{k}}; i_{l}\geq 2 i_{l+1} \rbrace\) form a basis of  and
and  , called the Cartan–Serre basis of admissible monomials.
, called the Cartan–Serre basis of admissible monomials.
The degree-wise linear dual of the Koszul dual dga coalgebra  is a dga algebra, which is anti-isomorphic to the Λ
algebra of [BCK+66]. Notice that its homology gives the second page of the Adams spectral sequence which computes homotopy groups of spheres. The dga algebra Λ is generated by the elements {λ
i
}
i≥0 of degree |λ
i
|=i and satisfies the relations
is a dga algebra, which is anti-isomorphic to the Λ
algebra of [BCK+66]. Notice that its homology gives the second page of the Adams spectral sequence which computes homotopy groups of spheres. The dga algebra Λ is generated by the elements {λ
i
}
i≥0 of degree |λ
i
|=i and satisfies the relations
Its differential is the unique derivation extending
The mod-p Steenrod algebra can be treated in the same way. For more details, we refer the reader to [Wan67, Pri70].
3.7 Résumé
3.7.1 Quadratic Data and Koszul Dual Constructions

- The quadratic algebra: :
-
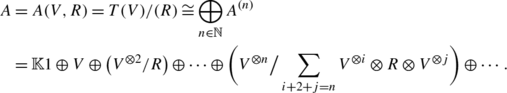
- The quadratic coalgebra: :
-

- Koszul dual coalgebra of an algebra: :
-

- Koszul dual algebra of a coalgebra: :
-
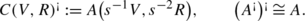
- Koszul dual algebra of an algebra: :
-
When V is finite dimensional, the linear dual of the desuspension of
 is the quadratic algebra A
!≅A(V
∗,R
⊥).
is the quadratic algebra A
!≅A(V
∗,R
⊥).
Examples:
T(V)!≅D(V ∗) and S(V)!≅Λ(V ∗).
3.7.2 Koszul Duality Theory
- Twisting morphism: :
-

- Koszul complexes: :
-
 and
and  ,
, 
with the syzygy degree:
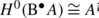 and
and  .
.
The quadratic data (V,R) is Koszul when one of the following equivalent assertions is satisfied.
-
1.
the right Koszul complex
 is acyclic,
is acyclic, -
2.
the left Koszul complex
 is acyclic,
is acyclic, -
3.
the inclusion
 is a quasi-isomorphism,
is a quasi-isomorphism, -
4.
the projection
 is a quasi-isomorphism,
is a quasi-isomorphism, -
5.
H n(B• A)=0 for n≥1,
-
6.
 for n≥1,
for n≥1, -
7.
H •(B• A) is a sub-coalgebra of T c(sV),
-
8.
the Yoneda algebra \(\mathrm{Ext}_{A}(\mathbb{K},\mathbb{K})\) is generated by its weight 1 elements [when V is finite dimensional].
Examples:
T(V), D(V), S(V), Λ(V).
3.7.3 Generating Series or Hilbert–Poincaré Series

3.7.4 Inhomogeneous Koszul Duality Theory
- Quadratic-linear data: :
-
(V,R), with R⊂V⊕V ⊗2.
- Quadratic analog: :
-
\(qR:=\mathrm{proj}_{V^{\otimes 2}}(R)\) and qA:=A(V,qR).

 induces a coderivation
induces a coderivation  , (ql
1) and (ql
2) imply d
φ
well-defined and (d
φ
)2=0.
, (ql
1) and (ql
2) imply d
φ
well-defined and (d
φ
)2=0. - Koszul dual dga coalgebra: :
-
 .
.
A(V,R) Koszul algebra when (ql 1), (ql 2) and qA quadratic Koszul algebra. In this case:
-
quasi-free resolution:
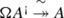 ,
, -
Poincaré–Birkhoff–Witt theorem: \(qA \cong \operatorname{gr} A\),
-
Koszul complex:
 acyclic.
acyclic.
Example:
\(A=U(\mathfrak{g})\), universal enveloping algebra of a Lie algebra \(\mathfrak{g}\),
-
 ,
, -
Original Poincaré–Birkhoff–Witt theorem: \(S(V) \cong \operatorname{gr} U(\mathfrak{g})\),
-
Original Koszul complex: \(U(\mathfrak{g}) \otimes_{\kappa}\varLambda^{c}(s\mathfrak{g})\) acyclic.
Example:
 , the mod-2 Steenrod algebra,
, the mod-2 Steenrod algebra,
-
Cartan–Serre basis,
-
the dga algebra
 is the Λ algebra.
is the Λ algebra.
3.8 Exercises
Exercise 3.8.1
(Koszul implies quadratic).
Let A be a connected weight graded algebra (see Sect. 1.5.10). Its bar construction BA splits with respect to the weight and we consider the same syzygy degree as in Sect. 3.3.1. Show that if the homology of BA is concentrated in syzygy degree 0, then the algebra has a quadratic presentation.
Exercise 3.8.2
(Two-sided Koszul complex).
Let (V,R) be a quadratic data. Under the notation of Sect. 2.1.4, we define the two-sided Koszul complex on  by the differential \(d^{l}_{\kappa}\otimes \operatorname {Id}_{A} + \operatorname {Id}_{A} \otimes d^{r}_{\kappa}\) and we denote it by
by the differential \(d^{l}_{\kappa}\otimes \operatorname {Id}_{A} + \operatorname {Id}_{A} \otimes d^{r}_{\kappa}\) and we denote it by  . Show that the quadratic data is Koszul if and only if the morphism of dg A-bimodules
. Show that the quadratic data is Koszul if and only if the morphism of dg A-bimodules

is a resolution of A.
(★) When (V,R) is a quadratic-linear data satisfying conditions (ql 1) and (ql 2), we add the term \(\operatorname {Id}_{A}\otimes d_{\varphi}\otimes \operatorname {Id}_{A}\) to the differential defining the two-sided Koszul complex. Prove the same result in this case.
Exercise 3.8.3
(Dual numbers algebra).
Show that, for the quadratic algebra of dual numbers \(A=\mathbb{K}[\varepsilon ]/ (\varepsilon ^{2}=0)\), with ε of degree 0, the cobar construction of  is isomorphic to the dga algebra
is isomorphic to the dga algebra  , where |t
n
|=n−1 and d(t
n
)=−∑
i+j=n
(−1)i
t
i
t
j
.
, where |t
n
|=n−1 and d(t
n
)=−∑
i+j=n
(−1)i
t
i
t
j
.
Exercise 3.8.4
(Inhomogeneous algebra ★).
Let A be an inhomogeneous quadratic algebra. Show that if A is Koszul, then f κ :A !→BA is a quasi-isomorphism of dga coalgebras.
Exercise 3.8.5
(Koszul complex of the symmetric algebra).
Prove that (Λ c(sV)⊗S(V),d κ ) is acyclic over ℤ.
Hint.
Use a suitable filtration.
Exercise 3.8.6
(Koszul complexes ★).
Consider the three functors S, Λ and Γ (cf. Exercise 1.8.6). Show that there are acyclic complexes Λ⊗S, Γ⊗Λ. Show that S⊗Λ is not acyclic in characteristic p and defines the Cartier homomorphism, see for instance [Pir02b].
Exercise 3.8.7
(Koszul complex in local cohomology ★).
Let A be a commutative algebra concentrated in degree 0. Let x be an element of A. We define the “Koszul complex” by
concentrated in degrees 0 and 1, where the boundary map defined by d(a):=ax. More generally, for n elements {x 1,…,x n } of A, the “Koszul complex” is defined by the tensor product
of chain complexes.
Show that the degree −1 map
is a twisting morphism from the symmetric cofree coalgebra on the suspension of the basis {x 1,…,x n } to the algebra A.
Prove that the “Koszul complex” \(K^{A}_{\bullet}(x_{1}, \ldots, x_{n})\) is isomorphic to the twisted tensor product \(\varLambda^{c}(sx_{1}, \ldots , sx_{n}\mathbb{K}) \otimes_{\tau}A\).
Considering the canonical twisting morphism κ:Λ c(sx 1,…,sx n )→S(x 1,…,x n ), show that the “Koszul complex” \(K^{A}_{\bullet}(x_{1}, \ldots, x_{n})\) is isomorphic to the relative tensor product
where A is considered a left S(x 1,…,x n )-module.
We say that {x 1,…,x n } is a regular sequence when the image of x i in A/(x 1,…,x i−1)A has no nonzero divisor, for 1≤i≤n. When it is the case, prove that the Koszul complex \(K^{A}_{\bullet}(x_{1}, \ldots, x_{n})\) is a resolution of A/(x 1,…,x n )A by free A-modules.
This chain complex is used to compute local cohomology (see [Wei94, Sects. 4.5–4.6]).
Exercise 3.8.8
(Homological degree).
Let (V,R) be a quadratic data such that V is concentrated in degree 0. We consider the bar construction B• A of the quadratic algebra A=A(V,R) as a chain complex with the homological degree.
Show that this chain complex splits with respect to the weight grading: B•
A=⨁
n∈ℕ(B•
A)(n). For n≥1, prove that the sub-chain complex (B•
A)(n) is finite, concentrated in degrees 1≤•≤n and that  .
.
Show that the quadratic data (V,R) is Koszul if and only if the homology of the bar construction B• A is concentrated on the diagonal ⨁ n∈ℕ H n ((B• A)(n)).
Exercise 3.8.9
(Double Hilbert–Poincaré series).
Pursuing the preceding exercise, we require here the vector space V to be finite dimensional. In this case, show that all the components (B m A)(n) of the bar construction of A are finite dimensional, for any m,n∈ℕ.
We define the double Hilbert–Poincaré series of A by
Show that the quadratic data is Koszul if and only if the double Hilbert–Poincaré series has only nontrivial coefficients in powers x m t n for m=n. Prove that it is also equivalent to \(F^{A}(x,t)=f^{A^{!}}(xt)\).
Prove the functional equation f A(t)F A(−1,t)=1 and recover the equation of Theorem 3.5.1.
Exercise 3.8.10
(Every augmented algebra is inhomogeneous Koszul).
Let A be an augmented associative algebra.
-
1.
Show that \(V:=\bar{A}\) and \(R:=\{a\otimes b - ab\mid a,b \in \bar{A}^{\otimes 2} \}\) is a quadratic-linear presentation of A satisfying conditions (ql 1) and (ql 2).
-
2.
Prove that qA is nilpotent and that the Koszul dual dg coalgebra
 is isomorphic to the bar construction of the algebra A.
is isomorphic to the bar construction of the algebra A. -
3.
Finally, show that this quadratic-linear presentation is Koszul and that the Koszul resolution is nothing but the bar–cobar resolution.
Exercise 3.8.11
(BCKQRS spectral sequence as twisted convolution algebra ★).
Show that the first page E
1
X of the spectral sequence of [BCK+66] for any spectrum X is equal to the convolution algebra  as follows: H
•(X) and
as follows: H
•(X) and  are
are  -modules and
-modules and

Show that  .
.
References
A. K. Bousfield, E. B. Curtis, D. M. Kan, D. G. Quillen, D. L. Rector, and J. W. Schlesinger, The mod−p lower central series and the Adams spectral sequence, Topology 5 (1966), 331–342.
A. Braverman and D. Gaitsgory, Poincaré-Birkhoff-Witt theorem for quadratic algebras of Koszul type, J. Algebra 181 (1996), no. 2, 315–328.
C. Chevalley and S. Eilenberg, Cohomology theory of Lie groups and Lie algebras, Trans. Amer. Math. Soc. 63 (1948), 85–124.
H. Cartan and S. Eilenberg, Homological algebra, Princeton University Press, Princeton, N. J., 1956.
R. Fröberg, Koszul algebras, Advances in commutative ring theory (Fez, 1997), Lecture Notes in Pure and Appl. Math., vol. 205, Dekker, New York, 1999, pp. 337–350.
—, Homologie et cohomologie des algèbres de Lie, Bull. Soc. Math. France 78 (1950), 65–127.
Clas Löfwall, On the subalgebra generated by the one-dimensional elements in the Yoneda Ext-algebra, Algebra, algebraic topology and their interactions (Stockholm, 1983), Lecture Notes in Math., vol. 1183, Springer, Berlin, 1986, pp. 291–338.
Yu. I. Manin, Some remarks on Koszul algebras and quantum groups, Ann. Inst. Fourier (Grenoble) 37 (1987), no. 4, 191–205.
—, Quantum groups and noncommutative geometry, Université de Montréal Centre de Recherches Mathématiques, Montreal, QC, 1988.
J. P. May, The cohomology of restricted Lie algebras and of Hopf algebras, J. Algebra 3 (1966), 123–146.
—, Homology, Classics in Mathematics, Springer-Verlag, Berlin, 1995, Reprint of the 1975 edition.
D. I. Piontkovskiĭ, On Hilbert series of Koszul algebras, Funktsional. Anal. i Prilozhen. 35 (2001), no. 2, 64–69, 96.
—, Polynomial functors over finite fields (after Franjou, Friedlander, Henn, Lannes, Schwartz, Suslin), Astérisque (2002), no. 276, 369–388, Séminaire Bourbaki, Vol. 1999/2000.
L. E. Positsel’skiĭ, The correspondence between Hilbert series of quadratically dual algebras does not imply their having the Koszul property, Funktsional. Anal. i Prilozhen. 29 (1995), no. 3, 83–87.
A. Polishchuk and L. Positselski, Quadratic algebras, University Lecture Series, vol. 37, American Mathematical Society, Providence, RI, 2005.
S. B. Priddy, Koszul resolutions, Trans. Amer. Math. Soc. 152 (1970), 39–60.
Jan-Erik Roos, On the characterisation of Koszul algebras. Four counterexamples, C. R. Acad. Sci. Paris Sér. I Math. 321 (1995), no. 1, 15–20.
V. A. Ufnarovski, Combinatorial and asymptotic methods in algebra, Algebra VI, Encyclopedia Math. Sci., vol. 57, Springer, Berlin, 1995, pp. 1–196.
J. S. P. Wang, On the cohomology of the mod−2 Steenrod algebra and the non-existence of elements of Hopf invariant one, Illinois J. Math. 11 (1967), 480–490.
C. A. Weibel, An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38, Cambridge University Press, Cambridge, 1994.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Loday, JL., Vallette, B. (2012). Koszul Duality for Associative Algebras. In: Algebraic Operads. Grundlehren der mathematischen Wissenschaften, vol 346. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-30362-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-642-30362-3_3
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-30361-6
Online ISBN: 978-3-642-30362-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


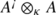 is acyclic,
is acyclic, is acyclic,
is acyclic, is a quasi-isomorphism,
is a quasi-isomorphism, is a quasi-isomorphism.
is a quasi-isomorphism. , thereby defining a coderivation
d
φ
of the coalgebra
, thereby defining a coderivation
d
φ
of the coalgebra
 .
.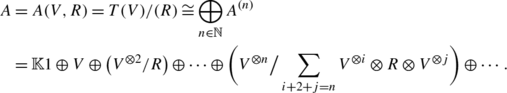


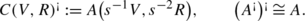
 is the quadratic algebra A
!≅A(V
∗,R
⊥).
is the quadratic algebra A
!≅A(V
∗,R
⊥).
 and
and  ,
, 
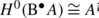 and
and  .
. is acyclic,
is acyclic, is acyclic,
is acyclic, is a quasi-isomorphism,
is a quasi-isomorphism, is a quasi-isomorphism,
is a quasi-isomorphism, for n≥1,
for n≥1,
 induces a coderivation
induces a coderivation  , (ql
1) and (ql
2) imply d
φ
well-defined and (d
φ
)2=0.
, (ql
1) and (ql
2) imply d
φ
well-defined and (d
φ
)2=0. .
.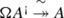 ,
, acyclic.
acyclic. ,
, is the Λ algebra.
is the Λ algebra. is isomorphic to the bar construction of the algebra A.
is isomorphic to the bar construction of the algebra A.