Terahertz Scattering

Abstract

Terahertz (THz) Time Domain Spectroscopy (TDS) measurements have the unique ability to detect both the amplitude and phase of the electric field, simultaneously. This eliminates complications introduced by Kramers–Kronig relations typically used in near-infrared spectroscopy. Many materials of interest contain resonant features in their refractive indices in the far-infrared (THz) spectrum, while their packaging materials are generally transparent. Thus, an important application for THz TDS is the ability to see inside packaging materials and detect the material features of their contents. Such applications are promising for security screening (concealed drugs, explosives, etc.) in post offices and airports as well as for non-destructive evaluation (NDE) of products on an assembly line or tissue damage due to burns or cancer [1–6].

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

Terahertz (THz) Time Domain Spectroscopy (TDS) measurements have the unique ability to detect both the amplitude and phase of the electric field, simultaneously. This eliminates complications introduced by Kramers–Kronig relations typically used in near-infrared spectroscopy. Many materials of interest contain resonant features in their refractive indices in the far-infrared (THz) spectrum, while their packaging materials are generally transparent. Thus, an important application for THz TDS is the ability to see inside packaging materials and detect the material features of their contents. Such applications are promising for security screening (concealed drugs, explosives, etc.) in post offices and airports as well as for non-destructive evaluation (NDE) of products on an assembly line or tissue damage due to burns or cancer [1–6].

The advancement of these technologies is complicated, however, because the wavelength of THz waves are on the same order as geometric features of the samples [7–10]. For example, spectral material features may be obscured by things like a transparent covering layer on the order of 100 microns (for example, the thickness of a piece of paper), a rough surface on the order of 10’s of microns (sandpaper or fingerprint impressions), or scattering from grains or air bubbles on the order of 10’s of microns. In addition, many materials of interest have relatively high absorption at THz frequencies. In particular, THz waves have skin depths of only a few millimeters in objects that contain high water content, such as the human body.

While carefully prepared samples may be studied in a controlled laboratory environment, it is expected that most practical applications of THz technology will be restricted to a reflection geometry. Measurements will probably also require some signal processing to correct for the frequency-dependent geometric scattering from layers, rough surfaces, and particles. The effects of these scattering phenomena are briefly introduced in this chapter.

5.2 Terahertz Reflection and Transmission from Samples with Smooth Planar Interfaces

This section addresses scattering phenomena that may occur at an interface between two media. Transmission and reflection coefficients are introduced to define the field above and below the interface. The etalon effect is briefly considered for a thin layer of material. Finally, scattering from random media is introduced and methods to detect material features from rough surface scattering are discussed.

5.2.1 Reflection and Transmission at a Single Interface

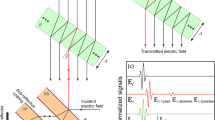
This section will consider the simplest transmission and reflection configurations, such as might be encountered while using prepared samples in a laboratory setting. Figure  5.1a shows a horizontally polarized plane wave incident on a smooth interface between two infinite half-spaces. The incident field is given by,

$$\begin{aligned} \bar{E}_i(f,\overline{k}_i) = \hat{y}E_0 e^{ixk_{xi}-izk_{zi}}e^{-i2\pi ft}, \end{aligned}$$

(5.1)

where $f$ is the frequency (in Hz) and $t$ is time. In the remainder of this chapter, time-dependence will be suppressed. In (5.1), $k_{xi} = k\sin \theta _i$ and $k_{zi} = k\cos \theta _i$ are the horizontal and vertical components of the incident wave vector, $\overline{k}_i = k_{xi} \hat{x} + k_{zi} \hat{z}$ and $\theta _i$ is the incident angle. Throughout this chapter, $k = 2\pi / \lambda$ will be used to represent the wavenumber, where $\lambda = c/f$ is the wavelength and $c = 3 \times 10^8$ m/s is the speed of light in free space. This standard convention in electromagnetics is different from the terminology sometimes used in spectroscopy where “wavenumber” is often defined as $1/\lambda$. We note that the notation in this chapter is different from other chapters in this text where wavenumber is represented as $K$, and $k$ is used for the extinction coefficient.

Fig. 5.1

Panel A Plane of incidence for reflection and transmission at a smooth interface between media $0$ (free space) and $1$. The horizontally polarized incident field, $\bar{E}_i$ is reflected at the specular angle, $\theta _s = \theta _i$. The refractive index, $N_1$, may be dependent on the THz frequency.  Note, the incident, transmitted and reflected electric fields and the y-axis are illustrated as vectors pointing into the page. Panel B Reflected and transmitted pulses from a single layer of material for normal incidence, $\theta _r = \theta _i = 0$

For infinite planar surfaces the reflected and transmitted fields, $\bar{E}_r$ and $\bar{E}_t$, are given by the horizontal Fresnel reflection and transmission coefficients,

$$\begin{aligned} R_{01}^h = \frac{N_0\cos \theta _i - N_1\cos \theta _t}{N_0\cos \theta _i + N_1\cos \theta _t}, \end{aligned}$$

(5.2)

$$\begin{aligned} T_{01}^h = 1 + R_{01}^h. \end{aligned}$$

(5.3)

In (5.2) and (5.3), $R_{01}$ is the reflection coefficient for a field reflected from medium 1 into medium 0, $T_{01}$ is the transmission coefficient for a field transmitted from medium 0 into medium 1, and $\theta _t$ is the refracted angle inside medium 1. The complex index of refraction, $N_1$, is generally frequency-dependent in the THz portion of the spectrum so that

$$\begin{aligned} N(f) = \sqrt{\epsilon (f)\mu }, \end{aligned}$$

(5.4)

where

$$\begin{aligned} \epsilon (f) = \epsilon ^{\prime }(f) + i\epsilon ^{\prime \prime }(f). \end{aligned}$$

(5.5)

The real part, $\epsilon ^{\prime }(f)$, and imaginary part, $\epsilon ^{\prime \prime }(f)$, of the complex relative permittivity in (5.5) often contain unique spectral information which can be used for material detection and identification. The relative permeability, $\mu$, of non-magnetic materials is 1. Figure  5.2 shows the complex permittivity for $\alpha$-lactose monohydrate, calculated from the Lorentz parameters. It has been shown that the 1st derivative of the reflection coefficient magnitude or the 2nd derivative of the reflection coefficient phase may yield a similar signature to the imaginary part of the permittivity when $\epsilon ^{\prime } \gg \epsilon ^{\prime \prime }$ [11–13].

Fig. 5.2

Relative permittivity for alpha-lactose-monohydrate calculated from the Lorentz parameters. The imaginary part shows peaks near 0.54, 1.2, and 1.4 THz which may be used for material identification

The primary objective of THz spectroscopy is to gain information about a material from either the transmitted or reflected fields. For smooth surfaces, the reflected angle is called the “specular” angle and is given by the law of reflection, $\theta _r = \theta _i$. In general, the extraction of $N_1$ from (5.2) is complicated by the dependence of $\theta _t$ on $N_1$ due to Snell’s Law of Refraction [14]. The process of extracting $N_1$ is greatly simplified if the angle of incidence is chosen to be normal. The transmitted field is preferred over the reflected field for THz spectroscopy, because it is more heavily influenced by the absorption features and because most materials of interest have relatively low reflectivity.

It is difficult to accurately account for the transfer functions of all of the individual components in a THz TDS system. This problem is by-passed by making an additional reference measurement without the sample material in place. Thus, normalizing the sample measurement by the reference measurement removes the unknowns and isolates the material parameters in a process called deconvolution [14]. Thus, for a given geometry with fixed incident and transmitted or reflected angles, the electric field of the sample and reference THz pulses are measured as time-domain waveforms and the corresponding complex frequency spectra, $\overline{E}_\mathrm{sample}(f)$ and $\overline{E}_\mathrm{ref}(f)$, are then computed using numerical Fast Fourier Transforms (FFT’s). Finally, the ratio gives the deconvolved sample spectrum,

$$\begin{aligned} {E}_\mathrm{deconv}(f) = \frac{{E}_\mathrm{sample}(f)}{{E}_\mathrm{ref}(f)}. \end{aligned}$$

(5.6)

For transmission measurements the reference is the electric field with the source and receiver in the same position, but without a sample in the propagation path. The reference for reflection measurements is the specular reflection from a mirror. Although it is more practical, the reflection configuration presents a number of challenges. First, it is difficult to align the emitter, sample, and detector precisely at the specular angle to capture the reflected signal. Similarly, the deconvolution operation requires the mirror to be placed at exactly the same location as the sample. For example, if the mirror is misplaced by only a few hundred microns there may be several wavelengths difference in the propagation path between the sample and reference measurements. This subtle difference can result in a large error in the phase and ultimately the extracted material properties. In addition, it is more difficult to extract the material properties from reflection measurements because the calculation of $\theta _t$ requires a-priori knowledge of the material’s index of refraction. Finally, an even more important challenge for reflection spectroscopy is that most materials of interest have a relatively small reflection coefficient (on the order of $10$ percent) making it difficult to acheive the signal to noise ratio (SNR) needed to identify spectral features [15]. For these reasons it is expected that the detection and identification procedures used in security or medical screening applications will rely on comparison of reflection spectra of the in situ samples with absorption spectra from a library of known materials, derived from laboratory measurements made in transmission mode.

5.2.2 Reflection and Transmission from a Layer

Transmission though thin pellet samples in a laboratory environment will generally be used to extract material properties, which can be recorded in a database or library of known material signatures. Samples are prepared by pressing powder in a hydraulic press to create a pellet with smooth level surfaces on each side. However, interference between the internal reflections within the pellet (etalon effect) may still obscure spectral features of the sample material. This section will briefly describe the complexities associated with transmission at normal incidence through a single pellet with just two interfaces as illustrated in Fig.  5.1b.

For an electric field at normal incidence, the effective reflection, and transmission coefficients for a layer of thickness, $d$, can be written as [16],

$$\begin{aligned} R_\mathrm{eff} = \frac{R_{01} + R_{10}\exp (i2k_1d)}{1 + R_{01}R_{10}\exp (i2k_1d)}, \end{aligned}$$

(5.7)

and

$$\begin{aligned} T_\mathrm{eff} = \frac{T_{01}T_{10}\exp (ik_1d)}{1 + R_{01}R_{10}\exp (i2k_1d)}, \end{aligned}$$

(5.8)

where $k_1 = 2\pi f / N_1 c$ is the wavenumber inside region $1$. Extraction of the refractive index from a thin sample as illustrated in Fig.  5.1b will generally require (5.7) or (5.8) to be solved using numerical methods. If the sample is thick enough so that only the first transmitted pulse can be detected, then $R_{10}$ in the denominator of $T_\mathrm{eff}$ goes to zero, and $N_1$ can be extracted more easily using the methods in the literature [14]. This is the most desirable scenario, but is difficult to achieve in practice because thin samples can become brittle and fall apart. Therefore, the sample material is often mixed with a transparent binding material (such as polyethylene or Teflon). The grain sizes of the sample and binding material must be small enough to avoid scattering within the sample. The samples must also be pressed with sufficient pressure to reduce the size of air voids within the sample. Volume scattering will be considered in the second part of this chapter.

In more practical applications of THz technology, accounting for the etalon effect in the layers above a material of interest (clothing, packaging material, etc.) is imperative. This has been done using optimization routines within an inverse model for a single layer [17].

5.3 Random Media

As discussed above, THz TDS may be used to extract spectroscopic information from homogeneous materials with smooth surfaces. However, most naturally occurring materials will contain randomly distributed particles and/or surface protrusions or indentations which are on the same order as THz wavelengths. This is illustrated in panel $A$ of Fig.  5.3. Scattering from random rough surfaces may dominate over volume scattering within materials that are opaque (small skin depths) as shown in (Fig.  5.3b), and discussed in the following section. Scattering from inhomogeneities randomly distributed throughout materials with smooth surfaces (Fig.  5.3c) will be discussed in the second half of this chapter.

Fig. 5.3

Most materials of interest for THz TDS must be modeled as random media (panel A). The scattered field above random rough surfaces (panel B) will be discussed in Sect.  5.3.1. Scattering from inhomogeneities randomly located inside a medium (panel C) will be discussed in the second half of this chapter

For either case the scattered field will be the sum of the mean field and a fluctuating field,

$$\begin{aligned} \overline{E}_s(f,\overline{k}_i,\overline{k}_s) = \overline{E}_m(f,\overline{k}_i,\overline{k}_s) + \overline{E}_f(f,\overline{k}_i,\overline{k}_s), \end{aligned}$$

(5.9)

where $\overline{k}_s$ is the scattered wave vector in the $\theta _s$ direction, and the expected value of the fluctuating field is equal to zero, $\langle \overline{E}_f(f,\overline{k}_i,\overline{k}_s) \rangle = 0$. It is important to note that since the fluctuating part of the field is (by definition) phase incoherent the phase structure corresponding to the material spectrum is contained solely within the mean (or coherent) field component. Although the incoherent field averages to zero, the incoherent power does not, and may therefore be used to obtain spectral information.

5.3.1 Terahertz Reflection from Random Rough Surfaces

Since most materials are opaque at THz frequencies, it is expected that more practical detection systems will need to operate in a reflection configuration. Furthermore, many common surfaces will have roughness on the order of THz wavelengths (hundreds of microns), and cause the spectroscopic signatures to be altered by scattering. Since the surface of most materials will have some random roughness, it will be necessary to average a number of measurements in order to characterize a typical sample material. In fact, dozens or possibly hundreds of sample measurements may be required. The complexity of the rough surface scattering physics motivates the development of mathematical models and computer simulations that can accurately and efficiently provide these answers.

A rough surface can be considered as an ergotic random process where the height at any given location is a random variable, $\zeta$. It is reasonable to assume that for most random rough surfaces all of the heights will have the same probability distribution and the same mean value. For a zero-mean surface the root-mean-square (rms) height is given by

$$\begin{aligned} h = \sqrt{ \left\langle \zeta ^2(x,y) \right\rangle }. \end{aligned}$$

(5.10)

Along a single line in the y-dimension, the covariance between two points $\zeta (x_1)$ and $\zeta (x_2)$, on a random rough surface is

$$\begin{aligned} \left\langle \zeta (x_1)\zeta (x_2) \right\rangle = h^2 C(x_1 - x_2), \end{aligned}$$

(5.11)

where $C(x_1 - x_2)$ is the autocorrelation function. The correlation length is defined as the horizontal distance, $l_c$, that causes the autocorrelation function to decrease by $1/e$, where $e = 2.7183$.

The strength of a wave reflected from a rough surface will depend on three factors: material properties, viewing geometry (incident and detection angles), and rough surface statistics. The impact of the surface on the scattering depends on the surface height relative to a wavelength. As wavelength decreases (with increasing frequency) a surface will appear more rough to the incident plane wave, resulting in more diffuse scattering. According to the Fraunhofer Criterion a surface can be considered rough if it causes a $\frac{\pi }{8}$ phase shift as compared to a smooth surface [18, 19]. Thus, a surface is “rough” if the rms height, $h$, satisfies the inequality

$$\begin{aligned} h \ge \frac{\lambda }{32 \cos \theta _i}. \end{aligned}$$

(5.12)

The scattered field, $\overline{E}_s$, from a horizontally polarized wave incident on a rough surface will have both horizontal and vertical components. The horizontal component is given by [20],

$$\begin{aligned} \bar{E}_{s}^{h} (\bar{r})= \hat{y} \left[ \frac{ike^{ikr}}{4\pi r} \right] \int \limits _{S^{\prime }} \mathrm{d}S^{\prime } \left[ \hat{y} \cdot \left( \hat{k}_s \times \left[ \hat{n} \times \overline{E}(\overline{r}^{\prime }) \right] + \eta \left[ \hat{n} \times \overline{H}(\overline{r}^{\prime }) \right] \right) e^{-i\overline{k}_s \cdot \overline{r}^{\prime }} \right], \end{aligned}$$

(5.13)

where it has been assumed that the detector is in the plane of incidence. In (5.13), $r$ is the distance from the origin to the observation point, and $\bar{r}^{\prime }$ is a vector from the origin to a patch of area, dS’, on the surface, S’. $\overline{E}$ and $\overline{H}$ are the electric and magnetic fields, respectively, on the surface. The surface normal, $\hat{n}$, points outward from the surface, and the impedance of the (non-magnetic) surface material is $\eta \approx 377/\sqrt{\epsilon _1}$ ohms, where $\epsilon _1$ is the relative permittivity of the surface material.

Although (5.13) is exact, the integral is difficult to solve for random rough surfaces. The integration may be solved using numerical techniques, such as Method of Moments (MoM) [21] or Finite Difference Time Domain (FDTD) [22, 23].

At a distance, $r$, from a scatterer, the differential cross-section, $\sigma _d$, gives the relative amount of scattered power

$$\begin{aligned} \sigma _d(f,\overline{k}_i,\overline{k}_s) = 4\pi r^2 \frac{|\overline{E}_s(f,\overline{k}_i,\overline{k}_s)|^2}{|\overline{E}_i(f,\overline{k}_i,\overline{k}_s)|^2 } \mathrm{d}\Omega _s, \end{aligned}$$

(5.14)

with units of area. In (5.14), $\mathrm{d}\Omega _s = \sin \theta _s \mathrm{d}\theta _s \mathrm{d}\phi _s$ is the differential solid angle in the scattered direction, $\hat{k}_s$. Note, this is similar to THz TDS deconvolution as defined in (5.6), where the normalized intensity is

$$\begin{aligned} I_\mathrm{deconv}(f,\overline{k}_i,\overline{k}_s) = \frac{|\overline{E}_s(f,\overline{k}_i,\overline{k}_s)|^2}{|\overline{E}_{ref}(f,\overline{k}_i,\overline{k}_s=\mathrm{specular})|^2}. \end{aligned}$$

(5.15)

Thus, THz TDS intensity measurements will be proportional to differential cross-section calculations.

The dimensions of rough surfaces are generally larger than the incident beam. Therefore, the differential cross-section is often normalized by the incident beam cross-section to give the (dimensionless) scattering coefficient,

$$\begin{aligned} \gamma (f,\overline{k}_i,\overline{k}_s) = \frac{\sigma _d(f,\overline{k}_i,\overline{k}_s)}{ A_0 \cos \theta _i }, \end{aligned}$$

(5.16)

Fig. 5.4

Panel A Angular distribution of the scattering coefficient above two random rough conductive surfaces at two frequencies, simulated with the MoM. At each frequency the rougher surface (surface 2) diverts more energy away from the specular angle. For both surfaces, more scattering occurs at the higher frequency. Panel B Spectral derivatives for specular reflection measured [24] by a THz TDS system from a smooth lactose surface compared with lactose with rough surface $1$ and $2$, as in panel A. The peak near $0.54$ THz corresponds to the peak in the extinction coefficient in Fig.  5.2

where $A_0$ is the area of the rough surface projected onto the x-y plane. Figure  5.4a shows the scattering coefficients for two rough conductive surfaces at two frequencies. The scattering coefficients were calculated using MoM [21] for 1D surfaces of length $2L$, where $L = 25\lambda$. The heights of surfaces $1$ and $2$ are both Gaussian random variables with rms heights of $21\,\upmu \mathrm{m}$ and $55 \,\upmu \mathrm{m}$, respectively, and their correlation lengths are $161\,\upmu \mathrm{m}$ and $151 \,\upmu \mathrm{m}$, respectively. Each case shows the average scattering coefficient from $200$ independent surface realizations.

For both surfaces in Fig.  5.4a the peak (main lobe) is centered at the specular angle. The width of the specular peak is proportional to $1/(2L)$, and the height of the main lobe decreases exponentially with increasing rms height, frequency, and incident angle. At each frequency the rougher surface (surface $2$) diverts more energy away from the specular angle. For both surfaces, more scattering occurs at the higher frequency. The scattering at the specular angle decreases with increasing frequency as the diffuse scattering increases. For very rough surfaces, the coherent peak disappears completely, as illustrated by surface $2$ in Fig.  5.4a at $2.0$ THz.

Terahertz TDS measurements were made in reflection mode to demonstrate the ability to detect material features from rough surface scattering at the specular angle [24]. The sample materials were prepared at the Indian Head Division, Naval Surface Warfare Center (IHD NSWC) [25], and THz TDS measurments were conducted at the Northwest Electromagnetics and Acoustics Research Laboratory (NEAR-Lab) at Portland State University. Lactose powder was mixed with a (transparent) polytetrafluoroethylene (PTFE) binding material in a 20 % / 80 % PTFE/lactose weight ratio and pressed into circular pellets 2 inches in diameter. The sample thickness, approximately 9 mm, was large enough so that all etalon reflections could be time-gated out without significant loss of frequency resolution. A smooth surface sample was compared with two rough surface samples. The rough surface samples were impressed with the same roughness statistics as surface $1$ and surface $2$ by inserting a piece of 80 grit and 40 grit sandpaper in the bottom of the die, respectively. The samples and THz TDS transmitter and receiver were placed inside an acrylic enclosure purged with Nitrogen to remove narrow-band water vapor attenuation. The incident (collimated) beam was centered half-way between the center and the edge of the 2 in lactose pellet, which was rotated (in 12 degree increments) about its center to create 30 surface realizations. Reflection spectra were obtained by deconvolution using a gold mirror as the reference. Figure  5.4b shows the negative derivatives of the reflected power with respect to frequency for each surface. As discussed earlier, the $1$st derivative of the reflection coefficient magnitude (and thus also power) can reveal a spectral signature similar to the imaginary part of the permittivity when $\epsilon ^{\prime } \gg \epsilon ^{\prime \prime }$ [11–13], a condition satisfied by lactose (Fig. ). Thus, the spectral feature of lactose near $0.54$ THz is clearly apparent in Fig.  5.4b for the smooth surface, but becomes smaller as the surface roughness increases because more energy is diverted away from the specular angle.

Since the scattered power decreases exponentially with increasing frequency and disappears altogether for very rough surfaces, it can be more helpful to work with the diffuse scattering (incoherent power) from rough surfaces. Diffuse scattering will be produced at all angles and thus no particular alignment is necessary. Improvement in the SNR of the diffuse signatures may be realized by averaging over many scatter angles. In addition, signal processing techniques such as correlation detection [26] and Cepstrum filtering [27] have been applied to improve detections algorithms for diffuse scattering.

5.3.1.1 Rough Surface Scattering Approximations

Insight into scattering behavior can be gained by considering approximate solutions for (5.13). The two most common analytic approximations, the Kirchhoff Approximation and Small Perturbation Method, will be introduced in this section.

Kirchhoff Approximation

The Kirchhoff Approximation assumes the facets of a rough surface can be approximated locally as tangent planes. For surfaces with large radius of curvature the Kirchhoff Approximation simplifies (5.13) to give [18, 20],

$$\begin{aligned} \bar{E}_{s}^{h} (\bar{r}) =\hat{y} \left[ \frac{ike^{ikr}}{4\pi r} \right] E_0 \int \limits _{A_0} \left[ a\frac{\delta }{\delta x}\zeta (x,y) - b \right] e^{ i(\overline{k}_i - \overline{k}_s) \cdot \overline{r}^{\prime }} \mathrm{d}x^{\prime } \; \mathrm{d}y^{\prime }, \end{aligned}$$

(5.17)

where $A_0$ is the total surface area, with dimensions $2L_x \times 2L_y$, and the coefficients are given by $a = (1-R_{01}^h) \sin \theta _i + (1+R_{01}^h) \sin \theta _s$, and $b = (1+R_{01}^h) \cos \theta _s - (1-R_{01}^h) \cos \theta _i$. It is important to note that in (5.17) the emitter and detector are assumed to be in the xz plane. In this case, only tangent planes of the surface which are perpendicular to the xz plane are relevant in the integration. Although these tangent planes have no slope in the y-direction, a two-dimensional integration is still necessary to account for the width of the planes. Since the local normal of each of these planes will be parallel to the xz plane, the local polarization of the incident wave is still in the y-direction and the horizontal reflection coefficient can be used to compute the a and b coefficients. More general scattering scenarios are presented in the literature [18, 20].

The scattered field from the Kirchhoff Approximation may be solved numerically for a random surface realization, $\zeta (x,y)$, in (5.17). However, if the surface has small slopes, then (5.17) can be simplified further [20],

$$\begin{aligned} \overline{E}_s(\overline{r}) = \hat{y} \left[ \frac{ike^{ikr}}{4\pi r} \right] E_0 \left[- b \right] \int \limits _{A_o} e^{ i(\overline{k}_i - \overline{k}_s) \cdot \overline{r}^{\prime }} \mathrm{d}x^{\prime } \; \mathrm{d}y^{\prime }. \end{aligned}$$

(5.18)

The Kirchhoff Approximation is valid for all frequencies for which the radius of curvature is much larger than a wavelength. However, at large angles of incidence, shadowing and multiple reflections in-between facets of the surface may occur. The basic form of the Kirchhoff Approximation, presented here, does not account for these effects.

If the surface has a Gaussian probability density function, then the scattering coefficient can be solved analytically [20],

$$\begin{aligned} \gamma = \frac{k^2}{4\pi A_0 \cos \theta _i} \left| - b \right|^2 ( |<I>|^2 + D_I ) , \end{aligned}$$

(5.19)

where the first and second terms within the parenthesis represent the coherent and incoherent scattered intensity, respectively. If the transmitter and receiver are both in the $xz$ plane, and the surface area includes many correlation lengths, then the coherent scattering is given by [20],

$$\begin{aligned} <I> = A_0 \exp \left[-\frac{1}{2}k_{dz}^2 h^2 \right] sinc(k_{dx}L_x), \end{aligned}$$

(5.20)

where $sinc(x) = \sin (x)/x$, $k_{dx}= k (\sin \theta _i - \sin \theta _s)$ and $k_{dz}=k(\cos \theta _i - \cos \theta _s)$. It is important to note that this is similar to the scattered field from a flat plate of width $2L_x$, but here the rough surface attenuates the field by an exponential factor which is dependent on the rms height, angle of incidence, and wavelength.

Small Perturbation Method

For surfaces that have small rms height, $kh \ll 1$, the Small Perturbation Method (SPM) can be used to estimate the scattering coefficient for a Gaussian surface [20],

$$\begin{aligned} \gamma ^{(1)} = \left[ 4 k^4 h^2 l_c^2 \cos ^2 \theta _s \cos \theta _i \right] \left| \frac{(k_1^2 - k^2)}{(k_{z}+k_{1z})(k_{zi}+k_{1zi})} \right|^2 \exp \left[ - \frac{1}{4} k_{d\rho }^2 l_c^2 \right]. \end{aligned}$$

(5.21)

where the superscript on the scattering coefficient indicates a first-order approximation. In the medium above the rough surface, the vertical component of the scattered wave vector is given by $k_z = k\cos \theta _s$, and $k_{d \rho }$ is the difference between the horizontal components of the incident and scattered wave vectors where $k_{d\rho }^2= k^2(\sin ^2\theta _s + \sin ^2\theta _i - 2 \sin \theta _s \sin \theta _i)$. Similarly, the vertical components of the incident and scattered wave vectors are given by $k_{z1i} = k_1\cos \theta _i$ and $k_{1z} = k_1\cos \theta _s$, respectively.

The SPM model is useful for frequencies at which the small height approximation is valid. Therefore, SPM is only applicable for a band of frequencies bracketed by the Fraunhofer Criterion (5.12) and the small height requirement, $kh \ll 1$.

5.4 Volume Scattering and Absorption

This section considers an electromagnetic wave propagating in a material that has volume inhomogeneities (i.e., grains or bubbles), as shown in the right-hand part of Fig.  5.3. The energy in an electromagnetic wave propagating through such a material will be scattered and absorbed by the particles. This is commonly observed (experimentally) as a loss of energy from the incident or coherent wave, but the scattering will also in general re-distribute energy into a scattered electric field that propagates in other directions (much as rough surface scattering produces energy in non-specular directions). The strength of the scattering depends on the size of the scatterers relative to the THz wavelength; the dielectric contrast between the scatterer and the background; and the shape, concentration, and orientation of the scatterers.

In random media, the exact positions and characteristics of the particles are not precisely known, but often their properties can be described in terms of the particle statistics. Given these statistics, it is possible to predict the mean field properties, either with analytical approximations or numerical calculations (using Monte Carlo techniques). In this section, several of the more commonly used approaches and approximations for calculating the volume scattering and absorption are provided.

5.4.1 Scattering from Individual Particles

Consider the case of a single particle of permittivity $\epsilon _p$ (which differs from the background permittivity $\epsilon$) illuminated by the incident electric field as defined in (5.1). In the far field, the field scattered from the particle will be a spherical wave with dependence $e^{ikr}/r$, where $r$ is the distance from the particle to the observation point. The electric field scattering in the direction $\hat{k}_s$ is

$$\begin{aligned} \bar{E}_s = \hat{e}_s f_s(\hat{k}_s,\hat{k}_i) E_o \frac{e^{ikr}}{r} \end{aligned}$$

(5.22)

and $f_s(\hat{k}_s,\hat{k}_i)$ is the scattering amplitude from direction $\hat{k}_i$ into direction $\hat{k}_s$. The scattered power can be determined by integrating over all scattered angles to give the scattering cross-section

$$\begin{aligned} \sigma _s = \int \mathrm{d}\Omega | f_s(\hat{k}_s,\hat{k}_i) |^2 \end{aligned}$$

(5.23)

where $\mathrm{d}\Omega$ is a differential solid angle. In addition to scattering, the particles may also introduce absorptive loss, which is quantified by the absorption cross-section $\sigma _a$. The extinction cross-section, $\sigma _e = \sigma _s + \sigma _a$ accounts for both effects.

The analytic solution for the scattering amplitude (and hence the far-field scattered field) can be found by expressing the incident, scattered, and internal fields in terms of a complete orthonormal basis, such as spherical vector wave functions. Electromagnetic boundary conditions are then imposed at the particle boundaries, resulting in expressions for the unknown expansion coefficients [28]. Typically, this process only yields closed form solutions for canonical objects (e.g., spheroids, cylinders, etc.); more complicated objects require numerical approaches.

The scattered field can be computed using the T-matrix [29, 30] method (see [31] for a recent review on the approach), which represents the scattered field in terms of the regular vector spherical wave functions $\overline{M}^{(1)}_{mn}$ and $\overline{N}^{(1)}_{mn}$ as

$$\begin{aligned} \overline{E}_s(\overline{r}) = \sum _{m,n} [ a_{mn}^{s(M)} \overline{M}_{mn}(kr, \theta , \phi ) + a_{mn}^{s(N)} \overline{N}_{mn}(kr, \theta , \phi )] \end{aligned}$$

(5.24)

where $\theta$ and $\phi$ are the elevation and azimuthal angles in spherical coordinates and $a_{mn}^{s(M)}$ and $a_{mn}^{s(N)}$ are the (unknown) coefficients of the spherical wave functions which can be expressed in terms of the T-matrix as

$$\begin{aligned} \left[ \begin{array}{c} \bar{a}^{s(M)} \\ \bar{a}^{s(N)} \end{array} \right] = \left[ \begin{array}{cc} \overline{\overline{T}}^{(11)} \overline{\overline{T}}^{(12)} \\ \overline{\overline{T}}^{(21)} \overline{\overline{T}}^{(22)} \end{array} \right] \left[ \begin{array}{c} \bar{a}^{e(M)} \\ \bar{a}^{e(N)} \end{array} \right]. \end{aligned}$$

(5.25)

and each of the sub-matrices have dimensions $L_\mathrm{max} \times L_\mathrm{max}$, where $L_\mathrm{max}$ is determined by the number of spherical harmonics necessary in the expansion in (5.24).

The scattering from spherical particles of radius $a$ is referred to as Mie scattering [32, 33], and for spherical scatterers the T-matrix is diagonal with

$$\begin{aligned} T_{mnm^{\prime }n^{\prime }}^{(11)} = \delta _{m m^{\prime }} \delta _{n n^{\prime }} T_n^{(M)}; \;\; T_{mnm^{\prime }n^{\prime }}^{(22)} = \delta _{m m^{\prime }} \delta _{n n^{\prime }} T_n^{(N)}; \;\; T_{mnm^{\prime }n^{\prime }}^{(12)} =T_{mnm^{\prime }n^{\prime }}^{(21)} =0\nonumber \\ \end{aligned}$$

(5.26)

where

$$\begin{aligned} T_n^{(M)}&= \frac{j_n(k_s a) \left[ k a j_n(ka) \right] ^{\prime } - j_n(ka) \left[k_s a j_n(k_s a) \right] ^{\prime }}{j_n(k_s a) \left[ k a h_n(ka) \right] ^{\prime } - h_n(ka) \left[k_s a j_n(k_s a) \right] ^{\prime }} \nonumber \\ T_n^{(M)}&= \frac{\left[ k_s^2 a^2 j_n(k_s a) \left[ k a j_n(ka) \right] ^{\prime } \right] - \left[ k^2 a^2 j_n(ka) \left[ k_s a j_n(k_s a)\right]^{\prime } \right]}{\left[ k_s^2 a^2 j_n(k_sa) \left[ k a h_n(ka) \right] ^{\prime }\right] - \left[ k^2a^2 h_n(ka) \left[k_s a j_n(k_s a) \right] ^{\prime } \right]} \end{aligned}$$

(5.27)

where $j_n$ and $h_n$ are the spherical Bessel and Hankel functions, respectively, and the prime indicates differentiation. The scattering and extinction cross-section for spheres can then be written in terms of the T-matrix elements as

$$\begin{aligned} \sigma _s&= \frac{2 \pi }{k^2} \sum _{n=1}^{\infty } (2n+1) (|T_n^{(M)}|^2+|T_n^{(N)}|^2), \end{aligned}$$

(5.28)

$$\begin{aligned} \sigma _e&= -\frac{2 \pi }{k^2} \sum _{n=1}^{\infty } (2n+1) \{Re(T_n^{(M)}+T_n^{(N)})\}. \end{aligned}$$

(5.29)

The above expressions account rigorously for the scattering and absorption from spherical particles. However, the computation requires a summation over spherical harmonics, and the larger the particle the more terms are required in the summation. For small dielectric spheres ($ka \ll 1$) the only term that needs to be retained is the electric dipole term. Thus, the scattering and absorption cross-sections for small particles (called Rayleigh scattering) can be simplified to

$$\begin{aligned} \sigma _s&= \frac{8 \pi }{3} k^4 a^6 \left| \frac{\epsilon _p-\epsilon }{\epsilon _p+2\epsilon } \right| ^2 = \frac{8 \pi }{3} k^4 a^6 \left| y \right| ^2, \end{aligned}$$

(5.30)

$$\begin{aligned} \sigma _a&= k \frac{Im\{ \epsilon _p\} }{\epsilon } \frac{4 \pi a^3}{3} \left| \frac{3 \epsilon }{\epsilon _p+2\epsilon } \right| ^2, \end{aligned}$$

(5.31)

and $y=(\epsilon _s-\epsilon )/(\epsilon _s + 2 \epsilon )$.

5.4.2 Scattering from Randomly Distributed Collections of Particles

Many inhomogeneous materials can be modeled as a collection of finite scatterers randomly distributed in a background media as shown in Fig.  5.3. The presence of these scatterers will introduce scattering and absorption to an electromagnetic wave propagating through the media. To compute the loss associated with this scattering and absorption, consider the scattering and absorption of a wave passing through a small volume $dV$ which contains a large number of particles (with a density of $n_0$ particles per unit volume) but is also larger than $\lambda ^3$.

The first case to consider is when the randomness of the particle separation is not much smaller than a wavelength, so that that their positions will not introduce coherent, correlated scattering. Under this condition, the independent scattering assumption can be utilized, and the scattering from the collection of particles is computed as the product of the particle number density and the scattering from an individual particle. The scattering, absorption, and extinction coefficients ($\kappa _s$, $\kappa _a$, $\kappa _e$ respectively) are defined as the cross-sections per unit volume, and under an independent scattering approximation these can be written as

$$\begin{aligned} \kappa _s&= n_0 \sigma _s, \; \; \; \kappa _a = n_0 \sigma _a \end{aligned}$$

(5.32)

$$\begin{aligned} \kappa _e&= \kappa _s + \kappa _a = n_0 (\sigma _s + \sigma _a). \end{aligned}$$

(5.33)

The physical interpretation of the above can be seen in the context of a THz wave of intensity $I$ traveling through a volume of scatterers over a distance $\Delta z$ and with a cross-sectional area $S$. The power extinguished due to scattering and absorption is then

$$\begin{aligned} \Delta P = - I \kappa _e S \Delta z \end{aligned}$$

(5.34)

giving the solution for the intensity as a function of distance $z$ as

$$\begin{aligned} I = I_0 e^{-\kappa _e z}. \end{aligned}$$

(5.35)

Thus $\kappa _e$ is the attenuation per unit distance due to scattering and absorption.

For many materials, the particles are not a single size, but can be described with a size distribution $p(a)$. Using the independent scattering assumption, the coefficients for the multi-size particle mixture can be written,

$$\begin{aligned} \kappa _s&= \int \limits _0^\infty \mathrm{d}a \; p(a) \; \sigma (a) \end{aligned}$$

(5.36)

$$\begin{aligned} n_0&= \int \limits _0^\infty \mathrm{d}a \; p(a) \end{aligned}$$

(5.37)

where the integration is over the particle radius, $a$. For Rayleigh scattering under the independent scattering assumption, particles with size distribution $p(a)$ give

$$\begin{aligned} \kappa _s&= \frac{8 \pi }{3} k^4 \left| \frac{\epsilon _p-\epsilon }{\epsilon _p+2\epsilon } \right| ^2 \int \limits _0^\infty \mathrm{d}a \; p(a) \; a^6 \end{aligned}$$

(5.38)

$$\begin{aligned} \kappa _a&= k \frac{Im\{ \epsilon _p\} }{\epsilon } \frac{4 \pi }{3} \left| \frac{3 \epsilon }{\epsilon _p+2\epsilon } \right| ^2 \int \limits _0^\infty \mathrm{d}a \; p(a) \; a^3, \end{aligned}$$

(5.39)

and $\kappa _e = \kappa _s + \kappa _a$.

As an example, consider a material composed of a randomly distributed collection of lactose (dielectric properties given in Fig.  5.2) spheres of radius $a$ in a background of air, with the lactose particles having a fractional volume of $f_v$. Let us assume that the particle concentration is sufficiently small that the independent scattering assumption is valid, and thus the total loss due to scattering and absorption through a distance $l$ of the material is given by $\kappa _e l$ with $\kappa _e$ given in (5.33). (Note: the independent scattering assumption for this example is examined in the next section, and it is shown that it can over-predict the amount of scattering—indicating an effective media calculation is needed.) The scattering and absorption cross-sections can be calculated with (5.30) and (5.31) if the particles are small (Rayleigh), but the general solution requires the Mie expression in (5.28) and (5.29).

The total wave extinction is due to both scattering and absorption, and the portion of the loss caused by absorption versus scattering is dependent on the particle radius. Consider the results shown in the left-hand plot of Fig.  5.5, which shows the predicted loss for single size particles with a fractional volume of 5 %, computed for three different particles radii: $a=8 \,\upmu \mathrm{m}$ (dotted line), $a= 50 \,\upmu \mathrm{m}$ (dashed line), and $a=200 \,\upmu \mathrm{m}$ (solid line). The smallest particles ($a=8 \,\upmu \mathrm{m}$) are Rayleigh scatterers at all frequencies in the 0.0–3.0 THz band, and the wave extinction through the particles is dominated by absorption. Thus, the spectral features of the extinction prominently show the peaks present in material absorption spectra (see Fig.  5.2). The largest particles ($a=200 \,\upmu \mathrm{m}$) are in the Mie regime. These particles have strong classical scattering resonances, and thus the features visible in the THz spectra are due to scattering, not the material absorption. The mid-size particles transition from Rayleigh into the Mie regime as a function of frequency, hence the lowest lactose peak (0.54 THz) is evident in the extinction curve, while the higher peaks are obscured by scattering losses.

Note the example above considered dielectric spheres in a background of air. A more common mixture in THz transmission measurements is pellets formed from pressing a sample material of interest under strong pressure to attempt to remove residual air and form a homogeneous sample. However, small residual air gaps are present in the mixture, and these can lead to scattering losses. The scattering losses can be estimated by modeling the air gaps as scatterers in a background of the dielectric material [34].

Fig. 5.5

Left-hand plot THz wave extinction (loss) for a randomly distributed collection of spherical lactose particles. The particles are a single size, and the loss is computed for three different radii: $a=8 \,\upmu \text{ m}$ (dotted line), $a= 50 \,\upmu \mathrm{m}$ (dashed-dot, and dashed lines) and $a=200 \,\upmu \mathrm{m}$ (solid line). Plot shows frequency dependence of the loss computed under the independent scattering assumption for a fractional volume of 5 %. The total extinction loss is shown in black, and is the sum of the scattering loss (red) and absorption loss (blue). Right-hand plot extinction loss as a function of fractional volume shown as predicted by the independent scattering assumption and QCA, calculated at $1.0$ THz for particles with $a= 50 \,\upmu \text{ m}$. Note the overprediction in scattering loss under the independent scattering assumption, indicating the losses in the left-hand plot are higher than expected. See text for discussion

5.4.2.1 Dense Media Calculations

In dense media, particles are close together giving rise to correlated scattering and the independent scattering approximation is not valid. In this situation, the scattering calculation needs to take into account the interaction between particles based on the statistics of their positions. There are two general approaches to achieving this. The first is to analytically compute the expectation operator to obtain an expression for the mean field properties. The second approach is to numerically calculate the field for a given ensemble of particles (taking into account correlated scattering) and then use Monte Carlo averaging to obtain the mean field statistics. The numerical approach is discussed in the next section.

One method of obtaining an analytic solution is to use the Quasi-Crystalline Approximation (QCA) [28]. In this formulation, the multi-particle conditional probability can be written using Bayes’ rule to generate a hierarchy of equations, and under the QCA, the resulting equation is truncated at the bivariate level. Thus, for QCA, the particle distribution statistics are represented with a pair distribution function, $g(r)$, which is a bivariate statistic whose value is proportional to the probability of finding any two particle separated by a distance of $r$. For statistically isotropic media in which non-penetrable particles are randomly positioned, the pair distribution function is given by the Percus Yevick (PY) pair distribution function. Several other types of particle distributions can be considered, including densely packed particles with a known size distribution or particles that exhibit some attraction or clustering behavior [35].

An approximate solution under QCA is obtained by representing the scattered wave in terms of an effective (complex) wavenumber

$$\begin{aligned} K_\mathrm{eff}=\sqrt{\epsilon _\mathrm{eff}} \omega /c. \end{aligned}$$

(5.40)

where the real part of $K_\mathrm{eff}$ represents the coherent phase progression of the wave in the random media, and the imaginary part represents the attenuation due to scattering and absorption. This effective media model can be used in the equation for the exciting field coefficient, and terms with the effective wavenumber $K_\mathrm{eff}$ balanced to satisfy a generalized Lorentz-Lorenz law. Then the Ewald-Oseen extinction theorem is used to balance the integral equation for waves traveling with the background wavenumber $k$. Physically, this ensures that the medium generates a wave that extinguishes the incident wave. This process yields a single scalar equation in the form of the Ewald-Oseen extinction theorem,

$$\begin{aligned} K_\mathrm{eff} - k = - \frac{\pi i n_0}{k^2} \sum _n (T_n^{(M)}X_n^{M}+T_n^{(N)} X_N^{(N)})\; (2n+1) . \end{aligned}$$

(5.41)

In (5.41), $X_n^{M}$ and $X_n^{N}$ are unknown amplitudes that satisfy a system of simultaneous equations resulting from the Lorentz-Lorenz law (see [28] for full detail). In general, a closed form solution can only be obtained in the low-frequency limit (i.e., small $ka$), which yields

$$\begin{aligned} K_\mathrm{eff}^2&= k^2 + \frac{3 f_v k^2 y}{1-f_v y} \left\{ 1 + i \frac{2}{3} \frac{ (ka)^3y}{1-f_vy} \times \left[ 1 + 4 \pi n_0 \int \limits _0^\infty \mathrm{d}r \; r^2 [ g(r)-1] \right] \right\} \quad \end{aligned}$$

(5.42)

where $f_v$ is the fractional volume, and $y$ is defined in (5.30). For Rayleigh particles described by the PY pair distribution (single size non-penetrable particles, statistically isotropic random placement) this reduces to

$$\begin{aligned} K_\mathrm{eff}^2&= k^2 + \frac{3 f_v k^2 y}{1-f_v y} \left\{ 1 + i \frac{2}{3} k^3 a^3 y \frac{(1-f_v)^4}{(1-f_vy)(1+2f_v)^2} \right\} . \end{aligned}$$

(5.43)

For larger values of $ka$, the solution to (5.41) can be determined numerically.

The QCA solution accounts for multiple scattering between the particles and hence can predict correlated scattering phenomenon. However, the derivation assumes that the wave moves between the particles in the background media (dielectric with permittivity $\epsilon$). For high concentrations of particles, a more accurate approach would be to use the wavenumber of the effective media for the propagating wave - or replace the wavenumber $k$ with the effective wavenumber $K_\mathrm{eff}$. This approach is called the QCA with coherent potential (QCA-CP) [28].

For dense media, the effective wavenumber, $K_\mathrm{eff}$, characterizes the coherent wave propagation, and thus the imaginary part of $2 K_\mathrm{eff}$ represents the amount of power (per unit length) extinguished in the media due to scattering and absorption. This is analogous to the extinction coefficient in (5.33), which was derived for sparse media using the independent scattering assumption. The choice of which expressions to use to estimate ($\kappa _e$ or $2 Im\{K_\mathrm{eff} \}$) depends on particle density.

An example of dense media scattering is presented in the plot in the right-hand of Fig.  5.2. The extinction loss is plotted as a function of fractional volume, $f_v$, for lactose spheres of radius $a= 50 \,\upmu \text{ m}$ in a background of air. The extinction coefficient $\kappa _e$ computed with (5.29) is shown as a dash-dot line, and the quantity $2 Im\{K_\mathrm{eff}\}$ obtained from the QCA approximation using (5.41) is shown as a dashed line. Under both approximations, the scattering increases as the particle density increases. However, since $\kappa _e$ is proportional to the particle density, it increases linearly with an increase in the fractional volume of the particles ($n_0 = f_v/v_0$) with $v_0$ denoting the volume of a single particle. Clearly this is non-physical, since in the limit of $f_v=1.0$ the material is homogenous, and the absence of particles means there should be no scattering. In contrast, the imaginary part of the QCA effective wavenumber (which accounts for absorption and scattering losses) is seen to initially increase as a function of $f_v$, agreeing at low densities with the independent scattering approximation, but then peaks and begins to decrease as the $f_v$ increases further. Thus, for appreciable particle densities, the independent scattering assumption overpredicts the amount of scattering. Comparing the curves in the right-hand plot of Fig.  5.2 at 5 % fractional volume, it can be seen the losses in the left-hand plot (under the independent scattering assumption) are about 25 % higher than predicted with a dense media (QCA) calculation (and thus the scattering is over-predicted).

5.4.3 Numerical Calculations and Monte Carlo Simulations

In 5.4.1, the T-matrix expressions were presented for a single particle, and explicit expressions were provided for Mie scattering for spherical particles. The T-matrix method can also be used for systems of particles with random positions. However, for collections of particles, each particle is excited not only by the incident electromagnetic field, but by the field scattered by all the other particles in the collection. This can be represented mathematically by writing the exciting field for the $l$th particle as

$$\begin{aligned} \bar{a}^{(e,l)} = \sum _{j=1, j\ne l}^{J} \overline{\overline{\sigma }}(k \overline{r}_{lj}) \; \overline{\overline{T}} \; \overline{a}^{(e,j)} + e^{i \overline{k}_i \cdot \overline{r}_l} \overline{a}_{\text{ inc}} \end{aligned}$$

(5.44)

where $\overline{a}_{\text{ inc}}$ is a vector of the incident field coefficients, $\overline{\overline{\sigma }}(k\overline{r})$ is a $2L_{\text{ max}} \times 2L_{\text{ max}}$ matrix of terms accounting for a coordinate transformation, $\overline{r}_{lj}= \overline{r}_j - \overline{r_l}$ is the vector pointing from center of the $l$th particle to the center of the $j$th particle, and $\overline{\overline{T}}$ is the T-matrix for the particles, as given in (5.27) for spherical particle. The physical interpretation of (5.44) is that the excitation for the $l$th particle in the system is a combination of the incident wave and the waves scattered from all the other ($j=1..J, j \ne l$) particles in the system. Once $\overline{a}^{(e,l)}$ is determined, the scattered field coefficients can be computed using (5.24) to compute the scattered field coefficients and hence the scattered field.

The expression in (5.44) is a rigorously derived expression for the scattered field that includes all orders of multiple scattering. However, the solution for the coefficients depend on the exact position and nature (shape, orientation, etc.) of the particles; they are thus difficult to solve exactly for most practical problems. For some problems, an iterative numerical approach can be employed [36].

Another option is to calculate the solution using a numerical approach based on the discretization of Maxwell’s equations. For time-domain THz systems, a particularly appropriate method is the Finite Difference Time Domain (FDTD) approach, because the broadband data is generated in a single simulation pass. The FDTD method originally reported by Yee is based on a discrete approximation of the point form of Maxwells equations [37]. This basic algorithm breaks the simulation space into discrete points where the electric and magnetic fields are sampled in space and time. Furthermore, FDTD allows computation of dielectric media which can contain both volume scatterers and rough interfaces; the complexity of the material is limited only on the ability to capture the material characteristics in a discretely sampled representation. FDTD has been used extensively for electromagnetic scattering calculations, and has more recently applied to THz sensing [23]; see [22] for a complete background.

The electromagnetic field calculated for a single ensemble of particles represents the response for a single realization, but does not provide the mean field properties. In the previous section, the mean (or coherent) field was obtained by computing an analytical expectation operator. For numerical computations, a Monte Carlo approach can be used to generate a number of realizations drawn from the same statistical characterization, and then computing the mean field by coherently averaging over a sufficiently large number of realizations. To separate the coherent and incoherent components, the scattered field is averaged to give the coherent scattered field. The coherent scattered field is calculated by

$$\begin{aligned} \langle \overline{ E}_s \rangle = \frac{1}{N_r} \sum _{q=1}^{N_r} \overline{E}_s^{q} \end{aligned}$$

(5.45)

where $q$ is the realization index with $q = 1,2, . .N_r$ realizations, and $\overline{E}_s^{q}$ is the scattered field from the elemental volume of many scatterers (includes their coherent near and intermediate range interactions). The incoherent field is the difference between the total field and the coherent field $\overline{\mathcal{E}}_s^{q} = \overline{ E}_s^{q} - \langle \overline{ E}_s \rangle$. Calculation of the scattering coefficient $\kappa _s$ from the incoherent scattered field $\overline{ \mathcal{E}}_s$ can be expressed as

$$\begin{aligned} \kappa _s = \frac{1}{V} \int \limits _{0}^{\pi } \text{ d}\theta _s \sin (\theta _s) \int \limits _{0}^{2 \pi } \text{ d} \phi _s \frac{R^2}{N_r} \sum _{q=1}^{N_r} | \overline{\mathcal{E}}_s^q|^2. \end{aligned}$$

(5.46)

Note that the Monte Carlo approach is a valid approach for computing the field propagating through a random distribution of particles, as well as for computing the field scattered from a rough surface interface.

5.5 Conclusions

This chapter provided short introduction into eletromagnetic phenomenon observed in THz applications. In particular, it described the reflection and scattering of THz waves from flat or rough interfaces, and the scattering and absorption of THz waves through materials with volume inhomogeneities (such as grains). Since the length scale of many naturally occurring media are comparable to the THz wavelength, some of the scattering effects can be quite pronounced, and can be visible in the material spectra