Complex Refractive Index Determination Using Planar and Converging Beam Transfer Functions

Abstract

Terahertz time domain spectroscopy can help us to determine the complex refractive index of materials. To achieve this a theoretical model of the spectrometer has to be implemented; a usual method for refractive index determination is to fit a theoretically calculated transfer function to the experimental data. Material parameter extraction models based on transfer functions can be of varying complexity based on the requirements for accuracy and also the difficulty of factoring all experimental parameters. Here, we are going to show how algorithms based on transfer functions with different complexity can be setup. It will be described how a transfer function can be used to extract the refractive index of material and the key stages of the analysis, the fitting algorithm, and the need for phase unwrapping. Transfer functions of an increasing complexity will be shown, with and without the etalon term, using planar or converging beam.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

4.1 Material Parameter Extraction Using a Transfer Function

Terahertz time domain spectroscopy can help us to determine the complex refractive index of materials. To achieve this a theoretical model of the spectrometer has to be implemented; a usual method for refractive index determination is to fit a theoretically calculated transfer function to the experimental data. Material parameter extraction models based on transfer functions can be of varying complexity based on the requirements for accuracy and also the difficulty of factoring all experimental parameters. There is a lot of research that treats a planar THz wave case, one of the first publications in the subject were from Duvillaret et al. [1, 2], where a transfer function is used with and without etalon effects. The same group in [2] extends their work in a treatment that also calculates the thickness of the sample. There is an ongoing research that treats the problem of material parameter determination in time domain experiments usually focussing in specific material systems [3–7].

At present, the most commonly used refractive index extraction methods are based on theoretical transfer functions that assume a plane wave and neglect the etalon effect. The etalon effect can be ignored if the data are truncated, so multiple reflections are not present. This is acceptable in thick samples or scattering samples but limits the accuracy of parameter extraction on thin samples with a strong etalon effect. Furthermore, the effect of the converging beam until now has not been investigated; using a planar THz beam treatment is correct when parallel beams are used and is likely to incur an acceptably small accuracy penalty when only slow focusing beams are used. However, this may restrict the accuracy of the calculated refractive index especially when strongly converging THz beams are used, e.g., in THz imaging. There is published research calculating or characterizing the beam of a THz system [8–12] and limited experimental investigation showing the difference on the material parameter extraction when a converging beam or plane beam was used [13]. Recently, we have presented our work, which compares a traditional planar algorithm to a converging beam algorithm [14]. Furthermore, there is recent work on Gaussian beam propagation used for THz material parameter extraction without taking into account multiple reflections [15].

Here, we are going to show how algorithms based on transfer functions with different complexity can be setup. It will be described how a transfer function can be used to extract the refractive index of material and the key stages of the analysis, the fitting algorithm, and the need for phase unwrapping. Transfer functions of an increasing complexity will be shown, with and without the etalon term, using planar or converging beam. Results shown will be analyzed using the algorithms as examples to show what is the expected behavior of transfer function extraction algorithms and also to show where a complex THz extraction algorithm can be useful.

4.2 Planar Transfer Function Algorithm

4.2.1 Experimental and Theoretical Transfer Function

A transfer function fully characterizes the effect of the material on an arbitrary input electric field, it describes mathematically the relation of input and output signals on a system, which is linear and time-invariant. It can be written as,

$$\begin{aligned} Y(\omega ) = H(\omega )X(\omega ) \end{aligned}$$

(4.1)

where $X(\omega )$ is the input electric field in the frequency domain, $Y(\omega )$ is the spectrum of the output electric field, and $H(\omega )$ is the transfer function of the material. Time invariance and linearity can be assumed true in a THz spectrometer. In the case of a THz spectrometer the input should be the THz electromagnetic wave generated by the emitter and the output should be the wave after it is transmitted through the investigated material system. In practice the experimental transfer function is easily calculated when performing a THz-TDS experiment using the relation:

$$\begin{aligned} H_{\rm experiment} (\omega ,\tilde{n})=\frac{S_{\rm sample} (\omega )}{S_{\rm reference} (\omega )} \end{aligned}$$

(4.2)

The transfer function is the ratio of one measurement with the sample and one measurement without the sample, usually called, reference scan. As everything in the system, up to the material, and after it, is the same for both measurements, all these elements cancel out and the ratio of the reference and sample scan reveals only the transfer function of the sample.

The complex refractive index can be determined by comparing the experimental transfer function to a theoretical transfer function of the material. Both of the transfer functions are dependent on the complex refractive index. To construct the theoretical transfer function the electric field propagation through the material is modeled using the Fresnel coefficients and propagation in their usual terminology.

$$\begin{aligned} R_{ab}&=\frac{\tilde{n}_a -\tilde{n}_b }{\tilde{n}_a +\tilde{n}_b }\end{aligned}$$

(4.3)

$$\begin{aligned} P_a&=\exp \left( {-\frac{i\tilde{n}_a \omega l}{c}} \right)\end{aligned}$$

(4.4)

$$\begin{aligned} E(\omega )&=n(\omega )\cdot P_1 (\omega ,l_1 )\cdot T_{12} \cdot P_2 (\omega ,l_2 )\cdot T_{21} \cdot P_1 (\omega ,l_1 )\nonumber \\&\quad \cdot \sum _{k=0}^\infty {[R_{21} \cdot P_2 (\omega ,l_2 )\cdot R_{21} \cdot P_2 (\omega ,l_2 )} ]^{k} \end{aligned}$$

(4.5)

This is the electric field of the THz wave passing through the air, which is material 1, and a bulk sample, material 2, then air again, and finally it reaches the detector antenna. Here the length of propagation in air is chosen to be $l_1$ from the emitter to the sample and equal from the sample to the detector. The length of propagation in the sample has been chosen to be $l_2$. The sum series represents the internal reflections in the sample that can be omitted for simplified analysis. In order to extract a transfer function for the system we will have to divide this with a reference electric field, which is only propagation in air; the transfer function including the etalon effect of the sample will be

$$\begin{aligned} H_{{\rm model}} (\omega ,\tilde{n})&= \frac{{E(\omega )_{{\rm sample}} }}{{E(\omega )_{{\rm reference}} }}\nonumber \\&= \frac{{T_{12} \cdot P_{2} (\omega ,l_{2} ) \cdot T_{{21}} \cdot \sum \nolimits _{{k = 0}}^{\infty } {[R_{{21}} \cdot P_{2} (\omega ,l_{2} ) \cdot R_{{21}} \cdot P_{2} (\omega ,l_{2} )} ]^{k} }}{{P_{1} (\omega ,l_{2} )}} \end{aligned}$$

(4.6)

This expression is a function of the complex refractive index; therefore, we have to vary the refractive index in this expression in order to equalize it to the experimental transfer function. When the fit is correct, of course the refractive index of the material versus frequency is revealed. The Newton–Raphson method maybe the simplest method that can be used to fit, which is an iterative method for finding the roots of functions.

$$\begin{aligned} \tilde{n}_{{x + 1}} = \tilde{n}_{x} - \frac{{f(\tilde{n}_{x} )}}{{f^{\prime }(\tilde{n}_{x} )}} \end{aligned}$$

(4.7)

The variable parameter $\tilde{n}$ is the complex refractive index, which is estimated for each frequency component. The function used contains the difference of the natural logarithm of each transfer function, the function is calculated and the root is found for each frequency component.

$$\begin{aligned} f(\omega ,\tilde{n}) = \ln (H_{{\rm model}} (\omega ,\tilde{n})) - \ln (H_{{\rm experiment}} (\omega ,\tilde{n})) \end{aligned}$$

(4.8)

The method would also work with a function that would be the difference of the transfer functions. The reason why natural logarithm is considered more convenient is because it naturally derestricts the phase of the theoretical transfer function; therefore, there is no need to unwrap its phase. Except Newton–Raphson it is possible to also use minimization algorithms to extract the refractive index, the target is to find an algorithm that will scale favorably with number of points in order to give acceptable computation times. However, in general, a parameter extraction algorithm will usually complete within a minute; therefore, algorithm efficiency is rarely a problem.

In Fig. 4.1, it can be seen how a planar algorithm with internal reflections can be used to extract the refractive index of quartz and how mismatching the thickness will create ripples in the refractive index, which show that the modeled etalon is not matching the real thickness of the sample. It has to be noted that experimental errors especially related with the delay line, such as starting points or stepping errors can give similar effects as they affect the delays between the reference pulse and the delayed pulse and pulse echoes observed with transmission through the sample. In essence, these are violations of the time-invariance condition that usually stem from instabilities of temperature or laser noise. Therefore, although an extraction algorithm can be used to determine thickness it is better if thickness is measured with an alternative method to reduce uncertainty and reveal potential errors.

When deciding on an appropriate transfer function for the experiment the number of reflections should be considered. The simpler case is to completely ignore reflection terms in the theoretical transfer function; then the data should also be truncated before the first reflection, which also limits frequency resolution. The importance of etalon effects depends on the nature of the sample: transparent, thin, high index samples with polished faces will exhibit strong etalon effects. Thick, porous samples with scattering surfaces have negligible etalon effects but may show other types of complex behavior that may require use of the Kramers–Kronig relation to be analyzed.

Fig. 4.1

Real part of the refractive index for a 0.5 mm quartz sample, the extraction was made by a planar algorithm that used the transfer function of Eq. 4.6 and by varying the thickness of the sample by 10 $\upmu\rm {m}$ steps

4.2.2 Phase Unwrapping

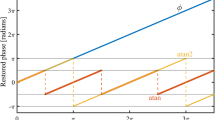
Phase unwrapping is a process, which is applied to the experimental transfer function to recover the correct phase. The reason for phase unwrapping is that the output of sinusoidal functions is ambiguous, that is, to say for a given output of a sinusoidal function there are multiple solutions. Therefore, when using the output of sinusoidal functions to calculate the phase of a transmitted EM wave, this is restricted between the range of plus and minus $\pi$. However, the real solution is a multiple number of 2$\pi$’s of the calculated phase. As an example let us assume propagation through a thickness d of material of refractive index n, so that is given by $\exp (-in\omega d/c)$; there are multiple values of n such that $n\omega d/c$ differs by 2$\pi$. In the case of the experimental transfer function the phase has a saw tooth appearance however it should vary sequentially as the frequency varies because the wavelength is becoming smaller with respect to the sample thickness. Because we know from physics that discontinuities in phase are not due to discontinuities of the refractive index we can attribute them to phase changes of 2$\pi$. Thus, the phase unwrapping algorithm works by detecting erroneous jumps in phase, which are then corrected by a multiple of 2$\pi$’s; the results can be seen in Fig. 4.2. The phase unwrapping should begin at the peak of high SNR and extrapolate to zero frequency as this produces the most accurate results. Starting the phase unwrapping at low or high frequencies where the SNR is low usually puts an artificial bias to the calculated refractive index.

In conclusion, the Newton–Raphson method applied to the raw transfer function converges on a complex number, which is a root of a function for which there are multiple solutions; phase unwrapping allows the Newton–Raphson method to converge to the correct solution. Taking the natural logarithm of the transfer functions can separate the amplitude and phase of the theoretical transfer function into the real and imaginary terms, this improves the fitting process because it produces a linear imaginary term and ensures that the phase of at least the theoretical transfer function is no longer ambiguous.

Fig. 4.2

Phase unwrapping of a transfer function

4.3 Modeling a Converging Beam

At the focus of a THz spectrometer the wavefront is planar, but it still contains a spectrum of wavevectors; consequently, it is not a plane wave and the propagation through the sample cannot be represented by a single-phase retardation. Therefore, even if the sample is placed in the focus of the spectrometer a converging beam has to be theoretically used. Here we will build a converging focusing beam of a THz setup using a summation of plane waves propagated at different angles. This analysis of converging beam through the sample does not depend on the position of the sample.

In order to define our problem, axes are taken with the z-axis normal to the plane of the sample and y-axis parallel to the dipole transmitter axis. It is convenient to let x, y and z to be unit vectors along the axes. The field of a transmitting dipole is expressed as an angular spectrum of plane waves and then the angles, which are used to form an image of the dipole antenna on the sample, are limited. The electric field of a transmitting dipole can be derived [16] from a Hertz vector along y using

$$\begin{aligned} {\mathbf E } = \nabla \nabla \cdot {\varvec{\Pi }} + {\mathbf k }^{2} \varvec{\Pi } \end{aligned}$$

(4.9)

and $\varvec{\Pi }$ has only a $y$ component

$$\begin{aligned} \varvec{\Pi }_{y} = \frac{{e^{{ikr}} }}{r} \end{aligned}$$

(4.10)

Specifically,

$$\begin{aligned} E_{x} = \frac{{\partial ^{2} \varvec{\Pi }}}{{\partial x\partial y}},\quad E_{y} = \left( {k^{2} \varvec{\Pi }+ \frac{{\partial ^{2} \varvec{\Pi }}}{{\partial y^{2} }}} \right),\quad E_{z} = \frac{{\partial ^{2} \varvec{\Pi }}}{{\partial y\partial z}} \end{aligned}$$

(4.11)

The spherically symmetric quantity $\varvec{\Pi }_{y}$ can be written

$$\begin{aligned} \varvec{\Pi }= \frac{{e^{{ikr}} }}{r} = \frac{i}{{2\pi }}\int \limits _{{ - \infty }}^{\infty } {\int \limits _{{ - \infty }}^{\infty } {\frac{{e^{{i\mathbf k \varvec{\cdot }\mathbf r }} }}{{\sqrt{k^{2} - k_{1} ^{2} - k_{2} ^{2} } }}dk_{1} dk_{2} } } \end{aligned}$$

(4.12)

where $k_{1}^{2} + k_{2}^{2} + k_{3}^{2} = k^{2} = \omega ^{2} /c^{2}$, where ${\mathbf k_1}$, ${\mathbf k_2}$ and ${\mathbf k_3}$ are the orthogonal components of the wavevector $k$, and ${\mathbf k_3}$ is the propagation direction.

4.3.1 Angular Weighting Function

We will introduce a weighting function $W(k_{1},k_{2})$ to account for the fact that waves with only a limited range of directions contribute to the image. This will take into account the effect of the parabolic lenses used in a typical Terahertz experiment. The simplest model would be a sharp cutoff at some angle; however, this would create large oscillations in the field along the $z$-axis, which may complicate the results. These oscillations can be thought of as Fresnel diffraction; as one moves along the axis different numbers of Fresnel zones are included in the angular spectrum. It is clear that the easiest case to analyze would be a gentle cut-off and an obvious model is a Gaussian. The beam out of a silicon lens can be approximated with a Gaussian as shown in [17]. In neither case can the necessary integral be done analytically but we know that if we use a smooth (Gaussian-like) cutoff in the angular spectrum this should produce a smooth focus without diffraction oscillations. Of course, in most experiments the parabolic lens is going to most likely impose a cutoff value for the angles of the experiment. This cutoff is going to be more important for low frequencies where the diffraction can make the spread of angles emitted by the antenna greater than the acceptance angle of the parabolic. Therefore, it is also important that we match the dependence of the angular spread as a function of frequency. Although it is possible to characterize or simulate the beam profile of a THz system [8–11] it is quite impractical as it is quite likely that small changes such as a new antenna or different lenses would make a significant and difficult to predict change. Therefore, the easiest way to find the appropriate weighting function for a measurement is to try different functions and different frequency dependencies and choose the one that better fits our data. Of course the type of parabolics, the gap of the antennas, the existence, or not of a silicon lens, can give significant insight on the parameters that should be chosen.

4.3.2 Transmission of the Converging Beam Through a Slab

The electric field components are obtained by doing the differentiations set out above in Eq. 4.11, this introduces factors of

$$\begin{aligned} {\mathbf E }(k_{1} ,k_{2} ) = \left( {\frac{{k_{1} k_{2} }}{{k^{2} }}, - \frac{{(k^{2} - k_{2}^{2} )}}{{k^{2} }},\frac{{k_{2} k_{3} }}{{k^{2} }}} \right) \end{aligned}$$

(4.13)

This shows that ${\mathbf k } \cdot {\mathbf E } = 0$ so $\mathbf E$ is perpendicular to $\mathbf k$ as is required for a transverse wave. $\mathbf E$ lies in the plane of $\mathbf k$ and $\mathbf y$, also,

$$\begin{aligned} \left| E \right|^{2} = 1 - k_{2}^{2} /k^{2} = 1 - \cos ^{2} \alpha \end{aligned}$$

(4.14)

where $\alpha$ is the angle between $\mathbf k$ and y-axis, so the magnitude of E is $\sin \alpha$ as required for dipole radiation. To work out the reflection and transmission coefficients this electric field must be resolved into components $\mathbf E _{\parallel }$ in the plane of incidence and $\mathbf E _{\perp }$ normal to the plane of incidence. The plane of incidence is that containing k and z so the vector $\mathbf k \times \mathbf z = (k_2, -k_1, 0)$ is perpendicular to it and a unit vector in this direction is ${\mathbf p } = (k_{2} /\bar{k}, - k_{1} /\bar{k},0)$ where $\bar{k}^{2} = k_{1}^{2} + k_{2}^{2}$. The perpendicular component of $\mathbf E$ normalized is therefore

$$\begin{aligned} {\mathbf E }_{ \bot } = ({\mathbf E } \cdot {\mathbf p }){\mathbf p } = \frac{{k_{1} }}{{\bar{k}}}{\mathbf p } = \left( {\frac{{k_{1} k_{2} }}{{\bar{k}^{2} }}, - \frac{{k_{1}^{2} }}{{\bar{k}^{2} }},0} \right) \end{aligned}$$

(4.15)

and the parallel component can be computed as

$$\begin{aligned} {\mathbf E }_{\parallel } = {\mathbf E } - {\mathbf E }_{ \bot } = \left( { - \frac{{k_{1} k_{2} k_{3}^{2} }}{{k^{2} \bar{k}^{2} }}, - \frac{{k_{2}^{2} k_{3}^{2} }}{{k^{2} \bar{k}^{2} }},\frac{{k_{2} k_{3} }}{{k^{2} }}} \right) \end{aligned}$$

(4.16)

At the first surface of the sample the angle of incidence is given by $\cos \theta _{1} = k_{3} /k$ or $\sin \theta _{1} = \bar{k}/k$ and the angle of the transmitted wave $\theta _{2}$ by $n_{1} \sin \theta _{1} = n_{2} \sin \theta _{2}$. The path length in the sample is $D/\cos \theta _{2}$ where D is the sample thickness and this introduces a phase shift represented by multiplying the electric fields by $P_{2} = \exp ( - ikD(n_{2} \cos \theta _{2} - n_{1} \cos \theta _{1})).$

The reflection and transmission coefficients are:

$$\begin{aligned} \begin{array}{l} \displaystyle r_{ \bot } = \frac{{n_{i} \cos \theta _{i} - n_{t} \cos \theta _{t} }}{{n_{i} \cos \theta _{i} + n_{t} \cos \theta _{t} }}\qquad r_{\parallel } = \frac{{n_{t} \cos \theta _{i} - n_{i} \cos \theta _{t} }}{{n_{i} \cos \theta _{t} + n_{t} \cos \theta _{i} }}\\ [12pt] \displaystyle t_{ \bot } = \frac{{2n_{i} \cos \theta _{i} }}{{n_{i} \cos \theta _{i} + n_{t} \cos \theta _{t} }}\qquad t_{\parallel } = \frac{{2n_{i} \cos \theta _{i} }}{{n_{i} \cos \theta _{t} + n_{t} \cos \theta _{i} }} \end{array} \end{aligned}$$

(4.17)

where $n_i$ and $n_t$ are the refractive indices and $\theta _i$ and $\theta _t$ are the angles of incidence and transmission appropriate for the interface involved.

The direct transmission through the sample then involves, transmission through the first interface, propagation to the second interface and transmission through the second interface, which multiplies the field by $T_{2} P_{2} T_{1}$ where, $T_{1} = t(\theta _{1} ,\theta _{2})$ and $T_{2} = t(\theta _{2} ,\theta _{1})$.

Transmission with one pair of internal produces a factor of $T_{2} (P_{2}^{2} R^{2} )P_{2} T_{1}$. For a thin sample the above series can be summed to yield an overall factor $F = T_{2} [1 - P_{2}^{2} R^{2} ]^{{ - 1}} (P_{2} /P_{1} )T_{1}$.

The electric field of the emerging wave is then:

$$\begin{aligned} {\mathbf E } = F_{\parallel } {\mathbf E }_{\parallel } + F_{ \bot } {\mathbf E }_{ \bot } \end{aligned}$$

(4.18)

The emerging waves are focused on the detector. The focusing lens or mirror is a device that introduces phase delays so that all the waves arrive at the detector simultaneously. The signal at the detector is therefore obtained by summing over all $k_1$ and $k_2$. As mentioned above we will introduce a weighting function $W(k_{1} ,k_{2})$ at least to cutoff the waves traveling at large angles to the axis. The final result is that the detected signal is

$$\begin{aligned} \int {\int {\frac{{W(k_{1} ,k_{2} )}}{{k_{3} }}} } \left( {F_{\parallel } (k_{3} ){\mathbf E }_{\parallel } + F_{ \bot } (k_{3} ){\mathbf E }_{ \bot } } \right)dk_{1} dk_{2} \end{aligned}$$

(4.19)

The x and z components are antisymmetric in either $k_1$ or $k_2$ and so the integrals vanish and, as expected, there is only a y component at the focus. If we convert to polar coordinates $\bar{k} = k\sin \theta$ and $k_{3} = k\cos \theta$ the final result is

$$\begin{aligned} - \pi \int _{0}^{{\theta _{\max }}} W (\theta )[\cos ^{2} \theta F_{\parallel } (\theta ) + F_{ \bot } (\theta )]\sin \theta d\theta \end{aligned}$$

(4.20)

The upper limit of $\infty$ is irrelevant because the weight $W(\bar{k})$ is intended to reduce the integrand to zero at some finite $\bar{k}$. The reference signal can be obtained by writing $n_{1} = n_{2} = 1$ when $F_{\parallel }$ and $F_{ \bot }$ are both equal to unity. The transfer function is therefore obtained by dividing, Eq.4.20 with

$$\begin{aligned} \int _{0}^{{\theta _{\max }}} W (\theta )(1 + \cos ^{2} \theta )\sin \theta d\theta \end{aligned}$$

(4.21)

These values must be compared with the transfer function for a plane wave, which in this notation is just $F_{ \bot } (0)$. The calculation of the transmission of the converging beam through the sample requires the numerical evaluation of these integrals during the fitting process; however, the integrands are smooth and this is not a significant computational burden.

4.3.3 Phase Unwrapping in a Converging Algorithm

In the converging beam case, it is difficult to perform phase unwrapping because each wave for a single frequency undergoes a different phase shift. Whereas in the case of the planar beam we could derive the logarithm of the theoretical transfer function and thus extract the phase; we cannot do the same in the converging beam. Therefore, the converging beam transfer function is fitted to the experimental amplitude and raw phase. To improve the extraction process we use a plane wave algorithm first to find the approximate value for the refractive index, which is then set as the initial refractive index value for the converging beam extraction. The fitting process used again is the Newton–Raphson method.

4.3.4 Simulated Data

Simulated data were produced in order to show how the converging beam algorithm works. To produce simulated converging beam data a reference scan from a converging beam setup was used. The converging beam code was applied to this reference scan with a known angular distribution, refractive index and thickness. The simulated data used in Fig. 4.3 had an angular distribution of $\pm 30\,^{\circ }$ for all frequencies, refractive index of $2.0 - 0.005i$, and thickness of 2 mm. Figure 4.3 shows the converging beam algorithm extracting the correct complex refractive index. Figure 4.4 shows the plane wave extraction on the same data, there are oscillations present on the complex refractive index, which are consistent with the sample thickness. The plane wave algorithm fails to remove these etalon oscillations, which originate from the amplitude of the transfer function.

Figure 4.5 shows the converging beam extraction on the same data; however, the extraction parameters use an angular distribution of $\pm 25\,^{\circ }$ where as the data were produced with an angular spectrum of $\pm 30\,^{\circ }$. The complex refractive index has oscillations similar to the plane wave extraction. The oscillations are due to the incorrect calculation of the phase and amplitude, which is caused by the difference between the actual length of propagation in the data and the assumed length of propagation for the extraction. The amplitude of the oscillations in the complex refractive index decreases with increasing frequency because the number of wavelengths present in the sample increases; therefore, the total effect of these wavelengths has a smaller effect on the error. The simulated data show that the plane wave approximation is theoretically inadequate for simulated converging beams and that in order to correctly extract the converging beam data the correct angular distribution must be used.

Fig. 4.3

The resultant complex refractive index extracted using converging algorithm for simulated converging beam data. The simulated data had an angular distribution of $\pm 30\,^{\circ }$, refractive index $2.0-0.005i$ and thickness of 2 mm

Fig. 4.4

The resultant complex refractive index extracted using plane wave algorithm for simulated converging beam data. The simulated data had an angular distribution of $\pm 30\,^{\circ }$, refractive index $2.0-0.005i$ and thickness of 2 mm

Fig. 4.5

Extraction using converging beam algorithm with a mismatch of angle $\pm 25\,^{\circ }$. The simulated data had an angular distribution of $\pm 30\,^{\circ }$, refractive index $2.0-0.005i$, and thickness of 2 mm

4.4 Experimental Data

Figure 4.6 shows the converging beam algorithm processed on data from a THz-TDS setup for a 2 mm crystalline quartz window. The setup had a converging geometry (f:2) and the sample was placed in the beam focus. The setup used photoconductive emitter and receiver with Si lenses. For these results we have used a square weighting function with smooth edges that vary its width to match our sample better. The angular spread used starts from the planar option and increased in small steps. The angular spread also varies with frequency using an 1/f dependence. There is also a hard cutoff, which restricts the angle to 0.35 radians and is significant at low frequencies (${<}500$ GHz). Figure 4.6 shows how the converging beam algorithm extracts the complex refractive index of quartz and that when using different angular spectra, there is difference in the amplitude of the etalon oscillations, which can be used to judge how good is the match with the experimental conditions. In a converging beam geometry such as the one used here, the THz beam is undergoing in average higher phase retardation than the nominal thickness of the sample. This difference is depending on the spread of angles in the experiment. This results in that using the planar algorithm the thickness is slightly underestimated and therefore the refractive index will be slightly overestimated. This can also be seen in Fig. 4.6.

Fig. 4.6

The resultant complex refractive index extracted for a 2 mm quartz sample placed at the focus of the beam in THz-TDS setup

The results shown in Fig. 4.6 were taken in a setup with a slow focusing lens system. Still, there are improvements over the plane wave algorithm (0 radians line) if we use as a criterion the refractive index oscillations, which we know is an artifact of the data extraction process. However, comparison between the algorithms can be quite difficult to quantify objectively; the refractive index oscillations in the planar case are approximately $2\cdot 10^{-3}$, which for a lot of purposes may not present a problem. What all this analysis shows is that the extraction algorithm should be chosen according to the required accuracy and taking into account the complexity of the algorithm. There are a lot of options in building an extraction algorithm based on a transfer function and a lot of decisions in which the scenario fits best with each case.

4.5 Conclusions

We have described in this chapter how a transfer function can be used to extract the refractive index of materials investigated in a THz-TDS and the key stages of the analysis such as the fitting algorithm and the need for phase unwrapping. Transfer functions of an increasing complexity have been shown with and without the etalon term, using planar or converging beam. The etalon effect can be ignored if the data are truncated, so multiple reflections are not present. This is generally acceptable in thick samples or scattering samples but limits the accuracy of parameter extraction on thin samples with a strong etalon effect. Also, using a planar THz beam treatment is correct when parallel beams are used and is likely to incur an acceptably small accuracy penalty when only slow focusing beams are used. However, this may restrict the accuracy of the calculated refractive index especially when strongly converging THz beams are used, e.g., in THz imaging.

We have shown that refractive index oscillations present in analyzed THz data are an artifact of the data extraction process and show a mismatch between the experimental data and the theoretical transfer function. The extracted refractive indices in Fig. 4.1 show how minimization of the refractive index oscillations can help to identify the thickness of a sample. Similarly, in Fig. 4.6 we have analyzed with a converging beam algorithm, data that were taken in a setup with a slow focusing lens system, and we have used the minimization of refractive index oscillations to identify the correct angular profile for extraction. However, concluding, we should stretch that almost any mismatch between the experiment and the theoretical transfer function will result to oscillations in the refractive index, e.g., delay line errors such as time offset between reference and sample scan or changing sampling interval; tilted sample orientation; wrong phase interpolation, etc. Therefore, someone has to be very careful to draw conclusions only based on the refractive index oscillations as thickness or angular profile may mask other experimental errors. The thickness of the sample or the angular profile of the THz-TDS should be measured experimentally in order for the results of an extraction algorithm to be verified.

Therefore, there are a lot of options in building a transfer function extraction algorithm and a lot of decisions in which scenario fits best with each case. Comparison between algorithms can be quite difficult to quantify objectively; the refractive index oscillations in the planar case are approximately $2 \cdot 10^{-3}$, which for a lot of purposes may not present a problem. This shows that the extraction algorithm should be chosen according to the required accuracy and taking into account the complexity of the algorithm.