Terahertz Spectroscopy: Ellipsometry and Active Polarization Control of Terahertz Waves

Abstract

The principles and experimental methods of terahertz (THz) wave ellipsometry are described. The procedure to determine diagonal and off-diagonal components of the complex dielectric tensor for materials using THz time domain spectroscopy in transmission and oblique reflection geometries are explained. The measured optical activity in artificial chiral grating structures is also described as applications of this technique.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

11.1 Introduction

Terahertz (THz) time domain spectroscopy (TDS) provides phase- sensitive information on electromagnetic responses and enables one to determine complex dielectric functions of materials. It is natural to extend this technique to polarization-sensitive measurements, to determine both the diagonal and off-diagonal components of the complex dielectric tensor. It has strong potential for various applications including magneto-optical measurements for non-contact Hall mobility measurements [1, 2], detection of chiral molecules and sensing for biological applications [3, 4]. Recently, with improved sensitivity of polarization rotation [5], quantum hall effects have been clearly confirmed in the THz frequency region [6].

In this section, first, a method for THz time domain ellipsometry in transmission mode is described. Experimental results for the measurement of polarization effects of artificial chiral structures are given. Second, THz-TDS for magneto-optical effects measured in oblique reflection mode are given. Explicit expressions between polarization parameters and dielectric tensors are formulated. As an application, the results of active polarization control of THz waves are also demonstrated.

11.2 Transmission-Mode Time Domain Ellipsometry

11.2.1 Method of Polarization State Measurement with Wire-Grid Polarizers

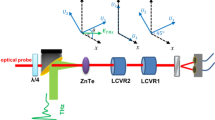
In THz-TDS, a nonlinear optical crystal or a detection antenna is used for THz-wave detection. They are sensitive to the direction of polarization of a THz wave. Therefore, a wire-grid polarizer (WGP) is usually placed in front of these devices, in order to determine the polarization direction of a detected THz wave. Placing another WGP in front of the WGP enables one to measure the polarization states of a THz wave. Here, electro-optic (EO) sampling measurement with ZnTe crystal is considered as shown in Fig. 11.1. WGP1 is placed in order to make the polarization direction of detected THz wave oriented parallel to x-axis to maximize the sensitivity of THz-wave detection.

Fig. 11.1

Schematics of experimental setup for polarization state measurements of a THz wave with wire-grid polarizers

The relation between the electric field vector incident on WGP2, $\tilde{E}$, and the electric field vector incident on ZnTe crystal, $\tilde{F}$, is described as

$$\begin{aligned} \tilde{F}&=[\begin{array}{ll}{1}&\quad {0}\end{array}]\left[\begin{array}{ll}\cos {\theta }&{-\sin }{\theta }\\ \sin {\theta }&\quad {\cos }{\theta }\end{array}\right] \left[\begin{array}{ll}{1}&\quad {0}\\ {0}&\quad {0}\end{array}\right]\left[\begin{array}{ll}\cos {\theta }&\quad {\sin }{\theta }\\ {-\sin }{\theta }&\quad \cos {\theta }\end{array}\right]\tilde{E}\nonumber \\&=\left[\begin{array}{ll}{\cos }^{2}{\theta }&\quad {\sin }{\theta } \cos {\theta }\end{array}\right]\left[\begin{array}{l}\tilde{E}_{x}\\ \tilde{E}_{y}\end{array}\right], \end{aligned}$$

(11.1)

where $\theta$ is the angle between the y-axis and the direction of polarization for WGP2 as shown in Fig. 11.1. Therefore, each component of $\tilde{E}$ is determined by performing measurements with different values of $\theta _{1}$ and $\theta _{2}$. From the measured amplitude ${\theta }$ from the measurement at $\theta _{1}$ and $\theta _{2}$, $\tilde{E}$ is calculated as

$$\begin{aligned}&{}\left[\begin{array}{l}\tilde{E}_{x}\\ \tilde{E}_{y}\end{array}\right]=\left[\begin{array}{ll}\cos ^{2}{\theta }_{1}&\quad {\sin }{\theta }_{1} \cos {\theta }_{1}\\ \cos ^{2}{\theta }_{2}&\quad \sin {\theta }_{2}\cos {\theta }_{2}\end{array}\right]^{-1}\left[\begin{array}{l}\tilde{F}_{1}\\ \tilde{F}_{2}\end{array}\right]\nonumber \\&=\frac{1}{{\cos }{\theta }_{1}\cos {\theta }_{2}{\sin }({\theta }_{2}-{\theta }_{1})} \left[\begin{array}{ll}\sin {\theta }_{2}\cos {\theta }_{2}&\quad -\sin {\theta }_{1} \cos \theta _{1}\\ -\cos ^{2}{\theta }_{2}&\quad \cos ^{2}{\theta }_{1} \cos \theta _{1}\end{array}\right]\left[\begin{array}{l}\tilde{F}_{1}\\ \tilde{F}_{2}\end{array}\right]. \end{aligned}$$

(11.2)

If we set $\theta _{1}={-\pi }/4$ and $\theta _{2}=\pi /4$,

$$\begin{aligned} \left[\begin{array}{l}\tilde{E}_{x}\\ \tilde{E}_{y}\end{array}\right]=\left[\begin{array}{l}\tilde{F}_{1}-\tilde{F}_{2}\\ \tilde{F}_{1}+2{\tilde{F}}_{2}\end{array}\right]. \end{aligned}$$

(11.3)

However, when $\tilde{E}_{x}$ is very small, it is difficult to measure $\tilde{E}_{x}$ with high accuracy from the difference between $\tilde{F}_{1}$ and $\tilde{F}_{2}$. In this case, it may be better to set $\theta _{1}=0$ and $\theta _{2}=\pi /4$, and the resulting relations are described as :

$$\begin{aligned} \left[\begin{array}{l}\tilde{E}_{x}\\ \tilde{E}_{y}\end{array}\right]=\left[\begin{array}{l}\qquad \tilde{F}_{1}\\ -\tilde{F}_{1}+2{\tilde{F}}_{2}\end{array}\right]. \end{aligned}$$

(11.4)

In this case $\tilde{E}_{x}$ is simply equal to $\tilde{F}_{1}$, and that value can be obtained with high accuracy.

Polarization azimuth rotation $\theta$ and ellipticity angle $\eta$ are calculated from the following relationships.

$$\begin{aligned} \theta&=\tan ^{-1}\left(\frac{\mathrm{Re}\{\tilde{E}_{x}^{*}\tilde{E}_{y}\}}{|\tilde{E}_{x}|^{2}-|\tilde{E}_{y}|^{2}}\right)\end{aligned}$$

(11.5)

$$\begin{aligned} \eta&=-\sin ^{-1}\left(\frac{\mathrm{Im}\{\tilde{E}_{x}^{*}\tilde{E}_{y}\}}{|\tilde{E}_{x}|^{2}-|\tilde{E}_{y}|^{2}}\right) \end{aligned}$$

(11.6)

11.2.2 Calculation of Dielectric Tensor

The dielectric tensor of samples from polarization measurements can be obtained. The relationship between the reference wave $\tilde{\varvec{E}}_{\mathrm{ref}}$, measured without a sample, and that transmitted through a sample $\tilde{\varvec{E}}_{\mathrm{sample}}$ is described by the square matrix $\tilde{T}$ as,

$$\begin{aligned} \tilde{\varvec{E}}_{\mathrm{sample}}=\tilde{T}\tilde{\varvec{E}}_{\mathrm{ref}}. \end{aligned}$$

(11.7)

The experimental results with different reference waves $\tilde{\varvec{E}}_{\mathrm{ref}}^{1}$ and $\tilde{\varvec{E}}_{\mathrm{ref}}^{2}$ can be des- cribed as;

$$\begin{aligned} \left[\begin{array}{ll}\tilde{\varvec{E}}_{\mathrm{sample}}^{1}&\quad \tilde{\varvec{E}}_{\mathrm{sample}}^{2}\end{array}\right]=\tilde{T}\left[\begin{array}{ll}\tilde{\varvec{E}}_{\mathrm{ref}}^{1}&\quad \tilde{\varvec{E}}_{\mathrm{ref}}^{2}\end{array}\right] \end{aligned}$$

(11.8)

Because $\tilde{\varvec{E}}_\mathrm{sample}^{1},\tilde{\varvec{E}}_\mathrm{sample}^{2},\tilde{\varvec{E}}_\mathrm{ref}^{1}, \tilde{\varvec{E}}_\mathrm{ref}^{2}$ can be measured by using the method described in the Sect. 11.2.1, matrix $\tilde{T}$ is determined from the following equation;

$$\begin{aligned} \tilde{T}=\left[\begin{array}{ll}\tilde{\varvec{E}}_{\mathrm{sample}}^{1}&\quad \tilde{\varvec{E}}_{\mathrm{sample}}^{2}\end{array}\right]\left[\begin{array}{ll}\tilde{\varvec{E}}_{\mathrm{ref}}^{1}&\quad \tilde{\varvec{E}}_{\mathrm{ref}}^{2}\end{array}\right]^{-1}. \end{aligned}$$

(11.9)

In the case of a magnetized isotropic medium, the dielectric tensor is presented in the following form:

$$\begin{aligned} \tilde{\varepsilon }=\left(\begin{array}{c@{\quad }c@{\quad }c} \tilde{\varepsilon }_{xx}&\tilde{\varepsilon }_{xy}&0\\ -\tilde{\varepsilon }_{xy}&\tilde{\varepsilon }_{xx}&0\\ 0&0&\tilde{\varepsilon }_{zz}\end{array}\right). \end{aligned}$$

(11.10)

When light propagates through such media in the z-direction, the eigen modes have circular polarization $(\mathbf{e }_{\pm }=\frac{1}{2}(1, \pm i)^{T})$ and its eigen values of refractive index have the following relationship to the complex permittivity,

$$\begin{aligned} \varepsilon _{0}\tilde{n}_{\pm }^{2}=\tilde{\varepsilon }_{xx}{\pm }\,{i}\tilde{\varepsilon }_{xy}. \end{aligned}$$

(11.11)

In this case, matrix $\tilde{T}$ is described as follows,

$$\begin{aligned} \tilde{T}=\left[\begin{array}{ll}\tilde{t}_{x}&\quad \tilde{t}_{xy}\\ -\tilde{t}_{xy}&\quad \tilde{t}_{x}\end{array}\right], \end{aligned}$$

(11.12)

and two measurements are not necessary to obtain matrix $\tilde{T}$. If we set $\tilde{\varvec{E}}_{\mathrm{ref}}=(0, \tilde{E}_{\mathrm{ref}})$, matrix $\tilde{T}$ is simply obtained with the following Eq. (11.7);

$$\begin{aligned} \left[\begin{array}{l}\tilde{t}_{xy}\\ \tilde{t}_{x}\end{array}\right]=\tilde{E}_{\mathrm{sample}}/\tilde{E}_{\mathrm{ref}}. \end{aligned}$$

(11.13)

The matrix $\tilde{T}$ can also be diagonalized with circular polarization eigenmodes as follows;

$$\begin{aligned} \tilde{T}=\left[\begin{array}{cc}\tilde{t}_{x}&\quad \tilde{t}_{xy}\\ -\tilde{t}_{xy}&\quad \tilde{t}_{x}\end{array}\right]=\left[\begin{array}{ll}\mathbf{e }_{+}&\quad \mathbf{e }_{-}\end{array}\right]\left[\begin{array}{cc}\tilde{t}_{+}&\quad 0\\ 0&\quad \tilde{t}_{-}\end{array}\right]\left[\begin{array}{cc}\mathbf{e }_{+}&\quad \mathbf{e }_{-}\end{array}\right]^{-1}, \end{aligned}$$

(11.14)

where $\tilde{t}_{+}$ and $\tilde{t}_{-}$ are transmittances for left and right circularly polarizations, respectively, being related to $\tilde{t}_{x}$ and $\tilde{t}_{xy}$;

$$\begin{aligned} \tilde{t}_{\pm }=\tilde{t}_{x}\,{\pm }\,i\tilde{t}_{xy}. \end{aligned}$$

(11.15)

In the case of a plate sample in air, $\tilde{t}_{\pm }$ is described, taking account of the Fresnel constants on the interfaces and phase change inside the sample, as follows

$$\begin{aligned} \tilde{t}_{\pm }=\frac{\tilde{E}_{\mathrm{sample}}^{\pm }}{\tilde{E}_{\mathrm{ref}}^{\pm }}&=\frac{2}{\tilde{n}_{\pm }+1}\cdot \frac{2\tilde{n}_{\pm }}{\tilde{n}_{\pm }+1}\cdot \frac{\tilde{n}_{\pm }-1}{\tilde{n}_{\pm }+1}\mathrm{exp}\left(\begin{array}{ll}\frac{i{\omega }L}{c}\tilde{n}_{\pm }\end{array}\right)/\mathrm{exp}\left(\begin{array}{ll}\frac{i{\omega }L}{c}\end{array}\right)\nonumber \\&=\frac{4\tilde{n}}{(\tilde{n}_{\pm }+1)^{2}}\mathrm{exp}\left[\begin{array}{ll}\frac{i{\omega }L}{c}(\tilde{n}_{\pm }-1)\end{array}\right]. \end{aligned}$$

(11.16)

where $\tilde{n}_{+}$ and $\tilde{n}_{-}$ are complex refractive indices of the sample for left and right circularly polarizations, respectively, L is the thickness of the sample and $\omega$ is the angular frequency of THz wave $\tilde{n}_{\pm }$ can be obtained by solving (11.13), (11.15), (11.16) numerically. Each component of the dielectric tensor is obtained with (11.11):

$$\begin{aligned} \tilde{\varepsilon }_{xx}&=\frac{\tilde{n}_{+}^{2}+\tilde{n}_{-}^{2}}{2{\varepsilon }_{0}}\end{aligned}$$

(11.17)

$$\begin{aligned} \tilde{\varepsilon }_{xy}&=\frac{\tilde{n}_{+}^{2}-\tilde{n}_{-}^{2}}{2i{\varepsilon }_{0}}. \end{aligned}$$

(11.18)

Fig. 11.2

Schematic illustrations of experimental setup and sample

Fig. 11.3

Time domain THz waveforms of transmitted waves obtained in the cross-Nichol arrangement (a), with WGP2 $-45^{\circ }$ (b) and $+45^{\circ }$ (c). The green curves show reference signals measured without any sample. The red, blue, and black curves show the signals for right- and left- twisted gammadion samples and cross-patterned samples, respectively. By Fourier transform, the corresponding x- and y-elements of the electric field in the frequency domain are calculated and shown in (d) and (e). In addition, absolute values of electric field are shown in (d). The relative delays between the signals with and without a sample correspond to the propagation delay times of the THz pulses during the propagation through the samples (From [16])

Fig. 11.4

Absolute values of diagonal (a) and off-diagonal (b) elements for the Jones matrix of the sample. Spectra of rotation angle (c) and ellipticity (d). Effective complex dielectric tensor of the sample for left- (blue) and right-twisted (red) gammadion samples and cross-patterned sample (black). Green curves show the results of the Si substrate (e)–(h) (From [16])

11.2.3 Example of Polarization Measurements

In this section, the procedure explained previously is employed to demonstrate the polarization rotation angle and complex dielectric tensor using transmission-mode measurements of an artificial planar periodic structure with chirality. Recent progress on the design and fabrication of artificial subwavelength structures, such as metamaterials, has revealed several novel functions for controlling light [7]. For example, metal chiral structures have been proposed to show optical activity [8], and chirality-dependent polarization-sensitive effects have been reported [9–15]. The development of such artificial structures for THz wave control is important because polarimetry in the THz region is hampered by a lack of good polarization devices in this frequency range.

Figure 11.2 shows schematic illustrations of the experimental setup and sample. Arrays of achiral (cross) and chiral (gammadion patterns) structures were fabricated by depositing a thin gold film on to a resist layer placed upon a high-resistance Si substrate and patterned by electron-beam lithography. The resulting samples, without lift-off treatment, have two metal layers with complementary patterns. The gratings are arranged in a two-dimensional square periodic structure with a period of 100 $\upmu$m. The thicknesses of the gold film and the resist layer are 100 and 180 nm, respectively. Because these structures have fourfold symmetry, around the normal to the substrate, the samples are in-plane isotropic and the dielectric tensor is presented by Eq. (11.10). It was experimentally confirmed that no birefringence was observed at normal incidence. The THz wave, generated by optical rectification with a ZnTe crystal, is focused onto the sample at normal incidence down to a diameter of about 1 mm.

The polarization state of a transmitted wave is determined by using the method explained in the previous sections. The cross-Nicol method (with (11.4)) was used to measure the $\tilde{\varvec{E}}_{x}$ component with high sensitivity, and 45 $^{\circ }$ polarizer method (with (11.3)) to measure the $\tilde{\varvec{E}}_{y}$ component. Detailed information about the sample fabrication and experimental setup is described in [16]. Waveforms of the electric fields obtained with the cross-Nicol configuration are shown in Fig. 11.3a and those obtained with the angle of WGP2 at $-45$ and $+45\,^{\circ }$ with x-axis are shown in Figs. 11.3b and c, respectively. The green curves show the signals without sample indicating the waveform of the incident wave, $\tilde{\varvec{E}}_{\mathrm{ref}}$. In Fig. 11.3a, the chiral samples show pronounced orthogonal components of the electric fields and the sign of the electric fields are opposite for right- and left-twisted gammadion samples. This shows that polarization rotation occurs for chiral patterns, and the rotation direction is reverted depending on the chirality of the unit cell pattern. The frequency-domain spectra of the x-component amplitude shown in Fig. 11.3d are almost the same for right- and left- twisted patterns, and much larger than that of the cross pattern. The slight difference observed between the spectra of left- and right-twisted patterns is mainly due to the limitation of reproducibility in the pattern fabrication.

Matrix $\tilde{T}(\omega )$ is obtained by using (11.13). Figure 11.4a and b shows the obtained values of $|\tilde{t}_{x}|$ and $|\tilde{t}_{xy}|$. The errors indicate the standard deviations for the statistical fluctuation after repeating the measurements eight times. The polarization azimuth rotation and ellipticity angle spectra for the incident linear polarization are calculated using (11.5) and (11.6). Figure 11.4c and d shows the corresponding spectra obtained. Rotations of about $1.5\,^\circ$ are observed at 0.4 and 1.2 THz and about $1\,^\circ$ at 0.8 THz. From the obtained $\tilde{T}(\omega )$ matrix for the sample, the complex effective dielectric tensor of the sample as a whole can aslo be determined, including the Si substrate, following the procedure explained above. Figure 11.4e–h shows the spectra of the calculated elements of effective dielectric tensor. The mechanism of polarization rotation of the wave in such a structure will be explained in Sect. 11.3.

11.3 Reflection Mode Time Domain Magneto-Optical Ellipsometry

Reflection mode measurements enable one to investigate the optical properties of materials that are opaque in the frequency region of interest, by analyzing the polarization azimuth rotation $\phi$ and ellipticity angle $\eta$ of the reflected light wave. In the case of Magneto-optical Kerr effect (MOKE) measurements, MOKE data are usually analyzed using the small magneto-optical response approximation (SMRA). With SMRA, one assumes that: (i) the off-diagonal component of the dielectric tensor, $\tilde{\varepsilon }_{xy}$, is small compared to the diagonal component, $\tilde{\varepsilon }_{xx}$(i.e., $|Q| \ll 1$, where $Q=i \tilde{\varepsilon }_{xy}/\tilde{\varepsilon }_{xx}$); and (ii) the change of the diagonal component induced by the magnetic field is negligible. Since in this approximation $\phi$ and $\eta$ are proportional to $\tilde{\varepsilon }_{xy}$, one can obtain the real and imaginary part of $\tilde{\varepsilon }_{xy}$ directly from $\phi$ and $\eta$, using the complex refractive index measured with no magnetic field. However, if the medium has a large magneto-optical response, additional measurements are needed to determine the components of the dielectric tensor. This can be done, for example, using a conventional ellipsometry techniques that involve measurements of three polarization-dependent reflection coefficients [17–20]. In the THz frequency region, there are even more opportunities. Specifically, THz measurements are performed in the time domain, so that information on the temporal evolution of the electric field on the THz wave can be obtained. This information allows one to obtain both the amplitude and phase of the THz wave [21, 22], and can be used to obtain the diagonal and off-diagonal components of the dielectric tensor, from experimental data acquired with a conventional MOKE scheme without using SMRA.

In this part, a method is introduced that enables one to determine the real and imaginary parts of $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ from complex reflection coefficients that are obtained in MOKE measurements with oblique incidence [23]. Of course, the method described here can be employed to other materials with off-diagonal components of the dielectric tensor, e.g., chiral media.

11.3.1 MOKE Signal at Oblique Incidence

We assume that the interface coincides with plane $z=0$ and a permanent magnetic field $\mathbf{H}$ is along the $-z$ direction, while the wave vector of the incident light wave is at angle $\theta _{0}$ with the interface normal, as shown in Fig. 11.5. For this magneto-optical experiment, this is often referred to as the polar Kerr geometry. For this reason, the measured spectrum will be referred to here as the “magneto-optical Kerr effect spectrum”. It is necessary to note that the Voigt or Cotton-Mouton effect also contributes to the measured signal, since the incidence angle is finite. In the Cartesian coordinate system {xyz}, the dielectric tensor of the magnetized isotropic medium is presented in the same as (11.10).

Fig. 11.5

Illustration of the reflection problem in the plane of incidence, for the Cartesian coordinate systems {xyz} and $\{{xy^\prime z^\prime }\}$ [23]

In order to obtain the reflection coefficients and the polarization state of the reflected waves, it is convenient to introduce a Cartesian system $\{xy{^\prime }z{^\prime }\}$ with the ${z^\prime }$ axis along the wave vector of the transmitted wave. In this Cartesian coordinate system, the dielectric tensor of the magnetized medium can be presented in the following form:

$$\begin{aligned} \tilde{\varepsilon }=\left(\begin{array}{ccc}\tilde{\varepsilon }_{xx}&\tilde{\varepsilon }_{xy}\cos {\theta }&\quad -\tilde{\varepsilon }_{xy}\sin \tilde{\theta }\\ -\tilde{\varepsilon }_{xy}\cos \tilde{\theta }&\quad \tilde{\varepsilon }_{xx} + \tilde{\Delta }\sin ^{2}\tilde{\theta }&\quad \tilde{\Delta }\sin \tilde{\theta }\cos \tilde{\theta }\\ \tilde{\varepsilon }_{xy}\sin \tilde{\theta }&\quad \tilde{\Delta }\sin \tilde{\theta }\cos \tilde{\theta }&\quad \tilde{\varepsilon }_{zz} + \tilde{\Delta }\cos ^{2}\tilde{\theta }\\ \end{array}\right) \end{aligned}$$

(11.19)

where $\tilde{\Delta } \equiv \tilde{\varepsilon }_{zz}-\tilde{\varepsilon }_{xx}$ and $\tilde{\theta }$ is the refraction angle in medium 1. The evolution equation for the amplitude of the transmitted light wave is described as follows [24]:

$$\begin{aligned} \left[\begin{array}{ll} \tilde{n}^{2}\left(\delta _{ij}-\delta _{iz\prime },\delta _{jz\prime }\right)-\tilde{\varepsilon }_{ij}\end{array}\right]=0, \end{aligned}$$

(11.20)

where $\tilde{n}$ is the complex refractive index of the sample and the subscripts indicate Cartesian axes ${x, y^\prime }$ and ${z^\prime }$. Equation (11.20) has nontrivial solutions when

$$\begin{aligned}&\left(\begin{array}{ll}\tilde{\varepsilon }_{zz}\cos ^{2}\tilde{\theta } +\varepsilon _{xx}\sin ^{2}\tilde{\theta }\end{array}\right)\tilde{\eta }^{4}- \left[\begin{array}{ll}\tilde{\varepsilon }_{xx}\tilde{\varepsilon }_{zz}\left( \begin{array}{ll}1+\cos ^{2}\tilde{\theta }\end{array}\right)+\left( \begin{array}{ll}\tilde{\varepsilon }^{2}_{xx}+\tilde{\varepsilon }^{2}_{xy}\end{array}\right) \sin ^{2}\tilde{\theta }\end{array}\right]\tilde{\eta }^{2}\nonumber \\&\quad +\tilde{\varepsilon }_{zz}\left( \begin{array}{ll}\tilde{\varepsilon }^{2}_{xx}+\tilde{\varepsilon }^{2}_{xy}\end{array} \right)=0. \end{aligned}$$

(11.21)

This equation, along with the Snell’s law (i.e., $\tilde{\eta }\sin \tilde{\theta }=n_{0}\sin {\theta }_{0}$ where $\tilde{\theta }$ is the complex refraction angle and n $_{0}$ is the refractive index of free space) allows one to arrive at two eigenvalues of the refractive index $\tilde{\eta }$ and the relevant refraction angle $\tilde{\theta }$. Correspondingly, the transmitted light wave can be presented in the following form:

$$\begin{aligned} {\tilde{\mathbf{E }}}_{T}={{\tilde{\mathbf{E }}}}_{A} e^{{-\mathrm{i}\left({\frac{\omega }{{c}}}\right){{\tilde{n}}}A^{{z^{\prime }}}}}+{{\tilde{\mathbf{E }}}}_{B} e^{{-\mathrm{i}\left({\frac{\omega }{{\text{ c}}}} \right){{\tilde{n}}}B^{{z\prime }}}} \end{aligned}$$

(11.22)

Here, subscripts A and B label the modes, i.e., the solutions of (11.21). The magneto-optical response of the medium also results in a nonzero longitudinal component of the transmitted light wave, i.e., $\tilde{\mathbf{E }}_{A,B}$, have nonzero projection on the propagation axis ${z^\prime }$. Therefore, the amplitudes of both p and ${z^\prime }$ components of the transmitted wave are obtained in terms of its s component as $\tilde{E}_{pk}=\tilde{\xi }_{k}\tilde{E}_{sk}$ and $\tilde{E}_{z\prime k}=\tilde{\zeta }_{k}\tilde{E}_{sk}$. Subscript k labels eigenmodes A and B, while coefficients $\tilde{\xi }_{k}$ and $\tilde{\zeta }_{k}$ can be obtained from (11.19) and (11.20), respectively as follows:

$$\begin{aligned} \tilde{\xi }_{k}=\frac{\tilde{n}^{2}-\tilde{\varepsilon }_{xx}- \frac{\tilde{\varepsilon }^{2}_{xy} \sin ^{2}\tilde{\theta }_{k}}{\tilde{\varepsilon }_{xx}+\tilde{\Delta } \cos ^{2}\tilde{\theta }_{k}} }{\tilde{\varepsilon }_{xy} {\cos }^{2}\tilde{\theta }_{k}+\frac{\tilde{\Delta } \sin ^{2} \tilde{\theta }_{k}\cos {\tilde{\theta }}_{k}}{\tilde{\varepsilon }_{xx}+ \tilde{\Delta } \cos ^{2}\tilde{\theta }_{k}}}\end{aligned}$$

(11.23)

$$\begin{aligned} \tilde{\zeta }_{k}=\frac{\tilde{\varepsilon }^{2}_{xy}\tilde{\Delta }(\tilde{n}^{2}_{k}-\tilde{\varepsilon }_{xx})}{\tilde{\varepsilon }_{zz}\tilde{\varepsilon }_{xy}}\sin \tilde{\theta }_{k} \end{aligned}$$

(11.24)

The polarization effects will be restricted to the p-polarized incident light wave; however, the magneto-optical response ensures the existence of the both s- and p-polarized components in the reflected and transmitted waves (see Fig. 11.5). In the Cartesian system {xyz}, in which the vacuum-medium interface coincides with the plane $z=0$, the electric $(\tilde{\mathbf{E }})$ and magnetic $(\tilde{\mathbf{H }})$ fields of the incident (subscript I) and reflected (subscript R) waves can be presented in the following form:

$$\begin{aligned} \tilde{\mathbf{E }}_{I}=(0, \quad \tilde{E}_{Ip}\cos {\theta }_{0}, \quad \tilde{E}_{Ip}\sin {\theta }_{0})\nonumber \\ \tilde{\mathbf{H }}_{I}=\frac{n_{0}}{c}(\tilde{E}_{Ip},0,0) \end{aligned}$$

(11.25)

$$\begin{aligned} \tilde{\mathbf{E }}_{R}=(\tilde{E}_{RS},\quad -\tilde{E}_{Rp}\cos {\theta }_{0},\quad \tilde{E}_{Rp}\sin {\theta }_{0})\\\tilde{\mathbf{H }}_{R}=\frac{n_{0}}{c}(-\tilde{E}_{Rp},\quad -\tilde{E}_{RS}\cos {\theta }_{0},\quad \tilde{E}_{RS}\sin {\theta }_{0}) \end{aligned}$$

(11.26)

As shown in (11.22), the transmitted wave consists of two eigenmodes; the complex amplitude in the Cartesian system {xyz} and relevant electric and magnetic fields are expressed by the following:

$$\begin{aligned} \tilde{\mathbf{E }}_{k}=(\tilde{E}_{sk}&, \quad \tilde{E}_{pk}\cos \tilde{\theta }_{k} -\tilde{E}_{zk}\sin {\theta }_{k},\quad \tilde{E}_{pk}\sin \tilde{\theta }_{k} +\tilde{E}_{zk}\cos \tilde{\theta }_{k})\\&\tilde{\mathbf{H }}_{k}=\frac{n_{k}}{c}(-\tilde{E}_{pk},\quad \tilde{E}_{sk}\cos \tilde{\theta }_{k},\quad -\tilde{E}_{sk}\sin {\theta }_{k}) \end{aligned}$$

(11.27)

where $k =A,B$. The continuity of the tangential components of the electric and magnetic field at $z=0$ gives

$$\begin{aligned}&{}\tilde{E}_{RS}=\tilde{E}_{sA}+\tilde{E}_{sB}\nonumber \\&\tilde{E}_{Ip}\cos {\theta }_{0}-\tilde{E}_{Rp}\cos {\theta }_{0}=\tilde{\chi }_{A}\tilde{E}_{sA}+\tilde{\chi }_{B}\tilde{E}_{sB}\nonumber \\&-n_{0}\tilde{E}_{Ip}-n_{0}\tilde{E}_{Rp}=-\tilde{n}_{A}\tilde{\xi }_{A}\tilde{E}_{sA}-\tilde{n}_{B}\tilde{\xi }_{B}\tilde{E}_{sB}\nonumber \\&-n_{0}\tilde{E}_{RS}\cos {\theta }_{0}=\tilde{n}_{A}\tilde{E}_{sA}\cos \tilde{\theta }_{A}+\tilde{n}_{B}\tilde{E}_{sA}\cos \tilde{\theta }_{A} \end{aligned}$$

(11.28)

where

$$\begin{aligned} \tilde{\chi }_{k}=\tilde{\xi }_{k}\cos \tilde{\theta }_{k}-\tilde{\zeta }_{k}\sin \tilde{\theta }_{k}. \end{aligned}$$

(11.29)

The Solution for (11.28) gives the following expressions for the amplitude reflection coefficients:

$$\begin{aligned} \tilde{r}_{pp}&=\frac{\tilde{E}_{Rp}}{\tilde{E}_{Ip}}=\frac{(\tilde{n}_{A}\tilde{\xi }_{A}-\tilde{n}_{0}\tilde{\chi }_{A}/\cos {\theta }_{0})\tau _{B}-(\tilde{n}_{B}\tilde{\xi }_{B}-\tilde{n}_{0}\tilde{\chi }_{B}/\cos {\theta }_{0})\tau _{A}}{(\tilde{n}_{A}\tilde{\xi }_{A}+\tilde{n}_{0}\tilde{\chi }_{A}/\cos {\theta }_{0})\tau _{B}-(\tilde{n}_{B}\tilde{\xi }_{B}+\tilde{n}_{0}\tilde{\chi }_{B}/\cos {\theta }_{0})\tau _{A}}\end{aligned}$$

(11.30)

$$\begin{aligned} \tilde{r}_{sp}&=\frac{\tilde{E}_{RS}}{\tilde{E}_{Ip}}=\frac{2n_{0}(\tilde{n}_{B}\cos \tilde{\theta }_{B}-\tilde{n}_{A}\cos \tilde{\theta }_{A})}{(\tilde{n}_{A}\tilde{\xi }_{A}+\tilde{n}_{0}\tilde{\chi }_{A}/\cos {\theta }_{0})\tau _{B}-(\tilde{n}_{B}\tilde{\xi }_{B}+\tilde{n}_{0}\tilde{\chi }_{B}/\cos {\theta }_{0})\tau _{A}} \end{aligned}$$

(11.31)

where

$$\begin{aligned} \tau _{k}=\tilde{n}_{k}\cos \tilde{\theta }_{k}+n_{0}\cos {\theta }_{0}. \end{aligned}$$

(11.32)

It should be noted here that (11.30) and (11.31) are valid for an oblique angle of incidence and any magnitude of the magneto-optical response. Since $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$ are functions of three complex variables; $\tilde{\varepsilon }_{xx}$, $\tilde{\varepsilon }_{xy}$, $\tilde{\varepsilon }_{zz}$ we can calculate $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ from the obtained complex reflection coefficients, as long as $\tilde{\varepsilon }_{zz}$ is known. For example, $\tilde{\varepsilon }_{zz}$ can be obtained with reflection measurement at normal incidence because the reflection coefficients at normal incidence, $\tilde{r}_{n}$ is described as $\tilde{r}_{n}=(1-\sqrt{\tilde{\varepsilon }_{zz}})/(1+\sqrt{\tilde{\varepsilon }_{zz}})$.

By using conventional formulas for the polarization azimuthangle $\phi$ and ellipticity angle $\eta$ in terms of the Cartesian components of the electric field $\mathbf{E}$ [25];

$$\begin{aligned} \phi&=\frac{1}{2}\tan ^{-1}\left(\frac{2\mathrm{Re}\{\tilde{E}_{x}\tilde{E}_{y}^{*}\}}{|\tilde{E}_{x}|^{2}-|\tilde{E}_{y}|^{2}}\right),\nonumber \\ \eta&=\frac{1}{2}\sin ^{-1}\left(\frac{2\mathrm{Im}\{\tilde{E}_{x}\tilde{E}_{y}^{*}\}}{|\tilde{E}_{x}|^{2}+|\tilde{E}_{y}|^{2}}\right), \end{aligned}$$

(11.33)

One can now readily obtain $\phi$ and $\eta$, in terms of $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$, with (11.30) and (11.31):

$$\begin{aligned} &\phi =-\frac{1}{2}\arg \left(\frac{\tilde{r}_{pp}-i\tilde{r}_{sp}}{\tilde{r}_{pp}+i\tilde{r}_{sp}}\right)\\ \eta =\tan ^{-1}&\left(\frac{|\tilde{r}_{pp}-i\tilde{r}_{sp}|-|\tilde{r}_{pp} +i\tilde{r}_{sp}|}{|\tilde{r}_{pp}-i\tilde{r}_{sp}|+|\tilde{r}_{pp}+i\tilde{r}_{sp}|} \right) \end{aligned}$$

(11.34)

The procedure based on (11.30), (11.31), and (11.34) will be outlined for the evaluation of $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ from ellipsometric experiments below.

At the end of this section, the obtained Eqs. (11.30) and (11.31) are compared with the result of SMRA. The difference between mode A and B is reduced to the difference of the sign of magneto-optical response; therefore, $+$ and $-$ subscripts are used instead of A and B. Substituting the SMRA condition, i.e.,$|Q|\equiv |i\tilde{\varepsilon }_{xy}|/|\tilde{\varepsilon }_{xx}|\ll 1$ and $\tilde{\Delta }\approx 0$ in Eq. (11.21), the following is obtained:

$$\begin{aligned} \tilde{n}_{k}=\tilde{n}\left(1\pm \frac{i\tilde{\alpha }\tilde{Q}}{2}\right),\end{aligned}$$

(11.35)

$$\begin{aligned} \sin \tilde{\theta }_{k}=\frac{n_{0}\sin {\theta }_{0}}{\tilde{n}}\left(1\pm \frac{i\tilde{\alpha }\tilde{Q}}{2}\right), \end{aligned}$$

(11.36)

where $\tilde{\alpha }=\sqrt{{n}^{2}_{0}sin^{2}{\theta }_{0}/\tilde{\varepsilon }_{zz}-1}$. $\tilde{n}=\sqrt{\tilde{\varepsilon }_{zz}}$ is the index of refraction of medium 1 without a magnetic field. With these variables, the quantities $\tilde{\xi }_{k}, \tilde{\zeta }_{k}$ and $\tilde{\chi }_{k}$ can be reduced to the following:

$$\begin{aligned} \tilde{\xi }_{k}&=\frac{\mp \tilde{\alpha }-i\tilde{Q}\sin ^{2}\tilde{\theta }+i(\tilde{\alpha }^{2}\tilde{Q}/2)\tan ^{2}\tilde{\theta }}{\cos \tilde{\theta }},\end{aligned}$$

(11.37)

$$\begin{aligned} \tilde{\zeta }_{k}&=i\tilde{Q}\sin \tilde{\theta },\end{aligned}$$

(11.38)

$$\begin{aligned} \tilde{\chi }_{k}&=\mp \tilde{\alpha }-2i\tilde{Q}\sin ^{2}\tilde{\theta }. \end{aligned}$$

(11.39)

Substituting these into (11.30) and (11.31), one obtains

$$\begin{aligned} \tilde{r}_{pp}&=\frac{\tilde{n}\cos {\theta }_{0}-\tilde{n}\cos {\theta }_{0}}{\tilde{n}\cos {\theta }_{0}+\tilde{n}\cos {\theta }_{0}}\end{aligned}$$

(11.40)

$$\begin{aligned} \tilde{r}_{sp}&=\frac{i\tilde{Q}n_{0}\tilde{n}\cos {\theta }_{0}}{(\tilde{n}\cos {\tilde{\theta }}+n_{0}\cos {\theta }_{0})(\tilde{n}\cos {\theta }+n_{0}\cos {\theta }_{0})\cos \tilde{\theta }} \end{aligned}$$

(11.41)

These are the same as (2.31) in [26].

11.3.2 Analysis Based on Intensity Measurements

Before considering in detail the time domain THz ellipsometry, a conventional MOKE technique is revisited for optical frequencies based on light intensity measurements. With MOKE intensity-based measurement techniques, the polarization azimuth angle $\phi$ and ellipticity angle $\eta$ of the reflected electromagnetic wave under the magnetic field are obtained [27]. Since $\phi$ and $\eta$ depend only on the ratio $\tilde{r}_{sp}/\tilde{r}_{pp}$, see (11.34), both the real and imaginary parts of $\tilde{r}_{sp}/\tilde{r}_{pp}$ can be determined from the MOKE experiment.

When the SMRA conditions are fulfilled (i.e., when the magneto-optical response is small $|Q|\ll 1$, and dependence of $\tilde{\varepsilon }_{xx}$ on the magnetic field is negligible), $\phi$ and $\eta$ are less than a few degrees. In such a case, (11.30), (11.31) and (11.34) are reduced to the following SMRA equation [26]:

$$\begin{aligned} \left(\begin{array}{l} \phi \\ \eta \end{array}\right)=\left(\begin{array}{l} \mathrm{Re}\\ \mathrm{Im} \end{array}\right)\frac{n_0\tilde{\varepsilon }_{xy}}{(\tilde{\varepsilon }_{xx}-n_0^2)\sqrt{\tilde{\varepsilon }_{xx}}} \frac{\cos \theta _0}{\cos (\theta _0+\tilde{\theta })} \end{aligned}$$

(11.42)

In (11.42), $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ are separated; therefore, if $\tilde{\varepsilon }_{xx}$ is measured independently (e.g. from the reflectivity at zero magnetic field), the real and imaginary part of $\tilde{\varepsilon }_{xy}$ can be determined directly from the measured values of $\phi$ and $\eta$.

When the magneto-optical response is large, SMRA cannot be applicable. In such case, the diagonal component of the dielectric tensor is not negligible and one needs to perform additional measurements to determine $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$, even in the case of normal incidence. In particular, this can be done using the conventional ellipsometry technique [17–20]. In this technique, $\tilde{R}_{pp}=\tilde{r}_{pp}/\tilde{r}_{ss}$, $\tilde{R}_{sp}=\tilde{r}_{sp}/\tilde{r}_{ss}$, and $\tilde{R}_{ps}=\tilde{r}_{ps}/\tilde{r}_{ss}$ can be measured by rotating the analyzer with a finite angular frequency [18], while $\tilde{\varepsilon }_{xx},\tilde{\varepsilon }_{xy}$, and $\tilde{\varepsilon }_{zz}$ are obtained by fitting the measured reflection coefficients [19] using exact equations [20].

11.3.3 Analysis Based on the Time Domain THz Ellipsometry

In this section, we explain a method to determine $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ from experimentally obtained $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$ values, when $\tilde{\varepsilon }_{zz}$ is obtained from independent measurements. The method is based on time domain THz spectroscopy one; more specifically as “time-domain THz ellipsometry”. The THz spectroscopy technique enables us to reveal the temporal evolution of the THz electric field [21, 22] and to obtain the phase and amplitude of the reflected THz wave, and the complex reflection coefficient. This technique gives both the real and imaginary parts of $\tilde{r}_{pp}/\tilde{r}_{pp}$ and $\tilde{r}_{sp}/\tilde{r}_{p}$, where $\tilde{r}_{p}$ is a reflection coefficient that is determined from a given $\tilde{\varepsilon }_{zz}$ [28]. As described below, this procedure allows one to arrive at real and imaginary parts of $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$, therefore, to obtain $\phi$ and $\eta$, see (11.34).

The case where the incident wave $\tilde{\mathbf{E }}_\mathrm{in}$ has p-polarization is considered:

$$\begin{aligned} \tilde{\mathbf{E }}_\mathrm{in}=\tilde{E}_\mathrm{in}\mathbf{e }_{p} \end{aligned}$$

(11.43)

where $\mathbf{e }_{s,p}$ are eigenvectors for s- and p- polarization. The refracted wave $\tilde{\mathbf{E }}_{r}^{B}$ in the case with an external magnetic field, is;

$$\begin{aligned} \tilde{\mathbf{E }}^{B}_{r}=\tilde{E}^{B}_{r,p}\mathbf{e }_{p}+\tilde{E}^{B}_{r,s}\mathbf{e }_{s}=(\tilde{r}^{B}_{pp}\mathbf{e }_{p}+\tilde{r}^{B}_{sp}\mathbf{e }_{s})\tilde{E}_{in}. \end{aligned}$$

(11.44)

The refracted wave $\tilde{\mathbf{E }}_{r}^{0}$, in the case without external magnetic field, is;

$$\begin{aligned} \tilde{\mathbf{E }}^{0}_{r}=\tilde{E}^{0}_{r,p}\mathbf{e }_{p}=\tilde{r}_{p}\tilde{E}_{in}\mathbf{e }_{p}. \end{aligned}$$

(11.45)

The detected THz electric fields after a polarizer, with angle to p-polarization is $\varphi$, are described as follows;

$$\begin{aligned} \tilde{E}^{B,\varphi }_{r}&=(\tilde{r}_{pp}\cos {\varphi }+\tilde{r}_{sp}\sin {(\varphi )})\tilde{E}_\mathrm{in}f(\varphi )\end{aligned}$$

(11.46)

$$\begin{aligned} \tilde{E}^{0,\varphi }_{r}&=(\tilde{r}_{p}\cos {\varphi }\tilde{E}_{in}f{(\varphi )} \end{aligned}$$

(11.47)

where $f{(\varphi )}$ is detection efficiency that depends on the polarization of THz wave.

The ratio $\tilde{\epsilon }^{B,\varphi }\equiv \tilde{E}^{B,\varphi }_{r}/\tilde{E}^{B,0}_{r}$ is measured for two different polarizer angles $\varphi _1$ and $\varphi _2$;

$$\begin{aligned} \tilde{\epsilon }^{B,\varphi ,i}=\frac{\tilde{r}_{pp}\cos {\varphi }_{j}+\tilde{r}_{sp}\sin {\varphi _{j}}}{\tilde{r}_{p}\cos {\varphi }_{j}}(j=1,2). \end{aligned}$$

(11.48)

Here, $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$ can be calculated from (11.48) as follows;

$$\begin{aligned} \tilde{r}_{pp}&=\frac{\tilde{\epsilon }^{B,{\varphi }_{1}}\tan {\varphi }_{2}-\tilde{\epsilon }^{B,{\varphi }_{2}}\tan {\varphi }_{1}}{\tan {\varphi }_{2}-\tan {\varphi }_{1}}\tilde{r}_{p}\end{aligned}$$

(11.49)

$$\begin{aligned} \tilde{r}_{sp}&=\frac{\tilde{\epsilon }^{B,{\varphi }_{1}}-\tilde{\epsilon }^{B,{\varphi }_{2}}}{\tan {\varphi }_{1}-\tan {\varphi }_{2}}\tilde{r}_{p}. \end{aligned}$$

(11.50)

In summary, $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$ can be obtained by measuring complex THz electric fields at two different polarizer angles with and without external magnetic fields. If we set $\varphi _{1}=\pi /4$ and $\varphi _{2}=-\pi /4$, (11.49) and (11.50) are simplified as follows;

$$\begin{aligned} \tilde{r}_{pp}&=\frac{\tilde{\epsilon }^{B,\pi /4}+\tilde{\epsilon }^{B,-\pi /4}}{2}\tilde{r}_{p}\end{aligned}$$

(11.51)

$$\begin{aligned} \tilde{r}_{sp}&=\frac{\tilde{\epsilon }^{B,\pi /4}-\tilde{\epsilon }^{B,-\pi /4}}{2}\tilde{r}_{p} \end{aligned}$$

(11.52)

The next step includes rewriting (11.30) and (11.31) to obtain $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ as functions of $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$;

$$\begin{aligned} \tilde{\varepsilon }_{xx}&=\tilde{\varepsilon }_{xx}(\tilde{r}_{pp}, \tilde{r}_{sp},\tilde{\varepsilon }_{zz}).\nonumber \\ \tilde{\varepsilon }_{xy}&=\tilde{\varepsilon }_{xy}(\tilde{r}_{pp}, \tilde{r}_{sp}, \tilde{\varepsilon }_{zz}). \end{aligned}$$

(11.53)

Following these nonlinear simultaneous equations, $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ are calculated from the measured $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$ and the $\tilde{\varepsilon }_{zz}$ given by using numerical calculations, such as the Newton-Raphson method [29].

The procedure to obtain $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ is summarized in Fig. 11.6. The numbers in Fig. 11.6 correspond to the following numbers.

• 1. Measure the incident THz waves, $E_\mathrm{in}(t)$, and the reflected THz wave, $E_\mathrm{out}(t)$, without external magnetic field.

• 2. Calculate $\tilde{r}_{p}=\mathcal F [E_\mathrm{out}(t)]/\mathcal F [E_\mathrm{in}(t)]$, where $\mathcal F [\ldots ]$ corresponds to a Fourier transformation.

• 3. Measure the reflected waves with and without external magnetic field, $E^{\pi /4}_{\mathrm{out},B}(t)$ and $E^{-\pi /4}_\mathrm{out}(t)$, with the wire-grid polarizer $\varphi =\pi /4$.

• 4. Measure the reflected THz waves with and without external magnetic field, $E^{-\pi /4}_{\mathrm{out},B}(t)$ and $E^{-\pi /4}_\mathrm{out}(t)$, with the wire-grid polarizer $\varphi =-\pi /4$.

• 5. Calculate the ratios $\mathcal F [E^{\pm \pi /4}_{\mathrm{out},B}(t)]/\mathcal F [E^{\pm \pi /4}_{\mathrm{out},B}(t)]$. These correspond to $\tilde{\epsilon }^{B,\varphi _{i}}$ in (11.48).

• 6. Calculate $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$ using (11.51) and (11.52). $\phi$ and $\eta$ can be obtained from (11.34).

• 7. Obtain $\tilde{\varepsilon }_{zz}$ from $\tilde{r}_{p}$ with numerical calculation.

• 8. Obtain $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$ from $\tilde{r}_{pp}, \tilde{r}_{sp}; \tilde{\varepsilon }_{zz}$ with numerical calculations.

Fig. 11.6

Schematic illustration of the calculation procedure

11.3.4 Analysis Example

In this section, the procedure explained above can be employed to obtain the complex dielectric tensor using the results of the THz MOKE measurements for n-type InAs.

The first step is to measure the complex reflectivity coefficient $\tilde{r}_{p}$ in the absence of the magnetic field. A numerical method for the misplacement phase error correction is effective for THz time domain reflection-mode spectroscopy [30, 31]. Since the crystal symmetry does not permit any current parallel to the magnetic field, it is natural to assume that the field along z axis (see Fig. 11.1) does not change the longitudinal component of the dielectric tensor, i.e., $\tilde{\varepsilon }_{zz}(\mathbf{H})=\tilde{\varepsilon }_{zz}(\mathbf{H}=0)$. Within this approximation, $\tilde{\varepsilon }_{zz}$ can be calculated from $\tilde{r}_{p}$ [21, 22]. The measured THz spectra of $\tilde{r}_{p}$ and $\tilde{\varepsilon }_{zz}$ are shown in Fig. 11.7. Second, by using the experimental procedure described above with a 45$^{\circ }$ angle of incidence, $\tilde{r}_{pp}/\tilde{r}_{p}$ and $\tilde{r}_{sp}/\tilde{r}_{p}$ are measured, which allows us to obtain $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$, as shown in Fig. 11.4.

Fig. 11.7

The spectra of a $\tilde{r}_{p}$ and b $\tilde{\varepsilon }_{zz}$. $\tilde{\varepsilon }_{zz}$ is calculated from measured value of $\tilde{r}_{p}$ [23]

Fig. 11.8

Spectra of (a) Re$\{\tilde{r}_{pp}\}$, (b) Im$\{\tilde{r}_{sp}\}$, (c) Re$\{\tilde{r}_{sp}\}$, and (d) Im$\{\tilde{r}_{sp}\}$obtained from measured $\tilde{r}_{pp}/\tilde{r}_{p}$, $\tilde{r}_{sp}/\tilde{r}_{p}$, and $\tilde{r}_{p}$ [23]

From the above complex reflection coefficients $\tilde{r}_{pp}$ and $\tilde{r}_{sp}$, the polarization plane azimuth angle $\phi$ and ellipticity angle $\eta$ of the reflected wave (i.e., MOKE signal) can be obtained, as shown in Fig. 11.9 [28]. In this system, the dielectric response in the THz frequency region originates from the intraband motion of conduction electrons. Therefore, one can use the Drude model to describe the THz response. In the Drude model framework, the components of the dielectric tensor in the presence of the magnetic field are as follows:

$$\begin{aligned} \tilde{\varepsilon }_{xx}&=\varepsilon _{b}\left[1-\frac{\omega ^{2}_{p}(\omega ^{2}+i\omega \Gamma )}{(\omega ^{2}+i\omega \Gamma )^{2}-\omega ^{2}\omega ^{2}_{c}}\right], \nonumber \\ \tilde{\varepsilon }_{xy}&=\frac{i\omega ^{2}_{p}\varepsilon _{b}\omega \omega _{c}}{(\omega ^{2}+i\omega \Gamma )^{2}-\omega ^{2}\omega ^{2}_{c}} ,\nonumber \\ \tilde{\varepsilon }_{zz}&=\varepsilon _{b}\left[1-\frac{\omega ^{2}_{p}}{\omega ^{2}+i{\omega }{\Gamma }}\right], \end{aligned}$$

(11.54)

where $\varepsilon _{b}$ is the background dielectric constant, $\omega _{p}=\sqrt{Ne^{2}/\varepsilon _{b}m^{*}}$ is the plasma frequency, $N$ and $m^{*}$ are the carrier density and effective mass, $\Gamma$ is the damping constant, and $\omega _{c}=e|H|/m^{*}c$ is the cyclotron frequency (Fig. 11.8). Solid lines in Fig. 11.9 represent this Drude model fitting, which are obtained using (11.30), (11.31) and (11.34) at $\omega _{p}=1.8$ THz (the corresponding carrier density is $2.1\times 10^{16}$ cm$^{-3})$, $\varGamma = 0.75$ THz, $\omega _c= 0.46$ THz, $\varepsilon _{b}=16.3$ and $m^* =0.026m_{e}$. One can observe a pronounced resonance feature in the vicinity of the plasma frequency. This effect is often referred to as the magnetoplasma resonance [32].

Fig. 11.9

The measured spectra of $\phi$ (circles) and $\eta$ (dots) calculated from measured and $\tilde{r}_{pp}$/$\tilde{r}_{p}$ and $\tilde{r}_{sp}$/$\tilde{r}_{p}$. Solid curves show the results of Drude model fitting [23]

By using the measured complex reflection coefficients $\tilde{r}_{pp}$, $\tilde{r}_{sp}$, and $\tilde{\varepsilon }_{zz}$, obtained in the first step, one can reconstruct the diagonal and off-diagonal component of the dielectric tensor by inversely solving (11.30) and (11.31). Here, the Newton-Raphson method for this procedure was employed [29].

Figure 11.10 shows the spectra of the obtained complex dielectric tensor. For comparison, the complex dielectric tensor calculated with the Drude model is also shown; the parameters of which are obtained above. One can observe from Fig. 11.10 that $\tilde{\varepsilon }_{xx}$ and $\tilde{\varepsilon }_{xy}$, directly calculated from the complex reflection coefficients and do not rely on the particular mechanism of the MOKE, correspond to the ones calculated using the Drude model with parameters obtained from the measured MOKE signal. A slightly bigger (in comparison with other components) discrepancy between the calculated Im$\{{\tilde{\varepsilon }}_{xy}\}$ and its MOKE fitting is due to the smallness of the magnitude of Im$\{{\tilde{\varepsilon }}_{xy}\}$.

Finally, the conventional analysis based on SMRA are compared with the results obtained above. Figure 11.11 shows the frequency dependence of the off-diagonal component of the dielectric tensor, $\tilde{\varepsilon }_{xy}$, obtained from the measured $\phi$ and $\tilde{\varepsilon }_{zz}$ by using SMRA (i.e., assuming that and $|Q|\ll 1$ and $\tilde{\varepsilon }_{xx}\approx \tilde{\varepsilon }_{zz}$) and by using the refined method. One can observe from Fig. 11.11 that the obtained off-diagonal component of the dielectric tensor, $\tilde{\varepsilon }^{ex}_{xy}$, shows better correspondence with the Drude fitting of measured MOKE signals than $\tilde{\varepsilon }_{xy}$, which was calculated in the SMRA framework. Results of the THz experiment presented here are apparently beyond the range of applicability of SMRA ($|Q|\approx 0.5$ and $|\phi +i\eta |\approx 0^{-1}$) and require a more rigorous treatment.

Figure 11.12a and b shows the spectra for the polarization rotation $\phi$ and ellipticity angle $\eta$, respectively, calculated from the measured off-diagonal component of the dielectric tensor $\tilde{\varepsilon }^{ex}_{xy}$ using SMRA, calculated from the exact formulae developed above, and measured by the experiment. The correspondence of the measured values and those calculated using the exact expression shows the correctness of the analysis. One can observe from Fig. 11.11 that SMRA results in a nonnegligible deviation in the polarization rotation and ellipticity angle from those measured, particularly in the vicinity of the plasma resonance of 1.8 THz.

Fig. 11.10

Frequency dependence of (a) $\mathrm{Re}{\{\tilde{\varepsilon }_{xx}\}}$, (b) $\mathrm{Im}{\{\tilde{\varepsilon }_{xx}\}}$, (c) $\mathrm{Re}{\{\tilde{\varepsilon }_{xy}\}}$, and (d) $\mathrm{Im}{\{\tilde{\varepsilon }_{xy}\}}$ obtained from measured spectra of $\tilde{r}_{pp}, \tilde{r}_{sp}$, and $\tilde{r}_{p}$(dots) and calculated spectra from Drude model with parameters obtained by fitting of MOKE signals (lines) [23]

Fig. 11.11

Off-diagonal component of the dielectric tensor obtained from rigorous calculations with our method (circles), SMRA (solid line), and Drude model fitting (bold line) with MOKE [23]

Fig. 11.12

Polarization azimuth (a) and ellipticity angle (b) calculated from the experimentally determined dielectric tensor using SMRA (dotted lines), calculated using exact formulas (thin solid lines), and measured in the experiment (bold broken lines) [23]

Fig. 11.13

SMRA versus exact analysis [23]. a Frequency dependence of the magneto-optical constant Q and the error $\delta$. b The relation between $\delta$ and the magnitude of MOKE signal

In order to describe the difference between the refined method and SMRA, a value is introduced, $\delta =|\tilde{\varepsilon }_{xy}-\tilde{\varepsilon }^\mathrm{SMRA}_{xy}|/|\tilde{\varepsilon }_{xy}|$; this is a quantitative measure of the SMRA imposed error. Note that here the dielectric tensor is used to calculate the Drude model with parameters obtained from the MOKE signal fits described previously. From this tensor, one can calculate the MOKE signal $\phi +i{\eta }$, and calculate $\tilde{\varepsilon }^\mathrm{SMRA}_{xy}$ from $\phi +i{\eta }$ using SMRA. Figure 11.13a shows the frequency dependence of $\delta$ and $|Q|=|\tilde{\varepsilon }_{xy}/\tilde{\varepsilon }_{xx}|$ in the frequency range from 0.5 to 2.5 THz. In Fig. 11.13b, $\delta$ is plotted versus $\phi +i{\eta }$, using frequency as a parameter, where the dotted line and bold line correspond to the frequency regions above and below $\omega _{p}$.

One can observe that with $\omega > \omega _{p}$, $\delta$ increases monotonically as $|\phi +i{\eta }|$ increases. With $\omega < \omega _{p}$, $\delta$ does not reduce monotonically as is reduced. From Fig. 11.13a and b it can be noticed that the small MOKE signal does not always correspond to a small $\tilde{\varepsilon }_{xy}(i.e., |Q| \ll 1)$. In other words, SMRA may fail even when $|\phi +i{\eta }|$ is relatively small. Note that in metals, for which the magneto-optical response is conventionally studied by using the MOKE technique, $|Q|$ is of the order of 10$^{-2}$, and SMRA is usually valid. However, a more careful analysis is necessary when the frequency of the incident wave is resonant to the intrinsic longitudinal electromagnetic modes of the medium, such as plasmons, optical phonons, longitudinal excitons, etc.

11.4 Active Polarization Control of Terahertz Wave

In the optical region, photoelastic modulators are commonly used for highly sensitive polarization measurements [27]. Such polarization modulation devices are required to develop THz polarimetry. If optical activity is induced by an external stimulus, such as photoexcitation in an artificial structure that was introduced in the Sect. 11.2, the polarization state of the THz wave can be modulated. In this section, the optical activity in the THz region induced by photoexcitation on silicon is discussed with a subwavelength chiral-patterned metal mask [31]. Two-dimensional arrays of gold chiral masks are fabricated on a silicon substrate, which is an achiral medium. In contrast to the case of visible light waves [9–11, 15], for THz waves gold-patterned films are too thin to induce three-dimensional effects. No significant polarization effect was observed for single-layered metal chiral grating samples, as previously reported [16]. However, significant THz optical activity was observed, illuminating a single-layered chiral grating patterned on silicon samples. The metal chiral gratings and photogenerated carrier distribution form a conducting three-dimensional chiral structure.

Figure 11.14a shows optical microscopic images of the samples. Arrays of achiral (cross) and chiral (gammadion) patterns are fabricated with electron-beam lithography and consist of 100 nm thick gold film on a high resistance Si substrate. A thin Cr film of 5 nm thickness exists between the gold film and the substrate to improve adhesion. The structures are arranged in a two-dimensional square lattice with a period of 100 $\upmu$m.

Figure 11.14b shows a schematic description of the experimental setup of THz wave polarization measurements. A regenerative amplified Ti:sapphire laser is used as a light source. It is divided into three beams and is used for the generation and detection of THz radiation and photoexcitation of the sample. The optical rectification and free-space electro-optic sampling with ZnTe crystals were employed for THz generation and detection, respectively. To detect the polarization state of THz radiation, the time domain waveforms were measured with wire-grid polarizers, as described in the Sect. 11.2 [33].

Fig. 11.14

a Optical microscopic images of the samples. b illustration of excitation. Pump beam and THz wave normally incident on the sample. The polarization azimuth rotation angle $\theta$ of the transmitted THz wave is measured. c Illustration of complimentary double-layered structure, created by the photoexcitation of carriers in semiconductor substrate (From [33])

Both the pump beam and THz radiation are incoming on the sample surface at normal incidence, and their diameters are approximately 3 and 2 mm, respectively. The directions of the pump beam and THz pulse are horizontally and vertically polarized, respectively. The THz pulse arrives at the sample at a delay $\tau =70$ ps after the photoexcitation. Since the lifetime of photocarriers is much longer than the duration of the THz pulse, the response of the carrier can be considered to be in a quasi-steady-state regime.

Figure 11.15 shows the measured transmission spectra and polarization-rotation spectra of chiral and achiral structures. One can observe that an increase in the pump power results in the suppression of the transmittance. The polarization-rotation spectra are shown in Fig 11.15b. The polarization rotation without photoexcitation is negligibly small. However, polarization rotation is observed at around 1 THz, when the chiral gammadion-patterned samples are photoexcited, and the sign of polarization rotation depends on the chirality of the patterns. The magnitude of the polarization rotation increases with pump power. One can observe, from Fig. 11.15b, that there is no polarization effect in the achiral cross-patterned sample. This indicates that the observed polarization effect originates from the structure chirality. The polarization rotation effects was not found to depend on the incident polarization direction.

Fig. 11.15

Experimental results of transmission and polarization-rotation spectra. a Transmission spectra and b polarization-rotation spectra at different photoexcitation powers. Top, middle and bottom figures are the results of the samples with cross, right-twisted, and left-twisted metal patterns, respectively (From [23])

The mechanism of the observed polarization effect can be understood by comparison with the enhancement of optical activity in complementary double-layered chiral structures whose experimental data are shown in Fig. 11.4. In that case, the coincidence of the resonant frequency of the complementary double layers, because of Babinet’s principle, and the local enhanced electric fields near the edges of two layers at close lateral positions contributed to realize a large optical activity [16]. In the case illustrated in Fig. 11.14, the photoexcitation generates a chiral distribution of photocarriers at the surface and inside the semiconductor substrate. The gold metal mask and photocarriers form a double-layered complementary metallic grating, and optical activity results. The present technique of active THz polarization control is based on the formation of a three-dimensional chiral morphology of semiconducting material system.

To examine the validity of the observed phenomena, numerical calculations of transmission spectra and polarization-rotation spectra were performed with the rigorous coupled-wave analysis method. The dielectric response function $\epsilon (z,\omega )$ for the photoexcited region, based on the Drude model, was introduced taking into account the carrier density attenuation along the z direction as follows,

$$\begin{aligned} \epsilon (z,\omega )=\epsilon _{Si}+\Delta \epsilon (\omega )\mathrm{exp}(-z/{d}),\end{aligned}$$

(11.55)

$$\begin{aligned} \Delta \epsilon (\omega )=\frac{{\omega ^{2}_{p}}}{{\omega \left({\omega -i\gamma }\right)}} \end{aligned}$$

(11.56)

where $\epsilon _{Si}$ is the dielectric constant of silicon without photoexcitation, the attenuation length $d = 9.8$ $\mu$m is the penetration depth of the pump beam [34]. The damping constant of the Drude model is assumed to be $\gamma /2\pi = 0.5$ THz. The excitation level is expressed by $\omega _{p}$ in (11.56); larger $\omega _{p}$ indicates stronger excitation because $\omega _{p}$ is proportional to the square root of the photoexcited carrier density. The results of the calculation are shown in Fig. 11.16. The suppression of the transmission spectra and the enhancement of optical activity with photoexcitation are well reproduced.

Fig. 11.16

Results of numerical calculation of transmission and polarization-rotation spectra. Numerical calculation results of a transmission spectra and b polarization-rotation spectra of the left-twisted gammadion structure at different photoexcitation levels, identified by $\omega _{p}$ (From [23])

In conventional schemes, carrier lifetime limits the switching time of photocarrier-induced effects. In the present case, however, the photo-induced optical activity decays much faster than the lifetime of photocarriers in silicon (${\sim }\mu$s). Numerical calculations and experiments were performed to clarify the mechanism of such fast decaying, and found that the gammadion-patterned carrier distribution becomes uniform within about 250 ns, and the optical activity vanishes. By using a semiconductor substrate with a shorter lifetime of carriers or faster carrier diffusion, a faster response of active polarization control can be achieved.

11.5 Conclusion

In this chapter, THz time domain ellipsometry, which makes use of the vectorial nature of THz waves, has been described. Using this method, all the components of the complex dielectric tensor, including off-diagonal parts, can be obtained with high accuracy by extracting both information of amplitude and phase from the x and y components of a THz time domain wave vector. As examples of application, optical activity was observed in artificial chiral grating structures. Such structures can also be used as active polarization modulators. THz ellipsometry can develop new applications for THz-TDS, such as detection of quantum hall [6] and magneto-optical effects. These methods could be employed as powerful spectroscopic tools in the future.