Individual Versus Ecological Analyses

Abstract

Analyses of disease maps frequently require the use of an ecological approach, partially because aggregates of cases allow such measures as rates to be computed. In addition, group averages of individual measures often are more readily available, tend to reduce impacts of measurement error, and help to preserve the confidentiality of individuals in each aggregation group. Given this context, the resulting problematic issue concerns drawing sound inferences about individuals from such grouped data. The general drawback to this type of inference is known as the ecological fallacy: most often a difference exists between an ecological regression and the regression based upon individuals underlying it (i.e., aggregate-level relationships do not necessarily hold at the individual level).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Analyses of disease maps frequently require the use of an ecological approach, partially because aggregates of cases allow such measures as rates to be computed. In addition, group averages of individual measures often are more readily available, tend to reduce impacts of measurement error, and help to preserve the confidentiality of individuals in each aggregation group. Given this context, the resulting problematic issue concerns drawing sound inferences about individuals from such grouped data. The general drawback to this type of inference is known as the ecological fallacy: most often a difference exists between an ecological regression and the regression based upon individuals underlying it (i.e., aggregate-level relationships do not necessarily hold at the individual level). Well-recognized impacts corrupting inference are aggregation bias (i.e., distortions of the information content of data attributable to loss of variability through observation aggregation), confounding variables (i.e., hidden or unknown variables lurking about in a study that cause distortions through their correlations with the response variable), and nonlinearity. One interesting exchange about this topic appears in the Annals of the Association of American Geographers (2000).

In this chapter, results of experiments with Syracuse, NY pediatric lead poisoning data demonstrate selected nonstandard spatial statistical analyses concerning individual versus ecological inference.

2 Spatial Autocorrelation Effects

Frequently georeferenced data comprise geographic aggregates, with geographic variability constituting part of the focus of a study. Accordingly, analyses of disease maps are further complicated by the presence of spatial autocorrelation (SA) effects associated with georeferenced data, especially because less is known about impacts of these effects on binomial or Poisson random variables. Generally speaking, variance inflation is the principal impact of positive SA in linear statistical analyses. This holds for binomial and Poisson variables, too, where it operates as a source of overdispersion.

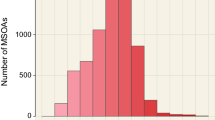
Consider a P-by-Q regular square tessellation network of locations. Simple binomial models were estimated for P = 91 and Q=92 (i.e., n = 8,372), and the Syracuse pediatric blood lead level (BLL) data parameter estimates based upon the three current threshold values of concern: 5 micrograms/deciliter (μg/dl; the detection level), 10 μg/dl (the concern threshold), and 20 μg/dl (the intervention threshold); these data contain 8,343 child-parcel matched locations, with global parameter estimates reported in Table 2.1. Impacts of SA in this numerical example are illustrated in Fig. 2.1. As SA latent in the data increases from none, to a moderate level, and then to a marked level, variance indeed increases, with the principal impact being a noticeable decrease in kurtosis (i.e., peakedness; Fig. 2.1a). In other words, the distribution is being flattened, with more extreme counts becoming increasingly likely, and more central counts becoming increasingly less likely.

Table 2.1 Logistic model comparisons when spatial autocorrelation is induced via the mean response: numerical results preserving ${{\hat \alpha}_{\textrm{0}}}$ and VAR(${{\hat \alpha}_{\textrm{0}}}$), based upon the entire Syracuse pediatric blood lead levels (BLLs) data

Fig. 2.1

Binomial distribution histograms for n = 8,372. Left (a): impacts of spatial autocorrelation. Right (b): comparable binomial histograms based upon the logistic regression intercept term variance

The moderate levels of positive SA (msa) employed to construct Fig. 2.1 are those more commonly encountered in the real world. These levels are accompanied by a noticeable, but not a dramatic, distortion of the affiliated histogram. The strong level of positive SA (ssa) employed to construct Fig. 2.1 is rarely encountered in the real world. Nevertheless, it distorts histograms in a way that makes them more closely resemble a uniform distribution, even when the sample size implies a bell-shaped curve should be expected. Figure 2.2 portrays the impact of near-perfect positive SA. It demonstrates that further increasing the level of positive SA results in additional squashing of the more central frequencies, essentially forcing all counts to be either of the two extremes of the range of counts. In other words, the frequency distribution now is sinusoidal in form.

Fig. 2.2

Binomial distribution histograms for n = 8,372: impacts of near-perfect positive spatial autocorrelation

3 Aggregation Impacts

For independent and identically distributed (iid) observations, the number of ways the total number of individuals (P) can be allocated to n aggregate groups is given by the following Stirling number of the second kind (Abramowitz and Stegun, 1964):

$$\frac{{\textrm{1}}}{{{\textrm{n!}}}}\sum\limits_{{\textrm{k}} = {\textrm{0}}}^{\textrm{n}} {{{{\textrm{(}} - {\textrm{1)}}}^{{\textrm{n}} - {\textrm{k}}}}\frac{{{\textrm{n!}}}}{{{\textrm{k!(n}} - {\textrm{k)!}}}}{{\textrm{k}}^{\textrm{P}}}} $$

(2.1)

One reason to note SA impacts, beyond variance inflation, is that the clustering of similar values on a map means the actual number of geographic areal unit aggregates is constrained to be less than the quantity rendered by expression (1). Accordingly, positive SA reduces within areal unit variation, and hence accentuates between areal unit variation. For example, if all of an even number of observations were linked pairs (i.e., correlated), with the net effect being that P/2 is the total number of items for allocation, then for two groups and 10 observations, this constraint reduces the number of possible groups from 511 to 15. In other words, SA may well help data analysts contend with the ecological fallacy to some degree.

3.1 The Syracuse Data

BLL data were collected by the Onondaga County Health Department for children, ages 0–6, residing in the City of Syracuse during 1992–1996, and then made digitally available for scientific analysis, with confidentiality being maintained by masking names with unique identification numbers. These data have undergone considerable editing and cleaning, and have been geocoded using the 2002 cadastral property tax map, which contains 35,500 parcels (Griffith et al., 2008). This data set comprises a total of 16,383 BLL measurements, of which 37 fail to have addresses that matched any of the city parcel addresses (i.e., they are located outside of the city boundaries), and 73 final address matchings fail to have consistent block and block group allocations (which introduces a small amount of noise into some of the aggregate data analyses). Repeated measures for children are summarized by retaining only the maximum BLL for each child. These observations are geographically distributed across 8,208 parcel locations in the City (see Fig. 2.3), with three parcels failing to link to census tracts (of which there are 57) or census block groups (of which there are 147), and an additional two parcels failing to link to census blocks (of which there are 2,025).

Fig. 2.3

The geographic distribution of individual BLLs across the City of Syracuse. Black: 0–5 μ g/dl; dark gray: 5–10 μg/dl; μ medium gray: 10–20 μ g/dl; and, light gray: 20–47 μ g/dl

The handful of cases available for a non-geographic analysis that had to be set aside for a geographical analysis introduce some, but not much, noise into the analysis. In all cases for BLL > 5 μg/dl, regardless of geographic aggregation, the simple constant mean logistic regression model yields an intercept estimate of 0.6965, with a standard error of 0.0234 (see Table 2.2). In other words, the geographic aggregation does not distort this parameter estimate or the inference that accompanies it. Rather, ecological distortion enters here in terms of the deviance statistic. Although somewhat meaningless for a binary variable, the individual data analysis is accompanied by a deviance statistic of 1.27. This value increases to 2.06 for census blocks, to 6.02 for census block groups, and to 19.81 for census tracts. Results for BLL > 10 and >20 μg/dl (see Table 2.2) are consistent with these findings. Not only may the deviance statistic be detecting a mixture of heterogeneous Bernoulli random variables, but it also may be detecting the presence of SA.

Table 2.2 Logistic regression estimation results for a constant mean model specification, for threshold BLL values and the different levels of geographic aggregation

In summary, for the simple intercept-only logistic regression model, ecological distortions appear to manifest themselves most noticeably through the deviance statistic, with aggregate data cross-tabulated by geographic areal units rendering the same inference as individual data.

3.2 Previous Findings for Syracuse

Griffith et al. (1998) report findings based upon a spatial analysis of part of the database employed here. Their study found that the general pattern of elevated BLLs across the City persists through successive levels of aggregation, from the individual child through 1990 census tract groupings. Conspicuous SA is identifiable at each level of geographic aggregation. On both substantive and empirical grounds, housing value is the single covariate that is strongly associated with elevated BLLs. Pediatric lead poisoning tends to be a completely preventable inter-city/poverty disease.

Griffith et al. (1998) also report sets of socio-economic/demographic census variables that strongly covary with pediatric lead poisoning at aggregate levels. In additional to housing value (e.g., median house value, percentage renter occupied), these include:

• census tracts: population density, percentage in cohort < 18 years of age

• census block group: population density, percentage black, number of cases

• census block: percentages black and Hispanic, number of cases, percentage in cohort < 18 years of age

Covariate surrogates for SA also appear in the models. In addition, the census block resolution is sufficiently fine that many geographic areas are non-residential, resulting in many areal units having zeroes; this is one problematic feature associated with using fine resolution census geographies or individual data for analysis purposes.

4 Spatial Autocorrelation in the Syracuse Data

Two sources of SA in the Syracuse BLL data are of particular interest. The first is latent in the BLL values themselves: children who are neighbors tend to have similar BLLs. The second is latent in the housing value covariate: neighboring houses tend to have a similar market value.

4.1 Spatial Autocorrelation in the Syracuse Data: LN(BLL + 1) Values

A Thiessen polygon partitioning of the Syracuse city surface based upon locations with children for which BLL values have been measured appears in Fig. 2.4. Below-detection-level BLL anomalies are conspicuous, whereas high BLL anomalies are not, according to a simple normal quantile plot of individual LN(BLL + 1) values, where one is the maximum likelihood translation parameter estimate for aligning the log-BLL values with a bell-shaped curve (see Fig. 2.5).

Fig. 2.4

Thiessen polygon surface partitioning of the City of Syracuse, for the locations of children for which BLL values were obtained during 1992–1996

Fig. 2.5

Normal quantile plot for individual log-BLL values

SA for individual LN(BLL + 1) value locations (a total of 8,208 parcels), portrayed with a semivariogram plot (see Fig. 2.6) for distance not exceeding roughly a third of the span of the geographic landscape, is weak-to-moderate and positive. Based upon roughly 37.3 million distance pairs, where distance has been standardized to the unit square, the following spherical and circular semivariogram models¹ (where ${{\hat \gamma}_{{\textrm{ij}}}}$ denotes semivariance) best describe these data:

$${\textrm{penta}} - {\textrm{spherical model:}}\,{{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{0}}{\textrm{.14}} + {\textrm{0}}{\textrm{.03}}\left[ {\frac{{15}}{8}\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.32}}}} - \frac{5}{4}{{\left( {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.32}}}}} \right)}^3} + \frac{3}{8}{{\left( {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.32}}}}} \right)}^5}} \right]{\textrm{ , }}$$

$${{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} \le {\textrm{ 0}}{\textrm{.32}};$$

$${{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{0}}{\textrm{.14}} + {\textrm{0}}{\textrm{.03 }} = {\textrm{ 0}}{\textrm{.17 , }}{{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} > {\textrm{ 0}}{\textrm{.32}}$$

$${\textrm{spherical model:}}\,{{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{0}}{\textrm{.14}} + 0.03\left[ {\frac{3}{2}\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.26}}}} - \frac{1}{2}{{\left( {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.26}}}}} \right)}^3}} \right]{\textrm{ , }}{{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} \le {\textrm{ 0}}{\textrm{.26}}$$

$${{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{0}}{\textrm{.14}} + {\textrm{0}}{\textrm{.03 }} = {\textrm{ 0}}{\textrm{.17 , }}{{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} > {\textrm{ 0}}{\textrm{.26}}$$

Fig. 2.6

Semivariogram plot for LN(BLL + 1) values, City of Syracuse, NY. Black asterisks denote observed values; gray open circles denote spherical model predicted values

These models respectively yield 0.074 and 0.075 relative error sums of squares. The scatterplot reveals very marked in situ variability of log-BLL values, and a well-defined geographic pattern to their covariation.

4.2 Spatial Autocorrelation in the Syracuse Data: Appraised House Value

The correlation between individual log-BLLs and 2002 appraised house values is –0.29 (see Fig. 2.7 ).

Fig. 2.7

Scatterplot and trend line portraying the relationship between BLL and 2002 appraised house value

In general, house values tend to display strong positive SA. Indices for the City of Syracuse, calculated with median values for geographic aggregates, are as follows (also see Fig. 2.7):

aggregation unit	Moran Coefficient (MC)	Geary Ratio (GR)	n
census tract	0.40902	0.62080	56 (#32 missing)
census block group	0.55331	0.45103	145 (#32.001 and #32.002 missing)
census block	0.66111	0.32304	1,485 (540 blocks missing)

These statistics are based upon 2002 assessed values, per $10,000, for houses in which children were tested for pediatric lead poisoning (a total of 7,057 houses). Areal units without residential properties were set aside during the SA index computations. These results simply indicate that latent SA in the geographic aggregations is moderate and positive, increasing with increasingly finer resolution.

SA for individual residential properties, portrayed with a semivariogram plot (see Fig. 2.8) for distance not exceeding a third of the span of the geographic landscape, is strong and positive. Based upon roughly 16.9 million distance pairs, where distance has been standardized to the unit square, the following spherical and circular semivariogram models (again where ${{{\hat \gamma }}_{{\textrm{ij}}}}$ denotes semivariance) best describe these data:

$${\textrm{circular model:}}\,{{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{1}}{\textrm{.58}} + {\textrm{4}}{\textrm{.82}}\frac{{\textrm{2}}}{{{\pi }}}\left[ {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.18}}}}\sqrt {{\textrm{1}} - {{\left( {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.18}}}}} \right)}^{\textrm{2}}}} + {\textrm{SI}}{{\textrm{N}}^{ - {\textrm{1}}}}\left( {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.18}}}}} \right)} \right]{\textrm{ , }}$$

$${{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} \le {\textrm{0}}{\textrm{.18 ;}}$$

$${{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{1}}{\textrm{.58}} + {\textrm{4}}{\textrm{.82 }} = {\textrm{ 6}}{\textrm{.40 , }}{{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} > {\textrm{ 0}}{\textrm{.18}}$$

$${\textrm{spherical model:}}\,{{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{1}}{\textrm{.47}} + {\textrm{4}}{\textrm{.96}}\left[ {\frac{3}{2}\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.21}}}} - \frac{1}{2}{{\left( {\frac{{{{\textrm{d}}_{{\textrm{ij}}}}}}{{{\textrm{0}}{\textrm{.21}}}}} \right)}^3}} \right]{\textrm{ , }}{{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} \le {\textrm{ 0}}{\textrm{.21}}$$

$${{{\hat \gamma }}_{{\textrm{ij}}}} = {\textrm{1}}{\textrm{.47}} + {\textrm{4}}{\textrm{.96 }} = {\textrm{ 6}}{\textrm{.43, }}{{\textrm{d}}_{{\textrm{ij}}}}{\textrm{ }} > {\textrm{ 0}}{\textrm{.21}}$$

Fig. 2.8

Semivariogram plot for 2002 appraised house values, City of Syracuse, NY. Black asterisks denote observed values; gray circles denote circular model predicted values

These models respectively yield 0.005 and 0.008 relative error sums of squares. The scatterplot reveals sizeable in situ variability of house values, a pronounced geographic pattern to their covariation, and a not surprising city-wide trend possibility.

Including house value in the logistic regression specification accounts for some of the SA in BLLs. Because appraised house values are not reported for apartment complexes, the values for these locations were set to 0, and then an indicator variable was created to differentiate these rental locations from the other residential locations (the numeral 1 denotes non-rental, and –1 denotes rental). Logistic regression estimation results for this situation appear in Table 2.3. As expected, house value is negatively related, whereas rental property is positively related, to elevated BLLs. Inclusion of the housing variables reduces overdispersion across the individual and ecological analyses (see Sect. 3.1). In addition, ecological bias now is detectable in all of the parameter estimates as well as their corresponding standard errors (Green, 1993; Wrigley, 1995; Holt et al., 1996). Although inferences tend not to be dramatically altered for BLL > 5 or 10 μg/dl, nevertheless they are altered. The case of BLL > 20 μg/dl illustrates how ecological analysis findings can deviate radically from individual-based findings. Furthermore, the rareness of BLLs > 20 creates numerical problems with estimation of the house value binary 0–1 indicator variable parameter, which had to be set aside for its aggregate analyses. This complication resulted in a loss of observations: 121 blocks, five block groups, and one census tract.

Table 2.3 Logistic regression estimation results when house value is used as a covariate, for threshold BLL values and the different levels of geographic aggregation

5 Spatial Autocorrelation in the Syracuse Data: Other Sources

Other sources of SA (e.g., geographic concentration of poverty, siblings)—which may well represent the presence of confounders—beyond house value can be captured in part by employing a spatial filter (SF) model specification. Spatial filtering involves regressing a disease map variable on a set of synthetic variates representing distinct map patterns that accounts for SA. Griffith (2003) develops one form of spatial filtering whose synthetic variates are the set of n eigenvectors extracted from matrix (I – ii ^T/n)C(I – ii ^T/n), the matrix appearing in the numerator of the MC index of SA, where C is a binary 0–1 n-by-n geographic weights matrix (i.e., c _ij = 1 if areal units i and j are neighbors, and 0 otherwise), and i is an n-by-1 vector of ones.² This procedure is similar to executing a principal components analysis in which the covariance matrix is given by (I – ii ^T/n)C(I – ii ^T/n). But rather than using the resulting eigenvectors to construct linear combinations of attribute variables, the eigenvectors themselves (instead of principal components scores) are the desired synthetic variates, each containing n elements, one for each areal unit. The extracted eigenvector $\frac{1}{{\sqrt n }}$ i relates to the mean response, and the remaining (n–i) extracted eigenvectors relate to distinct map patterns characterizing latent SA—whose MCs are given by standardizing their corresponding eigenvalues (Tieflesdorf and Boots, 1995)—that can materialize with matrix C. Furthermore, for a given geographic landscape surface partitioning, the eigenvectors represent a fixed effect in that matrix (I – ii ^T/n)C(I – ii ^T/n) does not, and hence they do not, change from one attribute variable to another.

Because this eigenfunction decomposition yields n eigenvectors, a spatial scientist needs to restrict attention to only those eigenvectors describing substantive positive/negative (e.g., MC > 0.25) SA, reducing the candidate set to a more manageable number for describing a given disease map. Supervised stepwise selection from this set of eigenvectors is a useful and effective approach to identifying the subset of eigenvectors that best describes latent SA in a particular disease map. This procedure begins with only the intercept included in a regression specification. Next, at each step an eigenvector is considered for addition to the model specification. For the stepwise generalized linear binomial model regression, the eigenvector that produces the greatest reduction in the log-likelihood function chi-square test statistic is selected, but only if it produces at least a prespecified minimum reduction; this is the criterion used to establish statistical importance of an eigenvector. At each step all eigenvectors previously entered into a SF equation are reassessed, with the possibility of removal of vectors added at an earlier step. The forward/backward stepwise procedure terminates automatically when some prespecified threshold chi-square statistic values are encountered for entry and removal of all candidate eigenvectors.

SFs were constructed for the three geographic aggregations from the 15 candidate eigenvectors for census tract, the 37 for block group, and the 483 for block surface partitionings. Spatial filtering results appear in Table 2.4. Although SA is being accounted for in the parameter estimations for these models, ecological bias still persists. The constructed SFs represent moderate-to-strong levels of positive SA:

Aggregation unit	BLL >5		BLL >10		BLL >20
	MC	GR	MC	GR	MC	GR
census tract	0.52360	0.46773	0.57387	0.42043	0.82900	0.19180
census block group	0.78798	0.21419	0.80439	0.24604	0.89953	0.22550
census block	0.96443	0.28303	0.90625	0.29532	0.97343	0.31957

Table 2.4 Ecological logistic regression estimation results when house value is used as a covariate and spatial autocorrelation is accounted for, for threshold BLL values

Individual results are not available here, since eigenvectors were not computed for the set of individual locations (see Fig. 2.4 for a possible surface partitioning supporting this purpose). Of note is that, as before, the rareness of BLLs > 20 continues to create numerical problems with estimation of the house value binary 0–1 indicator variable parameter, which has been removed from the model specification.

6 Bayesian Analysis Using Gibbs Sampling (BUGS) and Model Prediction Experiments

The parallel analyses of individual and ecological data in preceding sections reveal the presence of positive spatial dependence beyond house value, most likely attributable to other unmeasured cofounders with spatial structure, in elevated pediatric BLLs. These parallel analyses also document the presence of ecological biases. A previous ecological investigation of these data uncovers population density, an indicator of urban poverty that could not be detected with the individual-level data, as a covariate of elevated BLLs. This finding illustrates Darby et al.’s contention that “the ecological result [is not always the one] that is wrong” (2001, p. 202). But even findings reported here from ecological analyses conducted by changing geographic aggregation resolution do not agree. This ecological variation arises from a suppression of within-areal unit variability, a finding established in Sect. 2.3.1: “within-area information … is vital for analysis and interpretation” (Wakefield and Salway, 2001, p. 136). Wakefield (2003) notes that this is particularly true for regression analyses, in which SA components potentially account for unmeasured confounders. Accordingly, the question of interest now asks if this within-areal unit variation can be recovered. Richardson and Montfort (2000) argue that one method of recovery is to posit a parametric form for this variation in order to adjust the corresponding individual-level model, noting that even a parametric form that describes the variation poorly is better than none at all. Wakefield and Salway (2001) allude to the use of random effects, which is explored in this section.

The experiments conducted to explore the utility of random effects estimates as surrogates for within-areal unit variation include those ecological covariates found in the previous study (Griffith et al., 1998). Besag et al. (1991) suggest that these random effects could be spatially structured using a conditional autoregressive (CAR) covariance specification. Wakefield and Salway (2001) suggest that the simplest approach is to employ non-spatial random effects. As a compromise between these two specifications, a SF is employed here to specify spatially structured random effects; the SF becomes the mean of the effects. As is done in the tradition of principal components regression, this SF is computed exogenously, and then its coefficient—which subsequently is distributed across the linear combination of eigenvectors—is estimated; this procedure is analogous to introducing starting values in nonlinear regression estimation (e.g., logistic regression). Next, this analysis is repeated with a proper CAR specification for spatially structured random effects.

Various different completed analyses facilitate exploring relationships between individual- and ecological-based model predictions. One hypothesis evaluated here may be stated as follows:

The variance of a spatially structured ecological random effects term is directly proportional to the within areal unit variability suppressed by undertaking an ecological analysis.

Preparatory work for assessing this hypothesis involved a Bayesian analysis of the pediatric BLL data. This analysis was executed with the WinBUGS software (the Windows version of BUGS; Thomas et al., 2004), employing a SF model specification, normal priors for the parameter estimates and the random effects term, a gamma prior for the inverse of the error variance, a 25,000-iteration burn-in period, and 500,000 subsequent Markov chain Monte Carlo (MCMC) iterations that then had only every hundredth one retained (weeding), yielding chains of length 5,000 for estimation purposes. With regard to diagnostics, accompanying temporal correlograms and time series plots suggest the generated chains are sound. A CAR comparison also is made, using a 5,000-iteration burn-in period, and 100,000 subsequent MCMC iterations that then had only every hundredth one retained, yielding chains of length 1,000 for estimation purposes.

A second hypothesis evaluated here may be stated as follows:

Individual level prediction improves by adding to its model specification those neighborhood variables identified as important factors with ecological modeling.

The resulting model is labeled mixed here.

6.1 Results for the 2000 Census Tracts

Results of parameter estimation for both generalized linear and BUGS binomial regressions are reported in Table 2.5. For the most part, the BUGS results corroborate the frequentist generalized linear model results. The SFs capture strong positive SA. Maps for two eigenvectors common to all three SFs (i.e., E ₃ and E ₉) appear in Fig. 2.9. One conspicuous difference between these two sets of results is the standard errors for BLL > 5 μg/dl and BLL > 10 μg/dl: Bayesian-based standard errors tend to be noticeably larger in these two cases. Nevertheless, models for BLL > 5 μg/dl and BLL > 10 μg/dl appear to furnish respectable descriptions of the ecological data.

Fig. 2.9

Eigenvectors common to the spatial filters for the BLL >5 μg/dl, BLL > 10 μg/dl, and BLL > 20 μg/dl. Left (a): eigenvector E ₃. Right (b): eigenvector E ₉

Table 2.5 Tract-level ecological logistic regression results when selected socio-economic/demographic variables are used as covariates and spatial autocorrelation is accounted for, for threshold BLL values

The suppressed variation induced by aggregation for ecological analysis is for appraised house values. The following battery of descriptive statistics for the 5,000 MCMC generated random error terms, aggregated by census tract, were calculated: mean, median, standard deviation, minimum value, maximum value, skewness, and kurtosis. Next, a stepwise regression was executed using these statistics as predictor variables, and the standard deviation of house value as the regressor variable. Kurtosis was the single statistic selected in the stepwise analysis for BLL > 5  μg/dl; it accounts for roughly 15% of the variability in the standard deviation of house values. The standard deviation was the single statistic selected in the stepwise analyses for BLL > 10 μg/dl and BLL > 20 μg/dl; it accounts for, respectively, roughly 6.6% and 4.6% of the variability in the standard deviation of house values. Meanwhile, replacing kurtosis with this standard deviation for BLL > 5 results in roughly 4.6% of the variability in the standard deviation of house values being accounted for. The ideal result would be for nearly 100% of the variability in the standard deviation of house values to be accounted for by the standard deviation in estimated random error terms. Therefore, the hypothesis positing direct proportionality between these two statistics is not supported here. Apparently the type of approach promoted by Richardson and Montfort (2000) can neither be recaptured nor receive empirical guidance from ecological Bayesian spatial modeling.

Of note is that random effects results from a proper CAR model also were generated for BLL > 5 μg/dl. Here the spatial autoregressive parameter estimate is 0.7870 (SE = 0.2063), indicating the presence of strong, positive SA; now the degrees of freedom are 13. These random effects failed to exhibit any covariation whatsoever with the suppressed variability.

A cross-tabulation of individual observed and prediction results for 0 (non-elevated BLL) and 1 (elevated BLL) appear in Table 2.6; predicted probabilities less than 0.5 have been classified as and rounded to 0, whereas those greater than 0.5 have been classified as and rounded to 1. As the ecological fallacy warns, applying an ecological model to individuals is unsuccessful here. Of note is that even the individual-level model predictions loose reliability as elevated BLL increasingly becomes a rare event. Nevertheless, as Darby et al. (2001) argue, enhanced model results are obtained by formulating a mixed individual-ecological model specification. Not only are covariates like population density detectable at the aggregate level, while not at the individual level, but adding these covariates to an individual-level model also improves predictability for BLL > 5 μg/dl, and very marginally for BLL > 10 μg/dl. Of note is that any individual-model gains by including these ecologically determined covariates is lost as these covariates become statistically nonsignificant in their ecological analyses.

Table 2.6 Cross-tabulations of observed and model predicted elevated BLLs, for threshold BLL values

Because the results here were so poor, analyses were not repeated for either the census block group or census block aggregations.

7 Discussion and Implications

The empirical case study explored here reveals that geographic aggregation combined with SA can cause diagnostic statistics to be misleading. Nevertheless, four general ecological inference conclusions can be drawn from findings summarized here. First, spatial filtering may furnish a blurred, but still unsatisfactory, glimpse of within-areal unit covariation by serving as the spatial structuring term for random effects. Second, the failure of estimated random effects to furnish a useful within-areal units variability surrogate implies that the Richardson-Montfort suggestion of specifying individual-level covariance structure a priori should be a more fruitful pursuit. But guidelines for undertaking this task remain to be established; the ultimate goal is to be able to draw the same statistical inferences from aggregate-level data that would be drawn from individual-level data, but without having the individual details. Third, a posited covariance structure should include prominent attributes identified via ecological analysis, resulting in a mixed formulation, as advocated by Darby et al. (2001). Prominent ecological covariates that remain invisible at an individual level of analysis offer the potential to dramatically improve statistical description. In addition, these ecologically-based attributes may at least partially account for SA that impacts upon individual data. Finally, the ability to develop far better ecological-level predictive models for rare events is a continuing need.