Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

12.1 Introduction

In spite of the complex dynamics exhibited by even the simplest of nonlinear time delay systems, there exists a host of coupled nonlinear time delay systems which admit exact solutions. Particularly, certain coupled systems of nonlinear delay differential equations modelling traffic flow [1–3], called the car following models, possess exact analytic solutions in terms of Jacobian elliptic functions under periodic boundary conditions. However, under open boundary conditions, they admit shock-like solutions, representing the stationary propagation of a traffic jam [2,3]. We will closely follow here the approach of Tutiya and Kanai [4] in the following discussion just to illustrate how exact solutions can arise in delay systems.

12.2 The Car-Following Models

It is interesting to note that one can treat a traffic flow, including pedestrian flow, as a compressible fluid from a macroscopic point of view, or as a many-body problem of driven particles in a microscopic sense. Consequently, models can be developed based either on hydrodynamic equations or in terms of coupled ordinary differential equations, and even in terms of cellular automata.

Consider for example, the highway traffic. One can model it as a system of particles moving in one dimension in a definite direction interacting with each other asymptotically, see Fig.12.1.

In this one-dimensional picture one essentially considers contrasting density patterns, which change quite irregularly as the density of particles increases, and which finally take the form of a stable traffic jam propagating backwards with constant speed. One can introduce a set of coupled delay- differential equations of the following form to represent the traffic flow:

$$\dot{x}_{n}(t) = F(\varDelta x_{n}(t-\tau)), \qquad \varDelta x_{n}(t) = x_{n-1}(t) - x_{n}(t), \qquad n = 1,2,\cdots$$
((12.1))

where \(x_{n}(t)\), \(n = 1,2,\cdots\), denotes the position of the nth car at time t and \(\varDelta x_{n}(t)\) is the distance between the nth car and the one in front of it (that is the \((n-1)\)th). In the above car following model described by (12.1), one can observe that it represents the solution where the velocity of each car, \(\dot{x_{n}}(t)\), is determined in terms of the distance that separates it from its predecessor with a delay τ, that is in terms of \(\varDelta x_{n}(t-\tau)\). The function \(F(x)\) in (12.1), often called optimal velocity function, is usually determined from real traffic data.

Fig. 12.1
figure 1

An illustration of one-lane traffic with the assumption that cars overtaking and colliding are prohibited [4]

Full size image

Two typical models correspond to the following forms:

  1. (i)

    Newell model: \(F = V\left[1-exp\left(-\frac{\gamma}{V} \left(\varDelta x_{n}(t-\tau) - L\right)\right)\right]\), where r, V, L are parameters.

  2. (ii)

    Tanh model: \(F = \xi + \eta tanh \left(\frac{\varDelta x_{n}(t-\tau)-\rho}{2A}\right)\), where ξ, η, ρ and A are parameters. Exact solutions to these two models can be deduced using the so called Hirota bilinearization method [5], well known in the theory of soliton systems (see for example [6]).

12.3 The Newell Model

The Newell equation reads as

$$\begin{array}{*{20}l} \dot{x_{n}}(t) &=& V\left[1-exp\left(-\frac{\gamma}{V} \left(\varDelta x_{n}(t-\tau) - L\right)\right)\right],\\ \varDelta x_{n}(t) &=& x_{n-1}(t) - x_{n}(t), \qquad n = 1,2,\cdots \end{array}$$
((12.2))

Here V is the maximum allowed velocity of the car, γ is the slope of the optimal velocity of function at \(\varDelta x_{n} = L\) corresponding to the sensitivity of the driver to changes in the traffic situation, and L is the minimum headway. In Fig.12.2, the optimal velocity function F is shown as a function of the headway \(\varDelta x_{n}\), where the parameters have been deduced from empirical data [4].

Fig. 12.2
figure 2

The optimal velocity function for the Newell model. The values of the parameters are as follows: \(V=120\), \(\gamma=6\) and \(L=5\), where V indicates the maximum allowed velocity, γ is the derivative of F at \(\varDelta x_n=L\), and L is the minimum distance between cars (adapted from [4])

Full size image

Now, in order to eliminate the background uniform flow, one can change the dependent variable \(x_{n}(t)\) to \(y_{n}(t)\) as

$$y_{n}(t) = x_{n}(t) - (V_{0}t-L_{0}n),$$
((12.3))

where the velocity \(V_{0}\) and headway \(L_{0}\) satisfy the condition

$$V_{0} = V\left[1-exp\left(-\frac{\gamma}{V}(L_{0}-L)\right)\right],$$
((12.4))

which is required of a uniform solution. Substituting (12.3) and (12.4) into (12.1), the Newell equation (12.3) can be rewritten as

$$\dot{y_{n}}(t) = (V-V_{0}) [1-exp(-s_{n} (t-\tau)],$$
((12.5a))

where

$$s_{n}(t) = \frac{\gamma}{V}(y_{n-1}(t)-y_{n}(t)).$$
((12.5b))

Now differentiating (12.5 b) once and using (12.5 a), we can rewrite (12.5) as

$$\frac{1}{\alpha_0} \dot{s_{n}}(t) = -exp\left(-s_{n-1}(t-\tau)\right) + exp\left(-s_{n}(t-\tau)\right),$$
((12.6a))

where

$$\alpha_{0} = \gamma\left(1-\frac{V_0}{V}\right) = \gamma exp\left[-\frac{\gamma}{V}(L_{0}-L)\right].$$
((12.6b))

One can now reexpress the above Newell equation in Hirota’s bilinear form. For this purpose, let us define

$$\psi_{n}(t) = exp(-s_{n}(t)).$$
((12.7))

Then from (12.6) one has

$$\frac{1}{\alpha_0} \frac{\dot{\psi_{n}}(t+\tau)}{\psi_{n}(t+\tau)} = \psi_{n-1}(t) - \psi_{n}(t).$$
((12.8))

Following the standard bilinearization procedure (for example for the nonlinear Schrödinger equation see for instance [6]), one can introduce the bilinearizing transformation

$$\psi_{n}(t) = \frac{g_{n}(t)} {f_{n}(t)}.$$
((12.9))

Then (12.5) can be rewritten as

$$\frac{1}{\alpha_0} \frac{\dot{g_{n}}(t+\tau) f_{n}(t+\tau) - g_{n}(t+\tau) \dot{f_{n}}(t+\tau)} {f_{n}(t+\tau) g_{n}(t+\tau)} = \frac{g_{n-1}(t) f_{n}(t) - g_{n}(t) f_{n-1}(t)}{f_{n-1}(t) f_{n}(t)}$$
((12.10))

Consequently (12.10) can be decoupled as

$$\begin{array}{*{20}l} \dot{g_{n}}(t+\tau) f_{n}(t+\tau) - g_{n}(t+\tau) \dot{f_{n}}(t+\tau)\nonumber \\ = \lambda (g_{n-1}(t) f_{n}(t) - g_{n}(t) f_{n-1}(t)), \end{array}$$
((12.11a))
$$f_{n-1}(t) f_{n}(t) = \frac{\alpha_0}{\lambda} f_{n}(t+\tau) g_{n}(t+\tau).$$
((12.11b))

Here λ is a constant. Equations (12.11) are now in the required bilinear form.

Following the standard procedure of Hirota bilinearizition method [5], one can assume that

$$f_{n}(t) = 1+exp(an+2bt),$$
(12.12a))
$$g_{n}(t) = u+v exp(an + 2bt),$$
((12.12b))

where a, b, u and v are constants. Substituting (12.12) back into (12.11), one obtains a shock-like solution of the form

$$f_{n}(t) = 1 + exp[2b(t-n\tau)],$$
((12.13a))
$$g_{n}(t) = \frac{b}{{\alpha_0}(1-e^{-2b\tau})} \left\{1 + exp(2b[t-\tau(n+1)])\right\},$$
((12.13b))

where b is a free parameter. Using (12.13) and (12.9) in (12.7) one can finally obtain the solution

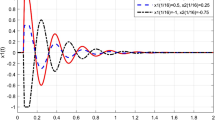
$$s_{n}(t) = log \frac{\alpha_{0} sinh(b\tau)}{b} \frac{cosh[b(t-n\tau)]}{cosh[b(t-(n+1)\tau)]}.$$
((12.14))

Solution (12.14) represents a shock-like structure moving with velocity \(U = \frac{1}{\tau}\) representing a traffic jam backwards. Here open boundary conditions have been assumed. A plot of the function (12.14) is shown in Fig.12.3 to show the solitary nature and shock-like structure. In addition one can also obtain an elliptic function wave solution of the form

$$s_{n}(t) = log \frac{2\alpha_{0} sn(\varOmega \tau) cn(\varOmega \tau) dn(\varOmega \tau)}{\varOmega [1-k^{2} sn^{2}(\varOmega \tau) sn^{2}(\phi+\varOmega \tau)] (1-k^{2} sn^{2}(\varOmega \tau) sn^{2} \phi)},$$
((12.15))

where \(\phi = \varOmega (t-2\tau n)\), and sn, cn, and dn are Jacobian elliptic functions with modulus k, while the parameter Ω satisfies a certain transcendental equation [4].

Fig. 12.3
figure 3

Solution \(s_{n}(t)\) as a function of t for various values of n. The other parameters are fixed at \(\alpha_{0}\) = 5, b = 1, τ = 2

Full size image

12.4 The tanh Car-Following Model

Consider the car following model introduced in [2,3],

$$\dot x_n = \xi + \eta tanh \left(\frac{\varDelta x_{n} (t-\tau)-\rho}{2A}\right),$$
((12.16))

where ξ,η,ρ and A are constant parameters. Defining the distance variable

$$h_{n}(t) = \frac{(\varDelta x_{n}(t)-\rho)}{2A},$$
((12.17))

Equation (12.16) can be rewritten as

$$\dot{h}_{n}(t+\tau) = \frac{\eta}{2A} \left[tanh h_{n-1}(t) - tanh h_{n}(t)\right].$$
((12.18))

Several specific elliptic function solutions to (12.18) can be given [2,3]:

$$(i) tanh\ h_{n}(t) = a sn \varOmega (t-2n\tau)+b,$$
((12.19))
$$(ii) tanh\ h_{n}(t) = \frac{b}{sn \varOmega (t-2n\tau)+a} + c,$$
((12.20))
$$(iii) tanh\ h_{n}(t) = \frac{b}{sn^{2} \varOmega(t-2n\tau)+a}+c.$$
((12.21))

In the above Ω is a free parameter, while the parameters a, b, and c can be fixed in terms of Ω, A, η and τ.

Other interesting solutions can be given again by bilinearizing the system (12.16). Defining

$$\psi_n = tanh h_n,$$
((12.22))

Equation (12.17) can be rewritten as

$$\dot {\psi}_{n}(t+\tau) = \frac{\eta}{2A} \left[1-(\psi_{n}(t+\tau))^2\right] \left(\psi_{n-1}(t)-\psi_{n}(t)\right)$$
((12.23))

Again defining

$$\psi_{n}(t) = \frac{g_{n}(t)}{f_{n}(t)},$$
((12.24))

one can rewrite (12.23) into a system of bilinear equations,

$$\begin{array}{*{20}l} \dot{g_{n}}(t+\tau) f_{n}(t+\tau) - g_{n}(t+\tau) \dot{f_{n}}(t+\tau) \nonumber \\ = \lambda \left[(g_{n-1}(t) f_{n}(t) - g_{n}(t) f_{n-1}(t))\right], \end{array}$$
((12.25a))
$$f_{n-1}(t) f_{n}(t) = \frac{\eta}{2A\lambda} \left[f_{n}^{2}(t+\tau) - g_{n}^{2}(t+\tau)\right],$$
((12.25b))

where λ is a constant.

Making now the substitution

$$f_{n}(t) = 1+ exp(2bt-an), \,\,g_{n}(t) = u + v exp(bt-an)$$
((12.26))

into (12.25), and finding consistent forms of u and v, one can obtain the solution

$$\begin{array}{*{20}l} f_{n}(t) &=& 1 + exp(2bt-an),\nonumber \\ g_{n}(t) &=& \left[1-\frac{2bA}{\eta(1-e^{-2b\tau})}\right]+\left[1+e^{-2b\tau} exp(2bt-an)\right], \end{array}$$
((12.27))

where the constant parameters a and b are related by

$$e^{a} = \frac{bA/\eta+1-e^{2b\tau}}{bA/\eta-1+e^{-2b\tau}}.$$
((12.28))

Using the above forms of \(f_{n}(t)\) and \(g_{n}(t)\), then one obtains the exact solution to the tanh car following model (12.16) as

$$\varDelta x_{n}(t) = \rho + A log \left( \frac{2\eta sinh (b\tau) cosh \left(bt-\frac{a}{2}n\right)}{bA cosh\left[b(t-\tau)-\frac{a}{2}n\right]}-1 \right)$$
((12.29))

This is another shock wave solution with velocity \(U = \frac{2b}{a}\) which represents a traffic jam propagating backwards, see Fig.12.4. Apart from the above type of solutions one can also construct explicit elliptic function waves propagating with velocity \(U=\frac{1}{2\tau}\) and as a limiting form a kink like solution can also be obtained. For details see for example [2,4].

Fig. 12.4
figure 4

The plot of the function \(\varDelta x_{n}(t)\) Vs t for different values of n, while the other parameters are held fixed

Full size image

12.5 Other Developments

Modeling of vehicular traffic is a complex dynamical problem, which has been attracting the attraction of scientists for more than half a century (for a review, see [7]). Yet the precise mechanism for generation and propagation of traffic jams is not fully understood. In this chapter, we have presented a couple of simple car following models which possess exact shock like solutions representing jams propagating backwards. More general models require detailed numerical analysis.

In the case of sparse traffic, it is well known that there exists a uniform flow equilibrium where vehicles follow each other with the same velocity while oscillations may arise when the traffic becomes more dense. One of the typical oscillations [8] is a stop-and-go-wave, where the velocity breaks down and vehicles become densely packed on a section of the highway and the congestion propagates upstream as a density wave with a characteristic wave speed. Several models exist to reproduce some aspects of such a flow. More general models than the simple car following model (12.1) start with the dynamical equation for the acceleration of the ith vehicle,

$$\dot{v}_{i}(t) = f\left(h_{i}(t-\tau_{1}), \dot{h}_{i}(t-\tau_{2}), v_{i}(t-\tau_3)\right).$$
((12.30))

Here \(v_{i}\) is the velocity of the ith vehicle, while \(h_{i}\) is the bumper to bumper distance between the ith and \((i+1)\)th vehicles called the headway. The reaction time delays \(\tau_1, \tau_2, \tau_3 (\geq 0)\) are generally different, but often assumed to be same for simplicity. Here

$$\dot{h}_{i}(t) = x_{i+1}(t)-x_{i}(t)-l,$$
((12.31))

where \(x_{i}\) is the position of the front bumper of the ith vehicle and l is the length of the vehicle. The time derivative then gives

$$\dot{h}_{i}(t) = v_{i+1}(t)-v_{i}(t),$$
((12.32))

With suitable functional forms of the function f and appropriate boundary conditions, one may numerically analyze Eq. (12.30) to get detailed microscopic dynamics and macroscopic properties of traffic flow. For details see [8–10] for example.

In all the above models time-delay plays a crucial role.