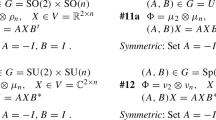Abstract
We introduce a partial order on classical and quantum mixed states which reveals that these sets are actually domains: Directed complete partially ordered sets with an intrinsic notion of approximation. The operational significance of the partial orders involved conclusively establishes that physical information has a natural domain theoretic structure. For example, the set of maximal elements in the domain of quantum states is precisely the set of pure states, while the completely mixed ensemble \(I/n\) is the order theoretic least element ⊥.
In the same way that the order on a domain provides a rigorous qualitative defini- tion of information, a special type of mapping on a domain called a measurement provides a formal account of the intuitive notion “information content.” Not only is physical information domain theoretic, but so too is physical entropy: Shannon entropy is a measurement on the domain of classical states; von Neumann entropy is a measurement on the domain of quantum states.
These results yield a foundation from which one can (a) reason qualitatively about probability, (b) derive the lattices of Birkhoff and von Neumann in a unified manner, suggesting that domains may provide a formalism for the logic of partial belief, and (c) develop new techniques for studying phenomena like noise and entanglement. Along the way, new lines of investigation open up within various subdisciplines of physics, mathematics and theoretical computer science.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
One of the great lessons of the differential and integral calculus is that we can conquer the infinite, and in particular, the continuous, by means of the discrete. An infinite sum may be understood as a limit of finite sums, the area beneath a curve as the limit of areas of approximating rectangles, the line tangent to a curve at a point is the limit of the secant lines joining points nearby.
The philosophy espoused is unambiguous: The ideal can be realized as a limit of the partial; the abstract, as a limit of the concrete; the continuous, a limit of the discrete, and so on. And this powerful ideology, as it arises in the context of recursive functionals, is part of what the axioms of domain theory are intended to capture. But even in Scott’s prelude to the subject, it is difficult to keep the imagination from wandering beyond the confines of computation [16]:
Maybe it would be better to talk about information; thus, \(x\sqsubseteq y\) means that x and y want to approximate the same entity, but y gives more information about it. This means we have to allow incomplete entities, like x, containing only partial information.
In its purest interpretation, domain theory is a branch of mathematics which offers an exclusively qualitative account of information: A proposal for how we might find information structured in a universe where all things arise as a limit of the partial.
Physics of course is also the study of information. But with one caveat: In physics, the term “information” normally manages to escape rigorous mathematical definition, and in those cases where it does not, its formulations tend toward the purely quantitative. But what is self-evident is that only qualitative accounts of physical phenomena are capable of imparting “structural laws of general validity.” From A. Einstein,
I do not believe in micro- and macro-laws, but only in (structural) laws of general validity.
Now this is not to say that physics ought to be done in laboratories without numbers, simply that our understanding of physical reality should be mathematically expressible in such a way that the laws of nature are clearly delineated from the conventions of man.
Thus, at least on the surface, there is a good match between what domain theory offers, and what physics needs: Domain theory can provide the structures of reality, physics in turn can explicate the reality of the structures. A research program in this direction begins with the demonstration contained herein that the density operator formulation of quantum mechanics is an instance of domain theory: Its partial elements are the mixed states, its total or idealized elements are the pure states.
The route to this discovery passes through the measurement formalism, a theory [8] which allows for the quantitative expression \(\mu:D\rightarrow[0,\infty)^{\ast}\) of the qualitative notion captured by a domain \((D,\sqsubseteq)\). In doing so, it yields an indispensable methodology for uncovering the structural aspects of information which often enough seem to appear in purely quantitative disguise. Such is the case with classical and quantum information, for instance, which are normally formulated in terms of Shannon and von Neumann entropy.
Our method of transport is a philosophy still advocated in certain studies on the foundations of physics [3, 9, 13]: Every formal idea should represent a meaningful physical notion, and each successive mathematical development ought to have a clear counterpart in physical reality. To illustrate, the partial order on classical states is defined inductively in terms of Bayesian state update, which corresponds to the process by which an observer looks for an object and updates his knowledge according to what he finds. Similarly, the partial order on quantum states relies on the physical notion of a measurement process.
On our way, this vehicle escorts classical and quantum probability into a genuine formal realization of the Bayesian ideal, elegantly captured by F. P. Ramsey [14]: “Probability is the logic of partial belief.”

Concretely, we introduce the domain of classical states, which has Shannon entropy as a measurement. The partial order on classical states extends to yield a domain of quantum states with von Neumann entropy as a measurement. As already mentioned, the operational significance of the partial orders involved unquestionably demonstrates that physical information has a natural domain theoretic structure. By recognizing this structure, the present work achieves unity across various subdisciplines of physics and information theory. For example, the Birkhoff-von Neumann contrast, between classical and quantum, which arises in the logical aspect, is in perfect harmony with Shannon and von Neumann entropy, which arises in more “pragmatic” pursuits. All of these are part of a single, and it would appear, more complete, picture of physical reality.
2 Classical States
The information an observer has a priori about the result of an event in which one of n different outcomes is possible can be described by a function \(x:\{1,\ldots,n\}\rightarrow[0,1]\) that assigns a probability x i indicating the degree to which outcome i is likely. These are called classical states.
Definition 1
The classical n-states are
where \(x=(x_1,\ldots,x_n)\) and \(n\geq 1\).
In this section we will introduce a natural partial order on classical states that is probably best referred to as the Bayesian order. Before doing so, here is a brief indication of how this order was discovered and our original motivation for studying it.
In contrast to a classical n-state, a quantum n-state is a self-adjoint, positive, trace one, linear operator \(\rho:\mathcal{H}^n\rightarrow\mathcal{H}^n\) on a n dimensional complex Hilbert space \(\mathcal{H}^n\). In particular, ρ is an \(n\times n\) matrix of complex numbers whose n eigenvalues \(\lambda_i\geq 0\) for \(1\leq i\leq n\) add up to one. Thus, to each quantum state ρ we can associate a classical state \(\mathrm{spec}(\rho)=(\lambda_1,\ldots,\lambda_n)\).
Thus, if we have a partial order ⊑ on Δ n, we might be able to use the connection between quantum and classical given above to derive a natural candidate for a partial order on quantum states as follows:
And then the questions start: (i) Can we really order matrices by ordering their eigenvalues? (ii) How exactly do we form the list \((\lambda_1,\ldots,\lambda_n)\), when in actuality the eigenvalues \(\mathrm{spec}(\rho)\) of ρ only form a set? (iii) How do we order classical states?
The first two questions will be answered in the next section, but the short answers are: (i) Yes, if we have the right order on Δ n, and (ii) quantum measurement. Let us then get on with the answering of (iii).
2.1 Two States and the Parabola
Begin by imagining \(n+1\) boxes

In one of these boxes, there lies a tenured position in the land of free expression. There are two observers searching frantically for its location. The knowledge an observer has about its location is a classical state \(x\in\varDelta^{n+1}\), formed by assigning a probability x i which indicates the likelihood that the tenured position is located in box i:

For example, if the observer is frustrated beyond belief because he has no earthly idea which box contains the tenured position, then his knowledge would be the completely mixed state
indicative of the fact that he regards all boxes as equally likely:

On the other hand, if the observer knows the tenured position is located in box i, then his knowledge would be the pure state
where the one occurs at index i:

In general, the actual location is always represented by a pure state. This much is independent of all observers.
Let k be the actual location of the tenured position, \(x\in\varDelta^{n+1}\) represent the knowledge of the first observer and \(y\in\varDelta^{n+1}\) the knowledge of the second observer:

In the interest of holding the reader’s attention, let \(x\neq y\). If ⊑ is a partial order on \(\varDelta^{n+1}\) that expresses what it means for one state to be more informative than another, and in this order we have \(x\sqsubseteq y\), then observer one knows less about the location of the tenured position than observer two.
But now suppose that each observer looks into box i only to discover that it does not contain the tenured position. Then \(x_i <1\) and \(y_i <1\). In addition, the knowledge of the first observer changes to
while the state of the second observer’s knowledge updates to \(p_i(y)\):

Because the second observer knew more than the first before observation, and because they have both increased their knowledge by the same amount (they both now additionally know that it is not in box i), we must conclude that the second still knows more than the first. That is,
whenever \(i\neq k\). But this reasoning should apply in all situations, i.e., it should not depend on the actual location of the tenured position: We should allow for the reality that k could be any of the values in \(\{1,\ldots,n+1\}\). Thus, we arrive at a potential definition of \((\varDelta^{n+1},\sqsubseteq)\) in terms of \((\varDelta^n,\sqsubseteq)\):
This leaves just one question: How do we order Δ 2? The answer appears when we imagine that the order ⊑ on Δ n is known, and then use it to formally express some of the well-known intuitions used in physics when reasoning about classical states as information:
-
The completely mixed state should be the least element of \((\varDelta^n,\sqsubseteq)\),
$$(\forall x)\,\bot\sqsubseteq x,$$ -
The set of pure states should be the set of maximal elements,
$$\max(\varDelta^n)=\{e_i:1\leq i\leq n\},$$ -
The observer’s a priori uncertainty, Shannon entropy
$$\mu x=-\sum_{i=1}^nx_i\log x_i,$$should be a measurement in the sense of domain theory [8]. In particular, as states become more informative, uncertainty should decrease:
$$x\sqsubseteq y\Rightarrow \mu x\geq \mu y,$$i.e., as a map from the poset Δ n to the poset \([0,\infty)^{\ast}\) of nonnegative reals in their opposite order, it should be monotone.
-
The mixing law should be respected by ⊑:
$$x\sqsubseteq y\ \mathrm{and}\ p\in[0,1]\Rightarrow x\sqsubseteq(1-p)x+py\sqsubseteq y.$$The state \((1-p)x+py\) is a mixture of x and y whose composition consists of \((1-p)\) percent x and p percent y. Thus, the mixing law says that if y is more informative than x, then any mixture of the two is more informative than x, but less informative than y.
This leaves only one way of ordering Δ n.
Definition 2
For \(x,y\in\varDelta^2\), we order classical two states by
We will prove the uniqueness of this order after explaining its derivation. For the latter, look at the graph of Shannon entropy μ on two states:

Remembering that the order ⊑ on Δ 2 should be defined so that Shannon entropy \(\mu:\varDelta^2\rightarrow[0,\infty)^{\ast}\) is a measurement in the sense of domain theory (and hence monotone), a natural candidate for ⊑ appears when we flip the parabola upside down:

The order suggested by this picture is simply a copy of \([0,1/2]^{\ast}\) and \([1/2,1]\) joined at \(1/2\),

which is exactly how we defined the order on Δ 2 (Definition 2).
For its uniqueness, first realize that there are at least two reasonable interpretations of the mixing law: (i) (Informatically) When two comparable states are mixed, a loss of information is experienced from one point of view that is simultaneously a gain of information from the other, (ii) (Geometrically) The line connecting two comparable states moves up in the order.
Lemma 1
A partial order ⊑ on Δ n respects the mixing law iff the map \(f:[0,1]\rightarrow\varDelta^n\) given by \(f(t)=(1-t)x+ty\) is monotone for each pair of comparable states \(x\sqsubseteq y\).
Proof
The monotonicity of f implies the mixing law. For the converse, let \(s <t\). By the mixing law, \(x\sqsubseteq f(t)\sqsubseteq y,\) so applying the mixing law again to \(x\sqsubseteq f(t)\), gives
which finishes the proof since \(f(s)=\big(1-\frac{s}{t}\big)x+\frac{s}{t}f(t)\).
Now the uniqueness of \((\varDelta^2,\sqsubseteq)\) is transparent.
Theorem 1
There is a unique partial order on Δ 2 which satisfies the mixing law and has \(\bot=(1/2,1/2)\). It is the order on classical two states.
Proof
Let ≤ be any partial order on Δ 2 which respects the mixing law and has least element \(\bot=(1/2,1/2)\).
Because \(\bot\leq e_1=(1,0)\), Lemma 1 implies that the straight line path f 1 from \(f_1(0)=\bot\) to \(f_1(1)=e_1\) is monotone. Similarly, the line f 2 from \(f_2(0)=\bot\) to \(f_2(1)=e_2=(0,1)\) is monotone. Thus, \(\sqsubseteq\ \subseteq\ \leq\).
To prove \(\leq\ \subseteq\ \sqsubseteq\), suppose \(x\leq y\). First, we must have either \(x_1,y_1\leq 1/2\) or \(1/2\geq x_1,y_1\): Otherwise, the line f from \(f(0)=x\) to \(f(1)=y\) passes through ⊥, and since f is monotone by the mixing law, we have \(x=\bot\sqsubseteq y\). But this means that either \(x\sqsubseteq y\) or \(y\sqsubseteq x\). In the first case, the proof is done. In the latter, we must have \(y\leq x\), which by the antisymmetry of ≤, gives \(x=y\), and hence \(x\sqsubseteq y\).
Thus far, we have not defined terms like “domain” and “measurement.” At this stage, there is no need to. Let us simply point out that Δ 2 is a domain with Shannon entropy μ as a measurement such that
The precise definitions of these terms will become apparent as we proceed.
2.2 A Partial Order on Classical States
When an observer looks in box i and discovers that the object of his desire is not there, the classical state x representing his knowledge of its location collapses to one \(p_i(x)\) in a lower dimension as follows.
Definition 3
Let \(n\geq 2\). The projection which collapses the ith outcome is the partial map \(p_i:\varDelta^{n+1}\rightharpoonup\varDelta^n\) given by
for \(1\leq i\leq n+1\) and \(0\leq x_i <1\). It is defined on \(\mathrm{dom}(p_i)=\varDelta^{n+1}\setminus\{e_i\}\).
In the way of needless (but fun) geometric illustration, consider the case of the triangle Δ 3. If \(x=(x_1,x_2,x_3)\), then although \(p_i(x)\) is technically a member of Δ 2, we can still picture its effect on x as follows:

Recalling the definition of \((\varDelta^2,\sqsubseteq)\) from the last section, we can now completely specify the order on classical states.
Definition 4
Let \(n\geq 2\). For \(x,y\in\varDelta^{n+1}\), we define
where i ranges over the set \(\{1,\ldots,n+1\}\).
To be perfectly clear, notice that \(x,y\in\mathrm{dom}(p_i)\) iff \(x_i,y_i <1\). The following operators on classical states will prove indispensable in what follows.
Definition 5
Let \(n\geq 2\). For \(x\in\varDelta^n\), we set
We have \(x^-\in[0,1/n]\) and \(x^+\in[1/n,1]\).
For example, a state x is pure iff \(x^+=1\), while ⊥ is the unique classical state x with \(x^+=x^-\).
Lemma 2
Let \(x,y\in\varDelta^n\) for \(n\geq 2\). Then
-
(i)
If \(x\sqsubseteq y\) with \(x_i=1\), then \(y_i=1\).
-
(ii)
If \(x\sqsubseteq\bot\), then \(x=\bot\).
Proof
(i) Assume for \(n\geq 2\). For \(n+1\), suppose \(x_i=1\). First, we claim there is some \(k\neq i\) with \(y_k=0\). If not, then because \(n+1\geq 3\), there is some \(k\neq i\) such that
as the sum above involves at least two positive numbers. Because \(k\neq i\), \(x_k=0\), so the inductive hypothesis applied to \(p_k(x)\sqsubseteq p_k(y)\) gives
which contradicts \(y_k <1-y_i\). Thus, there is \(k\neq i\) with \(x_k=y_k=0\), and the inductive hypothesis applied to \(p_k(x)\sqsubseteq p_k(y)\) yields
finishing the proof.
(ii) We know \(x^+ <1\), since otherwise by (i) we would have \(\bot^+=1\). Now the proof is a trivial induction: Since \(x\sqsubseteq\bot\), we have \(p_i(x)\sqsubseteq p_i(\bot)=\bot_n\), and by the inductive hypothesis, \(p_i(x)=\bot_n\) for all \(i\in\{1,\ldots,n+1\}\). The only possibility is \(x=\bot\).
Lemma 3
For classical n-states \(x\sqsubseteq y\), either \(x=\bot\), \(y=\bot\) or there is an index \(k\in\{1,\ldots,n\}\) such that \(x_k\leq y_k\), \(x_k>x^-\) and \(y_k>y^-\)
Proof
The result is true for \(n=2\). Assume it for n. To prove it for \(n+1\), we start with \(x,y\neq\bot\). Immediately, we have \(x\neq y\) (otherwise, \(x\neq\bot\Rightarrow x_k=y_k=x^+>x^-\)), and by virtue of Lemma 2(i), \(x^+ <1\).
Now let i be an index with \(x_i\geq y_i\). Throughout, \(y_i <1\), since otherwise \(x=y\). Then either (1) \(p_i(x)\neq\bot_n\) or (2) \(p_i(x)=\bot_n\).
In case (1), we cannot have \(p_i(y)=\bot_n\) (Lemma 2(ii)), so the inductive hypothesis applies, yielding an index of \(p_i(x)\) and \(p_i(y)\) which we can relabel as an index k of x and y with
Then \(x_k>x^-\) and \(y_k>y^-\). In addition, since \(x_i\geq y_i\),
which finishes the proof in case (1).
In case (2), \(p_i(x)=\bot\). It helps to picture x as the \((n+1)\)-state
though our proof does not depend on this informal remark. Because \(x\neq\bot\), \({x_i\neq(1-x_i)/n}\), so either \((1-x_i)/n>x_i\) or \(x_i>(1-x_i)/n\).
The case \((1-x_i)/n>x_i\) is simple: Since \(x_i\geq y_i\), there must exist \(k\neq i\) with \(x_k\leq y_k\), or else we could derive \(x_i <y_i\). Then we have
which also makes it clear that \(x_k>x^-=x_i\) and \(y_k>y_i\geq y^-\).
For the last case, we have \(x_i>(1-x_i)/n\). First we eliminate the possibility \(y^+=1\). If \(y^+=1\), then there is an index j with \(y_j=0\). Delicately, we can take \(j\neq i\) because \(n+1\geq 3\). Then \(p_j(x)\neq\bot_n\) and \(p_j(y)\neq\bot_n\), so the inductive hypothesis applies to yield an index k
But \(x_k>x^-\) implies that \(k=i\). In addition, we have known from the start that \(y_i <1\), which means \(y_i=0\) because \(y^+=1\). But then \(0=y_i=y_k\geq x_k=x_i=0\), which contradicts \(x_i>(1-x_i)/n\geq 0\).
To finish case (2), we have \(x^+,y^+ <1\) and \(x_i=x^+>(1-x_i)/n\). What we will prove is that \(x_i>x^-\), \(y_i>y^-\) and \(x_i\leq y_i\). The first of these is clear. For the other two, let k be any index different from i. Then \(p_k(x)\neq\bot_n\), which means \(p_k(y)\neq\bot_n\) since \(p_k(x)\sqsubseteq p_k(y)\). By the inductive hypothesis, there is an index j such that
Again, \(x_j>x^-\) implies \(j=i\). Hence, \(y_i>y^-\). But this also gives us \({x_i(1-y_k)\leq y_i(1-x_k)}\), for all \(k\neq i\), which enables
ending in \((n-1)x_i+x_i y_i\leq (n-1)y_i+x_i y_i\).
Lemma 4
If \(x\sqsubseteq y\) in Δ n for \(n\geq 2\), then there is an index \(i\in\{1,\ldots,n\}\) such that \(x_i=x^-\geq y^-=y_i\).
Proof
If \(x=\bot\) the claim is trivial; thus, \(y\neq\bot\), by Lemma 2(ii). By Lemma 3, there is an index \(k\in\{1,\ldots,n\}\) such that \(x_k\leq y_k\), \(x_k>x^-\) and \(y_k>y^-\).
If \(x_k=1\leq y_k\), then \(x=y\) and the proof is done. If \(y_k=1\), then let i be an index where \(x_i=x^-\). We cannot have \(i=k\) since \(x_k>x^-\). Thus, \(x_i=x^-\geq y_i=0\).
Assume for n. For \(n+1\), \(p_k(x)\sqsubseteq p_k(y)\), and the inductive hypothesis applies to yield an index i of x and y with
Because \(x_k\leq y_k\), \(x_i\geq y_i\). But since \(x_k>x^-\) and \(y_k>y^-\), we have \(x_i=x^-\) and \(y_i=y^-\).
Now that we understand the behavior of minima, the nature of the maxima is immediate (and fundamental).
Proposition 1
Let \(x,y\in\varDelta^n\) and e i be the pure states in Δ n.
-
(i)
If \(x\sqsubseteq y\), then there is an index i such that \(x_i=x^+\leq y^+=y_i\).
-
(ii)
For any i, \(x_i=x^+\) if and only if \(x\sqsubseteq e_i\).
-
(iii)
If \(x\sqsubseteq y\) and \(x^+=y^+\), then \(x=y\).
Proof
All of these statements are proved by induction. The arguments below all assume that the respective claims are true for n and give the argument for the \(n+1\) case. That they are true for \(n=2\) is clear.
(i) By Lemma 4, there is an index k with \(x_k=x^-\geq y^-=y_k\), so we apply the inductive hypothesis to \(p_k(x)\sqsubseteq p_k(y)\) to obtain an index i such that
Since \(x_i\geq x^-=x_k\) and \(x_i\geq x_j\) for all \(j\neq k\) using \(p_k(x)^+=x_i/(1-x^-)\), we have \(x_i=x^+\). Similarly, \(y_i=y^+\). That \(x_i\sqsubseteq y_i\) now follows from
since \(x^-\geq y^-\).
(ii) Let i be an index where \(x_i=x^+\) and \(e_i\in\varDelta^{n+1}\) be the associated pure state whose value at index i is one. To prove that \(x\sqsubseteq e_i\), we must show that \(p_k(x)\sqsubseteq p_k(e_i)\) for all \(k\neq i\). Fix an arbitrary \(k\neq i\).
First, let j be the index of \(p_k(x)\) corresponding to index i in x. This index exists because \(k\neq i\). The value of \(p_k(x)\) at index j is
Second, \(p_k(e_i)\) is a pure state in Δ n whose value at index j is one. By the inductive hypothesis, \(p_k(x)\sqsubseteq p_k(e_i)\), for all \(k\neq i\), which means \(x\sqsubseteq e_i\).
For the converse, suppose \(x\sqsubseteq y:=e_i\). By (i), there is an index k such that \(x_k=x^+\) and \(y_k=y^+\). But y is pure, so we must have \(k=i\), which means \(x_i=x_k=x^+\).
(iii) Starting with \(x\sqsubseteq y\) and \(x^+=y^+\), we use Lemma 4 to project away the minima \(x_k=x^-\geq y^-=y_k\), obtaining \(p_k(x)\sqsubseteq p_k(y)\). Applying (i) to this pair yields an index i with
As in the proof of (i), \(x_i=x^+\) and \(y_i=y^+\). But since \(x_i=y_i>0\) and \(p_k(x)^+\leq p_k(y)^+\), we have \(x^-\leq y^-\), which gives \(x^-=y^-\). This means \(p_k(x)^+= p_k(y)^+\), and since \(p_k(x)\sqsubseteq p_k(y)\), the inductive hypothesis applies, leaving \(p_k(x)=p_k(y)\). Because we also have \(x_k=y_k\), the states x and y are equal.
Proposition 1(ii) shows that an outcome with maximum probability in a classical state has a certain qualitative character to it. In general, it is the only outcome we can say this about.
Theorem 2
Δ n is a partially ordered set for each \(n\geq 2\). Its maximal elements are the pure states,
and its least element is the completely mixed state \(\bot:=(1/n,\ldots,1/n)\)
Proof
The proof is by induction. It is true for \(n=2\). Assume the result for n. Then for \(n+1\), the reflexivity and transitivity are clear.
For antisymmetry, let \(x\sqsubseteq y\) and \(y\sqsubseteq x\). By Proposition 1(i), we have \(x^+\leq y^+\) and \(y^+\leq x^+\). By Proposition 1(iii), \(x=y\).
That the least element is ⊥ follows from \(p_i(\bot)=\bot_n\) for all i. For its maximal elements, first suppose \(x^+=1\) and that \(x\sqsubseteq y\). By Proposition 1(i), there is an index i with \(x_i=x^+=1\leq y^+=y_i\), so \(y_i=1\), which means \(x=y\). Hence, \(x\in\max(\varDelta^{n+1})\).
Conversely, if \(x\in\max(\varDelta^{n+1})\), then \(x\sqsubseteq e_i\) by Proposition 1(ii), where e i is the pure state corresponding to \(x_i=x^+\). By the maximality of x, \(x=e_i,\) which means \(x^+=1\).
The next result displays some fundamental properties of the order on classical states—the crucial degeneration lemma.
Lemma 5 (Degeneration)
If \(x\sqsubseteq y\) in Δ n, then
for all \(1\leq i,j\leq n\).
Proof
Both of these are proved by induction. For \(n=2\) they are easily seen to be true; we give the arguments for \(n+1\) assuming n.
For \((x_i=0\Rightarrow y_i=0)\), we can assume \(x^+,y^+ <1\): If \(x^+=1\), then \(x=y\) since x is maximal; If \(y^+=1\), then either \(y_i=0\), which finishes the proof, or \(y_i=1\), in which case Proposition 1(i) gives \(y_i=y^+=1\geq x^+=x_i>0\), contradicting \(x_i=0\). Thus, since \(x^+,y^+ <1\), any \(k\neq i\) yields \(p_k(x)\sqsubseteq p_k(y)\), and since \(x_i/(1-x_k)=0\), the inductive hypothesis gives \(y_i/(1-y_k)=0\) hence \(y_i=0\).
For the other claim, suppose \(y_i=y_j>0\) with \(i\neq j\). Then \(y^+ <1\). In addition, \(x^+ <1\) or else \(x=y\) and we are done. Then because \(n+1\geq 3\), there is \(k\in\{1,\ldots,n+1\}\setminus\{i,j\}\). For any such index, we have \(p_k(x)\sqsubseteq p_k(y)\), so the inductive hypothesis gives \(x_i/(1-x_k)=x_j/(1-x_k)\), i.e., \(x_i=x_j\).
The standard projections \(\pi_k:\varDelta^n\rightarrow[0,1]\) are \(\pi_k(x)=x_k\) for \(1\leq k\leq n\). Lemma 4 extends to increasing sequences as follows.
Lemma 6
If \((x_i)\) is an increasing sequence in Δ n, then
-
(i)
There is an index k with \(\pi_k(x_i)=x_i^-\) for all i.
-
(ii)
There is an index k with \(\pi_k(x_i)=x_i^+\) for all i.
Proof
(i) Before starting, a crucial consequence of Lemma 5 for the present argument is that
provided that \(x\sqsubseteq y\) and \(y^->0\). Thus, any increasing sequence \((x_i)\) with \(x_i^->0\) leads to a decreasing sequence of nonempty finite sets. The intersection of such a sequence must be nonempty, and any member k in this intersection will satisfy \(\pi_k(x_i)=x_i^-\) for all i.
Thus, for our sequence \((x_i)_{i\geq 1}\), we may assume that there is a least integer \(m\geq 1\) with \(x_m^-=0\). First, the proof is finished if we find k with \(\pi_k(x_i)=x_i^-\) for all \(i\leq m\), since then we have \(\pi_k(x_m)=0\) and hence \(\pi_k(x_i)=0\) for all \(i\geq m\), by Lemma 5, which means \(\pi_k(x_i)=x_i^-\) for all \(i\geq 1\).
The case \(m=1\) is trivial. If \(m>1\), then for the subsequence \((x_i)_{i <m}\), we have \(x_i^->0\) for \(i <m\), by the choice of m, so our opening remarks give \(\pi_k(x_i)=x_i^-\), for all \(i <m\), where k is any index in \(\{k:\pi_k(x_{m-1})=x_{m-1}^-\}\). By Lemma 4, there is k with \(\pi_k(x_{m-1})=x_{m-1}^-\) and \(\pi_k(x_m)=x_m^-\). This value of k gives \(\pi_k(x_i)=x_i^-\) for all \(i\leq m\).
(ii) We simplify modify the proof of Proposition 1(i) using (i).
Now we take our first step toward proving that Δ n is a domain.
Definition 6
A subset S of a poset is directed if it is nonempty and
A directed-complete partial order, or dcpo, is a poset in which every directed subset has a supremum.
A familiar example of a directed set is an increasing sequence: A sequence \((x_i)\) such that \(x_i\sqsubseteq x_{i+1}\) for all i. Joyfully, on classical states, one can always replace directed sets with increasing sequences, so we never have to think about the former.
Proposition 2
The classical states Δ n are a dcpo. In more detail,
-
(i)
If \((x_i)\) is an increasing sequence, then
$$\bigsqcup_{i\geq 1}x_i=(\lim_{i\rightarrow\infty} \pi_1(x_i),\ldots,\lim_{i\rightarrow\infty} \pi_n(x_i)).$$ -
(ii)
Every directed subset of Δ n contains an increasing sequence with the same supremum.
Proof
We first prove (i) by induction. It is true for \(n=2\). Assume for n. Given an increasing sequence \((x_i)\), Lemma 6 yields an index k such that \(\pi_k(x_i)=x_i^-\) for all i. The sequence \((p_k(x_i))\) is increasing in Δ n, so by the inductive hypothesis, we know that
exists for all \(j\neq k\). The sequence \((x_i^-)\) is decreasing and contained in \([0,1/(n+1)]\), so it has a limit \(s_k=\lim \pi_k(x_i) <1\), which means \((1-x_i^-)\) has a limit that is not zero. Thus,
exists for \(j\neq k\). Notice that
which means that \(s=(s_1,\ldots,s_{n+1})\) is a classical state. We claim that s is the supremum of \((x_i)\).
To avoid needless complication, we can assume \(x_i^+ <1,\) since otherwise \((x_i)\) has finitely many distinct elements, and then the claim is obvious. To prove that \(x_i\sqsubseteq s\) for all i, we must show
Fix an index j with \(s_j <1\). Then the sequence \((p_j(x_i))_{i\geq 1}\) is increasing in Δ n, so by the inductive hypothesis, it has a supremum
which is equal to \(p_j(s)\) since \(s_j=\lim_{i\rightarrow\infty}\pi_j(x_i) <1\). Hence, \(p_j(x_i)\sqsubseteq p_j(s)\) for all i and j with \(s_j <1\), which means \(x_i\sqsubseteq s\) for all i.
To prove that s is the supremum of \((x_i)\), let u be any upper bound of \((x_i)\). We must show that \(s\sqsubseteq u\), i.e.,
Let j be any index with \(s_j <1\) and \(u_j <1\). Then since \(p_j(x_i)\sqsubseteq p_j(u)\) for all i, we have \(p_j(s)=\bigsqcup_{i\geq 1} p_j(x_i)\sqsubseteq p_j(u)\), using the inductive hypothesis and that \(s_j <1\). Thus, \(s\sqsubseteq u\), which proves \(s=\bigsqcup x_i\).
The directed completeness of Δ n and (ii) now follow from a theorem in [8] provided there is a strictly monotone map \(f:\varDelta^n\rightarrow[0,\infty)^{\ast}\) which preserves suprema of increasing sequences. To see that \(f(x)= 1-x^+\) is one such map, if \((x_i)\) is an increasing sequence, Lemma 6(ii) yields an index k with \(\pi_k(x_i)=x_i^+\) for all i, so
which makes it clear that f preserves suprema of increasing sequences. That f is strictly monotone follows from Proposition 1(iii).
Definition 7
A map \(f:D\rightarrow E\) between dcpo’s is Scott continuous if it is monotone
and it preserves directed suprema:
for any directed set \(S\subseteq D\).
Corollary 1
A monotone map \(f:\varDelta^n\rightarrow E\) into a dcpo E is Scott continuous iff for each increasing sequence \((x_i)\) in Δ n, \(f\left(\bigsqcup x_i\right)=\bigsqcup f(x_i)\).
Proof
If \(S\subseteq\varDelta^n\) is directed, then \(\bigsqcup f(S)\sqsubseteq f(\bigsqcup S)\) by monotonicity. For the other direction, Proposition 2(ii) gives an increasing sequence \((x_i)\) in S with \(\bigsqcup S=\bigsqcup x_i\), enabling
confirming that f preserves suprema of all directed sets provided it does so for increasing sequences.
For instance, the map
is Scott continuous, while \(x\mapsto 1-x^+\) is Scott continuous as a map \(\varDelta^n\rightarrow[0,1]^{\ast}\). An amusing example of a Scott continuous map that is not Euclidean continuous is the natural retraction from Δ 2 onto
Generally speaking, the entropy of an event with probability p is − log p. If forced to choose a single probability representative of an entire classical state x, x + would be the most sensible choice, because of its qualitative significance in Proposition 1. Thus, one might say that \(s(x)=-\log x^+\) measures the entropy of a classical state.
Corollary 2
The map \(s:\varDelta^n\rightarrow[0,\infty)^{\ast}\) given by \(s(x)=-\log x^+\) is Scott continuous. It has the following properties:
-
(i)
For all \(x,y\in\varDelta^n\), if \(x\sqsubseteq y\) and \(s(x)=s(y),\) then \(x=y\).
-
(ii)
For all \(x\in\varDelta^n\), we have \(s(x)=0\) iff \(x\in\max(\varDelta^n)\).
-
(iii)
For all \(x\in\varDelta^n\), we have \(s(x)=\log n\) iff \(x=\bot\).
Proof
The map is well-defined because \(x^+\in[1/n,1]\). That s is strictly monotone follows from Proposition 1. (ii) and (iii) follow from combinations of direct calculation and applications of (i).
By the last result, a monotone map \(f:D\rightarrow\varDelta^n\) from a dcpo D is Scott continuous iff \(s\circ f\) is Scott continuous. We will take a closer look at entropy later on.
2.3 Symmetries for Classical States
We now establish the fundamental role played by the symmetric group
of bijections on the set \(\{1,\ldots,n\}\). These we also refer to as permutations or symmetries. The composition of \(x\in\varDelta^n\) and \(\sigma\in S(n)\) is written \(x\cdot\sigma\).
Definition 8
A state \(x\in\varDelta^n\) is monotone if \(x_i\geq x_{i+1}\) for all \(i <n\).
A classical state \(x\in\varDelta^n\) can be completely described by a monotone state \(x\cdot\sigma\) and a symmetry \(\sigma^{-1}\). The order on Δ n has an analogous representation.
Lemma 7
For states \(x,y\in\varDelta^2\), we have \(x\sqsubseteq y\) iff there is a permutation σ of \(\{1,2\}\) such that \(x\cdot\sigma=(x^+,x^-)\), \(y\cdot\sigma=(y^+,y^-)\) and \(x^+y^-\leq x^-y^+\).
Theorem 3
For \(x,y\in\varDelta^n\), we have \(x\sqsubseteq y\) iff there is a permutation σ of \(\{1,\ldots,n\}\) such that \(x\cdot\sigma\) and \(y\cdot\sigma\) are monotone and
for all i with \(1\leq i <n\)
Proof
By the last lemma, the claim is true for \(n=2\). Assume the result for \(n\geq 2\). For the case \(n+1\), we prove both implications separately.
First suppose \(x\sqsubseteq y\). Let k be an index with \(x_k=x^-\geq y^-=y_k\). By the inductive hypothesis applied to \(p_k(x)\sqsubseteq p_k(y)\), there is a permutation σ of \(\{1,\ldots,n\}\) such that \(p_k(x)\cdot\sigma\) and \(p_k(y)\cdot\sigma\) are monotone. Now compose σ with the natural bijection that maps indices of \(p_k(x)\) and \(p_k(y)\) to indices of x and y, and since there is no harm in doing so, call the resulting bijection \(\sigma:\{1,\ldots,n\}\rightarrow \{1,\ldots,n+1\}\setminus\{k\}\).
We extend σ to a permutation of \(\{1,\ldots,n+1\}\) by setting \(\sigma(n+1):=k\). It is then clear that \(x\cdot\sigma\) and \(y\cdot\sigma\) are monotone and that
for all \(1\leq i <n\). To finish this direction, we need to prove
Because \((x\cdot\sigma)_{n+1}=x_k=x^-\geq y^-=y_k=(y\cdot\sigma)_{n+1}\), we need only consider the case that \((y\cdot\sigma)_n< (x\cdot\sigma)_n\).
First, \(x^+<1\), since \((x\cdot\sigma)_n>0\Rightarrow (x\cdot\sigma)_1=x^+<1\). Next, \(y^+<1\), since otherwise \((y\cdot\sigma)_{n+1}=0\), in which case the inequality is trivial. Now let j be an index with \(x_j=x^+\leq y^+=y_j\). By the inductive hypothesis applied to \(p_j(x)\sqsubseteq p_j(y)\), we obtain a permutation π of \(\{1,\ldots,n\}\). Similar to the case of σ, we regard π as a bijection
and then extend it to a permutation of \(\{1,\ldots,n+1\}\) by setting \(\pi(1):=j\). Again \(x\cdot\pi\) and \(y\cdot\pi\) are monotone, and in this case we have
for \(2\leq i <n+1\). Because \(x\cdot\pi=x\cdot\sigma\) and \(y\cdot\pi=y\cdot\sigma\), setting \(i=n\) yields the desired inequality, finishing this direction.
For the other, let σ be a permutation of \(\{1,\ldots,n+1\}\) with \(x\cdot\sigma,y\cdot\sigma\) monotone and \((x\cdot\sigma)_i(y\cdot\sigma)_{i+1}\leq (x\cdot\sigma)_{i+1}(y\cdot\sigma)_i\) for all i with \(1\leq i <n+1\). First notice that slightly more is true:
for \(1\leq i\leq j\leq n+1\).
In the cases \((x\cdot\sigma)_i=0\) and \((y\cdot\sigma)_{j}=0\), \((*)\) is clear; if \((x\cdot\sigma)_i>0\) and \((y\cdot\sigma)_{j}>0\), then \((y\cdot\sigma)_{k}>0\) for \(k\leq j\) by monotonicity, which means \((x\cdot\sigma)_{k}>0\) for all \(i\leq k\leq j\) as well, since for \(k>i\) we have
assuming \((x\cdot\sigma)_{k-1}>0\). Without division by zero to worry about, \((*)\) is now clear.
To prove \(x\sqsubseteq y\) we must show \(p_k(x)\sqsubseteq p_k(y)\) for all k with \(x_k <1,y_k<1\). To this end, fix one such k. We restrict σ to a bijection
which then yields a permutation σ k of \(\{1,\ldots,n\}\) such that \(p_k(x)\cdot\sigma_k\) and \(p_k(y)\cdot\sigma_k\) are monotone. By (*), we have
for all \(1\leq i <n\). By the inductive hypothesis, \(p_k(x)\sqsubseteq p_k(y),\) finishing the proof.
The explicit nature of the representation using symmetries can be advantageous in establishing certain properties of the order.
Lemma 8
The map \(x\mapsto x\cdot\sigma\) is an order isomorphism of Δ n for each \(\sigma\in S(n)\)
Proof
Let \(f(x)=x\cdot\sigma\). To see that f is monotone, if \(x\sqsubseteq y\), then there is \(\nu\in S(n)\) with \(x\cdot\nu\) and \(y\cdot\nu\) monotone satisfying the inequalities of Theorem 3. But the same is true of \(x\cdot\sigma\) and \(y\cdot\sigma\) if we apply the permutation \(\sigma^{-1}\cdot\nu\) to each. Thus, \(f(x)=x\cdot\sigma\sqsubseteq y\cdot\sigma=f(y)\).
The same argument shows \(g(x)=x\cdot\sigma^{-1}\) is monotone. Because f and g are also inverse to one another, each is an order isomorphism.
It is now time to take a more in depth look at the order on classical states. To keep things simple initially, we start on the outside and work our way inward. The boundary of \(\varDelta^{n+1}\),
can be understood geometrically as \(n+1\) copies of Δ n identified at certain points. The same result holds order theoretically. That is, the dcpo \(\partial\varDelta^{n+1}\) is order isomorphic to \(n+1\) copies of the dcpo Δ n identified along their common boundaries.
Proposition 3
For \(n\geq 1\), we have an order isomorphism
for any of the standard projections \(\pi_i:\varDelta^{n+1}\rightarrow[0,1]\) with \(1\leq i\leq n+1\).
Proof
First, \(i_{n+1}:\varDelta^n\rightarrow\varDelta^{n+1}::x\mapsto(x,0)\) is an order embedding. It is order reflecting:
For its monotonicity, let \(x\sqsubseteq y\). By Theorem 3, there is \(\sigma\in S(n)\) with \(x\cdot\sigma\) and \(y\cdot\sigma\) monotone such that the usual inequalities hold.
Now extend σ to a permutation in \(S(n+1)\) by setting \(\sigma(n+1)=n+1\). Because the value of the state \(i_{n+1}(x)\) at index \(n+1\) is zero, \(i_{n+1}(x)\cdot \sigma\) and \(i_{n+1}(y)\cdot\sigma\) are monotone and satisfy the inequalities of Theorem 3. Thus, \(i_{n+1}(x)\sqsubseteq i_{n+1}(y)\).
The other n maps, i k for \(1\leq k\leq n\), which produce an \(n+1\) state having value zero at index k, all arise as the composition of isomorphisms (derived from right multiplication by a symmetry) followed by \(i_{n+1}\).
Thus, the boundary of the triangle Δ 3 is a dcpo made of three copies of Δ 2:

To get an idea of what the order is like on int(Δ n), we need to look a little closer. First, some long overdue notation.
Definition 9
The monotone classical states are denoted
For \(\sigma\in S(n)\),
Notice that \(\varDelta^n_1=\varLambda^n\).
As we have already seen, the order on monotone states can be characterized purely algebraically. For the sake of emphasis:
Lemma 9
For \(x,y\in \varLambda^n\), \(x\sqsubseteq y\) iff \((\forall\, 1\leq i <n)\,x_iy_{i+1}\leq y_ix_{i+1}\).
Just as was the case with its boundary, there is also a natural way of dividing Δ n itself into regions: For each \(n\geq 1\),
And just as before, these regions are identical (order-theoretically).
Proposition 4
Let \(n\geq 2\).
-
(i)
For each \(\sigma\in S(n)\), \(\varDelta^n_\sigma\) is closed under directed suprema in Δ n.
-
(ii)
For an increasing sequence \((x_i)\) in Δ n, there is \(\sigma\in S(n)\) with \(x_i\in\varDelta^n_\sigma\) for all i.
-
(iii)
The natural map
$$r:\varDelta^n\rightarrow \varLambda^n$$is a Scott continuous retraction whose restriction to \(\varDelta^n_\sigma\) is an order isomorphism \(\varDelta^n_\sigma\simeq\varLambda^n\) for each \(\sigma\in S(n)\).
Proof
(i) Since every directed set contains an increasing sequence with the same supremum, we only have to prove this result for increasing sequences \((x_i)\) in \(\varDelta^n_\sigma\). By Lemma 8 and the formula for suprema,
But the state on the far right is monotone because all the \(x_i\cdot\sigma\) are. This proves that \(\bigsqcup x_i\in\varDelta^n\) also belongs to \(\varDelta^n_\sigma\).
(ii) This is a straightforward induction using Lemma 6(i).
(iii) For \(\sigma\in S(n)\), we denote the order isomorphism in Lemma 8 by \(r_\sigma(x)=x\cdot\sigma\). Set \(r(x)=r_\sigma(x)\) for \(x\in\varDelta^n_\sigma\). This map is well defined and its restriction to \(\varDelta^n_\sigma\) is an order isomorphism: \(\varDelta^n_\sigma=r_\sigma^{-1}(\varLambda^n)\simeq\varLambda^n\).
It is monotone: If \(x\sqsubseteq y\), then by Theorem 3, there is \(\sigma\in S(n)\) with \(x,y\in\varDelta^n_\sigma\) which gives \(r(x)=r_\sigma(x)\sqsubseteq r_\sigma(y)=r(y)\).
It is Scott continuous: If \(\mu:\varDelta^n\rightarrow[0,\infty)^{\ast}\) is strictly monotone, Scott continuous and \(\mu r=\mu\), then r itself is Scott continuous, since it is monotone and has continuous measure \(\mu r\). Let \(\mu x=-\log x^+\) (Corollary 2).
Finally, \(r|_{\varLambda^n}=1_{\varLambda^n}\), which proves that r is a retraction.
Thus, we can think of Δ n as being n!-many copies of the retract Λ n identified along their common boundaries. For instance, Δ 3 splits into six different regions, all order isomorphic to Λ 3:

This, combined with an elementary analysis of Λ 3, allows us to determine the upper sets of \((\varDelta^3,\sqsubseteq)\) shown in Fig. 10.1.
We now have our first example of an intuition about classical states that has been formally justified. Consider a closed cylinder of volume V partitioned into smaller volumes V i as follows:

The cylinder is known a priori to contain a single molecule. With no other information available to us, our knowledge of the molecule’s location is \((p_1,p_2,p_3)\) where \(p_i=V_i/V\). Or is it? Well, it is if we assume that the volumes are labelled from left to right as 1,2,3. But if they have been labelled in the reverse order, as

then our knowledge is \((p_3,p_2,p_1)\).
Naturally, we intuitively understand that in the grand scheme of things it makes no difference how we label things—as long as all statements made about the experiment are made with respect to the same choice of labels, we will not encounter any trouble: What is physically true for one choice of labels is also true for any other. But that’s where the magic is! We have derived this simple truth: For each \(\sigma\in S(n)\), the map \(x\mapsto x\cdot\sigma\) is an order isomorphism.
In short, there is a definite physical reason why Δ n is divided into different regions \(\varDelta^n_\sigma\) all of which are “identical” (\(\varDelta^n_\sigma\simeq\varDelta^n_\nu\)). For the very same reason, measures of information content in such experiments tend to be symmetric.
Definition 10
A function \(f:\varDelta^n\rightarrow E\) is symmetric if for all \(\sigma\in S(n)\), we have \(f(x\cdot\sigma)=f(x)\).
Lemma 10
Let E be a dcpo. Then
-
(i)
Every function \(f:\varLambda^n\rightarrow E\) determines a unique symmetric extension \(\bar{f}:\varDelta^n\rightarrow E\) given by \(\bar{f}=f\circ r\) where r is the natural retraction.
-
(ii)
Monotonicity, strict monotonicity and Scott continuity are inherited by \(\bar{f}\) whenever they are possessed by f.
Proof
(i) For the uniqueness of \(\bar{f}\), if \(g:\varDelta^n\rightarrow E\) is another symmetric extension of f, then for any \(x\in\varDelta^n_\sigma\), we can write
using that g is symmetric, followed by the fact that \(g=f\) on Λ n, and then the fact that \(\bar{f}\) is a symmetric extension of f.
(ii) Each property is preserved by composition and satisfied by r.
Example 1
Canonical symmetric functions on Δ n
-
(i)
The maps \(\varDelta^n\rightarrow[0,1]::x\mapsto x^+\) and \(\varDelta^n\rightarrow[0,1]^{\ast}::x\mapsto 1-x^+\).
-
(ii)
Entropy \(s(x)=-\log x^+\).
-
(iii)
The natural retraction \(r:\varDelta^n\rightarrow\varLambda^n\).
-
(iv)
Shannon entropy
$$\mu x=-\sum_{i=1}^nx_i\log x_i.$$
As the last result illustrates, the retraction \(r:\varDelta^n\rightarrow\varLambda^n\) provides us with a general approach for solving problems involving classical states: First solve it for Λ n, and then for Δ n in general.
2.4 Approximation of Classical States
A decent understanding of approximation can provide insight about the nature of partiality. Partiality, as we will see in the next section, is imperative for a meaningful discussion on entropy.
Definition 11
Let D be a dcpo. For \(x,y\in D\), we write \(x\ll y\) iff for all directed sets \(S\subseteq D\),
The approximations of \(x\in D\) are
and D is called exact if \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{-.4ex} {\(\downarrow\)}}\(\downarrow\)}}} x\) is directed with supremum x for all \(x\in D\).
A continuous dcpo is exact, and in that case, the “way below” relation and our notion of approximation above are equivalent. In addition, the two notions also coincide on maximal elements.
Lemma 11
Let D be a dcpo. For each \(x\in D\), the set \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{-.4ex} {\(\downarrow\)}}\(\downarrow\)}}} x\) is directed with supremum x iff it contains a directed set with supremum x.
The ability to approximate classical states is provided by the mixing law.
Proposition 5
(The mixing law) If \(x\sqsubseteq y\) in Δ n, then
for all \(p\in[0,1]\)
Proof
Let z denote the classical state \((1-p)x+py\). Because \(x\sqsubseteq y\), there is a symmetry σ with \(x\cdot\sigma,y\cdot\sigma\) monotone. First,
for \(1\leq i <n\), which means \(z\cdot\sigma\) is monotone. Thus, \(x\sqsubseteq z\) follows from
while \(z\sqsubseteq y\) follows similarly.
A path from x to y in a space X is a continuous map
with \(p(0)=x\) and \(p(1)=y\). A segment of a path p is \(p[a,b]\) for \(b>a\). Any monotone path into Δ n with its Euclidean topology is Scott continuous. For instance, by the mixing law (Lemma 1), the straight line path from x to y,
is Scott continuous iff \(x\sqsubseteq y\).
Lemma 12
Let \(x\sqsubseteq y\) with \(x\in\varDelta^n\) and \(y\in\varLambda^n\). Then
-
(i)
If \(y_i>0\) for all i, then \(x\in\varLambda^n\).
-
(ii)
If \(x\ll y\), then \(x\in\varLambda^n\).
Proof
(i) The proof is by induction. For the \(n+1\) case, Lemma 4 gives an index i with \(x_i=x^-\geq y_i=y^-\), while the monotonicity of y yields \(y_{n+1}=y^-=y_i>0\). By degeneration (Lemma 5), \(x_{n+1}=x_i=x^->0\).
Now we can apply the inductive hypothesis to \(p_{n+1}(x)\sqsubseteq p_{n+1}(y)\), since \(p_{n+1}(y)\in\varLambda^n\) and all its values are positive, to deduce that \(p_{n+1}(x)\in\varLambda^n\). But since \(x_{n+1}=x^-\), we have \(x\in\varLambda^{n+1}\).
(ii) We apply (i). By the Scott continuity of \(\pi_{\bot y}\),
and since \(x\ll y\), we have \(x\sqsubseteq\pi_{\bot y}(t)\) for some \(t <1\). Because \(y\in\varLambda^n,\) \(\pi_{\bot y}(t)\in\varLambda^n\), and \(\pi_{\bot y}(t)_i>0\) for all i since \(t <1\). By (i), \(x\in\varLambda^n\).
Proposition 6
Let \(r:\varDelta^n\rightarrow\varLambda^n\) be the natural retraction.
-
(i)
If \(x,y\in\varDelta^n_\sigma\) and \(x\sqsubseteq y\), then \(\pi_{xy}(t)\in\varDelta^n_\sigma\) for all \(t\in[0,1]\).
-
(ii)
For \(x,y\in\varDelta^n\), we have \(x\ll y\) iff
$$(\forall\sigma\in S(n))(y\in\varDelta^n_\sigma\Rightarrow x\in\varDelta^n_\sigma)\ \ \mathrm{and} \ \ (r(x)\ll r(y)\ \mathrm{in}\ \varLambda^n)\,.$$
Proof
(i) This was shown in the proof of the mixing law. (ii) First recall that right multiplication by \(\sigma\in S(n)\), \(r_\sigma(x)=x\cdot\sigma\), is an order isomorphism of Δ n. If \(x\ll y\), then \(x\sqsubseteq y\), which means \(x,y\in\varDelta^n_\sigma\) for some \(\sigma\in S(n)\). Because r σ is an order isomorphism,
But \(r(x)=r_\sigma(x)\) and \(r(y)=r_\sigma(y)\), which means \(r(x)\ll r(y)\) in Δ n. However, \(r(x),r(y)\in\varLambda^n\) and in addition Λ n is closed under directed suprema in Δ n by Prop. 4(i), which means that the supremum in Λ n of a directed set \(S\subseteq\varLambda^n\) is equal to the supremum it has as a subset of Δ n. Thus, \(r(x)\ll r(y)\) in Λ n.
To finish this direction, suppose \(y\in\varDelta^n_\sigma\). Then \(x\cdot\sigma=r_\sigma(x)\ll r_\sigma(y)=y\cdot \sigma\) in Δ n, since r σ is an order isomorphism. But \(y\cdot\sigma\) is monotone, so Lemma 12 implies that \(x\cdot\sigma\) is too, i.e., \(x\in\varDelta^n_\sigma\).
For the other direction, if we choose any \(\sigma\in S(n)\) with \(y\in\varDelta^n_\sigma\), then \(x\in\varDelta^n_\sigma\). By assumption, we have \(r_\sigma(x)=r(x)\ll r(y)=r_\sigma(y)\) in Λ n. If we show that \(r_\sigma(x)\ll r_\sigma(y)\) in Δ n, then because r σ is an order isomorphism, we may conclude \(x\ll y\) in Δ n.
Let \((y_i)\) be an increasing sequence in Δ n with \(r_\sigma(y)=\bigsqcup y_i\). By Proposition 4, there is \(\nu\in S(n)\) with \(y_i\in\varDelta^n_\nu\) for all i, and hence \(y\cdot\sigma\in\varDelta^n_\nu\). Then because \(y\in\varDelta^n_{\sigma\cdot\nu}\), we have \(x\in\varDelta^n_{\sigma\cdot\nu}\) by assumption, so the following relation involves only states in Λ n:
Because \(x\cdot\sigma\ll y\cdot\sigma\) in Λ n, we must have \(x\cdot(\sigma\cdot\nu)\sqsubseteq y_i\cdot\nu\) for some i, i.e., \(r_\nu(r_\sigma(x))\sqsubseteq r_\nu(y_i)\) which gives \(r_\sigma(x)\sqsubseteq y_i\). Then \(r_\sigma(x)\ll r_\sigma(y)\) in Δ n, and now the proof is finished.
Theorem 4
The classical states Δ n are exact.
-
(i)
For every \(x\in\varDelta^n\), \(\pi_{\bot x}(t)\ll x\) for all \(t <1\).
-
(ii)
The approximation relation ≪ is interpolative: If \(x\ll y\) in Δ n, then there is \(z\in\varDelta^n\) with \(x\ll z\ll y\).
Proof
The exactness of Δ n follows from (i), the Scott continuity of \(\pi_{\bot x}\), and Lemma 11. To prove (i), we first show that \(\pi_{\bot x}(t)\ll x\) in Λ n for any \(x\in\varLambda^n\) and \(t <1\). Notice that \(\pi_{\bot x}(t)\in\varLambda^n\) for all \(t\in[0,1]\) by Proposition 6(i). Let \(x=\bigsqcup y_k\in\varLambda^n\) for an increasing sequence \((y_k)_{k\geq 1}\) in Λ n.
For \(i <n\) fixed, we will show that there is an integer k i such that
for all \(k\geq k_i\). If \(x_i=0\), then \(x_{i+1}=0\) by the monotonicity of x, and then we can take \(k_i=1\), by the monotonicity of each y k . Thus, we can assume \(x_i>0\).
If \(x_{i+1}=0\), then we can write
where \(\delta>0\) is some constant, and we use \(x=\bigsqcup y_k\). This makes it clear that such a k i exists in this case. Thus, we can also assume \(x_{i+1}>0\).
If \(x_i=x_{i+1}>0\), then because \(y_k\sqsubseteq x\), degeneration (Lemma 5) gives \(\pi_i(y_k)=\pi_{i+1}(y_k)>0\) for each k. In this case, we can again take \(k_i=1\). Thus, we assume \(x_i>x_{i+1}>0\). By the degeneration lemma, this also implies \(\pi_i(y_k)>0\) and \(\pi_{i+1}(y_k)>0\) for all k. But then we get
using \(x_i>x_{i+1}>0\), \(t <1\) and \(\bigsqcup y_k=x\). Thus, in this case there is also a large enough k i such that the desired inequality holds for all \(k\geq k_i\).
Then \(\pi_{\bot x}(t)\sqsubseteq y_k\) where \(k\geq\max\{k_i:1\leq i< n\}\), which proves \(\pi_{\bot x}(t)\ll x\) in Λ n for all \(t <1\). To finish the proof, let x be any classical state and \(r:\varDelta^n\rightarrow\varLambda^n\) the natural retract. We know
-
\(x\in\varDelta^n_\sigma\Rightarrow \pi_{\bot x}(t)\in\varDelta^n_\sigma\) for all \(t\in[0,1]\), and
-
\(r(\pi_{\bot x}(t))=\pi_{\bot r(x)}(t)\ll r(x)\) in Λ n, for all \(t <1\),
where the first follows from Proposition 6(i), and the second from what we proved above. By Prop. 6(ii), these two give \(\pi_{\bot x}(t)\ll x\) for all \(t<1\).
(ii) First, for any \(x\in\varDelta^n\), we have \(\pi_{\bot x}(s)\ll \pi_{\bot x}(t)\) whenever \(s<t\). This easily follows from (i): For \(p:=\pi_{\bot x}(t)\) we have
If \(x\ll y\), then \(x\sqsubseteq\pi_{\bot y}(t)\ll y\) for some \(t<1\). Thus,
so taking \(z:=\pi_{\bot y}((t+1)/2)\) finishes the proof.
The last result demonstrates the existence of a natural approximative structure on classical states: The dcpo Δ n can rightfully be called a domain. As we said at the start, domains normally have partial elements, and total or ideal elements. We now explain the relationship between the qualitative notion of approximation ≪ and the natural intuitive notions of “partiality” and “totality” for classical states.
Intuitively, a classical state x is partial iff it offers no certainty about any outcome iff \((\forall i)\, 0<x_i<1\) iff \((\forall i)\,x_i>0\). One may object that \(x=(1/2,1/2,0)\in\varDelta^3\) seems partial but is excluded from the above. However, only “some” of x is partial, the element \(p_3(x)=\bot\in\varDelta^2\). As a state in Δ 3, though, x is not genuinely partial because it imparts certainty about the third outcome.
On the other hand, if we assume that the order theoretic structure of Δ n has captured our intuitive understanding of classical states, we easily arrive at an alternative formulation of partiality: An object is partial when it approximates something. The latter of course is purely qualitative and provides exactly what one hopes for: A formalization of intuition.
Lemma 13 (Partiality)
For each \(x\!\in\!\varDelta^n,\) the set \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is nonempty iff \(x_i\!>\!0\) for all i.
Proof
If \(x\ll y\), there there is \(t<1\) with \(x\sqsubseteq\pi_{\bot y}(t)\). Because \(t<1\), \(\pi_{\bot y}(t)_i\!>\!0\), so degeneration (Lemma 5) gives \(x_i\!>\!0\). For the other direction, let \(x_i>0\) for all i.
Intuitively, because x is in the interior of Δ n, the line segment from ⊥ to x can be extended nontrivially to a point y on the boundary of Δ n, for which we then have \(x\ll y\). Formally now, we can assume \(x\neq\bot\). Then
Let y be the classical state defined pointwise by
for each \(1\leq i\leq n\). To see that y is in fact a classical state, notice that
Since \(0\leq 1/\lambda<1,\) \(\pi_{\bot y}(1/\lambda)=x\ll y\), which proves \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\neq\emptyset\).
The “opposite” of partiality is totality: A classical state is total when it imparts certainty about all of its outcomes. Thus, the total or ideal classical states are exactly the pure states e i , which we have already characterized qualitatively as being precisely \(\max(\varDelta^n)\). But the approximation relation can offer additional insight about the sense in which pure states are total.
To understand the connection between the two, let’s begin by thinking about \(x\ll y\), which we could say means that
-
All paths \((y_i)\) to y must qualitatively exceed x after some finite stage, which can be read as
-
All paths to y essentially begin with x, and finally
-
A process \((y_i)\) can only end up in state \(y=\bigsqcup y_i\) provided that it has the information represented by x: x is necessary for having y, i.e., the only way to know y is to first know x.
In each version of ≪ above, some reference to a process is made (a path is assumed to be generated by some process), providing us with a crucial distinction between ≪ and ⊑: \(x\ll y\) is a statement about processes, \(x\sqsubseteq y\) is a statement about information. The difference between these two becomes clear by considering states \(x,y,z\) with \(x\ll y\sqsubseteq z\) but not \(x\ll z\).
Example 2
Let \(\bot\neq x\ll y:=(1/2,1/2,0)\sqsubseteq z:=e_1\). Then \(x\not\ll z\). Here are two equivalent perspectives:
-
(i)
In terms of knowledge: We are not required to know that an object is not in box 3 before we can know that it is in box 1.
-
(ii)
In terms of processes: From an initial state of ⊥, one way to conclude the object is in box 1 is to begin by ruling out box 3 as a possibility, and then look in one of the others—but this does not describe all ways. We could just look in box 1.
Thus, ⊑ makes statements about potential evolutions of state; ≪
is concerned with what we must know in order to obtain information using the process of observation.
This example suggests that ≪ is capable of expressing a characteristic of totality: The only time we expect the implication
to hold nontrivially is when x is a state from which a unique outcome is likely, i.e., x approximates a unique pure state. When \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) satisfies the implication above, it is called an upper set.
Proposition 7 (Approximation of pure states)
Let \(n\geq 2\)
-
(i)
For all \(x\in\varDelta^n\), \(x\ll e_i\) iff \(x=\pi_{\bot e_i}(t)\) for some \(t<1\).
-
(ii)
For all \(x\in\varDelta^n\), \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is an upper set iff it is empty, all of Δ n, or contains a unique pure state.
Proof
(i) For \(n=2\) this is clear. Assume \(n\geq 3\). Because \(x\ll e_i\), there is \(s<1\) with \(x\sqsubseteq\pi_{\bot e_i}(s)\). By degeneration, \((\exists a>0)(\forall k\neq i)(x_k=a),\) which now makes the claim obvious.
(ii) For (⇒), every nonempty upper set contains at least one maximal element. By (i), either \(x=\bot\), or \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) contains a unique pure state.
For the other direction, we need to prove that \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is an upper set when it contains a unique pure state e i . Suppose \(x\ll y\sqsubseteq z\). First, because \(x\ll e_i\), it is routine to show that \(x_i=x^+\) and \(x_k=x^-\) for all \(k\neq i\). Because \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) contains a unique pure state, \(x\neq\bot\), which means \(x^+>x^->0\). To apply Proposition 6(ii), we first show \(z\in\varDelta^n_\sigma\Rightarrow x\in\varDelta^n_\sigma\).
Let \(z\cdot\sigma\) be monotone. Because \(x\sqsubseteq z\), \(x\cdot\sigma\sqsubseteq z\cdot\sigma\), which means there is an index k with \((x\cdot\sigma)_k=x^+\leq (z\cdot\sigma)_k=z^+\). By the monotonicity of \(z\cdot\sigma\) and degeneration,
which means \(x\cdot\sigma\) is monotone, since the only other value it assumes is x −.
To finish, we need to show \(r(x)\ll r(z)\) in Λ n. First, \(r(z)_2>0\), since otherwise \(r(z)=e_1\), for which we already know \(r(x)\ll r(e_i)=e_1=r(z)\). By degeneration, this also means \(r(y)_2>0\). Because \(r(x)\ll r(y)\) in Λ n, there is \(t<1\) with \(r(x)\sqsubseteq\pi_{\bot r(y)}(t)\). Thus,
where the strict inequality follows from \(r(y)_1>r(y)_2>0\) (which is a consequence of degeneration using \(r(x)_1>r(x)_2>0\) and \(r(x)\sqsubseteq r(y)\)). Because \(r(x)_i/r(x)_{i+1}=1\) for \(1<i<n\), it is clear that \(r(x)\ll r(z)\) in Λ n.
An approximation a of a pure state x defines a region \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} a\) of Δ n known in domain theory as a Scott open set.
Definition 12
A subset U of a dcpo D is Scott open if
-
U is an upper set: \((\forall x\in U)(\forall y\in D)\,x\sqsubseteq y\Rightarrow y\in U,\) and
-
U is inaccessible by directed suprema: For any directed set \(S\subseteq D\),
$$\bigsqcup S\in U\Rightarrow S\cap U\neq\emptyset\,.$$
The collection of all Scott open subsets of D is σ D .
Notice that a map \(f:D\rightarrow E\) between dcpo’s is Scott continuous in the sense defined earlier iff \(f^{-1}(U)\) is Scott open in D whenever U is Scott open in E.
Lemma 14
For all \(x\in\varDelta^n\), \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is an upper set iff it is Scott open.
Proof
If \(z=\bigsqcup S\in{\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\), then by interpolation (Theorem 4), there is \(y\in\varDelta^n\) with \(x\ll y\ll z\). Thus, by \(y\ll z\), there is \(s\in S\) with \(y\sqsubseteq s\), and since \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is an upper set, \(s\in{\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\). Interestingly, one can also show that \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is Scott open iff \(\uparrow ({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x)\) is Scott open.
The relation between approximation, partiality and purity can now be summarized as follows:
-
(i)
The partial elements are those \(x\in\varDelta^n\) with \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\neq\emptyset\).
-
(ii)
For a partial element \(x\in\varDelta^n\), \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} x\) is Scott open iff \(x=\pi_{\bot e_i}(t)\) for some i and some \(t<1\) iff (\(x=\bot\) or x approximates a unique pure state).
Thus, the “totality” of a pure state x is largely explained by the fact that \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} a\) is Scott open whenever \(a\ll x\). To complete the picture,
Lemma 15
A subset \(U\subseteq\varDelta^n\) is Scott open iff
-
Any monotone path from \(x\in U\) to a pure state lies in U, and
-
The line from ⊥ to \(x\in U\) has a segment contained in U,
and for pure states x, there is an equivalence between “approximation of x” and “Scott open set containing x”: Given any \(a\ll x\), the set \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} a\) is Scott open, while given any Scott open U with \(x\in U\), we can (by exactness) find an approximation \(a\in U\) of x with \(x\in{\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} a\subseteq U\).
Approximation can also describe things of a more concrete nature. Because of its close connection to the mixing law, which is especially evident in the case of pure states (Proposition 7(i)), we can sometimes reinterpret mixing as approximation. This, for instance, can be useful when one seeks to explain the sense in which certain forms of noise work “against” the state σ of a system.
Example 3
The depolarization channel The map \(d_p:\varDelta^n\rightarrow\varDelta^n\) by
describes the process by which a state \(\sigma\in\varDelta^n\) is depolarized with probability \(p>0\) (has all bias and hence all information removed from it) and is otherwise unaltered. But notice:
which means \(d_p(\sigma)\ll\sigma\) for \(p>0\). In particular, the effect of depolarization on a state is qualitative.
To say that the effect of noise is qualitative essentially means that while the state of the system has suffered, it has not been “degraded beyond recognition.” This is not always the case: Some forms of noise are more destructive than others and the order on classical states can at times capture this.
Example 4
Classical bit flipping A state \(\sigma\in\varDelta^2\) suffering the effect of a magnetic field is “flipped” with probability p and otherwise left alone
where * is the involution \((x,y)^{\ast}=(y,x)\). In this case, we have
i.e., the effect of the noise is qualitative iff the field is weak enough.
Those familiar with classical information theory may know what we call classical bit flipping by another name, the binary symmetric channel. In this important example, a bit (a “0” or a “1”) is transmitted correctly through a channel with probability \(1-p\) and reversed with probability p:

Given that information is sent through the binary symmetric channel, we want to determine the information that is actually received. The information sent is modelled by \(\sigma=(x,y)\in\varDelta^2\), where x is the probability that 0 is sent and y is the probability that 1 is sent. The effect that the channel has on information passing through it (σ) is captured by its channel matrix
To determine the information received when \((x,y)\) is sent, we calculate a distribution for the output using the channel matrix as follows:
All of this is implicit in the operator \(f_p(\sigma)=p\sigma^{\ast}+(1-p)\sigma\) of Example 4: The distribution for the output is \(f_p(\sigma)\), the 0 bit is \(e_1=(1,0)\), the 1 bit is \(e_2=(0,1)\), and reversing σ means applying the involution * to obtain σ *.
2.5 Entropy, Content and Partiality
We have already seen how the use of ⊑ on Δ n enables a precise formulation of what it means to say that a classical state is “information.” One of the advantages in taking this approach to defining information is that the structure of a domain can then be used to define the notion “information content,” i.e., we can say what it means to measure the content of information.
The idea introduced in [8] is this: Assuming that information is formally specified as a domain, measuring content means measuring partiality, i.e., the amount of partiality in an object. The importance of this conceptually is that partiality, as we have already seen, is intimately connected to the order theoretic structure of a domain.
To slightly motivate the formal definition we are about to see, suppose that \(\mu:\varDelta^n\rightarrow[0,\infty)\) is a measure of content on classical states. Then μ x is the amount of uncertainty (or partiality) in x. As we move up in the order ⊑ on Δ n, states become more informative, so uncertainty decreases:
That is, as a map from Δ n to \([0,\infty)^{\ast}\), μ is monotone. If μ is defined in terms of the usual formulae from physics (arithmetic, logarithms, other elementary functions), then it is continuous in the sense of analysis, and hence Scott continuous from Δ n to \([0,\infty)^{\ast}\).
The essence of the distinction between content and a random continuous map on a domain is subtle. Consider a pure state \(x\in\max(\varDelta^n)\) and one of its approximations \(a\ll x\), so that a is information any process must have before it can evolve to x. Then we also expect \(a\ll y\) provided that
-
(i)
y is a state from which it is possible to evolve to x, and
-
(ii)
y is “close enough” to x in content.
The first translates as “\(y\sqsubseteq x\)”; the second translates as “\(|\mu x-\mu y|<\varepsilon\),” on the assumption that μ measures information content. Putting everything together now, if μ is a measure of content, then we expect that
Because x is pure, we can replace \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} a\) with a Scott open set \(U\subseteq\varDelta^n\), as we saw in the last section.
Definition 13
A Scott continuous map \(\mu:D\rightarrow[0,\infty)^{\ast}\) on a dcpo is said to measure the content of \(x\in D\) if
whenever \(U\in\sigma_D\) is Scott open and
are the elements ε close to x in content. The map μ measures X if it measures the content of each \(x\in X\).
In order for a map μ to be regarded “a measure of content,” it must minimally be capable of distinguishing those elements which it claims are maximally informative. That is, μ must measure all of the objects which it regards as possessing no uncertainty \(\ker\mu:=\{x:\mu x=0\}\).
Definition 14
A measurement is a Scott continuous map \(\mu:D\rightarrow[0,\infty)^{\ast}\) on a dcpo that measures \(\ker\mu:=\{x\in D:\mu x=0\}\).
The measurement formalism [8] teaches that the ability to measure content is indicative of a purely structural relationship that exists between two classes of informative objects. Neither class need consist of numbers. This relationship is formally expressed by a map \(\mu:D\rightarrow E\) whose general nature is to reflect properties of simpler objects E onto more complex objects D.
The motivation for the idea stems from the empirical fact that it is often easier to reason about D in terms of E rather than deal with D directly [8]. Hence the reflective nature of μ: It confirms that we actually can learn about \(x\in D\) by studying the properties of its simplification \(\mu x\in E\).
Definition 15
A Scott continuous map \(\mu:D\rightarrow E\) between dcpo’s is said to measure the content of \(x\in D\) if
whenever \(U\in\sigma_D\) is Scott open and
are the elements ε close to x in content. The map μ measures X if it measures the content of each \(x\in X\).
Definition 16
A measurement is a Scott continuous map \(\mu:D\rightarrow E\) between dcpo’s that measures \(\ker\mu:=\{x\in D:\mu x\in\max(E)\}\).
These definitions are easily seen to be equivalent to the quantitative formulations we saw earlier by setting \(E=[0,\infty)^{\ast}\). To establish the reflective nature of content, we use the following relationship between the order ⊑ on a dcpo D and its Scott open sets 03C3; D :
Proposition 8
Let \(\mu:D\rightarrow E\) be a measurement and x an object that it measures.
-
(i)
If \(\mu x\in\max(E)\), then \(x\in\max(D)\).
-
(ii)
If \(\mu x=\bot\), then \(x=\bot\), provided \(\bot\in D\) exists.
-
(iii)
If \(y\sqsubseteq x\) and \(\mu x=\mu y\), then \(x=y\).
-
(iv)
If \(x_n\sqsubseteq x\) and \((\mu x_n)\) is directed with supremum \(\mu x\), then \(\bigsqcup x_n=x\).
In addition, the composition of measurements is again a measurement.
Proof
The proofs here are essentially taken verbatim from [8], where other properties of content can be found.
-
(i)
Let \(x\in U\). Then \(y\in\mu_\varepsilon(x)\subseteq U\), for some \(\varepsilon\in\sigma_E\). Since U was arbitrary, \(x\sqsubseteq y\). By antisymmetry, \(x=y\).
-
(ii)
If \(x\sqsubseteq y\), then \(\mu x=\mu y\), since \(\mu x\in\max(E)\), which gives \(y\in\ker\mu\). Since μ is a measurement, it measures y, so \(x=y\) by (iii).
-
(iii)
First, \(\mu(\bot)\sqsubseteq\mu x=\bot\), so \(\mu(\bot)=\bot=\mu x\). Since \(\bot\sqsubseteq x\), we can apply (i) to obtain \(x=\bot\).
-
(iv)
Let \(x_n\sqsubseteq u\) for all n. If \(x\in U\), then \(x\in\mu_\varepsilon(x)\subseteq U\), which means
$$\mu x=\bigsqcup \mu x_n\in\varepsilon,$$and so \(\mu x_n\in\varepsilon\) for some n, which gives \(x_n\in U\) and hence \(u\in U\). Since U was arbitrary, \(x\sqsubseteq u\). Thus, \(\bigsqcup x_n=x\).
Finally, if we have measurements \(D\stackrel{\mu}{\longrightarrow}E\stackrel{\lambda}{\longrightarrow}F\), then λ μ measures \(\ker\lambda\mu\) as follows. First, if \(x\in\ker\lambda\mu\) and \(x\in U\in\sigma_D\), then \(x\in\ker\mu\) so there is \(\varepsilon\in\sigma_E\) with \(x\in\mu_\varepsilon(x)\subseteq U\). Then, since \(\mu x\in\varepsilon\) and \(\mu x\in\ker\lambda\), there is \(\delta\in\sigma_F\) with \(\mu x\in\lambda_\delta(\mu x)\subseteq\varepsilon\). We have
which finishes the proof.
With the benefit of the abstract formulation of content, let us take a second look at uncertainty (\(E=[0,\infty)^{\ast}\)). By Proposition 8(i), we know that
for any measurement \(\mu:D\rightarrow[0,\infty)^{\ast}\). That is, quantitative certainty implies qualitative certainty. As a case in point, if \(D=\varDelta^n\), then, as we will see shortly, Shannon entropy \(\mu:D\rightarrow[0,\infty)^{\ast}\) given by
is a measurement. Thus, any classical state x with entropy \(\mu x=0\) is pure. But now we have an explanation for why such properties hold:
-
(i)
In the sense of the measurement formalism, μ is a measure of content between the domains Δ n and \([0,\infty)^{\ast}\), and
-
(ii)
Measures of content between domains always reflect maximality.
The same is true of the von Neumann entropy on quantum states (that we will see later). But the moral of the last result is what is most important: Subject to moderate hypotheses, information behaves in the same manner as its content.
Proposition 9
The natural retraction \(r:\varDelta^n\rightarrow\varLambda^n\) is a measurement.
Proof
To start, notice that \(\ker r=\max(\varDelta^n)\). Let \(U\subseteq\varDelta^n\) be a Scott open set that contains the pure state x. By exactness, there is \(\bot\neq a\ll x\) with \(a\in U\). By Prop. 6(ii), \(r(a)\ll r(x)\) in Λ n. Because x is pure, \(\varepsilon:= {\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} r(a)\) is a Scott open subset of Λ n (a corollary of Theorem 4 and Proposition 7). We claim \(x\in r_\varepsilon(x)\subseteq{\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} a\subseteq U\) as follows.
First, \(x\in r_\varepsilon(x)\) by \(r(a)\ll r(x)\). Then, if \(y\in r_\varepsilon(x)\), we have \(r(a)\ll r(y)\) in Λ n and \(y\sqsubseteq x\). To prove that \(a\ll y\) in Δ n and finish the proof, we must show \(y\in\varDelta^n_\sigma\Rightarrow a\in\varDelta^n_\sigma\).
For this subtle point, a takes its maximum at a unique index, because \(a\neq\bot\) and it approximates a pure state (Proposition 7(i)). Then \(r(a)\) does as well. Since \(r(a)\sqsubseteq r(y)\), degeneration implies the same is true of \(r(y)\) and hence of y. Thus, because y takes its maximum at a unique index, and because \(y\sqsubseteq x\in\max(\varDelta^n)\), we have \(y\in\varDelta^n_\sigma\Rightarrow x\in\varDelta^n_\sigma\), while \(a\ll x\) then implies \(a\in\varDelta^n_\sigma\).
We have made intuitive use of this fact numerous times: Whenever we prove a statement about classical states by first proving it for monotone states, we are implicitly appealing to the fact that \(r(x)\) provides a decent measure of the content of x.
Example 5
The standard variable \(v:\varDelta^n\rightarrow[0,\infty)^{\ast}\) given by
is a measurement with \(\ker v=\max(\varDelta^n)\). To prove as much, we need only show that its restriction to Λ n, \(\lambda:= v|_{\varLambda^n}\), is a measurement, since then \(v=\lambda\circ r\) must be another.
To this end, let \(U\subseteq\varLambda^n\) be a Scott open set and \(x\in\ker\lambda\). Because U is Scott open, there is \(t <1\) with \(a:=\pi_{\bot x}(t)\in U\). We then have
where
Example 6
The entropy \(s:\varDelta^n\rightarrow[0,\infty)^{\ast}\) given by
is a measurement with \(\ker s=\max(\varDelta^n)\). First, \(s(x)\geq v(x)\), using the classic inequality \(\log t\leq t-1\) for \(t>0\). Thus,
for any pure state x and \(\varepsilon>0\). Because v is a measurement, so is s.
Now for Shannon entropy.
Lemma 16
Let \(x\sqsubseteq y\) be monotone classical states in Δ n. Then there is \(k\in\{1,\ldots,n\}\) such that
-
(i)
\((\forall i <k)\,x_i\leq y_i\), and
-
(ii)
\((\forall i\geq k)\,x_i\geq y_i\).
Proof
First, since \(x\sqsubseteq y\), we have by induction that \(x_iy_{i+j}\leq y_ix_{i+j},\) for each \(j\in\{0,\ldots,n-i\}\). Thus, if \(x_i\geq y_i\), then \(x_{i+j}\geq y_{i+j}\) for each \(j\in\{0,\ldots,n-i\}\). Now let k be the least integer \(1\leq k\leq n\) with \(x_k\geq y_k\). Notice that such a k exists since \(x_n\geq y_n\). This finishes the proof.
The relative Shannon entropy of y given x is
where \(x,y\in\varDelta^n\). This quantity is always nonnegative and is zero iff \(x=y\).
Theorem 5
Let \(\mu:\varDelta^n\rightarrow[0,\infty)^{\ast}\) be the Shannon entropy on classical states
where the logarithm is natural. Then μ is a measurement. In addition,
-
(i)
For all \(x,y\in\varDelta^n\), if \(x\sqsubseteq y\) and \(\mu(x)=\mu(y),\) then \(x=y\).
-
(ii)
For all \(x\in\varDelta^n\), we have \(\mu(x)=0\) iff \(x\in\max(\varDelta^n)\).
-
(iii)
For all \(x\in\varDelta^n\), we have \(\mu(x)=\log n\) iff \(x=\bot\).
Proof
Because μ is symmetric, its Scott continuity follows if we show that its restriction to the dcpo Λ n is Scott continuous. First we prove its monotonicity into \([0,\infty)^{\ast}\).
Let \(x\sqsubseteq y\) be monotone classical states. By Lemma 16, there is an integer \({k\in\{1,\ldots,n\}}\) such that \(x_i\leq y_i\) for \(i <k\) and \(x_i\geq y_i\) for \(i\geq k\). Then
Notice that if \(x_k=0\) then the sum of the \(i>k\) vanishes, while the sum of the \(i <k\) blows up, but is nevertheless nonnegative. From the nonnegativity of this sum, we have
where the second inequality follows from \(\mu(y\|x)\geq 0\). This proves that μ is monotone into \([0,\infty)^{\ast}\).
If in addition to \(x\sqsubseteq y\) we also have \(\mu x=\mu y\), then the inequality above immediately gives \(\mu(y\|x)=0\), which implies \(x=y\). This establishes that μ is strictly monotone. For its Scott continuity, if \((x_i)\) is increasing, then
where the first equality uses Proposition 2 and the second uses the continuity of μ with respect to the Euclidean topology. By Lemma 1, μ is Scott continuous. Finally, μ is a measurement: For \(x\in\varDelta^n\), we have
using \(\log t\leq t-1\) for \(t>0\) and \(x^+\geq 1/n\), where v is the variable from Example 5. Since v is a measurement, \((1/n)\cdot v\) is a measurement, which means that μ is as well.
It is important to realize that the minimal account of content given here is more substantial than it may seem: There are natural mappings which do not measure content.
Example 7
Numbers are not enough. For \(n\geq 3\), consider
It is Scott continuous, symmetric and assumes its order theoretic minimum at ⊥. Furthermore, even though \(f(x)=0\) for all \(x\in\max(\varDelta^n)\), f does not measure the content of a single pure state.
For instance, suppose f measured the content of \(e_1\in\varDelta^3\). Then given any open \({U\subseteq\varDelta^n}\) with \(e_1\in U\), there would exist \(\varepsilon>0\) with \(e_1\in f_\varepsilon(e_1)\subseteq U\). Then \({(1/2,1/2,0)\in U}\). But because this applies to any open set U, we now have a proof that \(e_1\sqsubseteq(1/2,1/2,0)\).
More intuitively: Many states are assigned maximal measure by f which are not pure. For instance \(f(x,y,0)=0\) on Δ 3, even though the only time \((x,y,0)\) is pure is when \(x=1\) or \(y=1\).
Here is a summary.
Example 8
Canonical measures of content on Δn
-
(i)
The maps \(\varDelta^n\rightarrow[0,1]::x\mapsto x^+\) and \(\varDelta^n\rightarrow[0,1]^{\ast}::x\mapsto 1-x^+\).
-
(ii)
Entropy \(s(x)=-\log x^+\).
-
(iii)
The natural retraction \(r:\varDelta^n\rightarrow\varLambda^n\).
-
(iv)
Shannon entropy
$$\mu x=-\sum_{i=1}^nx_i\log x_i.$$
3 Quantum States
We now pursue the idea which motivated our study of the Bayesian order on classical states: The spectral order on quantum states. Later we will see that the spectral order can be characterized in a manner completely analogous to the order on classical states:
-
The inductive formulation, in terms of quantum projections, and
-
The symmetric formulation, in terms of unitary transformations.
These two accounts of the quantum order, when restricted to a class of states exhibiting classical behavior, are equivalent to the inductive and symmetric characterizations of the Bayesian order on classical states studied in the last section.
3.1 Essentials
An n-dimensional complex Hilbert space \(\mathcal{H}^n\) is an n-dimensional vector space over \({\Bbb C}\) with specified inner product \(\langle\cdot\mid\cdot\rangle\).
Definition 17
A base of \(\mathcal{H}^n\) is a sequence \((\psi_i)_{i=1}^n\) of unit vectors,
which are mutually orthogonal:
We write \(x\perp y\) to express the orthogonality of two vectors \(x,y\in\mathcal{H}^n\), and as is customary, extend this notation to subspaces of \(\mathcal{H}^n\) as follows:
where o is the zero of \(\mathcal{H}^n\).
Definition 18
A linear operator \(\rho:\mathcal{H}^n\rightarrow\mathcal{H}^n\) is self-adjoint if
for all \(\phi,\psi\in\mathcal{H}^n\), positive when
for all \(\psi\in\mathcal{H}^n\), and idempotent when \(\rho^2:=\rho\circ\rho=\rho\).
The spectral theorem of von Neumann [12], roughly speaking, states that each self-adjoint operator on a Hilbert space decomposes into a sum of simple operators called projections.
Definition 19
A projection or projector is a self-adjoint, linear, idempotent operator. The set of projections is denoted \({\Bbb P}^n\). A projection \(P\in{\Bbb P}^n\) is fully characterized by its subspace of fixed points \(\mathsf{fix}(P)\subseteq\mathcal{H}^n\).
All we need here is the finite dimensional case of the spectral theorem.
Theorem 6
A self-adjoint linear operator \(\rho:\mathcal{H}^n\rightarrow\mathcal{H}^n\) decomposes uniquely into a linear combination of mutually orthogonal projections
whose images span \(\mathcal{H}^n\). The set \(\mathsf{spec}(\rho)\subseteq{\mathbb R}\) is called the spectrum of ρ.
We write the fact that the images of the projections span \(\mathcal{H}^n\) as
where by idempotence we have \(\mathsf{fix}(P)=\mathsf{Im}(P)=P(\mathcal{H}^n)\).
Definition 20
The trace of a linear operator ρ on \(\mathcal{H}^n\) is
where \(\{\psi_i\}\) is any base of \(\mathcal{H}^n\). If A is any matrix representation of ρ, then \(\mathsf{tr}(\rho)=\sum A_{ii}\) is the sum of the elements on the diagonal of A.
The standard kinematical account of a quantum system includes both a description of the states a system can take, and of its observables, i.e., the measurements that can be performed on the system.
Definition 21
A density operator ρ on \({\mathcal{H}^n}\) is a self-adjoint, positive, linear operator with \(\mathsf{tr}(\rho)=1\). A quantum n-state is a density operator. The class of quantum n-states is denoted Ω n.
Definition 22
A quantum state ρ is pure if \(\mathsf{spec}(\rho)\subseteq\{0,1\}\). The set of pure states is written Σ; n.
A classical state is a distribution on the set of pure states \(\max(\varDelta^n)\). Similarly, Gleason’s theorem [5] establishes that density operators encode precisely the measures on the closed subspaces of \(\mathcal{H}^n\), i.e., density operators are distributions on the set of pure states.
Definition 23
A quantum n-measurement is a self-adjoint linear operator \(e:\mathcal{H}^n\rightarrow\mathcal{H}^n\).
For instance, if e is the energy observable, then its spectrum \(\mathsf{spec}(e)\) contains the actual energy values a system can assume. According to quantum mechanics, if the density operator of a system is ρ, then a measurement of the observable e yields \(\lambda\in\mathsf{spec}(e)\) as the result with probability
Now what we want to do is rewrite all of this in a form more amenable to the task at hand.
Definition 24
\({\Bbb L}^n\) is the set of closed subspaces of \(\mathcal{H}^n\).
By the spectral theorem, we can write a self-adjoint operator e as
By mutual orthogonality, \({e}\psi=\lambda\psi\ \Leftrightarrow\ P^\lambda_{e}\psi=\psi\), so the eigenspaces
give rise to a labeled collection of mutually orthogonal subspaces
which span \(\mathcal{H}^n\).
Definition 25
A decomposition of \(\mathcal{H}^n\) is a family of mutually orthogonal subspaces of \(\mathcal{H}^n\) of dimension at least one which span \(\mathcal{H}^n\). The decompositions of \(\mathcal{H}^n\) are denoted \({\Bbb D}^n\).
We will also refer to the union \(\bigcup\mathcal{D}\) of a decomposition \(\mathcal{D}\) as being the decomposition itself since the first characterizes the latter.
Definition 26
A spectral decomposition of \(\mathcal{H}^n\) is an injective function \(f:X\rightarrow{\Bbb L}^n\) defined on a nonempty set \(X\subseteq{\mathbb R}\) with \(f(X)\in{\Bbb D}^n\). The domain of f is written \({\mathsf{spec}(f)=X}\) and called the spectrum of f.
Equivalently, a spectral decomposition is a partial injection \(f:{\Bbb R}\rightharpoonup{\Bbb L}^n\) with \({\mathsf{Im}(f)\in{\Bbb D}^n}\) and \(\mathsf{spec}(f):=\mathsf{dom}(f)\).
Lemma 17
There is a one to one correspondence between self-adjoint operators on \(\mathcal{H}^n\) and spectral decompositions of \(\mathcal{H}^n\).
Thus, we frequently use the operator and decomposition language interchangeably. For example, here is an alternate formulation of quantum states:
Definition 27
A density operator is a spectral decomposition r with
and \(\mathsf{spec}(r)\subseteq[0,\infty)\).
In particular, a pure state \(r\in\varSigma^n\) is a decomposition \(r:\{0,1\}\to{\Bbb L}^n\) with
From this equation we see that the subspace r 1 is one-dimensional. In fact, r 1 serves to characterize r, since r 0 must then be a certain \(n-1\) dimensional subspace known as the orthocomplement of r 1,
We have proven the following.
Lemma 18
The pure states on \(\mathcal{H}^n\) are in bijective correspondence with the one dimensional subspaces of \(\mathcal{H}^n\).
So much for states. For observables, we will consider only those e on \(\mathcal{H}^n\) with the maximum number of distinguishable outcomes n. By simple renaming then, we can take \(\mathsf{spec}(e)=\{1,\ldots, n\}\). This convention highlights the role played by measurements: They are labelings, i.e., to each outcome \(1\leq i\leq n\), a measurement assigns those states e i of the system for which observable e has value i with certainty (probability one).
Definition 28
A labeling is a spectral decomposition
Notice that non-degeneration of \(\mathsf{spec}(e)\) implies that the decomposition \(\mathcal{D}_e\) consists only of one-dimensional subspaces (pure states), i.e., \(\mathcal{D}_e\) cannot be refined any further:
Definition 29
A decomposition \(\mathcal{D}\) is a refinement of decomposition \(\mathcal{D}'\) iff
Finally, the probabilities. Recall that the probability of obtaining outcome i in a measurement of observable e on a system with density operator r is given by
For a state r and a labeling e, \(\langle {r}|e_i\rangle\) denotes the ith diagonal element of the matrix representation of r when expressed in a base B in which all \(P^i_e\) diagonalize, and thus, by the spectral decomposition theorem, in which e itself diagonalizes. Writing \(P^i_e\cdot {r}\) in base B then yields
and thus
from which we conclude
In particular, \(\langle r|e_i\rangle\) does not depend on B, but only on r and e i , since it is equal to \(\mathsf{tr}(P^i_e\cdot {r})\). Further, since \(\mathsf{tr}(r)=1\),
which simply says that a measurement for observable e yields some outcome \(i\in\mathsf{spec}(e)\) with probability one.
Definition 30
For a state r and labeling e, we define
Notice that \(\mathsf{spec}(r|e)\) is a list, while \(\mathsf{spec}(r)\) is a set.
In general, \(\mathsf{spec}(r|e)\) may not consist of eigenvalues of r, i.e., elements of \(\mathsf{spec}(r)\). However, if r also diagonalizes in base B, then its diagonal consists of eigenvalues of r. And this is the case we are most interested in.
Definition 31
A state r admits a labeling e if
Any state admits at least n! labelings, corresponding with different permutations of \(\mathsf{spec}({r}|e)\). More generally, the following result tells us exactly when a labeling yields the spectrum of a state.
Proposition 10
The following are equivalent for state r and labeling e:
-
r admits labeling e.
-
\(\mathcal{D}_e\) is a refinement of \(\mathcal{D}_{r}\).
-
r diagonalizes in a base B in which e is diagonal.
-
r and e commute, that is, \([{r},e]={r}\cdot e-e\cdot {r}=0\).
The following are equivalent for states r and s:
-
They admit a joint labeling e.
-
They admit joint refinement \(\mathcal{D}\).
-
They diagonalize in a common base B.
-
They commute, that is, \([{r},{s}]=0\).
Additionally, states r and s admit labeling e iff
In particular we have in all the above cases that
whenever one of the inclusions applies
Proof
Given a base B, for all \(\psi\in B\) we have \(\psi\in\bigcup\mathcal{D}_e\) iff all \(\psi\in B\) are eigenvectors of e iff e diagonalizes in the base B. Thus, any self-adjoint operator e diagonalizes in a base B iff \(B\subseteq\bigcup\mathcal{D}_e\) .
We already showed above that r admits labeling e when there exists a base B in which both r and e diagnalize, that is, whenever B is included both in \(\bigcup\mathcal{D}_{r}\) and \(\bigcup\mathcal{D}_e\) and as such
where since e is non-degenerated we have
and thus \(\bigcup\mathcal{D}_e\subseteq\bigcup\mathcal{D}_{r}\) . Two states r and s then admit a joint labeling e whenever
The converses of these derivations is obvious. Whenever r and s admit diagonalization in a common base B, when representing them in B commutation reduces to commutation of reals. For the other results with respect to commutation, in particular the fact that self-adjoint operators diagonalize in a common base if they commute, we refer to relevant literature.
Lemma 19
Let r be a state and e be a labeling with \([r,e]=0\). Then
and
In particular, \(\mathsf{dim}(r_\lambda)\) does not depend on the choice of e, so neither do the multiplicities of eigenvalues.
Finally, the following result is indispensable and we will appeal to it time and time again (often implicitly).
Lemma 20 (Definability)
For any labeling e and classical state x, there is a unique quantum state \(r\in\varOmega^n\) with \([r,e]=0\) and \(\mathsf{spec}(r|e)=x\).
Although the notions decomposition, refinement and labeling as well as the representation of states and measurements as maps that label subspaces in terms of spectra are not standard in orthodox quantum theory [12], they prove to be useful in our setting since they highlight degeneration of spectra, a fundamental ingredient in the ordering of both classical and quantum states.
3.2 A Partial Order on Quantum States
Here is the spectral order on quantum states Ω n.
Definition 32
For states \({r},{s}\in\varOmega^n\), we write \(r\sqsubseteq {s}\) iff there exists a labeling e such that
-
e is admitted both by r and s,
-
\(\mathsf{spec}({r}|e)\sqsubseteq \mathsf{spec}({s}|e)\) in Δ n.
Though the order on quantum states only requires that there exist a single joint labeling, it nevertheless applies to all labels shared by r and s. This is like the way that \(x\sqsubseteq y\) for classical states implies \(x\cdot \sigma\sqsubseteq y\cdot\sigma\), for any \(\sigma\in S(n)\) with \(x,y\in\varDelta^n_\sigma\).
Proposition 11
If \(r\sqsubseteq s\) in Ω n, then \(\mathsf{spec}({r}|e)\sqsubseteq \mathsf{spec}({s}|e)\) in Δ n, for any labeling e with \([r,e]=[s,e]=0\).
Proof
We prove the equivalent statement that
whenever \([r,e]=[s,e]=[r,e']=[s,e']=0\). Since
and, since whenever \([r,e]=[s,e]=0\) we have
by Proposition 10, it follows that
where, since \({r}_\lambda\perp {r}_{\lambda'}\) and \({s}_\lambda\perp {s}_{\lambda'}\) for \(\lambda\not=\lambda'\), the subspaces \({r}_\lambda\cap {s}_{\lambda'}\) are mutually orthogonal for non-coincideng labels \((\lambda,\lambda')\) and thus mutually exclusive. Since their union includes \(\bigcup\mathcal{D}_e\) they span \(\mathcal{H}^n\), so they constitute a decomposition
with \(\mathcal{D}_e\) as a refinement.

Since \(\mathcal{D}_e\) is a refinement of \(\mathcal{D}_{r,s}\) it also follows that
where the quantity on the left does not depend on e. Since,
for \((\lambda,\lambda')\in \mathsf{spec}({r})\times\mathsf{spec}({s})\), we have
Thus, writing
it follows that the list \(\mathsf{spec}(r,s|e)\) contains a fixed collection of elements
where all \({(\lambda,\lambda')\in\mathsf{spec}({r})\times\mathsf{spec}({s})}\), independent on the choice of e except for the order of the elements in this list, that is, given e and e′ such that \([r,e]=[s,e]=[r,e']=[s,e']=0\) we have
for some permutation \(\sigma:\{1,\ldots,n\}\to\{1,\ldots,n\}\) and thus
But these are classical states, so
from which implication (10.5) follows.
The last result uses one of the two fundamental properties possessed by the Bayesian order on Δ n: It is symmetric, i.e., the map
is an order isomorphism, for any \(\sigma\in S(n)\). This label independence of the Bayesian order is a simple case of a more general notion satisfied by the spectral order which we will study in the section on symmetries. To hint at the connection: The equation
indicates that permuting the classical state \(\mathsf{spec}(r|e)\) is the same as permuting the subspaces \((e_i)_{i=1}^{i=n}\) of the labeling e.
The second crucial property of the Bayesian order on Δ n is that it is degenerative:
Here is the quantum version of the degeneration lemma for classical states.
Lemma 21
If \({r}\sqsubseteq {s}\) in Ω n then
and
where
Proof
Since \({r}\sqsubseteq {s}\) they admit a labeling e such that \(\mathsf{spec}({r}|e)\sqsubseteq \mathsf{spec}({s}|e)\) and thus by degeneration for classical states (Lemma 5), we have
so eq. (10.6) follows. Analogously, for
classical degeneration again yields
so eq. (10.7) follows.
Recall that an increasing sequence \((x_i)\) of classical states must be confined to some region \(\varDelta^n_\sigma\). Here is the analogous result for the spectral order.
Lemma 22
Let \(({r}_i)_{i\geq 1}\) be a sequence such that for all \(i\geq 1\) we have that \({r}_i\sqsubseteq {r}_{i+1}\). Then there exists a joint refinement \(\mathcal{D}_{(r_i)}\) of \((\mathcal{D}_{{r}_i})_{i\geq 1}\) and thus the states \(({r}_i)_{i\geq 1}\) admit joint labeling.
Proof
We agree that the first index for states refers to the sequence index and that the second refers to eigenvalues. First note that by Lemma 21, since \({r}_i\sqsubseteq {r}_{i+1}\) we have
We now proceed by induction.
As base case we take r 1 as its own refinement. Note that the spectrum of a state r decomposes in a zero and a non-zero part to which we refer as \(\mathsf{spec}_0({r})\). Let \(\mathcal{D}_i\) be the constructed joint refinement for \(({r}_1,\ldots,{r}_i)\). Set
where
Graphically, in terms of decompositions of \(\mathcal{H}^n\) in subspaces,

We now prove that \(\mathcal{D}_{i+1}\) is a joint refinement for \(({r}_1,\ldots,{r}_{i+1})\). Since \({r}_i\sqsubseteq {r}_{i+1}\) they admit a joint refinement \(\mathcal{G}\) so we have by Proposition 10 that
by Eqs. (10.8) and (10.9) and since
We moreover have
Since \(\mathcal{D}_i\) is a refinement for \(\mathcal{D}_{{r}_i}\) it also follows that
Thus,
The elements in \(\mathcal{D}\), \(\mathcal{E}\) and \(\mathcal{F}\) are mutually orthogonal since \(\mathcal{D}_i\), \({r}_{i,>0}\) and \({r}_{i+1,>0}\) consist of mutually orthogonal elements. Moreover, the sets \(\bigcup\mathcal{D}\), \(\bigcup\mathcal{E}\) and \(\bigcup\mathcal{F}\) are themselves mutually orthogonal since
-
\(\bigcup\mathcal{F}=\bigcup{r}_{i+1,>0}\perp{r}_{i+1,0}\supseteq\bigcup\mathcal{E}\) ,
-
\(\bigcup\mathcal{D}\subseteq{r}_{i,0}\perp\bigcup{r}_{i,>0}\supseteq\bigcup\mathcal{E}\) , and,
-
\(\bigcup\mathcal{D}\subseteq{r}_{i,0}\perp\bigcup{r}_{n,>0}\supseteq\bigcup{r}_{i+1,>0}=\bigcup\mathcal{F}\) ,
where the last inclusion follows from Eq. (10.9). Thus, \(\mathcal{D}_{i+1}\) is a decomposition of \(\mathcal{H}^n\). Since
-
\(\bigcup\mathcal{F}=\bigcup{r}_{i+1,>0}\),
-
\(\bigcup\mathcal{E}={r}_{i+1,0}\), and,
-
\(\bigcup\mathcal{D}\subseteq{r}_{i,0}\subseteq {r}_{i+1,0}\),
by eq. (10.8), it follows that
so \(\mathcal{D}_{i+1}\) is a refinement of \(\mathcal{D}_{r_{i+1}}\). Since
-
\(\bigcup\mathcal{E}=\bigcup{r}_{i+1,>0}\subseteq\bigcup{r}_{i,>0}\subseteq \bigcup\mathcal{D}_n\), by Eq. (10.9) and the inductive assumption,
-
\(\bigcup\mathcal{F}\subseteq\bigcup{r}_{i,>0}\subseteq\bigcup\mathcal{D}_i\), and,
-
\(\bigcup\mathcal{D}\subseteq\bigcup\mathcal{D}_i\),
it follows that \(\mathcal{D}_{i+1}\) is a refinement of \(\mathcal{D}_i\) and thus of all \(\mathcal{D}_{{r}_j}\) for \(1\leq j\leq i\).
Finally, consider an infinite sequence \(({r}_i)_{i\geq 1}\) such that for all \(i\geq 1\) we have that \({r}_i\sqsubseteq {r}_{i+1}\) and let \((\mathcal{D}_i)_{i\geq 1}\) be the corresponding series of refinements, each member being the above constructed common refinement of \((\mathcal{D}_{{r}_1},\ldots,\mathcal{D}_{{r}_i})\). Note that \((\bigcup\mathcal{D}_i)_{i\geq 1}\) is decreasing with respect to intersection. Then, since \(\mathcal{H}^n\) is n-dimensional, there can only be n distinct decompositions contained in \((\mathcal{D}_i)_{i\geq 1}\), that is \(n-1\) non-trivial refinements steps \(\mathcal{D}_{i}\mapsto\mathcal{D}_{{i+1}}\). Thus,
is equal to the intersection of a finitely many decreasing sets and thus must be equal to its smallest member, which is a common refinement for \((\mathcal{D}_{{r}_i})_{i\geq 1}\).
Theorem 7
Ω n is a partially ordered set for each \(n\geq 2\). Its maximal elements are the pure states,
while its least element is the completely mixed state
Proof
For reflexivity, consider any labeling e admitted by state r. Then, due to reflexivity in Δ n (Theorem 2), reflexivity in Ω n follows.
For anti-symmetry assume that \(r\sqsubseteq s\) and \(s\sqsubseteq r\). By Lemma 22 there exists a joint labeling e and thus by definition 32 we have
Due to anti-symmetry in Δ n we obtain \(\mathsf{spec}(r|e)=\mathsf{spec}(s|e)\) so \(r=s\) by Lemma 20.
For transitivity assume that \(r\sqsubseteq s\) and \(s\sqsubseteq t\). By Lemma 22 there exists a joint labeling e and thus we have
Thus, due to transitivity in Δ n we obtain \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(t|e)\) and thus by Definition 32 we have \(r\sqsubseteq t\).
Since \(\mathsf{spec}(r)=\{0,1\}\) for any \(r\in\varSigma^n\), when \(s\in\varOmega^n\) satisfies \(r\sqsubseteq s\) it follows for any labeling e admitted by r and s that we have
in Δ n for some permutation σ, so \(\mathsf{spec}(r|e)=\mathsf{spec}(s|e)\) since \(\mathsf{spec}(r|e)\in\max(\varDelta^n)\), and thus \(r=s\).
Conversely, for any state \(r\in\varOmega^n\) expressed in a base \(B\in\mathcal{D}_e\) in which it diagonalizes, we have
in Δ n for some permutation σ, so r has a pure state above it, and thus the pure quantum states are the only maximal elements of Ω n.
Since \(\mathsf{spec}(\bot)=\{{1/n}\}\) we have \(\mathcal{D}_\bot=\mathcal{H}^n\) and thus ⊥ admits any labeling. Given \(r\in\varOmega^n\) and labeling e admitted by e we then have
so \(\bot\sqsubseteq r\) and thus ⊥ is the least element of Ω n.
Examining the proofs given so far reveals that the technique used in defining the spectral order serves to distinguish an interesting class of partial orders on classical states for which the Bayesian order is the canonical member.
Corollary 3
If ⊑ is a symmetric and degenerative partial order on Δ n, then the relation in Definition 32 is a partial order on Ω n. Moreover,
-
\(\max(\varOmega^n)=\varSigma^n\) whenever \(\max(\varDelta^n)=\{e_i:1\leq i\leq n\}\), and
-
The completely mixed state is the bottom of Ω n whenever \((1/n,\ldots,1/n)\) is the bottom of Δ n.
By Lemma 20, we can define a quantum state r by specifying two pieces of information: (i) a labeling e which it admits, that is \([r,e]=0\), and (ii) a classical state x for which \(\mathsf{spec}(r|e):=x\). We use this idea in what follows.
Proposition 12
The quantum states Ω n are a dcpo. In more detail,
-
(i)
If \((r_i)_{i\geq 1}\) is an increasing sequence, then its supremum \(\bigsqcup_{i\geq 1}r_i\) exists and is implicitly defined by
$$\mathsf{spec}\Bigl(\,\,\bigsqcup_{i\geq 1}r_i\Bigm|e\Bigr)= \Bigl( \lim_{i\rightarrow\infty}\langle r_i|e_1\rangle,\ldots,\lim_{i\rightarrow\infty}\langle r_i|e_n\rangle \Bigr)$$((10.10))for some and thus any joint labeling e of \((r_i)_{i\geq 1}\).
-
(ii)
Every directed subset of Ω n contains an increasing sequence with the same supremum.
Proof
By Lemma 22 there exists a joint labeling e for \((r_i)_{i\geq 1}\) and thus by Definition 32 it follows that \(\left(\mathsf{spec}(r_i|e)\right)_{i\geq 1}\) is an increasing sequence in Δ n. Then by Proposition 2 we know that the pointwise limit
exists. We define a state r implicitly via
We first show that this state r is independent on the choice of e. Since
where we leave the proof of the first equality to the reader (straightforward verification via the inductive definition of \(\mathcal{D}_{(r_i)}\)), so
Note that by \(\bigcup\mathcal{D}_{(r_i)}=\bigcap_i\bigcup\mathcal{D}_{r_i}\) it also follows that for any joint labeling e of \((r_i)_{i\geq 1}\), since
we have \(\bigcup\mathcal{D}_e\subseteq\bigcup\mathcal{D}_{(r_i)}\), that is, \(\bigcup\mathcal{D}_{(r_i)}\) contains all joint labelings of \((r_i)_{i\geq 1}\) (and only those, so it is maximal with respect to this property).
If e is a joint labeling of \((r_i)_{i\geq 1}\) and \(\bigcap_i r_{i,\lambda_i}\not=\emptyset\), where
then there exists some \(e_j\in\mathcal{D}_e\) such that \(e_j\subseteq \bigcap_i r_{i,\lambda_i}\) for which we have
Since \(\lim_{i\rightarrow\infty}\langle {r_i}|e_j\rangle\) exists, \(\lim_{i\rightarrow\infty}\lambda_i\) exists and is equal to it. However, \((\lambda_i)_{i\geq 1}\) does not depend on any labeling so neither does its limit \(\lim_{i\rightarrow\infty}\lambda_i\). can define r now as follows without any reference to a labeling:
Next we prove that r is an upper bound of \((r_i)_{i\geq 1}\). By Proposition 2 we have
so for all \(i\geq 1\) we have \(\mathsf{spec}(r_i|e)\sqsubseteq\mathsf{spec}(r|e)\) and thus by definition of the order on quantum states it follows that \(r_i\sqsubseteq r\) for all \(i\geq 1\).
We now show that r is the least upper bound of \((r_i)_{i\geq 1}\). Let s be any upper bound of the sequence \((r_i)_{i\geq 1}\), i.e., for all \(i\geq 1\), \(r_i\sqsubseteq s\). We now prove that \(r\sqsubseteq s\). By the proof of Lemma 22 we know that there exists a finite subsequence of \((r_i)_{i\geq 1}\) (of which we can assume that it has n members) which yields the same common refinement of \((r_i)_{i\geq 1}\) for the given construction—since there are only \(n-1\) refinement steps possible. Denote this finite subsequence by \((r_{i_j})_{j=1}^{j=n}\). Then, since
they admit a common refinement and thus a common labeling e, which is also a common labeling for the whole sequence \((r_i)\), and which we can assume to be the one by means of which we defined r since the definition of r does not depend on the choice of labeling. In this labeling we then have for each \(i\geq 1\) that
in Δ n since for all \(i\geq 1\) we have \(\mathsf{spec}(r_i|e)\sqsubseteq\mathsf{spec}(s|e)\). Thus \(r\sqsubseteq s\) by definition of the order on quantum states.
We conclude \(r=\bigsqcup_{i\geq 1}r_i\) from which Eq. (10.10) then follows.
(ii) The map \(\varOmega^n\rightarrow[0,1]::r\mapsto \max(\mathsf{spec}(r))\) preserves suprema of increasing sequences and is strictly monotone.
Thus, we can think of \(\mathsf{spec}(\cdot|\cdot)\) as being Scott continuous in its first argument: For any observable e,
whenever \((r_i)\) is an increasing sequence in Ω n.
3.3 Symmetries for Quantum States
We introduce symmetries, the quantum analogue of permutations for classical states.
Definition 33
A unitary transformation is a surjective linear operator \(U:\mathcal{H}^n\to\mathcal{H}^n\) which preserves angles:
for all \(\psi,\phi\in\mathcal{H}^n\). U is called a quantum n-symmetry.
In particular, the inverse \(U^{-1}\) of a unitary operator U is unitary.
Lemma 23
Let U be a quantum symmetry on \(\mathcal{H}^n\). For any labeling e,
is a labeling, while for any state r,
is a state with \(\mathsf{spec}(U\cdot r)=\mathsf{spec}(r)\).
In both cases only the action of U on subspaces comes into play. Thus, two unitary operators U and \(U'\) related by \(U=re^{i\theta}\cdot U'\) with \(r>0\) and \(\theta\in[0,2\pi)\) should be thought of as equivalent. The linearity of the maps, in conjuction with the coincidence of the action of U and U′ on subspaces does force them to essentially be the same [4], e.g. \(\mathsf{span}(e^{i\theta}\psi)=\mathsf{span}(\psi)\), though for \(\psi\not=\phi\) and both nonzero we find \({\mathsf{span}(\phi+e^{i\theta}\psi)\not=\mathsf{span}(\phi+\psi)}\) for \(\theta\not=0\). Thus, a quantum n-symmetry should be conceived of as a class of unitary operators on \(\mathcal{H}^n\) with equivalent action on subspaces. We will freely represent such a class by one of its representatives.
Lemma 24
For a state r and a labeling e with \([r,e]=0\),
Proof
First note that
and
Next, following Eq. (10.3) we have
which completes the proof.
Now we give a symmetric characterization of the spectral order analogous to the symmetric characterization of the Bayesian order on classical states. Equation (10.11) leads us to the following dual formulations, which we call the active and passive (cfr. active and passive transformations in classical mechanics are those acting on the system and the reference frame, respectively). We assume for both theorems that a labeling e has been fixed in advance.
Theorem 8 (Active)
For \(r,s \in\varOmega^n\), we have \(r\sqsubseteq s\) iff there exists a quantum symmetry \(U:\mathcal{H}^n\rightarrow\mathcal{H}^n\) such that
-
\(\mathsf{spec}(U\cdot r|e)\) and \(\,\mathsf{spec}(U\cdot s|e)\) are monotone
-
\([r,e]=[s,e]=0\)
and
for all i with \(1\leq i <n\).
Theorem 9 (Passive)
For \(r,s \in\varOmega^n\), we have \(r\sqsubseteq s\) iff there exists a quantum symmetry \(U:\mathcal{H}^n\rightarrow\mathcal{H}^n\) such that
-
\(\mathsf{spec}(r|\,U\cdot e)\) and \(\mathsf{spec}(s|\,U\cdot e)\) are monotone
-
\([r,U\cdot e]=[s,U\cdot e]=0\)
and
for all i with \(1\leq i <n\).
Proof
Any labeling e′ can be obtained from a given one e as \(U\cdot e\) for some unitary transformation U. Indeed, in terms of linear operators this correspondence translates as \(e'=U\circ e\circ U^{-1}\) so \(e\cdot\psi=i\,\psi\) iff \(e'\cdot U(\psi)=i\,U(\psi)\), that is, \(\psi\in e_i\Leftrightarrow U(\psi)\in e_i'\) yielding the definition of \(U\cdot e\) in terms of labelings. The result then straightforwardly follows from Theorem 3 and Lemma 24.
The following is now merely an observation.
Proposition 13
The map \((U\cdot-):\varOmega^n\to\varOmega^n\) is an order isomorphism for any quantum symmetry \(U:\mathcal{H}^n\rightarrow\mathcal{H}^n\).
Theorem 8 is the quantum counterpart of Theorem 3 for classical states: The action on states \((U\cdot-):\varOmega^n\to\varOmega^n\) in terms of a unitary transformation U corresponds to the action on states \((-\cdot\sigma):\varDelta^n\to\varDelta^n\) in terms of a permutation σ. But what is the classical analogue of the passive formulation of the spectral order?
Definition 34
A classical labeling is an injective function
The standard labeling is 1 defined by \(1(i)=e_i\).
Like the quantum case, we can write a classical state x from the point of view of a classical labeling e as
where \(\langle\cdot|\cdot\rangle\) is the standard inner product on \({\mathbb R}^n\). For \(e=1\), \(\mathsf{spec}(x|1)=x\). Notice too that \(\langle e_i|e_j\rangle=0\) for \(i\neq j\), so the image of a classical labeling e is by definition a mutually orthogonal collection of pure states.
A classical labeling e induces a permutation \(1^{-1}\circ e\in S(n)\). Thus, a classical labeling is merely a way of rearranging a fixed set of n orthogonal pure states \(\max(\varDelta^n)\). By contrast, a quantum labeling corresponds to selecting n orthogonal pure states from an infinite set of potential pure states and arranging the n pure states chosen.
Because classical labelings and symmetries are essentially the same, Theorem 3 is the passive formulation of the Bayesian order when we fix the standard classical label 1 as our reference frame. All other classical labels e can be written as \(e=1\circ\sigma\) for some \(\sigma\in S(n)\), analogous to the quantum case. To summarize:

The equivalence of “symmetry” and “labeling” for classical states suggests the following analogy: Symmetries are to classical states as labelings are to quantum states. Though this is not entirely conceptually satisfying, it is a useful mathematical view of things. To illustrate, notice the strong resemblance between the following characterization of the spectral order, in terms of labels, and the symmetric characterization of the Bayesian order.
Theorem 10
For \(r,s \in\varOmega^n\), we have \(r\sqsubseteq s\) iff there is a quantum labeling e such that
-
\(\mathsf{spec}(r|e)\) and \(\,\mathsf{spec}(s|e)\) are monotone
-
\([r,e]=[s,e]=0\)
and
for all i with \(1\leq i <n\).
Compared to Theorem 8 and Theorem 9, in this result it is the act of labeling itself that transforms a state into a monotone classical state. In the classical case, it is obviously a permuation (classical label) which converts a state to monotone form.
As a second example, first recall that the symmetric group \(S(n)\) divides Δ n into order isomorphic regions,
where \(\varDelta^n_\sigma\simeq\varLambda^n\). Similarly, quantum states are divided into order isomorphic regions by the class of measurement operators:
where \(\varOmega^n|e:=\{r\in\varOmega^n:[r,e]=0\}\), i.e., the set of quantum states admitted by measurement e. Here is the quantum version of Proposition 4.
Proposition 14
Let \(n\geq 2\). Then
-
(i)
For each labeling e, \(\varOmega^n|e\) is closed under directed suprema.
-
(ii)
For an increasing sequence \((r_i)\), there is a labeling e with \(r_i\in\varOmega^n|e\) for all i.
-
(iii)
The natural map
$$q:\varOmega^n\rightarrow\varLambda^n$$is Scott continuous, strictly monotone and restricts to a retraction
$$r_e:\varOmega^n|e\simeq\varDelta^n\rightarrow\varLambda^n$$for each e.
Proof
The precise definition of q is as follows: For \(s\in\varOmega|e\), we define \(q(s):=r(\mathsf{spec}(s|e))\), where \(r:\varDelta^n\rightarrow\varLambda^n\) is the natural retraction.
In particular, the Bayesian order on classical states is an instance of the spectral order on quantum states, which is realized whenever we specify a labeling e. It may interest the reader to know that both authors claim that \(q:\varOmega^n\rightarrow\varLambda^n\) cannot be factored into a composition of monotone maps
where \(?:\varOmega^n\rightarrow\varDelta^n\) denotes a monotone map that probably doesn’t exist.
3.4 Approximation of Quantum States
Like classical states, the ability to approximate quantum states order theoretically is a consequence of the mixing law.
Proposition 15
If \(r\sqsubseteq s\) in Ω n, then
for all \(p\in[0,1]\).
Proof
First, \((1-p)r+ps\) is a density operator. Because \(r\sqsubseteq s\), there is a labeling e with \([r,e]=[s,e]=0\). Then
Next,
because \((1-p)r+ps\), r and s are diagonal when written in the base e. The result now follows from the mixing law for classical states.
Like the classical case, the mixing law is equivalent to saying that the path \(\pi_{rs}:[0,1]\rightarrow\varOmega^n\) from r to s given by
is Scott continuous iff \(r\sqsubseteq s\).
Lemma 25
If \(r\sqsubseteq s\) in Ω n and \(\mathsf{spec}(s)\subseteq(0,\infty)\), then
for any labeling e.
Proof
First recall that \([s,e]=0\) means that \(\mathcal{D}_e\) is a refinement of \(\mathcal{D}_s\). But the spectrum of s is positive, so Lemma 21 implies that \(\mathcal{D}_s\) is a refinement of \(\mathcal{D}_r\). Thus, \(\mathcal{D}_e\) is a refinement of \(\mathcal{D}_r\), which means \([r,e]=0\).
The last result is the quantum analogue of Lemma 12(i) for classical states. The next few results further demonstrate the parallel between \(\varDelta^n_\sigma\) for classical states and \(\varOmega^n|e\) for quantum states.
Proposition 16
Let \(n\geq 2\).
-
(i)
If \(r,s\in\varOmega^n|e\), then \(\pi_{rs}(t)\in\varOmega^n|e\) for all \(t\in[0,1]\).
-
(ii)
For \(r,s\in\varOmega^n\), we have \(r\ll s\) iff for any labeling e, if \(s\in\varOmega^n|e\), then \(r\in\varOmega^n|e\) and \(\mathsf{spec}(r|e)\ll\mathsf{spec}(s|e)\) in Δ n.
Proof
(i) This was established in the proof of the mixing law.
(ii) \((\Rightarrow)\) Let \(r\ll s\). Then for some \(t<1\), \(r\sqsubseteq\pi_{\bot s}(t)\). If \([s,e]=0\), then by (i), \([\pi_{\bot s}(t),e]=0\) for all t, since we always have \([\bot,e]=0\). However, because \(t<1\), the spectrum of \(\pi_{\bot s}(t)\) is positive, which is clear since
By Lemma 25, \([r,e]=0\). The other part is obvious.
(ii)\((\Leftarrow)\) Suppose \(s=\bigsqcup s_i\) for an increasing sequence \((s_i)\). Then there is a labeling e with \([s_i,e]=0\) for all i and \([s,e]=0\). By assumption, \([r,e]=0\), and since
we have \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(s_i|e)\) for some i, and hence \(r\sqsubseteq s_i\). Thus, \(r\ll s\).
Ω n is a domain: A dcpo with an intrinsic notion of approximation.
Theorem 11
The quantum states Ω n are exact. In addition,
-
(i)
For all \(r\in\varOmega^n\), \(\pi_{\bot r}(t)\ll r\) for all \(t <1\).
-
(ii)]
The approximation relation ≪ is interpolative: If \(r\ll s\) in Ω n, then there is \(q\in\varOmega^n\) with \(r\ll q\ll s\).
Proof
(i) By Prop. 16(i), \([\pi_{\bot r}(t),e]=0\) whenever \([r,e]=0\). Since
Proposition 16 (ii) gives \(\pi_{\bot r}(t)\ll r\) for all \(t <1\).
The map \(\pi_{\bot r}\) is Scott continuous, so r is the supremum of an increasing sequence of approximations. This implies that \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{-.4ex} {\(\downarrow\)}}\(\downarrow\)}}} r\) is directed with supremum r, proving the exactness of Ω n.
(ii) Mimic the argument for classical states to show \(\pi_{\bot r}(t_1)\ll\pi_{\bot r}(t_2)\) whenever \(t_1 <t_2\).
The notion of partiality derivable from ≪ on Ω n is worth taking a brief look at. As before, we call \(r\in\varOmega^n\) partial iff \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} r\neq\emptyset\).
Lemma 26 (Partiality)
For \(r\in\varOmega^n\), the set \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} r\neq\emptyset\) iff \(\mathsf{spec(r)}\subseteq(0,\infty)\).
Proof
The only direction which requires proof is \((\Leftarrow)\). Let e be a labeling with \([r,e]=0\). Let \(x:=\mathsf{spec}(r|e)\in\varDelta^n\). From the proof of Lemma 13 for classical states, there is \(y\in\varDelta^n\) such that \(\pi_{\bot y}(t)=x\) for some \(t <1\).
Let \(s\in\varOmega^n\) with \([s,e]=0\) and \(\mathsf{spec}(s|e)=y\). First, \(\pi_{\bot s}(t)=r\), since \(\pi_{\bot s}(t),r\in\varOmega^n|e\) and
Because \(t <1\), \(r=\pi_{\bot s}(t)\ll s\) in Ω n.
Thus, a quantum state which is partial cannot be pure. In addition, by exactness, all quantum states r arise as the supremum of an increasing sequence
of partial states which approximate r.
Lemma 27
(Approximation of pure states) Let \(n\geq 2\) and \(\psi\in\max(\varOmega^n)\) be a pure state. For all \(r\in\varOmega^n\), \(r\ll \psi\Leftrightarrow r=\pi_{\bot\psi}(t)\) for some \(t <1\).
Proof
Let \(r\ll\psi\). Let e be any labeling with \([\psi,e]=0\). Then \([r,e]=0\) and
Thus, by Prop. 7,
But \(\pi_{\bot\psi}(t)\in\varOmega^n|e\) and \(\mathsf{spec}(\pi_{\bot\psi}(t)|e) = \pi_{\bot y}(t)=x=\mathsf{spec}(r|e),\) so \(r=\pi_{\bot\psi}(t)\), since each is diagonal in e and their spectra are equal.
Thus, the order theoretic approximations of pure states ψ are precisely the mixtures of ψ with the completely mixed ensemble ⊥.
Example 9
The depolarization channel \(d_p:\varOmega^n\rightarrow\varOmega^n\) describes the process by which the density operator of a system has all bias removed from it with probability p
It can be rewritten as
very similar to the classical case we considered earlier. Just as in the classical case, we also have \(d_p(r)\ll r\) for \(p>0\).
3.5 Entropy
The word “measurement” is used in domain theory and in quantum mechanics. They are related as follows: Domain theoretically, to measure the content of an object x, we must do something to x that will convert the information it represents into a simpler form μ x that can be understood. Physically, as it turns out, the content of a quantum state r can be measured by selecting an appropriate quantum measurement e that converts r into a monotone classical state \(\mathsf{spec}(r|e)\). (We might think of e as a way of extracting classical information from r.) This defines the map
completely analogous to \(r:\varDelta^n\rightarrow\varLambda^n\) for classical states, which is a measurement in the sense of domain theory.
Proposition 17
The map \(q:\varOmega^n\rightarrow\varLambda^n\) is a measurement.
Proof
First, q is Scott continuous, strictly monotone, and preserves and reflects maximal elements. To show that it measures \(\ker q=\max(\varOmega^n)\), let \(\psi\in\varOmega^n\) and \(U\subseteq\varOmega^n\) be Scott open with \(\psi\in U\).
Then there is \(0 <t<1\) with \(a:=\pi_{\bot\psi}(t)\in U\). Because \(a\ll\psi\) in Ω n, \({q(a)\ll q(\psi)}\) in Λ n, which means \(\varepsilon:={\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} q(a)\) is a Scott open subset of Λ n. We claim that \({\psi\in q_\varepsilon(\psi)\subseteq\,\uparrow\!\!a\subseteq U}\). That \(\psi\in q_\varepsilon(\psi)\) is clear.
Now let \(s\in q_\varepsilon(\psi)\). Then there is a labeling e with \([s,e]=[\psi,e]=0\). Because \(a\ll\psi\), we must have \([a,e]=0\). But we also know
where \(r:\varDelta^n\rightarrow\varLambda^n\) is the natural retraction. Now the proof that r is a measurement gives
which implies that \(a\sqsubseteq s\), and thus \(s\in U\), finishing the proof.
In particular, we can measure the content of a quantum state with a classical state.
Example 10
The content of a density operator ρ can also be measured with its largest eigenvalue,
This is a measurement into \([0,1]\) since it factors as \(q(\rho)^+\). Similarly,
and
are measurements into \([0,\infty)^{\ast}\).
The measures of content in the last example are the quantum versions of the maps \(x\mapsto x^+\), \(x\mapsto 1-x^+\) and \(x\mapsto-\log x^+\) on classical states. The extension of Shannon entropy to quantum states is called von Neumann entropy.
Theorem 12
Let \(\sigma:\varOmega^n\rightarrow[0,\infty)^{\ast}\) be the von Neumann entropy on quantum states
where the logarithm is natural. Then σ is a measurement in the sense of domain theory. In addition,
-
(i)
For all \(r,s\in\varOmega^n\), if \(r\sqsubseteq s\) and \(\sigma(r)=\sigma(s),\) then \(r=s\).
-
(ii)
For all \(r\in\varOmega^n\), we have \(\sigma(r)=0\) iff \(r\in\max(\varOmega^n)=\varSigma^n\).
-
(iii)
For all \(r\in\varOmega^n\), we have \(\sigma(r)=\log n\) iff \(r=\bot\).
Proof
The von Neumann entropy σ factors as
where \(q:\varOmega^n\rightarrow\varLambda^n\) assigns to a quantum state its monotone spectrum, and \({\mu:\varLambda^n\rightarrow[0,\infty)^{\ast}}\) is Shannon entropy. Since q and μ have all the properties mentioned in this result, so does σ.
By now it is clear that quantum information is more intricate than classical information, if for no other reason than the superficial observation that a density operator is “more complicated” than a classical state. What we now want is a precise formulation of the intuitive idea that there is more information in the quantum than in the classical.
One hint is provided by Proposition 14: We can associate each classical state to a quantum state in such a way that information is conserved:
And this is what we now prove: While each classical state can be associated to a quantum state in such a way that information is conserved, the converse is never true.
Theorem 13
Let \(n\geq 2\). Then
-
There is an order embedding \(\phi:\varDelta^n\rightarrow\varOmega^n\) such that \(\sigma\circ\phi=\mu\).
-
For \(m\geq 2\), there is no order embedding \(\phi:\varOmega^n\rightarrow\varDelta^m\) with \(\mu\circ\phi=\sigma\).
Proof
For the first, Proposition 14 gives an embedding which preserves entropy. For the second, if there is an embedding of Ω n into Δ m which preserves entropy, it yields an injection of \(\max(\varOmega^n)\) into \(\max(\varDelta^m)\), which is impossible since the first of these sets is infinite, while the latter is finite.
The reader may be interested to know that the authors both claim that the above result holds independent of entropic considerations.
4 Synthesis
We now obtain a unified perspective on classical and quantum which leads to a methodology applicable in any setting where one has (i) a notion of state and (ii) a notion of state update as the result of observation.
4.1 Classical Projections
We first turn back to classical states to show that they admit a more general class of projectors and that the inductive definition of the Bayesian order extends to this larger class. First note that a classical projection
is undefined in the singleton
and has as “fixed points”
Any projection p i moreover has a complementary projector, namely
which is undefined in
This projector expresses the update that the observer experiences when he looks in box i and the object of his desire is actually there. Equivalently, this corresponds to looking in all boxes except box i and not finding the object. The condition
is however trivially satisfied whenever \(p_i^\perp\) is defined both in x and y. As such, one could have included it in Definition 2.7 providing an interpretation “whatever outcome we obtain when looking in box i, the corresponding collapse of knowledge preserves the partial order”.
We define general projectors, encoding knowledge update when looking in several boxes at once. Let \(n\geq 2\) and \(1\leq k\leq n\). The map which collapses all \(i_1,\ldots,i_k^\textit{th}\) outcomes is
for \(1\leq i_1,\ldots,i_k\leq n\) and \(0\leq{x_{i_1}},\ldots,{x_{i_j}},\ldots,{x_{i_k}} <1\). The projector corresponding to “looking in all boxes except” is
for \(1\leq i_1,\ldots,i_k\leq n\).
The set of projectors as defined constitute a Boolen algebra isomorphic to the powerset \(\mathcal{P}(\{1,\ldots, n\})\) when we adjoin the empty map
and the identity
In particular we have
that is, projections inherit orthogonality from the complementation of the Boolean algebra \(\mathcal{P}(\{1,\ldots, n\})\).
Proposition 18
Let \(x,y\in\varDelta^{n+1}\). Then
Proof
Given \(p_i:\varDelta^{n}\rightharpoonup\varDelta^{n-1}\) define \(\tilde{p}_i:\varDelta^{n}\rightharpoonup\varDelta^{n}\) via
where
Analogously we introduce the map
where
when assuming that \(i_1,\ldots,i_k\) is monotone and formally setting \(i_0=0\) and \(i_{k+1}=n+1\). We then have
from which the result follows by induction.
Clearly, we rely on the following.
Proposition 19
Projections commute with respect to composition
In particular, the Boolean algebra of projections is defined from concatenated action of projections
where \(\tilde{p}\) and \(\tilde{q}\) are defined as in the proof of Proposition 18.
4.2 Quantum Projections
We now show that the projective structure of classical states and its corresponding inductive definition of the Bayesian order are preserved by the natural embeddings of Δ n into Ω n. In particular, the classical projections become instances of Hilbert space projectors.
The Hilbert space projectors \({\Bbb P}^n\) also constitute an orthocomplemented lattice for the partial order
This lattice is however no longer distributive, e.g. [2, 3], and as such is not a Boolean algebra. Related to this, commutativity for projections as we have in Proposition 19 is not valid anymore for Hilbert space projectors.
Analogous to the introduction of \(\tilde{p}\) given p in order to be able to compose projections, we now will have to do the converse for Hilbert space projectors in order to state an inductive definition of the partial ordering ofthe quantum states.
Any projector \(P\in{\Bbb P}^n\) can be equivalently represented as a partial surjective map
which is undefined in \(\mathsf{fix}(P)^\perp\). When an isomorphism
is specified, with \(0\leq k=\mathsf{dim}(\mathsf{fix}(P))\leq n\), we can define
of which the codomain does not depend on P anymore.
Note that such a map \(P^\downarrow\) as well as P itself is fully characterized by its kernel, thus these maps are in bijective correspondence with the subspaces \({\Bbb L}^n\) via
and also with \(\{0,1\}\)-labeled decompositions, or equivalently, two element ordered decompositions, via
Abstracting over the \(\{0,1\}\)-labeling we set
Proposition 20
The following are equivalent for state r and projector P:
-
They admit joint labeling e.
-
\(\mathcal{D}_{r}\) and \(\mathcal{D}_P\) admit a joint refinement \(\mathcal{D}\).
-
They diagonalize in a common base B.
-
\([{r},P]=0\).
The following are equivalent for states r and s and projector P:
-
They admit joint labeling e, i.e., \(\mathcal{D}_{r}\), \(\mathcal{D}_{s}\) and \(\mathcal{D}_P\) admit a joint refinement \(\mathcal{D}\), i.e., they diagonalize in a common base B.
-
They pairwise admit joint labeling, i.e., \(\mathcal{D}_{r}\), \(\mathcal{D}_{s}\) and \(\mathcal{D}_P\) pairwise admit joint refinement, i.e., they pairwise diagonalize in a common base.
-
\([{r},P]=[{s},P]=[{r},{s}]=0\).
Proof
Equivalence of the first four conditions follows from Proposition 10 since P is a state up to normaliztion, that is,
Given a joint refinement \(\mathcal{D}\) for r,s and P any labeling e such that \(\bigcup\mathcal{D}_e=\bigcup\mathcal{D}\) is a joint labeling, and a base \(B\in\bigcup\mathcal{D}_e\) yields joint diagonalization. At its turn, given a base B in which r,s and P diagonalize then
is a joint refinement.
Whenever we have a joint refinement, a joint labeling or a joint base for s, t and P then we have pairwise existence of one too. For the converse statement we provide a proof. We are going to prove a more general statement however, namely, that whenever we have a set of decompositions \(\{\mathcal{D}_i\mid i\in I\}\), for technical simplicity envisioned as being finite, and such that for all \(i,j\in I\) we have that \(\mathcal{D}_i\) and \(\mathcal{D}_j\) admits a joint refinement, then \(\{\mathcal{D}_i\mid i\in I\}\) as a whole admits one. (This fact is implied by well-known results in the study of quantum structures [2, 3, 7, 13], though the terminology there is different from ours. For the sake of a self-contained discussion, we provide a complete proof.)
We call \(a,b\in{\Bbb L}^n\) compatible, denoted \(a\leftrightarrow b\), iff \(\{a,a^\perp\}\) and \(\{b,b^\perp\}\) admit joint refinement—in lattice terms this means that they generate a subalgebra of \({\Bbb L}^n\) which is Boolean [3]. Then we have that
Indeed, existence of a joint refinement for \(\{a,a^\perp\}\) and \(\{b,b^\perp\}\) implies
and since
are subspaces of \(\mathcal{H}^n\) this forces Eq. (10.12).
The fact that each \(\mathcal{D}_i\) is a decomposition, implying mutual orthogonality of its members, and that we have pairwise existence of a joint refinement for all decompositions in \(\{\mathcal{D}_i\mid i\in I\}\), implies that
We will now construct a joint refinement inductively, that is, we build a series \((d_i)\) containing all elements of \(\bigcup\{\mathcal{D}_i\mid i\in I\}\) and construct a joint refinement \(\mathcal{E}_{k+1}\)for \((d_1,\ldots,d_{k+1})\) given a joint refinement \(\mathcal{E}_k\) for \((d_1,\ldots,d_k)\), taking as base case \({\mathcal{E}_1:=\{d_1,d_1^\perp\}}\). Set
It clearly follows that \(\bigcup\mathcal{E}_{k+1}\subseteq\bigcup\mathcal{E}_{k}\) so we obtain a decreasing sequence.
We then also have that
-
\(\mathsf{span}(\mathcal{E}_1)=\mathcal{H}^n\), and,
-
\(\mathsf{span}(\mathcal{E}_{k+1}) =\mathsf{span}\left(\{a\cap d_{k+1},a\cap d_{k+1}^\perp\mid a\in\mathcal{E}_k\}\right) =\mathsf{span}\left(\mathcal{E}_k\right)\)
due to Eq. (10.12), what proves that the inductive procedure preserves spanning \(\mathcal{H}^n\). Mutual orthogonality of the elements in \(\mathcal{E}_{k+1}\) also follows construction.
It remains to be proven that
for all \(i\in I\). Let \(\#(d_i)\) be the length of \((d_i)\). From the construction it follows that the elements of \(\mathcal{E}_{\#(d_i)}\) are of the form \(a_1\cap\ldots\cap a_{\#(d_i)}\) where \(a_j\in\{d_j,d_j^\perp\}\). For every \(\mathcal{D}_i\) there is a subsequence of elements \(a_{i_j}\) such that \(d_{i_j}\in\mathcal{D}_i\). Let \(a_{i_1}\cap\ldots\cap a_{i_{\#\mathcal{D}_i}}\) be the corresponding subterm. We claim that the only non-empty such terms are those for which there is exactly one \(1\leq j\leq\#\mathcal{D}_i\) such that \(a_{i_j}=d_{i_j}\) and for all others \(k\not=j\) we have \(a_{i_j}=d_{i_k}^\perp\). That there is at most one follows from the fact that the elements in \(\mathcal{D}_i\) are mutually orthogonal. That there is necessarily one follows from the fact that we otherwise have \(d_{i_1}^\perp\cap\ldots\cap d_{i_{\#\mathcal{D}_i}}^\perp\) as this subterm what implies that any vector contained in it should be orthogonal to all \(d_{i_j}\in\mathcal{D}_i\), what is impossible since \(\mathcal{D}_i\) spans \(\mathcal{H}^n\). So every subterm \(a_{i_1}\cap\ldots\cap a_{i_{\#\mathcal{D}_i}}\) and thus also every term \(a_1\cap\ldots\cap a_{\#(d_i)}\) contains \(d_{i_j}\in\mathcal{D}_i\) and thus
so
for all \(i\in I\) what completes the proof.
It is well-known that projectors on \(\mathcal{H}^n\) induce maps on Ω n in terms of Luders’ rule [11], that is
for \(\mathsf{tr}(P\cdot r)>0\). Note that \(P:\varOmega^n\rightharpoonup\varOmega^n\) is still idempotent since
so we can set
Given an isomorphism
with \(0\leq k=\mathsf{dim}(\mathsf{fix}(P))\leq n\), and possibly induced by an isomorphism h on the underlying Hilbert spaces, we can define a map
This will be of our view of projectors in this section, except for an additional extension of the kernel to those density matrices that do not commute with P.
-
By a projector \(P^\downarrow[-]:\varOmega^n\rightharpoonup\varOmega^k\) we refer to the partial map induced by \(P\in{\Bbb P}^n\) which has as kernel those states \(x\in\varOmega^n\) which are such that either
-
\(\mathsf{tr}(P\cdot x)=0\)
-
\([x,P]\not=0\)
and with the images defined by Eq. (10.13).
-
When writing down \(P^\downarrow[-]\) we as such assume that an isomorphism h, or equivalently, g has been specified.
We introduce some dialectics analogous to that of labelings.
-
A state r admits a projector \(P^\downarrow[-]\) iff \(P^\downarrow[\,r\,]\) is defined.
Then by Proposition 20 P and r admit joint labeling.
Let \({\Bbb I}(k,n)\) be the collection of monotone maps of the form
for \(0\leq k\leq n\), where the monotonicity is with respect to the usual order on natural numbers, and let
Let
be the partial inverse for any given ι and let \({\Bbb P}^n|e\) be the projectors \(P\in{\Bbb P}^n\) that admit a given labeling e, that is,
Lemma 28
Given a labeling e of \(\mathcal{H}^n\) then \({\Bbb P}^n|e\,\cong\,{\Bbb I}^n\,\).
Proof
Given \(I\subseteq\{1,\ldots,n\}\) define \(\iota\in{\Bbb I}^n\) such that I is its range. It then follows that
via \(I\mapsto\iota\) due to monotonicity of ι.
We moreover have that \(P\in{\Bbb P}^n|e\) iff \(\bigcup\mathcal{D}_e\subseteq\bigcup\{\mathsf{fix}(P),\mathsf{fix}(P)^\perp\}\) iff there exists \({I_P\subseteq\{1,\ldots,n\}}\) such that \(e_i\in\mathsf{fix}(P)\Leftrightarrow i\in I_P\), and thus we have \({\Bbb P}^n|e\,\cong\,\mathcal{P}(\{1,\ldots,n\})\) via \(P\mapsto I_P\).
In Proposition 18, we characterized the Bayesian order in terms of projections. Here is the formulation for the spectral order in terms of quantum projections.
Theorem 14
Let \(n\geq 2\). For \(r,s\in\varOmega^n\), we have
-
for all projectors \(P^\downarrow[-]\) admitting both r and s, and,
-
provided there are enough projectors admitting both r and s,
where we adopt the base cases
-
\(\varOmega^0:=\emptyset\);
-
\(\varOmega^1:=\{(1)\}\) with \((1)\sqsubseteq(1)\) ;
-
For \(r,s\in\varOmega^2\) we have \(r\sqsubseteq s\) iff there exist \(p,q\in[0,1]\) with \(p\leq q\) and a pure state \(t\in\varSigma^n\) such that
$$r=(1-p)\bot +p t \quad s=(1-q)\bot +q t\,,$$with
$$\bot:=\left(\begin{array}{cc} \frac{1}{2}&0\\0&\frac{1}{2} \end{array}\right)\,.$$
Proof
Any self-adjoint operator on \(\mathcal{H}^2\) either has a non-degenerated spectrum or is ⊥. Excluding the latter case, given \(r\in\varOmega^2\) there exists a unique labeling e (up to permutation of the labels) such that r admits e. This labeling is obtained by setting \(e_1=r_+\) and \(e_2=r_+^\perp\), where \(r_+\) are the eigenvectors for eigenvalue \(\mathsf{max}(\mathsf{spec}(r))\). In view of Definition 32, it then follows that if e is admitted both by r and s and \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(s|e)\) then
with \(s_+=r_+\) is necessary and sufficient for \(r\sqsubseteq s\). Defining \(p,q\in[0,1]\) by
and the pure state \(t\in\varOmega^n\) such that \(t_1=e_1\) we obtain
what encodes \(s_+=r_+\) and \(\langle{r}|e_1\rangle\leq\langle{s}|e_1\rangle\) provided that \(p\leq q\).
Let \(r\sqsubseteq s\) according to Definition 32. We need to prove that r and s admit enough projectors and that they satisfy Eq. (10.14) with respect to those admitted. So let us first define what we mean by enough projectors.
We mean by this having at least enough to consitute a family of mutually orthogonal projectors \(\{P^i_e\mid 1\leq i\leq n\}\) that support the spectral decomposition of a labeling
One verifies that this is equivalent to saying that there exists a family of mutually orthogonal projectors \(\{P_i\mid 1\leq i\leq n\}\) such that \(\bigcap_i\bigcup\mathcal{D}_{P_i}\) is the decomposition of some labeling e. It is moreover not restrictive to assume that for all i we have \(\mathsf{dim}(\mathsf{fix}(P_i))=n-1\).
Since \(r\sqsubseteq s\) they admit a joint labeling e that admits projectors \({\Bbb P}^n|e\), among which we have those defined by \(\mathsf{fix}(P_i)=e_i\). Then \(\mathcal{D}_e=\bigcap_i\bigcup\mathcal{D}_{P_i}\) so r and s admit enough projectors.
We now show that \(r\sqsubseteq s\) implies \(P^\downarrow[\,r\,]\sqsubseteq P^\downarrow[\,s\,]\) provided \(P^\downarrow[-]\) is admitted both by r and s. By Proposition 20 we have, since there exists a pairwise common refinement for r, s and P, that they all together admit a joint labeling e for which we then moreover have \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(s|e)\in\varDelta^n\). Let
and set \(I^\perp_P:=\{0,\ldots,1\}\setminus I_P\). By Proposition 18 we then have that
Let \(\iota\in {\Bbb I}(k,n)\) with \(k=\mathsf{dim}(\mathsf{fix}(P))\) such that it range coincides with I P . Next, given any isomorphism \(h:\mathsf{fix}(P)\to\mathcal{H}^k\), and thus also a corresponding one on states
choose a labeling \((e'_i)\) of \(\mathcal{H}^k\) such that \(h(e_{\iota(i)})=e_{i}'\)—we slightly abusively refer to a base vector by the subspace of the labeling in which it is contained. We obtain commutation of the following maps

where \(\tilde{h}:{\Bbb L}^n\rightharpoonup{\Bbb L}^k\) is here the partial surjective map arising when \(h:\mathsf{fix}(P)\to\mathcal{H}^k\) is applied pointwisely to those one-dimensional \(a\in{\Bbb L}^n\) which are such that \(a\subseteq\mathsf{fix}(P)\). Indeed, we have
Since due to \(\bigcup\mathcal{D}_e\subseteq\bigcup\mathcal{D}_P\) we have
It then follows that
so
and thus
We then conclude \(P^\downarrow (r)\sqsubseteq P^\downarrow (s)\).
Conversely, assume that there exists mutually orthogonal projectors \({\{P_i\mid 1\leq i\leq n\}}\) such that \(\bigcap_i\bigcup\mathcal{D}_{P_i}\) is the decomposition of some labeling e and for which we have \({P^\downarrow[\,r\,]_i\sqsubseteq P^\downarrow[\,s\,]_i}\). Since r and s are admitted by all P i we have by the proof of Proposition 20 that there exists a joint labeling for r and s and all P i , which as such can only be e itself due to \(\mathcal{D}_e=\bigcap_i\bigcup\mathcal{D}_{P_i}\). By constructing the isomorphisms
for each projector P i such that we have commutation of

taking into account the isomorphisms \(g_i:\mathsf{fix}(P_i[-])\to\varOmega^k\) that are different for each P i , we can embed the quantum case for projectors P i and states r and s that admit a fixed labeling e in the classical one with projectors p i . Then \(r\sqsubseteq s\) follows from \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(s|e)\in\varDelta^n\) which itself results from the inductive definition for classical states.
Denote by \({\Bbb P}^n_\bullet\) projectors on \(n-1\) dimensional subspaces of \(\mathcal{H}^n\). We have the following analogy between classical and quantum states:

4.3 The Lattices of Birkhoff and Von Neumann
In the spectral order, quantum states are ordered by requiring of a labeling e that it commute with the states r and s under consideration. In the corresponding inductive formulation, a condition of commutation with states is imposed on projections. Knowing the structural importance of non-commutativity of observables in quantum mechanics, it may surprise the reader to learn that the lattices of Birkhoff and von Neumann [2], the powerset \(\mathcal{P}\{1,\ldots,n\}\) and the collection \({\mathbb L}^n\) of subspaces of \(\mathcal{H}^n\) ordered by inclusion, can be recovered from Δ n and Ω n in a purely order theoretic manner.
Recall here that the fundamentally different nature of quantum versus classical observables can also be explained in order theoretic terms, roughly, by the distributivity of \(\mathcal{P}\{1,\ldots,n\}\) versus the non-distributivity of \({\mathbb L}^n\) [3, 7, 13]. The relation between observables and these lattices is as follows.
A (real-valued) observable of a classical system, with pure states \(\varSigma_{\mathrm{cl}}^n\cong\{1,\ldots,n\}\), is a map \(a:\varSigma_{\mathrm{cl}}^n\to{\Bbb R}\) with range \(\mathsf{spec}(a)\) that assigns to each pure state the value of that observable. As a consequence, any proposition about the system of the form
encodes as the set \(a^{-1}(E)\). By considering all observables, that is, all such maps a, we obtain \(\mathcal{P}\{1,\ldots,n\}\cong\mathcal{P}(\varSigma_{\mathrm{cl}}^n)\) as the algebra of propositions about the system. Inclusion of sets encodes implication of propositions.
Envision the pure states \(\varSigma_{\mathrm{qm}}^n\) of a quantum system as the one-dimensional subspaces of \(\mathcal{H}^n\), that is, a pure state is the set of fixed points r 1 of a density operator r with \(\mathsf{spec}(r)\subseteq\{0,1\}\). For an observable on a quantum system, i.e., a self-adjoint operator A with spectrum \(\mathsf{spec}(A)\), any proposition about the system of the form
encodes as the fixed points of the projector \(P_A^E\), since the states included in it will yield an outcome in E in a measurement of the observable A (the probability of all other outcomes is zero). This set of fixed points is a subspace of \(\mathcal{H}^n\). By considering all observables, that is, all self-adjoint operators A, we obtain \({\Bbb L}^n\subset\mathcal{P}(\varSigma_{\mathrm{qm}}^n)\) as the algebra of propositions about the system. And once again, inclusion of subspaces encodes implication of propositions.
And so now, to briefly state things, in this section we establish the following: Though the domain of quantum states is grounded in commutativity, it is nevertheless a genuine quantum structure in the sense of present day theoretical physics.
Definition 35
Let D be a dcpo. An element \(x\in D\) is irreducible if
The set of irreducible elements in D is \(\mathrm{Ir}(D)\).
Our first result establishes that the irreducible states in Δ n have an unmistakable operational significance: They are precisely the states one derives by applying all possible combinations of projections p i to the initial state \(\bot\in\varDelta^n\).
Lemma 29
For \(x\in\varDelta^n\), the following are equivalent:
-
(i)
The state x is irreducible.
-
(ii)
For all \(i\in\{1,\ldots,n\}\), either \(x_i=x^+\) or \(x_i=0\).
-
(iii)
There is a nonempty subset \(X\subseteq\max(\varDelta^n)\) with \(x=\bigwedge X\).
Proof
Recall from Proposition 1(ii) that for any classical state x and any index i, \(x\sqsubseteq e_i\Leftrightarrow x_i=x^+\). This fact is used implicitly in what follows.
(i) ⇒ (ii): Let x be irreducible. Let \(y\in\varDelta^n\) be the classical state with \(y_i=y^+\Leftrightarrow e_i\in\ \uparrow\!x\cap\max(\varDelta^n)\) and \(y_i=0\) otherwise. Then y is a lower bound for \(\uparrow\!x\cap\max(\varDelta^n)\), so \(y\sqsubseteq x\). We claim that \(y=x\). If \(y^+ <x^+\), then
which contradicts the fact that x is a classical state. Then \(y^+\geq x^+\). But since \(y\sqsubseteq x\), we know \(y^+\leq x^+\). Thus, \(x^+=y^+\), which gives \(x=y\). This proves (ii).
(ii) ⇒ (i): The proof is by induction. It is true for \(n=2\). Assume it for Δ n, and let \(x\in\varDelta^{n+1}\) be a state of the desired form. We can assume x is not pure, since otherwise x is clearly irreducible.
Let \(y\in\varDelta^{n+1}\) be a lower bound for the set \(\uparrow\!x\cap\varDelta^{n+1}\). Because x is not pure, y cannot be pure either. Let i be any index with \(1\leq i\leq n+1\). Then \(p_i(x)\) has the form mentioned in (ii), so it is irreducible by the inductive hypothesis. The state \(p_i(y)\) is a lower bound of \(\uparrow\!\!p_i(x)\cap\max(\varDelta^n)\), so the irreduciblity of \(p_i(x)\) gives \(p_i(y)\sqsubseteq p_i(x)\). Then \(y\sqsubseteq x\). This puts \(x\in\mathrm{Ir}(\varDelta^{n+1})\).
(iii) ⇒ (i): Let y be the state with \(y_i=y^+\) iff \(e_i\in X\) and \(y_i=0\) otherwise. By (i)=(ii), y is irreducible, while \(X=\ \uparrow\!y\cap\max(\varDelta^n)\) gives
which shows that x is irreducible.
(i) ⇒ (iii): Obvious.
Now we prove that \(\mathcal{P}\{1,\ldots,n\}\) is recoverable from the irreducible elements of Δ n. Specifically, \(\mathrm{Ir}(D)\) in the order it inherits from D is order isomorphic to a subset of \(\mathcal{P}\bigl(\max(D)\bigr)\) ordered by reverse inclusion, so we must consider \(\mathrm{Ir}(D)\) in its dual order, \(\mathrm{Ir}(D)^{\ast}\). Second, since every \(x\in D\) has a maximal element above it, the empty set is not represented in \(\mathrm{Ir}(D)^{\ast},\) so we adjoin a least element 0 to obtain the poset
Proposition 21
For any \(n\geq 2\),
Proof
Let \(e:\{1,\ldots,n\}\rightarrow\max(\varDelta^n)\) be the natural bijection that takes an outcome i to its associated pure state \(e(i)=e_i\). An order isomorphism
is then given by
First, ϕ is surjective: Given \(\emptyset\neq X\in\mathcal{P}\{1,\ldots,n\}\),
using Lemma 29(iii). Next, it is an order embedding: For \(x,y\in\mathrm{Ir}(\varDelta^n)^{\ast}\),
Now we simply extend ϕ to an order isomorphism from \(\mathrm{Ir}(\varDelta^n)^{\ast}_\bot\) to \(\mathcal{P}\{1,\cdots,n\}\) by setting \(\varphi(0)=\emptyset\), and the proof is finished.
We turn now to the analogous result for quantum states. To stress the analogy with classical states we denote pure states now as \(\max(\varOmega^n)\) rather than as Σ; n.
First we prove the analogue of Proposition 1(ii) for quantum states. Denote by \(r^+\) the subspace of eigenvectors for the largest eigenvalue, that is \(r^+=r_\lambda\) for \(\lambda=\max\bigl(\mathsf{spec}(r)\bigr)\).
Lemma 30
For \(r\in\varOmega^n\) and \(t\in \max(\varOmega^n)\), we have
and thus
Proof
Let \(t\in\max(\varOmega^n)\) be such that \(t_1\subseteq r^+\). Define a labeling e that satisfies
-
\(e_1=t_1\),
-
\(e_2,\ldots,e_{\mathsf{dim}(r^+)}\in r^+\cap t_1^\perp\), and,
-
\(e_{\mathsf{dim}(r^+)+1},\ldots,e_n\in\bigcup\mathcal{D}_r\cap (r^+)^\perp\).
By Proposition 1(ii) we then have \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(t|e)\) and thus \(r\sqsubseteq t\).
Conversely, let \(t\in\max(\varOmega^n)\) be such that \(r\sqsubseteq t\). Then there exists labeling e such that \([r,e]=[t,e]=0\), that is \(\bigcup\mathcal{D}_e\subseteq\bigcup\mathcal{D}_r\cap\bigcup\mathcal{D}_t\), which implies since \(\mathcal{D}_t=\{t_1^\perp,t_1\}\) with t 1 one-dimensional that there exists \(i\in\{1,\ldots,n\}\) such that \(t_1=e_i\), say \(i=1\). Then
in Δ n. By Prop. 1(ii) it then follows that \(\langle r|e_i\rangle=\mathsf{spec}(r|e)^+\) so \(e_i\subseteq r^+\) and thus \(t_1\subseteq r^+\).
A quantum state is irreducible iff its spectrum can be viewed as an irreducible classical state.
Lemma 31
For \(r\in\varOmega^n\), the following are equivalent:
-
(i)
The state r is irreducible.
-
(ii)
There is a labeling e with \([r,e]=0\) and \(\mathsf{spec}(r|e)\in\mathrm{Ir}(\varDelta^n)\).
-
(iii)
Either there exists \(\lambda\in(0,1]\) such that \(\mathsf{spec}(r)=\{0,\lambda\}\) or \(r=\bot\).
In either case, \(\mathsf{spec}(r|e)\in\mathrm{Ir}(\varDelta^n)\) for any labeling e with \([r,e]=0\)
Proof
By Lemma 29, (ii) ⇔ (iii) is obvious. The rest of the proof essentially relies on the analogous result for classical states.
(i) ⇒ (iii) Let r be irreducible and e be a labeling with \([r,e]=0\). Let
By Lemma 29(iii), the infimum of X is an irreducible classical state, and we use this to implicitly define a quantum state \(s\in\varOmega^n\) by
By the definition of \(\mathsf{spec}(s|e)\), we immediately have \(\mathsf{spec}(r|e)\sqsubseteq\mathsf{spec}(s|e)\), which implies \(r\sqsubseteq s\) in Ω n.
We claim that \(r=s\). To prove this, we need only show that
for then we have
using the irreducibility of r.
Let \(t\in\,\uparrow\!r\cap\max(\varOmega^n)\). By Lemma 30, \(t_1\subseteq r^+\), and since \(r^+\subseteq s^+\), \(t_1\subseteq s^+\), which again by Lemma 30 gives \(t\in\,\uparrow\!s\cap\max(\varOmega^n)\). But why do we have \(r^+\subseteq s^+\)?
This is the crucial part of the argument: Since \([r,e]=0\), \(\bigcup \mathcal {D}_e\subseteq\bigcup \mathcal{D}_r\), so \(\mathcal{D}_e\) contains a subset S of cardinality \(\mathsf{dim}(r^+)\) whose union is contained in \(r^+\). Each element of S is a one dimensional subspace of \(\mathcal{H}^n\), so the usual bijection allows us to treat S as a collection of pure states.
For each pure state \(t\in S\), we have \([t,e]=0\), since \(t_1\in\mathcal{D}_e\), and \({t\in\,{\uparrow\!r}\cap\max(\varOmega^n)}\), using Lemma 30 and \(t_1\subseteq r^+\). Then by the definition of s, \(s\sqsubseteq t\), while Lemma 30 gives \(t_1\subseteq s^+\). But then, because \(s^+\) is a subspace, we clearly have
which proves \(r=s\). Thus, \(\mathsf{spec}(r|e)=\mathsf{spec}(s|e)\) is irreducible in Δ n.
(iii) ⇒ (i) Let \(r=\bot\). Then \(\uparrow\!\bot\cap\max(\varOmega^n)=\max(\varOmega^n)\). If \(s\sqsubseteq \max(\varOmega^n)\) (pointwisely) then by Lemma 30 it follows that
Thus \(s=\bot\) so \(s\sqsubseteq r\) and as such since trivially \(\bot\sqsubseteq\max(\varOmega^n)\) (pointwisely) we conclude \(\bot=\bigwedge\bigl(\uparrow\!\bot\cap\max(\varOmega^n)\bigr)\).
Let \(\mathsf{spec}(r)=\{0,\lambda\}\). First, \(r\sqsubseteq\uparrow\!r\cap\max(\varOmega^n)\) (pointwisely) is again trivial. Second, let \(s\sqsubseteq\uparrow\!r\cap\max(\varOmega^n)\) (pointwisely). Then,
so it follows by Lemma 30 that
Now define a labeling e that satisfies
-
\(e_1, \ldots, e_k\subseteq r^+\) for \(k:=\mathsf{dim}(r^+)\),
-
\(e_{k+1},\ldots, e_{k+l}\subseteq(r^+)^\perp\cap s^+\) for \(l:=\mathsf{dim}(s^+)-\mathsf{dim}(r^+)\), and,
-
\(e_{k+l+1},\ldots, e_{n}\subseteq(s^+)^\perp\) where \(1-l-k=1-\mathsf{dim}(s^+)\).
We have \([r,e]=[s,e]=0\), while Lemma 29 gives \(\mathsf{spec}(s|e)\sqsubseteq\mathsf{spec}(r|e)\) since \(\mathsf{spec}(r|e)\) is irreducible in Δ n. Thus, \(s\sqsubseteq r\).
Theorem 15
For any \(n\geq 2\),
Proof
An order isomorphism \(\varphi:\mathrm{Ir}(\varOmega^n)^{\ast}\rightarrow {\Bbb L}^n\setminus\{0\}\) is given by
For its surjectivity, given any \(A\in{\Bbb L}^n\setminus\{0\}\), define an irreducible quantum state \(r:\{0,\lambda\}\rightarrow{\Bbb L}^n\) by \(r_{\lambda}=A\) and \(r_0=A^{\perp}\), where \(\lambda=1/\mathsf{dim}(A)>0\). Then \(\varphi(r)=A\). The fact that it is an order isomorphism follows straightforwardly from quantum degeneration (Lemma 21).
The particular nature of this proof, which essentially relies on how we recover \(\mathcal{P}\{1,\ldots,n\}\) from Δ n, exhibits how much of the structure of Ω n is already present in the partial order on Δ n.
To summarize, we are able to recover \({\Bbb L}^n\), the basic quantum structure from which all other are derivable, from the domain of quantum states in a purely order theoretic manner. Here is an analogy worth remembering: Ω n is to \({\Bbb L}^n\) as density operators are to pure states. More to the point, in view of the fact that
-
The canonical order theoretic structure corresponding to quantum mechanics in terms of only pure states is \({\Bbb L}^n\),
we are tempted to claim that
-
The canonical order theoretic structure corresponding to quantum mechanics in terms of density operators is Ω n.
In short, because the density operator formulation offers a more complete picture than simply working with pure states, the domain Ω n offers a more complete picture than the lattice \({\Bbb L}^n\).
Finally, let us add one last twist to the story: Not only does this more complete picture emerge as the result of commutative considerations, but any natural approach to ordering states which allows non-commutativity seems destined to fail!
Fact 1
If we define \(r\sqsubseteq s\) for \(r,s\in\varOmega^n\) by either
-
(i)
“there exists a labeling e such that \(\mathsf{spec}(r|e)\sqsubseteq \mathsf{spec}(s|e)\) in Δ n,” or
-
(ii)
“for all labelings e we have \(\mathsf{spec}(r|e)\sqsubseteq \mathsf{spec}(s|e)\) in Δ n,”
where e does not necessarily commute with r and s, then in both cases, the relation ⊑ is not an information order.
Justification We will only provide explicit proofs of the following partial statements for the case of \(n=2\) (arguments in higher dimensions are essentially of the same nature):
-
In case (i), all states (including bottom) are above all pure states.
-
In case (ii), no state (including bottom) is strictly below a pure state.
Let r be a pure state with \(\psi\in r_1\) and let \(\psi^\perp\in r_0\). Then there exists a labeling e such that \(\psi+\psi^\perp\in e_1\) and \(\psi-\psi^\perp\in e_2\). For this labeling e we have \(\langle r|e_1\rangle=\langle r|e_2\rangle={1/2}\), that is, \(\mathsf{spec}(r|e)=\bot\) in Δ 2. Thus, for all \(s\in\varOmega^2\) we have \(\mathsf{spec}(r|e)\sqsubseteq \mathsf{spec}(s|e)\) in Δ 2. In case (i) this implies \(r\sqsubseteq s\) in Ω 2. In case (ii) this implies that we cannot have \(s\sqsubset r\) in Ω 2.
Thus, the commutativity implied by the existence of a joint labeling in the spectral order seems unavoidable if one wants to obtain a non-trivial partial order. This can be physically explained as follows: Quantum mechanics bears as one of its most fundamental principles that the maximal knowledge an observer can have about a system at a single point in time amounts to knowing the values of a class of observables that constitute a maximally commuting family; any knowledge beyond this is forbidden. Thus, on the assumption that a partial order on quantum states should make statements about knowledge we possess about a system, commutativity at some level is probably unavoidable.
5 Applications
We consider some basic applications of classical and quantum states.
5.1 A Calculus for Noise
One of the basic ideas in the measurement formalism [8] is that one can differentiate functions \(f:D\rightarrow E\) between collections of informative objects with respect to underlying notions of content. Speaking abstractly, it offers a definition of “informatic rate of change,” i.e., the rate at which (the content of) the output of a process changes with respect to (the content of) its input.
As we have seen, the domains of classical and quantum states have many natural notions of content, so in principle we ought to be able to study informatic rates of change in these settings as a means of improving our understanding about the behavior of various phenomena.
One such example arises easily in the study of noise: By modelling the effect of noise as a selfmap on classical or quantum states, we can apply the informatic derivative with respect to a preferred notion of content μ to gain a precise measure of the effect a given form of noise f has on a given state σ. For ease of exposition, we illustrate the idea on Δ 2. Here are some natural candidates for μ:
-
\(\mu x = 1 - x^+\)
-
\(\mu x = 2x^+x^-\)
-
\(\mu x = -x^+\log x^+ - x^-\log x^-\) (Shannon entropy)
We’ll use the first since it is the simplest.
Definition 36
A noise operator is a function \(f:\varDelta^2\rightarrow\varDelta^2\) such that \(f\sigma\sqsubseteq\sigma\).
The intuition in this definition is that noise qualitatively increases uncertainty. Now, suppose a system is in state σ when it suffers an unwanted interaction with its environment, which changes its state to f σ. How can we measure the effect of the noise on the state of the system?
First, we write down a “grammar” which allows for the description of noise: A simple class of noise operators \({\mathbb N}\) is
-
\(\bot,1\in{{\mathbb N}}\)
-
\(f,g\in{{\mathbb N}}\Rightarrow f\circ g\in{{\mathbb N}}\)
-
\(f,g\in{{\mathbb N}}\Rightarrow pf+(1-p)g\in{{\mathbb N}}\) for \(p\in[0,1]\),
-
\(f,g\in{{\mathbb N}}\ \&\ f\sqsubseteq g\Rightarrow pf^{\ast}+(1-p)g\in{{\mathbb N}}\) for \(p\in[0,1/2]\),
where * is the involution \((x,y)^{\ast}=(y,x)\). It is straightforward to check that the class of noise operators on Δ 2 are closed under the operations mentioned above.
Now the effect that channel \(f\in{{\mathbb N}}\) has on state σcan be systematically calculated as follows:
Theorem 16
If \(f,g\in{{\mathbb N}}\), then
-
\(d(\bot)_\mu(\sigma)=0\),
-
\(d(1)_\mu(\sigma)=1\),
-
\(d(f\circ g)_\mu(\sigma)=df_\mu(g\sigma)\cdot dg_\mu(\sigma)\),
-
\(d(pf+(1-p)g)_\mu(\sigma) = p df_\mu(\sigma)+(1-p)dg_\mu(\sigma)\),
-
\(d(pf^{\ast}+(1-p)g)_\mu(\sigma) = (1-p)dg_\mu(\sigma) - p df_\mu(\sigma),\)
for any \(\sigma\neq\bot\).
This theorem allows us to verify inductively that \(df_\mu(\sigma)\) is a measure of reliability. For instance, if \(df_\mu(\sigma)=0\), then the noise f has had a very strong effect on σ (as a channel, f is unreliable for the transmission of σ), while if \(df_\mu(\sigma)=1\), we intuitively expect \(f(\sigma)=\sigma\), i.e., f is completely reliable.
Lemma 32
If f is a noise operator and \(f\sigma=\sigma\), then either \(df_\mu(\sigma)\geq 1\) or it does not exist.
We now have a fun and systematic approach to an interesting problem: Determining the states that a particular type of noise does not affect.
Example 11
Consider the depolarization of a classical state,
For \(\sigma\neq\bot\), we have
so the only unaffected state is ⊥ for \(p>0\).
Example 12
The effect of a magnetic field on data stored on a disk is
For \(\sigma\neq\bot\), we have
Thus, if you are a state, it is better to be depolarized than flipped.
In quantum mechanics, the study of noise and how to beat it is called decoherence. In the quantum case, some neat measures of content arise, corresponding to the classical ones:
-
\(\mu x=1-x^+\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\Longrightarrow \ \mu\rho = 1-\mathrm{spec}(\rho)^+\),
-
\(\mu x = 2x^+x^-\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\Longrightarrow\ \mu\rho = 1-\mathrm{tr}(\rho^2)\),
-
\(\mu x = -x^+\log x^+ - x^-\log x^-\ \Longrightarrow\ \mu\rho = -\mathrm{tr}(\rho\log\rho)\).
For consistency, we use the first one here as well.
Example 13
Depolarization of quantum states is
Once again, \(df_\mu(r)=1-t\). But the reason is physical. For instance, in the two dimensional case we have
It affects the entire state in a uniform way. Quantum bit/phase flipping, by contrast, only affects “part” of r. Things get more interesting then.
5.2 The Axioms of Domain Theory
This work led to the introduction of a new class of domains, the exact domains. We will show in this section that exact domains offer a new perspective on the more traditional, continuous domains [1]. With the benefit of this new point of view, it then becomes possible to ask certain foundational questions that some domain theorists may find intriguing.
Recall that in the study of approximation on classical states, we learned that \(x\ll y\) is a statement which implicitly carries a specific context. In order to conclude \(x\ll z\) when \(y\sqsubseteq z\), we need to know that the statement \(y\sqsubseteq z\) is being made in the same context as \(x\ll y\). Aside from the case when x approximates a pure state (Prop. 7), there is another way of ensuring this: If all entities involved (\(x,y,z\)) can be regarded as necessary for a single state (\({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} z\neq\emptyset\)).
Proposition 22 (Context)
For all \(x,y,z\in\varDelta^n\), if \(x\ll y\sqsubseteq z\) and \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} z\neq\emptyset\), then \(x\ll z\).
Proof
First we prove that if \(x,y,z\in\varLambda^n\) with \(x\ll y\sqsubseteq z\) in Λ n and \(z_i>0\) for all i, then \(x\ll z\) in Λ n. Let \(z=\bigsqcup w_k\) where \((w_k)_{k\geq 1}\) is increasing in Λ n. Now we proceed just as in the proof of Theorem 4. For \(x_i=x_{i+1}>0\), we can take \(k_i=1\), since the monotonicity of w k implies
for all k, while in the case of \(x_i>x_{i+1}>0\), degeneration (Lemma 5) gives \({y_i>y_{i+1}>0}\), which accounts for the strict inequality in
The definition of limit again makes it clear that the required k i exists.
More generally, if \(x\ll y\sqsubseteq z\ll w\) in Δ n, we use Proposition 6(ii) to prove \(x\ll z\). First, \(z\in\varDelta^n_\sigma\Rightarrow x\in\varDelta^n_\sigma\) follows from Lemma 12(i) since \(z_i>0\) for all i using Lemma 13 and \(z\ll w\). And second, since Proposition 6(ii) gives \(r(x)\ll r(y)\sqsubseteq r(z)\) in Λ n, our opening argument now applies leaving \(r(x)\ll r(z)\) in Λ n.
The value of this observation is that it provides a theoretical explanation for why the approximation relation on Δ n is interpolative:
Lemma 33
If D is an exact dcpo such that for all \(x,y,z\in D\),
whenever \({\mathord{\mbox{\makebox[0pt][l]{\raisebox{.4ex} {\(\uparrow\)}}\(\uparrow\)}}} z\neq\emptyset\), then ≪ is interpolative. Moreover, a dcpo is continuous iff it is exact and \(x\ll y\sqsubseteq z\Rightarrow x\ll z\) for all \(x,y,z\in D\).
Proof
The proof given in [1] applies unchanged.
From this we can see that exact domains require precision when reasoning about approximation. By contrast, the single most important aspect of approximation on a continuous domain is not that it is interpolative [1], but rather that it is context independent. The present work seems to provide sufficient impetus for investigating domains beyond the continuous variety.
5.3 Qualitative Measures of Entanglement
Quantum entanglement is the essential feature in quantum communication schemes and quantum cryptographic protocols that distinguishes them from their classical counterparts. For the particular dialectics used here we refer to the standard literature on the matter.
We illustrate by means of a series of examples how the results of this paper can be applied to the study of entanglement. A full development on the matter is in preparation.
Example 14
Measures of entanglement of bipartite quantum systems. Let \(\mathcal{H}^n\) be a n-dimensional complex Hilbert space. According to Schmidt’s biorthogonal decomposition theorem [15], any bipartite state \(\varPsi\in\mathcal{H}^n\otimes\mathcal{H}^n\) can be rewritten as
with \((\psi_i)\) and \((\phi_i)\) orthonormal bases of \(\mathcal{H}^n\) and \((c_i)\) positive real coifficients which are as a set uniquely defined. In particular we have \(\sum_i c_i^2=1\) due to normalization of Ψ, so every \(\varPsi\in\mathcal{H}^n\otimes\mathcal{H}^n\) defines a unique classical state \(c:=(c_i^2)\). We can then qualitatively measure entanglement using the dcpo Λ n as
where r is the usual retraction on classical states.
Moreover, every measure of content
gives rise to a quantitative measure of entanglement
When taking as μ Shannon entropy we find the usual quantitative measure of entanglement for bipartite quantum systems.
The maximal element of Λ n then encodes the non-entangled states, that is, the pure tensors \(\psi\otimes\phi\). The minimal element of Λ n then encodes the maximally entangled state, that is
which does not depend on the choice of bases.
Since \(\mu:\varLambda^2\to[0,1]^{\ast}\) is a duality, using Λ 2 rather than in \([0,1]^{\ast}\) doesn’t teach us much for the case \(n=2\), that is, for a pair of qubits. For qutrits however, \(n=3\), we capture essential qualitative differences by valuating in Λ 3.
Consider for example the state
that is,
The state \(\mathsf{S}\) is entangled but this entanglement has essentially a qubit nature, that is, we can express the state by only using a subbase of \(\mathcal{H}^3\) that contains two vectors. In particular, the entanglement coincides with that of the EPR or singlet state so it is maximal as qubit entanglement.
On the other hand, the states
for \(1/3 <q<1\), that is,
exhibits genuine qutrit entanglement.
Unfortunately, for q ranging in \((\frac{1}{3},1)\) Shannon entropy ranges in \((0,1)\) so some \(\mathsf{T}_q\) have entropy higher than \(\mathsf{S}\) and some have entropy less than \(\mathsf{S}\). The valuation \(\mu\cdot\mathsf{Ent}\) as such doesn’t capture the qualitative feature that distinquishes between maximal qubit-type entanglement and essentially qutrit type entanglement.
However, Λ 3 does. Indeed, consider
that is,

in graphical terms. Since there is no value for \(q\in(\frac{1}{3},1)\) for which we have that \(\left({1/2},{1/2},0\right)\) and \(\left(q,(1-q)/2,(1-q)/2\right)\) compare in Λ 3, it follows for all \(\mathsf{T}_q\) with \(q\in(\frac{1}{3},1)\) that
The states \(\varPsi\in\mathcal{H}^3\otimes\mathcal{H}^3\) for which we have \(\mathsf{Ent}(\varPsi)\sqsubseteq\mathsf{Ent}(\mathsf{S})\) are those which are such that
for \(0\leq q\leq 1/3\), that is, that are convex combinations of \(\mathsf{S}\) and the maximally entangled state in \(\mathcal{H}^3\otimes\mathcal{H}^3\),
for which we set
Graphically,

where \(\downarrow\!\mathsf{Ent}(\mathsf{S})\) is the lower set of \(\mathsf{Ent}(\mathsf{S})\) in Λ 3.
The states \(\varPsi\in\mathcal{H}^3\otimes\mathcal{H}^3\) for which we have \(\mathsf{Ent}(\mathsf{S})\sqsubseteq\mathsf{Ent}(\varPsi)\) are those which are such that
for \(0\leq q\leq 1/2\), that is, convex combinations of \(\mathsf{S}\) and the minimally entangled state in \(\mathcal{H}^3\otimes\mathcal{H}^3\) (the pure tensor \(|00\rangle\)), for which we set
Graphically,

where \(\uparrow\!\mathsf{Ent}(\mathsf{S})\) is the upper set of \(\mathsf{Ent}(\mathsf{S})\) in Λ 3.
We can now refine our qualitative representation of entanglement for bipartite states using the order on quantum states.
Example 15
Qualitative entanglement of bipartite quantum systems In Example 14, the quantitative valuation \(\mu\cdot\mathsf{Ent}\) with μ Shannon entropy, that is, the usual valuation attributed to a bipartite quantum system in order to measure entanglement, can equivalently be defined as the von Neumann entropy of one of the quantum states \(\rho_1(\varPsi)\) or \(\rho_2(\varPsi)\) for \(\varPsi\in\mathcal{H}^n\otimes\mathcal{H}^n\) that arise by tracing over the other system.
Explicitly, for \(\varPsi=\sum_ic_i\psi_i\otimes\phi_i\) we obtain
Since the diagonals coincide, von Neumann entropy coincides and in either case gives the same value.
This implies that we can refine the valuation of entanglement \(\mathsf{Ent}\) in Example 14 as
where \(\varOmega^n\times\varOmega^n\) is ordered pointwisely, that is,
On \(\varOmega^n\times\varOmega^n\) we can then define as a measure of content
where μ is von Neumann entropy. This results in a quantitative measure of entanglement on \(\mathcal{H}^n\otimes\mathcal{H}^n\) that exactly coincides with the usual one. Indeed,
Note here in particular that \(\mathsf{Ent}^\varOmega\) “almost” turns the states in \(\mathcal{H}^n\otimes\mathcal{H}^n\) into a domain by setting
We obtain a preorder that has pure tensors as maximal elements and that has ⊥ as a minimum.
We however lose some anti-symmetry in this passage. In particular, when considering the Schmidt base, the order loses track of relative phases between base vectors. Indeed,
although
so these vectors do not encode the same state.
However, this can be fixed by taking into account their phases in defining the order. We will provide the details in a future paper.
Pure tensors avoid this since
for which we have
The maximally entangled states do not depend on the bases at all.
The essential difference between the qualitative valuations \(\mathsf{Ent}^\varOmega\) and \(\mathsf{Ent}\) is the fact that \(\mathsf{Ent}^\varOmega\) takes into account the identity of pure tensors above.
Example 16
Qualitative entanglement of multipartite quantum systems In Example 14 we measured entanglement of bipartite quantum systems using unicity of the coefficients in the Schmidt biorthogonal decomposition. There however does not exist a similar construction for arbitrary multipartite sytems, that is, there is no Schmidt-type decomposition theorem for arbitrary \(\mathcal{H}^n\otimes\ldots\otimes\mathcal{H}^n\).
In particular, up to now there was not even a satisfactory notion of maximal entanglement e.g. see [10]. Indeed, when considering three partite qubit states, for the Greenberger-Horn-Zeilinger state [6]
and the \(\mathsf{W}\)-state
there are conflicting arguments about which one is maximally entangled. The general favourite is however \(\mathsf{GHZ}\) in particular in view of its maximal violation of certain type of inequalities (e.g. Bell’s) that are characteristic for entanglement.
The solution of this conflict lies in specification of a context with respect to which one measures entanglement, in the sense of Example 15.
We propose here a qualitative measure for multipartite entanglement that favours \(\mathsf{GHZ}\) as the maximally entangled state, allong the lines of the valuation in Example 15 for bipartite entanglement.
Define
where \(\rho_i(\varPsi)\) arises by tracing over all systems except the ith. We can do this for example by considering the Schmidt decomposition for \(\mathcal{H}^n\otimes\left(\mathcal{H}^n\otimes\ldots\otimes\mathcal{H}^n\right)\) where the single Hilbert space encodes the ith system.
We then obtain for the above examples that
since we have
with respect to the 1st component and
since for example
and as such it follows that
Depicting only the part of Ω 2 containing the relevant pure states \(|0\rangle\) and \(|1\rangle\) here, that is, a copy of Δ 2, this represents graphically as \(\mathsf{Ent}^\varOmega(\mathsf{GHZ})\)

versus \(\mathsf{Ent}^\varOmega(\mathsf{W})\)
where the maps π 1, π 2 and π 3 represent the components of \(\mathsf{Ent}^\varOmega\).

We can define a quantitative measure of entanglement on \(\mathcal{H}^n\otimes\ldots\otimes\mathcal{H}^n\) via composition of \(\mathsf{Ent}^\varOmega\) and
where μ is again von Neumann entropy. We obtain as such the desired values on pure tensors and the maximally entangled state. In particular do we obtain
When one prefers to abstract over the identity of the pure tensors above, it is clear that all the above still holds by substituting Λ n for Ω n, that is, \(\mathsf{Ent}\) for \(\mathsf{Ent}^\varOmega\).
References
Abramsky, S., Jung, A.: Domain theory. In: Abramsky, S., Gabbay, D.M., Maibaum, T.S.E. (eds.) Handbook of Logic in Computer Science, vol. III. Oxford University Press, Oxford (1994)
Birkhoff, G., von Neumann, J.: The logic of quantum mechanics. Ann. Math. 37, 823–843 (1936)
Coecke, B., Moore, D.J., Wilce, A. (eds.): Current Research in Operational Quantum logic: Algebras, Categories, Languages. Kluwer Academic Publishers, Dordrecht (2000)
Faure, Cl.-A., Frölicher, A.: Modern projective Geometry. Kluwer Academic Publishers, Dordrecht (2000)
Gleason, A.M.: Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 6, 885–893 (1957)
Greenberger, D.M., Horn, M.A., Shimony, A., Zeilinger, A.: Bell’s theorem without inequalities. Am. J. Phys. 58, 1131 (1990)
Kalmbach, G.: Orthomodular Lattices. Academic Press, New York (1983)
Martin, K. A foundation for computation. Ph.D. Thesis, Department of Mathematics, Tulane University (2000)
Mackey, G.M.: The Mathematical Foundations of Quantum Mechanics. W. A. Benjamin, New York (1963)
van Loock, P., Braunstein, S.L.: Multipartite entanglement, 2002. arXiv:quantph/0205068
Lüders, G.: über die Zustandsänderung durch den Messprozess (German). Annalen der Physik 8, 322–328 (1951)
von Neumann, J.: Mathematische Grundlagen der Quantenmechanik. Springer, New York (1932); Translation, Mathematical Foundations of Quantum mechanics. Princeton University Press, Princeton (1955)
Piron, C.: Foundations of quantum physics. W. A. Benjamin, Reading (1976)
Ramsey, F.P.: Truth and probability, 1926. In: Braithwaite, R.B. (ed.) The Foundations of Mathematics and Other Logical Essays, Ch. 7. Routledge, London (1931)
Schmidt, E.: Math. Ann. 63, 433 (1907)
Scott, D.: Outline of a mathematical theory of computation. TechnicalMonograph PRG-2. (November 1970)
Acknowledgement
To Samson Abramsky and Prakash Panangaden – who supported the authors when ideas combining semantics and physics were far less popular than they are today. This paper appears in its original, unpublished form in tribute to a memorable time and place.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2010 Springer-VerlagBerlin Heidelberg
About this chapter
Cite this chapter
Coecke, B., Martin, K. (2010). A Partial Order on Classical and Quantum States. In: Coecke, B. (eds) New Structures for Physics. Lecture Notes in Physics, vol 813. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-12821-9_10
Download citation
DOI: https://doi.org/10.1007/978-3-642-12821-9_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-12820-2
Online ISBN: 978-3-642-12821-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)