On the Approximation of a Discrete Multivariate Probability Distribution Using the New Concept of t-Cherry Junction Tree

Abstract

Most everyday reasoning and decision making is based on uncertain premises. The premises or attributes, which we must take into consideration, are random variables, so that we often have to deal with a high dimensional discrete multivariate random vector. We are going to construct an approximation of a high dimensional probability distribution that is based on the dependence structure between the random variables and on a special clustering of the graph describing this structure. Our method uses just one-, two- and three-dimensional marginal probability distributions. We give a formula that expresses how well the constructed approximation fits to the real probability distribution. We then prove that every time there exists a probability distribution constructed this way, that fits to reality at least as well as the approximation constructed from the Chow–Liu dependence tree. In the last part we give some examples that show how efficient is our approximation in application areas like pattern recognition and feature selection.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The goal of our paper is to approximate a high dimensional joint probability distribution using two and three-dimensional marginal distributions, only.

The idea of such kind of approximations was given by Chow and Liu [7]. In their work they construct a first order tree taking into account the mutual information gains of all pairs of random variables. They proved that their approximation is optimal in the sense of Kullback–Leibler divergence [12, 15].

In order to give an approximation that uses lower dimensional marginal probability distributions, there are many algorithms developed. Most of them first construct a Bayesian network (directed acyclic graph) see [1] and then they obtain from this in several steps a junction tree. See [11] for a good overview.

Many algorithms were developed for obtaining a Bayesian Network. These algorithms start with the construction of the Chow–Liu tree and then this graph is transformed, by adding edges and then delete the superfluous edges using conditional independence tests. The number of conditional independence tests is diminished by searching the minimal d-separating set [2, 6].

After the graphical structure is determined a number of quantitative operations have to be performed on it (see [13] and [9]).

In our paper we suppose to be known just the three-dimensional marginals of the joint probability distribution (indeed that implies that the second and first order marginals are known, too). From this information we first construct a graphical model, and then a junction tree, named t-cherry-junction tree.

The construction of our graphical model is inspired by the graphical structure, named cherry tree, and t-cherry tree introduced by Bukszár and Prékopa in [3].

We emphasize that our method does not use the construction of the Bayesian network first, we are going to use just the third order marginals and the information contents related to them, and to certain pairs of random variables involved.

The paper is organized as follows:

• The second section contains the theory, formulas, and connections between them that are used in the third section.

• The third section contains the introduction of the concept of the t-cherry-junction tree, the formula that gives the Kullback–Leibler divergence associated to the approximation introduced, and a proof that the approximation associated to the t-cherry-junction tree is at least as good as Chow–Liu’s approximation is.

• The last section contains some applications of the approximation introduced in order to exhibit some advantages of this approach.

2 Preliminaries

2.1 Notations

Let X = (X ₁, X ₂, …, X _n )^T be an n-dimensional random vector with the joint probability distribution

$$P\!\left ({X}_{1} = {x}_{{i}_{1}}^{1},\ldots ,{X}_{ n} = {x}_{{i}_{n}}^{n}\right ),{i}_{ 1} = 1,\ldots ,{m}_{1},\ldots ,{i}_{n} = 1,\ldots ,{m}_{n}.$$

For this we will use also the abbreviation

$$P(\mathbf{X}) = P({X}_{1},{X}_{2},\ldots ,{X}_{n}).$$

This shorter form will be applied in sums and products, too. So we will write

$$\sum\limits_{\mathbf{X}}P(\mathbf{X}) = \sum\limits_{{i}_{1}=1}^{{m}_{1} }\cdots \sum\limits_{{i}_{n}=1}^{{m}_{n} }P({X}_{1} = {x}_{{i}_{1}}^{1},\ldots ,{X}_{ n} = {x}_{{i}_{n}}^{n})\left (= 1\right )$$

(3.1)

and for example if H = { j, k, l} is a three element subset of the index (vertex) set {1, 2, …, n} then X _H = (X _j , X _k , X _l )^T and

$$\sum\limits_{{\mathbf{X}}_{H}}P({\mathbf{X}}_{H}) = \sum\limits_{{i}_{j}=1}^{{m}_{j} } \sum\limits_{{i}_{k}=1}^{{m}_{k} } \sum\limits_{{i}_{l}=1}^{{m}_{l} }P({X}_{j} = {x}_{{i}_{j}}^{j},{X}_{ k} = {x}_{{i}_{k}}^{k},{X}_{ l} = {x}_{{i}_{l}}^{l})\left (= 1\right )$$

(3.2)

and

$$\prod\limits_{{\mathbf{X}}_{H}}P({\mathbf{X}}_{H}) = \prod\limits_{{i}_{j}=1}^{{m}_{j} } \prod\limits_{{i}_{k}=1}^{{m}_{k} } \prod\limits_{{i}_{l}=1}^{{m}_{l} }P({X}_{j} = {x}_{{i}_{j}}^{j},{X}_{ k} = {x}_{{i}_{k}}^{k},{X}_{ l} = {x}_{{i}_{l}}^{l})$$

(3.3)

P _a (X) will denote the approximating joint probability distribution of P(X).

2.2 Cherry Tree and t-Cherry Tree

The cherry tree is a graph structure introduced by Bukszár and Prékopa (see [3]). A generalization of this concept, called hyper cherry tree can be found in [4] by Bukszár and Szántai. Let be given a nonempty set of vertices V.

Definition 3.1.

The graph defined recursively by the following steps is called cherry tree:

• 1. Two vertices connected by an edge is the smallest cherry tree.

• 2. By connecting a new vertex of V , by two new edges to two existing vertices of a cherry tree, one obtains a new cherry tree.

• 3. Each cherry tree can be obtained from (1) by the successive application of (2).

Remark 3.1.

A cherry tree is an undirected graph. We emphasize that it is not a tree.

Definition 3.2.

We call cherry, a triplet of vertices formed from two existing vertices and a new one connected with them in step (2) of Definition 3.1.

For the cherry we will use the notation introduced in [4] by Bukszár and Szántai: ({l, m}, k), where l and m are the existing vertices, k is the newly connected vertex and {k, l}, {k, m} are the new edges.

Remark 3.2.

From a set of n vertices we obtain a cherry tree with n − 2 cherries.

Remark 3.3.

We denote by $\mathcal{H}$ the set of all cherries of the cherry tree and by ε the set of edges of the cherry tree.

Remark 3.4.

A cherry tree is characterized by a set V of vertices, the set $\mathcal{H}$ of cherries and the set ε of edges. We denote a cherry-tree by $\Delta = (V,\mathcal{H},\epsilon )$.

In our paper we need the concept of the t-cherry tree introduced by Bukszár and Prékopa in [3]. To get the concept of t-cherry tree one has to apply the more restrictive Step (2′) in Definition 3.1 instead of Step (2):

• (2′) By connecting a new vertex of V by two new edges to two connected vertices of a cherry tree, one obtains a new cherry tree.

Definition 3.3.

The graph defined recursively by (1), (2′) and (3) is called t-cherry tree.

Remark 3.5.

A pair of adjacent vertices from the t-cherry tree may be used several times, for connecting new vertices to them.

2.3 Junction Tree

The junction tree is a very prominent and widely used structure for inference in graphical models (see [5] and [12]).

Let X = { X ₁, …, X _n } be a set of random variables defined over the same probability field and X = (X ₁, …, X _n )^T an n-dimensional random vector.

Definition 3.4.

A tree with the following properties is called junction tree over X:

• 1. To each node of the tree, a subset of X called cluster and the marginal probability distribution of these variables is associated.

• 2. To each edge connecting two clusters of the tree, the subset of X given by the intersection of the connected clusters and the marginal probability distribution of these variables is associated.

• 3. If two clusters contain a random variable, than all clusters on the path between these two clusters contain this random variable (running intersection property).

• 4. The union of all clusters is X.

Notations:

• $\mathcal{C}$ – the set of clusters

• C – a cluster

• X _C – the random vector with the random variables of C as components

• P(X _C ) – the joint probability distribution of X _C

• $\mathcal{S}$ – the set of separators

• S – a separator

• X _S – the random vector with the random variables of S as components

• P(X _S ) – the joint probability distribution of X _S

The junction tree provides a joint probability distribution of X:

$$P(\mathbf{X}) = \frac{\prod\limits_{C\in \mathcal{C}}P({\mathbf{X}}_{C})} {\prod\limits_{S\in \mathcal{S}}P{({\mathbf{X}}_{S})}^{({\nu }_{S}-1)}},$$

where ν _S is the number of those clusters which contain all of the variables involved in S.

3 t-Cherry-Junction Tree

3.1 Construction of a t-Cherry-Junction Tree

Let X = { X ₁, …, X _n } be a set of random variables defined over the same probability field and denote by X = (X ₁, …, X _n )^T the corresponding n-dimensional random vector. Together with the construction of the t-cherry tree over the set of vertices V = { 1, …, n} we can construct a t-cherry-junction tree in the following way.

Algorithm 1. Construction of a t-cherry-junction tree.

• 1. The first cherry of the t-cherry tree identifies the first cluster of the t-cherry junction tree. The vertices of the first cherry give the indices of the random variables belonging to the first cluster.

• 2. Similar way each new cherry of the t-cherry tree identifies a new cluster of the t-cherry-junction tree. The separators contain pairs of random variables with indices corresponding to the connected vertices used in Step (2′) of Definition 3.3.

Theorem 3.1.

The t-cherry-junction tree constructed by Algorithm 1 is a junction tree.

Proof.

We can check the statements of Definition 3.4:

• The first statement of definition is obvious.

• The separator that connects two clusters contains the intersection of the two clusters. This follows from the construction of the separator sets.

• Let us suppose that there exists a variable X _m which belongs to two clusters on a path, so that on this path exist a cluster that does not contain X _m . This implies that on this past exist two neighboring cluster so that one of them contains X _m and the other one does not contain X _m . This means that in the t-cherry tree there are two cherries connected so that one of them contains the vertex m the other one does not contain the vertex m. According to the point (2) of Definition 3.1, m is a new vertex connected, but since X _m belongs already to another cluster, the vertex m belongs to another cherry, too. That is a contradiction, because that means that m is not a new vertex.

• The union of all sets associated to the clusters is X, because of the union of set of indices is V.

Remark 3.6.

To each cluster {X _l , X _m , X _k } a three-dimensional joint probability distribution P(X _l , X _m , X _k ) can be associated. To each separator {X _l , X _m } a two-dimensional joint probability distribution P(X _l , X _m ) can be associated.

The joint probability distribution associated to the t-cherry-junction tree is a joint probability distribution over the variables X ₁, …, X _n , given by

$$P(\mathbf{X}) = \frac{\prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l},{X}_{m},{X}_{k})} {\prod\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}P{({X}_{l},{X}_{m})}^{{\nu }_{lm}-1}} ,$$

(3.4)

where ${\nu }_{lm} = \#\{\{{X}_{l},{X}_{m}\} \subset C\vert C \in \mathcal{C}\}$.

3.2 The Approximation of the Joint Distribution Over X by the Distribution Associated to a t-Cherry-Junction Tree

Chow and Liu introduced a method to approximate optimally an n-dimensional, discrete joint probability distribution by the one- and two-dimensional probability distributions using first-order dependence tree. It is shown that the procedure presented in their paper yields an approximation with minimum difference of information, in the sense of Kullback–Leibler divergence.

In this part, we first give a formula for the Kullback–Leibler divergence between the approximated distribution associated to the t-cherry-junction tree and the real joint probability distribution; we then conclude what we have to take into account to minimize the divergence. For the proof of this theorem we need a lemma:

Lemma 3.1.

In a t-cherry-junction tree for each variable X _m ∈ X:

$$\begin{array}{rcl} \#\{\{{X}_{l},{X}_{m}\}\:\vert \:(\{{X}_{l},{X}_{m}\},{X}_{k}) \in \mathcal{C}\} = \#\{(\{{X}_{l},{X}_{m}\},{X}_{k})\:\vert \:(\{{X}_{l},{X}_{m}\},{X}_{k}) \in \mathcal{C}\}- 1& & \\ \end{array}$$

Proof.

Let denote $t = \#\{\{{X}_{l},{X}_{m}\}\:\vert \:(\{{X}_{l},{X}_{m}\},{X}_{k}) \in \mathcal{C}\}$ for a given X _m ∈ X.

• Case t = 0.

  The statement is a consequence on one hand of Definition 3.4 that is the union of all sets associated to the nodes (clusters) is X, so every vertex from X, have to appear at least in one cluster. On the other hand, if X _m would be contained in two clusters than there must exist one separator set containing this vertex (point 3) in Definition 3.4), but we supposed t = 0.

• Case t > 0.

  If two clusters contain a variable X _m , than all clusters from the path between the two clusters contain X _m (running intersection property). From this results that the clusters containing X _m are the nodes of a connected graph, and this graph is a first order tree. If this graph contains t + 1 clusters, than it contains t separator sets (definition of a tree in which we have separators instead of edges and clusters instead of nodes). From the definition of the junction tree (Definition 3.4) results that every separator set connecting two clusters contains the variables from the intersection of the clusters. So there are t separator sets that contain the variable X _m .

The goodness of the approximation of a probability distribution can be quantified by the Kullback–Leibler divergence between the real and the approximating probability distributions (see for example [8] or [15]). The Kullback–Leibler divergence expresses somehow the distance between two probability distributions. As smaller value it has as better the approximation is.

Theorem 3.2.

If we denote by P _a(X) the approximating joint probability distribution associated to the t-cherry-junction tree [see formula (3.4)], then the Kullback–Leibler divergence between the real and the approximating joint probability distribution is given by:

$$\begin{array}{rcl} I(P(\mathbf{X}),{P}_{a}(\mathbf{X}))& = -H(\mathbf{X}) - \sum\limits_{({X}_{l},{X}_{m},{X}_{k})\in \mathcal{C}}I({X}_{l},{X}_{m},{X}_{k}) & \\ & & \\ & \quad + \sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}({\nu }_{lm} - 1)I({X}_{l},{X}_{m}) + \sum\limits_{k=1}^{n}H({X}_{k}).& \\ \end{array}$$

(3.5)

Proof.

$$\begin{array}{rcl} I(P(\mathbf{X}),{P}_{a}(\mathbf{X}))&& = \sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2} \dfrac{P(\mathbf{X})} {{P}_{a}(\mathbf{X})}\\ && = \sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2}P(\mathbf{X}) - \sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2}{P}_{a}(\mathbf{X}) \\ && = -H(\mathbf{X}) - \sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2}\dfrac{\prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l},{X}_{m},{X}_{k})} {\prod\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}P{({X}_{l},{X}_{m})}^{{\nu }_{lm}-1}}\\ && = -H(\mathbf{X}) - \sum\limits_{\mathbf{X}}P(\mathbf{X}){\Bigg{[}\log }_{2} \prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l},{X}_{m},{X}_{k})\\ && \quad \hspace{91.20007pt} {-\,\log }_{2} \prod\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}P{({X}_{l},{X}_{m})}^{{\nu }_{lm}-1}\Bigg{]}\\ && = -H(\mathbf{X}) -\sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2} \prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l},{X}_{m},{X}_{k})\\ &&\quad+\, \sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2} \prod\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}P{({X}_{l},{X}_{m})}^{{\nu }_{lm}-1}\\ \end{array}$$

From Definition 3.4 follows that the union of the clusters of the junction tree is the set X. From the Lemma 3.1 we know that each vertex appears once more in clusters than in separator sets. So by adding and subtracting the sum

$$\sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2}\left [\prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l})P({X}_{m})P({X}_{k})\right ]$$

we obtain the following:

$$\begin{array}{rcl} &&I(P(\mathbf{X}),{P}_{a}(\mathbf{X}))\\ && = -H(\mathbf{X}) -\sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2} \frac{\prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l},{X}_{m},{X}_{k})} {\prod\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}P({X}_{l})P({X}_{m})P({X}_{k})}\\ && \quad + \sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2} \frac{\prod\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}P{({X}_{l},{X}_{m})}^{{\nu }_{lm}-1}} {\prod\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}\!{[P({X}_{l})P({X}_{m})]}^{{\nu }_{lm}-1}} \,-\,\sum\limits_{\mathbf{X}}P{(\mathbf{X})\log }_{2}\! \prod\limits_{{X}_{k}\in X}\!P({X}_{k})\\ && = -H(\mathbf{X}) -\sum\limits_{\mathbf{X}}P(\mathbf{X}) \sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}\log_{2} \frac{P({X}_{l},{X}_{m},{X}_{k})} {P({X}_{l})P({X}_{m})P({X}_{k})}\\ && \quad + \sum\limits_{\mathbf{X}}P(\mathbf{X})\sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}{({\nu }_{lm} - 1)\log }_{2} \frac{P({X}_{l},{X}_{m})} {P({X}_{l})P({X}_{m})} + \sum\limits_{{X}_{k}\in X}H({X}_{k}).\\ \end{array}$$

Since (X _l , X _m , X _k ) and (X _l , X _m ) are components of the random vector X, we have the relations:

$$\begin{array}{l} \sum\limits_{\mathbf{X}}P(\mathbf{X})\sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}\log_{2} \dfrac{P({X}_{l},{X}_{m},{X}_{k})} {P({X}_{l})P({X}_{m})P({X}_{k})}\\ \\ \quad = \sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}\sum\limits_{{({X}_{l},{X}_{m},{X}_{k})}^{T}}P{({X}_{l},{X}_{m},{X}_{k})\log }_{2} \dfrac{P({X}_{l},{X}_{m},{X}_{k})} {P({X}_{l})P({X}_{m})P({X}_{k})} \end{array}$$

and

$$\begin{array}{rcl} && \sum\limits_{\mathbf{X}}P(\mathbf{X})\sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}{({\nu }_{lm} - 1)\log }_{2} \dfrac{P({X}_{l},{X}_{m})} {P({X}_{l})P({X}_{m})}\\ && \quad = \sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}\sum\limits_{{({X}_{l},{X}_{m})}^{T}}({\nu }_{lm} - 1)P{({X}_{l},{X}_{m})\log }_{2} \dfrac{P({X}_{l},{X}_{m})} {P({X}_{l})P({X}_{m})}.\\ \end{array}$$

Taking into account these relations and applying the notion of the mutual information content for two and three variables:

$$\begin{array}{l} I({X}_{l},{X}_{m}) = \sum\limits_{{({X}_{l},{X}_{m})}^{T}}P{({X}_{l},{X}_{m})\log }_{2} \dfrac{P({X}_{l},{X}_{m})} {P({X}_{l})P({X}_{m})}, \\ I({X}_{l},{X}_{m},{X}_{k}) = \sum\limits_{{({X}_{l},{X}_{m},{X}_{k})}^{T}}P{({X}_{l},{X}_{m},{X}_{k})\log }_{2} \dfrac{P({X}_{l},{X}_{m},{X}_{k})} {P({X}_{l})P({X}_{m})P({X}_{k})}\end{array}$$

we obtain (3.5) and the statement of the theorem has been proved.

Observation 1. We can observe that for minimizing the Kullback–Leibler divergence between the real probability distribution and the approximation obtained from the t-cherry-junction tree we have to maximize the difference between the sum of the mutual divergence of the clusters and the sum of the mutual divergence of the separators denoted by S:

$$S = \sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}I({X}_{l},{X}_{m},{X}_{k}) -\sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}({\nu }_{lm} - 1)I({X}_{l},{X}_{m})$$

Observation 2. If we wish to compare two approximations of a joint probability distribution associated to two different t-cherry-junction trees, we have just to:

• Sum the information contents of the clusters

• Sum the information contents of the separators

• Make the difference between them

• Claim a t-junction-cherry tree be better than another one, if it produces greater value of S

3.3 The Relation Between the Approximations Associated to the First-Order Dependence Tree and t-Cherry-Junction Tree

A natural question is: can the t-cherry-junction tree give better approximation than the first order tree given by Chow and Liu does? Let us remind that Chow and Liu introduced a method for finding an optimal first order tree that minimizes the Kullback–Leibler divergence.

If pa(j) denotes the parent node of j, the joint probability distribution associated to the Chow–Liu first order dependence tree is given as follows:

$${P}_{Ch-L}(\mathbf{X}) = \prod\limits_{i=1}^{n}P({X}_{{ m}_{i}}\vert {X}_{pa({m}_{i})}),$$

where {m ₁, …, m _n } is a permutation of the numbers 1, 2, …, n and if pa(j) is the empty set, then by definition P(X _j | X _pa(j)) = P(X _j ).

In the following Algorithm 2 we will show how one can construct a t-cherry-junction tree from a Chow–Liu first order dependence tree. After this in Theorem 3.3 we prove that the t-cherry-junction tree constructed this way gives at least as good approximation of the real probability distribution as the Chow–Liu first order dependence tree does.

Algorithm 2. The construction of a t-cherry-junction tree from a Chow–Liu first order dependence tree.

Let us regard the spanning tree behind the Chow–Liu first order dependence tree. It is sufficient to give an algorithm for constructing a t-cherry tree from this spanning tree. Then by Algorithm 1 we can assign a t-cherry-junction tree to this t-cherry tree:

• 1. The first cherry of the t-cherry tree let be defined by any three vertices of the spanning tree which are connected by two edges.

• 2. We add a new cherry to the t-cherry tree by taking a new vertex of the spanning tree adjacent to the so far constructed t-cherry tree.

• 3. We repeat step (2) till all vertices from the spanning tree become included in the t-cherry tree.

Theorem 3.3.

If ${P}_{Ch-L}(\mathbf{X}) = \prod\nolimits_{i=1}^{n}P({X}_{{m}_{i}}\vert {X}_{pa({m}_{i})})$ is the approximation associated to the Chow–Liu first order dependence tree there always exists a t-cherry-junction tree with associated probability distribution P _t−ch(X) that approximates P(X) at least as well as P _Ch−L(X) does.

Proof.

We construct the t-cherry-junction tree from the Chow–Liu first order dependence tree using Algorithm 2.

The Kullback–Leibler divergence formally looks like it is given in (3.5).

In the case of the approximation obtained by the Chow–Liu method, the Kullback–Leibler divergence is given as follows (see [7]):

$$I(P(\mathbf{X}),{P}_{Ch-L}(\mathbf{X})) = -H(\mathbf{X}) -\sum\limits_{i=1}^{n}I({X}_{{ m}_{i}},{X}_{pa({m}_{i})}) + \sum\limits_{i=1}^{n}H({X}_{ i}).$$

(3.6)

Because the first and last terms of the Kullback–Leibler divergences are the same in the case of the two approximations (3.5) and (3.6), we denote the sums that we have to compare by S _{Ch − L} in the case of Chow–Liu’s approximation and S _{t − ch} in the case of t-cherry-junction tree approximation:

$${S}_{Ch-L} = \sum\limits_{{X}_{{m}_{ i}}\in X}I({X}_{{m}_{i}},{X}_{pa({m}_{i})})$$

(3.7)

and

$${S}_{t-ch} = \sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}I({X}_{l},{X}_{m},{X}_{k}) -\sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}({\nu }_{lm} - 1)I({X}_{l},{X}_{m})$$

(3.8)

In the case of formula (3.7) we can apply the formula

$$I(X,Y ) = H(X) - H(X\vert Y )$$

(see [8], Formula (2.43) on p. 16), while in the case of formula (3.8) we can apply

$$I(X,Y,Z) = H(Z) + I(X,Y ) - H(Z\vert X,Y )$$

which easily can be derived from formulae given in book [8].

So from (3.7) we get

$$\begin{array}{rcl} {S}_{Ch-L}& =&\sum\limits_{{X}_{{m}_{ i}}\in X}\left [H({X}_{{m}_{i}}) - H({X}_{{m}_{i}}\vert {X}_{pa({m}_{i})})\right ]\\ \\ \\ \\ & =&\sum\limits_{{X}_{{m}_{ i}}\in X}H({X}_{{m}_{i}}) -\sum\limits_{{X}_{{m}_{ i}}\in X}H({X}_{{m}_{i}}\vert {X}_{pa({m}_{i})}) \end{array}$$

(3.9)

and from (3.8) we get

$$\begin{array}{rcl}{ S}_{t-ch}&& = \sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}\left [H({X}_{k}) + I({X}_{l},{X}_{m}) - H({X}_{k}\vert {X}_{l},{X}_{m})\right ]\\ && \quad -\sum\limits_{\{{X}_{l},{X}_{m}\}\in \mathcal{S}}({\nu }_{lm} - 1)I({X}_{l},{X}_{m})\\ && = \sum\limits_{{X}_{k}\in X}H({X}_{k}) -\sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}H({X}_{k}\vert {X}_{l},{X}_{m}) \\ \end{array}$$

(3.10)

From (3.9) and (3.10) we conclude that we have to compare only

$$\begin{array}{rcl} \sum\limits_{{X}_{{m}_{ i}}\in X}H({X}_{{m}_{i}}\vert {X}_{pa({m}_{i})})& & \\ \end{array}$$

and

$$\sum\limits_{\{{X}_{l},{X}_{m},{X}_{k}\}\in \mathcal{C}}H({X}_{k}\vert {X}_{l},{X}_{m})$$

To each X _k corresponds an ${X}_{{m}_{i}}$ because these both are the vertices of X and each of them appears exactly once. The edge connecting ${X}_{{m}_{i}}$ and ${X}_{pa({m}_{i})}$ is contained in the t-cherry tree as it was constructed according to Step (2) in the proof of Theorem 3.3. From this we can conclude that for each X _k contained in a cluster {X _l , X _m , X _k } one of X _l and X _m is X _pa(k). Now we can apply the inequality (see book [8], Formula (2.130) on p. 36):

$$\begin{array}{rcl} H({X}_{k}\vert {X}_{i},{X}_{j}) \leq H({X}_{k}\vert {X}_{i})& & \\ \end{array}$$

with equality just in case X _k is conditionally independent of X _j . From this it is obvious that ${S}_{t-ch} \geq {S}_{Ch-L}$, and indeed the relation** between the Kullback–Leibler divergences of the two approximations is:

$$I(P(\mathbf{X}),{P}_{t-ch}(\mathbf{X})) \leq I(P(\mathbf{X}),{P}_{Ch-L}(\mathbf{X})).$$

This proves the statement of the theorem.

Observation 1. If the underlying dependence structure is a first order dependence tree than we got equality between the two divergences. (Because of the conditional independences that take place between the unlinked vertices of the first order dependence tree).

4 Some Practical Results of Our Approximation and Discussions

This section consists of three parts. In the first part we consider two different approximations of a given eight-dimensional discrete joint probability distribution:

• The approximation given by the Chow–Liu method

• The approximation corresponding to the t-cherry tree constructed by the algorithm given in the proof of Theorem 3.3

In the second part of this section we use the approximations to make some prediction, when the values taken by two out of eight random variables are known. From this information we are going to recognize the most probable values of the remaining six random variables. In the third part we use the influence diagram underlying the t-cherry-junction tree to make a feature selection.

Two Approximations of an Eight-Dimensional Discrete Probability Distribution

First we construct an eight-dimensional discrete probability distribution in the following way. The one-dimensional marginal distributions are generated randomly. Then the so called North-West corner algorithm was applied to determine an initial feasible solution of an eight-dimensional transportation problem, where the quantities to be transported were the marginal probability values. This way the “transported probabilities” are concentrated on 44 different directions, i.e. the constructed eight-dimensional discrete probability distribution is concentrated on 44 eight-dimensional vector instead of the possible 2,116,800. An other advantage is that this way we can get as high as possible positive correlations between the components of the random vector X. For having also high negative correlations, we combined the North-West corners with South-West corners.

Now we suppose that only the two and three-dimensional marginals of the eight-dimensional joint probability distribution are known. Using these we are going to construct a probability distribution associated to the t-cherry-junction tree. First we construct the Chow–Liu spanning tree and then transform the correspondent Chow–Liu dependence tree in a t-cherry junction tree using the Algorithm 2.

The first step is to calculate the mutual information contents of every pair and triplet of random variables. We then order them in descending way.

The Chow–Liu tree is constructed by a greedy algorithm from the two-dimensional information gains. In Table 3.1 the ordered mutual information gains are given. The mutual information gains used by Chow–Liu’s method are in boldface. In Fig. 3.1 the Chow–Liu tree can be seen.

Table 3.1 The mutual information gains in decreasing order for the construction of the Chow–Liu spanning tree

Table 3.3 The two variable mutual information contents ordered in decreasing way. The boldfaced ones are used in the t-cherry-junction tree

Fig. 3.1

The Chow–Liu spanning tree

The joint probability distribution associated to the constructed Chow–Liu dependence tree is:

$$\begin{array}{l} {P}_{Ch-L}(\mathbf{X}) \\ \quad = P({X}_{5})P({X}_{8}\vert {X}_{5})P({X}_{2}\vert {X}_{8})P({X}_{6}\vert {X}_{5})P({X}_{1}\vert {X}_{8})P({X}_{3}\vert {X}_{1})P({X}_{7}\vert {X}_{1})P({X}_{4}\vert {X}_{7})\\ \\ \quad = \dfrac{P({X}_{5}{X}_{8})P({X}_{2}{X}_{8})P({X}_{5}{X}_{6})P({X}_{1}{X}_{8})P({X}_{1}{X}_{3})P({X}_{1}{X}_{7})P({X}_{4}{X}_{7})} {P({X}_{8})P({X}_{5})P({X}_{8})P({X}_{1})P({X}_{1})P({X}_{7})}. \end{array}$$

The Kullback–Leibler divergence corresponding to the divergence between the real probability distribution and the approximation given by Chow–Liu method can be calculated as follows:

$$\begin{array}{rcl} & & I(P(\mathbf{X}),{P}_{Ch-L}(\mathbf{X})) \\ & & \quad = \sum\limits_{i=1}^{8}H({X}_{ i}) - H(\mathbf{X}) -\big{[}I({X}_{5},{X}_{8}) + I({X}_{2},{X}_{8}) + I({X}_{5},{X}_{6}) + I({X}_{1},{X}_{8}) \\ & & \qquad +\, I({X}_{1},{X}_{3}) + I({X}_{1},{X}_{7}) + I({X}_{4},{X}_{7})\big{]} \\ & & \quad = 16.908113 - 4.634363 - 10.990524 = 1.283226.\end{array}$$

The t-cherry-junction tree constructed by Algorithm 2 can be seen in Fig. 3.2. The three and the two variable mutual information contents corresponding to the clusters and separators of the t-cherry-junction tree are given in bold face in Tables 3.2 and 3.3

Table 3.2 The three variable mutual information contents ordered in decreasing way. The boldfaced ones are used in the t-cherry-junction tree

Fig. 3.2

The t-cherry-junction tree

The joint probability distribution associated to the constructed t-cherry-junction tree is:

$$\begin{array}{l} {P}_{t-ch}(\mathbf{X}) \\ =\! \dfrac{P({X}_{1}{X}_{5}{X}_{8})P({X}_{1}{X}_{7}{X}_{8})P({X}_{1}{X}_{5}{X}_{6})P({X}_{1}{X}_{3}{X}_{5})P({X}_{2}{X}_{5}{X}_{8})P({X}_{1}{X}_{4}{X}_{7})} {P({X}_{1}{X}_{8})P({X}_{1}{X}_{5})P({X}_{1}{X}_{5})P({X}_{5}{X}_{8})P({X}_{1}{X}_{7})}. \end{array}$$

The Kullback–Leibler divergence between the real probability distribution and the approximation associated to the t-cherry-junction tree is:

$$\begin{array}{rcl} & & I(P(\mathbf{X}),{P}_{t-ch}(\mathbf{X})) \\ & & \quad = \sum\limits_{i=1}^{8}H({X}_{ i}) - H(\mathbf{X}) -\big{[}\;I({X}_{1},{X}_{5},{X}_{8}) + I({X}_{1},{X}_{7},{X}_{8}) + I({X}_{1},{X}_{5},{X}_{6}) \\ & & \qquad +\, I({X}_{1},{X}_{3},{X}_{5}) + I({X}_{2},{X}_{5},{X}_{8}) + I({X}_{1},{X}_{4},{X}_{7}) - I({X}_{1},{X}_{8}) \\ & & \qquad -\, I({X}_{1},{X}_{5}) - I({X}_{1},{X}_{5}) - I({X}_{5},{X}_{8}) - I({X}_{1},{X}_{7})\big{]} \\ & & \quad = 16.908113 - 4.634363 - 20.129510 + 8.074578 = 0.218818.\end{array}$$

The real eight-dimensional distribution has 44 different vectors with probabilities different from 0. The Chow–Liu approximation has 453 vectors; the t-cherry-junction tree approximation has 93 vectors with probabilities different from zero. From the two Kullback–Leibler divergences calculated above we can observe easily that the approximation associated to the t-cherry-junction tree is much better (“closer” to the reality) than the approximation constructed from the Chow–Liu tree.

Application for Pattern Recognition

In this part we are testing our approximations for the following pattern recognition problem. We suppose that the values of X ₁ and X ₈ are known. For these given values we want to predict the most probable values of the other six random variables. In Table 3.4 one can see these predictions made with the help of the approximation.

Table 3.4 Comparison of the predicted values with the real ones in the case of the two different approximations

In the left side of the table the predicted values of the random variablesX ₂, …, X ₇ are given for the two different approximations. In the right side of the table the most probable values of the same random variables are given according to the real probability distribution (the same in the case of both approximations). The rows of the table are in ascending order according to the real probabilities. As the wrong predicted values are typed in boldface one easily can find them for each approximation. Let us observe that as long as the number of the wrong predicted values is 13 in the case of the Chow–Liu approximation, the same number equals only 2 in the case of the new t-cherry-junction tree approximation.

Feature Selection: Forecasting the Values of a Random Variable Which Depends on Many Others

The main idea of feature selection is to choose a subset of input random variables by eliminating features with little or no predictive information. In supervised learning the feature selection is useful when the main goal is to find feature subset that produces higher classification accuracy.

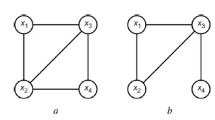
In practice many times we have a lot of attributes (random variables) that depend more or less on each other. The problem is how to select a few of them to make a good forecast of the variable we are interested in. The pairwise mutual information contents are not sufficient to make such a decision. To highlight this let us consider the following example. If we have four random variables with the relations between their pairwise mutual information contents: I(X ₂, X ₃) > I(X ₁, X ₃) > I(X ₃, X ₄), and want to take into account only two random variables to forecast the values of X ₃, we would use X ₂ and X ₁. But if we have the dependence diagram (see Fig. 3.3) we should decide in an other way. As X ₁ influences X ₃ only through X ₂ we should rather use X ₂ and X ₄ for the forecast of the values of X ₃. To solve such problems we give a method that uses the t-cherry-junction tree. If we are interested in forecasting a random variable X _i , we have to select from the cherry tree the clusters that contain X _i . We obtain in this way a sub junction tree. This results immediately from the properties of the junction tree. We have to take into consideration, just the variables that belong to this sub junction tree.

Fig. 3.3

A possible dependence diagram of four random variables

If in our earlier numerical example we are interested in the forecast of X ₈ we select from the t-cherry-junction tree the clusters that contain X ₈. From Fig. 3.2 these are (X ₁, X ₅, X ₈), (X ₁, X ₇, X ₈) and (X ₂, X ₅, X ₈). Now we** can conclude that for our purpose it is important to know the joint probability distribution of the random vector (X ₁, X ₂, X ₅, X ₇, X ₈)^T. This can be obtained as a marginal distribution of the distribution associated to the cherry tree, which can be also expressed as:

$$P({X}_{1},{X}_{2},{X}_{5},{X}_{7},{X}_{8}) = \dfrac{P({X}_{1},{X}_{5},{X}_{8})P({X}_{1},{X}_{7},{X}_{8})P({X}_{2},{X}_{5},{X}_{8})} {P({X}_{1},{X}_{8})P({X}_{5},{X}_{8})}.$$

Now to test our method we calculate the value of the conditional entropy H(X ₈ | X ₁, X ₂, X ₅, X ₇) = 0. 214946 from the real probability distribution. If we choose another random vector (X ₁, X ₂, X ₅, X ₇, X ₈)^T, then we get H(X ₈ | X ₁, X ₂, X ₅, X ₆) = 0. 235572.

It is interesting to see that I(X ₁, X ₂, X ₅, X ₆, X ₈) = 7. 210594 is greater than I(X ₁, X ₂, X ₅, X ₇, X ₈) = 7. 087809.