Keywords

1 Introduction

Quantum circuits is the most known and most used quantum computation model [1]. In quantum circuits the quantum gates, which are unitary Hilbert space operators, act on the quantum bits (qubits) and evolve their state from the initial state, which is the input to the quantum computation, towards the final state, which is measured and produces the output of the quantum computation [2, 3]. Most known quantum algorithms, such as Deutch [4], Grover [5] and Shor [6] quantum algorithms can be formulated as quantum circuits. Although quantum circuits are a powerful model, many physical problems and processes cannot be easily described as quantum circuits. This fact has initiated the quest for alternative models for quantum computation.

Quantum walks, first introduced in 1993, are quantum versions of classical random walks [7]. Since then, continuous and discrete quantum walks have been extensively studied and it has been proven that quantum walks are a universal model for quantum computation. Continuous quantum walks on graphs can reproduce quantum computations. In this model, quantum gates are implemented by scattering processes [8, 9]. On the other hand, discrete quantum walks have been proven to implement a universal quantum gate set and thus are able to execute any quantum computation [10]. Both continuous and discrete quantum walks on graphs are universal models for quantum computation, but building a physical quantum computing system based on the mathematical graph structures is not straightforward. In quantum walk models, graphs and wires do not represent qubits but basis states and cannot be mapped on a physical quantum computer architecture.

Feynman in 1982 introduced the concept of quantum cellular automata (QCAs) by examining the possibility of extending classical cellular automata (CAs) as models that can simulate quantum systems [11]. QCA evolution must be unitary, as is the evolution of all quantum systems. This fact causes several limitations on the use of QCAs as universal quantum computation models. The two most important limitations are imposed by the non-cloning theorem and the no-go lemma. The non-cloning theorem, that imposes the first limitation, forbids the cloning (copying) of an unknown quantum state [1]. Because of this, copies of the neighboring cell states are not available to the central cell, as is the case in classical CAs. Therefore, the evolution of the QCA cell states cannot be directly determined by the states of their neighbors. Several models have been proposed to circumvent this obstacle. Among them, a QCA with two qubits per cell has been introduced [12], and a relaxed unitary evolution has been proposed, in which probability is conserved and the evolution is linear, but the evolution is approximately unitary [13]. The second limitation is imposed by the no-go lemma, which states that except for the trivial case, unitary evolution of one-dimensional QCAs is impossible, i.e. in one dimension there exist no non-trivial homogeneous, local, linear QCA [14].

In QCAs one or more qubits are assigned to the QCA cells. The qubit states are quantum states and are described by wave functions, which are solutions to the Schrödinger equation. Quantum states should evolve both in space and time, whereas the states of qubits in the sites of the QCA have a trivial evolution. This is because their evolution in space is limited by the no-cloning theorem, which forbids the transfer of states between neighboring QCA cells. On the other hand, quantum walkers are quantum particles, the state of which evolves naturally in space. It is therefore possible that a model comprising quantum walks, which will reproduce quantum evolution in space, and QCAs, that will reproduce quantum evolution in time, can be developed so that it can serve as a universal model for quantum computation. Here we define the quantum walk on QCA lattices. The quantum particle (i.e. the quantum walker) is transferred between neighboring QCA sites and changes the quantum phase of the qubits according to a propagator, reproducing unitary space evolution. The QCA evolves in time reproducing unitary time evolution. Our results show that the development of a universal model of quantum computation based on quantum walks on the QCA lattice is possible.

2 Unitary Evolution of Quantum Walks on QCA Lattices

The most important characteristic of a quantum computing system is the reproduction of the solutions of the Schrödinger equation. The simplest solution is the plane wave:

$$\begin{aligned} \left| {\varPsi \left( {x,t} \right) } \right\rangle = A{e^{i\left( {kx - \omega t} \right) }} = A{e^{i\left( {px - Et} \right) /\hbar }} \end{aligned}$$
(1)

Where \(\varPsi \) is the wave function in Dirac notation, k is the wave vector and \(\omega \) the angular frequency. \(E=\hbar \omega \) is the energy and \(p=\hbar k\) is the momentum. The one-dimensional, time dependent Schrödinger equation:

$$\begin{aligned} i\,\hbar \,{\partial \over {\partial \,t}}\;\,\left| {\varPsi \left( {x,t} \right) } \right\rangle = H\,\left| {\varPsi \left( {x,t} \right) } \right\rangle \end{aligned}$$
(2)

where H is the Hamiltonian operator:

$$\begin{aligned} H =\left( { - {{{\hbar ^2}} \over {2\,m}}\,{{{\partial ^2}} \over {\partial {x^2}}} + V\left( {x,t} \right) } \right) \end{aligned}$$
(3)

has the following general solution:

$$\begin{aligned} \left| {\varPsi \left( {{x_b},{t_b}} \right) } \right\rangle = U\left( {x,t} \right) \;\left| {\varPsi \left( {{x_a},{t_a}} \right) } \right\rangle \end{aligned}$$
(4)

where U is a unitary operator:

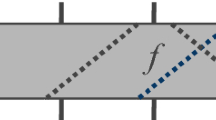
$$\begin{aligned} U\,\left( {x,t} \right) ={e^{{{ - i\,H\,t} \over \hbar }}} \end{aligned}$$
(5)

Both the simplest solution of (1) and the general solution of (4) describe the evolution of the wave function from an initial space-time point \((x_a, t_a)\) to a final space-time point \((x_b, t_b)\), as shown in Fig. 1. In the quantum circuit model, space is defined by an one-dimensional array of qubits and the computation proceeds in time steps, in each of which a number of quantum gates act on the qubits. In the proposed model we follow the same discretization scheme as in the quantum circuit model, i.e. qubits form the QCA lattice and the computation evolves in discrete time steps.

Fig. 1.
figure 1

Wave function evolution in space-time, from an initial space-time point \((x_a, t_a)\) to a final space-time point \((x_b, t_b)\). In the proposed model quantum walks evolve the wave function in space and QCAs in time.

Full size image

In the proposed model we consider one-dimensional QCAs in which the QCA cells form a one-dimensional lattice. Three qubits are allocated at each QCA cell, the a-qubit, which is the QCA qubit and a two-qubit quantum register, w, which comprises the two qubits necessary for the quantum walk. The state of the \(i^{th}\) QCA cell at computation step t is written as: \(\left| {a_i^t\,w_i^t} \right\rangle \). There are eight basis states for each QCA cell. The global state of the QCA at the computation step t, \(\left| {{Q^{t}}} \right\rangle \), is the tensor product of the states of its cells and is written as:

$$\begin{aligned} \left| {{Q^t}} \right\rangle = \left| { \cdot ~a_{i + 1}^t\,w_{i + 1}^t\,a_i^t\;w_i^t\,a_{i - 1}^t\,w_{i - 1}^t \cdots } \right\rangle \end{aligned}$$
(6)

The evolution of the global QCA state, from computation step t to computation step \(t+1\) is given by:

$$\begin{aligned} \left| {{Q^{t + 1}}} \right\rangle = U(x,t)\left| {{Q^t}} \right\rangle = A\left( t \right) \,W\left( x \right) \left| {{Q^t}} \right\rangle \end{aligned}$$
(7)

In our model the unitary operator U(x, t) is decomposed in a product of two operators, A(t), which describes the time evolution of the QCA and W(x), which describes the space evolution of the QCA qubit states by the action of the quantum walk. Since only U has to be unitary, the unitarity criterion on both operators A and W could be relaxed, as long as their product is unitary. Nevertheless, we choose not to relax this criterion and in our model we demand both A and W to be unitary. We describe below the action of these two operators.

Fig. 2.
figure 2

The QCA structure and the W operator acting on qubits along with the A operator described by Eq. 10. Shaded rectangles represent QCA cells and the qubits connected with the arrowed (red) lines, are the qubits affected by the quantum walk. (Color figure online)

Full size image

In the discrete quantum walk, a walker (which can be a particle or a quantum state) moves on the QCA lattice. The sites of this lattice are numbered by: \({i = 0, \pm 1, \pm 2, \cdots {\pm }n}\). The quantum walker tosses a quantum coin and moves to the right (towards \(+n\)) if the coin state is \(\left| 1 \right\rangle \), and to the left (towards \(-n\)) if the coin state is \(\left| 0 \right\rangle \). The state of the quantum walker found at location i is: \(\left| {{w_i}} \right\rangle = \left| {i,{c_i}} \right\rangle \), where i indicates the location and \(c_i\) the coin state. The quantum walk operator W is given by: \(W= S \cdot \left( {I \otimes C} \right) \), where I is the unit operator, and C is the coin operator, which can be any one-qubit unitary quantum operator, such as the Pauli, Hadamard or Phase-shift operators. The shift operator S that moves the quantum walker is given by:

$$\begin{aligned} S= \sum \limits _{i = -n}^n {\left| 1 \right\rangle \left\langle 1 \right| \otimes \left| {i + 1} \right\rangle \left\langle i \right| ~+~\left| 0 \right\rangle \left\langle 0 \right| \otimes \left| {i - 1} \right\rangle \left\langle i \right| } \end{aligned}$$
(8)

Figure 2 shows the QCA structure and the W operator acting on qubits. The global state of the QCA evolves according to evolution rules expressed by the operator A.

$$\begin{aligned} \left| {{Q^{t + 1}}} \right\rangle = A\,\left| {{Q^{t}}} \right\rangle \end{aligned}$$
(9)

This operator can be any two-qubit unitary quantum operator, for example it can comprise Controlled-NOT (CNOT) gates:

$$\begin{aligned} A = \cdots \otimes CN\otimes CN \otimes CN \otimes \cdots \end{aligned}$$
(10)

Figure 2 shows the A operator in the case of Eq. 10. The phase of the QCA qubit, \(\left| a_i \right\rangle \), is controlled by the location qubit of the quantum walk, \(\left| i \right\rangle \). The qubits connected by the arrowed (red) line, i.e. \(\left| c_i \right\rangle \) and \(\left| i \right\rangle \) are the qubits affected by the quantum walk, which transfers information about the states of neighboring QCA qubits. The QCA evolves in time by interaction between its qubit states, which in the case of Fig. 2 is a concatenation of CNOT quantum gates.

3 Simulation of Quantum Walks on QCA Lattices

We aim to develop a new quantum computation model that is closer to the structure of physical systems. We use our model to simulate the most basic quantum mechanical process: the motion of a particle (i.e. the quantum walker) in spaces where various potentials exist. Following Eq. 2, where the potential enters in the exponent, we formulate the problem by entering the values of the space potentials as phases of the QCA qubits and evolve the quantum walk in these spaces. It is well known that if the initial value of the quantum walker coin qubit is in state \(\left| 0 \right\rangle \), the quantum walk is directed towards the left direction from the starting point and when the coin is in state \(\left| 1 \right\rangle \) the quantum walk is directed towards the right. We start the evolution of the quantum walk with the initial coin state in superposition of the basis states \(1/\sqrt{2}\,\left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right) \) which results in symmetric quantum walk evolution towards both directions.

Fig. 3.
figure 3

Quantum walk on a QCA lattice, with potential increasing towards the right. The potential is shown by the red line. (Color figure online)

Full size image

Figure 3 shows the evolution of a quantum walk on a QCA lattice which encodes a potential that increases towards the right. The potential is shown by the red line. The quantum walk starts at location 0 with the initial coin state in the superposition described above. The red line shows the potential and the blue bars at lattice sites show the probability of the quantum walker to be found in the corresponding lattice sites. Our computation results reproduce the motion of the quantum walker towards the left, as expected.

Fig. 4.
figure 4

Quantum walk on a QCA lattice, with potential increasing towards the left. The potential is shown by the red line. (Color figure online)

Full size image

We simulated a quantum walk on a QCA lattice encoding a potential that is mirror symmetric to the previous one and increases towards the left, shown by the red line. Again, the quantum walk starts at location 0 with the same initial coin state superposition. Figure 4 shows the evolution of this quantum walk, reproducing a mirror symmetric probability distribution, characteristic of the motion of the quantum walker towards the right, as expected.

Fig. 5.
figure 5

Quantum walk on a QCA lattice, with a thin potential barrier. The barrier is shown by the red line. (Color figure online)

Full size image

We also simulated a quantum walk on a QCA lattice encoding a potential barrier shown in red in Fig. 5. The width of the potential barrier is small and the barrier is relatively transparent to the quantum particle, with a large transmission coefficient. Our computation results, shown in Fig. 5, reproduced the tunneling through a barrier, characteristic of quantum particles. The quantum walk starts at lattice site 0. The probability distribution is near zero inside the potential barrier and the non-zero to the left of the barrier.

Fig. 6.
figure 6

Quantum walk on a QCA lattice, with a large potential barrier and with potential increasing towards the right. Potential and barrier are shown by the red line. (Color figure online)

Full size image

Figure 6 shows the evolution of a quantum walk on a QCA lattice encoding both a potential gradient and a potential barrier. The potential distribution is shown by the red line. In this case the width of the potential barrier is large, and its transmission coefficient is near zero. Although the potential gradient drives the quantum walk towards the left, the particle is not transmitted through the barrier and the probability distribution to the left of the barrier is almost zero, as expected.

4 Conclusions

We developed a new quantum computation model based on quantum walks on quantum cellular automata lattices. This new model is closer to the structure of many quantum mechanical systems and processes. We used this model to simulate the most basic quantum mechanical processes, i.e. the motion of a particle in a one-dimensional space in which potential distributions exist. Our model reproduced qualitatively the expected motions in spaces with potential gradients and potential barriers, which were encoded as phases of the quantum cellular automaton qubits. Our results show that the development of an accurate universal quantum computation model based on quantum walks on quantum cellular automata lattices is possible.