Keywords

1 Introduction

The behavior of single-arrival single-server systems as shown in Fig. 1 is generally well understood, and relevant to most industries [1]. If an actual system can be observed, the lead time can easily be calculated using Little’s law [2].

Fig. 1.
figure 1

Illustration of a single-arrival single-queue single service system

Full size image

If the system is understood in more abstract terms, the Kingman equation (also known as Kingman formula or Kingman approximation) gives an approximation of the waiting time of the orders for a single process based on its utilization and variance [3]. Other calculations and approximations exist like [4,5,6] or [7]. These equations are valid over a wide range of assumptions and estimate the behavior of a steady state system quite well.

In industry, it is common practice to prioritize some orders over others to reduce the lead time and waiting time of the prioritized orders at the cost of an increased lead time and waiting time of the non-prioritized orders. Examples include the food industry with its limited product lifespan [8], maintenance tasks [9] or other resources [10], as well as general throughput improvements [11]. It is important to note that as long as the average system behavior does not change, the equations in [2,3,4,5,6] and [7] are still valid. Even if some orders are prioritized and accelerated, the slowdown of the not-accelerated orders will cause the overall system to keep a constant average lead time and waiting time.

Take for example Little’s law [2]. Little’s law is “not influenced by the arrival process distribution, the service distribution, the service order, or practically anything else” [12]. As prioritization does nothing but change the “service order,” prioritization has no effect on the average lead time. It does, however, affect the distribution of this lead time. As some orders are accelerated at the expense of others, the width of the distribution of the lead times and waiting times will increase, even though the mean remains unchanged.

Please also note that this paper uses orders as the item processed in the single-server single-queue system. However, the wide application of this prioritization makes the following simulations, discussions, and calculations equally valid for a system processing parts (as for example a machine), customers (for example in a supermarket, a hospital, or a call center), products (as for example a shipping warehouse), or many other applications.

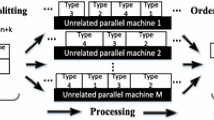
2 System Outline

The system simulated is a single-arrival single-server system as a simplification of more complex production systems. The arrival times and service times are randomly distributed. For the arrival times, we used an exponential distribution, as this is the most commonly used distribution to model inter-arrival times [13, 14]. The service times are modeled using a lognormal distribution, which is also commonly used for service times [13, 15]. The exponential distribution has only one parameter, which was used to adjust the mean value. The lognormal distribution has two parameters, hence besides the mean, it is also possible to influence the standard deviation. During this analysis, the standard deviation was set to be 25% of the mean value (i.e., the coefficient of variation is 25% for the service times). This is within the range of common values in the industry.

The utilization of the system has a major influence on the waiting time. Hence different systems were simulated using different utilizations. Table 1 gives an overview of the different settings to achieve different utilizations. Please note that the units of the mean times are here only for a complete understanding of the set-up, but does not influence the results. The lot size of arrivals and processing is both one. For simplicity, we also did not model any set-up changes, breakdowns, or other interruptions. Transport times were also assumed instantaneous.

Table 1. Overview of the mean inter-arrival times and service times to achieve different utilizations
Full size table

During the simulations, we measured the mean waiting time for each order type as well as the joint mean waiting time. We also measured the standard deviation of the waiting time for order types A and B individually as well as jointly. The 95% confidence interval of all of these was also determined. Each simulation experiment had a duration of 120,000 min, representing 20,000 orders processed or around one year of simulated time. Each simulation was repeated thirty-nine times to calculate the 95% confidence interval. For details on the set-up, see [16].

2.1 Un-prioritized Baseline System

As a baseline reference, we used a system without prioritization, using a simple first-come-first-served approach for the arriving orders. The layout is shown in Fig. 1.

2.2 Prioritized System

The main part of the analysis is the prioritized system. Two different order types were simulated, order type A and B. Order type A always has priority over order type B. This is simulated by having two different waiting queues, both of which have an independent first-in-first-out logic. Orders in the B queue are only processed if there are no more orders waiting in the A queue. The service time for both order types is identical and depending on the selected utilization as shown in Table 1 (Fig. 2).

Fig. 2.
figure 2

Illustration of a prioritized system with a double-arrival double-queue single-service system

Full size image

The percentage of prioritized orders was modified from 0.1% to 99.9% as shown in Table 2. The exponentially distributed inter-arrival times were adjusted accordingly to maintain a joint mean inter-arrival rate of 6 min between orders. Combining the 11 different percentages A with the 5 different utilizations gives a total of 55 simulation experiments in addition to the 5 utilizations of the baseline system.

Table 2. Mean inter-arrival times for order A and B for different percentages of A
Full size table

3 Simulation Results

3.1 Baseline System

As expected and predicted by theory, the waiting time of the queue of the baseline system was influenced by the utilization. The exponential relation is shown in Fig. 3. For a utilization of 100%, the average waiting time would approach infinity. These values serve as our baseline system.

Fig. 3.
figure 3

Waiting times in dependence of the utilization of the un-prioritized baseline system

Full size image

3.2 Prioritized System

Figure 4 shows the behavior of the systems under different utilizations and percentages of prioritized orders. For simplification, the percentage improvement of orders A and the percentage worsening of orders B compared to the baseline waiting time from Fig. 3 is shown. It is clearly visible that for low percentages of A, there is a substantial benefit for orders A with an up to 90% reduction in waiting time without much disadvantage for orders B. However, as the percentage of A increases, this benefit for A shrinks, whereas the disadvantage for orders B becomes exponential, with the waiting time being a multitude of the baseline.

Fig. 4.
figure 4

Waiting times relative to the baseline in dependence of the utilization and percentage prioritized orders of the prioritized system

Full size image

Figure 5 shows the impact on the coefficient of variation of the waiting time. For both orders A and B, this increases as the percentage of prioritized orders A increases. Hence, not only does the average waiting time increase, but the range of the fluctuations also increases. The full data including the confidence intervals can be found in [16].

Fig. 5.
figure 5

Coefficient of variation of the waiting times in dependence of the utilization and percentage prioritized orders of the prioritized system

Full size image

4 Conclusions

Overall, prioritizing important orders can have a significant benefit as long as it is done in moderation. In industry, often a general rule of thumb is used, recommending to prioritize no more than 30% of the workload. Since this number originates in industry, there is no academic reference for this that we are aware of. While this rule is an oversimplification, Fig. 4 shows that this is a workable assumption without having a too much negative effect on the not-prioritized orders. However, this is not a hard cut off, but rather a sliding scale, and prioritizing 35% or even 40% may also be possible, although the benefit shrinks and the disadvantages grow. It boils down to the tradeoff that has to be made between benefitting the prioritized products while disadvantaging everything else.

However, prioritizing an excessive number of orders will diminish the effect of this prioritization. The negative effect on the not-prioritized orders will multiply and become significant. Even worse, the range of the fluctuations increases faster than the mean waiting time. If the products are made to order (MTO), this means a prediction of a delivery date will become more difficult, as the actual delivery dates become more erratic. For a reasonable delivery performance, the promised delivery date now has to be much later, as this not only has to include the mean but also a substantial share of the outliers. If 95% of the true delivery dates should be within the estimate, the estimated delivery date needs to be the 95th percentile of the actual delivery dates.

Similarly, for made-to-stock (MTS) items, if the waiting and process time would always be constant, it would be sufficient to have one item in stock plus the coverage for the customer behavior. As the fluctuations of the waiting time and delivery time increase, more stock is needed to cover for these fluctuations. Again, if a 95% delivery performance is promised, there needs to be stock covering at least 95% of the shortest waiting times and processing times in addition to the customer behavior.

Overall, prioritizing too many orders will drastically push the promised delivery dates to the future (for MTO) or require significant increases in inventory (for MTS), or have a significant negative impact on the delivery performance (for both cases). Practitioners are strongly advised to prioritize no more than 30% of their order volume!